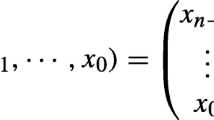Cryptographic properties of small bijective S-boxes with respect to modular addition

Abstract

We define affine equivalence of S-boxes with respect to modular addition, and explore its use in cryptanalysis. We have identified classes of small bijective S-boxes with respect to this new equivalence, and experimentally computed their properties.

1 Introduction

The study of Boolean functions has an important place in the design of cryptographic ciphers. The Advanced Encryption Standard (AES), which is a current standard of the U.S. National Institute of Standards and Technology (NIST), benefits from theoretically designed [11] S-boxes with high non-linearity [18] and flat differential profile [19]. Note that already in [19], the question was posed of whether the theoretical approach of constructing S-boxes is relevant when an attacker uses a notion of difference other than XOR. While not directly relevant to AES, there are various cipher designs that use addition modulo 2ⁿ instead of, or in addition to, an XOR operation. An example is the Ukrainian standard Kalyna [20] that is very similar to AES, but the initial and final key addition layer is realized with addition modulo 2⁶⁴.

Another example is the Russian standard GOST 28147-89 [25]. GOST 28147-89 has a Feistel structure, in which the round function contains key addition, which is realized modulo 2³², followed by an S-box layer (using small 4-bit S-boxes) and a diffusion layer realized by bit rotation. In the case of GOST, or a similar encryption scheme, an attacker is very likely to consider differential cryptanalysis based on differences with respect to modular addition instead of an XOR operation.

Recently, the interest in different types of differences in cryptanalysis was reawakened by the approach of [8], later expanded in [10]. This approach applies to the case when S-boxes with good cryptographic properties (such as high non-linearity and a flat differential profile) are used in the design of a cipher. However, the S-boxes contain a hidden weakness: they are cryptographically weak against other algebraic operations, which can be used by the attacker to mount a modified differential attack. The study in [10] focuses on differential attacks using a hidden algebraic structure in the whole cipher. An alternative additive operation is chosen so that one S-box is weakened, and also the linear layer remains linear with respect to the alternative operation. In a recent work [6], Brunetta et al. investigate the problem of determining possible alternative operations for which a linear permutation can be linear also for the new sum. They provide a procedure that can find a hidden sum for a given linear layer.

For a typical cipher design, it still might be difficult for an attacker to combine alternative notions of differences with diffusion layers that are linear with respect to an XOR operation, but can be non-linear with respect to alternative operations. On the other hand, we provide a toy example of a simple cipher design that resists standard differential cryptanalysis, but is nonetheless vulnerable against attacks based on alternative differences. However, our main focus is to abstract the question of actual attacks and ask: can we design S-boxes that are strong against differential cryptanalysis based on different algebraic operations? How difficult is it to find an S-box that is strong against attacks with respect to one type of operation and weak against attacks with respect to a different operation?

The main objective of this paper is an experimental study of the properties of small bijective vectorial Boolean functions, with respect to operations in the ring $\mathbb {Z}_{2^n}$, and their connection to standard S-box criteria with respect to operations in $\mathbb {F}_{2^n}$. While cryptographic applications are our main motivation, we believe that our research can be of interest to a general audience studying Boolean functions.

In practical terms, we restrict our study to small S-boxes with dimension n = 4. These S-boxes have been extensively studied and classified with respect to their linear and differential properties and applications to lightweight cipher designs [16]. Further studies have been conducted with respect to different cryptographic criteria [12, 24], resistance and protection against side-channel attacks [3, 15, 21], and multiplicative complexity [27]. Experimental studies use affine equivalence to restrict the space of all studied S-boxes to a small number of class representatives. This can be done only if the studied property is an invariant of affine equivalence. In our study, properties with respect to modular addition are not invariant under affine equivalence. We instead consider an equivalence relation corresponding to affine functions over $\mathbb {Z}_{2^n}$, which we call modular affine equivalence. In the theoretical part of the paper, we explore some properties of modular affine equivalence. In the experimental part of the paper, we use modular affine equivalence to reduce the space of the functions we need to study, and restrict the results to representatives of modular affine classes.

The main focus of the experiments is the study of the cryptographic quality of S-boxes with respect to differential cryptanalysis based on an alternative notion of difference. In the theoretical part, we generalise the standard S-box criterion, the so-called differential profile, and define a so-called D-criterion of an S-box. The D-criterion is based on differential uniformity with respect to modular addition. Theoretically, the non-linearity of S-boxes can be generalized with respect to any quasigroup [13] (a set with a binary operation whose Cayley table is a Latin square, i.e., each row and column is a permutation of the elements of the set). Affine equivalence and non-linearity of general permutations over $\mathbb {Z}_{n}$ was studied by Kumar et al. in [14], with a focus on the cryptanalysis of RC4. We use a similar notion of affine approximation to define a non-linearity criterion: the L-criterion expresses how well an S-box can be approximated by a (modular) affine function. Both the D- and the L-criterion are invariant under modular affine equivalence, and we used exhaustive enumeration over class representatives to compute the statistical distribution of S-box representatives with given values of D- and L-criteria. In a similar way, we have analysed the entire affine equivalence classes of optimal S-boxes (with respect to standard linear and differential cryptanalysis).

2 Notation

We use standard terminology related to vectorial Boolean functions (S-boxes) in accordance with [9]. However, we will slightly abuse notation to make some sections of the paper more readable. The notation we use is summarized as follows:

• Vectors and matrices are typed in boldface: for example, u for a row vector, and M for a matrix.

• Sets are denoted by blackboard-bold: for example, $\mathbb {A}$ for a set.

• The set of n-dimensional binary vectors is denoted by $\mathbb {F}_{2^n}$, with vector addition denoted by ⊕.

• The symbol $\mathbb {Z}$ denotes the set of integers. We use the standard notation $\mathbb {Z}_{N} = \mathbb {Z}/(N)$ to denote the ring of equivalence classes modulo N, and $\mathbb {Z}_{N}^{*}$ to represent the group of units of $\mathbb {Z}_{N}$. We represent elements of $\mathbb {Z}/(N)$ by positive integers {0,1,…,N − 1}. Addition in $\mathbb {Z}_{N}$ is denoted simply by + . Each integer x can be represented as a binary vector x = (x₀,x₁,…) using the standard binary expansion $x = \sum x_{i} 2^{i}$. If N = 2ⁿ, this binary expansion defines a natural¹ bijection $\iota : \mathbb {Z}_{2^n}\rightarrow \mathbb {F}_{2^n}: \iota (x) = \mathbf {x}$. In the case when we combine operations over $\mathbb {F}_{2^n}$ and $\mathbb {Z}_{2^n}$, we do not state this explicitly. For example, M ⋅ (x + (u ⊕v)) is shorthand for

  $$ \mathbf{M}\cdot \iota(x + \iota^{-1}(\mathbf{u} \oplus \mathbf{v})). $$

• Boolean functions are denoted by plain upper case letters. We use the term Boolean function for any function $F: \mathbb {F}_{2}^{n} \rightarrow \mathbb {F}_{2}^{m}$. We denote a coordinate (function) of F by $F_{i} : \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2}$, i.e., $F(\mathbf {x}) = \left (F_{0}(\mathbf {x}), \ldots , F_{m-1}(\mathbf {x}) \right )$. A component (function) of F is any non-zero linear combination of its coordinates. In general, the term “S-box” can denote any (non-linear) vectorial Boolean function used in cipher designs. In this article, we will focus on bijective S-boxes over $\mathbb {F}_{2^n}$.

• Functions on the set $\mathbb {Z}_{2^n}$ are denoted by Greek characters. For example, α, β.

• We will again use a natural bijection between bijective functions over $\mathbb {F}_{2^n}$ and bijective functions over $\mathbb {Z}_{2^n}$ (all of which can also be identified with elements of the permutation group ${\Sigma }_{2^{n}}$ of the set of integers {1,2,…,2ⁿ}). We associate a Boolean function $S:\mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ with a function $\sigma :\mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}$, such that S(ι(x)) = ι(σ(x)), where ι denotes again the standard binary expansion.

  To simplify notation, we will again omit ι in formulas. For example, we can write S(a + b) + c, instead of the more formal ι^− 1(S(ι(a + b))) + c. In a similar way, we will write (F ∘ π)(u), instead of (F ∘ ι ∘ π ∘ ι^− 1)(u).

• In all our experiments with n = 4, we use a shorthand representation for concrete S-boxes. Each S-box is written as a string of hexadecimal numbers. This string is read from left to right, and each hexadecimal digit represents the output ι(S(x)) of S corresponding to the inputs ι(0), ι(1), …, ι(15). For example, the string 1fd057a4923e6b8c encodes a function which maps 0000 to 0001, 0001 to 1111, 1111 to 1100, and so forth.

• We will extend the operators ⊕,+,∘ (representing XOR, modular addition, and functional composition, respectively) to apply to sets. If any of the arguments is a set, the result of the operation is a set. For example:

  $$ a + \mathbb{B} = \{ a + b : b \in \mathbb{B} \}, $$
  $$ \mathbb{A} + \mathbb{B} = \{ a + b : a\in \mathbb{A}, b \in \mathbb{B} \}. $$

3 Modular affine functions and modular affine equivalence

The notion of affine equivalence is important when studying the properties of large sets of S-boxes. Two S-boxes $S_{1}, S_{2}: \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ are affine equivalent, if there exist two bijective affine functions A₁,A₂, such that

$$ A_{1} \circ S_{1} = S_{2} \circ A_{2}. $$

Explicitly, S₁ and S₂ are affine equivalent if and only if

$$ \exists \mathbf{A}_{1},\mathbf{A}_{2},\mathbf{b}_{1},\mathbf{b}_{2}, \forall \mathbf{x} : S_{2}(\mathbf{x}) = \mathbf{A}_{1} \cdot S_{1}(\mathbf{A}_{2} \cdot x + \mathbf{b}_{2}) + \mathbf{b}_{1}, $$

(1)

with $\mathbf {x} \in \mathbb {F}_{2^n}$, A₁,A₂, invertible n × n matrices, and $\mathbf {b}_{1},\mathbf {b}_{2} \in \mathbb {F}_{2^n}$.

Let $a\in \mathbb {Z}_{2^n}^{*}, b \in \mathbb {Z}_{2^n}$. Let $\alpha : \mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}: \alpha (x) = ax+b$ be a bijective function with inverse α^− 1(x) = a^− 1x − a^− 1b. We will call α a modular affine function. Note that this is distinct from the notion of an affine vectorial Boolean function, which we call simply an affine function. The set of modular affine functions (understood as permutations) is closed under composition, and forms a subgroup of the permutation group ${\Sigma }_{2^{n}}$ of size 2ⁿ ⋅ 2^n− 1.

Using the binary expansion $\iota : \mathbb {Z}_{2^n}\rightarrow \mathbb {F}_{2^n}: \iota (x) = \mathbf {x}$, we can associate each function $\alpha : \mathbb {Z}_{2^n}\rightarrow \mathbb {Z}_{2^n}$ with a vectorial Boolean function $A: \mathbb {F}_{2^n}\rightarrow \mathbb {F}_{2^n}: A(\iota (x)) = \iota (\alpha (x)),$ simply written as A(x) = ax + b. The function $A: \mathbb {F}_{2^n}\rightarrow \mathbb {F}_{2^n}$ is in general not a linear function, and can have coordinate functions with algebraic degree higher than 1. For example, the function A(x) = x + 1 has coordinate functions A₀(x) = x₀ ⊕ 1, and $A_{i}(x) = x_{i} \oplus {\prod }_{j=0}^{i-1} x_{j},$ for each i > 0.

Using modular affine functions we can define modular affine equivalence (MAE for short) of S-boxes. Two S-boxes $S_{1}, S_{2}: \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ are modular affine equivalent, if there exist two modular affine functions A₁,A₂, such that

$$ A_{1} \circ S_{1} = S_{2} \circ A_{2}. $$

We can also write this condition as

$$ \exists a_{1},a_{2},b_{1},b_{2}, \forall x : S_{2}(x) = a_{1} \cdot S_{1}(a_{2} \cdot x + b_{2}) + b_{1}, $$

(2)

with $x \in \mathbb {Z}_{2^n}$, $a_{1},a_{2}\in \mathbb {Z}_{2^n}^{*},$ and $b_{1},b_{2} \in \mathbb {Z}_{2^n}$.

It is easy to see that if S₁ is bijective, then S₂ is bijective as well.

In [22], the notion of EA- and CCZ-equivalence [7] for functions over finite abelian groups was introduced. In particular, for the case of $\mathbb {Z}_{2^n}$ these equivalences are an extension of the MAE given here. However, unlike basic MAE, extended MAE² does not preserve the bijectivity of S-boxes. Thus, we will only work with basic modular affine equivalence further on.

3.1 Representatives of MAE classes

To efficiently work with MAE classes, we need to use some suitable representatives. Similar to affine equivalence (AE) classes, we can restrict our enumeration to S-boxes with zero constant term due to the following lemma (which follows from the definition of MAE):

Lemma 1

Let $S: \mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}$ be a function, such that S(0) = b, $b \in \mathbb {Z}_{2^n}$. Then $S^{\prime }: \mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}$ with $S^{\prime }(x) = S(x)-b$ is in the same MAE class, and $S^{\prime }(0) = 0$.

In addition to restricting to S-boxes with a zero constant term, we can normalize the value of S(1) using the following lemma:

Lemma 2

Let $S: \mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}$, such that S(0) = 0, and S(i) = j, for some $i,j \in \mathbb {Z}_{2^n}$ such that $\gcd (i, 2^{n}) = \gcd (j, 2^{n}) = 1$. Such i,j always exist if S(0) = 0 (as there are more remaining odd elements than even). Then $S^{\prime }:\mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}$, with $S^{\prime }(x) = j^{-1} S(i x)$ is in the same MAE class, and $S^{\prime }(1) = 1$, $S^{\prime }(0) = 0$.

We will call an S-box with the property S(0) = 0, S(1) = 1 a normalized S-box. As a consequence of Lemma 2, we only need to investigate normalized S-boxes.

In each MAE class of S-boxes there can be multiple normalized representatives. Given any S-box S₁ (that is, in general, not normalized), it suffices to go through all possible values of a₁,b₁ to enumerate all normalized S-boxes in the same MAE class. This can be summarized as follows:

Lemma 3

For each bijective function $S_{1}: \mathbb {Z}_{2^n} \rightarrow \mathbb {Z}_{2^n}$, and $(a_{1}, b_{1}) \in \mathbb {Z}_{2^n}^{*} \times \mathbb {Z}_{2^n}$, there exists a unique pair $(a_{2}, b_{2}) \in \mathbb {Z}_{2^n} \times \mathbb {Z}_{2^n}$, such that S₂(x) = a₁ ⋅ S₁(a₂ ⋅ x + b₂) + b₁, and satisfies S₂(0) = 0, S₂(1) = 1.

Proof

Let x = 0, we get

$$ a_{1} \cdot S_{1}(b_{2}) + b_{1} = 0. $$

Thus $b_{2} = S_{1}^{-1}(-a_{1}^{-1} b_{1})$. Because S₁ is bijective, the solution exists for any choice of a₁,b₁.

Let x = 1, we get

$$ a_{1} \cdot S_{1}(a_{2} + b_{2}) + b_{1} = 1. $$

From this we get

$$ S_{1}(a_{2} + b_{2}) = a_{1}^{-1}(1-b_{1}), $$

and consequently

$$ a_{2} = S_{1}^{-1}\left( a_{1}^{-1} (1-b_{1}) \right) - S_{1}^{-1}(-a_{1}^{-1} b_{1}). $$

Again, a₂ always exists because S₁ is bijective. □

Note that the a₂ computed in the proof of Lemma 3 is not necessarily odd. If a₂ is not odd, the computed S₂ is not a bijection, and as such it is not a member of the investigated MAE class.

To generate all normalized MAE representatives of the class that contains S₁, we can iterate through all choices of $(a_{1}, b_{1}) \in \mathbb {Z}_{2^n}^{*} \times \mathbb {Z}_{2^n}$, and generate the corresponding S₂’s. The maximum possible number of MAE representatives thus generated can be 2ⁿ ⋅ 2^n− 1. Because a₂ is not always invertible, some classes contain a smaller number of normalized representatives.

In our experiments, we enumerate all normalized bijective S-boxes. Then we use Lemma 3 to partition these S-boxes into MAE classes. In further experiments, we use a single S-box from each class to investigate those S-box properties that are invariant w.r.t. MAE.

If we want to decide whether two bijective S-boxes are in the same class, we can use Lemma 3 to generate normalized representatives of one of them, and check whether any normalized representative of the second S-box is in this set. A simpler algorithm is to use a system of equations similar to the proof of Lemma 3: for every choice of $(a_{1}, b_{1}) \in \mathbb {Z}_{2^n}^{*} \times \mathbb {Z}_{2^n}$, a potential b₂ is computed from S₁(b₂) + b₁ = S₂(0), and a potential a₂ is computed from a₁ ⋅ S₁(a₂ + b₂) + b₁ = S₂(1). If $a_{2} \in \mathbb {Z}_{2^n}^{*}$, modular affine equivalence is then decided by checking whether S₂(x) = a₁ ⋅ S₁(a₂ ⋅ x + b₂) + b₁ holds for each remaining x.

4 S-box characteristics with respect to modular addition

We assume that the reader is familiar with classical linear [17] and differential [2] cryptanalysis. These cryptanalytic techniques have influenced the design of modern block ciphers, with emphasis on the cryptographic strength of the S-boxes used. The cryptographic strength of S-boxes is typically measured by non-linearity and the maximum value of the differential profile.

When considering the non-linearity, we use the notion of Hamming distance between functions. In general, the Hamming distance between two vectors u,v is the number of coordinates i with u_i≠v_i. In the Boolean case, the Hamming distance of two functions $f, g: \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2}$ can be computed as a sum over integers: ${\sum }_{\mathbf {x} \in \mathbb {F}_{2^n}} f(\mathbf {x}) \oplus g(\mathbf {x})$. In the case of two S-boxes S₁, S₂ understood as functions over $\mathbb {Z}_{2^n}$, their Hamming distance is the size of the set $\{x \in \mathbb {Z}_{2^n} : S_{1}(x) - S_{2}(x) \neq 0 \}$.

The non-linearity of the function $F:\mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ is defined as the minimum (Hamming) distance between any component function of F and any affine (Boolean) function on n variables. A cryptographically strong S-box must have a high non-linearity. The non-linearity can be computed using the Walsh transform as follows [9]:

$$ \mathcal{N}\mathcal{L}(F) = 2^{n-1} - \frac{1}{2} \max_{\mathbf{v} \in \mathbb{F}_{2^n}*, \mathbf{u} \in \mathbb{F}_{2^n}} \left| {\sum}_{\mathbf{x} \in \mathbb{F}_{2^n}} (-1)^{\mathbf{v} F(\mathbf{x})^{T} \oplus \mathbf{u} \mathbf{x}^{T}} \right|. $$

(3)

The differential profile of a function F expresses the number of solutions of the equation F(x ⊕a) ⊕ F(x) = b for given $\mathbf {a} \in {\mathbb {F}_{2^n}}^{*}, \mathbf {b} \in \mathbb {F}_{2^n}$. The differential probability is then defined as

$$ p_{(a, b)} = \frac{\left| \mathbf{x} \in \mathbb{F}_{2^n} : F(\mathbf{x}\oplus\mathbf{a}) \oplus F(\mathbf{x}) = \mathbf{b} \right|}{2^{n}}. $$

A cryptographically strong S-box must also have a flat differential profile, i.e., its maximum over all possible values of a and b, should be as low as possible.

It is known how to construct S-boxes with good non-linearity and differential profile [11, 26]. The non-linearity and differential profile are invariant under affine equivalence. These properties of small S-boxes with n = 4 are known, as well as all 16 AE classes with optimal properties [16] (the non-linearity is 4, and the maximum of the differential profile is also 4, which is the best that can be achieved for bijective S-boxes with n = 4).

In standard cipher designs based on a substitution permutation network (SPN), S-boxes are the only source of non-linearity. Key additions can be understood as an addition of a constant, and diffusion layers are linear. Therefore, the security of the cipher directly depends on the properties of the S-box.

Consider now the following toy cipher design. The state of the cipher is represented as bit vectors of length w. The design repeats the following three operations in r rounds:

• Key addition is done in $\mathbb {Z}_{w}$: y = x + k.

• An S-box layer is applied, i.e., the state is split into n-bit substrings, and each substring x_i is replaced by y_i = S(x_i), where $S:\mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ is a chosen S-box.

• Diffusion is realized by a simple rotation by one bit.

Let us analyze this design using ordinary differential cryptanalysis. Suppose we use a bijective S-box with n = 4, and the best possible differential probability bounded by 4/16 = 2^− 2 (e.g., an S-box based on finite field inversion similar to AES). In the best attack scenario, the attacker can construct an iterative differential characteristic involving a single S-box in each round (e.g. when an input S-box difference of 0010 maps to an output difference of 0001). Because key-addition is now non-linear, a single bit difference propagates unchanged only if the corresponding subkey bit is 0. If the subkeys are independent, the maximum differential probability that an attacker can reach is 2^− 3r over r rounds. This means that a 6-round toy design with w = 16, or a 43-round design with w = 128, should be secure against standard differential attacks.

Now let us consider a different attacker. The attacker focuses on the first S-box (corresponding to the least significant bit in the state representation). Let x₁, and x₂ represent the n least significant plaintext bits (as integers in $\mathbb {Z}_{2^n}$), with even (modular) difference d = x₂ − x₁. Then the inputs of the first S-box are x₁ + k, and x₂ + k (here k is the corresponding subkey part), with the same modular difference d. Now let us suppose that also the outputs of the S-box y₁,y₂ have a modular difference y₂ − y₁ = d/2 with some probability p. Rotation doubles this modular difference, if the most significant bits of the state are the same. We can estimate this event to have probability 50%. If p is high enough, an attacker can construct an (iterative) modular differential distinguisher, with r-round probability (p/2)^r. For example³, if p = 1/2, a 6-round distinguisher has probability 2^− 12, and a 43-round distinguisher has probability 2^− 86. In our experiments (see Section 5) we have found S-boxes optimal w.r.t. standard differential cryptanalysis that have p as high as 12/16, which gives a distinguisher with probability 2^− 61 for a 43-round design.

This short analysis shows that with a suitable choice of S-boxes, our toy design can be secure against standard differential cryptanalysis. However, the same design with the same parameters and S-boxes is vulnerable against an attack based on modular differences.

This toy cipher example demonstrates that it is important to study S-box properties with respect to differences in $\mathbb {Z}_{2^n}$ (and possibly other notions of difference). It is not clear whether similar techniques can be adapted to linear cryptanalysis, or whether we can combine the modular differences and standard linear/differential techniques. However, the goal of this paper is not a study of cryptanalytic techniques, but rather a study of properties of (small) S-boxes.

With respect to modular differential cryptanalysis, we define the modular differential profile of an S-box $S: \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ as follows. For each pair $(d_{x}, d_{y}) \in \mathbb {Z}_{2^n}\setminus \{0\} \times \mathbb {Z}_{2^n}$, we define a quantity

$$ D_{(d_{x}, d_{y})}^{(S)} = \left| \left\{ x : S(x + d_{x}) - S(x) = d_{y} \right\} \right|. $$

When S is known from the context, we omit it from the superscript, writing just $D_{(d_{x}, d_{y})}$.

This definition, unlike the ordinary differential profile, is relative to the representation of numbers by bit-vectors, as discussed in Section 2. This means that if we choose a different bit encoding of numbers (bijection ι), an S-box S will be represented by a different function over $\mathbb {Z}_{2^n}$, with possibly different modular differential profile. This fact, however, does not change our statistical results, as we study the set of all S-boxes (of a fixed size). Note that given a cipher design, the attacker typically chooses the bit encoding of numbers with respect to the cipher design, and thus in cryptanalytic applications, we might consider ι to be fixed.

Note that unlike the XOR operation, modular addition is not its own inverse, and the quantity $D_{(d_{x}, d_{y})}$ is not necessarily even. We can normalize $D_{(d_{x}, d_{y})}$ to obtain a modular differential probability

$$ p_{(d_{x}, d_{y})} = \frac{D_{(d_{x}, d_{y})}}{2^{n}}. $$

We call the multiset of all $D_{(d_{x}, d_{y})}$ the modular differential profile of the S-box S:

$$ \mathbb{D} = \{ D_{(d_{x}, d_{y})} : (d_{x}, d_{y}) \in \mathbb{Z}_{2^n}\setminus\{0\} \times \mathbb{Z}_{2^n} \}. $$

The largest value of the modular differential profile $\mathbb {D}$ characterizes the resistance of an S-box against modular differential cryptanalysis. To simplify the text, we refer to this maximum as the D-criterion (of an S-box S).

Note that for a bijective S-box, the lower bound for the D-criterion is 2. Indeed, a bijective S-box is by definition a 1-to-1 function, thus $D_{(d_{x}, 0)} = 0$. Because there are n possible values of x, and n − 1 possible non-zero differences, at least one difference must occur more than once. Our experiments (see Section 5) show that both 3-bit and 4-bit S-boxes with D = 2 exist, although statistically, they are rare. It is not clear whether this holds in general for any n.

While the modular differential profile is quite a straightforward generalisation of the ordinary differential profile, in the case of non-linearity the situation is slightly different. The space of affine functions is restricted to functions ax + b with $a\in \mathbb {Z}_{2^n}^{*}$ (since a can only be odd, as ax + b with a even defines a non-invertible function). It is also not clear how to measure the distance between functions. We have decided to define modular non-linearity with a Hamming distance over symbols from $\mathbb {Z}_{2^n}$, but it might be interesting to generalise this to other distance metrics (e.g. Manhattan, or distance over concatenated binary strings representing outputs).

For each pair $(q,c) \in \mathbb {Z}_{2^n}^{*} \times \mathbb {Z}_{2^n}$, we define a quantity

$$ L_{(q,c)}^{(S)} = \left| \left\{ x : S(x) = qx + c \right\} \right|. $$

When S is known from the context, we omit it from the superscript, writing just L_(q,c).

The normalized L_(q,c) is a measurement of how close S is to an affine function:

$$ r_{(q,c)} = \frac{L_{(q,c)}}{2^{n}}. $$

Similarly to the modular differential criterion, we define the modular linear profile of S to be the multiset

$$ \mathbb{L} = \{ L_{(q,c)} : (q,c) \in \mathbb{Z}_{2^n}^{*} \times \mathbb{Z}_{2^n} \}. $$

The maximum of the modular linear profile $\mathbb {L}$ can be used as a measure of S-box resistance against modular cryptanalytic attacks. To simplify the text, we refer to this maximum as the L-criterion (of an S-box S).

We were not able to construct an attack on an SPN-like design based on linear approximations similar to a standard linear cryptanalysis. However, we can show the importance of the L-criterion with a simplified example based on the historical Enigma machine (see e.g., [23]). Encryption of a plaintext letter $x^{(t)} \in \mathbb {Z}_{2^n}$ to a ciphertext letter $y^{(t)} \in \mathbb {Z}_{2^n}$ is given by

$$ y^{(t)} = S_{3}(S_{2}(S_{1}(x^{(t)} + k_{1} + t) - (k_{1}+t) + k_{2}) - k_{2} + k_{3} ) - k_{3}. $$

Note that for the sake of simplicity, we have omitted many details from the real Enigma. Let us further suppose that S₁ = S₂ = S₃ = S, with a known modular linear profile with maximum L attained for some pair q,c. This means that the following equation

$$ y^{(t)} = q^{3} x^{(t)} + (q^{3}-q^{2}) k_{1} + (q^{2}-q) k_{2} + (q-1) + k_{3} + (q^{3}-q^{2})t +\text{const}, $$

holds with probability approximately $r_{(q,c)}^{3} = L^{3}/2^{3n}$. If the attacker can guess or find 3 pairs (x^(t),y^(t)) of inputs and corresponding outputs, he can compute the keys k₁,k₂,k₃ by solving a simple linear equation system. The expected data complexity of such an attack is thus 2⁹ⁿ/L⁹. In the case when n = 4, the lowest value of L is L = 2, giving data complexity 2²⁷. On the other hand, we have found cryptographically optimal 4-bit S-boxes⁴ with L as high as 10, in which case the expected number of input-output pairs is only 69.

4.1 Modular affine equivalence and S-box properties

In this section, we show that modular affine equivalence preserves the modular differential and linear profile of an S-box.

Assume that S₁ is modular affine equivalent to S₂, so that

$$ S_{2}(x)= a_{1} S_{1}(a_{2} x + b_{2}) + b_{1}. $$

Consider the equation S₂(x) = qx + c, $q\in \mathbb {Z}_{2^n}^{*}, c\in \mathbb {Z}_{2^n}$. We can rewrite this using S₁ as follows:

$$ a_{1} S_{1}(a_{2} x + b_{2}) + b_{1} = qx + c. $$

We can substitute y = a₂x + b₂, or $x = a_{2}^{-1} y - a_{2}^{-1} b_{2}$, respectively, to get

$$ a_{1} S_{1}(y) + b_{1} = q a_{2}^{-1} y - q a_{2}^{-1} b_{2} + c. $$

After division by a₁ and rearrangement of terms, we get:

$$ S_{1}(y) = (a_{1}^{-1} q a_{2}^{-1}) y + (a_{1}^{-1} c - a_{1}^{-1} q a_{2}^{-1} b_{2} - a_{1}^{-1} b_{1}) . $$

We can thus set $q^{\prime } = a_{1}^{-1} q a_{2}^{-1}$ and $c^{\prime } = a_{1}^{-1} c - a_{1}^{-1} q a_{2}^{-1} b_{2} - a_{1}^{-1} b_{1}$. Then

$$ L_{(q,c)}^{(S_{2})} = L_{(q^{\prime},c^{\prime})}^{(S_{1})}. $$

This means that the values in the modular linear profile are the same (albeit rearranged with respect to q,c), and the L-criterion is an invariant under modular affine equivalence.

A similar situation holds for the modular differential profile. Given

$$ S_{2}(x+d_{x}) - S_{2}(x) = d_{y}, $$

we can rewrite this as

$$ a_{1} S_{1}(a_{2} x + b_{2} + a_{2} d_{x}) + b_{1} - a_{1} S_{1}(a_{2} x + b_{2}) - b_{1} = d_{y}. $$

Again we can substitute $x = a_{2}^{-1} y - a_{2}^{-1} b_{2}$, and divide by a₁ to obtain

$$ S_{1}(y + a_{2} d_{x}) - S_{1}(y) = a_{1}^{-1} d_{y}. $$

Thus

$$ D_{(d_{x},d_{y})}^{(S_{2})} = D_{(a_{2} d_{x},a_{1}^{-1} d_{y})}^{(S_{1})}, $$

and the modular differential spectra contain the same values (albeit rearranged with respect to d_y). Thus, the D-criterion is an invariant under modular affine equivalence as well.

5 Experimental results

In this section, we summarize our experiments with small S-boxes. We have conducted a series of experiments with custom software implemented in Python (PyPy 7.0.0 with GCC 6.2.0, Python 3.6.1). The computation was parallelized and run on a cluster of 28 Intel i9-7940X 3.1GHz cores, using 128GB RAM, and 1TB M2 NVME SSD as storage. We have used 24 of the CPU cores for one week in real-time to find all representatives of MAE classes. The computation of the statistics was then simpler (details provided further on). Computing the statistics of the representatives in each of the G0-G15 affine classes took approximately 8 hours each.

5.1 Bijective S-boxes, n = 3

Our initial experiments were conducted with bijective S-boxes of dimension n = 3. We have performed an exhaustive search over this group of 8! S-boxes. They belong to 58 MAE classes. The distribution of MAE classes with respect to D- and L-criteria is summarized in Table 1. The rows and columns of the table are indexed by the values of D, and L, respectively. The numbers in the table represent the number of MAE classes for the given (D,L) combination.

Table 1 Distribution of MAE classes of 3-bit S-boxes with respect to D- and L-criterion

There are 6 classes that have D = 2, and 5 classes that have L = 2. One of these classes has both D = 2, and L = 2. We have not studied these S-boxes in more detail, due to the limited cryptographic interest in 3-bit S-boxes.

5.2 Bijective S-boxes, n = 4

Bijective S-boxes of size n = 4 are commonly used in cipher designs, such as GOST [25], Serpent [1], PRESENT [5], and others. There are 16! (approximately 2⁴⁴) S-boxes of this size. While it is not infeasible to enumerate this whole set, it requires a lot of computational resources (e.g., to store this set, we need at least 152 TB of storage). Their cryptographic properties can be more efficiently studied with the help of affine equivalence, as there are only 302 AE classes. Of these, 16 classes are considered optimal with respect to linear and differential cryptanalysis [16]. We will use the notation G0-G15 from [16] to denote the optimal classes.

When considering modular affine equivalence, the situation is more complicated. Each class can contain at most (2³ ⋅ 2⁴)² = 2¹⁴ elements (if every a₁,b₁,a₂,b₂ in (2) defines a different S-box), thus there are at least (approximately) 2⁴⁴/2¹⁴ = 2³⁰ classes. By performing an exhaustive search over S-boxes restricted to potential MAE class representatives (with S(0) = 0, and S(1) = 1, see Section 3.1), we were able to find 1277100855 MAE classes. This number is very close to the lower bound, since it can be expressed as

$$ \frac{(2^{4})!}{2^{14}} + 75105. $$

While the set is still relatively large, we were able to experimentally determine D- and L-criteria for each class in this set with moderate computational effort. The results are graphically summarized in Fig. 1. The figure is a heat-map depicting the relative frequencies of MAE classes for a given combination of the D-criterion (on the vertical axis), and the L-criterion (on the horizontal axis). Low frequencies are (dark) red, going through orange and yellow to green. White (empty) boxes depict combinations of D,L with no possible MAE class. All non-empty boxes contain at least one MAE class, with its relative frequency displayed as a percentage value. The numbers are for readability shortened to two decimal places, thus very small (but non-zero) relative frequencies can be shown as 0.00%.

Fig. 1

Statistical distribution of MAE classes of 4-bit S-boxes with respect to D- and L-criterion

The most common situation for a randomly selected S-box is D = L = 4, which happens in approx. 30% of the MAE classes. For approx. 95% MAE classes, the criteria are bounded by D,L ∈{4,5}. However, approximately 0.5% of the MAE classes satisfy D ≥ 8, or L ≥ 8 (this means, the distinguishers use events with at least 50% probability).

Classes better than average are very rare. The lowest values of D = 2,L = 2 cannot be obtained simultaneously. There are 170 classes with L = 2,D = 3, and 411 classes with L = 3,D = 2, respectively.

We provide some examples of cryptographically strong S-boxes (among the class representatives investigated) w.r.t. D- and L-criteria (we also give their differential uniformity δ_F, and non-linearity $\mathcal {N}{\mathscr{L}}$):

• D = 2, L = 3:

  • 012438c69ebf75da, first in lex-order, δ_F = 6, $\mathcal {N}{\mathscr{L}}=2$,

  • 012496ec37da5bf8, strong S-box with δ_F = 4, $\mathcal {N}{\mathscr{L}}=4$,

  • 013d95cf764ae2b8, weak S-box with δ_F = 16, $\mathcal {N}{\mathscr{L}}=0$,

  • 01462df75aec98b3, last in lex-order, δ_F = 8, $\mathcal {N}{\mathscr{L}}=2$.

• D = 3, L = 2:

  • 01325a9be7c68fd4, first in lex-order, δ_F = 6, $\mathcal {N}{\mathscr{L}}=2$,

  • 01357b962e8fdca4, strong S-box with δ_F = 4, $\mathcal {N}{\mathscr{L}}=4$,

  • 0135e8d46a29fcb7, weak S-box with δ_F = 12, $\mathcal {N}{\mathscr{L}}=0$,

  • 013fb8ac6e49d752, last in lex-order, δ_F = 6, $\mathcal {N}{\mathscr{L}}=2$.

We were also curious, whether S-boxes that are used in cipher designs have good properties with respect to modular addition. We have selected a list of S-boxes from [24]. In this set, D,L ∈{3,4,5,6,7}. While most of the S-boxes have the expected properties L = 4,D = 4, there are some examples of weaker S-boxes⁵:

• DES S5-1: D = 7, L = 4 (occurring with 0.53% probability in the global statistics). Namely, we have a differential probability

  $$ Pr(S(x+3)-S(x)=8)=7/16. $$

• GOST K8: D = 5, L = 7 (occurring with 0.36% probability in the global statistics). There exists an affine approximation with probability

  $$ Pr(S(x)=5x+1) = 7/16. $$

• HAMSI, Serpent S2 (G1): D = 7, L = 3 (occurring with 0.12% probability in the global statistics).

We have studied also the AE classes of DES S5-1 and GOST-K8. We have generated all MAE representatives within each AE class, and computed the relative frequencies of S-boxes with given values of D,L. We did not observe any irregularities within these AE classes, and the overall distribution is similar to Fig. 1. It is very rare to obtain S-boxes with such modular properties even in their AE class. The maximum value of the D-criterion is D = 13 in both cases. The maximum value of the L-criterion is L = 11 in the AE class of DES S5-1, and L = 12 in the AE class of GOST-K8. We have not studied whether this property can be exploited in attacks on the corresponding ciphers.

5.3 Bijective S-boxes, n = 4, optimal classes

In addition to the previous study of the distribution of MAE classes with respect to the specific values of the D- and L-criterion, we have also studied properties of 4-bit S-boxes from the 16 optimal classes. Although there is no reason to suspect different behaviour, we were mostly interested in extreme cases: whether there are classes of S-boxes with significantly better properties, and whether we can also find significantly weaker S-boxes with respect to modular addition in these classes.

On a technical note, if we wanted to explore all S-boxes in the 16 optimal classes, the required computational power would be 1303 times more than to explore all MAE class representatives. Again, it is possible to save time by working only with S-box representatives. To find S-box representatives for MAE classes within a single affine class, we use the following lemma.

Lemma 4

Let $\mathbb {A}$ denote the set of all affine permutations over $\mathbb {F}_{2^n}$. Let $\mathbb {M}$ denote the set of all modular affine permutations over $\mathbb {Z}_{2^n}$. Let $\mathbb {A}_{L} \subset \mathbb {A}$, $\mathbb {A}_{R} \subset \mathbb {A}$ be sets such that $\mathbb {M} \circ \mathbb {A}_{L} = \mathbb {A}_{R} \circ \mathbb {M} = \mathbb {A}$. Let $S: \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$ be a bijective S-box. Then $\mathbb {S} = \mathbb {A}_{L} \circ S \circ \mathbb {A}_{R}$ contains S-boxes from each MAE class contained in $\mathbb {S}^{*} = \mathbb {A} \circ S \circ \mathbb {A}$.

Proof

First, note that from the definition of $\mathbb {A}_{L}$, $\mathbb {A}_{R}$, it is easy to see that each S-box from $\mathbb {S}$ is also in $\mathbb {S}^{*}$. Each S-box $S^{*} \in \mathbb {S}^{*}$ can be written as

$$ S^{*} = \beta_{1} \circ S \circ \beta_{2}, $$

with $\beta _{1}, \beta _{2} \in \mathbb {A}$. Let $\alpha _{1}, \alpha _{2} \in \mathbb {M}$ be such that $\beta _{1} = \alpha _{1} \circ \beta _{1}^{\prime },$ with $\beta _{1}^{\prime } \in \mathbb {A}_{L}$, and $\beta _{2} = \beta _{2}^{\prime } \circ \alpha _{2},$ with $\beta _{2}^{\prime } \in \mathbb {A}_{R}$. Thus

$$ S^{*} = \beta_{1} \circ S \circ \beta_{2} = \alpha_{1} \circ \beta_{1}^{\prime} \circ S \circ \beta_{2}^{\prime} \circ \alpha_{2}. $$

Thus S^∗ is MAE equivalent to the S-box $S^{\prime } = \beta _{1}^{\prime } \circ S \circ \beta _{2}^{\prime }$, which is an element of $\mathbb {S}$. □

We use this lemma by computing smallest possible sets $\mathbb {A}_{L}$ and $\mathbb {A}_{R}$, and enumerating $\mathbb {S}$ instead of the larger $\mathbb {S}^{*}$:

• 1. Let $\mathbb {A}$ be the set of all affine functions $A : \mathbb {F}_{2^n} \rightarrow \mathbb {F}_{2^n}$, with n = 4.

• 2. Let $\mathbb {A}_{L}$ contain MAE representatives of all classes aA(x) + b. This set contains 20160 permutations, and is can be easily seen that it has the property $\mathbb {M}\circ \mathbb {A}_{L} = \mathbb {A}$.

• 3. Let $\mathbb {A}_{R}$ contain MAE representatives of all classes A(ax + b). This set again contains 20160 permutations, and has the property $\mathbb {A}_{R} \circ \mathbb {M} = \mathbb {A}$.

• 4. Compute $\mathbb {A}_{L} \circ S \circ \mathbb {A}_{R}$, where S is any normalized S-box in the selected AE class.

The results of the experiments are summarized in Figs. 2 and 3. We observe that in each AE class, the best S-boxes always have (D,L) = (2,3). The values (D,L) = (3,2) are only attained in classes G0, G1, G2, G8, G9, G10, G12, G14, and G15. Classes G4 and G13 contain S-boxes with (D,L) = (4,2). Classes G3, G5, G6, G7, and G11 have a minimum value of L = 3 (Fig. 4). Individual classes also slightly differ when considering high values of L and D:

• Nine AE classes (G0, G1, G2, G3, G4, G5, G7, G8, G12) have maximum possible value L = 9, all other AE classes contain some S-boxes with L = 10.

• Four AE classes (G5, G7, G8, G11) have a maximum possible value D = 11, other AE classes have D = 12.

Similarly to the global statistics, between 96% and 97% of S-boxes in each class have D,L ∈{4,5} (common S-boxes). Between 0.1% and 0.2% of S-boxes have D ≥ 8 or L ≥ 8 (bad S-boxes). The overview per class is presented in Fig. 5.

Fig. 2

Statistical distribution of MAE classes of 4-bit S-boxes with respect to D- and L-criterion, within 16 optimal AE classes, G0-G7

Fig. 3

Statistical distribution of MAE classes of 4-bit S-boxes with respect to D- and L-criterion, within the 16 optimal AE classes, G8-G15

Fig. 4

Statistical distribution of MAE classes of 4-bit S-boxes with respect to D- and L-criterion, within AE class G3 (containing finite field inverse)

Fig. 5

Statistical distribution of common and bad S-boxes within AE classes

6 Conclusion

The focus of this work was an experimental investigation of the properties of (small) S-boxes with respect to modular addition. We have computed statistics of representatives of classes of modular affine equivalence and experimentally computed their distribution with respect to the D- and L-criteria. Experiments have also produced examples of S-boxes that have good properties with respect to D- and L-criteria. On the other hand, there is a non-negligible amount of S-boxes that are very weak with respect to modular cryptanalysis. Our further analysis of the best 4-bit S-boxes in affine equivalence classes G0-G15 shows that each class contains a similar ratio (0.1% - 0.2%) of weak S-boxes. While these S-boxes are strong against classical linear and differential cryptanalysis, they either have a modular differential probability at least 1/2 (up to 12/16), or can be approximated by a modular affine function with probability at least 1/2 (up to 10/16).

In Section 4 we gave an example of a modular differential attack on a toy cipher based on GOST, which is resistant against classical differential cryptanalysis. It is an open question whether it is possible to exploit these properties to break some standard SPN based cipher designs. On the other hand, S-boxes which resist standard cryptanalysis, but are weak against modular cryptanalysis, are easy to find, and can be potentially used to insert backdoors in cipher designs. Such S-boxes can even be hidden inside larger S-boxes. For example, we can use our toy example design to construct a small bijective function on 16 bits, and only publish the final table of function values as an S-box. The hidden modular weakness can be more difficult to spot in this hidden structure with reverse-engineering similar to [4].

There are many questions left open. The representation of numbers as bitstrings (that is, the choice of the bijection ι) does not influence the overall statistics. However, we can ask how the choice of ι influences the properties of a concrete S-box we want to use. We have not considered general bounds or theoretical estimates for general n (or non-bijective S-boxes). There is also the question of combined differentials, where the input difference is considered with respect to one operation, and the output difference with respect to another, similar to the generalized non-linearity studied in [13]. Finally, a question can arise, whether there are concrete S-boxes that are good with respect to some larger set of generalized differences (and how to find them).