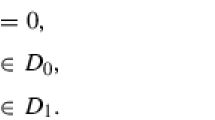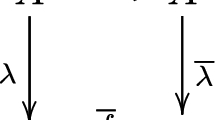New results on permutation polynomials of the form (x ^{p m} − x + δ)^s + x^{p m} + x over 𝔽 p ^2m

Abstract

Permutation polynomials over finite fields have significant applications in coding theory, cryptography, combinatorial designs and many other areas of mathematics and engineering. In this paper, we study the permutation behavior of polynomials with the form $(x^{p^{m}}-x+\delta )^{s}+x^{p^{m}}+x$ over the finite field $\mathbb {F}_{p^{2m}}$. By using the Akbary-Ghioca-Wang (AGW) criterion, we present several new classes of permutations over $\mathbb {F}_{p^{2m}}$ based on some bijections over the set $\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$ or the subfield $\mathbb {F}_{p^{m}}$.

1 Introduction

Let p be a prime, n be a positive integer and $\mathbb {F}_{p^{n}}$ be a finite field with p ⁿ elements. A polynomial $f(x)\in \mathbb {F}_{p^{n}}[x]$ is called a permutation polynomial (PP) over $\mathbb {F}_{p^{n}}$ if it induces a bijection from $\mathbb {F}_{p^{n}}$ to itself. A linearized polynomial or p-polynomial [10, Definition 3.49] over $\mathbb {F}_{p^{n}}$ is defined by

$$L(x)=\sum\limits_{i=0}^{n-1}a_{i}x^{p^{i}}\in \mathbb{F}_{p^{n}}[x].$$

It has a unique zero root in $\mathbb {F}_{p^{n}}$ if and only if L(x) permutes $\mathbb {F}_{p^{n}}$, which means that the equation L(x) + b = 0 has a unique nonzero solution for any $b\in \mathbb {F}_{p^{n}}\setminus \{0\}$. PPs are an interesting subject of mathematics and engineering, and have significant applications in coding theory, cryptography, combinatorial designs and so on. For more details of the recent advances and contributions to the area, the reader is referred to [4, 7, 12, 20] and the references therein.

Helleseth and Zinoviev [6] first proposed PPs of the form

$$\left( \frac{1}{x^{2}+x+\delta}\right)^{2^{l}}+x$$

for the goal of deriving new identities on Kloosterman sums over $\mathbb {F}_{2^{n}}$, where $\delta \in \mathbb {F}_{2^{n}}$ and l = 0 or 1. Yuan et al. [15, 16] further investigated the permutation behavior of the polynomials with the form

$$ (x^{p^{k}}-x+\delta)^{s}+L(x) $$

(1)

over $\mathbb {F}_{p^{n}}$, where k, s are integers, $\delta \in \mathbb {F}_{p^{n}}$ and L(x) is a linearized polynomial. Akbary et al. [1] proposed a criterion of PPs by the following lemma:

Lemma 1

[1] (The AGW criterion) Let A,S and $\overline {S}$ be finite sets with $\sharp S=\sharp \overline {S}$ , and let f : A → A , $h: S\rightarrow \overline {S}$ , λ : A → S and $\overline {\lambda }: A\rightarrow \overline {S}$ be maps such that $\overline {\lambda }\circ f=h\circ \lambda$ . If both λ and $\overline {\lambda }$ are surjective, then the following statements are equivalent:

• (1) f is a bijection (a permutation over A); and

• (2) h is a bijection from S to $\overline {S}$ and f is injective on λ ⁻¹(t)for each t ∈ S .

Yuan and Ding [17, 18] gave a unified treatment of some earlier constructions of PPs and get many new specific PPs by using the AGW criterion. Followed by Yuan and Ding’s work, many researchers began to study PPs having the form as in (1). They obtained many important results and advances, which can be seen in [3, 9, 19, 22, 23] and the references therein.

Very recently, Tu et al. [13, 14] presented several classes of PPs over $\mathbb {F}_{p^{2m}}$ with the form (1), where k = m, s and m are integers satisfying s ≡ 1(mod p ^m + 1) or s ≡ 1(mod p ^m − 1). For this kind of exponents s, Zeng et al. [21] proposed several classes of PPs based on trace functions over $\mathbb {F}_{2^{n}}$. This motivated Zha and Hu [24] to construct PPs of the form (1) with new such exponents s.

As we know, both $x^{p^{m}}-x$ and $x^{p^{m}}+x$ are not permutations on $\mathbb {F}_{p^{2m}}$. In this paper, we further study the permutation behavior of polynomials with the form

$$(x^{p^{m}}-x+\delta)^{s}+x^{p^{m}}+x$$

over $\mathbb {F}_{p^{2m}}$. By using the AGW criterion, we find some new exponents s and present several new classes of PPs over $\mathbb {F}_{p^{2m}}$ based on some bijections over the set $\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$ or the subfield $\mathbb {F}_{p^{m}}$.

The rest of this paper is organized as follows. In Section 2, some preliminaries needed later are presented. In Section 3, we propose three classes of PPs based on some bijections over the set $\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$. In Section 4, by determining some bijections over the subfield $\mathbb {F}_{p^{m}}$ we exhibit some new classes of PPs with exponents s = i p ^j(p ^m + 1) + p ^j or i p ^j(p ^m + 1) + 2p ^j for some integers i and j. Finally, we conclude the paper in Section 5.

2 Preliminaries

Throughout this paper, we always let p be an odd prime, and let j, s, m and n be positive integers. Denote the multiplicative group of $\mathbb {F}_{p^{m}}$ by $\mathbb {F}_{p^{m}}^{*}$. For each element δ in the finite field $\mathbb {F}_{p^{2m}}$, we denote $\delta ^{p^{m}}$ by $\overline {\delta }$ in analogy with the usual complex conjugation. Obviously, $\delta +\overline {\delta }\in \mathbb {F}_{p^{m}}$ and $\delta \overline {\delta }\in \mathbb {F}_{p^{m}}$. Denote the p-adic order of an integer m by v _p (m) and let v _p (m) = n if p ⁿ|m and p ⁿ⁺¹ ∤ m.

By the AGW criterion, we have the following propositions.

Proposition 1

Let $\delta \in \mathbb {F}_{p^{2m}}$ . The polynomial $f(x)=(x^{p^{m}}-x+\delta )^{s}+x^{p^{m}}+x$ induces a permutation on $\mathbb {F}_{p^{2m}}$ if and only if the polynomial

$$h(t)=(-t+\overline{\delta})^{s}-(t+\delta)^{s}$$

is a bijectionover the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$.

Proof

Note that the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$ can be denoted as $\{x^{p^{m}}-x| x\in \mathbb {F}_{p^{2m}}\}$. Let $\lambda (x)=\overline {\lambda }(x)=x^{p^{m}}-x$ and $h(x)=(x+\delta )^{s\cdot p^{m}}-(x+\delta )^{s}$. It can be verified that the following diagram commutes

For each t ∈ S, we have that $\lambda ^{-1}(t)=\{x\in \mathbb {F}_{p^{2m}}|x^{p^{m}}-x=t\}$ and f(x) = (t + δ)^s + t + 2x is injective on λ ⁻¹(t). Then by the AGW criterion, f permutes $\mathbb {F}_{p^{2m}}$ if and only if

$$h(t)=(t+\delta)^{s\cdot p^{m}}-(t+\delta)^{s}=(-t+\overline{\delta})^{s}-(t+\delta)^{s}$$

is a bijection over S. □

Remark 1

Let $\lambda \in \mathbb {F}_{p^{m}}^{*}$. We note that t ∈ S if and only if λ t ∈ S, where S is defined in Proposition 1.

Proposition 2

Let $\delta \in \mathbb {F}_{p^{2m}}$ . The polynomial $f(x)=(x^{p^{m}}-x+\delta )^{s}+x^{p^{m}}+x$ permutes $\mathbb {F}_{p^{2m}}$ if and only if the polynomial $g(x)=(x^{p^{m}}-x+\delta )^{s\cdot p^{j}}+x^{p^{m}}+x$ permutes $\mathbb {F}_{p^{2m}}$ for any integer j ≥ 0.

Proof

According to Proposition 1, the polynomials f(x) and g(x) permute $\mathbb {F}_{p^{2m}}$ if and only if $h(t)=(-t+\overline {\delta })^{s}-(t+\delta )^{s}$ and $h^{p^{j}}(t)$ permute S respectively. Moreover, the mapping h(t) is a bijection on S if and only if $h^{p^{j}}(t)$ is a bijection on S. Hence the proof is completed. □

3 Three classes of PPs over $\mathbb {F}_{p^{2m}}$ derived from bijections over the set $\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$

In this section, we present three classes of permutation polynomials over $\mathbb {F}_{p^{2m}}$ by applying Propositions 1 and 2.

Theorem 1

Let $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }=0$ . Then

$$f(x)=(x^{p^{m}}-x+\delta)^{s}+x^{p^{m}}+x$$

permutes$\mathbb {F}_{p^{2m}}$if and only ifs is odd and $\gcd (s,p^{m}-1)=1$.

Proof

By Proposition 1, f(x) permutes $\mathbb {F}_{p^{2m}}$ if and only if $h(t)=(-t+\overline {\delta })^{s}-(t+\delta )^{s}$ is a bijection on the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$. Since $\delta +\overline {\delta }=0$, we get $(t+\delta )^{p^{m}}+t+\delta =0$, which implies that t + δ = 0 or $(t+\delta )^{2(p^{m}-1)}=1$. It can be easily checked that

$$h(t)=(t+\delta)^{s}((-1)^{s}-1).$$

If s is even, h(t) = 0 is not a bijection on S. If s is odd and $\gcd (s,p^{m}-1)=i>1$, then there exist two different values t ₁,t ₂ ∈ S such that t ₁ + δ = β(t ₂ + δ) and h(t ₁) = h(t ₂), where $\beta \in \mathbb {F}_{p^{m}}$, β ⁱ = 1 and β ≠ 1. It follows that h(t) is not a bijection on S. If s is odd and $\gcd (s,p^{m}-1)=1$, then $\gcd (s,2(p^{m}-1))=1$. It can be verified that h(t) = 2(t + δ)^s is an injection on S, which implies that h(t) permutes S. Hence the proof is finished. □

Theorem 2

Let k be an integer with k < m and let $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . Then

$$f(x)=(x^{p^{m}}-x+\delta)^{s}+x^{p^{m}}+x$$

permutes$\mathbb {F}_{p^{2m}}$in thefollowing two cases:

• (i) s = p ^jor 2p ^j;

• (ii) s = (p ^k + 1) ⋅ p ^jwith $\frac {m-k}{\gcd (m,k)}$is odd.

Proof

By Propositions 1 and 2, we just need to prove that $h(t)=(-t+\overline {\delta })^{s}-(t+\delta )^{s}$ is a bijection on the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$ in the case of j = 0.

• (i) If s = 1, $h(t)=-2t+\overline {\delta }-\delta$ is an affine permutation of S. If s = 2, $h(t)=-2(\overline {\delta }+\delta )t+\overline {\delta }^{2}-\delta ^{2}$ is also an affine permutation of S since $\delta +\overline {\delta }\neq 0$.

• (ii) If s = p ^k + 1, then $h(t)=-(\overline {\delta }+\delta )t^{p^{k}}-(\overline {\delta }+\delta )^{p^{k}}t+\overline {\delta }^{p^{k}+1}-\delta ^{p^{k}+1}$. Since $\delta +\overline {\delta }\neq 0$, h(t) is a bijection on S if and only if

  $$h_{1}(t)=h((\overline{\delta}+\delta)t)=-(\overline{\delta}+\delta)^{p^{k}+1}(t^{p^{k}}+t)+\overline{\delta}^{p^{k}+1}-\delta^{p^{k}+1}$$

  is a bijection on S. Assume t ₁,t ₂ ∈ S with t ₁≠t ₂ and h ₁(t ₁) = h ₁(t ₂). It leads to $(t_{1}-t_{2})^{p^{m}}+(t_{1}-t_{2})=0$ and $(t_{1}-t_{2})^{p^{k}}+(t_{1}-t_{2})=0$. Let u = t ₁ − t ₂. Then we have u ≠ 0 and

  $$u^{p^{m}-1}=u^{p^{k}-1}=-1,$$

  which implies that $u^{p^{m-k}-1}=1$, i.e., $u\in \mathbb {F}_{p^{m-k}}^{*}$. We note that $u^{p^{k}-1}=-1$ has a solution u in $\mathbb {F}_{p^{m-k}}^{*}$ if and only if $\frac {m-k}{\gcd (k,m-k)}$ is even. Since $\gcd (k,m-k)=\gcd (m,k)$ and $\frac {m-k}{\gcd (m,k)}$ is odd, there is no solution of $u^{p^{k}-1}=-1$ over $\mathbb {F}_{p^{m-k}}^{*}$. Therefore, h ₁(t) and h(t) are bijections on S.

□

Lemma 2

[5] Let a, b be integers and $l=\gcd (a,b)$. Let a ^′ = a/l and b ^′ = b/l . Then

$$\gcd(p^{a}+1,p^{b}-1)=\left\{ \begin{array}{cl} p^{l}+1, &\mathrm{for\ odd}\ a^{\prime}\ \mathrm{and\ even}\ b^{\prime},\\ 2, &\text{otherwise}. \end{array} \right. $$

Theorem 3

Let k be an integer and $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . Then

$$f(x)=(x^{p^{m}}-x+\delta)^{s}+x^{p^{m}}+x$$

permutes$\mathbb {F}_{p^{2m}}$in the following cases:

• (i) p = 3,$s=\frac {(3^{k}+1)\cdot 3^{j}}{2}$or $\frac {(3^{2m}+3^{k+1}+2)\cdot 3^{j}}{2}$,where $\gcd (k,2m)=1$;

• (ii) $s=\frac {(p^{k}+1)\cdot p^{j}}{2}$or $\frac {(p^{2m}+p^{k+1}+p-1)\cdot p^{j}}{2}$,where v ₂(k) ≥ v ₂(2m).

Proof

Let $S_{1}=\{z\in \mathbb {F}_{p^{2m}}|z+\overline {z}=\delta +\overline {\delta }\}$ and ρ be a mapping from S ₁ to S with ρ(z) = z − δ. It is clear that ρ is a one to one mapping. According to Proposition 1, we need to prove that $h(t)=(-t+\overline {\delta })^{s}-(t+\delta )^{s}$ is a bijection on the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$, which is equivalent that

$$h\circ \rho(z)=(-1)^{s}(z-\delta-\overline{\delta})^{s}-z^{s}(:=h_{1}(z))$$

is a one to one mapping from $S_{1}=\{z\in \mathbb {F}_{p^{2m}}|z+\overline {z}=\delta +\overline {\delta }\}$ to S. Note that |S ₁| = |S|. It is sufficient to show that for any γ ∈ S, there is at most one solution z ∈ S ₁ of equation

$$ h_{1}(z)=\gamma. $$

(2)

Let $u=\frac {\overline {\delta }+\delta }{4}$ and $z=\eta +\frac {u^{2}}{\eta }+2u$, where $\eta \in \mathbb {F}_{p^{2m}}^{*}$ satisfying $\overline {\eta }+\eta =0$ or $\overline {\eta }\eta +u^{2}=0$. Then $z=\frac {(\eta +u)^{2}}{\eta }$ and $z-\delta -\overline {\delta }=\eta +\frac {u^{2}}{\eta }-2u=\frac {(\eta -u)^{2}}{\eta }$. Equation (2) can be written as

$$ h_{1}\left( \eta+\frac{u^{2}}{\eta}+2u\right)=\frac{(-1)^{s}(\eta-u)^{2s}-(\eta+u)^{2s}}{\eta^{s}}=\gamma. $$

(3)

By Proposition 2, we only consider the following exponents s in the case of j = 0.

• (i) Since $\gcd (k,2m)=1$, both $\frac {3^{k}+1}{2}$ and $\frac {3^{2m}+3^{k+1}+2}{2}$ are even. If $s=\frac {3^{k}+1}{2}$, (3) turns to be

  $$\begin{array}{@{}rcl@{}} h_{1}(\eta+\frac{u^{2}}{\eta}+2u)&=&\frac{(\eta-u)^{3^{k}+1}-(\eta+u)^{3^{k}+1}}{\eta^{(3^{k}+1)/2}}=\frac{-2u\eta^{3^{k}}-2u^{3^{k}}\eta}{\eta^{(3^{k}+1)/2}}\\ &=&-2u(\eta^{\frac{3^{k}-1}{2}}+(\frac{u^{2}}{\eta})^{\frac{3^{k}-1}{2}})=\gamma. \end{array} $$

  (4)

  Assume $\theta =\eta ^{\frac {3^{k}-1}{2}}$. Equation (4) turns to

  $$u\left( \theta+\frac{u^{3^{k}-1}}{\theta}\right)=\gamma.$$

  Since $\delta +\overline {\delta }\neq 0$ and $\eta \in \mathbb {F}_{3^{2m}}^{*}$, we obtain u ≠ 0 and 𝜃 ≠ 0. The above equation implies that

  $$\theta^{2}+\frac{\gamma}{2u}\theta+u^{3^{k}-1}=0,$$

  which has at most two solutions 𝜃 ₁ and 𝜃 ₂ with $\theta _{1}\theta _{2}=u^{3^{k}-1}$. Note that

  $$\gcd\left( \frac{3^{k}-1}{2},3^{2m}-1\right)=\frac{3^{\gcd(k,2m)}-1}{2}=1.$$

  Both 𝜃 ₁ and 𝜃 ₂ lead to one solution η ₁ and η ₂ respectively, where $\eta _{1}=\frac {u^{2}}{\eta _{2}}$. It is obvious that η ₁ and η ₂ give the same value z. Therefore, (2) has at most one solution of z.

  If $s=\frac {3^{2m}+3^{k+1}+2}{2}$, (3) leads to

  $$\begin{array}{@{}rcl@{}} h_{1}(\eta+\frac{u^{2}}{\eta}+2u)&=&\frac{(\eta-u)^{3^{k+1}+3}-(\eta+u)^{3^{k+1}+3}}{\eta^{(3^{2m}+3^{k+1}+2)/2}}=\frac{-2u^{3}\eta^{3^{k+1}}-2u^{3^{k+1}}\eta^{3}}{\eta^{(3^{2m}+3^{k+1}+2)/2}}\\ &=&-2u^{3}\left( \eta^{\frac{3^{2m}+3^{k+1}-4}{2}}+\left( \frac{u^{2}}{\eta}\right)^{\frac{3^{2m}+3^{k+1}-4}{2}}\right)=\gamma \end{array} $$

  (5)

  since $\eta ,u\in \mathbb {F}_{3^{2m}}^{*}$. Note that $\gcd (\frac {3^{2m}+3^{k+1}-4}{2},3^{2m}-1)=\gcd (\frac {3^{k+1}-3}{2},3^{2m}-1)=1$. Similarly, we can show that (2) has at most one solution of z.

• (ii) Since v ₂(k) ≥ v ₂(2m), we get k is even and p ^k ≡ 1(mod 4), which means that $\frac {p^{k}+1}{2}$ and $\frac {p^{2m}+p^{k+1}+p-1}{2}$ are both odd. If $s=\frac {p^{k}+1}{2}$, (3) turns to be

  $$\begin{array}{@{}rcl@{}} h_{1}\left( \eta+\frac{u^{2}}{\eta}+2u\right)&=&\frac{-(\eta-u)^{p^{k}+1}-(\eta+u)^{p^{k}+1}}{\eta^{(p^{k}+1)/2}}\\ &=&-2\left( \eta^{\frac{p^{k}+1}{2}}+\left( \frac{u^{2}}{\eta}\right)^{\frac{p^{k}+1}{2}}\right)=\gamma. \end{array} $$

  (6)

  From the known condition v ₂(k) ≥ v ₂(2m), we can deduce that $\frac {k}{\gcd (2m,k)}$ is even or both $\frac {k}{\gcd (2m,k)}$ and $\frac {2m}{\gcd (2m,k)}$ are odd. Then by Lemma 2, we obtain

  $$\gcd\left( \frac{p^{k}+1}{2},p^{2m}-1\right)=\frac{\gcd(p^{k}+1,p^{2m}-1)}{2}=1,$$

  which implies that (2) has at most one solution of z.

  If $s=\frac {p^{2m}+p^{k+1}+p-1}{2}$, (3) leads to

  $$\begin{array}{@{}rcl@{}} h_{1}\left( \eta+\frac{u^{2}}{\eta}+2u\right)&=&\frac{-(\eta-u)^{p^{k+1}+p}-(\eta+u)^{p^{k+1}+p}}{\eta^{(p^{2m}+p^{k+1}+p-1)/2}}\\ &=&-2\left( \eta^{\frac{p^{2m}+p^{k+1}+p-1}{2}}+\left( \frac{u^{2}}{\eta}\right)^{\frac{p^{2m}+p^{k+1}+p-1}{2}}\right)=\gamma \end{array} $$

  (7)

  since $\eta ,u\in \mathbb {F}_{p^{2m}}^{*}$. It can be checked that

  $$\gcd\left( \frac{p^{2m}+p^{k+1}+p-1}{2},p^{2m}-1\right)=\gcd\left( \frac{p^{k+1}+p}{2},p^{2m}-1\right)=1.$$

  This implies that (2) has at most one solution of z.

□

Remark 2

It is clear that the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$ can be denoted as the following simpler way

$$S=\{t\in\mathbb{F}_{p^{2m}}|t=a^{p^{m}}-a, a\in\mathbb{F}_{p^{2m}}\}.$$

4 Some classes of PPs over $\mathbb {F}_{p^{2m}}$ with exponents s = i p ^j(p ^m + 1) + p ^j or i p ^j(p ^m + 1) + 2p ^j

In this section, we present some new classes of permutation polynomials $f(x)=(x^{p^{m}}-x+\delta )^{s}+x+x^{p^{m}}$ over $\mathbb {F}_{p^{2m}}$ with exponents s = i p ^j(p ^m + 1) + p ^j or i p ^j(p ^m + 1) + 2p ^j, where $\delta \in \mathbb {F}_{p^{2m}}$. By Proposition 2, we just need to prove the case of j = 0 in the sequel. Firstly, we give some lemmas needed later.

Lemma 3

[14] For an odd prime p and a positive integer m, if $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }=0$ , then the polynomial $f(x)=(x^{p^{m}}-x+\delta )^{i(p^{m}+1)+1}+x^{p^{m}}+x$ permutes $\mathbb {F}_{p^{2m}}$ , where the integer i satisfies 0 < i < p ^m − 1and $\gcd (1+2i,p^{m}-1)=1$ .

Lemma 4

Let i be an integer and $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . The polynomial $f(x)=(x^{p^{m}}-x+\delta )^{i(p^{m}+1)+1}+x^{p^{m}}+x$ permutes $\mathbb {F}_{p^{2m}}$ if and only if the polynomial $g(x)=(x^{p^{m}}-x+\delta )^{i(p^{m}+1)+2}+x^{p^{m}}+x$ permutes $\mathbb {F}_{p^{2m}}$ .

Proof

According to Proposition 1, the polynomial f(x) permutes $\mathbb {F}_{p^{2m}}$ if and only if

$$\begin{array}{@{}rcl@{}} h_{1}(t)&=&(-t+\overline{\delta})^{i(p^{m}+1)+1}-(t+\delta)^{i(p^{m}+1)+1}\\ &=&(-t+\overline{\delta})^{i}(t+\delta)^{i}(-t+\overline{\delta}-(t+\delta))\\ &=&(-t^{2}+(\overline{\delta}-\delta)t+\overline{\delta}\delta)^{i}(-2t+\overline{\delta}-\delta) \end{array} $$

(8)

is a bijection over the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$. Similarly, the polynomial g(x) permutes $\mathbb {F}_{p^{2m}}$ if and only if

$$\begin{array}{@{}rcl@{}} h_{2}(t)&=&(-t+\overline{\delta})^{i(p^{m}+1)+2}-(t+\delta)^{i(p^{m}+1)+2}\\ &=&(-t+\overline{\delta})^{i}(t+\delta)^{i}((-t+\overline{\delta})^{2}-(t+\delta)^{2})\\ &=&(-t^{2}+(\overline{\delta}-\delta)t+\overline{\delta}\delta)^{i}(-2t+\overline{\delta}-\delta)(\overline{\delta}+\delta). \end{array} $$

(9)

is a bijection on S. Since $\delta +\overline {\delta }\neq 0$, the mappings of (8) and (9) are linear equivalent. This completes the proof. □

Lemma 5

Let i be an integer and $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . The polynomial $f(x)=(x^{p^{m}}-x+\delta )^{i(p^{m}+1)+1}+x^{p^{m}}+x$ permutes $\mathbb {F}_{p^{2m}}$ if the polynomial

$$ h^{\prime}(\lambda)=\lambda(\lambda^{2}-c^{2})^{i} $$

(10)

permutes $\mathbb {F}_{p^{m}}$for any $c\in \mathbb {F}_{p^{2m}}^{*}$with $c+c^{p^{m}}=0$.

Proof

As stated in Lemma 4, the polynomial f(x) permutes $\mathbb {F}_{p^{2m}}$ if and only if

$$h_{1}(t)=(-t^{2}+(\overline{\delta}-\delta)t+\overline{\delta}\delta)^{i}(-2t+\overline{\delta}-\delta)$$

is a bijection on the set $S=\{t\in \mathbb {F}_{p^{2m}}|t^{p^{m}}+t=0\}$.

If $\delta =\overline {\delta }$, then h ₁(t) = −2t(−t ² + δ ²)ⁱ. Assume 𝜃 ∈ S with 𝜃 ≠ 0. The mapping Φ : z↦𝜃 z from $\mathbb {F}_{p^{m}}$ to S is a bijection. Let t = 𝜃 z for $z\in \mathbb {F}_{p^{m}}$. The mapping h ₁(t) can be rewritten as

$$h_{1}(\theta z)=-2\theta z(-\theta^{2}z^{2}+\delta^{2})^{i}=(-1)^{i+1} 2\theta^{1+2i} z(z^{2}-\theta^{-2}\delta^{2})^{i}.$$

Note that h ₁(t) is a bijection over S if and only if the mapping

$$h_{1}^{\prime}(z)=z(z^{2}-\theta^{-2}\delta^{2})^{i}$$

is a bijection on $\mathbb {F}_{p^{m}}$. Since $\delta +\overline {\delta }\neq 0$, we have δ ≠ 0. Then 𝜃 ⁻¹ δ ≠ 0 and $\theta ^{-1}\delta +(\theta ^{-1}\delta )^{p^{m}}=0$.

If $\delta \neq \overline {\delta }$, the mapping ${\Phi }_{1}: z\longmapsto (\delta -\overline {\delta })z$ from $\mathbb {F}_{p^{m}}$ to S is a bijection. Let $t=(\delta -\overline {\delta })z$ for $z\in \mathbb {F}_{p^{m}}$. The mapping h ₁(t) turns to be

$$h_{1}((\delta-\overline{\delta})z)=(\delta-\overline{\delta})(-1)^{i+1} ((\delta-\overline{\delta})^{2}z^{2}+(\delta-\overline{\delta})^{2}z-\overline{\delta}\delta)^{i}(2z+1).$$

Since $\delta +\overline {\delta }\neq 0$, h ₁(t) is a bijection on S if and only if the mapping

$$h_{2}^{\prime}(z)=\left( z^{2}+z-\frac{\overline{\delta}\delta}{(\delta-\overline{\delta})^{2}}\right)^{i}(2z+1)$$

permutes $\mathbb {F}_{p^{m}}$. Let λ = 2z + 1. Then $\lambda \in \mathbb {F}_{p^{m}}$ and $h_{2}^{\prime }(z)$ is affine equivalent to the following mapping

$$h^{\prime\prime}(\lambda)=\lambda\left( \frac{\lambda^{2}-1}{4}-\frac{\overline{\delta}\delta}{(\delta-\overline{\delta})^{2}}\right)^{i} =\left( \frac{1}{4}\right)^{i} \lambda\left( \lambda^{2}-\left( \frac{\delta+\overline{\delta}}{\delta-\overline{\delta}}\right)^{2}\right)^{i}$$

over $\mathbb {F}_{p^{m}}$. It can be easily check that $\frac {\delta +\overline {\delta }}{\delta -\overline {\delta }}\neq 0$ and $\frac {\delta +\overline {\delta }}{\delta -\overline {\delta }}+(\frac {\delta +\overline {\delta }}{\delta -\overline {\delta }})^{p^{m}}=0$.

If the polynomial h ^′(λ) = λ(λ ² − c ²)ⁱ permutes $\mathbb {F}_{p^{m}}$ for any $c\in \mathbb {F}_{p^{2m}}^{*}$ with $c+c^{p^{m}}=0$, then $h_{1}^{\prime }(z)$ and h ^″(λ) are both permutations on $\mathbb {F}_{p^{m}}$. Hence the proof is finished. □

Lemma 6

[14] For $a,b\in \mathbb {F}_{p^{m}}$ , the equation x ^p − a x + b = 0has the unique solution in $\mathbb {F}_{p^{m}}$ if and only if a = 0or a is not a (p − 1)power in $\mathbb {F}_{p^{m}}^{*}$ .

Lemma 7

[11] Let p be an odd prime and k be a positive integer. Then $f(x)=x(x^{2}-t)^{\frac {p-1}{2}}$ is a permutation polynomial over $\mathbb {F}_{p^{k}}$ , where t is a non-square element in $\mathbb {F}_{p^{k}}$ .

Lemma 8

Let $c\in \mathbb {F}_{p^{2m}}^{*}$ with $c+c^{p^{m}}=0$ . Then $c^{2}\in \mathbb {F}_{p^{m}}$ and c ² is not a square in $\mathbb {F}_{p^{m}}$ .

Proof

Since $c\in \mathbb {F}_{p^{2m}}^{*}$ with $c+c^{p^{m}}=0$, we get $c^{p^{m}-1}=-1$, which implies that $c^{2p^{m}-2}=1$. It follows that $c^{2p^{m}}=c^{2}$, i.e., $c^{2}\in \mathbb {F}_{p^{m}}$.

If c ² is a square in $\mathbb {F}_{p^{m}}$, then we have $c\in \mathbb {F}_{p^{m}}$. From $c+c^{p^{m}}=0$ we get c = 0, which is a contradiction. □

With the above preparations, we have the following results by determining the permutation behavior of the polynomial in (10).

Theorem 4

Let $\delta \in \mathbb {F}_{p^{2m}}$ . The polynomial

$$f(x)=(x^{p^{m}}-x+\delta)^{(\frac{p-1}{2}\cdot p^{m}+\frac{p+1}{2})\cdot p^{j}}+x^{p^{m}}+x$$

permutes$\mathbb {F}_{p^{2m}}$.

Proof

The exponent $s=\frac {p-1}{2}\cdot p^{m}+\frac {p+1}{2}=\frac {p-1}{2}(p^{m}+1)+1$ implies $i=\frac {p-1}{2}$. Since $\gcd (1+2i,p^{m}-1)=1$, if $\delta +\overline {\delta }=0$, we get that f(x) is a permutation over $\mathbb {F}_{p^{2m}}$ by Lemma 3. Below we consider the case of $\delta +\overline {\delta }\neq 0$.

For any $c\in \mathbb {F}_{p^{2m}}^{*}$ with $c+c^{p^{m}}=0$, from Lemma 8 we have that $c^{2}\in \mathbb {F}_{p^{m}}$ and c ² is not a square in $\mathbb {F}_{p^{m}}$. By Lemma 7, we get that $h^{\prime }(\lambda )=\lambda (\lambda ^{2}-c^{2})^{\frac {p-1}{2}}$ is a permutation polynomial over $\mathbb {F}_{p^{m}}$. Then the desired conclusion of this theorem follows from Lemma 5. □

According to Lemma 4 and Theorem 4, we get the following corollary directly.

Corollary 1

Let $\delta \in \mathbb {F}_{p^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . The polynomial

$$f(x)=(x^{p^{m}}-x+\delta)^{(\frac{p-1}{2}\cdot p^{m}+\frac{p+3}{2})\cdot p^{j}}+x^{p^{m}}+x$$

permutes$\mathbb {F}_{p^{2m}}$.

Theorem 5

Let $\delta \in \mathbb {F}_{3^{2m}}$ . The polynomial

$$f(x)=(x^{3^{m}}-x+\delta)^{\frac{(3^{2m}+2\cdot3^{m}+3)\cdot 3^{j}}{2}}+x^{3^{m}}+x$$

permutes$\mathbb {F}_{3^{2m}}$.

Proof

The exponent

$$s=\frac{3^{2m}+2\cdot3^{m}+3}{2}=\frac{3^{m}+1}{2}(3^{m}+1)+1$$

implies $i=\frac {3^{m}+1}{2}$. Since $\gcd (1+2i,3^{m}-1)=1$, by Lemma 3 we get that f(x) is a permutation over $\mathbb {F}_{3^{2m}}$ if $\delta +\overline {\delta }=0$. Next we consider the case of $\delta +\overline {\delta }\neq 0$.

By Lemma 5, we need to prove that h ^′(λ) permutes $\mathbb {F}_{3^{m}}$. It is sufficient to prove that for any $\gamma \in \mathbb {F}_{3^{m}}$, the equation

$$ \lambda(\lambda^{2}-c^{2})^{\frac{3^{m}+1}{2}}=\gamma $$

(11)

has at most one solution for any $c\in \mathbb {F}_{3^{2m}}^{*}$ with $c+c^{3^{m}}=0$. Squaring both sides of (11) gives

$$\lambda^{2}(\lambda^{2}-c^{2})^{2}=\gamma^{2}.$$

The above equation leads to

$$\lambda^{3}-c^{2} \lambda=\gamma$$

or

$$\lambda^{3}-c^{2} \lambda=-\gamma.$$

It follows from Lemma 8 that $c^{2}\in \mathbb {F}_{3^{m}}$ and c ² is not a square in $\mathbb {F}_{3^{m}}$. By Lemma 6 the above two equations have one solution λ ₁ and λ ₂ respectively, where λ ₁ = −λ ₂. If γ = 0, we get λ ₁ = λ ₂ = 0. If γ ≠ 0, it can be verified that λ ₁ and λ ₂ are not the solutions of (11) simultaneously. That is to say, there is at most one solution λ of (11). The proof is completed. □

A direct consequence of Lemma 4 and Theorem 5 is the following.

Corollary 2

Let $\delta \in \mathbb {F}_{3^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . The polynomial

$$f(x)=(x^{3^{m}}-x+\delta)^{\frac{(3^{2m}+2\cdot3^{m}+5)\cdot 3^{j}}{2}}+x^{3^{m}}+x$$

permutes$\mathbb {F}_{3^{2m}}$.

Theorem 6

Let $\delta \in \mathbb {F}_{3^{2m}}$ . The polynomial

$$f(x)=(x^{3^{m}}-x+\delta)^{(2\cdot3^{2m-1}-3^{m-1})\cdot 3^{j}}+x^{3^{m}}+x$$

permutes$\mathbb {F}_{3^{2m}}$.

Proof

The exponent

$$s=2\cdot3^{2m-1}-3^{m-1}=(2\cdot3^{m-1}-1)(3^{m}+1)+1$$

implies i = 2 ⋅ 3^m−1 − 1. Since $\gcd (1+2i,3^{m}-1)=\gcd (3^{m}+3^{m-1}-1,3^{m}-1)=1$, by Lemma 3 we have that f(x) is a permutation over $\mathbb {F}_{3^{2m}}$ if $\delta +\overline {\delta }=0$.

Now we discuss the case of $\delta +\overline {\delta }\neq 0$. By Lemma 5, it suffices to prove that for each $\gamma \in \mathbb {F}_{3^{m}}$, the equation

$$ \lambda(\lambda^{2}-c^{2})^{2\cdot3^{m-1}-1}=\gamma $$

(12)

has a unique solution for any $c\in \mathbb {F}_{3^{2m}}^{*}$ with $c+c^{3^{m}}=0$. According to Lemma 8, $c^{2}\in \mathbb {F}_{p^{m}}$ and c ² is not a square in $\mathbb {F}_{p^{m}}$. If γ = 0, then λ = 0 is the unique solution of (12) since c ² is not a square in $\mathbb {F}_{3^{m}}$. If γ ≠ 0, then λ ≠ 0 and λ ² − c ²≠0. Raising both sides of (12) to the third powers gives

$$\lambda^{3}(\lambda^{2}-c^{2})^{-1}=\gamma^{3},$$

which implies that

$$ \left( \frac{1}{\lambda}\right)^{3}-c^{-2} \frac{1}{\lambda}=-\gamma^{-3}c^{-2}. $$

(13)

According to Lemma 6, there is exactly one solution λ of (13). We complete the proof. □

An immediate consequence of Lemma 4 and Theorem 6 is the following result.

Corollary 3

Let $\delta \in \mathbb {F}_{3^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . The polynomial

$$f(x)=(x^{3^{m}}-x+\delta)^{(2\cdot3^{2m-1}-3^{m-1}+1)\cdot 3^{j}}+x^{3^{m}}+x$$

permutes$\mathbb {F}_{3^{2m}}$.

Theorem 7

Let $\delta \in \mathbb {F}_{3^{2m}}$ . The polynomial

$$f(x)=(x^{3^{m}}-x+\delta)^{\frac{(3^{2m}-2\cdot3^{m}+3)\cdot 3^{j}}{6}}+x^{3^{m}}+x$$

permutes$\mathbb {F}_{3^{2m}}$.

Proof

The exponent

$$s=\frac{3^{2m}-2\cdot3^{m}+3}{6}=\frac{3^{m}-3}{6}(3^{m}+1)+1$$

implies $i=\frac {3^{m}-3}{6}$. Since $\gcd (1+2i,3^{m}-1)=\gcd (3^{m},3^{m}-1)=1$, as stated before, f(x) is a permutation over $\mathbb {F}_{3^{2m}}$ if $\delta +\overline {\delta }=0$.

Assume $\delta +\overline {\delta }\neq 0$. By Lemma 5, for any $\gamma \in \mathbb {F}_{3^{m}}$ we need to show that the equation

$$ \lambda(\lambda^{2}-c^{2})^{\frac{3^{m}-3}{6}}=\gamma $$

(14)

has at most one solution for any $c\in \mathbb {F}_{3^{2m}}^{*}$ with $c+c^{3^{m}}=0$. By Lemma 8 we have that $c^{2}\in \mathbb {F}_{3^{m}}$ is not a square in $\mathbb {F}_{3^{m}}$. Similarly as the proof of Theorem 6, there is a unique solution of (14) when γ = 0. Next we suppose γ ≠ 0. It leads to λ ≠ 0. Taking the sixth powers on both sides of (14), we obtain

$$ \lambda^{6}(\lambda^{2}-c^{2})^{-2}=\gamma^{6}. $$

(15)

We can deduced that

$$\lambda^{3}=\gamma^{3} c^{2}-\gamma^{3}\lambda^{2}$$

or

$$\lambda^{3}=-\gamma^{3} c^{2}+\gamma^{3}\lambda^{2},$$

which implies that

$$ \left( \frac{1}{\lambda}\right)^{3}-c^{-2}\left( \frac{1}{\lambda}\right)=\gamma^{-3}c^{-2} $$

(16)

or

$$ \left( \frac{1}{\lambda}\right)^{3}-c^{-2}\left( \frac{1}{\lambda}\right)=-\gamma^{-3}c^{-2}. $$

(17)

Then by Lemma 6, we get that (16) and (17) have one solution λ ₁ and λ ₂ respectively, where λ ₁ = −λ ₂≠0. It can be verified that λ ₁ and λ ₂ are not the solutions of (14) simultaneously. That is to say, there is at most one solution λ of (14). The proof is finished. □

Similarly, we can deduce the following result by Lemma 4 and Theorem 7.

Corollary 4

Let $\delta \in \mathbb {F}_{3^{2m}}$ with $\delta +\overline {\delta }\neq 0$ . The polynomial

$$f(x)=(x^{3^{m}}-x+\delta)^{\frac{(3^{2m}-2\cdot3^{m}+9)\cdot 3^{j}}{6}}+x^{3^{m}}+x$$

permutes$\mathbb {F}_{3^{2m}}$.

5 Conclusion

In this paper, we continued the work in [9, 14, 16, 19, 24] and proposed several new classes of permutation polynomials $f(x)=(x^{p^{m}}-x+\delta )^{s}+x^{p^{m}}+x$ over $\mathbb {F}_{p^{2m}}$ for some $\delta \in \mathbb {F}_{p^{2m}}$ by using the AGW criterion. Note that the AGW criterion can be used to investigate the permutation behavior of more explicit polynomials of the form $(x^{p^{m}}+ax+\delta )^{s}+bx^{p^{m}}+cx$ over $\mathbb {F}_{p^{2m}}$, where s is an integer and $a,b,c,\delta \in \mathbb {F}_{p^{2m}}$.