Analytical solution of thermally developing heat transfer in circular and parallel plates microchannels

Abstract

The heat transfer characteristics of the thermally developing flow in the circular and parallel plates microchannels under the constant wall temperature and the constant heat flux are studied analytically. The energy equations are solved by using the separation of variables combined with the Gram–Schmidt orthogonalization. The effect of the number of eigenvalues on the calculation accuracy of the local Nusselt number is first determined. The temperature distribution and the heat transfer coefficient at the entrance region are calculated considering the effects of the rarefaction (0 < Kn < 0.1) and the axial heat conduction (Pe > 50). It is found that the axial heat conduction can dramatically improve the heat transfer of the thermally developing flow when the Peclet number is less than 250. But when the Peclet number is greater than 500, the effect of the axial heat conduction can be omitted. Enhancing the rarefaction would weaken the influence of the axial heat conduction on the heat transfer, and the difference of the local Nusselt number between the two boundary conditions decreases as increasing Kn. Enhancing fluid axial heat conduction would increase the thermal entrance length. The thermal entrance length of the microtube is 3–4 times that of the parallel plates microchannel, and the correlations of the thermal entrance lengths are developed, which may provide guidance for thermal design and optimization of microchannel heat sinks.

1 Introduction

With the development of the modern micro-electro-mechanical system and the continuous improvement of packaging density, the heat dissipation requirements of nano-scale chips in conventional microelectronic devices have reached 10 MW/m². Such a large amount of heat dissipation puts forward higher requirements on the thermal management system. It is necessary to configure the best cooling system to ensure the device operates properly and prolong the cycle life of the device. While conventional heat exchangers are cumbersome and cannot handle such high heat flux density. The microchannel heat exchanger emerges as the engineering requires. The tiny size is a distinguishing feature of microchannels. The Knudsen number Kn, defined as the ratio of the mean free path λ to the length scale characteristic D_h [1], increases as the characteristic length decreases. As 0.001<Kn<0.1, the well-known Navier–Stokes equations are still appropriate for the fluid, but velocity slip and temperature jump boundary conditions are required to modify the fluid-solid interface.

When the channel is short in mini-structured devices, the entrance effect has to be taken into account. The heat transfer capacity of the thermally developing flow in a channel is significantly higher than that of the fully developed region because of the entrance effect. The convective heat transfer problem of the thermally developing flow in a channel is also named Graetz problem [2]. Shah and London [3] summarized plentiful results about the Graetz problem in various macro channels. In 1997, Barron et al [4] first extended the problem to include the effects of slip flow through the microtube (CM) with the constant wall temperature by using the Frobenius series method [5]. They found the Nusselt number increases as the Knudsen number, meaning that the rarefaction effect in the microchannel enhances the heat transfer, which is different from other results [6,7,8,9]. Larrode et al [7] and Tunc and Bayazitoglu [8] pointed out that the rarefaction effect weakens the heat transfer performance, and the results in Barron et al [4] are due to ignoring the temperature jump boundary condition during the calculation. Therefore, the flow and heat transfer characteristics in the microchannel still meet the Reynolds analogy [10, 11].

The velocity profile is fully developed for the Graetz problem. The problem of the thermally developing flow can be thus solved with some theoretical methods. Apart from the aforementioned series method, some other methods are also applied to study the Graetz problem. Chalhub et al [12] obtained the solution of the extended Graetz problem in isothermal parallel plates microchannels (PPM) based on the Generalized Integral Transform Technique. They considered the effects of the axial conduction and the rarefaction on the local Nusselt number and found the influence of the axial conduction declined as increasing the rarefaction. Haddout et al [13] also studied a similar problem in both CM and PPM. They degraded the energy equation into two first-order partial differential equations by using the self-adjoint formalism and indicated that the local Nusselt number was strongly influenced by the Peclet and Knudsen numbers. What’s more, the separation of variables was often employed to settle the extended Graetz problem [14, 15].

Nevertheless, it is worth noting that the influence of the axial fluid heat conduction, characterized by the Peclet number Pe, on the heat transfer performance of the thermally developing flow in microchannels was often ignored in most of the above analytical results. Many studies about the thermally developing flow were also based on the assumption of ignoring the axial heat conduction [16,17,18,19,20,21,22,23,24]. While the axial heat conduction even dominates the heat transfer process when the Peclet number is low enough [25,26,27,28]. However, it is not clear when the axial heat conduction should be considered. Tada and Ichimiya [29] pointed out that the effect of the axial heat conduction can be neglected when Pe>200. But Renksizbulut and Niazmand [30] demonstrated that the local Nusselt number was independent of Pe when Pe>50. Avci and Aydin [31] found that the axial heat conduction had little effect on heat transfer when Pe>5. While some investigations showed that the influence of the axial heat conduction on the convective heat transfer was obvious when Pe<100 [32,33,34,35,36,37,38,39,40,41,42,43]. The inconsistent results indicate that the importance of the axial heat conduction on heat transfer of the developing flow remains to be further determined.

The objective of this work is to determine the impacts of the axial heat conduction (Pe>50) and rarefaction (0<Kn<0.1) on forced convection heat transfer in both CM and PPM. The motivation is to figure out the criteria for ignoring or considering the effect of axial conduction in microchannels. Two types of thermal boundary conditions, namely constant wall temperature and constant heat flux, are taken into consideration. The energy equation is solved by using the separation of variables. The effect of the number of eigenvalues on the calculation accuracy of the local Nusselt number is first investigated. The Gram–Schmidt orthogonalization is utilized to solve the nonorthogonal boundary problems caused by considering the axial heat conduction. The heat transfer performance under different thermal boundary conditions is also compared. The thermal entrance lengths of different microchannels with different boundary conditions are also calculated, which may provide the guideline for the design of microchannel heat sinks.

2 Analysis

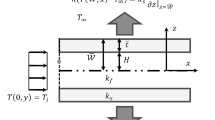
The velocity is fully developed for the Graetz problem as illustrated in figure 1 and the flow chart of the analytical solution is shown in figure 2. For laminar flow, the general form of the energy equation is expressed as follows [44]

$$ \rho c_{p} \frac{DT}{{Dt}} = \nabla \cdot \left( {\kappa \nabla T} \right) + Q + \beta T\frac{DP}{{Dt}} + \mu \Phi $$

(1)

where Q is internal heat generation, β is the coefficient of thermal expansion, μ is the dynamic viscosity, ρ is the density, c_p is the specific heat, κ is the thermal conductivity and Φ is the viscous dissipation function. The viscous dissipation can be ignored with the huge heat flux and small dynamic viscosity of air in the present work. With the assumption of ignoring the effects of viscous dissipation, natural convection, and radiation heat transfer, the energy equation of constant thermophysical properties and incompressible Newtonian fluid without internal heat generation in parallel plates and circular tubes can be simplified to

$$ \rho c_{p} u\frac{\partial T}{{\partial x}} = \kappa \left[ {\frac{1}{{r^{p} }}\frac{\partial }{\partial n}\left( {r^{p} \frac{\partial T}{{\partial n}}} \right) + \frac{{\partial^{2} T}}{{\partial x^{2} }}} \right] $$

(2)

Figure 1

Schematic diagram and coordinate system.

Figure 2

Flow chart of the analytical solution.

The geometry factor p (or n) is 0 (or y) in PPM and 1 (or r) in CM. Before solving the energy equation, defining the following non-dimensional quantities,

$$ \begin{aligned} {\text{CM}}:\quad A = \sqrt {\frac{1}{{1 + 4Kn_{u} }}} ,\;X = \frac{{A^{2} \left( {2 - A^{2} } \right)x}}{{r_{\it{o}} Pe}},\;Y = \frac{n}{{r_{o} }}A,\\\quad\overline{Pe} = \frac{Pe}{{A\left( {2 - A^{2} } \right)}} \\ {\text{PPM}}:\quad A = 1 + 12Kn_{u} ,\;B = \frac{{1 + 8Kn_{u} }}{{A^{2} }},\;Y = \frac{n}{Ab},\\ \quad\overline{Pe} = \frac{3}{8}PeA^{2} \\ \end{aligned} $$

(3)

where Kn_u, defined as Kn(2–σ_v)/σ_v, is the modified Knudsen number [45] and the corresponding tangential momentum accommodation coefficient σ_v is set as unity in this paper. Based on these non-dimensional quantities, Eq. (2) is transformed into

$$ \left( {B^{1 - p} - Y^{2} } \right)\frac{\partial \theta }{{\partial X}} = \frac{1}{{Y^{p} }}\frac{\partial }{\partial Y}\left( {Y^{p} \frac{\partial \theta }{{\partial Y}}} \right) + \frac{1}{{\overline{Pe}^{2} }}\frac{{\partial^{2} \theta }}{{\partial X^{2} }} $$

(4)

where θ is the no-dimensional temperature and defined as

$$ \theta { = }\left\{ {\begin{array}{*{20}c} {\frac{{T - T_{{{\text{in}}}} }}{{{{D_{h} q} \mathord{\left/ {\vphantom {{D_{h} q} \kappa }} \right. \kern-\nulldelimiterspace} \kappa }}}} & {constant\;heat\;flux} \\ {\frac{{T - T_{{\text{w}}} }}{{T_{{{\text{in}}}} - T_{{\text{w}}} }}} & {constant\;wall\;temperature} \\ \end{array} } \right. $$

(5)

where T_in is the inlet temperature of the working medium.

2.1 Constant heat flux

The non-dimensional boundary conditions for the constant heat flux are as follows

$$ \theta \left( {0,Y} \right) = 0 $$

(6)

$$ \theta \left( {\infty ,Y} \right) = \theta_{\infty } $$

(7)

$$ \left. {\frac{\partial \theta }{{\partial Y}}} \right|_{Y = 0} = 0 $$

(8)

$$ \left. {\frac{\partial \theta }{{\partial Y}}} \right|_{{Y = A^{2p - 1} }} = 1 $$

(9)

where θ_∞ is the no-dimensional temperature in the fully developed region. As Eq. (4) is a linear equation, according to the superposition principle, we have

$$ \theta { = }\overline{\theta } + \theta_{\infty } $$

(10)

For the new variable $\overline{\theta }$, the corresponding equation and the boundary conditions are

$$ \left( {B^{1 - p} - Y^{2} } \right)\frac{{\partial \overline{\theta }}}{\partial X} = \frac{1}{{Y^{p} }}\frac{\partial }{\partial Y}\left( {Y^{p} \frac{{\partial \overline{\theta }}}{\partial Y}} \right) + \frac{1}{{\overline{Pe}^{2} }}\frac{{\partial^{2} \overline{\theta }}}{{\partial X^{2} }} $$

(11)

$$ \overline{\theta }\left( {0,Y} \right) = - \theta_{\infty } $$

(12)

$$ \overline{\theta }\left( {\infty ,Y} \right) = 0 $$

(13)

$$ \left. {\frac{{\partial \overline{\theta }}}{\partial Y}} \right|_{Y = 0} = 0 $$

(14)

$$ \left. {\frac{{\partial \overline{\theta }}}{\partial Y}} \right|_{{Y = A^{2p - 1} }} = 0 $$

(15)

Due to the homogeneous boundary conditions in the Y direction, the equation has an infinite series solution of the following form

$$ \overline{\theta } = \sum\limits_{n = 1}^{\infty } {C_{n} e^{{ - \lambda_{n}^{2} X}} \phi_{n} } \left( Y \right) $$

(16)

where C_n, $\lambda_{n}^{2}$, $\phi_{n} (Y)$ are the coefficients, eigenvalues, and eigenfunctions respectively. Substituting Eq. (16) into Eqs. (11), (14), and (15) yields

$$ \frac{1}{{Y^{p} }}\frac{{\text{d}}}{{{\text{d}}Y}}\left( {Y^{p} \frac{{{\text{d}}\phi_{n} }}{{{\text{d}}Y}}} \right) + \left( {B^{1 - p} - Y^{2} + \frac{1}{{\overline{Pe}^{2} }}\lambda_{n}^{2} } \right)\lambda_{n}^{2} \phi_{n} = 0 $$

(17)

$$ \left. {\frac{{{\text{d}}\phi_{n} }}{{{\text{d}}Y}}} \right|_{Y = 0} = 0 $$

(18)

$$ \left. {\frac{{{\text{d}}\phi_{n} }}{{{\text{d}}Y}}} \right|_{{Y = A^{2p - 1} }} = 0 $$

(19)

In order to solve Eq. (17), choosing $\eta = \lambda_{n} Y^{2}$, $\omega (\eta ){ = }e^{{\frac{\eta }{2}}} \phi_{n} (\eta )$ gives

$$ \eta \frac{{{\text{d}}^{2} \omega }}{{{\text{d}}\eta^{2} }} + \left( {\frac{p + 1}{2} - \eta } \right)\frac{{{\text{d}}\omega }}{{{\text{d}}\eta }} + \left( {B^{1 - p} \lambda_{n} - p - 1 + \frac{{\lambda_{n}^{3} }}{{Pe^{2} }}} \right)\frac{\omega }{4} = 0 $$

(20)

$$ \left( { - \frac{\omega }{2} + \frac{{{\text{d}}\omega }}{{{\text{d}}\eta }}} \right)_{{\eta = \lambda_{n} A^{4p - 2} }} = 0 $$

(21)

Equation (20) is a confluence hypergeometric equation, also known as the Kummer’s equation [46]. The eigenvalues can be obtained by solving Eq. (21) with the characteristic of the Kummer’s equation. Equation. (21) is then transformed into

$$ \frac{4a}{{1 + p}}F\left( {a + 1,c + 1,z} \right) = F\left( {a,c,z} \right) $$

(22)

where the term F(a,c,z) is the Kummer’s confluent hypergeometric function and the related parameters are as follows

$$ a = \frac{1 + p}{4} - \frac{{\lambda_{n}^{3} }}{{4\overline{Pe}^{2} }} - \frac{{B^{1 - p} \lambda_{n} }}{4} $$

(23)

$$ c = \frac{1 + p}{2} $$

(24)

$$ z = \lambda_{n} A^{4p - 2} $$

(25)

$\lambda_{n}^{2}$ can be acquired by solving Eq. (22) using the FindRoot command in Mathematica. But when it comes to solving the coefficients C_n, it is necessary to discuss the orthogonality of $\phi_{n} (Y)$.

For the case Pe → ∞, namely ignoring the influence of the axial heat conduction, $\phi_{n} (Y)$ are mutually orthogonal and C_n can be calculated as follows

$$ C_{n} = \frac{{\int_{0}^{{A^{2p - 1} }} { - \theta_{\infty } \left( {B^{1 - p} - Y^{2} } \right)\phi_{n} Y^{p} {\text{d}}Y} }}{N\left( \phi \right)} $$

(26)

where the normalization integrals $N(\phi )$ is expressed as

$$ N\left( \phi \right) = \int_{0}^{{A^{2p - 1} }} {\left( {B^{1 - p} - Y^{2} } \right)\phi_{n}^{2} Y^{p} {\text{d}}Y} $$

(27)

Therefore, for CM,

$$ C_{{n,{\text{c}}}} = \frac{{\left( {2A^{2} - A^{4} } \right)\phi \left( A \right)}}{{\lambda_{n}^{2} A^{2} \left( {A^{2} - 2} \right)N\left( \phi \right)}} $$

(28)

For PPM,

$$ C_{{n,{\text{p}}}} = \frac{{\left( {1 - 3A^{2} B} \right)\phi_{n} \left( {A^{ - 1} } \right)}}{{2\lambda_{n}^{2} N\left( \phi \right)}} $$

(29)

However, $\phi_{n} (Y)$ are not mutually orthogonal when considering the axial heat conduction. For this case, the Gram-Schmidt orthogonal procedure is employed to fulfill the orthogonalization process. The steps of the orthogonal procedure are shown in “Appendix A”.

After determining C_n, $\lambda_{n}^{2}$, $\phi_{n} (Y)$, the temperature distribution and the local Nusselt number are also determined. For CM,

$$ Nu\left( x \right)_{{\text{c}}} = \frac{2}{{\sum\limits_{n = 1}^{\infty } {F_{{n,{\text{c}}}} e^{{ - 2A^{2} \left( {2 - A^{2} } \right)\lambda_{n}^{2} x^{*}}} } + \frac{4\gamma }{{1 + \gamma }}\frac{{2 - \sigma_{T} }}{{\sigma_{T} Pr}}Kn + \frac{{3A^{4} - 16A^{2} + 24}}{{24\left( {2 - A^{2} } \right)^{2} }}}} $$

(30)

where

$$ F_{{n,{\text{c}}}} = C_{{n,{\text{c}}}} \left[ {\phi_{n} \left( A \right) - \frac{4}{{A^{2} \left( {2 - A^{2} } \right)}}\int_{0}^{A} {\left( {1 - Y^{2} } \right)\phi_{n} \left( Y \right)Y{\text{d}}Y} } \right] $$

(31)

$$ x^{*} = \frac{x}{{D_{h} Pe}} $$

(32)

For PPM,

$$ Nu\left( x \right)_{{\text{p}}} = \frac{4}{{\sum\limits_{n = 1}^{\infty } {F_{{n,{\text{p}}}} e^{{ - \lambda_{n}^{2} \frac{32x^{*}}{{3A^{3} }}}} } + \frac{8\gamma }{{1 + \gamma }}\frac{{2 - \sigma_{T} }}{{\sigma_{T} Pr}}Kn + \frac{2}{15A} + \frac{2}{{105A^{2} }} + \frac{1}{3}}} $$

(33)

where

$$ F_{{n,{\text{p}}}} = C_{{n,{\text{p}}}} \left[ {\phi_{n} \left( \frac{1}{A} \right) - \frac{{3A^{2} }}{2}\sum\limits_{n = 1}^{\infty } {e^{{ - \lambda_{n}^{2} X}} } \int_{0}^{\frac{1}{A}} {\left( {B - Y^{2} } \right)\phi_{n} \left( Y \right){\text{d}}Y} } \right] $$

(34)

2.2 Constant wall temperature

When the wall temperature T_w is given, the non-dimensional boundary conditions for the energy equation are as follows

$$ \theta \left( {0,Y} \right) = 1 $$

(35)

$$ \theta \left( {\infty ,Y} \right) = \theta_{\infty } $$

(36)

$$ \left. {\frac{\partial \theta }{{\partial Y}}} \right|_{Y = 0} = 0 $$

(37)

$$ \theta \left( {X,A^{2p - 1} } \right) = k\left. {\frac{\partial \theta }{{\partial Y}}} \right|_{{Y = A^{2p - 1} }} $$

(38)

where k is defined as

$$ k = - \frac{{2^{3 - p} A^{2p - 1} \gamma }}{1 + \gamma }\frac{{2 - \sigma_{T} }}{{\sigma_{T} }}\frac{Kn}{{Pr}} $$

(39)

Equations (37) and (38) are the second and third homogeneous boundaries respectively. The energy equation with this kind of boundary has a solution of the following form

$$ \theta = \sum\limits_{n = 1}^{\infty } {C_{n} e^{{ - \lambda_{n}^{2} X}} \phi_{n} \left( Y \right)} $$

(40)

The eigenfunctions $\phi_{n} (Y)$ meet the following differential equation

$$ - \left( {B^{1 - p} - Y^{2} } \right)\lambda_{n}^{2} \phi_{n} = \frac{1}{{Y^{p} }}\frac{{\text{d}}}{{{\text{d}}Y}}\left( {Y^{p} \frac{{{\text{d}}\phi_{n} }}{{{\text{d}}Y}}} \right) + \frac{1}{{\overline{Pe}^{2} }}\lambda_{n}^{4} \phi_{n} $$

(41)

and the corresponding boundary conditions are

$$ \frac{{d\phi_{n} }}{dY} = 0 $$

(42)

$$ \phi_{n} \left( {A^{2p - 1} } \right) - k\left. {\frac{{d\phi_{n} }}{dY}} \right|_{{Y = A^{2p - 1} }} = 0 $$

(43)

Since the form of $\phi_{n} (Y)$ is similar to that under the constant heat flux, the Kummer equation can still be obtained through variable substitution, that is,

$$ \eta \frac{{{\text{d}}^{2} \omega }}{{{\text{d}}\eta^{2} }} + \left( {\frac{p + 1}{2} - \eta } \right)\frac{{{\text{d}}\omega }}{{{\text{d}}\eta }} + \left( {B^{1 - p} \lambda_{n} - p - 1 + \frac{{\lambda_{n}^{3} }}{{\overline{Pe}^{2} }}} \right)\frac{\omega }{4} = 0 $$

(44)

Solving the boundary conditions will obtain the eigenvalues, which can be expressed as

$$ \left( {\frac{1}{{A^{2p - 1} \lambda_{n} k}} + 1} \right)F\left( {a,c,z} \right) - \frac{4a}{{1 + p}}F\left( {a + 1,c + 1,z} \right) = 0 $$

(45)

C_n can be acquired by using the same procedure of that under the constant heat flux. Therefore, for CM, the local Nusselt number is

$$ Nu(x)_{{\text{c}}} = \frac{{ - A^{3} \left( {2 - A^{2} } \right)\sum\nolimits_{n = 1}^{\infty } {C_{n} \phi_{n} \left( {X,A} \right)e^{{ - 2A^{2} \left( {2 - A^{2} } \right)\lambda_{n}^{2} x^{*}}} } }}{{2k\sum\nolimits_{n = 1}^{\infty } {C_{n} e^{{ - 2A^{2} \left( {2 - A^{2} } \right)\lambda_{n}^{2} x^{*}}} \int_{0}^{A} {\left( {1 - Y^{2} } \right)\phi_{n} YdY} } }} $$

(46)

For PPM, the local Nusselt number is

$$ Nu(x)_{{\text{p}}} = \frac{{ - 8\sum\nolimits_{n = 1}^{\infty } {C_{n} \phi_{n} \left( {X,A} \right)e^{{ - \frac{32}{{3A^{3} }}\lambda_{n}^{2} x^{*}}} } }}{{3kA^{3} \sum\nolimits_{n = 1}^{\infty } {C_{n} e^{{ - \frac{32}{{3A^{3} }}\lambda_{n}^{2} x^{*}}} \int_{0}^{A} {\left( {1 - Y^{2} } \right)\phi_{n} YdY} } }} $$

(47)

3 Model validation

3.1 Number of eigenvalues

Note that there are infinite series in the expression of the local Nusselt number. But only limited eigenvalues need to be intercepted for the actual calculation. The number of eigenvalues that are a suitable compromise between the reasonable accuracy and solution cost needs to be determined. The number of eigenvalues mainly affects the local Nusselt number near the inlet, as shown in figure 3. When comparing the results in figure 3(a) and figure 3(b), it is found that the effect of N decreases as Kn increases. Because the entrance effect is not obvious when increasing the rarefaction effect. The maximum relative error between N = 15 and N = 20 in figure 3(a) is 0.44%, but the error between N = 15 and N = 20 in figure 3(c) is 3.37%, implying that the effect of N increases as Pe decreases. What’s more, it is obvious that more eigenvalues are required to calculate Nu(x) in CM from figure 3(a) and figure 3(d), and the maximum relative error between N = 20 and N = 25 in figure 3(d) is 1.58%. In this work, the first 20 eigenvalues are chosen to calculate Nu(x).

Figure 3

Effect of the number of eigenvalues on local Nusselt number with (a) Pe = ∞, Kn = 0, (b) Pe = ∞, Kn = 0.1, (c)Pe = 50, Kn = 0 in PPM; and with (d) Pe = ∞, Kn = 0 in CM.

3.2 Validation of Gram–Schmidt orthogonalization

In this work, the Gram–Schmidt orthogonalization was used to solve the heat transfer problem including the axial heat conduction. But the orthogonalization is an approximate method. The number of orthogonal functions needs to be determined during the orthogonalization. As the local Nusselt number can be obtained precisely when ignoring the axial heat conduction. We treated the analytical solution of Pe = ∞, Kn = 0 as a benchmark to verify the Gram–Schmidt orthogonalization, as shown in figure 4. What’s more, Shah and London [3] also summarized the results of the local Nusselt number in PPM with constant heat flux, which are also used to verify the results. The number of the orthogonal function also mainly affects the local Nusselt number near the inlet. The results of Shah and London [3] and the benchmark solution are almost overlapped. The maximum relative error is 0.64% when comparing the results of 20 orthogonal functions with the benchmark solution or the data in Shah and London [3]. Therefore, 20 orthogonal functions are adopted in this work to enhance the calculation accuracy.

Figure 4

Effect of the number of the orthogonal function on local Nusselt number.

3.3 Validation of analytic solutions

It is essential to verify the analytic solutions before discussing the heat transfer characteristics further. For the extended Graetz problem in CM or PPM, there are some available data that can be compared with the present results as shown in figure 5. Figure 5(a) depicts the results in CM with Pe = ∞ under the constant heat flux. Obviously, the present results are consistent with that in Shah and London [3] and Haddout et al [13], but some deviations are found when compared with that in Ameel et al [6]. It can be ascribed to the difference in the number of eigenvalues because only 8 eigenvalues were employed in Ameel et al [6]. Figure 5(b) describes the variation of the local Nusselt number in CM and PPM with Kn = 0 under the constant wall temperature. The data in Chalhub et al [12] and Kalyoncu and Barisik [15] are also plotted to compare the results. Good agreements can be found and the maximum relative errors between the present work and the literature data are less than 0.4% and 2% in PPM and CM, respectively.

Figure 5

Validation of analytic solutions: (a) constant heat flux in CM and (b) constant wall temperature in CM and PPM.

4 Results and discussion

4.1 Constant heat flux

Figure 6 displays the influence of the rarefaction on the local Nusselt number. The rarefaction is directly proportional to the Kn. As expected, the Nusselt number decreases as Kn increases in both the entrance region and the fully developed region. The reduction is more apparent in the entrance region, indicating the entrance effect is greatly affected by the rarefaction. It is expected that the entrance effect will disappear if Kn is large enough. Because the gas is thinner with increasing Kn, which decreases the collision frequency between the gas molecules. While the axial conduction depends on the heat conduction between the gas molecules. Therefore, increasing Kn would weaken the heat transfer. Besides, the reduction is also distinct for low Pe. Since the axial heat conduction is significantly diminished when enhancing the rarefaction. The effect of the rarefaction on the heat transfer is more prominent in PPM when compared with that in CM, which maybe since the boundary conditions have more effect on the double-connected channel.

Figure 6

Effect of Kn on Nu(x) in PPM with (a) Pe = 50 (b) Pe = 100 (c) Pe = ∞ and in CM with (d) Pe = 50, (e) Pe = 100 (f) Pe = ∞.

The influence of the axial heat conduction on the local Nusselt number is shown in figure 7. The results indicate that Nu(x) is inversely proportional to Pe, and the tendency is manifest when Pe < 250 with Kn = 0. The maximum relative error of Nu(x) between Pe = 500 and Pe = 1000 are 3.1% and 0.08% when Kn = 0 and 0.1 respectively in CM, and for PPM they are 6.0% and 0.1% respectively. The influence of Pe can be thus omitted when Pe>500. Because the speed of the axial heat conduction is far slower than that of the heat convection if Pe is high enough, resulting in a small axial temperature gradient and the axial heat conduction can be omitted. Besides, the axial heat conduction only affects Nu(x) at the entrance region and the effect gradually decreases along the streamwise direction. The fully developed Nusselt number is independent of Pe, which means the axial heat conduction only affects the local Nusselt number in the thermal entrance region [47]. It is worth noting that for the constant heat flux condition, the fluid temperature linear changes along the axial direction, which means the second derivative of the temperature along the axial direction can be ignored in the fully developed region. When comparing figure 7(a) and figure 7(b), it is obvious that the influence of Pe is greatly weakened as Kn increases. Similarly, the influence of Pe on Nu(x) is more apparent in PPM in comparison with that in CM.

Figure 7

Effect of Pe on Nu(x) in PPM with (a) Kn = 0, (b) Kn = 0.01, (c) Kn = 0.1; and in CM with (d) Kn = 0, (e) Kn = 0.01, (f) Kn = 0.1.

The above results reveal that due to the entrance effect, the heat transfer coefficient at the entrance region is much higher than that of the fully developed region. Therefore, it is necessary to determine the thermal entrance length to clarify the influence range of the entrance effect. Based on the definition of the thermal entrance length $L_{{{\text{th}}}}^{*}$ [48], it can be calculated with the following expression

$$ Nu(L_{{{\text{th}}}}^{*} ) = 1.05Nu_{\infty } $$

(48)

where Nu_∞ is the fully developed Nusselt number.

The variation of the thermal entrance length is shown in figure 8. The symbol mark in the figure is the calculated value. The results in Shah and London [3], who gave the thermal entrance length of ignoring the axial heat conduction and rarefaction, are also used to make a contrast. The good result of the comparison supports the present work. Moreover, Colin [49] have summarized the thermal entry length without axial conduction for CM under constant heat flux boundary condition, and the results are also plotted in figure 8(b). The same trend can be found but some differences were also observed especially for low Kn. Note that the results in Colin [49] come from Ameel et al [6]. The deviation can be ascribed to the fewer eigenvalues used in Ameel et al [6], as mentioned in section 3.3. While the Nusselt number at the entrance region is more sensitive to the number of the eigenvalue for low Kn. Despite this, the results in Ameel et al [6] or Colin [49] also verify our results because the relative error of the thermal entry length is within 3.8%. Besides, it is found that Pe has a distinct influence on the thermal entrance length when Pe is low. While the thermal entrance length hardly changes when Pe > 500. Note that the thermal entrance length increases for increasing fluid axial heat conduction (i.e., decreasing Pe). For example, in the case of the fluid heating situation, finite axial heat conduction would reduce the temperature of the fluid at any cross section, and hence a longer duct length would be required to achieve the fully developed temperature profile. In addition, the thermal entrance length, on the whole, decreases as Kn increases and the reduction is apparent for low Pe. When 0 ≤ Kn ≤ 0.1 and Pe ≥ 50, the correlations of the thermal entrance lengths are obtained by using the curve fitting. For PPM,

$$ L_{{{\text{th}}}}^{*} = a + bKn + cKn^{1.5} + dKn^{2} $$

(49)

Figure 8

Variation of thermal entrance length in (a) PPM and (b) CM.

The corresponding coefficients are shown in table 1. For CM,

$$ \begin{aligned} L_{{{\text{th}}}}^{*}& = \left( { - 0.5913 + 0.5967Kn + 5.044Kn^{1.5} - 7.796Kn^{2} } \right)\\ &\quad\left( { - 0.073 - 2.767Pe^{ - 1.8} } \right)\\ \end{aligned}$$

(50)

Table 1 Coefficients in Eq. (49).

The results of the Eqs. (49) and (50) are shown by the solid line in figure 8 and good agreements can be found between the correlations and the calculated values.

4.2 Constant wall temperature

The influence of Kn on Nu(x) with the constant wall temperature is shown in figure 9. Similar to the results under the constant heat flux, Nu(x) is a decreasing function of Kn. As Kn increases, the collision frequency between the gas molecules becomes weak. And the entrance effect is greatly affected by Kn, especially for low Pe, which is due to the fact that the axial conduction enhances the entrance effect and the effect of the rarefaction is more evident. The influence of the rarefaction on the heat transfer performance is more obvious in PPM compared with that in CM.

Figure 9

Effect of Kn on Nu(x) in PPM with (a) Pe = 50, (b) Pe = 100, (c) Pe = ∞; and in CM with (d) Pe = 50, (e) Pe = 100, (f) Pe = ∞.

The influence of the axial heat conduction on the local Nusselt number is shown in figure 10. The local Nusselt number increases as Pe decreases, especially when Pe < 250. The maximum relative error of Nu(x) between Pe = 100 and Pe = 500 are 36.2%, 15.5%, and 1.6% in CM when Kn = 0, 0.02, and 0.1 respectively, indicating the effect of the axial conduction is obvious when Pe > 100, especially for low Kn. And the maximum relative error of Nu(x) between Pe = 500 and Pe = 1000 in CM are 3.3%, 1.5%, and 0.1% when Kn = 0, 0.02, and 0.1 respectively, and for PPM they are 6.9%, 1.8% and 0.1% respectively. Therefore, when Pe > 100, the effect of the axial heat conduction on the entrance effect cannot be ignored in the slip regime until Pe > 500, rather than Pe > 100 in the existing literature. Likewise, the influence of the axial heat conduction attenuates as Kn increases. Besides, the influence is more obvious in PPM in comparison with that in CM. But the difference decreases as Kn increases, indicating that increasing Kn would downgrade the effect of the channel shape on the heat transfer.

Figure 10

Effect of Pe on Nu(x) in PPM with (a) Kn = 0, (b) Kn = 0.01, (c) Kn = 0.1 and in CM with (d) Kn = 0, (e) Kn = 0.01 and (f) Kn = 0.1.

The influence of Pe on Nu(x) gradually decreases along the streamwise direction. But it is worth noting that Pe has an influence on Nu_∞ under the constant wall temperature, as shown in figure 11. Since the fully developed Nusselt number with the constant wall temperature strongly depends on the first eigenvalue, which is affected by both Kn and Pe. However, the effect of Pe on Nu_∞ is small when Pe ≥ 50, and the effect decreases as Kn increases.

Figure 11

Variation of the fully developed Nu with Pe in PPM.

The effects of Pe and Kn on the thermal entrance length are shown in figure 12. Different from the results under the constant heat flux, the thermal entrance length increases first and then decreases as Kn increases. The peak values of $L_{{{\text{th}}}}^{*}$ arise when Kn is 0.4 or 0.5. $L_{{{\text{th}}}}^{*}$ is gradually getting shorter as Pe increases and almost keeps unchanged when Pe > 500. Besides, $L_{{{\text{th}}}}^{*}$ of CM is about 3–4 times that of PPM. This is because two surfaces are in contact with the fluid in PPM, the thermal boundary layer is thus formed faster and shortens $L_{{{\text{th}}}}^{*}$. When 0 ≤ Kn ≤ 0.1 and Pe ≥ 50, the correlations of $L_{{{\text{th}}}}^{*}$ are obtained by using the curve fitting. For PPM,

$$ L_{{{\text{th}}}}^{*} = a + bKn + cKn^{1.5} + dKn^{2} + eKn^{2.5} $$

(51)

Figure 12

Variation of thermal entrance length in (a) PPM and (b) CM.

The corresponding coefficients are shown in table 2. For CM,

$$ \begin{aligned} L_{{{\text{th}}}}^{*} & = \left( { - 0.0665 + 0.0038Kn - 0.9Kn^{{1.5}} + 4.29Kn^{2} } \right. \\ & \quad \left. { - 4.14Kn^{{2.5}} } \right)\left( { - 0.504 - 33.33Pe^{{ - 1.83}} } \right) \\ \end{aligned} $$

(52)

Table 2 Coefficients in Eq. (51).

The results of the Eqs. (51) and (52) are shown by the solid line in figure 12 and a high degree of coincidence can be found between the correlations and the calculated values.

4.3 Comparison of heat transfer under different thermal boundaries

Figure 13 plots the influence of the rarefaction on the local Nusselt number in PPM and CM with different boundary conditions. The rarefaction effect has almost the same effect on the local Nusselt number in the two microchannels. Taking the results in PPM as an example, the local Nusselt number decreases significantly with the increase of Kn under the two thermal boundaries. When Kn = 0, the curves of Nu(x) with the two boundary conditions are almost parallel. As Kn increases, the two curves have an intersection or even almost overlap at the entrance region. The difference of the local Nusselt number with the two boundary conditions almost disappears when Kn = 0.1 in CM. But the difference is still obvious in the fully developed region in PPM, indicating the effect of the thermal boundary condition on the heat transfer performance is more important in PPM. The result indicates that the rarefaction effect would diminish the difference in the heat transfer performance between the two boundaries. At the same time, the result demonstrates the change of Kn has a greater influence on the heat transfer under the constant heat flux when compared with that under the other boundary.

Figure 13

Effect of Kn on Nu(x) under different boundary conditions in (a) PPM, and (b) CM.

In figure 14, the effect of the axial heat conduction on the heat transfer is depicted in PPM and CM with different boundary conditions. When the axial heat conduction is not considered, that is, Pe → ∞, the heat transfer coefficient with the constant wall temperature is always lower. As Pe decreases, Nu(x) under the constant wall temperature tends to exceed that under the constant heat flux. The phenomenon shows that the axial heat conduction would greatly enhance the heat transfer performance at the entrance region, especially for the constant wall temperature. In addition, it can be found that there is a fluctuation for Nu(x) near the inlet when Pe = 50 under the constant wall temperature boundary, which indicates that more eigenvalues are needed to calculate more accurate results for this case. While adding an eigenvalue will double the amount of calculation, so using the numerical methods to obtain the heat transfer coefficient of small Pe may reduce the cost.

Figure 14

Effect of Pe on Nu(x) under different boundary conditions in (a) PPM and (b) CM.

5 Conclusions

In this paper, the energy equations of the thermally developing flow in circular and parallel plates microchannels are solved by using the separated variable method combined with the Kummer function and Gram-Schmidt orthogonalization. The temperature distribution is obtained, and the expression of the dimensionless heat transfer coefficient is derived. By analyzing the influence of the axial heat conduction and the rarefaction on the heat transfer characteristic in microchannels with two boundary conditions, the following conclusions are drawn:

• (1) The number of eigenvalues mainly affects the results near the inlet. With increasing Kn and Pe, the entrance effect is not obvious and the effect of the number of eigenvalues on the Nusselt number decreases as well. More eigenvalues are needed to accurately calculate the local Nusselt number in CM comparatively with that in PPM. Besides that, more eigenvalues are required to obtain the local Nusselt number accurately for the constant wall temperature boundary condition when compared with that for the constant heat flux.

• (2) Considering the axial heat conduction will enhance the heat transfer capacity at the entrance region, especially when Pe < 50. While the maximum relative errors of Nu(x) between Pe = 500 and Pe = 1000 in CM and PPM are within 7%, even within 0.1% for Kn = 0.1. The effect of axial heat conduction on Nu can be thus ignored when Pe > 500. In the fully developed region, the axial heat conduction does not affect the Nusselt number under the constant heat flux but still has a small influence on the heat transfer under the constant wall temperature. In addition, enhancing the rarefaction would weaken the entrance effect and then weaken the influence of axial heat conduction on the heat transfer as well.

• (3) The thermal entrance length decreases with the increase of Kn under the constant heat flux, but it increases first and then decreases as Kn increases under the constant wall temperature. The thermal entrance length decreases as the axial fluid heat conduction fades away. Besides, the thermal entrance length in CM is 3–4 times that of PPM because PPM can be treated as a double-connected channel. Finally, the correlations of the thermal entrance length are proposed.

• (4) The influence of thermal boundary conditions on the heat transfer coefficient decreases as increasing Kn. Considering these two boundary conditions, the rarefaction effect has more influence on the heat transfer under the constant heat flux, and the effect of the axial heat conduction on the heat transfer is more apparent under the constant wall temperature.

Appendix A: Steps of Gram-Schmidt orthogonalization to obtain C n

For the eigenfunctions sequence {ϕ_n}, assuming that the orthogonalized function sequences are {g_n}, the relationship between the above two is as follows

$$ g_{1} = \phi_{1} $$

(A-1)

$$ g_{2} = \phi_{2} - a_{21} g_{1} = \phi_{2} - a_{21} \phi_{1} $$

(A-2)

$$ \begin{gathered} g_{3} = \phi_{3} - a_{32} g_{2} - a_{31} g_{1} = \phi_{3} - a_{32} \left( {\phi_{2} - a_{21} \phi_{1} } \right) - a_{31} \phi_{1} \hfill \\ \, = \phi_{3} - a_{32} \phi_{2} + \left( {a_{32} a_{21} - a_{31} } \right)\phi_{1} \hfill \\ \end{gathered} $$

(A-3)

$$ g_{n} = \phi_{n} - \sum\limits_{m = 1}^{n - 1} {a_{nm} } g_{m} $$

(A-4)

For the orthogonal function sequences {g_n}, there is the following orthogonal property when i ≠ j

$$ \int_{0}^{1} {g_{i} g_{j} } {\text{d}}Y = 0 $$

(A-5)

Substituting (A-1) and (A-2) into (A-5) yields

$$ \int_{0}^{1} {g_{1} g_{2} } {\text{d}}Y = \int_{0}^{1} {\phi_{1} \left( {\phi_{2} - a_{21} g_{1} } \right)} {\text{d}}Y = \int_{0}^{1} {\phi_{1} \phi_{2} } {\text{d}}Y - a_{21} \int_{0}^{1} {\phi_{1} g_{1} } {\text{d}}Y = 0 $$

(A-6)

then

$$ a_{21} = \frac{{\int_{0}^{1} {\phi_{1} \phi_{2} } {\text{d}}Y}}{{\int_{0}^{1} {\phi_{1} g_{1} } {\text{d}}Y}} = \frac{{ < \phi_{1} ,\phi_{2} > }}{{ < \phi_{1} ,g_{1} > }} $$

(A-7)

More generally,

$$ a_{nm} = \frac{{ < \phi_{n} ,g_{m} > }}{{ < g_{m} ,g_{m} > }} $$

(A-8)

Based on the inlet boundary condition, setting the coefficient of the eigenfunctions after the orthogonalization is B_n, namely

$$ \sum\limits_{n = 1}^{\infty } {C_{n} \phi_{n} (Y)} = \sum\limits_{n = 1}^{\infty } {B_{n} g_{n} (Y)} $$

(A-9)

and

$$ \sum\limits_{n = 1}^{\infty } {B_{n} g_{n} (Y)} = \theta (0,Y) $$

(A-10)

The coefficient B_n can be obtained based on the characteristics of the orthogonal function:

$$ B_{n} = \frac{{\int_{0}^{1/A} {\theta (0,Y)g_{n} {\text{d}}Y} }}{{\int_{0}^{1/A} {g_{n}^{2} {\text{d}}Y} }} $$

(A-11)

According to (A-1)–(A-4), we have

$$ \begin{aligned} \sum\limits_{{n = 1}}^{\infty } {B_{n} g_{n} (Y)} & = B_{1} \phi _{1} + B_{2} \left( {\phi _{2} - a_{{21}} \phi _{1} } \right) + B_{3} \left( {\phi _{3} - a_{{32}} \phi _{2} } \right. \\ & \quad \left. { + a_{{32}} a_{{21}} \phi _{1} - a_{{31}} \phi _{1} } \right) + B_{4} \left( {\phi _{4} - a_{{43}} \phi _{3} + a_{{43}} a_{{32}} \phi _{2} } \right. \\ & \quad \left. { - a_{{43}} a_{{32}} a_{{21}} \phi _{1} + a_{{43}} a_{{31}} \phi _{1} - a_{{42}} \phi _{2} + a_{{42}} a_{{21}} \phi _{1} - a_{{41}} \phi _{1} } \right) \\ & \quad + \cdots B_{n} \left( {\phi _{n} - \sum\limits_{{m = 1}}^{{m - 1}} {a_{{nm}} } g_{m} } \right) \\ \end{aligned} $$

(A-12)

After determining B_n, C_n can be calculated according to (A-9), that is

$$ \begin{aligned} & C_{1} = B_{1} - B_{2} k_{1,2} - \cdots - B_{N} k_{1,N} = B_{1} - \sum\limits_{i = n + 1}^{N} {B_{i} k_{1,i} } \\ & \vdots \\ & C_{n} = B_{n} - B_{n + 1} k_{n,n + 1} - \cdots - B_{N} k_{n,N} = B_{n} - \sum\limits_{i = n + 1}^{N} {B_{i} k_{n,i} } \\ & \vdots \\ & C_{N} = B_{N} \\ \end{aligned} $$

(A-13)

where

$$ \begin{aligned} k_{n,m} &= a_{m,n} k_{n,n} - a_{m,n + 1} k_{n,n + 1} - \cdots - a_{m,m - 1} k_{n,m - 1} = a_{m,n}\\&\quad - \sum\limits_{i = n + 1}^{m - 1} {a_{m,i} k_{n,i} } \\ k_{n,n} &= 1 \\ \end{aligned} $$

(A-14)