1 Introduction

Recent years saw a remarkable growth in the literature regarding non-Newtonian fluids. These fluids obey nonlinear constitutive relationship between the shear stress and deformation rate and have practical applications in chemical, metallurgical, civil and mining engineering and industries. There exist various constitutive relationships of non-Newtonian fluids in the literature. Among these the Walters-B [1] fluid is an important viscoelastic fluid. The nonlinearity and higher-order derivatives restrict the researchers to solve flow equations of Walters-B fluid by conventional methods. Moreover, there exists a strong singularity at the initial boundary. This complexity challenged mathematicians to develop methods that overcome this difficulty. Beard and Walters [1] used the first-order perturbation method to find the solution. The perturbation solution predicted the velocity overshoot within the boundary layer. Frater [2] was of the opinion that perturbation solution is responsible for overshoot in the velocity profile. Ariel [3] proposed a hybrid numerical technique to explain the stagnation-point flows of Walters-B liquid and reported the overshoot in the velocity. Dorrepaal et al [4] discussed the flow of Walters-B fluid near point of reattachment.

The flow over a stretching surface has frequent engineering applications such as polymer extrusion, artificial fibres and rolling and manufacturing of plastic films. In the process of melt-spinning, the extrudate from the die is usually drawn and at the same time stretched into a sheet, which is converted into a solid by gradual cooling process. The heat transfer at stretching surface influences the quality of the final product. Crane [5] investigated the attached flow with a stretching surface utilizing the boundary layer equations of a viscous fluid. McLeod and Rajagopal [6] studied the unique solution of a viscous fluid flow past a stretchable boundary. Mahapatra et al [7] explored the flow of Walters-B fluid near the stagnated region over a flat stretching surface. Lok et al [8] studied the non-orthogonal stagnated flow of a viscous fluid near a stretching sheet. Hussain et al [9] deliberated the stagnated flow of Walters-B liquid impinging obliquely over a stretching surface. Hayat et al [10] explored the three-dimensional flow of an elastico-viscous fluid over a stretching surface. Wang [11] analytically solved the problem of slip flow of a viscous fluid near the stagnation region. Labropulu et al [12] evaluated the slip effects in the stagnation-region of Walters-B liquid. Sajid et al [13] investigated the axisymmetric flow near a stagnation-point over a lubricated disk with power-law fluid as lubricant by introducing generalized slip boundary condition. Mehmood et al [14,15,16,17] considered the flow of an elastico-viscous fluid, micropolar, couple stress and Jeffrey fluids, respectively, towards an oblique stagnation point caused by a lubricated flat surface. Kushwaha and Sahu [18] discussed the heat transfer in the presence of the slip in the region between two heated parallel plates having the effects of viscous dissipation. Zhu et al [19] evaluated the effects of the velocity slip of the second order on the nanofluid flow in the presence of MHD.

In the last few years, attention has been paid to heat transfer in non-Newtonian fluids in many engineering and industrial activities, e.g. food processing, pharmaceutical process, hybrid power engines, microelectronics, fuel cells, hyperthermia, coolants in nuclear power plants, etc. Dandapat and Gupta [20] analysed the heat transfer in second-grade fluid over a stretchable surface. Sajid et al [21] discussed the micropolar fluid flow over a disk with combined effects of uniform rotation and linear radial stretching. Labropulu et al [22] calculated the heat transfer in oblique flow of a viscoelastic fluid towards a stretchable surface. The analysis was made by considering the non-Newtonian fluid in the oblique stagnation zone. Reza et al [23] discussed the heat transfer in stagnation flow of a elastico-viscous fluid impinging on a quiescent fluid. Hayat et al [24] studied the radiative and convective heat transfer phenomenon in Walters-B liquid flow. Hakeem et al [25] analysed the effects of thermal radiation and elastic deformation in Walters-B fluid. Ali et al [26] examined heat transfer due to thermal radiation and heat source/sink in a unsteady flow of a non-Newtonian fluid past an oscillatory stretching sheet. Seedak and Abdelmeguid [27] investigated the effects of thermal radiation with thermal diffusivity over a stretching sheet having variable heat flux. Babu and Sandeep [28], Raju and Sandeep [29] and Kumar et al [30] focused on the effects of non-linear thermal radiations by incorporating the Newtonian and non-Newtonian fluids in the presence and absence of the slip effects. Attia et al [31] and Prakashi et al [32] investigated the heat transfer in fluid flow between two porous plates and the porous channel.

The spectral methods are widely used to deal with the nonlinearity of a system of equations. Yuan et al [34] introduced the multidomain pseudo-spectral approximation based on the Legendre–Galerkin method. They solved nonlinear diffusion equations to check the stability and the rate of convergence of the method.

Keeping in view this literature, the current investigation is performed to predict the effects of the slip and thermal radiation on the oblique two-dimensional flow of Walters-B fluid near a stagnation point with uniform heat source/sink. Governing equations are solved mathematically using a numerical method named as Legendre wavelet spectral collocation method (LWSCM) proposed by Sajid et al [35]. No overshoot in the velocity reported in the work of Arial [3] and Hussain et al [9] is seen while applying the LWSCM numerical technique.

2 Problem formulation

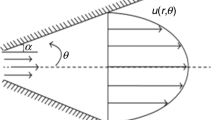
A steady, two-dimensional and incompressible oblique stagnation-point flow of Walters-B fluid over a stretchable sheet at \(y=0\) is considered (figure 1). The flow and heat transfer are studied by following [1, 9, 25].

Figure 1
figure 1

Flow geometry of physical problem.

Full size image
$$\begin{aligned}&\frac{\partial {\bar{u}}}{\partial {\bar{x}}} + \frac{\partial {\bar{v}}}{\partial {\bar{y}}}=0, \end{aligned}$$
(1)
$$\begin{aligned}&{\bar{u}}\frac{\partial {\bar{u}}}{\partial {\bar{x}}} + {\bar{v}} \frac{\partial {\bar{u}}}{\partial {\bar{y}}}= -\frac{1}{\rho } \frac{\partial {\bar{p}}}{\partial {\bar{x}}}+\nu {\bar{\nabla }}^{2} {\bar{u}}- \frac{k_0}{\rho } \Biggl [ \frac{\partial }{\partial {\bar{x}}}\bigg [ 2 {\bar{u}} \frac{\partial ^{2} {\bar{u}}}{\partial {\bar{x}}^{2}}+4 \bigg (\frac{\partial {\bar{u}}}{\partial {\bar{x}}}\bigg )^{2}+2{\bar{v}}\frac{\partial ^{2} {\bar{u}}}{\partial {\bar{x}} \partial {\bar{y}}} \nonumber \\&\quad +\, 2\frac{\partial {\bar{v}}}{\partial {\bar{x}}}\bigg (\frac{\partial {\bar{v}}}{\partial {\bar{x}}}+\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\bigg )\bigg ]+ \frac{\partial }{\partial {\bar{y}}}\bigg [\bigg ( {\bar{u}} \frac{\partial }{\partial {\bar{x}}}+ {\bar{v}} \frac{\partial }{\partial {\bar{y}}}\bigg ) \bigg (\frac{\partial {\bar{v}}}{\partial {\bar{x}}}+\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\bigg )+2\frac{\partial {\bar{v}}}{\partial {\bar{x}}} \frac{\partial {\bar{v}}}{\partial {\bar{y}}}+2 \frac{\partial {\bar{u}}}{\partial {\bar{x}}} \frac{\partial {\bar{u}}}{\partial {\bar{y}}} \bigg ] \Bigg ], \end{aligned}$$
(2)
$$\begin{aligned}&{\bar{u}}\frac{\partial {\bar{v}}}{\partial {\bar{x}}} + {\bar{v}} \frac{\partial {\bar{v}}}{\partial {\bar{y}}}= -\frac{1}{\rho } \frac{\partial {\bar{p}}}{\partial {\bar{y}}}+\nu {\bar{\nabla }}^{2} {\bar{v}}- \frac{k_0}{\rho } \Biggl [ \frac{\partial }{\partial {\bar{x}}} \bigg [ \bigg ( {\bar{u}} \frac{\partial }{\partial {\bar{x}}} + {\bar{v}} \frac{\partial }{\partial {\bar{y}}}\bigg ) \bigg (\frac{\partial {\bar{v}}}{\partial {\bar{x}}}+\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\bigg )\nonumber \\&\quad +\, 2 \frac{\partial {\bar{u}}}{\partial {\bar{x}}} \frac{\partial {\bar{u}}}{\partial {\bar{y}}}+2\frac{\partial {\bar{v}}}{\partial {\bar{x}}} \frac{\partial {\bar{v}}}{\partial {\bar{y}}} \bigg ]+ \frac{\partial }{\partial {\bar{y}}}\bigg [ 2 {\bar{u}}\frac{\partial ^{2} {\bar{v}}}{\partial {\bar{x}}\partial {\bar{y}}}+2{\bar{v}} \frac{\partial ^{2} {\bar{v}}}{\partial {\bar{y}}^{2}}+4 \bigg (\frac{\partial {\bar{v}}}{\partial {\bar{y}}}\bigg )^{2} + 2\frac{\partial {\bar{u}}}{\partial {\bar{y}}}\bigg (\frac{\partial {\bar{v}}}{\partial {\bar{x}}}+\frac{\partial {\bar{u}}}{\partial {\bar{y}}} \bigg ) \bigg ] \Biggr ], \end{aligned}$$
(3)
$$\begin{aligned}&{{\bar{u}}} \frac{\partial T}{\partial {{\bar{x}}}} + {{\bar{v}}}\frac{\partial T}{\partial {{\bar{y}}}} = \frac{k}{\rho c_p} \frac{\partial ^2 T}{\partial {{\bar{y}}}^2} - \frac{1}{\rho c_p} \frac{\partial q_r}{\partial {{\bar{y}}}}+ \frac{Q}{\rho c_p}(T-T_\infty ), \end{aligned}$$
(4)

where u(x, y) and v(x, y), respectively, are components of velocity in x and y directions; \(\nu \), \(\rho \) , \(c_p\), k, \(q_r\) and Q, respectively, are kinematic viscosity, density, specific heat, thermal conductivity, radiative heat flux and the heat source/sink. The Rossland approximation \( q_r = \frac{-4\sigma ^*}{3k^*} \frac{\partial T^4}{\partial {{\bar{y}}}}\) where \(\sigma ^*\) and \(k^*\), respectively, are the Stefan–Boltzmann constant and the mean absorption coefficient is used. Furthermore, T, \(T_w\) and \(T_{\infty }\), respectively, are the temperature of fluid inside boundary layer, at the wall and far away from the wall. Defining stream function from (1) such that

$$\begin{aligned} {{\bar{u}}} = \frac{\partial {{\bar{\psi }}}}{\partial {{\bar{y}}}}, \quad {{\bar{v}}} = -\frac{\partial {{\bar{\psi }}}}{\partial {{\bar{x}}}}. \end{aligned}$$
(5)

Substituting (5) into (2)–(4) and eliminating the pressure we have

$$\begin{aligned}&\frac{\partial ({{\bar{\psi }}},\; \nabla ^2 {{\bar{\psi }}} )}{\partial ({{\bar{x}}}, \; {{\bar{y}}})} + \frac{k_0}{\rho } \frac{\partial ({{\bar{\psi }}},\; \nabla ^4 {{\bar{\psi }}} )}{\partial ({{\bar{x}}}, \; {{\bar{y}}})}+ \nu \nabla ^4 {{\bar{\psi }}} =0, \end{aligned}$$
(6)
$$\begin{aligned}&\frac{\partial {{\bar{\psi }}}}{\partial {{\bar{y}}}} \frac{\partial T}{\partial {{\bar{x}}}} + \frac{\partial {{\bar{\psi }}}}{\partial {{\bar{x}}}}\frac{\partial T}{\partial {{\bar{y}}}} = \frac{k}{\rho c_p} \frac{\partial ^2 T}{\partial {{\bar{y}}}^2} - \frac{1}{\rho c_p} \frac{\partial q_r}{\partial {{\bar{y}}}}+ \frac{Q}{\rho c_p}(T-T_\infty ). \end{aligned}$$
(7)

The appropriate boundary conditions are [9]

$$\begin{aligned} {\bar{\psi }}= & {} 0, \qquad \frac{\partial {\bar{\psi }}}{\partial {\bar{y}}} =c{{\bar{x}}} + \frac{b}{\mu } \tau ^{12} |_{{{\bar{y}}}=0}, \qquad T= T_w + \alpha ^* \frac{\partial T}{\partial {{\bar{y}}}} \quad \text{ at } \quad {\bar{y}}=0, \end{aligned}$$
(8)
$$\begin{aligned} {\bar{\psi }}= {} a{\bar{x}}{\bar{y}} + \frac{1}{2} b {\bar{y}}^{2},\qquad T \rightarrow T_\infty \quad \text{ as } \quad {\bar{y}} \rightarrow \infty , \end{aligned}$$
(9)

where a, b and c are constants and \(\alpha ^* \) is thermal slip parameter. The heat transfer rate and skin friction coefficient at wall can be expressed as [26]

$$\begin{aligned} C_f = \frac{\tau _w}{\rho (c{{\bar{x}}})^2}, \quad \quad Nu_x = \frac{{{\bar{x}}} q_w}{k (T_w- T_{\infty })}, \end{aligned}$$
(10)

where

$$\begin{aligned} \tau _w= & {} \bigg \{\mu (\frac{\partial ^{2} {\bar{\psi }}}{\partial {\bar{y}}^{2}} -\frac{\partial ^{2} {\bar{\psi }}}{\partial {\bar{x}}^{2}})- k_{o}\Big [\frac{\partial {\bar{\psi }}}{\partial {\bar{y}}} (\frac{\partial ^{3} {\bar{\psi }}}{\partial {\bar{x}}\partial {\bar{y}}^{2}}-\frac{\partial ^{3} {\bar{\psi }}}{\partial {\bar{x}}^{3}})\nonumber \\&-\frac{\partial {\bar{\psi }}}{\partial {\bar{x}}} (\frac{\partial ^{3} {\bar{\psi }}}{\partial {\bar{y}}^{3}}-\frac{\partial ^{3} {\bar{\psi }}}{\partial {\bar{x}}^{2}\partial {\bar{y}}})+2{\bar{\psi }}_{{\bar{x}}{\bar{y}}}{\bar{\psi }}_{{\bar{x}}{\bar{x}}}+2{\bar{\psi }}_{{\bar{y}}{\bar{y}}} {\bar{\psi }}_{{\bar{x}}{\bar{y}}}\Big ]\bigg \}_{{{\bar{y}}}=0}. \end{aligned}$$
(11)
$$\begin{aligned} q_w= & {} -k \bigg ( 1+ \frac{16\sigma ^* T^3_\infty }{3kk^*} \bigg ) \bigg (\frac{\partial T}{\partial {{\bar{y}}}}\bigg )_{{{\bar{y}}} = 0} . \end{aligned}$$
(12)

Defining dimensionless variables

$$\begin{aligned} x= {\bar{x}} \sqrt{\frac{c}{\nu }}, \quad y= {\bar{y}} \sqrt{\frac{c}{\nu }},\quad \psi = \frac{{\bar{\psi }}}{\nu }, \end{aligned}$$
(13)

Eqs. (6)–(9) in dimensionless variables become

$$\begin{aligned}&\frac{\partial (\psi ,\; \nabla ^2 \psi )}{\partial ( x, \; y)} + We \frac{\partial ( \psi ,\; \nabla ^4 \psi )}{\partial ( x, \; y)}+ \nu \nabla ^4 \psi =0, \end{aligned}$$
(14)
$$\begin{aligned}&\frac{\partial \psi }{\partial y} \frac{\partial T}{\partial x} + \frac{\partial \psi }{\partial x}\frac{\partial T}{\partial y} = \frac{k}{\rho c_p} \frac{\partial ^2 T}{\partial y^2} - \frac{1}{\rho c_p} \frac{\partial q_r}{\partial y}+ \frac{Q}{\rho c_p}(T-T_\infty ), \end{aligned}$$
(15)
$$\begin{aligned}&\psi =0, \quad \frac{\partial \psi }{\partial y} = x + \beta \tau ^{12} |_{ y=0}, \quad T= T_w + \alpha \frac{\partial T}{\partial y} \quad \text{ at }\ \quad y=0, \end{aligned}$$
(16)
$$\begin{aligned}&\psi = \frac{a}{c} x y + \frac{1}{2} \gamma y^{2},\quad T \rightarrow T_\infty \quad \text{ as } \quad y \rightarrow \infty , \end{aligned}$$
(17)

where \(We= \frac{k_0 c}{\rho \nu }\), \(\gamma =\frac{b}{c}\), \(\beta =b \sqrt{\frac{c}{\nu }}\) and \(\alpha = \alpha ^* \sqrt{\frac{c}{\nu }}\), respectively, are viscoelastic parameter Weissenberg number, shear in freestream, velocity and thermal slip parameters. Introduce the similarity transformations

$$\begin{aligned} \psi (x,y) = xF(y) + G(y), \qquad \theta (y) = \frac{T- T_{\infty }}{T_w - T_{\infty }}, \end{aligned}$$
(18)

where F(y) and G(y), respectively, denote the component of the flow in normal and tangential directions. Applying Eq. (18) into Eqs. (14)–(17) and after integration, the following system of ordinary differential equations is obtained:

$$\begin{aligned}&F'''(y)- [F'(y)]^{2} + F(y)F''(y)+\frac{a^2}{c^2}+We\Big [F(y)F^{iv}(y)\nonumber \\&\quad +\,F'''(y)+[F''(y)]^{2}-2F'(y) \Big ]=0, \end{aligned}$$
(19)
$$\begin{aligned}&G'''(y) + G''(y) F(y) - G'(y) F'(y)+We\Big [G^{iv}(y) F(y)-G'''(y) F'(y)\nonumber \\&\quad +\,G''(y) F''(y)- G'(y) F'''(y) \Big ]=A\gamma , \end{aligned}$$
(20)
$$\begin{aligned}&\theta ''(y) +Pr_{eff}\; \theta '(y) \; F(y)+ \lambda \; Pr_{eff}\;\theta (y)=0, \end{aligned}$$
(21)
$$\begin{aligned}&F(0)=0, \quad \quad F'(0) = \frac{1+ \beta F''(0)}{3 \beta We F''(0) +1}, \quad \quad F'(\infty )= \frac{a}{c}, \end{aligned}$$
(22)
$$\begin{aligned}&G(0) =0,\;\; G'(0)=\frac{\beta G''(0)}{1+\beta We F''(0)} \bigg [1 - 2 We \bigg ( \frac{1+\beta F''(0)}{3 \beta We F''(0)+1} \bigg ) \bigg ],\nonumber \\&\quad G''(\infty )= \gamma , \end{aligned}$$
(23)
$$\begin{aligned}&\theta (0) = 1+ \alpha \; \theta '(0), \quad \quad \theta (\infty ) =0, \end{aligned}$$
(24)

where \(A=A(We, a/c)\) is the boundary layer displacement and \(Pr_{eff} = \frac{Pr}{ Nr+1}\) denotes the effective Prandtl number. It was the opinion of the Magyari and Pantokratoras [33] that energy equation (24) should not be solved by an approach using two parameters, i.e., Prandtl number and radiation parameter. They disclosed that in fact the study of heat transfer characteristics has similar consequences either with or without thermal radiation. It was emphasized that the flow problems involving thermal radiations admit the same solution for infinite parametric values of (Nr, Pr), which corresponds to the same effective Prandtl number. Equation (20) can be further simplified as

$$\begin{aligned}&G'(y) = \gamma H(y), \end{aligned}$$
(25)
$$\begin{aligned}&H''(y) +H'(y) F(y) - H(y) F'(y) + We \Big [H'''(y) F(y) - H''(y) F'(y)\nonumber \\&\quad + H'(y) F''(y) - H(y) F'''(y) \Big ] = A, \end{aligned}$$
(26)
$$\begin{aligned}&H(0)=\frac{\beta H'(0)}{1+\beta We F''(0)} \bigg [1 - 2 We \bigg ( \frac{1+\beta F''(0)}{3 \beta We F''(0) +1} \bigg ) \bigg ],\;\; H'(\infty )= 1. \end{aligned}$$
(27)

Employing Eq. (18) in Eq. (10), we have

$$\begin{aligned} Re_x C_f= & {} x F''(0)(1-3We) + \gamma H'(0) (1-2We), \end{aligned}$$
(28)
$$\begin{aligned} Re^{-1/2}_x Nu^*_x= & {} - \theta '(0), \end{aligned}$$
(29)

where \(Nu^*_x = \frac{Nu_x}{(1+Nr)}\) is local effective Nusselt number.

3 LWSCM

Consider the interval [0, T). The Legendre wavelets are defined as

$$\begin{aligned} \psi _{m,n} (t) = \bigg \lbrace \begin{array}{ll} (m+\frac{1}{2})^{1/2} 2^{k/2} L_m (2^{k} t - 2n +1), &{} \frac{n-1}{2^{k-1}}\le t<\frac{n}{2^{k-1}},\\ 0, &{} \text {otherwise}. \end{array} \end{aligned}$$
(30)

\(L_m (t)\) is mth-order Legendre polynomial having \(w(t) =1\) orthogonal weight function. One can obtain the Legendre polynomials using the relations

$$\begin{aligned} L_0 (t)= & {} 1,\nonumber \\ L_1 (t)= & {} t,\nonumber \\ L_{m+1}(t)= & {} \frac{2m+1}{m+1} t L_{m}(t)- \frac{m}{m+1} L_{m-1}(t), \quad m= 1,2,3 \ldots . \end{aligned}$$
(31)

\( x_0<x_1<x_2\cdot \cdot \cdot \cdot <x_{m-1}\), known as Legendre–Gauss collocation points, are roots of the \(L_m(x)\) in \((-1,1)\) and \( \lbrace w_j \rbrace ^{m-1} _{j=0} \) are corresponding weights:

$$\begin{aligned} w_j = \frac{2}{(1-x^{2} _j)(L'_M(x_j))^2} , \quad j=0,1, \ldots ,M-1. \end{aligned}$$
(32)

Any function \(f \in L^2[0,y_{\infty } )\) in terms of Legendre wavelets takes the form

$$\begin{aligned} f(x) = \sum \limits ^\infty _{n=1} \sum \limits ^\infty _{m=0} y_{n,m} \psi _{n,m} (x), \end{aligned}$$
(33)

where \(y_{n,m}\) can be approximated to

$$\begin{aligned} y_{n,m} \simeq \sum \limits ^{M-1} _{j=0} {\bar{w}}_j f(x_{nj}) \psi _{n,m} (x_{nj}), \end{aligned}$$
(34)

where

$$\begin{aligned} {\bar{w}}_j= & {} \frac{w_j}{2^k} , \quad x_{nj}= \frac{x_j}{2^k} + \frac{2n-1}{2^k}, \end{aligned}$$
(35)
$$\begin{aligned} n= & {} 1,2, \ldots , 2^{k-1}T, \quad j=0,1, \ldots M-1. \end{aligned}$$
(36)

Hence, Eq. (33) becomes

$$\begin{aligned}&f(x)\simeq \sum \limits ^\infty _{n=1} \sum \limits ^\infty _{m=0}\sum \limits ^{M-1} _{j=0} {\bar{w}}_j f(x_{nj}) \psi _{n,m} (x_{nj}) \psi _{n,m} (x). \end{aligned}$$
(37)
$$\begin{aligned}&\sum \limits ^\infty _{n=1} \sum \limits ^\infty _{m=0} \psi _{n,m}(x) \psi _{n,m} (t) = \delta (x-t) \end{aligned}$$
(38)

is an identity. Truncating this to \(M-1\) and \(2^{k-1}\,T\) and introducing

$$\begin{aligned} I_{nj}(x)=\sum \limits ^{M-1} _{m=0} {\bar{w}}_j \psi _{n,m} (x_{nj}) \psi _{n,m} (x), \end{aligned}$$
(39)

we have

$$\begin{aligned} f(x) \simeq \sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I_{nj}(x) f(x_{nj}). \end{aligned}$$
(40)

3.1 Solution by LWSCM

Consider the boundary value problems (19)–(24). We convert boundary value problems into initial value problems by assuming

$$\begin{aligned} F''(0)=s , \;\;\;\; G''(0)=r, \;\;\;\; \theta ' (0)=t. \end{aligned}$$
(41)

To obtain an approximate solution of these problems, we divide the domain \(0< y<T\) into subintervals for \(n= 1, \ldots , 2^{k-1}T\) by \( \Big [ \frac{n-1}{2^{k-1}}, \quad \frac{n}{2^{k-1}} \Big ) \). The functions F(y) and Z(y) can be approximated using Legendre wavelet interpolation on the nth subinterval as

$$\begin{aligned} F(y)\simeq & {} \sum \limits ^{2^{k-1}T} _{n=1} F_n(y) =\sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I_{nj}(y)\;F(y_{nj}) , \end{aligned}$$
(42)
$$\begin{aligned} G(y)\simeq & {} \sum \limits ^{2^{k-1}T} _{n=1} G_n(y) =\sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I_{nj}(y)\;G(y_{nj}) , \end{aligned}$$
(43)
$$\begin{aligned} \theta (y)\simeq & {} \sum \limits ^{2^{k-1}T} _{n=1} \theta _n(y) =\sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I_{nj}(y)\;\theta (y_{nj}) , \end{aligned}$$
(44)

and the derivatives can be written as

$$\begin{aligned} F^{m}(y)\simeq & {} \sum \limits ^{2^{k-1}T} _{n=1} F^{m}_n(y) =\sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I^{m}_{nj}(y)\;F(y_{nj}), \end{aligned}$$
(45)
$$\begin{aligned} Z^{m}(y)\simeq & {} \sum \limits ^{2^{k-1}T} _{n=1}Z^{m}_n(y) =\sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I^{m}_{nj}(y)\;Z(y_{nj}) , \end{aligned}$$
(46)
$$\begin{aligned} \theta ^m(y)\simeq & {} \sum \limits ^{2^{k-1}T} _{n=1} \theta ^m_n(y) =\sum \limits ^{2^{k-1}T} _{n=1} \sum \limits ^{M-1} _{j=0} I^m_{nj}(y)\;\theta (y_{nj}). \end{aligned}$$
(47)

Applying the points \(\{ {y}_{nj} \;| n=1,..., 2^{k-1}T, \;\; j=3,...,M-1 \}\) into Eqs. (19)–(24), we obtain

$$\begin{aligned}&F_{n}'''+ F_{n}'' F_{n} - F_{n}'^{2} +\frac{a^2}{c^2}+We\Big [F_{n} F_{n}^{iv}- 2F_{n}'''F_{n}'+ F_{n}''^{2} \Big ]=0 , \end{aligned}$$
(48)
$$\begin{aligned}&G'''_n + G''_n F_n - G'_n F'_n+We\Big [G^{iv}_n F_n-G'''_n F'_n+ G''_n F''_n- G'_n F'''_n \Big ]=A\gamma , \end{aligned}$$
(49)
$$\begin{aligned}&\theta ''_n +Pr_{eff}\; \theta '_n \; F_n+ \lambda \; Pr_{eff}\;\theta _n=0, \end{aligned}$$
(50)
$$\begin{aligned}&F_n(0)=0, \quad \quad F'_n(0) = \frac{1+ \beta F''_n(0)}{3 \beta We F''_n(0) +1}, \quad \quad F''_n(0)= s, \end{aligned}$$
(51)
$$\begin{aligned}&G_n(0) =0,\;\; G'_n(0)=\frac{\beta G''_n(0)}{1+\beta We F''_n(0)} \bigg [1 - 2 We \bigg ( \frac{1+\beta F''_n(0)}{3 \beta We F''_n(0)+1} \bigg ) \bigg ],\nonumber \\&\quad G''_n(0)= r, \end{aligned}$$
(52)
$$\begin{aligned}&\theta _n(0) = 1+ \alpha \; \theta '_n(0), \quad \quad \theta '_n(0) =t. \end{aligned}$$
(53)

An approximate value is chosen for s, r and t and the system of Eqs. (48)–(53) is solved for the first subinterval, i.e. \([0, 1/2^{k-1})\). The results of first subinterval are used as initial guess for second subinterval and this process is repeated for all subintervals. A root finding algorithm that satisfies \(F'(\infty )= a/c\), \(G''(\infty )=\gamma \) and \(\theta (\infty )=0\) is applied to modify the values of s, r and t, respectively.

4 Results and discussion

To find the solution of the problem, a numerical technique known as LWSCM is applied. A comparison of numerical data is made using available literature of Hussain et al [9] for no-slip boundary condition as shown in table 1. A deep analysis of this table demonstrates that the method has excellent agreement for the viscous case, and as the viscoelastic parameter increases the difference with the numerical data occurs. This is because of the undershoot and overshoot in the velocity profiles within the boundary layer observed in the work of Hussain et al [9]. However, the method implemented in this article has the ability to control the overshooting and undershooting phenomenon while solving these equations, which gives more accurate and stable solutions. Secondly, there is no limitation on the viscoelastic parameter by employing LWSCM; it is not possible to obtain the solutions beyond the critical value of viscoelastic parameter, i.e. \(We = 0.3257864\) by implementing the algorithm followed by [9]. Furthermore, this table also shows that the horizontal component of skin friction \(F''(0)\) increases on increasing the viscoelastic parameter Weissenberg number We for \(a/c>1\) and an opposite result is obtained for \(0<a/c<1\). It also indicates that for a fixed value of Weissenberg number We, horizontal skin friction component is an increasing function of stretching ratio parameter a/c. The influences of the We, a/c and slip parameter \(\beta \) on the horizontal and shear components of skin friction are numerically presented in table 2. It is observed that both \(F'(0)\) and \(H'(0)\) increase on increasing We and a/c, while they decrease with increase in slip \(\beta \). Table 3 shows the influences of the Weissenberg number We, stretching ratio parameter a/c, slip parameter \(\beta \), effective Prandtl number \(Pr_{eff}\), heat source/sink parameter \(\lambda \) and thermal slip parameter \(\alpha \) on the effective local Nusselt number \(-\theta '(0)\). It is clearly seen that decrease in \(Nu^*_x\) occurs due to increase in \(\lambda \) and \(\alpha \). Other parameters (We, a/c, \(\beta \) and \(Pr_{eff}\)) show increasing effects.

Figures 2 and 3 show the influence of the viscoelastic parameter We on the dimensionless horizontal velocity \(F'(y)\) in the presence of slip effects for the stretching ratio parameter \(a/c=1.2\), which correspond to the results that the stretching ratio parameter enhances the viscoelasticity effects. On the other hand, a increment in the Weissenberg number causes a decrease in the velocity profile for case \(0<a/c<1\). It is worth mentioning that no phenomenon of overshoot (for \(a/c>1\)) and undershoot (for \(a/c<1\)) in the velocity profile is observed. Figure 4 shows the effects of stretching ratio parameter a/c on the velocity profile. It is noted that the velocity increases for increasing a/c. Inverted boundary layer phenomenon is observed for \(a/c<1\). Figures 5 and 6 indicate the effects of slip parameter on the velocity profile for both the cases. These figures show the result that as slip is increased the velocity is increased for \(a/c>1\) and decreased for \(a/c<1\). The variation of shear component of skin friction \(H'(0)\) against We is plotted in figure 7. In the presence of slip, \(H'(0)\) is an increasing function of We. Figure 8 presents the effects of slip parameter on \(H'(0)\). An increase in slip parameter results in a decrease of \(H'(0)\). Figure 9 analyses the viscoelastic effects on the dimensionless temperature profile \(\theta \). Temperature and thermal boundary layer thickness decrease with increasing We, resulting from the fact that the viscoelasticity enhances the heat transfer rate, which causes reduction in fluid temperature inside the boundary layer. Figure 10 presents the change in temperature profile for various values of a/c. It is noticed that increase in the stretching ratio parameter causes a decrease in the temperature profile, which results in the enhancement of the heat transfer rate. Figure 11 is plotted to check the effects of slip parameter on the temperature profile. Increase in the slip parameter enhances the temperature. The effects of thermal slip \(\alpha \) on \(\theta (y)\) is plotted in figure 12. It can be seen that temperature inside the boundary layer decreases on increasing the thermal slip parameter. Figure 13 depicts the change in the temperature profile on changing the effective Prandtl number \(Pr_{eff}\). An increase in \(Pr_{eff}\) cause a decrease in temperature, which is due to the fact that thermal diffusivity reduces for large \(Pr_{eff}\). Figure 14 displays the heat source/sink effects on the temperature. Addition of heat source causes an increase in heat transfer rate, which results in an increase of temperature. On the other hand, addition of heat sink reduces the temperature.

Table 1 Comparison of the results for \(\beta =0\).
Full size table
Table 2 Effects of We, a/c and \(\beta \) on \(F''(0)\) and \(H'(0)\).
Full size table
Table 3 Effects of We, a/c, \(\beta \), \(Pr_{eff}\) and \(\lambda \) on \(-\theta '(0)\).
Full size table
Figure 2
figure 2

Effects of We on \(F'(y)\) when \(a/c>1\).

Full size image
Figure 3
figure 3

Effect of We on \(F'(y)\) when \(a/c<1\).

Full size image
Figure 4
figure 4

Effect of a/c on \(F'(y)\).

Full size image
Figure 5
figure 5

Effect of \(\beta \) on \(F'(y)\) when \(a/c>1\).

Full size image
Figure 6
figure 6

Effect of \(\beta \) on \(F'(y)\) when \(a/c<1\).

Full size image
Figure 7
figure 7

Effect of We on \(H'(y)\).

Full size image
Figure 8
figure 8

Effect of \(\beta \) on \(H'(y)\).

Full size image
Figure 9
figure 9

Effect of We on \(\theta (y)\).

Full size image
Figure 10
figure 10

Effect of a/c on \(\theta (y)\).

Full size image
Figure 11
figure 11

Effect of \(\beta \) on \(\theta (y)\).

Full size image
Figure 12
figure 12

Effect of \(\alpha \) on \(\theta (y)\).

Full size image
Figure 13
figure 13

Effect of \(Pr_{eff}\) on \(\theta (y)\).

Full size image
Figure 14
figure 14

Effect of \(\lambda \) on \(\theta (y)\).

Full size image

5 Conclusion

  • The undershoot and overshoot phenomenon in the velocity profiles within the boundary layer associated with the Walters-B fluid is controlled and a more accurate and stable solution is predicted.

  • It is observed that an increase in viscoelasticity enhances the fluid velocity for \(a/c >1\) and a reverse behaviour arises for \(0<a/c<1\). The temperature and thickness of thermal boundary layer increase with rising viscoelasticity of the fluid.

  • On increasing the stretching ratio parameter, the fluid velocity increases while temperature and thickness of thermal boundary layer decline. Inverted boundary layer phenomenon is observed for \(a/c<1\).

  • The presence of velocity slip enhances the velocity and temperature while an increment in thermal slip reduces the temperature.

  • Large value of effective Prandtl number reduces the temperature within the boundary layer.

  • Addition of heat source increases the temperature while addition of heat sink reduces the temperature.