Heat transfer between two parallel porous plates for Couette flow under pressure gradient and Hall current

Abstract

The aim of the present paper is to study the unsteady magneto-hydrodynamic viscous Couette flow with heat transfer in a Darcy porous medium between two infinite parallel porous plates considering Hall effect, and temperature dependent physical properties under constant pressure gradient. The parallel plates are assumed to be porous and subjected to a uniform suction from above and injection from below while the fluid is flowing through a porous medium that is assumed to obey Darcy’s law. A numerical solution for the governing nonlinear partial differential equations coupled with set of momentum equations and the energy equation including the viscous and Joule dissipations is adopted. The effect of the porosity of the medium, the Hall current and the temperature dependent viscosity and thermal conductivity on both the velocity and temperature distributions are investigated. It is found that the porosity number M has a marked effect on decreasing the velocity distribution (owing to a simultaneous increase in Darcy porous drag). Also the temperature T is decreased considerably with increasing porosity number. With increasing Hall current parameter m, the velocity component u (x-direction) is considerably increased, whereas velocity component w (z-direction) is reduced. Temperatures are decreased in the early stages of flow but effectively increased in the steady state with increasing m.

1 Introduction

The magnetic field on the Newtonian and non-Newtonian fluid flow has wide applications in chemical engineering, metallurgical engineering, and various industries. Researchers have considerable interest in the study of flow phenomenon between two parallel plates, because of its occurrence in rheomatic experiments to determine the constitutive properties of the fluid, in lubrication engineering, and in transportation and processing encountered in chemical engineering, etc. Devika et al (2013). Many research workers have paid their attention towards the application of fluid flow under the influence of magnetic field. Hartmann & Lazarus (1937), investigated the effect of a transverse uniform magnetic field on the flow of a viscous incompressible electrically conducting fluid between two infinite parallel plates. Exact solutions for the velocity fields were developed (Alpher 1961; Tao 1960; Sutton & Sherman 1965; Cramer & Pai 1973) under different physical effects. Attia (1998) examined the effect of Hall current on the velocity and temperature fields of an unsteady Hartmann flow with uniform suction and injection applied perpendicular to the plates. The influence of the dependence of the physical properties on temperature in the MHD Couette flow between parallel plates was studied (Soundalgekar et al 1979; Soundalgekar & Uplekar 1986; Klemp et al 1990; Attia & Kotb 1996; Attia 2005, 2007; Mostafa et al 2013).

The study of fluids flow through porous media has become very important in recent years because of its possible applications in many branches of Science and Technology, particularly in the field of Agricultural Engineering to study the underground water resources, seepage of water in river beds, in Chemical Engineering for filtration and purification process and in Petroleum Technology to study the movement of natural gas, oil and water through the oil reservoirs Ravikumar et al (2012). Many research workers have paid their attention towards the application of fluid flow in different category through porous medium in channels of various cross-sections (Nield & Kuznetsov 2010; Pal & Talukdar 2011; Das et al 2012; Attia & Mostafa 2013; Attia et al 2013, 2014).

In this paper, the transient Couette flow through a porous medium of a viscous, incompressible, electrically conducting fluid is investigated with heat transfer under constant pressure gradient. The viscosity and thermal conductivity of the fluid are assumed to vary with temperature while the Hall current is taken into consideration. The fluid is flowing between two electrically insulating porous plates and is acted upon by an axial constant pressure gradient, while the fluid is flowing through a porous medium that is assumed to obey Darcy’s law (Joseph et al 1982; Ingham & Pop 2002; Khaled & Vafai 2003). The upper plate moves with a uniform velocity while a uniform suction and injection and an external uniform magnetic field are applied perpendicular to the surface of the plates. The two plates are kept at two constant but different temperatures and the viscous and Joule dissipations are taken into consideration in the energy equation.

2 Description of the problem

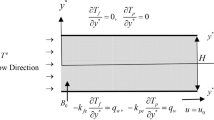
We have considered the fluid flows between two infinite horizontal parallel plates located at the y = ± h apart in the presence of uniform transverse constant magnetic field B _o applied parallel to y-axis which is normal to the planes of the plates in the positive direction, as shown in figure 1. We have considered the simple case where, B _o is fixed relative to the fluid. The two plates are porous, insulating and kept at two constant but different temperatures T ₁ for the lower plate and T ₂ for the upper plate with T ₂>T ₁. The upper plate moves with a uniform velocity U _o , whereas the lower plate is kept stationary. A constant pressure gradient $\vec {\nabla } p=-G$ is imposed in the axial x-direction, where G is prescribed constants and a uniform suction from above and injection from below, with velocity v _o, are applied impulsively at t = 0. The Hall effect is considered and accordingly, a z-component of the velocity is initiated. The viscosity and thermal conductivity of the fluid are dependent on temperature exponentially and linearly, respectively while the viscous and Joule dissipations are not neglected in the energy equation.

Figure 1

The geometry of the problem.

The flow in the porous medium deals with the analysis in which the differential equation governing the fluid motion is based on the Darcy’s law which considers the drag exerted by the porous medium. The fluid motion starts from rest at t = 0, and the no-slip condition at the plates implies that the fluid velocity has neither a z nor an x-component at y = ± h. The initial temperature of the fluid is assumed to be equal to T ₁ as the temperature of the lower plate. Since the plates are infinite in the x and z-directions, the physical quantities do not change in these directions which lead to one-dimensional problem.

3 Basic equations

The governing equations of this study are based on the conservation laws of mass, linear momentum and energy for both phases.

3.1 Momentum equations

The flow of the fluid is governed by the Navier–Stokes equation:

$$ \rho \frac{D\vec{\nu} }{Dt}=-\nabla p+\nabla .\left( {\mu \nabla \vec{\nu}} \right)+\vec J \wedge\vec B -\frac{\mu }{K}\vec {\nu}, $$

(1)

where, ρ is the density of the fluid, μ is the viscosity of the fluid, $\vec {{J}}$ is the current density, and $\vec {\nu }$ is the velocity vector of the fluid, which is given by:

$$\vec{{\nu}}=u(y,t)\vec{{i}}+{\nu}_{o} \vec{{j}}+w(y,t)\vec{{k}}. $$

If the Hall term is retained, the current density $\vec {{J}}$ is given by the generalized Ohm’s law (Hartmann & Lazarus 1937):

$$ \vec{{J}}=\sigma (\vec{{\nu}}\wedge \vec{{B}}_{o} -\beta (\vec{{J}}\wedge \vec{{B}}_{o} )), $$

(2)

where, σ is the electric conductivity of the fluid and β is the Hall factor (Sutton & Sherman 1965). Eq. (2) may be solved in $\vec {{J}}$ to yield:

$$ \vec{{J}}\wedge \vec{{B}}_{o} =-\frac{\sigma {B_{o}^{2}} }{1+m^{2}}((u+mw)\vec{{i}}+(w-mu)\vec{{k}}), $$

(3)

where, m is the Hall parameter and m = σβB _o . Thus, the two components of the momentum Eq. (1) read:

$$ \rho \frac{\partial u}{\partial t}+\rho v_{o} \frac{\partial u}{\partial y}=G+\mu \frac{\partial^{2}u}{\partial y^{2}}+\frac{\partial \mu }{\partial y}\frac{\partial u}{\partial y}-\frac{\sigma {B_{o}^{2}} }{1+m^{2}}(u+mw)-\frac{\mu }{\bar{{K}}}u, $$

(4)

$$ \rho \frac{\partial w}{\partial t}+\rho v_{o} \frac{\partial w}{\partial y}=\mu \frac{\partial^{2}w}{\partial y^{2}}+\frac{\partial \mu }{\partial y}\frac{\partial w}{\partial y}-\frac{\sigma {B_{o}^{2}} }{1+m^{2}}(w-mu)-\frac{\mu }{\bar{{K}}}w. $$

(5)

where, $\bar {{K}}$ is the Darcy permeability (Attia & Mostafa 2013) and the last term in the right sides of Eqs. (4) and (5) represent the porosity force in the x- and z-directions, respectively. It is assumed that the pressure gradient is applied at t = 0 and the fluid starts its motion from rest. Thus:

$$ t=0:u=w=0. $$

(6a)

For t>0, the no-slip condition at the plates implies that

$$ y=-h:u=w=0, $$

(6b)

$$ y=h:u=U_{o} ,\,\,w=0. $$

(6c)

3.2 Energy equations

The energy equation describing the temperature distribution for the fluid is given by Ingham & Pop (2002):

$$ \rho c_{p} \frac{\partial T}{\partial t}+\rho c_{p} \mathit{v}_{o} \frac{\partial T}{\partial y}=\frac{\partial }{\partial y}\left( {k\frac{\partial T}{\partial y}} \right)+\mu \left( {\left( {\frac{\partial u}{\partial y}} \right)^{2}+\left( {\frac{\partial w}{\partial y}} \right)^{2}} \right)+\frac{\sigma {B_{o}^{2}} }{1+m^{2}}\left( {u^{2}+w^{2}} \right), $$

(7)

where, T is the temperature of the fluid, c _p is the specific heat at constant pressure of the fluid, and k is thermal conductivity of the fluid. The last two terms in the right side of Eq. (7) represent the viscous and Joule dissipations, respectively.

The temperature of the fluid must satisfy the initial and boundary conditions:

$$ t=0:T=T_{1}, $$

(8a)

$$ t>0:T=T_{1} ,y=-h, $$

(8b)

$$ t>0:T=T_{2} ,y=h. $$

(8c)

The viscosity of the fluid is assumed to vary with temperature and is defined as, μ = μ _o f ₁(T). By assuming the viscosity to vary exponentially with temperature, the function f ₁(T) takes the form, f ₁(T) = exp(−a ₁(T − T ₁)) (Soundalgekar et al 1979). In some cases a ₁ may be negative, i.e. the coefficient of viscosity increases with temperature (Soundalgekar et al 1979; Joaquín et al 2010). Also the thermal conductivity of the fluid is varying with temperature as $k=k_{o} f_{2} \left (T \right )$. We assume linear dependence for the thermal conductivity upon the temperature in the form k = k _o (1 + b ₁(T − T ₁)), where the parameter b ₁ may be positive or negative (Eguia et al 2013).

3.3 Dimensionless equations

We introduce the following non-dimensional variables:

$$(\hat{{x}},\hat{{y}},\hat{{z}})=\frac{(x,y,z)}{h},\;\;\hat{{t}}=\frac{U_{o} t}{h},\;\hat{{G}}=\frac{hG}{\rho {U_{o}^{2}} },\;(\hat{{u}},\hat{{w}})=\frac{(u,w)}{U_{o} },\;\theta =\frac{T-T_{1} }{T_{2} -T_{1} }, $$

$\hat {{f}}_{1} (\theta )=e^{-a_{1} (T_{2} -T_{1} )\theta }=e^{-a\theta }, a$ is the viscosity variation parameter,

$\hat {{f}}_{2} (\theta )=1+b_{1} (T_{2} -T_{1} )\theta =1+b\theta , b$ is the thermal conductivity variation parameter,

S = v _o /U _o , is the suction parameter.

$Ha^{2}=\sigma {B_{o}^{2}} h^{2}/\mu _{o}$, Ha is the Hartmann number,

M = hμ _o /(ρU _o K), is the porosity parameter.

$R_{e} =\frac {\rho U_{0} h}{\mu _{0} }$, Reynolds number.

$\Pr =\mu _{o} c_{p} /k_{o}$, is the Prandtl number,

$Ec={U_{o}^{2}} /c_{p} (T_{2} -T_{1} )$, is the Eckert number.

Nu _L = (∂T/$\partial \hat {{y}})\hat {{y}}_{\mathrm {=-1}}$ is the Nusselt number at the lower plate,

Nu _U = (∂T/$\partial \hat {{y}})\hat {{y}}_{\mathrm {=1}}$ is the Nusselt number at the upper plate.

Using the above non-dimensional quantities, the governing dimensionless of the Momentum equations (4)–(8) read (the hats are dropped for simplicity):

$$ \frac{\partial u}{\partial t}+S\frac{\partial u}{\partial y}=G+\frac{f_{1} (\theta )}{R_{e} }\frac{\partial^{2}u}{\partial y^{2}}+\frac{1}{R_{e} }\frac{\partial f_{1} (\theta )}{\partial y}\frac{\partial u}{\partial y}-\frac{Ha^{2}}{R_{e} (1+m^{2})}(u+mw)-Mu, $$

(9)

$$ \frac{\partial w}{\partial t}+S\frac{\partial w}{\partial y}=\frac{f_{1} (\theta )}{R_{e} }\frac{\partial^{2}w}{\partial y^{2}}+\frac{1}{R_{e} }\frac{\partial f_{1} (\theta )}{\partial y}\frac{\partial w}{\partial y}-\frac{Ha^{2}}{R_{e} (1+m^{2})}(w-mu)-Mw. $$

(10)

With, the initial and boundary conditions:

$$ t=0:u=w=0, $$

(11a)

$$ t>0:y=-1,\,\,u=w=0, $$

(11b)

$$ t>0:y=1,u=1,\,\,w=0. $$

(11c)

In terms of the above non-dimensional quantities the governing dimensionless energy equations read:

$$\begin{array}{@{}rcl@{}} \frac{\partial \theta }{\partial t}+S\frac{\partial \theta }{\partial y}&=&\frac{1}{R_{e} \Pr }f_{2} (\theta )\frac{\partial^{2}\theta }{\partial y^{2}}+\frac{1}{R_{e} \Pr }\frac{\partial f_{2} (\theta )}{\partial y}\frac{\partial \theta }{\partial y}+\frac{Ec f_{1} (\theta )}{R_{e} }\left( {\left( {\frac{\partial u}{\partial y}} \right)^{2}+\left( {\frac{\partial w}{\partial y}} \right)^{2}} \right) \\ && +\frac{Ec Ha^{2}}{R_{e} (1+m^{2})}(u^{2}+w^{2}) \end{array} $$

(12)

With, the initial and boundary conditions:

$$ t=0:\theta =0, $$

(13a)

$$ t>0:\theta =0,y=-1, $$

(13b)

$$ t>0:\theta =1,y=1. $$

(13c)

4 Numerical method

The governing equations linear momentum (9–10) and energy (12) represent a system of coupled non-linear partial differential equations which are solved numerically under the initial and boundary conditions given by Eqs. (11) and (13) using the method of finite differences. The Crank–Nicolson implicit method is used at two successive time levels (Ames 1977). An iterative scheme is used to solve the linearized system of differential equations. The solution at a certain time step is chosen as an initial guess for next step and the iterations are continued till convergence, within a prescribed accuracy. Finally, the resulting block tri-diagonal system is solved using the generalized Thomas-algorithm (Ames 1977). Finite difference equations relating to the variables are obtained by writing the equations at the mid-point of the computational cell and then replacing the different terms by their second order central difference approximations in the y-direction. The diffusion terms are replaced by the average of the central differences at two successive time-levels. The computational domain is divided into meshes, were Δt and Δy represent time and space respectively.

We define the variables A = ∂u/∂y, B = ∂w/∂y and H = ∂𝜃/∂y to reduce the second order differential Eqs. (9), (10) and (12) to first order differential equations, and an iterative scheme is used at every time step to solve the linearized system of difference equations. All calculations are carried out for the non-dimensional variables and parameters given by, G = 5, Pr = 1, and Ec = 0.2. G is related to externally applied pressure gradient and the chosen given values for Pr and Ec are suitable for steam or water vapor. Grid-independence studies show that the computational domain $0<t<\infty$ and −1 < y < 1 is divided into intervals with step sizes Δt = 0.0001 and Δy = 0.005 for time and space, respectively. Smaller step sizes do not show any significant change in the results. Convergence of the scheme is assumed when all of the unknowns u, w, A, B, 𝜃 and H for the last two approximations differ from unity by less than 10⁻⁶ for all values of y in at every time step. Less than 7 approximations are required to satisfy this convergence criteria for all ranges of the parameters studied here.

5 Results and discussion

Figures 2–4 present the time development of the profiles of the velocity and temperature for various values of the Hall parameter m and for Ha = 1, S = 1, M = 1, a = 0.5 and b = 0.5. Figure 2, indicates that u increases with increasing m which can be attributed to the fact that an increment in m decreases the resistive force. Figure 3 shows that w decreases with increasing m which can be attributed to the fact that an increment in m increases the resistive force. Figure 4 shows that 𝜃 increases with increasing m for all values as a result of increasing the dissipations.

Figure 2

The evolution of the profile of: u; $\left ({\mathbf {a}}\right )m=0;\,\left ({\mathbf {b}}\right )m=1;\,\left ({\mathbf {c}} \right )m=2.\,\,(Ha=1$, S = 1, M = 1, a = 0.5, b = 0.5).

Figure 3

The evolution of the profile of w; (a) m = 1; (b) m = 2. (Ha =1, S = 1, M = 1, a = 0.5, b = 0.5).

Figure 4

The evolution of the profile of 𝜃; (a) m = 0; (b) m = 1; (c) m = 2. (Ha = 1, S = 1, M = 1, a = 0.5, b = 0.5).

Figures 5–7 show the time development of the profiles of the velocity and temperature for various values of the suction parameter S and for Ha = 1, m = 1, M = 1, a = 0.5 and b = 0.5. Figures 5 and 6 indicate that the velocity components u and w and their steady state time decrease with increasing the suction parameter S for all time. Figure 7 shows that the temperature 𝜃 and its steady state time decrease with increasing the suction parameter S for all time due to pumping fluid from lower cold regions to upper hot regions. Figures 6–8 show that the influence of the suction parameter on the velocity and temperature distributions becomes more pronounced as time develops.

Figure 5

The evolution of the profile of u; (a) S = 0; (b) S = 0.5; (c) S = 1. (Ha = 1, m = 1, M = 1, a = 0.5, b = 0.5).

Figure 6

The evolution of the profile of w; (a) S = 0; (b) S = 0.5; (c) S = 1. (Ha = 1, m = 1, M = 1, a = 0.5, b = 0.5).

Figure 7

The evolution of the profile of 𝜃: (a) S = 0; (b) S = 0.5; (c) S = 1. (Ha = 1, m = 1, M = 1, a = 0.5, b = 0.5).

Figure 8

The evolution of u at y = 0 for various values of a, and M: $\left ({\mathbf {a}} \right )M=0; \left ({\mathbf {b}} \right )M=1; \left ({\mathbf {c}} \right )M=2$. $\left ({Ha=1, m=1, S=1, b = 0.5} \right )$.

Figures 8–10 present the time progression of the velocity components u and w and the temperature 𝜃 at the center of the channel $\left ({\mathrm {y}=0} \right )$ for different values of M and a and for Ha = 1, m = 1, S = 1 and b = 0.5. Figures 8–9 indicate that u and w decrease with increasing M for all values as a result of the damping effect of the porosity. Figure 10 depicts that the temperature 𝜃 decreases with increasing M for all values as a result of the damping effect of the porosity which decreases the velocity and velocity gradients and, in turn, deceases the dissipations. By increasing the parameter, there is an increase in the velocity components and the temperature distribution for all values of M as shown in all figures.

Figure 9

The evolution of w at y = 0 for various values of a, and M: $\left ({\mathbf {a}} \right )M=0; \left ({\mathbf {b}} \right )M=1;\left ({\mathbf {c}} \right )M=2$. $\left ({Ha=1, m=1, S=1, b = 0.5}\right )$.

Figure 10

The evolution of 𝜃 at y = 0 for various values of a, and M: $\left ({\mathbf {a}} \right )M=0; \left ({\mathbf {b}} \right )M=1; \left ({\mathbf {c}} \right )M=2$. $\left ({Ha=1, m=1, S=1, b = 0.5} \right )$.

Figures 11 show the time development of the profiles of the velocity and temperature at the center of the channel $\left ({\mathrm {y}=0} \right )$ for various values of the Hartmann number H _a and for S = 1, m = 1, M = 1, a = 0.5 and b = 0.5. Figure 11a shows that with an increase of Hartmann number H _a , the magnitude of velocity component u is reduced because increase in the hydromagnetic drag force in Eq. (9). On the other hand, figure 11b indicates the increase in the velocity component w with a rise in Hartmann number Ha. Temperature 𝜃 is also reduced substantially with increasing Hartmann number H _a indicating that the regime is cooled with stronger magnetic fields (figure 11c).

Figure 11

The evolution of u, w, and 𝜃 aty =0 for various values of Hartmann numbers Ha:$\left ({\mathbf {a}} \right )u; \left ({\mathbf {b}} \right )w; \left ({\mathbf {c}} \right )\theta .\left ({S=1, m=1, a = 0.5, b = 0.5} \right )$.

Tables 1 and 2 present the variation of the Nusselt numbers at the lower and upper plates Nu _L and Nu _U , respectively, for different values of a and b and for Ha = 1, m = 1, S = 1 and M = 1. It is clear that increasing the parameters a or b there is a decrease in both Nu _L and Nu _U and its effect is more pronounced for Nu _U than Nu _L .

Table 1 Variation of the steady state Nusselt number at the lower plate Nu _L for various values of a and b $\left ({Ha=1,m=1,S=1,M=1} \right )$.

Table 2 Variation of the steady state Nusselt number at the upper plate Nu _U for various values of a and b $\left ({Ha=1,\,\,m=1,S=1,\,\,M=1} \right )$.

6 Conclusions

In the present work, the time varying MHD Couette flow through a porous medium between two parallel plates was investigated considering the Hall current under the action of a constant pressure gradient. The viscosity and thermal conductivity of the fluid are assumed to be temperature dependent. The effect of the porosity parameter M, the Hartmann number Ha, the Hall parameter m, the viscosity variation parameter a and the thermal conductivity variation parameter b on the velocity and temperature fields at the centre of the channel are discussed. The following conclusions are drawn from the study.

• (i) The Hall term gives rise to a velocity component w in the z-direction and affects the main velocity u in the x-direction.

• (ii) The parameter a has a marked effect on the velocity components u and w for all values of M. However, the parameter b has no significant effect on u or w.

• (iii) The porosity parameter M has a marked effect on the velocity and temperature distributions, however, its effect on the velocity and its steady state time is more pronounced than that for the temperature.

• (iv) The effect of Hartmann number H _a on the velocity components and temperature distribution has been studied. By increasing H _a , the x-component of the velocity u and temperature 𝜃 will decrease, while the z-component of the velocity w will increase.