1 Introduction

The blood flow in a stenosed artery and the effect of physical parameters on blood flow was analysed and studied in references [1,2,3,4]. Several investigators [5,6,7,8,9] discussed experimental and theoretical studies on blood flow, which are useful in the diagnosis and treatment of cardiovascular diseases. The presence of taper and its implications on physiologically significant parameters have been studied in [10, 11]. Many investigators [12,13,14,15,16] analysed the blood flow in a stenosed artery by assuming blood to be a Newtonian fluid. At low shear stress this is not applicable. Blood is generally assumed to be non-Newtonian due to the presence of formed elements. Haemoglobin is an iron-based protein inside red blood cells [4]. Several investigators [17,18,19,20,21,22,23,24] analysed the effects of magnetic field on blood flow through a stenosed artery. The practical applications of magnetic field in medicine has been investigated by Motta et al [25] and Midya et al [26]. Nadeem and Ijaz [27] analysed the effects of tapering on blood flow through stenosed artery.

Bugliarello and Sevilla [28] and Cokelet [29] experimentally showed that there exists a cell-free plasma layer in addition to a core region consisting of erythrocytes. Ponalagusamy [30] analysed the blood flow through stenosed arteries with axially variable peripheral layer thickness and variable slip at the wall, considering the fluids in both core and plasma regions as Newtonian. The effects of peripheral plasma layer thickness and yield stress on wall shear stress (WSS) and resistive impedance have been studied by Chaturani and Ponnalagarsamy [31]. Ponalagusamy and Tamil Selvi [32] developed a two-fluid model for blood where fluid in the core region is assumed to be Cassonian and the fluid in the peripheral region to be Newtonian taking slip velocity into account. Sankar and Lee [33] analysed the pulsatile flow of blood through stenosed arteries by assuming blood in the core region to be Cassonian fluid and plasma fluid to be Newtonian. Srivastava [34] investigated the two-phase model of blood flow through stenosed tubes in the presence of a peripheral layer. The problem of non-Newtonian and nonlinear blood flow through a stenosed artery has been analysed and solved by Chaturani and Ponnalagarsamy [35], where the non-Newtonian rheology of the flowing blood is characterized by a Herschel–Bulkley model. Ikbal et al [36] investigated mathematical model on non-Newtonian flow of blood through a stenosed artery in the presence of a transverse magnetic field by treating blood as a power-law fluid. The unsteady nature of blood flow has been further studied by Mustapha et al [37] and Eldesoky et al [38].

Jeffrey fluid belongs to the class of non-Newtonian fluid. The Jeffrey fluid as a generalization of Newtonian fluid and hence Newtonian fluid can be deduced from the Jeffrey fluid model as a special case. Many investigators have studied the flow of Jeffrey fluid in the presence of several factors. Akbar et al [39] have investigated a non-Newtonian fluid model for blood flow through a tapered artery with a stenosis by assuming blood as a Jeffrey fluid taking heat and mass transfer into account. Nallapu and Radhakrishnamacharya [40] developed a mathematical model of blood flow as a two-fluid model where the fluid in the core region is assumed to be a Jeffrey fluid and plasma in peripheral region to be a Newtonian fluid. Jyothi et al [41] analysed the flow of blood in a catherized tapered artery with nanoparticles considering blood as a Jeffrey fluid. The flow of Jeffrey fluid has been further discussed in references [42,43,44,45]. A non-Newtonian fluid model for blood flow through a tapered artery with a stenosis and variable viscosity by modelling blood as Jeffrey fluid has been developed by Ellahi et al [45]. It is of interest to mention that the combined effects of physiologically important parameters such as radially variable core viscosity and magnetic field have not been investigated in the aforementioned mathematical models.

It is argued that the non-homogeneity of blood should be accounted for while investigating the flow of blood in order to have a realistic model [46,47,48]. These facts imply that the viscosity of blood is a function of hematocrit in such a way that it varies radially more near the tube axis and decreases when one moves towards the arterial wall and becomes a constant in the peripheral plasma layer. Further, fluid dynamics of biological fluids under the influence of magnetic field emerges as a new trend to investigate their flow behaviour in the presence of a magnetic field. In view of these, a modest effort has been made to study the unsteady flow of blood as two-layered blood, where blood in the core region is assumed to be a Jeffrey fluid and plasma in peripheral layer to be Newtonian taking into account variable core viscosity and variable magnetic field.

2 Formulation of the problem

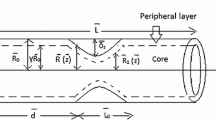
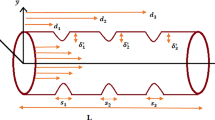
Let us consider an axially symmetric, pulsatile, laminar and fully developed flow of blood in a tapered artery with stenosis and radially variable transverse magnetic field. In the present study, the flow of blood is represented by a two-fluid model where the blood in the core region is assumed to be a Jeffrey fluid and the plasma in the peripheral region to be a Newtonian fluid. We consider a cylindrical coordinate system \((\bar{r}, \bar{\theta }, \bar{z})\), whose origin is located on the axis of tapered arterial stenosis (figures 1 and 2).

Figure 1
figure 1

Geometry of an axially non-symmetrical stenosed artery.

Full size image
Figure 2
figure 2

Geometry of the stenosed artery for different taper angles.

Full size image

The consistency function \(\bar{\mu }(\bar{r})\) may be written as follows:

$$\begin{aligned} \bar{\mu }(\bar{r}) = {\left\{ \begin{array}{ll} \bar{\mu _c}(\bar{r}) , 0\le \bar{r}\le \bar{R_1}(\bar{z})\\ \bar{\mu _p}, \bar{R_1}(\bar{z})\le \bar{r} \le \bar{R}(\bar{z}) \end{array}\right. } \end{aligned}$$
(1)

where \(\bar{\mu _c}(\bar{r})\) and \(\bar{\mu _p}\) are the viscosities of the central core fluid and the plasma, respectively; \(\bar{R_1}(\bar{z})\) and \(\bar{R}(\bar{z})\) are the radii of the central core region and the artery in the stenotic region. The momentum equations governing the unsteady incompressible Jeffrey fluid in the core region are [42]

$$\begin{aligned}&\frac{\partial \bar{v_c}}{\partial \bar{r}}+\frac{\bar{v_c}}{\bar{r}}+\frac{\partial u_c}{\partial \bar{z}}=0, \end{aligned}$$
(2)
$$\begin{aligned}&\quad \bar{\rho _c} \left( \frac{\partial }{\partial t}+\bar{v_c}\frac{\partial }{\partial \bar{r}}+\bar{u_c} \frac{\partial }{\partial \bar{z}}\right) \bar{u_c} = -\frac{\partial \bar{p}}{\partial \bar{z}} + \frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}(\bar{r} \bar{S}_{rz})+\frac{\partial }{\partial \bar{z}}(\bar{S}_{zz}) \\&\quad -\bar{\sigma }\bar{B_0}^2(\bar{r})\bar{u_c},\end{aligned}$$
(3)
$$\begin{aligned}&\quad \bar{\rho _c} \left( \frac{\partial }{\partial t}+\bar{v_c}\frac{\partial }{\partial \bar{r}}+\bar{u_c} \frac{\partial }{\partial \bar{z}}\right) \bar{v_c} = -\frac{\partial \bar{p}}{\partial \bar{r}} + \frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}(\bar{r} \bar{S}_{rr})+\frac{\partial }{\partial \bar{z}}(\bar{S}_{rz})-\frac{\bar{S}_{\theta \theta }}{\bar{r}}. \end{aligned}$$
(4)

The extra tensor \(\bar{S}\) for Jeffrey fluid is defined as follows:

$$\begin{aligned} \bar{S}=\frac{\bar{\mu _c}(\bar{r})}{(1+\lambda _1)}(\bar{\dot{\gamma }}+\bar{\lambda }_2 \bar{\ddot{\gamma }}) \end{aligned}$$
(5)

where \(\bar{\dot{\gamma }}\) is the shear rate, \(\bar{\ddot{\gamma }}\) is the rate of shear rate, \(\bar{\mu _c}(\bar{r})\) is the viscosity of core fluid and is given by \(\bar{\mu _c}(\bar{r}) = \bar{\mu _p}[1+\beta \bar{h}(\bar{r})]\), \(\bar{h}(\bar{r}) = h_m \left[ R_1^{m_2}-r^{m_2}\right] \), \(\lambda _1\) is the ratio of relaxation to retardation times, \(\bar{\lambda }_2\) is the retardation time, \(\bar{p}\) is the pressure, \(\bar{\rho _c}\) is the density of the core fluid, \(\bar{\sigma }\) is the electrical conductivity of the fluid and \(\bar{B_0}^2(\bar{r})\) is the variable magnetic field [39]; \(\bar{u_c}\) and \(\bar{v_c}\) are the velocity components in the core region along the z and r directions, respectively.

The momentum equations governing the unsteady Newtonian fluid in the peripheral plasma region are

$$\begin{aligned}&\frac{\partial \bar{v_p}}{\partial \bar{r}}+\frac{\bar{v_p}}{\bar{r}}+\frac{\partial \bar{u_p}}{\partial \bar{z}} = 0 \end{aligned}$$
(6)
$$\begin{aligned}&\quad \bar{\rho _p}\left( \frac{\partial }{\partial \bar{t}}+\bar{v_p} \frac{\partial }{\partial \bar{r}}+\bar{u_p}\frac{\partial }{\partial \bar{z}}\right) \bar{u_p} = -\frac{\partial \bar{p}}{\partial z} +\bar{\mu _p}\left[ \frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}\left( \bar{r}\frac{\partial \bar{u_p}}{\partial \bar{r}}\right) +\frac{\partial ^2 \bar{u_p}}{\partial \bar{z}^2}\right] \\&\quad -\bar{\sigma }\bar{B_0}^2(\bar{r})\bar{u_p} \end{aligned}$$
(7)
$$\begin{aligned}&\quad \bar{\rho _p}\left( \frac{\partial }{\partial \bar{t}}+\bar{v_p} \frac{\partial }{\partial \bar{r}}+\bar{u_p}\frac{\partial }{\partial \bar{z}}\right) \bar{v_p} = -\frac{\partial \bar{p}}{\partial \bar{r}} +\bar{\mu _p}\left[ \frac{1}{\bar{r}}\frac{\partial }{\partial \bar{r}}\left( \bar{r}\frac{\partial \bar{v_p}}{\partial \bar{r}}\right) +\frac{\partial ^2 \bar{v_p}}{\partial \bar{z}^2}-\frac{\bar{v_p}}{\bar{r}^2}\right] \end{aligned}$$
(8)

where \(\bar{\rho _p}\) is the density of plasma fluid and \(\bar{\mu _p}\) is the viscosity of fluid in plasma region; \(\bar{u_p}\) and \(\bar{v_p}\) are the velocity components of plasma in \(\bar{z}\) and \(\bar{r}\) directions respectively.

The following non-dimensional variables are introduced:

$$\begin{aligned} r&=\frac{\bar{r}}{\bar{R_0}}, z = \frac{\bar{z}}{\bar{L_0}}, t = \bar{\omega }\bar{t}, u_c = \frac{\bar{u_c}}{\bar{u_0}}, u_p = \frac{\bar{u_p}}{\bar{u_0}}, R_1 = \frac{\bar{R_1}}{\bar{R_0}}, M^2(r)=\frac{\bar{B_0}^2(\bar{r}) \bar{\sigma }\bar{R_0}^2}{\bar{\mu _p}},\\ p&= \frac{\bar{p}\bar{R_0}^2}{\bar{u_0}\bar{\mu _p}\bar{L_0}}, \rho = \frac{\bar{\rho _p}}{\bar{\rho _c}}, \alpha ^2 = \frac{\bar{\rho _p}\bar{\omega }\bar{R_0}^2}{\bar{\mu _p}}, Re = \frac{\bar{\rho }_p \bar{u}_0\bar{R}_0}{\bar{\mu }_p}. \end{aligned}$$
(9)

From literature [49, 50], the values of the average velocity (\(\bar{u}_0\)) of flow in a uniform artery and its radius (\(\bar{R}_0\)) are, respectively, taken as 1 cm/s and 0.1 cm.

The appropriate equations in non-dimensional form governing the pulsatile flow of Jeffrey fluid in the case of a slightly tapered artery with mild stenosis (taper angle \(< 3^o\) and \(\frac{\bar{\delta _s}}{\bar{R_0}}<< 1\)) are obtained as follows (see Appendix A).

In the core region \((0\le r\le R_1(r))\)

$$\begin{aligned} \frac{\alpha ^2}{\rho _0} \frac{\partial u_c}{\partial t} = -\frac{\partial p}{\partial z}+\frac{1}{1+\lambda _1}\left[ \frac{1}{r}\frac{\partial }{\partial r}\right] \left\{ 1+\beta h_m \left( R_1^{m_2}-r^{m_2}\right) \right\} \frac{\partial u_c}{\partial r}-M^2(r) u_c. \end{aligned}$$
(10)

In the peripheral plasma region \((R_1(r)\le r \le R)\)

$$\begin{aligned} \alpha ^2 \frac{\partial u_p}{\partial t} = -\frac{\partial p}{\partial z}+\frac{\partial ^2 u_p}{\partial r^2}+\frac{1}{r}\frac{\partial u_p}{\partial r}-M^2(r)u_p \end{aligned}$$
(11)

where \(M(r) = M e^{\alpha _1 (R-r)}\) [4].

The main motive mechanism for blood flow is the prevailing pressure gradient. The pressure gradient is given by \(-\frac{\partial p}{\partial z}(z,t) = A_0+A_1 \text{cos}(t)\).

The corresponding boundary conditions are

  1. (i)

    \(\frac{\partial u_c}{\partial r} = 0\) at \(r = 0\),

  2. (ii)

    \(u_c = u_p\) at \(r = R_1\),

  3. (iii)

    \((\tau )_p = (\tau )_c\) at \(r = R_1\) and

  4. (iv)

    \(u_p = 0\) at \(r = R\).

The non-dimensional form of flow geometry is given by

$$\begin{aligned} R(z) = {\left\{ \begin{array}{ll} \begin{aligned} (1 - \psi z)[1-B\left\{ (z-d)-(z-d)^{n_1}\right\} ], \\ d\le z\le d+1 \end{aligned}\\ 1-\psi z, {\text {otherwise}} \end{array}\right. } \end{aligned}$$
(12)

where \(B=\frac{\delta _s n_1^{\frac{n_1}{n_1-1}}}{n_1-1}\) , \(\psi = \tan \phi \) and \(\phi \) is the taper angle. For converging tapering, \(\phi \) becomes greater than 0, \(\phi < 0\) indicates diverging tapering and \(\phi = 0\) for the case of non-tapered artery (arterial stenosis).

3 Solution of the problem

The implicit difference scheme for Eq. (10) is as follows [51]:

$$\begin{aligned} u_c&= \frac{(u_c)_{i,j}^{k+1}+(u_c)_{i,j}^{k}}{2},\\ \frac{\partial u_c}{\partial t}&= \frac{(u_c)_{i,j}^{k+1}-(u_c)_{i,j}^{k}}{\Delta t},\\ \frac{\partial u_c}{\partial r}&= \frac{(u_c)_{i,j+1}^{k+1}-(u_c)_{i,j-1}^{k+1}+(u_c)_{i,j+1}^{k}-(u_c)_{i,j-1}^{k}}{4\Delta r}, \end{aligned}$$
$$\frac{\partial ^2 u_c}{\partial r^2}= \frac{(u_c)_{i,j+1}^{k+1}-2(u_c)_{i,j}^{k+1}+(u_c)_{i,j-1}^{k+1}+(u_c)_{i,j+1}^{k}-2(u_c)_{i,j}^{k}+(u_c)_{i,j-1}^{k}}{2(\Delta r)^2}.$$
(13)

Using these finite-difference approximations (13), Eq. (10) becomes

$$\begin{aligned}&\left[ \frac{X(r_j)}{2(\Delta r)^2}+\frac{S(r_j)}{4\Delta r}\right] (u_c)_{i,j+1}^{k+1}-\left[ \frac{X(r_j)}{(\Delta r)^2}+\frac{\alpha ^2}{\Delta t}+\frac{M^2(r_j)}{2}\right] (u_c)_{i,j}^{k+1}+\left[ \frac{X(r_j)}{2(\Delta r)^2}-\frac{S(r_j)}{4\Delta r}\right] (u_c)_{i,j-1}^{k+1}\\ &= -(A_0+A_1 \text{cos}(t^{k}))-\left[ \frac{X(r_j)}{2(\Delta r)^2}+\frac{S(r_j)}{4\Delta r}\right] (u_c)_{i,j+1}^{k}+\left[ \frac{X(r_j)}{(\Delta r)^2}+\frac{\alpha ^2}{\Delta t}+\frac{M^2(r_j)}{2}\right] (u_c)_{i,j}^{k}\\ &\quad -\left[ \frac{X(r_j)}{2(\Delta r)^2}-\frac{S(r_j)}{4\Delta r}\right] (u_c)_{i,j-1}^{k} \end{aligned}$$
(14)

where

$$\begin{aligned} X(r_j)= & {} r_j \left[ 1+\beta h_m\left( R_1^{m_2}-r_j^{m_2}\right) \right] , \\ S(r_j)= & {} \frac{1}{(1+\lambda _1)r_j}\left[ 1+\beta h_m\left( R_1^{m_2}-(m_2+1)r_j^{m_2}\right) \right] . \end{aligned}$$

Adopting the following implicit scheme:

$$\begin{aligned} u_p &= \frac{(u_p)_{i,j}^{k+1}+(u_p)_{i,j}^{k}}{2},\\ \frac{\partial u_p}{\partial t} &= \frac{(u_p)_{i,j}^{k+1}-(u_p)_{i,j}^{k}}{\Delta t},\\ \frac{\partial u_p}{\partial r} &= \frac{(u_p)_{i,j+1}^{k+1}-(u_p)_{i,j-1}^{k+1}+(u_p)_{i,j+1}^{k}-(u_p)_{i,j-1}^{k}}{4\Delta r}, \end{aligned}$$
$$\frac{\partial ^2 u_p}{\partial r^2} = \frac{(u_p)_{i,j+1}^{k+1}-2(u_p)_{i,j}^{k+1}+(u_p)_{i,j-1}^{k+1}+(u_p)_{i,j+1}^{k}-2(u_p)_{i,j}^{k}+(u_p)_{i,j-1}^{k}}{2(\Delta r)^2},$$
(15)

Eq. (11) becomes

$$\begin{aligned}&\left[ \frac{r_j}{2(\Delta r)^2}+\frac{1}{4\Delta r}\right] (u_p)_{i,j+1}^{k+1}-\left[ \frac{r_j}{(\Delta r)^2}+\frac{r_j \alpha ^2}{\Delta t}+\frac{M^2(r_j)}{2}\right] (u_p)_{i,j}^{k+1}\\&+\left[ \frac{r_j}{2(\Delta r)^2}-\frac{1}{4\Delta r}\right] (u_p)_{i,j-1}^{k+1} = -r_j(A_0+A_1 \cos(t^{k}))\\&-\left[ \frac{r_j}{2(\Delta r)^2}+\frac{1}{4\Delta r}\right] (u_p)_{i,j+1}^{k} +\left[ \frac{r_j}{(\Delta r)^2}+\frac{r_j \alpha ^2}{\Delta t}+\frac{M^2(r_j)}{2}\right] (u_p)_{i,j}^{k}\\&-\left[ \frac{r_j}{2(\Delta r)^2}-\frac{1}{4\Delta r}\right] (u_p)_{i,j-1}^{k} \end{aligned}$$
(16)

where \(M(r_j) = M e^{\alpha _1 (R-r_j)}\) [4]. Equations (14) and (16) are solved by the Thomas algorithm to obtain velocities in the core region and plasma region, respectively. In order to solve Eqs. (14) and (16) we need initial velocities for \(u_c\) and \(u_p\).

In the case of a two-fluid flow with radially variable magnetic field, the initial velocities for \(u_c\) and \(u_p\) can be numerically obtained from

$$\begin{aligned} 0= & {} (A_0+A_1)+\frac{1}{1+\lambda _1}\left[ \frac{\partial ^2 u_c}{\partial r^2}+\frac{1}{r} \frac{\partial u_c}{\partial r}\right] -M^2(r) u_c, \end{aligned}$$
(17)
$$\begin{aligned} 0= & {} (A_0+A_1)+\frac{\partial ^2 u_p}{\partial r^2}+\frac{1}{r}\frac{\partial u_p}{\partial r}-M^2(r) u_p. \end{aligned}$$
(18)

Using the following finite-difference approximations in Eqs. (17) and (18)

$$\begin{aligned} \frac{\partial u_c}{\partial r}&= \frac{(u_c)_{i,j+1}-(u_c)_{i,j}}{\Delta r}, \frac{\partial ^2 u_c}{\partial r^2} = \frac{(u_c)_{i,j+1}-2(u_c)_{i,j}+(u_c)_{i,j-1}}{(\Delta r)^2}, \\ \frac{\partial u_p}{\partial r}&= \frac{(u_p)_{i,j+1}-(u_p)_{i,j}}{\Delta r}, \frac{\partial ^2 u_p}{\partial r^2} = \frac{(u_p)_{i,j+1}-2(u_p)_{i,j}+(u_p)_{i,j-1}}{(\Delta r)^2}, \end{aligned}$$
(19)

we get the following difference equations:

$$\begin{aligned} -(A_0+A_1)(1+\lambda _1)r_j&= \left[ \frac{r_j}{(\Delta r)^2}+\frac{1}{\Delta r}\right] (u_c)_{i,j+1} -\left[ \frac{2r_j}{(\Delta r)^2}+\frac{1}{\Delta r}+(1+\lambda _1)r_j\right. \\&\left. M^2(r_j)\right] (u_c)_{i,j} +\frac{r_j}{\Delta r)^2} (u_c)_{i,j-1}, \end{aligned}$$
(20)
$$\begin{aligned} -(A_0+A_1) r_j&= \left[ \frac{r_j}{(\Delta r)^2}+\frac{1}{\Delta r}\right] (u_p)_{i,j+1} -\left[ \frac{2r_j}{(\Delta r)^2}+\frac{1}{\Delta r}+r_j M^2(r_j)\right] (u_p)_{i,j}\\&+\frac{r_j}{(\Delta r)^2} (u_p)_{i,j-1}. \end{aligned}$$
(21)

Solving this system of equations, initial values for \(u_c\) and \(u_p\) can be obtained.

The non-dimensional shear stress in the core region is given by

$$\begin{aligned} {\mathbf{S}}_{rz} = \frac{1+\beta h_m \left( R_1^{m_2}-r^{m_2}\right) }{1+\lambda _1} \frac{\partial u_c}{\partial r}. \end{aligned}$$
(22)

The non-dimensional form of shear stress in the plasma region is expressed as follows:

$$\begin{aligned} {\mathbf{S}}_{rz} = \frac{\partial u_p}{\partial r}. \end{aligned}$$
(23)

The non-dimensional shear stress at the wall is given as follows:

$$\begin{aligned} \tau _w = \left( \frac{\partial u_p}{\partial r}\right) _{r = R}. \end{aligned}$$
(24)

The flow rate \(Q_c(z,t)\) in the core region can be obtained from the relation

$$\begin{aligned} Q_c(z,t) = 2\sum _{r=0}^{R_1(z)} ru_c(r,z,t) \Delta r. \end{aligned}$$
(25)

The flow rate \(Q_p(z,t)\) in the peripheral plasma region is given by the relation

$$\begin{aligned} Q_p(z,t) = 2\sum _{r=R_1(z)}^{R(z)} ru_p(r,z,t) \Delta r. \end{aligned}$$
(26)

The total flow rate is \(Q(z,t) = Q_c(z,t)+Q_p(z,t)\), which implies

$$\begin{aligned} Q(z,t)&= 2\sum _{r = 0}^{R_1(z)}ru_c (r,z,t) \Delta r\\&+2\sum _{r = R_1(z)}^{R(z)}ru_p (r,z,t) \Delta r \end{aligned}$$
(27)

where \(R_1(z) = \gamma R(z), \gamma = 1-\frac{\delta (z)}{R(z)}\) and \(\delta (z)\) is the plasma layer thickness [4].

The flow resistance \(\lambda \) is defined as follows:

$$\begin{aligned} \lambda = \sum _0^z \left[ \frac{-\frac{\partial p}{\partial z} (z,t)}{Q(z,t)}\right] \Delta z \end{aligned}$$
(28)

where z is any point in the section of tapered arterial stenosis. Flow resistance values are obtained by substituting \( -\frac{\partial p}{\partial z}(z,t) = A_0+A_1{\mathrm{cos}} \) t and Eq. (27) in Eq. (28).

4 Results and discussion

The governing equations of the system are solved numerically using Crank–Nicholson finite-difference schemes to discretize the spacial derivatives. The flow region has been discretized by taking the step size in the radial direction \(\Delta r = 0.001\) and the time step size is taken to be \(\Delta t = 0.001\) in order to guarantee the convergence of the numerical solution to the sixth order. Hence, the solution domain (the \(r-z\) plane) is divided into 10,00,000 meshes in order to compute the required numerical results, which could be useful to predict the actual flow phenomenon. Also, it is observed that further reduction in \(\Delta r\) and \(\Delta t\) does not bring about any substantial change, which leads to the stability of the numerical techniques. MATLAB programming codes are developed to compute the numerical values for velocity profile, WSS and flow resistance for different values of the parameters involved in the present study.

When blood flows in a uniform artery, the variation of the axial velocity profiles of the one-fluid model for the steady flow of Newtonian fluid and the two-fluid model consisting of Jeffrey fluid in the core region and Newtonian fluid in the peripheral region along with the experimental results of [28] for blood containing 40% RBC has been displayed in figure 3. It is observed that the rheology of blood behaves like that of a Jeffrey fluid than that of a Newtonian fluid. A comparative study of the present numerical results with the corresponding steady-flow solutions obtained by [40] and the steady flow of Newtonian fluid has been shown in figure 3. One of the remarkable results is that the axial velocity obtained from the present study seems to be closer to the experimental result [28] for \(\beta = 2, m_2 = 2, h_m = 0.4, \lambda _1 = 0.1\). Based on the results obtained from the present investigation, one may infer that the Jeffrey parameter, variable viscosity and the plasma layer thickness affect the axial flow velocity. Hence it is important to analyse the effect of these parameters in this blood flow model. It is pertinent to point out here that good agreement between the present results and the experimental results [28] has been found, in the sense that the experimental results lie within the range of the presently computed values as displayed in figure 3.

Figure 3
figure 3

Velocity distribution with radial distance.

Full size image

The axial variation of WSS for different values of parameters involved in the present study is depicted in figures 4–7. Figures 4– 7 show that there is an increase in the WSS until it reaches the midpoint of the stenotic region, and decreases in the downstream of the region. The effect of maximum stenotic height (\(\delta _s\)) can be observed from figure 4. As the stenotic height increases, the WSS increases. Figure 5 shows the variation of WSS with axial distance for different values of radially variable magnetic field. Increase in parameter \(\alpha _1\) causes WSS to increase. The magnitude of WSS is comparatively lower in the case of Jeffrey fluid without magnetic field. Therefore the presence of magnetic field induces higher shear stress at the wall.

Figure 4
figure 4

Variation of wall shear stress with axial distance for different values of maximum stenotic height (\(\delta _s\)) taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \alpha ^2 = 1, \lambda _1 = 0.1, \gamma = 0.8\) and \(t = 1.\)

Full size image
Figure 5
figure 5

Variation of wall shear stress with axial distance for different values of M and \(\alpha _1\) taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \alpha ^2 = 1, \lambda _1 = 0.1, \gamma = 0.8\) and \(t = 1.\)

Full size image

Figure 6 is plotted to see the axial variation of WSS in the presence of a constant magnetic field and variable magnetic field for the cases of converging tapered (\(\psi = 0.01\)), non-tapered (\(\psi = 0\)) and diverging tapered artery (\(\psi = - 0.01\)). It can be observed from figure 6 that WSS increases in the upstream of the stenotic region, reaches maximum at the midpoint of the throat and decreases in the downstream of the region. WSS is found to be more in converging tapered artery than in non-tapered and diverging tapered artery. The variation of WSS in case of variable magnetic field is comparatively higher than in constant magnetic field. It is pertinent to note that as compared with Jeffrey fluid with variable magnetic fluid, WSS is higher in the case of constant magnetic field. Figure 7 shows the effects of time parameter t together with pulsatile Reynolds number \(\alpha ^2\). The results presented in figure 7 reveal that WSS is negatively increased as the pulsatile Reynolds number \(\alpha ^2\) increases for a given value of time t.

Figure 6
figure 6

Axial variation of wall shear stress for different values of \(\psi \) with respect to constant magnetic field and variable magnetic field taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \alpha ^2 = 1, \lambda _1 = 0.1, \gamma = 0.8\) and \(t = 1.\)

Full size image
Figure 7
figure 7

Axial variation of wall shear stress for different values of \(\alpha ^2\) and t taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \lambda _1 = 0.3, \gamma = 0.8, M = 2\) and \(\alpha _1 = 0.1.\)

Full size image

The important predictions of the present investigation are enumerating the combined effects of different values of Jeffrey parameter \((\lambda _1)\), the plasma layer thickness (in terms of \(\gamma \)), the magnetic parameter (M), the parameter (\(\alpha _1\)) involved in the expression of radially variable magnetic field, the taper angle (\(\psi \)), the parameters involved in the expression of core fluid viscosity (\(\beta , h_m, m_2\)) , time t, the pulsatile Reynolds number (\(\alpha ^2\)) and the axial distance (z) on the resistive impedance (figures 8–12). Figure 8 displays the influence of peripheral layer thickness on the resistive impedance when the other parameters are held constant. The increase in the peripheral plasma layer thickness (or a decrease in the parameter \(\gamma \)) leads to a decrease in the resistive impedance. Figure 8 reveals that for a lower value of peripheral plasma layer thickness, the percentage of increase in the axial variation of flow resistance becomes high but this behaviour becomes less dominant for a higher value of peripheral plasma layer thickness.

Figure 8
figure 8

Axial variation of flow resistance (\(\lambda \)) for different values of \(\lambda _1\) and \(\gamma \) taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \alpha ^2 = 1, M = 1, \alpha _1 = 0.1\) and \(t = 1.\)

Full size image

Figure 9 depicts the effect of radially variable magnetic field on resistive impedance. It is observed from figure 9 that the blood flow experiences higher resistive impedance for larger values of magnetic field parameter M. It is of interest to mention that the nature of radially varying magnetic field induces higher flow resistance in comparison with that of a constant applied magnetic field. Blood flowing through the tapered arterial stenosis experiences lower flow resistance in the case of Jeffrey fluid without magnetic field than in the presence of magnetic field. Hence, it can be argued that the presence of magnetic field slows down the blood flow, which is further aggravated by increasing the parameter \(\alpha _1\) involved in the expression of radially variable magnetic field. As the value of the parameter \(\alpha _1\) increases, the rate of increase in the flow resistance is less for the lower value of magnetic number M whereas it becomes higher for the higher value of magnetic number M. Figure 10 displays the axial variation of flow resistance with respect to constant and variable magnetic fields in the case of converging tapered, non-tapered and diverging tapered artery. The nature of radially variable magnetic field makes flowing blood to experience more resistive impedance. Converging tapered artery exhibits comparatively high resistive impedance than non-tapered and diverging tapered arteries.

Figure 9
figure 9

Variation of resistive impedance (\(\lambda \)) with axial distance for different values of M and \(\alpha _1\) taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \alpha ^2 = 1, \lambda _1 = 0.1, \gamma = 0.8\) and \(t = 1.\)

Full size image
Figure 10
figure 10

Axial variation of flow resistance (\(\lambda \)) for different values of \(\psi \) with respect to constant magnetic field and variable magnetic field taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \alpha ^2 = 1, \lambda _1 = 0.1, \gamma = 0.8\) and \(t = 1.\)

Full size image

The numerical values of flow resistance for different values of axial distance and the parameters (\(\beta , h_m, m_2\)) involved in the core viscosity have been computed and displayed in figure 11. Hematocrit is the main factor that determines the blood viscosity. The resistance to flow increases as hematocrit level increases. Increase in \(\beta \) leads to increase in flow resistance. The pertinent role of the parameter \(m_2\) involved in the profile of core viscosity has been studied and it is observed that increase in the parameter \(m_2\) leads to decrease in the flow resistance, which is a new information, for the first time, added to the literature. The significance of unsteady nature of blood flow can be observed from figure 12. As time parameter t increases, the resistance to flow increases. The magnitudes of flow resistances are higher in the case of blood flow in unsteady state than in steady state.

Figure 11
figure 11

Variation of flow resistance with axial distance for different values of parameters \(\beta , h_m, m_2\) involved in variable viscosity taking \(\psi = 0.01, \alpha ^2 = 1, \lambda _1 = 0.1, \gamma = 0.8, M = 1, \alpha _1 = 0.1\) and \(t = 1.\)

Full size image
Figure 12
figure 12

Axial variation of flow resistance for different values of \(\alpha ^2\) and t taking \(\beta = 2, h_m = 0.4, m_2 = 2, \psi = 0.01, \lambda _1 = 0.1, \gamma = 0.8, M = 1\) and \(\alpha _1 = 0.1.\)

Full size image

5 Conclusion

The present mathematical model sheds new light on investigating the combined effects of Jeffrey parameter, peripheral layer thickness, magnetic field parameter, taper angle, hematocrit, the parameters (\(\beta , m_2\)) involved in profile of core viscosity and time on the physiologically important quantities such as WSS and resistive impedance. Two-fluid models have been considered where the fluid in the core region is assumed to be a Jeffrey fluid and plasma in the peripheral plasma region as a Newtonian fluid with variable viscosity under the influence of variable magnetic field. Furthermore, the parameters involved in the present investigation certainly bear the potential to influence the flow characteristics such as flow velocity, WSS and flow resistance to considerable extent. The flow variables such as velocity, WSS and flow resistance are computed numerically. It is pertinent to point out here that there is a good agreement between the present results and the experimental results [28] and it has been found that that the experimental results lie within the range of the presently computed values of axial velocity as displayed in figure 3.

It is well known that accurately measuring the arterial WSS in the case of pulsatile flow in a tapered stenosed tube is very difficult and 20–50% experimental errors might occur in the estimation of WSS [7]. Furthermore, the inter-correlation between the fluid characteristics and atherosclerotic infection exposes a prevailing association during higher value of WSS, pulsatile nature of WSS, intimal condensing and plaque formation [2, 6, 46]. Hence, a precise prediction of WSS distribution is particularly useful in the thorough understanding of the effects of blood flow on endothelial cells. In view of importance of analysing the variation of WSS with respect to parameters involved in the present work, figures 4–7 have been prepared for the WSS distribution. It is observed that WSS is increased by increasing the values of Jeffrey parameter, magnetic number (Hartmann number), the parameters \(\beta \), \( \alpha _1\), hematocrit and the nature of converging tapered artery. The increase in the peripheral plasma layer thickness (or a decrease in the parameter \(\gamma \)), the parameter (\(m_2\)) and pulsatile Reynolds number (\(\alpha ^2\)) leads to a decrease in WSS.

The resistive impedance has been thought to be one of the physiologically important flow variables, which is to be investigated along with the effects of other parameters on it due to the fact that it envisages whether the required amount of blood (carrying nutrients and oxygen) supply to vital organs (heart, brain, kidneys, etc.) is ensured or not. The influence of the radially variable magnetic field and constant magnetic field on the flow resistance and WSS has been thoroughly investigated due to their various applications in medical sciences, including transport of drugs using magnetic particles as drug carriers for targeted drug delivery, reducing blood flow at the time of surgery, separating red cells from blood and cancer tumour treatment. The peripheral plasma layer thickness, the rheological behaviour of blood as a Jeffrey fluid, the constant applied magnetic field, the diverging tapered arterial stenosis and the power-law parameter involved in the core fluid viscosity reduce the resistance to flow, which, in turn, leads to normalizing the exiting abnormal blood flow to a greater extent and ultimately preventing sudden death.

It is theoretically observed in the present study that as compared with the case of flow in a non-tapered arterial stenosis, the percentage increase in WSS at the midpoint of stenotic region (\(z = 2.5\)) due to the presence of convergent tapering in the stenosed artery becomes 12.39% while the percentage decrease in WSS (at \(z = 2.5\)) due to the presence of divergent tapering in the stenosed artery becomes 10.41%. Further, the percentage increase in the flow resistance (at \(z = 3.0\)) due to the presence of convergent tapering in the stenosed artery becomes 41.84% while the percentage decrease in the flow resistance (at \(z = 3.0\)) due to the presence of divergent tapering in the stenosed artery becomes 24.67%. The observed results show that the effect of tapering in blood vessel on flow characteristics (WSS and flow resistance) is significant even for the case of mild tapering (\(\psi = 0.05\) or −0.05).

Although the present analysis enlightens the effects of pulsatility, radially variable magnetic field and core fluid viscosity, non-uniform cross-section of artery and non-Newtonian rheology on the flow characteristics, the mathematical model has to be further extended by taking into account several properties of blood. Apart from the pulsatile nature of the blood flow, blood is a concentrated mixture of viscoelastic particles. Blood flow in the arteries shows many other fluid dynamic complexities such as curvature, viscoelastic nature, tapering, narrowing and branching, and hence velocity, flow rate, WSS and resistive impedance will be affected by these phenomena [52]. Further, the motion and nature of the arterial wall are to be considered. Hence, an active research has to be performed in these directions to develop a realistic model that overcomes the limitations of this study. In view of this, a modest effort will be made to investigate the problem of blood flow by incorporating the factors mentioned earlier (two or three factors at a time, impossible to consider all the factors simultaneously) and the numerical findings will be published in the future papers.