Numerical solution of fuzzy boundary value problems using Galerkin method

Abstract

This paper proposes a new technique based on Galerkin method for solving nth order fuzzy boundary value problem. The proposed method has been illustrated by considering three different cases depending upon the sign of coefficients with benchmark example problems. To show the applicability of the proposed method, an application problem related to heat conduction has also been studied. The results obtained by the proposed methods are compared with the exact solution and other existing methods for demonstrating the validity and efficiency of the present method.

1 Introduction

In recent years, the study of fuzzy differential equations (FDEs) has been expanding rapidly as a new branch of fuzzy mathematics. The concept of fuzzy set theory was first developed by Zadeh [1]. FDEs play an important role for modelling physical and engineering problems because they may mimic the real situation to handle the systems under uncertainty. But, it is too difficult to obtain exact solutions of FDEs, due to the complexity in fuzzy arithmetic. For example, addition is not the inverse operation of subtraction. In a similar manner multiplication is not the inverse operation of division too. Hence, one may need reliable and efficient numerical techniques to handle the corresponding FDEs.

There exist a variety of papers dealing with FDEs and their applications. Some of these are reviewed and cited here for better understanding of the present investigation. Chang and Zadeh [2] first introduced the concept of a fuzzy derivative, followed by Dubois and Prade [3], who defined and used the extension principle in their approach. Other fuzzy derivative concepts were proposed by Puri and Ralescu [4] and Goetschel and Voxman [5] as an extension of the Hukuhara derivative of multivalued functions. The FDEs and fuzzy initial value problems (FIVPs) are studied by Kaleva [6, 7] and Seikkala [8].

Bede [9] described the exact solutions of FDEs in his note in an excellent way. Buckley and Feuring [10] applied two analytical methods for solving nth order linear differential equations with fuzzy initial conditions. In the first method, they simply fuzzified the crisp solution to obtain a fuzzy function and then checked whether it satisfies the differential equation or not. And the second method was just the reverse of the first method. Ahmada et al [11] studied analytical and numerical solutions of FDEs based on the extension principle. Oregan et al [12] obtained the exact solution of fuzzy first-order boundary value problems (BVPs). In all the above-cited papers they have converted the FDEs to coupled or uncoupled system of differential equations depending on the sign of the coefficients. Very recently, a new analytical method has been developed by Tapaswini and Chakraverty [13] based on fuzzy centre, where only two crisp uncoupled differential equations are required to solve with respect to sign of the coefficients.

All fuzzy initial value problems (FIVPs) or fuzzy boundary value problems (FBVPs) may not be solved exactly. Sometimes, it is even impossible to find their analytical solutions. Hence, various numerical methods are proposed by different authors for solving FDEs, which are discussed in the following paragraph.

A few authors have also investigated numerical methods to obtain the solution of FBVPs. Wintner-type result for fuzzy IVPs and a superlinear-type result for FBVPs are investigated by Oregan et al [12]. A new condition has been developed by Chen et al [14] to show that the two-point FBVPs and fuzzy integral equation are equivalent. Generalized differentiability concept has been applied by Khastan and Nieto [15] to obtain the solution of two-point FBVPs. Nonhomogeneous FBVPs using collocation method has been studied by Mohammed and Fadhel [16]. Jamshidi and Avazpour [17] applied shooting method for second-order fuzzy boundary value problems (SOFBVPs) under generalized differentiability. Undetermined fuzzy coefficients method has been applied by Guo et al [18] to obtain the solution of SOFBVPs. Dahalan et al [19] implemented half-sweep alternating group explicit method to obtain the numerical solution. Optimal homotopy asymptotic method (OHAM) has been applied by Jameel and Ismail [20] to solve nth order two-point FBVPs. Also, some application problems have been modelled through FBVPs, e.g., Chen et al [21] solved two-point boundary value undamped uncertain dynamical systems.

It is revealed from the above literature review that various authors applied different methods to solve FDEs. In general these methods are sometimes problem dependent and less efficient for large systems. Also less work has been done in the field of FBVP. Hence, here an alternative attempt has been made by using Galerkin’s method to solve FBVPs. The novelty of the method is that this method along with the r-cut form converts the FDE into a crisp linear system of equations, which may very easily be solved by any well-known methods. Moreover the sign of the coefficients in the FDE plays an important role. As such different signs of the coefficients may also be handled in a straightforward way by using the proposed method. The powerfulness of the procedure has been demonstrated first by a few simple (fuzzy) mathematical example problems. And finally an application problem has also been considered to show the efficacy and applicability of the method.

This paper is organized as follows. In section 2, we have given basic preliminaries related to the present investigation. Next, the proposed method has been investigated in section 3. Further, in section 4, various numerical examples along with one application problem related to heat transfer have been solved and discussed. Finally in the last section conclusions are drawn.

2 Preliminaries

In this section, we present some notations, definitions and preliminaries, which are used further in this paper [13, 22,23,24].

Definition 2.1

Fuzzy number

A fuzzy number $\widetilde{U}$ is convex normalized fuzzy set $\widetilde{U}$ of the real line $R$ such that

$$ \{ \mu_{{\widetilde{U}}} (x):R \to [0, \, 1],\quad \forall \, x \in R\} $$

where $\mu_{{\widetilde{U}}}$ is called the membership function of the fuzzy set and it is piecewise continuous.

Definition 2.2

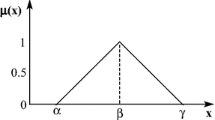
Triangular fuzzy number

A triangular fuzzy number $\widetilde{U}$ is a convex normalized fuzzy set $\widetilde{U}$ of the real line $R$ such that

• 1. There exists exactly one $x_{0} \in R$ with $\mu_{{\widetilde{U}}} (x_{0} ) = 1$ ($x_{0}$ is called the mean value of $\widetilde{U}$), where $\mu_{{\widetilde{U}}}$ is called the membership function of the fuzzy set.

• 2. $\mu_{{\widetilde{U}}} (x)$ is piecewise continuous.

Let us consider an arbitrary triangular fuzzy number $\widetilde{U} = (a, \, b, \, c)$. The membership function $\mu_{{\widetilde{U}}}$ of $\widetilde{U}$ will be defined as follows:

$$ \mu_{{\widetilde{U}}} (x) = \left\{ {\begin{array}{*{20}l} {0,} \hfill & {x \le a} \hfill \\ {\frac{x - a}{b - a},} \hfill & {a \le x \le b} \hfill \\ {\frac{c - x}{c - b},} \hfill & {b \le x \le c} \hfill \\ {0,} \hfill & {x \ge c} \hfill \\ \end{array} } \right.. $$

The triangular fuzzy number $\widetilde{U} = (a, \, b, \, c)$ can be represented with an ordered pair of functions through r-cut approach, viz. $[\underline{u} (r),\bar{u}(r)] = [(b - a)r + a, \, - (c - b)r + c],$ where $r \in [0,{ 1}]$.

It may be noted that the lower and upper bounds of the fuzzy numbers satisfy the following requirements:

• i. $\underline{u} (r)$ is a bounded left continuous non-decreasing function over $\left[ {0, 1} \right].$

• ii. $\bar{u}(r)$ is a bounded right continuous non-increasing function over $\left[ {0, 1} \right]$.

• iii. $\underline{u} \left( \alpha \right) \le \overline{ u} \left( \alpha \right), 0 \le \alpha \le 1$

Definition 2.3

Fuzzy arithmetic

For any two arbitrary fuzzy numbers $\widetilde{x} = [\underline{x} (r),\bar{x}(r)],$ $\widetilde{y} = [\underline{y} (r),\bar{y}(r)]$ and scalar ${\text{k}}$, the fuzzy arithmetic is defined as follows:

• i. $\widetilde{x} = \widetilde{y}$ if and only if $\underline{x} (r) = \underline{y} (r)$ and $\bar{x}(r) = \bar{y}(r)$

• ii. $\widetilde{x} + \widetilde{y} = [\underline{x} (r) + \underline{y} (r), \, \bar{x}(r) + \bar{y}(r)]$

• iii. $\widetilde{x} \times \widetilde{y} = \left[ \begin{aligned} \hbox{min} \left( {\underline{x} (r) \times \underline{y} (r),\underline{x} (r) \times \bar{y}(r),\bar{x}(r) \times \underline{y} (r),\bar{x}(r) \times \bar{y}(r)} \right), \hfill \\ \hbox{max} \left( {\underline{x} (r) \times \underline{y} (r),\underline{x} (r) \times \bar{y}(r),\bar{x}(r) \times \underline{y} (r),\bar{x}(r) \times \bar{y}(r)} \right) \hfill \\ \end{aligned} \right]$

• iv. $k\widetilde{x} = \left\{ \begin{aligned} [k\bar{x}(r),k\underline{x} (r)],\quad k < 0 \hfill \\ [k\underline{x} (r),k\bar{x}(r)],\quad k \ge 0 \hfill \\ \end{aligned} \right.$.

Definition 2.4

[15, 25] Let $F :\;(a,b) \to R_{F}$ and $t_{0} = (a,b)$. $X$ is called differentiable at $t_{0}$ if there exists $F'(t_{0} ) \in R_{F}$ such that

• (1) for all $h > 0$ sufficiently close to 0, the Hukuhara difference $F(t_{0} + h)\varTheta \, F(t_{0} )$ and $F(t_{0} )\varTheta \, F(t_{0} - h)$ exist and (in metric $D$)

$$ \mathop {\lim }\limits_{{h \to 0^{ + } }} \frac{{F(t_{0} + h)\varTheta F(t_{0} )}}{h} = \mathop {\lim }\limits_{{h \to 0^{ + } }} \frac{{F(t_{0} )\varTheta F(t_{0} - h)}}{h} = F^{\prime}(t_{0} ), $$

or

• (2) for all $h > 0$ sufficiently close to 0, the Hukuhara difference $F(t_{0} )\varTheta F(t_{0} + h)$ and $\, F(t_{0} - h)\varTheta F(t_{0} )$ exist and (in metric $D$)

$\mathop {\lim }\limits_{{h \to 0^{ + } }} \frac{{F(t_{0} )\varTheta F(t_{0} + h)}}{ - h} = \mathop {\lim }\limits_{{h \to 0^{ + } }} \frac{{ \, F(t_{0} - h)\varTheta F(t_{0} )}}{ - h} = F^{\prime}(t_{0} ).$

Chalco-Cano and Roman-Flores [25] used Definition 2.4 to obtain the following results.

3 Proposed method

In this section, we propose a new technique based on Galerkin type to solve $n$th order FDE. Accordingly let us consider the general form of the problem as

$$ \widetilde{y}^{(n)} (t;r) + a_{n - 1} (t)\widetilde{y}^{(n - 1)} (t;r) + \cdots + a_{1} (t)\widetilde{y}'(t;r) + a_{0} (t)\widetilde{y}(t;r) = \widetilde{g}(t;r), $$

(1)

where $a_{i} (t), \, 0 \le i \le n - 1,$ is continuous on some interval $I,$ subject to fuzzy boundary conditions

$$ \widetilde{y}(a;r) = \left[ {\underline{\beta } (r), \, \bar{\beta }(r)} \right], \, \widetilde{y}(b;r) = \left[ {\underline{\gamma } (r), \, \bar{\gamma }(r)} \right] $$

and $\widetilde{y}(t;r)$ is the solution to be determined.

Now an approximate solution is assumed involving the unknown fuzzy constants $\widetilde{c}_{i}$, for $i = 1, \, 2, \, 3, \, \ldots , \, n$ as

$$ \widetilde{y}(t;r) = \widetilde{\phi }_{0} (t;r) + f\sum\limits_{i = 1}^{n} {\widetilde{c}_{i} \varPsi_{i} (t)} $$

(2)

where $\widetilde{\phi }_{0} (t;r) = \left[ {M\underline{\beta } (r) + N\underline{\gamma } (r),M\bar{\beta }(r) + N\bar{\gamma }(r)} \right]$, $M = \frac{b - t}{b - a}$, $N = \frac{t - a}{b - a}$ $f = (t - a)(b - t)$, and $\varPsi_{i} (t) = t^{i - 1}$.

Now one may write Eq. (2) as

$$ \widetilde{y}(t;r) = \widetilde{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\widetilde{c}_{i} \phi_{i} (t)} $$

(3)

where $\phi_{i} (t) = f \, \varPsi_{i} (t)$.

Here it can be clearly seen that $\widetilde{y}(t;r)$ satisfies the given boundary conditions. Next, by substituting Eq. (3) in Eq. (1), the residual $\widetilde{R}(t; \, r ,\widetilde{c}_{1} , \, \widetilde{c}_{2} , \ldots , \, \widetilde{c}_{n} )$ may be obtained as

$$ \begin{aligned} \widetilde{R}(t; \, r ,\widetilde{c}_{1} , \, \widetilde{c}_{2} , \ldots , \, \widetilde{c}_{n} ) =& \left( {\widetilde{\phi }_{{_{0} }}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\widetilde{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\widetilde{\phi }_{{_{0} }}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\widetilde{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \hfill \\ & + a_{1} (t)\left( {\widetilde{\phi }_{{_{0} }}^{'} (t;r) + \sum\limits_{i = 1}^{n} {\widetilde{c}_{i} } \phi_{i} '(t)} \right) + a_{0} (t)\left( {\widetilde{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\widetilde{c}_{i} } \phi_{i} (t)} \right) - \widetilde{g}(t;r) \hfill \\ \end{aligned} . $$

(4)

The residual $\widetilde{R}(t; \, r ,\widetilde{c}_{1} , \, \widetilde{c}_{2} , \ldots , \, \widetilde{c}_{n} )$ is then orthogonalized with the functions $\phi_{j}$ for $j = 1, \, 2 \, , \ldots , \, n$. This gives

$$ \int\limits_{a}^{b} {\widetilde{R}(t;r, \, \widetilde{c}_{1} , \, \widetilde{c}_{2} , \ldots , \, \widetilde{c}_{n} )} \phi_{j} (t)dt = 0. $$

(5)

Solving the above system (5) one may obtain the fuzzy constants $\widetilde{c}_{i}$. Next, substituting the value of these constants in Eq. (3) one may have the approximate solution of the nth order FBVP. To compare the results of proposed method we have also applied the method of Bede [9] to find the exact solution. Now three cases as below may arise:

Case 1

When the coefficients $a_{n - 1} (t), \, a_{n - 2} (t), \ldots ,a_{1} (t), \, a_{0} (t)$ are all positive.

From Eq. (1) we have

$$ \underline{y}^{(n)} (t;r) + a_{n - 1} (t)\underline{y}^{(n - 1)} (t;r) + \cdots + a_{1} (t)\underline{y} '(t;r) + a_{0} (t)\underline{y} (t;r) = \underline{g} (t;r), $$

(6)

$$ \bar{y}^{(n)} (t;r) + a_{n - 1} (t)\bar{y}^{(n - 1)} (t;r) + \cdots + a_{1} (t)\bar{y}'(t;r) + a_{0} (t)\bar{y}(t;r) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} (t;r). $$

(7)

In view of Eqs. (6) and (7), (by using Eq. (3)) we have the residues $\underline{R} (t;r,\underline{c}_{1} ,\underline{c}_{2} , \ldots ,\underline{c}_{n} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )$, respectively, as

$$ \begin{aligned} \underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} ) =& \left( {\underline{\phi }_{{_{0} }}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\underline{\phi }_{{_{0} }}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \hfill \\ &+ a_{1} (t)\left( {\underline{\phi }_{0}^{'} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} '(t)} \right) + a_{0} (t)\left( {\underline{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} (t)} \right) - \underline{g} (t;r) \hfill \\ \end{aligned} $$

(8)

and

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} ) =& \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \hfill \\ &+ a_{1} (t)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0}^{'} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} '(t)} \right) + a_{0} (t)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} (t)} \right) - \bar{g}(t;r) \hfill \\ \end{aligned} . $$

(9)

The residual $\widetilde{R}(t; \, r , {\widetilde{\text{c}}}_{1} ,{\widetilde{\text{c}}}_{2} , \ldots ,{\widetilde{\text{c}}}_{n} ) = [\underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )]$ is then orthogonalized with the functions $\phi_{j}$ for $j = 1, \, 2, \, \ldots , \, n$. This gives

$$ \int\limits_{a}^{b} {\left\{ {\left( {\underline{\phi }_{{_{0} }}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\underline{\phi }_{{_{0} }}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \, + a_{0} (t)\left( {\underline{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} (t)} \right) - \underline{g} (t;r)} \right\}} \phi_{j} dt $$

(10)

$$ \int\limits_{a}^{b} {\left\{ {\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots + a_{0} (t)\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} (t)} \right) - \bar{g}(t;r)} \right\}} \phi_{j} dt $$

(11)

We may write Eqs. (10) and (11) as

$$ \int\limits_{a}^{b} {\sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{j} \left\{ {\phi_{{_{i} }}^{(n)} (t) + \cdots \, + a_{0} (t)\phi_{i} (t)} \right\}} dt = \int\limits_{a}^{b} {\phi_{j} \left\{ {\underline{g} (t;r) - \left( {\underline{\phi }_{{_{0} }}^{(n)} (t) + \cdots \, + a_{0} (t)\underline{\phi }_{0} (t)} \right)} \right\}} dt, $$

(12)

$$ \int\limits_{a}^{b} {\sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{j} \left\{ {\phi_{{_{i} }}^{(n)} (t) + \cdots \, + a_{0} (t)\phi_{i} (t)} \right\}} dt = \int\limits_{a}^{b} {\phi_{j} \left\{ {\bar{g}(t;r) - \left( {\bar{\phi }_{{_{0} }}^{(n)} (t) + \cdots \, + a_{0} (t)\bar{\phi }_{0} (t)} \right)} \right\}} dt. $$

(13)

Let us assume

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\phi_{{_{i} }}^{(n)} (t) + a_{n - 1} (t)\phi_{{_{i} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\phi_{i} (t)} \right\}} dt = \alpha_{ji} , $$

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\underline{g} (t;r) - \left( {\underline{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\underline{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\underline{\phi }_{0} (t)} \right)} \right\}} = \underline{f}_{j} (t;r) $$

and

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\bar{g}(t;r) - \left( {\bar{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\bar{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\bar{\phi }_{0} (t)} \right)} \right\}} dt = \bar{f}_{j} (t;r) $$

Then the following system is obtained:

$$ \begin{array}{*{20}c} {\sum\limits_{i = 1}^{n} {\alpha_{ji} \underline{c}_{i} } = \underline{f}_{j} (t;r)} \\ {\sum\limits_{i = 1}^{n} {\alpha_{ji} \bar{c}_{i} } = \bar{f}_{j} (t;r)} \\ \end{array} \quad {\text{for}}\quad j = 1, \, 2, \, \ldots , \, n. $$

(14)

The above system (14) can be written in the form of a linear system of equations $AX = B$ as follows:

$$ A = \left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } \\ {A_{2} } & {A_{1} } \\ \end{array} } \right]_{2n \times 2n} $$

where

$$ A_{1} = \left[ {\begin{array}{*{20}c} {\alpha_{11} } & {\alpha_{12} } & {\alpha_{13} } & \cdots & {\alpha_{1n} } \\ {\alpha_{21} } & {\alpha_{22} } & {\alpha_{23} } & \cdots & {\alpha_{2n} } \\ {\alpha_{31} } & {\alpha_{32} } & {\alpha_{33} } & \cdots & {\alpha_{3n} } \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {\alpha_{n1} } & {\alpha_{n2} } & {\alpha_{3n} } & \cdots & {\alpha_{nn} } \\ \end{array} } \right]_{n \times n} ,A_{2} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & \cdots & \vdots \\ \vdots & \vdots & \vdots & \cdots & 0 \\ 0 & 0 & 0 & \cdots & 0 \\ \end{array} } \right]_{n \times n} , $$

$$ X = [\underline{c}_{1} ,\underline{c}_{2} , \ldots ,\underline{c}_{n} ,\bar{c}_{1} ,\bar{c}_{2} , \ldots , \, \bar{c}_{n} ] $$

and $B = [\underline{f}_{1} (t;r), \, \underline{f}_{2} (t;r), \ldots ,\underline{f}_{n} (t;r),\bar{f}_{1} (t;r),\bar{f}_{2} (t;r), \ldots ,\bar{f}_{n} (t;r)]$. The fuzzy constants $\widetilde{c}_{i}$ for $i = 1,2, \ldots ,n$ are obtained by solving the above system of equations (Eq. (14)). Substituting these constants in Eq. (3) we get the approximate solution of the FBVP.

Case 2

When the coefficients $a_{n - 1} (t), \, a_{n - 2} (t), \ldots ,a_{1} (t), \, a_{0} (t)$ are all negative.

From Eq. (1) we have

$$ \underline{y}^{(n)} (t;r) + a_{n - 1} (t)\bar{y}^{(n - 1)} (t;r) + \cdots + a_{1} (t)\bar{y}'(t;r) + a_{0} (t)\bar{y}(t;r) = \underline{g} (t;r), $$

(15)

$$ \bar{y}^{(n)} (t;r) + a_{n - 1} (t)\underline{y}^{(n - 1)} (t;r) + \cdots + a_{1} (t)\underline{y} '(t;r) + a_{0} (t)\underline{y} (t;r) = \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {g} (t;r). $$

(16)

In view of Eqs. (15) and (16), (by using Eq. (3)) we may have the residues $\underline{R} (t;r,\underline{c}_{1} ,\underline{c}_{2} , \ldots ,\underline{c}_{n} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )$, respectively, as

$$ \begin{aligned} \underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} ) =& \left( {\underline{\phi }_{{_{0} }}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\bar{\phi }_{{_{0} }}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \hfill \\ & + a_{1} (t)\left( {\bar{\phi }_{0}^{'} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} '(t)} \right) + a_{0} (t)\left( {\bar{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} (t)} \right) - \underline{g} (t;r) \hfill \\ \end{aligned} $$

(17)

and

$$ \begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} ) & = \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {\phi }_{0}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\underline{\phi }_{0}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) \\ & \quad + a_{1} (t)\left( {\underline{\phi }_{0}^{'} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} '(t)} \right) + a_{0} (t)\left( {\underline{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} (t)} \right) - \bar{g}(t;r). \\ \end{aligned} $$

(18)

The residual $\widetilde{R}(t; \, r , {\widetilde{\text{c}}}_{1} ,{\widetilde{\text{c}}}_{2} , \ldots ,{\widetilde{\text{c}}}_{n} ) = [\underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )]$ is then orthogonalized with the functions $\phi_{j}$ for $j = 1, \, 2, \, \ldots , \, n$. This gives

$$ \int\limits_{a}^{b} {\underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} )} \phi_{j} dt $$

(19)

$$ \int\limits_{a}^{b} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )} \phi_{j} dt. $$

(20)

We may write Eqs. (19) and (20) as

$$ \begin{aligned} & \int\limits_{a}^{b} {\phi_{j} \left\{ {\sum\limits_{i = 1}^{n} {\underline{c}_{i} \phi_{{_{i} }}^{(n)} (t)} + a_{n - 1} (t)\sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t) + \cdots + a_{0} (t)\sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} (t)} \right\}} dt \\ &\quad = \int\limits_{a}^{b} {\phi_{j} \left\{ {\underline{g} (t;r) - \left( {\underline{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\bar{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\bar{\phi }_{0} (t)} \right)} \right\}} dt \\ \end{aligned} $$

(21)

$$ \begin{aligned} & \int\limits_{a}^{b} {\phi_{j} \left\{ {\sum\limits_{i = 1}^{n} {\bar{c}_{i} \phi_{{_{i} }}^{(n)} (t)} + a_{n - 1} (t)\sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t) + \cdots + a_{0} (t)\sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} (t)} \right\}} dt \\ & \quad= \int\limits_{a}^{b} {\phi_{j} \left\{ {\bar{g}(t;r) - \left( {\bar{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\underline{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\underline{\phi }_{0} (t)} \right)} \right\}} dt. \\ \end{aligned} $$

(22)

Again by taking

$$ \int\limits_{a}^{b} {\phi_{j} \phi_{{_{i} }}^{(n)} (t)} dt = \eta_{i,i} $$

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {a_{n - 1} (t)\phi_{{_{i} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\phi_{i} (t)} \right\}} dt = \delta_{i,i} , $$

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\underline{g} (t;r) - \left( {\underline{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\bar{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\bar{\phi }_{0} (t)} \right)} \right\}} = \underline{f}_{j} (t;r) $$

and

$$ \int\limits_{a}^{b} {\phi_{i} \left\{ {\bar{g}(t;r) - \left( {\bar{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\underline{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{0} (t)\underline{\phi }_{0} (t)} \right)} \right\}} = \bar{f}_{j} (t;r) $$

the following system is obtained:

$$ \left( {\sum\limits_{i = 1}^{n} {\eta_{ji} \underline{c}_{i} } + \sum\limits_{i = 1}^{n} {\delta_{ji} \bar{c}_{i} } } \right) = \underline{f}_{j} (t;r). $$

(23)

The above system (23) may again be represented as a system of linear equation $AX = B$ such as

$$ A = \left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } \\ {A_{2} } & {A_{1} } \\ \end{array} } \right]_{2n \times 2n} $$

where

$$ A_{1} = \left[ {\begin{array}{*{20}c} {\eta_{11} } & {\eta_{12} } & {\eta_{13} } & \cdots & {\eta_{1n} } \\ {\eta_{21} } & {\eta_{22} } & {\eta_{23} } & \cdots & {\eta_{2n} } \\ {\eta_{31} } & {\eta_{32} } & {\eta_{33} } & \cdots & {\eta_{3n} } \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {\eta_{n1} } & {\eta_{n2} } & {\eta_{3n} } & \cdots & {\eta_{nn} } \\ \end{array} } \right]_{n \times n} ,\quad A_{2} = \left[ {\begin{array}{*{20}c} {\delta_{11} } & {\delta_{12} } & {\delta_{13} } & \cdots & {\delta_{1n} } \\ {\delta_{21} } & {\delta_{22} } & {\delta_{23} } & \cdots & {\delta_{2n} } \\ {\delta_{31} } & {\delta_{32} } & {\delta_{33} } & \cdots & {\delta_{3n} } \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {\delta_{n1} } & {\delta_{n2} } & {\delta_{3n} } & \cdots & {\delta_{nn} } \\ \end{array} } \right]_{n \times n} , $$

$$ X = [\underline{c}_{1} ,\underline{c}_{2} , \ldots ,\underline{c}_{n} ,\bar{c}_{1} ,\bar{c}_{2} , \ldots , \, \bar{c}_{n} ] $$

and $B = [\underline{f}_{1} (t;r), \, \underline{f}_{2} (t;r), \ldots ,\underline{f}_{n} (t;r),\bar{f}_{1} (t;r),\bar{f}_{2} (t;r), \ldots ,\bar{f}_{n} (t;r)]$. The fuzzy constants $\widetilde{c}_{i}$ for $i = 1,2, \ldots ,n$ are obtained by solving the above system of equations Eq. (23). Substitute these constants in Eq. (3) to get the approximate solution of Eqs. (15) and (16) for this case.

Case 3

When the coefficients $a_{n - m - 1} (t), \, a_{n - m - 2} (t), \ldots ,a_{1} (t), \, a_{0} (t)$ for $n \ge m$ are negative. From Eq. (1) we have

$$ \begin{aligned} &\underline{y}^{(n)} (t;r) + a_{n - 1} (t)\underline{y}^{(n - 1)} (t;r) + \cdots + a_{n - m} (t)\underline{y}^{(n - m)} (t;r) + a_{n - m - 1} (t)\bar{y}^{(n - m - 1)} (t;r) + \cdots \\ & \quad + a_{0} (t)\bar{y}(t;r) = \underline{g} (t;r), \\ \end{aligned} $$

(24)

$$ \begin{aligned} & \bar{y}^{(n)} (t;r) + a_{n - 1} (t)\bar{y}^{(n - 1)} (t;r) + \cdots + a_{n - m} (t)\bar{y}^{(n - m)} (t;r) + a_{n - m - 1} (t)\underline{y}^{(n - m - 1)} (t;r) + \cdots \\ \quad + a_{0} (t)\underline{y} (t;r) = \bar{g}(t;r). \\ \end{aligned} $$

(25)

We may have the residues $\underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} )$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )$, respectively, as

$$ \begin{aligned} & \underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} ) = \left( {\underline{\phi }_{{_{0} }}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\underline{\phi }_{{_{0} }}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \\ & \quad + a_{n - m} (t)\left( {\underline{\phi }_{{_{0} }}^{(n - m)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - m)} (t)} \right) + a_{n - m - 1} (t)\left( {\bar{\phi }_{{_{0} }}^{(n - m - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - m - 1)} (t)} \right) + \cdots \\ & \quad + a_{0} (t)\left( {\bar{\phi }_{0} (t;r) + \sum\limits_{i = 0}^{n} {\bar{c}_{i} } \phi_{i} (t)} \right) - \underline{g} (t;r) \\ \end{aligned} $$

(26)

$$ \begin{aligned} & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} ) = \left( {\bar{\phi }_{{_{0} }}^{(n)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} \phi_{{_{i} }}^{(n)} (t)} } \right) + a_{n - 1} (t)\left( {\bar{\phi }_{{_{0} }}^{(n - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - 1)} (t)} \right) + \cdots \\ & \quad + a_{n - m} (t)\left( {\bar{\phi }_{{_{0} }}^{(n - m)} (t;r) + \sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - m)} (t)} \right) + a_{n - m - 1} (t)\left( {\underline{\phi }_{{_{0} }}^{(n - m - 1)} (t;r) + \sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - m - 1)} (t)} \right) + \cdots \\ & \quad + a_{0} (t)\left( {\underline{\phi }_{0} (t;r) + \sum\limits_{i = 0}^{n} {\underline{c}_{i} } \phi_{i} (t)} \right) - \bar{g}(t;r) \\ \end{aligned} $$

(27)

The residual $\widetilde{R}(t; \, r , {\widetilde{\text{c}}}_{1} ,{\widetilde{\text{c}}}_{2} , \ldots ,{\widetilde{\text{c}}}_{n} ) = [\underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} ),\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )]$ is then orthogonalized with the functions $\phi_{j}$ for $j = 1, \, 2, \, \ldots , \, n$ as done in previous cases. Next we get

$$ \int\limits_{a}^{b} {\underline{R} (t; \, r ,\underline{c}_{1} , \, \underline{c}_{2} , \ldots , \, \underline{c}_{n} )} \phi_{j} dt $$

(28)

and

$$ \int\limits_{a}^{b} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {R} (t; r,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{1} , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{2} , \ldots , \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}} {c}_{n} )} \phi_{j} dt $$

(29)

Eqs. (28) and (29) are now written as

$$ \begin{aligned} & \int\limits_{a}^{b} {\phi_{j} \left\{ {\sum\limits_{i = 1}^{n} {\underline{c}_{i} \phi_{{_{i} }}^{(n)} (t)} + \cdots + a_{n - m} (t)\sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - m)} (t) + a_{n - m - 1} (t)\sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - m - 1)} (t) + a_{0} (t)\sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{i} (t)} \right\}} dt \\ & = \int\limits_{a}^{b} {\phi_{j} \left\{ {\underline{g} (t;r) - \left( {\underline{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\underline{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{n - m} (t)\underline{\phi }_{{_{0} }}^{(n - m)} (t) + a_{n - m - 1} (t)\bar{\phi }_{{_{0} }}^{(n - m - 1)} (t) + \cdots + a_{0} (t)\bar{\phi }_{0} (t)} \right)} \right\}} dt \\ \end{aligned} $$

(30)

$$ \begin{aligned} & \int\limits_{a}^{b} {\phi_{j} \left\{ {\sum\limits_{i = 1}^{n} {\bar{c}_{i} \phi_{{_{i} }}^{(n)} (t)} + \cdots + a_{n - m} (t)\sum\limits_{i = 1}^{n} {\bar{c}_{i} } \phi_{{_{i} }}^{(n - m)} (t) + a_{n - m - 1} (t)\sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{{_{i} }}^{(n - m - 1)} (t) + a_{0} (t)\sum\limits_{i = 1}^{n} {\underline{c}_{i} } \phi_{i} (t)} \right\}} dt \\ & = \int\limits_{a}^{b} {\phi_{j} \left\{ {\bar{g}(t;r) - \left( {\bar{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\bar{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{n - m} (t)\bar{\phi }_{{_{0} }}^{(n - m)} (t) + a_{n - m - 1} (t)\underline{\phi }_{{_{0} }}^{(n - m - 1)} (t) + \cdots + a_{0} (t)\underline{\phi }_{0} (t)} \right)} \right\}} dt \\ \end{aligned} $$

(31)

Again by assuming

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\phi_{{_{i} }}^{(n)} + a_{n - 1} \phi_{{_{i} }}^{(n - 1)} (t) + \cdots + a_{n - m} \phi_{{_{i} }}^{(n - m)} (t)} \right\}} dt = \xi_{ji} $$

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {a_{n - m - 1} (t)\phi_{{_{i} }}^{(n - m - 1)} (t) + \cdots \, + a_{1} (t)\phi_{{_{i} }}^{'} (t) + a_{0} \phi_{i} (t)} \right\}} dt = \mu_{ji} , $$

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\underline{g} (t;r) - \left( {\underline{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\underline{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{n - m} \underline{\phi }_{{_{0} }}^{(n - m)} (t) + a_{n - m - 1} \bar{\phi }_{{_{0} }}^{(n - m - 1)} (t) + \cdots + a_{0} (t)\bar{\phi }_{0} (t)} \right)} \right\}} = \underline{f}_{j} (t;r) $$

and

$$ \int\limits_{a}^{b} {\phi_{j} \left\{ {\bar{g}(t) - \left( {\bar{\phi }_{{_{0} }}^{(n)} (t) + a_{n - 1} (t)\bar{\phi }_{{_{0} }}^{(n - 1)} (t) + \cdots \, + a_{n - m} \bar{\phi }_{{_{0} }}^{(n - m)} (t) + a_{n - m - 1} \underline{\phi }_{{_{0} }}^{(n - m - 1)} (t) + \cdots + a_{0} (t)\underline{\phi }_{0} (t)} \right)} \right\}} = \bar{f}_{i} (t;r) $$

the following system is

$$ \left( {\sum\limits_{i = 1}^{n} {\xi_{ji} \underline{c}_{i} } + \sum\limits_{i = 1}^{n} {\mu_{ji} \bar{c}_{i} } } \right) = \underline{f}_{j} (t;r)\quad {\text{for}}\quad j = 1, \, 2, \ldots , \, n. $$

(32)

Eq. (32) is written finally in the form of $AX = B$ as

$$ A = \left[ {\begin{array}{*{20}c} {A_{1} } & {A_{2} } \\ {A_{2} } & {A_{1} } \\ \end{array} } \right]_{2n \times 2n} $$

where

$$ A_{1} = \left[ {\begin{array}{*{20}c} {\xi_{11} } & {\xi_{12} } & {\xi_{13} } & \cdots & {\xi_{1n} } \\ {\xi_{21} } & {\xi_{22} } & {\xi_{23} } & \cdots & {\xi_{2n} } \\ {\xi_{31} } & {\xi_{32} } & {\xi_{33} } & \cdots & {\xi_{3n} } \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {\xi_{n1} } & {\xi_{n2} } & {\xi_{3n} } & \cdots & {\xi_{nn} } \\ \end{array} } \right]_{n \times n} ,\quad A_{2} = \left[ {\begin{array}{*{20}c} {\mu_{11} } & {\mu_{12} } & {\mu_{13} } & \cdots & {\mu_{1n} } \\ {\mu_{21} } & {\mu_{22} } & {\mu_{23} } & \cdots & {\mu_{2n} } \\ {\mu_{31} } & {\mu_{32} } & {\mu_{33} } & \cdots & {\mu_{3n} } \\ \vdots & \vdots & \vdots & \cdots & \vdots \\ {\mu_{n1} } & {\mu_{n2} } & {\mu_{3n} } & \cdots & {\mu_{nn} } \\ \end{array} } \right]_{n \times n} , $$

$X = [\underline{c}_{1} ,\underline{c}_{2} , \ldots ,\underline{c}_{n} ,\bar{c}_{1} ,\bar{c}_{2} , \ldots , \, \bar{c}_{n} ]$ and $B = [\underline{f}_{1} (t;r), \, \underline{f}_{2} (t;r), \ldots ,\underline{f}_{n} (t;r),\bar{f}_{1} (t;r),\bar{f}_{2} (t;r), \ldots ,\bar{f}_{n} (t;r)]$. The fuzzy constants $\widetilde{c}_{i}$ for $i = 1, \, 2, \, \ldots , \, n$ are obtained by solving the above system of equations [Eq. (32)] as done previously. These constants are substituted in Eq. (3) to get the approximate solution of the BVP.

4 Numerical implementation of the proposed method

In the following paragraphs, example problems are solved using the proposed method with different cases and are also compared with exact solutions. We also obtain the exact solution by following the method of Bede [9].

Example 1

Let us consider the following second-order fuzzy linear differential equation with positive coefficients (Case 1):

$$ \widetilde{y}'' + \widetilde{y} + t = 0 $$

(33)

subject to the fuzzy boundary conditions

$$ \widetilde{y}(0) = \widetilde{y}(1) = [0.1r - 0.1, \, 0.1 - 0.1r]. $$

The exact fuzzy solution are found, Bede [9], as

$$ \begin{aligned} & \underline{Y} (t; \, r) = - t + (0.1r - 0.1)\cos (t) + (1.13376 + 0.0546302r)\sin (t), \\ & \bar{Y}(t; \, r) = - t + (0.1 - 0.1r)\cos (t) + (1.24303 - 0.0546302r)\sin (t). \\ \end{aligned} $$

Let the approximate solution of Eq. (33) be

$$ \widetilde{y}(t;r) = \widetilde{\phi }_{0} (t;r) + \sum\limits_{i = 1}^{3} {\widetilde{c}_{i} \phi_{i} (t)} $$

(34)

where $\widetilde{\phi }_{0} (t;r) = [(0.1r - 0.1), \, (0.1 - 0.1r)]$.

Now, $\widetilde{y}(t;r)$ can be written as

$$ \widetilde{y}(t;r) = \widetilde{\phi }_{0} (t;r) + t(1 - t)(\widetilde{c}_{1} + t\widetilde{c}_{2} + t^{2} \widetilde{c}_{3} ) $$

(35)

which satisfies the fuzzy boundary condition.

Therefore residue $\widetilde{R}$ can be written as

$$ \begin{aligned} & \underline{R} (t,r,\underline{c}_{1} ,\underline{c}_{2} ,\underline{c}_{3} ) = ( - 0.1 + 0.1r) + t + ( - 2 + t - t^{2} )\underline{c}_{1} + (2 - 6t + t^{2} - t^{3} )\underline{c}_{2} + t(6 - 12t + t^{2} - t^{3} )\underline{c}_{3} , \\ & \bar{R}(t,r,\bar{c}_{1} ,\bar{c}_{2} ,\bar{c}_{3} ) = (0.1 - 0.1r) + t + ( - 2 + t - t^{2} )\bar{c}_{1} + (2 - 6t + t^{2} - t^{3} )\bar{c}_{2} + t(6 - 12t + t^{2} - t^{3} )\bar{c}_{3} . \\ \end{aligned} $$

(36)

Here the residue $\widetilde{R}$ is orthogonalized to the functions $\phi_{1} (t)$, $\phi_{2} (t)$ and $\phi_{3} (t)$. This gives

$$ \begin{aligned} & \int\limits_{0}^{1} {\widetilde{\phi }_{1} (t;r)\widetilde{R}(t;r,\widetilde{c}_{1} ,\widetilde{c}_{2} ,\widetilde{c}_{3} )dt = 0} , \\ & \int\limits_{0}^{1} {\widetilde{\phi }_{2} (t;r)\widetilde{R}(t;r,\widetilde{c}_{1} ,\widetilde{c}_{2} ,\widetilde{c}_{3} )dt = 0} , \\ \end{aligned} $$

(37)

and

$$ \int\limits_{0}^{1} {\widetilde{\phi }_{3} (t;r)\widetilde{R}(t;r,\widetilde{c}_{1} ,\widetilde{c}_{2} ,\widetilde{c}_{3} )dt = 0} . $$

(38)

On solving the above equations we get the following system:

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {0.0595238} & {0.0297619} & {0.0123016} & 0 & 0 & 0 \\ {0.0297619} & {0.0218254} & {0.0130952} & 0 & 0 & 0 \\ {0.0170635} & {0.0154762} & {0.0111472} & 0 & 0 & 0 \\ 0 & 0 & 0 & {0.0595238} & {0.0297619} & {0.0123016} \\ 0 & 0 & 0 & {0.0297619} & {0.0218254} & {0.0130952} \\ 0 & 0 & 0 & {0.0170635} & {0.0154762} & {0.0111472} \\ \end{array} } \right] \, \left\{ {\begin{array}{*{20}c} {\underline{c}_{1} } \\ \begin{aligned} \underline{c}_{2} \hfill \\ \underline{c}_{3} \hfill \\ \end{aligned} \\ {\bar{c}_{1} } \\ \begin{aligned} \bar{c}_{2} \hfill \\ \bar{c}_{3} \hfill \\ \end{aligned} \\ \end{array} } \right\} \\ & \quad = \left[ {\begin{array}{*{20}c} {0.0133333 + 0.00333333r} \\ {0.00785714 + 0.00166667r} \\ {0.005 + 0.000952381r} \\ \begin{aligned} 0.02 - 0.00333333 \, r \hfill \\ 0.0111905 - 0.00166667r \hfill \\ 0.00690476 - 0.000952381r \hfill \\ \end{aligned} \\ \end{array} } \right]. \\ \end{aligned} $$

Solving for $\widetilde{c}_{1}$, $\widetilde{c}_{2}$ and $\widetilde{c}_{3}$ from the above system, we get

$$ \widetilde{c}_{1} = [0.132778 + 0.054623 \, r, \, 0.242024 - 0.054623 \, r] $$

$$ \widetilde{c}_{2} = [0.190205 + 0.00469417 \, r, \, 0.199594 - 0.00469417 \, r] $$

and

$$ \widetilde{c}_{3} = [ - 0.0187767 - 0.00469417 \, r, \, - 0.028165 + 0.00469417 \, r]. $$

By substituting the values of fuzzy constants to Eq. (35), we have

$$ \begin{aligned} \underline{y} (t;r) & = (0.1r - 0.1) + t(t - 1)(0.132778 + 0.054623r + t(0.190205 + 0.00469417r) \\ \quad + t^{2} ( - 0.0187767 - 0.00469417r)), \\ \bar{y}(t;r) & = \, (0.1 - 0.1r) + t(t - 1)(0.242024 - 0.054623r + t(0.199594 - 0.00469417r) \\ & \quad + t^{2} ( - 0.028165 + 0.00469417r)). \\ \end{aligned} $$

Hence from this one may have the final solution as $\widetilde{y}(t;r) = [\underline{y} (t;r),\widetilde{y}(t;r)]$. Now the results obtained by the proposed method are compared with the exact solution for particular value of $t$. The solution bounds are shown in tables 1 and 2. Corresponding fuzzy plots are given in figure 1.

Table 1 Fuzzy solution of Example 1 at $t = 0.1$.

Table 2 Fuzzy solution of Example 1 at $t = 0.01$.

Figure 1

Fuzzy solution of Example 1 for Case 1 using the proposed method.

Example 2

Now, we take the following second-order fuzzy linear differential equation

$$ \widetilde{y}'' + \widetilde{y} = t, \, t \in [0, \, 1] $$

(39)

subject to the fuzzy boundary conditions as

$$ \widetilde{y}(0) = (3 + r, \, 5 - r),\quad \widetilde{y}(1) = (r,{ 2} - r). $$

Exact fuzzy solution are obtained again by following the method of Bede [9] as

$$ \underline{Y} (t{ ; }r) = t + (3 + r)\cos (t) - (3 + r)\cot (1)\sin (t) + (r - 1){\text{cosec}}(1)\sin (t), $$

$$ \overline{Y} (t{ ; }r) = t + (5 - r)\cos (t) - (5 - r)\cot (1)\sin (t) + (1 - r){\text{cosec}}(1)\sin (t). $$

Now, by using the proposed method we have $\widetilde{\phi }_{0} (t;r) = [(1 - t)(3 + r) + tr, \, (1 - t)(5 - r) + (2 - r)t]$.

Subsequently, by applying the procedure discussed previously, we get the following system of equations:

$$ \left[ {\begin{array}{*{20}c} {\frac{3}{10}} & {\frac{3}{20}} & {\frac{19}{210}} & 0 & 0 & 0 \\ {\frac{3}{20}} & {\frac{13}{105}} & {\frac{79}{840}} & 0 & 0 & 0 \\ {\frac{19}{210}} & {\frac{79}{840}} & {\frac{103}{1260}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{3}{10}} & {\frac{3}{20}} & {\frac{19}{210}} \\ 0 & 0 & 0 & {\frac{3}{20}} & {\frac{13}{105}} & {\frac{79}{840}} \\ 0 & 0 & 0 & {\frac{19}{210}} & {\frac{79}{840}} & {\frac{103}{1260}} \\ \end{array} } \right] \, \left\{ {\begin{array}{*{20}c} {\underline{c}_{1} } \\ \begin{aligned} \underline{c}_{2} \hfill \\ \underline{c}_{3} \hfill \\ \end{aligned} \\ {\bar{c}_{1} } \\ \begin{aligned} \bar{c}_{2} \hfill \\ \bar{c}_{3} \hfill \\ \end{aligned} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{1}{6} + \frac{r}{6}} \\ {\frac{1}{20} + \frac{r}{12}} \\ {\frac{1}{60} + \frac{r}{20}} \\ \begin{aligned} \, \frac{1}{2} - \frac{r}{6} \hfill \\ \frac{13}{60} - \frac{r}{12} \hfill \\ \frac{7}{60} - \frac{r}{20} \hfill \\ \end{aligned} \\ \end{array} } \right]. $$

On solving the above system we have obtained the fuzzy constants $\widetilde{c}_{i}$ for $i = 1, \ldots 3$ and putting these values in Eq. (39) we have

$$ \begin{aligned} & \underline{y} (t;r) = (1 - t)(3 + r) + tr + t(1 - t)\left( {\frac{14(2332 + 1435r)}{36777} - \frac{14( - 557 + 41r)t}{12259} - \frac{14}{299}(1 + r)t^{2} } \right), \\ & \bar{y}(t;r) = (1 - t)(5 - r) + (2 - r)t + t(1 - t)\left( { - \frac{14( - 5202 + 1435r)}{36777} - \frac{14(475 + 41r)t}{12259} + \frac{14}{299}( - 3 + r)t^{2} } \right). \\ \end{aligned} $$

Again, it may be worth mentioning that the results obtained by proposed method are compared with exact solution for different values of $t$, which are tabulated in tables 3 and 4. Plots for Example 2 are depicted in figure 2.

Table 3 Fuzzy solution of Example 2 at $t = 0.1$.

Table 4 Fuzzy solution of Example 2 at $t = 0.01$.

Figure 2

Fuzzy solution of Example 2 using the proposed method.

Example 3

Consider the following FDE (Case 2):

$$ \widetilde{y}'' - \widetilde{y} = 1 \, $$

(40)

subject to the fuzzy boundary conditions as

$$ \widetilde{y}(0) = [r - 1, \, 1 - r],\widetilde{y}(0) = [r - 1, \, 1 - r],\quad \widetilde{y}(1) = [r + (e - 2), \, e - r]. $$

We have obtained the exact fuzzy solution as follows:

$$ \begin{aligned} & \underline{Y} (t{ ; }r) = - 1 + e^{t} + (r - 1)\cos (t) + (r - 1)\sin (t)\tan \left( {\frac{1}{2}} \right) \\ & \bar{Y}(t{ ; }r) = - 1 + e^{t} + (1 - r)\cos (t) + (1 - r)\sin (t)\tan \left( {\frac{1}{2}} \right). \\ \end{aligned} $$

Next, by following the proposed method we have

$$ \widetilde{\phi }_{0} (t;r) = [(1 - t)(r - 1) + t(r + (e - 2)), \, (1 - t)(1 - r) + t(e - r)]. $$

The following system is now obtained as

$$ \left[ {\begin{array}{*{20}c} {\frac{1}{3}} & {\frac{1}{6}} & {\frac{1}{10}} & {\frac{1}{30}} & {\frac{1}{60}} & {\frac{1}{105}} \\ {\frac{1}{6}} & {\frac{2}{15}} & {\frac{1}{10}} & {\frac{1}{60}} & {\frac{1}{105}} & {\frac{1}{168}} \\ {\frac{1}{10}} & {\frac{1}{10}} & {\frac{3}{35}} & {\frac{1}{105}} & {\frac{1}{168}} & {\frac{1}{252}} \\ {\frac{1}{30}} & {\frac{1}{60}} & {\frac{1}{105}} & {\frac{1}{3}} & {\frac{1}{6}} & {\frac{1}{10}} \\ {\frac{1}{60}} & {\frac{1}{105}} & {\frac{1}{168}} & {\frac{3}{20}} & {\frac{13}{105}} & {\frac{79}{840}} \\ {\frac{1}{105}} & {\frac{1}{168}} & {\frac{1}{252}} & {\frac{1}{10}} & {\frac{1}{10}} & {\frac{3}{35}} \\ \end{array} } \right] \, \left\{ {\begin{array}{*{20}c} {\underline{c}_{1} } \\ \begin{aligned} \underline{c}_{2} \hfill \\ \underline{c}_{3} \hfill \\ \end{aligned} \\ {\bar{c}_{1} } \\ \begin{aligned} \bar{c}_{2} \hfill \\ \bar{c}_{3} \hfill \\ \end{aligned} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{r}{6} - \frac{1}{4} - \frac{e}{12}} \\ {\frac{r}{12} - \frac{7}{60} - \frac{e}{20}} \\ {\frac{r}{20} - \frac{1}{15} - \frac{e}{30}} \\ \begin{aligned} \, - \frac{r}{6} + \frac{1}{12} - \frac{e}{12} \hfill \\ - \frac{r}{12} + \frac{1}{20} - \frac{e}{20} \hfill \\ - \frac{r}{20} + \frac{1}{30} - \frac{e}{30} \hfill \\ \end{aligned} \\ \end{array} } \right]. $$

And the solution may be found to be

$$ \begin{aligned} & \underline{y} (t) = (1 - t)(r - 1) + t(r + e - 2) + t(1 - t)\left( \begin{aligned} &- \frac{7}{86476182}(10608211 + 1848717e - 6748420r) \hfill \\& - \frac{14}{14412697}( - 138672 + 148304e - 48203r)t \hfill \\& - \frac{7}{335179}( - 1345 + 897e + 2242r)t^{2} \hfill \\& \end{aligned} \right), \\ & \bar{y}(t) = (1 - t)(1 - r) + t(e - r) + t(t - 1)\left( \begin{aligned}& - \frac{7}{86476182}( - 2888629 + 1848717e + 6748420r) \hfill \\& - \frac{14}{14412697}( - 235078 + 148304e + 48203r)t \hfill \\ &- \frac{7}{335179}(3139 + 897e - 2242r)t^{2} \hfill \\& \end{aligned} \right). \\ \end{aligned} $$

Again the solution obtained by proposed method is compared with the exact solution. Results are given in tables 5 and 6, and plots for this example are shown in figure 3.

Table 5 Fuzzy solution of Example 2 at $t = 0.1$.

Table 6 Fuzzy solution of Example 2 at $t = 0.01$.

Figure 3

Fuzzy solution of Example 3 for Case 2 using the proposed method.

Example 4

Next, we consider the following FDE (Case 3):

$$ \widetilde{y}'' - 3\widetilde{y}' + 2\widetilde{y} = 0 { } $$

(41)

subject to the fuzzy boundary conditions

$$ \widetilde{y}(0) = [r + 1, \, 3 - r], $$

$$ \widetilde{y}(1) = [r + 2, \, 4 - r]. $$

The exact fuzzy solution for this problem may be obtained as follows:

$$ \begin{aligned} & \underline{Y} (t;r) = \frac{{e^{ - 1 - 2t} \left( { - 3e^{3t} + 3e^{4t} + 2e^{2 + 3t} - 2e^{1 + 4t} } \right)}}{ - 1 + e} + \frac{{(1 - r)e^{ - 1 - 2t} \left( { - e^{2} + e^{3} + e^{1 + t} - e^{3 + t} } \right)}}{ - 1 + e}, \\ & \bar{Y}(t;r) = \frac{{e^{ - 1 - 2t} \left( { - 3e^{3t} + 3e^{4t} + 2e^{2 + 3t} - 2e^{1 + 4t} } \right)}}{ - 1 + e} + \frac{{(r - 1)e^{ - 1 - 2t} \left( { - e^{2} + e^{3} + e^{1 + t} - e^{3 + t} } \right)}}{ - 1 + e}. \\ \end{aligned} $$

Here we may have $\widetilde{\phi }_{0} (t;r) = [(1 - t)(r + 1) + t(r + 2), \, (1 - t)(3 - r) + t(4 - r)]$and

$$ \left[ {\begin{array}{*{20}c} {\frac{4}{15}} & {\frac{2}{15}} & {\frac{17}{210}} & 0 & {\frac{1}{20}} & {\frac{1}{20}} \\ {\frac{2}{15}} & {\frac{4}{35}} & {\frac{37}{420}} & {\frac{1}{20}} & 0 & {\frac{1}{70}} \\ {\frac{17}{210}} & {\frac{37}{420}} & {\frac{7}{90}} & {\frac{1}{20}} & {\frac{1}{70}} & 0 \\ 0 & {\frac{1}{20}} & {\frac{1}{20}} & {\frac{4}{15}} & {\frac{2}{15}} & {\frac{17}{210}} \\ {\frac{1}{20}} & 0 & {\frac{1}{70}} & {\frac{2}{15}} & {\frac{4}{35}} & {\frac{37}{420}} \\ {\frac{1}{20}} & {\frac{1}{70}} & 0 & {\frac{17}{210}} & {\frac{37}{420}} & {\frac{7}{90}} \\ \end{array} } \right] \, \left\{ {\begin{array}{*{20}c} {\underline{c}_{1} } \\ \begin{aligned} \underline{c}_{2} \hfill \\ \underline{c}_{3} \hfill \\ \end{aligned} \\ {\bar{c}_{1} } \\ \begin{aligned} \bar{c}_{2} \hfill \\ \bar{c}_{3} \hfill \\ \end{aligned} \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\frac{r}{3}} \\ {\frac{1}{60} + \frac{r}{6}} \\ {\frac{1}{60} + \frac{r}{10}} \\ \begin{aligned} \, \frac{2}{3} - \frac{r}{3} \hfill \\ \frac{7}{20} - \frac{r}{6} \hfill \\ \frac{13}{60} - \frac{r}{10} \hfill \\ \end{aligned} \\ \end{array} } \right]. $$

Hence the solutions are

$$ \begin{aligned} & \underline{y} (t;r) = (1 + r)(1 - t) + (2 + r)t + (1 - t)t \\ & \left( {\frac{7( - 1709 + 2434r)}{10022} - \frac{7( - 3079 + 2394r)t}{10022} + \frac{{21(105 + 298r)t^{2} }}{10022}} \right), \\ & \bar{y}(t;r) = (3 + r)(1 - t) + (4 - r)t + (1 - t)t \\ & \left( { - \frac{7( - 3159 + 2434r)}{10022} + \frac{7( - 1709 + 2394r)t}{10022} - \frac{{21( - 701 + 298r)t^{2} }}{10022}} \right). \\ \end{aligned} $$

Here also above results are compared with the exact solution and are incorporated in tables 7 and 8. Corresponding plots for this example are shown in figure 4.

Table 7 Fuzzy solution of Example 4 at $t = 0.1$.

Table 8 Fuzzy solution of Example 4 at $t = 0.01$.

Figure 4

Fuzzy solution of Example 4 for Case 3 using the proposed method.

Example 5

Let us now consider the following FDE (Case 2):

$$ \widetilde{y}''' - t\widetilde{y} = (t^{3} - 2t^{2} - 5t - 3 )e^{t} , \, 0 \le t \le 1 $$

(42)

subject to the fuzzy boundary conditions

$$ \widetilde{y}(0) = [0.2r - 0.2, \, 0.2 - 0.2r],\quad \widetilde{y}'(0) = [0.2r + 0.8, \, 1.2 - 0.2r],\quad \widetilde{y}(1) = [0.2r - 0.2, \, 0.2 - 0.2r]. $$

Here we may have $\widetilde{\phi }_{0} (t;r) = [(0.2r - 0.2) + t(1 - t)(0.2r + 0.8), \, (0.2 - 0.2r) + t(1 - t)(1.2 - 0.2r)]$ and applying the procedure as discussed in section 3, one may have

$$ \underline{y} (t;r) = (0.2r - 0.2) + (0.8 + 0.2r)(1 - t)t + t(1 - t)\left\{ \begin{aligned} ( - 8.27196 - 0.21426r) \hfill \\ + t(1.06088 + 0.00826r) \hfill \\ + t^{2} (0.57229 + 0.00819r) \hfill \\ + t^{3} (0.20881 + 0.00009) \hfill \\ \end{aligned} \right\}, $$

$$ \bar{y}(t;r) = .(0.2 - 0.2r) + (1.2 - 0.2r)(1 - t)t + t(1 - t)\left\{ \begin{aligned} ( - 8.70050 + 0.21426r) \hfill \\ + t(1.07710 - 0.00826r) \hfill \\ + t^{2} (0.58867 - 0.00819r) \hfill \\ + t^{3} (0.20900 - 0.00009) \hfill \\ \end{aligned} \right\}. $$

Here also above results are compared with the special case $r = 1$ [26] and are incorporated in table 9. Corresponding plots for this example are shown in figure 5.

Table 9 Fuzzy solution of Example 4.

Figure 5

Fuzzy solution of Example 3 for Case 2 using the proposed method.

Example 6

In this example we have considered a 1-mm diameter, 50-mm long aluminium pin fin as shown in figure 6 used to enhance the heat transfer from a surface wall maintained at $300^{ \circ } {\text{C}}.$ The governing differential equation is

Figure 6

A pin-fin Seshu [27].

$$ k\frac{{d^{2} \widetilde{T}}}{{dx^{2} }} = \frac{Ph}{{A_{c} }}(\widetilde{T} - \widetilde{T}_{\infty } ) $$

(43)

subject to the fuzzy boundary conditions

$$ \widetilde{T}(0;r) = [20r + 280,{ 320} - 20r], \, \frac{{d\widetilde{T}}}{dx}(L) = [0.8r - 0.8,0.2 - 0.2r]. $$

Here the considered parameters are defined as below.

$$ \begin{aligned} & k = {\text{coefficient of thermal conductivity,}} \\ & P = p{\text{erimeter,}} \\ & A_{c} = {\text{cross-sectional area,}} \\ & h = {\text{convective heat transfer coefficient,}} \\ & \widetilde{T}_{w} = {\text{fuzzy wall temperature,}} \\ & \widetilde{T}_{\infty } = {\text{ambient temperature}} .\\ \end{aligned} $$

Let $k = 200\,{\rm W/m}/^{ \circ } {\rm C}$ for aluminium, $h = 20\,{\rm W/m}^{2} {^{ \circ } {\text{C}}}, \, \widetilde{T}_{\infty } = 30^{ \circ } {\text{C}}.$ Thus Eq. (43) is reduced to

$$ \frac{{d^{2} \widetilde{T}}}{{dx^{2} }} = 400(\widetilde{T} - 30). $$

The exact bounds of the fuzzy solutions are found as follows:

$$ \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{T} (x;r) = e^{ - 20x} (220.212 + 30e^{20x} + 29.7878e^{40x} + 17.603r + 2.39702e^{40x} r), $$

$$ \bar{T}(x;r) = e^{ - 20x} (255.428 + 30e^{20x} + 34.5721e^{40x} - 17.6127r - 2.3873e^{40x} r). $$

Here we may have $\widetilde{\phi }_{0} (t;r) = [(20r + 280) + x(0.8r0.8), \, (320 - 20r) + x(0.2 - 0.2r)].$ Fuzzy solutions are obtained using the present procedure and are presented in tables 9–13. Tables 9 and 11 gives the lower and upper bounds of the fuzzy solutions, respectively, along with the comparison of Bede [9] for $r = 0.6$ with different values of $x$. Also comparisons have been made in table 12 with the crisp solution obtained by Bede [9] and Seshu [27] for different values of $x$ and $r = 1$. Similarly table 13 incorporates the solution bounds for $x=0.2$ with different values of $r$.

Table 10 Comparison of various lower bound solutions for uncertain temperature in a fin for $r = 0.6$.

Table 11 Comparison of various upper bound solutions for uncertain temperature in a fin for $r = 0.6$.

Table 12 Comparison of the solutions for uncertain temperature in a fin for $r = 1$.

Table 13 Comparison of various bound solutions for uncertain temperature in a fin for $x = 0.2$.

It is worth mentioning that the main value of the paper may not be the example problems as discussed above. Here the main contribution is the new Galerkin type method to handle nth order FDEs. As such some known FDEs are solved as test problems to have the confidence on the proposed method. The solutions by the proposed method in all the test problems are found to be very close to the exact solutions. Finally the proposed method has been applied to an application problem too. The proposed method may be found to be a straightforward and alternate way to handle nth order FBVPs.

5 Conclusions

In this paper, the Galerkin method has been successfully applied to find fuzzy solution of nth order fuzzy boundary value problems. The proposed methodology is applied for both positive and negative coefficient of the fuzzy differential equations. Also the obtained results are compared with the exact as well as other existing method(s) and are found to be in good agreement.