MHD free convection heat transfer of a water–Fe₃O₄ nanofluid in a baffled C-shaped enclosure

Abstract

In this paper, the effect of a baffle on free convection heat transfer of a water–Fe₃O₄ nanofluid in a C-shaped enclosure in the presence of a magnetic field is investigated numerically. The enclosure is subjected to a constant magnetic field. The vertical wall on the left side is maintained at a constant hot temperature of T_h, and the right one is kept at a constant cold temperature of T_c. The rest of the walls are insulated. The governing equations are discretized by the control volume method and solved simultaneously by the SIMPLE algorithm. The numerical results show very good agreement with other published works. The results indicate that by increasing the enclosure’s aspect ratio, the Nusselt number is increased. It is also found that the volume fraction of nanoparticles can be raised in order to achieve increased cooling in the enclosure. By increasing the aspect ratio, the effect of the nanoparticles on the enhancement of the Nusselt number is more pronounced. Also, the maximum effect of the baffle on the heat transfer is seen at the bottom of the hot wall. Generally, increasing the baffle length produces increases in the Nusselt number. The maximum cooling level is occurred for AR = 0.7 and B_f = 0.2.

Introduction

Free convection heat transfer has achieved a big interest in recent years due to its wide applications in various areas, including cooling electronic devices, chemical processing equipment and collecting solar energy [1,2,3]. In the integrated electrical circuit boards, an effective cooling process is required to ensure the satisfactory performance of the electronic components in high temperature range. In the last few decades, free convection heat transfer has created great interest for researchers in science, engineering and electronics industry. The main objective of the researchers is to find different strategies for increasing efficiency and cooling the heat that is created on electronic devices with specific geometries [4, 5]. Alami et al. [6] investigated the height of the isothermal blocks on the free convection heat transfer in a T-shaped cavity with the air passage. The examined parameters were the Rayleigh number, Prandtl number and the height of the blocks. The results showed that the heat transfer changes with the Rayleigh number for smooth or ribbed vertical channels. Bilgen [7] studied the heat transfer in a cavity with the thin fin on the hot wall, numerically and predicted the position and size of the fin on the heat transfer and found that the Nusselt number decreases with increasing the fin length.

In most of the conducted studies, the fluid within the enclosure has a low conductivity, which limits the heat transfer rate that is why particular attention has been paid for using nanofluids [8,9,10]. It is expected that the addition of nanoparticles to the base fluid would increase the conductivity coefficient and consequently, the heat transfer. Many researchers have stated that by adding nanoparticles with low volume fractions (1–5%), the thermal conductivity coefficient of the nanofluid could be increased up to 20% [11, 12]. Mahmoudi et al. [13] numerically solved the free convection of the copper–water nanofluid in a square-shaped cavity containing a horizontal heat source on the vertical side. They investigated the influence of some parameters including the Rayleigh number, position of the heat source and the volume fraction of nanofluids on the heat transfer of the cavity and found that the most effective one is the dimension of the heat source where the heat transfer rate is decreased by increasing the length of the heat source. Jou and Tzeng [14] conducted a numerical study of the heat transfer parameters for nanofluids in a two-dimensional enclosure. They concluded that increasing the volume fraction of the nanoparticles would lead to an increase in the heat transfer rate. The numerical study of the nanofluids influence on the free convection of water–copper nanofluids in a two-dimensional enclosure is investigated by Khanafer et al. [15]. They proved that at any Grashof number, the heat transfer rate is increased with increasing the copper particles dispersed in water. Ahmed and Rashed [16] investigated numerically the problem of natural convection heat transfer of micropolar nanofluid inside a rectangular enclosure saturated with anisotropic porous medium. They showed in anisotropic porous medium, the increase in the permeability ratio leads to a decrease in the fluid activity and vortex strength. Rashad et al. [17] studied magnetohydrodynamic effect on natural convection in a cavity filled with a porous medium saturated with a nanofluid. MHD mixed convection of Cu–water nanofluid in a two-sided lid-driven porous cavity with a partial slip is investigated by Sivasankaran et al. [18]. They concluded that the average heat transfer rate increased on increasing the Darcy number for both cases of direction of the moving wall. Mansour et al. [19] considered numerical simulation for MHD natural convection in a square enclosure using a nanofluid with the influence of thermal boundary conditions. They found that an increase in the Hartmann number resulted in a clear reduction in the rate of heat transfer. Numerical investigation of the effect of an inclined magnetic field on the mixed convection flow in a trapezoidal enclosure in the presence of internal heat generation or absorption has been done by Rashad et al. [20]. They showed that the heat transfer rate increased on decreasing the Richardson number, that is, the forced convection produced heat transfer enhancement and this decreased on increasing the magnetic field strength. Natural convection analysis by entropy generation and heatline visualization using lattice Boltzmann method in nanofluid-filled cavity included with internal heaters-Empirical thermo-physical properties is studied by Rahimi et al. [21]. Natural convective boundary layer flow over a non-isothermal vertical plate embedded in a porous medium saturated with a nanofluid is investigated by Gorla and Chamkha [22]. Ismael et al. [23] investigated the entropy generation due to conjugate free convection in a square domain. They suggested a novel gauge for evaluation of the thermal performance. Armaghani et al. [24] studied the entropy generation and natural convection of nanofluids in an inclined porous media-layered cavity. They used the thermal performance criteria for obtaining the best value of the porous layer, nanofluid volume fraction and other parameters. Armaghani et al. [25] carried out numerical investigation of water–alumina nanofluid natural convection heat transfer and entropy generation in a baffled L-shaped cavity. They used the thermal performance criteria for introducing the best aspect ratio and baffled length of an L-shaped cavity. Recently, Snoussi et al. [26] have studied numerically the natural convection heat transfer in a nanofluid-filled U-shaped enclosure.

Studying the effects of the presence of a magnetic field has important applications in physics and engineering. Mass and heat transfer problems in the presence of a magnetic field have attracted the interests of scientists and engineers for many decades [27,28,29]. Kasayipour et al. [30] investigated the mixed convection heat transfer in a T-shaped enclosure subjected to a magnetic field and realized that by increasing the Reynolds number, Richardson number and the volume fraction of nanoparticles, an increase in the heat transfer would occur. Makulati et al. [31] studied the free convection heat transfer of the water–alumina nanofluid in a C-shaped enclosure in the presence of the magnetic field and concluded that by increasing the Hartmann number, the effect of the nanofluid on the Nusselt number is decreased; also, they realized that the effect of the enclosure angle on the heat transfer is decreased by increasing the enclosure aspect ratio. Chamkha et al. [32] studied the entropy generation and natural convection of CuO–water nanofluid in a C-shaped cavity under a magnetic field.

Since baffle is a tool for controlling and increasing heat transfer rate, they have many applications in various industries. Therefore, a numerical study of the baffle effect on free convection heat transfer of water–Fe₃O₄ nanofluids in the C-shaped enclosure in the presence of a magnetic field is investigated in this study. In this regard, the effects of parameters such as the Rayleigh number, the Hartmann number, and the aspect ratio of the enclosure, the baffle length and the nanoparticles volume fraction on the rate of heat transfer are investigated.

Problem description

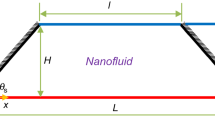
The physical model of this study is a C-shaped enclosure with a baffle, which is indicated in Fig. 1. The enclosure is subjected to a constant magnetic field, the left-side wall is maintained at the hot temperature T_h, the right-side wall is kept at the cold temperature T_c, and the rest of the walls are insulated. The baffle with the temperature T_c has a significant effect on the flow behavior and can disrupt the flow pattern. The aspect ratio and the baffle length are defined as AR = H/L and B_f = a/L, respectively. The enclosure is filled with a Fe₃O₄–water nanofluid. The direction of the gravity force is downward, and the enclosure is subjected to a constant magnetic field of magnitude B₀ in the horizontal direction.

Fig. 1

C-Shaped enclosure with baffle subjected to the magnetic field

Governing equations

The assumptions of this problem are:

• Laminar flow without energy generation and storage and with no viscous dissipation.

• A thermal equilibrium exists between the pure fluid and the solid particles.

• The nanofluid is an incompressible Newtonian fluid.

With considering the single-phase approach for modeling the nanofluid flow and heat transfer, the dimensionless governing equations (continuity, momentum and energy) of the problem by applying the Boussinesq approximation are as follows [31]:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$

(1)

$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} \nu_{\text{f}} }}\left[ {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right]$$

(2)

$$\begin{aligned} U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} & = - \frac{\partial P}{\partial Y} + \frac{{\mu_{\text{nf}} }}{{\rho_{\text{nf }} \nu_{\text{f}} }}\left[ {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right] \\ & \quad + \frac{{\left( {\rho \beta } \right)_{\text{nf}} }}{{\rho_{\text{nf}} \beta_{\text{f}} }}Ra \cdot Pr \cdot \theta - \frac{{\rho_{\text{f }} \sigma_{\text{nf }} }}{{\rho_{\text{nf }} \sigma_{\text{f}} }}Ha^{2} \cdot Pr \cdot V \\ \end{aligned}$$

(3)

$$U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \frac{{\alpha_{\text{nf}} }}{{\alpha_{\text{f}} }}\left[ {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right],$$

(4)

where the dimensionless parameters used in the equations are:

$$X = \frac{x}{L},Y = \frac{y}{L},U = \frac{uL}{{\alpha_{\text{f}} }},V = \frac{vL}{{\alpha_{\text{f}} }},P = \frac{pL}{{\rho_{\text{nf}} \alpha_{\text{f}}^{2} }},\theta = \frac{{T - T_{\text{C}} }}{{T_{\text{h}} - T_{\text{C}} }}.$$

(5)

With the dimensionless numbers of Rayleigh, Prandtl and Hartmann are defined as follows:

$$Ra = \frac{{g\beta L^{3} \left( {T_{\text{h}} - T_{\text{C}} } \right)}}{{\nu_{\text{f}} \alpha_{\text{f}} }},\quad Pr = \frac{{\nu_{\text{f}} }}{{\alpha_{\text{f}} }},\quad Ha = B_{0} L\sqrt {\frac{{\sigma_{\text{f}} }}{{\rho_{\text{f}} \nu_{\text{f}} }}} .$$

(6)

Boundary conditions

The hydrodynamic boundary conditions of the present problem are the no-slip and no-penetration conditions at the walls U, V = 0. The thermal boundary condition for the left-side wall and the hot source is Ө = 1, for the inner cold horizontal and vertical wall with baffle is Ө = 0, and for the insulated walls, the temperature gradient is zero. The heat transfer rate can be expressed in the form of the Nusselt number. The local Nusselt number on the hot wall is defined as follows:

$$Nu = - \frac{{k_{\text{nf}} }}{{k_{\text{f}} }}\left( {\frac{\partial \theta }{\partial X}} \right)_{X = 0} .$$

(7)

The average Nusselt number is achieved by integrating through the hot wall:

$$Nu_{\text{m}} = \mathop \smallint \limits_{0}^{1} Nu {\text{d}}Y.$$

(8)

Physical properties of nanofluids

The nanofluids thermo-physical properties are calculated according to the following formulas [32,33,34]:

$$\rho_{\text{nf}} = \left( {1 - \varphi } \right)\rho_{\text{f}} + \varphi \rho_{\text{s}}$$

(9)

$$\left( {\rho \beta } \right)_{\text{nf}} = \left( {1 - \varphi } \right)\left( {\rho \beta } \right)_{\text{f}} + \varphi \left( {\rho \beta } \right)_{\text{s}}$$

(10)

$$\left( {\rho c_{\text{p}} } \right)_{\text{nf}} = \left( {1 - \varphi } \right)\left( {\rho c_{\text{p}} } \right)_{\text{f}} + \varphi \left( {\rho c_{\text{p}} } \right)_{\text{s}}$$

(11)

$$\alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }}$$

(12)

$$\frac{{\sigma_{\text{nf}} }}{{\sigma_{\text{f}} }} = 1 + \frac{{3\left( {\gamma - 1} \right)\varphi }}{{\left( {\gamma + 2} \right) - \left( {\gamma - 1} \right)\varphi }},\quad \gamma = \frac{{\sigma_{\text{s}} }}{{\sigma_{\text{f}} }}.$$

(13)

The dynamic viscosity of the nanofluids is given by Brinkman [35] as follows:

$$\mu_{\text{nf}} = \mu_{\text{f}} \left( {1 - \varphi } \right)^{ - 2.5} .$$

(14)

K_nf is the thermal conductivity coefficient of nanofluids proposed by Patel’s model [36]. For two independent components of suspended spherical particles, the model is as follows:

$$k_{\text{nf}} = k_{\text{f}} \left[ {1 + \frac{{k_{\text{s}} A_{\text{s}} }}{{k_{\text{f}} A_{\text{f}} }} + ck_{\text{s}} Pe\frac{{A_{\text{s}} }}{{k_{\text{f}} A_{\text{f}} }}} \right],$$

(15)

where k_s and k_f are the conductivity coefficient of the Fe₃O₄–water nanofluid and pure water, respectively. C = 36,000 is proposed for Fe₃O₄–water nanofluid [37].

$$\frac{{A_{\text{s}} }}{{A_{\text{f}} }} = \frac{{d_{\text{f}} }}{{d_{\text{s}} }}\frac{\varphi }{1 - \varphi }.$$

(16)

The diameter of the solid nanoparticles is d_s = 100 nm, and the molecular size of the water-based fluid is:

$$d_{\text{f}} = 2A^{0},A^{0}=0.1nm$$

(17)

$$Pe = \frac{{u_{\text{s}} d_{\text{s}} }}{{\alpha_{\text{f}} }},$$

(18)

in which u_s is the Brownian motion of nanoparticles speed:

$$u_{\text{s}} = \frac{{2k_{\text{b}} T}}{{\pi \mu_{\text{f}} d_{\text{s}}^{2} }},$$

(19)

where $k_{\text{b}} = 1.3807 \times 10^{ - 23} \;{\text{J}}\,{\text{K}}^{ - 1}$ is the Boltzmann constant. nf, f and s indices refer to the properties of nanofluids, water and Fe₃O₄ nanoparticles, respectively. Pr = 6.2 is considered for pure water. The thermo-physical properties of the water and Fe₃O₄ are provided in Table 1.

Table 1 Thermo-physical properties of pure water and Fe₃O₄ nanoparticle [38]

Numerical solution and validation

For modeling the desired geometry, a program is written in FORTRAN. Equations (1)–(4) together with the mentioned boundary conditions are discretized using the finite difference method based on the control volume. The solution field is discretized using staggered grids. For solving the algebraic equations, the SIMPLE algorithm, which is detailed in Ref. [39], has been used. The convergence criteria are as follows:

$$\mathop \sum \limits_{j} \mathop \sum \limits_{i} \sqrt {\left[ {\left. {\frac{{\delta^{{\text{n}} + 1} - \delta^{\text{n}} }}{{\delta^{\text{n} + 1} }}} \right|_{i,j} } \right]^{2} } \le 10^{ - 8} ,$$

(20)

in which n is the iteration number and δ indicates the general variable (U, V, θ). Convergence rate is shown in Fig. 2.

Fig. 2

Convergence rate

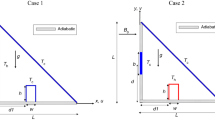
Figure 3 shows the comparison of the written code for a C-shaped enclosure with nanofluids. The average Nusselt is plotted for an enclosure with three inner walls in the cold temperature and three outer walls in the hot temperature [40]. The nanofluid is a suspension of copper and water. The comparison is conducted for Ra = 10⁵ in different aspect ratios and different volume fractions. It can be concluded that the results are in good agreement with the results of Ref. [40].

Fig. 3

Comparison of average Nusselt between current work and Mahmudi and Hashemi [40]

After controlling the program performance, it is required to check the independence of the solutions in terms of the grid numbers. In this regard, the influence of the grid number on the Nusselt number of the hot wall for a C-shaped enclosure has been investigated for different Rayleigh numbers, Hartmann numbers, aspect ratios, baffle lengths and volume fractions of nanoparticles. Sample of such surveys for Ha = 30, AR = 0.3, B_f = 0.3, Ra = 105 and φ = 0.04 is given in Table 2. It is clear that for grids smaller than 100 × 100, the solution remained the same. The grid structure of the enclosure is shown in Fig. 4.

Table 2 Effect of the grid number on the average Nusselt number

Fig. 4

Grid sample

Results

Effect of Rayleigh and Hartmann number

In this section, the effects of the Rayleigh and Hartmann numbers on the fluid and temperature fields and the free convection heat transfer rate is investigated. The parametric values AR = 0.3 and B_f = 0.2 are considered.

In Fig. 5, the streamlines and isotherms for different Rayleigh numbers and Ha = 15 are plotted for water and nanofluid. The results show that with increasing the Rayleigh number, and consequently, increasing the buoyancy force, the streamlines are drawn to the walls. This leads to increase the flow velocity near the wall. Also, the maximum of the stream function is observed in the center of the contour. It can be seen that a stronger vortex is formed by increasing the Rayleigh number.

Fig. 5

Streamlines and isotherms for different Rayleigh numbers in Ha = 15 (solid line) for pure water and (dashed line) for nanofluid φ = 0.04

For lower Rayleigh numbers, where the conduction is dominant, thermal layers with parallel and perpendicular isotherms are formed in the central area of the enclosure. By increasing the Rayleigh number, the temperature gradient is more intense in the vicinity of the walls and thermal boundary layers are formed near the hot and cold walls and also the baffle.

The effect of the different Rayleigh numbers of the nanofluid (φ = 0.04) on the local Nusselt is plotted for Ha = 15 in Fig. 6. The result shows that by increasing the Rayleigh number, the level of the heat transfer is increased, due to the increase in the buoyancy force. Also, it can be observed that in the top corner of the hot wall, the process is reversed due to the speed slowdown in this area and dominance of the conduction heat transfer.

Fig. 6

Effect of Rayleigh numbers of nanofluid on local Nusselt number (Ha = 15, φ = 0.04)

In Fig. 7, the effect of the Rayleigh number and the volume fraction of the nanoparticles on the average Nusselt is plotted. As it was expected from Fig. 5, the heat transfer is increased by increasing the Rayleigh number. Also, it was observed that adding the nanoparticles in the base fluid increases the Nusselt number slightly.

Fig. 7

Effect of Rayleigh number and volume fraction of nanofluid on the average Nusselt number (Ha = 15)

In Fig. 8, the streamlines and isotherms are plotted for water and nanofluid for different Hartman numbers and Ra = 10⁵. It can be observed that the streamlines are drawn to the bottom of the wall as the Hartmann number is increased, which weakens the vortices and decreases the velocity flow.

Fig. 8

Streamlines and isotherms for different Hartman numbers (Ra = 10⁵) (solid line) for pure fluid and (dashed line) for nanofluid (φ = 0.04)

The streamlines are tending to be parallel with the vertical walls from in a complicated manner by increasing the magnetic field. In other words, with increasing the Hartmann number, the Lorentz force is strengthened and overcomes the buoyancy forces and the conduction heat transfer becomes dominant. By increasing the thermal conductivity, the surface temperature becomes higher, which results in a reduction in the temperature gradient of the nanofluid compared to that of the pure fluid. The capability and capacity of the fluid for heat transfer are increased by using nanofluids.

The effect of different Hartmann numbers on the local Nusselt number is shown in Fig. 9. It can be seen that increasing the magnetic field would result in reduced local Nusselt numbers through the hot source due to the dominance of the Lorentz force on the bouncy force. Due to the reduction in the velocity component and the decreasing effect of the magnetic field on the Nusselt, the heat transfer is reduced starting from the top of the hot wall.

Fig. 9

Effect of Hartman number of nanofluids on the local Nusselt number (φ = 0.04, Ra = 10⁵)

In Fig. 10, the effect of the Rayleigh and Hartmann numbers on the average Nusselt is plotted. The results show a reduction in the heat transfer by increasing the Hartmann number. As it was expected from Fig. 5, by increasing the Rayleigh number, the heat transfer is increased due to the increase in the buoyancy properties.

Fig. 10

Effect of Rayleigh and Hartmann numbers of nanofluid on the average Nusselt number (φ = 0.04)

The effect of the enclosure aspect ratio and baffle length

In this section, the effects of the aspect ratio and the baffle length on the flow and temperature fields as well as the free convection heat transfer rate are investigated. The values Ra = 10⁵ and Ha = 15 are fixed in this section.

The streamlines and isotherms for various aspect ratios are presented for base fluid (pure water) and nanofluid (φ = 0.04) in Fig. 11. It can be observed that by increasing the aspect ratio, the vortices become smaller due to the reduced space.

Fig. 11

Streamlines and isotherms for different aspect ratios (B_f = 0.2) (solid line) for pure fluid and (dashed line) for nanofluid (φ = 0.04)

Also, it is shown that by increasing the aspect ratio, the isotherms become closer to the hot wall as a result of the flow reduction between the hot and cold walls, which yields an increase in the heat transfer.

The effect of the aspect ratio on the local Nusselt at the hot wall is plotted in Fig. 12. Generally, increasing the aspect ratio leads to an increase in the Nusselt number. Moving toward the top of the hot wall, the Nusselt number is reduced because of the buoyancy force. The effect of the baffle length on the Nusselt number for AR = 0.7 is more significant due to the close proximity of the baffle to the hot wall.

Fig. 12

Effect of enclosure aspect ratio on local Nusselt number (φ = 0.04, B_f = 0.2)

The effect of the aspect ratio and the volume fraction on the average Nusselt number is shown in Fig. 13. According to the results, the Nusselt number increases as a result of increasing AR. Also, it is obvious from the figure that using a nanofluid instead of a pure fluid increases the Nusselt number. Consequently, if it is desired to increase the cooling capacity of a system using a nanofluid, the volume fraction of nanoparticles can be increased.

Fig. 13

Effect of aspect ratio for different volume fractions of nanofluids on average Nusselt number (B_f = 0.2)

In Fig. 14, the streamlines and isotherms for base fluid and nanofluid are plotted for various lengths of the baffle. It can be observed that by increasing the baffle length, the space for nanofluid flow is reduced and hence, the vortices become smaller. Also, the isotherms become closer to the hot wall, which consequently increases the heat transfer.

Fig. 14

Streamlines and isotherms for different baffle lengths (AR = 0.3) (solid line) for pure fluid and (dashed line) for nanofluid (φ = 0.04)

The effect of the baffle length on the local Nusselt number is plotted in Fig. 15 for AR = 0.3. According to the results, generally, increasing the baffle length increases the Nusselt number with the maximum effect being at the bottom of the hot wall.

Fig. 15

Effect of baffle length on local Nusselt number (φ = 0.04, AR = 0.3)

In Fig. 16, the effect of the baffle length and the aspect ratio on the average Nusselt is plotted. It can be observed that increasing the baffle length increases the heat transfer, except for AR = 0.7 and B_f = 0.3, due to the division of the enclosure into two parts. The maximum cooling level occurs for AR = 0.7 and B_f = 0.2.

Fig. 16

Effect of baffle length and aspect ratio on average Nusselt number (φ = 0.04)

Conclusions

In this work, the effect of a baffle on free convection heat transfer of a water–Fe₃O₄ nanofluid in a C-shaped enclosure under a magnetic field was analyzed numerically. The governing equations were solved using the SIMPLE algorithm. A parametric study of the Rayleigh number, magnetic field, aspect ratio, baffle length and the volume fraction of the nanoparticles on the streamlines, isotherms, and the local and average Nusselt number was performed. The following conclusions are obtained:

• 1. The Nusselt number is increased by increasing the enclosure aspect ratio AR.

• 2. By increasing the volume fraction of the nanoparticles, the enclosure cooling can be enhanced.

• 3. The effect of the nanoparticles on the Nusselt number is more pronounced for higher enclosure aspect ratios.

• 4. The maximum effect of the baffle on the heat transfer is observed at the bottom of the hot wall.

• 5. Generally, increasing the baffle length leads to an increase in the heat transfer.

• 6. Under the considered parametric values, the maximum cooling level occurs for AR = 0.7 and B_f = 0.2.