Introduction

Over the last few years, a little word with big potential has been swiftly insinuating itself into the world’s perception that the word is ‘nano.’ Nano has moved from the world of the future to the world of the present due to the fastest growth in nanotechnology, and many applications are already standard. As nanomaterials possess unique chemical, physical, and mechanical properties, these can be used for a wide variety of applications like next-generation computer chips, aerospace components, spacecraft applications, the elimination of pollutants, and numerous others. Eventually, the development of nanoproducts is leading toward the next industrial revolution. There are plenty of research articles on different types of nanofluids (consisting of a single or multiple nanoparticles) including their preparation and issues with agglomeration or sedimentation [1]. In this context, Huminic and Huminic [2] carried out a detailed review of the application of hybrid nanofluids in diverse fields of thermal systems. Muneeshwaran et al. [3] focused on enhanced heat transfer using a hybrid nanofluid. Such an approach for enhancing heat transfer has also been explored by several researchers using mono/hybrid nanofluid [4, 5] through the porous structure (which has inherent flow hindering characteristics) [6].

Before designing any thermal system/device, understanding the proper thermo-fluid flow characteristics is of utmost importance. Therefore, various researchers are devoted to analyzing the convective dynamics along with the thermal performance in various geometries under various situations [7]. The study is necessary because of its practical relevancy in various engineering fields, for instance electronics cooling, heat exchanging devices, chemical reactors, material processing, food processing, and others [8, 9]. At the same time, it is essential to comprehend the complex convective dynamics under the various thermal boundary conditions. In general, a vast pool of the literature is available based on a constant heat source along the heated wall. However, in real-world applications, it is difficult to maintain heat sources as a constant source. Rather it is more practical to mimic the actual real model of the heating strategy, a nonuniform heating situation. Modeling of nonuniform temperature profiles could be implemented easily following mathematical functions in the form of linear, sinusoidal or half-sinusoidal, or others. In this context, Biswas et al. [10] reported the benefit of nonuniform heating over constant heating (at the bottom) of a porous cavity with sliding cold walls. The same group has also reported enhanced heat transfer (up to 74%) during buoyant convection in a bottom-heated porous cavity keeping the fixed mean temperature of heating [11]. The study on buoyant convection in various cavities heated sinusoidally could be found without [12, 13] or with [14, 15] porous medium. Applying the nonuniform temperature on the bottom and left sidewall, Bhowmick et al. [16] studied buoyant convection in an air-filled cavity containing a heated cylinder, and they observed enhanced heat transfer with sinusoidal heating at a higher wavelength. Sivasankaran and Pan [17] examined the impact of sinusoidal temperature (on the sidewalls), amplitude, and phase deviation on free convection and found an increasing trend of heat transfer with the increasing Ra, and phase deviation. Cheong et al. [18] examined free convection in a porous medium-filled wavy cavity heated nonuniformly and observed that nonuniform heating as well as a wavy wall affects the heat transfer. Considering lower Pr (Prandtl number) fluid-filled porous trapezoidal enclosures, Basak et al. [19] analyzed the impact of nonuniform heating and concluded that the square cavity offers more heat transfer in comparison with the trapezoid-shaped cavity.

The study has also been extended to the area of nanofluid flow under nonuniform heating. In a recent study, Sheremet and Öztop [20] studied the effect of sinusoidal heating on a different nanofluid (Al2O3, CuO, TiO2)-filled cavities containing porous fin and found that the addition of nanoparticles suppresses the heat transfer. In another study, Sheremet et al. [21] examined thermal convection in a nonuniformly heated wavy-walled cavity filled with nanofluid. They ascertained that a rise in the undulation number and its peaks increases the heat transfer. Wang et al. [22] analyzed the effects of sinusoidal heating (on the sidewall) on free convection of non-Newtonian nanofluids flow in a rectangular cavity. The effect of sinusoidal heating, varying the thermal profiles on a U-shaped cavity filled with hybrid nanofluid, has been analyzed by Asmadi et al. [23], and they reported that sinusoidal heating worsens heat transfer compared to uniform heating. The effect of sinusoidal heating on nanofluidic thermal convection in the thick-walled porous cavity has been investigated by Alsabery et al. [24], and they found enhanced heat transfer significantly. Utilizing Cu–Al2O3/water hybrid nanofluid, Tayebi and Chamkha [25] studied the thermal performance of a sinusoidally heated (at the sidewall) cavity.

When an external magnetic field is imposed on a thermo-fluidic system, the transport process is modulated significantly and the associated phenomena are termed Magnetohydrodynamics (MHD). There is plenty of research finding on the above topics [26,27,28,29,30,31,32,33]. Applying the MHD, Pordanjani et al. [34] investigated the Al2O3–water nanofluid thermal convection in a cavity containing heated obstacles on the cavity sidewalls. They observed that magnetic field intensity reduces heat transfer. Magnetohydrodynamic (MHD) nanofluidic convection under the influence of sinusoidal heating profile (on the sidewalls) has also been investigated by Mejri et al. [35] (using Al2O3–water nanofluid) and Sajjadi et al. [36] (using Cu–water nanofluid under the horizontal magnetic field). Furthermore, Malik and Nayak [37] analyzed the thermal convection in a porous cavity filled with Cu–water nanofluid, heated partially with a sinusoidal profile, and found that the thermo-fluid flow structure is significantly modulated by the involved flow parametric values. In a recent study, Biswas et al. [38, 39] analyzed the effect of a nonuniform heating strategy in the form of multi-frequency half-sinusoidal heating at the bottom of the porous cavity containing Cu–Al2O3/water hybrid nanofluid under the external magnetizing impact, and they found that multi-frequency heating is always better relative compared to uniform heating. The study of nonuniform heating has also been extended to different geometry [40], linearly varying temperatures [41], and others.

Tolerating the key challenges in impending engineering and technological applications, the present work explores the fundamental flow physics of natural convection under the externally induced magnetizing field within an intricate porous composition in a half-sinusoidally heated domain. The assorted scientific relevance of such problems imitated, for example cooling of electronic devices, heat exchangers, process industries, MEMs applications, and plenty of others. For that reason, thermal management by convection within the porous matrix and magnetic field between the source and sink has always been a significant topic of concern. This kind of impact with localized heating and cooling originates from more intricate thermo-fluid occurrences in the presence of varying multi-physical conditions [42]. Other relevant works on thermo-fluidic convection in different geometry under sinusoidal heating could be found in the open literature. Considering air-filled partial porous cavity heated nonuniformly, Omara et al. [43] studied the double-diffusive free convection and found that at higher spatial frequency mass transfer declines. Cimpean and Pop [44] examined the free convection of nanofluid flow through the porous inclined cavity heated nonuniformly at the sidewalls. They reported that the cavity orientation and the periodic thermal conditions at the boundaries can effectively control thermal behavior. Effects of various heating temperature profiles on the convection of Cu–Al2O3/water hybrid nanofluidic flow in a U-shaped cavity have been investigated by Asmadi et al. [23], and they reported that isothermal heating offers the best thermal performance, while the nonuniform heating performed the worst. Pati et al. [45] explored the best heating strategy in a circular pipe for forced convection and concluded that the periodic heat flux condition is the optimal choice for the best thermal performance. Astanina et al. [46] considered a cubical thermal system subjected to nonuniform heating at the left vertical wall and observed that constant temperature heating offers a higher energy transport rate. Utilizing Fe3O4–water nanofluid in a wavy triangular cavity subjected to nonuniform heating, Shekaramiz et al. [47] examined the MHD convection and found that both the undulations and nonuniform heating affect thermal behavior.

During an exhaustive survey of the obtainable literature, it is observed that the sinusoidal heating application is relevant in a diversity of thermal fluid flow dynamic systems for exploring heat transfer on top of appropriate control over it. Subsequently, the aim of this exploration is to study the MHD natural convection of Cu-Al2O3/water hybrid nanofluid in a porous enclosure heated half-sinusoidally on the bottom wall with partially cooled sidewalls. The heating profile is applied at the source wall of the enclosure implementing important controlling parameters like amplitude (I) and frequency (f). The heated fluid rejects heat through the partially cooled sidewalls. Therefore, the current work is originated to scrutinize the thermo-fluid flow and heat transfer impact of such a half-sinusoidally heated enclosure underneath a choice of key parameters like Ram, Ha, Da, ε, and φ. Furthermore, the impact of a cooler position is also explored for achieving superior heat transfer. To find out the case of optimal heating strategy, the constant heating condition has also been studied and compared with the applied half-sinusoidal nonuniform heating. The present study contributes new flow features and results by exploring the impact of a spatially active magnetic field on the thermo-fluid flow of a hybrid nanofluid-saturated porous system. A thorough investigation is undertaken by considering different geometric parameters (such as partial cooler positions at the sidewalls) and flow-controlling parameters like magnetic field intensity, temperature modulating parameters, porous medium porosity and permeability, and nanoparticles’ concentration. Furthermore, the heat energy transport within the thermal system is properly illustrated by using Bejan’s heatlines. To capture realistic thermal behaviors of the hybrid nanofluid flow, the experimentally obtained thermo-physical properties (thermal conductivity and viscosity) are used during the simulations instead of their mathematical models. The incorporation of amplitude and frequency of heating profile in conjunction with different multi-physical states is another vital aspect of the present study and is a novel attempt in this field. These facts generate newer results and provide newer insights, especially due to the interaction of partial magnetic field and hybrid nanofluid flowing in a porous domain, and make this work novel in this thermal area. Although the present investigation is performed to understand the fundamental aspects, the outcome findings are useful to the design and operation of similar thermal devices involving multi-physical transport processes.

Problem description

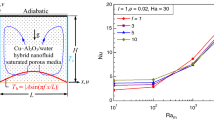
The computational domain of the problem geometry is a two-dimensional enclosure filled with hybrid nanofluid and porous substances subjected to the nonuniform heating from the bottom and cooled partially from the sidewalls as illustrated in Fig. 1. The domain is a square enclosure of length L with the bottom wall being heated at temperature following the half-sinusoidal thermal profile of Th = A sin(πf x/L), whereas the sidewalls are partially cooled (length 0.5L at temperature Tc) and the rest of the sidewalls are adiabatic. To explore the impacts of the cooler positions (on the sidewalls), different combinations of the cooler positions are also analyzed. The top horizontal wall is thermally insulated. Cu-Al2O3/water hybrid nanofluid is used as a working medium within the enclosure. The Brinkman–Forchheimer–Darcy extended model is adopted for the porous media with the supposition of a local thermal equilibrium model between hybrid nanofluid and porous medium [48]. All boundaries are regarded as impermeable and no-slip states. The working medium is supposed to be Newtonian, steady, laminar, and incompressible, and the Boussinesq approximation is valid. On the solid walls, impermeable and no-slip conditions are assumed [49]. A uniform magnetic field (of strength B) is applied horizontally.

Fig. 1
figure 1

Schematic computational geometry with boundary conditions (a), heat flow visualization (b)

Full size image

For the hybrid nanofluid flow, a single-phase homogeneous model is adopted [5, 8] and there is no agglomeration/sedimentation (of particles) due to a lower concentration of < 3% of Cu and Al2O3 particles (spherical size of ~ 1 nm). The host fluid is water (of Pr = 5.83), and it passes through the porous structure [50]. Here, the induced magnetic Reynolds number is insignificant [51]. The Hall effect and Joule heating are also supposed to be insignificant [52]. Furthermore, the influences of radiation and viscous dissipation effects [53] are negligible.

With the above assumptions, the nondimensional coupled transport equations are derived [25] as

$$\frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0$$
(1)
$$\frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}}} \right) \, = \, - \frac{{\rho_{{{\text{bf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{\partial P}{{\partial X}} + \, \frac{{\nu_{{{\text{hnf}}}} \Pr }}{{\nu_{{{\text{bf}}}} \varepsilon }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) \, - \left( {\frac{{\nu_{{{\text{hnf}}}} \Pr }}{{\nu_{{{\text{bf}}}} {\text{Da}}}} + \frac{{F_{{\text{c}}} \sqrt {U^{2} + V^{2} } }}{{\sqrt {{\text{Da}}} \, \varepsilon^{3/2} }}} \right)U$$
(2)
$$\begin{aligned} \frac{1}{{\varepsilon^{2} }}\left( {U\frac{\partial V}{{\partial X}} + V\frac{\partial V}{{\partial Y}}} \right) \, & = \, - \frac{{\rho_{{{\text{bf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{\partial P}{{\partial Y}} + \, \frac{{\nu_{{{\text{hnf}}}} \Pr }}{{\nu_{{{\text{bf}}}} \varepsilon }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) - \left( {\frac{{\nu_{{{\text{hnf}}}} \Pr }}{{\nu_{{{\text{bf}}}} {\text{Da}}}} + \frac{{F_{{\text{c}}} \sqrt {U^{2} + V^{2} } }}{{\sqrt {{\text{Da}}} \, \varepsilon^{3/2} }}} \right)V \, \\ & - \frac{{\rho_{{{\text{bf}}}} }}{{\rho_{{{\text{hnf}}}} }}\frac{\sigma }{{\sigma_{{{\text{bf}}}} }}{\text{Ha}}^{2} \Pr V + \frac{{(\rho \beta )_{{{\text{hnf}}}} }}{{\rho \beta_{{{\text{bf}}}} }}{\text{Ra}}_{{\text{m}}} \frac{{{\text{Pr}}}}{{{\text{Da}}}}\theta \\ \end{aligned}$$
(3)
$$\left( {U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}}} \right) \, = \, \frac{{\alpha_{{{\text{hnf}}}} }}{{\alpha_{{{\text{bf}}}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(4)

The dimensionless variables of U, V, X, Y, θ, and P are as follows

$$\begin{gathered} (X, \, Y) = (x, \, y) \, / \, H; \, (U, \, V) = (u, \, v) \, H/ \, \alpha_{{{\text{bf}}}} ; \hfill \\ \theta \, = \, (T \, - \, T_{{\text{c}}} )/(T_{{\text{h}}} - T_{{\text{c}}} ); \, P = (p - p_{{\text{a}}} )H^{2} /\rho_{{{\text{bf}}}} \alpha_{{\text{f}}}^{2} \hfill \\ \end{gathered}$$
(5a)
$$\begin{gathered} \Pr = \frac{{\nu_{{{\text{bf}}}} }}{{\alpha_{{{\text{bf}}}} }};{\text{ Da}} = \frac{K}{{H^{{2}} }}; \, F_{{\text{c}}} = \frac{1.75}{{\sqrt {150} }}; \, \hfill \\ {\text{Ra}} = \frac{{g\beta_{{{\text{bf}}}} {(}T_{{\text{h}}} - T_{{\text{c}}} {)}H^{3} }}{{\nu_{{{\text{bf}}}} \alpha_{{{\text{bf}}}} }};{\text{ Ra}}_{{\text{m}}} = {\text{Ra}} \times {\text{Da; Ha}} = {\text{BH}}\sqrt {\frac{{\sigma_{{{\text{bf}}}} }}{{\mu_{{{\text{bf}}}} }}} \hfill \\ \end{gathered}$$
(5b)

The followings are the boundary conditions for the computation:

  1. (a)

    \(\theta = I\sin (\pi f \, X \, )\), V = U = 0 for the heated bottom wall (Y = 0)

  2. (b)

    \(\, \frac{\partial \, \theta }{{\partial Y}} = {0}\), V = U = 0, for the adiabatic top wall (Y = 1)

  3. (c)

    \(\theta = 0\), V = U = 0, for the upper half portion of the cold sidewalls (i.e., at X = 0, 1)

  4. (d)

    \(\, \frac{\partial \, \theta }{{\partial X}} = {0}\), V = U = 0, for the lower half portion of the adiabatic sidewalls (i.e., at X = 0, 1)

where the symbols I and f indicate the nondimensional amplitude [I = A/(Tm − Tc)] and multi-frequency of the half-sinusoidal heating profile, respectively. I varies in the range of 0.1 and 1, while f varies from 1 to 7 in the current study. For obtaining the global heat transfer parameter, the average Nusselt number (Nu) is formulated as

$${\text{Nu}} = \left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{bf}}}} }}} \right)\int\limits_{0}^{1} {\left( { - \frac{\partial \theta }{{\partial Y}}\left| {_{Y = 0} } \right.} \right)} {\text{d}}X$$
(6)

The flow structure is envisaged by using stream function (\(\psi\)) and streamlines. The stream function (\(\psi\)) is defined as

$$\frac{\partial \psi }{{\partial Y}} = U\;{\text{and}}\; - \frac{\partial \psi }{{\partial X}} = V$$
(7)

Additionally, the formation of heat energy transport corridors from the half-sinusoidally heated bottom wall to the cold partial sidewalls is reflected by heatlines. These heatlines are acquired from heat function (\(\Pi\)) [54] which is given as

$$- \frac{\partial \Pi }{{\partial X}} = V\theta - \frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{bf}}}} }}\frac{\partial \theta }{{\partial Y}}\;{\text{and}}\;\frac{\partial \Pi }{{\partial Y}} = U\theta - \frac{{k_{{{\text{hnf}}}} }}{{k_{{{\text{bf}}}} }}\frac{\partial \theta }{{\partial X}}$$
(8)

The effective thermo-physical properties of the base fluid (bf) water (Pr = 5.83), and Cu–Al2O3 nanoparticles (hnf) are mentioned in Table 1 [55]. The effective thermo-physical properties of hybrid nanofluid are calculated from the correlations, which are listed in Table 2. However, in this study, the thermal and dynamic viscosity are taken from the experimentally available data of Suresh et al. [55] (instead of calculating them from theoretical models [56]). The reason for this consideration is to predict the correct properties for Cu–Al2O3/water hybrid nanofluid.

Table 1 Properties of the host fluid (water) and nanoparticles (Cu and Al2O3) [55]
Full size table
Table 2 Correlations for evaluating effective thermo-physical properties of hybrid nanofluid [32]
Full size table
Table 3 Experimental data of hybrid nanofluid viscosity and thermal conductivity [55]
Full size table

Simulation methodology

The governing transport Eqs. (1) –(4) are numerically solved by our in-house code. The finite volume method is adopted to discretize the nondimensional transport equations. The domain of interest is divided into fine control volumes through the proper meshing distributed nonuniformly along the x and y directions. Then the nondimensional equations are solved iteratively over the fine control volumes by using the alternate direction implicit (ADI) scheme and the tridiagonal matrix algorithm (TDMA). The computations are performed using the FORTRAN-based code following the SIMPLE algorithm [57]. The developed code comprises of state-of-the-art computation algorithms for complex problem geometry involving various multi-physical scenarios. A third-order upwind scheme (QUICK) is utilized for the convective terms as reflected in the momentum and energy equations. The diffusion terms are based on the central differencing scheme (second order). The computation is carried out in an iterative process, and residuals for each conservation equation are obtained by limiting to < 10−10, respectively. The above computation code has already been validated broadly for different fluid flow and heat transfer problems in our preceding works comprising of natural or mixed convection, and bioconvection under various multi-physical scenarios [58]. For ease of understanding the various steps/activities during the entire numerical procedure, a computation process flowchart is presented in Fig. 2.

Fig. 2
figure 2

Flowchart for the FEM solution procedure

Full size image

Code validation

Apart from the above validation, an in-house experimental study validation of the present solver has also been conducted [59]. Furthermore, another validation study is demonstrated by simulating the porous enclosure heated at the left and cooled at the right, and filled with Cu–water nanofluid as published by Nguyen et al. [59]. The comparison between the published results and the present results is made through the estimated average Nu and stream function (\(\left| \psi \right|_{\max }\)) for Pr = 6.2 by varying porosity ε =(0.4–0.8) but fixed values of φ = 5%, Ram = 103, Da = 10−2, as shown in Table 3. The comparison shows the present code efficacy is quite acceptable with the published results [59]. Furthermore, the local velocity, as well as temperature distribution on the same problem domain [60], is also compared using the streamlines and isotherms as shown in Fig. 3 when Ra = 105, Da = 10−2, ε = 0.4, \(\varphi_{{{\text{Cu}}}}\) = 5%, Pr = 6.2. Here, the governing equations along with the property relations are utilized for the Cu–water nanofluid flow considering \(\varphi_{{{\text{Al}}_{{2}} {\text{O}}_{{3}} }}\) = 0. The comparison shows reasonably good agreement with the published results [59]. This comparison confirms the accuracy of the present solver for further extensive simulation.

Table 4 Comparison between the published results [59] and present results through average Nu and stream function (\(\left| \psi \right|_{\max }\)) for Pr = 6.2, varying porosity ε (= 0.4–0.8), fixed values of φ = 5%, Ram = 103, Da = 10−2
Full size table
Fig. 3
figure 3

Comparison of the computed results with the published results [59] through the streamlines and isotherms for Ra = 105, Da = 10−2, φCu = 5%, ε = 0.4, Pr = 6.2

Full size image

Furthermore, the accuracy of the finite volume method-based code is also verified through the extensive validation study with the benchmark experimental results of Ho et al. [60]. The geometry is basically a square cavity filled with Al2O3–water nanofluid. Using the present solver, mean Nusselt numbers for the various temperature difference (∆T = 2–10 °C) are calculated and presented in Fig. 4 for Pr = 6.2 and φ = 0%. The comparison shows that the present results are in good agreement with the published experimental data. Similar findings have also been reported by Geridonmez and Oztop [61]. This comparison further confirms the accuracy of the present solver.

Fig. 4
figure 4

Comparison of the computed results with the published experimental results of Ho et al. [60] and numerical results of Geridonmez and Oztop [61] through the streamlines and isotherms for various temperature differences (∆T = 2–10 °C), φ = 0% (of Al2O3–water nanofluid), Pr = 6.2

Full size image

Mesh refinement

The grid independency analysis has been carried out in a hybrid nanopowder blended fluid medium with nonuniform half-sinusoidally heated partially cooled cavity using staggered uniform grid sizes. Taking into contemplation of fluid and heat flow field a range of values of heating profile frequencies at fixed parameters like Ram = 103, Da = 10−3, Ha = 30, \(\varepsilon\) = 0.6, φ = 0.1%, and I = 1.0, the problem is solved on varying coarse to the fine grids as 120 × 120, 140 × 140, 160 × 160, 180 × 180, and 200 × 200. The simulated results are extracted in Table 4 using the average Nusselt values (Nu) of the heat source. The subsequent adaptation in Nu value due to fine-tuning in grid size is also mentioned in the brackets which is calculated on the preceding coarse grid dimension. This is intensely scrutinized that with grid fine-tuning of 140 × 140, 160 × 160, 180 × 180, and 200 × 200, the error is < 1%. Therefore, the grid size of 160 × 160 is chosen for the entire numerical investigation.

Table 5 Mesh sensitivity test through average Nusselt number (Nu) by varying frequency f when Ram = 103, Da = 10−3, Ha = 30, \(\varepsilon\) = 0.6, φ = 0.1%, I = 1.0
Full size table

Results and discussion

In the present exploration, the outcome of bottom wall heating (with different frequencies and amplitudes) on the heat transfer and hybrid nanofluid flow in a square porous cavity imposing an MHD field is analyzed amid natural convection mode. The enclosed space is heated half-sinusoidally at the bottom wall and cooled the upper half of the sidewalls on either side. The impacts of significant parameters are examined systematically for a range of parametric values such as Darcy–Rayleigh number (10 ≤ Ram ≤ 104), Darcy value (10–5 ≤ Da ≤ 10–1), Hartmann number (0 ≤ Ha ≤ 70), volume fraction (0 ≤ φ ≤ 2%), treating porosity value that is changed to 0.1 ≤ ε ≤ 1.0 at different amplitudes (0.1 ≤ I ≤ 1.0), and frequency range that is taken as f = 1, 3, 5, 7. To find out the case of optimal heating strategy, the constant heating condition has also been studied and compared with nonuniform heating. The extracted results are demonstrated using fluid flow through streamlines, temperature distribution by isotherms, the flow of heat flux by heatlines contours, and system heat transport rate by average and local Nusselt (Nu) value. The above study is continued for different positions of the cold zone in the sidewall as described in Table 5. However, to avoid repetition, symmetric cases (like case BM, BT and MT) are not presented in the analysis. Each section develops a simple correlation (through the regression analysis) to find out the trend of average Nu, taking into consideration of subsequent controlling parameters. This will be very helpful for the designer to predict the thermal performance of any data set.

Table 6 Different study cases combining the positions of half of the cold sidewalls
Full size table

Convective strength in terms of Ram and frequency (f)

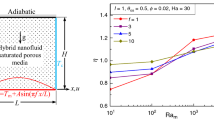
The convective flow regime of the present scheme in Fig. 5 (for small to elevated Darcy–Rayleigh numbers Ram = 10–104) is explored with present parameters (Da = 10−3, Ha = 30, ε = 0.6, φ = 0.1%, f = 1, I = 1). The first row of Fig. 5 depicts the contours of streamlines, whereas the second row presents isotherms and the third row depicts the heatline contours. It is to be mentioned that this section demonstrates the results of half-sinusoidal bottom heating and cooling by the upper half portion (= 0.5L) of the sidewalls. Therefore, the middle of the bottom wall produces high thermal convection due to high temperature that in turn develops upward flow about the middle vertical plane as expected. This flow reaches cold sidewalls after striking the top adiabatic wall. It completes a cycle and returns to the bottom-heated wall guided by the side adiabatic walls. Ultimately, with the effect of half-sinusoidal heating and partial cooling, here comes into picture one couple of clockwise (CW) and counterclockwise (CCW) circulation cells within the entire cavity. At lower Ram, heat production is primarily governed by the conduction mode; however, at high Ram = 104 the flow structure differs mainly owing to the convection mode. The formed convective cells are symmetrical at the low range of Ram (= 10, and 102), and this shape becomes asymmetrical due to higher thermal convection at higher Ram. The increase in strength of cells as Ram rises is noted as usual. It predicts abrupt change in flow strength at higher Ram. Corresponding isotherms (second row) at the lower range of Ram (= 10, and 102) represent a semicircular shape, and the thermal layer spreads continuously from bottom to top (from high-temperature zone to low-temperature zone). The isotherm contour positions drastically change to distorted symmetric curves and squeeze the isotherms in the middle that in turn produces a high-temperature zone of filament. This formation of filament raises the density of isotherms at the bottom wall indicating high heat transfer as Ram increases. Here, the heatlines (third row) reflect that energy flux from the bottom wall source disseminates toward the partial cold sidewalls at low Ram. The dynamics of heat flow occur symmetrically about the mid-vertical plane. It is interesting to show that, with the increasing Ram, the corridor of energy transfer becomes thinner and forms the heat energy vortices nearer to the bottom source wall. It occupies the whole cavity space at a higher Ram of 104. It is revealed that the heatlines start from the heated bottom wall, and terminate at the cold walls at a lower Ram of 10. The sinusoidal temperature difference (higher at the middle, lower at the sides) at the bottom wall is the reason for this. Such a detailed understanding of the heat flow dynamics due to the multi-frequency heating in a porous thermal system is very limited in the earlier literature except very few [10, 38]. Furthermore, to find out the case of optimal heating strategy, the constant heating condition has also been studied and compared with nonuniform heating. Overall, the increasing rate of heat transportation with changing the frequency of nonuniform heating f (= 1–7) is noted at about 4.71–370.77% (for Ram = 10), 5.03–301.88% (for Ram = 102), − 9.71–38.87% (for Ram = 103), and 4.09–32.62% (for Ram = 104) relative to low constant heating (average Nu = 1.373–9.652). In general, nonuniform heating offers the best thermal performance during the conduction mode of heat transfer (which is at lower Ram) compared to the convection dominance.

Fig. 5
figure 5

Impact of convective strength on flow structures varying Ram at Da = 10−3, Ha = 30, ε = 0.6, φ = 0.1%, f = 1, I = 1.0 for Case 1 (TT)

Full size image

The frequency (f) of sinusoidal heating alters the flow physics remarkably; therefore, this section presents the impact of frequency (f = 3, 5, 7) on streamlines, isotherms, and heatlines by Fig. 6 (similar to Fig. 5) at Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, φ = 0.1%, I = 1.0 for Case 1 (TT). As the rise in the frequency at the bottom heating distributes high -emperature as well as low-temperature zone (following the spatial nonuniform sinusoidal heating profile) throughout the wall (for one frequency, high temperature at middle and low temperature at sides), this reduces the strength of velocity at the middle. This results in the decrease in flow strength of the convective cell as frequency increases as observed from the contours of streamlines (first row). However, a rise in frequency decreases the thermal boundary layer thickness at the bottom heating wall by indicating enhancement of heat transfer. This has been revealed by the corresponding isotherms (second row). The significant change in the pattern of isotherms at the bottom wall is due to the localized heating and cooling effect accordingly to the frequency. Heatlines (third row) show the drop in strength of heat energy vortices as frequency rises. Heatlines cut the cooling wall as heat flux flows along the path of the contours. These contours cut to the bottom wall according to the number of frequency. As the frequency increases, there are no significant changes in the heatlines contours, but the strength of the active heat energy corridors increases and it reflects higher heat transfer.

Fig. 6
figure 6

Impact of convective strength on flow structures with varying f at Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, φ = 0.1%, I = 1.0 for Case 1 (TT)

Full size image

For a better understanding of the heat transfer phenomenon under the different parameters, the variation of local Nu at the heating wall with respect to various frequencies (f) and Ram is plotted in Fig. 7 for Da = 10−3, Ha = 30, ε = 0.6, φ = 0.1%, I = 1.0 for Case 1 (TT). Figure 7a illustrates the local Nu distribution along the heated wall for the varying Ram when f = 1. It shows that there is a positive peak about the mid-horizontal plane and a negative peak at both ends of the horizontal wall following the half-sinusoidal temperature profile. For the value Ram ≥ 102, the peak value of the local Nu increases due to more heat exchange, and there forms a down peak at the mid-horizontal point due to the decrease in the temperature gradient. An increase in frequency shows positive peak and the negative peak of local Nu according to the number of frequencies (as shown in Fig. 7b). These positive and negative magnitude rise as frequency increases, which indicates the enhanced number of a heating cooling zone with the augmentation of local heat transfer along the heated wall. For the single frequency, significant cooling at the sidewalls is also noted. The partial side cooling decreases with the increase in frequency. In the middle of the bottom wall, Nu drops due to the maximum temperature of the adjacent fluid. This drooping at the middle is less at the lower Ram. However, the average Nu rises for both the cases of rising in f and Ram. As Ram increases, average Nu increases monotonically for Ram ≥ 102 due to the strong convection dominance (as shown in Fig. 7c). This increasing trend is noticeable for the increasing f. Overall, the average Nu is an increasing function of both f and Ram. Compared to constant heating, spatial heating at a higher frequency offers the best heat transfer up to 370.77% (for Ram = 10). However, the enhancement is reduced up to 32.62% (for Ram = 104) as the convection effect increases.

Fig. 7
figure 7

Impact of convective strength on the heat transfer: a local Nu varying Ram, b local Nu varying f, and c average Nu varying f, at Da = 10–3, Ha = 30, ε = 0.6, φ = 0.1%, I = 1.0 for Case 1 (TT)

Full size image

In order to predict the trend of the average Nu curve for the involved critical controlling parameters (like f and Ram), a MATLAB code is developed through the regression analysis. As an output, Eq. (9) for the average Nu at different Ram and f is obtained.

$${\text{Nu}} = b_{1} + b_{2} {\text{Ra}}_{{\text{m}}} + b_{3} f + b_{4} {\text{Ra}}_{{\text{m}}} f + b_{5} {\text{Ra}}_{{\text{m}}}^{0.05} + b_{6} f^{2}$$
(9)

The coefficients for the above equation are given below.

b1

− 7.257994572302756

b2

0.000552499476406

b3

0.513396317868404

b4

− 0.000028799850383

b5

7.446986836555025

b6

0.023581250008177

Emphasis of amplitude (I)

The control of amplitude (I) of half-sinusoidal heat source on the streamlines, isotherms, heatline contours, and Nu values is demonstrated in Fig. 8 for the invariable parameters of Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, f = 1, φ = 0.1% for Case 1 (TT). An increase in the amplitude of sinusoidal heating rises the middle temperature by its amplitude and thorough wall to maintain the sinusoidal curve. Thus, bottom heating generates a middle plume for the initiation of convection. This convection force is aggravated by the amplitude of heating. Thus, it is obvious that an increase of I from 0.1 to 1.0 in the thermo-fluid porous enclosure leads the improvement in fluid recirculation potency with the production of vortex cells and consequential augmentation in the heat exchange rate (first row). This enhancement for the increase in I leads to a rise in the effective thermal activities of the flow medium. Isotherms at lower I (= 0.1) present such that the flow phenomenon is controlled by the conduction mode of heat transfer (second row). More concentration at the bottom wall at higher I (= 1.0) is noted with the high-temperature region at the top of the cavity. The effect of heat flow transmission is satisfactorily and symmetrically disseminated in the view like human lungs noted in the heatlines. The strength of energy circulation rises as I increase.

Fig. 8
figure 8

Varying amplitude (I) on flow structures at Ram = 103, Da = 10−3, Ha = 30, φ = 0.1%, f = 1 for Case 1 (TT)

Full size image

The variation of average and local Nu magnitude with I for different f is shown in Fig. 9 at Ram = 103, Da = 10–3, Ha = 30, φ = 0.1% for Case 1 (TT). From the local Nu variation (Fig. 9a), it is clear to get the enhancement of the cooling effect at the side bottom corner (due to the rise in amplitude). This is because of the very low temperature of the bottom wall at the corner at lower I and the relatively higher fluid temperature of the fluid at this zone at higher I. However, no middle cooling zone is observed for all I. The positive peak value of Nu rises with I indicating higher average Nu as I rise. The average Nu (Fig. 9b) value rises monotonically with I for all f due to continual increment in the heat input. When the spatial heating strategy for the varying f and I is compared (keeping all other parameters fixed) with the constant heating (average Nu = 5.937), an increase in the amplitude of spatial heating from I = 0.1 to 1 and frequency f = 1–7 is observed, although spatial heating is only beneficial only at the higher value of I = 1 and f > 3. Overall, higher amplitude and frequency of spatial heating could be opted for a better heating strategy compared to uniform heating.

Fig. 9
figure 9

Varying amplitude (I) effect on heat transfer a local Nu and b average Nu at Ram = 103, Da = 10−3, Ha = 30, φ = 0.1% for Case 1 (TT)

Full size image

Similar regression analysis is carried out to find Eq. (10) for the average Nu for different values of I and f.

$${\text{Nu}} = b_{1} + b_{2} I + b_{3} f + b_{4} If + b_{5} I^{2} + b_{6} f^{2}$$
(10)

The coefficients for the above equation are given below.

b1

0.136248095843796

b2

3.027284639468801

b3

− 0.263324153501370

b4

0.440694548095590

b5

1.649007524799697

b6

0.039525208387055

Permeability of porous media (Da) impact 

Variations of permeability of porous media permeability (expressed by Da) with fixed Ram = 103, Ha = 30, φ = 0.1%, ε = 0.6, and I = 1 are described in Fig. 10 for low to the high value of Da (10−4 to 10−1) (in columns). Normally, a smaller Da is allied to higher resistance to the porous matrix. The flow of hybrid nanofluid and heat flux happens within the enclosure with higher resistance. With higher Da = 10−1, as predictable with the improved permeability lesser may be flow resistance. From the streamlines (first row), it is evident that the shape of the convective cell becomes symmetrical as Da rises and weakens the flow strength. This is due to a fall in flow Rayleigh number despite low resistance to flow at higher Da, which weakens the thermal convection, as observed from the isotherms. It shows a very low-temperature zone in the middle of the enclosure at higher Da values (second row). This diminishing effect of heat transfer reduces the energy vortex strength as Da rises and it vanishes the energy vortex at higher Da (third row). This clearly reflects a reduction in the heat energy transport from the heat source to the heat sink, which is supported by the average Nu.

Fig. 10
figure 10

Varying Da on flow structures at Ram = 103, Ha = 30, and φ= 0.1%, I = 1.0, f = 1 for Case 1 (TT)

Full size image

The heat transport phenomenon is described by local and average Nu presented in Fig. 11. There is no change in the cooling effect at side corners as local Nu (Fig. 11a) remains the same for all Da. Only the peak Nu values drop as Da increases. It is to be mentioned that side cooling is noted for variation in f and I. However, average Nu curves (Fig. 11b) reproduce a continually leaning with a rising value of Da. But it can be seen that for every value of Da, the Nu value enhances with the rise in frequency as observed. So, an assessment of Da magnitude may control the thermo-flow process in half-sinusoidal heating and partial cooling cavity. So, the growing rate of heat transfer with changing frequency f (= 1–7) is noted at about − 4.91–26.60% (for Da = 10−5), 0.16–30.13% (for Da = 10−4), 6.57–201.04% (for Da = 10−2), and 5.14–369.82% (for Da = 10−1) relative to the uniform heating (average Nu = 10.61–1.38).

Fig. 11
figure 11

Effect of varying Da on the heat transfer a local Nu and b average Nu with frequency f on heat transfer at Ram = 103, Ha = 30, and φ = 0.1%, I = 1.0 for Case 1 (TT)

Full size image

Regression analysis provides Eq. (11) for the average Nu for different values Da and f.

$${\text{Nu}} = b_{1} + b_{2} {\text{Da}} + b_{3} f + b_{4} {\text{Da}}f + b_{5} {\text{Da}}^{{{0}{\text{.05}}}} + b_{6} f^{2}$$
(11)

The coefficients for the above equation are given below.

b1

28.758002722903026

b2

21.517156616798648

b3

0.329137443178308

b4

3.202734150372621

b5

− 33.734759353796086

b6

0.025328999831053

Strength of magnetic field (Ha) impact 

The magnetic field intensity effect caused by the horizontal imposed magnetizing field (denoted by Ha number) on contours of isotherms, streamlines, heatlines, and heat transfer is shown in Fig. 12 for varying Ha = 0, 50, and 70 by keeping constant parameters at Ram = 103, Da = 10−3, φ = 0.1%, ε = 0.6, and I = 1. The magnetic force term (containing the Ha in the Y–momentum equation) opposes the flow and, therefore, diminishes the flow strength of convective cells in the streamlines; stream function value drops as Ha rises (first row). The decrease in the convection is felt in the isotherms as Ha rises (second row). Energy circulation in the heatlines weakens their strength (third row).

Fig. 12
figure 12

Varying Ha on flow structures at Ram = 103, Ha = 30, and φ = 0.1%, I = 1.0, f = 1 for Case 1 (TT)

Full size image

The effect of varying Ha with frequency f on the local as well as global heat transfer at Ram = 103, Da = 10−3, and φ = 0.1%, I = 1.0 for Case 1 (TT) are depicted in Fig. 13. The local Nu variation (as shown in Fig. 13a) at different Ha reveals the dropping of peak Nu value as Ha rises predicting a reduction in heat transport. Side corner cooling does not differ from the variation of Ha. The variation of average Nu curves explains a steady declining trend with the increasing magnetizing field strength Ha as shown in Fig. 13b. The declining tendency of Nu curves is almost alike for every ‘f’ value. But the heat exchange rate enhances with the rise of frequency at all values of Ha. Consequently, the heat energy transport process is exaggerated meticulously. Normally, the enhancing rate of heat transport with altering frequency f (= 1–7) is in the range of − 2.70–44.95% (for Ha = 0, no magnetizing field), − 2.73–45.42% (for Ha = 10), -7.93–45.66% (for Ha = 50), and -10.86–57.74% (for Ha = 70) compared to constant heating conditions (average Nu = 5.825–4.753). It is interesting to note that the average Nu is a decreasing function of increasing Ha and it is true for both the constant heating and nonuniform heating. However, spatial heating provides a major advantage over constant heating, when the frequency of the nonuniform heating increases beyond f > 1. This is due to the local thermal modulation by spatial heating. Thus, heat transfer enhancement is noted with the increasing frequency even the magnitude of Ha increases. It implies the dampening effect of Ha could be compensated by the nonuniform heating strategy with higher frequency (f > 1). This could be a better choice for superior thermal management. Such a finding has not been reported clearly in the earlier literature.

Fig. 13
figure 13

Effect of varying Ha with frequency f on the heat transfer (a) local Nu and (b) average Nu at Ram = 103, Da = 10−3, and φ = 0.1%, I = 1.0 for Case 1 (TT)

Full size image

The regression analysis results in Eq. (12) for the average Nu for different Ha and f.

$${\text{Nu}} = b_{1} + b_{2} {\text{Ha}} + b_{3} f + b_{4} {\text{Ha}}f + b_{5} {\text{Ha}}^{{2}} + b_{6} f^{2}$$
(12)

The coefficients for the equation are given below.

b1

5.759110926188033

b2

− 0.007398034292213

b3

− 0.098220219690554

b4

0.001207838111009

b5

− 0.000216259808709

b6

0.068902250016544

Hybrid nanoparticles volume fraction (φ) impact

The increase in volume fraction φ (= 0.33% and 2%) of solid Cu/Al2O3 hybrid nanoparticles with water solution as flow medium on the contour of streamline isotherm, heatlines, and heat exchange are expressed in Fig. 14 for steady values of Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, I = 1. The addition of nanoparticles enhances thermal conduction that in turn raises heat transport. This addition raises the viscosity which results in a drop in flow velocity (first row). Here, this is fairly marked that the addition of hybrid nanoparticles in pure water manages to fall in flow strength, causing a drop in heat transport rate. Flow strength drops as φ rises. As such, there is no significant change in the isotherms (second row). The basis is because the increase in φ governs to heighten in viscosity of working hybrid nanofluid in a such half-sinusoidal heating system, which leads to a reduction in the energy recirculation strength (third row). Therefore, reduction in the buoyancy effect, and heat transmission rate compared to the host fluid (φ = 0). The consequence of volume fraction alteration of hybrid nanoparticles for varying ‘f’ values on the local Nu and average Nu is characterized in Fig. 15 at Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, I = 1.0. The figure markedly imitates that with the augmentation in ‘f’ average Nu increases for all values of φ. In general, the increasing rate of heat transfer with changing frequency f (= 1–7) is up to 37.11% (for φ = 0, no particle) and 64.91% (for φ = 2%). A higher frequency of spatial heating always offers superior heat transfer.

Fig. 14
figure 14

Inclusion of hybrid nanoparticles (φ) on a flow structures at Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, I = 1.0, f = 1 for Case 1 (TT)

Full size image
Fig. 15
figure 15

Inclusion of hybrid nanoparticles (φ) on heat transfer a local Nu and b average Nu at Ram = 103, Da = 10−3, Ha = 30, ε = 0.6, I = 1.0 for Case 1 (TT)

Full size image

Here, the regression analysis finds Eq. (13) for average Nu for different φ and f.

$${\text{Nu}} = b_{1} + b_{2} \varphi + b_{3} f + b_{4} \varphi f + b_{5} \varphi^{2} + b_{6} f^{2}$$
(13)

The coefficients for the equation are given below.

b1

5.504265696967

b2

− 92.8650607388

b3

− 0.09882876926

b4

9.263435727398

b5

1535.815310207

b6

0.071897708377

Porosity of porous medium (ε) impact

The impact of the porosity index (ε) on the thermal performance of hybrid nanofluid in the considered cavity is illustrated in Fig. 16 keeping other parameters (Ram = 103, Ha = 30, Da = 10−3, I = 1) constant. The results show augmented flow fluid features in the enclosure with enhancement in porosity value. As porosity increases that in turn allows the flowing ability, this enhances thermal convection. So, under partial cooling, as ε increases, the buoyancy-dominated circulation gains its strength as observed in the streamlines (first row). On the whole, a slight change is noted in the patterns of streamlines, isotherms (second row), and heatlines (third row) low to high porosity. This governs to significantly enhances in average Nu value with rising porosity. This ensures that, as the porosity augments, flow encounters less resistance. The heat flow corridor along with the strength of the energy vortex rises as porosity rises.

Fig. 16
figure 16

Porosity impact on the flow structures at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0, f = 1 for Case 1 (TT)

Full size image

At a higher value of frequency, f > 1, the buoyancy impact increases appreciably, governing a rise in fluid motion. This outcome is also further influenced by the higher value of porosity which is in Fig. 17 in terms of local Nu, and average Nu at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0, and f = 1 for Case 1 (TT). The local Nu value of peaks rises as ε rises (as shown in Fig. 17a), which is due to the reduction in the flow resistance and increase in the heat transfer. This is clearly reflected by the average Nu plot (as shown in Fig. 17b) for the increasing f. In general, an increase in the spatial frequency heat transfer enhances and it is true for any porosity value. Normally, heat transport increases with the changing frequency, f (= 1–7), and the enhancement is noted about 3.09–82.29% for the range of ε = 0.1–1.0 in comparison with the uniform heating (average Nu = 4.001–6.478). In fact, at the lower porosity, nonuniform heating (having a higher frequency f ≥ 3) offers better heat transfer compared to the constant heating.

Fig. 17
figure 17

Porosity impact on heat transfer a local Nu and b average Nu at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0 for Case 1 (TT)

Full size image

Here, regression analysis provides Eq. (14) for the average Nu for different ε and f.

$${\text{Nu}} = b_{1} + b_{2} \varepsilon + b_{3} f + b_{4} \varepsilon f + b_{5} \varepsilon^{2} + b_{6} f^{2}$$
(14)

The coefficients for the equation are given below.

b1

2.958769479810177

b2

5.036471336431086

b3

0.127837820738562

b4

− 0.233729492976186

b5

− 1.980157529914127

b6

0.064461354242423

Cooler positional impact

The important aspect of this study is the local positioning of the cooler wall in the sidewalls. The previous section focuses on the thermal transport phenomenon considering the position of the cooler at the left top and right top position on both the sidewalls. This cooler position on both walls symmetrically may be at the middle of the sidewalls or may be at the bottom position of the sidewalls. The different positions despite the same cooling length may alter the flow physics, which is necessary for this study. Again, the position of the cooler at different locations asymmetrically may show other pertinent phenomena. The combination of cooler may be left top–right middle (TM), left top–right bottom (TB), and left middle–right bottom (MB), which may produce other perspectives of the transport into the fluid. All these cases (as given in Table 5) of the location of cold sidewalls are scrutinized for a detail studying of transport by contours of flow, temperature, and heat flux by Figs. 18 and 19 at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0, f = 1. Figure 18 describes the cases of symmetrical position (TT, MM, and BB), and Fig. 16 shows the asymmetrical position (TM, TB, and MB). Figure 18 shows two opposite directional same shaped convective cells symmetrically about the middle vertical plane of the enclosure. For TT case, the vortex occupies almost the whole of the enclosure which is lesser for BB case. Streamlines in BB case show the center of the vortex to move at the lower zone of the enclosure with a high concentration of lines at the bottom. Flow strength is higher in TT case and then decreases in MM case; it becomes lesser in BB case. The phenomenon is such that the movement of the cold zone from top to bottom decreases the flow strength by lowering the center of each vortex. The reason for the phenomenon is that by lowering the cold zone, flow moves directly toward the cold zone without much traveling up to the top adiabatic wall and less flow space in between the hot and cold walls. Flow becomes weaker at the upper portion for BB case, and consequently, a low-temperature zone happens at the upper portion as observed in the isotherms. Temperature contours on sidewalls shift according to the cold zone locations at sidewalls. The heatlines show the decreasing strength of the energy cell as the cooler position on the sidewalls moves downward. However, the magnitude of average Nu increases by downward the location of the cooler position. Thus, there are less heat transport in TT case and maximum heat transport in BB case. The enhancement percentage of heat transfer in BB case is 8.95% relative to the TT case.

Fig. 18
figure 18

Cooler positional impact on flow structures at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0, f = 1

Full size image
Fig. 19
figure 19

Cooler positional impact on a flow structures and b heat transfer at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0, f = 1

Full size image

Figure 19 shows the unequal vortices with an asymmetrical position of convective cells due to the asymmetrical position of cooler walls. Convective cells adjacent to the top cooling zone develop high strength of flow and low vortex strength for bottom zone cooling as noted. The involved one flow convective cell is higher and the other is minimum for TB case or vice versa. Therefore, the maximum strength of the left convective cell is noted for the TB case, and the minimum strength of the right cell is also noted in the same case. The reason for the larger vortex is due to the involvement of a large flow field due to the interaction of the hot wall to the cold top position. The central plume direction in the middle vertical plane distorts isotherms according to the position of the cooler as noted. Heatlines produce the energy cells depending on the position of the cooler. Therefore, the same cooling length by virtue of its position alters the isolines and consequent heat transport. Heat transport is minimum at TM case, and it is maximum for MB case. The maximum heat transfer in MB case is due to energy transport in the nearby interaction. Compared to TB case, the increase in heat transfer is 5.88% for MB case. Heat transfer for asymmetrical cooling for any case is higher relative to TT case. However, BB case shows maximum heat transfer compared to an asymmetrical case. This has been shown for all frequencies of heating from Fig. 20. The impact of different cooler positions for the varying f, is reflected by the local and global heat transfer by the Nusselt number as shown in Fig. 20 at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0. The MB case is better in asymmetrical cooling; BB is the better choice in symmetrical cooling; however, BB is the highest option for heat transfer. Compared to TT, enhancement for BB is 8.95% (f = 1), 18.79% (f = 3), 20.86% (f = 5), 18.56% (f = 7). Furthermore, spatial heating with varying f offers superior heat transfer compared to uniform heating condition and enhances heat transfer up to 56.19% at a higher frequency. This analysis clearly reflects the benefit of spatial heating over uniform heating for the different cooler positions. The local Nu variation (in Fig. 20a) is symmetrical for TT, BB, and MM cases, and it becomes asymmetrical for TM, TB, and MB cases for unequal heat transfer in the sidewalls. For the symmetrical cooling wall, the local Nu value becomes negative and the same magnitude is at the bottom corners, but for asymmetrical cooling, this does not happen. Such detailed insight into the local thermo-fluid flow dynamics as well as global heat transport characteristics due to the different cooler position variations in a porous thermal system subjected to multi-frequency heating is not reported in the previously published literature. This is a major advantage of the present study.

Fig. 20
figure 20

Positional impact on cooler on a local heat transfer (local Nu) and b average heat transfer (Nu) at Ram = 103, Da = 10−3, φ = 0.1%, Ha = 30, I = 1.0

Full size image

The local variation of vertical velocity (V) and temperature (θ) (in Fig. 21) of fluid at the mid-horizontal plane in the cavity is presented for different values of I (Fig. 21a, b) and f (Fig. 21c, d) and at different cooler locations (Fig. 21e, f). The shape of the variation of velocity with respect to I and f is symmetrical about the mid-vertical plane and shows the negative velocity near the walls and positive velocity at the center due to the formed two vortices. The variation of velocity becomes asymmetrical when the cooler position becomes asymmetrical (TM, TB, and MB). The strength of the vortex is controlled by velocity magnitude. For lowering the cooling position over the vertical wall, velocity fluctuation is noted to be less. The temperature variation at this mid-horizontal position shows the high temperature at the center and is symmetrical for TT, MM, and BB conditions of cooler walls. It becomes asymmetrical as observed in the case of velocity which indicates the difference in heating on both sides near the wall. Maximum temperature and symmetrical variation are observed for the BB case. The central temperature rises as I rises, but f decreases. More fluctuation of velocity is noted with respect to I relative to f. The positive peak and negative peak of velocity rise with I. In context to this analysis, such details about the local thermal characteristics of a thermal system under multi-frequency heating (following the half-sinusoidal profile) are not reported in the previously published literature. Therefore, the present study will enrich the readers' insight into the present study.

Fig. 21
figure 21

Local distribution of vertical velocity (V) component and temperature profiles (θ) at Ram = 103, Da = 10–3, φ = 0.1%, Ha = 30 for varying (a, b) I, (c, d) f, and (e, f) cooler positions

Full size image

Conclusions

This work provides newer insights into thermal fluid flow due to the presence of a half-sinusoidal heating profile, partial magnetic field, hybrid nanofluid, and porous substance. The characteristics of this multi-physical thermal system are examined for parametric controls of Ram, Da, Ha, ε, φ, and f along with different cooler positions. The notable findings are concluded as:

  • Heat transportation characteristics due to convection strength are enhanced significantly for varying Ram and maximize at higher Ram = 104 and f = 7, which reproduces the selection of Ram and f value.

  • Control of buoyancy dominance and permeability of porous structure counter the flow resistance with an increase in Darcy value. This leads to a drop in heat exchange rate at higher Da. But heat exchange enhancements are observed for all Da with rising frequency f.

  • With the increase in magnetizing field strength, the impact of buoyancy dominance resisted by magnetic-induced force ensues in a diminution in heat transfer rate. But heat transfer augmentations are monitored for all Ha with intensifying frequency f.

  • With more inclusion of hybrid nanosize particles with water, the heat transport rate decreases relative to reference pure water (φ = 0). On the contrary, the heat transfer escalations are being observed for all φ with increasing frequency f.

  • Spatial multi-frequency heating with the appropriate setting of I and f values (of the half-sinusoidal heating profile) can enhance up to 370.77% compared to the uniform condition. Higher amplitude and frequency of spatial heating could be opted for a better heating strategy compared to the uniform heating.

  • Sinusoidal heating at the bottom wall generates a cooling effect on the bottom corners. This cooling effect remains the same by variation of Ram, Da, Ha, ε, and φ. But frequency and amplitude alter the cooling effect at these zones.

  • MB case is the better choice in asymmetrical cooling, and BB is better in symmetrical cooling; however, BB position offers a better option for the highest heat transfer. Heat transfer for asymmetrical cooling for any case is higher relative to the TT case. However, the BB case shows maximum heat transfer compared to an asymmetrical case.

  • The regression analysis determines the useful correlations on the average Nu involving various controlling parameters.

The ample lessons with this problem allowing for such a special type of heat source and partial cooling with multi-physical settings can be the potential research endeavor considering different shapes of geometry and its orientation, partially active magnetic field varying active width, numbers of bands, interspatial distance between bands, and other multi-physical conditions both experimentally and numerically, which are not covered in the present study.