Soliton solutions, lump solutions, mixed interactional solutions and their dynamical analysis of the $(2+1)$-dimensional Calogero–Degasperis system

Abstract

This paper focusses on a class of non-isospectral $(2+1)$-dimensional Calogero–Degasperis system, which is a more general form of the classical nonlinear Schrödinger equation. Primarily, according to the plane wave seed solutions, we analyse the modulational instability of this system and obtain the formation mechanism of different localised waves. Secondly, based on the known Lax pair, we construct the generalised $(n, N-n)$-fold Darboux transformation of this system. As an application of the resulting Darboux transformation, we not only show the interaction structures of the multisoliton solutions, but also analyse its long-time asymptotic behaviours and list the relevant physical properties. In order to explore the relationship with differential geometry, we also show the multisoliton surfaces. Subsequently, we give some higher-order lump solutions and analyse their large-parameter asymptotic states. We also give some mixed interactional solutions to better understand the interaction phenomena of different localised waves, whose propagation structures and characteristics are shown graphically. These results and phenomena may be helpful to understand some physical phenomena in nonlinear optics, fluids and Bose–Einstein condensates.

1 Introduction

In 2011, using the inverse Miura mapping method, Tsuchida has proposed the following Calogero–Degasperis (CD) system [1]:

$$\begin{aligned} \begin{array}{l l} \text {i}Q_t+Q_{xy}-fQ-Qg=O, \vspace{0.05in}\\ \text {i}R_t-R_{xy}+gR+Rf=O,\vspace{0.05in}\\ f_x=(QR)_y,\vspace{0.05in}\\ g_x=(RQ)_y, \end{array} \end{aligned}$$

(1)

which can describe many physical phenomena, such as nonlinear optics, soliton propagation and interaction in fluids and Bose–Einstein condensates [2,3,4]. In system (1), Q and R are two matrices of order $\ell _1 \times \ell _2$ and $\ell _2 \times \ell _1$, respectively, O is a zero matrix, $\text {i}$ is an imaginary unit, x and y are space variables, t is the time variable and the subscripts x, y and t denote the partial derivative of the corresponding unknown functions. Other unknown functions and their related meanings can be learned from ref. [1]. If we consider three matrices $Q,\ R$ and O in system (1) as scalars $q,\ r$ and 0, respectively, system (1) has the following form:

$$\begin{aligned} \begin{array}{l l} \text {i}q_t+q_{xy}-fq-gq=0, \vspace{0.05in}\\ \text {i}r_t-r_{xy}+gr+fr=0,\vspace{0.05in}\\ f_x-(qr)_y=0,\vspace{0.05in}\\ f_x-g_x=0, \end{array} \end{aligned}$$

(2)

where q and r are potential functions containing x, y and t in the complex field, whereas f and g are potential functions containing x, y and t in the real field. It is worth noting that f and g are not necessarily equal due to the influence of integral constants. The Lax pair of system (2) are as follows [1]:

$$\begin{aligned} \psi _{x}=M \psi , \ \ \psi _{t}=2\zeta \psi _y+N\psi , \end{aligned}$$

(3)

where

$$\begin{aligned} M=\left( \begin{array}{cc} -\text {i}\zeta &{} q \\ r &{} \text {i}\zeta \\ \end{array} \right) ,\quad N=\left( \begin{array}{cc} -\text {i}f &{} \text {i}q_y \\ -\text {i}r_y &{} \text {i}g\\ \end{array} \right) , \end{aligned}$$

and $\psi =\psi (x,y,t)=(\psi _1(x,y,t), \psi _2(x,y,t))^\textrm{T}$ (T stands for transpose) is the eigenfunction in the complex field. Meanwhile, it must satisfy the compatibility condition $\psi _{xt}=\psi _{tx}$ and $\psi _{xy}=\psi _{yx}$, $\zeta \in \mathbb {C}$ is a spectral parameter and satisfies the relation $\zeta _t=2\zeta \zeta _y$. In fact, system (2) can be viewed as a zero-curvature equation $M_t-N_x+[M,\,N]-2\zeta M_y=0$ with $[M,\, N]\equiv MN-NM$. When choosing the reduction $r=-q^*$, the superscript $*$ indicates complex conjugate. So from system (2) the reduced CD system can be given as follows:

$$\begin{aligned} \begin{array}{l l} \text {i}q_t+q_{xy}-fq-gq=0, \vspace{0.05in}\\ f_x+|q|^2_y=0,\vspace{0.05in}\\ f_x-g_x=0. \end{array} \end{aligned}$$

(4)

The corresponding Lax expressions of system (4) are still consistent with (3) except that r is replaced by $-q^*$. We mainly investigate the reduction of non-isospectral $(2+1)$-dimensional CD system (4).

For system (4), many researchers have studied its reduced form. A classic example is the $(2+1)$-dimensional nonlinear Schrödinger (NLS) equation, which can be obtained by making $f=g$ in system (4). Li et al [5] studied the variable coefficient ($2+1$)-dimensional NLS equation. By using the Hirota method with auxiliary functions, not only the multisoliton solutions are obtained, but also the effects of coefficients and wave numbers on the soliton interaction are revealed. These multisolitons include parabolic, cubic, quasiperiodical and polyline solitons. Chen et al [6] mainly discussed about the breathers and rogue wave solutions of the $(2+1)$-dimensional NLS equation with the help of the modified Darboux transformation (DT). In addition, the dynamic characteristics of Akhmediev breathers and Kuznetsov–Ma solitons are discussed in graphical form. Zhang et al [7], with the help of classical and generalised N-fold DT, mainly studied the elastic interaction between solitons and the related properties of higher-order rogue wave solution, while Peng et al [8] studied the non-local PT symmetric rational and semi-rational solutions using Hirota bilinear and long wave limit methods for $(2+1)$-dimensional NLS equation. Wang et al [9] proposed a simple and effective method to establish the breather and rogue wave solutions for the $(2+1)$-dimensional NLS equation. Zuo et al [10], as a special case of the optical solitons, studied the Hermite–Gaussian vortex solitons and displayed the relevant images. However, as far as we know, the modulational instability (MI), multisoliton, soliton surfaces, higher-order lump, mixed interaction solutions, dynamics analysis of soliton and large-parameter asymptotic of lump have not been studied using the generalised $(n, N-n)$-fold DT for system (4). Generalised DT plays an important role in solving nonlinear integrable equations [11,12,13,14]. However, the extension of the generalised DT to higher-dimensional non-isospectral nonlinear integrable equations including $(2+1)$-dimensional and $(3+1)$-dimensional Lax integrable systems still needs further research. Therefore, our next major task in this paper is to extend the generalised $(n, N-n)$-fold DT to solve the reduction non-isospectral $(2+1)$-dimensional CD system (4).

This article is organised as follows: In §2, based on the plane-wave background, we will not only divide the MI region in detail and analyse the MI of system (4), but also give the excitation principles of different localised waves in different regions. In §3, we establish the generalised $(n, N-n)$-fold DT. In §4, we establish abundant multisoliton structures by using (N, 0)-fold DT and show the related dynamic characteristics of multisolitons by using asymptotic analysis technique. In order to better understand the differential geometric properties of system (4), we also give the relevant structures of soliton surface. In §5, according to the generalised $(1, N-1)$-fold DT, we set up the position and shape controllable higher-order lump and use the large-parameter asymptotic analysis method to give the properties of the higher-order lump at infinity as the parameters change for system (4). In §6, with the help of the generalised $(2,N-2)$-fold DT, we give mixed lump-breather interactional structures. The relevant contents are summarised in §7.

2 MI analysis for the reduced $(2+1)$-dimensional CD system (4)

MI, also known as parametric instability, is an extremely common and momentous physical phenomenon in fluid mechanics, optics, plasma physics and condensed matter physics. With the development of nonlinear problems, researchers have found that the generation mechanism of different localised waves can be determined by numerical analysis method [12,13,14,15,16,17,18]. We can clearly understand the excitation principle of different localised waves through the detailed division of modulation stability (MS) and MI regions. Next, in order to analyse the MI of system (4), we start from the following plane-wave seed solutions:

$$\begin{aligned} \begin{array}{ll} q_0= c{\textrm{e}}^{\text {i}(kx+my+\mu t)}, \quad g_0=f_0=-\dfrac{km+\mu }{2}, \end{array} \end{aligned}$$

(5)

where $c,\ k,\ m$ and $\mu$ are arbitrary real constants. Subsequently, we can reconstruct solutions (5) after adding perturbations as follows:

$$\begin{aligned} \begin{array}{ll} q\!=\! q_0(1\!+\!\tau _{1+}\textrm{e}^{\text {i}\Omega (-\alpha x\!-\!\beta t+y)}\!+\!\tau _{1-}^*\textrm{e}^{-\text {i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \vspace{0.02in}\\ g\!=\!g_0(1\!+\!\tau _{2+}\textrm{e}^{\text {i}\Omega (-\alpha x\!-\!\beta t+y)}\!+\!\tau _{2-}^*\textrm{e}^{-\text {i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \vspace{0.02in}\\ f\!=\!f_0(1\!+\!\tau _{3+}\textrm{e}^{\text {i}\Omega (-\alpha x\!-\!\beta t+y)}\!+\!\tau _{3-}^*\textrm{e}^{-\text {i}\Omega (-\alpha ^*x-\beta ^*t+y)}), \end{array} \end{aligned}$$

(6)

where $\tau _{1\pm },\ \tau _{2\pm }$ and $\tau _{3\pm }$ are the complex small perturbations, $\Omega$ is the real modulational frequency and $\alpha$ and $\beta$ are the complex propagation parameters. Substituting eq. (6) into system (4), we will establish the following six linear algebraic equations:

$$\begin{aligned} \left\{ \begin{array}{ll} \dfrac{c}{2}\left[ 2\Omega (\Omega \alpha +\alpha m+\beta -k)\tau _{1+}\right. \\ \quad \left. +(km+\mu )\tau _{2+}+(km+\mu )\tau _{3+}\right] =0,\vspace{0.02in}\\ \dfrac{c}{2}\left[ 2\Omega (\Omega \alpha -\alpha m-\beta +k)\tau _{1-}\right. \\ \quad \left. +(km+\mu )\tau _{2-}+(km+\mu )\tau _{3-}\right] =0,\vspace{0.02in}\\ \text {i}\Omega [c^2\tau _{1+}+c^2\tau _{1-}+\tfrac{1}{2}\alpha (km+\mu )\tau _{3+}]=0,\vspace{0.02in}\\ \text {i}\Omega [c^2\tau _{1+}+c^2\tau _{1-}+\tfrac{1}{2}\alpha (km+\mu )\tau _{3-}]=0,\vspace{0.02in}\\ \text {i}\Omega \alpha (km+\mu )\tau _{2+}-\text {i}\Omega \alpha (km+\mu )\tau _{3+}=0,\vspace{0.02in}\\ \text {i}\Omega \alpha (km+\mu )\tau _{2-}-\text {i}\Omega \alpha (km+\mu )\tau _{3-}=0. \end{array}\right. \end{aligned}$$

(7)

According to eqs (7), we know that the necessary and sufficient condition for it to have a non-zero solution is that the relevant parameters $\alpha ,\ \beta ,\ \Omega ,\ c, \ k\ \textrm{and}\ m$ meet the following relationship:

$$\begin{aligned} \begin{array}{ll} \beta _{\pm }=-\alpha m+k\pm \sqrt{\Omega ^2\alpha ^2-4c^2}. \end{array} \end{aligned}$$

(8)

To facilitate the analysis, we must restrict $\alpha$ in relation (8) to be a sufficiently small complex number. However, it is inconvenient to give this sufficiently small complex number and we use $\alpha =\frac{\text {i}}{2}$ instead. When $\alpha =\tfrac{\text {i}}{2}$, we take $\beta _{+}$, where $k=1,\ m=120$. Next, we specify the MI gain as $G_1=|\Im (\Omega \beta _{+})|$ where $\Im$ represents the imaginary part. Thereby, we can obtain the following conclusion: MI generation factor of $G_1$ is the other regions except the lines $\Omega =\pm 4\sqrt{900-c^2}$ and $-30\le c \le 30$.

In order to avoid the restriction of $\alpha$ in relation (8), the relevant parameters can still satisfy the following conditions so that eqs (7) has a non-zero solution.

$$\begin{aligned} \alpha= & {} \dfrac{2 \sqrt{(\Omega ^2-m^2)c^2}}{\Omega ^2-m^2},\nonumber \\ \beta= & {} \dfrac{-\Omega ^2 k+k m^2+4m \sqrt{(\Omega ^2-m^2)c^2}}{-\Omega ^2+m^2}. \end{aligned}$$

(9)

From (9), we can redefine the MI gain $G_2=|\Im (\Omega \beta )|$, where $k=1$ and $m=2$, so that we can clearly understand that the MI regions of $G_2$ is the other regions except $c=0$ and $\Omega ^2>4$.

In figures 1(a1) and 1(a2), for the MI gain $G_1$, its surface shape and density distribution can be clearly seen. In figures 1(a2) and 1(a3), we also clearly mark the MI and MS regions. It is worth noting that $\Omega =0$ for the MI region and it can excite the breather or lump in figure 1(a2). In figure 1(a2), we can observe that the red region is the MS areas, and solitons or plane waves can be excited in this region. Figure 1(a3) is the enlarged image of the MS areas of figure 1(a2). For the explanation of why $\Omega =0$ for MI, please refer to refs [19, 20]. For the MI gain $G_2$, the relevant surface structure, density and MI, MS distributions are shown in figures 1(b1) and 1(b2). Certainly, the relevant localised waves will be excited in the corresponding region in figure 1(b2), which will be described only a little here. By the above analysis, we clearly know that the MI region can excite breather and lump, and the MS region can excite the soliton and the plane wave.

We have to emphasise that we have given the relevant parameter values in advance, which is helpful for the analysis. We can certainly assign other values to related parameters and use the same analysis method to analyse the MI gains. However, it will no longer be described.

Fig. 1

Surface (a1) and density (a2) distribution of the MI gain $G_1$ when $k=1,\ m=120,\ \alpha =\tfrac{\text {i}}{2}$; (a3) enlarged image of the MS areas of (a2); (b1) Surface (top) and density (below) distribution of the MI gain $G_2$ when $k=1,\ m=2$; (b2) MI and MS distribution areas of $G_2$.

3 Generalised $(n, N-n)$-fold DT of CD system (4)

As per our knowledge of DT, we can easily give the following gauge transformation:

$$\begin{aligned} \tilde{\psi }=T{(\zeta )}\psi \, \end{aligned}$$

(10)

where $\psi$ satisfies Lax pair (3) and the form of $T(\zeta )$ will be given below. Meanwhile, $\tilde{\psi }=(\tilde{\psi }_1, \tilde{\psi }_2)^\textrm{T}$ needs to satisfy the same form of the Lax pair as (3). And $\tilde{\psi }$ should be subjected to $\tilde{\psi }_{x}=\tilde{M} \tilde{\psi },\ \tilde{\psi }_{t}=2\zeta \tilde{\psi }_y+\tilde{N}\tilde{\psi }$, where $\tilde{M},\ \tilde{N}$ have the same forms as $M,\ N$, respectively, except that $q,\ r,\ f,\ g$ are replaced by $\tilde{q},\ \tilde{r},\ \tilde{f},\ \tilde{g}$. Similarly, as per our knowledge of DT, we can also obtain the following relationships:

$$\begin{aligned} T_{x}+ & {} TM-\tilde{M}T=0,\nonumber \\ T_{t}+ & {} TN-\tilde{N}T-2\zeta T_y=0. \end{aligned}$$

(11)

By symbolic computation, the following DT matrix T can be obtained:

$$\begin{aligned} T(\zeta ) = \left( \begin{array}{cc} \zeta ^{N}+\sum \limits _{j=0}^{N-1}A^{(j)}\zeta ^{j} &{} \sum \limits _{j=0}^{N-1}B^{(j)} \zeta ^{j} \vspace{0.05in}\\ \sum \limits _{j=0}^{N-1}C^{(j)} \zeta ^{j} &{} \zeta ^{N}+\sum \limits _{j=0}^{N-1}D^{(j)}\zeta ^{j} \end{array} \right) , \end{aligned}$$

(12)

where N is a positive integer, $A^{(j)},\ B^{(j)},\ C^{(j)}$ and $D^{(j)} \ (j=0,1,\ldots ,N-1)$ are unknown functions containing $x,\ y$ and t, and their specific forms will be given later. In terms of (11) and conventional N-fold DT knowledge, the potential function transformations of system (2) will be obtained as follows:

$$\begin{aligned} \begin{array}{ll} \tilde{q}_N=q_0+2\text {i}B^{(N-1)},\ \ \tilde{r}_N=r_0-2\text {i}C^{(N-1)},\\ \tilde{f}=f_0-2\text {i}A^{(N-1)}_y,\ \ \tilde{g}=g_0+2\text {i}D^{(N-1)}_y. \end{array} \end{aligned}$$

(13)

According to our research, the structures of the new solution generated are extremely unsatisfactory by transformation (13). Based on $r=-q^*$, we will construct the generalised $(n, N-n)$-fold DT for system (4). In terms of DT matrix (12), we can obtain the following reduced DT matrix:

$$\begin{aligned} T(\zeta ) = \left( \begin{array}{cc} \zeta ^{N}+\sum \limits _{j=0}^{N-1}A^{(j)}\zeta ^{j} &{}\sum \limits _{j=0}^{N-1}B^{(j)} \zeta ^{j} \vspace{0.05in}\\ -\sum \limits _{j=0}^{N-1}{B^{(j)}}^{*} \zeta ^{j} &{}\zeta ^{N}+\sum \limits _{j=0}^{N-1}{A^{(j)}}^{*}\zeta ^{j} \end{array} \right) . \end{aligned}$$

(14)

According to (10), (11) and (14), we have the following potential function transformations for system (4):

$$\begin{aligned} \begin{array}{ll} \tilde{q}_N=q_0+2\text {i}B^{(N-1)},\ \ \tilde{f}_N=f_0-2\text {i}A^{(N-1)}_y,\ \\ \tilde{g}_N=g_0+2\text {i}A^{(N-1)^*}_y, \end{array} \end{aligned}$$

(15)

where $q_0,\ f_0$ and $g_0$ are the seed solutions. To obtain the new form solutions for system (4), we have to determine $A^{(N-1)},\ B^{(N-1)}$ in (15). However, determination of these unknown functions will be our next research focus. According to $\zeta =\zeta _i\ (i=1,2,\ldots ,n)$, let $\psi (\zeta _i)=\left( \psi _1(\zeta _i),\psi _2(\zeta _i)\right) ^{\textrm{T}}$ be n linearly independent solutions for Lax pair (3), in which $1\le n\le N$. Then the unknown functions $A^{(j)}$ and $B^{(j)}\ (j=0,1,\ldots ,N-1)$ are determined from $T(\zeta _i)\psi (\zeta _i)=0$, that is, they can be given in the following equations:

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\zeta _i)\psi ^{(0)}(\zeta _i)=0,\\ T^{(0)}(\zeta _i)\psi ^{(1)}(\zeta _i)+T^{(1)}(\zeta _i)\psi ^{(0)}(\zeta _i)=0,\\ T^{(0)}(\zeta _i)\psi ^{(2)}(\zeta _i)+T^{(1)}(\zeta _i)\psi ^{(1)}(\zeta _i)\\ +T^{(2)} (\zeta _i)\psi ^{(0)}(\zeta _i)=0,\\ \ldots ,\\ \sum \limits _{j=0}^{r_i}T^{(j)}(\zeta _i)\psi ^{(r_i-j)}(\zeta _i)=0, \end{array} \right. \end{aligned}$$

(16)

where $N=\sum _{i=1}^n(n+r_i) \ (i=1,2,\ldots ,n)$, $T^{(j)}\ (j=0,1,2,\ldots )$ is obtained by

$$\begin{aligned} T(\zeta _i+\varepsilon )=\sum \limits _{\vartheta =0}^NT^{(\vartheta )}(\zeta _i)\varepsilon ^\vartheta ,\end{aligned}$$

while $\psi ^{(j)}\ (j=0,1,2,\ldots )$ are obtained by the expansion $\psi (\zeta _i+\varepsilon )=\psi ^{(0)}(\zeta _i)+\psi ^{(1)}(\zeta _i)\varepsilon +\psi ^{(2)}(\zeta _i)\varepsilon ^2+\cdots ,$ the coefficients

$$\begin{aligned}\psi ^{(\vartheta )}(\zeta _i)= & {} \left( \dfrac{1}{\vartheta !} \dfrac{\partial ^\vartheta }{\partial \zeta _i^\vartheta }\psi _1(\zeta _i),\ \dfrac{1}{\vartheta !} \dfrac{\partial ^\vartheta }{\partial \zeta _i^\vartheta }\psi _2(\zeta _i)\right) ^{\textrm{T}}\\{} & {} (\vartheta =0,1,2,\ldots ).\end{aligned}$$

According to (16), we will choose n appropriate spectral parameters $\zeta _i$ and 2N $A^{(j)}$, $B^{(j)}$. Once the seed solutions $q_0,\ f_0$ and $g_0$ of system (4) are given, then the exact expressions of $A^{(N-1)}$ and $B^{(N-1)}$ will be obtained in (15) as follows:

$$\begin{aligned} \begin{array}{ll} A^{(N-1)}=\dfrac{\Delta A^{(N-1)}}{\Delta _N},\qquad B^{(N-1)}=\dfrac{\Delta B^{(N-1)}}{\Delta _N}, \end{array} \end{aligned}$$

(17)

where $\Delta _N=\;$det$([\Delta ^{(1)}_{m_1+1},\Delta ^{(2)}_{m_2+1},\ldots ,\Delta ^{(n)}_{m_n+1}]^{\textrm{T}})$ and $\Delta ^{(i)}_{m_i+1}=(\Delta ^{(i)}_{j,s})_{2(m_i+1)\times 2N}$ and the form of $\Delta ^{(i)}_{j,s}\ (1\le j\le 2m_i+2,\ 1\le s \le 2N)$ is as follows:

$$\begin{aligned} \Delta ^{(i)}_{j,s}=\! \left\{ \begin{array}{l} \sum _{\vartheta =0}^{j-1}C_{N-s}^\vartheta \zeta _i^{N-s-\vartheta }\psi _{1i}^{j-1-\vartheta },\\ \qquad \!\! \text {for}\ \ 1\le j\le m_i+1,\ 1\le s\le N, \\ \sum _{\vartheta =0}^{j-1}C_{2N-s}^\vartheta \zeta _i^{2N-s-\vartheta }\psi _{2i}^{j-1-\vartheta },\\ \qquad \!\!\text {for}\ \ 1\le j\le m_i+1,\ N+1\le s\le 2N, \\ \sum _{\vartheta =0}^{j-(N+1)}C_{N-s}^\vartheta \zeta _i^{(N-s-\vartheta )*}\psi _2{i}^{(j-1-N-\vartheta )*},\\ \!\!\qquad \text {for}\ \ m_i+2\le j\le 2(m_i+1),\ 1\le s\le N, \\ -\sum _{\vartheta =0}^{j{-}(N{+}1)}C_{2N{-}s}^\vartheta \zeta _i^{(2N{-}s{-}\vartheta )*}\psi _{1i}^{(j{-}N{-}1{-}\vartheta )*},\\ \!\!\qquad \text {for}\ \ m_i{+}2{\le } j{\le } 2(m_i{+}1),\ N{+}1{\le } s{\le } 2N, \end{array} \right. \end{aligned}$$

while $\Delta A^{(N-1)}$ and $\Delta B^{(N-1)}$ will be uniquely determined by the determinant $\Delta N$ substituting its first and $(N+1)$th columns via the vector $(g^{(1)},\ldots ,g^{(n)})^{\textrm{T}}$ with $g^{(i)}=(g_j^i)_{2(m_i+1)\times 1}$, where

$$\begin{aligned} g_j^i= \left\{ \begin{array}{ll} -\sum \limits _{\vartheta =0}^{j-1}C_{N}^\vartheta \zeta _i^{N-\vartheta }\psi _{1i}^{(j-1-\vartheta )},\\ \ \qquad \text {for}\ \ 1\le j\le m_i+1, \\ -\sum \limits _{\vartheta =0}^{j-N-1}C_{N}^\vartheta \zeta _i^{(N-\vartheta )*}\psi _{2i}^{(j-N-1-\vartheta )*},\\ \ \qquad \text {for}\ \ m_i +2\le j\le 2(m_i+1). \end{array} \right. \end{aligned}$$

Table 1 Relevant physical quantities for one-soliton solution in the x, y direction.

In general, the transformations (10) and (15) are called the generalised $(n,N-n)$-fold DT. In the generalised $(n,N-n)$-fold DT, n denotes the number of spectral parameters used, while $N-n$ represents the sum of the derivative orders of the Taylor expansion for eigenfunction $\psi (\zeta _i) \ (i=1,2,\ldots ,n)$. In this article, we will establish higher-order lump and rich mixed interaction solutions for system (4) by adopting the generalised $(n,N-n)$-fold DT.

Remark 1

When $n=N, r_i=0 \ (1\le i \le N)$, the N-fold DT included in the (N, 0)-fold DT and the generalised $(n,N-n)$-fold DT will reduce to the (N, 0)-fold DT, from which if we do not use Taylor expansion at every $\zeta _i$, the soliton and breather solutions will be obtained. The generalised $(n,N-n)$-fold DT will reduce to the generalised $(1,N-1)$-fold DT, when $n=1$ and $r_1=N-1$, and from the plane-wave background, the lump solutions of system (4) will be obtained. The generalised $(n,N-n)$-fold DT will reduce to the generalised $(2,N-2)$-fold DT. When $n=2$ and $r_1+r_2=N-2$, we can certainly obtain the mixed lump–breather interaction structures for system (4). When $2<n<N$, we will certainly obtain interaction phenomena with higher order and abundant structures, but these phenomena will not be described in this paper. With the help of this method, in the subsequent three sections we will generate some multisoliton, higher-order lump and mixed interaction solutions from the non-zero background and plane-wave background for system (4), respectively.

Fig. 2

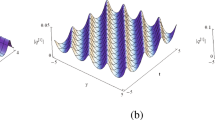
Surface (top) and density (below) plots for one-soliton solutions q and f using (20) with different spectral parameters: (a1), (a2) $\zeta _1=2\text {i}$; (a3), (a4) $\zeta _1=\tfrac{\text {i}}{2}$.

4 Multisoliton solutions, asymptotic analysis and soliton surfaces of system (4)

In this section, based on the constant seed solutions and transformation (15), we will use (N, 0)-fold DT to establish the multisoliton solutions of system (4) and analyse its elastic interaction and related dynamic characteristics. We consider the constant seed solutions $q_0=0$ and $f_0=g_0=-1$ of system (4), and substitute the seed solutions into Lax pair (3) to obtain the following form solution with $\zeta =\zeta _\kappa$:

$$\begin{aligned}{} & {} \psi _\kappa =\left( \begin{array}{cc} \psi _{1\kappa } \\ \psi _{2\kappa } \end{array} \right) = \left( \begin{array}{cc} \textrm{e}^{\tfrac{-2\text {i}\zeta _\kappa ^2x-2\zeta _\kappa t-(1+\text {i})y}{2\zeta _\kappa }} \vspace{0.05in}\\ \textrm{e}^{\tfrac{2\text {i}\zeta _\kappa ^2x+2\zeta _\kappa t+(1+\text {i})y}{2\zeta _\kappa }} \\ \end{array} \right) ,\quad \nonumber \\{} & {} \kappa =1,2,\ldots ,N. \end{aligned}$$

(18)

In the same background, in terms of transformation (15), we find that the shape and properties of f and g are similar. Therefore, to save space, we only show the multisoliton solutions of q and f and analyse their elastic interaction.

4.1 One-soliton solutions and dynamic analysis

When $N=1$, $\zeta _1=b\text {i}$, where b is an arbitrary constant, in terms of (15), we can obtain the following solutions:

$$\begin{aligned} \tilde{q}_1=2\text {i}B^{(0)},\quad \tilde{f}_1=-1-2\text {i}A^{(0)}_y, \end{aligned}$$

(19)

where

$$\begin{aligned} \begin{array}{llll} &{}\Delta _{1}=\left| \begin{array}{cc} \psi _{11} &{} \psi _{21} \\ \psi _{21}^* &{} -\psi _{11}^* \end{array}\right| ,\ \Delta A^{(0)}=\left| \begin{array}{cc} -\zeta _1\psi _{11} &{} \psi _{21} \\ -\zeta _1^*\psi _{21}^* &{} -\psi _{11}^* \end{array}\right| ,\\ &{}\Delta B^{(0)}=\left| \begin{array}{cc} \psi _{11} &{} -\zeta _1\psi _{11} \\ \psi _{21}^* &{} -\zeta _1^*\psi _{21}^* \end{array}\right| . \end{array} \end{aligned}$$

For the convenience of analysing the relevant physical properties of one-soliton, solutions (19) can be rewritten as

$$\begin{aligned} \tilde{q}_1= & {} 2b\textrm{e}^{\tfrac{y\text {i}}{b}}{{\,\textrm{sech}\,}}\bigg (\dfrac{2b^2x-y-2bt}{b}\bigg ),\nonumber \\ \tilde{f}_1= & {} -1+2{{\,\textrm{sech}\,}}^2\bigg (\dfrac{2b^2x-y-2bt}{b}\bigg ). \end{aligned}$$

(20)

From (20), it is easy to observe that $\tilde{q}_1$ is a bright one-soliton structure, while $\tilde{f}_1$ is a bell-shaped one-soliton structure. Relevant physical quantities propagating in different directions are listed in table 1. For q and f, the energies are defined as

$$\begin{aligned}{} & {} E_{q}=\int _{-\infty }^{\infty }|q|^{2}\textrm{d}x+\int _{-\infty }^{\infty }|q|^{2}\textrm{d}y,\\{} & {} E_{f+1}=\int _{-\infty }^{\infty }(f+1)^2 \textrm{d}x+\int _{-\infty }^{\infty }(f+1)^2 \textrm{d}y, \end{aligned}$$

respectively. We can easily observe that the physical quantities of one-soliton solutions depend on the spectral parameter $\zeta _1$. In figures 2(a1) and 2(a2), the bell-shaped one-soliton structure of $\tilde{q}_1$ and $\tilde{f}_1$ propagating in the x direction are shown when $\zeta _1=2\text {i}$ (i.e., $b=2)$. In figures 2(a3) and 2(a4), $\tilde{q}_1$ and $\tilde{f}_1$ propagating in the y direction are shown when $\zeta _1=\tfrac{\text {i}}{2}$ (i.e., $b=\tfrac{1}{2})$.

4.2 Two-soliton solutions and their asymptotic analysis

When $N=2$, $\zeta _1=b_1\text {i}$, $\zeta _2=b_2\text {i}$, where $b_1$ and $b_2$ are positive arbitrary constants, in terms of (15), we can get the following solutions:

$$\begin{aligned} \tilde{q}_2=2\text {i}B^{(1)},\quad \tilde{f}_2=-1-2\text {i}A^{(1)}_y, \end{aligned}$$

(21)

where

$$\begin{aligned}{} & {} \Delta _{2}=\left| \begin{array}{cccc} \zeta _{1}\psi _{11} &{}\quad \psi _{11} &{} \quad \zeta _{1}\psi _{21} &{}\quad \psi _{21}\\ \zeta _{2}\psi _{12} &{} \quad \psi _{12} &{} \quad \zeta _{2}\psi _{22} &{} \quad \psi _{22} \\ \zeta _1^*\psi _{21}^* &{} \quad \psi _{21}^* &{} \quad -\zeta _1^*\psi _{11}^* &{}\quad -\psi _{11}^* \\ \zeta _2^*\psi _{22}^* &{} \quad \psi _{22}^* &{} \quad -\zeta _2^*\psi _{12}^* &{} \quad -\psi _{12}^* \end{array}\right| ,\\{} & {} \Delta {A^{(1)}}=\left| \begin{array}{cccc} -\zeta _1^2\psi _{11} &{} \psi _{11} &{} \zeta _1\psi _{21} &{} \psi _{21} \\ -\zeta _2^2\psi _{12} &{} \psi _{12} &{} \zeta _2\psi _{22} &{} \psi _{22} \\ -{(\zeta _1^2)}^*\psi _{21}^* &{} \psi _{21}^* &{} -\zeta _1^*\psi _{11}^* &{} -\psi _{11}^* \\ -{(\zeta _2^2)}^*\psi _{22}^* &{} \psi _{22}^* &{} -\zeta _2^*\psi _{12}^* &{} -\psi _{12}^* \end{array}\right| ,\\{} & {} \Delta {B^{(1)}}=\left| \begin{array}{cccc} \zeta _{1}\psi _{11} &{} \psi _{11} &{} -\zeta _1^2\psi _{11} &{}\psi _{21}\\ \zeta _{2}\psi _{12} &{} \psi _{12} &{} -\zeta _2^2\psi _{12} &{} \psi _{22} \\ \zeta _1^*\psi _{21}^* &{} \psi _{21}^* &{} -{(\zeta _1^2)}^*\psi _{21}^* &{} -\psi _{11}^* \\ \zeta _2^*\psi _{22}^* &{} \psi _{22}^* &{} -{(\zeta _2^2)}^*\psi _{22}^* &{} -\psi _{12}^* \end{array}\right| . \end{aligned}$$

The solutions (21) can be rewritten as

$$\begin{aligned}{} & {} \tilde{q}_2=-\dfrac{4(b_1^2-b_2^2)\left[ -b_1\textrm{e}^{\tfrac{y\text {i}}{b_1}}\cosh (\xi _2)+b_2\textrm{e}^{\tfrac{y\text {i}}{b_2}}\cosh (\xi _1)\right] }{(b_1+b_2)^2\cosh (\xi _1-\xi _2)+(b_1-b_2)^2\cosh (\xi _1+\xi _2)-4b_1b_2\cos \left( y\tfrac{b_1-b_2}{b_1b_2}\right) }, \qquad \qquad \qquad \,\,\,\, \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \tilde{f}_2=\dfrac{\begin{array}{c}4(b_1+b_2)(b_1-b_2)^2\left[ \sqrt{J_1J_2}\cosh \left( \xi _1+\xi _2+\tfrac{1}{2}\ln {\tfrac{J_1}{J_2}}\right) +\sqrt{J_3J_4}\cosh \left( \xi _1-\xi _2-\tfrac{1}{2}\ln {\tfrac{J_3}{J_4}}\right) \right. \\ \quad \left. +(b_1+b_2)[\cosh (2\xi _2)+\cosh (2\xi _1)-2]\right] \end{array}}{\left[ (b_1+b_2)^2\cosh (\xi _1-\xi _2)+(b_1-b_2)^2\cosh (\xi _1+\xi _2)-4b_1b_2\cos \left( y\tfrac{b_1-b_2}{b_1b_2}\right) \right] ^2}-1,\qquad \quad \quad \,\,\,\, \end{aligned}$$

(23)

where

$$\begin{aligned} \xi _1= & {} \dfrac{2b_1^2x-y-2b_1t}{b_1}, \ \ \xi _2=\dfrac{2b_2^2x-y-2b_2t}{b_2},\vspace{0.05in}\\ J_1= & {} -2(b_1+b_2)\cos \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg )\\{} & {} +2(b_1-b_2)\sin \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg ),\\ J_2= & {} -2(b_1+b_2)\cos \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg )\\{} & {} -2(b_1-b_2)\sin \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg ),\vspace{0.05in}\\ J_3= & {} 2(b_1+b_2)\left[ \cos \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg )-\sin \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg )\right] ,\\ J_4= & {} 2(b_1+b_2)\left[ \cos \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg )+\sin \bigg (y\dfrac{b_1-b_2}{b_1b_2}\bigg )\right] . \end{aligned}$$

Asymptotic analysis is an extremely useful technique to analyse the elastic collision of solitons [21,22,23,24,25,26]. According to solutions (22), to study whether the interaction between two solitons is elastic, we have the following asymptotic analysis:

(i) The analysis of solution $\tilde{q}_2$ is as follows:

$\bullet$ Before the interaction $(t\rightarrow -\infty )$:

$$\begin{aligned}{} & {} \tilde{q}_2\rightarrow \eta _1^{-}=2b_1\textrm{e}^{\tfrac{y\text {i}}{b_1}}{{\,\textrm{sech}\,}}\left[ \xi _1+\ln {\bigg (\dfrac{b_1-b_2}{b_1+b_2}\bigg )}\right] ,\quad \nonumber \\{} & {} \xi _1 \sim 0,\quad \xi _2\rightarrow +\infty ,\vspace{0.05in}\nonumber \\{} & {} \tilde{q}_2\rightarrow \eta _2^{-}=2b_2\textrm{e}^{\tfrac{y\text {i}}{b_2}}{{\,\textrm{sech}\,}}\left[ \xi _2+\ln {\bigg (\dfrac{b_2-b_1}{b_2+b_1}\bigg )}\right] ,\quad \nonumber \\{} & {} \xi _2 \sim 0,\quad \xi _1 \rightarrow +\infty , \end{aligned}$$

where $\eta _1^{-}$, $\eta _2^{-}$ are the asymptotic expressions of $\tilde{q}_2$ before the interaction.

$\bullet$ After the interaction $(t\rightarrow +\infty )$:

$$\begin{aligned} \begin{array}{ll} \tilde{q}_2\rightarrow \eta _1^{+}=2b_1\textrm{e}^{\tfrac{y\text {i}}{b_1}}{{\,\textrm{sech}\,}}\left[ \xi _1+\ln {\bigg (\dfrac{b_1+b_2}{b_1-b_2}\bigg )}\right] , \quad \\ \xi _1 \sim 0,\quad \xi _2 \rightarrow -\infty ,\vspace{0.05in}\\ \tilde{q}_2\rightarrow \eta _2^{+}=2b_2\textrm{e}^{\tfrac{y\text {i}}{b_2}}{{\,\textrm{sech}\,}}\left[ \xi _2+\ln {\bigg (\dfrac{b_2+b_1}{b_2-b_1}\bigg )}\right] , \quad \\ \xi _2 \sim 0,\quad \xi _1 \rightarrow -\infty , \end{array} \end{aligned}$$

(24)

where $\eta _1^{+}$, $\eta _2^{+}$ are the asymptotic expressions of $\tilde{q}_2$ after the interaction.

(ii) The analysis of solution $\tilde{f}_2$ is as follows:

$\bullet$ Before the interaction $(t\rightarrow -\infty )$:

$$\begin{aligned} \begin{array}{ll} \tilde{f}_2+1\rightarrow \nu _1^{-}=2{{\,\textrm{sech}\,}}^2\left[ \xi _1+\ln {\bigg (\dfrac{b_1-b_2}{b_1+b_2}\bigg )}\right] , \quad \\ \xi _1 \sim 0,\quad \xi _2\rightarrow +\infty ,\vspace{0.05in}\\ \tilde{f}_2+1\rightarrow \nu _2^{-}=2{{\,\textrm{sech}\,}}^2\left[ \xi _2+\ln {\bigg (\dfrac{b_1-b_2}{b_1+b_2}\bigg )}\right] , \quad \\ \xi _2 \sim 0,\quad \xi _1 \rightarrow +\infty , \end{array} \end{aligned}$$

(25)

where $\nu _1^{-}$, $\nu _2^{-}$ are the asymptotic expressions of $\tilde{f}_2+1$ before the interaction.

$\bullet$ After the interaction $(t\rightarrow +\infty )$:

$$\begin{aligned} \begin{array}{ll} \tilde{f}_2+1\rightarrow \nu _1^{+}=2{{\,\textrm{sech}\,}}^2\left[ \xi _1+\ln {\bigg (\dfrac{b_1+b_2}{b_1-b_2}\bigg )}\right] , \quad \\ \xi _1 \sim 0,\quad \xi _2 \rightarrow -\infty ,\vspace{0.05in}\\ \tilde{f}_2+1\rightarrow \nu _2^{+}=2{{\,\textrm{sech}\,}}^2\left[ \xi _2+\ln {\bigg (\dfrac{b_1+b_2}{b_1-b_2}\bigg )}\right] , \quad \\ \xi _2 \sim 0,\quad \xi _1 \rightarrow -\infty , \end{array} \end{aligned}$$

(26)

where $\nu _1^{+}$, $\nu _2^{+}$ are the asymptotic expressions of $\tilde{f}_2+1$ after the interaction.

After the above analysis (23)–(26), the relevant physical quantities of two-soliton $\tilde{q_2}$ and $\tilde{f}_2+1$ are listed in different directions in tables 2 and 3. By comparing these physical quantities, we notice that the relevant physical quantities of the two-soliton before and after the interaction remain unchanged, but the phase is opposite, and so it is an elastic interaction. In order to understand these physical quantities more intuitively, we show the relevant images in figure 3 when the spectral parameters $\zeta _1=\tfrac{\text {i}}{2}$ and $\zeta _2=2\text {i}$ and $t=-4,\,0,\,4.$ In figure 3, we can easily observe the propagation and strong interaction of two-soliton, which will not be described here.

Table 2 Relevant physical quantities for two-soliton solution $\tilde{q}_2$ in the x, y direction.

Table 3 Relevant physical quantities for two-soliton solution $\tilde{f}_2+1$ in the x, y direction.

When $N=3$, similar to the method of $N=1,\ 2$, we can certainly obtain the three-soliton solutions, but the relevant dynamic features and physical properties will not be described due to space constraints. When the parameters $\zeta _1=\tfrac{\text {i}}{2},\ \zeta _2=2\text {i},\ \zeta _3=\tfrac{\text {i}}{3}$, we only plot the structures of three-soliton as shown in figure 4.

Fig. 3

Structural plots of the two-soliton solutions q and f via the (22) with two spectral parameters $\zeta _1=\tfrac{\text {i}}{2},\ \zeta _2=2\text {i}$ when $t=-4,\,0,\,4.$

Fig. 4

Structural plots of the three-soliton solutions q and f with three spectral parameters $\zeta _1=\tfrac{\text {i}}{2},\ \zeta _2=2\text {i},\ \zeta _3=\tfrac{\text {i}}{3}$ when $t=-4,\,0,\,4$.

4.3 Soliton surfaces

The soliton equation has many connections with differential geometries. Since the famous report of Gauss in 1827, the soliton theory has been widely applied to differential geometry surfaces and soliton surface theory developed by Sym can establish the general relationship between integrable systems and geometry [27,28,29]. Meanwhile, soliton surface method provides a geometric interpretation for many integrable systems, such as spin, vortex, chiral field and so on [30, 31]. Recently, research on soliton surface has become extremely popular. However, there are no studies on the soliton surfaces of $(2+1)$-dimensional non-isospectral problem. In this section, we will study the soliton surfaces of system (4) according to the previous soliton solutions.

Based on the seed solutions $q_0=0$ and $f_0=g_0=-1$, we can get the eigenfunctions matrix of system (4) as follows:

$$\begin{aligned} \Phi (\zeta )= \left( \begin{array}{cc} \textrm{e}^{\tfrac{-2\text {i}\zeta ^2x-2\zeta t-(1+\text {i})y}{2\zeta }} &{} -\textrm{e}^{\tfrac{-2\text {i}\zeta ^2x+2\zeta t+(1-\text {i})y}{2\zeta }} \vspace{0.05in}\\ \textrm{e}^{\tfrac{2\text {i}\zeta ^2x+2\zeta t+(1+\text {i})y}{2\zeta }} &{} \textrm{e}^{\tfrac{2\text {i}\zeta ^2x-2\zeta t-(1-\text {i})y}{2\zeta }} \\ \end{array} \right) , \nonumber \\ \end{aligned}$$

(27)

and $\text {det}(\Phi (\zeta ))=2\cosh (\tfrac{y+2\zeta t}{\zeta })\ne 0$, $M,\ N \in SU(2)$. By applying Sym formula $\Phi (\zeta )^{-1}\tfrac{\textrm{d}}{\textrm{d}\zeta }\Phi (\zeta )$ [31], we can obtain the N-soliton surface $(F_1, F_2, F_3)$ of system (4), the analytic form of which is defined as

$$\begin{aligned} \Phi ^{[N]}(\zeta )^{-1}\dfrac{\textrm{d}}{\textrm{d}\zeta }\Phi ^{[N]}(\zeta )= \left( \begin{array}{cc} \text {i}F_3+F_0 &{} \text {i}F_1-F_2 \vspace{0.05in}\\ \text {i}F_1+F_2 &{} -\text {i}F_3+F_0 \\ \end{array} \right) . \nonumber \\ \end{aligned}$$

(28)

According to (14) and (27), we can determine that $\Phi ^{[N]}(\zeta )=T(\zeta )\Phi (\zeta )$ in (28). It is worth noting that $\zeta$ satisfies the non-isospectral relation $\zeta _t=2\zeta \zeta _y$. When $N=1,\ 2,\ 3$, we will give the soliton surface structures satisfying the non-isospectral conditions as shown in figures 5–7, respectively. In figures 5(a1)–5(a3), based on the isospectral parameter $\zeta =1$, we show the structures of one-soliton surface for $t=-3,\,0,\,3$, which have pretty good symmetry. In figures 5(b1)–5(b3), based on the non-isospectral parameter $\zeta =\tfrac{2y+4}{3-4t}$, we show the structures of one-soliton surface for $t=-1,\,0,\,1$. In figures 6(a1)–6(a3), based on the isospectral parameter $\zeta =1$, we show the structures of two-soliton surface for $t=-3,\,0,\,3$, which have pretty good symmetry. In figures 6(b1)–6(b3), based on the non-isospectral parameter $\zeta =\tfrac{2y+4}{3-4t}$, we show the structures of two-soliton surface for $t=-1,\,0,\,1$. In figure 7, based on the isospectral parameter $\zeta =1$, we show the structures of three-soliton surface for $t=-3,\,0,\,3$, which also have pretty good symmetry.

Fig. 5

One-soliton surfaces for system (4) with isospectral parameters for $t=-3,\,0,\,3$: (a1)–(a3) $\zeta =1,\ \zeta _1=2\text {i},\ (x,y)\in [-3,3]\times [-3,3]$. One-soliton surfaces for system (4) with non-isospectral parameters for $t=-1,\,0,\,1$: (b1)–(b3) $\zeta =\tfrac{2y+4}{3-4t},\ \zeta _1=2\text {i},\ (x,y)\in [-1,1]\times [-1,1]$.

Fig. 6

Double-soliton surfaces for system (4) with isospectral parameters for $t=-3,\,0,\,3$: (a1)–(a3) $\zeta =1,\ \zeta _1=\tfrac{\text {i}}{2},\ \zeta _2=2\text {i},\ (x,y)\in [-3,3]\times [-3,3]$. Double-soliton surfaces for system (4) with non-isospectral parameters for $t=-1,\,0,\,1$: (b1)–(b3) $\zeta =\tfrac{2y+4}{3-4t},\ \zeta _1=\tfrac{\text {i}}{2},\ \zeta _2=2\text {i},\ (x,y)\in [-1,1]\times [-1,1]$.

Fig. 7

Three-soliton surfaces for system (4) with isospectral parameters for $t=-3,\,0,\,3$: (a1)–(a3) $\zeta =1,\ \zeta _1=\tfrac{\text {i}}{2},\ \zeta _2=\text {2i},\ \zeta _3=\tfrac{\text {i}}{3},\ (x,y)\in [-3,3]\times [-3,3]$.

5 Higher-order lump solutions and large-parameter asymptotic analysis for system (4)

In this section, we still only show the higher-order lump solutions of q and f and analyse them. According to (15) and generalised $(1,N-1)$-fold DT, higher-order lump solutions of system (4) will be established based on one spectral parameter. Subsequently, substituting (5) into Lax pair (3), we get the following form solution for system (4):

$$\begin{aligned} \psi= & {} \left( \begin{array}{ll} \psi _1 \\ \psi _2 \end{array} \right) = \left( \begin{array}{cc} \left( C_1\textrm{e}^{\gimel [x+\text {i}y+(2\text {i}\zeta -m) t+\delta (\varepsilon )]}+C_2\textrm{e}^{-\gimel [x+\text {i}y+(2\text {i}\zeta -m) t+\delta (\varepsilon )]}\right) \textrm{e}^{\tfrac{\text {i}(kx+my+\mu t)}{2}} \vspace{0.05in}\\ \left( C_1m_{-}\textrm{e}^{\gimel [x+\text {i}y+(2\text {i}\zeta -m) t+\delta (\varepsilon )]}+C_2m_{+}\textrm{e}^{-\gimel [x+\text {i}y+(2\text {i}\zeta -m) t+\delta (\varepsilon )]}\right) \textrm{e}^{\tfrac{-\text {i}(kx+my+\mu t)}{2}} \\ \end{array} \right) , \end{aligned}$$

(29)

with

$$\begin{aligned}{} & {} m_{\mp }=\dfrac{2c}{\text {i}k+2\text {i}\zeta \mp \sqrt{-4c^2-k^2-4k\zeta -4\zeta ^2}},\\{} & {} \gimel =\dfrac{\sqrt{-4c^2-k^2-4k\zeta -4\zeta ^2}}{2},\\{} & {} \delta (\varepsilon )=\sum \limits _{i=0}^{N}(e_i+\text {i}d_i)\varepsilon ^{2i}, \end{aligned}$$

where $\varepsilon$ is an extremely small parameter, usually refer to $e_i$ and $d_i \ (i = 0, 1, 2, \ldots , N)$ as real control parameters, while $C_1$ and $C_2$ are real numbers. According to (29) and the (N, 0)-fold DT, we can certainly get the breather solutions. However, the main goal of this section is to give the higher-order lump solutions and analyse them. Thus, two forms of Taylor expansion about spectral parameter $\zeta$ will be given later. Then, we can set $\zeta =\zeta _1+\varepsilon ^2$ in (29). Meanwhile, $\psi$ needs to expand through Taylor series around $\varepsilon =0$, and the following expressions can be obtained:

$$\begin{aligned} \psi (\varepsilon ^2)= & {} \sum \limits _{\vartheta =0}^{\infty }\psi ^{(\vartheta )}\varepsilon ^{2\vartheta }\nonumber \\= & {} \psi ^{(0)}+\psi ^{(1)}\varepsilon ^{2}+ \psi ^{(2)}\varepsilon ^{4}+\psi ^{(3)}\varepsilon ^{6}+\cdots , \end{aligned}$$

(30)

where $\psi ^{(\vartheta )}=(\psi _1^{(\vartheta )},\ \psi _2^{(\vartheta )})^{\textrm{T}}$ $(\vartheta =0, 1, 2, \ldots )$ can be uniquely obtained through (16) and (29).

In order to acquire the higher-order lump solutions of system (4) by means of symbolic computation, let $M=-\tfrac{k}{2}\pm c\text {i}$ and consider the following two expansion types:

Type I: Take $C_1=-C_2=\tfrac{1}{\varepsilon },\ c=k=1,\ \zeta = \zeta _1+ \varepsilon ^2$ with $\zeta _1=M$ and use Taylor series expansion at $\varepsilon =0$ for (29). Subsequently, the vectors $\psi ^{(\vartheta )}=(\psi _1^{(\vartheta )},\psi _2^{(\vartheta )})^{\textrm{T}}$ can be obtained, which are polynomials containing $x,\ y,\ t$, and then the lump solutions of system (4) can be acquired. Under this expansion type, the related expansion of (29) are as follows:

$$\begin{aligned} \psi _1^{(0)}&=(-2+2\text {i})[(3+\text {i})t-\text {i}y-x-\text {i}d_0-e_0]\nonumber \\ {}&\quad \times \textrm{e}^{\tfrac{\text {i}}{2}(x+y+t)},\nonumber \\ \psi _2^{(0)}&=(2-2\text {i})[(3+\text {i})t-\text {i}y-x-\text {i}d_0-e_0+1]\nonumber \\ {}&\quad \times \textrm{e}^{-\tfrac{\text {i}}{2}(x+y+t)},\nonumber \\ \psi _1^{(1)}&=\bigg \{\bigg (-\dfrac{16}{3}+\dfrac{88}{3}\text {i}\bigg )t^3-4[(1+7\text {i})x+(\text {i}-7)y\nonumber \\&\quad +(\text {i}-7)d_0+(1+7\text {i})e_0]t^2 -8\bigg \{\bigg (-\dfrac{1}{2}-\text {i}\bigg )x^2\nonumber \\&\quad +[(2-\text {i})y-(1+2\text {i})e_0+(2-\text {i})d_0]x \nonumber \\&\quad +\bigg (\dfrac{1}{2}+\text {i}\bigg )y^2+[(2-\text {i})e_0+(1+2\text {i})d_0]y\nonumber \\&\quad -\bigg (\dfrac{1}{2}+\text {i}\bigg )e_0^2+(2-\text {i})d_0e_0\nonumber \\&\quad -\dfrac{5}{8}-\dfrac{3}{4}\text {i}+\bigg (\dfrac{1}{2}+\text {i}\bigg )d_0^2\bigg \}t\nonumber \\&\quad -\dfrac{2}{3}(1-\text {i})d_0^3+(2-2\text {i})(\text {i}e_0+\text {i}x-y)d_0^2\nonumber \\&\quad +\dfrac{1}{2}(1-\text {i})[8\text {i}e_0y+8\text {i}xy+4e_0^2+8xe_0\nonumber \\&\quad +4x^2-4y^2+1]d_0-\dfrac{2}{3}(1+\text {i})e_0^3\nonumber \\&\quad -2(1-\text {i})(\text {i}x-y)e_0^2-2\bigg [(1+\text {i})x^2\nonumber \\&\quad -2(1-\text {i})yx-(1+\text {i})\bigg (y+\dfrac{1}{2}\bigg )\left( y-\dfrac{1}{2}\right) \bigg ]e_0\nonumber \\&\quad +\dfrac{1}{6} (1-\text {i})(-4\text {i}x^3+12\text {i}xy^2+12 x^2y \nonumber \\&\quad -4y^3-3\text {i}x+12\text {i}d_1+3y+12e_1)\bigg \}\textrm{e}^{\tfrac{\text {i}}{2}(x+y+t)},\nonumber \\ \psi _2^{(1)}&=\bigg \{\bigg (\dfrac{16}{3}-\dfrac{88}{3}\text {i}\bigg )t^3+4[(1+7\text {i})x\nonumber \\&\quad +(\text {i}-7)y+(\text {i}-7)d_0+(1+7\text {i})e_0-1-7\text {i}]t^2\nonumber \\&\quad +8\bigg \{\bigg (\dfrac{1}{2}+\text {i}\bigg )d_0^2+[(2-\text {i})e_0+(2-\text {i})x-2\nonumber \\&\quad +\text {i}+(1+2\text {i})y]d_0-\bigg (\dfrac{1}{2}+\text {i}\bigg )e_0^2\nonumber \\ {}&\quad +[(-1-2\text {i})x+1+2\text {i}+(2-\text {i})y]e_0\nonumber \\&\quad -\bigg (\dfrac{1}{2}+\text {i}\bigg )x^2+[1+2\text {i}+(2-\text {i})y]x \nonumber \\&\quad -\dfrac{9}{8}-\dfrac{7}{4}\text {i}+\bigg (\dfrac{1}{2}+\text {i}\bigg )y^2+(-2+\text {i})y\bigg \}t\nonumber \\&\quad +\dfrac{2}{3}(1-\text {i})d_0^3-2(1-\text {i})(\text {i}e_0+\text {i}x-\text {i}-y)d_0^2\nonumber \\&\quad -4(1-\text {i})\bigg [\dfrac{1}{2}e_0^2+(\text {i}y+x-1)e_0 -\dfrac{1}{2}y^2\nonumber \\&\quad +(\text {i}x-\text {i})y+\dfrac{1}{2}x^2-x+\dfrac{5}{8}\bigg ]d_0+\dfrac{2}{3}(1+\text {i})e_0^3\nonumber \\&\quad +(2-2\text {i})(\text {i}x-\text {i}-y)e_0^2+2\bigg \{(-1-\text {i})y^2\nonumber \\&\quad +\left[ 2-2\text {i}+(-2+2\text {i})x\right] y+\dfrac{5}{4}+\dfrac{5}{4}\text {i}\nonumber \\&\quad +(1+\text {i})x^2-(2+2\text {i})x\bigg \}e_0+\dfrac{2}{3}(1+\text {i})x^3\nonumber \\&\quad +(-2+2\text {i})(\text {i}+y)x^2+(-2+2\text {i})x\bigg (\text {i}y^2-\dfrac{5}{4}\text {i}\nonumber \\&\quad -2y\bigg )-\dfrac{1}{6}(1-\text {i})(-12\text {i}y^2-4y^3+12\text {i}d_1\nonumber \\&\quad +3\text {i}+15y+12e_1)\bigg \}\textrm{e}^{-\dfrac{\text {i}}{2}(x+y+t)}. \end{aligned}$$

(31)

Type II: Take $C_1=-C_2=c=k=1,\ \zeta = \zeta _1+\varepsilon ^2$ with $\zeta _1\ne M$ (e.g., $\zeta _1=M+1)$ and adopt Taylor series expansion at $\varepsilon =0$ for (29).

If we choose Type-II, we will get periodic wave (PW) solutions. However, this is not our main objective. In this paper, we only choose $M=-\tfrac{k}{2}+c\text {i}$ and mainly consider three cases: $N=1,\ 2,\ 3$ based on Type I. To facilitate the calculation, we only consider parameters $c=k=m=\mu =1$.

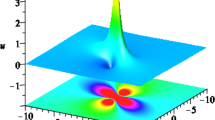
5.1 First-order lump solutions and maximal peak amplitude

When $N=1$, in terms of transformation (15), from the seed solutions (5) and combining with the generalised (1, 0)-fold DT, we can acquire the following two expressions:

$$\begin{aligned} \begin{array}{ll} \tilde{q}_1=\textrm{e}^{\text {i}(x+y+t)}+2\text {i}B^{(0)},\ \ \tilde{f}_1=-1-2\text {i}A^{(0)}_y,\ \ \end{array} \end{aligned}$$

(32)

in which

$$\begin{aligned}A^{(0)}=\dfrac{\Delta A^{(0)}}{\Delta _1},\ B^{(0)}=\dfrac{\Delta B^{(0)}}{\Delta _1}, \end{aligned}$$

where

$$\begin{aligned} \begin{array}{llll} \Delta _{1}=\left| \begin{array}{cc} \psi _1^{(0)} &{} \psi _2^{(0)} \\ \psi _2^{(0)^*} &{} -\psi _1^{(0)^*} \end{array}\right| ,\\ \Delta A^{(0)}=\left| \begin{array}{cc} -\zeta _1\psi _1^{(0)} &{} \psi _2^{(0)} \\ -\zeta _1^*\psi _2^{(0)^*} &{} -\psi _1^{(0)^*} \end{array}\right| ,\\ \Delta B^{(0)}=\left| \begin{array}{cc} \psi _1^{(0)} &{} -\zeta _1\psi _1^{(0)} \\ \psi _2^{(0)^*} &{} -\zeta _1^*\psi _2^{(0)^*} \end{array}\right| .\ \end{array} \end{aligned}$$

By using Type I, from (31) and (32), we get first-order lump solutions of system (4) and rewrite solutions (32) as

$$\begin{aligned} \begin{array}{cc} \tilde{q}_1=\bigg (\dfrac{\daleth _1}{\daleth _2}+1\bigg )\textrm{e}^{\text {i}(x+y+t)},\ \ \tilde{f}_1=\dfrac{\daleth _3}{\daleth _2^2}-1, \end{array} \end{aligned}$$

(33)

where

$$\begin{aligned} \begin{array}{ll} \daleth _1=8\text {i}(y+d_0-t)-8\bigg (x+e_0-3t-\dfrac{1}{2}\bigg )^2\\ \qquad \,\,\,-8(y+d_0-t)^2+2, \vspace{0.05in}\\ \daleth _2=4\bigg (x+e_0-3t-\dfrac{1}{2}\bigg )^2+4(y+d_0-t)^2+1, \vspace{0.05in}\\ \daleth _3=64(y+d_0-t)\bigg (x+e_0-3t-\dfrac{1}{2}\bigg ). \end{array} \end{aligned}$$

From this expression, we can see that there are two parameters $e_0$ and $d_0$, which can change the position of the first-order lump. In figure 8, we exhibit relevant structures of q and f, from which we can clearly see the structures of first-order lump q and f. They have single peak and double troughs, double peaks and double troughs, respectively. The position coordinate, maximal peak amplitude of first-order lump are listed in table 4, and t is an arbitrary time. In figures 8(a1)–8(a3) and 8(b1)–(b3), when the parameters $e_0=d_0=0$, we show the propagation process at different time, and clearly observe their propagation characteristics, which will not be described here. In figures 8(a4) and 8(b4), when time $t=0$, we show the structures with parameters $e_0=d_0=3$, and find that the parameters can control the position.

Table 4 Coordinate and maximal peak amplitude for lump solutions (33).

5.2 Second-order lump solutions and large-parameter asymptotic analysis

When $N=2$, in terms of transformation (15), from seed solution (5) and adopting the generalised (1, 1)-fold DT, we can acquire the following two expressions:

$$\begin{aligned} \begin{array}{ll} \tilde{q}_2=\textrm{e}^{\text {i}(x+y+t)}+2\text {i}B^{(1)},\ \ \tilde{f}_2=-1-2\text {i}A^{(1)}_y,\ \ \end{array} \end{aligned}$$

(34)

in which

$$\begin{aligned}A^{(1)}=\dfrac{\Delta A^{(1)}}{\Delta _2},\ B^{(1)}=\dfrac{\Delta B^{(1)}}{\Delta _2},\end{aligned}$$

where

$$\begin{aligned} \begin{array}{llll} \Delta _{2}=\left| \begin{array}{cccc} \zeta _1\psi _1^{(0)} &{} \psi _1^{(0)} &{} \zeta _1\psi _2^{(0)} &{}\psi _2^{(0)}\\ \zeta _1^*\psi _2^{(0)^*} &{} \psi _2^{(0)^*} &{} -\zeta _1^*\psi _1^{(0)^*} &{} -\psi _1^{(0)^*} \\ \zeta _{1}\psi _1^{(1)}+\psi _1^{(0)} &{} \psi _1^{(1)} &{} \zeta _1\psi _2^{(1)}+\psi _2^{(0)} &{} \psi _2^{(1)} \\ \zeta _1^*\psi _2^{(1)^*}+\psi _2^{(0)^*} &{} \psi _2^{(1)^*} &{} -\zeta _1^*\psi _1^{(1)^*}-\psi _1^{(0)^*} &{} -\psi _1^{(1)^*} \end{array}\right| .\ \end{array} \end{aligned}$$

$\Delta A^{(1)}$ and $\Delta B^{(1)}$ can be obtained by determinant $\Delta _2$ replacing its first and third columns by the vector $(-\zeta _1^2\psi _1^{(0)},\ -\zeta _1^{2*}\psi _2^{(0)^*},\ -\zeta _1^2\psi _1^{(1)}-2\zeta _1\psi _1^{(0)},\ -\zeta _1^{2*}\psi _2^{(1)^*}-2\zeta _1^*\psi _2^{(0)^*})^{\textrm{T}}$.

Because the second-order lump solutions are very complex, we will not give its specific form here. From (34), by using Type I, the second-order lump solutions can be acquired for system (4). According to (29), its solutions will contain four arbitrary parameters $e_j,\ d_j\ (j=0,1)$, which control the position and split shape. As shown in figure 9, we can not only observe the propagation characteristics of the second-order lump at different times and strong interaction, but also clearly see that it splits into triangles.

However, as the parameters $e_1,\ d_1$ increase, we find that the first-order lumps after splitting are very similar in shape. Large-parameter asymptotic is an extremely effective method to explore whether the first-order lumps after splitting are the same when the parameters $e_1$ and $d_1$ tend to infinity  [32]. Thus, we have the following large-parameter asymptotic analysis:

(i) Large-parameter asymptotic analysis about $d_1$ is as follows:

For solution $\tilde{q}_2$ in (34), we take

$$\begin{aligned} \begin{array}{ll} t=e_0=e_1=d_0=0,\ \ \\ d_1=\tau _1d^3+\tau _2d^2+\tau _3d +\tau _4,\ \\ \tau _i \in \mathbb {R},\ i=1,2,3,4, \end{array} \end{aligned}$$

where d is the new control parameter we introduce. For $\tilde{q}_2$, under the first transformations $x=X+ad$ and $y=Y+bd\ (a,b \in \mathbb {R})$, we can obtain the following governing polynomial:

$$\begin{aligned}{} & {} \mathcal {F}_1(a,b)=16a^6+48a^4b^2+48a^2b^4+16b^6\nonumber \\{} & {} \qquad \quad \qquad \quad +48a^3\tau _1-144ab^2\tau _1+36\tau _1^2. \end{aligned}$$

(35)

The roots of the governing polynomial (35) are related to the central positions of the separated first-order lump. So we define these roots as the central point of the corresponding first-order lump. Therefore, we can control the central positions of the separated first-order lump by adjusting central point (a, b) and $\tau _1$. Equation (35) is a polynomial of degree 6, which allows three double roots to exist. However, these central points are arbitrary, but we find that the limits at any central points are the same when d tends to infinity. In order to study the properties of the separated first-order lump at infinity, we will give the three specific double roots and analyse the asymptotic behaviour of the separated first-order lump as follows:

When $\tau _1=-18$, for governing polynomial (35), we can get three sets of values for $a,\ b$. Let central points $(a,b)=(a_j,b_j)\ (j=1,2,3)$. We get

$$\begin{aligned}(a_1,b_1)=(3,0), \quad (a_2,b_2)=\bigg (-\dfrac{3}{2},\dfrac{3\sqrt{3}}{2}\bigg )\end{aligned}$$

and

$$\begin{aligned}(a_3,b_3)=\bigg (-\dfrac{3}{2},-\dfrac{3\sqrt{3}}{2}\bigg ),\end{aligned}$$

respectively. For $(a_1,b_1)$, we take

$$\begin{aligned}X=\hat{X}-\frac{\tau _2-9}{18}\quad \textrm{and}\quad Y=\hat{Y}.\end{aligned}$$

For $(a_2,b_2)$, we take

$$\begin{aligned}X=\hat{X}-\dfrac{-\tau _2-18}{36}\quad \textrm{and} \quad Y=\hat{Y}-\frac{\sqrt{3}\tau _2}{36}.\end{aligned}$$

For $(a_3,b_3)$, we take

$$\begin{aligned}X=\hat{X}-\frac{\tau _2+18}{-36}\quad \textrm{and} \quad Y=\hat{Y}-\frac{\sqrt{3}\tau _2}{-36}.\end{aligned}$$

Parameter $\tau _2$ can adjust the central point of the lump slightly and its role will be shown later. In terms of (5) and (34), we have the following asymptotic limit expression for the three double roots:

$$\begin{aligned} \begin{array}{ll} \lim \limits _{d \rightarrow \infty }\left( \dfrac{\tilde{q}_2-q_0}{\textrm{e}^{\text {i}(x+y)}}\right) =\dfrac{-8\text {i}\hat{Y}-4}{4\hat{X}^2+4\hat{Y}^2+1}. \end{array} \end{aligned}$$

(36)

When $\tau _1=18$, for governing polynomial (35), we can also get three sets of values for $a,\ b$. Then, we can get

$$\begin{aligned}(a_1,b_1)=(-3,0)\quad \textrm{or} \quad (a_2,b_2)=\bigg (\frac{3}{2},\frac{3\sqrt{3}}{2}\bigg )\end{aligned}$$

or

$$\begin{aligned}(a_3,b_3)=\bigg (\frac{3}{2},-\frac{3\sqrt{3}}{2}\bigg ),\end{aligned}$$

respectively. For $(a_1,b_1)$, we take

$$\begin{aligned}X=\hat{X}-\frac{\tau _2-9}{18}\quad \textrm{and} \quad Y=\hat{Y}. \end{aligned}$$

For $(a_2,b_2)$, we take

$$\begin{aligned}X=\hat{X}-\frac{\tau _2+18}{-36}\quad \textrm{and} \quad Y=\hat{Y}-\frac{\sqrt{3}\tau _2}{-36}.\end{aligned}$$

For $(a_3,b_3)$, we take

$$\begin{aligned}X=\hat{X}-\frac{-\tau _2-18}{36}\quad \textrm{and} \quad Y=\hat{Y}-\frac{\sqrt{3}\tau _2}{36}.\end{aligned}$$

In terms of (5) and (34), we have the following asymptotic limit expression for the three double roots:

$$\begin{aligned} \begin{array}{ll} \lim \limits _{d \rightarrow \infty }\left( \dfrac{\tilde{q}_2-q_0}{\textrm{e}^{\text {i}(x+y)}}\right) =\dfrac{-8\text {i}\hat{Y}-4}{4\hat{X}^2+4\hat{Y}^2+1}. \end{array} \end{aligned}$$

(37)

(ii) Large-parameter asymptotic analysis about $e_1$ is as follows:

For solution $\tilde{q}_2$ in (34), we take

$$\begin{aligned} \begin{array}{ll} t=e_0=d_0=d_1=0,\ \ \\ e_1=\tau _{5}d^3+\tau _{6}d^2 +\tau _{7}d+\tau _{8},\ \ \\ (\tau _\varrho \in \mathbb {R},\ \varrho =5,6,7,8), \end{array} \end{aligned}$$

where d is the new control parameter introduced by us. For $\tilde{q}_2$, under the first transformations $x=X+ad$ and $y=Y+bd\ (a,b \in \mathbb {R})$, we obtain the following governing polynomial:

$$\begin{aligned}{} & {} \mathcal {F}_2(a,b)=16a^6+48a^4b^2+48a^2b^4+16b^6\nonumber \\{} & {} \qquad \quad \qquad \quad +48b^3\tau _{5}-144a^2b\tau _{5}+36\tau _{5}^2. \end{aligned}$$

(38)

When $\tau _{5}=-18$, for governing polynomial (38), we get three sets of values for $a,\ b$. Let $(a,b)=(a_j,b_j)\ (j=1, 2, 3)$, we get

$$\begin{aligned}(a_1,b_1)= & {} (0,3) \quad \text {or}\quad (a_2,b_2)\\ {}= & {} \bigg (\dfrac{3\sqrt{3}}{2},-\dfrac{3}{2}\bigg )\quad \textrm{or} \quad (a_3,b_3)\\ {}= & {} \bigg (-\dfrac{3\sqrt{3}}{2},-\dfrac{3}{2}\bigg ),\end{aligned}$$

respectively. For $(a_1,b_1)$, we take

$$\begin{aligned}X=\hat{X}+\dfrac{1}{2}\quad \textrm{and} \quad Y=\hat{Y}-\dfrac{\tau _{6}}{18}.\end{aligned}$$

For $(a_2,b_2)$, we take

$$\begin{aligned}X=\hat{X}-\bigg (\dfrac{\sqrt{3}\tau _{6}}{36}-\dfrac{1}{2}\bigg )\quad \textrm{and} \quad Y=\hat{Y}+\dfrac{\tau _{6}}{36}.\end{aligned}$$

For $(a_3,b_3)$, we take

$$\begin{aligned}X=\hat{X}+\bigg (\dfrac{\sqrt{3}\tau _{6}}{36}+\dfrac{1}{2}\bigg )\quad \textrm{and} \quad Y=\hat{Y}+\dfrac{\tau _{6}}{36}.\end{aligned}$$

$\tau _{6}$ has the same effect as $\tau _2$. In terms of (5) and (34), we have the following asymptotic limit expression for the three double roots:

$$\begin{aligned} \begin{array}{ll} \lim \limits _{d \rightarrow \infty }\left( \dfrac{\tilde{q}_2-q_0}{\textrm{e}^{\text {i}(x+y)}}\right) =\dfrac{-8\text {i}\hat{Y}-4}{4\hat{X}^2+4\hat{Y}^2+1}. \end{array} \end{aligned}$$

(39)

When $\tau _{5}=18$, for governing polynomial (38), we also get three sets of values for $a,\ b$. Then, we get

$$\begin{aligned}(a_1,b_1)=(0,-3)\quad \textrm{or} \quad (a_2,b_2)=\bigg (\dfrac{3\sqrt{3}}{2},\dfrac{3}{2}\bigg )\end{aligned}$$

or

$$\begin{aligned}(a_3,b_3)=\bigg (-\dfrac{3\sqrt{3}}{2},\dfrac{3}{2}\bigg ),\end{aligned}$$

respectively. For $(a_1,b_1)$, we take

$$\begin{aligned}X=\hat{X}+\dfrac{1}{2}\quad \textrm{and} \quad Y=\hat{Y}-\dfrac{\tau _{6}}{18}.\end{aligned}$$

For $(a_2,b_2)$, we take

$$\begin{aligned}X=\hat{X}+\bigg (\dfrac{\sqrt{3}\tau _{6}}{36}+\dfrac{1}{2}\bigg )\quad \textrm{and} \quad Y=\hat{Y}+\dfrac{\tau _{6}}{36}.\end{aligned}$$

For $(a_3,b_3)$, we take

$$\begin{aligned}X=\hat{X}-\bigg (\dfrac{\sqrt{3}\tau _{6}}{36}-\dfrac{1}{2}\bigg )\quad \textrm{and} \quad Y=\hat{Y}+\dfrac{\tau _{6}}{36}.\end{aligned}$$

In terms of (5) and (34), we have the following asymptotic limit expression for the three double roots:

$$\begin{aligned} \begin{array}{ll} \lim \limits _{d \rightarrow \infty }\left( \dfrac{\tilde{q}_2-q_0}{\textrm{e}^{\text {i}(x+y)}}\right) =\dfrac{-8\text {i}\hat{Y}-4}{4\hat{X}^2+4\hat{Y}^2+1}. \end{array} \end{aligned}$$

(40)

By this analysis, based on the specific double roots, when $\tau _2=0$ or $\tau _{6}=0$, we can find that the specific central point of the separated first-order lump is $(ad+\frac{1}{2},bd)$. According to (36), (37), (39) and (40), we can find that the shape and properties of the separated first-order lump are identical when d tends to infinity for $\tilde{q}_2$ in (34). In order to observe the properties of these separated first-order lump more intuitively for $\tilde{q}_2$ in (34), we show the relevant images under the specific parameter d in figures 10(a1)–10(a5). For example, in figures 10(a1) and 10(a5), we can fix the central point of the lump on $y=\tfrac{1}{2}$ at $(\tfrac{1}{2},10)$ and $(\tfrac{1}{2},-30)$, respectively by adjusting slightly. In figures 10(a2) and 10(a4), we can fix the central point of the lump on the x-axis at (15, 0) and $(-15,0)$ by adjusting slightly. Concurrently, we can clearly find that the lumps are symmetric about $y=\tfrac{1}{2}$ in figures 10(a1) and 10(a5), while the lumps are symmetric about the x-axis in figures 10(a2) and 10(a4). In figure 10(a3), we show the strong interaction structure and fix the central point at $(\tfrac{1}{2},0)$. We also notice that the shape and size of these lumps are identical with the increase in d in figure 10. Certainly, we can also obtain the expression of the asymptotic limit of the separated first-order lump by the above analysis for $\tilde{f}_2$. We will not describe it again due to space constraints.

Fig. 8

Surface (top) and density (bottom) plots for the first-order lump solutions (32) with different control parameters and time: (a1)–(a3) and (b1)–(b3) $e_0=d_0=0$, (a4) and (b4) with $e_0=d_0=3$.

Fig. 9

Surface (top) and density (bottom) plots for the second-order lump solutions (34) with different control parameters and time: (a1), (b1), (a3), (b3) $e_j=d_j=0\ (j=0,1)$ except $e_1=100$; (a2), (b2) $e_j=d_j=0$; (a4), (b4) $e_j=d_j=0\ (j=0,1)$ except $d_1=100$.

Fig. 10

Density plots for the second-order lump solution q via (34) based on different large-parameters $e_1,\ d_1$ when $t=0$. (a1) $\tau _{5}=-18,\ \tau _{6}=\tau _{7}=\tau _{8}=0,\ d=\tfrac{10}{3}$, (a2) $\tau _1=-18,\ \tau _2=\tau _3=\tau _4=0,\ d=\tfrac{29}{6}$, (a3) $d=0$, (a4) $\tau _1=18,\ \tau _2=\tau _3=\tau _4=0,\ d=\tfrac{31}{6}$ and (a5) $\tau _{5}=18,\ \tau _{6}=\tau _{7}=\tau _{8}=0,\ d=10$.

5.3 Third-order lump solutions and large-parameter asymptotic analysis

When $N=3$, from transformation (15) and plane-wave seed solutions (5) and combining with the generalised (1, 2)-fold DT, we can acquire the third-order lump solutions

$$\begin{aligned} \begin{array}{ll} \tilde{q}_3=\textrm{e}^{\text {i}(x+y+t)}+2\text {i}B^{(2)},\ \ \tilde{f}_3=-1-2\text {i}A^{(2)}_y,\ \ \end{array} \end{aligned}$$

(41)

in which

$$\begin{aligned}A^{(2)}=\dfrac{\Delta A^{(2)}}{\Delta _3},\ B^{(2)}=\dfrac{\Delta B^{(2)}}{\Delta _3},\end{aligned}$$

where

$$\begin{aligned} \begin{array}{llll} \Delta _{3}=\left| \begin{array}{cccccc} \zeta _1^2\psi _1^{(0)} &{} \zeta _1\psi _1^{(0)} &{} \psi _1^{(0)} &{} \zeta _1^2\psi _2^{(0)} &{} \zeta _1\psi _2^{(0)} &{} \psi _2^{(0)} \\ \zeta _1^{2^*}\psi _2^{(0)^*} &{} \zeta _1^*\psi _2^{(0)^*} &{} \psi _2^{(0)^*} &{} -\zeta _1^{2^*}\psi _1^{(0)^*} &{} -\zeta _1^*\psi _1^{(0)^*} &{} -\psi _1^{(0)^*} \\ \zeta _1^2\psi _1^{(1)}+2\zeta _1\psi _1^{(0)} &{} \zeta _{1}\psi _1^{(1)}+\psi _1^{(0)} &{} \psi _1^{(1)} &{} \zeta _1^2\psi _2^{(1)}+2\zeta _1\psi _2^{(0)} &{} \zeta _1\psi _2^{(1)}+\psi _2^{(0)} &{} \psi _2^{(1)} \\ \zeta _1^{2^*}\psi _2^{(1)^*}+2\zeta _1^*\psi _2^{(0)^*} &{} \zeta _1^*\psi _2^{(1)^*}+\psi _2^{(0)^*} &{} \psi _2^{(1)^*} &{} -\zeta _1^{2^*}\psi _1^{(1)^*}-2\zeta _1^*\psi _1^{(0)^*} &{} -\zeta _1^*\psi _1^{(1)^*}-\psi _1^{(0)^*} &{} -\psi _1^{(1)^*} \\ \zeta _1^2\psi _1^{(2)}+2\zeta _1\psi _1^{(1)}+\psi _1^{(0)} &{} \zeta _1\psi _1^{(2)}+\psi _1^{(1)} &{} \psi _1^{(2)} &{} \zeta _1^2\psi _2^{(2)}+2\zeta _1\psi _2^{(1)}+\psi _2^{(0)} &{} \zeta _1\psi _2^{(2)}+\psi _2^{(1)} &{} \psi _2^{(2)} \\ \zeta _1^{2^*}\psi _2^{(2)^*}+2\zeta _1^*\psi _2^{(1)^*}+\psi _2^{(0)^*} &{} \zeta _1^*\psi _2^{(2)^*}+\psi _2^{(1)^*} &{} \psi _2^{(2)^*} &{} \zeta _1^{2^*}\psi _1^{(2)^*}+2\zeta _1^*\psi _1^{(1)^*}+\psi _1^{(0)^*} &{} \zeta _1^*\psi _1^{(2)^*}+\psi _1^{(1)^*} &{} \psi _1^{(2)^*} \end{array}\right| .\ \end{array} \end{aligned}$$

$\Delta A^{(2)}$ and $\Delta B^{(2)}$ can be obtained by the determinant $\Delta _3$ replacing its first and fourth columns by the vector $(-\zeta _1^3\psi _1^{(0)},\ -\zeta _1^{3^*}\psi _2^{(0)^*},\ -\zeta _1^3\psi _1^{(1)}-3\zeta _1^2\psi _1^{(0)},\ -\zeta _1^{3^*}\psi _2^{(1)^*}-3\zeta _1^{2^*}\psi _2^{(0)^*},\ -\zeta _1^3\psi _1^{(2)}-3\zeta _1^2\psi _1^{(1)}-3\zeta _1\psi _1^{(0)},\ -\zeta _1^{3^*}\psi _2^{(2)^*}-3\zeta _1^{2^*}\psi _2^{(1)^*}-3\zeta _1^*\psi _2^{(0)^*})^{\textrm{T}}$.

By using Type I, in terms of (41), it is easy for us to obtain the third-order lump solutions for system (4). According to (29), its solutions will contain six arbitrary parameters $e_j,\ d_j\ (j=0,1,2)$, which control the position and split shape. As shown in figure 11, we can clearly see the propagation, strong interaction and arrangement shape of the third-order lump with different parameters at different time.

We know that $e_0$ and $d_0$ can control the position change of the third-order lump, $e_1$ and $d_1$ can control splitting and arrange into triangles, $e_2$ and $d_2$ can control splitting and arrange into pentagons. Next, we will only conduct large-parameter asymptotic analysis for $e_2$ and $d_2$ to explain the shape and properties of the separated first-order lump when d tends to infinity.

(i) Large-parameter asymptotic analysis about $e_2$ is as follows:

For solution $\tilde{q}_3$ in (41), we take

$$\begin{aligned} \begin{array}{ll} t=e_0=e_1=d_0=d_1=d_2=0,\ \\ e_2=\tau _1d^5+\tau _2d^4+\tau _3d^3+\tau _4d^2+\tau _5d+\tau _6\ \\ (\tau _i \in \mathbb {R},\ i=1,2,3,4,5,6), \end{array} \end{aligned}$$

where d is the new control parameter introduced by us. For $\tilde{q}_3$, under the first transformations $x=X+ad$ and $y=Y+bd\ (a,b \in \mathbb {R})$, we obtain the following governing polynomial:

$$\begin{aligned} \mathcal {F}_3(a,b)&=32(a^2+b^2)(16a^{10}+80a^8b^2\nonumber \\ {}&+160a^6b^4+160a^4b^6+80a^2b^8\nonumber \\ {}&+16b^{10} -360a^5\tau _1+3600a^3b^2\tau _1\nonumber \\ {}&-1800ab^4\tau _1+2025\tau _1^2). \end{aligned}$$

(42)

Equation (42) is a polynomial of degree 12, which allows the existence of six double roots. Similarly, in terms of the correlation analysis of second-order lump, we define these roots as the central point of the corresponding lump. However, these central points are also arbitrary, but we find that the limits at any central points are the same when d tends to infinity. In order to study the properties of the separated first-order lump at infinity, we will give five specific double roots and analyse the asymptotic behaviour of the separated first-order lump as follows:

When $\tau _1=\tfrac{4}{45}$, for governing polynomial (42), we get five sets of values for $a,\ b$. Let central points $(a,b)=(a_j,b_j)\ (j=1,2,3,4,5,6)$. We get

$$\begin{aligned} (a_1,b_1)= & {} (0,0), \quad (a_2,b_2)=(1,0),\\ (a_3,b_3)= & {} \bigg (\frac{\sqrt{5}}{5+\sqrt{5}},\frac{\sqrt{5}\sqrt{2\sqrt{5}+5}}{5+\sqrt{5}}\bigg ),\\ (a_4,b_4)= & {} \bigg (\frac{\sqrt{5}}{5+\sqrt{5}},-\frac{\sqrt{5}\sqrt{2\sqrt{5}+5}}{5+\sqrt{5}}\bigg ),\\ (a_5,b_5)= & {} \bigg (\frac{\sqrt{5}}{\sqrt{5}-5},\frac{\sqrt{-10\sqrt{5}+25}}{\sqrt{5}-5}\bigg ) \end{aligned}$$

and

$$\begin{aligned}(a_6,b_6)=\bigg (\frac{\sqrt{5}}{\sqrt{5}-5},-\frac{\sqrt{-10\sqrt{5}+25}}{\sqrt{5}-5}\bigg ),\end{aligned}$$

respectively. Because of the complexity of the latter four roots, we only analyse the first and second roots here. For $(a_1,b_1)$, we take $X=\hat{X}+\tfrac{1}{2}$ and $Y=\hat{Y}$ and for $(a_2,b_2)$, we take $X=\hat{X}+(\tfrac{9\tau _2}{4}+\tfrac{1}{2})$ and $Y=\hat{Y}$. In terms of (5) and (41), we have the following asymptotic limit expression for the three double roots:

$$\begin{aligned} \begin{array}{ll} \lim \limits _{d \rightarrow \infty }\left( \dfrac{\tilde{q}_3-q_0}{\textrm{e}^{\text {i}(x+y)}}\right) =\dfrac{8\text {i}\hat{Y}-8\hat{X}^2-8\hat{Y}^2+2}{4\hat{X}^2+4\hat{Y}^2+1}. \end{array} \end{aligned}$$

(43)

(ii) Large-parameter asymptotic analysis about $d_2$ is as follows:

For solution $\tilde{q}_3$ in (41), we take

$$\begin{aligned} \begin{array}{ll} t=e_0=e_1=e_2=d_0=d_1=0,\ \\ d_2=\tau _{7}d^5+\tau _{8}d^4+\tau _{9}d^3+\tau _{10}d^2+\tau _{11}d+\tau _{12}\ \\ (\tau _\varrho \in \mathbb {R},\ \varrho =7,8,9,10,11,12), \end{array} \end{aligned}$$

where d is the new control parameter introduced by us. For $\tilde{q}_3$, under the first transformations $x=X+ad$ and $y=Y+bd\ (a,b \in \mathbb {R})$, we obtain the following governing polynomial:

$$\begin{aligned} \mathcal {F}_4(a,b)&=32(a^2+b^2)(16a^{10}+80a^8b^2+160a^6b^4\nonumber \\ {}&\quad + 160a^4b^6+80a^2b^8+16b^{10} \nonumber \\ {}&\quad -1800a^4b\tau _{7} +3600a^2b^3\tau _{7}\nonumber \\ {}&\quad -360b^5\tau _{7} +2025\tau _{7}^2). \end{aligned}$$

(44)

When $\tau _{7}=\tfrac{4}{45}$, for governing polynomial (42), we get five sets of values for $a,\ b$. Let central points $(a,b)=(a_j,b_j)\ (j=1,2,3,4,5,6)$. We get

$$\begin{aligned} (a_1,b_1)= & {} (0,0),\quad (a_2,b_2)=(0,1),\\ (a_3,b_3)= & {} \Bigg (\frac{\sqrt{5}\sqrt{2\sqrt{5}+5}}{5+\sqrt{5}},\frac{\sqrt{5}}{5+\sqrt{5}}\Bigg ),\\ (a_4,b_4)= & {} \Bigg (-\frac{\sqrt{5}\sqrt{2\sqrt{5}+5}}{5+\sqrt{5}},\frac{\sqrt{5}}{5+\sqrt{5}}\Bigg ),\\ (a_5,b_5)= & {} \Bigg (\frac{\sqrt{-10\sqrt{5}+25}}{\sqrt{5}-5},\frac{\sqrt{5}}{\sqrt{5}-5}\Bigg ) \end{aligned}$$

and

$$\begin{aligned}(a_6,b_6)=\Bigg (-\frac{\sqrt{-10\sqrt{5}+25}}{\sqrt{5}-5},\frac{\sqrt{5}}{\sqrt{5}-5}\Bigg ),\end{aligned}$$

respectively. Because of the complexity of the latter four roots, we only analyse the first and second roots here. For $(a_1,b_1)$, we take $X=\hat{X}+\tfrac{1}{2}$ and $Y=\hat{Y}$ and for $(a_2,b_2)$, we take $X=\hat{X}+\tfrac{1}{2}$ and $Y=\hat{Y}+\tfrac{9\tau _{8}}{4}$. In terms of (5) and (41), we have the following asymptotic limit expression for the three double roots:

$$\begin{aligned} \begin{array}{ll} \lim \limits _{d \rightarrow \infty }\left( \dfrac{\tilde{q}_3-q_0}{\textrm{e}^{\text {i}(x+y)}}\right) =\dfrac{8\text {i}\hat{Y}-8\hat{X}^2-8\hat{Y}^2+2}{4\hat{X}^2+4\hat{Y}^2+1}. \end{array} \end{aligned}$$

(45)

By the above analysis, based on the specific double roots, when parameters $\tau _2=0$ or $\tau _{8}=0$, we can find that the specific central point of the separated first-order lump is $(ad+\frac{1}{2},bd)$. According to (43) and (45), we find that the shape and properties of the separated first-order lump are identical when the parameter d tends to infinity for $\tilde{q}_3$ in (41). In figure 12, the density plots of the separated first-order lump are displayed for $\tilde{q}_3$ in (41). The related symmetry, strong interaction and shape size can be easily observed from these figures, and so we will not describe them again.

Fig. 11

Surface (top) and density (bottom) plots for third-order lump solutions (41) with different control parameters and time: (a1), (b1) $t=e_j=d_j=0\ (j=0,1,2)$; (a2), (b2) $t=1,\ e_j=d_j=0$; (a3), (b3) $t=e_j=d_j=0$ except $e_2=6000$; (a4), (b4) $t=e_j=d_j=0$ except $e_0=4,\ d_0=2,\ d_1=600$.

Fig. 12

Density plots for third-order lump solution q via (41) based on different large parameters $e_2,\ d_2$ when $t=0$ and same control parameter $d=20$ and other parameters $\tau _i=\tau _\varrho =0$ except (a1) $\tau _{7}=\tfrac{4}{45}$, (a2) $\tau _1=\tfrac{4}{45}$, (a4) $\tau _1=-\tfrac{4}{45}$ and (a5) $\tau _{7}=-\tfrac{4}{45}$. All parameters of (a3) are 0.

6 Mixed interaction phenomenon of different localised waves

In this section, for fundamental solution (29), we will use the generalised $(2,N-2)$-fold DT and only adopt two spectral parameters to exhibit the interaction phenomenon of different localised waves for system (4). According to the control parameters $e_0$ and $d_0$, we can regulate the intensity of the interaction. Next, we will only consider two cases: $N=2$ (the generalised (2, 0)-fold DT) and $N=3$ (the generalised (2, 1)-fold DT). To facilitate calculation, we only consider parameters $c=k=m=\mu =1$.

6.1 Application of the generalised (2,0)-fold DT

When $N=2$, we will use the generalised (2, 0)-fold DT and only adopt two spectral parameters $\zeta _1$ and $\zeta _2$. In this application, we know that there are three cases: (i) Using Taylor expansion for two spectral parameters, (ii) using Taylor expansion for only one spectral parameter and (iii) neither spectral parameter uses Taylor expansion.

In Case (i), when using Type I at $\zeta _1$ and Type II at $\zeta _2$, interaction structures of first-order lump and first-order PW will be produced. When using Type II at $\zeta _1$ and $\zeta _2$, interaction structures of two first-order PWs will be produced. In Case (ii), when using Type I at $\zeta _1$ or $\zeta _2$, the interaction structures of one-breather and first-order lump will be generated. In Case (iii), two-breather rather than novel interactions will be produced. In the following, for Case (ii), we only consider the interaction structures between one-breather and first-order lump. Subsequently, we will use Type I at $\zeta _1$ and choose $\zeta _2=2\text {i}$.

Based on the generalised (2, 0)-fold DT and combining with plane-wave seed solutions (5), we can acquire the following two expressions:

$$\begin{aligned} \begin{array}{ll} \tilde{q}=\textrm{e}^{\text {i}(x+y+t)}+2\text {i}B^{(1)},\ \ \tilde{f}=-1-2\text {i}A^{(1)}_y,\ \ \end{array} \end{aligned}$$

(46)

where $A^{(1)}$ and $B^{(1)}$ can be determined by

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\zeta _1)\psi ^{(0)}(\zeta _1)=0,\vspace{0.05in}\\ T(\zeta _2)\psi (\zeta _2)=0, \end{array} \right. \end{aligned}$$

(47)

in which

$$\begin{aligned}A^{(1)}=\frac{\Delta A^{(1)}}{\Delta _2},\;\; B^{(1)}=\frac{\Delta B^{(1)}}{\Delta _2},\end{aligned}$$

where

$$\begin{aligned} \begin{array}{llll} \Delta _{2}=\left| \begin{array}{cccc} \zeta _1\psi _1^{(0)} &{} \psi _1^{(0)} &{} \zeta _1\psi _2^{(0)} &{}\psi _2^{(0)}\\ \zeta _1^*\psi _2^{(0)^*} &{} \psi _2^{(0)^*} &{} -\zeta _1^*\psi _1^{(0)^*} &{} -\psi _1^{(0)^*} \\ \zeta _2\psi _{11} &{} \psi _{11} &{} \zeta _2\psi _{21} &{} \psi _{21} \\ \zeta _2^*\psi _{21}^* &{} \psi _{21}^* &{} -\zeta _2^*\psi _{11}^* &{} -\psi _{11}^* \end{array}\right| .\ \end{array} \end{aligned}$$

$\Delta A^{(1)}$ and $\Delta B^{(1)}$ can be uniquely determined by determinant $\Delta _2$ replacing its first and third columns by the vector $(-\zeta _1^2\psi _1^{(0)},\ -\zeta _1^{2^*}\psi _2^{(0)^*},\ -\zeta _2^2\psi _{11},\ -\zeta _2^{2^*}\psi _{21}^*)^{\textrm{T}}$, where $\psi _{11}=\psi _1|_{\zeta =\zeta _2},\ \psi _{21}=\psi _2|_{\zeta =\zeta _2}$.

By symbolic computation, from solutions (46), we know that there are two parameters $e_0,\ d_0$ in the solutions that control the position. Then, the interaction structures between first-order lump and one-breather will be obtained. To save space, we will no longer show complex analytical solutions here, but we will only show the interaction structures of q as shown in figure 13 based on appropriate parameter combinations. From figure 13, we can clearly see the propagation characteristics and strong interaction of the breather and lump under different parameters at different time.

6.2 Application of the generalised (2,1)-fold DT

When $N=3$, we will use the generalised (2, 1)-fold DT and only adopt two spectral parameters $\zeta _1$ and $\zeta _2$. In this application, we know that there are two cases: (i) Using Taylor expansion for two spectral parameters and (ii) using Taylor expansion for only one spectral parameter.

Fig. 13

Surface (top) and density (bottom) plots of interaction structures between one-breather and first-order lump for q via (47) based on different control parameters: (a1)–(a3) $e_0=d_0=0$; (a4) $e_0=d_0=3$.

Fig. 14

Surface (top) and density (bottom) plots of interaction structures between one-breather and second-order lump for f via (48) based on different control parameters when $t=0.$ (a1) $e_j=d_j=0\ (j=0,1)$; (a2) $e_j=d_j=0$ except $e_1=100$; (a3) $e_j=d_j=0$ except $d_1=100$.

However, this paper will mainly discuss Case (ii). For Case (ii), we obtain the new interaction structures between one-breather and second-order lump. Subsequently, we will use Type I at $\zeta _1$ and choose $\zeta _2=2\text {i}$. Now, from plane-wave seed solutions (5) and combining with the generalised (2, 1)-fold DT, we can acquire the following two expressions:

$$\begin{aligned} \begin{array}{ll} \tilde{q}=\textrm{e}^{\text {i}(x+y+t)}+2\text {i}B^{(2)},\ \ \tilde{f}=-1-2\text {i}A^{(2)}_y,\ \ \end{array} \end{aligned}$$

(48)

where $A^{(2)}$ and $B^{(2)}$ need to be obtained by the following equations:

$$\begin{aligned} \left\{ \begin{array}{ll} T^{(0)}(\zeta _1)\psi ^{(0)}(\zeta _1)=0,\vspace{0.05in}\\ T^{(0)}(\zeta _1)\psi ^{(1)}(\zeta _1)+T^{(1)}(\zeta _1)\psi ^{(0)}(\zeta _1)=0,\vspace{0.05in}\\ T(\zeta _2)\psi (\zeta _2)=0, \end{array} \right. \end{aligned}$$

(49)

in which

$$\begin{aligned}A^{(2)}=\frac{\Delta A^{(2)}}{\Delta _3},\quad B^{(2)}=\frac{\Delta B^{(2)}}{\Delta _3},\end{aligned}$$

where

$$\begin{aligned} \begin{array}{llll} \Delta _{3}=\left| \begin{array}{cccccc} \zeta _1^2\psi _1^{(0)} &{} \zeta _1\psi _1^{(0)} &{} \psi _1^{(0)} &{} \zeta _1^2\psi _2^{(0)} &{} \zeta _1\psi _2^{(0)} &{} \psi _2^{(0)} \\ \zeta _1^2\psi _1^{(1)}+2\zeta _1\psi _1^{(0)} &{} \zeta _{1}\psi _1^{(1)}+\psi _1^{(0)} &{} \psi _1^{(1)} &{} \zeta _1^2\psi _2^{(1)}+2\zeta _1\psi _2^{(0)} &{} \zeta _1\psi _2^{(1)}+\psi _2^{(0)} &{} \psi _2^{(1)} \\ \zeta _1^{2^*}\psi _2^{(0)^*} &{} \zeta _1^*\psi _2^{(0)^*} &{} \psi _2^{(0)^*} &{} -\zeta _1^{2^*}\psi _1^{(0)^*} &{} -\zeta _1^*\psi _1^{(0)^*} &{} -\psi _1^{(0)^*} \\ \zeta _1^{2^*}\psi _2^{(1)^*}+2\zeta _1^*\psi _2^{(0)^*} &{} \zeta _1^*\psi _2^{(1)^*}+\psi _2^{(0)^*} &{} \psi _2^{(1)^*} &{} -\zeta _1^{2^*}\psi _1^{(1)^*}-2\zeta _1^*\psi _1^{(0)^*} &{} -\zeta _1^*\psi _1^{(1)^*}-\psi _1^{(0)^*} &{} -\psi _1^{(1)^*} \\ \zeta _2^2\psi _{11} &{} \zeta _2\psi _{11} &{} \psi _{11} &{} \zeta _2^2\psi _{21} &{} \zeta _2\psi _{21} &{} \psi _{21} \\ \zeta _2^{2^*}\psi _{21}^* &{} \zeta _2^*\psi _{21}^* &{} \psi _{21}^* &{} -\zeta _2^{2^*}\psi _{11}^* &{} -\zeta _2^*\psi _{11}^* &{} -\psi _{11}^* \end{array}\right| .\ \end{array} \end{aligned}$$

$\Delta A^{(2)}$ and $\Delta B^{(2)}$ can be determined by determinant $\Delta _3$ replacing its first and fourth columns through the vector $(-\zeta _1^3\psi _1^{(0)},\ -\zeta _1^3\psi _1^{(1)}-3\zeta _1^2\psi _1^{(0)},\ -\zeta _1^{3^*}\psi _2^{(0)^*},\ -\zeta _1^{3^*}\psi _2^{(1)^*}-3\zeta _1^{2^*}\psi _2^{(0)^*},\ -\zeta _2^3\psi _{11},\ -\zeta _2^{3^*}\psi _{21}^*)^{\textrm{T}}$, where $\psi _{11}=\psi _1|_{\zeta =\zeta _2},\ \psi _{21}=\psi _2|_{\zeta =\zeta _2}$.

By symbolic computation, from solutions (48) and (49), we know that there are four control parameters $e_j, d_j$ $(j=0, 1)$. Then, the interaction structures between one-breather and second-order lump will be acquired. Similarly, we will omit the expression of complex solutions and only show the related structures of f in figure 14.

7 Conclusions

In this paper, we have studied the $(2+1)$-dimensional non-isospectral CD system (4), which may describe many physical phenomena in nonlinear optics, fluids and Bose–Einstein condensates. The main results of this paper are summarised as follows:

• (i) MI, excitation principle and regional distribution of different localised waves were analysed and marked as shown in figure 1.

• (ii) Generalised $(n,N-n)$-fold DT was successfully extended to non-isospectral $(2+1)$-dimensional CD system (4) for the first time.

• (iii) Using the (N, 0)-fold DT, multisoliton solutions were established and relevant structures are shown in figures 2–4. The relevant dynamic characteristics are given using the asymptotic analysis technique in tables 1–3. Meanwhile, we have given the relevant figures of soliton surface (see figures 5–7).

• (iv) Using the generalised $(1,N-1)$-fold DT, higher-order lump solutions based on parametric control were acquired and analysed using the large-parameter asymptotic analysis method, and relevant structures are shown in figures 8–12.

• (v) Using the generalised $(2,N-2)$-fold DT, the mixed interaction structures between the breather and lump were obtained, and relevant structures are shown in figures 13 and 14.

The above results are reported for the first time. We hope that the results in this paper will help to explain some novel physical phenomena.