Two bursting patterns induced by system solutions approaching infinity in a modified Rayleigh–Duffing oscillator

Abstract

In this paper, the mechanism of system solutions approaching infinity is explored based on a modified Rayleigh–Duffing oscillator with two slow-varying periodic excitations. System solutions approaching infinity is a new novel route to bursting oscillation, and are not reported yet. The system can be separated into a fast subsystem and a slow subsystem according to the slow–fast analysis method. We find that there is a critical value for the fast subsystem, which limits the original region of the stable equilibrium point and the stable limit cycle, the right of which is the divergent region. When the control parameter slowly varies closely to the critical value $\delta _{\mathrm{CR}}$, both the stable equilibrium point and the stable limit cycle quickly leave the original region and approach positive infinity. The mechanism of two different bursting forms called bursting oscillation of point/point and bursting oscillation of cycle/cycle induced by system solutions approaching infinity are explored. This paper provides a new possible route to bursting oscillation unrelated to bifurcations and deepens the comprehension of bursting dynamics behaviours. Lastly, the accuracy of our study is verified by overlapping the transformed phase portraits onto the bifurcation diagrams.

1 Introduction

Various nonlinear natural systems are characterised by interactions between dynamical processes that run at quite different time-scales [1,2,3,4,5]. These can often be modelled as slow–fast systems, where system behaviours can be separated into interacting slow and fast changing variables. In the study of slow–fast dynamics, a special mode of oscillation called bursting oscillation, which is often observed in physics, biology, mechanics, chemistry, etc. [6,7,8,9] has attracted widespread attention. Bursting oscillation is a waveform that switches between a relatively large-amplitude oscillation and a nearly harmonic small-amplitude excursion. Normally speaking, if all the state variables behave in the static states stage or the microamplitude vibrations, the system is in quiescent state [10]. If all the state variables exhibit large-amplitude vibrations, we say the system is in a spiking state [11]. Two patterns of bifurcations can be found in bursting dynamics, one leading to the system switching from a quiescent state to a spiking state, and the other leading to the system switching from a spiking state to a quiescent state [12, 13].

Nonlinear systems with slow-varying periodic excitations are special forms of a slow–fast system [14, 15], which can be expressed in the form

$$\begin{aligned} \dot{{x}}=f(x,\mu ,A\cos (\omega t)) \end{aligned}$$

(1.1)

with a magnitude difference between the forcing frequency $\omega$ and the natural frequency $\omega _{N}$. In order to investigate the coupling of the two frequencies, system (1.1) can be rewritten in the form [16, 17]

$$\begin{aligned} \dot{{x}}=f(x,\mu ,\delta ), \hbox {(fast subsystem)} \nonumber \\ \delta =A\cos (\omega t), \hbox {(slow subsystem)} \end{aligned}$$

(1.2)

Fig. 1

Bursting oscillation of point/point (a–c) for $\mu =-0.01$ and bursting oscillation of point/point (d–f) for $\mu =0.5$ with different values of parameter F when $\gamma =1.0$, $\alpha =2.0$, $\beta =1.0$ and $\omega =0.01$. (a) $F=0.001$, (b) $F=0.002$, (c) $F=0.003$, (d) $F=1.0$, (e) $F=1.5$ and (f) $F=2.0$.

Fig. 2

Solutions of eq. (2.2) for $F=10.0$, $\mu =1.0$, $\alpha =2.0$, $\beta =1.0$ and $\omega =0.01$. (a) $\gamma =1.0$ and (b) $\gamma =-1.0$.

in which $\delta$ can be considered as a generalised slow-varying state variable. Then, system (1.2) becomes a generalised autonomous system. Considering $\delta$ as a control parameter, many results related to the effect of different time-scales are obtained. For example, Lakrad and $\hbox {Schiehlen}$ [18] investigated the effects of slow-varying periodic forcing excitation on a shallow arch model, and a novel bursting pattern induced by the bifurcation delay was analysed. Simo and $\hbox {Woafo}$ [19] found that the forcing excitation can affect the dynamical behaviours of the bursting oscillations generated by double-well in Duffing oscillator. Kovacic and $\hbox {Lenci}$ [20] showed that when the system takes a low-valued angular excitation frequency, the response exhibits a form of bursting oscillation, induced by the fast oscillations around the slow flow in a forced damped purely nonlinear oscillator. Zhang et al [21] revealed a novel vibration form called the slow–fast oscillation phenomenon when the frequency of the periodic electrical load is much smaller than the natural frequency of the hydraulic generating system. Ma and Cao [22] presented the bifurcation mechanisms of the periodic and chaotic bursting oscillations induced by delayed pitchfork bifurcation based on the jerk circuit system driven by parametric excitation. Han et al [23] proposed a general method for analysing bursting induced by two slow-changing excitations, and based on this, bursting patterns induced by amplitude $\hbox {modulation}$ [24] and pulse-shaped $\hbox {explosion}$ [25] are discussed. Wang et al [26] explored the mechanism of possible bursting oscillations in the Filippov system.

Fig. 3

Bifurcation diagram of system (2.1) for the fixed parameters $F=0.02$, $\gamma =1.0$, $\alpha =2.0$, $\beta =1.0$ and $\delta =-0.5$. H means Hopf bifurcation, which exhibits at $\mu =0$. Solid red line indicates stable equilibrium branch and red dotted lines indicate the maximum and minimum amplitudes of stable oscillations bifurcated from H.

Fig. 4

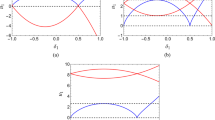
System solutions approaching positive infinity related to stable equilibrium E near $\delta _{\mathrm{CR}} =1/\gamma$. Solid red lines indicate stable equilibrium curves and blue dashed lines indicate critical lines $\delta _{\mathrm{CR}} =1/\gamma$. (a) $\gamma =2$, $\delta _{\mathrm{CR}} =0.5$, (b) $\gamma =1.5$, $\delta _{\mathrm{CR}} =0.66667$, (c) $\gamma =1.2$, $\delta _{\mathrm{CR}} =0.83333$ and (d) $\gamma =1$, $\delta _{\mathrm{CR}} =1.0$.

$\hbox {Izhikevich}$ [27] has given a good conclusion of possible routes to bursting oscillation related to codimension-1 bifurcations in the general smooth systems. However, other approaches that lead to bursting dynamics unrelated to bifurcations still need to be focussed on. For our study, a new dynamic mechanism named ‘system solutions approaching infinity’ resulting in bursting oscillation is revealed, which is independent of bifurcations. For this purpose, we consider a parametrically-driven extended Rayleigh–Duffing oscillator [28] with three-well potential modelled by

$$\begin{aligned}&\ddot{{x}}-\mu (1-\dot{{x}}^{2})\dot{{x}} +(1-\gamma \cos \omega t)(x+\alpha x^{3} +\beta x^{5})\nonumber \\&\quad =F\cos \omega t, \end{aligned}$$

(1.3)

where $\alpha$ and $\beta$ are two positive constant parameters,$\gamma$ is the parametric excitation amplitude, the two cosine functions $\cos \omega t$ are periodic excitations and F is the forcing excitation amplitude. The case considered in this paper is that the natural frequency $\omega _{N}$ of system (1.3) is much greater than the periodic excitation frequency $\omega$, i.e. there is an order of magnitude difference between them. Then, the effect of two time-scales appears. The effective method to solve the slow–fast dynamics is the slow–fast analysis method, which is proposed by $\hbox {Rinzel}$ [29]. According to the slow–fast analysis method, system (1.3) turns into a combination of a slow subsystem and a fast subsystem. The main dynamic behaviour of system (1.3) is determined by the fast subsystem, and the slow subsystem plays a regulatory role in the main dynamic behaviour of the system.

In this paper, two different bursting patterns induced by system solutions approaching infinity are investigated in detail, and are presented in figure 1. We can easily see that the two bursting patterns are related to stable equilibrium point and stable limit cycle, respectively. The rest of this paper is organised as follows. In §2, we summarise some of the results related to stabilities and bifurcations of the fast subsystem by treating the cosine function $\cos \omega t$ as a control parameter. In §3, the mechanism of system solutions approaching infinity related to the stable equilibrium point and the stable limit cycle are explored. In §4, we propose the mechanism of two different bursting forms induced by system solutions approaching infinity. Finally, a brief conclusion is given in §5.

2 Bifurcation analysis

Considering $\cos \omega t$ as a control parameter $\delta$, we obtain a fast subsystem given by

$$\begin{aligned} \left\{ {\begin{array}{l} \dot{{x}}=y \\ \dot{{y}}=F\delta +\mu (1-y^{2})y-(1-\gamma \delta )(x+\alpha x^{3}+\beta x^{5}) \\ \end{array}} \right. \end{aligned}$$

(2.1)

and a slow subsystem by $\dot{{\delta }}=-\omega \sin \omega t$.

E(x, 0) is a generalised form of the equilibrium point of system (2.1), where x depends on the real roots of the algebraic equation

$$\begin{aligned} F\delta -(1-\gamma \delta )(x+\alpha x^{3}+\beta x^{5})=0. \end{aligned}$$

(2.2)

It is easy to see that if the roots of eq. (2.2) exist, $\gamma$ and $\delta$ must satisfy $1-\gamma \delta \ne 0$. However, if the parameters $\gamma$ and $\delta$ satisfy the equation $1-\gamma \delta =0$, i.e.,

$$\begin{aligned} \delta =\frac{1}{\gamma }, \end{aligned}$$

(2.3)

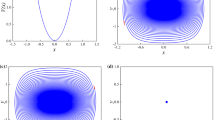
eq. (2.2) has no equilibrium point. And we also find that if $1-\gamma \delta \approx 0$, x approaches positive or negative infinity (see figure 2).

Now, we analyse the bifurcation behaviours of system (2.2) when $1-\gamma \delta \ne 0$. At the equilibrium point E, we linearise system (2.1), and the Jacobian matrix is obtained, which can be expressed as

$$\begin{aligned} J=\left( {\begin{array}{cc} 0&{}1 \\ -(1-\gamma \delta )(1+3\alpha x^{2}+5\beta x^{4})&{}\mu \\ \end{array}} \right) \end{aligned}$$

(2.4)

and the characteristic equation can be written as

$$\begin{aligned} F(\lambda )=\lambda ^{2}-\mu \lambda +(1-\gamma \delta )(1+3\alpha x^{2}+5\beta x^{4})=0.\nonumber \\ \end{aligned}$$

(2.5)

According to the Routh–Hurwitz criterion [30], we can conclude that E is stable for $\mu <0$ and $1-\gamma \delta >0$ and unstable for $\mu >0$. Therefore, at the critical value $\mu =0$, a pair of pure imaginary root of eq. (2.5) may exist, indicating the occurrence of a Hopf bifurcation, which results in the instability of the equilibrium point E and the appearance of a limit cycle with the oscillation frequency $\Omega _{H}^{2} =(1-\gamma \delta )(1+3\alpha x^{2}+5\beta x^{4})$ (shown in figure 3).

3 System solutions approaching infinity

The results of stability and bifurcation behaviours are summed up in §2. On the basis of the results above, we shall reveal the mechanism of transition in this section, which plays a significant part leading to bursting behaviours.

3.1 System solutions approaching infinity related to the stable attractor E

In order to analyse the new novel route of system solutions approaching infinity to bursting oscillations clearly, we fix the parameters as $F=0.02$, $\mu =-0.01$, $\alpha =2$, $\beta =1$ and $\omega =0.01$. In this condition, the system solutions approaching infinity is related to the stable equilibrium point. The equilibrium branch represented by the change of the system solutions with the slow-varying parameter $\delta$ is shown in figure 4. We can see that there are two distinctly different parts of the equilibrium branch with the increase in the control parameter $\delta$, i.e. a flat section on the left part and a steep section on the right part, and most values of $\delta$ are on the flat section. By increasing $\delta$ gradually, system solutions also increase gradually. When $\delta$ approaches the critical value $\delta _{\mathrm{CR}}$, a sudden steep transition of the stable equilibrium point E takes place, i.e. the system solution of the attractor E jumps to the positive infinity quickly from the flat section of the original place. This type of sharp transition is defined as ‘system solutions of stable equilibrium point attractor approaching infinity’.

Fig. 5

Numerical simulation of the relationship of critical value $\delta _{\mathrm{CR}}$ and $\gamma$.

It is easy to find that $\delta _{\mathrm{CR}}$ strongly depends on the parameter $\gamma$ (see figure 5). The $\delta {-}\gamma$ curve is a monotonous decreasing function. At the beginning, by increasing $\gamma \approx \text{0 }$ to $\gamma =0.5$ gradually, $\delta _{\mathrm{CR}}$ decreases sharply almost in a straight line. Then, $\delta _{\mathrm{CR}}$ decreases gently when $\gamma$ increases from $\gamma =0.5$ to $\gamma =1.0$.

Fig. 6

System solutions approaching positive infinity related to stable limit cycle near $\delta _{\mathrm{CR}} =1/\gamma$. The red dotted lines indicate the maximum and minimum amplitudes of stable oscillations, blue dashed lines indicate critical lines $\delta _{\mathrm{CR}} =1/\gamma$. (a) $\gamma =2$, $\delta _{\mathrm{CR}} =0.5$, (b) $\gamma =1.5$, $\delta _{\mathrm{CR}}=0.66667$, (c) $\gamma =1.2$, $\delta _{\mathrm{CR}}=0.83333$ and (d) $\gamma =1$, $\delta _{\mathrm{CR}} =1.0$.

3.2 System solutions approaching infinity related to the stable limit cycle

The route of system solutions approaching infinity related to stable attractor E has been analysed in §3.1. In this subsection, we shall present the other route of system solutions approaching infinity related to the stable limit cycle. We fix $F=0.02$, $\mu =1.5$, $\alpha =2$, $\beta =1$ and $\omega =0.01$. As $\mu$ varies from negative to positive, the stable attractor is a stable limit cycle and the equilibrium point E is always unstable. The change process of the system solution behaviours with $\delta$ is presented in figure 6. When $\delta$ changes from negative to positive and approaches $\delta _{\mathrm{CR}}$, the limit cycle surrounding the unstable equilibrium point E follows a sharp transition to infinity. Considering that the stable attractor is a stable limit cycle, the sharp transition in this parameter condition can be classified as ‘system solutions of stable limit cycle attractor approaching infinity’.

Fig. 7

Spiking state and quiescent state areas in the stable region $(-\delta _{\mathrm{CR}} ,\delta _{\mathrm{CR}} )$. (a) The mode $\cos \omega t$ visits the quiescent state area, (b) the mode $\cos \omega t$ visits the quiescent and spiking areas and (c) the mode $\cos \omega t$ visits the divergent area.

Fig. 8

Bursting oscillation of point/point. (a) Phase diagram on the space of (x, y) and (b) time series.

4 Bursting induced by system solutions approaching infinity

We have explored in details, the two routes of system solutions approaching infinity. Based on this, we turn to eq. (1.3) with the modulation frequency $0<\omega \ll 1$, and explore two attractive bursting patterns induced by the two routes of system solutions approaching infinity therein.

Fig. 9

Slow–fast analysis of bursting oscillation of point/point. Blue arrows indicate the directions of the trajectory and green solid line indicates the stable equilibrium point curve. (a) Transformed phase portrait on the space of $(\delta ,x)$ and (b) transformed phase portrait overlapped with the bifurcation curve and the critical value curve.

Fig. 10

Bursting oscillation of cycle/cycle. (a) Phase portrait on the space of (x, y) and (b) time history.

4.1 Spiking state and quiescent state areas

As previously mentioned, if we want the bursting phenomena to occur, an important factor is that the dynamic behaviour of system (2.1) must be able to switch between a spiking state and a quiescent state. Generally, the spiking state is a stable limit cycle with a relatively large amplitude, and the quiescent state is a stable equilibrium point or a stable limit cycle with a nearly small $\hbox {amplitude}$ [31, 32]. In this paper, as the critical value is represented by the cosine function $\cos \omega t$, when $\delta$ slowly varies through the transition of the quiescent state area critical line, i.e. $\delta$ can visit the spiking state and the quiescent state areas periodically and bursting oscillation is generated (see figure 7).

The fast subsystem can exhibit interesting dynamics of important characteristics similar to those of the quiescent state and spiking state. Before the sudden steep transition, the stable equilibrium point or the stable limit cycle stays near the origin. This dynamical behaviour is relatively smooth and mild, which can be regarded as the quiescent state. When $\delta$ approaches the critical value, the sudden steep transition takes place. This dynamical behaviour is violent and catastrophic, which can be considered as the spiking state.

Fig. 11

Slow–fast analysis of bursting oscillation of point/point. Burgundy arrows indicate the directions of the trajectory and black dotted line indicates the unstable equilibrium point curve. (a) Transformed phase portrait, (b) transformed phase portrait overlapped with the bifurcation curve and the critical value curve and (c) local enlargement of the overlay.

In figure 7, we can see that this is the only one quiescent state critical line. According to the different regions where the control parameter $\delta$ passes through, the crossing modes can be divided into three cases. In the first case, $\delta$ always stays in the quiescent state area, and the system may behave in a periodic oscillation. In the second case, $\delta$ can visit the quiescent state area and the spiking state area, and bursting oscillation is formed. In the third case, $\delta$ is big enough to enter the divergent area, and then the system diverges. The stable region $(-\delta _{\mathrm{CR}} ,\delta _{\mathrm{CR}} )$ also can be separated into two parts, a quiescent state area and a spiking state area. The main body of the stable area is quiescent state area, which takes up most of the parameter space.

4.2 Bursting oscillation of point/point

The schematic diagrams of parameter spatial distribution of the quiescent state and spiking state have been presented. Next, we shall explore the two bursting oscillations induced by system solutions approaching infinity. In this subsection, bursting oscillation of point/point is explored first.

Since the forcing excitation frequency $\omega$ is small, according to the slow–fast analysis method, we can treat the slow-varying excitation $\cos \omega t$ as a state variable $\delta$. And then, eq. (2.1) becomes a new three-dimensional system with three variables $(x,y,\delta =\cos \omega t)$. By projecting the new three-dimensional system on the subspace $(\delta ,x)$ or $(\delta ,y)$, we can obtain the transformed phase portrait [33], which exhibits the relationships between the new state variable $\delta$ and the other two variables x and y.

When we fix the parameters as $F=0.02$, $\mu =-0.01$, $\gamma =1.0$, $\alpha =2.0$, $\beta =1.0$ and $\omega =0.01$, the related phase diagram and time history are presented in figure 8. It can be easily seen that the trajectory switches between two equilibrium points. In order to investigate the dynamical mechanism of this oscillation, we superimposed the transformed phase portrait in the plane of $(\delta ,x)$ onto the bifurcation diagram, shown in figure 9, and the critical value of $\delta$ is $\delta _{\mathrm{CR}} =1/\gamma =1.0$.

In such a case, the stable attractor is an equilibrium E. The trajectory follows almost strictly along E for a long time interval, corresponding to the quiescent state. When $\delta$ approaches the critical value $\delta _{\mathrm{CR}} =1.0$, system (2.1) undergoes a catastrophic transition from the origin of the stable equilibrium point E to the positive infinity, which leads to the spiking state. When $\delta$ arrives at the maximum value 1.0, then it starts to decrease. From figure 4d, we can see that the solutions of system approach zero in the extreme time, leading to the trajectory undergoing an oscillation to the stable equilibrium E with high frequency quickly. Figure 9 shows that the amplitude of the high frequency decreases gradually, corresponding to the quiescent state. When $\delta$ reaches the minimum value − 1, the next evolution begins.

Bursting oscillation of point/point is a common bursting type, which is investigated so $\hbox {much}$ [34,35,36]. However, the mechanism of bursting oscillation of point/point in this paper is different from that of the previous study, as the transition between the spiking state and the quiescent state is not bifurcation, but system solutions approaching infinity.

4.3 Bursting oscillation of cycle/cycle

Bursting oscillation of point/point has been discussed in §4.2. In this subsection, we shall explore the other bursting oscillation induced by system solutions approaching infinity, i.e. bursting oscillation of cycle/cycle.

For this purpose, we fix the parameters as $F=0.02$, $\mu =1.5$, $\gamma =1.0$, $\alpha =2.0$, $\beta =1.0$ and $\omega =0.01$. The stable attractor in this condition is a stable limit cycle. The phase diagram and time history are shown in figure 10, from which we can see that the trajectory always moves in the stable limit cycle. The mechanism of this bursting also can be revealed by superimposing the phase diagram in the space of $(\delta ,x)$ onto to the bifurcation diagram of the control parameter $\delta$ (see figure 11).

The trajectory first moves in the vector field of the stable limit cycle, and behaves in a high-frequency oscillation with a relatively small amplitude. This movement can be considered as the quiescent state. When $\delta$ slowly changes to the critical value $\delta _{\mathrm{CR}} =1.0$, a sudden sharp transition takes place, leading to the trajectory approaching infinity, corresponding to the spiking state. After reaching the maximum value 1.0, $\delta$ begins to decrease. The amplitude of the oscillations decreases sharply in a narrow parameter interval. Then, the trajectory enters the quiescent state area. The oscillation becomes mild and oscillates in the limit cycle oscillation with a small amplitude. When $\delta$ reaches the minimum value − 1, the next evolution starts.

5 Conclusions

The modified Rayleigh–Duffing oscillator behaves in different bursting dynamics under different parameter conditions. In this paper, we reveal a novel route to bursting oscillation, called system solutions approaching infinity, which is not reported yet. The system exhibits one critical value, and when the periodic control parameter slowly varies through the critical value, a sudden sharp transition takes place, leading to the system solution approaching infinity. Based on this phenomenon, we present an explanation of a new novel mechanism for two different patterns of bursting oscillations, which are common and well-studied. Our research provides a special scheme connecting the quiescent state and the spiking state independent of bifurcations, and gives a new idea of the possible mechanism of bursting dynamics.