1 Introduction

The free surface of a fluid contained in a tank subjected to an external excitation exhibits a disordered form. This phenomenon is called sloshing. If a tank partially filled with magnetic fluid is subjected to an external magnetic field, magnetic field acts on the magnetic fluid and influences the free surface fluid movement. A ferrofluid is a stable colloidal solution of the magnetic nanoparticles dispersed in a solvent. Due to the unusual combination of liquid and magnetic properties, it is possible, among other things, to make them flow using magnetic fields.

Magnetic fields are used to control the ferrofluids flow, giving rise to new phenomena with many technical applications [1]. Application of variable or non-uniform magnetic field does not cause any movement of the ferrofluid completely contained in a hermetic tank. To cause a fluid displacement, there is initially a magnetisation heterogeneity. Presence of an interface is a sufficient condition. Magnetisation discontinuity between two media with different magnetic susceptibilities produces a pressure field at the interface which will deform it.

Deformation of the interface between the magnetic and the nonmagnetic fluids in the presence of a magnetic field, known as Cowley–Rosensweig instability (CRI), was investigated by Cowley and Rosensweig [2] and has been widely studied by several others later, see [3,4,5,6,7,8]. A normal magnetic field has a destabilising influence on a flat interface between a magnetic and a non-magnetic fluid, while interfacial tension and gravity have stabilising influence. CRI is similar to Rayleigh–Taylor instabilities (RTI), see [9, 10]. Among recent studies on RTI, the nonlinear Rayleigh–Taylor stability of the cylindrical interface between the vapour and the liquid phases of a fluid was studied by Seadawy and El-Rashidy [11] and a novel approach was developed by El-Dib et al [12] to study two rotating superposed infinite hydromagnetic Darcian flows through porous media under the influence of a uniform tangential magnetic field.

Some experiments on the stability of a flat interface between ferromagnetic and non-magnetic fluids, in the presence of uniform, normal, magnetic and gravitational fields were discussed by Cowley and Rosensweig [2]. Viscous effects and contribution of magnetic field induced by the discontinuity surface deformation on the development of infinitesimal waves are presented by Brancher [3]. Using multiple scales method, Malik and Singh [4] investigated nonlinear surface instability of two superposed magnetic fluids. It is shown that instability exists when the applied magnetic field, which is normal to the fluid surface, is slightly larger than the critical magnetic field. Nonlinear analysis shows that the fluid free-surface form is a combination of waves with different wave numbers and wavelengths. A ferrofluid slab bounded below by a fixed boundary and above by a vacuum was considered by Twombly and Thomas [5]. If the fluid is subjected to a vertical magnetic field of sufficient strength, surface waves appear. Equations describing this phenomenon were derived and a local stability criterion was also obtained and applied to three periodic structures: rolls, squares and hexagons.

Peak pattern formation on a magnetic fluid-free surface subjected to a normal magnetic field at the undisturbed interface was investigated theoretically by Friedrichs and Engel [6]. Perturbation energy minimisation procedure was used to study the relative stability of the ridge, square and hexagon plan forms. Previous studies were extended to take into account the finite depth fluid layer. Furthermore, the theoretical analysis showed that when the wave number changes, the square configuration becomes rather susceptible to the increase in wave number. Results were compared with the previous investigations and recent experimental findings.

The CRI of the ferrofluid has been the subject of several recent researches. Rotation and magnetic field effects on the nonlinear CRI of two superposed ferrofluids were investigated by Devi and Hemamalini [7]. It was considered that the system was subjected to uniform parallel rotation and normal magnetic field. Surface tension acts at the interface. Multiple scales method was used to obtain solution and dispersion relations for nonlinear problem of the CRI. The stability problem was discussed afterwards.

Bashtovoi et al [13] experimentally studied the magnetic fluid stability in the presence of tangential magnetic field and instability dynamics. Nonlinear instability theory, shape of a flat magnetic fluid surface, solitary and cnoidal wave theories on the cylindrical surface are developed. Asymptotic behaviour of weakly nonlinear dispersive waves at the interface of two semi-infinite superposed magnetic fluids in the presence of an applied magnetic field was investigated by Elhefnawy [14]. Stability was discussed both analytically and numerically, for tangential and normal magnetic fields, and stability diagrams were obtained. Comparing the results for the normal field with results obtained for a tangential field, they have observed that both fields play a dual role. They redistribute stable and unstable regions in the stability chart but with different effects. When the normal field is stabilising for small wave numbers, tangential field is destabilising for a range of wave numbers and vice versa.

Motion of liquid with a free surface is of great concern in many engineering disciplines such as fuel sloshing of the rocket propellant, oscillation of oil in large storage tanks, oscillation of water in a reservoir due to earthquake, sloshing of water in pressure-suppression pools of boiling water reactors and several others. Lateral sloshing of the magnetic fluid in a rectangular container in vertically applied non-uniform magnetic fields has been investigated by Sawada et al [15]. Assuming a potential flow and using perturbation method, they have obtained nonlinear sloshing responses up to the third-order perturbation in the vicinity of the first resonant frequency. Theoretical nonlinear solutions agree with experimental results. However, nonlinear solutions are slightly larger than the experimental data in the lower frequency range because the amplitude of the free surface oscillation does not vanish with decrease in frequency. In fact, in this range, linear solutions are in better agreement with experimental values. Velocity amplitude decreases when the magnetic field intensity increases. Also, power spectra were calculated from the velocity data. The spatial distributions of the dominant peaks were in good agreement with nonlinear theoretical results. However, other power spectra deviate from theoretical lines.

The flat interface between two magnetic fluids can be parametrically excited by periodically oscillating magnetic field oriented in normal direction to the fluids. The interface stability problem of two magnetic viscous fluids has been studied by Bajaj and Malik [16]. Beyond a critical value of wave number and excitation amplitude, the plane interface becomes unstable and standing waves appear. Standing wave solutions are found to exist for a given value of external frequency and steady magnetic field.

Nonlinear parametric instability of three-mode resonated standing waves raised at the interface of a viscous magnetic fluid bounded layer excited by both alternating magnetic field and longitudinal modulated gravity force was studied theoretically by Sirwah [17]. The system is assumed to be excited by a parametric force together with an oscillating magnetic field along normal direction to the unperturbed flat interface. Using multiple scales technique, non-secularity conditions considering uniformly convergent analytical solutions in different cases of resonance were obtained. Consequently, an autonomous coupled system of nonlinear ordinary differential equations controlling the amplitudes and phases of the modulated resonant waves was constructed. Accordingly, steady-state solutions as well as existence conditions of both stable (periodic) and turbulent (chaotic) motions are determined. Some numerical applications based on the analytical treatment were given to demonstrate the effects of various parameters on the behaviour of the modified amplitudes with time as well as phase-plane trajectory. Zakaria and Sirwah [18] provided an extensive stability analysis of the surface waves between layers of two immiscible infinite magnetic liquids. This subject seems to have a long history with relevance to fluid mechanics as well as technological and industrial applications. Gravitation and uniform oblique magnetic field effects were taken into account. Analytical solutions of the nonlinear problem were achieved in the perturbation analysis methods framework, in order to treat finite amplitude waves and then determine stability criteria of the considered problem. Various stability criteria of the travelling waves were investigated. Also, solitary wave solutions at the liquid–liquid interface were discussed. Influence of different parameters governing the system stability behaviour was discussed.

Bae et al [19] have analysed the dynamic behaviour of the magnetic fluid that sloshes due to the pitching motion of the container. This analysis shows that the surface of the magnetic fluid rises towards the location of intensity of the magnetic field when sloshing does not occur and when sloshing occurs simultaneously with the application of the magnetic field, the elevation of the surface as a result of the magnetic field is maintained. Further, the wave motion of the surface is small because the magnetic body force dominates the effect of sloshing if the excitation frequency of sloshing is small. Likewise, the wave motion of the fluid surface is smaller when a magnetic field is not applied if the excitation frequency increases. The results also show that when the intensity of the magnetic field is strong, the fluid surface rises in that location and if the intensity of the magnetic field is weak, the height of the fluid surface is lower than the initial level obtained in the absence of a magnetic field.

A weakly non-linear approach for small-amplitude capillary-gravity waves that propagate along the interface of two finite-thickness layers of viscous magnetic fluids and formed by the interaction of the first and the second harmonics of the fundamental mode was developed by Sirwah [20]. The fluids under consideration are assumed to have constant densities, viscosity and permeability, taking into account a constant surface tension. Fluids were assumed to be excited by a uniform tangential magnetic field. The influence of each tangential field and Weber number on the stability of linear waves has been considered. Numerical simulation results show that tangential field as well as Weber number have regular stabilising influence. Furthermore, he has concluded that the effect of wave number on the stability criteria depends strongly on tangential field values and Weber number. A pair of coupled nonlinear partial differential equations with complex coefficients which model, up to cubic order, the evolution of the interacting waves has been derived. Solutions of evolution equations (corresponding to sinusoidal wave trains) were obtained and then formal series expansion for the wave profile, in wave steepness powers was derived. The method of multiple scales was used by Lee [21] to analyse the propagation of nonlinear wave on a liquid and a subsonic gas interface in the presence of magnetic field taking into account surface tension. Amplitude evolution was governed by the nonlinear Schrödinger equation which is a criterion for modulation instability.

The studies carried out on the evolution of the interface of a magnetic fluid filling a reservoir when the system is subjected to an external magnetic field are carried out without taking into account the effects of the walls. Interface evolution of the magnetic fluid in a finite size tank which is subjected to external magnetic field is investigated in this study. Section 2 is devoted to the presentation of the physical problem. Equations governing the fluid motion and magnetic field with boundary conditions are given for both magnetic fluid and magnetic field at the rigid tank walls and at the free surface. By the appropriate selection of variables, we give dimensionless equations governing the magnetic fluid sloshing in §3. Resolution method based on the multiple scale variables is presented in §4. Linear solution is exposed in §5. We analyse, in §6, the effects of external magnetic field on the dispersion relation and magnetic fluid-free surface evolution. Stable and unstable zones depending on the wave number and how these are influenced by the horizontal and vertical components of the external magnetic field are presented. In Conclusion, major results of this study are discussed.

2 Problem formulation

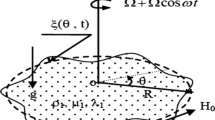
We consider two-dimensional sloshing of an incompressible inviscid magnetic fluid (ferrofluid), with free surface, in a rectangular tank of length L and depth h. The free surface is the interface between the magnetic fluid and air. Cartesian coordinates are considered with x-axis in the plane of the undisturbed free surface and y-axis is positive in the direction upward normal to the undisturbed free surface (see figure 1). The lower region in the tank (\(y\le 0\)), labelled 1, is occupied by the magnetic fluid of density \(\rho \) and magnetic permeability \(\mu _{1}\); the remaining space is occupied by air with magnetic permeability \(\mu _{2}\). Both media are subjected to a uniform magnetic field, oblique to the interface and is given by

$$\begin{aligned} \vec {H}_{0}=H_{01}\vec {e}_{x}+H_{02}\vec {e}_{y}. \end{aligned}$$
(1)

Assuming that the magnetic permeability of air is very close to that for a vacuum, magnetic inductions in the magnetic fluid and air are respectively

$$\begin{aligned} \vec {B}_{0}^{(1)}=\mu _{1}\vec {H}_{0}^{(1)} =\mu _{0}(\vec {H}_{0}+\vec {M}_{0}^{(1)}) \end{aligned}$$
(2)

and

$$\begin{aligned} \vec {B}_{0}^{(2)}=\mu _{2}\vec {H}_{0}^{(2)}=\mu _{0}\vec {H_{0}}, \end{aligned}$$
(3)

where

$$\begin{aligned} \vec {H}_{0}^{(j)}=H_{01}^{(j)}\vec {e}_{x}+H_{02}^{(j)} \vec {e}_{y}, \quad j=1,2 \end{aligned}$$
(4)

(see [22,23,24]) and \(\vec {M}_{0}^{(1)}\) is the magnetic fluid magnetisation given by

$$\begin{aligned} \vec {M}_{0}^{(1)}=\chi _{1}(H_{0})\vec {H_{0}} \end{aligned}$$
(5)

with \(\chi _{1}(H_{0})\) representing the magnetic fluid susceptibility.

Fig. 1
figure 1

Problem scheme.

Full size image

For a linear magnetisable magnetic fluid, corresponding to low applied magnetic field \(\vec {H_{0}}\), the magnetic fluid susceptibility is assumed to be constant, \(\chi _{1}(H_{0})=\chi _{1}\) and the magnetic fluid induction becomes

$$\begin{aligned} \vec {B}_{0}^{(1)}=\mu _{1}\vec {H}_{0}^{(1)}=\mu _{0}(1+\chi )\vec {H_{0}}. \end{aligned}$$
(6)

When the magnetic fluid interface is in equilibrium and assuming that there are no free currents at this interface, the normal magnetic induction component and tangential magnetic field component are continuous. We write

$$\begin{aligned} \vec { n}\cdot (\vec {B}_{0}^{(2)}-\vec {B}_{0}^{(1)})=0 \end{aligned}$$
(7)

and

$$\begin{aligned} \vec { n}\wedge (\vec {H}_{0}^{(2)}-\vec {H}_{0}^{(1)})=0 \end{aligned}$$
(8)

at the magnetic fluid interface.

In other terms, these conditions give

$$\begin{aligned} H_{01}^{(1)}= H_{01}^{(2)} \end{aligned}$$
(9)

and

$$\begin{aligned} \mu _{1} H_{02}^{(1)}=\mu _{2} H_{02}^{(2)}. \end{aligned}$$
(10)

Motion of the incompressible inviscid magnetic fluid in the rectangular tank under capillary-gravity forces is assumed to be irrotational. It can be described by the velocity potential (see [7, 14, 18, 25,26,27,28]), such that

$$\begin{aligned} \Phi _{xx}+ \Phi _{yy}=0, ~~~~0\le x\le L, ~~~~-h\le y \le \eta (x,t), \end{aligned}$$
(11)

where \(\Phi (x,y,t)\) is the velocity potential of the magnetic fluid.

In magneto-quasistatic case with negligible displacement current, Maxwell’s equations are reduced to Gauss law \(\vec {\nabla }\cdot \vec {B}\) and Ampere law (no currents) \(\vec {\nabla }\wedge \vec {H}=\vec {0}\). From Ampere law, the magnetic field \(\vec {H}^{(j)}\), \(j=1,2\) can be expressed in terms of the magnetic scalar potential \(\Psi ^{(j)}(x,y,t)\) in each region occupied by the fluid and air, i.e.,

$$\begin{aligned} \vec {H}^{(j)}=\vec {H}_{0}^{(j)}-\vec {\nabla }\Psi ^{(j)}, \quad j=1,2, \end{aligned}$$
(12)

where \(\vec {H}_{0}^{(j)}\), \(j=1,2\) are unperturbed oblique magnetic fields in regions 1 and 2 respectively.

Taking into account that magnetic fluid susceptibility is constant and combining eq. (12) with Gauss law, the magnetic scalar potential \(\Psi ^{(j)}\), \(j=1,2\) must obey Laplace equations:

$$\begin{aligned} \Psi ^{(1)}_{xx}+ \Psi ^{(1)}_{yy}=0, \quad 0\le x \le L, \quad -h\le y \le \eta (x,t) \end{aligned}$$
(13)

and

$$\begin{aligned} \Psi ^{(2)}_{xx}+ \Psi ^{(2)}_{yy}=0, \quad 0\le x \le L, \quad \eta (x,t) \le y \le +\infty , \end{aligned}$$
(14)

where \(y=\eta (x,t)\) is the free surface elevation.

On the rigid boundaries \(y=-h\), \(x=0\) and \(x=L\), normal fluid velocities as well as tangential components of the magnetic field vanish leading to

$$\begin{aligned}&\Phi _{y} = 0 ~~~~ \mathrm{at} ~ y=-h \end{aligned}$$
(15)
$$\begin{aligned}&\Psi ^{(1)}_{x} = 0 ~~~~~ \mathrm{at} ~ y=-h \end{aligned}$$
(16)
$$\begin{aligned}&\Phi _{x} = 0 ~~~~~~ \mathrm{at} ~ x=0,\quad x=L \end{aligned}$$
(17)
$$\begin{aligned}&\Psi ^{(1)}_{y} = 0 ~~~~ \mathrm{at} ~ x=0,\quad x=L. \end{aligned}$$
(18)

The jump in tangential components of the magnetic field is zero across the free surface, which gives

$$\begin{aligned}&(\Psi ^{(1)}_{x}-\Psi ^{(2)}_{x})-\eta _{x}(H_{02}^{(1)}-H_{02}^{(2)} +\Psi ^{(1)}_{y}-\Psi ^{(2)}_{y}) = 0 \nonumber \\&\quad \mathrm{at} ~ y=\eta (x,t). \end{aligned}$$
(19)

Additionally, as no free surface charges are present, normal component of the magnetic induction must be continuous at the free interface, which requires

$$\begin{aligned}&\eta _{x}(\mu _{1}\Psi ^{(1)}_{x}-\mu _{2}\Psi ^{(2)}_{x} -\mu _{1}H_{01}^{(1)}+\mu _{2}H_{01}^{(2)})\nonumber \\&\quad -(\mu _{1}\Psi ^{(1)}_{y}-\mu _{2}\Psi ^{(2)}_{y}) = 0 ~~~~ \mathrm{at} ~ y=\eta (x,t). \end{aligned}$$
(20)

The kinematics condition at the interface is given by

$$\begin{aligned} \eta _{t}-\Phi _{y}+\eta _{x}\Phi _{x}=0 ~~~~ \mathrm{at} ~ y=\eta (x,t). \end{aligned}$$
(21)

The balance of the normal component of total stress tensor at the interface gives the condition:

$$\begin{aligned}&\rho \Phi _{t}+\frac{1}{2}\nabla \Phi \nabla \Phi +\rho g\eta \nonumber \\&\quad -\sigma \eta _{xx}(1+\eta _{x}^{2})^{-3/2} +\frac{1}{2}\frac{(1-\eta _{x}^{2})}{(1+\eta _{x}^{2})}\nonumber \\&\quad \times \left\{ \begin{array}{lll} \mu _{1}(H_{02}^{2(1)}-H_{01}^{2(1)})-\mu _{2}(H_{02}^{2(2)}-H_{01}^{2(2)})\\ -2\mu _{1}H_{02}^{(1)}\Psi ^{(1)}_{y}+2\mu _{1}H_{02}^{(2)}\Psi ^{(2)}_{y}\\ +2\mu _{1}H_{01}^{(1)}\Psi ^{(1)}_{x}-2\mu _{2}H_{01}^{(2)}\Psi ^{(2)}_{x}\\ -\mu _{1}(\Psi ^{2(1)}_{x}-\Psi ^{2(1)}_{y})+\mu _{2}(\Psi ^{2(2)}_{x}-\Psi ^{2(2)}_{y})\\ \end{array}\right\} \nonumber \\&\quad +\frac{2\eta _{x}}{\Big (1+\eta _{x}^{2}\Big )}\nonumber \\&\quad \times \left\{ \begin{array}{lll} \mu _{1}H_{01}^{(1)}\Psi ^{(1)}_{y}+\mu _{1}H_{02}^{(1)}\Psi ^{(1)}_{x}-\mu _{2}H_{01}^{(2)}\Psi ^{(2)}_{y} \\ -\mu _{2}H_{02}^{(2)}\Psi ^{(2)}_{x}-\mu _{1}\Psi ^{(1)}_{x}\Psi ^{(1)}_{y}+\mu _{2}\Psi ^{(2)}_{x}\Psi ^{(2)}_{y}\\ \end{array}\right\} \nonumber \\&\quad =0 ~~~~\mathrm{at} ~ y=\eta (x,t). \end{aligned}$$
(22)

Using the dimensionless variables

$$\begin{aligned}&(\tilde{x}, \tilde{y},\tilde{L}, \tilde{h},\tilde{\eta }) =\frac{1}{L}(x, y, L, h, \eta ),\\&\tilde{t}=\sqrt{\frac{g}{L}}t,\quad \tilde{\phi } =\frac{1}{L\sqrt{gL}}\phi ,\\&\tilde{H}^{(j)} = \sqrt{\frac{\mu _{1}}{\rho g L}}H^{(j)}, \quad \tilde{\psi }^{(j)} = \frac{1}{L} \sqrt{\frac{\mu _{1}}{\rho g L}}\psi ^{(j)} \end{aligned}$$

eqs (11)–(22) gives

$$\begin{aligned}&\tilde{\Phi }_{\tilde{x}\tilde{x}}+ \tilde{\Phi }_{\tilde{y}\tilde{y}}=0, \quad 0\le \tilde{x}\le \tilde{L}, \quad -\tilde{h}\le \tilde{y} \le \tilde{\eta }(\tilde{x},\tilde{t}) \end{aligned}$$
(23)
$$\begin{aligned}&\tilde{\Psi }^{(1)}_{\tilde{x}\tilde{x}}+ \tilde{\Psi }^{(1)}_{\tilde{y}\tilde{y}}=0, \quad 0\le \tilde{x}\le \tilde{L}, \quad -\tilde{h}\le \tilde{y } \le \tilde{\eta }(\tilde{x},\tilde{t}) \end{aligned}$$
(24)

and

$$\begin{aligned}&\tilde{\Psi }^{(2)}_{\tilde{x}\tilde{x}}+ \tilde{\Psi }^{(2)}_{\tilde{y}\tilde{y}}=0, ~~~~0\le \tilde{x}\le \tilde{L}, ~~~~\tilde{\eta }(\tilde{x},\tilde{t}) \le \tilde{y }\le +\infty \end{aligned}$$
(25)
$$\begin{aligned}&\tilde{\Phi }_{\tilde{y}} = 0 \quad \mathrm{at} ~ \tilde{y}=-\tilde{h} \end{aligned}$$
(26)
$$\begin{aligned}&\tilde{\Psi }^{(1)}_{\tilde{x}} = 0 \quad \mathrm{at} ~ \tilde{y}=-\tilde{h} \end{aligned}$$
(27)
$$\begin{aligned}&\tilde{\Phi }_{\tilde{x}} = 0 \quad \mathrm{at} ~ \tilde{x}=0,\quad \tilde{x}=\tilde{L} \end{aligned}$$
(28)

and

$$\begin{aligned}&\tilde{\Psi }^{(1)}_{\tilde{y}} = 0,\quad \mathrm{at} ~\tilde{x}=0,\quad \tilde{x}=\tilde{L} \end{aligned}$$
(29)
$$\begin{aligned}&(\tilde{\Psi }^{(1)}_{\tilde{x}}-\tilde{\Psi }^{(2)}_{\tilde{x}}) -\tilde{\eta }_{\tilde{x}}(\tilde{H}_{02}^{(1)}-\tilde{H}_{02}^{(2)}\nonumber \\&\quad +\tilde{\Psi }^{(1)}_{\tilde{y}}-\tilde{\Psi }^{(2)}_{\tilde{y}})= 0\quad \mathrm{at} ~ \tilde{y}=\tilde{\eta }(\tilde{x},\tilde{t}) \end{aligned}$$
(30)
$$\begin{aligned}&\tilde{\eta }_{\tilde{x}}(\tilde{\Psi }^{(1)}_{\tilde{x}} -\mu \tilde{\Psi }^{(2)}_{\tilde{x}}-\tilde{H}_{01}^{(1)}\nonumber \\&\quad +\,\mu \tilde{H}_{01}^{(2)}) -(\tilde{\Psi }^{(1)}_{\tilde{y}}-\mu \tilde{\Psi }^{(2)}_{\tilde{y}}) = 0 \quad \mathrm{at} ~ \tilde{y}=\tilde{\eta }(\tilde{x},\tilde{t}) \end{aligned}$$
(31)
$$\begin{aligned}&\tilde{\eta }_{\tilde{t}}-\tilde{\Phi }_{\tilde{y}} +\tilde{\eta }_{\tilde{x}}\tilde{\Phi }_{\tilde{x}}=0 \quad \mathrm{at} ~ \tilde{y}=\tilde{\eta }(\tilde{x}, \tilde{t}) \end{aligned}$$
(32)
$$\begin{aligned}&\tilde{\Phi }_{\tilde{t}}+\frac{1}{2}\tilde{\nabla }\tilde{\Phi } \tilde{\nabla }\tilde{\Phi }+\tilde{\eta } -\tilde{\sigma } \tilde{\eta }_{\tilde{x}\tilde{x}}(1+\tilde{\eta }_{\tilde{x}}^{2})^{-3/2}\nonumber \\&\quad {+}\frac{1}{2}\frac{(1{-}\tilde{\eta }_{\tilde{x}}^{2})}{(1+\tilde{\eta }_{\tilde{x}}^{2})} \left\{ \begin{array}{lllll} (\tilde{H}_{02}^{2(1)}{-}\tilde{H}_{01}^{2(1)}){-}\mu (\tilde{H}_{02}^{2(2)}{-}\tilde{H}_{01}^{2(2)})\\ {-}2\tilde{H}_{02}^{(1)}\tilde{\Psi }^{(1)}_{\tilde{y}}{+}2\mu \tilde{H}_{02}^{(2)}\tilde{\Psi }^{(2)}_{\tilde{y}}\\ {+}2\tilde{H}_{01}^{(1)}\tilde{\Psi }^{(1)}_{\tilde{x}}{-}2\mu \tilde{H}_{01}^{(2)}\tilde{\Psi }^{(2)}_{\tilde{x}}\\ {-}(\tilde{\Psi }^{2(1)}_{\tilde{x}}{-}\tilde{\Psi }^{2(1)}_{\tilde{y}}){+}\mu (\tilde{\Psi }^{2(2)}_{\tilde{x}}{-}\tilde{\Psi }^{2(2)}_{\tilde{y}})\\ \end{array}\right\} \nonumber \\&\quad +\frac{2\tilde{\eta }_{\tilde{x}}}{(1+\tilde{\eta }_{\tilde{x}}^{2})}\nonumber \\&\quad \times \left\{ \begin{array}{lll} \tilde{H}_{01}^{(1)}\tilde{\Psi }^{(1)}_{\tilde{y}}+\tilde{H}_{02}^{(1)}\tilde{\Psi }^{(1)}_{\tilde{x}}-\mu \tilde{H}_{01}^{(2)}\tilde{\Psi }^{(2)}_{\tilde{y}} \\ -\mu \tilde{H}_{02}^{(2)}\tilde{\Psi }^{(2)}_{\tilde{x}}-\mu \tilde{\Psi }^{(1)}_{\tilde{x}}\tilde{\Psi }^{(1)}_{\tilde{y}}+\mu \tilde{\Psi }^{(2)}_{\tilde{x}}\tilde{\Psi }^{(2)}_{\tilde{y}}\\ \end{array}\right\} \nonumber \\&\quad =0 \quad \mathrm{at} ~ \tilde{y}=\eta (\tilde{x},\tilde{t}), \end{aligned}$$
(33)

where \(\tilde{\sigma }=\sigma /\rho g L^{2}\) is the dimensionless capillary coefficient.

3 Solution method

In order to simplify equations, we shall remove the tilde.

To obtain approximate solution of eqs (23)–(33), we use multiple scales method [29, 30] by introducing the spatial and temporal scales \(x_{n}=\varepsilon ^{n}x\) and \(t_{n}=\varepsilon ^{n}t\ (n=1,2,\ldots )\). \(\varepsilon \) is a small parameter corresponding to the steepness ratio of the wave. The following expansions of the variables are assumed:

$$\begin{aligned}&\eta (x,t) = \sum _{n=1}^{2} \varepsilon ^{n}\eta _{n} (x_{0},x_{1};t_{0}, t_{1})+O\big (\varepsilon ^{3}\big ) \end{aligned}$$
(34)
$$\begin{aligned}&\Phi (x,y,t) = \sum _{n=1}^{2} \varepsilon ^{n}\Phi _{n} (x_{0},x_{1},y; t_{0}, t_{1})+O\big (\varepsilon ^{3}\big ) \end{aligned}$$
(35)
$$\begin{aligned}&\Psi ^{(1)}(x,y,t) = \sum _{n=1}^{2} \varepsilon ^{n}\Psi _{n}^{(1)} (x_{0},x_{1},y; t_{0}, t_{1})+O\big (\varepsilon ^{3}\big ) \end{aligned}$$
(36)
$$\begin{aligned}&\Psi ^{(2)}(x,y,t) = \sum _{n=1}^{2} \varepsilon ^{n}\Psi _{n}^{(2)} (x_{0},x_{1},y; t_{0}, t_{1})+O\big (\varepsilon ^{3}\big ). \end{aligned}$$
(37)

Substituting expansions (34)–(37) in eqs (23)–(33) and equating terms with equal powers of \(\varepsilon \), we obtain the following first-order system of equations.

3.1 First-order system of equations

At the first order \(n=1\), the system of equations is given by

$$\begin{aligned}&\Phi _{1x_{0}x_{0}}+ \Phi _{1yy}=0,\quad ~0\le x_{0}\le L,\nonumber \\&\qquad -h \le y \le \eta _{1}(x_{0},t_{0}) \end{aligned}$$
(38)
$$\begin{aligned}&\Psi ^{(1)}_{1x_{0}x_{0}}+ \Psi ^{(1)}_{1yy}=0,\quad ~0\le x_{0} \le L,\nonumber \\&\qquad -h\le y \le \eta _{1}(x_{0},t_{0}) \end{aligned}$$
(39)

and

$$\begin{aligned}&\Psi ^{(2)}_{1x_{0}x_{0}}+ \Psi ^{(2)}_{1yy}=0,\quad 0\le x_{0} \le L,\nonumber \\&\qquad \eta _{1}(x_{0},t_{0}) \le y \le +\infty . \end{aligned}$$
(40)

At the bottom of the tank \(y=-h\)

$$\begin{aligned}&\Phi _{1y}=0 \end{aligned}$$
(41)
$$\begin{aligned}&\Psi _{1x_{0}}^{(1)}=0. \end{aligned}$$
(42)

On the left and right vertical rigid boundaries \(x_{0}=0\) and L

$$\begin{aligned}&\Phi _{1x_{0}}=0 \end{aligned}$$
(43)
$$\begin{aligned}&\Psi _{1y}^{(1)}=0 \end{aligned}$$
(44)

At the free surface \(y=\eta _{1}(x_{0},t_{0})\), we have: Continuity of normal and tangential magnetic field components given by

$$\begin{aligned}&(\Psi ^{(1)}_{1x_{0}}-\Psi ^{(2)}_{1x_{0}})-\eta _{1x_{0}} (H_{02}^{(1)}-H_{02}^{(2)}) = 0 \end{aligned}$$
(45)
$$\begin{aligned}&(\Psi ^{(1)}_{1y}-\mu \Psi ^{(2)}_{1y})+ \eta _{1x_{0}} (H_{01}^{(1)}-\mu H_{01}^{(2)})= 0. \end{aligned}$$
(46)

Kinematics and dynamical conditions are

$$\begin{aligned}&\eta _{1t_{0}}=\Phi _{1y} \end{aligned}$$
(47)
$$\begin{aligned}&\Phi _{1t_{0}}+\eta _{1}-\sigma \eta _{1x_{0}x_{0}}-H_{02}^{(1)} \Psi _{1y}^{(1)}+\mu H_{02}^{(2)}\Psi _{1y}^{(2)}\nonumber \\&\quad \quad +H_{01}^{(1)}\Psi _{1x_{0}}^{(1)}-\mu H_{01}^{(2)}\Psi _{1x_{0}}^{(2)}=0. \end{aligned}$$
(48)

The second-order system of equations is given in Appendix.

4 Linear solutions

In this section, we developed first-order solution. This solution satisfies the velocity and magnetic potentials Laplace eqs (38)–(40) and conditions (41)–(46).

Solution of the first-order problem is given in the form of progressive waves with respect to the lower scales by

$$\begin{aligned} \eta _{1}(x_{0},t_{0})=\sum _{n=1}^{\infty }A_{n}\,\cos (k_{n}x_{0}) \,\sin (\omega _{n}t_{0}) \end{aligned}$$
(49)
$$\begin{aligned} \Phi _{1}(x_{0},y, t_{0})= & {} \sum _{n=1}^{\infty }\frac{A_{n} \omega _{n}}{k_{n}\,\tanh (k_{n}h)} \frac{\cosh [k_{n}(y+h)]}{\cosh (k_{n}h)}\nonumber \\&\times \cos (k_{n}x_{0})\cos (\omega _{n}t_{0}) \end{aligned}$$
(50)
$$\begin{aligned} \Psi _{1}^{(1)}(x_{0},y, t_{0})= & {} \sum _{n=1}^{\infty }B_{n}[ H_{01}^{(1)} \,\sin (k_{n}x_{0})\nonumber \\&-H_{02}^{(1)}\,\cos (k_{n}x_{0})]\nonumber \\&\times \frac{\sinh [k_{n}(y+h)]}{\cosh (k_{n}h)}\, \sin (\omega _{n}t_{0}) \end{aligned}$$
(51)
$$\begin{aligned} \Psi _{1}^{(2)}(x_{0},y, t_{0})= & {} \sum _{n=1}^{\infty }B_{n}[H_{01}^{(2)} \,\tanh (k_{n}h) \,\sin (k_{n}x_{0})\nonumber \\&+H_{02}^{(2)}\,\cos (k_{n}x_{0})]\mathrm{e}^{-k_{n}y}\,\sin (\omega _{n}t_{0}),\nonumber \\ \end{aligned}$$
(52)

where \(A_{n}\) is an unknown function denoting the amplitude of the propagating wave mode n. \(\omega _{n}\) and \(k_{n}\) are frequency and wave number of mode n and

$$\begin{aligned} B_{n} =\frac{A_{n}(1-\mu )}{(1+\mu ~\tanh (k_{n}h))}. \end{aligned}$$

To verify the normal velocity conditions at the vertical tank boundaries, we set

$$\begin{aligned} k_{n}=n\pi . \end{aligned}$$
(53)

Introduction of solutions given by (49)–(52) in the dynamic condition at the interface (48) and taking into account kinematics condition (47) leads to the following dispersion relation:

$$\begin{aligned} \omega _{n}^{2}&= k_{n} (1+\sigma k_{n}^{2})\,\tanh (k_{n}h) -\frac{(1-\mu )^{2}k_{n}^{2}~\tanh (k_{n}h)}{\mu (1+\mu ~ \tanh (k_{n}h))}\nonumber \\&\quad \times [(H_{02}^{(1)})^{2}-\mu \tanh (k_{n}h)(H_{01}^{(1)})^{2}]. \end{aligned}$$
(54)

Considering the case of infinite depth, \(\tanh (k_{n}h)\rightarrow 1\), see Browaeys [31], with the same considerations and hypotheses, we obtain the following dispersion relation:

$$\begin{aligned} \omega _{n}^{2}= & {} k_{n} (1+\sigma k_{n}^{2})\nonumber \\&-\frac{(1-\mu )^{2} k_{n}^{2}}{\mu (1+\mu )} [(H_{02}^{(1)})^{2}-\mu (H_{01}^{(1)})^{2}]. \end{aligned}$$
(55)

The second member of the dispersion relation contains two terms. The first term is related to gravito-capillary effects (see Lamb [32]). The second term results from the magnetic field components. Term related to the vertical component of the magnetic field is negative, while the term related to the horizontal component is positive. All the parameters composing this dispersion relation are analysed to determine the sign of the eigenfrequencies when the wave number increases.

5 Results and discussion

Orientation of the magnetic field applied to a magnetic fluid in a reservoir influences the nature of the movement of the free surface. The motion of the free surface is progressive, representing the superposition of the eigenmodes and is not always possible as manifestation of the eigenmode is a consequence of the existence of eigenfrequencies. Gravito-capillary effects on the eigenfrequencies and eigenmodes were studied by Meziani and Ourrad [33].

Fig. 2
figure 2

Square eigenfrequencies vs. wave number values for \(\sigma =0.01\), \(\mu =0.001\) and \(H_{01}^{(1)}=0.1\). Infinite depth at the top figure and finite depth at bottom figure. (\(\centerdot \centerdot \centerdot \)) Without magnetic field, \((+ + +)\) with vertical magnetic field \(H_{02}^{(1)}\) and \((- - -)\) with horizontal and vertical magnetic fields \(H_{01}^{(1)}\) and \(H_{02}^{(1)}\). \((\mathbf{a} )\ H_{02}^{(1)}=0.1\), \((\mathbf{b} ) \ H_{02}^{(1)}=0.2\) and \((\mathbf{c} )\ H_{02}^{(1)}=0.3\).

Full size image

Relations (54) and (55), which give the square of the eigenfrequencies vs. wave numbers contain, in addition to gravity, four parameters which are: magnetic fluid depth, horizontal and vertical components of the external applied magnetic field, magnetic permeability ratio between the outside medium and the magnetic fluid and finally surface tension. In the following, we study the effects of all parameters on the eigenfrequencies and free surface eigenmodes.

5.1 Effects of infinite and finite depths

Analysis of dispersion relations obtained in finite and infinite depths shows clearly that fluid depth does not have a significant influence on the evolution of eigenfrequencies.

Figures 2a–2c show the evolution of the square of the eigenfrequencies with the wave number. These curves show evolution when the horizontal component of the magnetic field is fixed and vertical component of the magnetic field increases. In all the figures, the horizontal component of the magnetic field is fixed at \(H_{01}^{(1)}=0.1\).

In each case, we present curves for the cases of finite depth as well as for the infinite depth. For each curve, we show that the simple lines indicate the square of the eigenfrequency evolution when we take into account only the gravito-capillary effects. The solid lines with the squares indicate the square of the eigenfrequency evolution by taking into account, in addition to gravito-capillary effects, the influence of the vertical component of the applied magnetic field. The third curve indicates the square of the eigenfrequencies by taking into account all the terms, namely, the gravito-capillary effect and the vertical and horizontal components of the magnetic field.

In figure 2a, square of the eigenfrequencies are represented for vertical magnetic field component value equal to \(H_{02}^{(1)}=0.1\). We find that the square of the eigenfrequencies remain always positive when the wave number increases. In this case, the magnetic fluid-free surface remains stable.

Moreover, as the vertical component of the magnetic field increases, figure 2b shows that the square of the eigenfrequencies have two thresholds \(k_{1c}\) and \(k_{2c}\) which are given in tables 1 and 2. We note that the threshold values remain constant as well in both finite depth and infinite depth cases.

For \( k \leqslant k_{1c}\) and \(k \geqslant k_{2c}\), square of the eigenfrequencies are real and positive, implying that magnetic fluid-free interface remains stable. For \( k_{1c}<k < k_{2c}\), eigenfrequencies are imaginary corresponding to the interface of the unstable magnetic field. The instability region grows further as the vertical magnetic field component increases (see tables 3 and 4).

Beyond a critical value of the vertical component of the magnetic field, the magnetic fluid-free surface becomes unstable (see figure 2c).

Table 1 Threshold values \(k_{1c}\) and \(k_{2c}\) limiting unstable zone for \(\sigma =0.01\), \(\mu =0.001\), with vertical and no horizontal magnetic field components in infinite depth case.
Full size table
Table 2 Threshold values \(k_{1c}\) and \(k_{2c}\) limiting unstable zone for \(\sigma =0.01\), \(\mu =0.001\), with vertical and no horizontal magnetic field components in finite depth case.
Full size table
Table 3 Threshold values \(k_{1c}\) and \(k_{2c}\) limiting unstable zone for \(\sigma =0.01\), \(\mu =0.001\), with vertical and horizontal magnetic field components in infinite depth case.
Full size table
Table 4 Threshold values \(k_{1c}\) and \(k_{2c}\) limiting unstable zone for \(\sigma =0.01\), \(\mu =0.001\), with vertical and horizontal magnetic field components in finite depth case.
Full size table

5.2 Effect of the horizontal magnetic field

Application of horizontal external magnetic field allows us to give magnetic fluid-free interface from unstable to stable situation. Magnetic fluid interface stabilisation process is shown in figures 3a–3d. In figure 3a curves show that despite the application of the horizontal magnetic field component, beyond a critical wave number value, magnetic fluid-free interface becomes unstable. This resulted from the negative value of the square of eigenfrequencies. When the horizontal component of the magnetic field increases, it is found (see figure 3b) that the negative values of the square of the eigenfrequencies become low for greater wave numbers.

Fig. 3
figure 3

Effect of horizontal magnetic field on system eigenfrequencies values for \(\sigma =0.1\), \(\mu =0.05\) and \(H_{02}^{(1)}=0.3\). Infinite depth at the top figure and finite depth at bottom figure. \((\circ \circ \circ )\) Without magnetic field, \((+ + +)\) with vertical magnetic field \(H_{02}^{(1)}\) and \((---)\) with horizontal and vertical magnetic fields \(H_{01}^{(1)}\) and \(H_{02}^{(1)}\). \((\mathbf{a} )\ H_{01}^{(1)}=0.7\), \((\mathbf{b} )\ H_{01}^{(1)}=0.8\), \((\mathbf{c} )\ H_{01}^{(1)}=1.1\) and \((\mathbf{d} )\ H_{01}^{(1)}=1.2\).

Full size image

This process continues as the amplitude of the horizontal component gradually increases. We then go back to values where the magnetic fluid-free interface instability zone is circumscribed between the critical values of two wave numbers (figure 3c) and reach a stable situation (figure 3d), for even higher components of the horizontal magnetic field.

The magnetic fluid-free interface is destabilised by applying a vertical magnetic field of small amplitude. To restore this interface stability, we must apply a horizontal magnetic field whose amplitude is significantly greater than that of the vertical magnetic field.

5.3 Effect of the magnetic permeability ratio

In this section, we have investigated the magnetic fluid interface stability based on the magnetic permeability rate.

Fig. 4
figure 4

Effect of the magnetic permeability ratio on system eigenfrequency values for \(\sigma =0.1\), \(H_{01}^{(1)}=0.3\) and \(H_{02}^{(1)}=0.3\). \((\circ \circ \circ )\ \mu =0.05\), \((\square \square \square )\ \mu =0.1\), \((\times \times \times )\ \mu =0.12\), \((\triangle \triangle \triangle )\ \mu =0.2\) and \((\star \star \star )\ \mu =0.5\). \((\mathbf{a} )\) Infinite depth case and \((\mathbf{b} )\) finite depth case.

Full size image

This parameter, noted \(\mu \), is the ratio of the magnetic permeability of the surrounding space to that of themagnetic fluid. Figures 4a and 4b show the square of the eigenfrequencies vs. wave numbers in infinite and finite depth cases for five permeability ratios. Eigenfrequencies vs. waves numbers are shown by taking into account all terms in the dispersion relation.

For low values of magnetic permeability ratio, solid lines with empty circles, eigenfrequencies become imaginary beyond a critical value of wave number. The magnetic fluid-free interface becomes rapidly unstable.

The free surface shows limited instability zone when permeability ratio increases and becomes completely stable for higher ratios. Therefore, when the magnetic fluid is subjected to an external magnetic field, free interface instability does not depend only on the orientation and amplitudes of the external magnetic field, but also on permeability ratio. In other words, interface instability is closely related not only to the nature of the magnetic fluid but also to the medium that contains it.

5.4 Effects of surface tension

The last aspect of this investigation is the influence of surface tension on magnetic fluid-free interface stability when the magnetic fluid is subjected to oblique external magnetic field.

Fig. 5
figure 5

Effect of the surface tension on system eigenfrequency values for \(\mu =0.001\) and \(H_{01}^{(1)}=0.3\). \((\circ \circ \circ )\ \sigma =0.01\), \((\square \square \square )\ \sigma =0.05\), \((\times \times \times )\ \sigma =0.1\), \((\triangle \triangle \triangle )\ \sigma =0.5\) and \((\star \star \star )\ \sigma =1\). \((\mathbf{a} ) \ H_{02}^{(1)}=0.1\), \((\mathbf{b} ) \ H_{02}^{(1)}=0.3\) and \((\mathbf{c} )\ H_{02}^{(1)}=0.6\).

Full size image

Figures 5a–5c include the evolution of square eigenfrequencies with the wave number for five surface tension values when vertical component of the external magnetic field increases and horizontal component is constant.

For the weak vertical magnetic field component, magnetic fluid-free interface is unstable for weak surface tension values, while for great values of the surface tension, magnetic fluid-free interface is stable (figure 5a).

By increasing the vertical component of the external magnetic field, the magnetic fluid interface becomes unstable even for large surface tension values. See change in evolution of the curve in solid lines with inverted triangles between figures 5a and 5b. Also, for high surface tension, unstable zone appears (curve with square in figure 5b).

For a large value of the external magnetic field vertical component, the stability disappears for any surface tension value. The surface tension plays a stabilising role. The stabilising effect is quickly influenced by the applied vertical magnetic field.

6 Conclusion

In this study, we have developed a linear solution of the magnetic fluid-free surface evolution when it is subjected to an oblique external magnetic field. The method adopted to construct the linear solution is well explained. The dispersion relation obtained in the case of finite depth is similar to that obtained for the infinite depth case. A detailed analysis of all the parameters involved in this relationship is performed. Stability of the free surface depends not only on the applied external magnetic field, but also on the ratio of magnetic permeability and surface tension.