Nonlinear hydromagnetic instability of oscillatory rotating rigid-fluid columns

Abstract

The current paper is concerned with the nonlinear stability analysis of rotating magnetic fluid columns. The rotation sources are a mixture of both uniform and oscillating behavior. The motivation behind tackling this topic is the increasing interest in atmospheric and oceanic motions. The system consists of two magnetic phase fluid that fills two infinite vertical cylinders. An azimuthal uniform magnetic field is penetrated on the system. The governing equations of motion, in terms of the Coriolis force and reduced pressure, along with Maxwell’s equation in the quasi-static approximations are considered. Consequently, the disturbance of the interface has an azimuthal behavior. The fluids are fully saturated in porous media. In light of the implication of the nonlinear boundary conditions, the solutions of the linearized equations of motion resulted in a nonlinear characteristic dispersion equation. Utilizing the homotopy perturbation technique, this equation is analyzed. A modification of the latter equation is made to seem like a nonlinear Klein–Gordon equation. The stability criteria are realized in linear as well as nonlinear approaches. A set of diagrams is graphed to illustrate the effects of several non-dimensional numbers on the stability profile in resonance as well as non-resonance cases.

1 Introduction

Ferrofluid or magnetic fluid is a stable colloidal suspension of a nanoscale magnetic particle in a carrier liquid; for an illustration, see Rosensweig [1]. In this work, Rosensweig provided a framework for identifying the behavior of magnetic fluids. In other words, magnetic fluids, as iron, behave like magnetized materials due to the action of a magnetic field. Simultaneously, they exhibit the same properties as the ordinary fluids. Moreover, Rosensweig [1] showed important applications for them in seals, cooling, and other implementations. It was shown that the presence of a normal field at the interface exerted a destabilizing influence, and simultaneously the tangential one had a stabilizing effect on the stationary configuration of ferrofluids. This stabilizing influence has been claimed to hold for two perfect fluids in a relative motion. Furthermore, recent interest in magnetic fluids has concentrated on biomedical, pharmaceutical, flow manipulation, and other small scale applications; for instance, see Lűbbe et al. [2]. They provided an overview of the applications of ferrofluids along with magnetic fields. Moreover, they advanced several medical applications, especially in the anticancer process. Furthermore, they have a wide range of applications in the surface of separation between two magnetic fluids. Therefore, the stability properties of magnetic fluids, involving the interface and implication of magnetic fields, are of great practical interest for both existing and future practical applications. The effect of radial and axial magnetic fields of various strengths, on natural convection in a vertical cylindrical annular cavity, has been numerically studied by Sankar et al. [3]. They found that the magnetic field has a more effective mechanism when it is perpendicular to the direction of the primary flow. This phenomenon has a serious implication for the design of magnetic systems for stabilizing or weakening the convective effects. The stability in a layer channel flow fill of magnetic fluids was investigated by Yecko [4]. Yecko [4] obtained the neutral curves of stability, and his analysis showed that the stability characteristics mainly depend on the magnetic properties of the material. Furthermore, the stabilization/destabilization of the tangential/normal fields was shown by Rosensweig [1].

Girish et al. [5] studied the flow in the annular region between three vertical coaxial cylinders. They showed that the axial velocity profile was reduced by an increase in the Grashof number. However, for larger Grashof number, the axial velocity alters moderately in the passage bounded by an isothermal wall for both thermal cases. El-Dib and Mady [6] studied the linear and nonlinear stability profile of Rayleigh–Taylor instability of two magnetized fluids in the presence of tangential/normal magnetic field intensity. Their analysis resulted in a transcendental integro-Duffing equation. The stability criteria were theoretically formulated and numerically confirmed. Venkatachalappa et al. [7] reported the effect of axial or radial magnetic fields on a double-diffusive natural convection in a vertical cylindrical annular cavity. They aimed to present a numerical study to understand the effect of magnetic field on a double-diffusive convection in the annular cavity. They found that the magnetic field suppresses the double-diffusive convection only for small buoyancy ratios. With regard to porosity of different sizes and locations of the heater, its influence on the average Nusselt number is small at the low Darcy number, while it becomes significant at higher values of Darcy number. Furthermore, increasing porosity increases the average Nusselt number. Sankar et al. [8] examined a two-dimensional, axisymmetric cylindrical annular enclosure along with the important geometrical parameters. They found that porosity, at different sizes and locations of the heater, has an influence on the average Nusselt number, and its effect becomes of significance of higher values of Darcy number.

Understanding the rotating fluids is fundamental to explaining/predicting atmospheric or oceanographic phenomena. In addition, this topic is important in addressing technological problems ranging from the centrifugal to spinning shell; for instance, see Roberts and Soward [9]. Most of the examinations of rotating fluids have been motivated by geophysical applications because rotation properties are of principal importance in these circumstances. Sympathetic atmospheric and oceanic motions are of vital interest. Rotating fluids are identified in relation to the dispersion of pollution by biochemical into the atmosphere and the oceans, for illustration see Hopfinger [10]. Neumann et al. [11] analyzed explicit criteria that indicate the appropriateness of rotating packed beds for the perseverance of industrial applications for gas–liquid, vapor–liquid, and liquid–liquid interfaces. For this objective, distinguishing decision trees were familiarized in order to simplify the documentation of developments on this topic. Recently, a review of instability and consequent natural convection in rotating porous media was presented by Vadasz [12]. He showed that Taylor–Proudman columns and geophysical flows happening in rotating porous media are equivalent what takes place in pure fluids. The effect of Coriolis acceleration was also discussed. The interest in studying the fluid dynamics in rotating systems comes from the appearance of a specific category of waves, known as inertial waves, which is widely encountered in nature. Therefore, the instability of a rotating cylindrical fluid column has drawn a great deal of interest in accordance with its wide applications, ranging from the liquid atomization, through combustion enhancement nozzle design of the spray and the breakdown of vortex cores, to combination and painting processes, as well as astronomical telescopes. For instance, see Basta et al. [13]. Venkatachalappa et al. [14] performed a numerical calculation to investigate the effect of rotation on the axisymmetric flow in two vertical cylinders rotating at different angular velocities. They found that when the rotation of the outer cylinder is on low speed, the outer boundary flow is confined to a thin region. Meanwhile, the return flow occupies a major portion of the annulus for moderating the Grashof number. The classical work on the linear stability of a fluid cylinder has been attracting a great deal of interest in plasma physics, practical engineering, astrophysics, and many other practical applications. To the best of our knowledge, Rayleigh [15] was considered the first scientist who worked on this topic. Rayleigh [15] showed that a non-rotating inviscid column is unstable to an axisymmetric deformation whose wavelength in the axial direction is greater than the circumference of the column and stable for all non-axisymmetric disturbances. After more than fifty years, Hocking and Micheal [16] found that the liquid column, when acted upon by a uniform angular velocity $\Omega$, becomes stable according to the planar azimuthal wave number $m$, provided that

$$\sigma \ge \frac{\rho R^{3} \Omega^{2} }{m(m + 1)},$$

(1)

where $\sigma$ stands for the surface tension, $\rho$ refers to the incompressible fluid density, and $R$ is the undisturbed fluid column.

Hocking and Micheal [16] first derived the stability criterion of a perfect liquid column subjected to the axial disturbance in the following form:

$$\Phi \ge \frac{1}{{k^{2} - 1}},$$

(2)

where $\Phi$ is the ratio of the surface tension of the centrifugal force and the inertia to the viscous force, $k$ is the axial wavenumber which is normalized to the fluid column $R$.

Additionally, Hocking and Micheal [16] showed that the stability criterion for the viscous column should be independent of the following rotational Reynolds number:

$$R_{e} = \frac{{R^{2} \Omega }}{\nu }\,,$$

(3)

where $\nu$ represents the kinematic viscosity of the fluid column.

Joseph et al. [17] are the first to formulate a general stability criterion. This criterion was obtained by minimizing an appropriate potential function. Throughout this study, they deliberated the movement of two fluid rings with different densities and viscosities and rotating with same angular velocity. Furthermore, their results gave a partial explanation of stability and shape of the rollers of viscous oils that rotate in the water.

Undoubtedly, the instability at the fluid interface, moving between two porous media, is of excessive significance in numerous applications, including groundwater hydrology, oil production, civil engineering, and other uses. Nayfeh [18] provided an extensive investigation of the stability at the interface of two different fluids of different densities and viscosities throughout permeable media. He also investigated the instability of the interface between two moving liquids. The results showed that nonlinearity was destabilizing owing to the decrease in the surface tension force. Additionally, the deviations of Darcy's law were found to be stabilizing when the flow was from the denser to the lighter fluid and vice-versa. Raghavan and Marsden [19] introduced a new approach at which a liquid interface between two immiscible fluids may become unstable. This stability was similar to that of Kelvin–Helmholtz instability. They showed that the aligned flow of liquids may stabilize density gradients. Bishnoi and Agrawal [20] studied the stability of the density of stratified flows throughout porous media. They revealed physical situations where the flow is governed by Darcy’s law. Their analysis included a relationship that revealed two or three-dimensional disturbances. Sharma and Kumar [21] investigated Rayleigh–Taylor instability of a Newtonian viscous fluid above an Oldroydian visco-elastic fluid throughout porous media. Their analysis involved a horizontal magnetic field and a uniform rotation. They showed that the system becomes unstable for a viscous fluid overlying an Oldroydian visco-elastic fluid throughout porous media. Recently, Moatimid and Zekry [22] investigated the nonlinear instability of a non-Newtonian fluid of the Walters’ B type. The fluids filled the regions inside and outside a vertical circular cylinder. The fluids are saturated in porous media. Several special cases were reported upon convenient data choices. They showed that the nonlinear stability approach divided the phase plane into several parts of stability/instability. Xu and Li [23] examined the nonlinear stability approach of an infinite horizontal fluid layer saturated in porous media. They proved that the nonlinear stability is global and exponential.

The current article offers an extension to our previous work as given by El-Dib et al. [24] to include the nonlinear stability analysis of a uniform/periodic rotating liquid column. Therefore, the rotation is a mixture which displays uniform and oscillating behavior. The fluid column is held by capillary forces in the existence of an azimuthal magnetic field for non-axisymmetric and two-dimensional perturbations. A weakly nonlinear approach is based on the concept of the linear solutions of the governing equations of motion along with the implication of the convenient nonlinear boundary conditions. To crystallize the presentation of the problem, the rest of the manuscript is organized as follows: Sect. 2 reports general features of our previous work [24]. Section 3 is devoted to examining nonlinear stability analysis by modifying the homotopy perturbation method (HPM). This section involves a detailed analysis of the resonance as well as non-resonance cases. Finally, Sect. 4 is devoted to presenting the concluding remarks in light of the findings of the analysis.

2 Problem statement and relevant equations

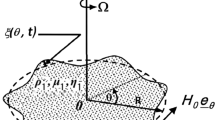
A system consisting of two infinitely long liquid columns that are composed of an incompressible, inviscid, and homogenous liquid is deliberated. The liquids are saturated in porous media; for the sake of simplicity, they are of unit porosity. The gravitational force $(g)$, which acts vertically downwards, is taken into account. It is convenient to work with the cylindrical polar coordinates $(r,\,\theta ,\,z)$. The velocity components are taken as $(u,\,v,\,w)$, and uniform and periodic angular velocities of rotation are given as: $\underline{\Omega } = (\Omega + \tilde{\Omega }\,\cos \omega t)\,\underline{e}_{z}$. Therefore, the column performs a rigid-body rotation around its vertical axis of symmetry. In equilibrium configuration, the interface represents a circular cylinder of the radius $R$. An azimuthal uniform magnetic field of strength $H_{0}$ acts on both fluids. It is presumed that the inner liquid column has a uniform density $\rho_{1}$, magnetic permeability $\mu_{1}$, and kinematic viscosity $\eta_{1}$. The outer column is embedded in an unbounded rotating liquid, having a uniform density $\rho_{2}$ and magnetic permeability, kinematic viscosity $\eta_{2}$ and the symbol $\kappa$ refer to the medium permeability. Keep in mind that the latter parameter is assumed to be of the same value in both media. Generally, the subscripts 1 and 2 refer to inner and outer magnetic columns, respectively. A schematic diagram of the configuration of the physical model is sketched in Fig. 1.

Fig. 1

Sketch of the physical model

The non-steady perturbed equations of motion are written in a rotating frame of reference as given by Weidman et al. [25]. Therefore, the fundamental governing equations of motion, for a bulk of magnetic fluid phases, are written as:

$$\frac{{{\text{d}}\underline{V} }}{{{\text{d}}t}} + 2(\underline{\Omega } \wedge \underline{V} ) = - \frac{1}{\rho }\nabla \pi - g\underline{e}_{z} - \frac{\eta }{\kappa }\underline{V} ,$$

(4)

with the incompressibility condition that is given by

$$\nabla \cdot \underline{V} = 0,$$

(5)

where $\pi = p - \rho ((\Omega + \tilde{\Omega }\,\cos \omega t)\underline{e}_{z} \wedge \underline{r} )^{2} \,/\rho$ is defined as “reduced pressure”, $p$ represents hydrostatic pressure. In other words, it can be said that the centrifugal force is included in the hydrostatic pressure to yield a new pressure, which is called the reduced pressure. The Coriolis force is represented by the term $2(\underline{\Omega } \wedge \underline{V} )$.

The following analysis is considered as in the Kelvin–Helmholtz model, so that the total velocity vector can be represented by $\underline{V} \,(u,\,r(\Omega + \tilde{\Omega }\,\cos \omega t) + v,\,\,w)$, where $r\,(\Omega + \tilde{\Omega }\,\cos \omega t)$ gives a non-perturbed velocity. For more opportunities and without any loss of generality, only two-dimensional disturbances are supposing. Therefore, one may assume that $w = 0\,.$

On the other hand, for simplicity, it is assumed that no free surface currents act in any of the two regions. Subsequently, Ampere’s law requires the magnetic field $\underline{H}$ to be curl-free. Consequently, the magneto-quasi-static approximation is valid for the problem at hand; for illustration, see Melcher [26]. In view of the validity of the quasi-static approximation, a scalar function $\varphi$ representing scalar magnetic potential may be introduced as follows:

$$\underline{H} = - \nabla \varphi \,.$$

(6)

Each of the two regions has a uniform magnetic permeability; it follows that Gauss’ law requires that scalar magnetic field should obey the following Laplace’s equation:

$$\nabla^{2} \varphi = 0.$$

(7)

In the equilibrium state, the equilibrium hydrostatic pressure may be given as

$$\pi_{j}^{(0)} = - \rho_{j} gz + C(t)_{j} ,\,\,\,\,j = 1,2$$

(8)

where the superscript $(0)$ refers to equilibrium state and $C(t)_{j}$ is a time-dependent constant of integration.

From the continuity of the normal stress at the interface, the jump of the pressure is found to be zero whence:

$$C(t)_{1} - C(t)_{2} = \frac{\sigma }{R} + (\rho_{2} - \rho_{1} )gc + \tfrac{1}{2}(\mu_{2} - \mu_{1} )H_{0}^{2} ,$$

(9)

where $\sigma$ is the amount of surface tension.

Simultaneously, as stated in the problem formulation, the motion is considered in the plane $z = c$ for instance. Therefore, $C(t)_{1}$ and $C(t)_{2}$ remain constant during the motion.

2.1 Perturbation equations

To complete the formulation of the boundary-value problem, the surface geometry and the supplement magnetic equations, along with the corresponding appropriate nonlinear boundary conditions, must be addressed. After a limited, but a finite departure from the initial configuration, the surface deflection may be expressed by considering the standard normal modes analysis; for instance, see Chandrasekhar [27]. In light of this concept, the surface deflections $\xi (\theta ;t)$ may be represented as a sinusoidal wave of finite amplitude, where after disturbance, the interface becomes as follows:

$$r = R + \xi (\theta ;t),$$

(10)

where

$$\xi (\theta ,t) = \gamma (t)\,e^{im\theta } + c.c.\,\,\,\,\,(0 \le \theta \le 2\pi ),$$

(11)

herein $\gamma (t)$ is an unknown function of time $t$, representing the amplitude of the perturbations of the initial surface of the column which determines the behavior of the amplitude of the disturbance of interface; the integer m is an azimuthal wavenumber which is assumed to be real, integer, and positive, and $c.c.$ refers to the complex conjugate of the preceding term.

It is appropriate to define bounding surface as the locus of points satisfying the relation $r = R + \xi (\theta ,t)$, then the unit normal vector to the interface will be given by

$$\underline{n} = \left( {\underline{e}_{r} - \frac{i\,m}{r}\xi \,\underline{e}_{\theta } } \right)\left( {1 - \frac{{m^{2} }}{{r^{2} }}\xi^{2} } \right)^{ - 1/2} .$$

(12)

It follows that all disturbances are assumed to be of two-dimensional form. By the two-dimensional disturbances, the flow field depends on the azimuthal direction of propagation, which will be along with $\theta$- azimuthal and r-horizontal directions. The limiting case of a very long longitudinal wavelength is considered here, so that the dependence of the variable z can be ignored.

Therefore, along with the two-dimensional flow case, the various perturbations may be represented in the following form:

$$\Re (r,\theta ,t) = \hat{\Re }(r,t)\,e^{im\theta } ,$$

(13)

where $\hat{\Re }(r,\,t)$ stands for any linear physical quantity.

For two-dimensional flow, the linearized form of the equations of motion may be written as:

$$Lu - 4\,(\Omega + \tilde{\Omega }\,\cos (\omega t))v = - \frac{1}{\rho }\frac{\partial \,\pi }{{\partial \,r}},$$

(14)

$$Lv + 4(\Omega + \tilde{\Omega }\,\cos (\omega t))u = - \frac{im}{{\rho \,r}}\pi ,$$

(15)

and

$$\frac{\partial \,u}{{\partial \,r}} + \frac{imv}{r} + \frac{u}{r} = 0,$$

(16)

where an operator $L$ is defined as: $L \equiv \frac{\partial }{\partial t} + \frac{\eta }{\kappa } + im(\Omega + \tilde{\Omega }\,\cos \omega t)$.

Typically, for two-dimensional flow, one may identify a stream function $\psi \left( {r,\,\theta ;t} \right)$ such that:

$$Lu = - \frac{im}{r}\,\psi ,\,{\text{and}}\,Lv = \frac{\partial \psi }{{\partial r}}.$$

(17)

The stream function may be determined by eliminating the pressure of equations of motion. For this purpose, a combination of Eqs. (13), (14) and (17) yields

$$\left( {r^{2} \frac{{\partial^{2} }}{{\partial \,r^{2} }} + r\frac{\partial }{\partial \,r} - m^{2} } \right)\,\,\hat{\psi }(r,t) = 0,$$

(18)

which has the solution:

$$\hat{\psi }(r,t) = A_{1}^{*} (t)\,r^{m} + A_{2}^{*} (t)\,r^{ - m} .$$

(19)

For the finite solutions, one may obtain

$$\psi_{1} (r,\theta ,t) = A_{1} (t)\,r^{m} e^{i\,m\,\theta } \,\,\,\,\,\,\,\,\,\,\,\,\,\,(r \le R),$$

(20)

and

$$\psi_{2} (r,\theta ,t) = A_{2} (t)\,r^{ - m} e^{i\,m\,\theta } \,\,\,\,\,\,\,\,\,(r \ge R),$$

(21)

where A₁(t) and A₂(t) are arbitrary time-dependent functions to be determined from the advantages of the nonlinear boundary conditions.

Once more, returning back to the magnetic part, in accordance with two-dimensional flow considered here, Laplace’s equation, as given in Eq. (7) that governs the magnetic potential $\hat{\varphi }(r,t)$, may be written as:

$$\left( {r^{2} \frac{{\partial^{2} }}{{\partial \,r^{2} }} + r\frac{\partial }{\partial \,r} - m^{2} } \right)\,\,\hat{\varphi }\,(r,t) = 0,$$

(22)

which has the following solutions:

$$\varphi_{1} (r,\theta ,t) = B_{1} (t)\,r^{m} e^{i\,m\,\theta } \,\,\,\,\,\,\,\,\,\,\,\,\,\,(r \le R),$$

(23)

and

$$\varphi_{2} (r,\theta ,t) = B_{2} (t)\,r^{ - m} e^{i\,m\,\theta } \,\,\,\,\,\,\,\,\,(r \ge R),$$

(24)

where B₁(t) and B₂(t) are time-dependent functions to be determined from the acceptable nonlinear boundary conditions.

To study the interface stability of the flow under consideration, two-dimensional small disturbances are introduced into governing equations of motion as well as the boundary conditions. For this objective, consider a small perturbation about initial configuration of the cylindrical interface. The qualified nonlinear boundary conditions will be presented in the next subsection.

2.2 Nonlinear boundary conditions

In light of the system adopted here, there are two relevant categories of boundary conditions. The first deals with the conditions at an infinite/finite distance from the interface. Simultaneously, the second one occurs at the surface of separation. The former expresses the requirements as magnetic field and velocities tend to zero at infinity. The interface boundary conditions must be satisfied on the surface of separation, which is located at $r = R + \xi$. The last conditions may be represented as follows:

• (i) At the boundary between the two fluids, it is required that fluid velocity field satisfies an equation expressing the assumed material character of dividing surface. This is called the kinematic boundary condition, hence, one gives

  $$u_{j} = \frac{\partial \,\xi }{{\partial \,t}} + im\,\left( {\Omega_{j} + \tilde{\Omega }_{j} \,\cos (\omega t) + \frac{{v_{j} }}{r}} \right)\,\xi \,\,\,\,\,\,\,\,\,\,j = 1,2\,\,\,\,\,\,r = R.$$

  (25)

• (ii) For the magnetic path, in the absence of the surface currents, the jump in the tangential components of the magnetic field is zero across the interface; this leads to

  $$\left\| {\frac{{\partial \phi }}{{\partial \theta }}} \right\| + im\xi \left\| {\frac{{\partial \phi }}{{\partial {\mkern 1mu} r}}} \right\| = 0{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} r = R,$$

  (26)

  where || || represents the jump across the interface; it is defined as $\left\| \bullet \right\| = ( \bullet )_{1} - ( \bullet )_{2} .$

Additionally, the normal magnetic displacement is continuous at the interface. Thus, one finds

$$\left\| {\mu \frac{{\partial \phi }}{{\partial {\mkern 1mu} r}}} \right\| - \frac{{im}}{{r^{2} }}\left( {\left\| {\mu \frac{{\partial \phi }}{{\partial \theta }}} \right\| - rH_{0} \left\| \mu \right\|} \right)\xi = 0{\mkern 1mu} ,{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} r = R.$$

(27)

The remaining boundary condition may be stated as: At the boundary two fluids, the fluid and magnetic stresses must be balanced. The derivation follows the work of Melcher [26] as follows:

$$\left\| {\sigma_{i\,j} } \right\|\,\,n_{j} \,\, = - \sigma (\nabla \cdot \underline{n} )\,n_{i} ,$$

(28)

where $n_{i}$ and $n_{j}$ are the components of the unit vector $\underline{n}$. The components of these stresses consist of the following hydrodynamic pressure and magnetic stresses:

$$\sigma_{rr} = - P + \tfrac{1}{2}\mu (H_{r}^{2} - H_{\theta }^{2} ),$$

(29)

$$\sigma_{\theta \theta } = - P - \tfrac{1}{2}\mu (H_{r}^{2} - H_{\theta }^{2} ),$$

(30)

and

$$\sigma_{r\theta } = \mu \,H_{r} H_{\theta } ,$$

(31)

where $\sigma_{rr}$ and $\sigma_{\theta \theta }$ are defined as the normal stresses and $\sigma_{r\theta }$ represents the shear one.

At this end, one may proceed to derive the nonlinear characteristic equation that governs the surface evolution, keeping in mind that the elevation function ξ is finite.

2.3 Derivation of the nonlinear characteristic equation

To solve the linearized equations of motion of the system under consideration, the favorable nonlinear boundary conditions are required. For this purpose, in light of the two-dimensional finite disturbances, the boundary-value problem is well defined. As customary in the hydrodynamic stability theory as established by Chandrasekhar [27], all perturbed physical quantities have exponential time dependence and a periodic spatial one.

Substituting from Eqs. (20) and (21) into Eq. (25), and from Eqs. (23) and (24) into Eqs. (26) and (27), the solutions corresponding to the nonlinear boundary conditions are related to the interface displacement $\xi$ as

$$\psi_{1} (r,\theta ;\,t) = \frac{i}{m}\frac{{(\xi_{t} + im(\Omega_{1} + \tilde{\Omega }_{1} \cos (\omega t))\,\xi )R^{2} }}{(R + m\xi )}\left( \frac{r}{R} \right)^{m} ,\,\,\,\,\,\,r \le R,$$

(32)

$$\psi_{2} (r,\theta ;\,t) = \frac{i}{m}\frac{{(\xi_{t} + im(\Omega_{2} + \tilde{\Omega }_{2} \cos (\omega t))\,\xi )R^{2} }}{(R - m\xi )}\left( \frac{R}{r} \right)^{m} ,\,\,\,\,\,r \ge R,$$

(33)

$$\phi _{1} (r,{\mkern 1mu} \theta ;{\mkern 1mu} t) = - \frac{{iR(\mu _{1} - \mu _{2} )H_{0} \xi }}{{(\mu _{1} + \mu _{2} )(R + m\xi )}}\left( {\frac{r}{R}} \right),{\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} {\mkern 1mu} r \le R$$

(34)

and

$$\phi_{2} (r,\,\theta ;\,t) = - \frac{{iR(\mu_{1} - \mu_{2} )H_{0} \xi }}{{(\mu_{1} + \mu_{2} )(R - m\xi )}}\left( \frac{R}{r} \right),\,\,\,\,\,\,\,\,r \ge R$$

(35)

The above distributions of velocity stream functions $\psi_{1} (r,\theta ;t)$, $\psi_{2} (r,\theta ;t)$ and magnetic potential functions $\phi_{1} (r,\theta ;t)$ and $\phi_{2} (r,\theta ;t)$ contain nonlinear terms in the elevation parameter $\xi$. This nonlinearity occurs because of the usage of the nonlinear boundary condition.

To evaluate the distribution of the pressure, substitute from Eqs. (32) and (33) into Eq. (15) to find

$$\pi_{1} (r,\theta ;\,t) = - \frac{{\rho_{1} }}{m\kappa }\left( {\frac{{R^{2} }}{R + m\xi }} \right)\left[ \begin{gathered} \kappa \xi_{tt} + \eta_{1} \xi_{t} + m\kappa (m - 2)(\Omega_{1} + \tilde{\Omega }_{1} \cos (\omega t))^{2} \xi + \hfill \\ i\left( {2i\kappa \left( {m - 1} \right)(\Omega_{1} + \tilde{\Omega }_{1} \cos (\omega t))\xi_{t} + m\eta_{1} (\Omega_{1} + \tilde{\Omega }_{1} \cos (\omega t))\xi } \right) \hfill \\ \end{gathered} \right]\left( \frac{r}{R} \right)^{m} ,\,\,\,\,\,r \le R$$

(36)

and

$$\pi_{2} (r,\theta ;\,t) = \frac{{\rho_{2} }}{m}\left( {\frac{{R^{2} }}{R - m\xi }} \right)\left[ \begin{gathered} \kappa \xi_{tt} + \eta_{2} \xi_{t} + m\kappa (m - 2)(\Omega_{2} + \tilde{\Omega }_{2} \cos (\omega t))^{2} \xi + \hfill \\ i\left( {2i\kappa (m - 1)(\Omega_{2} + \tilde{\Omega }_{2} \cos (\omega t))\xi_{t} + m\eta_{2} (\Omega_{2} + \tilde{\Omega }_{2} \cos (\omega t))\xi } \right) \hfill \\ \end{gathered} \right]\left( \frac{R}{r} \right)^{m} .\,\,\,\,\,r \ge R$$

(37)

At this stage, by inserting Eqs. (32–37) into the normal stress tensor as given in Eq. (28), the stream functions $\psi_{1} (r,\theta ;t)$, $\psi_{2} (r,\theta ;t)$ and magnetic potential functions $\phi_{1} (r,\theta ;t)$ and $\phi_{2} (r,\theta ;t)$ are replaced by their equivalents in terms of the surface elevation parameter $\xi$. This procedure gives a very complicated nonlinear equation in the parameter $\xi$. Keeping in mind that the surface deflection function $\xi$ is small, the implication of the binomial expansion is convenient. The calculations are lengthy but straightforward. Up to the third order of $\xi$, one finds a nonlinear equation in the interface displacement ξ. To save a space on the paper, it will now be omitted. Actually, the nonlinear characteristic equation has a complex nature. In the foregoing analysis, the two parts of the nonlinear characteristic equations will be presented. To simplify the calculations, it is convenient to write the nonlinear characteristic equation in a non-dimensional form:

To simplify the numerical calculations, it is appropriate to impose the nonlinear characteristic equation in terms of convenient non-dimensional quantities. For this objective, consider the following non-dimensional parameters:

$$\rho _{2} = \rho \,\rho _{1} ,\,\,\,\Omega _{2} = \hat{\Omega }\,\Omega _{1} ,\,\tilde{\Omega }_{2} = \Omega ^{*} \,\tilde{\Omega }_{1} ,\eta _{2} = \eta \,\eta _{1} ,\,\mu _{2} = \mu \,\mu _{1} \,{\text{and}}\,H_{0}^{2} = H_{0}^{{*2}} \mu _{1} \sqrt \kappa /\sigma .$$

For straightforwardness, the “$*$” mark may be ignored from the magnetic field intensity $H_{0}^{*2}$ in the following analysis. After employing this choice, the following non-dimensional numbers will appear in the dispersion relation:

• Taylor numbers $\hat{T}a = 4\Omega_{1}^{2} \kappa^{2} /\eta_{1}^{2}$ and $Ta^{*} = 4\tilde{\Omega }_{1}^{2} \,\kappa^{2} /\eta_{1}^{2}$ characterize the importance of the centrifugal "forces" or the so-called inertial forces due to the rotation of fluid relative to the viscous forces.

• Weber numbers $\hat{W}e = \rho_{1} \,\Omega_{1}^{2} \kappa \sqrt \kappa /\sigma$ and $We^{*} = \rho_{1} \,\tilde{\Omega }_{1}^{2} \kappa \sqrt \kappa /\sigma$ distinguish the ratio between the inertial and surface tension forces. They indicate whether the kinetic or surface tension energy is dominant or not.

• Ohnesorge number $Oh = \lambda_{1} /\sqrt {\sigma \rho_{1} \sqrt \kappa }$ relates viscous forces to an inertial and surface tension force, where $\lambda_{1} = \rho_{1} \eta_{1}$ represents the dynamic viscosity.

Along with the previous non-dimensional procedure, owing to the real nature of the surface deflection, it is appropriate to split the real and imaginary parts as follows:

The real part yields

$$\begin{aligned} & a_{0} \xi_{tt} + a_{1} \xi_{t} + \left( {c_{0} + c_{2} \cos 2\omega t + c_{3} \cos \omega t} \right)\xi + a_{2} \xi_{tt} \xi + a_{2} \xi_{t}^{2} + a_{3} \xi_{t} \xi \\ & \quad + \left( {a_{4} + d_{1} + c_{7} \cos 2\omega t + c_{8} \cos \omega t} \right)\xi^{2} + a_{5} \xi_{tt} \xi^{2} - a_{5} \xi \xi_{t}^{2} + a_{6} \xi_{t} \xi^{2} \\ & \quad + \left( {a_{7} + d_{2} + c_{12} \cos 2\omega t + c_{13} \cos \omega t} \right)\xi^{3} = 0. \\ \end{aligned}$$

(38)

Simultaneously, the imaginary part results in

$$\begin{aligned} & \left( {b_{1} + c_{1} \cos \omega t} \right)\xi_{t} + \left( {b_{2} + c_{4} \cos \omega t + c_{5} \omega \sin \omega t} \right)\xi + \left( {b_{3} + c_{6} \,\cos \omega t} \right)\xi_{t} \xi \\ & \quad + \left( {b_{4} + c_{9} \cos \omega t + c_{10} \omega \sin \omega t} \right)\xi^{2} + \left( {b_{5} + c_{11} \cos \omega t} \right)\xi_{t} \xi^{2} \\ & \quad \left( {b_{6} + c_{14} \cos \omega t + c_{15} \omega \sin \omega t} \right)\xi^{3} = 0, \\ \end{aligned}$$

(39)

where coefficients $a_{i} ,\,b_{i} ,\,c_{i} \,{\text{and}}\,\,d_{i}$ are given in “Appendix”.

The differentiation Eq. (38) will be added to Eq. (39) to give the well-known Ince equation; for instance, see Moussa [28]. Actually, this equation is more general than the well-known nonlinear Mathieu equation. The following Section will be devoted to analyzing the stability profile of this equation. A modified approach depending mainly on the HPM will be adapted.

3 Nonlinear stability analysis by utilizing a modified formulation of the HPM

The perturbation methods are widely applied techniques utilized in the practical engineering problems. The classical perturbation techniques, ranging from the straightforward method to the multiple time scale techniques, are all known for their dependence on the existence of a small parameter in the considered problem. Often, the absence of this parameter forces the user to consider weakness in the problem. To eliminate the limitation of “small parameter”, which is assumed in the perturbation method, a new technique based on the homotopy terminology will be adopted. The Chinese mathematician He [29] has proposed this new perturbation method which does not require a small parameter in the equation. The new method takes full advantage of the traditional perturbation methods and homotopy technique. These advantages may be summarized as follows:

• To obtain an optimal solution, choosing the zero-order equation is arbitrary.

• A few iterations are sufficient to achieve an accurate approximate solution.

• In order to reach successful results, it is possible to add and subtract any term.

Accordingly, away from using the classical perturbation technique, a nonlinear problem is transformed into an infinite number of simple linear problems. Effectively, letting the small parameter float and converge to the unity, the problem will be converted into a special perturbation problem with incorporating a small parameter. Therefore, the method receives the abbreviation HPM. This method is effective, processing and powerful. The new scheme has been applied to linear and nonlinear ordinary and partial differential equations. In analyzing the Duffing equation with a displacement time-delay, El-Dib [30] utilized two perturbation techniques to analyze damped Duffing equation with a time delayed displacement variable as well as the nonlinear frequency analysis. Recently, Moatimid et al. [31] provided approximate solutions of coupled nonlinear oscillation by utilizing the multiple scales in view of the homotopy approach. Throughout this approach, the analytical approximate is assumed as a sum of an infinite series that converges rapidly to an accurate solution. Furthermore, the stability analysis revealed both the resonant and non-resonant cases. Recently, Fedorov et al. [32] demonstrated that the HPM may be employed to obtain an analytical approximate solution to their model. They showed that the obtained solutions were in good agreement with the existing numerical methods. Additionally, their analysis revealed different HPM operators.

The dependent variable in the nonlinear characteristic that is composed of Eqs. (38) and (39) is $\xi \left( {\theta ,t} \right)$. This equation contains the partial derivative with respect to the time $t$. It may be modified to become like a Klein–Gordon equation. Recently, El-Dib et al. [33] aimed to provide a modification of the HPM by adding and subtracting a second-order differential operator to the homotopy equation. This approach may be accomplished throughout the construction of the given homotopy equation as follows:

$$\Im (\xi ) + \delta \,\left( {\Re (\xi ) + N_{2} (\xi ) + N_{3} (\xi )} \right) = 0;\,\,\delta \in \left[ {0,1} \right],$$

(40)

where the linear and nonlinear operators that correspond to the above homotopy equation are chosen as follows:

The linear terms may be listed along with two partitions $\Im (\xi )$ and $\Re (\xi ).$ The partition $N_{2} (\xi )$ refers to all the second-order nonlinear terms. The last partition $N_{3} (\xi )$ denotes all the cubic nonlinear terms. In order to obtain an optimal solution, one may impose any linear term of the first order on the second one. These terms may be listed as follows:

$$\Im (\xi ) = \xi_{tt} - \xi_{\theta \theta } + \omega_{0}^{2} \xi ,$$

(41)

where $\omega_{0}^{2} = c_{0} /\left( {a_{0} + b_{1} } \right).$

$$\begin{aligned} \Re (\xi ) & = \xi_{\theta \theta } + \frac{1}{{a_{0} + b_{1} }}\left( {c_{1} \cos \omega t\xi_{tt} + \left( {a_{1} + b_{2} + c_{4} \cos \omega t - (c_{1} - c_{5} )\,\omega \sin \omega t} \right)\xi_{t} } \right. \\ & \quad + \left( {c_{2} \cos 2\omega t + (c_{3} + c_{5} \omega^{2} )\cos \omega t - \omega \,c_{4} \sin \omega t} \right)\xi , \\ \end{aligned}$$

(42)

$$\begin{aligned} N_{2} (\xi ) & = \left( {a_{2} + b_{3} + c_{6} \cos \omega t} \right)\left( {\xi \xi_{tt} + \xi_{t}^{2} } \right) + \,\left( {a_{3} + 2b_{4} + 2c_{9} \cos \omega t - (c_{6} - 2c_{10} )\omega \sin \omega t} \right)\xi_{t} \xi \\ & \quad + \left( {a_{4} + d_{1} + c_{7} \cos 2\omega t + (c_{8} + c_{10} \,\omega^{2} )\cos \omega t - \omega c_{9} \sin \omega t} \right)\xi^{2} , \\ \end{aligned}$$

(43)

and

$$\begin{aligned} N_{3} (\xi ) & = \left( {a_{5} + b_{5} + c_{11} \cos \omega t} \right)\xi^{2} \xi_{tt} - \left( {a_{5} - 2b_{5} - 2c_{11} \cos \omega t} \right)\xi \xi_{t}^{2} \\ & \quad + \left( {a_{6} + 3b_{6} + 3c_{14} \cos \omega t - (c_{11} - 3c_{15} )\omega \sin \omega t} \right)\xi_{t} \xi^{2} \\ & \quad + \left. {\left( {a_{7} + d_{2} + c_{12} \cos 2\omega t + (c_{13} + c_{15} \,\omega^{2} )\cos \omega t - \omega \,c_{14} \sin \omega t} \right)\xi^{3} } \right)\,. \\ \end{aligned}$$

(44)

It should be noted that as $\delta \to 1,$ the additional term $\xi_{\theta \theta }$ will disappear and the homotopy Eq. (40) will be reduced to the original equation that is composed of Eqs. (38) and (39).

At this end, one may expand the variable $\xi \left( {\theta ,t;\delta } \right)$ as follows:

$$\xi \left( {\theta ,t;\,\delta } \right) = \xi_{0} (\theta ,t) + \delta \xi_{1} (\theta ,t) + \delta^{2} \xi_{2} (\theta ,t) + \cdots$$

(45)

Substituting from Eq. (45) into Eq. (40), as $\delta \to 0$, one gets the following linear wave equation:

$$\Im (\xi_{0} ) = 0.$$

(46)

The solution of the above wave equation may be formulated in analogy with the traveling wave solution. Therefore, the solution of Eq. (46) may be written as:

$$\xi_{0} (\theta ,t) = A\cos \Theta ,$$

(47)

where $\Theta = \varpi t + K\theta + B$, $\varpi$ is a modified frequency and $K$ is a synthetic wavenumber. Additionally, $A$ and $B$ are two arbitrary integration constants.

Actually, owing to the verification of Eq. (46), the parameters $\varpi$ and $K$ are restricted by the following criterion:

$$\varpi^{2} = K^{2} + \omega_{0}^{2} .$$

(48)

Equation (48) states that the characteristic parameters $\varpi$ and $K$ are connected along only with the linear part. The contribution of the nonlinearity will be enhanced and determined later. Employing the expansion as given in Eq. (45) into the homotopy equation, that is given by Eq. (40), equates the identical powers of $\delta$ to zero. The calculations will be maintained only up to the first-order. Therefore, one finds

$$\delta^{1} :\xi_{1tt} - \xi_{1\theta \theta } + \omega_{0}^{2} \xi_{1} = - \left( {\Re (\xi ) + N_{1} (\xi_{0} ) + N_{2} (\xi_{0} )} \right).$$

(49)

Substituting from Eq. (47) into the right-hand side of Eq. (49), one gets

$$\begin{aligned} \xi_{1tt} - \xi_{1\theta \theta } + \omega_{0}^{2} \xi_{1} & = r_{0} + r_{1} \cos \omega t + r_{2} \sin \omega t + r_{3} \cos 2\omega t + r_{4} \cos \Theta + r_{5} \sin \Theta + r_{6} \cos 2\Theta + r_{7} \sin 2\Theta \\ & \quad + r_{8} \cos 3\Theta + r_{9} \sin 3\Theta + r_{10} \cos (\Theta + \omega t) + r_{11} \sin (\Theta + \omega t) + r_{12} \cos (\Theta - \omega t) \\ & \quad + r_{13} \sin (\Theta - \omega t) + r_{14} \cos (\Theta + 2\omega t) + r_{14} \cos (\Theta - 2\omega t) + r_{15} \cos (2\Theta + \omega t) \\ & \quad + r_{16} \sin (2\Theta + \omega t) + r_{17} \cos (2\Theta - \omega t) + r_{18} \sin (2\Theta - \omega t) + r_{19} \cos (2\Theta + 2\omega t) \\ & \quad + r_{19} \cos (2\Theta - 2\omega t) + r_{20} \cos (3\Theta + \omega t) + r_{21} \sin (3\Theta + \omega t) + r_{22} \cos (3\Theta - \omega t) \\ & \quad + r_{23} \sin (3\Theta - \omega t) + r_{24} \cos (3\Theta + 2\omega t) + r_{24} \cos (3\Theta - 2\omega t). \\ \end{aligned}$$

(50)

where $r_{i} ,(i = 0,1,....,24)$ are given in “Appendix”.

The following subsections present the stability analysis; the procedure may be classified into two categories: the first case is concerned with the non-resonant case, and the second deals with the resonant one.

3.1 Stability analysis of the non-resonance case

There are many perturbation problems that may be properly called singular even though they are not of the layer-type. A large class of such problems involves the secular type. The existence of the secular term yields an unbounded solution. Therefore, to obtain a uniform valid expansion of the analytic approximate perturbed solution, the secular terms must be avoided. The foregoing Eq. (50) reveals a source of the secular terms. Obviously, these terms are represented as the coefficients of the trigonometric functions $\cos \Theta \,\,$ and $\sin \Theta$. Therefore, the elimination of these secular terms leads to the following solvability conditions:

$$\left( {a_{0} + b_{1} } \right)(\varpi^{2} - \omega_{0}^{2} ) + \frac{{A^{2} }}{4}\left[ {(4a_{5} + b_{5} )\varpi^{2} - a_{7}^{2} - d_{2} } \right] = 0,$$

(51)

and

$$4(a_{1} + b_{2} ) + \,A^{2} (a_{6} + 3b_{6} ) = 0.$$

(52)

The cancelation of the parameter $A^{2}$ between the above two equations yields the following transition curve:

$$(a_{0} + b_{1} )(a_{6} + 3b_{6} )(\varpi^{2} - \omega_{0}^{2} ) + (a_{1} + b_{2} )\left[ {(4a_{5} + b_{5} )\varpi^{2} - 3(a_{7} + d_{2} )} \right] = 0,$$

(53)

where $d_{2} = \hat{d}_{2} H_{0}^{2}$, and $\hat{d}_{2}$ are given in the “Appendix”.

The frequency equation as given in Eq. (53) may be reformulated to become:

$$\varpi^{2} = \alpha \,H_{0}^{2} + \beta ,$$

(54)

where $\alpha ,\,\,\beta$ are given in the “Appendix”.

Consequently, the stability criterion requires that the $\varpi^{2}$ as given in Eq. (54) must have a real and positive nature. This restriction may be accomplished in light of the following criterion:

$$\alpha \,H_{0}^{2} + \beta > 0.$$

(55)

In addition, the natural frequency $\omega_{0}^{2}$, as given in Eq. $\omega_{0}^{2}$(41), must be positive, and $\omega_{0}^{2}$ may be reformulated to become:

$$\alpha_{1} H_{0}^{2} + \beta_{1} > 0\,,$$

(56)

where $\alpha_{1}$ and $\beta_{1}$ are known from the context.

As stated before, the implication of the inequalities (55) and (56) must be taken into consideration. Therefore, all the following figures are plotted in a certain domain, where these criteria are automatically satisfied. Furthermore, the calculations indicated that the parameters $(\alpha \,{\text{and}}\,\alpha_{1} )$ are always of positive significance. This shows a stabilizing influence on the tangential magnetic field, which is an early result. It is verified by many authors; for instance, see Melcher [26], and many references therein.

Our main focus is on the inequalities (55) and (56). For this purpose, magnetic field intensity $Log\,H_{0}^{2}$ will be plotted versus the non-dimensional radius ($R$). In the following figures, stable region, corresponding to equality of (55), is referred to by the letter $S_{1}$. Simultaneously, unstable region is symbolized by the letter $U_{1}$. On the other hand, these two regions are referred to by letters $S_{2}$, and $U_{2}$, in analogy to the second condition (56). It is convenient to indicate the influence of various physical parameters in stability configuration. Therefore, the following figures are plotted for a system having the particulars:

$$m = 2,\,\rho = 0.3,\,\mu = 0.8,\,\lambda = 2,\,\hat{\Omega } = 0.1,\,\Omega^{*} = 0.7,\,Oh = 0.1,\,\hat{T}a = 1.5,\,Ta^{*} = 2,\hat{W}e = 0.3\,{\text{and}}\,We^{*} = 0.8.$$

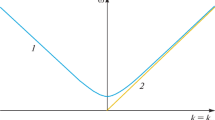
Figure 2 is depicted to indicate the stability picture in light of the relations (55) and (56). Throughout this figure, the transition curve $\varpi^{2} = 0$ is plotted in red; meanwhile, the transition curve $\omega_{0}^{2} = 0$ is graphed in blue. As seen, blue curve has no implication in the stability picture. Therefore, the stability is judged by the red curve. Consequently, the following figures considered the transition curve as only $\varpi^{2} = 0$.

Fig. 2

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the two criteria (55) and (56)

Figure 3 is plotted to indicate the influences of Taylor number $Ta^{*}$. It follows that $Ta^{*}$ has a stabilizing effect. This role is enhanced with the increasing of the non-dimensional radius $R$. Actually, this mechanism comes from the definition of this parameter. As previously indicated from the mathematical formula, it is proportional to the rotation of the centrifugal force and inversely proportional to the viscosity of the fluid.

Fig. 3

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criterion (55) for various values of $Ta^{*}$

Figure 4 displays the influences of Weber number $\hat{W}e$ on the stability profile. All physical parameters are held fixed except $\hat{W}e$. This figure shows that $\hat{W}e$ exerts a destabilizing influence. Once more, this mechanism is enhanced with the increasing of the non-dimensional radius $R$. This result is in good agreement with the result that has already been obtained by El-Sayed et al. [34].

Fig. 4

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criterion (55) for various values of $\hat{W}e$

Figure 5 is established to indicate the influences of $We^{*}$ on the stability picture. All the physical parameters are held fixed except $We^{*}$. As seen, this figure shows that $We^{*}$ exerts a destabilizing influence. This role is enhanced at large values of the non-dimensional values of the radius $R$. This result corresponds to the result that has already been obtained by El-Sayed et al. [34].

Fig. 5

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criterion (55) for various values of $We^{*}$

Figure 6 is depicted to indicate the influences of the azimuthal wave number $m$ on the stability picture. All the physical parameters are held fixed except $m$. As seen, this figure shows that the parameter $\hat{T}a$ plays a dual role in the stability picture. This result gives an excellent quantitative agreement with the result that has already obtained by El-Dib et al. [24].

Fig. 6

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criterion (55) for various values of $m$

Figure 7 is depicted to indicate the influences of the ratio periodic angular velocity $\Omega^{*}$ on the stability picture. All physical parameters are held fixed except $\Omega^{*}$. As seen, this figure shows that the $\Omega^{*}$ has a destabilizing influence. This result is in agreement with the result that has already obtained by El-Dib et al. [24].

Fig. 7

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criterion (55) for various values of $\Omega^{*}$

Figure 8 is pictured to indicate the influences of the ratio constant angular velocity $\hat{\Omega }$ on the stability picture. All the physical parameters are held fixed except $\hat{\Omega }$. As seen, this figure shows that the $\hat{\Omega }$ has a destabilizing influence. This result is in agreement with the result that has already obtained by El-Dib et al. [24].

Fig. 8

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criterion (55) for various values of $\hat{\Omega }$

For more appropriateness, an analytical approximate solution of the interface deflection can be derived. Typically, this procedure can be accomplished directly with the cancelation of the secular terms of the solution of the governing differential equation of the surface deflection. Therefore, to achieve a uniform valid expansion of Eq. (50), one may find out the following expansion:

$$\begin{aligned} \xi_{1} (\theta ,t) & = q_{0} + q_{1} \cos \omega t + q_{2} \sin \omega t + q_{3} \cos 2\omega t + q_{4} \cos 2\Theta + q_{5} \sin 2\Theta + q_{6} \cos 3\Theta \\ & \quad + q_{7} \sin 3\Theta + q_{8} \cos (\Theta + \omega t) + q_{9} \sin (\Theta + \omega t) + q_{10} \cos (\Theta - \omega t) + \,q_{11} \sin (\Theta - \omega t) \\ & \quad + q_{12} \cos (2\Theta + \omega t) + q_{13} \sin (2\Theta + \omega t) + q_{14} \cos (2\Theta - \omega t) + q_{15} \sin (2\Theta - \omega t) \\ & \quad + q_{16} \cos (3\Theta + \omega t) + q_{17} \sin (3\Theta + \omega t) + q_{18} \cos (3\Theta - \omega t) + q_{19} \sin (3\Theta - \omega t) \\ & \quad + q_{20} \cos (\Theta + 2\omega t) + q_{21} \cos (\Theta - 2\omega t) + q_{22} \cos (2\Theta + 2\omega t) + q_{23} \cos (2\Theta - 2\omega t) \\ & \quad + q_{24} \cos (3\Theta + 2\omega t) + q_{25} \cos (3\Theta - 2\omega t). \\ \end{aligned}$$

(57)

where $q_{i} = \frac{{r_{i} }}{{(D_{tt} - D_{\theta \theta } + \omega_{0}^{2} )}},\,\,\,i = 0,1,2, \ldots ,24.$

As a final result in the case of non-resonant, the analytic approximate periodic solution of the previous nonlinear characteristic equation may be written as follows:

$$\xi (\theta ,t) = \mathop {\lim }\limits_{\delta \to 1} \left( {\xi_{0} (\theta ,t) + \delta \,\xi_{1} (\theta ,t)} \right).$$

(58)

3.2 Stability analysis of the resonance case

The following analysis describes the resonance cases. Many resonance cases may appear. These resonance cases can be classified into sub-harmonic resonance and super-harmonic ones. The analysis adopted here depends mainly on the concept of expanded frequency; for instance, see El-Dib and Moatimid [35], so the frequency of the periodic rotation may be expanded as follows:

$$\omega^{2} = \varpi^{2} + \delta \,\sigma ,$$

(59)

where $\sigma$ is a small parameter to be determined later.

Substituting from Eq. (59) into the relation (48), one finds

$$\omega_{0}^{2} = \omega^{2} - K^{2} - \delta \,\sigma .$$

(60)

The homotopy equation, as given in Eq. (49), becomes:

$$\Im^{*} (\xi ) + \delta \,\left( { - \sigma \,\xi + \Re (\xi ) + N_{2} (\xi ) + N_{3} (\xi )} \right) = 0;\,\,\delta \in \left[ {0,1} \right],$$

(61)

where $\Im^{*} (\xi ) = \xi_{tt} - \xi_{\theta \theta } + (\omega^{2} - K^{2} )\xi$.

Employing the expansion, as given in Eq. (45) into the new homotopy Eq. (61), equates the identical powers of $\delta$ to zero. The calculations will be maintained only up to the first-order. Therefore, one gets

$$\delta^{0} :\xi_{0tt} - \xi_{0\theta \theta } + (\omega^{2} - K^{2} )\xi_{0} = 0,$$

(62)

and

$$\delta^{1} :\xi_{1tt} - \xi_{1\theta \theta } + (\omega^{2} - K^{2} )\xi_{1} = - \left( { - \sigma \xi_{0} + \Re (\xi_{0} ) + N_{1} (\xi_{0} ) + N_{2} (\xi_{0} )} \right),$$

(63)

The traveling solution of Eq. (62) may be written as:

$$\xi_{0} (\theta ,t) = \tilde{A}\cos \tilde{\Theta }\,\,,$$

(64)

where $\tilde{\Theta } = \omega \,t + K\theta + \tilde{B}$, $\tilde{A}\,\,,\,\,{\text{and}}\,\,\tilde{B}$ are arbitrary constants.

Substituting from Eq. (64) into the right-hand side of Eq. (63), one finds

$$\begin{aligned} \xi_{1tt} - \xi_{1\theta \theta } + (\omega^{2} - K^{2} )\xi_{1} & = r_{0} + r_{1} \cos \omega t + r_{2} \sin \omega t + r_{3} \cos 2\omega t + \tilde{r}_{4} \cos \tilde{\Theta } + r_{5} \sin \tilde{\Theta } \\ & \quad + \tilde{r}_{6} \cos 2\tilde{\Theta } + \tilde{r}_{7} \sin 2\tilde{\Theta } + \,\tilde{r}_{8} \cos 3\tilde{\Theta } + \tilde{r}_{9} \sin 3\tilde{\Theta } + \tilde{r}_{10} \cos (K\,\theta - \omega t + \tilde{B}) \\ & \quad + \tilde{r}_{11} \cos (K\,\theta + 2\omega t + \tilde{B}) + \tilde{r}_{12} \sin (K\,\theta + 2\omega t + \tilde{B}) \\ & \quad + \tilde{r}_{13} \cos (K\,\theta + 3\omega t + \tilde{B}) + \tilde{r}_{14} \cos (2K\,\theta + \omega t + 2\tilde{B}) \\ & \quad + \tilde{r}_{15} \sin (2K\,\theta + \omega t + 2\tilde{B}) + \tilde{r}_{16} \cos (2K\,\theta + 3\omega t + 2\tilde{B}) \\ & \quad + \tilde{r}_{17} \sin (2K\,\theta + 3\omega t + 2\tilde{B}) + \tilde{r}_{18} \cos (2K\,\theta + 4\omega t + 2\tilde{B}) \\ & \quad + \tilde{r}_{19} \cos (3K\,\theta + \omega t + 3\tilde{B}) + \tilde{r}_{20} \cos (3K\,\theta + 2\omega t + 3\tilde{B}) \\ & \quad + \tilde{r}_{21} \sin (3K\,\theta + 2\omega t + 3\tilde{B}) + \tilde{r}_{22} \cos (3K\,\theta + 4\omega t + 3\tilde{B}) \\ & \quad + \tilde{r}_{23} \sin (3K\,\theta + 4\omega t + 3\tilde{B}) + \tilde{r}_{24} \cos (3K\,\theta + 5\omega t + 3\tilde{B}) \\ & \quad + \tilde{r}_{25} \cos (K\,\theta + \tilde{B}) + \tilde{r}_{26} \cos (2K\,\theta + 2\tilde{B}). \\ \end{aligned}$$

(65)

Consequently, to acquire a uniform valid expansion of the analytic approximate perturbed solution, the secular terms must be ignored. The foregoing Eq. (65) contains the source of secular terms. Generally, these terms are presented as a coefficient of the trigonometric functions $\cos \tilde{\Theta }\,\,$ and $\sin \tilde{\Theta }$. The cancelation of these secular terms reaches the following solvability conditions:

$$(\sigma + K^{2} )(a_{0} + b_{1} ) + \frac{{\tilde{A}^{2} }}{4}\left( {4\omega^{2} a_{5} + \omega^{2} b_{5} - 3a_{7} - d_{2} } \right) = 0,$$

(66)

and

$$a_{1} + b_{2} + \frac{{\tilde{A}^{2} }}{4}\left( {a_{6} + b_{6} } \right) = 0,$$

(67)

The cancelation of the parameter $\tilde{A}^{2}$ between the above two equations yields the following value of the parameter $\sigma$:

$$\sigma = \frac{1}{{a_{6} + 3b_{6} }}\left( \begin{gathered} \omega^{2} (4a_{1} a_{5} + 4a_{5} b_{2} + a_{1} b_{5} + b_{2} b_{5} ) - K^{2} (a_{0} a_{6} + a_{6} b_{1} + 3a_{0} b_{6} + 3b_{1} b_{6} ) - \hfill \\ 3(a_{1} a_{7} + a_{7} b_{2} + a_{1} d_{2} + b_{2} d_{2} ) \hfill \\ \end{gathered} \right).$$

(68)

Substituting from Eq. (68) into Eq. (60), then setting $\delta \to 1$, one finds

$${\rm E}\,\omega^{2} + F = 0,$$

(69)

where ${\rm E}\,\,{\text{and}}\,\,F$ are constants. They are known from the context.

The stability criterion requires that the $\omega^{2}$ in the frequency equation, as given in Eq. (69), must have a real and positive nature. This restriction may be accomplished in light of the following criterion:

$$\tilde{\alpha }_{1} \,H_{0}^{2} + \tilde{\beta }_{1} > 0,$$

(70)

where $\tilde{\alpha }_{1}$ and $\tilde{\beta }_{1}$ are known from the context.

In addition, as stated above, the natural frequency $\omega^{2} - K^{2}$ must be positive and this requires

$$\tilde{\alpha }_{2} \,H_{0}^{2} + \tilde{\beta }_{2} > 0,$$

(71)

where $\tilde{\alpha }_{2}$ and $\tilde{\beta }_{2}$ are known from the context.

Our study focuses on the relations (70) and (71). For this purpose, the magnetic field intensity $Log\,H_{0}^{2}$ will be plotted versus the non-dimensional radius ($R$). As previously shown, the stable region corresponding to the equality of Eq. (70) is referred to in the following figures by letter $S_{1}$. Simultaneously, the unstable region is symbolized by letter $U_{1}$. On the other hand, these two regions are referred to by letters $S_{2}$, and $U_{2}$, in analogy to the second condition (71). It is convenient to illustrate the influence of various physical parameters on the stability configuration. Therefore, the following figures are plotted for a system having the particulars:

$$m = 3,\,\rho = 0.3,\,\mu = 1.5,\,\lambda = .2,\,\hat{\Omega } = 0.5,\,\Omega^{*} = 5,\,K = 2,\,Oh = 3,\,\hat{T}a = 0.5,\,Ta^{*} = 2,\hat{W}e = 0.3\,{\text{and}}\,We^{*} = 8.$$

Figure 9 is depicted to indicate the stability picture in light of the relations (70) and (71). Throughout this figure, the transition curve $\omega^{2} = 0$ is plotted in yellow; meanwhile, the transition curve $\omega^{2} - K^{2} = 0$ is graphed in black. As seen, the two curves are coincident. Consequently, the following figures considered only the transition curve as $\omega^{2} = 0$.

Fig. 9

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71)

Figure 10 is depicted to indicate the influences of Taylor number $\hat{T}a$ on the stability picture. Throughout this figure, all physical parameters are held fixed except the parameter $\hat{T}a$; it is shown that $\hat{T}a$ has a stabilizing effect. This influence is enhanced at large values of the non-dimensional radius $R$. As seen previously, this parameter does not change its mechanism. Therefore, Taylor number has a stabilizing influence on the resonance as well as non-resonance cases.

Fig. 10

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71) for various values of $\hat{T}a$

Figure 11 displays the influences of Weber number $\hat{W}e$ on stability configuration. All physical parameters are held fixed except $\hat{W}e$. This figure shows that the $\hat{W}e$ plays a destabilizing influence. Once more, this mechanism is enhanced with the increasing of the non-dimensional radius $R$. This result is in good agreement with the result that has already been obtained by El-Sayed et al. [34]. This same role has happened in the previous case.

Fig. 11

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71) for various values of $\hat{W}e$

Figure 12 indicates the influences of $We^{*}$ on stability picture. All the physical parameters are held fixed except $We^{*}$. As seen, this figure shows that $We^{*}$ exerts a destabilizing influence. This result corresponds to the result that has already been obtained by El-Sayed et al. [34]. This same role has happened in the previous case.

Fig. 12

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71) for various values of $We^{*}$

Figure 13 indicates the influences of Ohnesorge number $Oh$ on stability picture. All the physical parameters are held fixed except $Oh$. As seen, this figure shows that $Oh$ has a destabilizing influence. This influence is enlarged at small values of the non-dimensional radius $R$.

Fig. 13

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71) for various values of $Oh$

Figure 14 is depicted to indicate the influences of the ratio periodic angular velocity $\Omega^{*}$ on the stability picture. All physical parameters are held fixed except $\Omega^{*}$. As seen, this figure shows that $\Omega^{*}$ has a destabilizing influence. This result is in agreement with the result that has already been obtained by El-Dib et al. [24]. This same role has happened in the previous case.

Fig. 14

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71) for various values of $\Omega^{*}$

Figure 15 illustrates the influences of the ratio constant angular velocity $\hat{\Omega }$ on the stability picture. All the physical parameters are held fixed except $\hat{\Omega }$. As seen, this figure shows that $\hat{\Omega }$ exerts a destabilizing influence. This result is in agreement with the result that has already been obtained by El-Dib et al. [24]. This same role has happened in the previous case.

Fig. 15

Variation of magnetic field intensity with non-dimensional radius to depict the contribution of the criteria (70) and (71) for various values of $\hat{\Omega }$

4 Concluding remarks

The current paper is concerned with a novel approach in examining the nonlinear stability analysis of an azimuthal surface wave between two cylindrical liquid columns. Typically, the problem is modulated in light of the cylindrical coordinate system. A simplified modulation is done for the problem by assuming two infinite incompressible magnetic cylindrical fluids. The system is pervaded by rotation, namely uniform and oscillatory rotation. Along with the great importance of the porous medium, the problem considered a little configuration of this phenomenon. The inspiration in examining the topic of rotating fluids opportunities is attributed to the growing awareness of atmospheric and oceanic motions. Moreover, the problem acquires its importance from industrial applications for gas–liquid, vapor–liquid, and liquid–liquid interfaces. Additionally, a uniform tangential azimuthal magnetic field is taken into consideration. For straightforwardness, the magnetic field did not permit any existence of free surface currents at the surface deflection. Moreover, the procedure of the problem is accomplished in two dimensions. Indeed, the problem meets its practical importance of a geophysical point of view. Simultaneously, as in our previous work, the nonlinear analysis is based on the solution of the linear equations of motion together with the incrimination of the convenient nonlinear boundary conditions. A nonlinear characteristic dispersion equation of the surface deflection is realized. Some special cases are confirmed in light of convenient data choices. The stability analysis is analyzed in the linear as well as nonlinear approaches. To simplify the mathematical treatment, the stability analysis is performed in light of the HPM. The basic results of the work may be summarized in the following points:

• A mix of a uniform and oscillatory rotation is modulated in the configuration of the problem.

• A nonlinear characteristic equation of the surface deflection is showed to be similar to the well-known Ince equation.

• The HPM is adapted to analyze the stability profile, which yields a Klein-Gordon, as indicated in Eq. (40).

• A traveling wave solution for the nonlinear characteristic partial differential equation throughout the zero and first orders is given in Eqs. (47), (57) and (64).

• To be more precise, it is better to introduce the main key finding of the previous study. To be clearer, the main outcome will be presented in the following table:

Physical parameter	Non-resonant	Resonance
Taylor number $\hat{T}a$	–	S
Taylor number $Ta^{*}$	S	–
Weber number $\hat{W}e$	U	U
Weber number $We^{*}$	U	U
Ohnesorge number $Oh$	–	U
Non-dimensional $\Omega^{*}$	U	U
Non-dimensional $\hat{\Omega }$	U	U
Azimutal wavenumber $m$	D	-

Keep in mind that letter S refers to stable influence, U indicates for unstable effect and D stands for dual role.

Appendix

The coefficients that appear in the Eqs. (4) and (5) may be listed as follows:

$$\begin{aligned} & a_{0} = - \frac{{R^{2} }}{m}(1 + \rho ),\,\,\,a_{1} = - \frac{{Oh\,R^{2} }}{m}(1 + \lambda ),\,\,\,a_{2} = R(1 - \rho ),\,\,a_{3} = Oh\,R(1 - \lambda ), \\ & a_{4} = \frac{1}{{R^{2} }}\left( { - 2 + m(7m + 2(2\hat{W}e + We^{*} )\,R^{3} - m(2\hat{W}e + We^{*} )\,R^{3} + m(2 + m)(2\hat{W}e\hat{\Omega }^{2} + We^{*} \Omega^{*2} )\,R^{3} \rho )} \right), \\ & a_{5} = 2m(1 + \rho ),a_{6} = 2m\,Oh(1 + \lambda ), \\ & a_{7} = \frac{{m^{2} }}{{2R^{3} }}\left( { - 16m + 3m^{2} + 2(2 - m)(2\hat{W}e + We^{*} )R^{3} - 2(2 + m)(2\hat{W}e\hat{\Omega }^{2} + We^{*} \Omega^{*2} )\,R^{3} \rho } \right), \\ & b_{1} = - \frac{1}{m}(m - 1 + (1 + m)\rho \hat{\Omega })R^{2} Oh\sqrt {\hat{T}a} ,\,b_{2} = - \frac{1}{2}(Oh)^{2} \sqrt {\hat{T}a} \,R^{2} (1 + \lambda \,\hat{\Omega }), \\ & b_{3} = - \frac{1}{2}Oh\sqrt {\hat{T}a} \,R^{2} (2 - 3m + (2 + 3m)\rho \,\hat{\Omega }), \\ & b_{4} = \frac{m}{2}(Oh)^{2} \sqrt {\hat{T}a} \,R^{2} (1 - \lambda \,\hat{\Omega }),\,\,\,b_{5} = - \frac{1}{2}Oh\sqrt {\hat{T}a} \,R^{2} ( - 2 + m + (2 + m)\rho \,\hat{\Omega }), \\ & b_{6} = m^{2} (Oh)^{2} \sqrt {\hat{T}a} \,(1 + \lambda \,\hat{\Omega }), \\ & c_{0} = c_{0a} - c_{0b} H_{0}^{2} , \\ \end{aligned}$$

$$\begin{aligned} & c_{0a} = \frac{1}{8R}\left( {8 - 8m^{2} + \left( {8\hat{W}e + Ta^{*} \,(Oh)^{2} } \right)R^{3} (m - 2) + (2 + m)\left( {8\hat{W}e\,\hat{\Omega }^{2} + Ta^{*} \,(Oh)^{2} \Omega^{*2} } \right)} \right), \\ & c_{0b} = \frac{{m(1 - \mu )^{2} }}{(1 + \mu )}, \\ & c_{1} = - \frac{{Oh\,\sqrt {Ta^{*} } R^{2} }}{m}( - 1 + m + (1 + m)\,\rho \,\Omega^{*} ),\,\,c_{2} = \frac{{(Oh)^{2} \,\sqrt {Ta^{*} } R^{2} }}{8}( - 2 + m + (2 + m)\,\rho \,\Omega^{*} ), \\ & c_{3} = \frac{{(Oh)^{2} \,\sqrt {\hat{T}a\,Ta^{*} } R^{2} }}{2}( - 2 + m + (2 + m)\,\rho \,\hat{\Omega }\,\Omega^{*} ),\,\,c_{4} = - \frac{{(Oh)^{2} \,\sqrt {Ta^{*} } R^{2} }}{2}(1 + \lambda \,\Omega^{*} ),\, \\ & c_{5} = \sqrt {We^{*} } R^{2} (1 + \rho \,\Omega^{*} ), \\ & c_{6} = \frac{{ - Oh\sqrt {Ta^{*} } R}}{2}(2 - 3m + (2 + 3m)\rho \,\Omega^{*} ),\,\,c_{7} = \frac{{m\,R\,We^{*} }}{2}(2 - m + (2 + m)\rho \,\Omega^{*2} ), \\ & c_{8} = 2m\,R\,\sqrt {\hat{W}e\,We^{*} } (2 - m + (2 + m)\,\rho \,\hat{\Omega }\,\Omega^{*} ),\,\,c{}_{9} = \frac{{m(Oh)^{2} \,\sqrt {Ta^{*} } R}}{2}(1 + \lambda \,\Omega^{*} ), \\ & c_{10} = - m\,R\,\sqrt {We^{*} } (1 - \rho \,\Omega^{*} ),\,\,c_{11} = m\,Oh\sqrt {Ta^{*} } (m - 2 + (2 + m)\rho \,\Omega^{*} ), \\ & c_{12} = m^{2} \,\,We^{*} (m - 2 + (m + 2)\rho \,\Omega^{*2} ),\,c_{13} = - 4m^{2} \,\sqrt {\hat{W}e\,We^{*} } (2 - m + (2 + m)\,\rho \,\hat{\Omega }\,\Omega^{*} ), \\ & c_{14} = m^{2} \,(Oh)^{2} \sqrt {Ta^{*} } (1 + \lambda \,\Omega^{*} ),\,c_{15} = - 2m^{2} \,We^{*} (1 + \rho \,\Omega^{*} ),d_{1} = - \frac{{4m^{2} \mu (1 - \mu )H_{0}^{2} }}{{R(1 + \mu )^{2} }},\,\hat{d}_{2} = \frac{{2m^{3} (1 - \mu )^{2} }}{{R^{2} (1 + \mu )}}. \\ \end{aligned}$$

The coefficients that appear in Eq. (16) may be listed as follows:

$$\begin{aligned} & r_{0} = \frac{{A^{2} (a_{4} + d_{1} )}}{{2\left( {a_{0} + b_{1} } \right)}},\,\,r_{1} = - \frac{{A^{2} (c_{10} \omega^{2} + c_{8} )}}{{2(a_{0} + b_{1} )}},\,\,r_{2} = \frac{{A^{2} c_{9} \omega }}{{2\left( {a_{0} + b_{1} } \right)}},\,\,r_{3} = - \frac{{A^{2} c_{7} }}{{2\left( {a_{0} + b_{1} } \right)}}, \\ & r_{4} = \frac{{A\left( {4a_{5} A^{2} \varpi^{2} - 3a_{7} A^{2} + 4a_{0} K^{2} + A^{2} b_{5} \varpi^{2} - 3A^{2} d_{2} + 4b_{1} K^{2} } \right)}}{{4(a_{0} + b_{1} )}}, \\ & r_{5} = \frac{{A\varpi \left( {a_{6} A^{2} + 4a_{1} + A^{2} b_{6} + 4b_{2} } \right)}}{{4(a_{0} + b_{1} )}}, \\ & r_{6} = \frac{{A^{2} \left( {2a_{2} \varpi^{2} - a_{4} + 2b_{3} \varpi^{2} - d_{1} } \right)}}{{2(a_{0} + b_{1} )}},\,\,r_{7} = \frac{{\varpi \,A^{2} \left( {a_{3} + 2b_{4} } \right)}}{{2(a_{0} + b_{1} )}},\, \\ & r_{8} = - \frac{{A^{3} \left( {a_{7} - 3b_{5} \varpi^{2} + d_{2} } \right)}}{{4\left( {a_{0} + b_{1} } \right)}},\,\,r_{9} = \frac{{\varpi \,A^{3} \left( {a_{6} + 3b_{6} } \right)}}{{4(a_{0} + b_{1} )}} \\ & r_{10} = \frac{{A\left( {A^{2} \left( {(\omega + \varpi )\left( {c_{11} \varpi - 3c_{15} \omega } \right) - 3c_{13} } \right) + 4c_{1} \varpi (\omega + \varpi ) - 4c_{5} \omega (\omega + \varpi ) - 4c_{3} } \right)}}{{8\left( {a_{0} + b_{1} } \right)}}, \\ & r_{11} = \frac{{A\left( {3A^{2} c_{14} \omega + 3A^{2} c_{14} \varpi + 4c_{4} \omega + 4c_{4} \varpi } \right)}}{{8(a_{0} + b_{1} )}},\, \\ & r_{12} = \frac{{A\left( {A^{2} \left( {(\varpi - \omega )\left( {3c_{15} \omega + c_{11} \varpi } \right) - 3c_{13} } \right) + 4c_{1} \varpi (\varpi - \omega ) + 4c_{5} \omega (\varpi - \omega ) - 4c_{3} } \right)}}{{8\left( {a_{0} + b_{1} } \right)}}, \\ & r_{13} = \frac{{A\left( { - 3A^{2} c_{14} \omega + 3A^{2} c_{14} \varpi - 4c_{4} \omega + 4c_{4} \varpi } \right)}}{{8(a_{0} + b_{1} )}},\,\,r_{14} = \frac{{ - A\left( {3A^{2} c_{12} + 4c_{2} } \right)}}{{8(a_{0} + b_{1} )}}, \\ & r_{15} = \frac{{A^{2} \left( { - c_{10} \omega^{2} + 2c_{6} \varpi^{2} + c_{6} \omega \varpi - 2c_{10} \omega \varpi - c_{8} } \right)}}{{4(a_{0} + b_{1} )}},\,\,r_{16} = \frac{{A^{2} c_{9} \left( {\omega + 2\varpi } \right)}}{{4(a_{0} + b_{1} )}}, \\ & r_{17} = \frac{{A^{2} \left( { - c_{10} \omega^{2} + 2c_{6} \varpi^{2} - c_{6} \omega \varpi + 2c_{10} \omega \varpi - c_{8} } \right)}}{{4(a_{0} + b_{1} )}},\,\,\,r_{18} = \frac{{A^{2} c_{9} \left( {2\varpi - \omega } \right)}}{{4(a_{0} + b_{1} )}} \\ & r_{19} = - \frac{{A^{2} c_{7} }}{{4\left( {a_{0} + b_{1} } \right)}},\,\,\,r_{20} = \frac{{A^{3} \left( {(\omega + 3\varpi )\left( {c_{11} \varpi - c_{15} \omega } \right) - c_{13} } \right)}}{{8\left( {a_{0} + b_{1} } \right)}},\,\,r_{21} = \frac{{A^{3} c_{14} \left( {\omega + 3\varpi } \right)}}{{8(a_{0} + b_{1} )}}, \\ & r_{22} = \frac{{A^{3} \left( {(3\varpi - \omega )\left( {c_{15} \omega + c_{11} \varpi } \right) - c_{13} } \right)}}{{8\left( {a_{0} + b_{1} } \right)}},\,\,\,r_{23} = \frac{{A^{3} c_{14} \left( {3\varpi - \omega } \right)}}{{a_{0} + b_{1} }},\,\,r_{24} = - \frac{{A^{3} c_{12} }}{{8\left( {a_{0} + b_{1} } \right)}} \\ \end{aligned}$$

The coefficients that appear in Eq. (20) may be listed as follows:

$$\alpha = \frac{{3\hat{d}_{2} (a_{1} + b_{2} )}}{{(a_{1} + b_{2} )(4a_{5} + b_{5} ) - (a_{6} + 3b_{6} )(a_{0} + b_{1} )}},\,\,{\text{and}}\,\,\beta = \frac{{3a_{7} (a_{1} + b_{2} ) - (a_{6} + 3b_{6} )(a_{0} + b_{1} )\omega_{0}^{2} }}{{(a_{1} + b_{2} )(4a_{5} + b_{5} ) - (a_{6} + 3b_{6} )(a_{0} + b_{1} )}}.$$

The coefficients that appear in Eq. (31) may be listed as follows:

$$\begin{aligned} & \tilde{r}_{4} = \frac{{A\left( {4a_{5} A^{2} \omega^{2} - 3a_{7} A^{2} + 4a_{0} K^{2} + A^{2} b_{5} \omega^{2} - 3A^{2} d_{2} + 4b_{1} K^{2} + 4\sigma (a_{0} + b_{1} )} \right)}}{{4(a_{0} + b_{1} )}}, \\ & \tilde{r}_{10} = - \frac{{A(4c_{4} + 3A^{2} c_{12} )}}{{2\left( {a_{0} + b_{1} } \right)}},\,\,\tilde{r}_{11} = \frac{{A\left( {4\omega^{2} (c_{1} - c_{5} ) - 4c_{3} + A^{2} (2\omega^{2} c_{11} - 3c_{13} - 6A^{2} \omega^{2} c_{15} )} \right)}}{{8(a_{0} + b_{1} )}}, \\ & \tilde{r}_{12} = \frac{{A\omega (4c_{4} + 3A^{2} c_{12} )}}{{4\left( {a_{0} + b_{1} } \right)}},\,\,\tilde{r}_{13} = - \frac{{A(4c_{2} + 3A^{2} c_{12} )}}{{8\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{14} = \frac{{A(\omega^{2} c_{6} - c_{8} + \omega^{2} c_{10} )}}{{4\left( {a_{0} + b_{1} } \right)}}, \\ & \tilde{r}_{15} = \frac{{A^{2} \omega \,c_{9} }}{{4\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{16} = \frac{{A^{2} (3\omega^{2} c_{6} - c_{8} + 3\omega^{2} c_{10} )}}{{4\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{17} = \frac{{3A^{2} \omega \,c_{9} }}{{4\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{18} = - \frac{{A^{2} \,c_{7} }}{{4\left( {a_{0} + b_{1} } \right)}}, \\ & \tilde{r}_{19} = - \frac{{A^{3} \,c_{12} }}{{8\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{20} = \frac{{A^{3} (2\omega^{2} c_{11} - c_{13} + 2\omega^{2} c_{15} )}}{{8\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{21} = \frac{{A^{3} \omega \,c_{14} }}{{4\left( {a_{0} + b_{1} } \right)}}, \\ & \tilde{r}_{22} = \frac{{A^{3} (4\omega^{2} c_{11} - c_{13} + 4\omega^{2} c_{15} )}}{{8\left( {a_{0} + b_{1} } \right)}},\,\,\,\tilde{r}_{23} = \frac{{A^{3} \omega \,c_{14} }}{{2\left( {a_{0} + b_{1} } \right)}},\,\,\,\,\tilde{r}_{24} = - \frac{{A^{3} c_{12} }}{{8\left( {a_{0} + b_{1} } \right)}}, \\ & \tilde{r}_{25} = - \frac{{A(4c_{3} + 3A^{2} c_{13} )}}{{8\left( {a_{0} + b_{1} } \right)}},\,\,\,\,\,\tilde{r}_{26} = - \frac{{A^{2} c_{7} }}{{4\left( {a_{0} + b_{1} } \right)}}. \\ \end{aligned}$$