Exact solutions to complex Ginzburg–Landau equation

Abstract

In this paper, the trial equation method and the complete discrimination system for polynomial method are applied to retrieve the exact travelling wave solutions of complex Ginzburg–Landau equation. Both the Kerr and power laws of nonlinearity are considered. All the possible exact travelling wave solutions consisting of the rational function-type solutions, solitary wave solutions, triangle function-type periodic solutions and Jacobian elliptic functions solutions are obtained, and some of them are new solutions. In addition, concrete examples are presented to ensure the existence of obtained solutions. Moreover, four types of representative solutions are depicted to present the nature of the obtained solutions.

1 Introduction

The study of optical solitons occupies an important position in the field of nonlinear optics. In the past few decades, the propagation of solitons in long distance fibres has attracted much attention, and many valuable results have been achieved [1,2,3,4,5,6,7,8]. Nonlinear Schrödinger’s equation (NLSE) shows an outstanding performance in modelling and governing this physical phenomenon [9,10,11,12,13,14,15,16]. This paper will study the complex Ginzburg–Landau equation (CGLE), which is a variant of the Schrödinger’s equation and describes the dynamics of soliton propagation on the basis of nonlinear perturbation effects.

The focus of our study is to find a suitable method to deal with such an equation. Modified simple equation method [17], simplest equation method [18], multiple exp-function method [19, 20], transformed rational function method [21, 22], Lie symmetry method [23], Riemann–Hilbert formulation [24], F-expansion method [25], Q-function method [26], and other efficacious methods [27,28,29,30,31,32,33,34] are some of the methods which were used to obtain approximate and exact solutions of nonlinear partial differential equations. In recent years, Liu proposed the complete discrimination system for polynomial method [35,36,37] and trial equation method [38,39,40,41] to seek the exact travelling wave solutions of various nonlinear partial differential equations. Because of the good applicability and efficiency of Liu’s method, the method has been widely used since it was proposed. For instance, Liu [42] and Wang et al [43] respectively solved the nonlinear Schrödinger equation and Camassa–Holm–Degasperis–Procesi equation by applying Liu’s method. Kai [44] applied the complete discrimination system for polynomial method to solve the variant Boussinesq equations and proved that each solution acquired can be realised. Therefore, solving nonlinear partial differential equations successfully has proved the effectiveness of Liu’s method.

In this paper, the complete discrimination system for polynomial method and trial equation method will be employed to solve the complex Ginzburg–Landau equation. Moreover, both Kerr law and the power-law nonlinearity are considered in this paper, and the corresponding exact travelling wave solutions are given. In addition, concrete examples are also presented to ensure the existence of such solutions. Furthermore, some numerical simulations are carried out to reveal the nature of the solutions.

2 Mathematical analysis

The dimensionless form of complex Ginzburg–Landau equation [45,46,47,48] is presented as follows:

$$\begin{aligned}&iq_t+aq_{xx}+bF(|q|^2)q=\frac{1}{|q |^2q^*} \left[ a|q|^2(|q|^2)_{xx}\right. \nonumber \\&\quad \left. -\beta \{ (|q^2|)_x \}^2 \right] +rq, \end{aligned}$$

(1)

where x denotes the non-dimensional distance along the fibrer t is the non-dimensional time, a, b, $\alpha$, $\beta$ and $\gamma$ represent real-valued constants. The coefficients a and b arise from the group velocity dispersion (GVD) and nonlinearity, respectively. The terms with $\alpha$, $\beta$ and $\gamma$ come from perturbation effects, and in particular, $\gamma$ comes from the detuning effect.

In eq. (1), F is a real-valued algebraic function, $F (|q|^2)q$ needs to satisfy the smoothness and is k times continuously differentiable, so that

$$\begin{aligned} F (|q|^2 ) q \in \bigcup _{m,n=1}^\infty C^k ((-n,n)\times (-m,m);R^2). \end{aligned}$$

(2)

Then we define wave variable $\xi$ as

$$\begin{aligned} \xi =k(x-vt), \end{aligned}$$

(3)

where k is a constant and v is the velocity of the soliton.

Therefore, we can obtain the equation of q(x, t) which consists of phase and amplitude components.

$$\begin{aligned} q(x,t)=g(\xi )\mathrm {e}^{i(-\kappa x+\omega t+\theta )}, \end{aligned}$$

(4)

where the function g denotes the pulse shape, $\kappa$ denotes the soliton frequency, $\omega$ represents the soliton wave number and $\theta$ is the phase constant.

By substituting eq. (4) into eq. (1), we can obtain [46]

$$\begin{aligned} k^2(a-4\beta )g{''}-(\omega +a\kappa ^2+\gamma )g+bF(g^2)g=0. \end{aligned}$$

(5)

Based on Kerr law and power-law nonlinearity, eq. (5) will be used to seek exact travelling wave solutions in the following sections.

3 Complete discrimination system for the fourth-order polynomial

In Liu’s method, the nonlinear partial differential equations are simplified to the following elementary integral:

$$\begin{aligned} \int \frac{\mathrm {d}\eta }{\sqrt{G(\eta )}}=\pm (\eta -\eta _0), \end{aligned}$$

(6)

where $G(\eta )$ is a polynomial and $\eta _0$ is an integral constant.

In this paper, the fourth-order polynomial is the focus of our attention and it can be described as follows:

$$\begin{aligned} G(\eta )=\eta ^4+p\eta ^2+q. \end{aligned}$$

(7)

Then, the complete discrimination system is presented as

$$\begin{aligned} D_1= & {} 4,\quad D_2=-p,\quad D_3=-2p^3+8pq,\nonumber \\ D_4= & {} 4p^4q-32p^2q^2+64q^3,\quad E_2=-32pq, \end{aligned}$$

(8)

where $E_2$ is the discriminant of $\Delta _2(G)$.

According to the complete discrimination system for $G(\eta )$, the roots of $G(\eta )$ can be classified, and the detailed classification will be given in §4 and 5.

4 Kerr law

The Kerr law of nonlinearity describes the phenomenon that a light wave in an optical fibre encounters nonlinear responses from non-harmonic motion of electrons with an external electric field [48]. In the case of Kerr law nonlinearity, $F(u)=u$, so that eq. (5) can be simplified as

$$\begin{aligned} k^2(a-4\beta )g{''}-(\omega +a\kappa ^2+\gamma )g+bg^3=0. \end{aligned}$$

(9)

By multiplying $g{'}$ on both sides of the equation and integrating eq. (9) once, we obtain the following equation:

$$\begin{aligned} \frac{1}{2}{g{'}}^2-\frac{1}{2}\sigma g^2+\frac{1}{4}\tau g^4=e, \end{aligned}$$

(10)

where

$$\begin{aligned} \sigma =\frac{\omega +a\kappa ^2+r}{k^2(a-4\beta )},\quad \tau =\frac{b}{k^2(a-4\beta )} \end{aligned}$$

and e is an arbitrary constant.

Then eq. (10) is given by

$$\begin{aligned} {g{'}}^2=-\tau {'}g^4+\sigma g^2+e{'}, \end{aligned}$$

(11)

where

$$\begin{aligned} \tau {'}=\frac{b}{2k^2(a-4\beta )}, \end{aligned}$$

$e{'}=2e$ and is an arbitrary constant.

In order to solve eq. (11), when $\tau {'}<0$, we have the following transformation:

$$\begin{aligned} \eta =(-\tau ')^{{1}/{4}}g,\quad \xi _1=(-\tau ')^{{1}/{4}}\xi . \end{aligned}$$

(12)

Then eq. (11) is changed to

$$\begin{aligned} \eta _{\xi _1}^2=G(\eta )=\eta ^4+p\eta ^2+q, \end{aligned}$$

(13)

where

$$\begin{aligned} p=\frac{\sigma }{\sqrt{-\tau {'}}},\quad q=e{'}. \end{aligned}$$

If $\tau {'}>0$, by the following transformation

$$\begin{aligned} \eta =(\tau {'})^{{1}/{4}}g,\quad \xi _1=(\tau {'})^{{1}/{4}}\xi . \end{aligned}$$

(14)

Then, eq. (11) is given by

$$\begin{aligned} \eta _{\xi _1}^2=-G(\eta )=-(\eta ^4+p\eta ^2+q), \end{aligned}$$

(15)

where

$$\begin{aligned} p=\frac{-\sigma }{\sqrt{\tau {'}}},\quad q=-e{'}. \end{aligned}$$

For solving eqs (13) and (15), the complete discrimination system of the fourth-order polynomial introduced in §3 is applied, and the solutions in nine cases are discussed separately.

Case 4.1. When $D_2<0$, $D_3=0$ and $D_4=0$, $G(\eta )$ has a pair of conjugate complex roots of multiplicities two, i.e.

$$\begin{aligned} G(\eta )=((\eta -l)^2+s^2)^2, \end{aligned}$$

(16)

where $s>0$. In this case, according to eq. (13), we have

$$\begin{aligned} \pm (\xi _1-\xi _0)=\int \frac{\mathrm{d}\eta }{(\eta -l)^2+s^2}=\frac{1}{s}\,\mathrm{arctan}\frac{\eta -l}{s}. \end{aligned}$$

(17)

For example, when $a=1$, $\beta =0$, $k=\kappa ={1}/{\sqrt{2}}$, $b=-1$, $\omega ={1}/{4}$ and $\gamma ={1}/{4}$, we have $l=0$, $s=1$. Then, we obtain the solutions of eq. (13) as

$$\begin{aligned} \eta =\pm \mathrm{tan}(\xi _1-\xi _0). \end{aligned}$$

(18)

Therefore, we have

$$\begin{aligned} q(x,t)=\pm \mathrm{tan} \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] \mathrm {e}^{i\left( -\frac{\sqrt{2}}{2}x+\frac{1}{4} t+\theta \right) }. \end{aligned}$$

(19)

Case 4.2. When $D_2=0$, $D_3=0$ and $D_4=0$, $G(\eta )$ has a real root of multiplicities four, i.e.

$$\begin{aligned} G(\eta )=\eta ^4. \end{aligned}$$

(20)

By using eq. (13), we have

$$\begin{aligned} \pm (\xi _1-\xi _0)=\int \frac{\mathrm {d}\eta }{\eta ^2}=-\frac{1}{\eta ^{-1}}. \end{aligned}$$

(21)

For example, when $a=1$, $\beta =0$, $k=\kappa ={1}/{\sqrt{2}}$, $b=-1$, $\omega =-{1}/{4}$ and $\gamma =-{1}/{4}$, we have

$$\begin{aligned} \eta =\pm \frac{1}{\xi _1-\xi _0}. \end{aligned}$$

(22)

Hence, the solutions of eq. (1) are given by

$$\begin{aligned} q(x,t)=\pm \frac{\mathrm {e}^{i(-\frac{\sqrt{2}}{2}x-\frac{1}{4} t+\theta )} }{{(\sqrt{2}}/{2})(x+\sqrt{2}t)-\xi _0 }. \end{aligned}$$

(23)

Case 4.3. When $D_2>0$, $D_3=0$, $D_4=0$ and $E_2>0$, $G(\eta )$ has two distinct real roots of multiplicities two, i.e.

$$\begin{aligned} G(\eta )=(\eta -\mu )^2(\eta -\nu )^2, \end{aligned}$$

(24)

where $\mu > \nu$.

For $\tau ^{\prime }<0$, according to eq. (13), we have

$$\begin{aligned} \pm (\xi _1-\xi _0)= & {} \int \frac{\mathrm {d}\eta }{(\eta -\mu )(\eta -\nu )}\nonumber \\= & {} \frac{1}{\mu -\nu }\,\mathrm{ln}\bigg |\frac{\eta -\mu }{\eta -\nu }\bigg |. \end{aligned}$$

(25)

For $\eta >\mu$ or $\eta <\nu$, according to eq. (25), we have

$$\begin{aligned} \eta= & {} \frac{\nu -\mu }{\mathrm {e}^{\pm (\mu -\nu )(\xi _1-\xi _0)}-1}\nonumber \\= & {} \frac{\nu -\mu }{2} \left[ \pm \mathrm{coth} \frac{(\mu -\nu )(\xi _1-\xi _0)}{2} -1 \right] +\nu . \end{aligned}$$

(26)

For $\nu<\eta <\mu$, we have

$$\begin{aligned} \eta= & {} \frac{\nu -\mu }{-\mathrm {e}^{\pm (\mu -\nu )(\xi _1-\xi _0)}-1}\nonumber \\= & {} \frac{\nu -\mu }{2} \left[ \pm \mathrm{tanh} \frac{(\mu -\nu )(\xi _1-\xi _0)}{2} -1 \right] +\nu , \end{aligned}$$

(27)

where eqs (26) and (27) are solitary wave solutions.

For instance, when $a=1$, $\beta =0$, $k=\kappa ={1}/{\sqrt{2}}$, $b=-1$, $\omega =-1$ and $\gamma =-\frac{1}{2}$, we have $\mu =1,\nu =-1$. Then, the solutions of eq. (13) can be obtained as

$$\begin{aligned} \pm (\xi _1-\xi _0)=\frac{1}{2}\bigg |\frac{\eta -1}{\eta +1}\bigg |. \end{aligned}$$

(28)

Therefore, we have

$$\begin{aligned} q(x,t)=\pm \mathrm{coth} \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] \mathrm {e}^{i(-\frac{\sqrt{2}}{2}x- t+\theta )}. \end{aligned}$$

(29)

Case 4.4. When $D_2>0$, $D_3=0$, $D_4=0$ and $E_2=0$, $G(\eta )$ has a real root of multiplicities three and a real root of multiplicity one. When $D_2>0$, we have $p<0$, but it is in contradiction with $D_3=0$ and $E_2=0$. Therefore, this condition does not exist in this paper.

Case 4.5. When $D_2D_3<0$ and $D_4=0$, $G(\eta )$ has a real root of multiplicities two and a pair of conjugate complex roots. As $D_4=0$, we have $p^2=4q$ or $q=0$. If $p^2=4q$, we have $D_2D_3=0$ and it is in contradiction with the known restrictions. If $q=0$, we have $D_2D_3\ge 0$ and it is also contradictory to the known restrictions. So this condition does not exist.

Case 4.6. When $D_2>0$, $D_3>0$ and $D_4>0$, $G(\eta )$ has four distinct real roots such that

$$\begin{aligned} G(\eta )=(\eta -\alpha _1)(\eta -\alpha _2)(\eta -\alpha _3)(\eta -\alpha _4), \end{aligned}$$

(30)

where $\alpha _1>\alpha _2>\alpha _3>\alpha _4$. Then, we have

$$\begin{aligned} \pm (\xi _1-\xi _0)=\int \frac{\mathrm {d}\eta }{(\eta -\alpha _1)(\eta -\alpha _2) (\eta -\alpha _3)(\eta -\alpha _4)}. \end{aligned}$$

(31)

When $\alpha _4>0$, if $\eta >\alpha _1$ or $\eta <\alpha _4$, according to eq. (31) and the definition of Jacobian elliptic functions, we have

$$\begin{aligned} \eta =\frac{\alpha _2(\alpha _1-\alpha _4)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -\alpha _1(\alpha _2-\alpha _4)}{(\alpha _1-\alpha _4)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -(\alpha _2-\alpha _4)} \end{aligned}$$

(32)

and if $\alpha _3<\eta <\alpha _2$, then we get

$$\begin{aligned} \eta =\frac{\alpha _4(\alpha _2-\alpha _3)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -\alpha _3(\alpha _2-\alpha _4)}{(\alpha _2-\alpha _3)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -(\alpha _2-\alpha _4)}, \end{aligned}$$

(33)

where

$$\begin{aligned} m^2=\frac{(\alpha _1-\alpha _4)(\alpha _2-\alpha _3)}{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}, \end{aligned}$$

For $\alpha _4<0$, if $\alpha _1>\eta >\alpha _2$, we can similarly get the following solutions:

$$\begin{aligned} \eta =\frac{\alpha _3(\alpha _1-\alpha _2)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -\alpha _2(\alpha _1-\alpha _3)}{(\alpha _1-\alpha _2)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -(\alpha _1-\alpha _3)} \end{aligned}$$

(34)

and if $\alpha _4<\eta <\alpha _3$, we have

$$\begin{aligned} \eta =\frac{\alpha _1(\alpha _3-\alpha _4)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -\alpha _4(\alpha _3-\alpha _1)}{(\alpha _3-\alpha _4)\mathrm{sn^2}\left[ \pm \frac{\sqrt{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)}}{2}(\xi _1-\xi _0),m\right] -(\alpha _3-\alpha _1)}, \end{aligned}$$

(35)

where

$$\begin{aligned} m^2=\frac{(\alpha _1-\alpha _2)(\alpha _3-\alpha _4)}{(\alpha _1-\alpha _3)(\alpha _2-\alpha _4)} \end{aligned}$$

and eqs (32)–(35) are elliptic functions double periodic solutions.

For example, when $a=1$, $\beta =0$, $k=\kappa ={1}/{\sqrt{2}}$, $b=-1$, $\omega =-5$ and $\gamma =-{1}/{2}$, we have $p=-10,q=9$. Then, we have $\alpha _1=3,\alpha _2=1,\alpha _3=-1,\alpha _4=-3 , m=\pm {1}/{2}$. Hence, when $1<\eta <3$, we obtain

$$\begin{aligned} \eta =\frac{-\mathrm{sn^2}\left[ \pm 2(\xi _1-\xi _0),\pm \frac{1}{2}\right] -4}{\mathrm{sn^2}\left[ \pm 2(\xi _1-\xi _0),\pm \frac{1}{2}\right] -4}. \end{aligned}$$

(36)

Therefore, the solutions to eq. (1) are

$$\begin{aligned} q(x,t)=\frac{\left\{ -\mathrm{sn^2} \left\langle \pm 2 \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] ,\pm \frac{1}{2} \right\rangle -4 \right\} \mathrm {e}^{i(-\frac{\sqrt{2}}{2}x- 5t+\theta )}}{\mathrm{sn^2} \left\langle \pm 2 \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] , \pm \frac{1}{2} \right\rangle -4}. \end{aligned}$$

(37)

Case 4.7. When $D_2D_3>0$ and $D_4<0$, $G(\eta )$ has two distinct real roots and a pair of conjugate complex roots, i.e.

$$\begin{aligned} G(\eta )=(\eta -\mu )(\eta -\nu )((\eta -l)^2+s^2), \end{aligned}$$

(38)

where $\mu >\nu$ and $s>0$. Then, we have

$$\begin{aligned} \pm (\xi _1-\xi _0)=\int \frac{\mathrm {d}\eta }{(\eta -\alpha _1)(\eta -\alpha _2)(\eta -\alpha _3)(\eta -\alpha _4)}. \end{aligned}$$

(39)

By the following transformation

$$\begin{aligned}&a_1=\frac{1}{2}(\mu +\nu )c_1-\frac{1}{2}(\mu -\nu )d_1, \end{aligned}$$

(40)

$$\begin{aligned}&b_1=\frac{1}{2}(\mu +\nu )d_1-\frac{1}{2}(\mu -\nu )c_1,\end{aligned}$$

(41)

$$\begin{aligned}&c_1=\mu -l-\frac{s}{m_1},\end{aligned}$$

(42)

$$\begin{aligned}&d_1=\mu -l-sm_1,\end{aligned}$$

(43)

$$\begin{aligned}&\lambda =\frac{s^2+(\mu -l)(\nu -l)}{s(\mu -\nu )},\end{aligned}$$

(44)

$$\begin{aligned}&m_1=\lambda \pm \sqrt{\lambda ^2+1}, \end{aligned}$$

(45)

the solutions of eqs (13) and (15) can be obtained as

$$\begin{aligned} \eta =\frac{a_1 \mathrm{cn}\left[ \pm \frac{\sqrt{\mp 2sm_1(\mu -\nu )}}{2mm_1}(\xi _1-\xi _0),m \right] +b_1}{c_1 \mathrm{cn}\left[ \pm \frac{\sqrt{\mp 2sm_1(\mu -\nu )}}{2mm_1}(\xi _1-\xi _0),m \right] +d_1}, \end{aligned}$$

(46)

where

$$\begin{aligned} m^2=\frac{1}{1+m_1^2}, \end{aligned}$$

and expression (46) is an elliptic function double periodic solution. For example, when $a=1$, $\beta =0$, $k=\kappa =\frac{1}{\sqrt{2}}$, $b=-1$, $\omega ={1}/{2}$ and $\gamma ={1}/{2}$, we have $p=3,q=-4$. Then, we obtain $\mu =1$, $\nu =-1$ and $l=0$, $s=2$. Hence, we have

$$\begin{aligned}&b_1=c_1=0, \quad a_1=3,\nonumber \\&d_1=-3,\quad m=\pm \frac{\sqrt{5}}{5}, \end{aligned}$$

(47)

Therefore, the solutions can be shown as

$$\begin{aligned} q(x,t)= & {} -\mathrm{cn} \left\langle \pm \sqrt{5} \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] ,\right. \nonumber \\&\left. \pm \frac{\sqrt{5}}{5} \right\rangle \mathrm {e}^{i\left( -\frac{\sqrt{2}}{2}x+\frac{1}{2} t+\theta \right) }. \end{aligned}$$

(48)

Case 4.8. When $D_2D_3\le 0$ and $D_4>0$, $G(\eta )$ has two pairs of conjugate complex roots, i.e.

$$\begin{aligned} G(\eta )=((\eta -l_1)^2+s_1^2)((\eta -l_2)^2+s_2^2), \end{aligned}$$

(49)

where $s_1\ge s_2 > 0$. If

$$\begin{aligned}&a_1=l_1 c_1 +s_1d_1, \end{aligned}$$

(50)

$$\begin{aligned}&b_1=l_1d_1-s_1c_1, \end{aligned}$$

(51)

$$\begin{aligned}&c_1=-s_1-\frac{s_2}{m_1}, \end{aligned}$$

(52)

$$\begin{aligned}&d_1=l_1-l_2, \end{aligned}$$

(53)

$$\begin{aligned}&\lambda =\frac{(l_1-l_2)^2+s_1^2+s_2^2}{2s_2s_2}, \end{aligned}$$

(54)

$$\begin{aligned}&m_1=\lambda +\sqrt{\lambda ^2-1}, \end{aligned}$$

(55)

then the solutions of eq. (13) are presented as

$$\begin{aligned} \eta =\frac{a_1 \mathrm{sn} \left[ \pm \varepsilon (\xi _1-\xi _0),m \right] +b_1 \mathrm{cn} \left[ \pm \varepsilon (\xi _1-\xi _0),m \right] }{c_1 \mathrm{sn} \left[ \pm \varepsilon (\xi _1-\xi _0),m \right] +d_1 \mathrm{cn} \left[ \pm \varepsilon (\xi _1-\xi _0),m \right] }, \end{aligned}$$

(56)

where

$$\begin{aligned} m^2=\frac{m_1^2-1}{m_1^2} \end{aligned}$$

and

$$\begin{aligned} \varepsilon =\frac{s_2\sqrt{(c_1^2+d_1^2)(m_1^2c_1^2+d_1^2)}}{c_1^2+d_1^2} \end{aligned}$$

and eq. (56) is an elliptic functions double periodic solution.

For instance, when $a=1$, $\beta =0$, $k=\kappa ={1}/{\sqrt{2}}$, $b=-1$ and $\omega =\gamma =1$, we have

$$\begin{aligned} b_1=5,\quad c_1=-\frac{5}{2},\quad a_1=d_1=0,\quad \varepsilon =2. \end{aligned}$$

(57)

By using eqs (56) and (57), we have

$$\begin{aligned} \eta =\frac{ -2\mathrm{cn} [ \pm 2(\xi _1-\xi _0),\pm \frac{\sqrt{3}}{2}]}{\mathrm{sn}[ \pm 2(\xi _1-\xi _0),\pm \frac{\sqrt{3}}{2}]}. \end{aligned}$$

(58)

So we get the solutions as

$$\begin{aligned} q(x,t)=\frac{-2\mathrm{cn} \left\langle \pm 2 \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] ,\pm \frac{\sqrt{3}}{2} \right\rangle \mathrm {e}^{i\left( -\frac{\sqrt{2}}{2}x+t+\theta \right) }}{\mathrm{sn} \left\langle \pm 2 \left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] ,\pm \frac{\sqrt{3}}{2} \right\rangle }. \end{aligned}$$

(59)

Case 4.9. When $D_2>0$, $D_3>0$ and $D_4=0$, $G(\eta )$ has two single real roots and a real root with multiplicities two, i.e.

$$\begin{aligned} G(\eta )=(\eta -\alpha _1)(\eta -\alpha _2)(\eta -\alpha _3)^2, \end{aligned}$$

(60)

where $\alpha _1>\alpha _2$ and $\alpha _1 \ne \alpha _3,\alpha _2 \ne \alpha _3$. Let

$$\begin{aligned} c_1=\frac{\alpha _1-\alpha _2}{2} \left( \frac{\alpha _1+\alpha _2}{2}-\alpha _3\right) . \end{aligned}$$

(61)

According to eq. (13), we have

$$\begin{aligned} \pm (\xi _1-\xi _0)=\int \frac{\mathrm {d}\eta }{(\eta -\alpha _3)\sqrt{(\eta -\alpha _1)(\eta -\alpha _2)}}. \end{aligned}$$

(62)

From eq. (61), we have $c_1 \ne \pm 1$. For $c_1^2-1>0$, we have

$$\begin{aligned} \pm (\xi _1-\xi _0)=- \frac{1}{\sqrt{c_1^2-1}}\mathrm{ln}\bigg |\frac{y-c_2}{y+c_2}\bigg |. \end{aligned}$$

(63)

When $c_1^2-1<0$, we have

$$\begin{aligned} \pm (\xi _1-\xi _0)= -\sqrt{1-c_1^2} \,\mathrm{arctan}\frac{c_1+1}{1-c_1}y, \end{aligned}$$

(64)

where

$$\begin{aligned} c_2=\sqrt{\frac{c_1+1}{c_1-1}} \end{aligned}$$

and

$$\begin{aligned} y=\sqrt{1-\frac{\alpha _1-\alpha _2}{\left( \eta -\frac{\alpha _1+\alpha _2}{2}\right) +\frac{\alpha _1-\alpha _2}{2}}}. \end{aligned}$$

For instance, when $a=1$, $\beta =0$, $k=\kappa ={1}/{\sqrt{2}}$, $b=-1$ and $\omega =\gamma =-{1}/{2}$, we have $p=-1,q=0$. Then, $\eta$ is given by

$$\begin{aligned} \eta =\frac{1}{\mathrm{cos}(\xi _1-\xi _0)}. \end{aligned}$$

(65)

Therefore, the solution can be obtained as

$$\begin{aligned} q(x,t)=\frac{\mathrm {e}^{i\left( -\frac{\sqrt{2}}{2}x-\frac{1}{2} t+\theta \right) }}{\hbox {cos}\left[ \frac{\sqrt{2}}{2}(x+\sqrt{2}t)-\xi _0 \right] }. \end{aligned}$$

(66)

5 Power law

Power-law nonlinearity can be regarded as a generalisation of Kerr’s power-law nonlinearity. In this case, $F(u)=u^n$, so that eq. (5) can be given as

$$\begin{aligned} k^2(a-4\beta )g{''}-(\omega +a\kappa ^2+\gamma )g+bg^{2n+1}=0. \end{aligned}$$

(67)

Let

$$\begin{aligned} g=U^{{1}/{n}}. \end{aligned}$$

(68)

Then, eq. (67) can be transformed into

$$\begin{aligned}&k^2(a-4\beta )[ nUU{''}+(1-n){U{'}}^2]\nonumber \\&\quad -n^2(\omega +a\kappa ^2+\gamma )U^2+n^2bU^4=0. \end{aligned}$$

(69)

Let

$$\begin{aligned} A_1= & {} k^2(a-4\beta )n,\quad A_2=k^2(a-4\beta )(1-n),\nonumber \\ A_3= & {} n^2(\omega +a\kappa ^2+\gamma ),\quad A_4=n^2b. \end{aligned}$$

(70)

Then, eq. (69) is changed into

$$\begin{aligned} A_1UU{''}+A_2{U{'}}^2-A_3U^2+A_4U^4=0. \end{aligned}$$

(71)

Then, we use the trial equation method to solve the equation. By taking

$$\begin{aligned} {U{'}}^2=b_4U^4+b_3U^3+b_2U^2+b_1U+b_0, \end{aligned}$$

(72)

to eq. (71), we have

$$\begin{aligned}&(2A_1b_4+A_2b_4+A_4)U^4\nonumber \\&\quad +\left( \frac{3}{2}A_1b_3+A_2b_3\right) U^3\nonumber \\&\quad +(A_1b_2+A_2b_2-A_3)U^2\nonumber \\&\quad +\left( \frac{A_1}{2}b_1+A_2b_1\right) U+A_2b_0=0. \end{aligned}$$

(73)

Then, we obtain the following algebraic equations:

$$\begin{aligned}&2A_1b_4+A_2b_4+A_4=0, \end{aligned}$$

(74)

$$\begin{aligned}&\frac{3}{2}A_1b_3+A_2b_3=0,\end{aligned}$$

(75)

$$\begin{aligned}&A_1b_2+A_2b_2-A_3=0,\end{aligned}$$

(76)

$$\begin{aligned}&\frac{A_1}{2}b_1+A_2b_1=0,\end{aligned}$$

(77)

$$\begin{aligned}&A_2b_0=0. \end{aligned}$$

(78)

Solving eqs (74)–(78), we get a family of values to the parameters

$$\begin{aligned} b_1= & {} b_3=0,\quad b_4=\frac{-n^2b}{k^2(a-4\beta )(n+1)},\nonumber \\ b_2= & {} \frac{n^2(\omega +a\kappa ^2+\gamma )}{k^2(a-4\beta )}. \end{aligned}$$

(79)

For $b_0$, its value has two cases, namely $b_0=0$ or $b_0$ is an arbitrary constant, and we shall discuss the exact solutions of CGLE in detail under these two conditions.

Case I: $b_0=0$

If $b_0=0$, eq. (72) can be transformed into

$$\begin{aligned} {U^{\prime }}^{2}=b_4U^4+b_2U^2. \end{aligned}$$

(80)

In order to obtain the solutions of eq. (1) with the power-law nonlinearity, six cases are discussed separately as follows:

Case 5.1.1. When $b_4>0,b_2>0$, according to eq. (80), we have

$$\begin{aligned} \pm (\xi -\xi _0)=\int \frac{\mathrm {d}U}{U\sqrt{b_4U^2+b_2}}. \end{aligned}$$

(81)

To solve eq. (81), we have

$$\begin{aligned} \pm (\xi -\xi _0)=\frac{1}{\sqrt{b_2}}\mathrm{ln} \Big | \sqrt{1+\frac{b_2}{b_4U^2}}+\frac{\sqrt{b_2}}{\sqrt{b_4}U}\Big |. \end{aligned}$$

(82)

Then, the solutions of eq. (1) can be presented as

$$\begin{aligned} q(x,t)=\left\{ \frac{2\mathrm {e}^{\pm \sqrt{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}} \left[ k(x+2a\kappa t)-\xi _0 \right] } \sqrt{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}}}{\sqrt{\frac{-n^2b}{k^2(a-4\beta )(n+1)}} \left\langle \mathrm {e}^{ 2\sqrt{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}} \left[ k(x+2a\kappa t)-\xi _0 \right] }-1\right\rangle } \right\} ^{{1}/{n}} \mathrm {e}^{i(-\kappa x+\omega t+\theta )}. \end{aligned}$$

(83)

Case 5.1.2. When $b_4>0,b_2<0$, we have

$$\begin{aligned} \pm (\xi -\xi _0)=\frac{\mathrm{arccos}(\frac{\sqrt{-b_2}}{\sqrt{b_4}U})}{\sqrt{-b_2}}. \end{aligned}$$

(84)

Then, we get the solution as

$$\begin{aligned} q(x,t)=\left\{ \! \frac{\sqrt{-\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}}}{\sqrt{\frac{-n^2b}{k^2(a-4\beta )(n+1)}}\mathrm{cos} \left\langle \sqrt{-\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}} \left[ k(x+2a\kappa t)-\xi _0 \right] \right\rangle } \! \right\} ^{{1}/{n}}\mathrm {e}^{i(-\kappa x+\omega t+\theta )}. \end{aligned}$$

(85)

Case 5.1.3. When $b_4<0,b_2>0$, similar to Case 5.1.1, we can obtain the solutions as

$$\begin{aligned} q(x,t)=\left\{ \frac{2\mathrm {e}^{\pm \sqrt{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}} \left[ k(x+2a\kappa t)-\xi _0 \right] } \sqrt{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}}}{\sqrt{\frac{-n^2b}{k^2(a-4\beta )(n+1)}} \left\langle \mathrm {e}^{ 2\sqrt{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}} \left[ k(x+2a\kappa t)-\xi _0 \right] }-1\right\rangle } \right\} ^{{1}/{n}}\mathrm {e}^{i(-\kappa x+\omega t+\theta )}. \end{aligned}$$

(86)

Case 5.1.4. When $b_4<0,b_2<0$, the case has no solution when U is a real function according to eq. (81).

Case 5.1.5. When $b_4=0,b_2>0$, we get

$$\begin{aligned} q(x,t)=\mathrm {e}^{\pm \sqrt{\frac{(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}}\left[ k(x+2a\kappa t)-\xi _0 \right] +i(-\kappa x+\omega t+\theta )}. \end{aligned}$$

(87)

Case 5.1.6. When $b_4>0,b_2=0$, then we have

$$\begin{aligned} q(x,t)= & {} \left\langle \pm \frac{1}{\sqrt{\frac{-n^2b}{k^2(a-4\beta )(n+1)}} \left[ k(x+2a\kappa t)-\xi _0 \right] } \right\rangle ^{{1}/{n}}\nonumber \\&\times \,\mathrm {e}^{i(-\kappa x+\omega t+\theta )}. \end{aligned}$$

(88)

Case II: $b_0$ is an arbitrary constant

If $b_0$ is an arbitrary constant, eq. (72) is given by

$$\begin{aligned} {U{'}}^2=b_4U^4+b_2U^2+b_0. \end{aligned}$$

(89)

In order to solve eq. (89), when $b_4>0$, we have the following transformation:

$$\begin{aligned} \eta =(b_4)^{{1}/{4}}U,\quad \xi _1=(b_4)^{{1}/{4}}\xi . \end{aligned}$$

(90)

Fig. 1

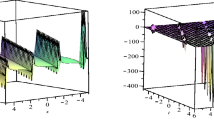
(a) The 3D graph of the triangle function-type periodic solution q(x, t) appearing in eq. (19), when $\xi _0=0,\theta ={\pi }/{2}$ and (b) the corresponding 2D graph for q(x, t) , when $t=1$.

Fig. 2

(a) The 3D graph of the rational function-type solution q(x, t) appearing in eq. (23), when $\xi _0=0,\theta ={\pi }/{2}$ and (b) the corresponding 2D graph for q(x, t), when $t=1$.

Fig. 3

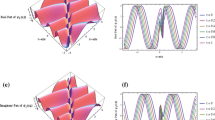
(a) The 3D graph of the solitary wave solution q(x, t) appearing in eq. (29), when $\xi _0=0,\theta ={\pi }/{2}$ and (b) the corresponding 2D graph for q(x, t), when $t=1$.

Fig. 4

(a) The 3D graph of Jacobian elliptic functions solution q(x, t) appearing in eq. (48), when $\xi _0=0,\theta =\frac{\pi }{2}$ and (b) the corresponding 2D graph for q(x, t), when $t=1$.

Then eq. (89) can be changed into

$$\begin{aligned} \eta _{\xi _1}^2=G(\eta )=\eta ^4+p\eta ^2+q, \end{aligned}$$

(91)

where

$$\begin{aligned} p=\frac{\frac{n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}}{ \left[ \frac{-n^2b}{k^2(a-4\beta )(n+1)} \right] ^{{1}/{2}}} ,\quad q=b_0. \end{aligned}$$

If $b_4<0$, by the following transformation

$$\begin{aligned} \eta =(-b_4)^{{1}/{4}}U,\quad \xi _1=(-b_4)^{{1}/{4}}\xi \end{aligned}$$

(92)

eq. (89) can be changed as

$$\begin{aligned} \eta _{\xi _1}^2=-G(\eta )=-(\eta ^4+p\eta ^2+q), \end{aligned}$$

(93)

where

$$\begin{aligned} p=\frac{\frac{-n^2(\omega +a\kappa +\gamma )}{k^2(a-4\beta )}}{ \left[ \frac{n^2b}{k^2(a-4\beta )(n+1)} \right] ^{{1}/{2}}} ,\quad q=-b_0. \end{aligned}$$

Similarly, applying the complete discrimination system of the fourth-order polynomial introduced in §3, we can also obtain the rational function-type solutions, solitary wave solutions, triangle function-type periodic solutions and Jacobian elliptic functions solutions. Other conditions are just the same and so we do not intend to show it here.

6 Numerical simulations for CGL equations

In this section, the numerical simulations of CGL equations are carried out. According to the solutions obtained above, four types of representative solutions are chosen to carry out numerical simulations. The real part of eqs (19), (23), (29) and (48) is calculated to draw the 3D and the corresponding 2D graphs. In addition, we only focus on the positive one if there is a plus-minus sign in the selected solutions. Numerical simulation for triangle function-type periodic solution is shown in figure 1, numerical simulation for rational function-type solution is shown in figure 2, numerical simulation for solitary wave solution is shown in figure 3 and numerical simulation for Jacobian elliptic functions solution is shown in figure 4.

By implementing numerical simulations, the evolution of four types of solutions are presented clearly, and the existence of the solutions are also proved.

7 Conclusions

This paper aims at finding all possible exact travelling wave solutions of the CGL equation with Kerr and power laws of nonlinearity. By applying the complete discrimination system for polynomial method and trial equation method, the rational function-type solutions, solitary wave solutions, triangle function-type periodic solutions and Jacobian elliptic function solutions are obtained, and some of them are new solutions. In particular, the solutions with concrete parameters are given to prove the existence of each solution. Moreover, four types of obtained solutions are drawn to show the nature of the solutions. The results show that the technique adopted by us for solving is efficacious and powerful, and the obtained solutions can help one to study the nonlinear dynamics of optical soliton propagations more deeply.