1 Introduction

The concept of solitons is one of the fundamental unifying ideas in modern physics and mathematics [1]. The soliton theory can be applied to diverse branches of physics such as plasmas physics, fluid dynamics, nonlinear optics, Bose–Einstein condensates (BECs), and nuclear physics [2–9]. The study of solitons in those physical systems reveals some exciting problems from both fundamental and application points of view [10–20].

In nonlinear optics, solitons are the focus of intense research interest due to their potential applications in telecommunication and ultrafast signal processing systems [21]. Solitons can be regarded as the balance between group velocity dispersion (GVD) and nonlinear effects [22]. They have various applications in pulse amplification, optical switch and pulse compression [23], and some studies on solitons have been carried out both theoretically and experimentally [24–28]. General analytic soliton solutions have been investigated [24], and nonlinear optics models giving rise to the appearance of solitons in a narrow sense have been considered [25]. Gazeau [26] was concerned with the evolution of solitons driven by random polarization mode dispersion. Under some parametric conditions, Choudhuri and Porsezian [27] have solved the higher-order nonlinear Schrödinger (NLS) equation with non-Kerr nonlinearity, and the interaction dynamics of solitons was reconsidered in [28].

In BECs, solitons can be viewed as fundamental nonlinear excitations [29]. Recently, with various methods, bright, dark and gap matter–wave solitons in BECs have been created [30]. These solitons have attracted much theoretical and experimental interests [31–34]. Some matter–wave solitons in a system of three-component Gross–Pitaevskii equation arising from the context of spinor BECs with time-modulated external potential and scattering lengths are presented in [31]. A family of non-autonomous soliton solutions of BECs with the time-dependent scattering length in an expulsive parabolic potential was obtained in [32]. Becker et al [33] studied the dynamics of apparent soliton stripes in elongated BECs experimentally and theoretically. Kanna et al [34] studied the dynamics of non-autonomous solitons in two- and three-component BECs.

In this paper, we shall study the properties and features of oscillating solitons in nonlinear optics, which can be described by the following variable-coefficient NLS (vcNLS) equation [21]:

$$ i\frac{\partial u}{\partial z}+i\,\beta_{1}(z)\frac{\partial u}{\partial t}+\beta_{2}(z)\frac{\partial^{2} u}{\partial t^{2}}+\gamma(z)|u|^{2}u=0, $$
(1)

where u(z,t) is the temporal envelope of solitons, z is the longitudinal coordinate and t is the time in the moving coordinate system. β 1(z) is the reciprocal of the group velocity, β 2(z) represents the GVD coefficient and γ(z) is the nonlinearity coefficient. Equation (1) can reduce to the standard vcNLS equation while β 1(z) = 0, and some studies on the standard vcNLS equation has been made.

However, eq. (1) has not been investigated due to the existence of β 1(z). With the help of the Hirota’s bilinear method, analytic soliton solutions for eq. (1) will be obtained. The relevant properties and features of oscillating solitons will be illustrated. The influence of β 1(z) will be analysed for the first time.

This paper is structured as follows. In §2, analytic soliton solutions for eq. (1) will be presented. In §3, the properties and features of oscillating solitons will be disucssed, and the influence of β 1(z) will be analysed. Finally, our conclusions will be presented in §4.

2 Analytic soliton solutions for eq. (1)

At first, the dependent variable transformation can be introduced as [35–38]

$$ u(z,t)=\frac{g(z,t)}{f(z,t)}, $$
(2)

where g(z,t) is a complex differentiable function and f(z,t) is a real one. With symbolic computation, the bilinear forms for eq. (1) are obtained as

$$\begin{array}{@{}rcl@{}} iD_{z}\,g\cdot f +i\beta_{1}(z)D_{t}\,g\cdot f&+&\beta_{2}(z){D_{t}^{2}}\,g\cdot f=0, \end{array} $$
(3)
$$\begin{array}{@{}rcl@{}}\beta_{2}(z){D_{t}^{2}}\,f\cdot f-\gamma(z)gg^{*}&=&0, \end{array} $$
(4)

where the asterisk denotes the complex conjugate. D z and D t [39] are the Hirota’s bilinear operators, and are defined by

$$ {D_{z}^{m}}\,{D_{t}^{n}}(a\cdot b) = \left( \frac{\partial}{\partial z} - \frac{\partial}{\partial z^{\prime}} \right)^{m}\,\left( \frac{\partial}{\partial t} - \frac{\partial}{\partial t^{\prime}} \right)^{n}\, a (z,t)\, b(z^{\prime},t^{\prime})\bigg|_{z^{\prime}= z,\ t^{\prime}= t}. $$
(5)

With the following power series expansions for g(z, t) and f(z, t):

$$\begin{array}{@{}rcl@{}} g(z,t)&=&\varepsilon g_{1}(z,t) + \varepsilon^{3}g_{3}(z,t) + \varepsilon^{5}g_{5}(z,t) + \cdots, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} f(z,t)&=&1 + \varepsilon^{2}f_{2}(z,t) + \varepsilon^{4}f_{4}(z,t) + \varepsilon^{6}f_{6}(z,t) +\cdots, \end{array} $$
(7)

where ε is a formal expansion parameter, bilinear forms (3) and (4) can be solved. Substituting expressions (6) and (7) into bilinear forms (3) and (4) and equating coefficients of the same powers of ε to zero, yield recursion relations for g n (z,t)s and f n (z,t)s. Then, the analytic soliton solutions for eq. (1) can be derived.

To get the analytic soliton solutions for eq. (1), we assume

$$ g(z,t)= g_{1}(z,t),\qquad f(z,t)= 1+ f_{2}(z,t), $$
(8)

where

$$\begin{array}{@{}rcl@{}} g_{1}(z,t)\,=\,\mathrm{e}^{\theta_{1}},\quad \theta_{1} \,=\, \left[a_{11}(z)+i\,a_{12}(z)\right]\,z+(b_{11}+i\,b_{12})t+k_{11}+i\,k_{12}, \end{array} $$
(9)

with b 11, b 12, k 11 and k 12 are real constants. a 11(z) and a 12(z) are the differentiable functions to be determined. With g 1(z,t), and collecting the coefficient of ε in eq. (3), we obtain the constraints on a 11(z) and a 12(z) as

$$\begin{array}{@{}rcl@{}} a_{11}(z)&=&\frac{1}{z}\int \left[-b_{11}\beta_{1}(z)-2 b_{11} b_{12} \beta_{2}(z)\right] \, \mathrm{d}z,\\ a_{12}(z)&=&\frac{1}{z}\int \big[b_{11}^{2}\beta_{2}(z)-b_{12}\beta_{1}(z)-b_{12}^{2}\beta_{2}(z)\big]\,\mathrm{d}z. \end{array} $$

Substituting g 1(z,t) into eq. (4), and collecting the coefficient of ε 2, we get

$$\begin{array}{@{}rcl@{}} f_{2}(z,t)=M\mathrm{e}^{\theta_{1}+\theta_{1}^{*}} \end{array} $$
(10)

where

$$\begin{array}{@{}rcl@{}} M=\frac{\gamma(z)}{8 b_{11}^{2}\beta_{2}(z)},\qquad \beta_{2}(z)=c\,\gamma(z), \end{array} $$

and c is an arbitrary constant.

Without loss of generality, we set ε = 1, and can write the analytic soliton solutions as

$$\begin{array}{@{}rcl@{}} u(z,t)&=&\frac{g(z,t)}{f(z,t)}= \frac{g_{1}(z,t)}{1 + f_{2}(z,t)}\\ &=&\frac{1}{\sqrt{M}}\mathrm{e}^{i\left[a_{12}(z)z+b_{12}t+k_{12}\right]}\text{sech}\left[a_{11}(z)z+b_{11}t+k_{11}+\frac{1}{2}\ln M\right]. \end{array} $$
(11)

3 Discussion

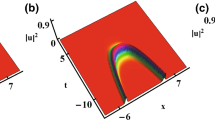
In figure 1, oscillating solitons are exhibited in nonlinear optics. In this case, nonlinearity is assumed to be constant; γ(z) = 0.01 in figure 1. When β 1(z) = 2 exp(−0.5z) + sin(2z) as in figure 1a, the solitons are stable at first, and then exhibit periodic soliton propagation. We can adjust the soliton propagation status in comparison with figure 1a. By changing β 1(z) the stable solitons can be changed to oscillating solitons when β 1(z) = 2 exp(−0.5z 2) (see figure 1b).

Figure 1
figure 1

Solitons in nonlinear optics. The parameters are c = 1, k 11 = −1, k 12 = 2, b 11 = 1, b 12 = −1, γ(z) = 0.01 with (a) β 1(z) = 2 exp(−0.5z) + sin(2z), (b) β 1(z) = 2 exp(−0.5z 2) + sin(2z).

Full size image

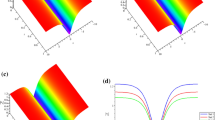
If nonlinearity γ(z) is also taken as a function in figure 1b, the periodic and oscillation state of solitons can be changed. When γ(z) = sin(z), the periodicity of soliton increases, and the oscillation of solitons is enhanced (figure 2a). Increasing the coefficient of γ(z) results in the decrease of the periodic and oscillation state of solitons, which can be seen in figure 2b with γ(z) = 1.5 sin(2z).

Figure 2
figure 2

Solitons in nonlinear optics with the same parameters as given in figure 1, but with (a) β 1(z) = 2 exp(−0.5z 2) + sin(2z), γ(z) = sin(z), (b) β 1(z) = 2 exp(−0.5z 2) + sin(2z), γ(z) = 1.5 sin(2z).

Full size image

By changing the values of β 1(z) and γ(z), we get different propagation status of solitons in figure 3. For β 1(z) and γ(z), if we transform the function type, the change of the phase shift is opposite. Moreover, when β 1(z) and γ(z) are linear combinations of trigonometric functions with different periods, the periodic propagation status of solitons is disrupted as shown in figure 3b. Soliton oscillations are sometimes weakened, and sometimes exacerbated. Thus, the soliton propagation status can be controlled with β 1(z) and γ(z) in nonlinear optics.

Figure 3
figure 3

Solitons in nonlinear optics with the same parameters as given in figure 1, but with (a) β 1(z) = 1.5 sin(2z), γ(z) = exp(−0.5z 2), (b) β 1(z) = 1.5 sin(2z) + cos(z), γ(z) = 1.5 cos(2z) + sin(z).

Full size image

4 Conclusions

In this paper, oscillating solitons in nonlinear optics were obtained. The vcNLS equation (see eq. (1)), which can be used to describe the soliton propagation, was investigated analytically. The bilinear forms (3) and (4) were derived, and the analytic soliton solutions (11) were obtained. According to solutions (11), the oscillating solitons were exhibited with different values of β 1(z) and γ(z) (see figures 1–3), and the influences of β 1(z) and γ(z) were analysed. The results have shown that the status of the soliton propagation can be controlled with β 1(z) and γ(z) in nonlinear optics. Results of this paper might be of potential use in the design of the dispersion-managed optical communication system and mode-locked fibre lasers.