1 Introduction

Nonlinear evolution equations (NLEEs) depict many physical scenarios that occur in many areas of physics, engineering, and applied mathematics. It is indeed important to investigate the exact explicit solutions of NLEEs so as to have a better understanding of the phenomena modeled by the underlying NLEEs. To obtain the exact solutions of NLEEs, many effective methods have been developed, such as the inverse scattering method [1, 2], the homogeneous balance method [3, 4], the Darboux transformation method [5, 6], Hirotäs bilinear method [7, 8], the variable separation approach [9], the extended tanh method [10, 11], the Lie group method [12, 13], and extended homoclinic test technique [14, 15].

Generally speaking, the interactions between soliton solutions for some nonlinear partial differential equations are considered to be completely elastic. That is to say, the soliton amplitude, velocity, and wave shape will not alter after nonlinear collisions [1]. However, for some soliton equations, when certain conditions between the wave speeds and velocities are satisfied, the completely non-elastic interactions between soliton solutions will occur. For example two or more solitons may fuse to a single soliton [16, 17]. On the contrary, at a specific time, a single soliton may fission to two or more solitons [18]. These two types of phenomena were called as soliton fission and soliton fusion, respectively [18]. In fact, in many nonlinear science fields such as the plasma physics, gas dynamics, laser and optical physics, hydrodynamics, nuclear physics, electromagnetics, and passive random walker dynamics [19], people have observed the similar phenomena. Therefore, it plays a very important role to discuss the elastic interactions between the solitary waves in certain integrable or non-integrable system with strong physical backgrounds, and it may provide theoretical tools in supporting and understanding the relevant dynamical behavior.

In this work, we consider the (\(3+1\))-dimensional Yu–Toda–Sasa–Fukuyama (YTSF) equation:

$$\begin{aligned}&(\varPhi (v)v_z-4v_t)_x+3v_{yy}=0,\nonumber \\&\quad \varPhi (v)=\partial _x^2 +4v+2v_x\partial _x^{-1}, \end{aligned}$$
(1)

where \(v:R_x\times R_y\times R_z\times R_t\rightarrow R\). Using the potential \(v=u_x\) gives the (\(3+1\))-dimensional potential-YTSF equation [20]:

$$\begin{aligned} -4u_{xt}+u_{xxxz}+4u_xu_{xz}+2u_{xx}u_z+3u_{yy}=0. \end{aligned}$$
(2)

It is well known that YTSF equation is an extension of the Bogoyavlenskii–Schif equation, and it is not a integrable system [21]. The linearly solitary wave solution of YTSF equation was firstly given using the strong symmetry [21]. The non-traveling wave solution was found using auto-Bäcklund transformation and the generalized projective Riccati equation method [22, 23]. Moreover, some soliton-like solutions and periodic solutions for the potential-YTSF equation were obtained by Hirotäs bilinear method, the tanh–coth method, and the exp-function method [13, 20, 24]. Recently, Darvishi and Najafi [25] obtained some breather cross-kink solutions by modification of the extended homoclinic test technique. In this work, we discuss further the (\(3+1\))-dimensional potential-YTSF equation by new methods including the extended homoclinic test technique and homoclinic breather limit method. New exact solutions including kinky breather-wave solution, rational breather-wave solution, and solitary solution are obtained. Besides, a new nonlinear dynamical behavior of kinky wave, kink degeneracy, is investigated, and the completely non-elastic interaction between kink solitary wave and rational breather-wave solution is presented. Eventually, rational breather waves are drowned or swallowed up by kink wave in the interaction between kink wave and rational breather wave as \(t\rightarrow \infty \).

Now, we propose a homoclinic (heteroclinic) breather limit method (HBLM), to seek kink degeneracy phenomenon of the potential-YTSF equation. We take the following four steps [26]:

  • Step 1 By Painlevé analysis, a transformation \(u=T(f)\) is made for some new and unknown function f.

  • Step 2 By using the transformation in step 1, original equation can be converted into Hirotas bilinear form \( G(D_{t}, D_{x}, f)=0\), where the D-operator is defined by

    $$\begin{aligned}&D_{x}^{m}D_{y}^{k}f\cdot g\\&\quad =\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x^{'}}\right) ^m\left( \frac{\partial }{\partial y}-\frac{\partial }{\partial y^{'}}\right) ^kf(x,y,t) \\&\qquad \cdot \, g(x^{'},y^{'},t^{'})|_{(x,y,t)=({x^{'},y^{'},t^{'}})}. \end{aligned}$$

  • Step 3 Solve the above equation to get kinky breather-wave solution by using extended homoclinic test approach (EHTA) [25].

  • Step 4 Let the period of periodic wave go to infinite in kinky breather-wave solution; we can obtain rational breather-wave solution; and at the same time, we get kink degeneracy phenomenon.

2 Kink degeneracy and rational breather-wave solution

Firstly, we obtain an exact kinky breather-wave solution by using the extended homoclinic test technique. We suppose that

$$\begin{aligned} \xi =x+az, and \end{aligned}$$
(3)

then, Eq. (2) reduces to

$$\begin{aligned} -4u_{\xi \,t}+au_{\xi \xi \xi \xi }+6au_{\xi }u_{\xi \xi }+3u_{yy}=0, \end{aligned}$$
(4)

whose Painlevé analysis and Lax pairs are given in [13] together with some exact solutions. By using Painleve analysis we can assume that

$$\begin{aligned} u(\xi ,y,t)=2(lnf)_{\xi }, \end{aligned}$$
(5)

for some unknown real function \(f(\xi ,y,t)\) and Eq. (5) into Eq. (4), we can be reduced into the following bilinear form

$$\begin{aligned} (-4D_{\xi }D_{t}+aD^{4}_{\xi }+3D_y^{2})f\cdot f=0. \end{aligned}$$
(6)

With regard to Eq. (6), using the extended homoclinic test technique, we are going to seek the solution of the form

$$\begin{aligned} f(\xi ,y,t)={e}^{-p\eta }+b_{0}\cos ({p_{1}(\xi -\beta \,t+\omega _{1})}) +b_{1}{e}^{p\eta }, \end{aligned}$$
(7)

where \(\eta =\xi +\alpha \,y+\beta \,t+\omega \) and \(\alpha , \beta , \omega , \omega _{1}, p, p_{1}, b_{0}, b_{1}\) are some constants to determine later. Substituting Eq. (7) into Eq. (6), we get

$$\begin{aligned}&[2b_{1}b_{0}(-4\beta {p}^{2}-4{p_{1}}^{2}\beta -6a{p}^{2}p_{1}^{2}\nonumber \\&\quad +\,ap_{1}^{4}+ap^{4}+3\,{p}^{2}{\alpha }^{2})\cos (p_{1}(\xi -\beta \,t+\omega _{1}))\nonumber \\&\quad +\,8apb_{0}b_{1}p_{1}(p-p_{1}) (p+p_{1})\nonumber \\&\quad \times \,\sin (p_{1}(\xi -\beta \,t+\omega _{{1}}))]{\mathrm{e}^{p\eta }}+ [2b_{0}(-4\beta \,p^{2}\nonumber \\&\quad -\,6ap^{2}p_{1}^{2}-4p_{1}^{2}\beta +ap_{1}^{4}+ap^{4}+3p^{2}\alpha ^{2})\nonumber \\&\quad \times \,\cos (p_{1}(\xi -\beta \,t+\omega _{1}))-8apb_{0}p_{1}(p-p_{1})\nonumber \\&\quad \times \,(p+p_{1})\sin (p_{1} (\xi -\beta \,t+\omega _{1}))]{\mathrm{e}^{-p\eta }}\nonumber \\&\quad +\,8(3p^{2}\alpha ^{2}b_{1}-4\beta \,{p}^{2}b_{1}+4ap^{4} b_{1}\nonumber \\&\quad -\,\beta \,b_{0}^{2}{p_{1}}^{2}+ab_{0}^{2}p_{1}^{4})=0. \end{aligned}$$
(8)

Equating all coefficients of different powers of \({e}^{p\eta },{e}^{-p\eta }, \cos (p_{1}(\xi -\beta \,t+\omega _{1})), \sin (p_{1}(\xi -\beta \,t+\omega _{1}))\) and constant term to zero, we obtain the set of algebraic equation for \(\alpha ,\beta ,\omega ,\omega _{1},p,p_{1},b_{1},b_{0}\). From Eq. (8), we have

$$\begin{aligned} \left\{ \begin{array}{l} 8apb_{0}p_{1}(p-p_{1})(p+p_{1})=0\\ -4\beta {p}^{2}-4{p_{1}}^{2}\beta -6a{p}^{2}p_{1}^{2}+ap_{1}^{4}\\ \quad +\,ap^{4}+3\,{p}^{2}{\alpha }^{2}=0\\ 3p^{2}\alpha ^{2}b_{1}-4\beta \,{p}^{2}b_{1}+4ap^{4}b_{1}\\ \quad -\,\beta \,b_{0}^{2}{p_{1}}^{2}+ab_{0}^{2}p_{1}^{4}=0. \end{array}\right. \end{aligned}$$
(9)

Solving Eq. (9) with the aid of Maple, we get

$$\begin{aligned} p_{1}=\pm \,p,b_{1}=\frac{b^{2}_{0}(\beta -ap^{2})}{4(\beta +2ap^{2})}, \alpha =\sqrt{\frac{8\beta +4ap^{2}}{3}}, \end{aligned}$$
(10)

where \(\beta ,\omega ,\omega _{1},p\) and \(b_{0}\) are some free real constants. Substituting Eq. (10) with Eq. (3) into Eq. (7), we obtain the solution as

$$\begin{aligned} \begin{aligned} f(x,y,z,t)={e}^{-p\zeta }+b_{0}\cos (p\vartheta )+b_{1}{e}^{p\zeta }, \end{aligned} \end{aligned}$$
(11)

where \(\zeta =x+az+\alpha \,y+\beta \,t+\omega \), \(\vartheta =x+az-\beta \,t+\omega _{1}\). If \(0< b_{1}\in \mathbf {R}\), then we obtain the exact kinky breather-wave solution as follows:

$$\begin{aligned}&u(x,y,z,t)\nonumber \\&\quad =\frac{2p(2\sqrt{b_{1}}\sinh (p\zeta +\frac{1}{2}\ln (b_{1})) -b_{0}\sin (p\vartheta ))}{2\sqrt{b_{1}}\cosh (p\zeta +\frac{1}{2}\ln (b_{{1}}))+b_{0}\cos (p\vartheta )}. \end{aligned}$$
(12)

Especially, if we choose the arbitrary \(b_{0}=-2 \), Eq. (12) can be rewritten as:

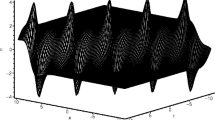
$$\begin{aligned} u=\frac{2p\left( \sqrt{\frac{\beta -ap^{2}}{\beta +2ap^{2}}} \sinh \left( p\zeta +\frac{1}{2}\ln \left( \frac{\beta -ap^{2}}{\beta +2ap^{2}}\right) \right) +\sin (p\vartheta )\right) }{\sqrt{\frac{\beta -ap^{2}}{\beta +2ap^{2}}}\cosh \left( p\zeta +\frac{1}{2}\ln \left( \frac{\beta -ap^{2}}{\beta +2ap^{2}}\right) \right) -\cos (p\vartheta )}, \end{aligned}$$
(13)

where \(\beta >ap^{2}\) or \(\beta <-2ap^{2}\) when \(a>0\), \(\beta >-2ap^{2}\) or \(\beta <ap^{2}\) when \(a<0\). Solution u(x, y, z, t) represented by Eq. (12) is kinky breather wave which has speed \(\beta \), and the forward-direction (or backward-direction) wave shows breather feature as trajectory along the straight line \( x=-(\alpha \,y+az+\beta t+\omega ) \); meanwhile, it takes on kinky feature as trajectory along the straight line \(x=-(az-\beta t+\omega _1)\) for (3+1)-dimensional potential-YTSF equation. Especially, this wave shows both breather and kink feature to space variable t. Besides, it also has a periodic feature with period \(\frac{2\pi }{p}\) (see Fig. 1).

Fig. 1
figure 1

Kinky breather-wave solution as \(\beta =2,\, p=\frac{1}{4},\, b_{0}=2,\, \alpha =-1,\, \omega _{1}=\omega =y=z=0\)

Full size image

Secondly, let p tends to zero in Eq. (13), and we can get the following rational breather-wave solution as follows:

$$\begin{aligned} u(x,y,z,t)={\frac{8x+8az+\frac{8}{3}\sqrt{6\beta }y +4\omega +4\omega _{1}}{\mathfrak {R}}}, \end{aligned}$$
(14)

where \(\mathfrak {R}=(x+az+\beta \,t+\frac{2}{3}\sqrt{6} \sqrt{\beta }y+\omega )^{2}+(x+az-\beta \,t+\omega _{1})^{2} -\frac{3a}{\beta }\). The solution u(x, y, z, t) represented by Eq. (14) is a new rational breather-wave solution. Notice that u tends to zero in Eq. (14) when the \(t\rightarrow \pm \infty \) and notice that the rational breather-wave solution has one upper lump and one down deep hole. The deep hole is hidden under the plane wave, and it is a bright-dark solitary wave solution, so it is no longer the kinky. Such a surprising feature of weakly dispersive long wave is first obtained. Meanwhile, this shows that kink is degenerated as a rational breather-wave solution when the period of breather wave tends to infinite in the breather kink wave (see Fig. 2). This is a new nonlinear phenomenon up to now.

Fig. 2
figure 2

Rational breather-wave solution as \(a=\omega _{1}=\omega =1,\beta =3,y=z=0\)

Full size image

Now, we study the potential function of the (\(3+1\))-dimensional potential-YTSF equation. By Eq. (14) to give u(x, y, z, t), the potential function:

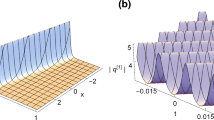
$$\begin{aligned} v=-u_{x}= & {} \frac{4\left( 2x+2az+\frac{2\sqrt{6\beta }}{3}y +\omega +\omega _{1}\right) ^{2}}{\mathfrak {R}^{2}}\nonumber \\&-\frac{8}{\mathfrak {R}}, \end{aligned}$$
(15)

The solution Eq. (15) is actually a dark rogue wave [27] solution which is a point of hot discussion. The amplitude of the rogue wave solution Eq. (15) depends on the four parameters \(a, \beta , \omega _{1}\), and \(\omega _{2}\). It has one down hole and two small upper peaks. The main peak forms a much deeper hole. Figure 3 shows the time structure of the potential function v(x, 0, 0, t). We can also see that an obvious feature of this solution is localized in \(x-\)directions. Thus, it indicates that the obtained solution is the rational rogue wave of (\(3+1\))-dimensional potential-YTSF equation.

Fig. 3
figure 3

Time structure of the rational rogue solution as \(a=-2,\, \beta =1,\, \omega _{1}=\omega =4,\, y=z=0\)

Full size image

3 Interaction between kink wave and rational breather-wave solution

3.1 Kink-wave solution

Here, we construct single solitary wave solution of the (\(3+1\))-dimensional potential-YTSF equation with the help of its bilinear form. Substituting the ansätz with regard to Eq. (5), using the extended homoclinic test technique, we are going to seek the solution of the form

$$\begin{aligned} f(\xi ,y,t)=1+{e}^{a_{3}\xi +b_{3}y+c_{3}t}, \end{aligned}$$
(16)

into Eq. (6) which will produce the dispersion relation

$$\begin{aligned} c_{3}=\frac{aa_{3}^{4}+3b_{3}^{2}}{4a_{3}}. \end{aligned}$$
(17)

So, we can obtain the single traveling solitary wave solution

$$\begin{aligned} u(x,y,z,t)=\frac{2a_{3}{e}^{a_{3}\xi +b_{3}y+c_{3}t}}{1+{e}^{a_{3}\xi +b_{3}y+c_{3}t}}. \end{aligned}$$
(18)

The solution Eq. (18) shows the single kink soliton feature, the solution \(u\rightarrow 2a_{3}\), when \(t\rightarrow +\infty \), and the solution \(u\rightarrow 0\), when \(t\rightarrow -\infty \).

3.2 Rational breather-wave solution

In this section, we construct rational breather-wave solution of the (\(3+1\))-dimensional potential-YTSF equation with the help of its bilinear form. Inspired by the equation Eq. (14), substituting the ansätz

$$\begin{aligned} f(\xi ,y,t)= & {} 1+({a_{1}\xi +b_{1}y+c_{1}t})^{2}\nonumber \\&+\,({a_{2} \xi ^{2}+b_{2}y^{2}+c_{2}t}^{2}), \end{aligned}$$
(19)

into Eq. (6) will produce the following relation

$$\begin{aligned} \begin{aligned}&c_{1}=\frac{3a(a_{1}^{4}+2a_{1}^{2}a_{2}+a_{2}^{2})}{4a_{1}},b_{2}=-a(a_{2}+a_{1}^{2})^{2},\\&b_{1}=0, c_{2}=\frac{-9a^{2}a_{2}(3a_{1}^{2}a_{2}^{2} +a_{1}^{6}+3a_{1}^{4}a_{2}+a_{2}^{3})}{16a_{1}^{2}}. \end{aligned} \end{aligned}$$
(20)

So, we can obtain the rational breather-wave solution by inserting Eq. (20) with Eq. (19) into Eq. (5) which is in the form of

$$\begin{aligned}&u(\xi ,y,t)\nonumber \\&\quad =(4(a_{1}^{2}+a_{2})\xi +3a(a_{1}^{2}+a_{2})^{2}t)\nonumber \\&\qquad \times \left( 1+\left( a_{1}\xi +\frac{3a(a_{1}^{2}+a_{2})^{2}t}{4a_{1}}\right) ^{2}-a(a_{1}^{2}+a_{2})^{2}y^{2}\right. \nonumber \\&\qquad \left. +\,a_{2}\xi ^{2}+{\frac{9a^{2}a_{2}(3a_{1}^{2}a_{2}^{2} +a_{1}^{6}+3a_{1}^{4}a_{2}+a_{2}^{3}){t}^{2}}{16a_{1}^{2}}}\right) ^{-1}. \end{aligned}$$
(21)

Some asymptotic behaviors of the obtained solution Eq. (21) can be found, the solution \(u\rightarrow 0\), when \(t\rightarrow \pm \infty \). It does not possess the feature of kink solitary wave. Moreover, the solution Eq. (21) is algebraically decaying, rather than exponentially decaying. From the Fig. 4, we know that the rational breather-wave solution has one upper lump and one down deep hole. The deep hole is hidden under the plane wave, and it is a bright-dark solitary wave solution (see Fig. 4).

Fig. 4
figure 4

Rational breather-wave solution as \(a=a_{2}=-\frac{1}{4},\, a_{1}=-1,\, x=0,\, t=0\)

Full size image

3.3 Interaction

In this section, we study the completely non-elastic interaction between kink solitary wave solution and rational breather-wave solution for the (\(3+1\))-dimensional potential-YTSF equation. To obtain the completely non-elastic interaction between solitary wave solution and rational kink-wave solution, we turn the above function \(f(\xi ,y,t)\) into the following new ansätz function

$$\begin{aligned} f(\xi ,y,t)= & {} 1+({a_{1}\xi +b_{1}y+c_{1}t})^{2}\nonumber \\&+\,(a_{2}\xi ^{2}+b_{2}y^{2}+c_{2}t^{2}) +\delta {e}^{a_{3}\xi +b_{3}y+c_{3}t}. \end{aligned}$$
(22)

The function \(f(\xi ,y,t)\) contains an exponential function and a rational function. Substituting Eq. (22) into Eq. (6), we can get the following relations among the parameters,

$$\begin{aligned} \begin{aligned}&b_{2}=-aa_{3}^{4}, b_{1}=0, c_{2}=\frac{9}{16}a^{2}a_{3}^{6} -c_{1}^{2}, c_{3}=\frac{aa_{3}^{3}}{4},\\&b_{3}=0, a_{1}=\frac{3aa_{3}^{3}}{4c_{1}}, a_{2}=\frac{a_{3}^{3}(16c_{1}^{2}-9a^{2}a_{3}^{6})}{16c_{1}^{2}}. \end{aligned} \end{aligned}$$
(23)

So, we can obtain new explicit solitary wave solution of (\(3+1\))-dimensional potential-YTSF equation by inserting Eq. (23) with Eq. (24) into Eq. (5) which is in the form of

$$\begin{aligned} u(\xi ,y,t)=\frac{a_{3}(\chi +2\delta {e}^{\frac{1}{4} a_{3}(4\xi +aa_{3}^{2}t)})}{1+\frac{\chi ^{2}}{16}-aa_{3}^{4}y^{2} +\delta {e}^{\frac{1}{4}a_{3}(4\xi +aa_{3}^{2}t)}}, \end{aligned}$$
(24)

where \(\chi =4a_{3}\xi +3aa_{3}^{3}t,\) and \(a_{3},c_{1}, \delta \) are arbitrary constants. New asymptotic behaviors of the obtained solution Eq. (24) can be got with \(\frac{aa_{3}}{4}>0\), the solution \(u\rightarrow 2a_{3}\) as \(t\rightarrow +\infty \), and solution \(u\rightarrow 0\) as \(t\rightarrow -\infty \). The asymptotic behaviors show the single kink wave finally drowns or swallows up rational breather wave varying with evolution of time t. In fact, the solution Eq. (24) is a rational kink-wave solution. That is to say, it is a solitary wave solution with x and t (or z and t), and at the same time is also a rational kink-wave solution with x, y and t (or z, y and t). It is algebraically decaying, and it is also exponentially decaying. Hence, it is a mixed exponential–algebraic solitary wave solution. It reflects the completely non-elastic interaction between two different solitary waves. Figure 5 shows the process of interaction, and rational breather waves are drowned or swallowed by kink wave (see Fig. 5).

Fig. 5
figure 5figure 5

Spatial structures interaction at different times as \(a=-\frac{1}{2},\, a_{3}=\frac{1}{2},\, \delta =-\frac{1}{16},\, x=0\)

Full size image

Now, we study the soliton interaction of the (\(3+1\))-dimensional potential-YTSF equation. In fact, noting \(f_{1}=1, f_{2}=(a_{1}\xi +b_{1}y+c_{1}t)^{2}+a_{2}\xi ^{2} +b_{2}y^{2}+c_{2}t^{2}, f_{3}=\delta {e}^{a_{3}\xi +b_{3}y+c_{3}t},\) then any combinations among \(f_{1}, f_{2}\) and \(f_{3}\) will form a solitary wave. So, we can obtain the solitary waves \(S_{1}, S_{2}\) and \(S_{3}\) with the following functions

$$\begin{aligned} \left\{ \begin{array}{l} S_{1}: f_{13}=1+\delta {e}^{a_{3}\xi +b_{3}y+c_{3}t},\\ S_{2}: f_{12}=1+\frac{\chi ^{2}}{16}-aa_{3}^{4}y^{2},\\ S_{3}: f_{23}=1+\frac{\chi ^{2}}{16}-aa_{3}^{4}y^{2} +\delta {e}^{a_{3}\xi +b_{3}y+c_{3}t}. \end{array} \right. \end{aligned}$$
(25)

The solitary waves \(S_{1}\) and \(S_{3}\) are solutions of (\(3+1\))-dimensional potential-YTSF equation. Note the velocity of the single kink solitary wave solution \(S_{1}\) is \(v_{k}=-\frac{aa_{3}^{2}}{4}\) on the x-axis. Notice \(S_{3}\) is a rational breather solitary in the condition of \(\delta =0\), and the velocity is \(v_{r}=-\frac{3aa_{3}^{2}}{4}\) on the x-axis [28]. So, we obtain the relation \(\varDelta (v_{r}, v_{k})\) of between \(v_{r}\) and \(v_{k}\):

$$\begin{aligned} \varDelta (v_{r}, v_{k})=v_{r}-v_{k}=-\frac{aa_{3}^{2}}{2}. \end{aligned}$$
(26)

If \(\varDelta (v_{r}, v_{k})=0\), then \(v_{r}\equiv v_{k}\), and under this condition, \(a_{3}=0\), no interaction of the solitary wave solution occurs. If \(\varDelta (v_{r}, v_{k})>0\), then \(v_{r}>v_{k}\), and under this condition, the fission of the solitary wave solution will occur. Obviously, when \(t\rightarrow -\infty \), the solution u represents a rational solitary wave solution. When \(t\rightarrow +\infty \), the solution u turns into two solitary waves: the kink solitary wave solution and the rational solitary wave solution. If \(\varDelta (v_{r}, v_{k})<0\), then \(v_{r}<v_{k}\). Under this condition, the fusion of the solitary wave solutions will occur. It is clear that when \(t\rightarrow -\infty \), the solution u represents two solitary waves: the kink solitary wave solution and the rational solitary wave solution. When \(t\rightarrow +\infty \), the rational solitary wave solution disappears, and only the kink solitary wave solution exists. Like this phenomenon, the process of interaction of rational breather wave is drowned or swallowed by kink solitary wave, when \(t\rightarrow \infty \)(see Fig. 5). Our results are different from the previous literatures [13, 18, 20–23]. The above analysis shows that the mixed exponential–algebraic solitary wave solution is instability. These are new dynamical phenomenon for (\(3+1\))-dimensional potential-YTSF equation, which has not been reported.

4 Conclusions

In summary, based on Hirotä bilinear form, applying the homoclinic breather limit method to the (\(3+1\))-dimensional potential-YTSF equation, exact kinky breather-wave solution, rational breather-wave solution, kink-wave solution, and mixed exponential–algebraic solitary wave solutions are obtained. Furthermore, we investigated new dynamical features of kinky wave including kink degeneracy, and rational breather wave is drowned or swallowed by kink wave. At the same time, the completely non-elastic interaction between kink wave and rational breather wave for (\(3+1\))-dimensional potential-YTSF equation is presented. The result obtained in this work shows that the mixed exponential–algebraic solitary wave solution is instability. These results might be helpful to understand the propagation processes for nonlinear waves in fluid mechanics.