Charged analogue of Vlasenko–Pronin superdense star with variable cosmological term

Abstract

The set of three static spherically symmetric solutions of the Einstein–Maxwell field equations by Maurya and Gupta, Astrophys. Space Sci. 333, 149 (2011) are modified by introducing the variable cosmological term. Motivated by Tiwari et al, Indian J. Pure Appl. Math. 31, 1017 (2000), some particular values of the cosmological term are taken to obtain well-behaved solutions of the Einstein–Maxwell field equations. All the results given by Maurya and Gupta can be obtained as particular cases of our solutions by choosing a cosmological term equal to zero.

1 Introduction

Maurya and Gupta [1] have presented three well-behaved charged fluid models. Only one model can be reduced to the neutral Vlasenko–Pronin superdense star [2], by removing the charge while the other two models cannot be neutralized. These models are solutions of the Einstein–Maxwell field equations

$$ R_{\mathit{ab}}-\frac{1}{2}Rg_{{ab}}=\kappa T_{{ab}},\quad a,b,c=1,2,...,4, $$

(1)

where R _{a b} , R, g _{a b} , κ, and T _{a b} are the Ricci tensor, Ricci scalar, metric tensor, coupling constant, and energy–momentum tensor respectively. Here, the left-hand side of the equation describes the geometry whereas the right-hand side represents the matter content of the space-time. In 1917, to stabilize the Universe against the attractive effect of gravity, Einstein introduced the cosmological constant, Λ, in the field equations given by eq. (1) [3], which then takes the form

$$ R_{{ab}}-\frac{1}{2}Rg_{{ab}}-{\Lambda} g_{{ab}}=\kappa T^{(m)}_{{ab}},\quad a,b,c=1,2,...,4. $$

(2)

Here notation $T^{(m)}_{{ab}}$ is used, as this part of the equation represents the matter contents. Presently, we consider a problem of charged perfect fluid for which we have

$$ T^{(m)}_{{ab}}=(c^{2}\rho+p)u_{a}u_{b}+pg_{{ab}}+\frac{1}{4\pi}\left[F_{ac}{F^{c}_{b}}-\frac{1}{4}F_{cd}F^{cd}g_{{ab}}\right], $$

(3)

with u ^a as the velocity four-vector, ρ as the density, p as the pressure, and F ^ab as the electromagnetic field tensor. The components are

$$ T^{a(m)}_{b}=\text{diag}\left( c^{2}\kappa \rho +\frac{q^{2}}{r^{4}},-\kappa p+\frac{q^{2}}{r^{4}},\ -\kappa p-\frac{q^{2}}{r^{4}}, -\kappa p-\frac{q^{2}}{r^{4}}\right). $$

(4)

In modern cosmology, the term Λ represents the dark energy. It is also equivalent to vacuum energy because it is the energy density of vacuum. Therefore, in the field equations, the variable cosmological term is referred to as the vacuum content of the energy–momentum tensor, i.e. $T^{(v)}_{{ab}}=({1}/{\kappa }){\Lambda }(r) g_{{ab}}$. Hence the energy–momentum tensor is a composition of its matter and the vacuum contents, i.e. $T_{{ab}}=T^{(m)}_{{ab}}+T^{(v)}_{{ab}}$. For our problem the energy–momentum tensor becomes

$$ T_{{ab}}=(c^{2}\rho+p)u_{a}u_{b}+pg_{{ab}}+\frac{1}{4\pi}\left[F_{ac}{F^{c}_{b}}-\frac{1}{4}F_{cd}F^{cd}g_{{ab}}\right]+T^{(v)}_{{ab}}. $$

(5)

This approach not only resolves some problems arising in cosmology (e.g. see [4,5]) but also satisfies the Bianchi identity. The conservation of energy–momentum tensor still holds by considering conservation of T _{a b} as a whole, instead of taking conservation of $T^{(m)}_{{ab}}$ and $T^{(v)}_{{ab}}$ separately. The equation of continuity with Λ is given as follows:

$$ \frac{\mathrm{d}}{\mathrm{d}r}\left( p-\frac{\Lambda}{8\pi}\right)+\frac{1}{2}(c^{2}\rho+p)\nu^{\prime}=\frac{1}{8\pi r^{4}}\frac{\mathrm{d}}{\mathrm{d}r}r^{4}E^{2}. $$

(6)

For Robertson–Walker metric, Chen and Wu [6] and Abdel-Rahman [7] replaced Λ by the square of the scale factor. Berman [5,8,9] found that the relation Λ∝t ⁻² is true for some static models. Beesham [10] also suggested that Λ cannot be a constant but a variable of coordinates. Later on, using the idea of variable cosmological term, a number of cosmological models have been discussed, e.g. [11–14]. Tiwari and co-workers in their papers [15–23] strongly argued the importance of variable cosmological term in the field of astrophysics and cosmology.

2 Basic field equations

The charged spheres are described by considering the most general spherically symmetric static metric

$$ \mathrm{d}s^{2}=\mathrm{e}^{\nu (r)}\mathrm{d}t^{2}-\mathrm{e}^{\lambda (r)}\mathrm{d}r^{2}-r^{2}\mathrm{d}\theta^{2}-r^{2}\sin^{2}\theta \mathrm{d}\phi^{2}. $$

(7)

For this metric, the field equations become

$$ {\frac{\lambda^{\prime}}{r}} \mathrm{e}^{-\lambda}+\frac{(1-\mathrm{e}^{-\lambda})}{r^{2}}=\kappa c^{2}\rho+E^{2}+{\Lambda}(r), $$

(8)

$$ \frac{\nu^{\prime}}{r} \mathrm{e}^{-\lambda}-\frac{(1-\mathrm{e}^{-\lambda})}{r^{2}}=\kappa p-E^{2}-{\Lambda}(r), $$

(9)

$$ \left[\frac{\nu^{\prime\prime}}{2}-\frac{\nu^{\prime}\lambda^{\prime}}{4}+\frac{{\nu}^{\prime2}}{4}+\frac{\nu^{\prime}-\lambda^{\prime}}{2r}\right]\mathrm{e}^{-\lambda}=\kappa p+E^{2}-{\Lambda}(r), $$

(10)

$$ \left( r^{2}E\right)^{\prime} =r^{2}\sigma \mathrm{e}^{\lambda} . $$

(11)

Here prime denotes differentiation with respect to r and E(r) represents the electric field intensity within the sphere of radius r and σ is the charged density.

To find solutions of eqs (8)–(10), we consider the substitutions, suggested by Durgapal and Bannerji [24], x=C ₁ r ², y ²=e^ν, and z=e^−λ. These substitutions transform eqs (8)–(10) into simpler form

$$ \frac{1-z}{x}-2\ \dot{z} =\frac{E^{2}}{C_{1}}+\frac{\kappa c^{2}\rho}{C_{1}}+{\Lambda}, $$

(12)

$$ 4z\frac{\dot{y}}{y}-\frac{1-z}{x}=\frac{\kappa p}{C_{1}}-\frac{E^{2}}{C_{1}}-{\Lambda},\\ $$

(13)

$$ 4xz\frac{\ \ \ddot{y}}{y}+(4z+2x\dot{z})\frac{\dot{y}}{y}+\dot{z} =\frac{\kappa p}{C_{1}}+\frac{E^{2}}{C_{1}}-{\Lambda}, $$

(14)

$$ \sigma^{2} =\frac{4cz}{x}\left( x\dot{E}+E\right)^{2}, $$

(15)

where the dot denotes differentiation with respect to the variable x. The system of differential eqs (12)–(15) is underdetermined. Eliminate one of the unknowns p from the system by substituting the value of p from eq. (13) into eq. (14) to get

$$ 4x^{2}z\ddot{y}+2x^{2}\dot{y}\dot{z}+ \left( 1-z+x\dot{y}-2x\frac{E^{2}}{C_{1}}\right)y=0. $$

(16)

The number of unknowns are more than the number of equations. So, as in [1] the following physically reasonable ansatz for the gravitational potential z and the electric field intensity E are considered

$$ z=(1-x)^{2},\quad \frac{E^{2}}{C_{1}}=\frac{\alpha x}{2}, $$

(17)

for some positive parameter α. In the interior of the star, z = e^−λ = (1−x) ² is regular and well-behaved at the origin. The electric field intensity is continuous, bounded and increasing function from the origin to the boundary of the sphere. These values of z and E transform eq. (16) into

$$ 4(1-x)^{2}\ddot{y}-4(1-x)\dot{y}+(1-\alpha)y=0. $$

(18)

Here, like [1], α = 1, α > 1 and 0 ≤ α < 1 generate new classes of solutions of eqs (7)–(9).

3 New models

Case 1.

0≤α<1

Equation (18) can be transformed to a standard Cauchy–Euler equation by the substitution $\tilde {x}=(1-x)$

$$ 4\tilde{x}^{2}\frac{\mathrm{d}^{2}y}{\mathrm{d}\tilde{x}^{2}}+4\tilde{x}\frac{\mathrm{d}y}{\mathrm{d}\tilde{x}}+(1-\alpha)y=0, $$

(19)

which leads to the solution

$$ y=c_{1}\cos[\sqrt{(1-\alpha)}\log \sqrt{(1-x)}]+c_{2}\sin[\sqrt{(1-\alpha}\log \sqrt{(1-x)}], $$

(20)

for some arbitrary constants of integration c ₁ and c ₂. Some physical consideration can fix these constants. Equations (12) and (13) give expressions of density and pressure where an arbitrary function Λ(x) is involved. Some values may be assigned to Λ. Here, we consider Λ=Λ₀+8π p and Λ=Λ₀−8π p as suggested by Tiwari et al [25]. Then eqs (12) and (13) yield

$$ \frac{\kappa p}{C_{1}}=\frac{\kappa}{\kappa\mp8\pi}\left[\frac{2(1 \,-\, x)\sqrt{1-\alpha}[c_{1}\sin \beta -c_{2}\cos \beta ]}{[c_{1}\cos \beta +c_{2}\sin \beta ]}\,+\,\!(x\,-\,2) \,+\, \frac{\alpha x}{2} \,+\, \frac{{\Lambda}_{0}}{C_{1}}\right],\\ $$

(21)

$$\begin{array}{@{}rcl@{}} \frac{\kappa c^{2}\rho}{C_{1}}&=&6\,-\,5x-\frac{\alpha x}{2}\,-\,\frac{{\Lambda}_{0}}{C_{1}} -\frac{8\pi} {\kappa\mp8\pi}\! \left[\frac{2(1\,-\,x)\sqrt{1-\alpha}[c_{1}\sin \beta \,-\, c_{2}\cos \beta ]}{[c_{1}\cos \beta +c_{2}\sin \beta ]}\right.\\ &&+\left.(x-2)+\frac{\alpha}{2}+\frac{{\Lambda}_{0}}{C_{1}}\right], \end{array} $$

(22)

where $[\sqrt {(1-\alpha )}\log \sqrt {(1-x)}]=\beta$. The expressions for the pressure gradient and density gradient are furnished as

$$\begin{array}{@{}rcl@{}} \frac{\kappa c^{2}}{C_{1}}\frac{\mathrm{d}\rho}{\mathrm{d}x}&=&-\frac{\alpha}{2}-5-\frac{8\pi} {\kappa\mp8\pi}\left[\frac{3\alpha}{2}-\frac{2\sqrt{1-\alpha}{[c_{1}\sin \beta -c_{2}\cos \beta ]}}{[c_{1}\cos \beta +c_{2}\sin \beta ]}\right.\\ &&\left.-\frac{(1-\alpha)[c_{1}\sin \beta -c_{2}\cos \beta]^{2}}{[c_{1}\cos \beta +c_{2}\sin \beta ]^{2}}\right], \end{array} $$

(23)

$$\begin{array}{@{}rcl@{}} \frac{\kappa}{C_{1}}\frac{\mathrm{d}p}{\mathrm{d}x}&=&\frac{\kappa}{\kappa\mp8\pi} \left[\frac{3\alpha}{2}- \frac{2\sqrt{1-\alpha}{[c_{1}\sin \beta -c_{2}\cos \beta ]}}{[c_{1}\cos \beta +c_{2}\sin \beta]} \right.\\ &&\left.-\frac{(1-\alpha)[c_{1}\sin \beta -c_{2}\cos \beta ]^{2}}{[c_{1}\cos \beta +c_{2}\sin \beta]^{2}}\right]. \end{array} $$

(24)

Case 2.

α=1

For α=1, eq. (18) yields

$$\begin{array}{@{}rcl@{}} y=c_{3}\log (1-x)+c_{4}, \end{array} $$

(25)

where c ₃ and c ₄ are constants of integration. Expressions for density, pressure, pressure gradient, and density gradient are

$$ \frac{\kappa p}{C_{1}}=\frac{\kappa}{\kappa\mp8\pi}\left[-\frac{4c_{3}(1-x)}{c_{3}\log (1-x)+c_{4}}-2+\frac{3x}{2}+\frac{{\Lambda}_{0}}{C_{1}}\right], $$

(26)

$$\begin{array}{@{}rcl@{}} \frac{\kappa c^{2}\rho}{C_{1}}&=&6-\frac{11x}{2}-\frac{{\Lambda}_{0}}{C_{1}}-\frac{8\pi}{\kappa\mp8\pi}\left[-\frac{4c_{3}(1-x)}{c_{3}\log (1-x)+c_{4}}-2\right.\\ &&\left.+\frac{3x}{2}+\frac{{\Lambda}_{0}}{C_{1}}\right], \end{array} $$

(27)

$$\begin{array}{@{}rcl@{}} \frac{\kappa c^{2}}{C_{1}}\frac{\mathrm{d}\rho}{\mathrm{d}x}&=& -~ \frac{11}{2}-\frac{8\pi}{\kappa\mp8\pi}\left[\frac{4c_{3}}{c_{3}(1-x)+c_{4}}\right.\\ &&\left.-~ \frac{4{c_{3}}^{2}}{(c_{3}\log(1-x)+c_{4})^{2}}+\frac{3}{2}\right],\\ \end{array} $$

(28)

$$ \frac{\kappa} {C_{1}}\frac{\mathrm{d}p}{\mathrm{d}x}=\frac{4c_{3}}{c_{3}(1-x)+c_{4}}- \frac{4{c_{3}}^{2}}{(c_{3}\log(1-x)+c_{4})^{2}}+\frac{3}{2}. $$

(29)

Case 3.

α>1

Equation (18) gives

$$ y=c_{5}\cosh \beta +c_{6}\sinh \beta , $$

(30)

where c ₅ and c ₆ are constants and $\beta =[\sqrt {(\alpha -1)}\log \sqrt {(1-x)}].$ Density, pressure, pressure gradient, and density gradient for this model are

$$\begin{array}{@{}rcl@{}} &&{\kern-.7pc}\frac{\kappa p}{C_{1}}=\frac{\kappa}{\kappa\mp8\pi}\left[-\frac{2(1-x)\sqrt{\alpha-1}[c_{5}\sinh \beta +c_{6}\cosh \beta ]}{[c_{5}\cosh \beta +c_{6}\sinh \beta ]}\right.\\ &&\qquad\left.+(x-2)+\frac{\alpha x}{2}+\frac{{\Lambda}_{0}}{C_{1}}\right], \end{array} $$

(31)

$$\begin{array}{@{}rcl@{}} &&{\kern-.7pc}\frac{\kappa c^{2}\rho}{C_{1}}=6-5x-\frac{\alpha x}{2}-\frac{{\Lambda}_{0}}{C_{1}}-\frac{8\pi} {\kappa\mp8\pi} \\ &&{\kern2pc}\times\left[- \frac{2(1 \,-\, x)\sqrt{\alpha \!-1}[c_{5}\sinh \beta +c_{6}\cosh \beta ]}{[c_{5}\cosh \beta +c_{6}\sinh \beta ]}\right.\\ &&{\kern2pc}\left.+~ (x \,-\, 2) \,+\, \frac{\alpha x}{2} \,+\, \frac{{\Lambda}_{0}}{C_{1}}\right], \\ \end{array} $$

(32)

$$\begin{array}{@{}rcl@{}} &&{\kern-.7pc}\frac{\kappa c^{2}}C_{1}\frac{\mathrm{d}\rho}{\mathrm{d}x}=-\frac{\alpha}{2}-5-\frac{8\pi} {\kappa\mp8\pi}\left[\frac{3\alpha}{2}+\frac{2\sqrt{\alpha-1}{[c_{5}\sinh \beta +c_{6}\cosh \beta ]}}{[c_{5}\cosh \beta +c_{6}\sinh \beta ]}\right.\\ &&\qquad\qquad\left.-\frac{(\alpha-1)[c_{5}\sinh \beta +c_{6}\cosh \beta ]^{2}}{[c_{5}\cosh \beta +c_{6}\sinh \beta ]^{2}}\right], \end{array} $$

(33)

$$\begin{array}{@{}rcl@{}} {\kern-.1pc}\frac{\kappa}{C_{1}}\frac{\mathrm{d}p}{\mathrm{d}x}&=&\frac{\kappa}{\kappa\mp8\pi}\left[\frac{3\alpha}{2}+\frac{2\sqrt{\alpha-1}{[c_{1}\sinh \beta +c_{2}\cosh \beta ]}}{[c_{5}\cosh \beta +c_{6}\sin \beta ]}\right.\\ &&\left.+\frac{(\alpha-1)[c_{5}\sinh \beta +c_{6}\cosh \beta]^{2}}{[c_{5}\cosh \beta +c_{6}\sinh \beta ]^{2}}\right]. \end{array} $$

(34)

4 Properties of solutions

The models given in the previous must satisfy some conditions to be physically acceptable and to fix the arbitrary constants.

• (1) Pressure p should be zero at boundary, i.e. p=0 at r=a.

• (2) Density ρ and pressure p must have non-zero finite values at r=0.

• (3) ρ and p should be monotonically decreasing from the centre towards the boundary, i.e. (dρ/dr)<0 and (dp/dr)<0.

• (4) At the centre, the pressure–density ratio should be positive and less than 1, i.e.

  $$0<\frac{(p)_{r=0}}{(\rho)_{r=0}}<1.$$

• (5) The pressure–density ratio (p/c ² ρ) must decrease monotonically with the increase of radius

  $$ \left( \frac{\mathrm{d}}{\mathrm{d}x}\frac{p}{c^{2}\rho}\right)_{{\small{\textit{x}=0}}}<0. $$

  (35)

• (6) Velocity of sound should be less than that of light throughout the model and should be decreasing towards the surface, i.e.

  $$ \left( \frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{\mathrm{d}p}{\mathrm{d}\rho}\right)\right)_{{\small{\textit{x}=0}}}<0. $$

  (36)

• (7) The central red shift Z ₀ and the surface red shift Z _a must be positive, finite, and bounded i.e.

  $$ {\kern-2.3pc}Z_{0}=[(\mathrm{e}^{\nu/2}- 1)]_{r =0} > 0 \quad \text{and}\quad Z_{a}=[(\mathrm{e}^{\lambda(a)/2} - 1)]>0. $$

  (37)

• (8) The solution should be free from physical and geometric singularities.

• (9) At r=a our models must meet the Reissner–Nordstrom exterior solution

  $$\begin{array}{@{}rcl@{}} &&{}\mathrm{d}s^{2}=(1-2M/r+\mathrm{e}^{2}/r^{2})\mathrm{d}t^{2}-(1-2M/r+\mathrm{e}^{2}/r^{2})^{-1}\mathrm{d}r^{2}\\ &&{\kern-.8pc}-r^{2}(\mathrm{d}\theta^{2}+\sin^{2}\theta \mathrm{d}\phi^{2}). \end{array} $$

  (38)

  This requires the continuity of the total charge q=r ² E, e^λ, and e^ν across the boundary. Therefore,

  $$ \mathrm{e}^{-\lambda(a)}=1-2M/a+\mathrm{e}^{2}/a^{2}, $$

  (39)
  $$ \mathrm{e}^{-\nu(a)}=y^{2}_{(r=a)}=1-2M/a+\mathrm{e}^{2}/a^{2}, $$

  (40)
  $$ q(a)=\mathrm{e}. $$

  (41)

Case 1.

0≤α<1

For 0≤α<1, at r=0, we have

$$ \left[\frac{\kappa c^{2}\rho}{C_{1}}\right]_{r=0}=6-\frac{{\Lambda}_{0}}{C_{1}}-\frac{8\pi} {\kappa-8\pi}\left[\frac{-2\sqrt{1-\alpha}c_{2}}{c_{1}} -2+\frac{{\Lambda}_{0}}{C_{1}}\right]>0, $$

(42)

$$ \left[\frac{\kappa p} {C_{1}}\right]_{r=0}=\frac{\kappa}{\kappa-8\pi}\left[\frac{-2\sqrt{1-\alpha}c_{2}}{c_{1}}-2+\frac {{\Lambda}_{0}}{C_{1}}\right]>0. $$

(43)

Also,

$$ \frac{p_{r=0}}{c^{2}\rho_{r=0}}<1. $$

(44)

Equations (42)–(44) give limits for c ₂/c ₁, which appear to be

$$ \frac{0.2{\Lambda}_{0}}{C_{1}\sqrt{1-\alpha}} -\frac{4.0}{\sqrt{1-\alpha}} < \frac{c_{2}}{c_{1}} < \frac{0.9{\Lambda}_{0}}{C_{1}\sqrt{1-\alpha}} -\frac{6.7}{\sqrt{1-\alpha}},\quad\text{for}{}\quad{\Lambda}={\Lambda}_{0}+8\pi p,\\ $$

(45)

where C ₁>0. On the boundary on setting $x_{r}=C_{1}a^{2}=\tilde {x}$ where a is the radius of sphere we get the value c ₂/c ₁.

$$ \frac{c_{2}}{c_{1}}=\frac{\sin(\sqrt{1-\alpha}\log \sqrt{1-\tilde{x}})-F_{1}\cos(\sqrt{1-\alpha}\log \sqrt{1-\tilde{x}})} {\cos(\sqrt{1-\alpha}\log \sqrt{1-\tilde{x}})+F_{1}\sin(\sqrt{1-\alpha}\log \sqrt{1-\tilde{x}})}, $$

(46)

where

$$ {F_{1}}=\frac{(4-(2+\alpha)\tilde{x})}{4(1-\alpha)\sqrt{1-\tilde{x}}}+\frac{{\Lambda}_{0}}{2C_{1}(1-\alpha)\sqrt{1-\tilde{x}}}, $$

(47)

ρ and p are monotonically decreasing from the centre towards the boundary. The velocity of sound at the centre is given by

$$\begin{array}{@{}rcl@{}} {}\left[\frac{\mathrm{d}p}{c^{2}\mathrm{d}\rho}\right]_{r=0}=\frac{ \left[\frac{\kappa}{\kappa-8\pi} \left( \frac{3\alpha}{2}+\frac{2c_{2}\sqrt{1-\alpha}}{c_{1}}-(1-\alpha)\frac{{c_{2}}^{2}}{{c_{1}}^{2}}\right)\right]}{\left[\frac{-\alpha}{2} -5-\frac{8\pi}{\kappa-8\pi}\left( \frac{3\alpha}{2}+\frac{2c_{2}\sqrt{1-\alpha}}{c_{1}}-(1-\alpha)\frac{{c_{2}}^{2}}{{c_{1}}^{2}} \right)\right]}<1, \end{array} $$

(48)

for all values of 0<α≤1 and c ₂/c ₁. The pressure–density ratio

$$\begin{array}{@{}rcl@{}} &&{\kern-1.5pc} \left[\frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{p}{c^{2}\rho}\right) \right]_{x=0} \\ &=&2C_{1}\frac{\kappa}{\kappa-8\pi}\left( \left[\frac{\frac{c_{2}}{c_{1}}\sqrt{1-\alpha}(2-\alpha)} {\left( 6-\frac{{\Lambda}_{0}}{C_{1}} -\frac{\kappa}{\kappa-8\pi}(-2\frac{c_{2}}{c_{1}}\sqrt{1-\alpha} -2+\frac{{\Lambda}_{0}}{C_{1}})\right)^{2}}\right]\right.\\ \end{array} $$

$$\begin{array}{@{}rcl@{}} &&+\frac{10-6\frac{B^{2}}{{c_{1}^{2}}}(1-\alpha)+8\alpha}{\left( 6-\frac{{\Lambda}_{0}}{C_{1}} -\frac{\kappa}{\kappa-8\pi}(-2\frac{c_{2}}{c_{1}}\sqrt{1-\alpha} -2+\frac{{\Lambda}_{0}}{C_{1}})\right)^{2}}\\ &&{}\left.+\left[\frac{\frac{{\Lambda}_{0}}{C_{1}}\left( \frac{{c_{2}}^{2}}{{c_{1}}^{2}}(1-\alpha)-\frac{c_{2}}{c_{1}}\sqrt{1-\alpha}\right)} {\left( -\frac{{\Lambda}_{0}}{C_{1}}-\frac{\kappa}{\kappa-8\pi}\left( -2\frac{c_{2}}{c_{1}}\sqrt{1-\alpha} -2+\frac{{\Lambda}_{0}}{C_{1}}\right)\right)^{2}}\right]\right)<0, \end{array} $$

(49)

for all values of 0≤α<1 and c ₂/c ₁. So pressure–density ratio is maximum at the centre.

The gravitational redshift is given by

$$ Z=\frac{1}{c_{1}\cos \beta +c_{2}\sin \beta} -1. $$

(50)

At r=0 its value is

$$ (Z)_{r=0}=\frac{1-c_{1}}{c_{1}}. $$

(51)

As gravitational redshift should be positive and must be finite, at the centre the arbitrary constant c ₁ lies between zero and one, i.e. 0<c ₁<1 . After differentiating eq. (50) with respect to x, we get

$$ \left[\frac{\mathrm{d}^{2}Z}{\mathrm{d}r^{2}}\right]_{r=0}=C_{1}\frac{c_{2}}{c_{1}}\frac{\sqrt{1-\alpha}}{c_{1}}<0, $$

(52)

for all values of 0≤α<1. The expression on the right-hand side is negative indicating that the gravitational redshift is maximum at the centre and monotonically decreases in the outward direction.

Case 2.

α=1

For the second model, ρ is finite at r=0. ρ and p are monotonically decreasing from the centre towards the boundary. The inequalities, i.e. p _r=0>0, ρ _r=0>0 and

$$ \frac{p_{r=0}}{c^{2}\rho_{r=0}}<1 $$

(53)

yield

$$ -\frac{0.08{\Lambda}_{0}}{4C_{1}}-0.9< \frac{c_{3}}{c_{4}} < \frac{{\Lambda}_{0}}{4C_{1}}-\frac{1}{2}. $$

(54)

For this model, boundary conditions yield

$$ \frac{c_{3}}{c_{4}}=\frac{-C_{1}[4-3\tilde{x}]-2{\Lambda}_{0}}{8C_{1}(1-\tilde{x})+[C_{1}(4-3\tilde{x})-2{\Lambda}_{0}] \log(1-\tilde{x})}. $$

(55)

Also the velocity of sound at the centre is given by

$$\begin{array}{@{}rcl@{}} \left[\frac{\mathrm{d}p}{c^{2}\mathrm{d}\rho}\right]_{r=0}= \frac{\left[\left( \frac{3}{2}+\frac{4c_{3}}{c_{4}}-\frac{4{c_{3}}^{2}}{{c_{4}}^{2}}\right)\right]} {\left[\frac{-11}{2} -\frac{8\pi}{\kappa-8\pi}\left( \frac{3}{2}+\frac{4c_{3}}{c_{4}}-\frac{4{c_{3}}^{2}}{{c_{4}}^{2}}\right)\right]}<1, \end{array} $$

(56)

for α=1 and for all values of c ₃/c ₄.

$$\begin{array}{@{}rcl@{}} \left[\frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{p}{c^{2}\rho}\right) \right]_{x=0}&=&2C_{1}\frac{\left( \frac{2c_{3}}{c_{4}}-\frac{24{c_{3}}^{2}}{{c_{4}}^{2}}-2\right)} {6-\frac{{\Lambda}_{0}}{C_{1}} -\frac{8\pi}{\kappa-8\pi}\left[-\frac{4c_{3}}{c_{4}}-2+\frac{{\Lambda}_{0}}{C_{1}}\right]}\\ &&+\frac{\left( \frac{4{c_{3}}^{2}{\Lambda}_{0}}{C_{1}{c_{4}}^{2}}-\frac{4c_{3}{\Lambda}_{0}}{C_{1}c_{4}}- \frac{25{\Lambda}_{0}}{2C_{1}}\right)}{6-\frac{{\Lambda}_{0}}{C_{1}} -\frac{8\pi}{\kappa-8\pi}\left[-\frac{4c_{3}}{c_{4}}-2+\frac{{\Lambda}_{0}}{C_{1}}\right]}<0, \end{array} $$

(57)

for all values of c ₃/c ₄. So pressure–density ratio is maximum at the centre. Gravitational redshift is given by

$$ Z=\frac{1}{c_{3}\log(1-x)+c_{4}}-1 $$

(58)

and

$$ (Z)_{r=0}=\frac{1-c_{4}}{c_{4}}. $$

(59)

We have 0<c ₄<1 because gravitational redshift should be positive and must be finite at the centre. By differentiating eq. (58) with respect to x, we get

$$ \left[\frac{\mathrm{d}Z}{\mathrm{d}x}\right]_{r=0}=\frac{c_{3}}{c_{4}}\frac{C_{1}}{c_{4}}<0. $$

(60)

The expression on the right-hand side is negative indicating that the gravitational redshift is maximum at the centre and monotonically decreases in the outward direction.

Case 3.

α>1

Here the conditions p _r=0>0, ρ _r=0>0 and the condition given by eq. (53) gives

$$ \frac{0.2{\Lambda}_{0}}{C_{1}\sqrt{\alpha-1}}-\frac{4}{\sqrt{\alpha-1}} < \frac{c_{6}}{c_{5}} < \frac{0.9{\Lambda}_{0}}{C_{1}\sqrt{\alpha-1}} -\frac{6.7}{\sqrt{\alpha-1}}. $$

(61)

Boundary conditions imply

$$ \frac{c_{6}}{c_{5}}=\frac{\sinh(\sqrt{\alpha-1}\log \sqrt{1-\tilde{x}})-F_{2}\cosh (\sqrt{\alpha-1}\log \sqrt{1-\tilde{x}})} {F_{2}\sinh(\sqrt{\alpha-1}\log \sqrt{1-\tilde{x}})-\cosh(\sqrt{\alpha-1}\log \sqrt{1-\tilde{x}})}, $$

(62)

where

$$ {F_{2}}=\frac{((2+\alpha)\tilde{x}-4)}{4\sqrt{(\alpha-1)}{(1-\tilde{x})}}+\frac{{\Lambda}_{0}}{2C_{1}(1-\tilde{x})\sqrt{\alpha-1}}. $$

(63)

(dρ/dr) < 0 and (dρ/dr) < 0 show that ρ and p are monotonically decreasing. Also the velocity of sound at the centre appears to be

$$\begin{array}{@{}rcl@{}} \left[\frac{\mathrm{d}p}{c^{2}\mathrm{d}\rho}\right]_{x=0}&=&\frac{\left[\frac{\kappa}{\kappa-8\pi} \left( \frac{3\alpha}{2}+\frac{2c_{6}\sqrt{\alpha-1}}{c_{5}}-(\alpha-1)\frac{{c_{6}}^{2}} {{c_{5}}^{2}}\right)\right]}{\left[\frac{-\alpha}{2} -5-\frac{8\pi}{\kappa-8\pi}\left( \frac{3\alpha}{2}+\frac{2c_{6}\sqrt{\alpha-1}}{c_{5}} -(\alpha-1)\frac{{c_{6}}^{2}}{{c_{5}}^{2}} \right)\right]}, \end{array} $$

(64)

where sound satisfies the inequality

$$0<\left[\frac{\mathrm{d}p}{c^{2}\mathrm{d}\rho}\right]_{r=0}<1, $$

for all values of α>1 and c ₆/c ₅.

$$\begin{array}{@{}rcl@{}} {}\left[\frac{\mathrm{d}}{\mathrm{d}x}\left( \frac{p}{c^{2}\rho}\right) \right]_{x=0} \\ &&{\kern-6.8pc} =2C_{1}\frac{\kappa}{\kappa-8\pi}\left[8\alpha \,-\, 10+\frac{\sqrt{\alpha-1}\frac{c_{6}}{c_{5}} (2-\alpha) -6\frac{{c_{6}}^{2}}{{c_{5}}^{2}}(1-\alpha)}{\left( 6-\frac{{\Lambda}_{0}}{C_{1}}-\frac{\kappa}{\kappa-8\pi} (-2\frac{c_{5}}{c_{6}}\sqrt{\alpha-1} -2+\frac{{\Lambda}_{0}}{C_{1}})\right)^{2}}\right]\\ &&{} +2C_{1}\frac{\kappa}{\kappa-8\pi}\left[\frac{\frac{{\Lambda}_{0}}{C_{1}}\left( \frac{{c_{6}}^{2}} {{}{c_{5}^{2}}}(1-\alpha)-\frac{c_{6}}{c_{5}}\sqrt{\alpha-1}\right)} {\left( -\frac{{\Lambda}_{0}}{C_{1}}-\frac{\kappa}{\kappa-8\pi}\left( -2\frac{c_{6}}{c_{5}}\sqrt{\alpha-1} -2+\frac{{\Lambda}_{0}}{C_{1}}\right)\right)^{2}}\right]. \end{array} $$

(65)

The expression on the right-hand side is negative for all values of α>1 and c ₆/c ₅. Here pressure–density ratio is maximum at the centre. Gravitational redshift is given by

$$ Z=\frac{1}{c_{5}\cosh \beta+c_{6}\sinh \beta}-1 $$

(66)

and

$$ (Z)_{x=0}=\frac{1-c_{5}}{c_{5}}. $$

(67)

We have 0<c ₅<1 because gravitational redshift should be positive and finite at the centre. While differentiating eq. (66) with respect to x, we get

$$ \left[\frac{\mathrm{d}Z}{\mathrm{d}x}\right]_{x=0}=C_{1}\frac{c_{6}}{c_{5}}\frac{\sqrt{1-\alpha}}{c_{5}}<0, $$

(68)

for all values of α>1. The expression on the right-hand side is negative indicating that the gravitational redshift is maximum at the centre and monotonically decreases in the outward direction.

The expression for mass is written as follows:

$$ m(a)=\frac{a\tilde{x}}{2}\left[2-\tilde{x}+\frac{\alpha \tilde{x}}{2}\right], $$

(69)

for all values of α such that e^−λ=1−2M/a+e ²/a ², where M=m(a) and Y ² _(r=a)=1−2M/a+e ²/a ² gives

$$ c_{1}=\frac{(1-\tilde{x})}{{\cos(\sqrt{1-\alpha}\log \sqrt{1-\tilde{x}})+({c_{2}}/{c_{1}})\sin(\sqrt{1-\alpha}\log \sqrt{1-\tilde{x}})}}, $$

(70)

$$ c_{3}=\frac{(1-\tilde{x})}{1+({c_{3}}/{c_{4}})\log(1-\tilde{x})}, $$

(71)

$$ c_{5}=\frac{(1-\tilde{x})}{{\cosh(\sqrt{\alpha-1}\log \sqrt{1-\tilde{x}})-({c_{6}}/{c_{5}})\sinh(\sqrt{\alpha-1}\log \sqrt{1-\tilde{x}})}}. $$

(72)

5 Conclusion

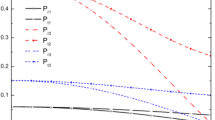
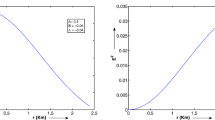
We have discussed solutions of the Einstein–Maxwell field equations of the charged fluid spheres having static spherically symmetric metric. By considering some substitutions, new classes of solutions of the field equations are found. Density, pressure, density gradient, pressure gradient and some other pressure–density relations are calculated. Two specific values of the cosmological term, Λ, are chosen to get new solutions. The conditions for well-behaved and regular models are discussed in detail in §4. Properties of solutions and boundary conditions are checked for all the cases in detail. Λ is related to pressure, and therefore, contributes to the effective gravitational mass of the astrophysical system.

All the solutions presented by Maurya and Gupta in ref. [1] can be recovered as particular cases of the solutions obtained in our paper by taking Λ=0. It is noted that the effect of Λ on pressure and density is that pressure increases and density decreases for increasing values of Λ. It is also noted that the cosmological term also has effects on the bounds /limits for the ratio of constants involved in the solutions.