1 Introduction

The term ‘compact object’ is mainly used in astronomy to describe collectively white dwarfs, neutron stars and black holes. It is well known that stars are an isolated body that is bounded by self-gravity, and which radiates energy supplied by an internal source. Most compact objects are formed to a point of the stellar evolution when the internal radiation pressure from the nuclear fusions of a star cannot balance the external gravitational force and the star collapses under its own weight. It is familiar that the model of a compact star can be obtained by solving Einstein’s field equations in the context of general theory of relativity. There are large numbers of papers on the exact solution of Einstein’s field equations for spherically symmetric perfect fluid spheres (Delgaty & Lake 1998; Stephani et al. 2003). Durgapal et al. (1982) have obtained two new classes of solutions of field equations with constant proper mass densities. Stewart (1982) has solved field equations for finding interior solutions for spherically symmetric, static, and conformal flat anisotropic fluid spheres. According to Ruderman (1972), the pressure inside the highly compact astrophysical objects such as an X-ray pulsar, Her-X-1, X-ray buster 4U 1820-30, the millisecond pulsar PSR J1614-2230, LMC X-4, etc., that have a core density beyond the nuclear density (\(10^{15}\) g/cc) show anisotropic nature, i.e., the pressure inside these compact objects can be decomposed into two parts: the radial pressure \(p_{r}\) and the transverse pressure \(p_{t}\). The existence of a solid stellar core, the presence of a type-3A superfluid, pion condensation, different kinds of phase transitions, a mixture of two gases, etc., are reasonable for pressure anisotropy (Sawyer 1972; Letelier 1980; Sokolov 1980; Kippenhahn & Weigert 1990). A large number of works have been done by assuming pressure anisotropy (Herrera & Santos 1997; Dev & Gleiser 2003; Sharma & Maharaj 2007; Rahaman et al. 2010, 2012; Bhar & Murad 2016).

To obtain the maximum value of the mass-to-radius ratio for a model of a compact star is an important problem in relativistic astrophysics since “the existence of such a bound is intriguing because it occurs well before the appearance of an apparent horizon at \(M = R/2\)” as proposed by Guven & Murchadha (1999). The authors have investigated the upper limit of M/R for compact general relativistic configurations by assuming that inside the star the radial stress pr is different from the tangential pressure pt. It was also investigated by them that if the density is monotonically decreasing and radial pressure is greater than the tangential pressure then the upper bound 8/9 is still valid to the entire bulk if m is replaced by the quasi-local mass. Several bounds on the mass–radius ratio and anisotropy parameter have also been found for models in which the anisotropic factor is proportional to \(r^2\) Mak et al. (2002). Bounds on m/r for static objects with a positive cosmological constant were obtained by Andréasson & Böhmer (2009). According to Heintzmann & Hillebrandt (1975), for an arbitrarily large anisotropy, in principle, there is neither limiting mass nor limiting redshift and they also proposed that semi-realistic equations of state lead to a mass of 3–\(4 \,M_{\odot }\) for neutron stars with an anisotropic equation of state (EoS). Bowers & Liang (1974) have analytically obtained the maximum equilibrium mass and surface redshift in the case of incompressible neutron matter. For a relativistic stellar model, the value of the redshift cannot be arbitrarily large. Bondi (1992) considered the relation between redshift and the ratio of the trace of the pressure tensor to local density and proved that when anisotropic pressures are allowed, considerably larger redshift values can be obtained. Ivanov (2002) obtained the maximum value of the redshift for anisotropic stars. For realistic anisotropic star models, the surface redshift cannot exceed the values 3.842 or 5.211 when the tangential pressure, respectively, satisfies the strong or the dominant energy condition (DEC), whereas this bound in the perfect fluid case is 2.

The dynamical stability of spherically symmetric gravitational equilibria of cold stellar objects made of bosons and fermions was proposed by Jetzer (1990). Using the Einstein–Klein–Gordon equation, Jetzer & Scialom (1992) explored the dynamical instability of the static real scalar field. Bhar et al. (2015) studied the behavior of static spherically symmetric relativistic objects with locally anisotropic matter distribution considering the Tolman VII form for the gravitational potential grr in curvature coordinates together with the linear relation between the energy density and the radial pressure. Bhar (2015b) proposed a model of a superdense star admitting conformal motion in the presence of a quintessence field by taking Vaidya & Tikekar (1982) ansatz motivated by the accelerating phase of our present universe. Ivanov (2018) proposed a physically realistic stellar model with a simple expression for the energy density with a conformally flat interior and discussed all the physical properties without graphic proofs. Recently, Sharma et al. (2020) obtained a new class of solutions by revisiting the Vaidya–Tikekar stellar model in the linear regime and discussed the impact of the curvature parameter K of the Vaidya–Tikekar model, which characterizes a departure from homogeneous spherical distribution, on the mass–radius relationship of the star. Mustafa et al. (2020) considered spherically symmetric space–time with an anisotropic fluid distribution. In particular, they used the Karmarkar condition to explore the compact star solutions.

To study the model of a compact star by utilizing Finch & Skea (1989) metric potential is a very interesting platform to the researchers. Hansraj & Maharaj (2006) obtained charged Finch–Skea stars and these models are given in terms of Bessel functions and obey a barotropic EoS. Sharma & Ratanpal (2013) obtained the model of stars with a quadratic EoS with the Finch–Skea geometry and this work was extended by Pandya et al. (2015) for a generalized form of the gravitational potential. Kalam et al. (2014) proposed quintessence stars with both dark energy and anisotropic pressures. A charged anisotropy stellar model in the background of Finch–Skea geometry has been obtained by Maharaj et al. (2017) and the exact solutions have been expressed in terms of elementary functions, Bessel functions, and modified Bessel functions. Bhar (2015a) proposed a new model of an anisotropic strange star, which admits the Chaplygin EoS. The study of a compact star model in the context of Finch–Skea geometry has been conducted in matter distributions with lower dimensions also (Banerjee et al. 2013; Bhar et al. 2014). Relativistic solutions of anisotropic charged compact objects in hydrodynamical equilibrium with Finch–Skea geometry in the usual four and higher dimensions have been studied by Dey & Paul (2020).

Inspired by all of these earlier works, in the present paper, we obtain a new model of a singularity-free compact star by assuming a physically reasonable anisotropic factor along with the metric potential \(g_{rr}.\) Our paper is arranged as follows: in Section 2,  the basic field equations have been discussed. In the next section, we have described the metric potential \(g_{rr}\). Section 4 is devoted to the description of the new model. In Section 5, we matched our interior solution to the exterior Schwarzschild line element. Physical analysis of the obtained model is described in Section 6. In the next section, the stability condition of the present model has been discussed and finally, some comparative study of the present model for different values of n is given in Section 8.

2 Interior space–time and Einstein field equations

The structure of compact and massive stars is determined by Einstein’s field equations:

$$\begin{aligned} G_{\mu \nu }& = {} \kappa \frac{G}{c^4} T_{\mu \nu }, \end{aligned}$$
(1)

where \(G_{\mu \nu }\) and \(T_{\mu \nu }\) are the Einstein tensor and energy-momentum tensor, respectively. G and c, respectively, denote the universal gravitational constant and speed of the light.

A non-rotating spherically symmetry 4D space–time in Schwarzschild coordinates \(x^{\mu }=(t,\,r,\,\theta ,\,\phi )\) is described by the line element

$$\begin{aligned} \mathrm{d}s^{2}=-A^{2}\,\mathrm{d}t^{2}+B^{2}\,\mathrm{d}r^{2}+r^{2}(\mathrm{d}\theta ^{2}+\sin ^{2}\theta \,\mathrm{d}\phi ^{2}), \end{aligned}$$
(2)

where A and B are static, i.e., functions of the radial coordinate r only, and these are called the gravitational potentials. They satisfy Einstein’s field Equation (1).

We also assume that inside the stellar interior, the matter is anisotropic in nature, and therefore, we write the corresponding energy–momentum tensor as

$$\begin{aligned} T_{\nu }^{\mu }=(\rho +p_r)u^{\mu }u_{\nu }-p_{t} g_{\nu }^{\mu }+(p_r-p_{t})v^{\mu }v_{\nu }, \end{aligned}$$
(3)

with \( u^{i}u_{j} =-v^{i}v_j = 1 \) and \(u^{i}v_j= 0\). Here the vector \(v^{i}\) is the space-like vector and \(u^i\) is the fluid 4-velocity and it is orthogonal to \(v_{i}\), \(\rho \) is the matter density, \(p_{t}\) and \(p_{r}\) are, respectively, the transverse and radial pressures of the fluid and these two pressure components act in the perpendicular direction to each other.

The Einstein field equations assuming \(G=1=c\) are given by

$$\begin{aligned} \kappa \rho& = {} \frac{1}{r^2}\left( 1-\frac{1}{B^2}\right) +\frac{2B'}{B^3r}, \end{aligned}$$
(4)
$$\begin{aligned} \kappa p_{r}& = {} \frac{1}{B^2}\left( \frac{1}{r^2}+\frac{2A'}{Ar}\right) -\frac{1}{r^2}, \end{aligned}$$
(5)
$$\begin{aligned} \kappa p_{t}& = {} \frac{A''}{AB^2}-\frac{A'B'}{AB^3}+\frac{1}{B^3rA}(A'B-B'A). \end{aligned}$$
(6)

The mass function for our present model is obtained as

$$\begin{aligned} m(r)& = {} 4\pi \int _0^{r}\omega ^{2}\rho (\omega )\,\mathrm{d}\omega . \end{aligned}$$
(7)

Using (4)–(6), we obtain

$$\begin{aligned} \frac{2A'}{A}& = {} \frac{\kappa r p_{r}+\frac{2m}{r^2}}{1-\frac{2m}{r}}, \end{aligned}$$
(8)
$$\begin{aligned} \frac{\mathrm{d}p_{r}}{\mathrm{d}r}& = {} -(\rho +p_{r})\frac{A'}{A}+\frac{2}{r}(p_{t}-p_{r}). \end{aligned}$$
(9)

Combining (8) and (9), one can finally obtain

$$\begin{aligned} \frac{\mathrm{d}p_{r}}{\mathrm{d}r}& = {} -\frac{\rho +p_{r}}{2}\frac{\left( \kappa r p_{r}+\frac{2m}{r^2}\right) }{\left( 1-\frac{2m}{r}\right) }+\frac{2}{r}(p_{t}-p_{r}). \end{aligned}$$
(10)

Equation (10) is called the Tolman–Oppenheimer–Volkoff (TOV) equation of a hydrostatic equilibrium for the anisotropic stellar configuration and \(\kappa = 8\pi \) being Einstein’s constant.

Where ‘prime’ indicates differentiation with respect to radial coordinate r. Our goal is to solve Equations (4)–(6).

3 Choice of the metric potential

In system (4)–(6), we have three equations with five unknown (\(\rho ,\,p_{r},\,p_{t},\,A,\,B\)). To solve this system, we are free to choose any two of them. Now by our previous knowledge of algebra we know that there are \({5 \atopwithdelims ()2 }=10\) possible ways to choose any two unknowns. Sharma & Ratanpal (2013), Bhar et al. (2016a), and Bhar & Ratanpal (2016) choose \(B^2\) along with \(p_{r}\), Bhar & Rahaman (2015) choose \(\rho \) along with \(p_{r}\), Murad & Fatema (2015) and Thirukkanesh et al. (2018) choose \(A^2\) with \(\Delta \) to model different compact stars. However, a very popular technique is to choose \(B^2\) along with an EoS, i.e., a relation between the matter density \(\rho \) and radial pressure \(p_{r}\). Several papers were published in this direction (Komathiraj & Maharaj 2007; Sharma & Maharaj 2007; Sunzu et al. 2014; Bhar 2015a; Bhar & Murad 2016; Bhar et al. 2016b, 2017; Thomas & Pandya 2017).

To solve Equations (4)–(6), let us assume the expression of the coefficient of \(g_{rr}\), i.e., \(B^2\) as

$$\begin{aligned} B^2& = {} \left( 1 + \frac{r^2}{R^2}\right) ^n, \end{aligned}$$
(11)

where \(n\ne 0 \) is a real number. If one takes \(n=0\), then from Equation (4), we get \(\rho =0\), which is not physically reasonable. The gravitational potential \(B^2\) is well behaved and finite at the origin. It is also continuous in the interior and it is important to realize that this choice for \(B^2\) is physically reasonable. For \(n=1\), the metric potential reduces to well-known Finch & Skea (1989) potential. The metric potential in (11) was used earlier by Pandya et al. (2015) to model a compact star by using a proper choice of the radial pressure \(p_{r}\) and they proved that the model is compatible with observational data.

Assuming \(G=c=1\) and by using (11) in (4), the expression for matter density is obtained as

$$\begin{aligned} \kappa \rho& = {} \frac{1 - \left( 1 + \frac{r^2}{R^2}\right) ^{-n}}{r^2} + \frac{2 n \left( 1 + \frac{r^2}{R^2}\right) ^{-1 - n}}{R^2}. \end{aligned}$$
(12)

4 Proposed model

Using the expression of \(B^2\), Equations (5) and (6) become

$$\begin{aligned} \kappa p_{r}& = {} \left( 1 + \frac{r^2}{R^2}\right) ^{-n}\left( \frac{1}{r^2}+\frac{2A'}{Ar}\right) -\frac{1}{r^2}, \end{aligned}$$
(13)
$$\begin{aligned} \kappa p_{t}& = {} \frac{A''}{A}\left( 1 + \frac{r^2}{R^2}\right) ^{-n}-\frac{A'}{A}\frac{n r \left( 1 + \frac{r^2}{R^2}\right) ^{-1 - n}}{R^2}\nonumber \\&+\frac{1}{rA}\left\{ A'-\frac{Anr}{R^2} \left( 1 + \frac{r^2}{R^2}\right) ^{-1}\right\} \left( 1 + \frac{r^2}{R^2}\right) ^{-n}. \end{aligned}$$
(14)

From Equations (13) and (14), it is clear that once we have the expression for A, one can obtain the expressions for \(~p_{r}\) and \(p_{t}\) in a closed form. Instead of a choice for A, for our present model, we introduce the anisotropic factor \(\Delta \), the difference between these two pressures, i.e., \(p_{t}-p_{r}\). This anisotropic factor measures the anisotropy inside the stellar interior and it creates an anisotropic force, which is defined as \({2\Delta }/{r}\). This force may be positive or negative depending on the sign of \(\Delta \), but at the center of the star, the force is zero since the anisotropic factor vanishes there.

Figure 1
figure 1

EoS parameters (top) \(\omega _{r}\), (middle) \(\omega _{t}\), and (bottom) \(({p_{r}+2p_{t}})/{\rho }\) are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image
Figure 2
figure 2

Matter density \(\rho \) is plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figure.

Full size image

From (13) and (14), we obtain

$$\begin{aligned}&\frac{A''}{A}-\frac{A'}{A}\frac{1}{r}\left( 1+\frac{n r^2}{r^2 + R^2}\right) +\frac{-1 + (1 + \frac{r^2}{R^2})^n}{r^2} \nonumber \\&\quad=\frac{n}{r^2 + R^2}+\kappa \left( 1+\frac{r^2}{R^2}\right) ^n\Delta . \end{aligned}$$
(15)

To solve equations (13) and (14), we choose the expression of \(\Delta \) as

$$\begin{aligned} \kappa \Delta& = {} \frac{1}{r^2} - \frac{\left( 1 + \frac{r^2}{R^2}\right) ^{-n} ((1 + n) r^2 + R^2 )}{r^2(r^2 + R^2)}. \end{aligned}$$
(16)

Whenever we choose the expression, one has to remember that the expression of \(\Delta \) is to be chosen in such a manner that (i) it should vanish at the center of the star, (ii) it does not suffer from any kind of singularity, (iii) \(\Delta \) is positive inside the stellar interior, and finally (iv) the field equation can be integrated easily with this choice of \(\Delta \). To obtain the model of a compact star, Maharaj et al. (2014), Murad & Fatema (2015), and Dey & Paul (2020) choose a physically reasonable choice of \(\Delta \) to find the exact solutions for the Einstein–Maxwell equations. Our present choice of the anisotropic factor satisfies the above conditions, which will be verified in the coming section and therefore this choice is physically reasonable.

Figure 3
figure 3

(Top) Radial pressure \(p_{r}\) and (bottom) transverse pressure \(p_{t}\) are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image

Solving (13) and (14) with the help of (16), we get the following equation:

$$\begin{aligned} A''=A' \left( 1 + \frac{n r^2}{r^2 + R^2}\right) \frac{1}{r}. \end{aligned}$$
(17)

Solving (17), we obtain another metric coefficient as

$$\begin{aligned} A^2& = {} \left( D + \frac{C (r^2 + R^2)^{1 + \frac{n}{2}}}{2 + n}\right) ^2, \end{aligned}$$
(18)

where C and D are constants of integrations which can be obtained from the matching conditions. Using the expression for \(A^2\), the expressions for radial and transverse pressures are obtained as

$$\begin{aligned}\kappa p_{r} &= \frac{ 2 C (2 + n) \left( 1 + \frac{r^2}{R^2}\right) ^{-n} (r^2 + R^2)^{\frac{n}{2}}}{ D (2 + n) + C (r^2 + R^2)^{1 +\frac{ n}{2}}}\nonumber \\&\quad -\frac{1 - \left( 1 + \frac{r^2}{R^2}\right) ^{-n}}{r^2}, \end{aligned}$$
(19)
$$\begin{aligned}&\kappa p_{t}=\frac{\big (C (4 + n) (r^2 + R^2)^{1 + \frac{n}{2}}-D n (2 + n)\big )\left( 1 + \frac{r^2}{R^2}\right) ^{-n}}{ D (2 + n) (r^2 + R^2) + C (r^2 + R^2)^{2 + \frac{n}{2}}}. \end{aligned}$$
(20)
Figure 4
figure 4

Anisotropic factor \(\Delta \) is plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figure.

Full size image
Table 1 Values of the constants \(R,\,C,\) and D for the compact star PSR J1614-2230 whose observed mass and radius are given by \((1.97 \pm 0.04)\,\;M_{\odot }\) and \(9.69_{-0.2}^{+0.2}\) km, respectively (Demorest et al. 2010).
Full size table
Table 2 Values of the constants \(R,\,C\) and D for the compact star EXO 1785-248 whose observed mass and radius are given by \((1.3\pm 0.2)\;M_{\odot }\) and \(8.849_{-0.4}^{+0.4}\) km, respectively (Ozel et al. 2009).
Full size table

5 Boundary condition

To fix the different constants, in this section, we match our interior space–time continuously to the exterior Schwarzschild space–time

$$\begin{aligned}\mathrm {d}s_+^{2}& =\left( 1-\frac{2M}{r}\right) ^{-1}\mathrm {d}r^{2}+r^{2}( \mathrm{d}\theta ^{2}+\sin ^{2}\theta \,\mathrm{d}\phi ^{2}) \nonumber \\&\quad -\left( 1-\frac{2M}{r}\right) \mathrm {d}t^{2}, \end{aligned}$$
(21)

outside the event horizon, i.e., \(r>2M\), where M is a constant representing the total mass of the compact star corresponding to our interior space–time:

$$\begin{aligned} \mathrm{d}s_{-}^2& = {} \left( 1 + \frac{r^2}{R^2}\right) ^{n}\,\mathrm{d}r^2+r^2(\mathrm{d}\theta ^2+\sin ^2 \theta \,\mathrm{d}\phi ^2) \nonumber \\&\quad -\left( D + \frac{C (r^2 + R^2)^{1 + \frac{n}{2}}}{2 + n}\right) ^2 \mathrm{d}t^2. \end{aligned}$$
(22)

A smooth matching of the metric potentials across the boundary is given by the first fundamental form, i.e., at the boundary \(r=r_b\)

$$\begin{aligned} g_{rr}^+=g_{rr}^- , \quad ~g_{tt}^+=g_{tt}^-, \, \, \, \, \end{aligned}$$
(23)

and the second fundamental form implies

$$\begin{aligned} p_i(r=r_b-0)=p_i(r=r_b+0), \end{aligned}$$
(24)

where i takes the values of r and t.

From the boundary conditions \(g_{tt}^+=g_{tt}^-\) and \(p_{r}(r_b)=0\), we get the following two equations:

$$\begin{aligned}&1-\frac{2M}{r_b}=\left( D + \frac{C (r_b^2 + R^2)^{1 + \frac{n}{2}}}{2 + n}\right) ^2, \end{aligned}$$
(25)
$$\begin{aligned}&\frac{1 - \left( 1 + \frac{r_b^2}{R^2}\right) ^{-n}}{r_b^2}=\frac{ 2 C (2 + n) \left( 1 + \frac{r_b^2}{R^2}\right) ^{-n} (r_b^2 + R^2)^{\frac{n}{2}}}{ D (2 + n) + C (r_b^2 + R^2)^{1 +\frac{ n}{2}}}. \end{aligned}$$
(26)

  • Determination of R:  Now the boundary condition \(g_\mathrm{rr}^+=g_\mathrm{rr}^-\), implies

    $$\begin{aligned} R& = {} \frac{r_b}{\sqrt{\left( 1 -\frac{2M}{r_b}\right) ^{-\frac{1}{n}} - 1}}. \end{aligned}$$
    (27)

  • Determination of C and D: Solving Equations (25) and (26), we obtain the expressions C and D as

    $$\begin{aligned} C& = {} -\frac{(R^2 + r_b^2)^{-\frac{n}{2}} \sqrt{\frac{-2 M + r_b}{r_b}}\left( 1-\left( 1 + \frac{r_b^2}{R^2}\right) ^n\right) }{ 2 r_b^2} , \end{aligned}$$
    (28)
    $$\begin{aligned} D& = {} -\frac{C(r_b^2 + R^2)^{1 + \frac{n}{2}}}{2 + n} + \sqrt{1 - \frac{2M}{r_b}}. \end{aligned}$$
    (29)

So, we have matched our interior space–time to the exterior Schwarzschild space–time at the boundary \(r=r_{b}\). Obviously, it is clear that the metric coefficients are continuous at \(r=r_{b}\), but the transverse pressure \(p_{t}\) does not vanish at the boundary and therefore it is not continuous at the junction surface. To take care of this situation, let us use the Darmois Israel (1966), Israel (1967) formation to determine the surface stresses at the junction boundary. The intrinsic surface stress–energy tensor \(S_{ij}\) is given by Lancozs equations in the following form:

$$\begin{aligned} S^{i}_{j}=-\frac{1}{8\pi }(\kappa ^{i}_j-\delta ^{i}_j\kappa ^{k}_k), \end{aligned}$$
(30)

where \(\kappa _{ij}\) represents the discontinuity in the second fundamental form, written as

$$\begin{aligned} \kappa _{ij}=K_{ij}^{+}-K_{ij}^{-}, \end{aligned}$$
(31)

\(K_{ij}\) being the second fundamental form is presented by

$$\begin{aligned} K_{ij}^{\pm }=\left. -n_{\nu }^{\pm }\left[ \frac{\partial ^{2}X_{\nu }}{\partial \xi ^{i}\partial \xi ^{j}}+\Gamma _{\alpha \beta }^{\nu }\frac{\partial X^{\alpha }}{\partial \xi ^{i}}\frac{\partial X^{\beta }}{\partial \xi ^{j}} \right] \right|_S, \end{aligned}$$
(32)

where \(n_{\nu }^{\pm }\) are the unit normal vectors defined by

$$\begin{aligned} n_{\nu }^{\pm }=\pm \left| g^{\alpha \beta }\frac{\partial f}{\partial X^{\alpha }}\frac{\partial f}{\partial X^{\beta }} \right| ^{-\frac{1}{2}}\frac{\partial f}{\partial X^{\nu }}, \end{aligned}$$
(33)

with \(n^{v }n_{\nu }=1\). Here \(n^{v }\) is of unit magnitude, and \(\xi ^{i}\) is the intrinsic coordinate on the shell. − and \(+\) correspond to interior and exterior Schwarzschild space–time, respectively.

Figure 5
figure 5

(Top) \({\mathrm{d}\rho }/{\mathrm{d}r}\) and (bottom) \({\mathrm{d}p_{r}}/{\mathrm{d}r},\,{\mathrm{d}p_{t}}/{\mathrm{d}r}\) are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image

Using the spherical symmetry nature of the space–time surface stress–energy tensor can be written as \(S^{i}_j=\mathrm{diag}(-\sigma ,\mathcal {P})\), where \(\sigma \) and \(\mathcal {P}\) are the surface energy density and surface pressure, respectively.

The expressions for the surface energy density \(\sigma \) and the surface pressure \(\mathcal {P}\) at the junction surface \(r = r_{b}\) are obtained as

$$\begin{aligned}&\sigma =-\frac{1}{4\pi r_b}\left[ \sqrt{1-\frac{2M}{r_b}}-\left( 1 + \frac{r_b^2}{R^2}\right) ^{-\frac{n}{2}}\right] , \end{aligned}$$
(34)
$$\begin{aligned}\mathcal {P}&=\frac{1}{8\pi r_b}\left[ \frac{1-\frac{M}{r_b}}{\sqrt{1-\frac{2M}{r_b}}}-\frac{\left( 1 + \frac{r_b^2}{R^2}\right) ^{-\frac{n}{2}}}{D (2 + n) + C (r_b^2 + R^2)^{1 + \frac{n}{2}}}\right. \nonumber \\&\quad \times \{D (2 + n) + C (r_b^2 + R^2)^{\frac{n}{2}}\big ((3 + n) r_b^2 + R^2\big ) \}\Bigg ]. \end{aligned}$$
(35)

6 Physical analysis of the present model

  1. 1.

    Regularity of the metric functions at the center:  We observe from equations (11) and (18) that the metric potentials take the following values at the center of the star:

    $$\begin{aligned} B^2|_{r=0}& = {} 1, \end{aligned}$$
    (36)
    $$\begin{aligned} A^2|_{r=0}& = {} \Big (\frac{D (2 + n) + C R^{2+n}}{2 + n}\Big )^2. \end{aligned}$$
    (37)

    The above two equations imply that metric functions are free from singularity and positive at the center.

  2. 2.

    Behavior of pressure and density:  From Equations (12), (19) and (20), the central density and central pressure are obtained as

    $$\begin{aligned} \rho _\mathrm{c}& = {} \frac{3 n}{\kappa R^2}~>0, \end{aligned}$$
    (38)
    $$\begin{aligned} p_\mathrm{c}& = {} \frac{-D n (2 + n) + C (4 + n)R^{2+n}}{R^2 \big (D (2 + n) + C R^{2+n}\big )}>0. \end{aligned}$$
    (39)

    From Equation (38), we obtain \(n>0\). Therefore, we can conclude that the dimensionless parameter n can never be negative. So \(n \in R^{+}\), R being the set of real numbers. Now Equation (39) holds if

    $$\begin{aligned} \frac{C}{D}>\frac{n(2+n)}{(4+n)R^{2+n}}. \end{aligned}$$

    Also, it is well known that for a physically acceptable model, \(\rho -p_{r}-2p_{t}\) should be positive everywhere within the stellar interior. By employing \(\rho -p_{r}-2p_{t}\) at the center of the star we get

    $$\begin{aligned} \frac{n(2+n)}{2R^{n+2}}~>\frac{C}{D}. \end{aligned}$$

    Hence, we obtain a reasonable bound for \(\frac{C}{D}\) as

    $$\begin{aligned} \frac{n(2+n)}{(4+n)R^{2+n}}<~\frac{C}{D}~<\frac{n(2+n)}{2R^{n+2}}. \end{aligned}$$

    The surface density of the star is obtained as

    $$\begin{aligned} \kappa \rho _s& = {} \frac{1 - \left( 1 + \frac{r_b^2}{R^2}\right) ^{-n}}{r_b^2} + \frac{2 n \left( 1 + \frac{r_b^2}{R^2}\right) ^{-1 - n}}{R^2}. \end{aligned}$$
    (40)

    The EoS parameters \(\omega _{r}\) and \(\omega _{t}\) are obtained from the following formulae:

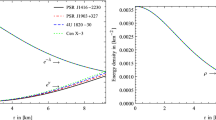
    $$\begin{aligned} \omega _{r}=\frac{p_{r}}{\rho },\quad ~\omega _{t}=\frac{p_{t}}{\rho }. \end{aligned}$$

    The profiles of \(\omega _{r}\) and \(\omega _{t}\) have been plotted in Figure 1.

    Next, we are interested to find out the pressure and density gradient denoted as follows: (i) density gradient: \({\mathrm{d}\rho }/{\mathrm{d}r}\), (ii) radial pressure gradient: \({\mathrm{d}p_{r}}/{\mathrm{d}r}\), and (iii) transverse pressure gradient: \({\mathrm{d}p_{t}}/{\mathrm{d}r}\). Differentiating Equations (12), (19), and (20) with respect to r, we get the following expressions for \(\rho ',\, p_{r}'\) and \(p_{t}'\) (overdashed denotes differentiation with respect to r) as

$$\begin{aligned}\kappa \rho '&=\frac{2}{r^3} \Bigg[\frac{\left( 1 + \frac{r^2}{R^2}\right) ^{-n}}{(r^2 + R^2)^2}\Big \{(1-n-2 n^2)r^4\nonumber \\&\quad + (2 + n) r^2 R^2 + R^4\Big \}-1 \Bigg], \end{aligned}$$
(41)
$$\begin{aligned}\kappa p_{r}'&=\frac{2 - 2 \left( 1 +\frac{r^2}{R^2}\right) ^{-n} }{r^3} - \frac{2 n \left( 1 +\frac{r^2}{R^2}\right) ^{-1-n}}{ r R^2}\nonumber \\&\quad -2 C (2 + n) r \Psi _1(r), \end{aligned}$$
(42)
$$\begin{aligned}\kappa p_{t}' &=\frac{2 r \left( 1 + \frac{r^2}{R^2}\right) ^{-n}}{ ( D (2 + n) (r^2 + R^2) + C (r^2 + R^2)^{2 + \frac{n}{2}} ) ^2}\nonumber \\&\quad \times \Big \{D^2 n (1 + n) (2 + n)^2 + C D n^2 (2 + n) \nonumber \\&\quad \times (r^2 + R^2)^{1 + \frac{n}{2}} - C^2 (1 + n) (4 + n) \nonumber \\&\quad \times (r^2 + R^2)^{2 + n}\Big \}, \end{aligned}$$
(43)

where

$$\begin{aligned} \Psi _1(r)& = {} \frac{D n (2 + n) + 2 C (1 + n) (r^2 + R^2)^{1 + \frac{n}{2}}}{ (D (2 + n) + C (r^2 + R^2)^{1 + \frac{n}{2}} )^2}\Omega ,\\ \Omega& = {} \frac{(r^2 + R^2)^{-1 + \frac{n}{2}}}{\left( 1 +\frac{r^2}{R^2}\right) ^{n}}. \end{aligned}$$

All of \(\rho ',\,p_{r}'\), and \(p_{t}'\) should be negative for \(r~\in ~(0,\,r_b)\). We shall verify it with the help of graphical analysis.

Table 3 The numerical values of the central density \(\rho _{c}\), surface density \(\rho _{s}\), central pressure \(p_{c}\), the value of the radial adiabatic index \(\Gamma _{r}\) at the center and surface transverse pressure \(p_{t}(r_b)\) have been obtained for different values of n for the compact star PSR J1614-2230.
Full size table
Table 4 The numerical values of the central density \(\rho _{c}\), surface density \(\rho _{s}\), central pressure \(p_{c}\), the value of the radial adiabatic index \(\Gamma _{r}\) at the center and surface transverse pressure \(p_{t}(r_b)\) have been obtained for different values of n for the compact star EXO 1785-248.
Full size table

6.1 The compact stars PSR J1614-2230 and EXO 1785-248

To obtain the values of the constants \(R,\,C,\) and D in the expressions of different model parameters, we have considered two compact stars PSR J1614-2230 and EXO 1785-248. The observed and estimated masses and radii of these two stars have been given in Tables 1 and 2, respectively. Using the expressions for \(R,\,C,\) and D from Equations (27) to (29), the numerical values of these parameters have been determined for different values of n and presented in Tables 1 and 2.

By using the mentioned values in Table 1 for the compact star PSR J1614-2230, we generated the plots of matter density \((\rho )\), radial pressure (\(p_{r}\)), transverse pressure (\(p_{t}\)), and anisotropic factor \((\Delta )\) in Figures 2–4, respectively. The matter density \(\rho \) is a positive, finite, and monotonically decreasing function of r, i.e., the maximum values of these physical model parameters are attained at the center of the star. The radial and transverse pressures \(p_{r}\) and \(p_{t}\) show the same behavior as \(\rho \). Figure 4 shows that \(\Delta >0\) for our model, i.e., anisotropic force is repulsive in nature and it is necessary for the construction of compact object (Gokhroo & Mehra 1994). Moreover, at the center of the star \(\Delta \) vanishes. \(\rho ',\,p_{r}'\), and \(p_{t}'\) all are plotted in Figure 5 and the figures indicate that all of them take a negative value and it once again verifies that \(\rho ,\,p_{r}\), and \(p_{t}\) are monotonically decreasing. The EoS parameters \(\omega _{r}\) and \(\omega _{t}\) are plotted in Figure 1. From the profiles, we see that \(\omega _{r}\) is monotonically decreasing and \(\omega _{t}\) is a monotonically increasing function of r,  also \(0<\omega _{r},\,\omega _{t}<1\) indicate that the underlying matter distribution is non-exotic in nature. The ratio of stress tensor to energy \((p_{r}+2p_{t} )/ \rho \) is monotonically decreasing and has been shown graphically in Figure 1.

One interesting thing we can note that for larger values of n, for the model parameters \(\omega _{t}\) and \(({p_{r}+2p_{t}})/{\rho }\), the central values of these two physical quantities increase and at \(r=7.3\) km, irrespective of n, all the curves coincide. Moreover for \( 0< r <7.3 \), as n increases, the profile corresponding to a small value of n is dominated by the profile corresponding to the value of n larger than previous one. On the other hand, for \( 7.3< r < r_b \), the nature of the curves for these two physical quantities become the reverse of the former.

6.2 Energy conditions

To be a physically reasonable model, one of the most important properties that should be satisfied by our model is energy conditions viz, null energy condition (NEC), weak energy condition (WEC), strong energy condition (SEC), and DEC. These energy conditions are followed if the following inequalities hold simultaneously:

$$\begin{aligned} \mathrm {NEC}:&:&T_{\mu \nu }\beta ^\mu \beta ^\nu \ge 0~\text{ or }~ \rho +p_i \ge 0, \end{aligned}$$
(44)
$$\begin{aligned} \mathrm {WEC}:&:&T_{\mu \nu }\alpha ^\mu \alpha ^\nu \ge 0~\text{ or }~\rho \ge 0, \,~\rho +p_i \ge 0, \end{aligned}$$
(45)
$$\begin{aligned} \mathrm {DEC}:&:&T_{\mu \nu }\alpha ^\mu \alpha ^\nu \ge 0 ~\text{ or }~ \rho \ge |p_i|, \end{aligned}$$
(46)
$$\begin{aligned} \mathrm {SEC}:&:&T_{\mu \nu }\alpha ^\mu \alpha ^\nu - {1 \over 2} T^\lambda _\lambda \alpha ^\sigma \alpha _\sigma \ge 0 ~\text{ or }~ \rho +\sum _i p_i \ge 0, \end{aligned}$$
(47)

where i takes the value of r and t for radial and transverse pressures. \(~\alpha ^\mu \) and \(\beta ^\mu \) are time-like vector and null vector, respectively, and \(T_{\mu \nu } {\alpha}^{\mu} \) is a non-space-like vector. To check all the inequalities stated above, we have drawn the profiles of left-hand sides of (44)–(47) in Figure 6 in the interior of the compact star PSR J1614-2230 for different values of n. The figures show that all the energy conditions are satisfied by our model of a compact star.

Figure 6
figure 6

All the energy conditions are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image

6.3 The behavior of mass function

The gravitational mass in a sphere of radius r is given by

$$\begin{aligned} m(r)& = {} 4\pi \int _0^{r}\omega ^{2}\rho (\omega )\,\mathrm{d}\omega =\frac{r}{2}\left[ 1 - \left( 1 + \frac{r^2}{R^2}\right) ^{-n}\right] . \end{aligned}$$
(48)

The compactness factor u(r) and surface redshift \(z_{s}\) are defined by

$$\begin{aligned} u(r)& = {} \frac{4\pi }{r}\int _0^{r}\omega ^{2}\rho (\omega )\,\mathrm{d}\omega =\frac{1}{2}\left[ 1 - \left( 1 + \frac{r^2}{R^2}\right) ^{-n}\right] ,\nonumber \\ \end{aligned}$$
(49)
$$\begin{aligned} z_\mathrm{s}& = {} \frac{1}{\sqrt{1-2u(r_b)}}-1. \end{aligned}$$
(50)

One can easily check that \(\lim _{r \rightarrow 0} m(r)=0\), which indicates that the mass function is regular at the center of the star. What is more, \(\left( 1+r^2/R^2\right) ^n>1\), therefore, \(\left( 1+r^2/R^2 \right) ^{-n}<1\) and hence \(m(r)>0\). As n increases, \(\left( 1+r^2/R^2\right) ^{-n}\) decreases and therefore mass function increases. So, m(r) is a monotonically increasing function of r. The twice maximum allowable mass-to-radius ratios are obtained as 0.5997 and 0.4693 for the compact stars PSR J1614-2230 and EXO 1785-248, respectively, and these values lie in the range \({2M}/{r_b}<{8}/{9}\), i.e., Buchdahl’s limit is satisfied (Buchdahl 1959). The surface redshift of these two stars is obtained as 0.5806 and 0.372699, respectively.

Figure 7
figure 7

(Top) \(p_{r}\) versus \(\rho \) and (bottom) \(p_{t}\) versus \(\rho \) are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image

6.4 Equation of state (EoS)

To construct a model of a compact star, it is a very common choice among the researchers to use any specific EoS, which gives a relationship between the pressure and the density. We still do not know the relationship between the matter density and the pressures. To check the variation of pressure with density, we have plotted \(p_{r}\) versus \(\rho \) and \(p_{t}\) versus \(\rho \) in Figure 7, from which one can predict possible EoS. For the complexity in the expressions of \(\rho ,\,p_{r}\), and \(p_{t}\), it is very difficult to obtain a well-known relation between them. With the help of the numerical analysis, we have obtained the best-fitted curve, which gives us a prediction about the relationship between the matter density and pressure. We have drawn the profiles for the compact star PSR J1614-2230 by taking different values of the dimensionless constant n mentioned in the figures.

6.5 Mass–radius curves

The mass–radius relation for different values of the dimensionless parameter n for the compact star PSR J1614-2230 is shown in Figure 8. In the following table, we have given the maximum allowable mass for different values of n and we have also obtained the corresponding radius from the figure.

n

Maximum mass (\( M/M_{\odot }\))

Radius (km)

10

2.915

12.01

15

2.831

11.81

25

2.738

11.44

60

2.648

11.04

1000

2.572

10.7

Figure 8
figure 8

Maximum allowable mass versus radius is plotted against r inside the stellar for different values of n mentioned in the figure.

Full size image

It is evident from the calculation that the maximum mass of compact star decreases as n increases.

Figure 9
figure 9

(Top) The variation of the mass function and (bottom) \({\partial M}/{\partial \rho _{c}}\) are plotted with respect to central density \(\rho _{c}\) inside the stellar interior for different values of n mentioned in the figures.

Full size image

7 Stability analysis

7.1 Harrison–Zeldovich–Novikov stability criterion

A stability condition for the model of compact star proposed by Harrison (1965) and Zeldovich & Novikov (1971) depending on the mass and central density of the star. They suggested that for stable configuration \({\partial M}/{\partial \rho _{c}}>0\), otherwise the system will be unstable, where M and \(\rho _{c}\) denote the mass and central density of the compact star.

For our present model

$$\begin{aligned} \frac{\partial M}{\partial \rho _{c}}=\frac{4}{3}\pi r_b^3 \left( 1+\frac{\kappa }{3n}\rho _{c} r_b^2\right) ^{-n-1}. \end{aligned}$$
(51)

The above expression of \({\partial M}/{\partial \rho _{c}}\) is positive and hence the stability condition is well satisfied. The variation of the mass function and \({\partial M}/{\partial \rho _{c}}\) with respect to the central density is depicted in Figure 9.

7.2 Stability under three forces

The stability of our present model under three different forces viz, gravitational force, hydrostatics force, and anisotropic force can be described by the following equation:

$$\begin{aligned} -\frac{M_G(\rho +p_{r})}{r^{2}}\frac{B}{A}-\frac{\mathrm{d}p_{r}}{\mathrm{d}r}+\frac{2}{r}(p_{t}-p_{r})=0, \end{aligned}$$
(52)

known as the TOV equation, where \(M_G(r) \) represents the gravitational mass within the radius r, which can be derived from the Tolman–Whittaker formula and Einstein’s field equations and is defined by

$$\begin{aligned} M_G(r)=r^{2}\frac{A'}{B}. \end{aligned}$$
(53)

Plugging the value of \(M_G(r)\) in Equation (52), this equation can be rewritten as

$$\begin{aligned} F_{g}+F_h+F_a=0, \end{aligned}$$
(54)

where

$$\begin{aligned}&F_{g}=-\frac{ C (2 + n) r \left( 1 + \frac{r^2}{R^2}\right) ^{-n} (r^2 + R^2)^{-1 + \frac{n}{2}}\Psi _1(r) }{4 \pi }, \end{aligned}$$
(55)
$$\begin{aligned}&F_h=\frac{1}{4\pi r^3}\left[ -1 + \left( 1 + \frac{r^2}{R^2}\right) ^{-n} \right. \nonumber \\&\quad \left. + \frac{r^2 \left( 1 + \frac{r^2}{R^2}\right) ^{-n} \xi (r)}{(r^2 + R^2) (D (2 + n) + C (r^2 + R^2)^{1 + \frac{n}{2}} )^2}\right] , \end{aligned}$$
(56)
$$\begin{aligned}&\quad F_a=\frac{1 - \frac{\left( 1 + \frac{r^2}{R^2}\right) ^{-n} ((1 + n) r^2 + R^2 )}{r^2 + R^2}}{4 \pi r^2} \end{aligned}$$
(57)

and

$$\begin{aligned}\xi (r)&=D^2 n (2 + n)^2 + C D n (2 + n) (r^2 + R^2)^{\frac{n}{2}}\Phi \\&\quad +C^2 (r^2 + R^2)^{1 + n}\big [(4 + n (7 + 2 n)) r^2 + n R^2\big ],\\\Phi& =(4 + n) r^2 + 2 R^2 . \end{aligned}$$
Figure 10
figure 10

Gravitational, hydrostatics, and anisotropic forces are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image

The three different forces acting on the system are shown in Figure 10 for different values of n. The figures show that gravitational force is negative and dominating in nature, which is counterbalanced by the combined effect of hydrostatics and anisotropic forces to keep the system in equilibrium.

7.3 Causality condition and method of cracking

For a physically acceptable model, the radial and transverse velocity of sound should lie in the range \(V_{r}^{2},\,V_{t}^{2}~\in ~[0,\,1]\), known as causality condition. Where radial \((V_{r}^{2})\) and transverse velocity \((V_{t}^{2})\) of sound are defined as

$$\begin{aligned} V_{r}^{2} = \frac{p_{r}'}{\rho '}, \quad V_{t}^{2}= \frac{p_{t}'}{\rho '}. \end{aligned}$$
(58)

The expressions for \(\rho ',\,p_{r}'\), and \(p_{t}'\) have been given in Equations (41)–(43).

Figure 11
figure 11

(Top) The square of the radial velocity \((V_{r}^2)\), (middle) the square of the transverse velocity \((V_{t}^2)\), and (bottom) the stability factor \(V_{t}^2-V_{r}^2\) are plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figures.

Full size image

Now, due to the complexity of the expression it is very difficult to verify the causality condition analytically. The profiles of \(V_{r}^2\) and \(V_{t}^2\) are shown in Figure 11. It is clear from the figure that both \(V_{r}^2\) and \(V_{t}^2\) lie in the reasonable range. So, it can be concluded that the causality condition is well satisfied. Next, we want to concentrate on the stability factor of the present model, which is defined as \(V_{t}^2-V_{r}^2\). For the stability of a compact star model, Herrera (1992) proposed the method of ‘cracking’ and using this method, Abreu et al. (2007) proposed that for a potentially stable configuration, \(V_{t}^2-V_{r}^2 < 0\). From Figure 11 (bottom panel), we see that the stability factor is negative and hence we conclude that our model is potentially stable everywhere within the stellar interior.

7.4 Adiabatic index

For a particular stellar configuration, Bondi (1964) examined that a Newtonian isotropic sphere will be in equilibrium if the adiabatic index \(\Gamma > 4/3\) and it gets modified for a relativistic anisotropic fluid sphere. Based on these results, the stability of an anisotropic stellar configuration depends on the adiabatic index \(\Gamma _{r}\) given by

$$\begin{aligned} \Gamma _{r}& = {} \frac{\rho +p_{r}}{p_{r}}\frac{\mathrm{d}p_{r}}{\mathrm{d}\rho },\nonumber \\& = \frac{2 r^2 (D n (2 + n) + 2 C (1 + n) \chi ^{1 + \frac{n}{2}})}{\chi (D (2 + n) \big (1- \left( 1 + \frac{r^2}{R^2}\right) ^n ) + C \chi ^{\frac{n}{2}} \Psi _2(r) )}V_{r}^2, \end{aligned}$$
(59)

where

$$\begin{aligned} \Psi _2(r)& = {} (5 + 2 n) r^2+R^2-\left( 1 + \frac{r^2}{R^2}\right) ^n (r^2 + R^2),\\ \chi& = {} r^2 + R^2, \end{aligned}$$

and the expression of \({\mathrm{d}p_{r}}/{\mathrm{d}\rho }\) has been given in the previous subsection.

Figure 12
figure 12

\(\Gamma _{r}\) is plotted against r inside the stellar interior for the compact star PSR J1614-2230 for different values of n mentioned in the figure.

Full size image

For our present model, the profiles of \(\Gamma _{r}\) are shown in Figure 12 for different values of n. From the figure, we see that the profile of the radial adiabatic index is a monotonically increasing function of r and \(\Gamma _{r} >4/3\) everywhere within the stellar configuration and hence the condition of stability is satisfied.

8 Discussion

The present paper provides a new generalized model of a compact star by assuming a physically reasonable metric potential together with a pressure anisotropy. We matched our interior solution to the exterior Schwarzschild line element at the boundary to fix the values of the different constants. From the boundary conditions we have obtained the values of \(R,\,C\), and\(\,D\) for the compact stars PSR J1614-2230 and EXO 1785-248 with masses 1.97 and \(1.3\, M_{\odot }\), respectively, and radii 9.69  and 8.85 km, respectively, in Tables 1 and 2 for different values of the dimensionless parameter n. From the tables, it is clear that the numerical values of the constants C and D decrease with increasing n, whereas the numerical values of R increase with n increasing. One notable thing is that the numerical values of C decrease rapidly whereas the numerical value of D decreases steadily. All the profiles are depicted for the compact star PSR J1614-2230. We have plotted the profiles of matter density (\(\rho \)), radial pressure (get the following expressions\(p_{r}\)), and transverse pressure (\(p_{t}\)) for different values of n and we see that all are positive and monotonically decreasing functions of r. The values of the model parameters such as central density, surface density, central pressure, surface transverse pressure, and the central value of the radial adiabatic index for the above-mentioned two stars are presented in Tables 3 and 4. We also note that the central values of pressure and density decreases with increasing n, it is evident from Table 2 as well as from Figures 2 and  3. On the other hand, the surface density of the star increases as n increases. Plugging G and c in the expression of \(\rho \) and \(p_{r}\), we obtained the central density and central pressure for different values of n, which lie in the range \(1.57\times 10^{15}{- }1.64\times 10^{15}~\, \mathrm {g/cm}^3\) and \(2.05\times 10^{35}{- }2.26\times 10^{35} \,\mathrm {dyn/cm}^2\), respectively. It can also be noted that the surface density lies in the range \(7.43\times 10^{14}{- }7.62\times 10^{14} \, \mathrm {g/cm}^3\) for the compact star PSR J1614-2230. Also, the central density and central pressure for different values of n lies in the range \(1.36\times 10^{15}{- }1.32\times 10^{15}\, \mathrm {g/cm}^3\) and \(8.802\times 10^{34}{- }1.005\times 10^{35} \, \mathrm {dyn/cm}^2\), respectively, and surface density lies in the range \(6.96\times 10^{14}{- }7.14\times 10^{14}\, \mathrm {g/cm}^3\) for the compact star EXO 1785-248. From the figure, it is clear that the transverse pressure \(p_{t}\) always dominates the radial pressure \(p_{r}\) and it creates a positive pressure anisotropy and hence repulsive force toward the boundary. With the help of graphical representation, we have shown that our model satisfies all the energy conditions, and \((p_{r}+2p_{t})/\rho \) is monotonically decreasing and \(<1\). The radial adiabatic index \(\Gamma _{r} > 4/3\) and the causality conditions are satisfied by our model. The stability conditions of the model have been tested under different conditions. The EoS parameter \(\omega _{r}\) is a monotonically decreasing function of r but \(\omega _{t}\) is monotonically increasing. Both of them lie in the range \(0< \omega _{r},\,\omega _{t} < 1\) (Figure 1). The forces acting on the present model are depicted in Figure 10 and it shows the effect of gravitational force (\(F_{g}\)) and anisotropic force (\(F_{a}\)) are increased with the increasing value of n. The central values of the radial adiabatic index for the compact stars PSR J1614-2230 and EXO 1785-248 are obtained in Tables 3 and 4. We see that the central values of the radial adiabatic index increases as n increases. So, one can conclude that the increasing value of n makes the system more stable in respect of the test of the adiabatic index. One can also note that the central values of radial and transverse velocities of sound increase with the increasing values of n. To check the behavior of the radial and transverse pressures with the matter density, we draw the profiles of \(p_{r}\) versus \(\rho \) and \(p_{t}\) versus \(\rho \) in Figure 7. The potential stability condition of the present model is also satisfied. So, we can conclude that solution obtained in this paper can be used as a successful model for the description of ultra-compact stars.

9 Conclusion

In the article, we have explored a new uncharged anisotropic solution by assuming modified Finch–Skea ansatz for the coefficient of \(g_{rr}\). We have assumed a physically reasonable anisotropic factor to generate our solution. However, the obtained physical parameters are well-behaved at the interior as well as possess finite values at the centre. In the construction of the stellar models we further assumed \(p_t > p_r\). The stability is examined by the relativistic adiabatic index, and the adiabatic radial and tangential sound speeds. The stellar models obtained in this paper could play a significant role in the description of internal structure of compact stars.