The P-DNS Method for Turbulent Fluid Flows: An Overview

Abstract

An overview of the Pseudo-Direct Numerical Simulation (P-DNS) method is presented. This is a multi-scale method aiming at numerically solving the unknown fields at two different scales, namely coarse and fine. The P-DNS method is built around four key ideas. The first one is that of numerically solving both scales, which facilitates obtaining solutions to problems of both concurrent multi-scale and hierarchical multi-scale types. The second key idea is that of computing off-line the fine solution via Direct Numerical Simulation in simplified domains, termed representative volume elements (RVEs), while the third idea is that of storing the basic (physics-informed) results obtained from this solution in a problem-independent unique dimensionless database. This database may be subsequently used for solving different problems at the coarse level, i.e. by using coarse meshes in the corresponding problem domains, via a surrogate model. In this sense P-DNS resembles Reduced Order Methods, which require a previous off-line evaluation of the modes to be used in the solution, sharing with them the benefit of solving the reduced problem, more precisely the coarse scale, in P-DNS terms, in a very efficient way. The fourth and last key idea of P-DNS is based on the fact that most of the high-frequency modes of a turbulent flow are convected by the fluid velocity of the low-frequency modes. Taking this into account the P-DNS technique is implemented in such a way that the fine instabilities are convected by the velocity field of the coarse solution. Finally, although the P-DNS method has been used to solve different computational mechanics problems, such as convection-diffusion and convection-reaction/absorption problems, the scope of this overview will be limited to its application to turbulent incompressible fluid flows, including both single phase and particle-laden flows.

1 Introduction

The primary challenge in numerical simulation of turbulent flows originates from the enormous range of scales that must be resolved. For accurate simulations, the size of the computational domain must typically be at least one order of magnitude larger than the largest energy containing waves, while the computational mesh must be fine enough to resolve the smallest dynamically significant length-scale, related to the turbulence kinetic energy dissipation, known as the Kolmogorov scale.

1.1 The DNS Approximation

The simulation of any physical phenomenon without relying on any empirical or modeling approach is known as Direct Numerical Simulation (DNS). DNS is a technique that allows solving problems that cannot be solved by theoretical methods. With sufficient computational resources, DNS can fully solve the governing equations that are accepted to reproduce the mechanics of a fluid flow, particularly in geometries of arbitrary complexity, providing the complete answer to the problem at hand. In practical fluid flow cases, it is well known that most interesting situations fall into unstable regimes and the challenge here is to simulate both the local details of the instabilities and their impact on the bulk flow. Accepting that the Navier–Stokes (N–S) equations provide a theoretical framework that governs the behavior of this type of fluid flows, their numerical solution with DNS not only allows one to understand the transfer mechanisms within the fluid flow, but also provides much more detailed information, in space and time, than a laboratory experiment. The DNS method could be thought at the same time as a numerical approach to obtain the same information as that of an analytical solution on arbitrary geometries, nonlinear situations and with general parameters. Another potential capacity of the DNS method that differentiates it from other numerical modeling techniques for fluid flows is the universality of its behavior, that is, its capacity to model the lower limit scale where molecular diffusion phenomena dominate, thus capturing all flow structures.

Since Orszag’s pioneering work in 1969 [1], many DNS studies have been performed on incompressible flows [2,3,4,5,6,7,8,9,10,11,12]. Unfortunately, despite the rapid development that hardware has undergone recently, the number of degrees of freedom required to handle turbulent flow issues with the DNS method makes this approach still unfeasible for engineering applications, even those with moderate Reynolds number. It is known that the computational resources for using DNS techniques in fluids scale as the Reynolds number raised to a power of 9/4. On the other hand, recent DNS studies allowed us to analyze flows in Reynolds numbers higher than those that can be achieved in laboratory experiments. The limitation of the latter stems from the need for large experimental facilities to produce high-velocity flows, in addition to the impossibility of observing unstable flow structures at very small scales and in situations with high intermittency. Therefore, any progress on the DNS method will help further improve our understanding of unstable fluids.

1.2 State of the Art Models to Reduce the DNS Computational Cost

The Reynolds Averaged Navier Stokes (RANS) approach [13, 14] was developed to considerably reduce the computational cost in the simulation of turbulent flows. It is based on averaging all the scales, incorporating their effects on the overall flow via models that rely on empirical coefficients obtained in experiments carried out in equilibrium conditions. The more advanced and powerful RANS methods are those classified as Reynolds Stress Models (RSM). They aim at transporting the full Reynolds stress tensor instead of relying on a turbulent eddy viscosity and the Boussinesq approximation. Some of the most advanced RSM are based on the Algebraic Reynolds Stress Model (ASM) [15], most notably in its explicit versions (EASM, see for example [16, 17]). However, the loss of details of the transient behavior of the flow in the necessary averaging process makes the RANS approach not adequate for many practical situations. Particularly, it usually fails to predict complex flow features, such as the transition from onset to almost fully developed turbulence, making it unsuitable in general for modeling turbulent flows.

Another widely used approach for modeling turbulent flows is the Large Eddy Simulation (LES) technique [18,19,20,21,22,23,24]. In LES, the large-scale motions (large eddies) are computed directly on the mesh, leaving only small (sub-grid) scale motions to be modeled. This leads to a considerable reduction in computational cost with respect to DNS. However, the limit between large and small eddies is not well-defined in LES, being typically a decision to be made by the users of the model according to their experience and the available computational resources. The good practices advise setting this limit where the fluid structures that remain to be modeled behave in a universal way, with an order of magnitude dictated by the molecular scales, mostly isotropic. In fact, obtaining LES solutions of accuracy close to that of DNS still requires very fine meshes, in particular near solid bodies, making LES unfeasible, in terms of computational costs, for the computer architectures existing today.

The hybridization of RANS and LES methods is a promising way to efficiently deal with separated turbulent flow simulations allowing to circumvent the drawback of LES to accurately solve the flow close to the solid walls [25, 26]. In this approach, the large eddies are resolved away from the walls, with the boundary layers covered by a RANS model. Examples of such global hybrid models are detached eddy simulation (DES) [27,28,29], scale-adaptive simulation (SAS) [30, 31], and Partially Averaged Navier-Stokes (PANS) models [32]. More advanced versions of DES include delayed DES (DDES), shear-layer-adapted (SLA) DDES (DDES-SLA), and improved DDES (IDDES) [33,34,35].

Despite the fact that RANS and LES only differ in how length or time scale information is provided for the modeled turbulent motions, it remains unaffordable to develop universally applicable RANS-LES hybrid methods. The problem is the incompatibility of both approaches in the region where they interact, since on the one hand the LES models only handle fluctuations of the subgrid, while RANS provides fluctuations that are a statistical average of all the scales, not only those of the subgrid. This poses a challenge that is still unresolved.

However, and as a brief summary, RANS remains the only approach to address most of the problems proposed by industry, even incorporating transient effects through U-RANS methodology, leaving the LES modeling approach reserved for situations where the relationship between mesh, accuracy and technological advances in terms of hardware, allow its use. As for DNS, everything indicates that it will have a growing role in science and technology and that efforts should be directed at finding better and more efficient ways to make use of it.

1.3 The Multi-scale Approximations

In general, the term multi-scale is used for problems where there are two or more different scales which, from the numerical point of view, cannot be treated as a unique single scale. In this sense, whether explicitly mentioned or not, all models to simulate turbulent flows are based on multi-scale approaches.

It is interesting to point out that the term multi-scale is used when there are different scales due to the physical characteristics of the material (multi-scale in density, multi-scale in elastic coefficients, etc.), and also when there are different scales in features of the solution behavior (multi-scale of frequencies, multi-scale of velocities, gradients, oscillations, etc.). Furthermore, from the modeling point of view, multi-scale phenomena can be classified into two main classes: hierarchical and concurrent. On one hand, hierarchical multi-scale phenomena are those where the physical characteristics of the constituent materials belong to two or more totally separated scales that are weakly coupled. Here, the large-scale variations decouple from the small-scale physics, or the large-scale variations appear homogeneous and quasi-static from the small-scale point of view. On the other hand, concurrent multi-scale phenomena, on the other hand, are those where their solution involves the sum of functions that belong to two or more scales, for example waves of very different lengths. The modeling here attempts to link methods appropriate for each scale together in a combined model, where the different scales of the system are considered concurrent and communicate with each other with some type of hand-shaking procedure [36, 37]. Hierarchical multi-scale phenomena are associated to composite materials such as concrete, FRP materials, porous materials, etc., while concurrent multi-scale phenomena are typically those governed by the advection–diffusion equations, most notably the fluid mechanics equations as applied to turbulent flows, among others [38]. A combination of both classes of multi-scale phenomena may also be found, for example in turbulent flows of particle-laden fluids, in which the fluid flow modeling part belongs to the category of concurrent multi-scale, but the combination of the density of the fluid with the density of the particles belongs to the category of hierarchical multi-scale.

The idea of treating homogeneous fluids as a multi-scale problem, within the frame of the finite element method (FEM) was first introduced by Hughes via the Variational Multi-Scale (VMS) framework [39]. Hughes presented a general procedure to derive numerical methods capable of dealing with concurrent multi-scale phenomena. Its development tries to rectify the simple fact that the direct application of the Galerkin method using standard bases, such as FEM, is not a robust approach for solving concurrent multi-scale phenomena. As for hierarchical multi-scale problems, there are many works aimig to modeling solids in this way, and the reader can see some of them in Reference [40].

In general, all multi-scale methods proceed along a similar path, with the solution decomposed into two different fields as $\varphi = \varphi^{\rm H} + \varphi^{\prime},$ where $\varphi^{\rm H}$ is solved numerically using a spatial discretization of characteristic element length H, and $\varphi^{\prime}$ is obtained approximately, either analytically or numerically, so that $\varphi^{\prime}$ is eliminated from the solution of the problem. Both $\varphi^{\rm H}$ and $\varphi^{\prime}$ can overlap or be disjoint, and $\varphi^{\prime}$ can be defined globally or locally, although its effect on the global problem will always be non-local [41].

The first approach to obtain $\varphi^{\prime}$ is proposed in [39], using analytical Green functions. The difficulty of applying this procedure to complex problems lead to the development of residual-based models. This kind of sub grid-scale models aim at providing an approximate analytical solution for $\varphi^{\prime}$ [42]. For this purpose, the scaling introduced is used to approximate the partial differential equations for the unresolved-scale quantities by solving ordinary differential equations or algebraic relations. Codina [41, 43] proposed a closed-form expression for the sub-grid scales based on a Fourier analysis of the problem of which they are the solution.

Alternative modeling strategies for the sub-grid scales are the addition of sub-grid viscosity [44], the use of a coarse time integration in the Galerkin method [45], or the use of bubble functions [46]. As a result of any of these procedures, algebraic scaling is combined with one scaling parameter for each equation, which can be identified as the inverse of the stabilization parameter of the more classical stabilized FEM [47].

The method of multiscale virtual power couples the macro- and micro-scale kinematical descriptors by means of kinematical insertion and homogenization operators. Micro-scale equilibrium equations as well as formulae for the homogenized (macro-scale) force- and stress-like quantities are derived a variational extension of the Hill-Mandel Principle that enforces the balance of the virtual powers of both scales [48, 49].

The FE² (FEM squared) method [50] is a hierarchical multi-scale approach admissible when the length scales of the structural problem and of the microstructure are separated. The FE² method links each integration point at the structural scale with a representative volume element (RVE), discretized using a FEM model of the microstructure. The prohibitive computational cost of this approach can be circumvented by solving the microscale problem with the fast Fourier transform [51], or even better using reduced basis homogenization schemes [52].

1.4 The P-DNS Ideas

The Pseudo-Direct Numerical Simulation (P-DNS) method, which was first introduced in [53], is a multi-scale method built around four key ideas.

The first key idea of P-DNS is that of numerically solving both scales, which facilitates obtaining solutions to problems of both concurrent multi-scale and hierarchical multi-scale types. The second key idea is that of computing off-line the fine scale solution via Direct Numerical Simulation in simplified domains, i.e. RVEs. The third idea is that of storing the basic (physics-informed) results obtained from this solution in a problem-independent unique dimensionless database. This database may be subsequently used for solving different problems at the coarse level, i.e. by using coarse meshes in the corresponding problem domains, via a surrogate model. In this sense P-DNS resembles Reduced Order Methods (ROM), which require a previous off-line evaluation of the modes to be used in the solution, sharing with them the benefit of solving the reduced problem, more precisely the coarse scale in P-DNS terms, in a very efficient way. The fourth and last key idea of P-DNS is based on the fact that most of the high-frequency modes of a turbulent flow are convected by the fluid velocity of the low-frequency modes. Taking this into account the P-DNS mexthod is implemented in such a way that the fine instabilities are convected by the coarse velocity field.

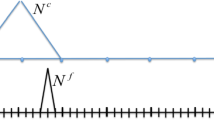
Figure 1 provides a summary of the P-DNS methodology, which comprises two steps, namely the off-line preparation of a dimensionless database and the on-line use of such database. On one hand, the off-line step of the method involves off-line DNS solutions in fine meshes of a collection of RVE problems, each of them associated to specific values of an input set of dimensionless parameters (${\hat{a}}_{1}, {\hat{a}}_{2}, \ldots , {\hat{a}}_n$). This input set, which details will be addressed later, is specifically designed to be computable with the information available in the global problem. Each RVE simulation computes relevant information, represented by $\tau_{i}$, which is stored as the output of the dimensionless database and associated to the corresponding input set values. On the other hand, the on-line step means solving a given global problem in a coarse mesh with a solution enriched with the fine mesh solution obtained from the database. To do this, during each time step of the global problem, the dimensionless inputs (${\hat{a}}_{1}, {\hat{a}}_{2}, \ldots , {\hat{a}}_n$) are computed in each RVE, which was previously convected in a Lagrangian way by the global velocity field. The downscale process is the evaluation of the reduced model in a database format to obtain the homogenized information from the fine-scale, $\tau_{i}$, which is up-scaled to enrich the coarse-scale solution.

Fig. 1

Summary of the P-DNS methodology

The concept of P-DNS originates from noticing a certain similarity between the microstructure in composite solid materials and the structures occurring in fluid flows, in particular, those related to turbulence. In a composite solid material, the overall rheological features come from the interaction of components with different properties and topology. On the other hand, in a turbulent flow of a fluid material, the overall behavior at the greater scales may be interpreted as the flow of a pseudo-fluid with particular rheological characteristics dependent on the instabilities present in the smaller scales. Behaviours like this are analogous to those seen in multiphase flows, where the apparent properties of the mixture are usually different from the simple averaging of those of the constituent phases.

The P-DNS method can also be understood as a variation of the VMS method, where the fine solution in the former is solved numerically while in the latter the idea lies in approximating the Green functions of the problem operator in order to stabilize the numerical solution scheme.

Also, from the point of view of homogenization methods, P-DNS can be perceived as the evolution of an FE² method in which the most expensive part of the computation is carried out off-line.

Finally, the P-DNS method can be framed as a Reduced Order Model (ROM) since from the methodological point of view it shares the idea of generating a priori an offline calculated database necessary to solve the main problem. In [54] the advantages and disadvantages of both methodologies are highlighted. This paper also discusses the drawback of standard ROM-type methods to solve problems in which space and time are not separate variables and that can be successfully solved by the P-DNS methodology.

The name P-DNS arises from the premise that in all multi-scale problems, the numerical result obtained with a very fine discretization is the correct one, without the need to introduce any additional theory (i.e. turbulence models), or any stabilization procedure for the transport equation terms (as in residual-based VMS techniques). As the coarse mesh is refined, P-DNS is designed so that it yields numerical results tending to the DNS solution, deemed here as the right solution, of the problem.

P-DNS, however, does not assume universality in the sub-grid (more specifically sub-coarse-mesh) model and, thus is free from the LES limitation that would have imposed a usually excessive requirement on the fine mesh size. Instead, it proposes to simulate (i.e. without turbulence models) the sub-grid instabilities in a fine mesh, and to re-insert their effect into the coarse mesh solution in a computationally efficient way.

The problem to face when developing numerical multi-scale approaches of practical value is that the fine-scale field $\varphi^{\prime}$ is generally non-local, except in one-dimensional problems, thus making it impossible to isolate a subdomain for an independent study. This is the main source of error of any multi-scale method and the accuracy of the solution will depend on how this aspect is addressed. In some problems, particularly those where the fine-scale solution is used to enrich the global solution, a direct approximation of $\varphi^{\prime}$ is generally used on the boundaries of each isolated subdomain through the Dirichlet boundary conditions (local solution). In other cases, for example when the goal is to incorporate disturbances on the mean solution, normally continuity conditions between subdomains may be employed, that is, Neumann-type or periodicity boundary conditions between subdomains (non-local solutions) for $\varphi^{\prime}$.

Finally, it is worth mentioning that although the P-DNS method arose as another way to solve turbulent homogeneous fluid flows, it was later generalized to solve convection-diffusion problems, which share with the first the property of not requiring stabilization or sufficiently fine meshes. for stable and accurate results. Convection-diffusion-reaction and convection-diffusion-absorption problems were also included in the scope of P-DNS [55].

More recently, the P-DNS method was extended to simulate turbulent particle-laden flows. In this case, P-DNS provides a solution to two very different problems, namely, the modulation of turbulence due to the presence of particles within the fluid, and the treatment of the mixture as a homogenized fluid using multi-scale techniques to obtain the homogenization parameters [56, 57].

The two sections that follow present an overview of the P-DNS methodology in two different contexts. Section 2 presents P-DNS as applied to homogeneous incompressible laminar and turbulent fluid flows. Special emphasis is placed on presenting both the so called internal and wall RVEs, suitable for representing the fine scale contribution in the bulk flow and inside boundary layers, respectively. Present challenges and possible solutions related to building an improved wall RVE suitable for developing boundary layers will also be briefly presented. Section 3, meanwhile, is devoted to the application of P-DNS to particle-laden fluid flows. The description of P-DNS for problems of transport of scalar quantities has been left out of this overview, and the reader is invited to consult [54, 55] for details.

2 The P-DNS Method for Turbulent Homogeneous Incompressible Fluid Flows

2.1 The Governing Equations

For homogeneous incompressible fluid flows, the N–S equations may be written as

$$\begin{aligned} \rho {A_{i}} = \frac{\partial {T_{ij}}}{\partial {x_{j}}}-\frac{\partial {p}}{\partial {x_{i}}} + {B_{i}}\end{aligned}$$

(1)

and

$$\begin{aligned} \frac{\partial u_{i}}{\partial x_i} = 0 \end{aligned}$$

(2)

for expressing momentum and mass conservation, where $u_{i}$ is the i-component of the velocity vector, p is the pressure and

$$\begin{aligned} T_{ij} = \mu \left( \frac{\partial u_{i}}{\partial x_j} + \frac{\partial u_j}{\partial x_i}\right) \end{aligned}$$

(3)

is the constitutive law for the viscous stresses tensor $T_{ij},\;\mu$ and $\rho$ the dynamic viscosity and the density of the fluid, $B_{i}$ a body force, and $A_{i}$ the acceleration, which will be written in an Arbitrary Lagrangian/Eulerian (ALE) form as

$$\begin{aligned} A_i = \frac{D^{\textbf{U}}u_{i}}{Dt} + (u_j-U_j)\frac{\partial u_{i}}{\partial x_j}, \end{aligned}$$

(4)

where the derivative $\frac{D^{\textbf{U}}u_{i}}{Dt}$ must be interpreted as the ALE time derivative with respect to a reference frame moving at velocity ${\textbf{U}},$ with

$$\begin{aligned} \begin{array}{l} \frac{D^{{\textbf{U}}} u_{i} }{D t}=\frac{\partial u_{i} }{\partial t}+U_j\frac{\partial u_{i} }{\partial x_j}. \end{array} \end{aligned}$$

(5)

2.2 Splitting of the Unknown Fields

As in all multi-scale approaches, the unknown fields are split into coarse and fine scale parts

$$\begin{aligned} u_{i} = {u^{c}_{i}} + {u^{f}_{i}}; \quad p = p^c + p^f, \end{aligned}$$

(6)

where ${u^{c}_{i}}$ and $p^c$ are the fields associated to a coarse mesh, and all subgrid effects are linked to ${u^{f}_{i}}$ and $p^f$.

A standard criteria in P-DNS is to consider that the coarse scale corresponds to a piecewise linear approximation in space via FEM or FVM procedures and that the fine scale comprises all higher order contributions.

After the splitting, the N–S equations read

$$\begin{aligned} \begin{array}{lll} \rho \left[ \frac{D^{\mathbf{u^{c}}} {{u^{c}_{i}}}}{D t} + {u^f_{j}} \frac{\partial u^{c}_{i}}{\partial x_j} \right] - \frac{\partial T^c_{ij}}{\partial x_j}+ \frac{\partial p^c}{\partial x_{i}}- B_{i}\\ + \rho \left[ \frac{D^{\mathbf{u^{c}}} {{u^{f}_{i}}}}{D t} + {{u^{f}_{j}}} \frac{\partial {u^{f}_{i}}}{\partial {x_{j}}} \right] - \frac{\partial T^f_{ij}}{\partial x_{j}}+ \frac{\partial p^{f}}{\partial x_{i}}=0 \end{array} \end{aligned}$$

(7)

where

$$\begin{aligned} \begin{array}{c} T^c_{ij} = \mu \left( \frac{\partial {u^{c}_{i}}}{\partial x_j} + \frac{\partial {u^c_{j}}}{\partial x_i}\right) \\ T^f_{ij} = \mu \left( \frac{\partial {u^{f}_{i}}}{\partial x_j} + \frac{\partial {u^{f}_{j}}}{\partial x_i}\right) \end{array} \end{aligned}$$

(8)

are the coarse and fine viscous shear stress tensors, respectively, and where it has been considered that the ALE reference frame moves at the coarse velocity $\mathbf {u^c}.$ Equation (7) is termed the “Lagrangian minus” version of the N–S equations, because a “fully Lagrangian” approach would require the frame to move with the full velocity field ${\textbf{u}}$ instead of $\mathbf{u^c}$.

In order to consider another approach, however, the term $\frac{D^{\mathbf {u^c}} {u^{c}_{i}} }{D t}$ may be transformed into $\frac{D^{\mathbf {u^c}} {u^{c}_{i}} }{D t} = \frac{\partial {u^{c}_{i}}}{\partial t}+ {u^c_{j}} \frac{\partial {u^c_{i}}}{\partial x_j}$, leading to what has been called “Eulerian plus” version of the momentum equations, namely

$$\begin{aligned} \begin{array}{lll} \rho \left[ \frac{\partial {u^c_{i}}}{\partial t}+ {u^c_{j}} \frac{\partial {u^c_{i}}}{\partial x_j} + {u^{f}_{j}} \frac{\partial {u^c_{i}}}{\partial x_j} \right] - \frac{\partial T^c_{ij}}{\partial x_j}+ \frac{\partial p^c}{\partial x_i}- B_i \\ + \rho \left[ \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^{f}_{i}}}{\partial x_j} \right] - \frac{\partial T^f_{ij}}{\partial x_j}+ \frac{\partial p^f}{\partial x_i}=0 \end{array} \end{aligned}$$

(9)

This is not termed “fully Eulerian” because the convection of the fine instabilities due to the coarse velocity field has been written in Lagrangian form.

Finally, the splitting of the mass conservation equation simply reads

$$\begin{aligned} \begin{array}{lll} \frac{\partial {u^c_{i}}}{\partial x_i}+\frac{\partial {u^{f}_{i}}}{\partial x_i}=0. \end{array} \end{aligned}$$

(10)

2.3 Weighted Residual Form for the Coarse Scale

The weighted residual form of Eq. (7) for the coarse scale is written as

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} N^{c,l} \Big \{ \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^c_{i}}}{\partial x_j} \right] - \frac{\partial T^c_{ij}}{\partial x_j}+ \frac{\partial p^c}{\partial x_i}- B_i \\ + \underbrace{ \rho \left[ \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^{f}_{i}}}{\partial x_j} \right] - \frac{\partial T^f_{ij}}{\partial x_j}+ \frac{\partial p^f}{\partial x_i} }_{\text {from DB (off-line)}} \Big \} d\Omega = 0. \\ \end{array} \end{aligned}$$

(11)

where $\Omega^l$ is the integration domain of node l, or in other terms the support of the standard FEM or FVM weighting functions $N^{c,l}$ associated to the coarse mesh, for instance piecewise linear weighting functions within each element for FEM, or constant and equal to 1 within each cell for FVM. The terms indicated by the underbrace are expected to be provided by the results of the off-line simulations stored in the RVE database.

Integrating by parts some terms of the previous equation leads to the weak form of the variational expression, which reads

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^c_{i}}}{\partial x_j} - B_i \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Omega +\cdots \\ \int_{\Gamma^l} N^{c,l} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Gamma_j+\cdots \\ \int_{\Omega^l} N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^{f}_{i}}}{\partial x_j} \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^f_{ij} - p^f{\delta_{ij}} \right) d\Omega +\cdots \\ \int_{\Gamma^l} N^{c,l} \left( T^f_{ij} - p^f{\delta_{ij}} \right) d\Gamma_j=0 \\ \end{array} \end{aligned}$$

(12)

where $\Gamma^l$ is the boundary of the nodal domain $\Omega^l$.

In the case of FEM, and limiting the study to linear weighting functions, the momentum equation results in

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^c_{i}}}{\partial x_j} - B_i \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Omega +\cdots \\ \int_{\Omega^l} N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^{f}_{i}}}{\partial x_j} \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^f_{ij} - p^f{\delta_{ij}} \right) d\Omega =0.\\ \end{array} \end{aligned}$$

(13)

As for the FVM version, with constant weighting functions, it reads

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^c_{i}}}{\partial x_j} - B_i \right] d\Omega - \cdots \\ \int_{\Gamma^l} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Gamma_j+\cdots \\ \int_{\Omega^l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} + {u^{f}_{j}} \frac{\partial {u^{f}_{i}}}{\partial x_j} \right] d\Omega - \cdots \\ \int_{\Gamma^l} \left( T^f_{ij} - p^f{\delta_{ij}} \right) d\Gamma_j=0. \end{array} \end{aligned}$$

(14)

2.4 Constrains to be Imposed to the Unknown Fields

In the following, some constrains are applied to the unknown fields, in preparation for the introduction of the internal RVEs, leaving the treatment of wall RVEs for a later section.

Recalling that the full solution of the problem is the sum of its coarse and its fine counterparts, and that this splitting is so far arbitrary, P-DNS assigns the translational and rotational aspects of ${\textbf{u}}$ solely to the coarse field ${\textbf{u}}^c$, which results in a fine field which has null mean value and null mean gradient inside $\Omega^l$. Introducing similar considerations for the pressure field p, it is possible to write the following constrains of the fine fields

$$\begin{aligned} \int_{\Omega^l} {u^{f}_{i}} d\Omega &= \int_{\Omega^l} p^fd\Omega =0;\\ \int_{\Omega^l} \frac{\partial {u^{f}_{i}}}{\partial x_j} d\Omega& = \int_{\Omega^l} \frac{\partial p^f}{\partial x_j} d\Omega =0\end{aligned}$$

(15)

Note that the constrains applied to the gradients of the fields may be rewritten as

$$\int_{\Omega^l} \frac{\partial {u^{f}_{i}}}{\partial x_j} d\Omega = \int_{\Gamma^l} {u^{f}_{i}} d\Gamma_j=0$$

(16)

and

$$\int_{\Omega^l} \frac{\partial p^f}{\partial x_j} d\Omega = \int_{\Gamma^l} p^fd\Gamma_j=0$$

(17)

which represent what P-DNS considers “weak periodic” boundary conditions. As will be explained later, strongly periodic conditions will in fact be imposed when simulating the fine fields, meaning that they are fulfilled for each pair of homologous points of opposite faces of the RVE, and not only on average. This strong periodicity is even more restrictive than the mentioned weak periodicity, therefore limiting even further the possibilities of variation of the velocity and pressure fields.

Furthermore, as an additional constrain, P-DNS considers both parts of the velocity field, i.e. both ${u^c_{i}}$ and ${u^{f}_{i}},$ to be incompressible, meaning that

$$\begin{aligned} \frac{\partial {u^c_{i}}}{\partial x_i}=\frac{\partial {u^{f}_{i}}}{\partial x_i}=0 \end{aligned}$$

(18)

Also, recalling that $\Omega^l$ has been defined as the domain associated to a generic coarse mesh node l, it is possible to assign to it a coarse velocity gradient $G^l_{ij}$ computed as the average of the gradients $G^e_{ij}$ of the elements sharing node l in the case of FEM or any desired interpolation scheme for computing a velocity gradient of cell l in the case of FVM.

Introducing all these constrains into the momentum equations, and approximating the gradient $\frac{\partial {u^c_{i}}}{\partial x_j}$ of the coarse field by the average gradient $G^l_{ij}$, it is possible to write, for FEM

$$\begin{aligned}&\int_{\Omega^l} N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} - B_i \right] d\Omega \\ &+ \cdots \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Omega \\ &+\cdots \int_{\Omega^l} N^{c,l} \rho \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} d\Omega \\ &+ \cdots \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( {u^{f}_{j}} \rho {u^{f}_{i}} \right) d\Omega =0 \end{aligned}$$

(19)

and for FVM

$$\begin{aligned}&\int_{\Omega^l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} - B_i \right] d\Omega \\ & - \cdots \int_{\Gamma^l} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Gamma_j\\ &+\cdots \int_{\Omega^l} \rho \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} d\Omega\\ & - \cdots \int_{\Gamma^l} \left( {u^{f}_{j}} \rho {u^{f}_{i}} \right) d\Gamma_j=0 \end{aligned}$$

(20)

As a last step, and to allow for the decoupling of the fine solution opening the possibility of off-line computations in separate independent subdomains (i.e. RVEs), P-DNS proposes to neglect the term $\int_{\Omega^l} \rho \frac{D^{\mathbf {u^c}} {u^{f}_{i}} }{D t} d\Omega$, an approximation whose validity has yet to be shown by the numerical results, which are presented in the next sections.

Finally, the coarse momentum equation to be solved is, for FEM

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} - B_i \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij} -T^\rho_{ij}- p^c{\delta_{ij}} \right) d\Omega =0 \end{array} \end{aligned}$$

(21)

and for FVM

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} - B_i \right] d\Omega - \cdots \\ \int_{\Gamma^l} \left( T^c_{ij} -T^\rho_{ij}- p^c{\delta_{ij}} \right) d\Gamma_j=0 \end{array} \end{aligned}$$

(22)

where

$$\begin{aligned} {T^{\rho }_{ij}} = \rho {u^{f}_{i}} {u^{f}_{j}} \end{aligned}$$

(23)

is named “inertial stress tensor”, being the only remaining contribution from the fine scale to the coarse one.

It must be noticed that, as P-DNS considers the fine fields as being convected by the coarse velocity field, the same applies for the inertial stress tensor (please see [58] for details).

2.5 The Coarse Scale Equations with Averaged Fine Scale Unknowns

The coarse scale solution requires solving the coarse scale equations, which from this point of view are not more than modified N–S equations that account for the effect of the fine scale solution through the added fine scale terms. In general, in every multi-scale solution, it is not necessary to obtain the instantaneous point-to-point solution of the fine scale. What is really needed, from an engineering point of view, is the overall effect of the fine scales space-averaged in spatial scales of the order of the local coarse mesh size. Therefore, P-DNS proposes to replace the instantaneous local inertial stress tensor by an averaged tensor defined in each $\Omega^l$ as

$$\begin{aligned} \widehat{T^{\rho }_{ij}}= \frac{1}{\Omega^l} \int_{\Omega^l} \left( \rho {u^{f}_{i}} {u^{f}_{j}} \right) d\Omega . \end{aligned}$$

(24)

Although this proposition may of course, in general, introduce approximation errors, this is not the case in the scope of P-DNS, for reasons that are different depending on the choice between FEM and FVM aproaches.

For the FEM, with linear weighting functions, $\frac{\partial N^{c,l}}{\partial x_j}$ is constant within each element included in $\Omega^l$, thus allowing us to perform this replacement within each element without incurring in approximations. The resulting equations to be solved at the coarse level mesh are then

$$\begin{aligned} \begin{array}{l} \int_{\Omega } N^{c,l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} - B_i \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij} -\widehat{T^\rho_{ij}}- p^c{\delta_{ij}} \right) d\Omega =0 \\ \int_{\Omega^l} \frac{\partial {u^c_{i}}}{\partial x_i} d\Omega =0. \end{array} \end{aligned}$$

(25)

For the case of FVM, being $N^{c,l}$ constant and equal to 1 inside $\Omega^l$, it is even easier to see that the proposed replacement does not imply any approximation. The resulting coarse scale equations are in this case

$$\begin{aligned} \begin{array}{l} \int_{\Omega^l} \rho \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t} - B_i \right] d\Omega + \cdots \\ \int_{\Gamma^l} \left( T^c_{ij} -\widehat{T^\rho_{ij}}- p^c{\delta_{ij}} \right) d\Gamma_j=0 \\ \int_{\Gamma^l} {u^c_{j}} d\Gamma_j =0 \end{array} \end{aligned}$$

(26)

2.6 The Representative Volume Elements

The next step in the P-DNS process, however, does introduce an approximation. It consists on calculating the average of $T^\rho_{ij}$ not over $\Omega^l$, but over a cubic volume of dimensions larger than those of the coarse scale grid. i.e. over the RVE. In P-DNS, then, $\widehat{T^\rho_{ij}}$ is approximated as

$$\begin{aligned} \widehat{T^{\rho }_{ij}}= \frac{1}{\Omega^l} \int_{\Omega^l} \left( \rho {u^{f}_{i}} {u^{f}_{j}}\right) d\Omega \approx \frac{1}{\Omega^R} \int_{\Omega^R} \left( \rho {u^{f}_{i}} {u^{f}_{j}} \right) d\Omega \end{aligned}$$

(27)

where $\Omega^R$ is the volume of a RVE.

Regarding the size of the RVE, it must be large enough so as to include all the wavelengths not captured by the coarse mesh but at the same time small enough so as to limit the error introduced by the spatial averaging. Although P-DNS does not propose a strict mathematical definition of the optimal size of an RVE associated to a given spatial location in the global domain, its dimension should be between the local size of the coarse mesh up to twice its value. This relationship between RVE size and local coarse mesh size has already been conceptually depicted in Fig. 1.

As for the shape of the RVE, since in the P-DNS method the information about the fine scales required by each element or cell of the coarse mesh has been reduced to constant values, due to the already described averaging process, simple geometric shapes are sought for RVEs, such as cubes or cuboids. This makes them independent of the coarse mesh topology and facilitates the implementation of periodic or jump-periodic boundary conditions, which are required for the P-DNS formulation of the off-line fine scale problems.

2.7 Solving the Fine Problem

Solving the fine problem means finding a way of computing the value of the approximated inertial stress tensor defined in Eq. (27) whenever and wherever it is required during the solution of the coarse scale equations. P-DNS tackles this problem by (i) computing off-line equilibrium stresses and storing them in dimensionless databases, and (ii) dealing with non-equilibrium stresses via a memory model. The task of computing the equilibrium databases is also split in two steps, one aimed at computing inertial stresses to be used on the coarse problem bulk flow, namely the internal RVE database, and another one intended to deal with the coarse problem boundary layers, namely the wall RVE database. Both types of databases and the associated memory model are detailed in the following sections.

2.7.1 The Equilibrium Internal RVE

Let us turn first our attention to the development of an internal RVE, i.e. one aimed at modeling turbulence in the bulk flow, and its associated dimensionless database.

In P-DNS, RVEs are simple domains, i.e. cubes or cuboids, in which simulations of the standard N-S equations subject to simple boundary conditions are carried out in meshes fine enough so as to qualify as DNS solutions. As it will be explained later, these boundary conditions reduce to an applied velocity gradient, and in some special cases might include an applied pressure gradient.

Simple boundary conditions are a key feature of the P-DNS RVEs, and they are termed simple in the sense that they are able to be completely defined using a reduced set of parameters, such as the value of a velocity gradient and/or that of a pressure gradient. This is not a requirement of the fine problem itself, but a requirement of the form in which the RVE results, i.e. the RVE database, will be used when solving the global, or coarse, problem. The RVEs boundary conditions must be defined using parameters able to be computed during the solution of the global problem with local instantaneous information available at any given position of the global domain and at any given time step.

Moreover, for the RVE database to be computable off-line and to be ready for its use on any future global problem, it is required that both the definition of the RVE problem and the storage of the relevant information obtained from its DNS simulation are carried out in dimensionless form [53], as explained below.

2.7.2 The Equilibrium Internal RVE Dimensionless Database

Let $G_{ij}$ be a velocity gradient tensor. It can be written in a dimensionless form as

$$\begin{aligned} \begin{array}{l} Id_{ij}=\frac{G_{ij}H^{2}\rho }{\mu } \end{array} \end{aligned}$$

(28)

where $Id_{ij}$ is to be considered as an instability index tensor, with H a characteristic length. On one hand, from the global problem point of view, this index may be computed at any given position and at any time step using the available coarse field velocity, the properties of the global fluid problem, and some estimation of the local coarse mesh size. On the other hand, from the RVE point of view, it may be computed using the values of the velocity shear applied in the DNS simulation, the properties of the RVE problem fluid, and a length representative of the RVE size. It should be noted that this index tensor has a unique value for each individual RVE simulation, independent of space and time, as the results to be stored in the database are time-averaged equilibrium conditions also space averaged over the RVE domain.

The instability index tensor $Id_{ij}$ is intended to be computed whenever and wherever required in the coarse problem solution process and used as an input parameter to the RVE database. However, P-DNS does not make use of the full coarse velocity gradient tensor to this end. It is well known that shear is one of the main sources of flow instabilities, e.g. those of Kelvin-Helmholtz type. Although some flow instabilities are commonly associated to other sources, like for example the buoyancy-driven type, it should be noted that, even when the larger scales are clearly promoted by density differences, the rest of the scales (which P-DNS aims to model) are mostly related with the larger shear scales. Due to this, and to eliminate the rigid body rotations which do not introduce instabilities, $Id_{ij}$ will be computed using only the symmetrical component

$$\begin{aligned} {G^{s}_{ij}} = \frac{1}{2}\left[ \frac{\partial {u^{c}_{i}}}{\partial x_{j}}+\frac{\partial {u^{c}_{j}}}{\partial x_{i}}\right] \end{aligned}$$

(29)

of the coarse velocity gradient tensor. Furthermore, as it is shown in Appendix 1, with the appropriate tensor rotations and by taking advantage of the incompressibility restriction of the coarse velocity field, the nine components of $Id_{ij}$ may be reduced to only two dimensionless parameters, namely $Id_{1}$ and $Id_{2}$.

Now, from the point of view of an RVE, a given pair of $Id_{1}$ and $Id_{2}$ values correspond to a DNS simulation of a problem with a given shear applied as jump-periodic velocity boundary conditions between, say, the top and bottom faces of the cube or cuboid, and a different shear applied to, say, the left and right faces. This problem is simulated until a statistically steady “equilibrium” state is reached, which means that the inertial stress tensor ${\widehat{T}}^{\rho }_{ij}$ reaches a constant value ${\overline{T}}^{\rho }_{ij}$.

Before storing these equilibrium stresses in the database, they must be put in dimensionless form, using fluid properties and a characteristic length pertaining to the corresponding RVE simulation. In this case, it is defined as

$$\begin{aligned} \begin{array}{l} \widetilde{{\overline{T}}^{\rho }_{ij}} = \frac{{\overline{T}}^{\rho }_{ij}H^{2}\rho }{\mu^{2}}. \end{array} \end{aligned}$$

(30)

This dimensionless equilibrium inertial stress tensor is stored as an output value in the database, associated to the corresponding dimensionless input parameters $Id_{1}$ and $Id_{2}$.

It is worth mentioning here that, as already been said, this is an equilibrium database. The coarse problem, however, would certainly require to deal with inertial stresses that are not necessarily in equilibrium with the local instantaneous coarse velocity gradient. Tackling this problem requires an involved process, which P-DNS refers to as a memory model, which will be detailed later.

2.7.3 Simulating an Internal RVE

A RVE must be a three-dimensional (3D) domain, because turbulent flow instabilities appear in all three spatial directions even under two-dimensional applied shear forces. P-DNS proposes to represent a RVE by a cube of side length H, see Fig. 2.

Fig. 2

Sketch of the internal RVE

In the following, the coordinate system $\{x^R_i,i=1,3\}$ is considered local to the RVE, with origin in the geometrical center of the RVE. The unknown velocity and pressure fields inside the RVE will be denoted as $u^R_i$ and $p^R$, respectively. The RVE fields are split as

$$\begin{aligned} \begin{array}{l} u^R_i=G^R_{ij} x^R_j+{u^{f}_{i}} \\ \end{array} \end{aligned}$$

(31)

and

$$\begin{aligned} \begin{array}{l} p^R=\Pi^R_i x^R_i +p^f\\ \end{array} \end{aligned}$$

(32)

where $G^R_{ij}$ is a particular symmetrical velocity gradient with null main diagonal, and $\Pi^R_i$ is a pressure gradient. The velocity gradient $G^R_{ij}$ is associated to its dimensionless counterpart $Id_{ij}$ through Eq. (28). As for the pressure gradient, it is considered null for internal RVEs.

The weighted residual equation to be solved in an RVE for obtaining the fine scale solution is, for FEM

$$\begin{aligned} \begin{array}{l} \int_{\Omega^R} N^{f,l} \rho \left[ \frac{\partial u^R_i }{\partial t} + u^R_j \frac{\partial u^R_i}{\partial x_j} - B_i \right] d\Omega + \cdots \\ \int_{\Omega^R} \frac{\partial N^{f,l}}{\partial x_j} \left( T^R_{ij} - p^R{\delta_{ij}} \right) d\Omega =0 \\ \int_{\Omega^R} N^{f,l} \frac{\partial u^R_i}{\partial x_j} d\Omega =0 \end{array} \end{aligned}$$

(33)

and for FVM

$$\begin{aligned} \begin{array}{l} \int_{\Omega^R} \rho \left[ \frac{\partial u^R_i }{\partial t} + u^R_j \frac{\partial u^R_i}{\partial x_j} - B_i \right] d\Omega + \cdots \\ \int_{\Gamma^R} \left( T^R_{ij} - p^R{\delta_{ij}} \right) d\Gamma_j =0 \\ \int_{\Gamma^R} u^R_j d\Gamma_j =0 \end{array} \end{aligned}$$

(34)

Both forms represent solving the transient incompressible N-S equations in an Eulerian frame (i.e. the RVE frame). They are to be solved in a DNS mesh, which means simulating all the scales down to the smallest waves, or Kolmogorov scale. For this reason, its resolution does not require any convection stability scheme, and only incompressibility stability schemes should be taken into account.

As for the boundary conditions, they certainly cannot be of the Dirichlet type, as a strong imposition like that eliminates a large part of the possible instabilities. Therefore, less restrictive boundary conditions such as that of periodic nature are used. However, as they would obviously prevent the formation of waves of length 2H. Waves of this and larger lengths would be expected to be solved by the coarse problem. For this reason, and from the coarse problem point of view, the RVE must be seen as a domain that covers twice the local mesh size, as conceptually shown in Fig. 1. Due to this, RVEs associated to neighboring elements or cells may certainly overlap.

The physical problem to be solved in a RVE is then completely defined by a side length H, fluid properties $\rho$ and μ, an applied shear velocity $G^R_{ij}$. The shear velocity is imposed as jump periodic conditions between opposite faces of the cube. The magnitude of the jump is computed as $G^R_{ij} n_j$, being $n_j$ the unit normal to the corresponding face. The null pressure gradient is simply imposed as regular periodic conditions between opposite faces.

At the RVE level, the standard N-S equations are solved until reaching an equilibrium state, meaning that the moving average of the spatial mean of all inertial stresses reach steady values. The dimensionless counterparts of these steady values are stored as output parameters in the database for later use, associated to the correspondent input parameters $Id_{1}$ and $Id_{2}$ (see typical results in Fig. 3).

Fig. 3

Database for the six-components of the fine-scale inertial stress tensor for an internal RVE. Data available in [59]

2.8 Dealing with Boundary Layers: An Equilibrium Wall RVE

Internal RVEs are adequate for modeling zones of the flow in which both (i) the coarse solution varies almost linearly, and (ii) the inertial stresses are almost uniform, in a region of a size comparable with the RVE size H. None of these assumptions hold in boundary layers, i.e. near solid walls. To deal with these regions of the coarse flow problem a special type of inertial stresses database is required, intended to be used for computing the coarse solution in the first layer of coarse cells in solid boundaries.

The first attempt of P-DNS for dealing with this problem is the so-called wall RVE database, that relies on a DNS simulation of a null-pressure gradient developed turbulent flow fluid between two horizontal parallel plates, namely lower and upper, separated by a distance 2H and moving in opposite directions, at velocities $(-U,0,0)$ and (U, 0, 0), respectively ( Fig. 4). The boundary conditions are those typical of solid walls on the lower and upper plates, i.e. imposed velocity and null normal pressure gradient, and periodic between the other two pairs of faces. The simulation is performed over a domain of size $H \times H \times 2H$, while the averaging of the inertial stress tensor is carried out in the lower half of the domain. The upper half, meanwhile, is just an artifact for imposing adequate conditions on the top face of the RVE, and it is not intended to represent a physically correct flow between parallel plates. The velocity of the plates is fixed, inducing a purely 2D shear, leading to a 3D fine problem characterized by only one instability index Id associated to the applied velocity gradient $G_{xz}=U/H.$

Fig. 4

Sketch of the wall RVE

As in the internal RVE, the standard N-S equations are solved until reaching an “equilibrium state”, in which, taking a sufficiently large time window, the spatial-temporal average of all inertial stresses reaches a steady value. The dimensionless values of this equilibrium tensor is stored as output in the database for later use, associated to a single dimensionless instability index Id.

From the point of view of the coarse problem, this database is accessed when required from cells or elements in contact with solid walls. It is assumed that in those cells the coarse velocity will be almost parallel to the wall. In any given wall cell it is then possible to compute a single valued local coarse velocity gradient $G_{ns}$, where n stands for the direction normal to the wall and s for the local streamline direction. With this gradient it is possible to compute the local instability index Id with which to access the wall RVE database to recover the dimensionless inertial stresses required by the coarse equations of this particular cell.

Before describing how P-DNS deals with non-equilibrium conditions in the next section, we highlight that a more involved treatment of boundary layers will be presented in a later section.

2.9 Dealing with Out-of-Equilibrium RVEs: A Data-Driven Memory Model

In a previous section it was said that P-DNS aims at solving the coarse problem as the flow of a pseudo-fluid with properties related to the fine instabilities. Considering that, for P-DNS, a RVE is a portion of pseudo-fluid convected by the coarse velocity field, it may be assimilated to a virtual particle located at its center, which is responsible for storing and carrying the instabilities. As mentioned above, adopting a Lagrangian formulation allows for accurately and naturally convecting and spreading the instabilities, even using a coarse mesh. Good resolution may be obtained by using either the first [60, 61] or the second generation of the particle finite element method (PFEM-2) [62,63,64,65,66] or its finite volume version, called particle finite volume method (PFVM) [67]. The readers are referred to these publications for further details on these technologies.

It was also said that the inertial stresses stored in the databases correspond to equilibrium conditions, considered as functions of state $\widetilde{{\overline{T}}^{\rho }_{ij}} \left( Id_{1},Id_{2} \right)$ of two (or one in wall RVEs) instability indices. These stresses are however not enough to fully capture the complex rheological behavior of the pseudo-fluid, as its properties depend not only on the local present conditions on a given location of the coarse problem, but on the history of strain rates experienced by the pseudo-material, which may be costly tracked and stored in databases.

The aforementioned difficulty may be approached by using techniques from the memory fluids discipline. In [53], the authors propose a first approach to tackle this problem by means of a simplified algorithm, approximating the stress $\widetilde{T^{\rho }_{ij}}^{n+1}$ of a given RVE at time $t_{n+1}= t_n+\Delta t$ as a weighted average between: (i) the equilibrium stress $\widetilde{{\overline{T}}^{\rho }_{ij}}^{n+1}$ for the coarse conditions prevailing at the present RVE position, and (ii) the past RVE stress $\widetilde{T^{\rho }}_{ij}^{n}$. This is expressed as

$$\begin{aligned} \begin{array}{l} \widetilde{T^{\rho }_{ij}}^{n+1} = m \widetilde{T^{\rho }_{ij}}^{n} + (1-m) \widetilde{{\overline{T}}^{\rho }_{ij}}^{n+1} \end{array} \end{aligned}$$

(35)

where the weighting factor m is a memory factor defined as

$$\begin{aligned} m = e^{-\frac{\Delta t}{\tau }} \end{aligned}$$

(36)

where $\tau$ may be thought of as a relaxation time (measuring how long it takes for an RVE to forget its past). The larger the value of $\tau$, the greater the dependence of the current state on the previous state of the RVE.

In [53] $\tau$ was assumed to be a user-defined constant, but in [58] the authors introduce a somehow automatic and more precise technique to define $\tau$, a brief description of which follows.

The technique relies on the results of hundreds of off-line simulations of internal RVEs initially in equilibrium with a given imposed 2D strain, i.e. one in which $Id_{1}\ne 0$ and $Id_{2}=0$. RVEs in equilibrium with a given $Id_{1}=\text {Id}^A$ where subject to sudden changes of the applied shear leading to a different $Id_{1}=\text {Id}^B$. Figure 5 shows an example for the transition from $\text {Id}^A=400$ to $\text {Id}^B=200$, with the evolution of dimensional kinetic energy versus dimensional time t[s].

Fig. 5

A set of 100 RVE simulations with Id=400 for $t<0$ to Id=200 when $t \ge 0$. Realizations (dark lines) and ensemble averaging (thick white line) of total kinetic energy K(t)

By studying different transitions for several pairs $(Id^A,Id^B)$ of applied shears, in the range $\text {Id}=200$ to $\text {Id}=600$, the authors found that the internal RVEs behave as a dynamical system with a relaxation time of the order of the inverse of the mean applied shear, that is

$$\begin{aligned} \tau = C_\tau / \left( \frac{G^B+G^A}{2}\right) \end{aligned}$$

(37)

for all sudden transitions, no matter the size or direction of the jump, with $C_\tau \simeq 1$.

Tests of this proposed relaxation time in decaying turbulence problems soon revealed that the model required a more sophisticated approach. The main reason is the fact that, during the update of the state of particles/RVEs in each time step of the coarse problem, the initial state A is no necessarily in equilibrium with the local $\text {Id}^A$, thus rendering the applied velocity gradient $G^A$ as not adequate to be used in estimating the corresponding $\tau$.

The revised version of the memory model, as published in [58], proposes a more involved computation of the relaxation time, which is expressed as

$$\begin{aligned} \tau = C_\tau / \left( \frac{G^B+W_\tau (\beta ) \breve{G}^A}{2}\right) \end{aligned}$$

(38)

where $\breve{G}^A$ is an applied shear consistent with the actual initial stress state of the RVE, information which is obtainable from the database. Here,

$$\begin{aligned} \beta =\frac{\mid \breve{G}^A-G^B\mid }{\mid \breve{G}^A\mid +\mid G^B\mid } \end{aligned}$$

(39)

measures the relative magnitude of the jump, with $\beta$ approaching 0 for small jumps and 1 for large jumps, and is used as indication of how far is the RVE from equilibrium. The weighting factor $W_\tau (\beta )$ is introduced to control how much of the past information (i.e. $\breve{G}^A$) is used in actually computing the relaxation time. In the present model, it is defined as

$$\begin{aligned} W_\tau = C_{1} \beta^3 + C_{2} (1-\beta^3) \end{aligned}$$

(40)

where $C_{1}=6.8$ and $C_{2}=4.0$ are coefficients calibrated by adjusting the P-DNS results of a decaying homogeneous isotropic turbulence problem.

The memory model presented in [58] also incorporates a low Re correction, to account for the fact that in decaying turbulence it appears to be a constant relaxation time $\tau$ during the final period of decay. To mimic this behavior, $\breve{G}_A$ is freezed for low enough perturbation Reynolds, i.e. for $Re<=Re^*$. This value is chosen to be $Re^*=15$ (Tennekes and Lumley [68] suggest taking $Re^*$ of the order of 10).

2.10 Examples of Applications of P-DNS for Turbulent Fluid Flows

Next, a series of examples taken from references [53, 58] will be provided to demonstrate the effectiveness of the P-DNS method. The specific situation of developing boundary layers will be addressed in subsequent sections.

The cases of a Couette and Poiseuille flow are presented first to demonstrate that with the P-DNS technology, good results can be achieved with a small number of elements close to the walls. The case of mixing layers is then presented to illustrate the results for different mesh refinements and to demonstrate that P-DNS can obtain good results with coarser meshes than other methods, such as LES, require.

A case typically used to show the performance of any approximation of turbulence is that of decaying turbulence. In the examples shown in Ref [58], it can be seen that in P-DNS there is no strict limit on the split between the coarse mesh and the fine mesh. Acceptable results are obtained with very different partitions, something that other methods, such as LES, cannot do.

The backward-facing step and the flow around a square cylinder are already less academic examples than the previous ones. Despite the fact that in the former there is a developing boundary layer downstream that has not yet been considered, the results show excellent agreement between the stream-wise velocities, shear Reynolds stresses, and averaged friction and pressure coefficients. In all cases, there was no need for excessive mesh refinement near the domain walls or objects.

Finally, the Taylor–Green vortex (TGV) problem is a benchmark that allows for evaluating the ability of a simulation methodology to predict key physical processes such as vortex dynamics, turbulent transition, turbulent decay, and energy dissipation processes.

The standard notation $\langle \cdot \rangle$ is used from here on to denote time-averaged values. In addition, hereinafter, LES refers to the dynamic k-Equation Subgrid-Scale (DKSGS) LES method proposed by Kim and Menon [69]. This method employs an equation for the transport of the subgrid kinetic energy (k), enabling it to account for some non-local and history effects that are completely neglected by simpler algebraic LES models.

2.10.1 Poiseuille and Couette Flows

Consider two one-dimensional coarse meshes with only four and three finite volume 1D cells, respectively. With this mesh, the RVEs must resolve all the unsteadiness of the flow. The objective is to obtain the averaged incompressible flow field by solving the steady-state Navier-Stokes equations with a modified stress tensor from the RVE databases. Note that this test involves the coupling of the distinct treatment for the near-wall cells with the treatment for the internal cells.

Two classical flows between plates are solved: one driven by a pressure difference (Poiseuille flow) and the other by pure shear due to the movement of the walls (Couette flow).

Above a certain Reynolds number, it is well known that these flows become turbulent, resulting in average velocity profiles that are very different from those corresponding to the laminar cases, i.e. parabolic for Poiseuille and linear for Couette. Both problems result in turbulent regimes under the conditions and dimensions specified in Table 1.

Table 1 Setup of the one-dimensional tests

Figure 6 compares the results obtained by solving the problems using three different strategies: (1) using the coarse mesh without modeling non-captured scales (unresolved DNS, u-DNS); (2) using the coarse mesh while modeling the non-captured scales with the presented databases (P-DNS); and (3) using standard 3D DNS in a fine mesh capable of capturing all instability scales. In addition, for the Poiseuille flow, an estimate of the average velocity for smooth tubes derived from the classic experimentally-based Colebrook formula (or Moody chart [70]) is provided by employing the concept of equivalent hydraulic diameter. Even with a small number of cells, the results demonstrate that the mean velocity profile predicted by P-DNS method closely matches the DNS solution.

Fig. 6

One-dimensional tests. Poiseuille flow, streamwise velocity (a) and ratio of xy-component of stresses (b). Couette flow, streamwise velocity (c) and ratio of xy-component of stresses (d)

In [53], a Poiseuille flow in a 2D domain was also solved. In this instance, a refined coarse mesh was utilized, resulting in a separation of scales, which led to the coarse mesh capturing a portion of the flow’s unsteadiness. As previously described, in the Lagrangian formulation the computation is performed including virtual particles to transport velocity and instability data.

A snapshot showing the time-average velocity profiles in the channel is shown in Fig. 7. A spatially averaged time mean velocity is calculated for a time window of 100 s. The average streamwise velocity $\angle u^c_x \rangle = 0.378$ m/s, which leads to a $Re = 1.5 \times 10^{5}$, considering the equivalent hydraulic diameter of the channel. In this way, we were able to estimate a predicted friction factor $f_r = 0.014$, close to the value of 0.016 obtained from the Moody diagram for a smooth pipe.

Fig. 7

Two-dimensional Poiseuille test. Time-averaged streamwise velocities

2.10.2 Mixing Layer

The solution via P-DNS of the mixing layer that forms between two fluid streams moving with different velocities is examined next. The main feature present in the mixing layer is the self-similarity property, which is characterized by linear growth of the layer as well as the mean velocities and turbulent statistics being independent of the downstream distance non-dimensionalized by appropriate length and velocity scales.

This example was solved with three meshes of different refinement. It is very interesting to show how small dependence exists in the solution via P-DNS on the distribution of the turbulence between the coarse and fine mesh.

Figure 8 presents the configuration studied. Free-stream velocities selected are $U_{1} = 4$ m/s and $U_{2} = 13$ m/s in order to compare with the results of Yang et al. [71]. The initial velocity distribution is assumed to be that of an inviscid flow with a velocity distribution at the inlet section with a hyperbolic tangent profile. The so-called traction-free boundary conditions are adopted at the top and bottom boundaries of the computational domain, and an advective boundary condition is used at the outlet to prevent wave reflections.

Fig. 8

Mixing layers. Geometry and case configuration

The tree meshes analyzed are: Case A with a mesh composed by $128 \times 30$ cells and $\Delta t = 0.0005$ s, the Case B with $256 \times 61$ cells using $\Delta t = 0.00035$ s, and a Case C with $512 \times 121$ cells using $\Delta t = 0.0002\,\text{s}.$

Figure 9 presents snapshots of the solution on mesh and particles at a specific simulation time for which the flow is developed. While Case A barely shows the vortex street, Case C obtains a visually good definition of the phenomena. Moreover, in Case C flow structures observed in several experiments are clearly detected: in the screenshot presented, a paired vortex structure is followed by an unpaired vortex.

Fig. 9

Mixing-layer, screenshot of P-DNS solutions. Virtual particles coloured by an approximation to the effective viscosity $\nu_{\textrm{eff}} = T^{\rho }_{xy}/G_{xy}$ from 0 (white) to 0.001 (magenta). a Case A, b Case B, and c Case C. (Color figure online)

Figure 9 also shows how the relevance of the data from the fine scales is reduced when more structures are captured by the coarse mesh. This is reflected by the magnitude of the instabilities transported by virtual particles $\left( T^{\rho }_{xy} / G_{xy} \right)$, which decreases when the coarse mesh is refined. We observe that, using P-DNS, refining the coarse mesh could be considered equivalent to moving the limit between what is considered large and small scales.

Although the coherent vortices have been plausibly simulated, these are just qualitative results. In order to guarantee the accuracy, the statistical results must be examined. The streamwise averaged velocity at three different positions (x = 0.4, 0.45, 0.5 m) is shown in Fig. 10, compared with Oster’s experimental measurement. From the plots, it should be noticed that the numerical solution with P-DNS accomplishes the self-similarity condition for the mean velocity even using a coarse grid for the large scales. Moreover, when the coarse-scale grid is refined, the results converge to the experimental ones.

Fig. 10

Mixing layer case, P-DNS solutions. Normalized streamwise mean velocity in subfigures (a, c, e), and normalized Reynolds shear stresses in subfigures (b, d, f) for Cases A, B and C respectively. Experimental data are taken from [72]

Figure 10 also presents the Reynolds shear stress at the same three positions (namely x = 0.4, 0.45, 0.5 m). Due to the scales splitting, we can sum up the fluctuations of the large scales and the pre-computed data from the fine scales. In this sense, the Reynolds shear stress is computed as $\langle u^{\prime}_x u^{\prime}_y \rangle =\langle (u^c_x - \langle u^c_x\rangle) (u^c_y - \langle u^c_y\rangle )\rangle + \langle T^{\rho }_{xy}\rangle/\rho.$ Cases B and C, P-DNS presents a good agreement with experimental data and, in Case A, less than half of the real turbulent intensity is predicted. Authors explain the inaccurate results in Case A because of the fact of separating scales at a size where the fine scales cannot yet be considered homogeneous, a strong hypothesis used on the RVE simulations.

For the sake of brevity, more graphical comparisons are not included in this overview, but it is good to mention that performing simulations with the standard LES and employing coarser grids than those used by Yang (same as cases B and A), LES is not able to capture the instabilities.

2.10.3 Decaying Turbulence

Homogeneous isotropic turbulence refers to turbulence whose average properties are independent of position and direction. Decaying homogeneous and isotropic turbulence (DT) is one of the most important and extensively studied out-of-equilibrium problems in fluid dynamics and a focal point of the study of turbulence. The problem involves a cubical domain with an initial velocity field consistent with a given turbulence spectrum. This field is allowed to evolve until all the remaining mechanical energy has dissipated without any energy input. In this example, the objective is to first obtain DNS solutions of kinetic energy decay for different Reynolds numbers and then to evaluate the prediction of P-DNS of this energy decay for the same flow conditions but with coarser meshes, thus necessitating the modeling of finer scales. This example demonstrates that there is no precise physical–mathematical variable in P-DNS that defines the separation between the coarse scale and the fine scale. Particularly in this example, where there are no boundary conditions, acceptable solutions can be obtained with either a fine or coarse mesh for the coarse scale.

In a cubic domain of size $L=9(2\pi )$ cm, the initial conditions are synthetically generated to accomplish the von Kármán Pao energy spectrum (vKP) using the implementation of [73]. Null mean is imposed to the initial velocity, being $u'$ the RMS value of the fluctuations. By selecting different values for the kinematic viscosity $\nu$, both the fluctuation-based Reynolds number and the minimum grid size required to fully represent all turbulent length scales can be adjusted. In particular, two test cases are selected employing $\nu = 4 \times 10^{-4}$ (high $\nu$) and $\nu = 5.625 \times 10^{-5}$ (low $\nu$) which give $Re_{u'} \approx 60$ and $Re_{u'} \approx 500$ respectively.

For the DNS simulation, a mesh with 256 cells by side is able to reach the Kolmogorov scale in the high Reynolds case (low $\nu$). Figure 11 shows a comparison between the theoretical and the synthetically generated spectra for each case. In the low $\nu$ case, the so-called inertial subrange is cleary present, showing the characteristic -5/3 slope. In this range, a transfer of energy from larger to smaller eddies is carried out, ideally without any viscous dissipation, which is thought to occur exclusively in the dissipation range. This inertial subrange may not be clearly identified for lower Reynolds numbers, as shown in the high $\nu$ case. Figure 11 also presents a snapshot of the initial velocity condition for each case. DNS simulations are carried out using an adaptive time step to keep CFL ≤ 1, where CFL is the Courant-Friedrichs-Levy number, and simulated until a final time of $T_f=50\,\text{s}.$

Fig. 11

Decaying turbulence case. Top: Theoretical (input) and synthetic (computed) turbulence spectra for high (a) and low (b) viscosities. Dashed line represents the maximum wave number that the employed mesh can capture. Bottom: magnitude of the velocity field for these spectra, i.e. the initial conditions for high (c) and low (d) viscosities

As for the coarser meshes, grids of 32, 16, 8, and 4 cells by side are chosen. Initial conditions are obtained as follows:

• 1. Start by filtering the DNS velocity fields by successive averaging on 2³ subdomains to get initial velocity fields $u_{i}$ for cases 32³, 16³, 8³, and 4³.

• 2. Then, for each case:

  • (a) compute the initial coarse kinetic energy field, $k^c={u^c_{i}}{u^c_{i}}$,

  • (b) compute the initial fine kinetic energy field as $k^f = k_{\textrm{DNS}} - k^c$, where $k_{\textrm{DNS}}$ is the kinetic energy

  • (c) estimate the initial conditions of inertial stresses as $T^{\rho }_{ij}=\frac{2}{3} \rho k_f {\delta_{ij}}$.

In order to compare solutions, the total kinetic energy per unit mass K is estimated as

$$\begin{aligned} K(t) = K^c(t) + K^f(t) \end{aligned}$$

(41)

where $K^c$ is the coarse kinetic energy, computed as

$$\begin{aligned} K^c=\frac{1}{\Omega }\int_{\Omega } \frac{{u^c_{i}}(t) {u^c_{i}}(t)}{2}\ d\Omega , \end{aligned}$$

(42)

and $K^f$ is the fine kinetic energy, whose evaluation depends on the numerical model employed. For the P-DNS, it is computed as

$$\begin{aligned} K^f_{\text {P-DNS}} = \frac{1}{\Omega }\int_{\Omega } \frac{T_{ii}^\rho }{2\rho }\ d\Omega , \end{aligned}$$

(43)

Solutions obtained for high $\nu$ cases are presented in Fig. 12a, b. Here, the DNS prediction of the normalized total kinetic energy decay $K//K_0$ is compared with P-DNS and LES predictions using coarser meshes for the first three seconds of simulation. For LES the fine kinetic energy is

$$\begin{aligned} K^f_{\text {LES}} = \frac{1}{ \Omega }\int_{\Omega } \textrm{k} \ d\Omega . \end{aligned}$$

(44)

The most relevant conclusion is that P-DNS obtains reasonable results, even with the coarsest meshes. On the other hand, although LES solutions using 32³ cells are accurate, the results depart considerably from the DNS solution as meshes get coarser. Moreover, solutions for the low $\nu$ cases (high Reynolds), shown in Fig. 12c,d, lead to similar conclusions.

Fig. 12

Decaying turbulence case. Top: high $\nu$ case. Kinetic energy decay. Comparison of the DNS reference with P-DNS (a) and LES (b) solutions varying the coarse mesh discretization. Bottom: low $\nu$ case. Comparison of the DNS reference with P-DNS (c) and LES (d) solutions

2.10.4 3D Taylor–Green Vortex Flow

The 3D TGV problem is a canonical benchmark which allows testing the ability of a simulation methodology to predict key physical processes as vortex dynamics, turbulent transition, turbulent decay and energy dissipation processes. The test consists of a cubical volume of fluid with periodic boundary conditions that contains a smooth initial distribution of vorticity. As time advances the vortices roll-up, stretch and interact, eventually breaking down into turbulence. Because of the lack of external forces, the small-scales will dissipate all the energy in the fluid, which will eventually come to rest.

The purpose of dealing with this complex 3D problem is to evaluate the capability of the P-DNS approach with the proposed memory model to reproduce the physics of the flow using meshes coarser than that required to represent the DNS solution (data from [74] are used as reference). For comparison purposes, LES solutions are also computed.

The problem domain is a cube with a side length of $2\pi$ m. The problem is defined as a periodic flow pattern in a cubic domain. The initial conditions for the velocity can be seen in Fig. 13a. Analytic expression can be obtained from [58]. Structured uniform orthogonal hexahedral grids are chosen to discretize the domain. Although the DNS solution requires a grid of $512^3$, grids of $64^3$, $32^3$ and $16^3$ cells are also employed in order to evaluate the coarse and fine scales contribution. The total dimensionless simulation time is ${\hat{t}}_f = 20\,s$, where the final velocity field seen by the coarse scale is displayed in Fig. 13b.

Fig. 13

Taylor–Green vortex case. Snapshot of velocity fields at a ${\hat{t}}=0$ and b ${\hat{t}}=20$ in (m/s). Kinetic energy evolution for c P-DNS and d LES solutions using different discretizations. Dissipation rate for e P-DNS and f LES solutions

The problem is studied by computing the temporal evolution of the kinetic energy K(t) and its derivative $-dK/dt$, i.e. the kinetic energy dissipation rate, as presented in Fig. 13c–f. The reference solution shows two very distinct phases. First, there exists an initial phase in which the energy is mainly transferred from large to small scales until the dissipation peaks, at about ${\hat{t}}=8$ s, signaling that the energy cascade has reached its smallest scale. Then, the final phase begins, in which the smallest scales start to vanish, much like in the decaying turbulence problem discussed above. In the case of $\text{N} = 64^3$ cells, all solutions are close to the reference values, showing that the fine scale modeling is in this case irrelevant. For N=$32^3$ cells, however, after an early stage (up to ${\hat{t}}=5$) where all solutions are close to the reference, the energy evolution results begin to differ.

The LES method underestimates the energy decay, while the P-DNS method, in turn, although overestimates the energy decay during the late stage of the initial phase (i.e. between ${\hat{t}} = 5$ and ${\hat{t}} = 8$), shows a good agreement in most of the final phase, thus confirming the reliable prediction shown in the decaying turbulence problem presented previously.

2.10.5 Backward Facing Step

Separation of turbulent flows due sudden expansions occur in many practical engineering applications, both in internal flow systems such as diffusers, combustors and channels, and in external flows like those around airfoils and buildings. The flow subsequently reattaches downstream forming a recirculation bubble. Among the flow geometries used for the studies of separated flows, the most frequently selected is the backward-facing step (BFS). In this section, the turbulent BFS flow at $Re_{\textrm{h}}$ = 5000 is studied, where h = 1 is the step height. Figure 14 presents the configuration of the case study. The computational domain consists of a streamwise length L = 30 h, including an inlet section L = 10 h prior to the sudden expansion, vertical height H = 6 h and spanwise width W = 4 h. The coordinate system is placed at the lower step corner. The mean inflow velocity profile, U(y), imposed at the left boundary x = −L is a flat-plate turbulent boundary layer profile, with U₀ = 1 being the maximum mean inlet velocity.

Fig. 14

Backward Facing Step case configuration

Reference time-averaged flow results and turbulent statistics are taken from the experimental study in [75], and the DNS simulation, using a mesh of 6 M cells, reported in [76]. Simulations using P-DNS and LES are performed using a structured mesh of 142K cells, where the step height is discretized using 20 cells. It is known that the results are strongly influenced by the inlet velocity profiles, therefore the turbulent inflow data are generated using a digital filter based approach to match the experimental conditions [77]. Fixed total pressure is set at the outlet, symmetry conditions are imposed at the top boundary, while periodic conditions are set in the spanwise direction. Finally, no-slip boundary conditions are imposed at the bottom wall. The total simulation time is $t_f$ = 800 s, with a fixed time-step $\Delta t=0.02$ s. The time averaging is performed during the last 600 s, time-window long enough to obtain converged statistics. A snapshot of the P-DNS solution can be seen in Fig. 15.

Fig. 15

Backward Facing Step case solved with P-DNS. Snapshot of the instantaneous velocity field

Figure 16 presents the comparison of several time-averaged quantities measured in the wind tunnel (experiment) and the numerical solutions. The mean longitudinal and vertical velocities in global coordinates (U/U₀ and V/U₀ vs. y/h) are compared at four streamwise locations x/h, see Fig. 16a, b. Turbulence intensity profiles for the 3-velocity components $\langle \text{u}^{\prime 2} \rangle ^{1/2}$, $\langle \text{v}^{\prime 2} \rangle^{1/2}$, $\langle \text{w}^{\prime 2} \rangle^{1/2}$ normalized by $\text{U}_0$, and the Reynolds shear-stress component $\langle \text{u}^{\prime} \text{v}^{\prime}\rangle$ normalized by ${\text{U}_{0}^{2}}$ are shown in Fig. 16c–f respectively. The skin-friction coefficient ${\text{C}_{\rm f}}$ is shown in Fig. 16g. Finally, the wall static-pressure coefficient ${\text{C}_{\rm p}}$ measured in the plane of symmetry along the bottom wall downstream of the step is shown in Fig. 16h.

Fig. 16

Backward Facing Step case. Comparison between experimental data [75], and DNS [76], P-DNS and LES solutions. Averaged on slices at different x-locations: streamwise (a) and vertical (b) velocities, streamwise (c), vertical (d), tranversal (e) and shear (f) Reynolds stresses. Averaged on the ground: friction (g) and pressure (h) coefficients

The mean reattachment length $l_r$ can be identified based on the zero crossing of their ${\text{C}_{\rm f}}$ distribution. The experimental curve gives $l_r/\textrm{h}=6\pm 0.15$, which was confirmed through oil flow visualization. The reattachment length obtained by DNS is 6.1h, while a similar analysis leads to predictions of 6.05h and 5.1h by P-DNS and LES respectively.

2.10.6 Flow Around a Square Cylinder

A canonical configuration to study bluff body aerodynamics and vortex induced vibration phenomena is the flow around a square cylinder. For moderate and high Reynolds numbers (based on the inflow velocity U and the width D of the cylinder cross section) the flow separates from the upstream corners leading to an asymmetric shedding of vortices into the wake which induces alternating forces on the cylinder. This promotes structural vibration and is a source of fatigue and flow-induced noise for many engineering applications, explaining the relevance of its study.

Although most research on flow around cylindrical objects has been carried out for circular cylinders, a cylinder with square cross section is here studied. The main reason is that the separation points are fixed (the sharp corners) allowing to concentrate on the turbulent behavior in the fluid bulk without the need to focus in the wall treatment model, which is left for the next section on developing boundary layers.

As a reference study, the work of Trias et al. [78] is chosen. There, a DNS solution of the flow around a square cylinder at Re=22,000 is presented, where time-averaged flow results and turbulent statistics are discussed and validated with experimental data, conforming a complete dataset useful for our comparison purposes.

The configuration of the case study is presented in Fig. 17. The origin of coordinates is placed at the center of the cylinder, while the dimensions of the computational domain are 27D × 13D × πD in the stream-wise, cross-stream and span-wise direction, respectively, far enough to avoid introducing disturbances in the solution near the cylinder due to the boundary conditions.

Fig. 17

Flow around a square cylinder, case configuration

The domain is discretized with a parametric mesh of hexahedra with decreasing sizes towards the cylinder, being $\text{h}_{\min}=0.04D$ the mesh size on the cylinder surface. The mesh employed in the current numerical simulations contains approximately 2 million cells, a really low number, in comparison with the 300 million cells required for the DNS solution.

As boundary conditions, a constant inflow profile $\text{u} = \left(\text{U}; 0; 0\right)$ is imposed at the inlet, while fixed total pressure is set at the outlet. Also, symmetry conditions are imposed at the top and bottom boundaries, while periodic conditions are set in the span-wise direction. Finally, no-slip boundary conditions are imposed at the surface of the cylinder. Henceforward the results are presented in dimensionless form where D, U, D/U, and U²/2 are respectively the reference length, velocity, time, and kinematic pressure.

Regarding simulation control, second order discretization schemes are employed, while two orders of convergence of pressure and velocity residuals is required per time-step, being the time-step value adapted such that Co ≤ 1. Starting from a null velocity initial condition, the simulation is performed up to 300 dimensionless time units, while the time averaging is performed during the last 200 units, a time-window long enough to obtain converged statistics.

The solution obtained with P-DNS is compared with the reference DNS solution. A simulation with LES is also performed for comparison purposes. Table 2 summarizes several bulk quantities obtained from the simulations performed.

Table 2 Comparison of several bulk quantities among the current simulations and the DNS reference. From top to bottom: Strouhal number, the time-averaged drag a lift coefficients, the rms values of the fluctuations of the drag and lift coefficients, and the reattachment length

Main time-averaged flow features of the P-DNS simulation are presented through velocity streamlines in the Fig. 18a. The laminar upstream flow impinges on the front wall of the cylinder leading to high pressure values. The two large recirculations reported in the DNS reference at the top and bottom areas of the cylinder are well predicted, but the secondary recirculations near the upstream and downstream corners are not properly captured due to the lack of grid refinement.

Fig. 18

Flow around a square cylinder. Comparison between DNS simulation [78], P-DNS and LES solutions

When compared with those of LES, the P-DNS predictions for the averaged stream-wise, $\langle \text{u}\rangle$, and cross-stream, $\langle \text{v}\rangle$, velocities in the near cylinder region show a more accurate location of the main vortex, as evidenced by the mean velocities displayed for positive x coordinates in Fig. 18b, c. Instead, large curvatures of the mean flow, located at negative x coordinates, are only partially predicted by both approaches.

The improved reliability of P-DNS solutions is confirmed by evaluating the reattachment length $\text{l}_{\rm R}$, which indicates the length of the time-averaged separation region behind the cylinder. Using P-DNS with the automatic memory model results in $l_R = 1.04$ which is, again, closer to the DNS reference than the other numerical alternatives here employed (see last row of Table 2).

Time-averaged turbulent statistics are presented in Fig. 18d, e as profiles of the averaged streamwise normal stress, and the shear stress component predicted by the P-DNS and the LES simulations. A better agreement with the DNS reference results is generally obtained using P-DNS. Beyond the already mentioned accurate prediction of the main recirculation on sides, see Fig. 18a, it is noticeable the ability of P-DNS to predict mean turbulent statistics, i.e. the profile of the components of the time-averaged Reynolds stress tensor, see Fig. 18b, c, even using a much coarser mesh than that of the reference solution.

Solutions have similar accuracy regarding the DNS reference, which confirms an inherent ability of the P-DNS method to predict the turbulent flow behavior.

2.11 Recent Advances: Improved Wall RVE and Velocity Enrichment

The P-DNS method described so far has proven to be successful in problems in which the boundary layers were either fully developed, not relevant for the global problem, or not present at all. As the long term goal of P-DNS is to be a method of general applicability, able to work with very coarse meshes, it is evident that a better way of dealing with boundary layers is required.

2.11.1 A Wall RVE Based on Time Developing Boundary Layers

Of the variety of approaches that were explored by the researchers involved in the development of P-DNS, the approach presently being used is that of a time developing boundary layer wall RVE, or TDL-RVE. As it will be explained in detail hereafter, the idea is to perform a DNS simulation of a time developing boundary layer over a horizontal infinite flat plate under null pressure gradient conditions are reached. The initial condition is a uniform horizontal laminar flow. From the mathematical point of view, and once written in dimensionless form, this a unique problem that has to be solved only once to obtain the time evolution of the RVE-averaged quantities which will conform the desired output of the simulation. As for the DNS problem domain size and shape, P-DNS proposes a cube of sides $L_x \times L_y \times L_z$, with x aligned with the free stream flow, being z the coordinate normal to the plate, see Fig. 19. The base of this domain lays on the solid wall, i.e. the plate, of area $A_w=L_x L_y$. This domain has to be at least large enough so as to include all the relevant large scale vortices (whose size will be of the order of the ever-growing boundary layer thickness $\delta (t)$). This size is however a minimum requirement, in the sense that the resulting RVE-averaged quantities would lack of enough spatial statistics for their values to be smooth functions of time. This problem has to be addressed either by performing an additional wide enough time window averaging, by increasing the spatial statistics with a larger $A_w$, or by performing ensemble averaging from several independent simulation instances of the problem. We note that the flow remains laminar until $Re_\delta$, defined as

$$\begin{aligned} Re_\delta =\frac{\rho U \delta }{\mu }, \end{aligned}$$

(45)

reaches a given threshold value. Until then, the problem is essentially one-dimensional in the vertical direction, with analytical solution [79]. In the DNS simulation, however, the laminar-turbulent transition may happen earlier due to numerical tripping mechanisms.

Fig. 19

Sketch of the time developing boundary layer wall RVE

Although an infinite flat plate is a particular case of a boundary layer, the results obtained and tabulated in a database will be used for all global problems in the vicinity of solid walls of any geometry. Furthermore, it will be used in spatially developing steady state boundary layers, somehow stretching the concept of self similarity with its implied relationship between space and time. All these intended uses are approximations aimed at avoiding the need to create specialized databases for a large variety of solid wall geometries and flow characteristics. It is worth mentioning, however, that this approach leaves aside the effect of the pressure gradient, which is related to important flow phenomena, e.g. flow separation and recirculation. Therefore, further developments of the wall RVEs along these lines may be needed in the future to accurately represent particular types of flows.

Another important feature of the TDL-RVE, as explained below, is that not only the time evolution of the RVE-averaged inertial stresses tensor needs to be computed and stored in the database. Other relevant results like the time evolution of the wall shear stress sustained by the flat plate are also stored and lately used for solving the wall cells in coarse meshes.

2.11.2 A New Splitting: Enriched Velocity Fields

The coarse scale equations developed in previous sections, namely Eqs. (25) or (26) depending on the selected coarse numerical method, relied on the approximation of ${\textbf{u}}^c$ as a linear velocity profile, able to be represented in $\Omega^l$ by a constant velocity gradient $G_{ij}$. P-DNS, however, it is not to be seen only as a means of modelling turbulent flows, but as a method aimed at using very coarse grids, even in laminar cases. Due to this, and because a laminar boundary layer velocity profile is clearly far from being linear, the assumption of linear spatial variations for the coarse flow is abandoned in the TDL-RVE aproach, thus introducing a more complex field splitting and the concept of velocity enrichment, as explained below.

The RVE total velocity $u^R_i$ is in this case split into three parts, namely spatial average ${\widehat{u}}_i$, enrichment $u^e_i$, and fine ${u^{f}_{i}}$, so that

$$\begin{aligned} u^R_i = {\widehat{u}}_i + u^e_i + {u^{f}_{i}}. \end{aligned}$$

(46)

The spatial average is defined as

$$\begin{aligned} {\widehat{u}}_i = \frac{1}{\Omega^R} \int_{\Omega^R} u^R_i d\Omega , \end{aligned}$$

(47)

where $\Omega^R$ is the RVE domain, a cube of sides $L_x \times L_y \times H$, being $H<L_z$ the height of the RVE.

The fine part ${u^{f}_{i}}$ mainly represents turbulence, much like in the already described P-DNS methodology, and has the same already mentioned imposed constrains. Due to these constrains, its spatial average is null in the RVE. With this result and using Eqs. (46) and (47), it follows that the spatial average of the enrichment part is also null (Fig. 20).

Fig. 20

Conceptual representation of the triple splitting

In order to compute the enrichment part $u^e_i$ a plane surface $\Gamma^R_{xy}(z)$ is defined, obtained by cutting $\Omega^R$ with a horizontal plane located at a distance z above the plate. For any given z, it is possible to compute a corresponding surface average

$$\begin{aligned} u^z_i(z)=\frac{1}{\Gamma^R_{xy}(z)} \int_{\Gamma^R_{xy}(z)} u^R_i d\Gamma \end{aligned}$$

(48)

which is a velocity whose only non-null component is aligned with x and which is function of z only. The enrichment part $u^e_i$ is then defined as

$$\begin{aligned} u^e_i(z) = u^z_i(z) -{\widehat{u}}_i \end{aligned}$$

(49)

which is also a function of z only.

Finally, the fine part is then computed as

$$\begin{aligned} {u^{f}_{i}} = u^R_i -u^z_i, \end{aligned}$$

(50)

which is in accordance with the splitting defined in Eq. (46).

Now, from the coarse scale point of view, for any given boundary node or cell l, the value ${u^c_{i}}$ will take the place of the RVE averaged ${\hat{u}}_i$. With this in mind, using this new splitting, and after repeating many of the steps that led to the previously mentioned coarse scale equations, we get an updated version valid for boundary layer cells, which for the case of FEM reads

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} N^{c,l} \rho \left( \frac{\partial {u^c_{i}} }{\partial t} + {u^c_{j}} \frac{\partial {u^c_{i}} }{\partial x_j} - B_i \right) d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Omega - \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( \widehat{T^{\rho e}_{ij}} + \widehat{T^{\rho }_{ij}} - \widehat{T^{e}_{ij}}\right) d\Omega =0 \\ \\ \int_{\Omega^l} N^{c,l}\frac{\partial {u^c_{i}}}{\partial x_i} d\Omega =0 \end{array} \end{aligned}$$

(51)

while for the FVM version is

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} \rho \left( \frac{\partial {u^c_{i}} }{\partial t} + {u^c_{j}} \frac{\partial {u^c_{i}} }{\partial x_j} - B_i\right) d\Omega + \cdots \\ \int_{\Gamma^l} \left( T^c_{ij} - p^c{\delta_{ij}} \right) d\Gamma_j - \cdots \\ \int_{\Gamma^l} \left( \widehat{T^{\rho e}_{ij}} + \widehat{T^{\rho }_{ij}} - \widehat{T^{e}_{ij}}\right) d\Gamma_j =0 \\ \\ \int_{\Gamma^l} {u^c_{j}} d\Gamma_j=0. \end{array} \end{aligned}$$

(52)

Here, the novelty are two new averaged tensors, additional to the averaged inertial stresses $\widehat{T^{\rho }_{ij}}$ defined in Eq. (24), and both related to the newly added enrichment. Much like the inertial stresses, they will also be approximated by averaging them over an RVE and not over $\Omega^l$, that is

$$\begin{aligned} \begin{array}{lll} \widehat{T^{\rho e}_{ij}} &{} = \frac{1}{\Omega^R} \int_{\Omega^R} \left( \rho u^e_i u^e_j \right) d\Omega \\ &{} \approx \frac{1}{\Omega^l} \int_{\Omega^l} \left( \rho u^e_i u^e_j \right) d\Omega \end{array} \end{aligned}$$

(53)

and

$$\begin{aligned} \begin{array}{lll} \widehat{T^e_{ij}} &{} = \frac{1}{\Omega^R} \int_{\Omega^R} \mu \left( \frac{\partial u^e_i }{\partial x_j}+\frac{\partial u^e_j }{\partial x_i} \right) d\Omega \\ &{} \approx \frac{1}{\Omega^l} \int_{\Omega^l} \mu \left( \frac{\partial u^e_i }{\partial x_j}+\frac{\partial u^e_j }{\partial x_i} \right) d\Omega \\ \end{array} \end{aligned}$$

(54)

In this RVE, then, it is possible to write the inertial and viscous enrichment stresses as

$$\begin{aligned} \widehat{T^{\rho e}_{ij}} \cong \frac{1}{\Omega^R} \int_{\Omega^R} \left( \begin{array}{ccc} \rho u^e_{x} u^e_{x} &{} 0 &{} 0 \\ 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 \end{array} \right) d\Omega \end{aligned}$$

(55)

and

$$\begin{aligned} \widehat{T^e_{ij}} \cong \frac{1}{\Omega^R} \int_{\Omega^R} \left( \begin{array}{ccc} 0 &{} 0 &{} \mu \frac{\partial u^e_{x}}{\partial z} \\ 0 &{} 0 &{} 0\\ \mu \frac{\partial u^e_{x}}{\partial z} &{} 0 &{} 0 \end{array} \right) d\Omega \end{aligned}$$

(56)

where it is clear that only two scalar values are enough to fully define them.

There is, however, an additional value to be computed and stored in the TDL-RVE database: the viscous enrichment wall shear stress $\widehat{T^{we}}$, defined as

$$\begin{aligned} \widehat{T^{we}} = \frac{1}{\Gamma^R_{xy}(0)} \int_{\Gamma^R_{xy}(0)} \mu \frac{\partial u^e_{x}}{\partial z} d\Gamma . \end{aligned}$$

(57)

During the solution of the coarse scale problem, this value will be required for computing the enrichment shear force over the solid wall portion of $\Gamma^l$.

2.11.3 The Fine Problem and the TDL-RVE Database

As been already said, the fine problem to be solved at the RVE level is that of a time developing boundary layer over an infinite steady flat plate. This problem is to be solved just once in a domain large enough so as to represent the largest turbulent scale with a mesh fine enough so as to capture the smallest scales, i.e. the Kolmogorov scale.

The flow outside the boundary layer is assumed to be laminar, with a uniform velocity ${\textbf{U}}=(U,0,0)$ expressed in a local coordinate system with x aligned with the free stream velocity and with z normal to the flat plate. Both the free stream velocity U and the fluid properties $\rho$ and μ may be selected arbitrarily, because the results are going to be stored in dimensionless form, which is of course independent of the particular values selected for the simulation. As for the actual size of the domain, it is selected based on the maximum expected boundary layer thickness $\delta$ desired to be included in the database. This is, in principle, also an arbitrary value, but it must be kept in mind that it limits the validity range of the database. It may well occur that a given coarse problem asks for conditions that lay outside the available RVE database, thus requiring some form of extrapolation or additional RVE simulations in order to extend it.

Unlike the internal and wall RVE databases discussed so far, that of the TDL-RVE is not an equilibrium database, as the results to be computed, non-dimensionalized, and stored are in this case the time evolution of the desired fine stresses. The desired results to be stored as functions of time are the dimensionless averaged stresses $\widetilde{T^{\rho e}_{ij}}$, $\widetilde{T^{\rho }_{ij}}$, $\widetilde{T^{e}_{ij}}$ and $\widetilde{T^{we}}$, being the first three volumetric averages (i.e. on the RVE volume) and the last one a surface average (i.e. on the flat plate surface). These values are considered to be the outputs of the database.

As for the inputs, they are twofold: (i) a single instability index $Id_{1}$, to be described in detail later, and (ii) the time, which for this database to be general, it must also be stored in dimensionless form. Being U, $\rho$ and μ the only available parameters, the only possible way of defining a dimensionless time is

$$\begin{aligned} {\hat{t}}=\frac{\rho U^{2} t}{\mu }. \end{aligned}$$

(58)

Much like it was described in the previously discussed equilibrium wall RVE, the instability index $Id_{1}$ is the only dimensionless parameter required to specify the applied shear. The way in which this is computed and interpreted is, however, different in the TDL-RVE. In this case, for a given RVE of height H, it is defined as

$$\begin{aligned} Id_{1} = \frac{\rho {\hat{u}}_x(t) H}{\mu } \end{aligned}$$

(59)

where ${\hat{u}}_x(t)$ is the instantaneous volumetric average of the horizontal velocity at instant t. It is then possible to define a set of RVE heights, namely ${\mathcal {H}}=\{H_i\}$, with $i=1,N^{\rm H}$, and a set of instants ${\mathcal {T}}=\{t_j\}$, with $j=1,N^t$, and, for each pair $(H_i,t_j)$, compute the following dimensionless quantities:

• the instability index $Id_{1}$,

• the time ${\tilde{t}}$,

• the fine inertial stresses $\widetilde{T^{\rho }_{ij}}$,

• the enrichment inertial stress $\widetilde{T^{\rho e}_{ij}}$,

• the enrichment viscous stresses $\widetilde{T^{e}_{ij}}$, and

• the enrichment wall stress $\widetilde{T^{we}}$,

being the first two the inputs and the rest the outputs of a double entry database with $N^{\rm H}$ cols and $N^t$ rows.

2.11.4 Computable Database Inputs

The coarse problem solution process requires the databases to be consulted whenever and wherever required, which means at least for each coarse problem time step and for each element or cell in the coarse mesh.

The first dimensionless input to the TDL-RVE database, the instability index Id, is readily computable with the information locally available in any coarse element or cell. For any given coarse domain $\Omega^l$ pertaining to a wall degree of freedom l it is evaluated as

$$\begin{aligned} Id = \frac{\rho {u}^{c,l}_\xi H^l}{\mu } \end{aligned}$$

(60)

where $\rho$ and μ are the coarse problem fluid properties, ${u}^{c,l}_\xi$ is the projection of the coarse velocity ${\textbf{u}}^{c,l}$ onto the wall, and $H^l$ is the local mesh size.

The second input, namely the dimensionless time ${\tilde{t}}$, requires however knowledge of a freestream velocity U which is an information that is neither local nor precisely defined in the coarse problem. To tackle this problem, and assuming a coarse mesh locally structured near solid walls, the actual second dimensionless parameter that P-DNS uses as index in the database is the dimensionless quotient of two velocities, namely the shape index $I_s$. It is defined as

$$\begin{aligned} I_s=\frac{u^{c,l}_\xi }{u^{c,q}_\xi } \end{aligned}$$

(61)

where ${u}^{c,q}_\xi$ is the projection of the coarse velocity ${\textbf{u}}^{c,q}$ onto the wall, with q being the "upper" cell located immediately above cell l, i.e. its neighbor in the second layer of boundary cells. From the point of view of the TDL-RVE, this is computed as the quotient of the spatial average ${\hat{u}}_x(t)$ on the RVE over the spatial average on a domain ranging from $z=H$ to $z=2H$, which plays the role of "upper" RVE. In the TDL-RVE simulation process, the initial value of the shape index is $I_s=1.0$, indicating a uniform or piston flow, and decays to a minimum of approximately $I_s \approx 0.82$ at the time in which the boundary layer $\delta$ reaches 2H, staying almost constant from then on.

As for the pros and cons of this index, on one hand this is a dimensionless monotonically decaying function of time, thus making it an excellent replacement. On the other hand, however, is it possible for the coarse problem to produce values of $I_s$ outside the range $[0.82-1.0]$, e.g. when the boundary layer velocities are faster that those of the far field. In those cases, there is no valid data available in the database, and some form of extrapolation or ad-hoc approximation is required, a matter to be sorted out in future developments of the TDL-RVE procedure.

2.12 Examples of Applications of P-DNS for Developing Boundary Layers

The null pressure gradient flow over a semi-infinite flat plate is the most common case of developing boundary layer (BL), and is shown here as an example of the TDL-RVE detailed in Sect. 2.11. Two cases have been considered namely a fully laminar boundary layer and a turbulent boundary layer.

More examples of flows including complex geometries and pressure gradients are under development and are expected to be published in the near future.

2.12.1 The Flat Plate Laminar Boundary Layer

A laminar flow past a thin plate at zero incidence with null pressure gradient will be studied next. Figure 21 presents the case configuration. It is initialized with a free-stream velocity $U = 0.06 \frac{m}{s}$ and a the boundary layer will grow until an equilibrium state is reached.

Fig. 21

Flat plate: case configuration

The theoretical (numerical) solution of a developing laminar boundary layer was achieved by Blasius in 1908 [80]. Two quantities will be compared between the P-DNS simulation versus the Blasius exact solution, namely the boundary layer thickness $\delta$ and the friction factor $C_f$.

Figure 22 shows that the chosen mesh includes the whole boundary layer in the first row of cells along the plate. Considering that in order to reproduce a parabolic solution, such as the laminar BL, at least five point should be taken into consideration, the virtue of the enrichment detailed in Sect. 2.11 arises. Figure 23 shows the excellent agreement between both $\delta$ and $C_f$, for such a coarse mesh. $\delta$ value for the P-DNS simulation was calculated using the velocity in the wall cell and assuming a parabolic profile.

Fig. 22

Laminar flow past a thin plate. A representation of the RVE flow profile for different stations along the plate are presented

Fig. 23

Boundary layer thickness (a), and friction coefficient (b) for the flat plate laminar boundary layer

2.12.2 The Flat Plate Turbulent Boundary Layer

As for the turbulent case, the discretization will be the same used in the laminar case (Fig. 24). However, taking into account the crucial importance of the laminar sub-layer for the computation of $C_f$ for this case, using the same coarse mesh would be extremely ambitious. Therefore, the results presented in Fig. 25 show the remarkable agreement between P-DNS and the analytical solution proposed by Schlichting in [81]. In this case, the boundary layer reaches the second row of cells along the plate. In order to make a comparison, the turbulent wall-RVE demanded a mesh of 264 cells in the direction of growth of the BL, so that the laminar sub-layer and the Kolmogorov scale were captured.

Regarding the transition, there is no additional modelling rather than establishing a threshold for passing from the laminar database to the turbulent one.

Fig. 24

Turbulent flow past a thin plate. A representation of the RVE flow profile for different stations along the plate are presented. A single line profile is shown despite an averaged value is taken into account to calculate the necessary quantities

Fig. 25

Friction coefficient for the flat plate turbulent boundary layer

3 The P-DNS Method for Turbulent Particle-Laden Fluid Flows

This section describes the methodology for solving particle-laden fluid flows using P-DNS. Two separated scales are observed, the small where the particles interacts with each other and with the carrier fluid, and the global scale. This is a hierarchical multiscale problem, and the P-DNS solution is based on the assumption that the solution on a fine enough mesh is reliable.

Multiphase flows are defined as the simultaneous flow of two or more phases. Here, the continuous (or carrier) phase occupies a continually connected region of space, and may be either gaseous or liquid. The dispersed phase, which occupies disconnected (discrete) regions of space, can consist of either solids (particles), liquids (droplets), or gases (bubbles). In the following, the term ‘particles’ will be used regardless of whether their state is solid, fluid, or gas.

The multiscale and nonlinear interactions between the carrier and the dispersed phases lead to complex flow physics and pose unique modeling challenges. Also, many of these flows involve turbulence. The simultaneous presence of two of the most challenging topics in fluid mechanics, namely multiphase flows and turbulence, is still an unsolved problem that deserves more attention and this section is oriented to how P-DNS addresses this challenge. Two different applications of the P-DNS method to particle-laden fluids will be discussed here. One is how the particles modify the turbulence, causing turbulence to increase or decrease. A second application is how to use the P-DNS to model the motion of many millions of particles in a fluid, without the need to move the particles within the fluid, but considering instead an homogenized fluid with properties defined by a scalar function representing the concentration of particles. Both approaches will serve to better understand how to model complex problems that are still open to the fluid mechanics community.

3.1 Turbulent Modulation

Turbulence modulation by the dispersed phase changes the carrier flow’s stochastic behavior. Because different mechanisms operate at different length and time scales, carrier phase turbulent kinetic energy enhancement and attenuation occur simultaneously. Higher inertia, particle drag-induced dissipation, and effective viscosity explain particle-laden flow attenuation. Wake dynamics, self-induced vortex shedding, and buoyancy-induced instabilities due to density variations cause production [82].

The overall modulation depends on the relative strength of the mechanisms, which is a result of the characteristics of the particles, such as volume fraction $\epsilon_p$, mean diameter ${\bar{d}}_p$, mass loading $\phi_p$, also on the carrier phase flow properties, the inertial effects measured by the flow, Re, and the particle, $Re_p$, Reynolds numbers, and the response effects quantified by the Stokes number $S_t=\tau_p/\tau_e$, i.e. the ratio of the characteristic time of a particle, $\tau_p$, to a characteristic time of the flow $\tau_e$. Some models have been proposed to consider the relative influence of these phenomena and predict the turbulence modulation by effect of the dispersed phase [83,84,85]. However, these models have limited validity [86, 87]. Although numerical simulations can analyze turbulence modulation in specific multiphase configurations [88, 89], the computational power available does not support the experimental data needed to validate the numerical results [90]. Therefore, there still is a lack of a universal indicator for turbulence modulation. This is mainly due to the wide range of length and time scales in the particulate flow systems and the complexity of studying them, either numerically or experimentally.

Multiphase flows are intrinsically multiscale but, unlike what happens in solid mechanics, here the particles move relative to the bulk fluid and strongly interact with it, altering the global behavior. This characteristic makes the problem as a multiscale fluid–structure interaction one. Particle-fluid and particle-particle interactions at the microscale (order of some particle diameters $d_p$) lead to organized mesoscale structures (tens of $d_p$) that affect macroscale flow behavior [91]. Recent proposals have used multiscale numerical strategies. Luo et al. [92] proposed several gas-liquid system modeling and simulation methods for all scales. Other methods study the interaction of the discrete phase in the boundary layer near walls, including mass and heat transfer and fluid droplet collisions [93]. Particle-resolved direct numerical simulation of the microscale governing equations has been used to study gas-solid flows and quantify meso- and macroscale developments. These developments have improved their respective applications, but none have improved dispersed flow turbulence modulation modeling. This topic has few literature proposals. These are applied to energy-based turbulence models that account for turbulence modulation through Stokes number-only source terms. These extra source terms usually predict non-realistic attenuation and production rates, which does not improve simulation results. This suggests that a turbulence model suitable for particle-laden flows must be developed [94] and that a systematic study of high-fidelity simulations of particle-laden flows can provide further insights [95].

3.1.1 The Equation to be Solved for a Particle-Laden Flows

From the differential equations point of view, the only difference between a particle-laden flow and an unladen one is the variation in density at each point of the domain due to the spatially variable void fraction of particles. It is also necessary to add the forces that the relative movement of the particles with respect to the fluid make on it.

Since we intend to represent polydisperse multiphase systems, for reasons of informatics tractability it is convenient to define a concentration $c^k$ for each type of particle, defined as the ratio between the volume occupied by $n^k$ particles of type k and the total volume $\Omega$, namely

$$\begin{aligned} c^k = \left( \sum_{j=1}^{n^k} \Omega_j \right) /\Omega \end{aligned}$$

(62)

with $\Omega_j$ being the volume of the j-th particle belonging to the k-type of particles. What is left of the volume when all the k-type of particles are removed is called the fluid volume fraction $c(x_i,t)$:

$$\begin{aligned} c = 1- \sum_{k=1}^{K} c^k \end{aligned}$$

(63)

The averaged density of the remaining fluid when the particles are removed $\varrho$ is then:

$$\begin{aligned} \varrho = \rho c \end{aligned}$$

(64)

The above assumption leads to the following residual weighting differential equation to be solved for the continuous phase at the coarse scale. For the FEM:

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} N^{c,l} \rho c \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t}-B_i \right] d\Omega + \cdots \\ \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^c_{ij}-\widehat{T^{\rho }_{ij}} - p^c{\delta_{ij}} \right) d\Omega =0, \\ \\ \int_{\Omega^l} N^{c,l}\left( \frac{\partial c}{\partial t} + \frac{\partial c {u^c_{i}}}{\partial x_i} \right) d\Omega =0, \end{array} \end{aligned}$$

(65)

and for the FVM:

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} \rho c \left[ \frac{D^{\mathbf {u^c}} {u^c_{i}} }{D t}-B_i \right] d\Omega + \cdots \\ \int_{\Gamma^l} \left( T^c_{ij}-\widehat{T^{\rho }_{ij}} - p^c{\delta_{ij}} \right) d\Gamma_j =0, \\ \int_{\Omega^l} \frac{\partial c}{\partial t} d\Omega + \int_{\Gamma^l} c {u^c_{i}} d\Gamma_i =0, \end{array} \end{aligned}$$

(66)

with

$$\begin{aligned} \widehat{T^{\rho }_{ij}}= \frac{\rho }{\Omega^R} \int_{\Omega^R} {u^{f}_{i}} c u_j d\Omega \end{aligned}$$

(67)

Remark 1

The inertial stress tensor in Eq. (67) is not any more a symmetric tensor as in Eq. (27). This is due to the variation of the volume fraction and the use of an ALE reference frame.

Calling $f_i$ the sum of all the forces that the particles exert on the fluid and calling $g_i$ the vector of the acceleration of the particles (gravity or other accelerations) the source term $B_i$ in Eq. (65) is expressed as

$$\begin{aligned} B_i = \rho c g_i + f_i \end{aligned}$$

(68)

Equations (65) or (66) will be solved in the coarse mesh using explicitly the values of $\widehat{T^{\rho }_{ij}}$ obtained from an RVE.

Now, the dispersed phase model is presented where a Discrete Particle Method (DPM) is employed in both the coarse and fine scale mesh (RVE).

The acceleration of a particle will be given by Newton’s law,

$$\begin{aligned} \rho^k \frac{\pi \left( d^k\right)^3}{6} \frac{dv_i}{dx} = f_i^g+f_i^d+f_i^l \end{aligned}$$

(69)

where $f_i^g$ is the net force due to gravity, and $f_i^d$ and $f_i^l$ are the drag and lift forces. On the other hand, $\rho^k$ and $d^k$ are the density and the diameter of the particle of the set k.

The gravitational and buoyancy forces are computed as a single force acting on a spherical particle as:

$$\begin{aligned} f_i^g = \left( \rho^k - \rho \right) \frac{\pi \left( d^k\right)^3}{6} g_i \end{aligned}$$

(70)

The drag $f_i^d$ and lift $f_i^l$ forces that a spherical particle exerts on the fluid are function of the relative velocity between the surrounding fluid $u_{i}$ and the particle $v_i$. Namely,

$$\begin{aligned} f_i^d = C_D \, \rho^k \,\frac{ \pi \left( d^k\right)^{2}}{8} \sqrt{(u_j-v_j)\,(u_j-v_j)} \left( u_{i}- v_i \right) \end{aligned}$$

(71)

where $C_D$ is the drag coefficient whose expression can be found in [96]; and

$$\begin{aligned} f_i^l = C_L \rho^k \frac{ \pi \left( d^k\right)^3}{6} \left( \epsilon_{ijl}\left( u_j- v_j \right) \omega_l \right) \end{aligned}$$

(72)

where $\omega$ is the vorticity and $C_L$ is the lift coefficient whose expression is taken from [97].

Finally, the momentum transfer term that enforces the two-way coupling between the particles and the fluid-phase, is defined as

$$\begin{aligned} f_i^k = \frac{1}{\Omega^l} \sum_{j} \left( f_i^{k,d} + f_i^{k,l} \right)_j \end{aligned}$$

(73)

where the sum is over all the particles of the k-th set located in the volume $\Omega^l$.

3.1.2 Constructing a RVE for a Particle-Laden Flow

At the RVE level, the fluid with particles is solved using a high-fidelity simulation based on the DPM approach. The unit size cubic domain $\Omega^R$, as seen in Fig. 26, is discretized using a standard mesh of finite elements or finite volumes of cell volume $\Omega^f$, such as $\Omega^R = \cup \Omega^f$ and $\cap \Omega^f=0$. The particle-point approach considers the particles diameter smaller than the grid size. Also, the mesh size should be fine enough to represent most of the fluid wavelengths that may appear. This fact impose the largest particle diameter that is possible to treat with the RVE discretization.

Fig. 26

Sketch of the particle-laden RVE

To enable the construction of the database, the following simplifying hypotheses will be made:

• 1. A k sets of particles of density $\rho^k$ are considered. An average diameter ${\bar{d}}^k$ and a spread $\eta^k$ to define the diameters distribution with the Rosin-Rammler function is used. Any other distribution can be used. Each of these sets is denoted with an upper index k.

• 2. Initially the particles are equally distributed throughout the RVE domain with a concentration equivalent to the mean concentration obtained in the coarse mesh.

• 3. As in the coarse level a particle will be considered as a geometric point in a specified position. It will perceive drag and lift forces proportional to its diameter and the relative speed with the surrounding fluid.

• 4. An average concentration $c^k$ is defined for each set k of particles as

  $$\begin{aligned} c^k= \frac{1}{\Omega^R} \int_{\Omega^R} c^{kR} d\Omega \end{aligned}$$

  (74)

  where the concentration field $c^{kR}$ for the kth particle set is defined considering the contribution of the particles in a computational cell of volume $\Omega^f$ as

  $$\begin{aligned} c^{kR} = \frac{1}{\Omega^f} \sum_{j \in \Omega_f} \left[ \frac{\pi \left( d^k\right)^3}{6} \right]_j \end{aligned}$$

  (75)

• 5. During the time evolution on the RVE $c^k$ does not vary. This hypothesis enables us obtaining averaged statistics of the fine scale. In practice, for each particle of the kth set that leaves the RVE domain, another particle of equal diameter enters the RVE domain. This periodic condition is inspired on the periodicity that we already imposed to the $u^f$ and $p^f$.

• 6. In order to preserve momentum in the RVE, it will be considered that if a particle leaves the RVE with a velocity $v_i$, another particle of equal diameter enters with the same velocity from the opposite side.

• 7. To avoid the unaffordable task of evaluating the temporal transition of the movement of the fluid and the particles over time, at the coarse level, a memory-model will be used for the fluid, as described in [58].

The weighting average N-S equations to be solved at the RVE, for instance for a FEM formulation are:

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} N^R_l \left[ \frac{\partial \left( \rho^R c^R u^R_i\right) }{\partial t} + u^R_j \frac{\partial \left( \rho^R c^R u^R_i\right) }{\partial x_j} -\right. \cdots \\ \left. \rho^R c^R g_i^R - \sum_k f_i^k \right] d\Omega + \int_{\Omega^l} \frac{\partial N^{c,l}}{\partial x_j} \left( T^R_{ij}- p^R{\delta_{ij}} \right) d\Omega =0 \\ \\ \int_{\Omega^l} N^R_l\left( \frac{\partial c^R}{\partial t} + \frac{\partial c^R u^R_i}{\partial x_i} \right) d\Omega =0 \end{array} \end{aligned}$$

(76)

and its equivalent version for a FVM method.

The space of parameters for RVE has the following components: $Id_{1}$ and $Id_{2}$, the concentration $c^k$, the dimensionless mean diameter $\widetilde{d^k}$, the spread $\eta^k$ and the density ratio $\widetilde{r^k}$, for each set of particles k. The RVE outputs are the averaged values in time and space of the nine components of the dimensionless inertial stress tensor at equilibrium, computed as

$$\begin{aligned} \begin{array}{lll} \widetilde{T^{\rho }_{ij}} = \frac{1}{T} \int_{0}^T \frac{dt}{\Omega^R} \int_{\Omega^R} {u^{f}_{i}} c^R u^R_j d\Omega \end{array} \end{aligned}$$

(77)

3.2 Examples the Applications of P-DNS for the Modulation of the Turbulence

This section presents case studies where the P-DNS methodology is used to predict turbulence modulation. Firstly, the reported in [56] is presented, where a synthetic model from pre-computed (off-line) simulations of RVEs is built to characterize the nonlinear dynamic response of the multiphase system composed by water droplets in air. Secondly of particle-laden flows on the coarse scale are solved, evaluating the capacities incorporated when using the reduced model developed.

The results in this section are obtained using the DPM approach on both, coarse and fine, scales. The solution of the disperse phase is performed using a semi-implicit integration approach [98, 99]. This guarantees numerical stability using moderate time-steps when managing the wide range of times scales introduced by the polydispersion of particle sizes. As the computing requirements are proportional to the number of particles, the strategy of computational parcels is employed. A parcel ${\hat{p}}$ agglomerates a set of $N_{{\hat{p}}}$ particles. The main hypothesis is that nearby particles experience the same changes in their properties. The extensive quantities $\psi_{{\hat{p}}}$ are computed as:

$$\begin{aligned} \rho_{{\hat{p}}} \psi_{{\hat{p}}} = \sum_{i=1}^{N_{{\hat{p}}}} \rho_{p_i}\psi_{p_i} = N_{{\hat{p}}} \rho_p\psi_p. \end{aligned}$$

(78)

Thus, the governing equations are computed for an individual particle p and the effect of that particle is transferred back to the fluid $N_{{\hat{p}}}$ times. Note that the particle-point approach imposes a restriction on the largest particle diameter, which should be smaller than the mesh size h.

The equations for the continuum phase are solved with the standard finite volume method. The time-step is restricted such as the Courant number does not exceed the unity, while the pressure–velocity coupling is solved with the PIMPLE algorithm [67] imposing a convergence of three orders for the velocity and pressure residuals. Second-order operators are used for both the spatial and time discretizations.

3.2.1 Enhancement and Attenuation at the Fine-Scale

Turbulence modulation can be seen as the change of intensity of the time-averaged kinetic energy of the carrier flow due to the presence of the particles regarding the unladen flow. In this regard, this subsection analyzes the output of the RVE simulations performed in Ref [56] to highlight the impact of the input parameters to attenuate or enhance the turbulence.

The effect of the particles on the kinetic energy of the carrier flow is presented in Fig. 27, where the time-averaged kinetic energy obtained by 126 RVE simulations is displayed. Results are clustered in three subfigures according to the particle mean diameter: large particles (${\bar{d}}=0.005$), medium particles (${\bar{d}}=0.0005$) and small particles (${\bar{d}}=0.00005$). The cases with Id₂ = 0 and varying Id₁, $\epsilon_p$ and n are analyzed, while reference results for unladen RVEs (i.e. particle-free) under same shear stresses conditions.

The unladen cases show, as expected, that an increase in the shear stresses leads to an increase of the kinetic energy. When the presence of the discrete phase is included in the analysis, Fig. 27a shows that the presence of large particles increases the carrier flow turbulence if the particle concentration is above some threshold. The value of this threshold increases with the shear stress (i.e. the value of Id). For example, large particles in a concentration of $\epsilon_p\approx 10^{-4}$ noticeably enhance the carrier fluid turbulence when Id₁ = 100. However, a value of $\epsilon_p\gtrapprox 5\times 10^{-4}$ is required to modify the unladen situation when Id₁ = 500. From the analysis of individual simulations, the turbulence augmentation is obtained as a consequence of higher magnitudes of the averaged velocity field of the carrier phase. They are induced by the higher inertia of the particles and their constructive interaction with chaotic carrier flow patterns. On the other hand, small particles attenuate turbulence for almost all the configurations analyzed, with the exception of low concentrations with strong imposed shear stress (Fig. 27c). For medium size particles (Fig. 27b) there is again a critical minimum concentration over which turbulence modulation occurs. In this case, and similarly to small particles, high concentrations tend to attenuate the turbulent intensity of the carrier flow.

Fig. 27

Kinetic energy of the carrier phase (time-averaged) fixing Id₂ = 0. Results varying the particle mean diameter compared with the unladen case (a–c). Resulting classification map (d)

No apparent generalized dependence of the variation of kinetic energy on the spread parameter $\eta$ (filled and dashed lines compare same RVE configuration but different $\eta$) is discernible.

However, although the particle mean diameter ${\bar{d}}_p$ apparently is the most sensitive parameter to determine the turbulence modulation behavior, in some particular cases the dispersion could modify the results. For example, in the cases of kinetic energy enhancement considering large particles, the simultaneous presence of smaller particles, i.e. when $\eta =1.5$ is chosen, reduces the rate of turbulence increase. Also, for configurations with medium size particles near the critical concentration threshold, using small values of $\eta$ (large dispersion) produces a kinetic energy increase, which may be associated with the inclusion of large particles. This phenomenon is negligible when the concentration rises and the global results lead to turbulence attenuation due to the massive presence of small particles.

As expected, as the concentration parameter $\epsilon_p$ diminishes the results obtained in laden RVEs tend to the unladen cases for the same Id. However, even a very diluted presence of small particles is enough to completely modify the flow behavior: for example, with Id₁ = 100 and $\epsilon_p=1.5 \times 10^{-6}$, a strong attenuation is observed, and a lower volume fraction is needed to neglect the effects of those small particles.

Lastly, in Fig. 27d presents the classification map of regimes of interaction between particles and turbulence according to the results obtained in the RVE simulations. There, the relationship between the particles concentration and the Stokes number is displayed considering the regions of turbulence augmentation and attenuation. Every RVE simulation is plotted on the map, where a red circle denotes turbulence augmentation and blue square indicates turbulence attenuation (turbulent intensity, TKE, greater or lower than the unladen case). The cases with absolute TKE differences lower than 20% are considered neutral regarding turbulence modulation and marked with a black cross. The Stokes number considers the particle response time $\tau_p = \rho {d_{p}^{2}}/(18\nu )$ and the $\tau_e$ as the turnover time of large eddies.

Flows with larger timescale ratios induce turbulence enhancement (red region), while smaller timescale ratios lead to turbulence attenuation (blue region). The results of the RVE simulations agree with the general observation experimental and numerical collections [87, 100]. However, these references usually mention that the separation between them is defined by the timescale ratio $St=10$ for any mass loading. The results obtained here do not show such a fixed threshold. Instead, a dependence on the averaged distance between particles is noticeable. This value is mentioned as a critical parameter for turbulence modulation [101] and it could explain why the enhancement-attenuation threshold found on RVE simulations is not fixed to $St=10$.

3.2.2 Turbulent Particle-Laden Flow in a Channel

The unloaded and loaded cases of turbulent flow in a channel bounded by two parallel plates (Poiseuille flow) are studied in this section. Using direct numerical simulation (DNS), the objective of this section is to first obtain reference solutions for the flow with and without particles. Then, using a coarse mesh, the P-DNS method is utilized to predict the flow behavior. Finally, these results are compared to those derived from other numerical approaches to modeling turbulence for such a multiphase system.

The case study consists of flow at Re=57,000 in a 1.5x0.5x0.5 m domain simulating a ventilation air duct. The flow is driven by periodic boundary conditions in the longitudinal and transverse coordinate directions and a pressure jump of $\Delta p = 0.0151875 Pa$ between the inlet and outlet. To highlight the interaction between turbulence and particles without the additional effect of particle deposition, gravity is ignored. The initial solution for the air velocity field is obtained by running a simulation without particles until a statistically stationary state of fully developed turbulence is reached. Then, solid particles of $\rho =1000$ kg/m³ and 200 μm diameter are introduced at random positions, uniformly distributed across the entire computational domain, and with an initial velocity equal to the air velocity at the position of each particle. The volume fraction of the dispersed phase is $\epsilon^k=0.0005$.

For the DNS simulation, the domain is discretized using a mesh of 300x150x50 cells that has been refined towards the walls. Solving the equations for the carrier flow and the particles using second-order time and spatial schemes yields a DNS solution, without the need of additional turbulence modeling or boundary layer treatment. In contrast, a coarse mesh of 36 × 12 × 12 cells of equal size is used to obtain the P-DNS solution. It must be noticed that such coarse grid size, 0.04 cm, enables homogenizing the particles as their diameter (200 μm) is smaller than the fine grid size, 0.04/80 cm $\approx$ 500 μm. In addition, coarse mesh solutions with a static Smagorinsky LES model and an unsteady RANS solver with a standard k-$\epsilon$ model are obtained for further comparison. In the latter, standard wall functions are considered, but no additional term for turbulence modulation is introduced.

Figure 28 displays statistically converged solutions, i.e., the averages of the results computed by averaging over the two homogeneous directions and over a long enough simulation time. The mean streamwise velocity Fig. 28a and c and mean kinetic energy, Fig. 28b and d of the carrier phase along the wall-normal coordinate are respectively displayed for the unladen and laden cases. Due to the inertia introduced by the particles, the kinetic energy of laden DNS solutions increases as predicted. This increase in inertia causes a change in the average profile, which tends to be sharpened with an increase in flow rate. Even on a very coarse mesh, the P-DNS solution reproduces these mechanisms with regard to the energy value and its effect on the velocity with great accuracy.

Fig. 28

Mean velocity and mean kinetic energy for the unladen (a) and (b), and laden (c) and (d) cases. Comparisons of several numerical solutions

The obvious lack of precision of the other numerical methods utilized should also be noted. In the case of LES, although some inertia enhancement is predicted, the overall results are inaccurate due to the unresolved boundary layer. Solving with the URANS model, however, reveals negligible differences between the laden and unladen results, indicating that ensemble averaged solutions cannot predict turbulence modulation.

3.2.3 Expelled Saliva Droplets

The target of this section is to perform a set of numerical experiments to evaluate the influence of the turbulence modeling when a saliva exhalation event is simulated. The saliva (water) droplets are injected into the domain from a circular region whose initial direction conforms to a 30 degree spray cone angle. Particles are released in 0.2 s with an initial velocity equal to the surrounding flow and a temperature of 37 Celsius degrees. Temperature differences between the human body’s expelled air and droplets and the surrounding environment cannot be ignored. Consequently, the energy equation is added to the governing equations, and buoyancy effects are modeled by coupling the energy and momentum equations via the Boussinesq approximation [102]. In addition, the empirical Ranz-Marshall correlation is used to account for heat transfer from the surface of Lagrangian droplets to the surrounding [103, 104].

Aerosols are modeled under two conditions: (i) exhalation with a large quantity of water from the respiratory tract, and (ii) exhalation with the same droplets after drying out in typical ambient conditions. Utilizing the Rosin-Rammler distribution, the number of aerosols is imposed as a function of their diameter. The domain is discretized with a 952K hexahedral cell mesh that is refined toward the inlet. The coarse grid size enables homogenizing the particles as their diameters are smaller than the RVE grid size.

Each flow condition is resolved employing both the P-DNS method and a static Smagorinsky LES technique. Due to the fact that the primary difference between these two methods is the treatment of unresolved turbulence scales, the comparison is useful for determining the impact of modeling the turbulence modulation phenomenon. Note that the isotropic turbulence requirement of LES methods for non-simulated turbulent scales is assumed to be met for the employed cell length.

Figure 29b presents the predictions of P-DNS and LES for the penetration of droplets with the condition (i). Inertia allows more than 90% of particles to advance behind $\Pi_{1}$, but most of them are quickly stopped by the air, and then sink slowly towards the floor in close proximity to the inlet. Predictions by the P-DNS and LES techniques are quite similar, and their agreement on computing the accumulated volume behind planes is a consequence of a very similar prediction of flow pattern evolution. Figure 29c depicts a comparison of the predicted accumulated volume using P-DNS and LES when simulating condition (ii). The majority of aerosols are completely dragged by the main flow due to the smaller droplet size and, consequently, the smaller Stokes number and settling velocities. The inlet flow ceases at t = 0.2 s, after which the air velocity dissipates slowly while a large number of droplets are carried by the air’s inertia. At t = 1 s, for instance, roughly 30% of the droplets have reached the final plane $Pi_6$. Both the P-DNS and LES models predict comparable penetration lengths. However, there are more differences than in condition (i) because the particle trajectories are more intricate due to the flow’s complex structures.

Fig. 29

Expelled saliva case. a Geometry and sampling planes. Conditions (i) (b), and (ii) (c). Accumulated volume at different samplings distances

The similarity between P-DNS and LES results indicates that turbulence modulation can be neglected when analyzing the propagation of airborne pathogens in built environments. The primary reason is the low value of mass loading that results from exhaling saliva in an open space.

3.3 Using P-DNS to Solve a Particle-Laden Flows as a Scalar Concentration Function

In this chapter, the methodology previously proposed to solve particle-laden turbulent flows through a multiscale approach is extended by introducing a continuous function for the dispersed phase concentration. The proposed continuous model is especially useful for studying the motion of particle streams in which gravitational and inertial effects cause the particles to deviate from a simple trajectory following the surrounding flow, as would be the case for the limit of very small, massless particles. The results show an excellent comparison between the solutions obtained using the continuous model and simulations evaluating the forces on each particle individually. Distinct advantages of the continuous approach are a much lower computational overhead, a better load balance and ease of parallelization. This is, possibly, one of the most effective P-DNS applications.

As commented in the previous section, two different ways of treating the particles at the coarse mesh level have been used. One is using the DPM approach (for Discrete Particle Method) as presented previously, where each particle was represented in the coarse mesh by a point moving in a Lagrangian way due to acceleration and drag and non drag forces. Another way is using the CPM approach (for Continuous Particle Method), as will be explained now. In the so-called Eulerian-Eulerian approaches, the forces from the relative movement of the particles with respect to the fluid are typically modeled through simplified empirically calibrated theoretical arguments. Our proposal may shed light on the possibility of bringing improvements for more accurate modeling using first principles of mechanics. Here, at the RVE level, a particle will be considered as usual as a geometric point in a specified position which perceive drag and lift forces proportional to its diameter and the relative speed with the surrounding fluid using the following approximations. At the coarse level, a continuous function for the dispersed phase concentration will be used, that moves as an independent fluid with a velocity and a diffusion that will be obtained from the RVE. Moving a scalar function, instead of moving millions of independent particles, is a great advantage from a computational point of view.

3.3.1 The Quasi-Eulerian Time Integration

Consider a fluid of density $\rho^k$, moving with a velocity ${u^k_{i}}$. The mass conservation equation reads:

$$\begin{aligned} \frac{ \partial \rho^k}{\partial t}+\frac{\partial \left( \rho^k {u_{i}^{k}} \right) }{\partial x_i}=0 \end{aligned}$$

(79)

or, as a function of their corresponding concentrations:

$$\begin{aligned} \frac{\partial c^k}{\partial t}+\frac{\partial \left( c^k {u_{i}^{k}} \right) }{\partial x_i}=0 \end{aligned}$$

(80)

Equations (79) or 80 correspond to the mass conservation equations expressed in an Eulerian reference frame.

Splitting the concentration function in a constant part inside each RVE coming from the coarse mesh plus an incremental part corresponding to the fine mesh:

$$\begin{aligned} c^k = c^{kc} + c^{kf} \end{aligned}$$

(81)

with

$$\begin{aligned} \begin{array}{lll} c^{kc} = \frac{1}{\Omega^R} \int_{\Omega^R} c^{kR} d\Omega , \text { with } \\ \int_{\Omega^R} c^{kf} d\Omega =0, \text {and}\\ \int_{\Omega^R} \frac{\partial c^{kf}}{\partial x_i} d\Omega =0 \end{array} \end{aligned}$$

(82)

Therefore, the Eulerian mass conservation equation is:

$$\begin{aligned} \frac{\partial c^{kc}}{\partial t}+\frac{\partial c^{kf}}{\partial t}+\frac{\partial \left( c^{kc} {u_{i}^{k}} \right) }{\partial x_i}+\frac{\partial \left( c^{kf} {u_i^{k}} \right) }{\partial x_i}=0 \end{aligned}$$

(83)

Equation (83) can be transformed in a quasi-Eulerian version in the following form:

$$\begin{aligned} \frac{\partial c^{kc}}{\partial t}+\frac{D^{\mathbf {u^c}} c^{kf}}{D t}- {u^c_{i}} \frac{\partial c^{kf}}{\partial x_i} +\frac{\partial \left( c^{kc} {u_i^{k}} \right) }{\partial x_i}+\frac{\partial \left( c^{kf} {u_i^{k}} \right) }{\partial x_i}=0 \end{aligned}$$

(84)

or

$$\begin{aligned} \begin{array}{lll} \frac{\partial c^{kc}}{\partial t}+\frac{D^{\mathbf {u^c}} c^{kf}}{D t}- {u^c_{i}} \frac{\partial c^{kf}}{\partial x_i} +\frac{\partial \left( c^{kc} {u_i^{k}} \right) }{\partial x_i}+\\ c^{kf} \frac{\partial {u_i^{k}} }{\partial x_i}+{u_i^{k}} \frac{\partial c^{kf} }{\partial x_i}=0 \end{array} \end{aligned}$$

(85)

or

$$\begin{aligned} \begin{array}{lll} \frac{\partial c^{kc}}{\partial t} + \frac{D^{\mathbf {u^c}} c^{kf}}{Dt} + u_i^{kR}\frac{\partial c^{kf}}{\partial x_i} + \frac{\partial (c^{kc} {u_i^{k}})}{\partial x_i} + \\ c^{kf}\frac{\partial {u_i^{k}}}{\partial x_i} = 0, \end{array} \end{aligned}$$

(86)

where $u_i^{kR}$ is the velocity of the particles of type k inside the RVE defined as $u_i^{kR}={u_i^{k}}-u_i^c$.

The name quasi-Eulerian for the time integration comes from the fact that the terms in $c^{kc}$ must be integrated in time in a Eulerian form, while the terms in $c^{kf}$ must be integrated in a Lagrangian frame moving with ${u^c_{i}}$.

Similar to the splitting performed for the concentration field, the relative velocity of the particles is also split in two parts, a coarse and a fine variation, i.e.:

$$\begin{aligned} u^{kR}_i= u^{kc}_i + u^{kf}_i \end{aligned}$$

(87)

with

$$\begin{aligned}& u_i^{kc} = \frac{1}{\Omega^R} \int_{\Omega^R} u_i^{kR} d\Omega , \text { and }\\ &\int_{\Omega^R} u_i^{kf} d\Omega =0, \text {and}\\ &\int_{\Omega^R} \frac{\partial u_i^{kf}}{\partial x_i} d\Omega =0 \end{aligned}$$

(88)

Equation (86) may be written as:

$$\begin{aligned}& \frac{\partial c^{kc}}{\partial t}+ {u_i^{k}} \frac{\partial c^{kc}}{\partial x_i}+ c^{kc} \frac{\partial {u_i^{k}}}{\partial x_i}+ \frac{D^{\mathbf {u^c}} c^{kf}}{D t}- \cdots c^{kf} \frac{\partial \left( u_i^c +u_i^{kc}+u_i^{kf}\right) }{\partial x_i}\\ &\quad+ \left( u_i^{kc}+u_i^{kf}\right) \frac{\partial c^{kf}}{\partial x_i}=0 \end{aligned}$$

(89)

Equation (89) evidences the terms that must be integrated in an Eulerian way and those that must be integrated in the Lagrangian way.

Using a residual weighted formulation for Eq. (89), taking into account the constrains imposed in (88), and the condition that the RVE moves with a velocity ${u^c_{i}}$, the term corresponding to the Lagrangian time integration in Eq. (89) is identically null, leaving the following equation to be solved in the coarse mesh:

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} N_l^R \left( \frac{\partial c^{kc}}{\partial t}+ {u_i^{k}} \frac{\partial c^{kc}}{\partial x_i}+ c^{kc} \frac{\partial {u_i^{k}}}{\partial x_i}+ \cdots \right. \\ \left. c^{kf} \frac{\partial u_i^{kf}}{\partial x_i}+ u_i^{kf} \frac{\partial c^{kf}}{\partial x_i} \right) d\Omega =0 \end{array} \end{aligned}$$

(90)

also

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} N_l^R \left( \frac{\partial c^{kc}}{\partial t}+ \frac{\partial \left( {u_i^{k}} c^{kc}\right) }{\partial x_i}+ \frac{\partial s_i^k}{\partial x_i} \right) d\Omega =0 \end{array} \end{aligned}$$

(91)

For the case of the FVM:

$$\begin{aligned} \begin{array}{lll} \int_{\Omega^l} \frac{\partial c^{kc}}{\partial t} d\Omega + \int_{\Gamma^l} \left( c^{kc} {u_i^{k}} +s_i^k \right) d\Gamma_i=0 \end{array} \end{aligned}$$

(92)

The fields ${u_{i}^{k}}$ and ${s_{i}^{k}}={c^{kf}}{u_{i}^{kf}}$ are computed from the RVE. It must be taken into account that the RVE moves in a Lagrangian way with a velocity ${u^c_{i}}$.

Equation (91) can be seen as an advection-reaction equation for the concentration of particles. The second term in Eq. (91), that comes from the second and the third terms in Eq. (90), is the advection at a ${u_i^{k}}$ velocity, plus a reaction or an absorption, of the concentration function with a reaction/absorption coefficient $\frac{\partial {u_i^{k}}}{\partial x_i}$, which represents the global compressibility of the disperse phase. The third term represents a reaction/absorption of the concentration function due to their local compressibility at the fine mesh level.

Remark 2

In the P-DNS CPM methodology proposed in this work, the equation system to be solved at the coarse scale are the mass and the momentum conservation, Eqs. (65) and the mass conservation for the dispersed phase, Eq. (91). The momentum for the dispersed phase is considered when solving individually the particles at the fine-scale. The contribution of the fine scale is driven by the fields $T^{\rho }_{ij}$, $f^k_i$,${u^k_{i}}$ and ${s^{k}}$. This means that, when the time integration of the equations is performed, these fields are required at every time t. However, as mentioned before, the values stored in the RVE database were computed at equilibrium, as presented in Eqs. (77). To overcome this drawback, the memory-model presented in Sect. 2.9 is used. As shown above, for the fluid variables the relaxation time depends on the local fluid velocity gradients, see Eq. (38). A relaxation time derived from the behavior of an isolated particle is adopted for the disperse phase in [54], which reads

$$\begin{aligned} \tau^k = \frac{\rho^k {d^k}^{2}}{18\mu }. \end{aligned}$$

(93)

Remark 3

The equilibrium states for the fine scale fields are recovered from the condition prevailing at the RVE position from the pre-computed database. This dimensionless data must be rescaled as indicated in Table 1 according to type of variable involved. As an example, the inertial stress tensor is now dimensionalized as

$$\begin{aligned} T^{\rho , eq}_{ij} = \widetilde{T^{\rho }_{ij}} \frac{\mu^{2}}{\rho H^{2}} \end{aligned}$$

(94)

where $\widetilde{T^{\rho }_{ij}}=F\left( X \right)$ with

$$\begin{aligned} X = \left( Id_{1}; Id_{2}; {\tilde{g}}_l;c^k;\widetilde{d^k};\widetilde{\xi^k};\widetilde{r^k} \right) \end{aligned}$$

, being F the RVE database or a synthetic model of that dataset [56]. This multi-valuated and multi-dimensional function predicts the averaged fine scale response for the local conditions specified through the dimensionless parameters set X.

Remark 4

Due to the fact that the velocities computed on the RVE are relative to a moving frame, the total velocity of the particles ${u^k_{i}}$ should be computed as the sum of the velocity of the particles evaluated at the RVE $u^{kR}_i$, plus the velocity of the fluid in the coarse mesh ${u^c_{i}}$, this is

$$\begin{aligned} {u_i^{k}} = {u^c_{i}} + {u^{kR}_{i}} \end{aligned}$$

(95)

The equation to be solved in the RVE is the same as for the previous case, except that now the acceleration $\widetilde{g_{i}}$ must be introduced at the RVE level, both the gravitational and any other inertial or electromagnetic force that exists, and in addition to the tensor $\widetilde{T^{\rho }_{ij}}$ evaluated in the formulation above, we must now also calculate the average relative velocity of the particles ${\widetilde{u^{kR}_i}}$, the vector ${\widetilde{{s^{k}}_{i}}} = {\widetilde{c^{kf} u^{kf}_{i}}}$ and the average forces $\widetilde{\sum_{k}f_i^k}$ to be transmitted to the coarse mesh.

3.4 Examples of Application of P-DNS with Particles Transported as a Scalar Function

A collection of case studies with some complexity is discussed below in order to evaluate the advantages of the P-DNS method, in terms of efficiency and accuracy using the continuous particle model, which it is referred as CPM.

Each test is studied using a detailed DPM simulation to get a reference solution. For this task, the DPMFoam solver, distributed in the OpenFOAM platform, is used. Then, the prediction of the P-DNS-CPM, hereinafter termed just P-DNS, is computed.

The P-DNS implementation here presented uses OpenFOAM as the core library. Using the same configuration in the same platform guarantees a reliable comparison of the results. In both DPM and P-DNS procedures, the equations for the continuum phases are solved with the finite volume method, while the PIMPLE (PISO + SIMPLE) algorithm is used to perform the pressure–velocity coupling for transient flows [67]. Case studies employ first-order time integration schemes and second-order spatial FV discretizations.

The first test case evaluates the dynamics of a cloud of water particles in air at rest. Then, the same cloud of particles is analyzed in a fluid subject to crossflow. Finally, a prototype example where a pollutant plume ejected from a chimney to air is studied.

3.4.1 Dynamics of a Cloud of Particles in a Fluid

The target of the first example is predicting the settling velocity of the cloud and the acceleration from rest. Water droplets are initially placed in a 20 cm by 30 cm rectangular domain with a concentration of $c_{k} = 10$ ppm. The computational domain of 0.5 × 2 m is discretized with a 50 × 200 cell structured grid. The boundary conditions depict a bounded region with tangential velocity acting on the lateral surfaces.

The diameters of particles of (i) 80 μm and (ii) 10 μm are examined. To satisfy the initial concentration requirements in the DPM simulation, over 22 K particles were used in case (i) and over 114 K parcels of 100 particles were used in case (ii). At t = 0 s, $g_i$ (gravity) is activated and particles begin to fall. The time step is constrained to prevent the Courant number from exceeding unity.

The interaction with the surrounding gas modifies the cloud’s initial shape, as observed in Fig. 30a. b, which depict the concentration of the dispersed phase. Although each test considers the same amount of water, the results reveal that the evolution of the dispersed phase is highly dependent on the particle diameters. The cloud with larger particles descends more quickly, and its initial shape deforms and becomes skirted after 5 s. In contrast, the cloud composed of smaller particles exhibits a much larger deformation and produces an instability similar to Rayleigh–Taylor, as indicated by the fingers observed at time t = 5 s. Results indicate that by modeling the movement of the particles with a concentration field instead of moving them explicitly as such in the coarse scale simulation of the P-DNS method, it is possible to reproduce these dynamics with good agreement.

Fig. 30

Snapshots of the volume fraction of dispersed phase field for times $t=2.5$ and 5 s for a large and b small particles. In c the evolution of the averaged velocity

In Fig. 30c, the settling velocity of a cloud of 80 micron particles is observed to not increase asymptotically. This highlights the differences between the dynamic behaviour of a cloud and that of an isolated one. Taking the DPM solution as reference, the P-DNS method accurately reproduces the dispersed phase dynamics, with negligible differences found at the beginning of the simulation. The cloud of smaller particles shows even more complex dynamics, with initially accelerated sinking reaching velocities one order larger than an isolated water drop. A group of particles is dragged upwards due to shape deformation after 1.5 s, and the average falling velocity reaches a maximum around t = 2.5 s before decreasing and changing displacement direction. The P-DNS technique using the continuous particle approach (as a concentration) accurately reproduces these complex dynamics.

A more complicated case is to add a transversal air flow to the previous example. While gravity tends to settle the droplets, the cross-flow horizontally drags the cloud. These dynamics result in a complex interaction of the dispersed phase with the surrounding air presented in Fig. 31.

Fig. 31

Settling in cross flow. Snapshots of the concentration of the dispersed phase. Diameter of particles: 10 microns

The evolution of 10 μm droplets presented through concentration snapshots at specific solution times reveals that the shape deformation is distinct from the fluid at rest. As the outer particles are dragged upwards by the ascending surrounding flow, the bell-like shape observed at t = 2 s gradually changes to a horn-like shape. This behavior facilitates the sinking of inner droplets.

Using the DPM results as the reference solution, the P-DNS method is able to reproduce the complex nature of this particulate flow. In addition, the numerical scheme used to advect the continuum field that models the particles does not introduce artificial diffusion, allowing the complex evolution of the morphology of the dispersed phase to be accurately reproduced.

3.4.2 Pollutant Plume Ejected from a Chimney

The modeling of particulate flows in urban environments is relevant in the study of air pollution. This example prototypes a pollutant plume ejected from a chimney to air.

The case study considers that the particulate flow is subjected to gravitational forces and a crossflow. Figure 32 presents the geometry considered. The computational domain is discretized using 437K cubic cells, using a cell size of 0.02 m near the chimney and 0.04 far from it.

Fig. 32

Chimney. Geometry specification and measuring planes. Units are in meters

A constant horizontal velocity of magnitude U = 1 m/s is imposed at the inlet surface. The slip boundary condition is set at the building, chimney stack, top, bottom, front and back, while an outlet condition is considered at the remaining surface.

The simulation studies the ejection of particulate flow from the top of the chimney at a velocity of V = 2 m/s. Particles of 80 microns in diameter and density of 1000 kg/m³ compose the dispersed phase. As inlet boundary condition, the concentration is fixed to 100 ppm and the ejected mass flow rate of particles is assumed as 2.8 g/s. The reference data computed from a DPM solution are compared with the P-DNS predictions and from a third simulation which considers incompressible one-phase flow and the concentration of the particles as a passive scalar field, i.e. a tracer.

The interaction between the airflow and the particulate flow results in complex flow dynamics. This phenomenon is characterized by a turbulent behavior and the development of a trace visually identified as a fume plume. Figure 33 compares the particulate plume predicted at $t=8$ s by the P-DNS method, the tracer, and the DPM solutions. In the light of the results, the dispersed phase can not be assumed simply as a passive scalar. As Fig. 33 shows, the tracer does not keep trapped by the air recirculation behind the building, because lacks of a settling capability following the air in its movement which represents a dangerous prediction failure. Despite the chaotic evolution, the flow macrostructures developed in the reference simulation using DPM are well reproduced by the continuous model used in the P-DNS technique.

Fig. 33

Chimney. Comparison of the particulate flow at t = 8 s. a particle volume fraction with P-DNS, b particles in DPM, c concentration as a passive scalar (tracer)

A quantitative comparison of the results is performed evaluating the mean mass flow rate through sample planes placed at different locations. Four measuring planes normal to the streamwise direction and two normal to the y-direction are used, as depicted in Fig. 32. At time t, the mean mass flow rate through a given plane is the ratio of the dispersed-phase mass that has traversed the plane to the elapsed time.

The vertical planes ${\Pi_{p}^{x}}$ allow computing the streamwise distance reached by particles being dragged by the crossflow. The horizontal planes ${\Pi_{p}^{y}}$ measure the sinking, a sensitive parameter when designing chimneys to avoid the particulate cloud keeps trapped between buildings. This phenomenon is not only harmful to pedestrian’s health but also increases the risk of re-entry of the pollution indoors.

Figure 34 shows the evolution of the mass flow rate at the different sampling planes. At the initial stage, the flow rate measured at any plane is null. When the plume reaches a plane, the flow rate increases up to an approximately constant value. Figure 34a and b shows that arrival times are well predicted by the P-DNS method, but some discrepancies are found on the steady flow rate mainly at planes ${\Pi_{2}^{x}}$ and ${\Pi_{3}^{x}}$. The low flowrate measured at plane ${\Pi_{4}^{x}}$ indicates that more than 80% of the mass ejected to air sinks and remains trapped behind the building. The P-DNS simulation reproduces well the evolution of the settled mass as reported in Fig. 34c.

Fig. 34

Chimney. Mean flowrate at measuring planes. a horizontal planes ${\Pi_{1}^{x}}$ and ${\Pi_{3}^{x}}$, b horizontal planes ${\Pi_{2}^{x}}$ and ${\Pi_{4}^{x}}$, c vertical planes

Considering the dispersed phase as a passive scalar is equivalent to neglecting the mass of the particles. Therefore, the statistics collected from the tracer simulation do not agree with the reference data. Not considering the inertia leads to an excessive streamwise velocity of the particles, which is reflected by early arrival times to the planes and the overprediction of the penetration of the flume. In addition, as the gravity force does not influence the dynamics of the tracer, the settling flow rate is not correctly estimated, as seen in Fig. 34c.

The chimney ejects to the air more than 10 million particles per second. The detailed DPM simulation of this case study quickly turns intractable. Strategies as using computational parcels of particles, i.e. performing the detailed analysis for one particle and then applying the effect to many, could partially overcome this issue. But in general, DPM turns unaffordable when long simulation times or large computational domains are required. Employing a continuous field as proposed in this work is a realistic alternative for modeling the behavior of the dispersed phase accounting for the dynamics of the individual particles and their interaction with the surrounding flow.

3.4.3 Latest Applications: Electrostatic Spray Coating

One of the many interesting applications of P-DNS to solve particulate-laden fluid problems using a continuous formulation is the powder coating technology. Powder coating is a finishing process for metal surfaces where a dry powder, typically made of a mixture of resins, pigments, and other additives that are electrostatically charged, is sprayed onto the surface. The particles adhere to the metal surface, forming a smooth and even layer that is then cured with heat to create a strong and durable finish. The complex nature of the physics involved in sprays behavior poses a significant challenge for researchers and manufacturers to optimize the process and achieve consistent results. The goal is to achieve a uniform coating layer over the entire surface, using the least amount of dust and in the least amount of time. For this, the variables to regulate are: the intensity of the electric field to be introduced, the speed with which the spray gun moves, the distance between the material to be covered and the spray gun, the intensity of the particle jet, the inclination of the diffuser, among many others. The classical approach to solve this problem is the so-called Discrete Particle Model (DPM), which allows for the simulation of the particles’ interactions with the fluid and electrostatic fields. The main drawback of DPM is the requirement of significant computational resources, particularly for large-scale simulations. This can lead to long simulation times and high computing costs, which can limit its practical application in certain industries. In this example the extensions of the P-DNS CPM model for the coupling of the two-phase flow with an electric field is presented. Also the proposal enhances the continuous particulate phase modeling by consider turbulent dispersion and a simple but realistic strategy for the interaction of spray with target surfaces to quantitatively account for the coating finishing.

Recently, in [105], the painting process of a ship’s propeller that is fixed in a vertical position is studied using the P-DNS CPM model. A moving spray gun rotates around the target surface at a speed that may be variable, ejecting a particulate flow rate of 0.6666 g/sec. Considering particles with diameter of 60 microns and a density of 1500 kg/m³, it means 3.9 million of particles/sec. The impressive computational cost is alleviated using the P-DNS CPM proposal.

Figure 35 shows some snapshots at different time steps where the spray gun is turning at a velocity of 12 rpm, while the electrode in its tip is established at a electrical potential of − 90 kV.

Fig. 35

Painting a ship propeller. Snapshots of the particulate volume fraction

Figure 36 shows for the same case, the thickness of the paint layer on a center line of each of the 4 blades after completing one turn of the spray gun.

Fig. 36

Painting a ship propeller. Paint thickness over a line at the center of the blades after a revolution of the spray gun

4 Conclusions and Future Works

An overview with the main applications found in the literature of the P-DNS method has been exposed.

Like all multi-scale methods, P-DNS is based on spliting the unknown fields into a coarse scale plus a fine scale. Then, both scales are resolved numerically. The greatest originality of the method is to solve the fine scale off-line in a dimensionless way and for a series of RVEs with a simple geometric shape. This is possible thanks to three fundamental factors:

• 1. An iterative procedure where the solution of the fine scale in isolated subdomains uses boundary conditions obtained from the coarse scale.

• 2. The dimensionless form to write the problem in both, the coarse scale and the fine scale.

• 3. The averaging of results obtained from the fine scale allows for solving simpler geometries without requiring precise consideration of the original geometry at the coarse scale.

The results obtained with the P-DNS method are encouraging. For homogeneous fluids problems presented in the literature, using coarse and medium mesh sizes, P-DNS provides better match to the experimental data than LES. In addition, LES methods do not comply with the self-similarity property or the averaged symmetry over the time of the flow. Moreover, the standard LES using coarser grids may not even capture instabilities that P-DNS approach is capable of capturing. From a computational point of view, P-DNS may be cheaper than LES because it avoids the LES requirement of using fine enough meshes to capture every large eddy.

The accuracy of the P-DNS solution on the coarse mesh is highly influenced by the accuracy of the fine scale solution. Therefore, it is worthy to invest as much computational power as possible to increase the refinement level to compute the fine mesh solution, and the number of samples to properly capture the nonlinear variation of the database coefficients to the different parametric inputs.

The results shown in this overview indicate that the P-DNS method is very recommendable for solving homogeneous turbulent fluids flows problems. However, other potential and very attractive fields of application of the P-DNS technique are heterogeneous multiphase flows and active fluids, where the interaction of the different materials involved with the instabilities at the finest scales is very difficult to capture by any method other than the standard DNS.

The treatment of the particles as a continuous fluid has several advantages with respect to the discrete particle model (DPM), where the particles are treated in a Lagrangian frame. The main drawback of the Lagrangian treatment of the particles is that once the number becomes very large, it requires a prohibitive amount of computational power to track a sufficiently large sample of particles required for statistical convergence. Furthermore, on parallel machines load imbalances may occur, requiring frequent re and sub partitioning for multi-objective load balancing. None of this occurs for the CPM model using P-DNS. In this case, the treatment of the dispersed phase just requires an extra computing cost which is the evaluation of the RVE database. This overhead is constant regarding the number of particles. In any case, a quantitative comparison of computational times of P-DNS against DPM requires further study as it is problem-dependent.

The great advantage of P-DNS over other multiscale methods is that the fine scale is solved previously and only once (off-line) for a dimensionless system parametrized for certain physical characteristics. In this way, at the coarse scale level, only a scalar function must be transported, and the only additional work is to consult the velocity and the forces in a previously calculated database.

The results show an excellent agreement between the numerical solutions using DPM and CPM with P-DNS, with the great advantage that the continuous model has from a computational point of view.

The continuous method proposed is particularly useful to study the movement of particulate flows such as aerosols in which the gravitational and inertial effects combine so that the particles do not follow the trace of the surrounding flow. At the computational price of transporting an extra scalar field, the CPM approach via P-DNS allows solving problems where the behavior of the dispersed phase should invariably consider the dynamics of the individual particles.

In the future, other applications of the P-DNS method to particle-laden fluids will be tested or expanded, such as modeling and simulation of infectious diseases in air (studies already started in [56]), transport of pollutants in the atmosphere (studies already started in [54]), simulation of powder coating sprays (see [105]), analysis of corrosion due to rainwater drops in wind generators, study of the distribution of vacuum drops in cavitation problems, distribution of drops of nasal spray remedies, and many other applications where a fluid such as air or water carries particles of a different density.

Appendix 1: Computing the dimensionless parameters and obtaining the equilibrium stress tensor

• 1. Compute the velocity gradient ${\text{G}_{\rm ij}^{\rm org}} = \frac{\partial {u^c_{i}}}{\partial x_j}$ of the coarse velocity field ${\text{u}^{\rm c}_{\rm i}}$.¹

• 2. Obtain the transformation tensor ${S_{ij}}$ and the corresponding rotated velocity gradients $g_{1}$ and $g_{2}$ following the procedures in “The internal RVE case” section for an internal cell or in “The wall-RVE case” section in this appendix for a boundary cell.

• 3. Compute the dimensionless gradients on the rotated configuration as:

  $$\begin{aligned} Id_{1} = g_{1} \frac{\rho H^ 2}{\mu } \\ Id_{2} = g_{2} \frac{\rho H^ 2}{\mu } \end{aligned}$$

• 4. Enter the database with $|Id_{1}|$ and $|Id_{2}|$ (remember that the RVE simulations were computed for positive $Id_i$ values) to obtain the dimensionless equilibrium fine stresses ${\widetilde{T}}_{ij}^{\rho}$.

• 5. Recover the correct sign of the off-diagonal components of ${\widetilde{T}}_{ij}^{\rho}$ by computing

  $$\begin{aligned} {\widetilde{T}}_{xy}^\rho := sign(Id_{1}) {\widetilde{T}}_{xy}^\rho , \\ {\widetilde{T}}_{xz}^\rho := sign(Id_{2}) {\widetilde{T}}_{xz}^\rho , \\ {\widetilde{T}}_{yz}^\rho := sign(Id_{2}){\widetilde{T}}_{yz}^\rho . \end{aligned}$$

• 6. Obtain the dimensional equilibrium stress tensor:

  $$\begin{aligned} {\overline{T}}_{ij}^\rho = {\widetilde{T}}_{ij}^{\rho} \frac{\mu^{2}}{\rho H^ 2}. \end{aligned}$$

• 7. Finally, transform the tensor back to the coarse mesh coordinates:

  $$\begin{aligned} {\overline{T}}_{ij}^\rho = S_{ik} {\overline{T}}_{kl}^\rho S_{jl}. \end{aligned}$$

1.1 The internal RVE case

Starting with a real, symmetric, null trace tensor

$$\begin{aligned} G_{ij}^{symm} = \left( \begin{matrix} g_{11} &{} g_{12} &{} g_{13} \\ g_{12} &{} g_{22} &{} g_{23} \\ g_{13} &{} g_{23} &{} -(g_{11}+g_{22}) \\ \end{matrix} \right) ,\end{aligned}$$

(96)

which is typical of the symmetric part of a velocity gradient, the idea is to obtain, by orthogonal transformations, a tensor

$$\begin{aligned} {G_{ij}^{rot}} = \left( \begin{matrix} 0 &{} g_{1} &{} g_{2} \\ g_{1} &{} 0 &{} g_{2} \\ g_{2} &{} g_{2} &{} 0 \\ \end{matrix} \right) , \end{aligned}$$

(97)

where $|g_{1}|\ge |g_{2}|$. This can be achieved with the following procedure.

• (i) Rotate to the principal axes by computing

  $$\begin{aligned} V_{ik} G_{kl}^{symm} V_{jl} = \text{G}_{\rm ij}^{\sigma } = \left( \begin{matrix} \sigma_{1} &{} 0 &{} 0 \\ 0 &{} \sigma_{2} &{} 0 \\ 0 &{} 0 &{} \sigma_{3} \\ \end{matrix} \right) , \end{aligned}$$

  (98)

  where $\sigma_i$ are the eigenvalues, with $\sigma_{1}\le \sigma_{2} \le \sigma_3$, and where the rotation matrix $V_{ij}$ is built from the corresponding eigenvectors.

• (ii) Reorder the eigenvalues to obtain the configuration of maximum energy, by defining

  $$\begin{aligned} {R^{0}_{ij}} = \left( \begin{matrix} \cos (\theta ) &{} 0 &{} \sin (\theta ) \\ 0 &{} 1 &{} 0 \\ -\sin (\theta ) &{} 0 &{} \cos (\theta ) \\ \end{matrix} \right) , \end{aligned}$$

  where $\theta =90^{\circ}$ if $({\sigma_{1}}{\sigma_{2}})<0$, $\theta =0^{\circ}$ otherwise, and computing

  $$\begin{aligned} {R^{0}_{ik}} G_{kl}^{\sigma } {R^{0}_{jl}} = {\text{G}_{\rm ij}^{0}}. \end{aligned}$$

  (99)

• (iii) Rotate around first axis to make null a diagonal coefficient, by defining

  $$\begin{aligned} R^1_{ij} = \left( \begin{matrix} 1 &{} 0 &{} 0 \\ 0 &{} \cos (\theta ) &{} -\sin (\theta ) \\ 0 &{} \sin (\theta ) &{} \cos (\theta ) \\ \end{matrix} \right) , \end{aligned}$$

  where $\theta =90^{\circ}$ if $|{G_{22}^{0}} |<\varepsilon$, $\theta =\tan^{-1}\left( \sqrt{{G_{11}^{0}}/{G_{22}^{0}} + 1}\right)$ otherwise, and computing

  $$\begin{aligned} R^1_{ik} G_{kl}^{0} R^1_{jl} = G_{ij}^{1}. \end{aligned}$$

  (100)

• (iv) Rotate around third axis to make null the remaining diagonal coefficients, by defining

  $$\begin{aligned} {R^{2}_{ij}} = \left( \begin{matrix} \cos (\theta ) &{} -\sin (\theta ) &{} 0\\ \sin (\theta ) &{} \cos (\theta ) &{} 0\\ 0 &{} 0 &{} 1 \\ \end{matrix} \right) , \end{aligned}$$

  where $\theta^{0}=45^{\circ}$, and computing

  $$\begin{aligned} {R^{2}_{ik}} {G_{kl}^1} {R^{2}_{jl}} = {G_{ij}^{2}} \end{aligned}$$

  (101)

• (v) Rotate to obtain $xy \ne xz$, by defining

  $$\begin{aligned} R^3_{ij} = \left( \begin{matrix} \cos (\theta ) &{} 0 &{} -\sin (\theta )\\ 0 &{} 1 &{} 0 \\ \sin (\theta ) &{} 0 &{} \cos (\theta )\\ \end{matrix} \right) , \end{aligned}$$

  where $\theta^{0} = 90^{\circ}$ if $|{G_{23}}^{2} |\ne |{G_{13}^{2}}|,\;{\theta} = 0^{\circ}$ otherwise, and computing

  $$\begin{aligned} R^3_{ik} G_{kl}^2 R^3_{jl} = G_{ij}^{3}. \end{aligned}$$

  (102)

• (vi) Rotate to obtain $sign(xz) = sign(yz)$, by defining

  $$\begin{aligned} {R^{4}_{ij}} = \left( \begin{matrix} 1 &{} 0 &{} 0 \\ 0 &{} \cos (\theta ) &{} -\sin (\theta ) \\ 0 &{} \sin (\theta ) &{} \cos (\theta ) \\ \end{matrix} \right) , \end{aligned}$$

  where $\theta^{0}=180^{\circ}$ if $|{G_{23}}^{3}-{G_{13}^{3}} |> 0$, $\theta =0^{\circ}$ otherwise, and computing

  $$\begin{aligned} {R^{4}_{ik}} G_{kl}^3 R^4_{jl} = G_{ij}^{4}. \end{aligned}$$

  (103)

Finally, by defining

$$\begin{aligned} {S_{ij}} = R^4_{ik} R^3_{kl} R^2_{lm} R^1_{mn} R^{0}_{np} V_{pj} \end{aligned}$$

the full transformation can be expressed as

$$\begin{aligned} {G_{ij}^{rot}} = S_{ik} G_{kl}^{symm} S_{jl} \end{aligned}$$

(104)

and the opposite transformation as

$$\begin{aligned} G_{ij}^{symm} = S_{ki} G_{kl}^{rot} S_{lj}. \end{aligned}$$

(105)

1.2 The wall-RVE case

In this case, the process starts with a real, null trace but not necessarily symmetric tensor

$$\begin{aligned} {G_{ij}^{org}} = \left( \begin{matrix} g_{11} &{} g_{12} &{} g_{13} \\ g_{21} &{} g_{22} &{} g_{23} \\ g_{33} &{} g_{32} &{} -(g_{11}+g_{22}) \\ \end{matrix} \right) , \end{aligned}$$

(106)

typical of a full velocity gradient, a unit vector $n_{i}$ normal to the wall and a cell-centered velocity $U_i$. The idea is to express ${G_{ij}^{org}}$ in a new local coordinate system, where the unit vectors ${\hat{i}}$, ${\hat{j}}$, ${\hat{k}}$ represent the axes, so that the wall normal is aligned with the ${\hat{j}}$ direction and the tangential velocity ${U_{i}^{\tau}} = U_{i} - (U_{j} n_{j}) n_{i}$ is aligned with the ${\hat{i}}$ direction (Fig. 37).

Fig. 37

Procedure for elements on walls

• 1. Define the auxiliary variables as

  $$\begin{aligned} s= & {} n_{i} {\hat{j}}_i \\ m= & {} {\epsilon_{ijk}} {n_{j}} {\hat{j}}_k \end{aligned}$$

  where ${\epsilon_{ijk}}$ is the Levi–Civita tensor.

• 2. Rotate such as align boundary normal with y-direction

  $$\begin{aligned} R^1_{ij} = s {\delta_{ij}} + (1-s) m_im_j/\sqrt{m_km_k} + n_{i} {\hat{j}}_j - n_j {\hat{j}}_i \end{aligned}$$

  where ${\delta_{ij}}$ is the identity tensor and compute

  $$\begin{aligned} R^1_{ik} G_{kl}^{org} R^1_{jl} = G_{ij}^{1}. \end{aligned}$$

  (107)

• 3. Redefine the auxiliary variables as

  $$\begin{aligned} U^{\prime}_i= & {} R^1_{ij} U_j^\tau \\ s= & {} U^{\prime}_i{\hat{i}}_i \\ m= & {} {\epsilon_{ijk}} U^{\prime}_j{\hat{i}}_k \end{aligned}$$

• 4. Rotate such as align tangential velocity with x-direction

  $$\begin{aligned} R^2_{ij} = s {\delta_{ij}} + (1-s) m_im_j/\sqrt{m_km_k} + U^{\prime}_i {\hat{i}}_j - U^{\prime}_j {\hat{i}}_i \end{aligned}$$

  and compute

  $$\begin{aligned} R^2_{ik} G_{kl}^{1} R^2_{jl} = {G_{ij}^{rot}}. \end{aligned}$$

  (108)

Finally, by defining

$$\begin{aligned} {S_{ij}} = R^2_{ik} R^1_{kj} \end{aligned}$$

the full transformation can be expressed as

$$\begin{aligned} {G_{ij}^{rot}} = S_{ik} G_{kl}^{org} S_{jl} \end{aligned}$$

(109)

It is important to note that:

• The resulting tensor ${G_{ij}^{rot}}$ is aligned with boundary normal and tangential velocities.

• This tensor is expressed as

  $$\begin{aligned} {G_{ij}^{rot}} = \left( \begin{matrix} 0 &{} g_{1} &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{matrix} \right) , \end{aligned}$$

  (110)

  only if the unique non-zero component of ${G_{ij}^{org}}$ is uv (with u aligned to the tangential velocity and v to the wall normal). If this is not the case, the other non-zero components are neglected.