A pseudo-DNS method for the simulation of incompressible fluid flows with instabilities at different scales

Abstract

In this work, a new model for the analysis of incompressible fluid flows with massive instabilities at different scales is presented. It relies on resolving all the instabilities at all scales without any additional model, i.e., following the direct numerical simulation style. Nevertheless, the computation is carried out at two levels or scales, termed the coarse and the fine. The fine-scale simulation is performed on representative volume elements providing the homogenized stress tensor as a function of several dimensionless numbers characterizing the flow. Consequently, the effect of the fine-scale instabilities is transferred to the coarse level as a homogenized stress tensor, a procedure inspired by standard multi-scale methods used in solids. The present proposal introduces a new way for the treatment of the flow at the fine scale, simulating not only the coarse scale but also the fine scale with all the necessary detail, but without incurring in the excessive computational cost of the classical DNS. Another interesting aspect of the present proposal is the use of a Lagrangian formulation for convecting the eddies simulated on the fine mesh through the coarse domain. Several examples showing the potentiality of this methodology for the simulation of homogeneous flows are presented.

1 Introduction

Nearly all the fluid flow problems encountered in the engineering practice and the vast majority of natural fluid flows present instabilities at different scales, which are very difficult to either treat analytically or simulate numerically. In many cases, the effect of these instabilities cannot be neglected due to its impact upon the overall flow behavior. For this reason, accurate representation of these instabilities defines one of the focuses of current research in computational fluid dynamics (CFD). In the following, we shall use the term massively unstable flows to denominate any kind of flow that present instabilities simultaneously in a wide range of scales.

In modern engineering design, CFD simulations are having a tremendous impact on a variety of applications, like aerial, aquatic, and terrestrial vehicles, among many others. In process engineering, simulations play an equally important role, but the scenarios may be even more challenging due to the frequent presence of multiple phases. Despite a large number of associated drawbacks, researchers and users of numerical methods have managed such complexity by resorting to a lot of empiricism that over time is giving way to the greater role of simulation.

Numerical methods base their calculation power on the discretization of both the independent variables, usually space and time, and their primary dependent variables, which in the case of CFD problems are typically pressure and velocity. Mathematical models in fluid mechanics expressed in integral-differential form are converted by numerical methods into systems of usually nonlinear algebraic equations that must be solved at each degree of freedom (dof) produced by the discretization.

Due to the limitations in the computational resources available, not everything is amenable of being simulated, even when having a mathematical model sufficiently accurate for the physical phenomenon at hand. In many cases, part of the equations must be modeled using some empirical approximations. However, due to the limitations inherent of empirical approximations, the idea of fully resolving numerically the considered physical problem is gaining strength.

1.1 Ways of dealing with instabilities in a fluid flow simulation

The primary challenge in numerical simulation of massively unstable flows originates from the enormous range of scales that must be resolved. For accurate simulations, the size of the computational domain must typically be at least one order of magnitude larger than the largest energy containing waves, while the computational mesh must be fine enough to resolve the smallest dynamically significant length scale, related to the turbulence kinetic energy dissipation, or Kolmogorov scale [1].

The simulation of flows without relying on any empirical approximation is known as direct numerical simulation (DNS), a technique that allows for solving problems that cannot be solved by theoretical methods. Given enough computational resources, DNS is able to fully solve the governing equations in geometries of arbitrary complexity, providing the whole answer to the problem at hand, by simulating both the local details of instabilities and their impact on the bulk flow. This power goes well beyond that of theoretical tools, e.g., the theory of bifurcations. Besides, it provides much more information, fully detailed in space and time, than a real experiment. It could be thought as a numerical approach of obtaining the same information as that of an analytic solution. Another potential capability of the DNS method is that of exploring universality, that is, to arrive at the lower limit scale where molecular diffusion phenomena dominate, thus capturing all the flow structures.

From the pioneering work published by Orszag in 1969 [2], many DNS studies in incompressible flows have been carried out [3,4,5,6,7,8,9,10,11,12,13]. Unfortunately, despite the recent rapid hardware development, the number of degrees of freedom that is required to handle unstable flow problems via DNS makes this approach still unfeasible for engineering applications already at moderate Reynolds numbers. On the other hand, recent DNS studies allowed to analyze flows at Reynolds numbers higher than that achievable in laboratory experiments. The limitation of the latter originates from the need of having very large facilities to produce high-speed flows, in addition to the impossibility of observing unstable flow structures at very small scales and in situations with high intermittence. Therefore, any progress in DNS may help in further improving our understanding of unstable fluids.

In order to considerably reduce the computational cost in the simulation of unstable flows, the Reynolds-averaged Navier–Stokes (RANS) approach was developed [14, 15]. RANS is based on averaging all the scales, incorporating the effect of the averaged scales on the overall flow via models that rely on experimentally obtained empirical coefficients. The more advanced and powerful RANS methods are those classified as Reynolds stress models (RSM), which try to transport the full Reynolds stress tensor instead of relying on a turbulent eddy viscosity and the Boussinesq approximation. Some of the most advanced methods of this kind are based on the algebraic Reynolds stress model (ASM) [16], most notably in its explicit versions (EASM, see for example [17, 18]). However, the lost details of the transient behavior of the flow in the averaging process make RANS not adequate for many practical situations. Particularly, it usually fails to predict complex flow features, such as the transition from onset to almost fully developed turbulence, making it unsuitable in general for modeling massively unstable flows.

Yet another approach for modeling massively unstable flows is the large eddy simulation (LES) technique [19,20,21,22,23,24,25]. In LES, the large-scale motions (large eddies) are computed directly on the mesh, leaving only small (subgrid) scale motions to be modeled. This leads to a considerable reduction in computational cost in comparison with DNS. However, the limit between large and small eddies is not well defined in this technique, being typically a decision to be made by the user of the model according to his/her experience and the available computational resources. The good practices advise setting this limit where the structures that remain to be modeled behave in a universal way, with an order dictated by the molecular scales, mostly isotropic. In fact, obtaining LES solutions of accuracy close to that of DNS still requires very fine meshes and unfeasible computational costs for the computer architectures existing today.

Despite the drawbacks mentioned above, RANS is still the only approach up to addressing most of the problems proposed by the industry, with LES reserved for situations where the relationship between mesh and precision allows its use. As for DNS, everything indicates that it will have growing prominence in science and technology and that efforts should be directed toward finding better and more efficient ways of performing it.

1.2 Present proposal

To overcome the mentioned drawbacks of the existing approaches, we propose a new method suitable for analyzing massively unstable flows as a previous step to be considered as apt to model some kinds of turbulent flows.

The main idea that motivates our present work originates from noticing a certain similarity between the microstructure present in composite solid materials and the flow structures present in the flow of fluids, in particular, those originated from instabilities. In a solid composite material, the overall rheological characteristics come from the mixing of components with different properties and topology. On the contrary, in a massively unstable flow of a fluid material, the overall behavior, which may as well be interpreted as overall rheological characteristics of a different fluid material with different apparent viscosity and/or density, is mainly due to the instabilities present in each and every scale. This effect is seen in multiphase flows, where the apparent properties are usually different from the simple average of that of the present phases, but also in single-phase flows.

On the other hand, there exists a significant difference between the microstructure of a solid and the instabilities of fluid flow. While the former is discrete (that is, there is a finite set of scales to observe), the latter is continuum. Thus, multi-scale techniques normally used in solid mechanics like the so-called hierarchical multi-scale method (see, e.g., [26, 27]) must be adapted for modeling the fluid instabilities, treating them as concurrent multi-scales.

Unlike the standard treatment of flow instabilities via separation of the velocity field into an averaged and a fluctuating component, we propose to solve a concurrent multi-scale problem on two meshes: a coarse one for solving the large scale of the flow and a fine one to solve down to the Kolmogorov scale. In this sense, when simulating the large eddies on the coarse mesh, this methodology follows somehow the guidelines of the LES technique. In contrast, the present method was inspired by the multi-scale techniques used in solids and the one proposed for flows in porous media, developed in the framework of the virtual power principle [28].

Our method, however, does not assume universality in the subgrid model and thus is free from the LES limitation that would have imposed a usually excessive requirement on the fine mesh. Our approach, instead, proposes to simulate in the fine mesh, i.e., not to model, the subgrid instabilities, and to re-insert their effect into the coarse mesh problem in a computationally efficient way. The present proposal modifies also the treatment of the flow on the fine mesh, simulating it with all the necessary detail but without incurring into the limitations of the classical DNS. This is achieved by performing the fine mesh simulations in an off-line fashion, with results stored in a dimensionless form in a database for future use. In this work, this dimensionless database is computed from the relationship between some measure of the fine-scale stress tensor computed in a representative volume element (RVE) with respect to the stress tensor using the molecular viscosity. For using this off-line information, the table should be first converted in dimensional units prior to being upscaled to the coarse mesh. This is complemented with a Lagrangian formulation for convecting on the coarse mesh the instabilities simulated on the fine mesh, to further reduce computational costs and improve accuracy. It should be noted, however, that our proposal does not exclude the possibility of using a purely Eulerian approach, i.e., without Lagrangian particles moving over the fixed grid. Such a variant, along with a RANS-like mesh, may be thought as a new approach to algebraic Reynolds stress models.

Furthermore, although out of the scope of the present contribution, it is important to note that the off-line methodology that is part of pseudo-DNS opens the door to employing advanced acceleration techniques for these fine problem simulations. One possibility is the use of a priori searching by means of artificial intelligence techniques to arrive at a reduced model that represents better the phenomena occurring at the small scale. In this way, a remarkable increase in terms of accuracy versus computational cost may be reached when compared with the LES technique. Thus, it may become possible to introduce a method characterized by high precision at a reasonable cost into the industrial community.

We propose denominating our approach a pseudo-direct numerical simulation or pseudo-DNS method. Summarizing, then, the main differences between the present model and other approaches to turbulence problems are the following:

• The separation between coarse and fine scales is arbitrary, not related to any universality assumptions;

• Both the large and the small scales are resolved numerically in concurrent meshes, each one responsible for solving its corresponding range of scales;

• The small eddies are convected by virtual particles that move in a Lagrangian fashion, thus improving accuracy in resolving convection with no spurious numerical diffusion;

• The fine mesh problems are solved off-line beforehand and stored in a dimensionless form in a database.

These features circumvent the necessity of representing all the large eddies in the coarse mesh, defining an important advantage over LES approach in terms of the ratio between accuracy and efficiency.

As the first step in this development, only homogeneous fluid flow problems shall be considered in the present work. However, with this type of techniques, it may also be possible to deepen the understanding of the interaction of the instabilities in a context of multiphase flows. It is well known that instabilities in multiphase flows radically change their behavior in relation to the case of a single phase, but currently, the research of this topic still remains at an initial stage.

Another application that appears to be disruptive in modern technology is that of active fluids [13]. An active fluid is a densely packed soft material whose constituent elements can self-propel, e.g., dense suspensions of bacteria, microtubule networks, and artificial swimmers. These materials appear under the broad category of active matter and differ significantly in properties when compared to passive fluids, which can be directly described using Navier–Stokes equations. Even though systems behaving as active fluids have been observed and investigated in different contexts for a long time, scientific interest in properties directly related to the activity has emerged only in the past two decades. These materials have been shown to exhibit a variety of different states ranging from well-ordered patterns (laminar) to chaotic states (unstable turbulent flows). This property opens up ways to the modification of the rheological behavior of the fluids at convenience and even promote a given spatial distribution according to the needs. Recent experimental investigations have suggested that the various dynamic states exhibited by active fluids may have important technological applications. It is expected that the technique proposed here presents a new perspective to address the challenge of predicting the behavior of active fluids. Although in this article only homogeneous fluid problems will be solved, the fact of numerically simulating small scales opens then the door to the simulation of instabilities in multi-fluids, in particulate fluids and especially in active fluids.

The article is organized as follows: Section 2 presents the methodology in terms of how to split the solution concurrently between the coarse and the fine scales. Section 3 presents the details of the RVE that is used as the basis for the fine-scale simulation and the strategy to transfer the data back and forth between the coarse and the fine meshes. Section 4 describes the whole algorithm, the role of the Lagrangian formulation, and the way in which both meshes are coupled in order to have a numerically stable algorithm. Section 5 shows numerical examples to demonstrate the accuracy and feasibility of the proposed method for some simple but significant problems. Finally, Sect. 6 is devoted to remarks and conclusions.

2 Methodology

The pseudo-DNS approach is based on three main concepts:

• 1. The unknowns, velocity and pressure, are solved separately in two meshes, namely coarse and fine.

• 2. The fine mesh solution, in turn, is obtained by direct numerical simulation of many separate subproblems in small domains, i.e. the RVEs, subject to consistent boundary conditions taken from the coarse solution.

• 3. These RVEs are associated with virtual particles that move in a Lagrangian way according to the velocity field of the coarse scale.

The total number of degrees of freedom (DOF) obtained summing up that of both the coarse mesh and the set of RVE fine meshes is comparable to the total DOF of a full DNS model. The main advantage of the new approach, however, is that the fine mesh solution is not obtained at once for the whole domain, as in conventional DNS, but is computed on the small domain of the individual RVEs that are separate and independent.

Another key advantage of this approach is that we propose all RVEs to have the same geometry (e.g., a cube). As a consequence, the individual RVEs may be solved off-line beforehand, subject to simple boundary conditions, and the relevant results may be stored in a dimensionless form for later use. We seek then for a global solution comparable to a DNS solution but having solved off-line the most expensive part of the computations.

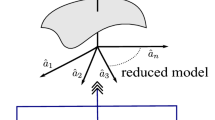
We begin by considering two different overlapped meshes, which we call coarse and fine, that cover the whole problem domain $\Omega$. A one-dimensional (1D) example with coarse and fine linear shape functions $N^{\mathrm{c}}$ and $N^{\mathrm{f}}$ is shown in Fig. 1. where a 1D illustration is introduced for the sake of clarity.

Fig. 1

One-dimensional example: coarse and fine meshes with linear shape functions. (Color figure online)

The unknown velocity and pressure fields, $u_i(x_j,t)$ and $p(x_j,t)$, are split into two parts corresponding to the coarse and fine meshes, with $u^{\mathrm{c}}$ and $p^{\mathrm{c}}$ representing the coarse fields and $u^{\mathrm{f}}$ and $p^{\mathrm{f}}$ the fine fields, giving

$$\begin{aligned}&u_i(x_j,t) = u^{\mathrm{c}}_i(x_j,t) + u^{\mathrm{f}}_i(x_j,t) \quad \text {and} \quad \nonumber \\&p(x_j,t) = p^{\mathrm{c}}(x_j,t) + p^{\mathrm{f}}(x_j,t) . \end{aligned}$$

(1)

This split is totally arbitrary, without the need for scale separation between the two meshes. The fine mesh, however, must be detailed enough so as to represent all the relevant small turbulent eddies, down to the Kolmogorov scale if required.

Independently of the approximation method used for solving the differential equations, we would end up with a system of equations that can be written as

$$\begin{aligned} \left[ \; \begin{matrix} K^{\mathrm{cc}} &{} K^{\mathrm{cf}} \\ K^{\mathrm{fc}} &{} K^{\mathrm{ff}} \end{matrix}\; \right] \left[ \; \begin{matrix} s^{\mathrm{c}} \\ s^{\mathrm{f}} \end{matrix}\; \right] = \left[ \; \begin{matrix} F^{\mathrm{c}} \\ F^{\mathrm{f}} \end{matrix}\; \right] \end{aligned}$$

(2)

where $s^{\mathrm{c}}$ and $s^{\mathrm{f}}$ represent the unknowns on both meshes, respectively. This system may be iteratively solved by computing an approximate coarse solution using the most recent fine solution available, i.e., by solving

$$\begin{aligned} K^{\mathrm{cc}}s^{\mathrm{c}} = F^{\mathrm{c}} - K^{\mathrm{cf}}s^{\mathrm{f}} \rightarrow s^{\mathrm{c}}, \end{aligned}$$

(3)

and then using the updated coarse fields to obtain an approximate fine solution from

$$\begin{aligned} K^{\mathrm{ff}}s^{\mathrm{f}} = F^{\mathrm{f}} - K^{\mathrm{fc}}s^{\mathrm{c}} \rightarrow s^{\mathrm{f}}, \end{aligned}$$

(4)

continuing the iterations until convergence. If the fine mesh is fine enough, the solution of the previous system would be equivalent to that of the full DNS solution.

The proposed approach, however, does not attempt to solve the fine mesh problem as a whole, but to approximately solve it via separated subdomains, independent from each other but influenced by the coarse solution (Fig. 2).

Fig. 2

One-dimensional example: coarse mesh and RVEs. (Color figure online)

Figures 3 and 4 show a simple one-dimensional example which serves also to show that, from a Fourier series point of view, a coarse mesh of uniform size h is able to capture wavelengths down to a value 3h, with all smaller wavelengths having to be captured by the fine mesh solution.

Fig. 3

One-dimensional problem. Representation of different wavelengths (in blue) with linear elements (in red). (Color figure online)

Fig. 4

One-dimensional problem. Wavelengths smaller than 2h are represented in the fine mesh (RVE). (Color figure online)

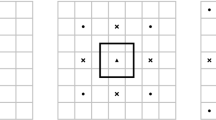
In the case of multi-dimensional general coarse meshes, the idea is to choose an RVE of size H twice the local element size h. Each point ${\mathbf {x}}$ in the domain may be associated with an RVE with its local coordinate system ${\mathbf {y}}$, as shown in Fig. 5.

Fig. 5

RVEs in the coarse mesh and the two coordinate system reference frames. (Color figure online)

In what follows, we consider that each RVE is assigned constant velocity and pressure gradients $G_{ij}$ and $H_i$, taken from the underlying coarse mesh fields, as

$$\begin{aligned} \begin{array}{ll} G_{ij} &{}= \left. \dfrac{\partial u^{\mathrm{c}}_i}{\partial x_j}\right| _{\mathbf {x}}, \\ H_i &{}=\left. \dfrac{\partial p^{\mathrm{c}}}{\partial x_i}\right| _{\mathbf {x}}. \end{array} \end{aligned}$$

(5)

These tensors are used to represent the state of the fluid in the coarse scale. They are used in the fine-scale problem for imposing consistent boundary conditions at each RVE (see Fig. 6). Around any arbitrary point ${\mathbf {x}}$, the coarse fields are therefore locally approximated in RVE coordinates as

$$\begin{aligned} \begin{array}{ll} u_i^{\mathrm{c}}({\mathbf {x}}+{\mathbf {y}}) &{} = u_i^{\mathrm{c}}({\mathbf {x}}) + G_{ij} y_j, \\ p^{\mathrm{c}}({\mathbf {x}}+{\mathbf {y}}) &{} = p^{\mathrm{c}}({\mathbf {x}}) + H_i y_i. \end{array} \end{aligned}$$

(6)

Using Eq. (1), we express the local approximations for the total fields as

$$\begin{aligned} \begin{array}{lll} u_i({\mathbf {x}}+{\mathbf {y}}) &{} = u_i^{\mathrm{c}}({\mathbf {x}}) + G_{ij} y_j + u_i^{\mathrm{f}}({\mathbf {y}}) &{}= u_i^{\mathrm{c}}({\mathbf {x}}) + u_i^{\mathrm{R}}({\mathbf {y}}),\\ p({\mathbf {x}}+{\mathbf {y}}) &{} = p^{\mathrm{c}}({\mathbf {x}}) + H_i y_i + p^{\mathrm{f}}({\mathbf {y}}) &{}= p^{\mathrm{c}}({\mathbf {x}}) + p^{\mathrm{R}}({\mathbf {y}}), \end{array}\nonumber \\ \end{aligned}$$

(7)

where, for later use, we have grouped the last two terms to define the RVE fields, $u_i^{\mathrm{R}}$ and $p^{\mathrm{R}}$, associated solely with the local RVE coordinates.

Fig. 6

The downscaling process: from coarse mesh cells to their RVE off-line representations. (Color figure online)

Fig. 7

Concurrent scales, coarse scale on top, and fine scale on bottom. (Color figure online)

The splitting of fields in Eq. (1) is so far arbitrary. Without any loss of generality, we chose to account for the RVE translation and rotation within the coarse-scale velocity (see Fig. 7) by imposing the following constraints to the fine fields in domain $\Omega ^{\mathrm{R}}$ of the RVE:

$$\begin{aligned} \displaystyle&\int _{\Omega ^{\mathrm{R}}} u^{\mathrm{f}}_i {\mathrm{d}}\Omega = 0, \end{aligned}$$

(8a)

$$\begin{aligned} \displaystyle&\int _{\Omega ^{\mathrm{R}}} \dfrac{\partial u^{\mathrm{f}}_i}{\partial x_i} {\mathrm{d}}\Omega = \displaystyle \int _{\Gamma ^{\mathrm{R}}} u_i^{\mathrm{f}} l_j {\mathrm{d}}\Gamma = 0, \end{aligned}$$

(8b)

$$\begin{aligned} \displaystyle&\int _{\Omega ^{\mathrm{R}}} p^{\mathrm{f}} {\mathrm{d}}\Omega = 0, \end{aligned}$$

(8c)

$$\begin{aligned} \displaystyle&\int _{\Omega ^{\mathrm{R}}} \dfrac{\partial p^{\mathrm{f}}}{\partial x_i} {\mathrm{d}}\Omega = \displaystyle \int _{\Gamma ^{\mathrm{R}}} p^{\mathrm{f}} l_j {\mathrm{d}}\Gamma = 0. \end{aligned}$$

(8d)

where $\Gamma ^{\mathrm{R}}$ is the boundary of the RVE and $l_j$ the outer normal vector. With these imposed constraints, the fine-scale fields are then constrained to have the following average values on an RVE:

$$\begin{aligned} \displaystyle&\frac{1}{\Omega ^{\mathrm{R}}} \int _{\Omega ^{\mathrm{R}}} u_i^{\mathrm{R}} {\mathrm{d}}\Omega = 0, \end{aligned}$$

(9a)

$$\begin{aligned} \displaystyle&\frac{1}{\Omega ^{\mathrm{R}}} \int _{\Omega ^{\mathrm{R}}} \dfrac{\partial u_i^{\mathrm{R}}}{\partial x_i} {\mathrm{d}}\Omega = \displaystyle \frac{1}{\Omega ^{\mathrm{R}}} \int _{\Gamma ^{\mathrm{R}}} u_i^{\mathrm{R}} l_j {\mathrm{d}}\Gamma = G_{ij}, \end{aligned}$$

(9b)

$$\begin{aligned} \displaystyle&\frac{1}{\Omega ^{\mathrm{R}}} \int _{\Omega ^{\mathrm{R}}} p^{\mathrm{R}} {\mathrm{d}}\Omega = 0, \end{aligned}$$

(9c)

$$\begin{aligned} \displaystyle&\frac{1}{\Omega ^{\mathrm{R}}} \int _{\Omega ^{\mathrm{R}}} \dfrac{\partial p^{\mathrm{R}}}{\partial x_i} {\mathrm{d}}\Omega = \displaystyle \frac{1}{\Omega ^{\mathrm{R}}} \int _{\Gamma ^{\mathrm{R}}} p^{\mathrm{R}} l_j {\mathrm{d}}\Gamma = H_i. \end{aligned}$$

(9d)

Additionally, the total average velocity on the RVE is

$$\begin{aligned}&\displaystyle \frac{1}{\Omega ^{\mathrm{R}}} \int _{\Omega ^{\mathrm{R}}} u_i({\mathbf {x}}+{\mathbf {y}})\ {\mathrm{d}}\Omega \nonumber \\&\quad = \displaystyle \frac{1}{\Omega ^{\mathrm{R}}} \int _{\Omega ^{\mathrm{R}}} \left[ u_i^{\mathrm{c}}({\mathbf {x}}+{\mathbf {y}}) + u_i^{\mathrm{f}}({\mathbf {y}})\right] \ {\mathrm{d}}\Omega = u_i^{\mathrm{c}}({\mathbf {x}}), \end{aligned}$$

(10)

meaning that the RVE is moving with the coarse velocity field evaluated at the RVE’s coordinate center ${\mathbf {x}}$.

As conclusion, the fine mesh problem has then been reduced to solving for the fields $u_i^{\mathrm{R}}$ and $p^{\mathrm{R}}$. In each RVE, the solution is obtained via a DNS simulation subject to the constraints given in Eq. (9), which may be easily imposed on a cubical domain, by one of the following options:

• (a) As a strict constraint, i.e., via Lagrange multipliers, or as successive offset corrections in iterative approaches.

• (b) Using jump-periodic conditions depending on $G_{ij}$ and H in the 3 sets of opposite faces, namely left and right, top and bottom, and front and back.

2.1 The coarse mesh problem

The overall problem is governed by the classical incompressible Navier–Stokes equations, namely

$$\begin{aligned} \begin{array}{l} \rho A_{i} = \dfrac{\partial T_{ij}}{\partial x_j}-\dfrac{\partial p}{\partial x_i} + B_i \\ T_{ij} = \mu \left( \dfrac{\partial u_i}{\partial x_j} + \dfrac{\partial u_j}{\partial x_i}\right) = 2 \mu \dfrac{\partial ^S u_i}{\partial x_j} \\ \dfrac{\partial u_i}{\partial x_i} = 0, \end{array} \end{aligned}$$

(11)

where $\mu$ and $\rho$ are the dynamic viscosity and density of the fluid, $T_{ij}$ the symmetrical stress tensor, and $A_{i}$ the acceleration that will be written in the arbitrary Lagrangian/Eulerian (ALE) reference frame. ALE form is adopted for the sake of generality, considering that the coarse scale is solved in the Lagrangian fashion, while RVEs are treated using an Eulerian frame. The corresponding expressions are:

$$\begin{aligned} A_i = \dfrac{D^Uu_i}{Dt} + (u_j-U_j)\dfrac{\partial u_i}{\partial x_j}, \end{aligned}$$

(12)

being $U_j$ the velocity of the reference coordinates and $\dfrac{D^Uu_i}{Dt}$ the ALE time derivative with respect to a reference frame moving at velocity $U_j$.

Making use of the field splitting of Eq. (1), the Navier–Stokes equations for a fluid of constant properties read

$$\begin{aligned}&\rho \dfrac{D^U \left( u^{\mathrm{c}}_i + u^{\mathrm{f}}_i\right) }{Dt} + \rho \left( u^{\mathrm{c}}_j + u^{\mathrm{f}}_j - U_j\right) \dfrac{\partial \left( u^{\mathrm{c}}_i + u^{\mathrm{f}}_i\right) }{\partial x_j} \nonumber \\&\quad -\, 2 \mu \dfrac{\partial }{\partial x_j} \left( \dfrac{\partial ^S\left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{\partial x_j}\right) + \dfrac{\partial \left( p^{\mathrm{c}}+p^{\mathrm{f}}\right) }{\partial x_i} - B_i = 0 ,\nonumber \\&\dfrac{\partial \left( u^{\mathrm{c}}_i + u^{\mathrm{f}}_i\right) }{\partial x_i} = 0. \end{aligned}$$

(13)

By making the reference frame move with the coarse-scale velocity, i.e., by setting $U_j = u^{\mathrm{c}}_j$, we get Eq. (13) in the form

$$\begin{aligned}&\rho \dfrac{D^U \left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{Dt} + \rho u^{\mathrm{f}}_j \dfrac{\partial \left( u^{\mathrm{c}}_i + u^{\mathrm{f}}_i\right) }{\partial x_j} \nonumber \\&\quad -\, 2 \mu \dfrac{\partial }{\partial x_j} \left( \dfrac{\partial ^S\left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{\partial x_j}\right) + \dfrac{\partial \left( p^{\mathrm{c}}+p^{\mathrm{f}}\right) }{\partial x_i} - B_i = 0\nonumber \\&\dfrac{\partial \left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{\partial x_i} = 0 \end{aligned}$$

(14)

By spatially averaging this equation over an RVE, we obtain

$$\begin{aligned}&\displaystyle \frac{1}{|\Omega ^{\mathrm{R}}|}\left[ \rho \displaystyle \int _{\Omega ^{\mathrm{R}}}\dfrac{D^U \left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{Dt} {\mathrm{d}}\Omega + \rho \displaystyle \int _{\Omega ^{\mathrm{R}}}u^{\mathrm{f}}_j \dfrac{\partial \left( u^{\mathrm{c}}_i + u^{\mathrm{f}}_i\right) }{\partial x_j} {\mathrm{d}}\Omega \right. \nonumber \\&\quad \left. -\, 2 \mu \displaystyle \int _{\Omega ^{\mathrm{R}}}\dfrac{\partial }{\partial x_j} \left( \dfrac{\partial ^S\left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{\partial x_j}\right) {\mathrm{d}}\Omega \right. \nonumber \\&\quad \left. + \displaystyle \int _{\Omega ^{\mathrm{R}}}\dfrac{\partial \left( p^{\mathrm{c}}+p^{\mathrm{f}}\right) }{\partial x_i} {\mathrm{d}}\Omega - \displaystyle \int _{\Omega ^{\mathrm{R}}}B_i {\mathrm{d}}\Omega \right] = 0\nonumber \\&\displaystyle \frac{1}{|\Omega ^{\mathrm{R}}|}\left[ \displaystyle \int _{\Omega ^{\mathrm{R}}}\dfrac{\partial \left( u^{\mathrm{c}}_i+u^{\mathrm{f}}_i\right) }{\partial x_i} {\mathrm{d}}\Omega \right] = 0\nonumber \\ \end{aligned}$$

(15)

It is easy to see that, using Eq. (8), several terms vanish, leading to

$$\begin{aligned}&\displaystyle \frac{1}{|\Omega ^{\mathrm{R}}|} \int _{\Omega ^{\mathrm{R}}}\left[ \rho \dfrac{D^U u^{\mathrm{c}}_i}{Dt} + \rho u^{\mathrm{f}}_j \dfrac{\partial u^{\mathrm{f}}_i}{\partial x_j}\right. \nonumber \\&\quad \left. -\, 2 \mu \dfrac{\partial }{\partial x_j} \left( \dfrac{\partial ^Su^{\mathrm{c}}_i}{\partial x_j}\right) + \dfrac{\partial p^{\mathrm{c}}}{\partial x_i} - B_i \right] {\mathrm{d}}\Omega = 0 \nonumber \\&\displaystyle \frac{1}{|\Omega ^{\mathrm{R}}|} \int _{\Omega ^{\mathrm{R}}}\dfrac{\partial u^{\mathrm{c}}_i}{\partial x_i} {\mathrm{d}}\Omega = 0 \end{aligned}$$

(16)

Furthermore, by using Eqs. (6) and (10), we get

$$\begin{aligned}&\rho \dfrac{D^U u^{\mathrm{c}}_i}{Dt} + \dfrac{\partial T^{\rho }_{ij}}{\partial x_j} + \dfrac{\partial p^{\rho }}{\partial x_i}\nonumber \\&\quad -\, 2 \mu \dfrac{\partial }{\partial x_j} \left( \dfrac{\partial ^Su^{\mathrm{c}}_i}{\partial x_j}\right) + \dfrac{\partial p^{\mathrm{c}}}{\partial x_i} - B_i = 0 \nonumber \\&\dfrac{\partial u^{\mathrm{c}}_i}{\partial x_i} = 0 \end{aligned}$$

(17)

where we have introduced the fine inertial deviatoric stress and the fine inertial pressure, defined as

$$\begin{aligned} \begin{array}{l} T^{\rho }_{ij}= \displaystyle \frac{1}{|\Omega ^{\mathrm{R}}|} \int _{\Omega ^{\mathrm{R}}}\left( \rho u^{\mathrm{f}}_i u^{\mathrm{f}}_j \right) ^{dev} {\mathrm{d}}\Omega , \\ p^{\rho }= \displaystyle \frac{1}{|\Omega ^{\mathrm{R}}|} \int _{\Omega ^{\mathrm{R}}}\dfrac{\delta _{ij}}{3} \left( \rho u^{\mathrm{f}}_i u^{\mathrm{f}}_j \right) {\mathrm{d}}\Omega . \end{array} \end{aligned}$$

(18)

The weighted residual form of the coarse-scale problem can thus be written as:

$$\begin{aligned}&\displaystyle \int _{\Omega } w_i^{\mathrm{c}} \rho \dfrac{D^U u^{\mathrm{c}}_i}{Dt} {\mathrm{d}}\Omega \nonumber \\&\quad - \displaystyle \int _{\Omega } \dfrac{\partial w_i^{\mathrm{c}}}{\partial x_j} \left[ T^{\rho }_{ij}+ p^{\rho }\delta _{ij} - 2 \mu \dfrac{\partial ^Su^{\mathrm{c}}_i}{\partial x_j} + p^{\mathrm{c}} \delta _{ij} \right] {\mathrm{d}}\Omega \nonumber \\&\quad - \displaystyle \int _{\Omega } w_i^{\mathrm{c}} B_i {\mathrm{d}}\Omega = 0, \nonumber \\&\displaystyle \int _{\Omega } q^{\mathrm{c}} \dfrac{\partial u^{\mathrm{c}}_i}{\partial x_i} {\mathrm{d}}\Omega = 0, \end{aligned}$$

(19)

where $w^{\mathrm{c}}_i$ and $q^{\mathrm{c}}$ are weight functions defined in the coarse mesh.

The momentum equation must still be integrated in time, in our case via a Lagrangian formulation. The Lagrangian integration in time of any function $f^t({\mathbf {x}}^t)$ whose reference coordinate moves at a velocity ${\mathbf {U}}$ is:

$$\begin{aligned} f^{\Delta t}({\mathbf {x}}^{\Delta t})= & {} f^0({\mathbf {x}}^0) + \displaystyle \int _0^{\Delta t} f^t({\mathbf {x}}^t)\ \mathrm{d}t \nonumber \\= & {} f^0({\mathbf {x}}^0) + f^{\theta \Delta t}({\mathbf {x}}^{\theta \Delta t}) \Delta t \end{aligned}$$

(20)

for some $0\le \theta \le 1$ with ${\mathbf {x}}^t = {\mathbf {x}}^0 + \displaystyle \int _{\tau =0}^{\tau =t} {\mathbf {U}}({\mathbf {x}}^{\tau })\ {\mathrm{d}}\tau$. The time integration of the weighted residual momentum equations in the coarse scale then reads

$$\begin{aligned}&\displaystyle \int _{\Omega }w_i^{\mathrm{c}} \rho \left( u_i^{\mathrm{c}}\right) _{{\mathbf {x}}^{t+\Delta t}}^{t+\Delta t}\, {\mathrm{d}}\Omega \nonumber \\&\quad = \displaystyle \int _{\Omega }w_i^{\mathrm{c}} \rho \left( u^{\mathrm{c}}_i\right) _{{\mathbf {x}}^{t}}^{t}\, {\mathrm{d}}\Omega + \displaystyle \int _t^{t+\Delta t} \displaystyle \int _\Omega \dfrac{\partial w_i^{\mathrm{c}}}{\partial x_j} \left( T^{\rho }_{ij}\right) _{{\mathbf {x}}^\tau }^\tau \, {\mathrm{d}}\Omega \, {\mathrm{d}}\tau \nonumber \\&\qquad + \displaystyle \int _t^{t+\Delta t} \displaystyle \int _\Omega \dfrac{\partial w_i^{\mathrm{c}}}{\partial x_j} \left( p^{\rho }\delta _{ij} \right) _{{\mathbf {x}}^\tau }^\tau \, {\mathrm{d}}\Omega \, {\mathrm{d}}\tau \nonumber \\&\qquad - 2 \mu \displaystyle \int _t^{t+\Delta t} \displaystyle \int _\Omega \dfrac{\partial w_i^{\mathrm{c}}}{\partial x_j} \left( \dfrac{\partial ^S u^{\mathrm{c}}_i}{\partial x_j} \right) _{{\mathbf {x}}^\tau }^\tau \, {\mathrm{d}}\Omega \, {\mathrm{d}}\tau \nonumber \\&\qquad + \displaystyle \int _t^{t+\Delta t} \displaystyle \int _\Omega \dfrac{\partial w_i^{\mathrm{c}}}{\partial x_j} \left( p^{\mathrm{c}} \delta _{ij} \right) _{{\mathbf {x}}^\tau }^\tau \, {\mathrm{d}}\Omega \, {\mathrm{d}}\tau \nonumber \\&\qquad + \displaystyle \int _t^{t+\Delta t} \displaystyle \int _\Omega w_i^{\mathrm{c}} \left( B_i \right) _{{\mathbf {x}}^\tau }^\tau \, {\mathrm{d}}\Omega \, {\mathrm{d}}\tau . \end{aligned}$$

(21)

Therefore, the coarse mesh problem reduces to solving Eqs. (21) and (20-b), where the inertial stresses $T^{\rho }_{ij}$ and pressure term $p^{\rho }$ must be provided by the fine mesh problem.

2.2 The fine mesh problem

Let us consider an RVE with center at position ${\mathbf {x}}_p^t$ moving with velocity $u^{\mathrm{c}}_i({\mathbf {x}}_p^t)$. At the RVE level, the equations to be solved are

$$\begin{aligned}&\rho \left[ \dfrac{D^U u^{\mathrm{c}}_i({\mathbf {x}}_p^t)}{Dt} + \dfrac{\partial u^{\mathrm{R}}_i}{\partial t} + u^{\mathrm{R}}_j \dfrac{\partial u^{\mathrm{R}}_i}{\partial x_j} \right] \nonumber \\&\quad - 2 \mu \dfrac{\partial }{\partial x_j} \left( \dfrac{\partial ^Su^{\mathrm{R}}_i}{\partial x_j}\right) + \dfrac{\partial p^{\mathrm{R}}}{\partial x_i} - B_i = 0 \nonumber \\&\dfrac{\partial u^{\mathrm{R}}_i}{\partial x_i} = 0 \end{aligned}$$

(22)

We now define weight functions $w^{\mathrm{R}}_i$ and $q^{\mathrm{R}}$ in the RVE’s fine mesh and require the fine solution to fulfill the following weighted residual form

$$\begin{aligned}&\displaystyle \int _{\Omega } w_i^{\mathrm{R}} \rho \left[ \dfrac{D^U u^{\mathrm{c}}_i({\mathbf {x}}_p^t)}{Dt} + \dfrac{\partial u^{\mathrm{R}}_i}{\partial t} + u^{\mathrm{R}}_j \dfrac{\partial u^{\mathrm{R}}_i}{\partial x_j} \right] {\mathrm{d}}\Omega \nonumber \\&\quad + \displaystyle \int _{\Omega } \dfrac{\partial w_i^{\mathrm{R}}}{\partial x_j} \left[ - 2 \mu \dfrac{\partial ^Su^{\mathrm{R}}_i}{\partial x_j} + p^{\mathrm{R}} \delta _{ij} \right] {\mathrm{d}}\Omega \nonumber \\&\quad - \displaystyle \int _{\Omega } w_i^{\mathrm{R}} B_i {\mathrm{d}}\Omega = 0, \displaystyle \int _{\Omega } q^{\mathrm{R}} \dfrac{\partial u^{\mathrm{c}}_i}{\partial x_i} {\mathrm{d}}\Omega = 0. \end{aligned}$$

(23)

This is solved by DNS with the restrictions of Eq. (9), which, in the current work, are applied via suitable boundary conditions (jump boundary conditions explained in Sect. 3). To impose these restrictions, the RVE problem requires information from the coarse solution at ${\mathbf {x}}_p^t$, namely the gradients $G_{ij}$ and $H_i$ and the acceleration $A_i=D^U u^{\mathrm{c}}_i({\mathbf {x}}_p^t)/Dt$. We propose to non-dimensionalize these three variables by defining the following dimensionless numbers:

$$\begin{aligned} \text {Id}_{ij}= & {} G_{ij} \dfrac{ H^2}{\nu }; \text {Ip}_i = -8 \; \text {sign}(H_i) \sqrt{\frac{|H_i|}{\rho H}} \frac{H^2}{\nu } ;\nonumber \\ \text {Ia}_i= & {} \dfrac{A_i \Delta t}{H} \frac{H^2}{\nu }. \end{aligned}$$

(24)

These numbers are passed from the coarse mesh to each RVE, which in turn returns the corresponding dimensionless inertial deviatoric stresses and pressures

$$\begin{aligned} {\tilde{T}}^{\rho }_{ij}= \dfrac{T^{\rho }_{ij}}{\mu \Vert G\Vert } ; ~~~ {\tilde{p}}^{\rho }= \dfrac{p^{\rho }}{\mu \Vert G\Vert } \end{aligned}$$

(25)

for the coarse formulation to use them after the corresponding re-dimensionalization.

3 Building an RVE

The solution on the fine mesh is obtained subdividing the total domain into small RVEs that are simulated separately by imposing consistent boundary conditions in accordance with the dimensionless parameters defined in Eq. (24). In this work, both density and viscosity are considered constant in all the domain (homogeneous fluids). But, in case of variations, an average of the density and the viscosity in all the RVE volume must be taken for the evaluation of Id, such as for the multiphase flow case.

An entire RVE database should include information about the stress response obtained on the fine mesh against variations of Id$_{ij}$, Ip$_i$ and Ia$_i$. However, a database like that would require a huge computational effort which is left for future work. Instead, we will consider only a subset of cases that are characterized by depending on the Id parameter only. In this case, the only relevant coarse mesh parameter is the velocity gradient $G_{ij}$, which is the averaged strain tensor on an RVE of size H. To eliminate the rigid body rotations, which do not introduce instabilities, the tensor must be transformed into a symmetrical form. It is well known that shear is one of the main sources of flow instabilities, e.g., those of Kelvin–Helmholtz type. Therefore, in order to obtain maximum instabilities, it is convenient to rotate the tensor G to a direction characterized by the presence of shear stresses only, that is, the direction for which the axial strain velocities (diagonal terms of $G_{ij}$) vanish. With the appropriate tensor rotations (detailed in Sect. 4.2), it is possible to obtain:

$$\begin{aligned} G_{ij}= & {} \left[ \; \begin{matrix} G_{xx} &{} G_{xy} &{} G_{xz} \\ G_{xy} &{} G_{yy} &{} G_{yz} \\ G_{xz} &{} G_{yz} &{} G_{zz} \\ \end{matrix}\; \right] \rightarrow G^\prime _{ij} = \left[ \; \begin{matrix} 0 &{} G^\prime _{xy} &{} G^\prime _{xz} \\ G^\prime _{xy} &{} 0 &{} G^\prime _{xz} \\ G^\prime _{xz} &{} G^\prime _{xz} &{} 0 \\ \end{matrix}\; \right] \rightarrow \nonumber \\ \text {Id}_{ij}= & {} \left[ \; \begin{matrix} 0 &{} \text {Id}_1 &{} \text {Id}_2 \\ \text {Id}_1 &{} 0 &{} \text {Id}_2 \\ \text {Id}_2 &{} \text {Id}_2 &{} 0 \\ \end{matrix}\; \right] \end{aligned}$$

(26)

which depends on only two parameters, Id$_1$ and Id$_2$. Choosing H as the size of the RVE, one must ensure that it is large enough so as to represent all the necessary wavelengths, and at the same time, sufficiently small so as to ensure validity of the constant velocity gradients hypothesis. In this context, $H = 2h$ is a good compromise, h being the local size of the coarse mesh.

Remark

A detail to be taken into account is that although this simplified problem has only two independent parameters, it still results in a dimensionless deviatoric inertial stress tensor with 5 different values due to symmetry and tracelessness, plus the additional dimensionless inertial pressure. Therefore, the off-line tables consist in 6 response surfaces (see conceptual example in Fig. 8).

Fig. 8

One of the 6 surfaces representing the dimensionless RVE stress tensor as a function of Id$_1$ and Id$_2$ parameters. P is a point laying on the surface that represents $\tilde{T}_{ij}=f_{ij}(Id_1=A,Id_2=B)$ with i, j sweeping the six tensor coefficients. (Color figure online)

Two different RVEs will be distinguished:

• An internal RVE for dealing with far-from-walls instabilities, and

• A wall RVE for instabilities in the vicinity of the domain solid walls.

3.1 Internal RVE

For the sake of simplicity, in this work only $G_{xy}$ velocity gradients are considered. In this case, the only non-dimensional number to be used is Id$_1$ (i.e., Id$_2=0$). The range of Id$_1$ will be limited in order to make the simulations affordable for a standard finite volume method (FVM) code on standard computer architecture. For future work, larger Ids should be solved using high-performance computing resources.

Figure 9 presents a general configuration of the internal RVE. In order to accomplish the constraint conditions for $u^{\mathrm{f}}_i$, both translation and rotation are considered in $u^{\mathrm{c}}_i$, leading to the set of constraints shown in Fig. 9.

Fig. 9

Configuration of the internal RVE. (Color figure online)

In the RVE, standard Navier–Stokes equations are solved for the unknowns $u^{\mathrm{R}}$ and $p^{\mathrm{R}}$. Therefore, satisfying the constraints leads to:

$$\begin{aligned} \left\{ \; \begin{aligned}&\int _{\Omega ^{\mathrm{R}}} u^{\mathrm{R}}_i\ {\mathrm{d}}\Omega = 0 \\&\dfrac{1}{\Omega ^{\mathrm{R}}}\int _{\Omega ^{\mathrm{R}}} \dfrac{\partial u^{\mathrm{R}}_i}{\partial x_j}\ {\mathrm{d}}\Omega = \dfrac{1}{\Omega ^{\mathrm{R}}}\int _{\Gamma } u^{\mathrm{R}}_i n_j \ {\mathrm{d}}\Gamma = G_{ij}\\ \end{aligned} \right. \end{aligned}$$

(27)

The former equation is satisfied as a global restriction (imposed using Lagrangian multipliers), while the latter is accomplished using periodic with jump boundary conditions, i.e.,

$$\begin{aligned} u^{\mathrm{R}}_i({\mathbf {x}}^+)= & {} u^{\mathrm{R}}_i({\mathbf {x}}^-)+ G_{ij}(x_j^+ - x_j^-) \qquad \nonumber \\&\rightarrow \dfrac{1}{\Omega ^{\mathrm{R}}}\displaystyle \int _{\Gamma } u^{\mathrm{R}}_i n_j \ {\mathrm{d}}\Gamma = G_{ij} \end{aligned}$$

(28)

where superscripts $+$ and − indicate opposite sides in the cube, i.e., left and right, top and bottom, and front and back pairs of faces.

A set of simulations for the range $0<=\mathrm{Id}_1<=1000$ was performed on the internal RVE. A structured mesh of $40\times 40\times 40$ cells was employed with a controlled time step fulfilling the Courant–Friedrichs–Lewy limit $C<=1$, where C is the Courant number. A standard unsteady FVM solver with second-order space and time discretization was employed in an ad hoc code developed by the authors [29], based on solver pimpleFoam (OpenFOAM$^{\textregistered }$suite).

Each simulation was carried out over time spans that depended on the Id, long enough for the instabilities to appear, and then continued until obtaining reliable and converged statistics. As an example, Fig. 10 shows a sequence of velocity snapshots in plane $Z=0$ corresponding to Id$_{1}=160$. In this case, the solution reaches a first orderly pattern and then remains steady up to $t=0.9$ s when instabilities appear, leading to a permanent non-repetitive transient flow pattern.

Fig. 10

Screenshots of the onset of the instability in plane $Z=0$. Velocity magnitude from 0 (blue) to 160 m/s (red). (Color figure online)

It should be noticed that the instabilities also occur on planes perpendicular to the direction of the shear stress applied (see Fig. 11), thus requiring the use of 3D RVEs even for 2D problems, as these transverse instabilities introduce large variations in the stress tensor.

Fig. 11

Internal RVE—velocity screenshots at $t=2$ s. Left: plane $Y=0$. Right: plane $X=0$. Velocity magnitude from 0 (blue) to 160 m/s (red). (Color figure online)

In Fig. 12, the equilibrium dimensionless xy inertial stress $\tilde{T}^{\rho }_{xy}$ for different Id$_{1}$ values is reported. In this simple case, the database may as well be represented by the function f(Id$_1)$ (shown by a red line) which is the least squares approximation of the data.

Fig. 12

Internal RVE—equilibrium dimensionless xy inertial stress $\tilde{T}^{\rho }_{xy}$ versus Id$_{1}$. f(Id$_1$) = $-0.00001898$ Id$_1^2+0.1945$ Id$_1$ + 9.352. (Color figure online)

Remark

In order to analyze the internal RVE simulation results, we have performed a spectral analysis which consisted in evaluating the time evolution of the x-component of the velocity signal on probes located at positions (H/2,H/2,H/2),(H,0,0), (0,H,0) and (0,0,H). From the obtained frequency spectra (Fig. 13 shows an example), it could be concluded that: (1) there are not significant spatial differences, enforcing the idea of homogeneous (but non-isotropic) instabilities, without spurious boundary effects, (2) the power of higher frequencies increases for increasing Id, and (3) the same occurs for increasing mesh refinement (until reaching fine mesh sizes close to the Kolmogorov scale).

Fig. 13

Internal RVE—example of velocity frequency spectrum. (Color figure online)

3.2 Wall RVE

A database for the wall RVE was also constructed. The case configuration is presented in Fig. 14. The velocity gradient tensor may be expressed as:

$$\begin{aligned} G^\prime _{ij} = \left[ \; \begin{matrix} 0 &{}\quad G^\prime _{xy} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{matrix}\; \right] \rightarrow \text {Id}_{ij} = \left[ \; \begin{matrix} 0 &{}\quad \text {Id}_1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 \\ \end{matrix}\; \right] . \end{aligned}$$

(29)

Therefore, once again the only varying parameter is Id$_1 = G^\prime _{xy}$.

In this case, the boundary conditions are imposed as solid walls moving in opposite directions in the top and bottom faces, with Dirichlet conditions for velocity $\mathbf {u}^{\mathrm{R}}({\mathbf {x}}^+) = [G^\prime _{xy}H; ~ 0; ~ 0]$ and $\mathbf {u}^{\mathrm{R}}({\mathbf {x}}^-) = [-G^\prime _{xy}H; ~ 0; ~ 0]$, and null normal pressure gradients. The remaining boundary conditions are those of the internal RVE, i.e., periodic (without jump) in streamwise and transversal directions.

The simulation is performed over a domain of size $H \times 2H \times H$, while the averaging of the inertial stress tensor and pressure is carried out in the RVE, namely the lower half of the domain. The upper half, meanwhile, is just an artifact for imposing adequate conditions on the top face of the RVE; it is not intended to represent a physically correct flow between parallel plates. In this regard, our numerical tests have shown that it is enough to have the upper plate at a distance 2H from the lower plate to reasonably represent the limiting case of an infinite separation distance between plates.

Fig. 14

Configuration of the wall RVE. (Color figure online)

Fig. 15

Wall RVE—equilibrium dimensionless inertial xy stress versus Id$_{1}$. $f(Id_1)=0.0119 Id_1^{0.7948}$. (Color figure online)

The equilibrium dimensionless xy inertial stress $\tilde{T}^{\rho }_{xy}$ for different Id$_{1}$ values is reported in Fig. 15. The flow is laminar for $\hbox {Id}_1 \lesssim 3000$. The function f(Id$_1)$ (shown by a red line) is a power law approximation of the data for $\hbox {Id}_1 \ge 4000$.

4 The algorithm

As mentioned above, adopting a Lagrangian formulation allows for accurately and naturally convecting and spreading the instabilities, even with a coarse mesh. Good resolution may be obtained by using either the first [30, 31] or the second generation of the particle finite element method (PFEM-2) [32,33,34,35] or its finite volume version, called particle finite volume method (PFVM) [29]. The readers are referred to these references for further details on these technologies. In the present work, the virtual particles convect not only the velocity, but also the inertial stress tensor.

The solution strategy is summarized in Algorithm 1.

4.1 Time evolution of uploaded inertial stress tensor

Let us rethink our problem as the task of solving, in the coarse mesh, the flow of a pseudo-fluid with properties determined not only by the real fluid physical properties but by the inertial stresses of the particles it convects, a combination that results in a complex rheological behavior. It is worth remembering, however, that the inertial stresses stored in the databases correspond to equilibrium conditions, to be considered as functions of state $T^{\mathrm{eq},t}_{ij}($Id$_1,$Id$_2)$ of the two Ids prevailing at the particle’s position ${\mathbf {x}}_p^{t}$ at time t (recall Fig. 8). This stresses are however not enough to fully capture the mentioned complex rheological behavior, for the pseudo-fluid properties depend not only on the local present conditions but on the history of strain rates experienced by the particle, which may be costly to track and store in databases.

The aforementioned difficulty may be approached by using techniques from the field of memory fluids. In this work, however, we propose a first approximation to tackle this problem by means of a simplified Step 6 in the algorithm, approximating the stress of particle p at any time $t^n \le t \le t^n+\Delta t$ and position ${\mathbf {x}}_p^{t}$ by solving the following initial value problem

$$\begin{aligned} \left\{ \begin{array}{cl} \displaystyle {\dfrac{\mathrm{d} T^\rho _{ij}}{\mathrm{d} t}} &{}= -\dfrac{1}{\tau } \Big ( T^\rho _{ij} - T^{\mathrm{eq},t^n+\Delta t}_{ij} \Big ) \\ T^\rho _{ij}(t^n) &{}= T^{\rho ,t^n}_{ij} \end{array} \right. \end{aligned}$$

(30)

where $\tau$ may be thought as a relaxation time (measuring how log it takes for a particle to forget its past), $T^{\rho ,t^n}_{ij}$ is the particle’s inertial stress tensor at the previous time step and $T^{\mathrm{eq},t^n+\Delta t}_{ij}$ is the equilibrium stress for the conditions prevailing at the particle’s position in the current time step, which is obtained from the database. The solution of this equation may be written as a weighted average with weight $0 \le {\mathrm{e}}^{-\frac{\Delta t}{\tau }} \le 1$, in the form

$$\begin{aligned} T^{\rho }_{ij}(t) = {\mathrm{e}}^{-\frac{(t-t^n)}{\tau }} T^{\rho ,t^n}_{ij} + \left( 1 - {\mathrm{e}}^{-\frac{(t-t^n)}{\tau }} \right) T^{\mathrm{eq},t^n+\Delta t}_{ij} , \end{aligned}$$

(31)

which for the discrete time $t=t^{n}+\Delta t$ becomes

$$\begin{aligned} T^{\rho ,t^n+\Delta t}_{ij} = {\mathrm{e}}^{-\frac{\Delta t}{\tau }} T^{\rho ,t^n}_{ij} + \left( 1 - {\mathrm{e}}^{-\frac{\Delta t}{\tau }} \right) T^{\rho ,t^n+\Delta t}_{ij}. \end{aligned}$$

(32)

The resulting updated particle stresses at time $t^n+\Delta t$ are then projected onto the coarse mesh. The larger the value of $\tau$, the greater the dependence of the current state on the previous state of the particle. In this work $\tau$ is assumed to be a user-defined constant, but in the future some relation with the local flow conditions may be discovered, based on more off-line numerical experiments.

4.2 Implicit treatment of the interaction between concurrent meshes

The previous section showed how to construct an RVE and how to transform the incoming strain rate tensor computed on the coarse mesh into the outcoming inertial stress tensor representing the fine scales effect on the coarse mesh problem. This direct relationship can lead to numerical instabilities if treated explicitly, imposing serious limitations on the allowable time steps and rendering the simulations costly or even impossible. Normally, the solution to this problem is to increase the implicit character of that relationship looking for an analysis of sensitivity of the response as a function of the cause. In the present work , only the analysis of the incidence of the coarse strain rate matrix $\mathbf {G}$ is presented, leaving the incidence of the coarse pressure gradient and acceleration to be included in future contributions, using the same strategy.

Let the direct relation mentioned above be expressed in compact tensorial notation as

$$\begin{aligned} T_{ij} \, = \, f_{ijkl} \, \left( \, G_{kl} \, \right) \end{aligned}$$

(33)

where sub- and supra-indices were omitted for the sake of simplicity. The strain rate tensor $\mathbf {G}$ is defined on the coarse mesh as

$$\begin{aligned}&G_{ij} = {\dfrac{1}{2}}\left( {\dfrac{\partial u_i^{\mathrm{c}}}{\partial x_j}}+ {\dfrac{\partial u_j^{\mathrm{c}}}{\partial x_i}} \right) \end{aligned}$$

(34)

A simple algebraic manipulation allows us to split it into its symmetrical part, related to the rate of deformation, and its antisymmetrical part, related to the rate of rotation, giving

$$\begin{aligned} \mathbf {G}= & {} \begin{pmatrix} G_{xx} G_{xy} G_{xz} \\ G_{yx} G_{yy} G_{yz} \\ G_{zx} G_{zy} G_{zz} \\ \end{pmatrix}\nonumber \\= & {} \underbrace{ \begin{pmatrix} G_{xx} &{}\quad {\dfrac{1}{2}}(G_{xy}+G_{yx}) &{}\quad {\dfrac{1}{2}}(G_{xz}+G_{zx}) \\ {\dfrac{1}{2}}(G_{xy}+G_{yx}) &{}\quad G_{yy} &{}\quad {\dfrac{1}{2}}(G_{yz}+G_{zy}) \\ {\dfrac{1}{2}}(G_{xz}+G_{zx}) &{}\quad {\dfrac{1}{2}}(G_{yz}+G_{zy}) &{}\quad G_{zz} \\ \end{pmatrix}}_{\mathbf {G^S} \text { (deformation) }} \nonumber \\&+\underbrace{ \begin{pmatrix} 0 &{}\quad {\dfrac{1}{2}}(G_{xy}-G_{yx}) &{}\quad {\dfrac{1}{2}}(G_{xz}-G_{zx}) \\ {\dfrac{1}{2}}(-G_{xy}+G_{yx}) &{}\quad 0 &{}\quad {\dfrac{1}{2}}(G_{yz}-G_{zy}) \\ {\dfrac{1}{2}}(-G_{xz}+G_{zx}) &{}\quad {\dfrac{1}{2}}(-G_{yz}+G_{zy}) &{}\quad 0 \\ \end{pmatrix} }_{\mathbf {G^A} \text { (rotation) }}\nonumber \\ \end{aligned}$$

(35)

Only the first, symmetrical part is to be sent to the RVE, because rigid body rotations do not induce instabilities. This symmetrical part is traceless, i.e., $\sum G_{ii} = 0$, due to the incompressibility constraint, being therefore identical to its own deviatoric part, i.e., ${\mathbf {G}}^{\mathbf {S}} = {\mathbf {G}}^{{\mathbf {S}},\text {Dev}}$.

Fig. 16

Partition of a strain rate tensor in its axial and shear components. (Color figure online)

One of the possible partitions of this tensor is the sum of a pure shear strain rate tensor and a pure axial strain rate tensor, i.e.,

$$\begin{aligned} \mathbf {G}^{\mathbf {S}} = \mathbf {G}^{{\mathbf {S}},\text {axial}} + \mathbf {G}^{{\mathbf {S}},\text {shear}}, \end{aligned}$$

(36)

as shown in Fig. 16. The axial strain rate tensor produces a flow that, due to incompressibility, simply redirects the incoming flows on some faces to outcoming flows on the rest of the faces, resembling symmetrical corner flows with a stagnation point at its center, as shown in Fig. 17. Theoretical arguments show that this kind of flow is stable, i.e., free from instabilities, which was confirmed numerically. On the other hand, the pure shear flow proved to become unstable above some critical value of a certain norm of the strain rate tensor, as was shown in the previous section.

Fig. 17

Velocity vector field for pure axial strain rate. Equivalent to a flow around four corners. (Color figure online)

Although this simple partition isolates the source of instabilities, it is clear that the norm or intensity of the original symmetrical strain rate tensor is lost in the process. We propose therefore to perform a norm preserving particular rotation of the original tensor, already mentioned in Eq. (26), leading to a different pure shear tensor $\mathbf {G}^{{\mathbf {S}},\text {shear,iso}}$, i.e., with null diagonal values, defined as

$$\begin{aligned} {\mathbf {G}}^{{\mathbf {S}},\text {shear,iso}} = \mathbf {R}^\mathbf {T} \mathbf {G}^\mathbf {S} \mathbf {R} \end{aligned}$$

(37)

where $\mathbf {R}$ is a particular rotation matrix that produces zero diagonal entries in the final strain rate tensor. Moreover, such a rotation produces a tensor defined by only two parameters, whose general form is

$$\begin{aligned} \mathbf {G}^{\mathbf {S},\text {shear,iso}} = \begin{pmatrix} 0 &{} a &{} b \\ a &{} 0 &{} c \\ b &{} c &{} 0 \\ \end{pmatrix} \end{aligned}$$

(38)

where $a=b$ or $a=c$ or $b=c$ depending on the order of magnitude of the eigenvalues relative to the frame of reference. This strain rate tensor $(\mathbf {G}^{\mathbf {S},\text {shear,iso}})$ is the information finally used to solve the RVE, or to access the off-line generated database.

We now face the task of returning to the coarse mesh the inertial stresses and pressure coming from the RVE, to contribute to the residual of the Navier–Stokes equations system and the resulting algebraic matrix. As already explained in Sect. 2, the momentum residual to be solved in the coarse mesh is modified to include the inertial stress tensor and pressure. In order to simplify the algebra, the total momentum residual may be split in two parts

$$\begin{aligned}&\mathcal {R}^{\mathrm{mom}} = \mathcal {R^{RVE}} + \mathcal {R^\mathrm{{rest}}} , \end{aligned}$$

(39)

where

$$\begin{aligned} \mathcal {R^{RVE}}= & {} \int _\Omega W_i \left( {\dfrac{\partial \sigma ^{\rho }_{ij}}{\partial x_j}} \right) {\mathrm{d}}\Omega \nonumber \\= & {} \int _\Omega W_i \left( -{\dfrac{\partial p^\rho }{\partial x_i}} + {\dfrac{\partial T_{ij}^{\rho }}{\partial x_j}} \right) {\mathrm{d}}\Omega . \end{aligned}$$

(40)

For the sake of brevity, $\mathcal {R^\mathrm{{rest}}}$ is not included in the following algebra because it depends on the original terms in the variational formulation of the Navier–Stokes equations, which do not change because of the presence of the RVE. Integrating by parts, as usual in FEM, or using Gauss’s theorem, as usual in FVM, we arrive at similar equations. To simplify the explanation, we choose in the following only the FEM formulation.

$$\begin{aligned} \mathcal {R^{RVE}}= & {} \int _\Omega W_i \left( -{\dfrac{\partial p^\rho }{\partial x_i}} + {\dfrac{\partial T_{ij}^{\rho }}{\partial x_j}} \right) {\mathrm{d}}\Omega =\nonumber \\= & {} - \int _\Omega {\dfrac{\partial W_i}{\partial x_j}} \left( -p^\rho \delta _{ij} + T^{\rho }_{ij} \right) {\mathrm{d}}\Omega \end{aligned}$$

(41)

Expressed in the incremental form usual in nonlinear problems solved by the Newton–Raphson method, given a seed solution $\{ \mathbf {u}^{c}, p^{c}\}^0$ (from the initial conditions or the previous iteration) that produces a non-null residual, i.e., $\mathcal {R^{RVE}}(\{ \mathbf {u}^{c} , p^{c} \}^0) \ne 0$, the solution process may be expressed as: find $\Delta \{ \mathbf {u}^{\mathrm{c}}, p^{\mathrm{c}}\}$ such that

$$\begin{aligned}&\mathcal {R^{RVE}} (\{ \mathbf {u}^{c} , p^{c} \}^0 + \Delta \{ \mathbf {u}^{\mathrm{c}}, p^{\mathrm{c}}\} ) \nonumber \\&\quad = \mathcal {R^{RVE}} (\{ \mathbf {u}^{c} , p^{c} \}^0) + {\dfrac{\partial \mathcal {R^{RVE}}}{\partial \mathbf {u}^{\mathrm{c}}}} \varvec{\Delta } \mathbf {u}^{\mathrm{c}} + {\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^{\mathrm{c}}}} \Delta p^{\mathrm{c}}\nonumber \\ \end{aligned}$$

(42)

with $\mathcal {R^{RVE}} (\{ \mathbf {u}^{c} , p^{c} \}^0 + \Delta \{ \mathbf {u}^{\mathrm{c}}, p^{\mathrm{c}}\} ) = 0$. In the previous expression, ${\dfrac{\partial \mathcal {R^{RVE}}}{\partial \mathbf {u}^{\mathrm{c}}}} \varvec{\Delta } \mathbf {u}^{\mathrm{c}} + {\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^{\mathrm{c}}}} \Delta p^{\mathrm{c}}$ are called the tangent matrices or the Jacobian matrices with respect to the unknowns.

Fig. 18

Conceptual view of the separation of scales for a 2D flow between parallel plates with two different coarse meshes. Left: large eddies (green) are represented in the coarse mesh velocity field, while small eddies (read an blue) appear in the fine mesh of each RVE, which moves with the virtual particles convected by the coarse velocity field. Right: the (very) coarse mesh is only able to represent the steady mean flow, leaving all the eddies to be represented in the fine mesh of each RVE, which in this cases move along the linear horizontal streamlines of the coarse flow. (Color figure online)

As the residual is a function of two kinds of unknowns, $p^\rho$ and $\mathbf {T}^\rho$, both computed from $\mathbf {u}^{\mathrm{c}}$ and $p^{\mathrm{c}}$, this Jacobian matrices should be computed as

$$\begin{aligned} {\dfrac{\partial \mathcal {R^{RVE}}}{\partial \mathbf {u}^{\mathrm{c}}}}&= {\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^\rho }} {\dfrac{\partial p^\rho }{\partial \mathbf {u}^{\mathrm{c}}}} + {\dfrac{\partial \mathcal {R^{RVE}}}{\partial \mathbf {T}^\rho }} {\dfrac{\partial \mathbf {T}^\rho }{\partial \mathbf {u}^{\mathrm{c}}}} \nonumber \\&= \Big ( \underbrace{{\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^\rho }}}_{1} \underbrace{{\dfrac{\partial p^\rho }{\partial \mathbf {G}^{\mathbf {S},\text {shear,iso}}}}}_{2} \nonumber \\&\quad + \underbrace{{\dfrac{\partial \mathcal {R^{RVE}}}{\partial \mathbf {T}^\rho }}}_{3} \underbrace{{\dfrac{\partial \mathbf {T}^\rho }{\partial \mathbf {G}^{\mathbf {S},\text {shear,iso}}}}}_{4} \Big ) \underbrace{{\dfrac{\partial \mathbf {G}^{\mathbf {S},\text {shear,iso}}}{\partial \mathbf {G^{S}}}}}_{5} {\dfrac{\partial \mathbf {G}^{\mathbf {S}}}{\partial \mathbf {u}^{\mathrm{c}}}}, \end{aligned}$$

(43)

that in indicial notation is written as

$$\begin{aligned} {\dfrac{\partial \mathcal {R^{RVE}}}{\partial u_i^{\mathrm{c}}}}&= {\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^\rho }} {\dfrac{\partial p^\rho }{\partial u_i^{\mathrm{c}}}} + {\dfrac{\partial \mathcal {R^{RVE}}}{\partial T^\rho _{jk}}} {\dfrac{\partial T^\rho _{jk}}{\partial u_i^{\mathrm{c}}}} \nonumber \\&= \Big ( \underbrace{{\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^\rho }}}_{1} \underbrace{{\dfrac{\partial p^\rho }{\partial G^{S,\text {shear,iso}}_{lm}}}}_{2} \nonumber \\&\quad + \underbrace{{\dfrac{\partial \mathcal {R^{RVE}}}{\partial T^\rho _{jk}}}}_{3} \underbrace{{\dfrac{\partial T^\rho _{jk}}{\partial G^{S,\text {shear,iso}}_{lm}}}}_{4} \Big ) \underbrace{{\dfrac{\partial G^{S,\text {shear,iso}}_{lm}}{\partial G^{S}_{np}}}}_{5} {\dfrac{\partial G^{S}_{np}}{\partial u_i^{\mathrm{c}}}}. \end{aligned}$$

(44)

In the above expression only terms 2 and 4 depend on the RVE solution, while term 5 depends on the transformation needed to arrive to a zero diagonal strain rate tensor $\mathbf {G}^{\mathbf {S},\text {shear,iso}}$ from $\mathbf {G}^{\mathbf {S}}$. The rest is simple algebra. To obtain an expression for the terms marked as 2 and 4, we have to resort to the inertial stresses and pressure databases. The same expression is also obtained for ${\dfrac{\partial \mathcal {R^{RVE}}}{\partial p^{\mathrm{c}}}}$, here omitted for brevity reasons. In this case terms 2 and 4 refer to the slopes of each of the six response surfaces (see Fig. 8) evaluated at the position defined by the current Ids. Regarding term 5, however, it is difficult to get an analytic expression to finally arrive to the exact tangent matrix. Instead, an approximate matrix, here called iteration matrix, is the easiest way to get at least some implicitness in the numerical algorithm. While this last strategy was adopted in this paper, this topic deserves more attention in the future.

Finally, it is highlighted again that even though the Jacobians may be approximated by the iteration matrices, the residual should be defined accurately through the off-line curves obtained for the relation between $\mathbf {T}^\rho$ and $p^\rho$ with respect to the current values of Id’s parameters.

4.3 Main features to be taken into account in the algorithm

There are three features that are key to the good performance of the proposed method, namely: (1) the dimensionless approach, (2) the Lagrangian form, and (3) the off-line computation of the equilibrium databases.

• 1. By using dimensionless input and output variables, all the internal RVEs may have the same geometry and dimensions. In particular, the same four-dimensional space-time cube of unit side will be used to average the results in all internal RVEs, with only a special but also unique treatment for wall RVEs. All RVEs are simulated off-line under simple boundary conditions, allowing the creation of an equilibrium database, expressed as tables or interpolating functions, of the behavior of the RVE under a broad set of strain rates. This database will provide information in real time during the computations of the coarse mesh solution.

• 2. Each RVE not only carries information of the average speed, but also of the instabilities. For this reason, it is essential at the coarse level to convect the information of the RVEs in Lagrangian form. In this way the transfer of information generated by the eddies induced within the RVE and that cannot reproduced by the coarse mesh is ensured (Fig. 18). This is the main advantage over the LES method in which all the trailers have to be transported by the coarse mesh.

• 3. The most expensive part of the algorithm is obtaining the RVE’s equilibrium solution, which requires 3D meshes with mesh size close to that of the Kolmogorov scale. Fortunately, these equilibrium computations can be carried out off-line once and for all. In the current work, we present a small database for low Id numbers obtained with standard FVM simulations (Sect. 3). However, to enlarge the database reaching higher Ids, it is possible to think on reducing the effort using one or both of the following procedures: a) reduction order methods, which could benefit from the same space-time geometry of all the RVEs, and/or b) a pseudo-spectral approximation (FFT + Chebyshev) taking advantage of the capabilities of GPGPU machines to obtain a sensible speedup.

5 Numerical tests

5.1 1D Poiseuille and Couette flows

The first two cases presented are not merely conceptual, but also allow to introduce the algorithmic procedure and its impact on the accuracy of the results. Let us consider two one-dimensional coarse meshes composed by only four and three 1D finite volume cells, respectively. With this meshes, all the unsteadiness of the flow must be resolved by the RVEs. The aim is to obtain the averaged incompressible flow field by solving the steady-state Navier–Stokes equations with a modified stress tensor obtained from to the RVE databases. Note also that this test involves the coupling between the distinct treatment for the near-to-wall cells and the interior cells.

Two classical flows between plates are solved: one driven by a pressure difference (Poiseuille flow) and the other by pure shear due to the movement of the walls (Couette flow). It is widely known that above certain Reynolds numbers these flows become turbulent, leading to average velocity profiles very different from those corresponding to the laminar cases, i.e., parabolic for Poiseuille and linear for Couette. For the conditions and dimensions presented in Fig. 19, both problems lead to turbulent regimes.

Fig. 19

One-dimensional tests configuration. (Color figure online)

Figure 20 presents a comparison between the results obtained solving the problems with three strategies: (1) using the coarse mesh without modeling non-captured scales (laminar), (2) using the coarse mesh while modeling the non-captured scales using the presented databases, and (3) using standard 3D DNS in a fine mesh able to capture all instability scales. Additionally, for the case of Poiseuille, an estimation of the average velocity for smooth tubes taken from the classic experimentally based Colebrook formula (or Moody chart, [36]) is included, by using the concept of equivalent hydraulic diameter.

Fig. 20

One-dimensional tests. Top: Poiseuille flow. Bottom: Couette flow. (Color figure online)

Results show that even using only a small number of cells, the mean velocity profile predicted by pseudo-DNS considerably agrees with the DNS solution. In the Poiseuille flow case, it is evident how the inertial stress tensor $T_{xy}^\rho$ increases the effective viscosity of the flow in the coarse field, reducing the velocity from a maximum of 4 m/s, obtained considering only laminar viscous stress ($T_{xy}^\mu$), to 0.55 m/s, which is a much better approximation to 0.42 m/s, the maximum mean velocity in the DNS simulation (see Fig. 20a). In the Couette flow case, the inclusion of data from finer scales results in changing the linear laminar flow profile to an S-shaped profile, which also agrees well with the DNS solution.

Moreover, having the DNS solution, it is possible to post-process the actual effective viscosity profile. The stresses predicted by pseudo-DNS are also in good agreement with these results, as observed in Fig. 20b–d.

5.2 2D Poiseuille flow

In this section, the turbulent flow between two infinite plates driven by a pressure difference between inlet and outlet is solved again. In this case, however, a much finer coarse mesh is used, leading to a split of scales which produces that part of the unsteadiness of the flow is captured by the coarse mesh. The computation is thus made including virtual particles to transport velocity and instability information.

The geometry is a 2D domain of $3L \times L$ with $L=1$ discretized using a structured grid with a cell size $h=0.1$. The case is set up with a kinematic viscosity $\nu =5$e$^{-6} \hbox {m}^2/\hbox {s}$ and a pressure difference of $\frac{p^{\mathrm{c}}_{\text {in}}-p^{\mathrm{c}}_{\text {out}}}{\rho } = 15\times 10^{-4}$ m$^2$/s$^2$. Boundary conditions for velocity are no-slip at the top and bottom walls and cyclic at the inlet and outlet. In the case of the pressure, zero gradient is set at the top and the bottom and a pressure “jump” is imposed at the inlet with respect to the outlet in order to impose the desired pressure gradient.

A laminar simulation is performed first, and then, the proposed solver is employed. The initial velocity field is the parabolic solution of a steady laminar solver, which has a maximum magnitude of 7.6 m/s. Using the average velocity, this results in $Re=10^6$ which indicates that the flow must be solved using a turbulence model. The adaptive time step used limits the Courant number to $C\le 5$. In order to update the fine stresses transported by particles, the relaxation parameter is fixed to $\tau =0.01$.

A snapshot showing the virtual particles and the average velocity profiles in the channel is shown in Fig. 21. A spatially averaged time mean velocity is calculated for a time window of 100 s, obtaining $U=|\overline{u_i}|=0.378$ m/s, which leads to a $Re=UD_h/\nu = 1.5\times 10^5$, where $D_h=2L$ is the equivalent hydraulic diameter of the channel. In this way, it is possible to estimate a predicted friction factor $f_r=2D_h (\partial p/\partial x) / U = 0.014$, close to the value $f_r=0.016$ obtained from the Moody diagram for a smooth pipe.

Fig. 21

Two-dimensional Poiseuille test. Left: mesh and particles. Particles are colored by the stress ratio $T_{xy}^{\rho }/T_{xy}^{\mu }$, and an arrow shows their transported velocity. Right: Averaged velocity profiles at $x=1.5$. (Color figure online)

5.3 Mixing layer

The mixing layer that forms between two fluid streams moving with different velocities has been the subject of extensive experimental and numerical studies due to the technological importance and its relevance for understanding the large coherent vortex structure. The main characteristic present in the mixing layer is the self-similarity property, which is characterized by linear growth of the layer as well as the mean velocities and turbulent statistics being independent of the downstream distance non-dimensionalized by appropriate length and velocity scales.

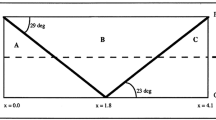
Figure 22 presents the case configuration. Free-stream velocities selected are $U_1=4$ m/s and $U_2=13$ m/s in order to compare with the results of Yang et al. [37]. The initial condition of velocity distribution is assumed to be that of an inviscid flow with a velocity distribution at the inlet section with a hyperbolic tangent profile. The so-called traction-free boundary conditions are adopted at the top and bottom boundaries of the computational domain, and an advective boundary condition is used at the outlet to prevent wave reflections.

Our pseudo-DNS Algorithm 1 is selected to simulate three cases which differ in grid resolution. We define a case A which employs a mesh composed by 128 $\times$ 30 cells and $\Delta t = 0.0005$ s, a case B with 256 $\times$ 61 cells using $\Delta t = 0.00035$ s, and a case C with 512 $\times$ 121 cells using $\Delta t = 0.0002$ s. Two particles per cell are initially seeded, and a requirement is imposed for having at least one and at most ten particles per cell during the simulation. A implementation of the particle-based second-order accurate methodology named PFVM, presented in [29], is used. Simulations are run up to a final time $T_\mathrm{f}=50$ s, and the mean fields are obtained by an averaging of the last 20 simulated seconds, a window large enough for obtaining reliable statistics.

In order to quantitatively compare results, some definitions must be introduced:

• $y_{0.5}$: y-position at which the time-averaged streamwise velocity, $<u>$, is equal to half the sum of the two free-stream velocities $U_1$ and $U_2$.

• $\theta = \displaystyle \int _{-\infty }^{\infty } \dfrac{<u>-U_1}{U_2-U_1} \left( 1 - \dfrac{<u>-U_1}{U_2-U_1}\right) dy$: momentum thickness at specific streamwise coordinate x.

• $\eta =\dfrac{y-y_{0.5}}{\theta }$: dimensionless transverse coordinate.

• $<u'>$ time-averaged streamwise mean fluctuating velocity

• $<v'>$ time-averaged transverse mean fluctuating velocity

Fig. 22

Mixing layers. Geometry and case configuration

In general, our numerical results are in good agreement with the experimental results of Oster [38] and they have similar characteristics as other numerical results as those obtained by Yang et al. [37] and Martha et al. [39]. Features reported as partial self-similarity, delayed instability due to non-perturbed inlet condition, and a large prediction of the time-averaged Reynolds shear stress near the exit boundary layer due to outflow boundary condition are also found in the test performed in this work.

Fig. 23

Pseudo-DNS solution screenshots. Left: Vorticity magnitude from 0 (white) to 1000 (magenta). Right: particles colored by an approximation to the effective viscosity $\nu _{\mathrm{eff}} = T^{\rho }_{xy}/G_{xy}$ from 0 (white) to 0.001 (magenta). (Color figure online)

Figure 23 presents snapshots of the solution on mesh and particles at a particular simulation time where the flow is developed. While case A barely shows the vortex street, case C obtains a visually good definition of the phenomena. Moreover, in case C flow structures observed in several experiments are clearly detected: in the screenshot presented, a paired vortex structure is followed by an unpaired vortex. Figure 23 also shows how the relevance (magnitude) of the data from the fine scales is reduced when more structures are captured by the coarse mesh. This is reflected by the magnitude of the instabilities transported by virtual particles ($T^{\rho }_{xy}/G_{xy}$), which decreases when the coarse mesh is refined. We observe that, using our algorithm, refining the coarse mesh could be considered equivalent to moving the limit between what is considered large and small scales.

Although the coherent vortices have been plausibly simulated, these are just qualitative results. In order to guarantee the accuracy, the statistical results must be examined. The streamwise averaged velocity at three different positions ($x = 0.4, 0.45, 0.5$ m) is shown in Fig. 24, compared with Oster’s experimental measurement. From the plots, it should be noticed that our numerical solution with pseudo-DNS accomplishes the self-similarity condition for the mean velocity even using a coarse grid for large scales. Moreover, when the coarse-scale grid is refined, the results converge to the experimental ones.

Fig. 24

Pseudo-DNS (pseudo-DNS) algorithm statistical results. Streamwise mean velocity. Experimental data are taken from [38]. (Color figure online)

Figure 25 presents the momentum thickness in the three cases, where the desired linear growth is obtained in cases B and C. The slope obtained by Yang et al. [37] using LES, with a mesh equivalent to case C, is similar to our pseudo-DNS algorithm (cases B and C). Discrepancies in the x coordinate where the instability starts are in accordance with the observations in the literature, where it is mentioned that the growth is greatly influenced by the inflow forcing. In our pseudo-DNS solution, the particle seeding at random positions of the inlet naturally introduces flow instabilities, while in the LES solution the inlet profile is not perturbed until it reaches the streamwise position $x=0.2$.

Fig. 25

Mixing layer growth. (Color figure online)

Figure 26 presents the Reynolds shear stress at the same three positions (namely $x = 0.4, 0.45, 0.5$ m). Due to our scales splitting, we can sum up the fluctuations of the large scales and the pre-computed data from the fine scales. In this sense, we compute the Reynolds shear stress as $<u'v'>=<u'v'>^{\mathrm{c}} + <T_{xy}^{\rho }>/\rho$. In cases B and C, pseudo-DNS presents a good agreement with experimental data and, in case A, less than half of the real turbulent intensity is predicted. We may explain the inaccurate results in case A because of the fact of separating scales at a size where the fine scales cannot yet be considered homogeneous, a strong hypothesis used on the RVE simulations.

Fig. 26

Pseudo-DNS statistical results. Reynolds shear stress. Experimental data are taken from [38]. (Color figure online)

Our case B is compared with the LES simulation results obtained from [37]. The cases have same flow conditions, but we are solving using a mesh with a cell size twice larger than the LES reference. As presented in Fig. 27 for the position of $x=0.4$, pseudo-DNS obtains lower differences with experimental time-averaged fluctuating velocities than LES even using this four times smaller mesh. In general, LES simulation tends to overpredict flow instabilities, being the biggest difference in the transverse fluctuating velocity. The latter is commonly found in two-dimensional simulation of mixing layers [7, 8] and is induced by the three-dimensionality of the actual flows [11].

For the sake of brevity, more graphical comparisons are not included in this work, but we can also mention that we have performed our own simulations with standard LES and, employing coarser grids than that used by Yang (same as our cases B and A), LES is not able to capture instabilities.

Fig. 27

Comparison between pseudo-DNS and LES solutions at $x=0.4$ using a structured grid of 512 $\times$ 126 cells. (Color figure online)

6 Summary and conclusions

A new approach to simulating fluid flows with physical instabilities at different scales was proposed. The different scale levels can be hierarchical or concurrent (separation of scales or a continuous variation of the size of the scales). The main features of the method presented are:

• Both large and small scales are simulated numerically, online and off-line, respectively. According to this strategy, the obligation of using very fine meshes is restricted to only one level.

• The separation of scales is arbitrary, with the only restriction of the small scales being isotropic, thus avoiding the need of reaching a resolution where the universality hypothesis is valid.

• Small eddies are convected by the coarse mesh velocity field by virtual Lagrangian particles.

• The fine scales are solved off-line over dimensionless, geometrically simple subregions which are universal, i.e., only dependent on the dimensionless numbers representing the stress state in the coarse mesh.

The proposal is expected to be beneficial for solving some cases of turbulent fluids flows as the preliminary numerical results presented here indicate. However, one of its main attractions may be the solution of heterogeneous, multiphase flows, and active fluids, where interaction of the different materials involved with the instabilities at the finest scales is very difficult to capture by any method other than the standard DNS. The proposed method is encouraging because, in the examples of homogeneous fluids presented, for coarse and medium mesh sizes, it provides better match to the experimental data than LES. In addition, LES methods do not comply with the self-similarity property or the averaged symmetry over the time of the flow. Moreover, the standard LES using coarser grids may not even capture instabilities that the present approach is capable of capturing.