Abstract
The past few decades have seen a significant spurt in developing lower-order, parsimonious models of large-scale dynamical systems used for design and control. These surrogate models effectively capture the most interesting dynamic features of the full-order models (FOMs) while preserving the input–output relation. Model order reduction (MOR) techniques have intensively been further developed to treat increasingly complex, multi-resolution models spanning a thousand degrees of freedom. This manuscript presents a state-of-the-art review of the moment-matching based order reduction methods for linear and nonlinear dynamical systems. We track the progress of moment-matching methods from their inception to how they have emerged as the most commonly adopted platform for reducing systems in large-scale settings. We discuss the frequency and time-domain notions of moment-matching between the original and reduced models. Moreover, we also provide some new results highlighting the extensive applications of this technique in reducing micro-electro-mechanical systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Large-scale models often emerge from all the branches of engineering and sciences. For instance, spatial discretization of partial differential equations (PDEs) using the finite volume [127, 178] or finite elements [57, 59], modeling complex fluid dynamics [40, 129, 170], VLSI systems [125, 173], disease modeling [147], micro or nano-electro-magnetic systems [113, 142], represent systems of scientific interest and are large-scale in nature. The need for higher accuracy necessitates enhanced details in these models, which inevitably increases the computational complexity. Furthermore, it is often desired to repeatedly simulate such systems for optimization and control, thus making untenable burdens on computational resources. Model order reduction intends to replace such high-fidelity systems with much cheaper models that can accurately replicate the input–output behavior as that of the original system while preserving some dominant properties such as stability and passivity [1, 10, 49, 119]. Such surrogate models are then reliably used to carry intense simulations to develop faster controllers for real-time applications [5, 61, 107, 131, 135, 146, 155].
One of the most successful MOR methods for reducing large-scale systems is the interpolatory method, also known as the moment-matching method [7, 9, 10, 12]. These methods produce a reduced-order model that interpolates the full-order system’s response at some predefined interpolation points. The main reason these methods are so successful is their numerical stability and that these methods involve less dense matrix transformations. These methods are also closely related to rational Krylov subspace methods. Some excellent reviews can be found in Refs. [21, 28, 65, 68, 69, 72].
This review aims to provide a complete understanding of moment-matching based model reduction methods and presents the most significant developments in this direction. To introduce the problem to first-time readers, we begin with the moment-matching methods in linear systems in Sect. 2. There, we discuss the moment-matching techniques in the frequency and time domain. We also explain the tangential interpolation problem for the multiple-input multiple-output systems and the notion of moments in second-order dynamical systems. Then, we point-out some open issues in these methods and provide some recent advancements in this direction. In Sect. 3, we present a comprehensive moment-matching based model reduction technique in nonlinear systems, based on the recently developed notion of steady-state interpolation. To illustrate the idea, we present numerical results for capturing highly oscillatory dynamics of MEMS switch through reduced modeling technique. We also discuss some of the prominent nonlinear MOR techniques based on Krylov subspace methods and present some open problems. Finally, we provide some concluding remarks in the end.
Throughout this manuscript, we study of MOR via moment-matching for a general class of continuous systems described in state-space representation given as:
where \(\varvec{x}(t) \in \mathbb {R}^{n}\) is known as the state-vector in control system parlance. This represents the vector of unknowns whose entries are called internal variables or state variables. Matrices \(\varvec{B}\in \mathbb {R}^{n \times m}\) and \(\varvec{C}\in \mathbb {R}^{n \times p}\) are the input and output matrices respectively, whereas \(\varvec{f},\varvec{h} : \mathbb {R}^{n} \rightarrow \mathbb {R}^n\) are the two nonlinear mappings. Vectors \(\varvec{u}(t) \in \mathbb {R}^{m}\) and \(\varvec{y}(t) \in \mathbb {R}^{p}\) are the inputs and outputs of the system. System (1) represents a multiple-input multiple-output (MIMO) system with \(m,p<<n\). However, for single-input single-output (SISO) systems, \(m=p=1\), and the matrices \(\varvec{B}\), \(\varvec{C}\) become vectors \(\varvec{b}\) and \(\varvec{c}^T\) whereas vectors \(\varvec{u}\) and \(\varvec{y}\) become scalars u and y respectively. Furthermore, if \(\varvec{f}(.)\) and \(\varvec{h}(.)\) are linear mappings, then system (1) is called a linear dynamical system otherwise a nonlinear (control-affine) system. Thus, system (1) essentially represents a large-scale, initial value problem that we are interested in solving for some predefined time-span, in the presence of some excitation function \(\varvec{u}(t)\).
The most common approach to obtain a reduced-order model of system (1) is via projection [39, 104, 171, 180], i.e., by projecting the dynamics of full-order model on a lower-dimensional manifold, spanning lesser degrees of freedom \((r<<n)\). This is followed by re-projecting the reduced dynamics onto the original space to obtain the approximation. The approximation ansatz is given as \(\varvec{x}(t)=\varvec{Vx_{r}}(t)\) with \(\varvec{x_{r}}(t) \in \mathbb {R}^{r}\) and where the columns of \(\varvec{V} \in \mathbb {R}^{n \times r}\) represent the basis for the reduced subspace. Substituting this approximation in Eq. (1) yields an over-determined systems of equations given as:
where \(\varvec{r}(t)\) is the residual vector due to the subspace approximation. In order to make this a well-posed problem, the Petrov-Galerkin condition is then imposed, i.e., \(\varvec{W}^{T}\varvec{r}(t)=0\). This gives:
where, it is usually required that \(\varvec{W^{T}V}=\varvec{I}\), such that \(\varvec{VW^{T}}\) is a projector onto an r-dimensional subspace. The various reduction methods vary in the choice of the projection matrices \(\varvec{V}\) and \(\varvec{W}\). However, one common aim is that the response of the reduced model Eq. (3) is “close” to the high-fidelity model Eq. (1).
In what follows, we discuss the moment-matching technique in linear time-invariant systems followed by nonlinear systems.
2 Moment Matching for Linear-Time Invariant Systems
Many mathematical and physical systems can be modeled as linear time-invariant (LTI) systems. To introduce the idea of MOR via moment-matching, consider a large-scale system of autonomous differential equations resulting from the spatial discretization of PDE’s represented in a continuous-time, state-space model as given below:
where n is the order of the state-space model (\(\varSigma _{L}\)) i.e., the states \(\varvec{x}(t) \in \mathbb {R}^{n}\) span an n-dimensional space, \(\varvec{E} \in \mathbb {R}^{n \times n}\) is the (non-singular) descriptor matrix, \(\varvec{A} \in \mathbb {R}^{n\times n}\) is the system matrix, \(\varvec{B} \in \mathbb {R}^{n\times m}\) is the input matrix and \(\varvec{C} \in \mathbb {R}^{n\times p}\) is the output matrix. The LTI system in Eq. (4) is called regular if the matrix \(\varvec{E}\) is nonsingular or descriptor system otherwise. In case of singular \(\varvec{E}\), Eq. (4) represents a system of differential-algebraic equations (DAEs) rather than ordinary differential equations (ODEs) which are more difficult to solve.
For LTI systems considered here, the impulse response is given as:
and the frequency domain transfer function, which is a \(p \times m\) matrix-valued rational function, is obtained by taking the Laplace transform of the impulse response given as:
which can also be written as
Using the Neumann expansion, we can rewrite the above expression as:
which can be further expanded via Taylor series as
Definition 1
[7] The moments of the LTI system Eq. (4) about the expansion point \(s=0\) are the negative coefficients of the Taylor series expression Eq. (9) expanded about \(s=0\) and are given as
The moments of system (4) at the point \(s=0\), are also the successive derivatives of the transfer function \(\varvec{H}(s)\) i.e.,
If the expansion is performed at some other point than \(s=0\) e.g. at \(s=\sigma\), then the moments of (4) about \(s=\sigma\) are computed by replacing the matrix \(\varvec{A}\) with \((\varvec{A}-\sigma \varvec{E})\) in Eq. (10) i.e.,
for \(i=0,1,\ldots\) and where it is assumed that the matrix pencil \((\varvec{A}-\sigma \varvec{E})\) is nonsingular.
Definition 2
[7] The coefficients of the Taylor series of transfer function \(\varvec{H}(s)\) about \(s=\sigma\) for \(\sigma \rightarrow \infty\), are defined as the Markov parameters of the LTI system (4) and are given as:
Furthermore, the ith Markov parameter is equal to ith derivative of the impulse response of system (4) at \(t=0\) i.e,
This implies that the first Markov parameter \(\varvec{M}_{0}\) is the system’s impulse response at \(t=0\).
2.1 Moment Matching in Frequency Domain
Model reduction via moment matching implies that a reduced-order model is to be obtained whose moments match the the full-order model moments at certain frequencies of interest. If the moments are matched about \(s=0\), the reduced-order model is called the Padé approximant, and the problem is known as Padé’s approximation. If the moments are matched at some other point \(s=\sigma\), the problem is known as shifted Padé’s approximation, and when the Markov parameters are matched, the problem is termed as Partial realization. It is often desired to match moments at more than one expansion point i.e., at specific frequency intervals, then we talk about the multipoint Padé or the rational interpolation problem. Thus, model reduction via moment matching is to construct a reduced order model (ROM) given as:
where \(\varvec{x_{r}}(t) \in \mathbb {R}^{r} (r<<n)\), and where the reduced system matrices are calculated using the projector \(\varvec{VW}^{T}\) given as:
such that the moments of \(\varvec{H}(s)\) match the reduced system’s moments having transfer function \(\varvec{H_{r}}(s)\) where
Now, this begs the questions on how to select the expansion points and, as such, obtain the projection matrices \(\varvec{V}\) and \(\varvec{W}.\) This is explained next.
2.1.1 SISO Case
For SISO systems, Eq. (4) simplifies to
and its ROM via Eq. (16) is given as:
where \(\varvec{W}^{T}\varvec{b} \in \mathbb {R}^{r}\) and \(\varvec{c}^{T}\varvec{V} \in \mathbb {R}^{r}\).
Theorem 1
[7, 71, 84] In order to match r moments between the full-order system (18) and reduced model (19) at the expansion point \(s=0\), it is required that the columns of projection matrix \(\varvec{V}\) used in Eq. (16) form a basis for the Krylov subspace \(\mathcal {K}_{r}(\varvec{A}^{-1}\varvec{E},\varvec{A}^{-1}\varvec{b})\). Furthermore the matrix \(\varvec{W}\) is selected such that the matrix \(\varvec{A_{r}}\) is nonsingular.
Remark 1
The subspace \(\mathcal {K}_{r}(\varvec{A}^{-1}\varvec{E},\varvec{A}^{-1}\varvec{b})\) is known as input Krylov subspace and the reduced scheme is known as the one-sided Krylov subspace method.
A typical choice of one-sided Krylov subspace method is \(\varvec{W}=\varvec{V}\). This has an advantage of preserving stability and passivity of reduced model for some specific large-scale models
Theorem 2
[7, 71, 84] In order to match 2r moments between the full-order system (18) and reduced model (19) at the expansion point \(s=0\), it is required that the columns of projection matrices \(\varvec{V}\)and \(\varvec{W}\) used in Eq. (16) form the basis for the Krylov subspaces given as \(\mathcal {K}_{r}(\varvec{A}^{-1}\varvec{E},\varvec{A}^{-1}\varvec{b})\) and \(\mathcal {K}_{r}(\varvec{A}^{-T}\varvec{E}^{T},\varvec{A}^{-T}\varvec{c})\) respectively, where \(\varvec{A}\) and \(\varvec{A_{r}}\) are assumed to be invertible.
This reduction scheme is known as two-sided Krylov subspace method, and this corresponds to matching double the number of moments than the one-sided method.
Theorem 3
[7, 71, 84] In order to match 2r moments between the full-order system (18) and reduced model (19) at the expansion point \(s=\sigma\), it is required that the columns of projection matrices \(\varvec{V}\)and \(\varvec{W}\) used in Eq. (16) form the basis for the Krylov subspaces given as \(\mathcal {K}_{r}((\varvec{A}-\sigma \varvec{E})^{-1}\varvec{E},\varvec{(}{A}-\sigma \varvec{E})^{-1}\varvec{b})\) and \(\mathcal {K}_{r}((\varvec{A}-\sigma \varvec{E})^{-T}\varvec{E}^{T},(\varvec{A}-\sigma \varvec{E})^{-T}\varvec{c})\) respectively, where \(\varvec{A}\) and \(\varvec{A_{r}}\) are assumed to be invertible.
Remark 2
This is achieved by substituting the matrix \(\varvec{A}\) by \((\varvec{A}-\sigma \varvec{E})\) in the respective Krylov subspaces as explained earlier.
Sometimes, one is interested in capturing the high-speed dynamics of the system at hand, which is achieved by matching moments at higher frequencies (\(s \rightarrow \infty\)) i.e, matching some of the Markov parameters.
Theorem 4
Let \(m_{1} \in \mathbb {Z}\) and \(0 \le m_{1} \le r\), then by selecting the matrix \(\varvec{V}\) used in Eq. (16) as a basis for Krylov subspace given as \(\mathcal {K}_{r}(\varvec{A}^{-1}\varvec{E},(\varvec{E}^{-1}\varvec{A})^{m_{1}}\varvec{A}^{-1}\varvec{b})\) matches the first \(m_{1}\) Markov parameters and the first \(r-m_{1}\) moments of system (18) and (19) resp.
Similarly, the matrix \(\varvec{W}\) is chosen such that \(\varvec{A_{r}}\) and \(\varvec{E_{r}}\) are non-singular. This immediately follows the number of moments, in this case, can be doubled by selecting the suitable input and output Krylov subspaces.
Theorem 5
Let \(m_{1},m_{2} \in \mathbb {Z}\) where \(0\le m_{1},m_{2}\le r\), then by selecting the matrices \(\varvec{V}\) and \(\varvec{W}\), used in Eq. (16), as the basis for Krylov subspaces given as \(\mathcal {K}_{r}(\varvec{A}^{-1}\varvec{E},(\varvec{E}^{-1}\varvec{A})^{m_{1}}\varvec{A}^{-1}\varvec{b})\) and \(\mathcal {K}_{r}(\varvec{A}^{-T}\varvec{E}^{T},(\varvec{E}^{-T}\varvec{A})^{m_{2}}\varvec{A}^{-T}\varvec{c})\) respectively, matches the first \(m_{1}+m_{2}\) Markov parameters and the first \(2r-m_{1}-m_{2}\) moments of system (18) and (19) respectively.
Now, if the aim is to match moments at multiple expansion points: \(\sigma _{1},\sigma _{2},\ldots ,\sigma _{k}\), then k different Krylov subspaces are to be constructed. In this case, the projection matrix is obtained by the union of all the respective Krylov subspaces such that a universal basis is found.
Theorem 6
The first \(r_{i}\) moments about \(\sigma _{i}\) are matched between systems (18) and (19) respectively, by selecting the matrix \(\varvec{V}\), used in Eq. (16), as follows:
where its assumed that (\(\varvec{A}-\sigma _{i}\varvec{E}\)) and (\(\varvec{A_{r}}-\sigma _{i}\varvec{E_{r}}\)) are both nonsingular and \(\varvec{W}\) is an arbitrary full rank matrix.
Similar to previous cases, a two-sided method can provide double the number of moments about each point \(\sigma _{i}\). All the theorems mentioned above are summed up in Table 1.
So far, it is not clear how to numerically obtain the projection matrices \(\varvec{V}\) and \(\varvec{W}\). An early attempt at this was the Asymptotic Waveform Evaluation (AWE) method [145] in which the moments were explicitly calculated rather than computing the matrices \(\varvec{V}\) and \(\varvec{W}\). The method became prominent due to its capability to reduce RC interconnect models containing thousands of variables. Later-on, a multi-point version of the method was proposed also in Ref. [53]. AWE based methods, however, had a numerical instability, that is, the vectors become linearly dependent and converge to an eigenvector of \(\varvec{A}\). This shortcoming was first pointed-out by Gallivan et al. [76] and later by Feldman and Freund [62]. Consequently, this led to the development of implicit based moment-matching methods, and the first significant contribution came via the Arnoldi method [13, 69]. This method employs a one-sided projection to iteratively construct a set of normalized vectors satisfying \(\varvec{V}^{T}\varvec{V}=\varvec{I}\). Within every iteration, a new vector is generated, which is orthogonal to all the previous ones. This results in an upper Hessenberg structure of the matrix \(\varvec{A_{r}}\) and the vector \(\varvec{b_{r}}\) becomes a multiple of the first unit vector. However, this algorithm also generates a linearly dependent set of basis vectors for a relatively large value of r. This is normally avoided by deflating the redundant columns of \(\varvec{V}\) to retain reduced models with a certain degree of accuracy [54]. This has been demonstrated by B. Salimbahrami [156] where a modified Gram-Schmidt orthogonalization scheme is employed.
Another key contribution towards implicit moment matching was the two-sided Lanczos method [62, 117], also known as the Padé via Lanczos (PVL) method. This method constructs two sequences of basis vectors which span the respective input and output Krylov subspaces satisfying \(\varvec{W}^{T}\varvec{V}=\varvec{I}\), resulting in an upper triangular structure of the matrix \(\varvec{A_{r}}\). Apart from matching moments, this method was initially proposed for obtaining reduced models based on the computation of eigenvalues [136]. Further work in this direction led to the development of partial realization via Lanczos method by Gragg and Lindquist [81]. The method was also extended to MIMO systems by Aliaga et al. [4] (also see Refs . [108, 109]). Boley [41] addressed the issue regarding the loss of biorthogonalization in classical Lanczos method. Later-on, new results also appeared in the areas of stability retention [85], error analysis [101] and in control literature [41, 174]. However, these studies didn’t present any new structure in projection technique for rational interpolation.
To retain passivity among the reduced models, the passive reduced-order interconnect macromodelling algorithm (PRIMA) was proposed by Odabasioglu et al. [137]. The idea was demonstrated in linear RLC systems. In order to match moments at multiple expansion points, the rational Lanczos method and the dual Arnoldi method were proposed by Grimme et al. [84]. Furthermore, the issue of unstable partial realizations in classical Krylov methods was addressed by the restarting techniques proposed in Ref. [85] and the implicitly restarted dual Arnoldi method by Jaimoukha and Kasemally [102].
2.1.2 MIMO Case
For the case of MIMO systems, (given in Eq. (4)), the block Krylov subspaces are defined as:
The block subspace for m starting vectors/columns of \(\varvec{B}\) can be considered as a union of m Krylov subspaces for each starting vector [156]. Thus, by using the block Krylov subspaces, all the above mentioned theorems for matching the moments/Markov parameters can be generalized for MIMO systems. For instance, one has to use the block versions, i.e, \(\mathcal {K}_{r}(\varvec{A}^{-1}\varvec{E},\varvec{A}^{-1}\varvec{B})\) and \(\mathcal {K}_{r}(\varvec{A}^{-T}\varvec{E}^{T},\varvec{A}^{-T}\varvec{C}^{T})\) that generalizes Theorem 2. Consequently, \(\frac{r}{m}\) moments are matched in one-sided method and \(\frac{r}{m}+\frac{r}{p}\) in the two-sided method.
2.1.3 Tangential Interpolation Problem
The notion of “interpolation” for MIMO systems implies that the interpolating matrix-valued rational function \(\varvec{H_{r}}(s)\) matches the origin function \(\varvec{H}(s)\) with respect to some predefined error. This would, in effect, require \(p\times m\) interpolation conditions for each interpolation point. As such, this will result in large size of reduced-order model r for even a moderate size of input and output dimensions m and p. Thus, for MIMO systems, it’s desired that the interpolating function matches the original function along certain specific directions or tangent directions. Consequently, this involves selecting interpolation points as well as the interpolation directions.
Tangential interpolation based moment matching for MIMO systems was presented in many studies such as in Refs. [7, 11, 21, 62, 71, 76, 139]. It is the extension of rational Krylov methods to MIMO systems when all tangent directions are the same. The tangential interpolation problem for descriptor systems was also proposed by Gugercin et al. [91] and for index one descriptor system by Antoulas et al. [11].
Definition 3
Let \(\varvec{w}_{i} \in \mathbb {C}^{m}\) be the (non-trivial) right tangent direction, we define \(\varvec{H_{r}}(s)\) to be the right tangent interpolant of \(\varvec{H}(s)\) at \(s=\sigma _{i}\) along \(\varvec{w}_{i}\) if
Similarly, the left tangential interpolant is defined as:
Definition 4
Let \(\varvec{v}_{i} \in \mathbb {C}^{p}\) be the (non-trivial) left tangent direction, then we define \(\varvec{H_{r}}(s)\) to be the left tangent interpolant of \(\varvec{H}(s)\) at \(s=\mu _{i}\) along \(\varvec{v}_{i}\) if
Remark 3
Given a set of r left interpolation points \(\{ \mu _{i}\}_{i=1}^{r}\), r left tangential directions \(\{\varvec{v}_{i}\}_{i=1}^{r}\), r right interpolation points \(\{ \sigma _{i}\}_{i=1}^{r}\), and r right tangential directions \(\{\varvec{w}_{i}\}_{i=1}^{r}\), we can formulate the model reduction problem via tangential interpolation as finding a degree-r reduced transfer function \(\varvec{H_{r}}(s)\) such that Eqs. (22) and (23) hold for \(i=1,2,..,r\).
Definition 5
Given a set of r left and r right tangential directions as \(\varvec{v}_{i}\) and \(\varvec{w}_{i}\) respectively, we define \(\varvec{H_{r}}(s)\) to be a bitangential Hermite interpolant of \(\varvec{H}(s)\), if \(\varvec{H_{r}}(s)\) satisfies both Eqs. (22) and (23). In addition to this, it is required that
holds for \(i=1,2,\ldots ,r\).
Theorem 7
[77] If the columns of matrices \(\varvec{V}\) and \(\varvec{W}\) used in Eq. (16) are selected as:
then the following tangential interpolation conditions are satisfied
with the assumption that \((\sigma \varvec{E}-\varvec{A})\) and \((\mu \varvec{E}-\varvec{A})\) are invertible. Furthermore, if Eq. (25) hold with \(\sigma =\mu\) then the bitangential Hermite condition, i.e,
is satisfied as well.
Remark 4
Theorem 7 demonstrates a left or right interpolation condition without the need to explicitly calculate the values that are interpolated.
The idea can be easily extended to the case of r interpolation points i.e., given a set of r left interpolation points \(\{ \mu _{i}\}_{i=1}^{r}\), r right interpolation points \(\{ \sigma _{i}\}_{i=1}^{r}\), r left tangent directions \(\{\varvec{v}_{i}\}_{i=1}^{r}\) and r right tangent directions \(\{\varvec{v}_{i}\}_{i=1}^{r}\) respectively, we can construct the matrices \(\varvec{V}\) and \(\varvec{W}\), that satisfy the Lagrange tangential interpolation conditions in Eqs. (22,23) and also the bitangential Hermite interpolation condition in Eq. (24) for \(\sigma _{i}=\mu _{i}\), given as follows:
and
The scheme can also be used for higher-order Hermite interpolation given as follows:
Theorem 8
Given the interpolation points \(\sigma ,\mu \in \mathbb {C}\) and the (nontrivial) tangent directions \(\varvec{v}\in \mathbb {C}^{p}\) and \(\varvec{w} \in \mathbb {C}^{m}\). Let the matrix pencils \((\sigma \varvec{E}-\varvec{A})\) and \((\mu \varvec{E}-\varvec{A})\) be invertible, then if the columns of matrix \(\varvec{V}\) used in Eq. (16) are constructed as
for \(k=1,..,N\), then
and if the columns of matrix \(\varvec{W}\) used in Eq. (16) are constructed as
for \(k=1,..,M\), then
and if both Eqs. (31) and (32) hold with \(\sigma =\mu\) then
for \(j=0,\ldots ,N+M-1\)
The main benefit of interpolatory model reduction methods is that it avoids solving large-scale Lyapunov or Riccati equations, making it a convenient reduction platform for large-scale systems. However, the main cost among these methods is solving the shifted linear systems that are sparse in most cases and can be solved using direct methods (e.g., Gaussian elimination). Also, one can prefer iterative solution methods for obtaining the reduction basis \(\varvec{V}\) and \(\varvec{W}\) when dealing with systems with millions of degrees of freedom.
2.1.4 Second-Order Systems
While modeling certain electrical or mechanical systems, one has to deal with models in second-order form. The model reduction techniques for such systems aim to construct reduced models that preserve the second-order structure [27, 123, 124, 158, 169]. To define the generalized notion of moments, consider a large-scale, MIMO, second-order, state-space model given as:
where the matrices \(\varvec{F,D}\) and \(\varvec{G}\) represent the mass, damping and stiffness matrices. The overall dimension of the systems is 2n with m inputs and p outputs. Since the mass, stiffness, and damping matrices in most of the practical systems are symmetric and positive definite, it is often recommended to represent the system (35) as a transformed state-space model given as follows:
As a result the symmetry and definiteness of matrix \(\varvec{E}\) are taken care of by matrices \(\varvec{F}\) and \(\varvec{G}\) and the symmetry of matrix \(\varvec{A}\) is maintained by matrices \(\varvec{G}\) and \(\varvec{D}\) respectively.
Definition 6
The ith moment of system (35) around expansion point \(s=0\) is defined as :
It is hereby assumed that matrix \(\varvec{G}\) is invertible so as to ensure that the matrix \(\varvec{A}\) remains nonsingular. The Markov parameter of system (35) is defined as:
with the condition that matrix \(\varvec{F}\) is invertible.
In order to evaluate the projection basis and hence the reduced second-order model, we first define the second-order Krylov subspace as follows:
Definition 7
[157] Given two matrices \(\varvec{X}_{1}\) and \(\varvec{X}_{2} \in \mathbb {R}^{n \times n}\) and another matrix \(\varvec{H}_{1} \in \mathbb {R}^{n \times m}\) whose columns represent the starting vectors, the second-order Krylov subspace is defined as:
where
Definition 8
The second-order input Krylov subspace is then defined as:
and the second-order output Krylov subspace is defined as:
Similar to first-order systems, the reduction techniques using only one second-order Krylov subspace are known as the one-sided Krylov subspace method, and the reduction techniques involving both the second-order Krylov subspaces are known as the two-sided Krylov subspace methods. Now consider the approximation ansatz given as \(\varvec{x}(t)=\varvec{Vx_{r}}(t), \varvec{V}\in \mathbb {R}^{n \times r}\). Substituting this approximation in Eq. (35) and pre-multiplying by \(\varvec{W}^{T} \in \mathbb {R}^{n \times r}\) yields a second-order reduced model of dimension 2r given as:
where
Using the formulation in Eq. (36), the second-order reduced model (43) is expressed in a transformed state-space given as:
where the projection matrices are defined as:
This formulation preserves the structure of the full-model. Now in order to obtain the projection basis to match any desired moments, all the previously mentioned theorems can be generalized for the second-order system in a similar fashion.
Theorem 9
[157, 158] In order to match the first \(r_{1}+ r_{2}\) moments between the original second-order model Eq. (35) and the reduced second-order model Eq. (43), it is required that the columns of projection matrices \(\varvec{V}\) and \(\varvec{W}\) used in Eq. (44) form the basis for the input and output second-order Krylov subspaces Eqs. (41) and (42) respectively. Also, it is assumed that the matrices \(\varvec{G}\) and \(\varvec{G}_{r}\) are invertible.
And similarly the rational interpolation can achieved as follows:
Theorem 10
[157, 158] In order to match first \(r_{i}\) moments about \(\sigma _{i}, i=1,..,k_{2}\) of the original and reduced models, it is assumed that matrices \(\varvec{V}\) and \(\varvec{W}\) are chosen as follows:
and
The first successful attempt in reducing second-order models came from Meyer, and Srinivasan [130] which involved the evaluation of the free-velocity and the zero-velocity gramians. This was followed by the much improved second-order balancing truncation method by Chahlaoui et al. [48]. However, balancing for second-order systems is not recommended from a numerical perspective. Instead, faster iterative schemes based on Arnoldi or Lanczos are more suitable for reducing systems in the second-order structure. An early attempt in this direction came from Su and Craig [169] and later by Bastian and Haase [27] in which Krylov subspace methods were employed. However, these methods could not match nonzero moments, and the number of moments matched was less than the classical Krylov subspace methods. Consequently, several papers appeared based on similar ideas [72, 120]. These methods obtained reduced models by applying different projection mappings to an equivalent state-space model while preserving its structure. Behnam et al. proposed two-different techniques in Ref. [158] for reducing second-order system by first reducing an equivalent state-space model followed by back conversion of the reduced model to second-order form. This resulted in matching double the number of moments than the second-order Krylov methods proposed in Refs. [23, 124, 157].
2.2 Moment Matching in Time-Domain
So far, we have discussed the frequency domain notion of moment matching for LTI systems for both SISO and MIMO systems. We saw that the reduced model obtained using Krylov subspaces results in a local approximation of frequency response. However, this cannot guarantee a good overall approximation of impulse response. Gunupudi and Nakhla [92], were among the first to present a scheme to match the first derivatives of time-response of full order model with that of the reduced one. Later-on Wang et al. [179] presented a passive model order reduction method based on Chebyshev expansion of the impulse response so as to match the transient responses of the full model and the reduced-order model. The Laguerre polynomial expansion based reduction framework was presented in Ref. [52]. This was later extended and further developed by Rudy [58]. However, the major contribution in this direction came from Astolfi [15] who also extended the idea further to nonlinear systems [16,17,18]. In the following, we describe the time-domain notion of moment matching based on Refs. [15,16,17].
Definition 9
The moments \(\varvec{\bar{\eta _{i}}}(\sigma )\) of the impulse response \({\hbar }(t)\) around a point \(s=\sigma\) is given by the weighted integrals over the time function and satisfy
Remark 5
Thus, the time-domain moments \(\varvec{\bar{\eta _{i}}}(\sigma )\) and the frequency-domain moments \(\varvec{\eta _{i}}(\sigma )\) only differ by a factor:
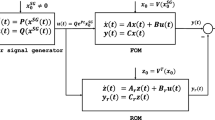
This result is used to develop the notion of moments in terms of steady-state response of system (4) interconnected with a linear signal generator.
Definition 10
[14] The 0-moment of system (4) at \(s=\sigma\) can also be defined as
where \(\varvec{V} \in \mathbb {R}^{n\times r}\) uniquely solves the linear Sylvester equation given as:
Proposition 1
[16] The moments of system (4), \(\varvec{\eta }_{0}(\sigma ), \varvec{\eta }_{1}(\sigma ),\ldots ,\varvec{\eta }_{k}(\sigma )\) can be uniquely determined by the elements of matrix \(\varvec{CV}\) i.e., there exists a one-to-one relation between the moments of system (4) and the elements of matrix \(\varvec{CV}\), with \(\varvec{V}\) being a unique solution of the following Sylvester equation
where \(\varvec{\Xi } \in \mathbb {R}^{r \times r}\) is any non-derogatory matrix and it is assumed that the pair (\(\varvec{\Psi },\varvec{\Xi }\)) is observable. Now, consider the following exogenous linear system (also known as signal generator):
with \(\varvec{\zeta }(t) \in \mathbb {R}^{r}\), \(\lambda (\varvec{E}^{-1}\varvec{A}) \cap \lambda (\varvec{\Xi }) = \emptyset\) and the triple \((\varvec{\Xi ,\Psi ,\zeta }(0))\) to be minimal i.e., the pair \((\varvec{\Psi },\varvec{\Xi })\) is observable and \((\varvec{\Xi },\varvec{\zeta }(0))\) is controllable such that the generated input signal \(\varvec{u}(t)\) is persistently exciting [20, 122].
Theorem 11
[16, 17] Consider system (4), \(\sigma \in \mathbb {C}\). Assume \(\lambda (\varvec{E^{-1}}\varvec{A}) \cap \lambda (\varvec{\Xi }) = \emptyset\). Let \(\varvec{V}\) satisfies the Sylvester equation (51) and \(\varvec{W}\) such that det(\(\varvec{W}^{T}\varvec{EV}\ne 0\)). Consider the interconnection of exogenous system (52) with system (4) as follows:
where the pair (\(\varvec{\Psi },\varvec{\Xi }\)) is observable. Then, the (well-defined) steady-state of the output of the said interconnection can be uniquely determined by the respective moments \(\varvec{\eta }_{0}(\sigma ),\varvec{\eta }_{1}(\sigma ),\ldots ,\varvec{\eta }_{k}(\sigma )\).
Remark 6
Connecting a linear signal generator with the full order system (4) is similar to providing exponential inputs to the system given as \(\varvec{u}(t)=\varvec{\Psi }(e^{\varvec{\Xi }t}\varvec{\zeta (0)})\). The (well-defined )steady-state of interconnected system is given as:
where \(\varvec{y}_{h}(t)\) represents the steady-state response of the system and for an asymptotically stable system, considered here, the transient response, represented by \(\varvec{y}_{p}(t)\) decays to zero at \(t \rightarrow \infty\).
Using Theorem 11, the reduced-order model via moment-matching can be obtained as follows:
Proposition 2
[17] Consider the full-order model (4) and the system described in Eq. (15). Fix \(\varvec{\Psi }\) and \(\varvec{\Xi }\) such that the pair (\(\varvec{\Psi },\varvec{\Xi }\)) is observable. Also assume that \(\lambda (\varvec{E^{-1}}\varvec{A}) \cap \lambda (\varvec{\Xi }) = \emptyset\) . Then, the reduced model (15) matches moments with system (4) at \((\varvec{\Xi ,\Psi ,\zeta }(0))\) if
where \(\varvec{V_{r}}\) uniquely solves the following Sylvester equation
Thus, moment-matching in the time-domain implies ma- tching the full order model’s steady-state response with the reduced model when both are excited by appropriate inputs from the signal generator. However, the steady-state response is interpolated for inputs other than those generated from the signal generator.
The time-domain illustration of moment-matching in terms of interpolation of steady-state response is depicted in Fig. 1. This kind of notion of moment-matching in terms of steady-state response is particularly useful in the sense that as it permits one to define moments even for those systems which don’t have a transfer function representation, such as the time-varying systems.
2.3 Issues and Recent Advancements in Linear Moment Matching
Model order reduction using Krylov subspace methods provides an indispensable platform for reducing large-scale problems; however, there are many issues related to the automatic generation of the reduced model. Although various algorithms have been developed in the past, these apply only to some specific class of problems or under some specific conditions. Next, we highlight some major relevant problems and provide an overview of some of the significant achievements in this direction.
2.3.1 Choice of Expansion Point(s)
The choice and number of interpolation points or shifts in Krylov subspace methods is an important factor in dictating the quality of the approximation. To address this issue, a lot of work has been carried out over the past years. In order for the reduced system to minimize the \(\mathcal {H}_{2}\)-norm error, various optimality conditions have been formulated either in terms of rational interpolation conditions [29,30,31, 45, 88, 90, 111, 128, 175] or in terms of Sylvester and Lyapunov equations [38, 93, 168, 183, 186]. For SISO systems, the interpolation conditions were first proposed by Meier and Luenberger [128]. Gugercin et al. proposed the iterative rational Krylov alogorithm (IRKA) [88, 89], which produces reduced models satisfying the first-order necessary conditions for \(\mathcal {H}_{2}\) optimality by selecting the interpolation points as the mirror images of the poles of reduced system. The idea was later extended to MIMO systems in Refs. [45, 90, 175]. Van Dooren et al. derived the optimality conditions for the case of repeated poles of \(\varvec{H_{r}}(s)\) [175]. Generally speaking, IRKA has been a significant success in obtaining optimal reduced models and as such finds applications in psychophysiology [105], optimal cooling of steel profiles [90] and many others. Recently, this method was also extended for the reduction of bilinear systems by Benner and Breiten [34]. The convergence of IRKA is guaranteed a priori in some situations [67], albeit fails in some cases [67, 90]. However, the choice of initial starting values remains an open question.
Druskin and Simoncini [56] proposed an adaptive computation of interpolation points for the rational Kry- lov methods. Though this method is less accurate than IRKA, it has a low computational cost. This was later followed by the SPARK algorithm by Panzer et al. [140] in which the choice of interpolation point(s), as well as the order of reduced model, is adaptively selected. Similar work was also presented in Ref. [66]. Based on the binary search principle, Bollhöfer and Bodendiek [42] presented adaptive rules for selecting the shifts. They showed a general scheme for selecting both the shifts and the moments by combining the adaptive shift selection scheme with the adaptive moment selecting method as presented earlier in Ref. [118]. However, the choice of selecting the reduced-order dimension remains unknown.
Besides the appropriate choice of interpolation point, it is often required in certain applications that the interpolation is carried out in certain frequency regions of interest. This requires weighting certain frequencies more than others. To allow frequency weighting, the weighted \(\mathcal {H}_{2}\) model reduction was first proposed by Halevi [93, 168] as the solution of Riccati and Lyapunov equations. However, a more efficient version of this scheme was introduced in SISO systems by Anić et al. [6] and for MIMO systems by Breiten et al. [44].
All the above methods described demand more or less heuristics, as the user has to manually pick and try several interpolation points and decide what works satisfactorily for his/her application. This is because of the absence of global error bounds for Krylov subspace methods, which will be discussed next. However, a general scheme that one can follow (as given in Ref. [58]) is that by selecting \(s=0\), the steady-state accuracy is improved as the DC gain of both the full-order and reduced-order model is matched. By selecting \(s\rightarrow \infty\), the resulting reduced system better approximates the transient response of the full-order system. Also, selecting multiple interpolation points across the frequency spectrum leads to a better approximation on a broader frequency band.
2.3.2 Global Error Indicator
Another major open issue in Krylov-based reduction is the lack of a global error bound between the full-order system and the reduced one. Earlier results in this direction led to the development of local error bounds for the transfer function only for a certain frequency range [25, 84]. Later, some heuristic error indicators were presented in Refs. [32, 84]. It was proposed that the error between the full-order model and the reduced model is approximately equal to one between two successive reduced-order models. However, no proof was provided. A deductible error estimator was presented first by Konkel et al. [110].
A posterior error indicator was presented by Feng and Benner [63], whereby a greedy algorithm determines the next interpolation point based on the largest error. However, the method is applicable only to some special LTI systems where the matrix \(\varvec{E}\) in Eq. (4) is symmetric positive definite. Similar requirement is mandated in the method presented by Panzer et al. [141] whereby global \(\mathcal {H}_{2}\) and \(\mathcal {H}_{\infty }\) error bounds are derived. Furthermore, it is also required that \(\varvec{A}+\varvec{A}^{T}>0\). Another study by Wolf et al. [182] proposed a gramian-based output error bound. However, the method is not computationally practical for large scale systems because it involves the explicit computation of observability gramian.
Thus, we conclude that the calculation of an exact global error bound in Krylov based reduction methods requires the involvement of the full-order system, and this would become practically challenging for large-scale settings. As such, this remains an open area of research.
2.3.3 Preserving Stability and Passivity
One of the most fundamental requirements in any reduction scheme is that the property of stability and passivity remains preserved in the reduced model to make sense of surrogate modeling. It is well-known that Krylov subspace-based reduced-order modeling techniques do not preserve stability or passivity in general. However, there are some appreciable efforts in this direction. Methods proposed in Refs. [70, 106] offer guaranteed stability and passivity of the reduced models if the original system is passive. Another set of methods were presented in Refs. [24, 85, 102]. These methods are based on post-processing schemes, in which the unstable poles of the reduced system are removed using explicitly restarted Lanczos and Arnoldi methods. Inspired by the relation between Löwner and Pick matrices, the interpolation-based passivity preserving methods were proposed in Refs. [8, 167].
Similar to the previous discussion, these methods are confined to a special class of LTI systems and extend only to one-sided Krylov methods. The interpolation-based methods are numerically costly than classical Krylov based MOR. As far as the restarted algorithms are considered, these apply to SISO systems only. Furthermore, after removing the unstable poles, these methods do not preserve moment matching property and, as such, do not always guarantee to obtain a stable a reduced model with a finite number of restarts, thus making this an open problem to be addressed.
3 Moment Matching for Nonlinear Systems
Since most of the practical real-life dynamical systems are inherently nonlinear in nature, this has led to a lot of research efforts from the past decades to reduce large-scale nonlinear systems. Special classes of large-scale systems such as bilinear systems, DAE systems and Hamiltonian systems have been successfully reduced, see e.g. Lall et al. [116], Soberg et al. [166], Al-Baiyat et al. [3] and Fujimoto [73]. Polynomial approximation of weakly nonlinear systems has been carried by Chen [51] , Rewienski and White [153, 154] and Benner [33]. Later-on, the idea of reducing certain nonlinear system by transforming them into quadratic bilinear form was proposed by Benner and Breiten [36], Gu [87] and Antoulas et al. [9]. Methods based on variational analysis were also proposed [35, 87, 144].
The concept of balancing for nonlinear systems was first proposed in Scherpen [164]. This further encouraged the development of energy-based methods and the notion of Hankel operator, see e.g., Gray and Mesko [82], Scherpen and Gray [163], Scherpen and Van-der-Schaft [165] and Fujimoto and Scherpen [74, 75]. Methods based on proper orthogonal decomposition (POD) were proposed by Willcox and Peraire [181], Kunisch and Volkwein [114], Hinze and Volkwein [94], Kunisch and Volkwein [115], Grepl et al. [83] and Astrid et al. [19]. Krylov subspace methods for special nonlinear system classes have also been studied in Refs. [43, 80].
The relation between moments and Sylvester equation was first proposed by Gallivan et al. [78, 79]. Based on this, the notion of nonlinear moments was firstly presented in Astolfi [14] followed by Ref. [15]. Since then, methods on linear moment matching and, especially, nonlinear moment-matching (NLMM) have been developed in many publications. A class of (nonlinear) parameterized ROMs achieving moment matching was defined in Ref. [96]. A two-sided, nonlinear moment matching theory was developed by Ionescu and Astolfi [97, 98]. The problem of MOR via moment-matching for linear and nonlinear differential time-delay systems with discrete and distributed-delays was studied by Scarciotti and Astolfi [160]. In addition to this, the online estimation of moments of linear and nonlinear systems from input/output measurements has been proposed in Ref. [161, 162]. The study presented new algorithms to construct ROM’s that asymptotically match the moments of an unknown nonlinear system to be reduced by solving a recursive, moving window, least-square estimation problem using input/output snapshot measurements. In reference to this, Maria et al. [176] developed a practical simulation-free, NLMM algorithm in which certain numerical simplifications are proposed that avoids the expensive solution of Sylvester PDE. Recently, Rafiq and Bazaz proposed a nonlinear MOR framework based on NLMM with dynamic mode decomposition (DMD) [152]. The framework involves the computation of the offline projection matrix \(\varvec{V}\) by the application of NLMM, whereas the underlying nonlinearity is approximated via DMD modes. Also, a parametric nonlinear MOR method based on NLMM has been proposed in Ref. [151](see also [148,149,150]). Faedo et al. [60] recently extended this idea to wave energy systems. Furthermore, an optimal \(\mathcal {H}_{2}\)-norm based MOR method using time-domain moment-matching was proposed by Ion Necoara and Ionescu [133].
As mentioned before, this manuscript focuses on interpolatory/moment-matching-based MOR methods, and as such, we will not discuss data-driven/snapshots based methods such as POD.
3.1 Moments of a Nonlinear System
Similar to the notion of moments for linear systems described in Sect. 2.2, we revisit the nonlinear enhancement of moment-matching for large-scale systems. The idea is based on the concepts emerging from output regulation of nonlinear systems [112], the center manifold theory [47] and the steady-state response of nonlinear-systems [46, 99, 100].
Consider a large-scale, nonlinear, time-invariant, exponentially stable, MIMO state-space model of the form
with non-singular descriptor matrix \(\varvec{E} \in \mathbb {R}^{n\times n}\), the vectors \(\varvec{x}(t) \in \mathbb {R}^{n}, \varvec{u} \in \mathbb {R}^{m}, \varvec{y}(t) \in \mathbb {R}^{p}\) and \(\varvec{f}(\varvec{x},\varvec{u}):\mathbb {R}^{n}\times \mathbb {R}^{m}\rightarrow \mathbb {R}^{n},\varvec{g}(\varvec{x}):\mathbb {R}^{n}\rightarrow \mathbb {R}^{p}\) are the two nonlinear, vector valued functions such that \(\varvec{f}(\varvec{0},\varvec{0})=\varvec{0}\) and \(\varvec{g}(\varvec{0})=\varvec{0}\). Also, the zero equilibrium, (calculated from \(\varvec{0}=\varvec{f}(\varvec{x},\varvec{0})\)), is assumed to be locally exponentially stable.
Consider the following nonlinear exogenous (signal generator) system:
where \(\varvec{\varpi }(\varvec{\zeta }) \in \mathbb {R}^{r}\rightarrow \mathbb {R}^{r}\) and \(\varvec{\varrho }(\varvec{\zeta }) \in \mathbb {R}^{r}\rightarrow \mathbb {R}^{m}\) are smooth mapping such that \(\varvec{\varpi }(\varvec{0})=\varvec{0}\) and \(\varvec{\varrho }(\varvec{0})=\varvec{0}\). It is hereby assumed that the exogenous system Eq. (58) is observable \((\varvec{\varrho },\varvec{\varpi },\varvec{\zeta _{0}})\), i.e., the output trajectories corresponding to any initial conditions do not coincide. Also, its is assumed that the point \(\varvec{\zeta _{0}}\) is a stable equilibrium (in ordinary sense of Lyapunov) such that inputs generated by such a system remain bounded. Furthermore, the input signal \(\varvec{u}(t)\) is assumed to be persistently exciting in time [99]. This implies that every point \(\varvec{\zeta ^{o}}\) is Poisson stable, such that no trajectory can decay to zero as \(t \rightarrow \infty\). When both the above conditions are met, we define the signal generator to be “neutrally stable” [99] i.e., if the output signal of such a signal generator is fed to the input of nonlinear system (57), the steady-state of output of such an interconnection is guaranteed to be well-defined. The signal generator thus essentially captures the requirement that one is interested in studying the the behavior of Eq. (57) only in specific circumstances. The interconnection of exogenous system (58) with nonlinear system (57) is given as:
The steady-state of such an interconnection is given as:
where the mapping \(\varvec{v}(\varvec{\zeta })\) is a local mapping defined in the neighborhood of \(\varvec{\zeta }=0\). Since the nonlinear system (57) is assumed to be exponentially stable, as such the transient solution decays exponentially, i.e., \(\lim \limits _{t \rightarrow \infty }\varvec{y_{h}}(t)=0\), and \(\varvec{y_{ss}}(t)=\varvec{g}(\varvec{v}(\varvec{\zeta }(t)))\) is the steady-state response of the interconnected system. Interconnecting the nonlinear system (57) with the signal generator (58) corresponds to exciting the nonlinear system with user-defined inputs.
In order to provide a generalized notion of moments for nonlinear systems, the following assumption is required (as provided in Ref. [17])
Assumption: The unique mapping \(\varvec{v}(\varvec{\zeta })\) solves the nonlinear Sylvester equation given as:
By the center manifold theory, the interconnected system (59) possesses a locally well-defined invariant manifold at \((\varvec{x_{eq}},\varvec{\zeta _{eq}}=(\varvec{0,0}))\), given as \(\mathcal {M}=\{ (\varvec{x},\varvec{\zeta }) \in \mathbb {R}^{n+r}:\varvec{x}=\varvec{v}(\varvec{\zeta })\}\) where \(\varvec{v}(\varvec{\zeta })\) solves Eq. (61).
Definition 11
[16, 17] The moment of system (57) at \(\varvec{\varpi (\varvec{\zeta })}\) is defined by function \(\varvec{g}(\varvec{v}(\varvec{\zeta }))\) under the aforesaid assumptions. Furthermore, the 0th nonlinear moment of system (57) at \((\varvec{\varpi }(\varvec{\zeta }(t))),\varvec{\varrho }(\varvec{\zeta }(t)),\varvec{\zeta _{0}})\) is related to the (locally well-defined) steady-state response \(\varvec{y_{ss}}(t)=\varvec{g}(\varvec{v}(\varvec{\zeta }(t)))\) where the mapping \(\varvec{v}(\varvec{\zeta })\) solves the nonlinear Sylvester equation (61).
Theorem 12
[16, 17] The moments of the nonlinear system (57) at \((\varvec{\varpi }(\varvec{\zeta }),\varvec{\varrho }(\varvec{\zeta }),\varvec{\zeta _{0}})\) coincide with the (well-defined) steady-state response of the output of the interconnected system Eq. (59) when the aforesaid assumptions hold.
Thus, similar to linear systems, a nonlinear reduced model can be defined that achieves moment-matching with original system (57) at \((\varvec{\varpi }(\varvec{\zeta }),\varvec{\varrho }(\varvec{\zeta }),\varvec{\zeta _{0}})\).
Definition 12
[16, 17] A reduced-order model defined as:
of dimension \(r~(r<<n)\) matches moments with the full-order system (57) at \((\varvec{\varpi }(\varvec{\zeta }),\varvec{\varrho }(\varvec{\zeta }),\varvec{\zeta _{0}})\) if the reduced nonlinear Sylvester equation given as:
is uniquely solved by \((\varvec{g_{r}}(\varvec{\zeta }))\) such that
Remark 7
Thus, moment-matching for nonlinear systems can be interpreted as the exact matching of the steady-state response of the FOM and ROM (cf. Fig. 2).
3.1.1 Illustration of Nonlinear Moment-Matching on MEMS Micro-Switch Model
In order to illustrate the idea of nonlinear moment-matching based MOR, we examine the time-dependent, large-amplitude dynamics of a highly nonlinear squeeze-film damping problem involving electrostatic, mechanical and fluidic components [121, 132, 138, 184]. This nonlinear benchmark model is used as a pressure sensor due to its extreme sensitivity to surrounding atmospheric conditions [103, 172, 185]. A finite-difference discretization scheme with M points along the length and N points for the width yields a system of nonlinear ODE of the form as Eq. (57) with dimension \((2+M)N\). The test signal (input excitation) is chosen as \(u_{\text {test}}=(3\cos (2\omega t )+7\cos (0.5\omega t))^{2}\) with \(\omega =2\pi \times 1e4\) and the output is taken as the center-point deflection of the beam. The full-order model of size \(n=374\) is integrated using an implicit Euler’s scheme, which resulted in a simulation time of 287.17 s. The reduced-order model of size \(r=15\) is constructed using the scheme proposed in Ref. [176] which involves solving a simplified version of Sylvester equation (61). The signal generated used in training phase is chosen as \(\dot{\varvec{\zeta }}(t)=16.5\sin (\pi t)+11e3\) whereas the test signal is kept the same. Figure 3 shows the full-order and the reduced-order systems’ response along-with the relative error-profile. It is seen that the reduced-order model effectively captures the oscillatory dynamics of the original system with a simulation time of 8.31 s.
Unlike linear-moment, where the interpolation points are implicitly/explicitly defined in the frequency range of interest, nonlinear moment-matching involves matching/interpolating the steady-state of FOM and ROM when both are excited by user-defined signal generator(s). For a more detailed analysis of choosing the appropriate signal generator for a system at hand and the numerical aspects involved, we refer the reader to Ref. [176].
3.2 Other Nonlinear MOR Methods
Besides the time-domain moment-matching method for nonlinear systems described above, there are other reduction schemes that use the Krylov subspaces to obtain the projection basis. One of the most simplest is the quadratic method [51] or the more accurate bilinearazation method by Bai et al. [22, 143]. These methods are the extension of linear moment-matching methods and fall in the category of frequency domain MOR methods. These methods either approximate the underlying nonlinearity by a polynomial of low degree [22, 51, 64, 143, 144] or transform into quadratic bilinear system [35, 86, 87]. Furthermore, there exist certain methods which involve efficient estimation of nonlinear function \(\varvec{f}(.)\) such as the empirical interpolation method by Barrault et al. [26] or the discrete empirical interpolation method by Chaturantabut and Sorensen [50], the best point interpolation method by Nguyen et al. [134] and the missing point estimate by Astrid et al. [19]. Here we discuss some effective methods of practice.
3.2.1 Quadratic Method
Proposed by Chen [51], this method approximates the nonlinear function \(\varvec{f}(.)\) as a kronecker product formulation of \(\varvec{x}\), which is given as:
where the matrices \(\varvec{A_{i}} \in \mathbb {R}^{n \times n}\) denote ith partial derivative of \(\varvec{f}\) at \(\varvec{x}=0\). The quadratic system thus obtained is given as:
The projection matrix \(\varvec{V}\), in this method, is obtained as the basis of the Krylov subspace given as:
and the reduced quadratic model is obtained by using the one-sided approximation ansatz \(\varvec{x}\approx \varvec{Vx}_{r}\) in Eq. (66) given as:
It is assumed that \(\varvec{f}(0)=0\) otherwise is taken as a part of input signal.
3.2.2 Bilinearization Method
Based on Carleman linearization of a nonlinear systems [159], the bilinear form was proposed in Refs. [22, 143]. This involves the use of first two terms of the series in Eq. (65) so as to approximate the nonlinear function as:
As such the bilinear, input-affine system is obtained as follows:
where \(\varvec{x}_{\otimes }=\begin{bmatrix} \varvec{x}(t)\\ \varvec{x}(t)\otimes \varvec{x}(t) \end{bmatrix},\quad \varvec{A}_{\otimes }=\begin{bmatrix} &{}\varvec{A_{1}}&{}\varvec{A_{2}}\\ {} &{}0&{}\varvec{A_{1}}\otimes \varvec{I}+\varvec{I}\otimes \varvec{A_{1}}\end{bmatrix}\) \(\varvec{N}_{\otimes }=\begin{bmatrix} &{}0&{}0\\ {} &{}\varvec{B}\otimes \varvec{I}+\varvec{I}\otimes \varvec{B}&{}0 \end{bmatrix},\varvec{B}_{\otimes }=\begin{bmatrix} \varvec{B}\\ 0 \end{bmatrix},\varvec{C^{T}}_{\otimes }=\begin{bmatrix} \varvec{C^{T}}\\ 0 \end{bmatrix}\) After transforming the nonlinear system to bilinear form Eq. (69), there are several choices of calculating the projection basis. One particular choice was proposed in Ref. [143]. It was shown that after constructing a series of Krylov subspaces for given \(r_{1},r_{2},\ldots ,r_{K}\), as follows:
and
for \(1<k<K\), the matrix \(\varvec{V}\) is calculated by taking the union of all the subspaces spanned by columns of \(\varvec{V_{k}}\), i.e.,
Another choice of transformation matrix \(\varvec{V}\) was proposed in Ref. [22], which matches as many multimoments as the reduced model and is given as:
and for \(k>1\)
and the final transformation matrix \(\varvec{V}\) is constructed in a similar fashion, i.e.,
After constructing the matrix \(\varvec{V}\), the reduced bilinear system is then obtained by using the approximation \(\varvec{x}_{\otimes }=\varvec{V}\hat{\varvec{x}}_{\otimes }\) in system (69) given as:
where \(\varvec{x}_{\otimes }=\varvec{V\hat{x}}_{\otimes }\), \(\hat{\varvec{A}}_{\otimes }=(\varvec{V}^{T}\varvec{A}_{\otimes }\varvec{V}), \hat{\varvec{N}}_{\otimes }=\varvec{V}^{T}\varvec{N}_{\otimes }\varvec{V}\), \(\hat{\varvec{B}}_{\otimes }=\varvec{V}^{T}\varvec{B}_{\otimes }\) and \(\hat{\varvec{C}}_{\otimes }=\varvec{CV}_{\otimes }\).
Another way of reducing bilinear systems is the balanced truncation (BT) for bilinear system method originally developed by Achar and Nakhla [2], later developed by Condon and Ivanov [126] and by Benner et al. [37]. This method is similar to standard BT method for linear systems. Although, this method outperforms moment-matching methods in terms of approximating quality, it involves solving the generalized Lyapunov equation which is computationally demanding.
3.2.3 Trajectory Piecewise Linear (TPWL) Method
TPWL method replaces the polynomial approximation of the nonlinear system with a piece-wise approximation. This method offers more robustness when dealing with strong nonlinearities. The idea is to linearize the nonlinear function \(\varvec{f}(.)\) at a number of linearization points \(\varvec{x}_{i} (i=0,1,\ldots ,l)\) in response to some training input. The nonlinear function \(\varvec{f}(.)\) is then approximated by the weighted sum of these linear models i.e., \(\varvec{f}(\varvec{x}(t))\approx \sum _{i=0}^{l}w_{i}(\varvec{f}(\varvec{x}_{i})+\varvec{A}_{i}(\varvec{x}(t)-\varvec{x}_{i}))\) and the original system is represented as:
where \(w_{i},i=0,1,\ldots ,l\) is a vector of weights and \(\varvec{A}_{i}\) is the Jacobian matrix of \(\varvec{f}(.)\) at \(\varvec{x}_{i}\). The projection matrix \(\varvec{V}\), in this case, is obtained as orthonormal basis of the following Krylov subspace which spans the reduced state-space.
The reduction is then performed by using the approximation ansatz \(\varvec{x}(t)=\varvec{Vx_{r}}(t)\) in Eq. (77).
Here, the weights \(\tilde{w}\) depend on \(\varvec{x_{r}}\) and can be computed using the information about the distances \(||\varvec{x_{r}}-\varvec{x_{r}}_{i}||\) of the (projected) linearization points \(\varvec{V}^{T}\varvec{x}_{i}\) from the current state \(\varvec{x_{r}}\). An error bound for TPWL was proposed in Ref. [154] along-with some discussion on stability and passivity preservation. A down-side of this method, however, is the choice of an appropriate training input. The reduced model loses accuracy if the training inputs are chosen far away from the actual inputs. This happens because the computed trajectory departs from the actual behavior of the state vector \(\varvec{x}(t)\).
In continuation with this, a polynomial piece-wise approximation was proposed by Dong and Roychowdhury [55] instead of a linear piece-wise approximation for each piece. Similar ideas later emerged in various studies such as in Refs. [177]. A more detailed review on piece-wise linearzation based reduction methods can be found in Ref. [95].
3.3 Issues in Nonlinear MOR
Although nonlinear MOR methods have seen a prominent success, there are still some unresolved queries/issues, which are enlisted as follows:
-
1.
A common issue among all nonlinear reduction methods is the lack of practical global error bounds for the reduced-order model.
-
2.
Nonlinear moment-matching based MOR method presented in Refs. [15,16,17,18] involves the a priori solution of the nonlinear, state-dependent, Sylvester-like PDE (61) which is computationally expensive.
-
3.
The choice of the signal generator in NLMM [176] is heuristic and requires repeated simulations.
-
4.
There is no a priori knowledge of acceptable training inputs and linearization points in the TPWL method.
-
5.
An optimal choice for the number of multi-moments in the bilinearization methods is not known.
4 Concluding Remarks
The idea of automatically extracting reduced-order models from large-scale dynamical systems is a central challenge. By and large, reduced-order modeling via moment-matching techniques for linear systems is relatively well explored, and a suite of efficient algorithms is available at our disposal. However, constructing optimal approximations of the large-scale models while preserving passivity or stability remains elusive. Furthermore, the systems arising while modeling complex fluids or in the simulation of electronics circuits are inherently nonlinear. Thus, employing nonlinear reduction techniques directly to these systems is desirable. The nonlinear model order reduction area though witnessed some notable achievements in the past few years, however certain issues (as discussed) remain challenging. Moment-matching-based MOR methods have seen a long history. Numerous modifications/advancements have appeared from time to time to make this technique a more robust platform for treating problems in large-scale settings. Some of these modifications are currently a work in progress, whereas others are yet to happen.
In this survey, we have reviewed the model order reduction problem from the moment-matching perspective. Both frequency and time-domain notions of the moment-matching technique are discussed. We have pointed out the differences and similarities among various methods. Several open problems are also exposed in the case of linear and nonlinear reduction methods.
Availability of data and material
Not applicable.
Code availability
Not applicable.
References
Akram N, Alam M, Hussain R, Ali A, Muhammad S, Malik R, Haq AU (2020) Passivity preserving model order reduction using the reduce norm method. Electronics 9(6):964
Al-Baiyat SA, Bettayeb M (1993) A new model reduction scheme for k-power bilinear systems. In: Proceedings of 32nd IEEE conference on decision and control, IEEE, pp 22–27
Al-Baiyat SA, Beyttayeb M, Al-Saggaf UM (1994) New model reduction scheme for bilinear systems. Int J Syst Sci 25(10):1631–1642
Aliaga J, Boley D, Freund R, Hernández V (2000) A Lanczos-type method for multiple starting vectors. Math Comput 69(232):1577–1601
Alla A, Haasdonk B, Schmidt A (2020) Feedback control of parametrized PDE’s via model order reduction and dynamic programming principle. Adv Comput Math 46(1):9
Anić B, Beattie C, Gugercin S, Antoulas AC (2013) Interpolatory weighted-\(\cal{H}_{2}\) model reduction. Automatica 49(5):1275–1280
Antoulas AC (2005) Approximation of large-scale dynamical systems. SIAM, Philadelphia
Antoulas AC (2005) A new result on passivity preserving model reduction. Syst Control Lett 54(4):361–374
Antoulas AC (2005) An overview of approximation methods for large-scale dynamical systems. Annu Rev Control 29(2):181–190
Antoulas AC, Sorensen DC, Gugercin S (2001) A survey of model reduction methods for large-scale systems. ContempMath 280:193–219
Antoulas AC, Beattie CA, Gugercin S (2010) Interpolatory model reduction of large-scale dynamical systems. In: Efficient modeling and control of large-scale systems. Springer, pp 3–58
Antoulas AC, Beattie CA, Gugercin S (2020) Interpolatory methods for model reduction. SIAM, Philadelphia
Arnoldi WE (1951) The principle of minimized iterations in the solution of the matrix eigenvalue problem. Q Appl Math 9(1):17–29
Astolfi A (2007) Model reduction by moment matching. In: 7th IFAC symposium on nonlinear control systems. Elsevier, pp 577–584
Astolfi A (2007) A new look at model reduction by moment matching for linear systems. In: 2007 46th IEEE conference on decision and control. IEEE, pp 4361–4366
Astolfi A (2008) Model reduction by moment matching for nonlinear systems. In: 2008 47th IEEE conference on decision and control. IEEE, pp 4873–4878
Astolfi A (2010) Model reduction by moment matching for linear and nonlinear systems. IEEE Trans Autom Control 55(10):2321–2336
Astolfi A (2010) Model reduction by moment matching, steady-state response and projections. In: 49th IEEE conference on decision and control (CDC). IEEE, pp 5344–5349
Astrid P, Weiland S, Willcox K, Backx T (2008) Missing point estimation in models described by proper orthogonal decomposition. IEEE Trans Autom Control 53(10):2237–2251
Åström KJ, Wittenmark B (1994) Adaptive control, 2nd edn. Addison-Wesley Longman Publishing Company, London
Bai Z (2002) Krylov subspace techniques for reduced-order modeling of large-scale dynamical systems. Appl Numer Math 43(1–2):9–44
Bai Z, Skoogh D (2006) A projection method for model reduction of bilinear dynamical systems. Linear Algebra Appl 415(2–3):406–425
Bai Z, Su Y (2005) Dimension reduction of large-scale second-order dynamical systems via a second-order Arnoldi method. SIAM J Sci Comput 26(5):1692–1709
Bai Z, Feldmann P, Freund RW (1997) Stable and passive reduced-order models based on partial Padé approximation via the Lanczos process. Numer Anal Manuscr 97(3):10
Bai Z, Slone RD, Smith WT, Ye Q (1999) Error bound for reduced system model by Padé approximation via the Lanczos process. IEEE Trans Comput Aided Des Integr Circuits Syst 18(2):133–141
Barrault M, Maday Y, Nguyen NC, Patera AT (2004) An ‘empirical interpolation’ method: application to efficient reduced-basis discretization of partial differential equations. CR Math 339(9):667–672
Bastian J, Haase J et al. (2003) Order reduction of second order systems. In: In Proceedings of 4th Mathmod, Citeseer
Baur U, Benner P, Feng L (2014) Model order reduction for linear and nonlinear systems: a system-theoretic perspective. Arch Comput Methods Eng 21(4):331–358
Beattie C, Gugercin S (2012) Realization-independent \(\cal{H}_{2}\)-approximation. In: 2012 IEEE 51st IEEE conference on decision and control (CDC). IEEE, pp 4953–4958
Beattie CA, Gugercin S (2007) Krylov-based minimization for optimal h 2 model reduction. In: 2007 46th IEEE conference on decision and control. IEEE, pp 4385–4390
Beattie CA, Gugercin S (2009) A trust region method for optimal h 2 model reduction. In: Proceedings of the 48h IEEE conference on decision and control (CDC) held jointly with 2009 28th Chinese Control conference. IEEE, pp 5370–5375
Bechtold T, Rudnyi EB, Korvink JG (2004) Error indicators for fully automatic extraction of heat-transfer macromodels for mems. J Micromech Microeng 15(3):430
Benner P (2004) Solving large-scale control problems. IEEE Control Syst Mag 24(1):44–59
Benner P, Breiten T (2012) Interpolation-based \(\cal{H}_{2}\) model reduction of bilinear control systems. SIAM J Matrix Anal Appl 33(3):859–885
Benner P, Breiten T (2012) Krylov-subspace based model reduction of nonlinear circuit models using bilinear and quadratic-linear approximations. In: Progress in industrial mathematics at ECMI 2010. Springer, pp 153–159
Benner P, Breiten T (2015) Two-sided projection methods for nonlinear model order reduction. SIAM J Sci Comput 37(2):B239–B260
Benner P, Damm T (2009) Lyapunov equations, energy functionals and model order reduction. Preprint, TU Chemnitz
Benner P, Køhler M, Saak J (2011) Sparse-dense sylvester equations in \(\mathcal{H} _{2}\)-model order reduction. Technical Report MPIMD
Benner P, Gugercin S, Willcox K (2015) A survey of projection-based model reduction methods for parametric dynamical systems. SIAM Rev 57(4):483–531
Bieker K, Peitz S, Brunton SL, Kutz JN, Dellnitz M (2020) Deep model predictive flow control with limited sensor data and online learning. In: Theoretical and computational fluid dynamics, pp 1–15
Boley DL (1994) Krylov space methods on state-space control models. Circuits Syst Signal Process 13(6):733–758
Bollhöfer M, Bodendiek A (2012) Adaptive-order rational Arnoldi method for Maxwell’s equations. In: Scientific computing in electrical engineering (Abstracts), pp 77–78
Breiten T (2013) Interpolatory methods for model reduction of large-scale dynamical systems. PhD thesis, Otto-von-Guericke Universität Magdeburg
Breiten T, Beattie C, Gugercin S (2015) Near-optimal frequency-weighted interpolatory model reduction. Syst Control Lett 78:8–18
Bunse-Gerstner A, Kubalińska D, Vossen G, Wilczek D (2010) \(\cal{H}_{2}\)-norm optimal model reduction for large scale discrete dynamical MIMO systems. J Comput Appl Math 233(5):1202–1216
Byrnes C, Isidori A (1989) Steady state response, separation principle and the output regulation of nonlinear systems. In: Proceedings of the 28th IEEE conference on decision and control. IEEE, pp 2247–2251
Carr J (1982) Applications of center manifold theory, vol 35. Applied Mathematical Sciences, Providence
Chahlaoui Y, Lemonnier D, Vandendorpe A, Van Dooren P (2004) Second order structure preserving balanced truncation. In: Symposium on math theory of network and systems
Chan J (2020) Entropy stable reduced order modeling of nonlinear conservation laws. J Comput Phys 423:109789
Chaturantabut S, Sorensen DC (2010) Nonlinear model reduction via discrete empirical interpolation. SIAM J Sci Comput 32(5):2737–2764
Chen Y (1999) Model order reduction for nonlinear systems. PhD thesis, Massachusetts Institute of Technology
Chen Y, Balakrishnan V, Koh CK, Roy K (2002) Model reduction in the time-domain using Laguerre polynomials and Krylov methods. In: Proceedings 2002 design, automation and test in Europe conference and exhibition. IEEE, pp 931–935
Chiprout E, Nakhla MS (1994) Asymptotic waveform evaluation. In: Asymptotic waveform evaluation. Springer, pp 15–39
Cullum JK, Willoughby RA (2002) Lanczos algorithms for large symmetric eigenvalue computations: theory, vol 1. SIAM, Philadelphia
Dong N, Roychowdhury J (2003) Piecewise polynomial nonlinear model reduction. In: Proceedings 2003. Design automation conference (IEEE Cat. No. 03CH37451). IEEE, pp 484–489
Druskin V, Simoncini V (2011) Adaptive rational Krylov subspaces for large-scale dynamical systems. Syst Control Lett 60(8):546–560
Dziuk G, Elliott CM (2013) Finite element methods for surface PDEs. Acta Numer 22:289
Eid R (2009) Time domain model reduction by moment matching. PhD thesis, Technische Universität München
Ern A, Guermond JL (2013) Theory and practice of finite elements, vol 159. Springer, Berlin
Faedo N, Piuma FJD, Giorgi G, Ringwood JV (2020) Nonlinear model reduction for wave energy systems: a moment-matching-based approach. Nonlinear Dyn 102(3):1215–1237
Far MF, Martin F, Belahcen A, Rasilo P, Awan HAA (2020) Real-time control of an IPMSM using model order reduction. IEEE Trans Ind Electron
Feldmann P, Freund RW (1995) Efficient linear circuit analysis by Padé approximation via the Lanczos process. IEEE Trans Comput Aided Des Integr Circuits Syst 14(5):639–649
Feng L, Benner P (2012) Automatic model order reduction by moment-matching according to an efficient output error bound. In: Scientific computing in electrical engineering (Abstracts), pp 71–72
Feng L, Zeng X, Chiang C, Zhou D, Fang Q (2004) Direct nonlinear order reduction with variational analysis. In: Proceedings design, automation and test in Europe conference and exhibition, vol 2. IEEE, pp 1316–1321
Feng L, Benner P, Korvink JG (2013) System-level modeling of mems by means of model order reduction (mathematical approximations)—mathematical background. System-Level Modeling of MEMS, pp 53–93
Feng L, Korvink JG, Benner P (2015) A fully adaptive scheme for model order reduction based on moment matching. IEEE Trans Compon Packag Manuf Technol 5(12):1872–1884
Flagg G, Beattie C, Gugercin S (2012) Convergence of the iterative rational Krylov algorithm. Syst Control Lett 61(6):688–691
Freund RW (1999) Reduced-order modeling techniques based on Krylov subspaces and their use in circuit simulation. In: Applied and computational control, signals, and circuits. Springer, pp 435–498
Freund RW (2000) Krylov-subspace methods for reduced-order modeling in circuit simulation. J Comput Appl Math 123(1–2):395–421
Freund RW (2000) Passive reduced-order modeling via Krylov-subspace methods. In: CACSD. conference proceedings. IEEE international symposium on computer-aided control system design (Cat. No. 00TH8537). IEEE, pp 261–266
Freund RW (2003) Model reduction methods based on Krylov subspaces. Acta Numer 12:267–319
Freund RW (2004) SPRIM: structure-preserving reduced-order interconnect macromodeling. In: IEEE/ACM international conference on computer aided design, 2004. ICCAD-2004. IEEE, pp 80–87
Fujimoto K (2008) Balanced realization and model order reduction for port-Hamiltonian systems. J Syst Des Dyn 2(3):694–702
Fujimoto K, Scherpen JM (2005) Nonlinear input-normal realizations based on the differential eigenstructure of Hankel operators. IEEE Trans Autom Control 50(1):2–18
Fujimoto K, Scherpen JM (2010) Balanced realization and model order reduction for nonlinear systems based on singular value analysis. SIAM J Control Optim 48(7):4591–4623
Gallivan K, Grimme E, Dooren PV (1994) Asymptotic waveform evaluation via a Lanczos method. Appl Math Lett 7(5):75–80
Gallivan K, Vandendorpe A, Van Dooren P (2004) Model reduction of MIMO systems via tangential interpolation. SIAM J Matrix Anal Appl 26(2):328–349
Gallivan K, Vandendorpe A, Van Dooren P (2004) Sylvester equations and projection-based model reduction. J Comput Appl Math 162(1):213–229
Gallivan K, Vandendorpe A, Van Dooren P (2006) Model reduction and the solution of Sylvester equations. MTNS, Kyoto, p 50
Goyal PK (2018) System-theoretic model order reduction for bilinear and quadratic-bilinear systems. PhD thesis, Universitätsbibliothek
Gragg WB, Lindquist A (1983) On the partial realization problem. Linear Algebra Appl 50:277–319
Gray WS, Mesko J (1997) General input balancing and model reduction for linear and nonlinear systems. In: 1997 European control conference (ECC). IEEE, pp 2862–2867
Grepl MA, Maday Y, Nguyen NC, Patera AT (2007) Efficient reduced-basis treatment of nonaffine and nonlinear partial differential equations. ESAIM Math Model Numer Anal 41(3):575–605
Grimme E (1997) Krylov projection methods for model reduction. PhD thesis, University of Illinois at Urbana Champaign
Grimme EJ, Sorensen DC, Van Dooren P (1996) Model reduction of state space systems via an implicitly restarted Lanczos method. Numer Algorithms 12(1):1–31
Gu C (2009) QLMOR: a new projection-based approach for nonlinear model order reduction. In: 2009 IEEE/ACM international conference on computer-aided design-digest of technical papers. IEEE, pp 389–396
Gu C (2011) QLMOR: a projection-based nonlinear model order reduction approach using quadratic-linear representation of nonlinear systems. IEEE Trans Comput Aided Des Integr Circuits Syst 30(9):1307–1320
Gugercin S (2005) An iterative rational Krylov algorithm (IRKA) for optimal \(\mathcal{H}_{2}\) model reduction. In: Householder symposium XVI, Seven Springs Mountain Resort, PA, USA
Gugercin S, Beattie C, Antoulas A (2006) Rational krylov methods for optimal \(\mathcal{H}_{2}\) model reduction. submitted for publication
Gugercin S, Antoulas AC, Beattie C (2008) \(\mathcal{H}_{2}\) model reduction for large-scale linear dynamical systems. SIAM J Matrix Anal Appl 30(2):609–638
Gugercin S, Stykel T, Wyatt S (2013) Model reduction of descriptor systems by interpolatory projection methods. SIAM J Sci Comput 35:1010–1033
Gunupudi PK, Nakhla MS (1999) Model-reduction of nonlinear circuits using Krylov-space techniques. In: Proceedings of the 36th annual ACM/IEEE design automation conference, pp 13–16
Halevi Y (1990) Frequency weighted model reduction via optimal projection. In: 29th IEEE conference on decision and control. IEEE, pp 2906–2911
Hinze M, Volkwein S (2005) Proper orthogonal decomposition surrogate models for nonlinear dynamical systems: error estimates and suboptimal control. In: Dimension reduction of large-scale systems. Springer, pp 261–306
Hochman A, Vasilyev DM, Rewienski MJ, White JK (2013) Projection-based nonlinear model order reduction. In: System-level modeling of MEMS, advanced micro and nanosystems. Wiley-VCH
Ionescu TC, Astolfi A (2013) Families of reduced order models that achieve nonlinear moment matching. In: 2013 American control conference. IEEE, pp 5518–5523
Ionescu TC, Astolfi A (2015) Nonlinear moment matching-based model order reduction. IEEE Trans Autom Control 61(10):2837–2847
Ionescu TC, Astolfi A, Colaneri P (2014) Families of moment matching based, low order approximations for linear systems. Syst Control Lett 64:47–56
Isidori A (1995) Nonlinear control systems, 3rd edn. Springer, Berlin
Isidori A, Byrnes CI (1990) Output regulation of nonlinear systems. IEEE Trans Autom Control 35(2):131–140
Jaimoukha IM, Kasenally EM (1995) Oblique production methods for large scale model reduction. SIAM J Matrix Anal Appl 16(2):602–627
Jaimoukha IM, Kasenally EM (1997) Implicitly restarted Krylov subspace methods for stable partial realizations. SIAM J Matrix Anal Appl 18(3):633–652
Kaczynski J, Ranacher C, Fleury C (2020) Computationally efficient model for viscous damping in perforated mems structures. Sens Actuators A 314:112201
Karatzas EN, Ballarin F, Rozza G (2020) Projection-based reduced order models for a cut finite element method in parametrized domains. Comput Math Appl 79(3):833–851
Kellems AR, Roos D, Xiao N, Cox SJ (2009) Low-dimensional, morphologically accurate models of subthreshold membrane potential. J Comput Neurosci 27(2):161
Kerns KJ, Yang AT (1998) Preservation of passivity during RLC network reduction via split congruence transformations. IEEE Trans Comput Aided Des Integr Circuits Syst 17(7):582–591
Kim D, Bae Y, Yun S, Braun JE (2020) A methodology for generating reduced-order models for large-scale buildings using the Krylov subspace method. J Build Perform Simul 13(4):419–429
Kim HM, Craig RR Jr (1988) Structural dynamics analysis using an unsymmetric block Lanczos algorithm. Int J Numer Methods Eng 26(10):2305–2318
Kim HM, Craig RR Jr (1990) Computational enhancement of an unsymmetric block Lanczos algorithm. Int J Numer Methods Eng 30(5):1083–1089
Konkel Y, Farle O, Sommer A, Burgard S, Dyczij-Edlinger R (2014) A posteriori error bounds for Krylov-based fast frequency sweeps of finite-element systems. IEEE Trans Magn 50(2):441–444
Krajewski W, Lepschy A, Redivo-Zaglia M, Viaro U (1995) A program for solving the l 2 reduced-order model problem with fixed denominator degree. Numer Algorithms 9(2):355–377
Krener AJ (1992) The construction of optimal linear and nonlinear regulators. In: Systems, models and feedback: theory and applications. Springer, pp 301–322
Kudryavtsev M, Rudnyi EB, Korvink JG, Hohlfeld D, Bechtold T (2015) Computationally efficient and stable order reduction methods for a large-scale model of mems piezoelectric energy harvester. Microelectron Reliab 55(5):747–757
Kunisch K, Volkwein S (1999) Control of the burgers equation by a reduced-order approach using proper orthogonal decomposition. J Optim Theory Appl 102(2):345–371
Kunisch K, Volkwein S (2008) Proper orthogonal decomposition for optimality systems. ESAIM Math Modell Numer Anal 42(1):1–23
Lall S, Krysl P, Marsden JE (2003) Structure-preserving model reduction for mechanical systems. Physica D 184(1–4):304–318
Lanczos C (1950) An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. United States Government Press Office, Los Angeles
Lee HJ, Chu CC, Feng WS (2006) An adaptive-order rational Arnoldi method for model-order reductions of linear time-invariant systems. Linear Algebra Appl 415(2–3):235–261
Li H, Song Z, Zhang F (2020) A reduced-order modified finite difference method preserving unconditional energy-stability for the Allen–Cahn equation. Numer Methods Part Differ Equ 37:1869–1885
Li RC, Bai Z et al (2005) Structure-preserving model reduction using a Krylov subspace projection formulation. Commun Math Sci 3(2):179–199
Liu CC, Wang CC (2014) Numerical investigation into nonlinear dynamic behavior of electrically-actuated clamped-clamped micro-beam with squeeze-film damping effect. Appl Math Model 38(13):3269–3280
Ljung L (1999) System Identification: Theory for the User, Information and System Sciences Series, 2nd edn. Prentice Hall, Upper Saddle River
Lohmann B, Salimbahrami B (2004) Order reduction using Krylov subspace methods. Autom Technol 52(1):30–38
Lohmann B, Salimbahrami B (2005) Reduction of second order systems using second order Krylov subspaces. IFAC Proc Vol 38(1):614–619
Maloberti F (2006) Analog design for CMOS VLSI systems, vol 646. Springer, Berlin
Martone R, Formisano A, Condon M, Ivanov R (2007) Krylov subspaces from bilinear representations of nonlinear systems. COMPEL Int J Comput Math Electr Electron Eng
Mazumder S (2015) Numerical methods for partial differential equations: finite difference and finite methods. Academic Press, London
Meier L, Luenberger D (1967) Approximation of linear constant systems. IEEE Trans Autom Control 12(5):585–588
Mendible A, Brunton SL, Aravkin AY, Lowrie W, Kutz JN (2020) Dimensionality reduction and reduced-order modeling for traveling wave physics. Theor Comput Fluid Dyn 34(4):385–400
Meyer DG, Srinivasan S (1996) Balancing and model reduction for second-order form linear systems. IEEE Trans Autom Control 41(11):1632–1644
Mohamed K (2019) Model order reduction method for large-scale RC interconnect and implementation of adaptive digital PI controller. IEEE Trans Very Large Scale Integr Syst 27(10):2447–2458
Nayfeh AH, Younis MI, Abdel-Rahman EM (2005) Reduced-order models for mems applications. Nonlinear Dyn 41(1–3):211–236
Necoara I, Ionescu TC (2020) \(\cal{H}_{2}\) model reduction of linear network systems by moment matching and optimization. IEEE Trans Autom Control 65(12):5328–5335
Nguyen NC, Patera AT, Peraire J (2008) A ‘best points’ interpolation method for efficient approximation of parametrized functions. Int J Numer Methods Eng 73(4):521–543
Nguyen VB, Tran SBQ, Khan SA, Rong J, Lou J (2020) POD-DEIM model order reduction technique for model predictive control in continuous chemical processing. Comput Chem Eng 133:106638
Nour-Omid B, Clough RW (1984) Dynamic analysis of structures using Lanczos co-ordinates. Earthq Eng Struct Dyn 12(4):565–577
Odabasioglu A, Celik M, Pileggi LT (2003) PRIMA: passive reduced-order interconnect macromodeling algorithm. In: The best of ICCAD. Springer, pp 433–450
Ouakad HM, Al-Qahtani HM, Hawwa MA (2016) Influence of squeeze-film damping on the dynamic behavior of a curved micro-beam. Adv Mech Eng 8(6):1687814016650120
Benner MHP, Termaten E (2001) Model reduction for circuit simulation. Lecture Notes in Electrical Engineering, vol 74. Springer, Cham
Panzer HK, Jaensch S, Wolf T, Lohmann B (2013) A greedy rational Krylov method for \(\cal{H}_{2}\) pseudooptimal model order reduction with preservation of stability. In: 2013 American control conference. IEEE, pp 5512–5517
Panzer HK, Wolf T, Lohmann B (2013) \(\cal{H}_{2}\) and \(\cal{H}_{\infty }\) error bounds for model order reduction of second order systems by Krylov subspace methods. In: 2013 European control conference (ECC). IEEE, pp 4484–4489
Pelesko JA, Bernstein DH (2002) Modeling MEMS and NEMS. CRC Press, Boca Raton
Phillips JR (2000) Projection frameworks for model reduction of weakly nonlinear systems. In: Proceedings of the 37th annual design automation conference, pp 184–189
Phillips JR (2003) Projection-based approaches for model reduction of weakly nonlinear, time-varying systems. IEEE Trans Comput Aided Des Integr Circuits Syst 22(2):171–187
Pillage LT, Rohrer RA (1990) Asymptotic waveform evaluation for timing analysis. IEEE Trans Comput Aided Des Integr Circuits Syst 9(4):352–366
Pillai AG, Samuel ER (2020) Minimal realized power systems for load frequency control using optimal theory based PID controller. IETE J Res 1–13
Proctor JL, Eckhoff PA (2015) Discovering dynamic patterns from infectious disease data using dynamic mode decomposition. Int Health 7(2):139–145
Rafiq D, Bazaz MA (2019) A comprehensive scheme for fast simulation of Burgers’ equation. In: 2019 Sixth Indian control conference (ICC). IEEE, pp 397–402
Rafiq D, Bazaz MA (2019) Model order reduction of non-linear transmission lines using non-linear moment matching. In: 2019 International conference on computing. Power and communication technologies (GUCON). IEEE, pp 394–399
Rafiq D, Bazaz MA (2020) A comprehensive scheme for reduction of nonlinear dynamical systems. Int J Dyn Control 8(2):361–369
Rafiq D, Bazaz MA (2020) A framework for parametric reduction in large-scale nonlinear dynamical systems. Nonlinear Dyn 102(3):1897–1908
Rafiq D, Bazaz MA (2020) Nonlinear model order reduction via nonlinear moment matching with dynamic mode decomposition. Int J Non-Linear Mech 128:103625
Rewienski M, White J (2003) A trajectory piecewise-linear approach to model order reduction and fast simulation of nonlinear circuits and micromachined devices. IEEE Trans Comput Aided Des Integr Circuits Syst 22(2):155–170
Rewieński M, White J (2006) Model order reduction for nonlinear dynamical systems based on trajectory piecewise-linear approximations. Linear Algebra Appl 415(2–3):426–454
Saini P, Dixit A, Gupta A, Sharma K (2020) Modeling and control of load frequency control (LFC) using model order reduction (MOR) techniques. Math Eng Sci Aerospace 11(1):1–11
Salimbahrami B (2005) Structure preserving order reduction of large scale second order models. PhD thesis, Technical University of Munich, Germany
Salimbahrami B, Lohmann B (2006) Order reduction of large scale second-order systems using Krylov subspace methods. Linear Algebra Appl 415(2–3):385–405
Salimbahrami SB (2005) Structure preserving order reduction of large scale second order models. PhD thesis, Technische Universität München
Sastry S (2013) Nonlinear systems: analysis, stability, and control, vol 10. Springer, Berlin
Scarciotti G, Astolfi A (2015) Model reduction of neutral linear and nonlinear time-invariant time-delay systems with discrete and distributed delays. IEEE Trans Autom Control 61(6):1438–1451
Scarciotti G, Astolfi A (2017) Data-driven model reduction by moment matching for linear and nonlinear systems. Automatica 79:340–351
Scarciotti G, Astolfi A (2017) Nonlinear model reduction by moment matching. Found Trends Syst Control 4(3–4):224–409
Scherpen JM, Gray WS (2000) Minimality and local state decompositions of a nonlinear state space realization using energy functions. IEEE Trans Autom Control 45(11):2079–2086
Scherpen JMA (1993) Balancing for nonlinear systems. Syst Control Lett 21(2):143–153
Scherpen JMA, Van der Schaft A (1994) Normalized coprime factorizations and balancing for unstable nonlinear systems. Int J Control 60(6):1193–1222
Sjöberg J, Fujimoto K, Glad T (2007) Model reduction of nonlinear differential-algebraic equations. IFAC Proc Vol 40(12):176–181
Sorensen DC (2005) Passivity preserving model reduction via interpolation of spectral zeros. Syst Control Lett 54(4):347–360
Spanos JT, Milman MH, Mingori DL (1992) A new algorithm for l2 optimal model reduction. Automatica 28(5):897–909
Su TJ, Craig RR Jr (1991) Model reduction and control of flexible structures using Krylov vectors. J Guid Control Dyn 14(2):260–267
Taira K, Hemati MS, Brunton SL, Sun Y, Duraisamy K, Bagheri S, Dawson ST, Yeh CA (2020) Modal analysis of fluid flows: applications and outlook. AIAA J 58(3):998–1022
Thomas D, Fabien C, Nissrine A, Ryckelynck D (2020) Model order reduction assisted by deep neural networks (rom-net). Adv Model Simul Eng Sci 7(1):1–27
Tian X, Sheng W, Tian F, Lu Y, Wang L (2020) Simulation study on squeeze film air damping. Micro Nano Lett 15(9):576–581
Uyemura JP (2002) Introduction to VLSI circuits and systems. Wiley, Delhi
Van Dooren P (1992) Numerical linear algebra techniques for large scale matrix problems in systems and control. In: Proceedings of the 31st IEEE conference on decision and control. IEEE, pp 1933–1938
Van Dooren P, Gallivan KA, Absil PA (2008) \(\cal{H}_{2}\)-optimal model reduction of mimo systems. Appl Math Lett 21(12):1267–1273
Varona MC, Nico S, Lohmann B (2019) Nonlinear moment matching for the simulation-free reduction of structural systems. In: IFAC Mechatronics and NolCoS, Vienna, Austria, IFAC, vol 52, pp 328–333
Vasilyev D, Rewienski M, White J (2003) A TBR-based trajectory piecewise-linear algorithm for generating accurate low-order models for nonlinear analog circuits and mems. In: Proceedings 2003. Design automation conference (IEEE Cat. No. 03CH37451). IEEE, pp 490–495
Vassilevski Y, Terekhov K, Nikitin K, Kapyrin I (2020) Parallel finite volume computation on general meshes. Springer, Berlin
Wang JM, Kuh ES, Yu Q (2000) Passive model order reduction algorithm based on Chebyshev expansion of impulse response of interconnect networks. In: Design automation conference. IEEE Computer Society, pp 520–525
Wang JM, Chu CC, Yu Q, Kuh ES (2002) On projection-based algorithms for model-order reduction of interconnects. IEEE Trans Circuits Syst I Fundam Theory Appl 49(11):1563–1585
Willcox K, Peraire J (2002) Balanced model reduction via the proper orthogonal decomposition. AIAA J 40(11):2323–2330
Wolf T, Panzer H, Lohmann B (2011) Gramian-based error bound in model reduction by Krylov subspace methods. IFAC Proc Vol 44(1):3587–3592
Yan WY, Lam J (1999) An approximate approach to \(\cal{H}_{2}\) optimal model reduction. IEEE Trans Autom Control 44(7):1341–1358
Younis MI, Abdel-Rahman EM, Nayfeh A (2003) A reduced-order model for electrically actuated microbeam-based MEMS. J Microelectromech Syst 12(5):672–680
Zamanzadeh M, Jafarsadeghi-Pournaki I, Ouakad HM (2020) A resonant pressure mems sensor based on levitation force excitation detection. Nonlinear Dyn 100:1105–1123
Žigić D, Watson LT, Beattie C (1993) Contragredient transformations applied to the optimal projection equations. Linear Algebra Appl 188:665–676
Funding
The Doctoral fellowship in favor of Danish Rafiq from Ministry of Human Resource Development (MHRD) India, via Grant No. 2017PHAELE006 is duly acknowledged.
Author information
Authors and Affiliations
Contributions
Danish Rafiq collected the data and wrote the manuscript. M. A. Bazaz helped in critical analysis and proof reading of the manuscript.
Corresponding author
Ethics declarations
Conflicts of interests
The authors declare no competing interests.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Rafiq, D., Bazaz, M.A. Model Order Reduction via Moment-Matching: A State of the Art Review. Arch Computat Methods Eng 29, 1463–1483 (2022). https://doi.org/10.1007/s11831-021-09618-2
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11831-021-09618-2