A Review on Model Reduction by Moment Matching for Nonlinear Systems

Abstract

The model reduction problem for nonlinear systems and nonlinear time-delay systems based on the steady-state notion of moment is reviewed. We show how this nonlinear description of moment is used to pose and solve the model reduction problem by moment matching for nonlinear systems, to develop a notion of frequency response for nonlinear systems, and to solve model reduction problems in the presence of constraints on the reduced order model. Model reduction of nonlinear time-delay systems is then discussed. Finally, the problem of approximating the moment of nonlinear, possibly time-delay, systems from input/output data is briefly illustrated.

Dedicated to Laurent: a pioneer in the land of control

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The model reduction problem has been widely studied for the prediction, analysis, and control of a wide class of physical behaviors. For instance, reduced order models are used to simulate or design weather forecast models, very large scale integrated circuits or networked dynamical systems [1]. The model reduction problem consists in finding a simplified description of a dynamical system maintaining at the same time specific properties. For linear system, the problem has been extensively studied exploiting a variety of techniques, some of them based on the singular value decomposition, see, e.g., [2,3,4] which make use of Hankel operators or, e.g., [5,6,7,8] which exploit balanced realizations, and some based on the Krylov projection matrices, see, e.g., [9,10,11,12,13,14,15], also called moment matching methods. The additional difficulties of the reduction of nonlinear systems carry the need to develop different or “enhanced” techniques. The problem of model reduction for special classes of systems, such as differential-algebraic systems, bilinear systems, and mechanical/Hamiltonian systems has been studied in [16,17,18,19]. Energy-based methods have been proposed in [7, 20, 21]. Other techniques, based on the reduction around a limit cycle or a manifold, have been presented in [22, 23]. Model reduction methods based on proper orthogonal decomposition have been developed for linear and nonlinear systems, see, e.g., [24,25,26,27,28]. Finally, note that some computational aspects have been investigated in [23, 26, 29, 30]. In addition, the problem of model reduction of time-delay systems is a classic topic in control theory. The optimal reduction (in the sense of some norm) is listed as an unsolved problem in systems theory in [31] and several results have been given using rational interpolations, see, e.g., [32,33,34], see also [35,36,37,38,39,40,41]. Recent results include model order reduction techniques for linear time-delay systems, see, e.g., [42,43,44], and for infinite dimensional systems, see, e.g., [45, 46] in which operators are used to provide reduced order models for linear systems. The goal of this chapter is to review the model reduction techniques for nonlinear, possibly time-delay, systems based on the “steady-state” notion of moment. We start introducing the interpolation approach to moment matching, which is how moment matching has been classically interpreted and applied to linear systems. We then move to the steady-state approach introduced in [47]. We present some results on the model reduction problem by moment matching for nonlinear systems, as given in [48], and develop a notion of frequency response for nonlinear systems. These techniques are extended to nonlinear time-delay systems [49] and the problem of obtaining a family of reduced order models matching two (nonlinear) moments is solved for a special class of signal generators. Finally the problem of approximating the moment of nonlinear (time-delay) systems, without solving the partial differential equation that defines it, is presented and solved [50, 51].

Notation. We use standard notation. $\mathbb {R}_{>0}$ denotes the set of positive real numbers; $\mathbb {C}_{<0}$ denotes the set of complex numbers with negative real part; $\mathbb {D}_{<1}$ denotes the set of complex numbers with modulo smaller than one; $\iota$ denotes the imaginary unit. Given a set of delays $\{\tau _j\}$, the symbol $\mathfrak {R}_T^n=\mathfrak {R}_T^n([-T,0],\mathbb {R}^n)$, with $T= \textstyle \max _j\{\tau _j\}$, indicates the set of continuous functions mapping the interval $[-T,0]$ into $\mathbb {R}^n$ with the topology of uniform convergence [52]. The symbol I denotes the identity matrix, $\sigma (A)$ denotes the spectrum of the matrix $A\in \mathbb {R}^{n\times n}$ and $\otimes$ indicates the Kronecker product. The vectorization of a matrix $A\in \mathbb {R}^{n\times m}$, denoted by ${{\mathrm{vec}}}(A)$, is the $nm \times 1$ vector obtained by stacking the columns of the matrix A one on top of the other, namely ${{\mathrm{vec}}}(A)=[a_1^{\top },a_2^{\top },\ldots ,a_m^{\top }]^{\top }$, where $a_i\in \mathbb {R}^n$ are the columns of A and the superscript $\top$ denotes the transposition operator. The superscript $*$ indicates the complex conjugate transposition operator. Let $\bar{s}\in \mathbb {C}$ and $A(s)\in \mathbb {C}^{n \times n}$. Then $\bar{s}\notin \sigma (A(s))$ means that $\det (\bar{s} I-A(\bar{s} ))\ne 0$. $\sigma (A(s))\subset \mathbb {C}_{<0}$ means that for all $\bar{s}$ such that $\det (\bar{s} I-A(\bar{s} ))=0$, $\bar{s} \in \mathbb {C}_{<0}$. $L_f h$ denotes the Lie derivative of the smooth function h along the smooth vector field f, as defined in [53, Chapter 1].

2 The Interpolation Approach

In this section we briefly recall the notion of moment and the related model reduction techniques as presented in [1]. We refer to this family of methods as “interpolation-based” methods. The key element to understand this framework is that the moment matching problem is interpreted as a problem of interpolation of points in the complex plane, which has been solved by the Nevanlinna-Pick theory (see, e.g., [54]).

Definition 2.1

Let $\{s_i\}$ be a sequence of distinct points in $Z\subset \mathbb {C}$ and let $\{w_i\}$ be an arbitrary sequence of points in $\mathbb {C}$. Given a space $\mathscr {W}$ of functions on Z, the interpolation problem consists in determining a function $W:Z\mapsto \mathbb {C}$ such that $W(s_i)=w_i$, for all $i=1,\ldots ,\nu$.

Consider a linear, single-input, single-output, continuous-time, system described by the equations

$$\begin{aligned} \dot{x} =Ax+Bu, \qquad y=Cx, \end{aligned}$$

(2.1)

with $x(t)\in \mathbb {R}^n$, $u(t)\in \mathbb {R}$, $y(t)\in \mathbb {R}$, $A\in \mathbb {R}^{n\times n}$, $B\in \mathbb {R}^{n\times 1}$ and $C\in \mathbb {R}^{1\times n}$. Let

$$ W(s)=C(sI-A)^{-1}B $$

be the associated transfer function and assume that (2.1) is minimal, i.e., controllable and observable. The k-moment of system (2.1) at $s_i$ is defined as the k-th coefficient of the Laurent series expansion of the transfer function W(s) in a neighborhood of $s_i\in \mathbb {C}$ (see [1, Chapter 11]), provided it exists.

Definition 2.2

Let $s_i\in \mathbb {C}\setminus \sigma (A)$. The 0-moment of system (2.1) at $s_i$ is the complex number $\eta _0 (s_i) = W(s_i)$. The k-moment of system (2.1) at $s_i$ is the complex number

$$ \eta _k (s_i) = \frac{(-1)^k}{k!} \left[ \frac{d^k}{ds^k} W(s)\right] _{s=s_i}, $$

with $k\ge 1$ integer.

Fig. 2.1

Diagrammatic illustration of the interpolation approach. Magnitude (top graph) and phase (bottom graph) plot of a given system (solid/blue line) and of a reduced order model (dashed/red line). The green circle represents the interpolation point

In the interpolation approach to moment matching, a reduced order model is such that its transfer function (and, possibly, derivatives of this) takes the same values of the transfer function (and, possibly, derivatives of this) of system (2.1) at $s_i$. This is graphically represented in Fig. 2.1 in which the magnitude (top) and phase (bottom) of the transfer function of a reduced order model (dashed/red line) matches the respective quantities of a given system (solid/blue line) at the point $s_i=30\iota$. Since a minimal system can be entirely described by its transfer function, such a system can be effectively reduced using this technique. In this framework, the problem of model reduction by moment matching can be formulated as the problem of finding the correct Petrov-Galerkin projectors $V\in \mathbb {R}^{n\times \nu }$ and $W\in \mathbb {R}^{n \times \nu }$, with $W^*V=I$, such that the model described by the equations

$$\begin{aligned} \dot{\xi }=F\xi +Gu, \qquad \psi =H\xi , \end{aligned}$$

(2.2)

with $\xi (t)\in \mathbb {R}^\nu$, $u(t)\in \mathbb {R}$, $\psi (t)\in \mathbb {R}$, $F\in \mathbb {R}^{\nu \times \nu }$, $G\in \mathbb {R}^{\nu \times 1}$, $H\in \mathbb {R}^{1\times \nu }$, and

$$\begin{aligned} \begin{array}{lll} F=W^*AV,&\quad G=W^*B,&\quad H=CV, \end{array} \end{aligned}$$

(2.3)

matches the moments of the given system at a set of points $s_i$. The problem of model reduction by moment matching using the Petrov-Galerking projectors is thoroughly described in [1] and it is the subject of intensive research, see, e.g., [9,10,11,12,13,14,15]. Herein we report a few results which are instrumental for the aims of the chapter. We invite the reader to refer to [1] for additional detail.

Proposition 2.1

[1] Consider $\nu$ distinct points $s_j\in \mathbb {C}\setminus \sigma (A)$, with $j=1,\ldots ,\nu$. The transfer function of the reduced order model (2.2), with

$$\begin{aligned} V=\left[ \begin{array}{lll}(s_1I-A)^{-1}B&\cdots&(s_\nu I-A)^{-1}B\end{array}\right] \end{aligned}$$

(2.4)

a generalized reachability matrix and W any left inverse of V, interpolates the transfer function of system (2.1) at the points $s_j$, with $j=1,\ldots ,\nu$.

Proposition 2.2

[1] Consider the point $s_0\in \mathbb {C}\setminus \sigma (A)$. The transfer function of the reduced order model (2.2), with

$$\begin{aligned} V=\left[ \begin{array}{llll}(s_0I-A)^{-1}B&(s_0I-A)^{-2}B&\cdots&(s_0 I-A)^{-\nu }B\end{array}\right] \end{aligned}$$

(2.5)

a generalized reachability matrix and W any left inverse of V, interpolates the transfer function of system (2.1) and its $\nu -1$ derivatives at the point $s_0$.

The techniques which result from these propositions are called rational interpolation methods by projection, or Krylov methods. We note that the matrix W is a free parameter since it has to satisfy only a “mild” constraint, namely that it is a left inverse of V. However, the selection of W such that the reduced order model exhibits specific properties is in general a difficult problem. The results presented to exploit the free parameters of the matrix W play, with different aims, on the possibility of interpolating more, somewhat special, points. The first of these results, which we recall here, provides a method for the so-called two-sided interpolation.

Proposition 2.3

[1] Consider $s_j\in \mathbb {C}\setminus \sigma (A)$, with $j=1,\ldots ,2\nu$, the generalized reachability matrix

$$\begin{aligned} \bar{V}=\left[ \begin{array}{lll}(s_1I-A)^{-1}B&\cdots&(s_\nu I-A)^{-1}B\end{array}\right] , \end{aligned}$$

(2.6)

and the generalized observability matrix

$$\begin{aligned} \bar{W}=\left[ \begin{array}{lll}(s_{\nu +1}I-A^*)^{-1}C^*&\cdots&(s_{2\nu } I-A^*)^{-1}C^*\end{array}\right] . \end{aligned}$$

(2.7)

Assume that $\det (\bar{W}^* \bar{V})\ne 0$, then the transfer function of the reduced order model (2.2) with and $V=\bar{V}$ and $W=\bar{W}( \bar{V}^*\bar{W})^{-1}$ interpolates the transfer function of system (2.1) at the points $s_j$, with $j=1,\ldots ,2\nu$.

Exploiting this result, the problem of preservation of passivity and stability has been solved in [55, 56], as reported here.

Lemma 2.1

[1] If the interpolation points in Proposition 2.3 are chosen so that $s_j$, with $j=1,\ldots ,\nu$, are stable spectral zeros, i.e., they are such that $W^*(-s_i)+W(s_i)=0$, and $s_{j+\nu }=-s_j$, with $j=1,\ldots ,\nu$, i.e., the interpolation points are chosen as zeros of the spectral factors and their mirror images, then the projected system is both stable and passive.

We can now indicate the following drawbacks in the Krylov methods.

• There is no systematic technique to preserve important properties of the system, for instance maintaining prescribed eigenvalues, relative degree, zeros, $L_2$-gain, or preserving compartmental constraints.

• When a method capable of preserving some of these properties (such as stability and passivity) is presented, it usually implies that specific moments are matched. Hence, the designer cannot chose arbitrary moments. Moreover, there is a lack of system theoretic understanding behind why a particular interpolation point is related to a property like passivity.

• In Lemma 2.1 all the free parameters (the matrix W) are used and no additional property can be preserved.

• Finally, the interpolation-based methods cannot be applied to nonlinear systems (or more general classes of systems), since for these we cannot define a transfer function.

A possible solution to these issues is offered by the “steady-state-based” approach to moment matching. While the first three points are addressed in [48], we focus the rest of the chapter on the last problem: the model reduction of general classes of nonlinear systems.

3 The Steady-State Approach

As just observed the interpolation approach cannot be extended to nonlinear systems for which the idea of interpolating points in the complex plane partially loses its meaning (see, however, [57, 58] for some results on the interpolation problem for nonlinear systems). In [48] (see also [14, 59]) a characterization of moment for system (2.1) has been given in terms of the solution of a Sylvester equation as follows.

Lemma 2.2

[48] Consider system (2.1), $s_i\in \mathbb {C}\setminus \sigma (A)$, for all $i=1,\ldots ,\eta$. There exists a one-to-one¹ relation between the moments $\eta _0(s_1)$, $\ldots$, $\eta _{k_1-1}(s_1)$, $\ldots$, $\eta _{0}(s_{\eta })$, $\ldots$, $\eta _{k_{\eta }-1}(s_{\eta })$, and the matrix $C\varPi$, where $\varPi$ is the unique solution of the Sylvester equation

$$\begin{aligned} A\varPi +BL=\varPi S, \end{aligned}$$

(2.8)

with $S\in \mathbb {R}^{\nu \times \nu }$ any non-derogatory² matrix with characteristic polynomial

$$\begin{aligned} p(s)=\prod _{i=1}^{\eta } (s-s_i)^{k_i}, \end{aligned}$$

(2.9)

where $\nu =\sum _{i=1}^{\eta } k_i$, and L is such that the pair (L, S) is observable.

The importance of this formulation, which has resulted in several developments in the area of model reduction by moment matching, see, e.g., [60, 61] and [49,50,51, 62,63,64,65,66], is that it establishes, through the Sylvester equation (2.8), a relation between the moments and the steady-state response of the output of the system. Before proceeding further we provide a formal definition of steady-state response. With abuse of notation, we indicate the state of a (linear, nonlinear, or more general) dynamical system as $x(t,x_0)$ to highlight the dependency on time and on the initial condition.

Definition 2.3

([67, 68]) Let $\mathscr {B}\subset \mathbb {R}^n$ and suppose $x(t,x_0)$ is defined for all $t\ge 0$ and all $x_0\in \mathscr {B}$. The $\omega$-limit set of the set denoted by $w(\mathscr {B})$, is the set of all points x for which there exists a sequence of pairs $\{x_k,t_k\}$, with $x_k\in \mathscr {B}$ and $\lim _{k\rightarrow \infty }t_k=\infty$ such that $\lim _{k\rightarrow \infty }x(t_k,x_k)=x$.

Definition 2.4

([67, 68]) Suppose the responses of the system, with initial conditions in a closed and positively invariant set $\mathscr {X}$, are ultimately bounded. A steady-state response is any response with initial condition $x_0\in w(\mathscr {B})$.

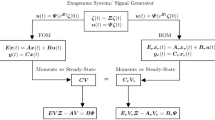
Exploiting the notion of steady-state response we can introduce the following result, which is illustrated in Fig. 2.2.

Fig. 2.2

Diagrammatic illustration of Theorem 2.1. The term denoting the steady-state response is circled

Theorem 2.1

[48] Consider system (2.1), $s_i\in \mathbb {C}\setminus \sigma (A)$, for all $i=1,\ldots ,\eta$, and $\sigma (A)\subset \mathbb {C}_{<0}$. Let $S\in \mathbb {R}^{\nu \times \nu }$ be any non-derogatory matrix with characteristic polynomial (2.9). Consider the interconnection of system (2.1) with the system

$$\begin{aligned} \dot{\omega }=S \omega , \qquad u=L\omega , \end{aligned}$$

(2.10)

with L and $\omega (0)$ such that the triple $(L,S,\omega (0))$ is minimal. Then there exists a one-to-one relation between the moments $\eta _0(s_1)$, $\ldots$, $\eta _{k_1-1}(s_1)$, $\ldots$, $\eta _{0}(s_{\eta })$, $\ldots$, $\eta _{k_{\eta }-1}(s_{\eta })$, and the steady-state response of the output y of such interconnected system.

Remark 2.1

[69] The minimality of the triple $(L,S,\omega (0))$ implies the observability of the pair (L, S) and the “controllability” of the pair $(S,\omega (0))$. This last condition, called excitability of the pair $(S,\omega (0))$, is a geometric characterization of the property that the signals generated by (2.10) are persistently exciting, see [70].

Remark 2.2

By one-to-one relation we mean that the moments are uniquely determined by the steady-state response of y(t) and vice versa. Exploiting this fact, in [50] the problem of computing the moments of an unknown linear systems from input/output data has been addressed. Therein an algorithm that, given the signal $\omega$ and the output y, retrieves the moments of a system for which the matrices A, B, and C are not known is devised.

The reduction technique based on this notion of moment consists in the interpolation of the steady-state response of the output of the system: a reduced order model is such that its steady-state response is equal to the steady-state response of the output of system (2.1) (provided it exists). Thus, the problem of model reduction by moment matching has been changed from a problem of interpolation of points to a problem of interpolation of signals. The output of the reduced order model has to behave as the output of the original system for a class of input signals, a concept which can be translated to nonlinear systems, time-delay systems, and infinite dimensional systems, [48, 49]. This fact also highlights how important for the moment matching techniques is to let the designer choose the interpolation points, which are related to the class of inputs to the system.

4 Model Reduction by Moment Matching for Nonlinear Systems

We can now extend the steady-state description of moment to nonlinear systems.³ Consider a nonlinear, single-input, single-output, continuous-time system described by the equations

$$\begin{aligned} \dot{x} =f(x,u), \qquad y=h(x), \end{aligned}$$

(2.11)

with $x(t)\in \mathbb {R}^n$, $u(t)\in \mathbb {R}$, $y(t)\in \mathbb {R}$, f and h smooth mappings, a signal generator described by the equations

$$\begin{aligned} \dot{\omega }=s(\omega ), \qquad u=l(\omega ), \end{aligned}$$

(2.12)

with $\omega (t)\in \mathbb {R}^v$, s and l smooth mappings, and the interconnected system

$$\begin{aligned} \dot{\omega }=s(\omega ), \qquad \dot{x} =f(x,l(\omega )), \qquad y=h(x). \end{aligned}$$

(2.13)

In addition, suppose that $f(0,0)=0$, $s(0)=0$, $l(0)=0$, and $h(0)=0$. Similarly, to the linear case the interconnection of system (2.11) with the signal generator captures the property that we are interested in preserving the behavior of the system only for specific input signals. The following assumptions and definitions provide a generalization of the notion of moment.

Assumption 2.1

The signal generator (2.12) is observable, i.e., for any pair of initial conditions $\omega _a(0)$ and $\omega _b(0)$, such that $\omega _a(0)\ne \omega _b(0)$, the corresponding output trajectories $l(\omega _a(t))$ and $l(\omega _b(t))$ are such that $l(\omega _a(t)) - l(\omega _b(t)) \not \equiv 0$, and Poisson stable⁴ with $\omega (0)\ne 0$.

Assumption 2.2

The zero equilibrium of the system $\dot{x} = f(x,0)$ is locally exponentially stable.

Lemma 2.3

[48] Consider system (2.11) and the signal generator (2.12). Suppose Assumptions 2.1 and 2.2 hold. Then there is a unique mapping $\pi$, locally defined in a neighborhood of $\omega =0$, which solves the partial differential equation

$$\begin{aligned} \frac{\partial \pi }{\partial \omega } s(\omega )=f(\pi (\omega ),l(\omega )). \end{aligned}$$

(2.14)

Remark 2.3

Lemma 2.3 implies that the interconnected system (2.13) possesses an invariant manifold described by the equation $x=\pi (\omega )$.

Definition 2.5

Consider system (2.11) and the signal generator (2.12). Suppose Assumption 2.1 holds. The function $h\,\!\circ \,\!\pi$, with $\pi$ solution of equation (2.14), is the moment of system (2.11) at (s, l).

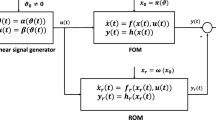
Theorem 2.2

[48] Consider system (2.11) and the signal generator (2.12). Suppose Assumptions 2.1 and 2.2 hold. Then the moment of system (2.11) at (s, l) coincides with the steady-state response of the output of the interconnected system (2.13).

Fig. 2.3

Diagrammatic illustration of Theorem 2.2. The term denoting the steady-state response is circled

The result is illustrated in Fig. 2.3 which represents the nonlinear counterpart of Fig. 2.2.

Remark 2.4

[48] If the equilibrium $x=0$ of the system $\dot{x} = f(x,0)$ is unstable, it is still possible to define the moment of system (2.11) at (s, l) in terms of the function $h\,\!\circ \,\!\pi$, provided the equilibrium $x=0$ is hyperbolic and the system (2.12) is Poisson stable, although it is not possible to establish a relation with the steady-state response of the interconnected system (2.13).

Remark 2.5

[48] While for linear systems it is possible to define k-moments for every $s_i\in \mathbb {C}$ and for any $k\ge 0$, for nonlinear systems it may be difficult, or impossible, to provide general statements if the signal u, generated by system (2.12), is unbounded. Therefore, we assume that the signal generator generates bounded signals. For linear systems this assumption implies that we consider only points $s_i\in \mathbb {C}$ that are distinct and with zero real part.

4.1 The Frequency Response of a Nonlinear System

In [48], see also [71, 72], a nonlinear enhancement of the notion of frequency response of a linear system has been derived exploiting the steady-state description of moment. Note that this result is loosely related to the analysis in [66] where a generalization of the phasor transform based on the notion of moment is proposed.

Consider system (2.11) and the signal generator (2.12). Let the signal generator (2.12) be such that

$$ s(\omega )= \left[ \begin{array}{cc} 0 &{} \bar{\omega }\\ -\bar{\omega }&{} 0 \end{array}\right] \omega , \qquad \qquad l(\omega ) = \left[ \begin{array}{cc} L_1&L_2 \end{array}\right] \omega , $$

with $\omega (0) \ne 0$, $\bar{\omega }\ne 0$, and $L_1^2+L_2^2 \ne 0$. Then, under Assumptions 2.1 and 2.2 the output of the interconnected system (2.13) converges toward a locally well-defined steady-state response, which, by definition, does not depend upon the initial condition x(0). Moreover, such a steady-state response is periodic, hence, if it has the same period of $l(\omega (t))$, it can be written in Fourier series as $h(\pi (\omega (t))) = \sum _{k=-\infty }^\infty c_k e^{\iota k \bar{\omega }t}$, with $c_k\in \mathbb {C}$. Consider now the operator ${\mathscr {P}}_+$ which acts on a Fourier series as follows

$$ {\mathscr {P}}_+\left( \sum _{k=-\infty }^\infty c_k e^{\iota k \bar{\omega }t}\right) = \sum _{k=0}^\infty \alpha _k e^{\iota k \bar{\omega }t}, $$

with $\alpha _k\in \mathbb {C}$. With this operator we can define the frequency response of the nonlinear system (2.11) as

$$ F(t, \omega (0),\bar{\omega }) = \frac{{\mathscr {P}}_+(h(\pi (\omega (t))))}{{\mathscr {P}}_+(l(\omega (t))}. $$

This function depends upon the frequency $\bar{\omega }$, just as in the linear case, and, unlike the linear case, upon the initial condition $\omega (0)$ of the signal generator and time. Note finally that if the system (2.11) were linear, hence described by the Eq. (2.1), then $F(t,\omega (0),\bar{\omega })$ would be constant with respect to t and equal to $|W(\iota \bar{\omega })|e^{\iota \angle {W(\iota \bar{\omega })}},$ where $W(s) = C(s I -A)^{-1} B$, $|\cdot |$ indicates the absolute value operator and $\angle$ the phase operator.

4.2 Moment Matching

We are now ready to introduce the notion of reduced order model by moment matching for nonlinear systems.

Definition 2.6

[48] Consider the signal generator (2.12). The system described by the equations

$$\begin{aligned} \dot{\xi }= \phi (\xi ,u),\qquad \psi = \kappa (\xi ), \end{aligned}$$

(2.15)

with $\xi (t) \in \mathbb {R}^\nu$, is a model at (s, l) of system (2.11) if system (2.15) has the same moment at (s, l) as (2.11). In this case, system (2.15) is said to match the moment of system (2.11) at (s, l). Furthermore, system (2.15) is a reduced order model of system (2.11) if $\nu <n$.

Lemma 2.4

Consider system (2.11), system (2.15) and the signal generator (2.12). Suppose Assumptions 2.1 and 2.2 hold. System (2.15) matches the moments of (2.11) at (s, l) if the equation

$$\begin{aligned} \phi (p(\omega ),l(\omega )) =\frac{\partial p}{\partial \omega } s(\omega ) \end{aligned}$$

(2.16)

has a unique solution p such that

$$\begin{aligned} h(\pi (\omega )) = \kappa (p(\omega )), \end{aligned}$$

(2.17)

where $\pi$ is the (unique) solution of equation (2.14).

In other words, we have to determine mappings $\phi$, $\kappa$, and p such that Eqs. (2.16) and (2.17) hold. We introduce the following assumption to simplify the problem.

Assumption 2.3

There exist mappings $\kappa$ and p such that $\kappa (0)=0$, $p(0)=0$, p is locally continuously differentiable, Eq. (2.17) holds and $\left. \det \frac{\partial p(\omega )}{\partial \omega }\right| _{\omega =0} \ne 0$, i.e., the mapping p possesses a local inverse $p^{-1}$.

Remark 2.6

[48] Similar to the linear case, Assumption 2.3 holds selecting $p(\omega ) = \omega$ and $k(\omega ) = h(\pi (\omega ))$.

Finally, as shown in [48], the system described by the equations

$$\begin{aligned} \begin{array}{l} \dot{\xi }= s(\xi ) -\delta (\xi )l(\xi ) + \delta (\xi ) u, \qquad \qquad \psi =h(\pi (\xi )), \end{array} \end{aligned}$$

(2.18)

where $\delta$ is any mapping such that the equation

$$\begin{aligned} \frac{\partial p}{\partial \omega }s(\omega )=s(p(\omega ))-\delta (p(\omega ))l(p(\omega ))+\delta (p(\omega ))l(\omega ), \end{aligned}$$

(2.19)

has the unique solution $p(\omega )=\omega$, is a family of reduced order models of (2.11) at (s, l).

4.3 Model Reduction by Moment Matching with Additional Properties

We can determine the conditions on the mapping $\delta$ such that the reduced order model satisfies additional properties. The proofs are omitted and can be found in [48].

4.3.1 Matching with Asymptotic Stability

Consider the problem of determining a reduced order model (2.18) which has an asymptotically stable zero equilibrium. This problem can be solved if it is possible to select the mapping $\delta$ such that the zero equilibrium of the system $\dot{\xi }= s(\xi ) - \delta (\xi ) l(\xi )$ is locally asymptotically stable. To this end, for instance, it is sufficient that the pair $\left( \left. \frac{\partial l(\xi )}{\partial \xi }\right| _{\xi =0},\left. \frac{\partial s(\xi )}{\partial \xi }\right| _{\xi =0}\right)$ is observable.

4.3.2 Matching with Prescribed Relative Degree

The problem of constructing a reduced order model which has a given relative degree $r\in [1,\nu ]$ at some point $\bar{\xi }$ can be solved selecting $\delta$ as follows.

Theorem 2.3

[48] For all $r \in [1,\nu ]$ there exists a $\delta$ such that system (2.18) has relative degree r at $\bar{\xi }$ if and only if the codistribution

$$\begin{aligned} d\mathcal{O}_{\nu } (\xi ) = \mathrm{span}\{d h(\pi (\xi )), \cdots , d L_s^{\nu -1} h(\pi (\xi ))\} \end{aligned}$$

(2.20)

has dimension $\nu$ at $\bar{\xi }$.

4.3.3 Matching with Prescribed Zero Dynamics

Consider system (2.18) and the problem of determining the mapping $\delta$ such that the model has zero dynamics with specific properties. If $\bar{\xi }$ is an equilibrium of system (2.18), the problem is solved selecting $\delta$ such that the codistribution (2.20) has dimension $\nu$ at $\bar{\xi }$ [48]. Then there is a $\delta$ such that the zero dynamics of system (2.18) have a locally exponentially stable equilibrium and there is a coordinate transformation, locally defined around $\bar{\xi }$, such that the zero dynamics are described by the equations

$$\begin{aligned} \begin{array}{rcl} \dot{z}_1 &{}=&{} z_2 + \hat{\delta }_{1} (z) z_1,\\ \dot{z}_2 &{}=&{} z_3 + \hat{\delta }_{2} (z) z_1,\\ &{}\!\!\vdots &{}\\ \dot{z}_{\nu -r} &{}=&{} \hat{f}(z) + \hat{\delta }_{\nu -r} (z) z_1, \end{array} \end{aligned}$$

(2.21)

where the $\hat{\delta }_{i}$ are free functions and

$$ \hat{f}(z)=\tilde{f}(\mathscr {Z})|_{\mathscr {Z}=[0,\ldots ,0,z_1,\ldots ,z_{\nu -r}]^{\top }}, $$

with $\mathscr {Z}=\varXi (\xi )$ and $\tilde{f}(\mathscr {Z})= L_s^{\nu } h(\pi (\varXi ^{-1}(\mathscr {Z})))$.

4.3.4 Matching with a Passivity Constraint

Consider now the problem of selecting the mapping $\delta$ such that system (2.18) is lossless or passive. For such a problem the following fact holds.

Theorem 2.4

[48] The family of reduced order models (2.18) contains, locally around $\bar{\xi }$, a lossless (passive, respectively) system with a differentiable storage function if there exists a differentiable function V, locally positive definite around $\bar{\xi }$, such that equation⁵

$$\begin{aligned} V_\xi s(\xi ) = h(\pi (\xi )) l(\xi ), \quad (V_\xi s(\xi ) \le h(\pi (\xi ))l(\xi ) \ \mathrm{respectively}), \end{aligned}$$

(2.22)

holds locally around $\bar{\xi }$ and

$$\begin{aligned} V_{\xi \xi }(\xi )>0. \end{aligned}$$

(2.23)

4.3.5 Matching with $L_2$-gain

We now consider the problem of selecting the mapping $\delta$ such that system (2.18) has a given $L_2$-gain.

Theorem 2.5

[48] The family of reduced order models (2.18) contains, locally around $\bar{\xi }$, a system with $L_2$-gain not larger than $\ell >0$, and with a differentiable storage function if there exists a differentiable function V, locally positive definite around $\bar{\xi }$, such that Eq. (2.23) holds and

$$\begin{aligned} V_\xi s(\xi ) + (h(\pi (\xi )))^2 \le \ell ^2 l^2(\xi ), \end{aligned}$$

(2.24)

holds locally around $\bar{\xi }$.

5 Model Reduction for Nonlinear Time-Delay Systems

Exploiting the steady-state notion of moment an extension of the model reduction method for nonlinear time-delay systems is given. To keep the notation simple we consider, without loss of generality, only delays (discrete or distributed) in the state and in the input, i.e., the output is delay-free. The neutral case is briefly discussed at the end of the section.

5.1 Definition of $\pi$: Nonlinear Time-Delay Systems

Consider a nonlinear, single-input, single-output, continuous-time, time-delay system described by the equations

$$\begin{aligned} \begin{array}{l} \dot{x} =f(x_{\tau _0},\ldots ,x_{\tau _{\varsigma }},u_{\tau _{\varsigma +1}},\ldots ,u_{\tau _{\mu }}),\qquad y=h(x),\\ x(\theta )=\phi (\theta ), \qquad \qquad \quad -T\le \theta \le 0, \end{array} \end{aligned}$$

(2.25)

with $x(t)\in \mathbb {R}^n$, $u(t)\in \mathbb {R}$, $y(t)\in \mathbb {R}$, $\phi \in \mathfrak {R}_T^n$, $\tau _0=0$, $\tau _j\in \mathbb {R}_{>0}$ with $j=1,\ldots ,\mu$ and f and h smooth mappings. Consider a signal generator (2.12) and the interconnected system

$$\begin{aligned} \begin{array}{lll} \dot{\omega }=s(\omega ),&\qquad \dot{x} =f(x_{\tau _0},\ldots ,x_{\tau _{\varsigma }},l(\omega _{\tau _{\varsigma +1}}),\ldots ,l(\omega _{\tau _{\mu }})),&\qquad y=h(x). \end{array} \end{aligned}$$

(2.26)

Suppose that $f(0,\ldots ,0,0,\ldots ,0)=0$, $s(0)=0$, $l(0)=0$ and $h(0)=0$.

Assumption 2.4

The zero equilibrium of the system $\dot{x}=f(x_{\tau _0},\ldots ,x_{\tau _{\varsigma }},0,\ldots ,0)$ is locally exponentially stable.

Lemma 2.5

[49, 53] Consider system (2.25) and the signal generator (2.12). Suppose Assumptions 2.1 and 2.4 hold. Then there exists a unique mapping $\pi$, locally defined in a neighborhood of $\omega =0$, which solves the partial differential equation

$$\begin{aligned} \frac{\partial \pi }{\partial \omega }s(\omega )=f(\pi (\bar{\omega }_{\tau _0}),\ldots ,\pi (\bar{\omega }_{\tau _{\varsigma }}),l(\bar{\omega }_{\tau _{\varsigma +1}}),\ldots ,l(\bar{\omega }_{\tau _{\mu }})), \end{aligned}$$

(2.27)

where $\bar{\omega }_{\tau _i}=\varPhi ^{s}_{\tau _i}(\omega )$, with $i=0,\ldots ,\mu$, is the flow of the vector field s at $-\tau _i$.

Remark 2.7

Lemma 2.5 implies that the interconnected system (2.26) possesses an invariant manifold, described by the equation $x=\pi (\omega )$. Note that the partial differential equation (2.27) is independent of time (as (2.14) in the delay-free case), e.g., if $s(\omega )=S\omega$ then $\bar{\omega }_{\tau _i}=e^{-S\tau _i}\omega$.

Definition 2.7

Consider system (2.25) and the signal generator (2.12). Suppose Assumption 2.1 holds. The function $h\,\!\circ \,\!\pi$, with $\pi$ solution of equation (2.27), is the moment of system (2.25) at (s, l).

Theorem 2.6

[49] Consider system (2.25) and the signal generator (2.12). Suppose Assumptions 2.1 and 2.4 hold. Then the moment of system (2.25) at (s, l) coincides with the steady-state response of the output of the interconnected system (2.26).

5.2 Reduced Order Models for Nonlinear Time-Delay Systems

In this section two families of models achieving moment matching are given.

Definition 2.8

Consider system (2.25) and the signal generator (2.12). Suppose Assumption 2.1 and 2.4 hold. Then the system

$$\begin{aligned} \dot{\xi }=\phi (\xi _{\chi _0},\ldots ,\xi _{\chi _{\hat{\rho }}},u_{\chi _{\hat{\rho }+1}},\ldots ,u_{\chi _{\rho }}), \qquad \psi =\kappa (\xi ), \end{aligned}$$

(2.28)

with $\xi (t)\in \mathbb {R}^{\nu }$, $u(t)\in \mathbb {R}$, $\psi (t)\in \mathbb {R}$, $\chi _0=0$, $\chi _j\in \mathbb {R}_{>0}$ with $j=1,\ldots ,\rho$, and $\phi$ and $\kappa$ smooth mappings, is a model of system (2.25) at (s, l) if system (2.28) has the same moment of system (2.25) at (s, l).

Lemma 2.6

Consider system (2.25) and the signal generator (2.12). Suppose Assumption 2.1 and 2.4 hold. Then the system (2.28) is a model of system (2.25) at (s, l) if the equation

$$\begin{aligned} \frac{\partial p}{\partial \omega }s(\omega )=\phi (p(\bar{\omega }_{\chi _0}),\ldots ,p(\bar{\omega }_{\chi _{\hat{\rho }}}),l(\bar{\omega }_{\chi _{\hat{\rho }+1}}),\ldots ,l(\bar{\omega }_{\chi _{\rho }})), \end{aligned}$$

(2.29)

where $\bar{\omega }_{\chi _i}=\varPhi ^{s}_{\chi _i}(\omega )$, with $i=0,\ldots ,\rho$, has a unique solution p such that

$$\begin{aligned} h(\pi (\omega ))=\kappa (p(\omega )), \end{aligned}$$

(2.30)

where $\pi$ is the unique solution of (2.27). System (2.28) is a reduced order model of system (2.25) at (s, l) if $\nu <n$, or if $\hat{\rho }<\varsigma$, or if $\rho <\mu$.

Similarly to the delay-free case we use part of the free mappings to obtain a simpler family of models.

Assumption 2.5

There exist mappings $\kappa$ and p such that $\kappa (0)=0$, $p(0)=0$, p is locally continuously differentiable, Eq. (2.30) holds and p has a local inverse $p^{-1}$.

Consistently with Lemma 2.6, a family of models that achieves moment matching at (s, l) is described by

$$\begin{aligned} \begin{array}{rl} \dot{\xi }&{}\!\!= \varPhi (\xi ,\bar{\xi }_{\chi _1},\ldots ,\bar{\xi }_{\chi _{\hat{\rho }}})+\frac{\partial p(\omega )}{\partial \omega }\gamma (\xi _{\chi _1},\ldots ,\xi _{\chi _{\hat{\rho }}}) +\, \frac{\partial p(\omega )}{\partial \omega }\sum _{j=\hat{\rho }+1}^{\rho }\delta _j(\xi )u_{\chi _j},\\ \psi &{}\!\!=\kappa (\xi ), \end{array}\end{aligned}$$

(2.31)

with

where $\bar{\xi }_{\chi _j}=\left[ \bar{\omega }_{\chi _j}\right] _{\omega =p^{-1}(\xi )}$, $\kappa$ and p are such that Assumption 2.5 holds, p is the unique solution of (2.29) and $\delta _j$ and $\gamma$ are free mappings.

Assumption 2.5 holds with the selection $p(\omega )=\omega$ and $\kappa (\omega )=h(\pi (\omega ))$. This yields a family of models described by the equations

$$\begin{aligned} \begin{array}{rl} \dot{\xi }&{}=s(\xi )-\!\!\!\sum \limits _{j=\hat{\rho }+1}^{\rho }\delta _j(\xi )l(\bar{\xi }_{\chi _j})-\gamma (\bar{\xi }_{\chi _1},\ldots ,\bar{\xi }_{\chi _{\hat{\rho }}})+\gamma (\xi _{\chi _1},\ldots ,\xi _{\chi _{\hat{\rho }}})+\sum _{j=\hat{\rho }+1}^{\rho }\delta _j(\xi )u_{\chi _j},\\ \psi &{}=h(\pi (\xi )), \end{array} \end{aligned}$$

(2.32)

where $\delta _j$ and $\gamma$ are arbitrary mappings such that Eq. (2.29), namely

$$ \begin{array}{rl} \frac{\partial p}{\partial \omega }s(\omega )=s(p(\omega ))&{}-\sum _{j=\hat{\rho }+1}^{\rho }\delta _j(p(\omega ))l(p(\bar{\omega }_{\chi _l}))-\,\gamma (p(\bar{\omega }_{\chi _1}),\ldots ,p(\bar{\omega }_{\chi _{\hat{\rho }}}))\\ &{}+\sum _{j=\hat{\rho }+1}^{\rho }\delta _j(p(\omega ))l(\omega _{\chi _j})+\gamma (p(\omega _{\chi _1}),\ldots ,p(\omega _{\chi _{\hat{\rho }}})), \end{array} $$

has the unique solution $p(\omega )=\omega$.

The nonlinear model (2.32) has several free design parameters, namely $\delta _j$, $\gamma$, $\chi _j$, $\hat{\rho }$ and $\rho$. We note that selecting $\gamma \equiv 0$, $\hat{\rho }=0$, $\rho =1$ and $\chi _1=0$ (in this case we define $\delta =\delta _1$), yields a family of reduced order models with no delays. This family coincides with the family (2.18) and all results of Sect. 2.4.3 are directly applicable: the mapping $\delta$ can be selected to achieve matching with asymptotic stability, matching with prescribed relative degree, etc. However, note that the choice of eliminating the delays may destroy some important dynamics of the model.

Remark 2.8

The results of this section can be extended to more general classes of time-delay systems provided that, for such systems, the center manifold theory applies. In particular, one can consider the class of neutral differential time-delay systems described by equations of the form

$$\begin{aligned} \begin{array}{l} d(\dot{x}_{\tau _0},\ldots ,\dot{x}_{\tau _{\varsigma _1}})=f(x_{\tau _{\varsigma _1+1}},\ldots ,x_{\tau _{\varsigma _2}},u_{\tau _{\varsigma _2+1}},\ldots ,u_{\tau _{\mu }}),\\ y=h(x), \end{array} \end{aligned}$$

(2.33)

with $x(t)\in \mathbb {R}^n$, $u(t)\in \mathbb {R}$, $y(t)\in \mathbb {R}$, $\tau _0=0$, $\tau _j\in \mathbb {R}_{>0}$ with $j=1,\ldots ,\mu$ and d, f, and h smooth mappings. The center manifold theory does not hold for this class of systems for a general mapping d. Specific cases have to be considered and we refer the reader to [73,74,75] and references therein. Note, however, that for the simple case

$$\begin{aligned} \begin{array}{l} \dot{x} +D\dot{x}_{\tau _1}=f(x_{\tau _2},\ldots ,x_{\tau _{\varsigma _1}},u_{\tau _{\varsigma _1+1}},\ldots ,u_{\tau _{\mu }}),\\ y=h(x), \end{array} \end{aligned}$$

(2.34)

with $D\in \mathbb {R}^{n\times n}$, the center manifold theory holds as for standard time-delay systems if the matrix D is such that $\sigma (D)\subset \mathbb {D}_{<1}$.

5.3 Exploiting One Delay to Match $h\,\!\circ \,\!\pi _a$ and $h\,\!\circ \,\!\pi _b$

In this section we show how to exploit the free parameters to achieve moment matching at two moments $h\,\!\circ \,\!\pi _a$ and $h\,\!\circ \,\!\pi _b$ maintaining the same number of equations describing the reduced order model. Consider system (2.25) and, to simplify the exposition, the signal generators described by the linear equation

$$\begin{aligned} \begin{array}{l} \dot{\omega }=S_a\omega , \qquad \qquad u=L_{ab}\omega , \end{array} \end{aligned}$$

(2.35)

Note that, as highlighted in [48], considering the model reduction problem for nonlinear systems when the signal generator is a linear system is of particular interest since the reduced order models have a very simple description, i.e., a family of reduced order models is described by a linear differential equation with a nonlinear output map. This observation holds true also in the case of time-delay systems, namely a nonlinear time-delay system can be approximated by a linear time-delay equation with a nonlinear output map. This structure has two main advantages. Firstly, the selection of the free parameters that achieve additional goals, such as to assign the eigenvalues or the relative degree of the reduced order model, is remarkably simplified. Secondly, the computation of the reduced order model boils down to the computation of the output map $h\,\!\circ \,\!\pi$. A technique to approximate this mapping is proposed in the next section. As a consequence of this discussion, a reduced order model of system (2.25) at $(S_a,L_{ab})$ is given by the family

$$\begin{aligned} \begin{array}{rcl} \dot{\xi }&{}=&{} F_0 \xi + F_1 \xi _{\chi }+G_2 u+G_3 u_{\chi },\\ \psi \!\!\!&{}=&{}\kappa _0(\xi )+\kappa _1(\xi _{\chi }), \end{array} \end{aligned}$$

(2.36)

with $\kappa _0$ and $\kappa _1$ smooth mappings, if there exists a unique matrix $P_a$ such that

$$\begin{aligned} \begin{array}{l} F_0 P_a + F_1 P_a e^{-S_a\chi }-P_a S_a=-G_2 L_{ab} -G_3 L_{ab} e^{-S_a\chi },\\ h(\pi _a(\omega ))=\kappa _0(P_a\omega )+\kappa _1(P_ae^{-S_a\chi }\omega ), \end{array} \end{aligned}$$

(2.37)

Consider now another signal generator described by the linear equation

$$\begin{aligned} \begin{array}{l} \dot{\omega }=S_b\omega , \qquad \qquad u=L_{ab}\omega , \end{array} \end{aligned}$$

(2.38)

and the problem of selecting $F_0$, $F_1$, $G_2$, $G_3$, $\kappa _0$, and $\kappa _1$ such that the reduced order model (2.36) matches the moments of system (2.25) at ($S_a,L_{ab}$) and ($S_b,L_{ab}$).

Proposition 2.4

Let $S_a\in \mathbb {R}^{\nu \times \nu }$ and $S_b\in \mathbb {R}^{\nu \times \nu }$ be two non-derogatory matrices such that $\sigma (S_a)\,\cap \,\sigma (S_b)=\emptyset$ and let $L_{ab}$ be such that the pairs $(L_{ab},S_a)$ and $(L_{ab},S_b)$ are observable. Let $\pi _a(\omega )=\pi (\omega )$ be the unique solution of (2.27), with $L=L_{ab}$ and $S=S_a$, and let $\pi _b(\omega )=\pi (\omega )$ be the unique solution of (2.27), with $L=L_{ab}$ and $S=S_b$. Then system (2.36) with the selection

$$\begin{aligned} \begin{array}{l} \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!F_1\!=\!(S_b-S_a-G_3(e^{-S_b\chi }-e^{-S_a\chi _3}))(e^{-S_b\chi }-e^{-S_a\chi })^{-1}\!\!\!\!,\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!F_0\!=\!S_a-G_2 L_{ab} -G_3L_{ab}e^{-S_a\chi } - F_1e^{-S_a\chi },\\ \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\kappa _0(\omega )\!=\!h(\pi _a(\omega ))-\kappa _1(e^{-S_a\chi }\omega ), \end{array} \end{aligned}$$

(2.39)

and $k_1$ a mapping such that

$$ \kappa _1\left( e^{-S_b\chi }\omega \right) - \kappa _1\left( e^{-S_a\chi }\omega \right) =h(\pi _b(\omega ))-h(\pi _a(\omega )), $$

is a reduced order model of the nonlinear time-delay system (2.25) achieving moment matching at ($S_a,L_{ab}$) and ($S_b,L_{ab}$), for any $G_2$ and $G_3$ such that $s_i\notin \sigma (F_0+F_1e^{-s\chi })$, for all $s_i\in \sigma (S_a)$ and $s_i\in \sigma (S_b)$.

Proof

As showed in the proof of Proposition 2.1 of [49], $F_0$ and $F_1$ solve the two Sylvester equations

$$\begin{aligned} \begin{array}{l} F_0 P_a + F_1 P_a e^{-S_a\chi }-P_a S_a=-G_2 L_{ab} -G_3 L_{ab} e^{-S_a\chi },\\ F_0 P_b + F_1 P_b e^{-S_b\chi }-P_b S_b=-G_2 L_{ab} -G_3 L_{ab} e^{-S_b\chi }, \end{array} \end{aligned}$$

(2.40)

with $P_a=P_b=I$. It remains to determine the mappings $\kappa _0$ and $\kappa _1$ that solve the matching conditions

$$\begin{aligned} \begin{array}{l} h(\pi _a(\omega ))=\kappa _0(\omega )+\kappa _1\left( e^{-S_a\chi }\omega \right) ,\\ h(\pi _b(\omega ))=\kappa _0(\omega )+\kappa _1\left( e^{-S_b\chi }\omega \right) . \end{array} \end{aligned}$$

(2.41)

Solving the first equation with respect to $\delta _0$ and substituting the resulting expression in the second yields

$$ \kappa _1\left( e^{-S_b\chi }\omega \right) - \kappa _1\left( e^{-S_a\chi }\omega \right) =h(\pi _b(\omega ))-h(\pi _a(\omega )), $$

from which the claim follows.

The family of linear time-delay systems with nonlinear output mapping characterized in Proposition 2.4 matches the moments $h\,\!\circ \,\!\pi _a$ and $h\,\!\circ \,\!\pi _b$ of the nonlinear system (2.25). Note that the matrices $G_2$ and $G_3$ remain free parameters and they can be used to achieve the properties discussed in Sect. 2.4.3. For instance, $G_2$ and $G_3$ can be used to set both the eigenvalues of $F_0$ and $F_1$.

Remark 2.9

Proposition 2.4 can be generalized to $\hat{\rho }>1$ delays, obtaining a reduced order model that match $(\hat{\rho }+1)\nu$ moments. The result can also be generalized to nonlinear generators $s_i(\omega )$ assuming that the flow $\varPhi _{\chi _i}^{s_i}(\omega )$ is known for all the delays $\chi _i$ and that $\gamma (\xi _{\chi _1},\ldots ,\xi _{\chi _{\hat{\rho }}})$ in (2.32) is replaced by $\hat{\gamma }_1(\xi _{\chi _1}) + \ldots + \hat{\gamma }_{\hat{\rho }}(\xi _{\chi _{\hat{\rho }}})$.

Remark 2.10

The number of delays in (2.25) does not play a role in Proposition 2.4. Thus, this result can be applied to reduce a system with an arbitrary number of delays always obtaining a reduced order model with, for example, two delays. This fact can be taken to the “limit” reducing a system which is not a time-delay system. In other words, a system described by ordinary differential equations can be reduced to a system described by time-delay differential equations with an arbitrary number of delays $\hat{\rho }$ achieving moment matching at $(\hat{\rho }+1)\nu$ moments.

6 Online Nonlinear Moment Estimation from Data

In this section we solve a fundamental problem for the theory we have presented, namely how to compute an approximation of the moment $h\,\!\circ \,\!\pi$ when the solution of the partial differential equation (2.13) or (2.27) is not known. Note, first of all, that the results of this section hold indiscriminately for delay-free and time-delay systems. In the following we do not even need to know the mappings f and h. In fact we are going to present a method to approximate the moment $h\,\!\circ \,\!\pi$ directly from input/output data, namely from $\omega (t)$ and y(t). Note that given the exponential stability hypothesis on the system and Theorem 2.2 (Theorem 2.6 for time-delay systems), the equation

$$\begin{aligned} y(t)=h(\pi (\omega (t)))+\varepsilon (t), \end{aligned}$$

(2.42)

where $\varepsilon (t)$ is an exponentially decaying signal, holds for the interconnections (2.13) and (2.26). We introduce the following assumption.

Assumption 2.6

The mapping $h\,\!\circ \,\!\pi$ belongs to the function space identified by the family of continuous basis functions $\varphi _j:\mathbb {R}^{\nu }\rightarrow \mathbb {R}$, with $j=1,\ldots ,M$ (M may be $\infty$), i.e., there exist $\pi _j\in \mathbb {R}$, with $j=1,\ldots ,M$, such that

$$ h(\pi (\omega )) = \sum _{j=1}^{M}\pi _j \varphi _j(\omega ), $$

for any $\omega$.

Let

$$ \begin{array}{rcl} \varGamma&\!=&\!\left[ \begin{array}{cccc} \pi _1 &{} \pi _2 &{} \ldots &{} \pi _N\end{array}\right] ,\\ \varOmega (\omega (t))&{}\!=&{}\!\left[ \begin{array}{cccc} \varphi _1(\omega (t)) &{} \varphi _2(\omega (t)) &{} \ldots &{} \varphi _N(\omega (t))\end{array}\right] ^{\top }, \end{array} $$

with $N\le M$. Using a weighted sum of basis functions, Eq. (2.42) can be written as

$$\begin{aligned} y(t)=\sum _{j=1}^{N}\pi _j \varphi _j(\omega (t))+ e(t)+\varepsilon (t)=\varGamma \varOmega (\omega (t))+ e(t)+\varepsilon (t), \end{aligned}$$

(2.43)

where $e(t)=\sum _{N+1}^{M}\pi _j \varphi _j(\omega (t))$ is the error caused by stopping the summation at N. Consider now the approximation

$$\begin{aligned} y(t)\approx \sum _{j=1}^{N}\widetilde{\pi }_j \varphi _j(\omega (t)) =\widetilde{\varGamma } \varOmega (\omega (t)), \end{aligned}$$

(2.44)

which neglects the approximation error e(t) and the transient error $\epsilon (t)$. Let $T_k^w=\{t_{k-w+1},\ldots ,t_{k-1},t_k\}$, with $0\le t_0< t_1< \ldots< t_{k-w}< \ldots< t_k< \ldots < t_q$, with $w>0$ and $q\ge w$, and $\varGamma _k$ be an on-line estimate of the matrix $\varGamma$ computed at $T_k^w$, namely computed at the time $t_k$ using the last w instants of time $t_i$ assuming that e(t) and $\epsilon (t)$ are known. Since this is not the case in practice, define $\widetilde{\varGamma }_k=\left[ \begin{array}{cccc} \widetilde{\pi }_1&\widetilde{\pi }_2&\ldots&\widetilde{\pi }_N\end{array}\right]$ as the approximation, in the sense of (2.44), of the estimate $\varGamma _k$. Finally, we can compute this approximation as follows.

Theorem 2.7

[64] Define the time-snapshots $\widetilde{U}_k\in \mathbb {R}^{w\times N}$ and $\widetilde{\varUpsilon }_k\in \mathbb {R}^{w}$ as

$$ \widetilde{U}_k=\left[ \begin{array}{cccc} \varOmega (\omega (t_{k-w+1}))&\ldots&\varOmega (\omega (t_{k-1}))&\varOmega (\omega (t_{k})) \end{array} \right] ^{\top } $$

and

$$ \widetilde{\varUpsilon }_k=\left[ \begin{array}{cccc} y(t_{k-w+1})&\ldots&y(t_{k-1})&y(t_k) \end{array} \right] ^{\top }. $$

If $\widetilde{U}_k$ is full rank then

$$\begin{aligned} {{\mathrm{vec}}}(\widetilde{\varGamma }_k)=(\widetilde{U}_k^{\top }\widetilde{U}_k)^{-1}\widetilde{U}_k^{\top }\widetilde{\varUpsilon }_k, \end{aligned}$$

(2.45)

is an approximation of the estimate $\varGamma _k$.

To ensure that the approximation is well-defined for all k, we give an assumption in the spirit of persistency of excitation.

Assumption 2.7

For any $k\ge 0$, there exist $\bar{K}>0$ and $\alpha >0$ such that the elements of $T_k^{K}$, with $K>\bar{K}$, are such that

$$ \frac{1}{K}\widetilde{U}_k^{\top }\widetilde{U}_k \ge \alpha I. $$

Note that if Assumption 2.7 holds (see [76] for a similar argument), $\widetilde{U}_k^{\top }\widetilde{U}_k$ is full rank. The next definition is a direct consequence of the discussion we have carried out.

Definition 2.9

The estimated moment of system (2.11) (or system (2.25)) is defined as

$$\begin{aligned} \widetilde{h\,\!\circ \,\! \pi }_{N,k}(\omega (t))=\widetilde{\varGamma }_k \varOmega (\omega (t)), \end{aligned}$$

(2.46)

with $\widetilde{\varGamma }_k$ computed with (2.45).

Equation (2.45) is a classic least-square estimator and an efficient recursive formula can be easily derived.

Theorem 2.8

[64] Assume that $\varPhi _k=(\widetilde{U}_k^{\top }\widetilde{U}_k)^{-1}$ and $\varPsi _k=(\widetilde{U}_{k-1}^{\top }\widetilde{U}_{k-1}+\omega (t_{k})\omega (t_{k})^{\top })^{-1}$ are full rank for all $t\ge t_r$ with $t_r\ge t_w$. Given ${{\mathrm{vec}}}(\widetilde{\varGamma }_r)$, $\varPhi _r$ and $\varPsi _r$, the least-square estimation

$$\begin{aligned} \begin{array}{l} {{\mathrm{vec}}}(\widetilde{\varGamma }_k)={{\mathrm{vec}}}(\widetilde{\varGamma }_{k-1})+\varPhi _k\omega (t_k)\!\left( y(t_k)-\omega (t_{k})^{\top }{{\mathrm{vec}}}(\widetilde{\varGamma }_{k-1})\right) -\\ \qquad \qquad \qquad \qquad \,\,-\varPhi _k\omega (t_{k-w})\!\left( y(t_{k-w})-\omega (t_{k-w})^{\top }{{\mathrm{vec}}}(\widetilde{\varGamma }_{k-1})\right) \!, \end{array} \end{aligned}$$

(2.47)

with

$$\begin{aligned} \begin{array}{l} \varPhi _k=\varPsi _k-\varPsi _k\omega (t_{k-w})(I+\omega (t_{k-w})^{\top }\varPsi _k\omega (t_{k-w}))^{-1}\omega (t_{k-w})^{\top }\varPsi _k \end{array} \end{aligned}$$

(2.48)

and

$$\begin{aligned} \begin{array}{l} \varPsi _k=\varPhi _{k-1}-\varPhi _{k-1}\omega (t_k)(I+\omega (t_k)^{\top }\varPhi _{k-1}\omega (t_k))^{-1}\omega (t_k)^{\top }\varPhi _{k-1}. \end{array} \end{aligned}$$

(2.49)

holds for all $t\ge t_r$.

Finally, the following result guarantees that the approximation converges to $h\,\!\circ \,\!\pi$.

Theorem 2.9

[64] Suppose Assumptions 2.1 (2.1 for time-delay systems), 2.2 (2.4 for time-delay systems), 2.6 and 2.7 hold. Then

$$ \lim _{t \rightarrow \infty } \left( h(\pi (\omega (t)))-\lim _{N \rightarrow M}\widetilde{h\,\!\circ \!\,\pi }_{N,k}(\omega (t))\right) =0. $$

7 Conclusion

In this chapter we have reviewed the model reduction technique for nonlinear, possibly time-delay, systems based on the “steady-state” notion of moment. We have firstly recalled the classical interpolation theory and we have then introduced the steady-state-based notion of moment. Exploiting this description of moment the solution of the problem of model reduction by moment matching for nonlinear systems has been given and an enhancement of the notion of frequency response for nonlinear systems has been presented. Subsequently, these techniques have been extended to nonlinear time-delay systems and the problem of obtaining a family of reduced order models matching two moments has been solved for nonlinear time-delay systems. The review is concluded with a recently presented technique to approximate the moment of nonlinear, possibly time-delay, systems, without solving any partial differential equation.