Recent Advances on Topology Optimization of Multiscale Nonlinear Structures

Abstract

Research on topology optimization mainly deals with the design of monoscale structures, which are usually made of homogeneous materials. Recent advances of multiscale structural modeling enables the consideration of microscale material heterogeneities and constituent nonlinearities when assessing the macroscale structural performance. However, due to the modeling complexity and the expensive computing requirement of multiscale modeling, there has been very limited research on topology optimization of multiscale nonlinear structures. This paper reviews firstly recent advances made by the authors on topology optimization of multiscale nonlinear structures, in particular techniques regarding to nonlinear topology optimization and computational homogenization (also known as FE²) are summarized. Then the conventional concurrent material and structure topology optimization design approaches are reviewed and compared with a recently proposed FE²-based design approach, which treats the microscale topology optimization process integrally as a generalized nonlinear constitutive behavior. In addition, discussions on the use of model reduction techniques is provided in regard to the prohibitive computational cost.

1 Introduction

1.1 Design of Monoscale Structures

Since the seminal paper by [6], topology optimization has undergone a remarkable development in both fields of academic research (e.g., [8, 25, 60]) and industrial application (e.g., [143]). Various approaches have been proposed, such as density-based methods (e.g., [5, 141]), evolutionary procedures (e.g., [59, 122, 123, 142]), level-set methods (e.g., [1, 13, 97, 113]) and others, all with the purpose of finding an optimal structural topology or material layout within a given design domain for specified objectives, constraints, and boundary conditions as is shown in Fig. 1. A critical review and comparison of the various design approaches has been recently presented by [103].

Fig. 1

Illustration of structural topology optimization

Early works on topology optimization were restricted to linear structural designs with the small deformation assumption (e.g., [8]). In pursuing more realistic designs, continuous efforts have been conducted to extend topology optimization to nonlinear structural designs considering various sources of nonlinearity, such as geometrical nonlinearity (e.g., [11, 12, 42, 76, 92, 111, 130]), material nonlinearity (e.g., [4, 78, 96, 131, 133, 134]), and both geometrical and material nonlinearities simultaneously (e.g., [58, 61, 68]).

1.2 Design of Multiscale Structures

Note that all above mentioned works focused on the design of monoscale structures, in other words the considered structures are made of homogeneous materials. In the recent years, there is an increasing use of high-performance heterogeneous materials such as fiber-reinforced composites, porous metallic materials, polymers and etc. When a structure made of these materials is under consideration, one has to account for material microscopic heterogeneities and constituent behaviors so as to assess the structural performance with more accuracy. Direct modeling of such structures including each individual microstructure is rather difficult or even impossible. Instead, a usual applied approach to bridge the two scales (structure and material), is homogenization (e.g., [47, 54, 55, 81]). By means of homogenization, one may evaluate the effective or homogenized constitutive behavior of the considered microstructure or Representative Volume Element (RVE) model and then use it to serve structural assessment rather than direct modeling it (e.g., [48, 118, 126, 127]). The key hypotheses of homogenization are the separation of scales and the periodicity. It is assumed that the microscopic length scale is much smaller than the macroscopic length scale such that the microscale RVE can be considered as periodically ordered pattern, while at the same time, the RVE is large enough to be considered in continuum mechanics framework, as is shown in Fig. 2.

Fig. 2

Illustration of a two-scale structure and periodically patterned RVE [118]

However, such approach encounters difficulties when geometrical and physical nonlinearities are present at the material scale. For such reason, computational homogenization approaches have been proposed (e.g. [30, 44, 66, 67, 70, 82, 83, 105]) and largely developed in the last decade [43] in order to assess the macroscopic influence of microscopic heterogeneities. Note that within the finite element analysis framework, this approach is also known as FE² following [30]. In general, it asserts that each point of the macroscopic discretization is associated with a RVE of the (nonlinear) microstructured material. Then for each macroscopic equilibrium iteration a nonlinear load increment needs to be computed for each of the (many) RVEs. In return the average stress across the RVE is then used as the macroscopic stress tensor without requiring effective constitutive relations. A schematic illustration of the first-order computational method [43] is shown in Fig. 3.

Fig. 3

Illustration of first-oder computational homogenization scheme [115]

A downside of this very general FE² method is the high computational burden. First, many nonlinear load steps need to be computed at the microscopic level which leads to a prohibitive amount of computing time. Second, when path-dependent constitutive behaviors are considered at the microscopic scale, the microscopic degrees of freedom and the history variables describing the material state need to be stored for each point within each RVE which leads to a distinct amount of additional storage requirements. In nonlinear topology optimization the multiscale dilemma is even more pronounced: not only is it required to solve the multiscale problem once, but for many different realizations of the structural topology. For these reasons, there has been very limited research on topology optimization of multiscale nonlinear structures within the above mentioned context. A first attempt towards FE²-based multiscale topology optimization has been recently made by the authors [115], where topology optimization is performed for a two-scale structure made of a nonlinear elastic RVE and an adaptive bi-level reduction strategy following [31, 32] is adopted to alleviate the computing cost. Note that, when a linear RVE is assumed, topology optimization of the structure made of this RVE is rather straightforward an extension of the standard monoscale design, because the effective constitutive of this RVEs can be explicitly determined by homogenization.

1.3 Concurrent Material and Structure Designs

Topology optimization has not only been applied for structural designs, but also for material microstructural design. By means of inverse homogenization, the continuously defined density model has also been used for tailoring material microstructures with prescribed constitutive properties [100, 101], extreme thermal expansion coefficients [45, 104], extreme viscoelastic behavior (e.g., [2, 19, 65, 129]), maximum stiffness and fluid permeability (e.g., [49, 50]) and recently hyperelastic properties [112]. Similar works have also been addressed by level-set methods (e.g., [17, 18]), ESO-type methods (e.g., [62, 63]). Some other works (e.g., [3, 38, 46, 69, 87–89, 106, 139]) fall also into this context. Up till now, topology optimization design of materials with extreme constitutive properties follows a rather standard routine [117]. An overview of material microstructural designs has been given by [14].

With the established models for material microstructural design, one comes up naturally with the idea of concurrent or integrate designs of both material ans structure. In other words, by topology optimization one determines not only the optimal spatial material layout distribution at the macroscopic structural scale, but also the optimal local use of the cellular material at the microscopic scale, as schematically shown in Fig. 4. The most commonly applied strategy is designing a universal material microstructure at the microscopic scale either for a fixed (e.g., [64, 106]) or concurrently changed (e.g., [26, 52, 124, 128, 144]) structure at the macroscopic scale. Obviously, such designs have not yet released the full potentiality of concurrent two-scale designs. A further step has been made by [138], where several different cellular materials are designed for a layered structure following a two-step design procedure. In fact, an earlier attempt to the topic traces back to [95], where simultaneous optimal designs are performed for both structure and element-wisely varying cellular materials following a decomposed design procedure [9, 109]. This work has later been extended to 3D [22] and to account for hyperelasticity [86]. Some more specific types of concurrent design have been give by (e.g., [40, 41, 75, 98, 99]) for the concurrent design of structural topology and composite laminate orientation and by [77] for the concurrent structural topology optimization and the shape optimization of closed liquid cell materials

Fig. 4

Illustration of concurrent topology optimization of material and structure [114]

Due to the intensive computational cost, though it was assumed that cellular materials vary from point to point at the macroscopic structural scale, in practice cellular materials are defined in an element-wise manner (e.g., [22, 95]) or from layer to layer (e.g., [138]). Concerning multiscale structural design, microscale cellular materials are optimized in response to the macroscale displacement solution, the optimized cellular materials in turn modify the macroscopic constitutive behavior. The equilibrium problem at the macroscopic scale is therefore in general nonlinear. Though this interface nonlinearity has been well acknowledged (e.g., [8, 109]), in practice it has been neglected in early works (e.g., [22, 95, 138]) for reasons that both scale design variables were updated simultaneously and no converged local material design results were required for macroscopic structural equilibrium.

Unlike previous design approaches, this nonlinearity has not been neglected but specially addressed in our recent work [114] treating the microscale material design integrally as a generalized nonlinear constitutive behavior. The nonlinear interface equilibrium due to the locally optimized or adapted materials is addressed by means of FE² method. It has been shown that this FE²-based design approach can provide similar topology solutions in comparison to the iterative design approach (e.g., [64, 128]), while requiring much less computing cost due to the reduced interchange between the two scales. Another advantage of treating the material optimization process as a generalized constitutive behavior is that the existing model reduction strategies for nonlinear heterogeneous materials can be applied straightforwardly to improve the design efficiency, as we have shown in [116].

1.4 Outline of this Paper

This paper is organized in the following manner. Nonlinear topology optimization for monoscale structure designs is reviewed at the first hand in Sect. 2 before dealing with multiscale structures. The general design procedure for multiscale nonlinear structures is summarized in Sect. 3. Section 4 reviews the inverse homogenization routine for extreme material microstructural designs. Based on the inverse homogenization, Sect. 5 presents two concurrent material and structure design approaches, namely iterative design approach and FE²-based design approach. Discussions on the use of model reduction techniques are given in Sect. 6 in regard to the prohibitive computational cost when dealing with multiscale computations. The paper ends with conclusions and perspectives in Sect. 7.

2 Nonlinear Topology Optimization

Among all exiting approaches for topology optimization, the Bi-directional Evolutionary Structural Optimization method (BESO; see, e.g., [60]) is applied to perform topology optimization for its robustness and the performance of the resulting structures (e.g., [58, 60]). In addition, as compared to continuously defined methods [8], the discrete nature of the BESO method omits the definition of additional pseudo-relationships between intermediate densities and material constitutive behavior, resulting in algorithmic advantages.

2.1 Topology Optimization Model

Topology design variables ${\varvec{\rho }}=(\rho _1,\dots ,\rho _{N_\mathrm{e}})^{T}$, are defined in an element-wise manner, where $N_\mathrm{e}$ is the total number of elements in the design domain. Within the framework of the BESO method (and others) the design variables take values of either 0 or 1, denoting void and solid materials,

$$\begin{aligned} \rho _{e} = 0\,\text{or}\,1,~e = 1, \dots , N_\mathrm{e}. \end{aligned}$$

(1)

whereas in practice an extremely small value $\rho _\mathrm{min}$ is attributed to voids to prevent the stiffness matrix singularity.

In linear elastic problems, topology design variables are usually associated with the material Young’s modulus or the element stiffness

$$\begin{aligned} \mathbf{k}_{e} = \rho _{e} \mathbf{k}_{0}, \end{aligned}$$

(2)

where $\mathbf{k}_{e}$ is the element stiffness matrix of the associated element and $\mathbf{k}_{0}$ is the element stiffness matrix with solid material.

In general nonlinearity, when there is no closed-form representation of the material’s constitutive law, topology design variables are defined is association with the element internal force vector $\mathbf{f}_\mathrm{int}^{e}$ as

$$\begin{aligned} \mathbf{f}_\mathrm{int}^{e} = \rho _{e}\int _{\varOmega _{e}} \mathbf{B}^{T}({\varvec{x}}){\varvec{\sigma }}({\varvec{x}})~\mathrm{d}{\varOmega _{e}}, \end{aligned}$$

(3)

where $\varOmega _{e}$ denotes the domain of element e. The linear strain-displacement matrix $\mathbf{B}$ relates the strain to element displacement vector $\mathbf{u}_{e}$ via

$$\begin{aligned} {\varvec{\varepsilon }}(\varvec{x}) = \mathbf{B}^{T}({\varvec{x}})\mathbf{u}_{e}. \end{aligned}$$

(4)

${\varvec{\sigma }}({\varvec{x}})$ is the stress response at point ${\varvec{x}}$ in response to the strain ${\varvec{\varepsilon }}(\varvec{x})$ computed according to the applied material constitutive law. In practice, for void elements the stress is set directly to zero and the tangent stiffness tensor is set to a small fraction of the initial stiffness tensor The effective tangent stiffness tensor is defined as a small fraction of the initial elastic tensor ${\mathbb {C}}^\mathrm{tan}=\rho _\mathrm{min}{\mathbb {C}}^\mathrm{initial}$ to avoid the singularity.

Two types of design objectives are usually adopted in nonlinear structural designs when the external force $\mathbf{f}_\mathrm{ext}$ is imposed, namely the end-compliance

$$\begin{aligned} f_\mathrm{c} = \mathbf{f}^{T}_\mathrm{ext} \mathbf{u}, \end{aligned}$$

(5)

and the complementary work

$$\begin{aligned} f_\mathrm{w} = \lim \limits _{n \rightarrow \infty } \left[ \frac{1}{2}\sum ^{n}_{i=1} \left( \mathbf{f}_\mathrm{ext}^{(i)} + \mathbf{f}_\mathrm{ext}^{(i-1)}\right) ^{T}\Delta \mathbf{u}^{(i)}\right] , \end{aligned}$$

(6)

where n is the number of load increments. The latter is applied to avoid degenerated topologies, especially when dealing with geometrical nonlinearity [12]. Without loss of generality, the end-compliance $f_\mathrm{c}$ is considered in the following.

The minimization of structural end-compliance considering a constraint on material volume fraction can be formulated as

$$\begin{aligned} \begin{array}{rl} \min\limits_{{\varvec{\rho }}}: & f_\mathrm{c}({\varvec{\rho }}, \mathbf{u})\\ \text{subject to}: & \mathbf{r}({\varvec{\rho }},\mathbf{u})=\mathbf{0}\\ :& V({\varvec{\rho }})=\sum \rho _{e}v_{e}=V_\mathrm{req}\\ :& \rho _{e}=0~\,\text{or}\,~1,~e = 1, \dots , N_\mathrm{e},\\ \end{array} \end{aligned}$$

(7)

in which $v_{e}$ is the element volume, $V({\varvec{\rho }})$ and $V_\mathrm{req}$ are the total and required material volumes, respectively. $\mathbf{u}$ is the converged displacement solution. $\mathbf{r}(\mathbf{u},{\varvec{\rho }})$ stands for the residual

$$\begin{aligned} \mathbf{r}({\varvec{\rho }},\mathbf{u})=\mathbf{f}_\mathrm{ext}- \sum _{e=1}^{N_\mathrm{e}}\rho _{e} \int _{\varOmega _{e}} \mathbf{B}^{T}{\varvec{\sigma }}~\mathrm{d}{\varOmega _{e}}. \end{aligned}$$

(8)

2.2 Sensitivity Analysis

To implement topology optimization, sensitivity of the design objective with respect to design variables needs to be provided. The derivation of the objective sensitivity requires applying the adjoint method [12]. Introducing a vector of Lagrangian multipliers ${\varvec{\lambda }}$, one may rewrite the objective in the following form without modifying the objective value

$$\begin{aligned} f^{*}_\mathrm{c}({\varvec{\rho }})=\mathbf{f}^{T}_\mathrm{ext}{} \mathbf{u}+{\varvec{\lambda }}^{T}{} \mathbf{r}, \end{aligned}$$

(9)

where the term ${\varvec{\lambda }}^{T}{} \mathbf{r}$ equals zero when the equilibrium of (8) is achieved, i.e., $f^{*}_\mathrm{c}=f_\mathrm{c}$.

Note that $\mathbf{f}_\mathrm{ext}$ is invariant to the variation of design variables, the derivative of the modified objective function $f^{*}_\mathrm{c}$ with respect to $\rho _{e}$ equals

$$\begin{aligned} \frac{\partial f^{*}_\mathrm{c}}{\partial \rho _{e}}=\mathbf{f}^{T}_\mathrm{ext}\frac{\partial \mathbf{u}}{\partial \rho _{e}}+{\varvec{\lambda }}^{T}\left( \frac{\partial \mathbf{r}}{\partial \mathbf{u}}\frac{\partial \mathbf{u}}{\partial \rho _{e}}+\frac{\partial \mathbf{r}}{\partial \rho _{e}}\right) . \end{aligned}$$

(10)

With the purpose of eliminating ${\partial \mathbf{u}}/{\partial \rho _{e}}$, regrouping the terms with ${\partial \mathbf{u}}/{\partial \rho _{e}}$ in (10) yields

$$\begin{aligned} \frac{\partial f^{*}_\mathrm{c}}{\partial \rho _{e}}=\left( \mathbf{f}^{T}_\mathrm{ext}-{\varvec{\lambda }}^{T}{} \mathbf{K}_\mathrm{tan}\right) \frac{\partial \mathbf{u}}{\partial \rho _{e}}+{\varvec{\lambda }}^{T}\frac{\partial \mathbf{r}}{\partial \rho _{e}}, \end{aligned}$$

(11)

where

$$\begin{aligned} \mathbf{K}_\mathrm{tan}=-\frac{\partial \mathbf{r}}{\partial \mathbf{u}} \end{aligned}$$

(12)

is the tangent stiffness matrix. Recall the symmetry of $\mathbf{K}_\mathrm{tan}$, i.e., $\mathbf{K}^{T}_\mathrm{tan}=\mathbf{K}_\mathrm{tan}$, the first term of the right-hand side of (11) can be eliminated by imposing

$$\begin{aligned} \mathbf{K}_\mathrm{tan}{\varvec{\lambda }}=\mathbf{f}_\mathrm{ext}, \end{aligned}$$

(13)

and yields

$$\begin{aligned} \frac{\partial f^{*}_\mathrm{c}}{\partial \rho _{e}}={\varvec{\lambda }}^{T}\frac{\partial \mathbf{r}}{\partial \rho _{e}}. \end{aligned}$$

(14)

Finally, according to the residual definition (8), the sensitivity of the objective equals

$$\begin{aligned} \frac{\partial f_\mathrm{c}}{\partial \rho _{e}}=\frac{\partial f^{*}_\mathrm{c}}{\partial \rho _{e}}=-{\varvec{\lambda }}^{T}\int _{\varOmega _{e}} \mathbf{B}^{T}{\varvec{\sigma }}~\mathrm{d}{\varOmega _{e}}. \end{aligned}$$

(15)

2.3 BESO Updating Scheme

In the BESO method [60], an evolutionary ratio $c_\mathrm{er}$ is defined to determine the required volume of material usage at each design iteration following

$$\begin{aligned} V^{(l)}= \mathrm{max} \left\{ V_\mathrm{req}, (1-c_\mathrm{er}) V^{(l-1)} \right\} , \end{aligned}$$

(16)

in which $V^{(l)}$ and $V^{(l-1)}$ denote the required volumes of the solid at the current (l-th) iteration and the previous iteration, respectively. Note that in general the volume of the solid of the structure decreases iteratively until the required volume $V_\mathrm{req}$ is achieved.

At each design iteration, the sensitivity numbers which denote the relative ranking of the elemental sensitivities are used to determine material removal and addition. The sensitivity number for the considered objective is defined as the opposite of the sensitivity divided by the element volume

$$\begin{aligned} \alpha _{e}= -\frac{\partial {f_\mathrm{c}}}{\partial \rho _{e}}\frac{1}{v_{e}}. \end{aligned}$$

(17)

Note that the division by element volumes can be omitted when uniform mesh is used.

In order to avoid mesh-dependency and checkerboard pattern, sensitivity numbers are smoothed by means of a filtering scheme [74, 102]

$$\begin{aligned} {\alpha }_{e}=\frac{\sum _{j=1}^{N_\mathrm{e}}w_{ej}{\alpha }_{j}}{\sum _{j=1}^{N_\mathrm{e}}w_{ej}}, \end{aligned}$$

(18)

where $w_{ej}$ is a linear weight factor

$$\begin{aligned} w_{ej}=\max (0,r_\mathrm{min}-\Delta (e,j)), \end{aligned}$$

(19)

determined according to the prescribed filter radius $r_\mathrm{min}$ and the element center-to-center distance $\Delta (e,j)$. A schematic illustration of the filtering scheme is shown in Fig. 5, where a checkerboard filed is filtered with $r_\mathrm{min}=1.5$ and $r_\mathrm{min}=3$ times of element length, respectively. It can be seen that the concerned field is smoothed by the filter scheme, for which reason the sensitivity numbers of void elements can be naturally obtained. By this scheme, void elements neighboring to the regions of high sensitivity numbers have higher potentiality to be recovered in the next iteration.

Fig. 5

A checkerboard field and filtered fields ($r_\mathrm{min}=1.5$ and 3)

It has been examined that the topology and the objective may encounter difficulties for convergence due to the discrete nature of the BESO material model. To improve the convergence of the solution, one may simply average the current sensitivity numbers with with their historical information [57]

$$\begin{aligned} {\alpha }^{(l)}_{e}\leftarrow \left({\alpha }^{(l)}_{e}+{\alpha }^{(l-1)}_{e}\right)/2. \end{aligned}$$

(20)

For variables updating, a threshold of sensitivity number $\alpha _\mathrm{th}$ is determined by means of a bisection algorithm from all sensitivity numbers satisfying the target volume at the current design iteration [59]. The design variables are updated according to

$$\begin{aligned} {\rho _{e}}=\mathrm{max} \left\{ \rho _\mathrm{min}, \mathrm{sign}(\alpha _{e}-\alpha _\mathrm{th}) \right\} , \end{aligned}$$

(21)

which means solids will be switched to voids if $\alpha _{e}$ is lower than $\alpha _\mathrm{th}$, accordingly voids will be switched back to solids when $\alpha _{e}$ is higher than $\alpha _\mathrm{th}$. The evolutionary design process stops when the objective value or the structural topology reaches convergence.

2.4 Numerical Example

A cantilever discretized into $100\times 50$ square shaped bilinear elements is considered as shown in Fig. 6. Element dimensions is $1\times 1$ mm$^2$ and assumed in plane strain condition. The left end of the cantilever is fixed and an external force is applied on the middle point of the right edge. In regard to topology optimization, inefficient or redundant materials are gradually removed according to the sensitivity ranking from an initial full solid design in an evolutionary rate of $c_\mathrm{er}=2\,\%$. Sensitivity numbers are filtered within a local zone controlled by a filter radius $r_\mathrm{min}= 6$ mm. The constraint on the volume fraction of solid is set to 60 %. For the purpose of comparison, the linear elastic topology solution obtained using the same parameter set is also given in Fig. 6.

Fig. 6

Illustration of a cantilever and its linear elastic topology design of 60 % volume fraction

In regard to nonlinear design, the present work is limited to nonlinear elasticity subjected to small deformations. The considered nonlinear constitutive behavior is governed by an isotropic compressible potential of the form

$$\begin{aligned} w({\varvec{\varepsilon }})=\frac{9}{2}\kappa \varepsilon _{m}+\frac{\varepsilon _{0}\sigma _{0}}{1+m}\left( \frac{\varepsilon _{eq}}{\varepsilon _{0}}\right) ^{1+m}. \end{aligned}$$

(22)

Here $\kappa$ denotes the bulk modulus, $\varepsilon _{m}=Tr({\varvec{\varepsilon }})/3$ is the hydrostatic strain, and $\varepsilon _{eq}$ is the equivalent strain defined by $\varepsilon _{eq}=\sqrt{2{\varvec{\varepsilon }_{d}}:{\varvec{\varepsilon }_{d}}/3}$ with ${\varvec{\varepsilon }}_{d}={\varvec{\varepsilon }}-\varepsilon _{m}{} \mathbf{1}$ and $\mathbf{1}$ being the second-order identity tensor. m is the strain-hardening parameter such that $0\le m \le 1$. $\sigma _{0}$ and ${\varepsilon _{0}}$ are the flow stress and reference strain, respectively. The stress-strain relationship is provided by:

$$\begin{aligned} {\varvec{\sigma }}=\frac{\partial w({\varvec{\varepsilon }})}{\partial {{\varvec{\varepsilon }}}}=\kappa Tr({\varvec{\varepsilon }})\mathbf{1} + \frac{2}{3}\frac{\sigma _{0}}{\varepsilon _{0}}\left( \frac{\varepsilon _{eq}}{\varepsilon _{0}}\right) ^{m-1}{\varvec{\varepsilon }}_{d}. \end{aligned}$$

(23)

This is a commonly used constitutive model for the representation of a number of nonlinear mechanical phenomena (e.g., [27, 90, 136]). In particular, the cases $m=0$ and $m=1$ correspond to perfectly rigid plastic and linearly elastic materials, respectively.

The following numerical parameters are chosen for the current test case: $m=0.5$, $\kappa =20$ MPa, $\sigma _{0}=1$ MPa, and $\varepsilon _{0}=1$. Nonlinear topology optimization designs are carried out for three different load forces 0.01 N, 0.2 N and 0.4 N and the corresponding topology design results are shown in Fig. 7a–c, respectively. The nonlinear design algorithm gives almost identical topology solution as is the case in linear elasticity when the load force is small, as can be viewed from Fig. 7a and the linear topology solution in Fig. 6. When the load force increases, the topology design result varies in response to the load force value as can be observed from Fig. 7b, c for $\mathbf{f}_\mathrm{ext}=0.2$ N and 0.4 N, respectively. From Fig. 7, one observes that materials move towards the left end of the cantilever to resist the increasing load force. The equivalent stress fields of the three topologies are also given in Fig. 7 on exaggeratedly deformed meshes. For the purpose of illustrations, the elements neighboring to the loading tip with high stress concentration are removed from the stress field plots.

Fig. 7

Nonlinear topology designs and the equivalent stress fields (deformation exaggerated 10 times). a $\mathbf{f}_\mathrm{ext}=0.01$ N, $f_\mathrm{c}=$ 2.5e−5 J. b $\mathbf{f}_\mathrm{ext}=0.2$ N, $f_\mathrm{c}=0.067$ J. c $\mathbf{f}_\mathrm{ext}=0.4$ N, $f_\mathrm{c}=0.456$ J

3 Design of Multiscale Structures

Topology optimization design of multiscale structures can be viewed as an extension of monoscale design except the material constitutive law is governed by a single RVE or multiple RVEs defined at the microscopic scale. In the case of linear elasticity, the effective or the homogenized constitutive behavior, i.e., the effective stiffness tensor of the RVEs can be explicitly determined by means of homogenization. In the contrary, when nonlinearities are present at the microscopic scale, one has to turn to FE²-type solution schemes because there exists no explicit closed-form representation for the constitutive behavior of the RVE. In the following, the FE² method [30], is firstly reviewed and summarized in Sect. 3.1. The implementation of a unified periodic boundary conditions [119] is briefly reviewed in Sect. 3.2. FE²-based nonlinear topology optimization model is given in Sect. 3.3. Section 3.4 carries out the design of a twoscale cantilever structure made of periodically patterned anisotropic short-fiber reinforced composite.

3.1 FE² Method

The FE² method assumes the hypothesis of the separation of scales and periodicity as is the case already shown in Fig. 2. Each macroscale material point is attributed with a prescribed RVE. At the macroscale the material appears to be homogeneous but with unknown mechanical properties. These mechanical properties are related to the heterogeneities of the RVE at the microscale which contribute strongly to the overall mechanical response observed at the larger scale.

Let ${\varvec{x}}$ and ${\varvec{y}}$ denote the position of a point at the macro and micro scales, respectively. Within the macroscopic domain $\varOmega$, the macroscopic displacement ${\bar{\varvec{u}}({\varvec{x}})}$, the macroscopic strain ${\bar{\varvec{\varepsilon }}({\varvec{x}})}$ and the macroscopic stress ${\bar{\varvec{\sigma }}({\varvec{x}})}$ are considered. Their microscopic counterparts at the microscale are the displacement ${\varvec{u}}({\varvec{x}},{\varvec{y}})$, the infinitesimal strain ${\varvec{\varepsilon }}({\varvec{x}},{\varvec{y}})$ and the stress ${\varvec{\sigma }}({\varvec{x}},{\varvec{y}})$. While the constitutive model for each material phase of the RVE at the microscale is assumed to be known, explicit constitutive relations on the macroscale that can account for the microstructural heterogeneities are rarely ever at hand. Therefore, the macroscopic stress can often only be computed as a function of the microscopic stress state by means of volume averaging according to

$$\begin{aligned} \bar{\varvec{\sigma }}({\varvec{x}})=\langle {\varvec{\sigma }}({\varvec{x}},{\varvec{y}})\rangle =\frac{1}{|\varOmega _{\upmu }|}\int _{\varOmega _{\upmu }}{\varvec{\sigma }}({\varvec{x}}, {\varvec{y}})~\mathrm{d}{\varOmega _{\upmu }}, \end{aligned}$$

(24)

in which ${\varvec{\sigma }}({\varvec{x}}, {\varvec{y}})$ is evaluated by solving the boundary value problem of the RVE by constraining $\langle {\varvec{\varepsilon }}({\varvec{x}},{\varvec{y}})\rangle$ equal to $\bar{\varvec{\varepsilon }}({\varvec{x}})$, i.e.,

$$\begin{aligned} \bar{\varvec{\varepsilon }}({\varvec{x}})=\langle {\varvec{\varepsilon }}({\varvec{x}},{\varvec{y}})\rangle =\frac{1}{|\varOmega _{\upmu }|}\int _{\varOmega _{\upmu }}{\varvec{\varepsilon }}({\varvec{x}}, {\varvec{y}})~\mathrm{d}{\varOmega _{\upmu }}, \end{aligned}$$

(25)

where periodic boundary conditions (p.b.c.) are usually applied to define this constraint in accordance with the assumed periodicity assumption. Note that when cracks, voids and rigid inhomogeneities are present in the RVE, the foregoing definitions for the macroscopic stress and stain tensors need to be extended [81].

The schematic illustration of the FE² method has already been shown in Fig. 3. In summary, the FE² method consists of the following steps:

• 1. evaluate $\bar{\varvec{\varepsilon }}({\varvec{x}})$ with an initially defined setting;

• 2. define p.b.c. on the RVE according to $\bar{\varvec{\varepsilon }}({\varvec{x}})$;

• 3. evaluate ${\varvec{\sigma }}({\varvec{x}},{\varvec{y}})$ by solving the RVE problem;

• 4. compute $\bar{\varvec{\sigma }}({\varvec{x}})$ via volume averaging ${\varvec{\sigma }}({\varvec{x}},{\varvec{y}})$;

• 5. evaluate the structural tangent stiffness matrix;

• 6. update ${\varvec{u}}({\varvec{x}})$ using the Newton–Raphson method;

• 7. repeat 2-6 until the equilibrium is achieved.

Note that in the case of linear elasticity, we have the following relationship

$$\begin{aligned} \bar{\varvec{\sigma }}({\varvec{x}})=\mathbb {C}^\mathrm{hom}:\bar{\varvec{\varepsilon }}({\varvec{x}}) \end{aligned}$$

(26)

in which the homogenized elastic stiffness tensor $\mathbb {C}^\mathrm{hom}$ can be determined by solving the RVE boundary value problem for six independent overall strain values in general 3D case.

3.2 Periodic Boundary Conditions

The microscale stress field ${\varvec{\sigma }}({\varvec{x}},{\varvec{y}})$ is evaluated by solving the RVE equilibrium problem subject to $\bar{\varvec{\varepsilon }}({\varvec{x}})$. By the assumption of periodicity, the displacement field of the RVE subjected to a given strain $\bar{\varvec{\varepsilon }}({\varvec{x}})$ can be written as the sum of a macroscopic displacement field and a periodic fluctuation field ${\varvec{u}}^{*}$ [81]

$$\begin{aligned} {\varvec{u}}({\varvec{x}},{\varvec{y}})=\bar{\varvec{\varepsilon }}({\varvec{x}})\cdot {\varvec{y}} + {\varvec{u}}^{*}({\varvec{y}}), \end{aligned}$$

(27)

such that

$$\begin{aligned} \langle {\varvec{\varepsilon }}({\varvec{x}},{\varvec{y}})\rangle =\bar{\varvec{\varepsilon }}({\varvec{x}}), \end{aligned}$$

(28)

because $\langle {\varvec{u}}^{*}\rangle$ vanishes for its periodicity.

In practice, (27) cannot be directly imposed on the boundaries because the periodic fluctuation term ${\varvec{u}}^{*}$ is unknown. The general expression of (27) needs to be transformed into a certain number of explicit constraints between the corresponding pairs of nodes on the opposite surfaces of the RVE [119]. Consider a 2D RVE as shown in Fig. 8, the displacements on a pair of opposite boundaries are

$$\begin{aligned} {\left\{ \begin{array}{ll} {\varvec{u}}({\varvec{x}},{\varvec{y}})^{k+}=\bar{\varvec{\varepsilon }}({\varvec{x}})\cdot {\varvec{y}}^{k+}+{\varvec{u}}^{*}({\varvec{y}})\\ {\varvec{u}}({\varvec{x}},{\varvec{y}})^{k-}=\bar{\varvec{\varepsilon }}({\varvec{x}})\cdot {\varvec{y}}^{k-}+{\varvec{u}}^{*}({\varvec{y}}) \end{array}\right. } \end{aligned}$$

(29)

where superscripts “$k+$” and “$k-$” denote the pair of two opposite parallel boundary surfaces that are oriented perpendicular to the kth direction. The periodic term ${\varvec{u}}^{*}$ can be eliminated through the difference between the displacements

$$\begin{aligned} {\varvec{u}}({\varvec{x}},{\varvec{y}})^{k+}-{\varvec{u}}({\varvec{x}},{\varvec{y}})^{k-}=\bar{\varvec{\varepsilon }}({\varvec{x}})\cdot ({\varvec{y}}^{k+}-{\varvec{y}}^{k-}). \end{aligned}$$

(30)

With specified $\bar{\varvec{\varepsilon }}({\varvec{x}})$, the right-hand side becomes a constant and such equations can be easily imposed in the the finite element analysis as nodal displacement constraint equations. At the same time, this form of boundary conditions meets the periodicity and continuity requirements for both displacement as well as stress when using displacement-based finite element analysis [120].

Fig. 8

An illustrative 2D rectangular RVE [115]

3.3 FE²-Based Multiscale Structural Design

In general, FE²-based multiscale structural design follows the same design algorithm that is presented in Sect. 2, except for the application of the FE² for the evaluation of structural performance. Similarly, topology design variables are defined in association with the element internal force vector $\bar{\mathbf{f}}_\mathrm{int}^{e}$ as

$$\begin{aligned} \bar{\mathbf{f}}_\mathrm{int}^{e} = \rho _{e}\int _{\varOmega _{e}}\bar{\mathbf{B}}^{T}({\varvec{x}})\bar{\varvec{\sigma }}({\varvec{x}})~\mathrm{d}{\varOmega _{e}}, \end{aligned}$$

(31)

where the effective stress $\bar{\varvec{\sigma }}({\varvec{x}})$ is computed via the volume averaging relation (24). The microscopic stress field ${\varvec{\sigma }}({\varvec{x}},{\varvec{y}})$ is determined from an underlying nonlinear microscale equilibrium problem subjected to a prescribed overall strain $\bar{\varvec{\varepsilon }}(\varvec{x})$. The macroscale strain is computed by the linear relation $\bar{\varvec{\varepsilon }}({\varvec{x}})=\bar{\mathbf{B}}^{T}({\varvec{x}})\bar{\mathbf{u}}_{e}$ with the specified matrix $\bar{\mathbf{B}}({\varvec{x}})$ and the nodal displacement vector of the e-th element $\bar{\mathbf{u}}_{e}$. In practice, for void elements the microscale solutions can be saved and the effective stress is set directly to zero. The effective tangent stiffness tensor is set to be a small fraction of the homogenized elastic tensor of the considered RVE as $\bar{\mathbb {C}}^\mathrm{tan}=\rho _\mathrm{min}\bar{\mathbb {C}}^\mathrm{hom}$ to avoid the singularity.

To be in consistence with Sect. 2, the structural end-compliance $f_\mathrm{c} = \bar{\mathbf{f}}^{T}_\mathrm{ext}\bar{\mathbf{u}}$, computed using the macroscale external force $\bar{\mathbf{f}}_\mathrm{ext}$ and the macroscale displacement solution $\bar{\mathbf{u}}$, is considered as the design objective to be minimized. The minimization of the end-compliance of multiscale structures considering a constraint on material volume fraction is defined in analogy to (7) in the form:

$$\begin{aligned} \begin{array}{rl} \min\limits_{{\varvec{\rho }}}: & f_\mathrm{c}({\varvec{\rho }}, \bar{\mathbf{u}})\\ \text{subject to}: & \bar{\mathbf{r}}({\varvec{\rho }},\bar{\mathbf{u}})=\mathbf{0}\\ :& V({\varvec{\rho }})=\sum \rho _{e}v_{e}=V_\mathrm{req}\\ :& \rho _{e}=0~\,\text{or}\,~1,~e = 1, \dots , N_\mathrm{e}.\\ \end{array} \end{aligned}$$

(32)

Here $\bar{\mathbf{r}}({\varvec{\rho }},\bar{\mathbf{u}})$ is the macroscale residual

$$\begin{aligned} \bar{\mathbf{r}}({\varvec{\rho }},\bar{\mathbf{u}})=\bar{\mathbf{f}}_\mathrm{ext}- \sum _{e=1}^{N_\mathrm{e}}\rho _{e} \int _{\varOmega _{e}} \bar{\mathbf{B}}^{T}\bar{\varvec{\sigma }}({\varvec{x}})~\mathrm{d}{\varOmega _{e}}. \end{aligned}$$

(33)

The sensitivity of $f_\mathrm{c}$ in the current context can also be derived in analogy to Sect. 2.2 and equals

$$\begin{aligned} \frac{\partial f_\mathrm{c}}{\partial \rho _{e}}=\frac{\partial f^{*}_\mathrm{c}}{\partial \rho _{e}}=-\bar{\varvec{\lambda }}^{T}\int _{\varOmega _{e}} \bar{\mathbf{B}}^{T}\bar{\varvec{\sigma }}({\varvec{x}})~\mathrm{d}{\varOmega _{e}}, \end{aligned}$$

(34)

where the adjoint solution $\bar{\varvec{\lambda }}$ is computed from

$$\begin{aligned} \bar{\mathbf{K}}_\mathrm{tan}\bar{\varvec{\lambda }}=\bar{\mathbf{f}}_\mathrm{ext}, \end{aligned}$$

(35)

using the macroscale tangent stiffness matrix $\bar{\mathbf{K}}_\mathrm{tan}$.

3.4 Numerical Example

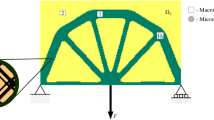
In this example, a two-scale cantilever structure made of periodically patterned anisotropic short-fiber reinforced composite as shown in Fig. 9 is to be designed. Following [136], both the matrix (phase 1) and the fibers (phase 2) are assumed to be isotropic and compressible materials characterized by the governing potential of Eq. (22). The matrix material is highly nonlinear: $m^\mathrm{(1)}=0.5$, $\kappa ^\mathrm{(1)}=20$ MPa, $\sigma ^\mathrm{(1)}_{0}=1$ MPa, and $\varepsilon ^\mathrm{(1)}_{0}=1$. The fibers are assumed to be linear elastic and much more rigid than the matrix: $m^\mathrm{(2)}=1$, $\kappa ^\mathrm{(2)}=20$ MPa, $\sigma ^\mathrm{(2)}_{0}=1000$ MPa, and $\varepsilon ^\mathrm{(2)}_{0}=1$. The RVE (Fig. 9) is discretized into $20\times 20$ square bilinear elements. The equivalent stress fields within the RVE in cases of biaxial stretching and uniaxial stretching combined with shear are shown in Fig. 10.

Fig. 9

Illustration of a two-scale cantilever made of periodically patterned short-fiber reinforced composite

Fig. 10

Equivalent stress fields (deformation exaggerated 50 times) of the short-fiber reinforced RVE for biaxial stretching (left, $\bar{\varepsilon }_{11}=\bar{\varepsilon }_{22}=0.002,\bar{\varepsilon }_{12}=0$) and uniaxial stretching with shear (right, $\bar{\varepsilon }_{11}=0.001, \bar{\varepsilon }_{22}=0,\bar{\varepsilon }_{12}=0.002$)

Topology optimization is carried out for the macroscale structure with the same BESO parameters that are used in Sect. 2.4, i.e., the evolutionary rate $c_\mathrm{er}=2\%$, the filter radius $r_\mathrm{min}= 6$ mm, the volume fraction constraint is 60%. It important to emphasize that it requires solving $4\times 100\times 50$ (4 Gauss integration points for each element) nonlinear RVE boundary value problems for each iteration of each load increment. This number would decrease progressively with iterations as the removed elements are no longer evaluated for the structural response.

For the purpose of comparison, designs are also carried out for the same three load forces, i.e., 0.01, 0.2 and 0.4 N as considered in Sect. 2.4 and the corresponding design results are shown in Fig. 11a–c. The topology shown in Fig. 11 is similar to the topologies of Figs. 6 and 7a, indicating that an external force load at the level of 0.01 N does not result in much difference in the design results. However, when the external load is increased to 0.2 and 0.4 N, one can observe obvious topological differences between the design results shown in Figs. 11b, c and 7b, c, respectively, which are due to the existence of the reinforcing fibers. The presence of fibers also results in lower end-compliance values, i.e., increased stiffness, of the design results (Figs. 7, 11).

Fig. 11

Design of two-scale structures in nonlinear elasticity. a $\mathbf{f}_\mathrm{ext}=0.01$ N, $f_\mathrm{c}=$ 2.2e$-$5 J. b $\mathbf{f}_\mathrm{ext}=0.2$ N, $f_\mathrm{c}=0.051$ J. c $\mathbf{f}_\mathrm{ext}=0.4$ N, $f_\mathrm{c}= 0.317$ J

The equivalent stress field of the topology solution in Fig. 11b is given in Fig. 12 together with the equivalent stress fields of the RVEs at several selected points. The elements neighboring the loading tip with high stress concentration are removed from the macroscale field plot for the purpose of illustration. From the deformed RVEs shown in Fig. 12, one can observe that the RVEs at points A and D are under compression, the RVE at point B is under tension, and the RVE at point C is subjected to a mechanical shear state, which are in agreement with their macroscale deformation states. One may also note from the stress fields that the presence of fibers results in higher stress concentrations at the interface of the matrix and the fibers. The higher stress concentrations are responsible for the initial material failure or crack at the microscopic scale which cannot be detected when using the conventional monoscale fracture analysis (e.g., [23]). There is also a potential application of such feature in stress-related topological designs (e.g., [10, 15, 16, 28, 51, 73, 140]), where the stress constraints may be considered to limit the maximum stress at the microscopic scale.

Fig. 12

The equivalent stress fields of the case b in Fig. 11 for the macro structure (deformation exaggerated 10 times) and for the micro RVEs at selected points (deformation exaggerated 50 times)

4 Material Microstructural Design

Before dealing with the concurrent material and structural designs in the next Sect. 5, the standard material microstructural design routine using the inverse homogenization (e.g., [62, 100, 117]) is reviewed firstly in this Section.

4.1 Homogenization Strategies

Within the scope of linear elasticity, there exits two equivalent approaches for the determination of the effective or the homogenized stiffness tensor $\mathbb {C}^\mathrm{hom}$ of periodically patterned microstructure [53]. One is the asymptotic approach, derived in a systematic way using the two-scale asymptotic expansion method [47]. Another is the energy-based approach [100] employing the average stress and strain theorem as is the relationship presented in Eq. (26).

By the asymptotic approach, the homogenized stiffness tensor is given by averaging the integral over a specified the RVE $\varOmega _{\upmu }$ as

$$\begin{aligned} C^\mathrm{hom}_{ijkl}=\frac{1}{|\varOmega _{\upmu }|} \int _{\varOmega _{\upmu }} C_{ijpq}\left(\varepsilon ^{0(kl)}_{pq}-\varepsilon ^{*(kl)}_{pq}\right) \mathrm{d}{\varOmega _{\upmu }}, \end{aligned}$$

(36)

where the Einstein index summation notation is used and $\varepsilon ^{*(kl)}_{pq}$ is the Y-periodic solution of

$$\begin{aligned} \int _{\varOmega _{\upmu }} C_{ijpq}\varepsilon ^{*(kl)}_{pq}\frac{\partial v_{i}}{\partial y_{j}} \mathrm{d}{\varOmega _{\upmu }} = \int _{\varOmega _{\upmu }} C_{ijpq}\varepsilon ^{0(kl)}_{pq}\frac{\partial v_{i}}{\partial y_{j}} \mathrm{d}{\varOmega _{\upmu }}, \end{aligned}$$

(37)

where v is $\varOmega _{\upmu }$-periodic admissible displacement field and $\varepsilon ^{0(kl)}_{pq}$ corresponds to the three (2D) or six (3D) linearly independent unit test strain fields.

The energy-based approach imposes the unit test strains directly on the boundaries of the RVE, inducing $\varepsilon ^{A(kl)}_{pq}$ which corresponds to the superimposed strain fields $(\varepsilon ^{0(kl)}_{pq}-\varepsilon ^{*(kl)}_{pq})$ in (36). Detailed implementation of periodic boundary conditions has been given in Sect. 3.2. Equation (36) can be rewritten in an equivalent form in terms of mutual energies

$$\begin{aligned} C^\mathrm{hom}_{ijkl}=\frac{1}{|\varOmega _{\upmu }|} \int _{\varOmega _{\upmu }} C_{pqrs} \varepsilon ^{A(ij)}_{pq} \varepsilon ^{A(kl)}_{rs} \mathrm{d}{\varOmega _{\upmu }}. \end{aligned}$$

(38)

Whilst most works apply the asymptotic approach for the design of material microstructures [see 14], its extension to nonlinear material designs is not straightforward. In contrast, the formulation of the energy-based approach (38) is more compact that facilitates the numerical implementation [100, 117] and its extension to nonlinear material designs is rather straightforward (e.g., [112]). In the following, the energy-based approach is employed.

4.2 Optimization Model

In finite element analysis, the RVE is discretized into $N_{\upmu }$ finite elements and the same number of topology design variables ${\varvec{\eta }}\in \mathbb {R}^{N_{\upmu }}$ are correspondingly defined in similar manner as is in Sect. 2 for structural design. The homogenized elastic stiffness tensor derived from the energy-based approach (38) can be approximately written in the form

$$\begin{aligned} C^\mathrm{hom}_{ijkl}=\frac{1}{|\varOmega _{\upmu }|}\sum ^{N_{\upmu }}_{e=1} (\mathbf{u}^{A(ij)}_{e})^{T}{} \mathbf{k}_{e}(\eta _{e})\mathbf{u}^{A(kl)}_{e} \end{aligned}$$

(39)

where $\mathbf{u}^{A(kl)}_{e}$ are element displacement solutions corresponding to the unit test strain fields ${\varvec{\varepsilon }}^{0(kl)}$. $\mathbf{k}_{e}=\eta _{e}{} \mathbf{k}_{0}$ is the element stiffness matrix and $\eta _{e}$ takes values $\eta _\mathrm{min}$ (a small positive value) and 1 indicating void and solid materials, respectively. $\mathbf{k}_{0}$ is the element matrix of solid material.

The mathematical formulation of the design of material microstructure with extreme properties reads as follows

$$\begin{aligned} \begin{array}{rl} \min\limits_{\varvec{\eta }}: & f_\mathrm{obj}(C^\mathrm{hom}_{ijkl}({\varvec{\eta }}))\\ \text{subject to}: & \mathbf{K}{} \mathbf{u}^{A(kl)}=\mathbf{0}, k,l=1,\dots ,d\\ :& V({\varvec{\eta }})=\sum v_{e}\eta _{e}=V_\mathrm{req}\\ :& \eta _{e}=0\,\text{or}\,1, e=1,\dots ,N_{\upmu } \end{array} \end{aligned}$$

(40)

where K is the global stiffness matrix, $\mathbf{u}^{A(kl)}$ is the displacement solution of the RVE with periodic boundary conditions corresponding to ${\varvec{\varepsilon }}^{0(kl)}$ imposed, d is the spatial dimension, $v_{e}$ is the element volume, $V({\varvec{\rho }})$ and $V_\mathrm{req}$ are the total and required material volumes, respectively.

The objective $f_\mathrm{obj}(C^{H}_{ijkl}({\varvec{\eta }}))$ is a function of the homogenized stiffness tensors. For instance, in the 2D case, the maximization of the material bulk modulus corresponds to the minimization of

$$\begin{aligned} f_\mathrm{obj}=-\left( C^\mathrm{hom}_{1111} + C^\mathrm{hom}_{1122} + C^\mathrm{hom}_{2211} + C^\mathrm{hom}_{2222}\right) \end{aligned}$$

(41)

and the maximization of material shear modulus corresponds to the minimization of

$$\begin{aligned} f_\mathrm{obj}=-C^\mathrm{hom}_{1212}. \end{aligned}$$

(42)

The sensitivity of the objective function ${\partial f_{obj}}/{\partial \eta _{e}}$ can be computed using [100]

$$\begin{aligned} \frac{\partial C^\mathrm{hom}_{ijkl}}{\partial \eta _{e}}=\frac{1}{|\varOmega _{\upmu }|}(\mathbf{u}^{A(ij)}_{e})^{T}{} \mathbf{k}_{0}{} \mathbf{u}^{A(kl)}_{e}, \end{aligned}$$

(43)

in accordance with the applied objective definition.

4.3 Numerical Example

Material microstructure designs are carried out using the same BESO updating scheme (Sect. 2.3). The square cellular material under consideration is discretized into $80\times 80$ square shaped bilinear elements ($1\times 1$ mm$^2$) and the same number of topology variables are correspondingly defined. Young’s modulus and Poisson’s ratio of solid material are set to 1 MPa and 0.3, respectively. The constraint of volume ratio of solid material is 60 %. The evolution rate is set to $c_\mathrm{er}=2\%$. In order to obtain the so-called one-length scale microstructure [8], i.e., avoid too detailed microstructures inside the cell, a larger filter radius should be used in comparison to conventional structural designs. Here, two radii $r_\mathrm{min} = 12$ mm and $r_\mathrm{min} = 8$ mm are considered for the purpose of comparison.

In structural compliance minimization designs, a full solid structure is usually chosen as the initial topology guess [60]. However, this cannot be employed for material designs because the applied periodic boundary conditions would result in a uniformly distributed sensitivity field, thus making the variable updating impossible. The influence of an initial guess on the final designs has been thoroughly discussed in (e.g., [45, 101, 104]). In the example, we simply follow [62] assigning four soft elements at the center to trigger topological changes. Microstructures with maximized bulk moduli and shear moduli are shown in Figs. 13 and 14, respectively. It can be observed that lower-valued filter radii result in more detailed microstructural features.

Fig. 13

Microstructures with maximized bulk moduli obtained using filter radii 12 mm (left, bulk modulus 0.2411 MPa) and 8 mm (right, bulk modulus 0.2404 MPa)

Fig. 14

Microstructures with maximized shear moduli obtained using filter radii 12 mm (left, shear modulus 0.1688 MPa) and 8 mm (right, shear modulus 0.1746 MPa)

5 Concurrent Material and Structure Design

This section reviews firstly the conventional decomposition strategy for concurrent material and structure design. Two concurrent material and structure design approaches, namely iterative design approach and FE²-based design approach, are then summarized and their performances are compared.

5.1 Problem Statement

Generalized mathematical formulations for concurrent cellular material and structure designs can be found in [109] and its application for continuous models has been given by [95]. Let x and y denote positions of a point at macroscopic and microscopic scales, respectively. The structural compliance minimization problem is stated in terms of two levels of design variables: the pointwise topology design variable $\rho (x)$ at the macroscale (structure) and the pointwise topology design variable $\eta (x,y)$ at the microscale (material).

Recall [8], using the principle of minimum potential energy, the minimum compliance problem in a displacement-based formulation is:

$$\begin{aligned} \begin{aligned}&\max _{(\rho ,\eta )\in \mathcal {A}_\mathrm{ad}}\ \min _{u\in {\mathcal {U}}}\\&\left\{ \frac{1}{2}\int _{\varOmega }C_{ijkh}\left( x,\rho (x), \eta (x,y) \right) \frac{\partial u_{i}}{\partial x_{j}}\frac{\partial u_{k}}{\partial x_{h}}\mathrm {d}{\varOmega }-l(u)\right\} . \end{aligned} \end{aligned}$$

(44)

Here $C_{ijkh}\left( x,\rho , \eta \right)$ is the fourth-order elastic stiffness tensor at material point x depending on both values of $\rho (x)$ and $\eta (x,y)$ at the two sales. U denotes the space of kinematically admissible displacement fields and l(u) is the loading potential term. Note that though Eq. (48) is defined under a linear assumption, $C_{ijkh}$ may depend in a nonlinear way on the design variables. $\mathcal {A}_\mathrm{ad}$ is the assembled admissible set of design variables consists of two defined admissible sets $\mathcal {A}_{\rho }$ and $\mathcal {A}_{\eta }$ for $\rho (x)$ and $\eta (x,y)$, respectively,

$$\begin{aligned} \mathcal {A}_\mathrm{ad}=\left\{ \rho ,\eta \ |\ \rho (x)\in \mathcal {A}_{\rho }, \eta (x,y)\in \mathcal {A}_{\eta }\right\} . \end{aligned}$$

(45)

In the case of discrete topology design models (e.g., BESO, [64, 114, 116, 128]), $A_{\rho }$ and $A_{\eta }$ are simply defined as:

$$\begin{aligned} \mathcal {A}_{\rho }=\left\{ \rho \ |\ \rho =0\,\text{or}\,1, \int _{\varOmega }\rho (x)\mathrm {d}{\varOmega }= V_\mathrm{req}^\mathrm{s}\right\} , \end{aligned}$$

(46)

and

$$\begin{aligned} \mathcal {A}_{\eta }=\left\{ \eta \ |\ \eta =0\,\text{or}\,1, \int _{\varOmega _{x}}\eta (x,y)\mathrm {d}{\varOmega ^{x}}= V_\mathrm{req}^{x}\right\} , \end{aligned}$$

(47)

where $V_\mathrm{req}^\mathrm{s}$ and $V_\mathrm{req}^{x}$ are the allowed material volume at the macro and micro scales, respectively. Note that, $V_\mathrm{req}^{x}$ can vary from point to point.

In the case of continuous topology optimization models (e.g., SIMP, [86, 95, 138]), the elastic stiffens tensor and $V_\mathrm{req}^{x}$ for macroacale point x are functions of $\rho (x)$. In the current context, the discrete-valued $\rho (x)$ indicates only the existence of an additional fine scale ($\rho (x)=1$) or not ($\rho (x)=0$). We can therefore extract $\rho (x)$ outside $C_{ijkh}$ and the remaining is the homogenized elastic stiffness tensor $C^{\hom }_{ijkh}$ depending on $\eta (x,y)$, i.e.

$$\begin{aligned} \begin{aligned}&\max _{(\rho ,\eta )\in \mathcal {A}_\mathrm{ad}}\ \min _{u\in {\mathcal {U}}}\\&\left\{ \frac{1}{2}\int _{\varOmega }\rho (x) ~ C^{\hom }_{ijkh}\left( x,\eta (x,y) \right) \frac{\partial u_{i}}{\partial x_{j}}\frac{\partial u_{k}}{\partial x_{h}}\mathrm {d}{\varOmega }-l(u)\right\} . \end{aligned} \end{aligned}$$

(48)

5.2 Problem Decomposition

The separation of the two scale variables and the interchange of the equilibrium and local optimizations of (48) result in a reformulated displacement-based problem

$$\begin{aligned} \max _{\rho \in \mathcal {A}_{\rho }}\ \min _{u\in {\mathcal {U}}}\left\{ \int _{\varOmega }\bar{w}\left( x,u,\eta (x,y)\right) \mathrm {d}{\varOmega }-l(u)\right\} , \end{aligned}$$

(49)

where the pointwise maximization of the strain energy density $\bar{w}$

$$\begin{aligned} \bar{w} = \max _{\eta \in \mathcal {A}_{\eta }}\ \frac{1}{2}~\rho (x) C^\mathrm{hom}_{ijkh}\left( x, \eta (x,y)\right) \frac{\partial u_{i}}{\partial x_{j}}\frac{\partial u_{k}}{\partial x_{h}} \end{aligned}$$

(50)

is treated as a subproblem for the prescribed $\rho (x)$ and u(x) at macroscale point x. From the reformulated form of (49), a hierarchical iterative solution strategy is straightforwardly established for the concurrent material and structure design.

The outer maximization problem of (49) is the “master” problem dealing with the macroscale material distribution in terms of $\rho (x)$ for the macroscale structure. The inner maximization problems of (49), i.e., (50), are the “slave” problems corresponding to the stiffness maximizations of the microscale materials in terms of $\eta (x,y)$ for the evaluated macroscale strain $\bar{\varepsilon }(x)$.

The middle layer minimization problem of (49) seeks kinematically admissible equilibrium displacements for the locally optimum energy function, for the given distribution of the macroscale topology of $\rho (x)$. Note that, since the locally optimum energies depend on the displacement field in a complex fashion via the optimization problems of (50), the equilibrium statement of (49) is in fact a constitutively nonlinear elastic problem.

5.3 Discretized Models

Within the context of finite element analysis, both topology design variables

$$\begin{aligned} {\varvec{\rho }}=(\rho _1,\dots ,\rho _ {N_\mathrm{s}})^{T}, \end{aligned}$$

(51)

and

$$\begin{aligned} {\varvec{\eta }}^{x}=(\eta ^{x}_1,\dots ,\eta ^{x}_{N_{x}})^{T}, \end{aligned}$$

(52)

written in vector form, are defined in an element-wise manner at both scales. ${N_\mathrm{s}}$ and ${N_{x}}$ are the numbers of discrete elements at the macro- and microscales, respectively. Here, the superscript x of ${\varvec{\eta }}^{x}$ denotes a vector of microscale topology variables at each macroscale point x.

Following the decomposition strategy presented in Sect. 5.2, the “master” problem of (49) is equivalent to the minimization of the macroscale end-compliance $\bar{f}_\mathrm{c}$, subjected to a material volume fraction constraint

$$\begin{aligned} \begin{array}{rl} \min _{{\varvec{\rho }},{\varvec{\eta }^{x}}}: & \bar{f}_\mathrm{c}({\varvec{\rho }}, \bar{\mathbf{u}})\\ \text{subject to}: & \bar{\mathbf{K}}({\varvec{\rho }},{\varvec{\eta }}^{x})\bar{\mathbf{u}}=\bar{\mathbf{f}}_\mathrm{ext}\\ :& V_{\rho }=\sum \rho _{i}v_{i}=V^\mathrm{s}_\mathrm{req}\\ :& \rho _{i}=0~\,\text{or}\,~1,~i = 1, \dots , N_\mathrm{s}.\\ \end{array} \end{aligned}$$

(53)

The macroscale stiffness matrix $\bar{\mathbf{K}}({\varvec{\rho }},{\varvec{\eta }}^{x})$ is governed by both scale variables:

$$\begin{aligned} \bar{\mathbf{K}}({\varvec{\rho }},{\varvec{\eta }}^{x})=\sum _{i=1}^{N_\mathrm{s}}\rho _{i}\int _{\varOmega _{i}}\bar{\mathbf{B}}^{T}\bar{\mathbf{C}}^\mathrm{hom}({\varvec{\eta }}^{x})\bar{\mathbf{B}}\mathrm{d}\varOmega _{i}, \end{aligned}$$

(54)

in which the homogenized stiffness matrix $\bar{\mathbf{C}}^\mathrm{hom}$ at macroscale point ${\varvec{x}}$, depending on the microscale material topology ${\varvec{\eta }}^{x}$, is computed via (39). The sensitivity of $\bar{f}_\mathrm{c}$ with respect to $\rho _{i}$ associated with the i-th macroscale element is

$$\begin{aligned} \frac{\partial \bar{f}_\mathrm{c}}{\partial \rho _{i}}=-\bar{\mathbf{u}}_{i}^{T}\int _{\varOmega _{i}}\bar{\mathbf{B}}^{T}\bar{\mathbf{C}}^\mathrm{hom}({\varvec{\eta }}^{x})\bar{\mathbf{B}}\mathrm{d}\varOmega _{i}\bar{\mathbf{u}}_{i}. \end{aligned}$$

(55)

The “slave” problems of Eq. (49), the microscale material stiffness maximizations subjected to microscale material volume fraction constraints, are defined at the macroscale points where $\rho ({\varvec{x}})=1$ in the following form

$$\begin{aligned} \begin{array}{rl} \max _{{\varvec{\eta }}^{x}}: &\bar{w}({\varvec{\eta }}^{x})\\ \text{subject to}: & \mathbf{K}^{x}({\varvec{\eta }}^{x})\mathbf{u}^{x}=\mathbf{0}\\ :& \langle {\varvec{\varepsilon }}(\mathbf{u}^{x})\rangle =\bar{\varvec{\varepsilon }}({\varvec{x}}) \\ :& V_{\eta }=\sum \eta _{j}v^{x}_{j}=V^{x}_\mathrm{req}\\ :& \eta _{j}=0\,\text{or}\,1,~j = 1, \dots , N_{x}.\\ \end{array} \end{aligned}$$

(56)

Note that, there exists no external force at the microscopic scale. The microscale systems are constrained by means of the imposed periodic boundary conditions, satisfying the equality between $\langle {\varvec{\varepsilon }}(\mathbf{u}^{x})\rangle$ and $\bar{\varvec{\varepsilon }}({\varvec{x}})$. The sensitivity of $\bar{w}({\varvec{\eta }}^{x})$ with respect to the $\eta ^{x}_{j}$ associated with the j-th microscale element is

$$\begin{aligned} \frac{\partial \bar{w}({\varvec{\eta }}^{x})}{\partial \eta ^{x}_{j}}=\frac{1}{2}~(\mathbf{u}^{x}_{j})^{T}{} \mathbf{k}^{x}_{0}\mathbf{u}^{x}_{j}, \end{aligned}$$

(57)

where $\mathbf{k}^{x}_{0}$ is the stiffness matrix of the element with full solid material when $\eta ^{x}_{j}=1$.

5.4 Concurrent Design Approaches

5.4.1 Iterative Design Approach

Following the decomposition strategy reviewed above, the straightforwardly developed concurrent design approach is summarized in Algorithm 1. The macroscale topology is updated iteratively until the chosen criterion convergence is achieved. For each macroscale design iteration, the microscale material stiffness maximizations are carried out and the homogenized elastic matrices of the currently optimized microscale topologies are evaluated to serve the next macroscale design iteration. This concurrent design algorithm has been mostly applied for continuous topology optimization designs (e.g., [22, 95, 138]), because the intermediate value of the macroscale variable can be imposed naturally to the microscale models as the upper bounds of volume fraction constraints and for the same reason the global convergence is guaranteed.

5.4.2 Simplified Design Approach

In the contrary, the concurrent design approach summarized in Algorithm 1 is not applicable when using discrete design schemes such as ESO-type methods [60]. Because of the discrete nature, the microscale volume fraction upper bounds are not linked to their corresponding macroscale variables. The discrete-valued $\rho (x)$ indicates only the existence of an additional fine scale when $\rho (x)=1$). The microscale volume fraction upper bounds are user-prescribed values within this context. Direct implementation of Algorithm 1 with discrete variables would result in the divergence of the design process [114]. In practical implementations (e.g., [64, 124, 125, 128]), a simplified version of Algorithm 1, as summarized in Algorithm 2, is adopted. Algorithm 2 in fact avoids solving the “slave” material stiffness maximization problems (56) while treating both scale variables ${\varvec{\rho }}$ and ${\varvec{\eta }}^{x}$ in an integral manner. The updating of the microscale variables uses directly the sensitivity of macroscale end-compliance $\bar{f}_\mathrm{c}$ with respect to the microscale variables ${\varvec{\eta }}^{x}$, i.e.,

$$\begin{aligned} \frac{\partial \bar{f}_\mathrm{c}}{\partial \eta ^{x}_{j}}=-\bar{\varvec{\varepsilon }}^{T}({\varvec{x}})\frac{\partial \bar{\mathbf{C}}^\mathrm{hom}({\varvec{\eta }}^{x})}{\partial \eta ^{x}_{j}} \bar{\varvec{\varepsilon }}({\varvec{x}}), \end{aligned}$$

(58)

where the evaluation of the derivative of $\mathbf{C}^\mathrm{hom}$ with respect to $\eta ^{x}_{j}$ follows (43). Algorithm 2 has been so far applied to the concurrent design cases when a universal microscale material is assumed and optimized concurrently with the macroscale topology. However, when it comes to multiple or pointwise microscale materials, Algorithm 2 is not applicable and results in the divergence of the design process according to our experiments. This is because the updating of the microsacle topologies are terminated once the associated macroscale elements are deleted while there is no guarantee that the deleted elements would not be recovered in the following iterations. When a universal microscale material ${\varvec{\eta }}^{\upmu }$ is assumed, the updating of the microscale variables uses the following sensitivity

$$\begin{aligned} \frac{\partial \bar{f}_\mathrm{c}}{\partial \eta ^{\upmu }_{j}}=-\sum _{i=1}^{N_\mathrm{s}} \bar{\mathbf{u}}_{i}^{T}\int _{\varOmega _{i}} \bar{\mathbf{B}}^{T}\frac{\partial \bar{\mathbf{C}}^\mathrm{hom}({\varvec{\eta }}^{\upmu })}{\partial \eta ^{\upmu }_{j}} \bar{\mathbf{B}}\mathrm{d}\varOmega _{i} \bar{\mathbf{u}}_{i}. \end{aligned}$$

(59)

5.4.3 FE²-Based Design Approach

Note that, both Algorithms 1 and 2 have neglected the interface nonlinearity of the nonlinear equilibrium statement of (49) due to local material optimizations. Unlike the iterative design approach, the scale-interface nonlinearity has been particularly addressed in our recent works [114, 116] by a FE²-based design approach, treating the microscale material optimization process integrally as a generalized nonlinear elastic behavior. In this context, the nonlinearity comes from the microscale optimizations. The microscale model is optimized upon the macroscale strain value at associated integration point. Then the effective stress is evaluated on the optimized microscale topology and returned to the upper scale. With the effective stress-strain relationship, scale-interface nonlinear equilibrium is then searched by means of Newton–Raphson method. The macroscale topology is then optimized using the converged solution.

Due to the particularity of the concerned nonlinearity, conventional Newton–Raphson solution scheme using tangent stiffness matrix is not applicable here. As can be observed in Fig. 15, the tangent stiffness matrix for $\mathbf{u}^{(1)}$ is in fact the linear stiffness matrix $\mathbf{K}_\mathrm{opt}(\mathbf{u}^{(1)})$ itself. Using this stiffness matrix results in the divergence of the solution of the scale-interface nonlinear equilibrium. The solution of this type of nonlinearity itself is still an open issue according to the authors’ knowledge. We propose to use an initial stiffness Newton–Raphson solution scheme based on a reasonable hypothesis that the structure constituted by the optimized materials ($\mathbf{K}_\mathrm{opt}(\mathbf{u}_{sol})$), is stiffer than the other structures ($\mathbf{K}_\mathrm{opt}(\mathbf{u}^{(1)}), \dots$) corresponding to the other admissible solutions. In this scheme, the applied initial stiffness matrix $\mathbf{K}_{0}$ is constructed assuming the microscale material is full of solid material. Though not rigorous enough, this solution scheme is capable of dealing with this scale-interface nonlinearity with satisfactory according to [114, 116].

Fig. 15

Initial stiffness Newton–Raphson solution scheme [114]

The FE²-based design approach is summarized in Algorithm 3. Since the microscale optimizations are treated as a generalized nonlinear material behavior, this algorithm does not suffer the divergence issue when using discrete variables as is the case of Algorithm 2. Unlike Algorithms 1 and 2, the FE²-based design algorithm uses only the effective stress-strain relationship while the homogenized elastic matrices are not required, which saves significant computing cost. Moreover, the extension of the FE²-based design algorithm is more straightforward to the cases when other geometrical or physical nonlinearities are present at the microscopic scale.

5.5 Numerical Examples

In this section, a two-scale half-MBB beam as shown in Fig. 16a is considered with the external force $\bar{\mathbf{f}}_\mathrm{ext} = 1 N$. The macroscale structure is discretized into $L\times H$ square shaped bilinear elements and each element is of dimensions $1\times 1$ mm$^2$. The assumed microscale material model is discretized into $40\times 40$ square shaped bilinear elements without specific unit due to the assumption of scale separation. Both scale topology design variables are defined in element-wise manner. At the microscopic scale, Young’s modulus and Poisson’s ratio of the solid material are set to 1 and 0.3, respectively. In the case of iterative design approach, the homogenized stiffness tensor of the microscale material serves as the constitutive law for the macroscale computation. In the case of FE²-based design approach, the macroscale constitutive behavior is governed by the effective stress-strain relations.

Fig. 16

A two-scale half-MBB beam and the optimized microstructures for different macroscale structure dimensions. (a). A two-scale half-MBB beam. (b). $L=8, H=16$. (c). $L=24, H=16$. (d). $L=40, H=16$. (e). $L=56, H=16$

The volume fraction of solid for the microscale material model is set to 60 %, i.e., a micro-porosity of 40 % is assumed. The required material volume fraction for macroscale design is also set to 60 %. The sensitivity filter radii $r_\mathrm{min}$ are set to 3$l_e$ and 6$l_e$ for macro- and microscale designs, respectively. Here, $l_e$ is the length of the element. Similar to the previous Sect. 4, due to the applied periodic boundary conditions, four soft elements at the center are assigned for the microscale model to trigger topological changes.

The iterative design approach (Algorithm 1) is not applicable here for reasons of the discrete nature of the BESO method. Please refer to [22, 95, 138] for the performance of this design approach on continuously defined models. In the following, tests on the performances of the simplified iterative design approach (Algorithm 2) and the FE²-based design approach (Algorithm 3) are given in Sects. 5.5.1 and 5.5.2, respectively.

5.5.1 Simplified Concurrent Design Approach

For simplicity, we assume firstly one universal material microstructure of topology ${\varvec{\eta }}^{\upmu }$ at the microscopic scale for the considered beam structure. By fixing the macroscale topology unchanged (${\varvec{\rho }}=\mathbf{1}$), Algorithm 2 recovers the design of an optimal material microstructure that maximizes the macroscopic structural stiffness [64]. Figure 16b–e gives the optimized material topologies for different dimensions of the beam structure. The topological transition from Fig. 16b–e due to the increase of the beam length can be clearly observed. The increased beam length requires more bending resistance and results a shift of material distribution along vertical direction to horizontal direction.

In the following the dimensions of beam is fixed to $40\times 16$ mm$^2$, both scale topologies ${\varvec{\rho }}$ and ${\varvec{\eta }}^{\upmu }$ are optimized following Algorithm 2. By our tests, when the evolution rate is set to $c_\mathrm{er}=2\,\%$, the optimization process diverges. As discussed, this algorithm updates both scale topologies iteratively and neglects the scale-interface equilibrium, resulting in mismatch between the two scales. For this reason, a smaller the evolution rate $c_\mathrm{er}=1\,\%$ is applied for both scales for stabilization consideration. The evolution of both scale topologies is captured in Fig. 17. By this approach, homogenization analysis needs to be carried out for the current optimized material topology. The homogenized stiffness tensor is then used for the macroscale assessment. Both scale topologies are updated iteratively and adaptively until the required material volume fractions are achieved.

Fig. 17

Design of the two-scale half-MBB beam using the concurrent design approach. a Iteration 9, $V_{\rho }=0.922, V_{\eta }=0.924, f_\mathrm{c} = 95.99 \text{J}$. b Iteration 24, $V_{\rho }=0.792, V_{\eta }=0.795, f_\mathrm{c} = 144.29 \text{J}$. c Iteration 56, $V_{\rho }=0.600, V_{\eta }=0.600, f_\mathrm{c} = 297.67 \text{J}$

Figure 18a gives the optimized topology for linear elasticity using the same BESO parameters setting. There is an obvious difference between the two topologies of Fig. 18a, b. According to [7], the effective Young’s modulus and Poisson’s ratio for the isotropic porous material with 40 % porosity obtained by inverse homogenization corresponding to the Hashin–Shtrikman (HS) upper bound equal to 0.34 MPa and 0.3, respectively. Assuming the linear design result (Fig. 18a) for this microstructure with 40 % porosity, its compliance value is 322.37 J. With the same amount of material usage at both scales, the iterative design approach results in a more rigid design with a concurrently optimized material microstructure as shown Fig. 17c with a compliance value 297.64 J.

Fig. 18

Comparison on the performances of two topology solutions. a Monoscale design result using isotropic material with 40 % porosity (HS upper bound), $f_\mathrm{c} = 322.37$ J. b Iterative design result, $f_\mathrm{c} = 297.67$ J with the material of Fig. 17c, $f_\mathrm{c} = 308.91$ J with the material of Fig. 16d

To validate the necessity of performing concurrent design, an additional comparison is given assuming Fig. 18b with the material microstructure of Fig. 17c, a microcrostructure with the same porosity 40 % but optimized for the full solid half-MBB beam. As expected, the result compliance value is 308.91 J, though still better than the compliance of the case Fig. 18a, is worse than the compliance of the case Fig. 17c.

As discussed in Sect. 5.4.2, the simplified iterative design approach (Algorithm 2) is not applicable when multiple or pointwise materials are assumed at the microscopic scale. Here, we show only the optimal material topologies for the full solid half-MBB beam structure in Fig. 19a. Microscale material models are defined in pointwise manner at Gauss integration points. The beam structure is discretized by $40\times 16$ elements and 4 Gauss points for each element, that means in total there are $40\times 16\times 4 = 2560$ microscale material models defined. Since the macroscale topology is not optimized, the evolution rate is set to $c_\mathrm{er}=2\,\%$ for all microscale models. It takes in total 35 design iterations and 12 h computing time. It requires solving the microscale problem for 3 times in the 2D case for the evaluation of the elastic stiffness tensor $\bar{\mathbb {C}}^\mathrm{hom}$, and this evaluation needs to be carried out for all 2560 microscale models for all 35 design iterations. In addition, the macroscale global stiffness matrix needs to be assembled for each design iteration so as to serve macroscale structural assessment. Note that, in Fig. 19a the optimized material topologies are enlarged for the purpose of illustration. By the separation of scales assumption, the optimized materials only represent the optimal solution at the microscopic scale for the associated integration points. Therefore, they are not necessarily continuous and represent only the tendency of the topological variations.

Fig. 19

Comparison on the microscale topology results by two different design approaches. a Simplified iterative design approach, $f_\mathrm{c} = 150.86$ J. b FE²-based design approach, $f_\mathrm{c} = 137.59$ J [114]

5.5.2 FE²-Based Design Approach

The same twoscale half-MBB beam structure has been investigated by FE²-based design approach in our recent work [114]. The nonlinear scale-interface equilibrium is particularly addressed by FE² method with the proposed initial stiffness Newton–Raphson solution scheme (Fig. 15). Unlike the iterative design approach with the microscale topologies updated iteratively along the design iteration, the microscale 2560 micro-optimizations are solved completely for each NR iteration of each design iteration. With the adopted convergence criterion on relative displacement variation, it takes in average 6 NR iterations to reach the equilibrium.

The same design problem of Fig. 19a is resolved by FE²-based design approach and the design result is shown in Fig. 19b. By the proposed initial stiffness Newton–Raphson solution scheme (Fig. 15), it takes 6 NR iterations to reach the equilibrium. The two topology results shown in Fig. 19a, b have quasi-identical topology layout. When the result of Fig. 19a is taken as a reference design, then the similarity between Fig. 19a, b validates the feasibility of proposed initial stiffness Newton–Raphson solution scheme.

Note that though 2560 complete micro-optimizations have been solved at each of the 6 NR iterations, the total computing time to obtain the result of Fig. 19b is 1.5 h, which is much less than the 12 h required by the simplified iterative design approach to obtain Fig. 19a. This is because FE²-based design approach uses the stress and strain relations instead of the stiffness tensors, which saves significantly the computing effort in regard to homogenization analyzes. Moreover, by the proposed initial stiffness Newton–Raphson scheme, $\mathbf{K}_{0}$ is assembled once and no additional assemblage of global stiffness matrix is required. One more interesting observation is that the result end-compliance of Fig. 19b is lower than that of Fig. 19a. Though rigorous reasons for this observation is not yet clear to our acknowledge, the low end-compliance value of Fig. 19b indicates potentially another advantage of FE²-based design approach against the iterative design approach.

Once the equilibrium is achieved, the macroscale topology is then optimized based on the converged solution response. The converged macroscale topology design result together with several typical microscale material topologies are shown in Fig. 20. Uniaxial materials may be sufficient at the main branches of the structure, while in order to have a higher structural performance, anisotropic materials have to be used at the joints of the main branches due to the more complex loading status. Concurrent topology optimization of the structure and of pointwisely defined materials would result in an end-compliance value almost 40 % lower (40 % stiffer in terms of structural stiffness) than those of Fig. 19a, b.

Fig. 20

Concurrent material and structure topology design result by FE²-based design approach, $f_\mathrm{c} = 190.16$ J [114]

6 Model Reduction

As has been discussed in the Introduction, the implementation of FE²-type solution schemes results in an extremely high computational burden in terms of both computing time and storage requirements. For instance, the realization of the test example of Fig. 12c requires approximately two weeks’ computing time because the time-comsuming multiscale nonlinear structure analysis need to be carried out for each of all design iterations.

One straightforward solution to alleviate the computational requirements is parallel computing (e.g., [85]), because the microscale problems are independent, embarrassingly parallel. Note that, the implementation of parallel computing contributes significantly in terms of limiting the computing time, but not necessarily reduces the computing cost. In the contrary, parallelization eventually results in higher computing cost due to additional interchanges between the two scales. For this reason, one needs to turn to alternative strategies by means of model reduction or simplification.

Reduced-Order Model (ROM) has been systematically researched and widely used in the fields of computational mechanics in order to reduce computing cost, data storage requirements as well as computing time (e.g., [33, 93]). Some other applications can also be found for the representation of material mircrostructure (e.g., [39, 118]) and structural optimization design (e.g., [94, 121]). In terms of reducing the computing effort for the evaluation of nonlinear RVEs at the microscopic scale, numerous ROMs can be found in literature for the representation or approximation of the effective constitutive behavior of nonlinear heterogeneous materials, using reduction strategies such as Proper Orthogonal Decomposition (POD, e.g., [135]), Proper Generalized Decomposition (PGD, e.g., [24, 29, 71]), hyper-reduction (e.g., [56, 84]), material map model (e.g., [108]), eigendeformation-based reduction (e.g., [91, 132]), Nonuniform Transformation Field Analysis (NTFA, e.g., [79, 80]), and Numerical EXplicit Potentials (NEXP, [136]). Note that, by simultaneous use of parallel computing and ROM (e.g., [36]), a further reduction in computational time can be achieved in multiscale analysis (e.g., [37]).

In the case of elasticity, the database-type methods such as material map model [107, 108] and NEXP [136] have shown promising performances in terms of both modeling accuracy and computing efficiency. The general idea of this type of methods is to compute off-line a certain number of RVE problems as a database, then the effective RVE behavior is approximated using the precomputed database by means of interpolation schemes. The on-line macroscale computation uses then directly the cheaper approximated constitutive behavior of the RVE without demanding solving full-scale RVE problems. By this reduction strategy, one in fact decomposes the two-scale modeling into the off-line RVE approximation construction phase and the on-line macroscale evaluation phase. This type of methods applies for viscoelastic materials (e.g., [110]) and nonlinear hyperelastic materials (e.g., [107, 108, 137]) and has also been extended for stochastic nonlinear elastic materials (e.g., [20, 21]). Recently the NEXP approximation has also been constructed using Neural Networks [72].

The development ROMs for the representation of RVE involving path-dependent constitutive laws, such as plasticity, is still a challenging subject under development. Here, we simply refer to methods of NTFA (e.g., [34, 35, 79, 80]) and adaptive POD approach for instance as implemented in [84] and [56].

Generally speaking, all these established ROMs apply straightforwardly to topology optimization of multiscale nonlinear structures as long as the macroscale equilibrium solution is provided. In [136], it has already been shown that the NEXP method can accurately approximate the nonlinear effective nonlinear behavior of the same short-fiber reinforced composite considered in Sect. 3.4. The implementation of the NEXP method to the design framework is therefore rather straightforward. The NEXP method has also been extended recently by the authors in [116] to represent the generalized nonlinear elastic behavior of microscale material optimizations with satisfactory performance. Figure 21 shows a twoscale topology design result for a finer discretized half-MBB beam problem with the use of an NEXP approximate constitutive behavior.

Fig. 21

Twoscale topology design result with the use of NEXP approximation [116]

Most of the existing ROMs require a set of a priori sampling experiments so as to build reduced bases or approximations. The choice of the experiment space and the sampling scheme are usually of great importance on the accuracy of the ROM. These difficulties can be alleviated when dealing with iterative structural optimization designs. The design domain can be easily localized using the solutions of the initial optimization design iterations. In addition, the involved reduced bases or the database can be adaptively updated or enriched, respectively in the following optimization design iterations. As we have presented in [115], a first attempt towards topology optimization of multiscale nonlinear structures, the bi-level reduced ROM [31, 32] for the considered nonlinear RVE is initially built using all microscale solutions at the first design iteration, then applied and adapted in the following design iterations.

7 Conclusions and Perspectives

This paper has reviewed recent advances on topology optimization of multiscale nonlinear structures. Key ingredients of two main sub-topics, namely design of multiscale structures and concurrent design of material and structure, are reviewed and their performances have been illustrated by numerical examples and comparisons.

As can be told from the present review, the realization of such type of designs is not challenging from technical perspective of view. The main difficultly lies on the unbearable computational burden and data storage requirement due to multiple realizations of FE² computing, for which reason we have discussed the existing and potential applications of model reduction techniques for multiscale structure designs.

To the best knowledge of the authors, this is a relatively new field that there has been very limited research, especially for the design of multiscale nonlinear structures. Many potential developments can be carried out with respect to the models for either optimization, multscale modeling, or model reduction.