On the strong convergence of the proximal point algorithm with an application to Hammerstein euations

Abstract

Let E be a real normed space. A new notion of quasi-boundedness for operators $A:E\rightarrow 2^E$ is introduced and the following general important result for accretive operators is proved: an accretive operator with zero in the interior of its domain is quasi-bounded. Using this result, a new strong convergence theorem for approximating a zero of an m-accretive operator is proved in a uniformly smooth real Banach space. This result complements the celebrated proximal point algorithm for approximating solutions of $0\in Au$ in a real Hilbert space where A is a maximal monotone operator. Furthermore, as an application of our theorem, a new strong convergence theorem for approximating a solution of a Hammerstein equation is proved. Finally, several numerical experiments are presented to illustrate the strong convergence of the sequence generated by our algorithm and the results obtained are compared with those obtained using some recent important algorithms.

1 Introduction

Let H be a real Hilbert space and $A:H\rightarrow 2^H$ be an operator (possibly nonlinear). A fundamental problem in nonlinear operator theory is that of finding an element

$$\begin{aligned} u\in H\qquad \text {such that} \qquad 0\in Au, \end{aligned}$$

(1.1)

where A is monotone, i.e., A satisfies the following inequality: $\langle x-y, \eta -\zeta \rangle \ge 0, ~~\forall ~~\eta \in Ax,~\zeta \in Ay.$ For example, if A is the subdifferential, $\partial f : H \rightarrow 2^H$ of a proper, lower semi-continuous and convex function $f:H\rightarrow (-\infty , \infty ]$, defined by $\partial f(x):=\big \{u\in H : ~f(y)-f(x)\ge \langle u,y-x\rangle ,~\forall y\in H\big \}$, then, $\partial f$ is a monotone operator and it is easy to see that a solution of the inclusion $0\in Au$corresponds to a minimizer of f. Furthermore, for an example where solutions of $0\in Au$, A monotone, represent solutions of variational inequality problems, the reader may see, for example, Rockafellar [54]; and for problems where solutions of $0\in Au$, A monotone, represent equilibrium state of a dynamical system, the reader may see Browder, [3].

Existence theorems have been proved for problem (1.1) (see, e.g., Browder [3], Martin [42]). Also, iterative algorithms for approximating solutions of the inclusion (1.1) have been studied extensively by numerous authors (see e.g., Bruck and Reich [8], Chidume and Chidume [14], Chidume [12, 13], Browder [3], Martin [42], Chidume et al. [15] and the references contained in them). One of the classical methods for approximating solution(s) of inclusion (1.1) is the celebrated proximal point algorithm (PPA) introduced by Martinet [41] and studied extensively by Rockafellar [54] and a host of other authors (see, e.g., Bruck and Reich [8] and Reich [45]).

Let E be a real normed space with dual space $E^*$, and let $J_q~(q>1)$ denote the generalized duality mapping from E to $2^{E^*}$. A set-valued mapping $A:E \rightarrow 2^E$ is said to be accretive if, $\forall x,y\in E$, there exists $j_q(x-y)\in J_q(x-y)$ such that

$$\begin{aligned} \langle \eta -\zeta , j_q(x-y)\rangle \ge 0, ~~\eta \in Ax,~\zeta \in Ay. \end{aligned}$$

(1.2)

The mapping A is called m-accretive if it is accretive and $R(I+\lambda A)$ (the range of range of $(I+\lambda A)$) is E, for all $\lambda >0$. In Hilbert spaces, accretive mappings are called monotone and m-accretive mappings are maximal monotone.

Let H be a real Hilbert space. If A is monotone, a classical result of Minty [43] states that for each $u \in H$ and $\lambda >0,$ there exists a unique $v\in H$ such that $(u-v)\in \lambda Av$, i.e., $u\in (I+\lambda A)v$. The mapping $J_{\lambda }:=(I+\lambda A)^{-1}$ is single-valued from H to H and nonexpansive. Furthermore, one has $J_{\lambda }(u)=u$ if and only if $0\in Au$ (for more on this see Sect. 7 of Reich [50]).

The proximal point algorithm for a maximal monotone operator (i.e., a monotone operator whose graph is not contained in the graph of any other monotone operator) is an iterative procedure that starts at a point $u_1\in H$, and generates inductively a sequence $\{u_n\}$ in H by $u_{n+1}=\Big ( I+\frac{1}{\alpha _n} A\Big )^{-1}u_n,$ where $\{\alpha _n\}$ is a sequence of positive numbers. Martinet [41] proved that the sequence $\{u_n\}$ converges weakly to a point $u^*\in H$ such that $0\in Au^*$. The question of whether the weak convergence established by Martinet can be improved to strong convergence remained open for many years. The answer is known to be affirmative if $A:=\partial f$ with f quadratic (see, e.g., Krasnoselskii [36], also Kryanev [37, 38]). Strong convergence of the PPA is also assured if $\alpha _n$ is bounded away from zero and A is strongly monotone i.e., there exists $k>0$ such that $\langle x-y, \eta -\zeta \rangle \ge k\Vert x-y\Vert ^2,~~\forall \eta \in Ax,\zeta \in Ay$ (see, e.g., Bruck and Reich [8], Reich [45] and Rockafellar [54]).

In 1976, Rockafellar [54] proved that the PPA converges weakly starting from any point. He then posed the following question: “Does the proximal point algorithm always converge strongly?”.

G$\ddot{u}$ler [34] gave a negative answer to this question. He proved (using a result of Bruck [7]) that in $l_2$, there exists a function f such that given any positive bounded sequence $\{\alpha _n\}$, there exists a starting point $u_1\in D(f)$ (domain of f) and the PPA starting from $u_1$ with $u_{n+1}=J_{\alpha _n}(u_n)$ converges weakly, but not strongly (see also Bauschke et al. [2]).

In [56], Solodov and Svaiter proposed a modification of the proximal point algorithm which guarantees strong convergence in a real Hilbert space. The authors themselves noted ([56], p 195) that “. . . at each iteration, there are two subproblems to be solved. . .” : (i) find an inexact solution of the proximal point algorithm, and (ii) find the projection of $x_0$ onto $C_k \cap Q_k.$ They also acknowledged that these two subproblems constitute a serious drawback in using their algorithm.

Kamimura and Takahashi [35] extended this work of Solodov and Svaiter [56] to the framework of arbitrary real Banach spaces that are both uniformly convex and uniformly smooth, where the operator A is maximal monotone. Reich and Sabach [49] extended this result to reflexive Banach spaces (see also Reem and Reich [53]).

In [39], Lehdili and Moudafi considered the technique of the proximal mapping and Tikhonov regularization to introduce and construct the so-called Prox–Tikhonov method. Using the notion of variational distance, they proved strong convergence theorems for their algorithm and its perturbed version, under appropriate conditions on the parameters of their algorithm.

Xu [57] also studied the recurrence relation Lehdili and Moudafi [39]. He used the technique of nonexpansive mappings to get convergence theorems for the perturbed version of the algorithm of Lehdili and Moudafi [39], under much relaxed conditions on the parameters.

In 2006, Xu [58] introduced and studied the following proximal type algorithm

Theorem 1.1

Let E be a reflexive Banach space that has a weakly continuous duality map $J_{\varphi }$with gauge $\varphi$and let A be an m-accretive operator in X such that $C=D(A)$is convex. Assume

• (i) $\lim _{n\rightarrow \infty } \alpha _n=0$ and $\sum _{n=1}^\infty \alpha _n=\infty$,

• (ii) $\lim _{n\rightarrow \infty } \lambda _n=\infty$.

Given $u,x_1\in C$, let $\{x_n\}$ be the sequence generated by

$$\begin{aligned} x_{n+1}=\alpha _n u +(1-\alpha _n)J_{\lambda _n}x_n,~~n\ge 1. \end{aligned}$$

(1.3)

Then $\{x_n\}$ converges strongly to a zero of A.

Qin and Su [59] extended and generalized the result of Xu [58]. They introduced and studied the following algorithm

Theorem 1.2

Let E be a uniformly smooth Banach space and A be an m-accretive operator in E such that $A^{-1}(0) \ne \emptyset$. Given a point $u\in C$ and given $\{\alpha _n\}$ in (0, 1) and $\{\beta _n\}$ in [0, 1], suppose $\{\alpha _n\}$, $\{\beta _n\}$ and $\{\lambda _n\}$ satisfy the conditions

• (i) $\lim _{n\rightarrow \infty } \alpha _n=0$ and $\sum _{n=1}^\infty \alpha _n=\infty$;

• (ii) $\lambda _n \ge \epsilon$,  $\forall ~n$ and $\beta _n\in [0,a)$, for some $a\in (0,1)$;

• (iii) $\sum _{n=1}^\infty |\alpha _{n+1}-\alpha _n|<\infty ,\quad \sum _{n=1}^\infty |\beta _{n+1}-\beta _n|< \infty$ and $\sum _{n=1}^\infty |\lambda _{n+1}-\lambda _{n}|< \infty$.

Let $\{x_n\}$ be the composite process defined by

$$\begin{aligned} {\left\{ \begin{array}{ll} y_n=\beta _n x_n +(1-\beta _n) J_{\lambda _n}x_n, &{} \\ x_{n+1}= \alpha _n u +(1-\alpha _n)y_n. \end{array}\right. } \end{aligned}$$

(1.4)

Then $\{x_n\}$ converges strongly to a zero of A.

Remark 1

The proximal point algorithm and its modifications listed above require either the computation of $\big ( I+\frac{1}{\alpha _n }A\big )^{-1}(u_n)$ or, the construction of two closed convex non-empty subsets of $E$ and the projection of the initial vector onto the intersection of the two closed convex subsets constructed.

Following this, Chidume posed the following question “ Can an iteration process be developed which will not involve the computation of $\big ( I+\frac{1}{\alpha _n }A\big )^{-1}(u_n)$ or the construction of two closed convex subsets of E and the projection of the initial vector onto the intersection of the two sets at each step of the iteration process, that will still guarantee strong convergence to a solution of $0\in Au$?”

This question was eventually resolved in the affirmative by Chidume and Djitte [26]. However, the following more general theorem has been proved.

Theorem 1.3

(Chidume, [11]). Let E be a uniformly smooth real Banach space with modulus of smoothness $\rho _E$, and let $A : E \rightarrow 2^E$ be a set-valued bounded m-accretive operator with $D (A)=E$ such that the inclusion $0\in Au$ has a solution. For arbitrary $u_1\in E$ define a sequence $\{u_n\}$ by,

$$\begin{aligned} u_{n+1}=u_n-\alpha _n\zeta _n-\alpha _n\beta _n(u_n-u_1), ~~~\zeta _n\in Au_n, ~~n\ge 1, \end{aligned}$$

(1.5)

where $\{\alpha _n\}$ and $\{\beta _n\}$ are e in (0,1) satisfying the following conditions:

• (i) $\lim _{n \rightarrow \infty }\beta _n =0$, $\{\beta _n\}$ is decreasing;

• (ii) $\sum _{n=1}^\infty \alpha _n\beta _n=\infty$,        $\sum _{n=1}^\infty \rho _E(\alpha _nM_1)<\infty$, for some constant $M_1$;

• (iii) $\lim _{n\rightarrow \infty } \frac{\Big (\frac{\beta _{n-1}-\beta _n}{\beta _n}\Big )}{\alpha _n\beta _n}=0$.

Assume that there exists a constant $\gamma _0>0$ such that $\frac{\rho _E(\alpha _n)}{\alpha _n}\le \gamma _0\beta _n$, then the sequence $\{u_n\}$ converges strongly to a zero of A.

Remark 2

Theorem 1.3 is a significant extension of the result of Chidume and Djitte [26] in the sense that Theorem 1.3 extends the theorem of Chidume and Djitte [26] from 2-uniformly smooth real Banach spaces to uniformly smooth real Banach spaces. Observe that Theorem 1.3 is restricted to m-accretive operators that are bounded.

2 Preliminaries

The following lemmas will be needed in the proof of our main theorems.

Lemma 2.1

Let E be a normed real linear space, and $J_q: E \rightarrow 2^{E^*},~~1<q<\infty ,$ be the generalized duality map. Then, the following inequality holds:

$$\begin{aligned}&\Vert x+y\Vert ^q\le \Vert x\Vert ^q+q\langle y,j_q(x+y)\rangle , \nonumber \\&\quad \forall ~ j_q(x+y)\in J_q(x+y),~\forall ~x,y\in E \end{aligned}$$

(2.1)

Lemma 2.2

(Reich, [51, 52]). Let E be a uniformly smooth real Banach space. Then, there exists a nondecreasing function $\rho : [0, \infty ) \rightarrow [0,\infty )$ satisfying the following condition:

$$\begin{aligned} \Vert x+y\Vert ^2 \le \Vert x\Vert ^2 + 2 \langle y , Jx \rangle + \mathrm{max}\{ \Vert x\Vert , 1 \} \Vert y \Vert \rho (\Vert y\Vert ) ,~\forall ~x,y\in E \end{aligned}$$

(see also, Xu and Roach [60] for another inequality).

Lemma 2.3

(Fitzpatrick et al. [33]) Let E be a real reflexive Banach space and let $A : D(A) \subset E \rightarrow E$ be an accretive mapping. Then A is locally bounded at any interior point of D(A).

3 Main result

Definition 3.1

A mapping $A:E\rightarrow 2^E$ is called quasi-bounded if for any $M>0$ there exists $C_M>0$ such that whenever $\langle \zeta , jx-j(x-y) \rangle \le M (2\Vert x\Vert +\Vert y\Vert ) ~~~ \mathrm{and} ~~~\Vert y\Vert \le M,~~~\Vert x\Vert \le M,~~\mathrm{for some}~j x\in Jx~~\mathrm{and} ~~j(x-y)\in J(x-y),$ then $\Vert \zeta \Vert \le C_M,~~\zeta \in Ay$.

Remark 3

A notion of quasi-boundedness for maps $A: E\rightarrow 2^{E^*}$, where $E^*$ is the dual space of E, is already defined (see e.g., Cioranescu [30], p 176, Exercise 9). If $x=0$ and E is a real Hilbert space, Definition 3.1 and that given for maps from $E\rightarrow 2^{E^*}$ coincide.

We now prove one of our main theorems.

Theorem 3.2

Let E be a smooth and reflexive real Banach space. Any accretive mapping $A: D(A) \subset E\rightarrow 2^E$ with $0\in int ~D(A)$ is quasi-bounded.

Proof

By Lemma 2.3, A is locally bounded at 0. This implies that there exist $r>0,~ M^*>0$ such that $B_E(0,r):=\{x\in E : \Vert x\Vert \le r \} \subset int ~D(A)$ and

$$\begin{aligned} \Vert \eta \Vert \le M^*,~~\forall ~x\in B_E(0,r),~~\eta \in Ax. \end{aligned}$$

Let $M>0$, $x\in B_E(0,r)$ and $y\in D(A)$. Assume that $\Vert y\Vert \le M$ and $\zeta \in Ay$ such that

$$\begin{aligned} \langle \zeta , Jx-J(x-y) \rangle \le M(2\Vert x\Vert + \Vert y\Vert ) . \end{aligned}$$

By the accretivity of A, $\langle \zeta -\eta ,J(y-x) \rangle \ge 0$, $\forall \eta \in Ax$. This implies that

$$\begin{aligned} \langle \zeta , J(x-y) \rangle \le \langle \eta , J(x-y) \rangle \le M^* (\Vert y\Vert +r). \end{aligned}$$

Furthermore,

$$\begin{aligned} \langle \zeta , Jx \rangle&=\langle \zeta , J(x-y)\rangle +\langle \zeta , Jx -J(x-y) \rangle \\&\le M^*(\Vert y\Vert +r)+ M(2\Vert x\Vert + \Vert y\Vert )\\&\le M^*(M+r)+M(2r+M). \end{aligned}$$

This implies that

$$\begin{aligned} |\langle \zeta , Jx \rangle | \le M^*(M+r)+M(2r+M), \forall x\in B_E(0,r). \end{aligned}$$

For $f\in B_{E^*}(0,1),$ by the reflexivity and smoothness of E, there exists $x\in B_E(0,r)$ such that $Jx=rf$. So,

$$\begin{aligned} |\langle \zeta , f\rangle | =\frac{1}{r}|\langle \zeta ,Jx\rangle |\le \frac{1}{r} \Big ( M^*(M+r)+M(2r+M) \Big ). \end{aligned}$$

Therefore,

$$\begin{aligned} \sup _{\Vert f\Vert \le 1}|\langle \zeta , f\rangle | \le \frac{1}{r} \Big ( M^*(M+r)+M(2r+M) \Big ). \end{aligned}$$

The quasi-boundedness of A follows. $\square$

We first prove the following Lemma.

Lemma 3.3

Let E be a uniformly smooth real Banach space and let $A:E\rightarrow 2^E$ be a set-valued m-accretive mapping such that the inclusion $0\in Au$ has a solution. For arbitrary $u_1\in E$, define inductively a sequence $\{u_n\}$ by

$$\begin{aligned} u_{n+1}=(1-\alpha _n\beta _n)u_n-\alpha _n\zeta _n,~~~~\zeta _n \in Au_n,~n\ge 1, \end{aligned}$$

(3.1)

where $\{\alpha _n\}$ and $\{\beta _n\}$ are sequences in (0, 1). Assume there exists a constant $\gamma _0>0$ such that if $\frac{\rho _E (\alpha _n)}{\alpha _n}\le \gamma _0\beta _n$, for some $M_0>0$ ($\rho _E$ is the function appearing in Lemma 2.2), then the sequence $\{u_n\}$ is bounded.

Proof

Let $u^*$ be a solution of the inclusion $0\in Au$, i.e., $0\in Au^*$ and let $u_1\in E$. Then, there exists $r>0$ such that $\Vert u^*\Vert \le \frac{r}{2}$ and $\Vert u_1-u^*\Vert \le \frac{r}{2}$. Define $B:=\{u\in E:\Vert u-u^*\Vert < r\}$. It suffices to show that $u_n\in B,~\forall n\ge 1.$ We show this by induction. Let $u\in B$, then $\Vert u\Vert \le \Vert u^*\Vert +r$. Sincce A is locally bounded at $0\in B$, there exist $m_1>0$, $k_1>0$ such that

$$\begin{aligned} \Vert \eta \Vert \le k_1, \quad \eta \in Av,\quad \forall v\in B_1(0,m_1)\subset B. \end{aligned}$$

Let $v\in B_1(0,m_1)$ such that $\omega _J(\Vert v \Vert )<m_1$, where $\omega _J$ is the modulus of continuity of J. By the accretivity of A, we have that

$$\begin{aligned} \langle \zeta , Ju \rangle \ge \langle \eta ,J(u-v) \rangle +\langle \zeta , Ju- J(u-v)\rangle , \quad \zeta \in Au. \end{aligned}$$

This implies that

$$\begin{aligned} \langle \zeta , J(-u) \rangle \le \langle \eta ,J(v-u) \rangle +\langle \zeta ,J(u-v)-Ju\rangle . \end{aligned}$$

Let $z=-u$. Then,

$$\begin{aligned} \langle \zeta , Jz \rangle&\le \langle \eta , J(v+z) \rangle +\langle \zeta , Jz-J(z+v) \rangle \\&\le \Vert \eta \Vert (\Vert v\Vert +\Vert z\Vert )+\Vert \zeta \Vert \Vert Jz-J(z+v)\Vert \\&\le k_1(m_1+\Vert u^*\Vert +r)+\Vert \zeta \Vert m_1 . \end{aligned}$$

Thus,

$$\begin{aligned} \sup _{\Vert z\Vert =\Vert Jz\Vert \le \Vert u^*\Vert +r}|\langle \zeta , Jz\rangle | \le k_1(m_1+\Vert u^*\Vert +r)+\Vert \zeta \Vert m_1. \end{aligned}$$

This implies that

$$\begin{aligned} (\Vert u^*\Vert +r)\Vert \zeta \Vert \le k_1(m_1+\Vert u^*\Vert +r)+\Vert \zeta \Vert m_1 , \end{aligned}$$

so that

$$\begin{aligned} \Vert \zeta \Vert \le \frac{ k_1(m_1+\Vert u^*\Vert +r) }{\Vert u^*\Vert +r-m_1}:=k_2. \end{aligned}$$

Setting $M=\max \{k_2,\Vert u^*\Vert + r\}$, we have

$$\begin{aligned} \langle \zeta , Jv-J(vu)\rangle \le M(2\Vert v\Vert +\Vert u\Vert ), \quad \Vert u\Vert \le M \quad and \quad \Vert v\Vert \le M. \end{aligned}$$

By Theorem 3.2, A is quasi-bounded. Thus, there exists $k>0$ such that

$$\begin{aligned} \Vert \zeta \Vert \le k, ~~~\forall u\in B. \end{aligned}$$

Define

$$\begin{aligned}&M_0:=\sup _{u\in B,~~\theta \in (0,1)}\big \{\Vert \theta u+\zeta \Vert \big \}+1, ~~~\zeta \in Au, \\&\gamma _0:=\min \left\{ 1,\frac{r^2}{8(r+1)M_0^2}\right\} . \end{aligned}$$

The quasi-boundedness of A and $u\in B$ guarantee that $M_0$ is well defined. Then, for $n=1$, by construction, $\Vert u_1-u^*\Vert \le r$. Assume $\Vert u_n-u^*\Vert \le r$, for some $n\ge 1$. We show that $\Vert u_{n+1}-u^*\Vert \le r$. For contradiction, suppose $r<\Vert u_{n+1}-u^*\Vert$. Now, using recursion formula (3.1), Lemma 2.2, and the condition that $\frac{\rho _E(\alpha _n)}{\alpha _n}\le \gamma _0 \beta _n,$ we have:

$$\begin{aligned} r^2<\Vert u_{n+1}-u^*\Vert ^2&=\Vert (1-\alpha _n\beta _n)u_n-\alpha _n\zeta _n-u^*\Vert ^2\\&\le \Vert u_n-u^*\Vert ^2-2\alpha _n\langle \zeta _n+\beta _nu_n,J(u_n-u^*)\rangle \\&\quad +\max \{\Vert u_n-u^*\Vert ,1\}\alpha _n\Vert \zeta _n \\&\quad + \beta _nu_n\Vert \rho _E (\alpha _n\Vert \zeta _n+\beta _nu_n\Vert )\\&\le \Vert u_n-u^*\Vert ^2-2\alpha _n\langle \zeta _n,J(u_n-u^*) \rangle \\&\quad -2\alpha _n\beta _n \langle u_n-u^*, J(u_n-u^*)\rangle \\&\quad -2\alpha _n\beta _n\langle u^*,J(u_n-u^*)\rangle \\&\quad +(r+1)M_0\rho _E (\alpha _n\Vert \zeta _n+\beta _nu_n\Vert )\\&\le \Vert u_n-u^*\Vert ^2-2\alpha _n\beta _n\Vert u_n-u^*\Vert ^2 \\&\quad +\alpha _n\beta _n(\Vert u^*\Vert ^2+\Vert u_n-u^*\Vert ^2)\\&\quad +(r+1)M_0\rho _E (\alpha _n\Vert \zeta _n+\beta _nu_n\Vert )\\&\le (1-\alpha _n\beta _n)\Vert u_n-u^*\Vert ^2 +\alpha _n\beta _n\Vert u^*\Vert ^2 \\&\quad +(r+1)M_0\frac{\rho _E (\alpha _nM_0)}{\alpha _nM_0}\alpha _nM_0\\&\le (1-\alpha _n\beta _n)\Vert u_n-u^*\Vert ^2 +\alpha _n\beta _n\Vert u^*\Vert ^2 \\&\quad +(r+1)M_0^2\gamma _0\beta _n\alpha _n\\&\le \left( 1-\frac{5\alpha _n\beta _n}{8}\right) r^2<r^2. \end{aligned}$$

This is a contradiction. Hence, $\Vert u_{n+1}-u^*\Vert \le r$. Therefore, $\{u_n\}$ is bounded.

$\square$

We now state and prove our strong convergence theorem.

Theorem 3.4

Let E be a uniformly smooth real Banach space and let $A:E\rightarrow 2^E$ be a set-valued m-accretive mapping such that the inclusion $0\in Au$ has a solution. For arbitrary $u_1\in E$, define inductively a sequence $\{u_n\}$ by

$$\begin{aligned} u_{n+1}=(1-\alpha _n\beta _n)u_n-\alpha _n\zeta _n,~~~~\zeta _n \in Au_n,~n\ge 1, \end{aligned}$$

(3.2)

where $\{ \alpha _n\}$$\{\beta _n\}$ are sequences in (0, 1) satisfying the following conditions:

• (i) $\lim _{n\rightarrow \infty }\beta _n=0$, $\{\beta _n\}$ is decreasing;

• (i) $\sum _{n=1}^\infty \alpha _n\beta _n=\infty$; $\quad \sum _{n=1}^\infty \rho _E(\alpha _nM_0)<\infty$, for some constant $M_0>0$;

• (i) $\lim _{n \rightarrow \infty } \frac{\Big (\frac{\beta _{n-1}}{\beta _n}-1\Big )}{\alpha _n\beta _n}=0.$

There exists a constant $\gamma _0>0$ such that $\frac{\rho _E(\alpha _n)}{\alpha _n}\le \gamma _0\beta _n$. Then, the sequence $\{u_n\}$ converges strongly to a zero of A.

Proof

We observe that the recurrence relation (3.2) is the same as the recurrence relation (1.5) in which $u_1\equiv 0$. This is possible since $u_1$ is an arbitrary element in domain of A which, in this case, is E. By Lemma 3.3, the sequence $\{u_n\}$ is bounded. The rest of the argument now follows exactly as in the proof of Theorem 1.3 (see, Chidume [11]). $\square$

The following estimates have been obtained for $\rho _E$ in $L_p$ spaces, $1<p<\infty$

$$\begin{aligned} \rho _E(t)\le {\left\{ \begin{array}{ll} \frac{1}{p}t^p, &{} 1<p<2;\\ \frac{(p-1)}{2}t^2, &{} p\ge 2; \end{array}\right. } \end{aligned}$$

where $t\ge 0$, (see e.g., Lindenstrauss and Tzafriri, [40], see also, Chidume, [10], p 18).

Prototype

For $L_p$ spaces, $2\le p<\infty ,$ let $\alpha _n=(n+1)^{-a}$ and $\beta _n=(n+1)^{-b}$, $n \ge 1$ with $0<b<a,~~\frac{1}{2}<a<1$ and $a+b<1$.

Now, we verify conditions (i)–(iii) and $\frac{\rho _E(\alpha _n)}{\alpha _n} \le \gamma _0 \beta _n$ given in Theorem 3.4.

Clearly, $\lim _{n\rightarrow \infty } \beta _n= \lim _{n\rightarrow \infty } \frac{1}{(n+1)^b} =0$ and the sequence $\beta _n$ is decreasing.

For (ii), using the fact that $a+b<1$, we have $\sum _{n=1}^\infty \alpha _n\beta _n= \sum _{n=1}^\infty \frac{1}{(n+1)^{a+b}}=\infty$.

Furthermore, the condition $\frac{1}{2}<a<1$ implies that

$$\begin{aligned} \displaystyle \sum _{n=1}^\infty \rho _E(\alpha _nM_0)\le \sum _{n=1}^\infty \left( \frac{p-1}{2}\right) \alpha _n^2M_0^2\le M_0^2\left( \frac{p-1}{2}\right) \displaystyle \sum _{n=1}^\infty \frac{1}{{(n+1)}^{2a}}<\infty . \end{aligned}$$

Next, for (iii), using the fact that $(1+x)^s\le 1+sx$, for $x>-1$ and $0<s<1$, we have

$$\begin{aligned} 0&\le \frac{\Big (\frac{\beta _{n-1}}{\beta _n}-1\Big ) }{\alpha _n \beta _n}=\Big [ \Big (1+\frac{1}{n} \Big )^b -1\Big ] \cdot (n+1)^{a+b}\\&\le b \cdot \frac{(n+1)^{a+b}}{n}=b \cdot \frac{n+1}{n} \cdot \frac{1}{(n+1)^{1-(a+b)}} \rightarrow 0 ~~\text {as } n \rightarrow \infty . \end{aligned}$$

Finally, using the fact that $\rho _E(t)\le \frac{(p-1)}{2}t^2$, $0<b<a$ and $\alpha _n=(n+1)^{-a} \le \beta _n=(n+1)^{-b}$, we obtain:

$$\begin{aligned} \begin{aligned} \frac{\rho _E(\alpha _n)}{\alpha _n}&\le \frac{(p-1)}{2\alpha _n} \cdot \alpha _n^2\\&=\frac{(p-1)}{2}\alpha _n=\frac{(p-1)}{2}(n+1)^{-a}\\&\le \frac{(p-1)}{2}(n+1)^{-b}= \gamma _0 \beta _n, \end{aligned} \end{aligned}$$

where $\gamma _0:=\frac{(p-1)}{2}.$ This completes the verification.

Similarly, for $L_p$ spaces, $1<p\le 2$, let $\alpha _n=(n+1)^{-a}$ and $\beta _n=(n+1)^{-b}$, $n \ge 1$ with $0<b<(p-1)a, ~~\frac{1}{p}<a<1$ and $a+b<1$, it can be shown that the conditions (i)–(iii) and $\frac{\rho _E(\alpha _n)}{\alpha _n} \le \gamma _0 \beta _n$ of Theorem 3.4 are satisfied.

4 Application to Hammerstein equations

A nonlinear integral equation of Hammerstein type, in abstract setting, is one of the form

$$\begin{aligned} u+KFu=0, \end{aligned}$$

(4.1)

where, $F:X\rightarrow X^*$ and $K: X^*\rightarrow X$ are monotone operators. For more on Hammerstein equation, the reader may consult Pascali and Sburlan [48], and for precise results on the existence of solution to Eq. (4.1), the reader may consult, for example, any of the following reference Brezis and Browder [4, 5], Browder and Gupta [6], Chepanovich [9], De Figueiredo and Gupta [31], Reich, [52].

For recent results on the approximation solution(s) of the Hammerstein Eq. (4.1), the reader may consult any of the following references: Chidume and Zegeye [20,21,22], Chidume and Djitte [26,27,28], Chidume and Ofoedu [19], Chidume and Shehu [16, 17], Djitte and Sene [32], Chidume et al. [24, 24] Chidume and Bello [25], Chidume et al. [23], Ofoedu and Onyi [46], Ofoedu and Malonza [47], Shehu [55], Minjibir and Mohammed [44], and the references contained in them.

We shall apply Theorem 3.4 to approximate a solution of Eq. (4.1).

Lemma 4.1

(Barbu [1]). Let E be a real Banach space, A be m-accretive set of $E \times E$ and let $B : E \rightarrow E$ be a continuous, m-accretive operator with $D(B) = E$. Then $A + B$ is m-accretive.

Lemma 4.2

Let E be a uniformly smooth real Banach space and $X := E \times E.$ Let $F, K : E \rightarrow E$ be m-accretive mappings. Let $A : X \rightarrow X$ be defined by $A([u, v]) = [F u -v, Kv + u]$. Then, A is m-accretive.

Proof

Define $S, T: E\times E \rightarrow E\times E$ as

$$\begin{aligned} S[u,v]=[Fu,Kv],\qquad T[u,v]=[-v,u]. \end{aligned}$$

Then, $A=S+T$. It is easy to verify that S is m-accretive and that T is m-accretive, continuous and $D(T ) = E.$ Hence, by Lemma  4.1, A is m-accretive.

$\square$

We note that $A[u,v]=0 ~\Leftrightarrow u$ solves Eq. (4.1) and $v=Fu$.

We now prove the following theorem.

Theorem 4.3

Let X be a uniformly smooth real Banach space and let $F,K:X\rightarrow X$ be m-accretive mappings. Define $E:=X\times X$ and let $A:E\rightarrow E$ be defined by $A([u, v]) = [F u -v, Kv + u]$. For arbitrary $u_1\in E$, define inductively a sequence $\{u_n\}$ by

$$\begin{aligned} u_{n+1}=(1-\alpha _n\beta _n)u_n-\alpha _n Au_n,~n\ge 1. \end{aligned}$$

(4.2)

Assume that the Hammerstein equation $u + KF u = 0$ has a solution. Then, the sequence $\{u_n\}$ converges strongly to $(u^* ,v^*)$, where $u^*$ is a solution of the Hammerstein equation $u+KFu=0$ with $v^*=Fu^*$.

Proof

By Chidume and Idu [18] (Lemma 6.3) and Lemma 4.2, E is uniformly smooth and A is m-accretive, respectively. Hence, the conclusion follows from Theorem 3.4. $\square$

Theorem 4.3 can also be stated as follows.

Theorem 4.4

Let X be a uniformly smooth real Banach space and let $F, ~K:X\rightarrow X$ be m-accretive mappings. For $(x_1,y_1),\,(u_1,v_1)\in X\times X$, define the sequences $\{u_n\}$ and $\{v_n\}$ in E, by

$$\begin{aligned} {\left\{ \begin{array}{ll} u_{n+1}=(1-\alpha _n\beta _n)u_n-\alpha _n(Fu_n-v_n) ,~~n\ge 1,&{}\\ v_{n+1}=(1-\alpha _n\beta _n)v_n-\alpha _n(Kv_n+u_n),~~n\ge 1. \end{array}\right. } \end{aligned}$$

(4.3)

Assume that the equation $u+KFu=0$ has a solution. Then, the sequences $\{u_n\}$ and $\{v_n\}$ converge strongly to $u^*$ and $v^*$, respectively, where $u^*$ is the solution of $u+KFu=0$ with $v^*=Fu^*$.

5 Numerical illustration

In this section, we present numerical examples to compare the convergence of the sequence generated by our algorithm: (Algorithm 3.2 of this paper), with respect to CPU and number of iterations with the following algorithms,

• (a) Algorithm 1.3 (Algorithm of Xu [58]),

• (b) Algorithm 1.4 (Algorithm of Qin and Su [59]) and

• (c) Algorithm 1.5 (Algorithm of Chidume [11]).

First, in Examples 1 and 2, we compare the convergence of the sequence of the algorithm (3.2) and algorithm (1.5). In these examples, we take $\alpha _n=\frac{1}{(n+1)^\frac{1}{2}}, ~\beta _n=\frac{1}{(n+1)^\frac{1}{4}},~n=1,2,\ldots ,$ as our parameters. Clearly, these parameters satisfy the hypothesis of Theorems 1.3 and 3.4. Furthermore, we use a tolerance of $10^{-8}$ and set maximum number of iterations $n=5000$.

Example 1

In Theorems 1.3 and 3.4, set $E={\mathbb {R}}^2$. Consider the mapping $A:{\mathbb {R}}^2\rightarrow {\mathbb {R}}^2$ defined by $A(u,v)=(u+v+\sin u, -u+v+\sin v).$ It is easy to see that A is accretive and (0, 0) is a solution of the problem $A(u,v)=(0,0)$.

Table of values choosing $u_1=(1,2)$
n	Algorithm (1.5)	Algorithm (3.2)
	$\Vert u_{n+1}\Vert$	$\Vert u_{n+1}\Vert$
1	0.2236	0.2236
5	0.1156	0.1022
10	0.3843	0.1289
15	0.2213	$6.297\times e^{-3}$
20	0.2002	$1.685 \times e^{-4}$
25	0.1817	$3.191\times e^{-6}$
30	0.1675	$4.978 \times e^{-8}$
32	0.1627	$9.127 \times e^{-9}$

Example 2

Let $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ be monotone nondecreasing. It is well known that the mapping $A_f:{\mathbb {R}}\rightarrow 2^{{\mathbb {R}}}$ defined by $A_fx:=\big [\displaystyle \lim _{t\rightarrow x^{-}}f(t), \displaystyle \lim _{t \rightarrow x^+}f(t)\big ]$ is maximal monotone, (see, e.g., Pascali and Sburlan [48]). Now, in Theorems 1.3 and 3.4, set $E={\mathbb {R}}$. Consider the mapping $f:{\mathbb {R}}\rightarrow {\mathbb {R}}$ defined by

$$\begin{aligned} f(x)= & {} {\left\{ \begin{array}{ll} x^2+1, &{} x\ge 0\\ 1, &{} -2<x<0\\ x+1, &{} x\le -2 \end{array}\right. } \quad \text {then}, \\ A_fx= & {} {\left\{ \begin{array}{ll} \{x^2+1\}, &{} x\ge 0\\ \{1\}, &{} -2<x<0\\ {[}-1,1], &{} x=-2\\ \{x+1\}, &{} x<-2. \end{array}\right. } \end{aligned}$$

It is easy to see that f is accretive (monotone) and thus A is accretive. Furthermore, $-2$ is the unique solution of the inclusion $0 \in Au$.

Table of values choosing $u_1=1$.
n	Algorithm (1.5)	Algorithm (3.2)
	$\Vert u_{n+1}+2\Vert$	$\Vert u_{n+1}+2\Vert$
1	3	3
5	1.5810	0.6841
10	1.3902	0.4209
100	1.1198	0.1199
500	0.9768	0.0231
1000	1.0059	0.0059
3000	0.9990	0.0009
4999	1.0124	0.0124

Next, in Example 3 we compare the convergence of the sequence of Algorithm (3.2) and Algorithms (1.3) and (1.4), and in Example 4, we compare the convergence of the sequence of Algorithms (3.2) and (1.4). In these examples, we consider the $L_p([0,1])$ spaces, $1<p<\infty$, with inner product and norm defined by

$$\begin{aligned}&\langle x,y \rangle := \int _{0}^1 x(t)y(t)\mathrm{d}t \\&\Vert x\Vert _p:=\Big (\int _{0}^1|x(t)|^p\mathrm{d}t\Big )^{\frac{1}{p}} \quad \forall x,y \in L_p([0,1]) \end{aligned}$$

and we choose the operator A such that the resolvent can be computed easily.

Example 3

In Theorems 1.1, 1.2 and 3.4, set $E=L_2([0,1])$. Consider the mapping ${A:L_2([0,1]) \rightarrow L_2([0,1])}$ defined by

$$\begin{aligned} (Au)(t):=(t+1)u(t) \quad \text { then, } \quad J_\lambda u(t)= \frac{u(t)}{1+\lambda (t+1)}. \end{aligned}$$

It is easy to see that A is accretive and the function $u(t)=0,~\forall ~t\in [0,1]$ is the only solution of the equation $Au(t)=0$. In algorithm (1.3), we take $\alpha _n=\frac{1}{n+1}$, $\lambda _n=n$, in algorithm (1.4), we take $\alpha _n=\frac{1}{n+1}$, $\beta _n=0.25$, $\lambda _n=5$, and in algorithm (3.2), we take $\alpha _n=\frac{1}{(n+1)^\frac{1}{2}}, ~\beta _n=\frac{1}{(n+1)^\frac{1}{4}},~n=1,2,\ldots ,$ as our parameters. Clearly, these parameters satisfy the hypothesis of Theorems 1.1, 1.2 and 3.4. Furthermore, we use a tolerance of $10^{-8}$ and set maximum number of iterations $n=20$.

Table of values choosing $u_1(t)=\sin t$
n	Algorithm (1.3)	Algorithm (1.4)	Algorithm (3.2)
	Time= 0.041	Time=21.21	Time= 0.21s
	$\Vert u_{n+1}\Vert$	$\Vert u_{n+1}\Vert$	$\Vert u_{n+1}\Vert$
1	0.3152	0.3061	0.4342
2	0.1945	0.2151	0.2103
3	0.1344	0.1641	0.06
5	0.0829	0.1102	$5.21 \times e^{-4}$
10	0.0429	0.0601	$1.16 \times e^{-7}$
14	0.0309	0.0441	$9.27 \times e^{-9}$
20	0.0219	0.0315	successful

Example 4

In Theorems 1.3 and 3.4, set $E=L_3([0,1])$. Consider the mapping $A:L_3([0,1]) \rightarrow L_3([0,1])$ defined by

$$\begin{aligned} (Au)(t):=u(t) \quad \text { then } \quad J_\lambda u(t)= \frac{u(t)}{1+\lambda }. \end{aligned}$$

It is easy to see that A is accretive and the function $u(t)=0,~\forall ~t\in [0,1]$ is the only solution of the equation $Au(t)=0$. In algorithm (1.4), we take $\alpha _n=\frac{1}{n+1}$, $\beta _n=0.25$, $\lambda _n=5$, and in algorithm (3.2), we take $\alpha _n=\frac{1}{(n+1)^\frac{1}{2}}, ~\beta _n=\frac{1}{(n+1)^\frac{1}{4}},~n=1,2,\ldots ,$ as our parameters. Clearly, these parameters satisfy the hypothesis of Theorems 1.2 and 3.4, respectively. Furthermore, we use a tolerance of $10^{-8}$ and set maximum number of iterations $n=20$.

Table of values choosing $u_1(t)= t^2+1$
n	Algorithm (1.4)	Algorithm (3.2)
	Time= 14.44	Time= 7.41s
	$\Vert u_{n+1}\Vert$	$\Vert u_{n+1}\Vert$
1	0.507	0.4223
2	0.2993	$6.77 \times e^{-3}$
3	0.2147	$9.92 \times e^{-4}$
5	0.1399	$8.32 \times e^{-5}$
10	0.076	$1.81\hbox {E}\times e^{-6}$
15	0.0522	$1.31 \times e^{-7}$
20	0.0398	$1.64 \times e^{-8}$

Remark 4

From the numerical comparisons above, we observe that the proposed method (Algorithm (3.2)) converges faster in terms of number of iteration and CPU time in all the examples considered. Thus, the proposed method which does not require the boundedness of the operator A or computation of the resolvent of A, would, perhaps, be a preferable alternative to the proximal and proximal type algorithms in any possible application.

5.1 Numerical experiments for solution of Hammerstein equation

Example 5

In Theorem 4.4, set $E={\mathbb {R}}^2$. Consider the mapping $F,K: {\mathbb {R}}^2 \rightarrow {\mathbb {R}}^2$ defined by

$$\begin{aligned} F(u_1,u_2)= & {} (u_1+u_2+\sin u_1, -u_1+u_2+\sin u_2), \\ K(v_1,v_2)= & {} (v_1+v_2, v_1+v_2). \end{aligned}$$

It is easy to see that F and K are accretive and the vector $[u, v]=[\mathbf{0}, \mathbf{0}]$ is the only solution of the equation $u+KFu=0$ with $v=Fu$. In Algorithm (4.3) we take $\alpha _n=\frac{1}{(n+1)^\frac{1}{2}}, ~\beta _n=\frac{1}{(n+1)^\frac{1}{4}},~n=1,2,\ldots ,$ as our parameters. Clearly, these parameters satisfy the hypothesis of Theorem 4.4. Furthermore, we use a tolerance of $10^{-8}$ and set maximum number of iterations $n=100$.

Table of values choosing $u_1=(0,5)^T,$$~~v_1=(-1,1)^T$
n	Algorithm (4.3)	Algorithm (4.3)
	$\Vert u_{n+1}\Vert$	$\Vert v_{n+1}\Vert$
1	4.2426	3.1301
5	1.4027	1.6546
10	0.0687	0.0651
20	7.547$\times e^{-3}$	8.35$\times e^{-3}$
30	7.25320$\times e^{-5}$	1.1242$\times e^{-5}$
60	9.771$\times e^{-7}$	1.5105$\times e^{-6}$
90	4.4384$\times e^{-8}$	6.8612$\times e^{-8}$
100	1.8315$\times e^{-8}$	2.8312$\times e^{-8}$

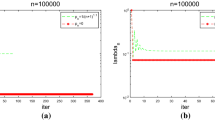
Example 6

In Theorem 4.4, set $E=L_{1.5}([0,1])$. Consider the mapping $F,K:L_{1.5}([0,1]) \rightarrow L_{1.5}([0,1])$ defined by

$$\begin{aligned} (Fu)(t)=tu(t)\qquad \text {and} \qquad (Ku)(t)=u(t) . \end{aligned}$$

It is easy to see that F and K are accretive and the function $[u(t), v(t)]=[0,0]~\forall ~t\in [0,1]$ is the only solution of the equation $u(t)+KFu(t)=0$ with $v(t)=Fu(t)$. In Algorithm (4.3) $\alpha _n=\frac{1}{(n+1)^\frac{1}{2}}, ~\beta _n=\frac{1}{(n+1)^\frac{1}{4}},~n=1,2,\ldots ,$ as our parameters. Clearly, these parameters satisfy the hypothesis of Theorem 4.4. Furthermore, we use a tolerance of $10^{-8}$ and set maximum number of iterations $n=15$.

Table of values choosing $u_1(t)=e^t,~~v_1(t)=4$
n	Algorithm (4.3)	Algorithm (4.3)
	$\Vert u_{n+1}\Vert$	$\Vert v_{n+1}\Vert$
1	2.8288	2.4342
4	0.4413	0.4391
6	0.1327	0.165
8	0.0598	0.0533
10	0.0325	0.0246
12	0.016	0.0157
14	0.0072	0.0093
15	0.0048	0.0069

Observations.

• 1. With respect to Example 1 in which A is an accretive (monotone) map of ${\mathbb {R}}^2$ into itself, and Example 2 in which A is a set-valued map from ${\mathbb {R}}$ to $2^{\mathbb {R}},$ with a tolerance of $10^{-8}$ and maximum number of iterations $n=5000,$ the sequence generated by our Algorithm (3.2) converges strongly to 0, a zero of the operator A in less than 15 iterations in Example 1, whereas Algorithm (1.5) has not converged after 30 iterations.

• 2. With respect to Example 3, where $E=L_2([0,1])$ and $A:L_2([0,1])\rightarrow L_2([0,1])$ is accretive, and with a tolerance of $10^{-8}$ and maximum number of iterations $n=20,$ the sequence generated by Algorithm (1.3) after 14 iterations in a time of 0.04 s has not converged to any zero of A;  also the sequence generated by algorithm (1.4) after 14 iterations; 21.21 s has not converged to a zero of A. We remark that Algorithms (1.3) and (1.4) both have resolvent operator. But, the sequence generated by our algorithm, Algorithm (3.2) after 0.21 s, converged to a zero of A after 5 iterations. With respect to this example, our algorithm in this paper which does not involve the resolvent operator is superior in terms of CPU time and number of iterations to Algorithms (1.3) and (1.4), both of which involve the resolvent operator. Consequently, the study of our algorithm in this paper for approximating zeros m-accretive operators makes big sense.

• 3. In Example 4, $E=L_3([0,1])$ and $A:L_3([0,1])\rightarrow L_3([0,1])$ as defined is accretive with the function $u(t)=0,~\forall ~t\in [0,1]$ being the only solution of $Au(t)=0$. With a tolerance of $10^{-8}$ and maximum number of iterations $n=20$, the sequence generated by Algorithm (1.4), which involves the resolvent after 20 iterations in 14.44 s has not converged to zero, the only zero of A, whereas, the sequence of our algorithm in this paper, Algorithm (3.2), after 7.41 s for the 20 iterations, already converged to zero after 3 iterations. Here again, our Algorithm (3.2) which does not involve the resolvent, for this example, is superior in terms of CPU time and number of iterations, to Algorithm (1.4) which involves the resolvent operator. Consequently, the study o f our algorithm which does not involve the resolvent operator for approximating zeros of accretive operators makes big sense.

• 4. In Examples 5 and 6, we present numerical experiments for solutions of Hammerstein Equations in ${\mathbb {R}}^2$ and $L_{1.5}([0,1]),$ respectively. In Example 5, with a tolerance of $10^{-8}$ and maximum number of iterations $n=100$, the sequence generated by our algorithm converged to a zero A in less than 20 iterations. In Example 6, with a tolerance of $10^{-8}$ and maximum number of iterations $n=15$, the sequence generated by our algorithm converges to a zero A after about 12 iterations. We observe that our algorithms involve m-accretive operators but do not involve resolvent operators.

Conclusion In this paper, a significant improvement of Theorem 1.3 is proved by dispensing with the restriction that A be bounded imposed in the theorem. This is achieved by first introducing a new notion of quasi-boundedness for operators $A:E\rightarrow 2^E$ and then proving a general theorem of independent interest on accretive operators, that: an accretive operator with zero in the interior of its domain is quasi-bounded. Using this result, a strong convergence theorem for approximating a solution of $0\in Au$ is proved. Furthermore, as an application of our theorem, a strong convergence theorem for approximating a solution a Hammerstein equation is proved. Finally, several numerical experiments are presented to illustrate the strong convergence of the sequence of our algorithm and the results obtained are compared with those obtained using some recent important algorithm.