Abstract
Tensor decomposition methods are inefficient when dealing with low-rank approximation of large-scale data. Randomized tensor decomposition has emerged to meet this need, but most existing methods exhibit high computational costs in handling large-scale tensors and poor approximation accuracy in noisy data scenarios. In this work, a Tucker decomposition method based on randomized block Krylov iteration (rBKI-TK) is proposed to reduce computational complexity and guarantee approximation accuracy by employing cumulative sketches rather than randomized initialization to construct a better projection space with fewer iterations. In addition, a hierarchical tensor ring decomposition based on rBKI-TK is proposed to enhance the scalability of the rBKI-TK method. Numerical results demonstrate the efficiency and accuracy of the proposed methods in large-scale and noisy data processing.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Tensor data are ubiquitous in scientific computing and numerical applications, such as color images, video sequences, and EEG signals [1, 2]. Compared to matrix factorization, tensor decomposition provides a more natural and efficient way to represent, store and compute such data [3,4,5,6,7]. Since observations are often noisy, incomplete, and redundant, low-rank tensor decomposition plays an increasingly important role in many machine learning tasks, such as network compression [8], image imputation [9] and data mining [10]. However, when dealing with large-scale problems, tensor decomposition solved by deterministic methods such as singular value decomposition (SVD) [11] and alternating least squares (ALS) [12] can be computationally expensive and resource-intensive.
Randomized sketching techniques offer the possibility of eliminating this limitation. The basic idea of randomized sketching is to capture a representative subset or subspace of the data in order to efficiently produce a satisfactory approximation. Extensive works have reveal that randomized sketching techniques can effectively reduce computational complexity, thus improve efficiency [13,14,15,16]. Without loss of generality, random sketching techniques are divided into non-iterative and iterative sketching in this work. Non-iterative sketching involves sketching the input data in a single pass, while iterative sketching employs power iteration to perform the sketching process.
With the development of sketching techniques, a number of randomized tensor decomposition have emerged to provide more computational efficiency and approximation accuracy. In the non-iterative sketching category, there are tensor decomposition methods based on Gaussian random projection [17,18,19,20], CountSketch sampling [21, 22], and leverage score sampling [23, 24]. In the iterative sketching category, there are tensor decomposition methods based on Gaussian random iterations [19, 25], power iteration [26, 27], and rank revealing projection [28, 29]. While existing methods offer effective solutions for handling large-scale data, many of them fail to capture critical information in the presence of noise, leading to reduced approximation accuracy.
The Krylov methods aim to search for more accurate approximations by constructing more efficient projection spaces. The traditional Krylov methods construct the projection space with random initial vectors [30, 31] or matrices [32]. However, when applying these methods directly to tensor decomposition, the iterative orthonormalization required to construct the projection space leads to high computational costs, limiting the applicability of these methods to large tensor, and simple initialization using randomized vectors or matrices may lead to poor convergence [33, 34]. Therefore, the randomized block Krylov iteration (rBKI) method [35] was proposed to improve on the existing Krylov methods by using cumulative sketches instead of random initial data to construct projection spaces, thus obtaining more accurate approximation with fewer iterations.
The aim of this work is to develop more efficient and accurate randomized tensor decomposition methods for large-scale and noisy data. Although the rBKI method has been widely used in matrix analysis [35,36,37], it has not yet attracted attention in tensor community. The main innovation of this work is the first incorporation of rBKI into tensor decomposition, enabling more efficient and accurate approximation of large-scale and noisy tensors. Specifically, the rBKI method is introduced into the Tucker decomposition (rBKI-TK) for searching significant subspace of each mode, thus capturing the key information when optimizing the multi-linear factors. Besides, a hierarchical tensor ring model is developed to improve the scalability of rBKI-TK method. Yu et al. cited and discussed our methods in their work, which uses the rBKI method in tensor train model [38].
The contribution of our work can be summarised below.
-
The rBKI-TK method offers more efficient processing of large-scale data and effectively reduce the noise interference.
-
The hierarchical tensor ring decomposition based on rBKI-TK can further reduce the storage cost, which is important for applying large-scale data to various tasks.
-
Numerical results demonstrate that the proposed methods exhibit significant efficiency and accuracy in processing large-scale and noisy data.
The following sections are organized as follows. In Sect. 2, some frequently used notations and definitions are outlined. In Sect. 3, main algorithms are presented. In Sect. 4, evaluations on both synthetic and real-world data are conducted. Finally, concluding remarks and future directions are depicted in Sect. 5.
2 Preliminaries
2.1 Notations
Throughout the paper, the terms “order” or “mode” are used to interchangeably describe a tensor data. For example, an Nth-order tensor can be unfolded into a mode-n unfolding matrix on each mode (\(n =1,2,\ldots ,N\)). Besides, a tensor set to [N \(=\) 3, I \(=\) 20, R \(=\) 3] represents a 3D tensor of dimension 20 and rank 3 on each mode. For better description, some frequently used notations are listed in Table 1.
2.2 Basic tensor decomposition models
Two basic tensor decomposition models studied in this work that are described below, and their corresponding diagrams are shown in Fig. 2.
Definition 1
Tucker decomposition of an Nth-order tensor  is expressed as an Nth-order core tensor interacting with N factor matrices. Suppose the Tucker-rank of
is expressed as an Nth-order core tensor interacting with N factor matrices. Suppose the Tucker-rank of  is \((R_1,R_2,\ldots ,R_N)\), also known as multilinear-rank, then it has the following mathematical expression,
is \((R_1,R_2,\ldots ,R_N)\), also known as multilinear-rank, then it has the following mathematical expression,

where \(\textbf{U}^{(n)}\in \mathbb {R}^{I_n\times R_n}\) is the mode-n factor matrix, and  is the core tensor reflecting the connections between the factor matrices.
is the core tensor reflecting the connections between the factor matrices.
Definition 2
Tensor ring (TR) decomposition of an Nth-order tensor  is expressed as a cyclic multilinear product of N third-order core tensors that can be shifted circularly. Given a TR-ranks of (\(J_1, J_2,\ldots , J_N\)), the TR operator in denoted by
is expressed as a cyclic multilinear product of N third-order core tensors that can be shifted circularly. Given a TR-ranks of (\(J_1, J_2,\ldots , J_N\)), the TR operator in denoted by  , and the element-wise TR decomposition is expressed below.
, and the element-wise TR decomposition is expressed below.

where  and
and  denotes the n-th TR-core and the \(i_n\)-th slice of the n-th TR-core, respectively.
denotes the n-th TR-core and the \(i_n\)-th slice of the n-th TR-core, respectively.
Note that, each TR-core  contains one dimension-mode (\(I_n\) in mode-2) and two rank-modes (\(R_{n-1}\) in mode-1 and \(R_n\) in mode-3). Besides, adjoin factors
contains one dimension-mode (\(I_n\) in mode-2) and two rank-modes (\(R_{n-1}\) in mode-1 and \(R_n\) in mode-3). Besides, adjoin factors  and
and  have a shared rank to ensure the contraction operation between them.
have a shared rank to ensure the contraction operation between them.
2.3 Low-rank approximation for matrix
The Low-rank approximation problem with respect to the Frobenius norm, and the \((1+\epsilon )\) quasi-optimal approximation is described as follows.
Definition 3
Low-rank approximation of any matrix \( \textbf{X} \in \mathbb {R}^{n \times d}\) with specific rank(\( \textbf{X}\)) = \(r \le \min (n,d)\), is to find a rank-k (\(k \le r\)) approximation \( \textbf{X}_k\) that minimizes the Frobenius norm as
Generally, the optimal rank-k approximation \(\textbf{X}_k\) can be obtained from the truncated SVD of \(\textbf{X}\), which is known as the Eckart-Young-Mirsky theorem [39]. Since SVD is prohibitive for large-scale data, randomized SVD addresses this limitation by using a variety of sketching techniques aimed at obtaining satisfactory approximation accuracy while significantly reducing storage and computational costs [13,14,15].
For a matrix \( \textbf{X} \in \mathbb {R}^{n \times d}\), the low-rank approximation based on randomized SVD consists of three main steps: 1) draw a sketch matrix \(\textbf{Y} = \textbf{X} \varvec{\Omega } \in \mathbb {R}^{n \times s}\) by employing a random sketching matrix \(\varvec{\Omega } \in \mathbb {R}^{d \times s}\) with a sketch-size \( k \le s \le \min (n,d)\); 2) compute the orthonormal basis \(\textbf{Q} \in \mathbb {R}^{n \times s}\) of \(\textbf{Y}\) to project the data onto the sketching space \(\textbf{Q}^{\top } \textbf{X} \in \mathbb {R}^{s \times d}\); 3) compute the low-rank approximation: \(\tilde{\textbf{X}} = \textbf{U} \textbf{U} ^{\top } \textbf{X}\) via truncated SVD of \(\textbf{Z} = \textbf{Q}^{\top } \textbf{X}\), i.e., \([\textbf{U, S, V}] = \text {svd}(\textbf{Z})\).
Definition 4
The \((1+\epsilon )\) quasi-optimal approximation can be described as the Frobenius norm error bound for the randomized rank-k approximation holds with high probability that
As \(\tilde{\textbf{X}}_k\) denotes the \((1+\epsilon )\) rank-k approximation in a s-dimension subspace spaned by \(\textbf{Q} \in \mathbb {R}^{n \times s}, s \ge k\), sketching can further speed up the low-rank approximation when \(s > k\). More theoretical analysis can be found in the work [40].
2.4 Low multilinear-rank approximation for tensor
Definition 5
The low multilinear-rank approximation [17] of an Nth-order tensor  with multilinear-rank \((R_1, R_2,\ldots , R_N)\) can be expressed as
with multilinear-rank \((R_1, R_2,\ldots , R_N)\) can be expressed as

where \(\textbf{U}^{(n)} \in \mathbb {R}^{I_n \times R_n}\) is the left singular matrix of the mode-n unfolding \({\textbf{X}}_{(n)}\).
Note that, Eq. (5) can be defined as a randomized low multilinear-rank approximation when \(\textbf{U}^{(n)}\) is obtained from a randomized SVD. More details can be found in work [17].
3 Methodology
3.1 Randomized block Krylov iteration (rBKI)
The Krylov methods have been extensively investigated in matrix approximation. Traditional Krylov methods tended to capture the key information of data by simply constructing a Krylov subspace in a vector-by-vector paradigm [30, 31], i.e.,
where \(\textbf{X}\in \mathbb {R}^{n \times d}\) is the input and \(\textbf{v}\in \mathbb {R}^{n}\) is a randomized initial vector. To improve the efficiency, block Krylov method was proposed to construct a Krylov subspace in a block-by-block paradigm [32], i.e.,
where \(\textbf{V}\in \mathbb {R}^{n \times s}\) is a random initial matrix.
However, when extended to large-scale data, these Krylov methods with random initial vectors or matrices may result in poor convergence [37], and the repeated orthonormalization required for constructing subspace results in high computational costs, limiting the applicability of these methods to large-scale data [33, 34]. Accordingly, randomized block Krylov iteration (rBKI) [35] was proposed to construct a Krylov subspace using sketches \(\textbf{W} = \mathbf {X\Omega }\) in a cumulative way instead of random initial data to capture more information about the original data with fewer iterations, i.e.,
where \(\varvec{\Omega } \in \mathbb {R}^{d \times s}\) is a random initial matrix. Empirically, \(q = 2 \) is sufficient to achieve a satisfactory approximate accuracy [35].
Compared with the existing popular randomized sketching methods: non-iterative method (e.g., Gaussian random projection), and power iteration method (\(\textbf{K} \doteq (\textbf{X}\textbf{X}^{\top })^q\textbf{W}\)), rBKI performs better in reducing the effect of tail singular values. Although the power iteration method construct the sketching space in an iterative way, \((\textbf{X}\textbf{X}^{\top })^q\textbf{W}\) focuses solely on computing the dominant eigenspace. In contrast, rBKI method accumulates important information of the original data when constructing \([\textbf{W}, (\textbf{X}\textbf{X}^{\top })\textbf{W},\ldots , (\textbf{X}\textbf{X}^{\top })^q\textbf{W}]\), minimizing the loss of information during the projection process. With a more accurate projection subspace, rBKI facilitates higher accuracy approximation.
For better understanding, given a tensor with setting of [N \(=\) 3, I \(=\) 10, R \(=\) 5], the clean data is drawn from \(\mathcal {N}(0,1)\) and the noisy data is corrupted by SNR \(=\) 0dB Gaussian random noise. The pseudocolor plot of singular value matrices of the clean data, noisy data, and projections based on three representative randomized SVD methods, namely Gaussian random projection (GR-SVD), Gaussian random power iteration (GRpi-SVD), and rBKI (rBKI-SVD), are presented in Fig. 1. As shown, rBKI-SVD performed better in eliminating tail singular values (i.e., noise interference) than the non-iterative GR-SVD and the GRpi-SVD method.
Besides, since rBKI constructs the subspace through a lower q-degree polynomials (8), it requires only \(q = \varTheta (\text {log} d / \sqrt{\epsilon } )\) iterations to achieve the (\(1+\epsilon \)) approximation to an \(n \times d\) matrix, which is more efficient than the power iteration that requires \(q = \varTheta (\text {log} d / \epsilon )\) iterations (Theorem 1 in [35]). Particularly, when the data have a rapid decay or a heavy-tail of singular value, rBKI can offer faster convergence performance, which is validated in the simulation section.
Moreover, the time complexity of several typical compared methods is presented in Table 2. Given a matrix \(\textbf{X} \in \mathbb {R}^{n \times d}\) with sketch-size s, according to the cost of each stage, the runtime of SVD is \(\mathcal {O}(n^2d)\) while that of the GR-SVD is \(\mathcal {O} (nds)\). With the number of iteration for rBKI of \(q = \varTheta (\text {log} d / \sqrt{\epsilon } )\) and for power iteration method of \(q = \varTheta (\text {log} d / \epsilon )\), the corresponding runtime is \(\mathcal {O}(nds\log d / \sqrt{\epsilon } + ns^2 \log ^2 d/ \epsilon + s^3 \log ^3 d/ \epsilon ^{\frac{3}{2}})\) and \(\mathcal {O}(nds\log d / \epsilon + ns^2 \log d/ \epsilon )\), respectively.
3.2 Tucker decomposition based on rBKI (rBKI-TK)
Tucker decomposition can be regarded as a higher-order SVD (HOSVD) model [3], and randomized sketching techniques can be used to achieve efficient low multilinear-rank approximation of large-scale tensors. Besides, the challenges posed by low approximation accuracy in noisy data scenarios can be addressed by leveraging the rBKI method. Therefore, the rBKI-based Tucker decomposition (rBKI-TK) is proposed to search for crucial projection subspace with fewer iterations, thus improving the optimization of multilinear factors.
When computing the Tucker decomposition (Eq. 1), the standard mode-n unfolding on  as \({\textbf{X}}_{(n)} \in \mathbb {R}^{I_n \times \prod _{p\ne n}I_p}\) is necessary to be performed first and then optimize factors in a form of matrix product as follows.
as \({\textbf{X}}_{(n)} \in \mathbb {R}^{I_n \times \prod _{p\ne n}I_p}\) is necessary to be performed first and then optimize factors in a form of matrix product as follows.
where \(\textbf{U}^{(n)} {\in }\mathbb {R}^{I_n\times R_n}\), and \({\textbf{C}}_{(n)} \left( {\bigotimes }_{p\ne n}\textbf{U}^{(p)}\right) ^{\top } {\in }\mathbb {R}^{R_n {\times } \prod _{p\ne n}I_p}\) can be computed by SVD [11] or ALS [12] algorithms.
Given an Nth-order tensor  with sketch-size \((S_1,S_2,\ldots ,S_N)\) and Tucker-rank \((R_1,R_2,\ldots ,R_N)\), the rBKI-TK method provides a low multilinear-rank approximation of
with sketch-size \((S_1,S_2,\ldots ,S_N)\) and Tucker-rank \((R_1,R_2,\ldots ,R_N)\), the rBKI-TK method provides a low multilinear-rank approximation of  through the following steps:
through the following steps:
-
1)
Draw a sketch \(\textbf{W}^{(n)} = {\textbf{X}}_{(n)}\mathbf {\Omega }^{(n)}\) to construct the mode-n block Krylov subspace
$$\begin{aligned} \textbf{K}^{(n)} \doteq [\textbf{W}^{(n)}, ({\textbf{X}}_{(n)}{\textbf{X}}_{(n)}^{\top })\textbf{W}^{(n)},\ldots , ({\textbf{X}}_{(n)}{\textbf{X}}_{(n)}^{\top })^q\textbf{W}^{(n)}], \nonumber \\ \end{aligned}$$(10)where \(\mathbf {\Omega }^{(n)}\in \mathbb {R}^{\prod _{p\ne n}I_p\times S_n}\) is a Gaussian random matrix.
-
2)
Compute the orthonormal basis \(\textbf{Q}^{(n)}\) via QR of \(\textbf{K}^{(n)}\) to project data \({\textbf{X}}_{(n)}\) onto the sketch subspace \(\textbf{Z}^{(n)} = \textbf{Q}^{(n)}{}^{\top }{\textbf{X}}_{(n)}\).
-
3)
Compute the factor matrices via \(\textbf{U}^{(n)} = \textbf{Q}^{(n)}{\tilde{\textbf{U}}}^{(n)}(:, 1:R_n)\), where \({\tilde{\textbf{U}}}^{(n)}\) is the left singular basis of the projection data \(\textbf{Z}^{(n)}\).
-
4)
Compute the core tensor
 , and obtain the low multilinear-rank approximation by
, and obtain the low multilinear-rank approximation by  .
.
The proposed rBKI-TK method offers the advantage of lower computational complexity and better denoising ability, which can be applied to large-scale and noisy data, thus has the potential for a wider range of applications. Details of the rBKI-TK method are presented in Algorithm 1.
3.3 Extensions to hierarchical tensor decomposition
Tensor Ring (TR) decomposition is a powerful tool for higher-order (three or more) tensor analysis [6]. When computing the TR decomposition, Eq. (2) can be rewritten in a TR mode-n unfolding form as
where \(\textbf{G}_{n(2)} \in \mathbb {R}^{I_n \times J_{n-1} J_n}\) and \(\textbf{G}^{\ne n}_{[2]} \in \mathbb {R}^{ \prod _{p\ne n} I_p \times J_{n-1} J_n }\) denotes the mode-2 unfolding of the nth core and the subchain except the nth core, respectively. Note that, the difference between the TR mode-n unfolding \(\textbf{X}_{[n]} \in \mathbb {R}^{I_n \times I_{n+1}\cdots I_N I_1 \cdots I_{n-1}}\) and the standard mode-n unfolding \({\textbf{X}}_{(n)} \in \mathbb {R}^{I_n \times I_1 \cdots I_{n-1}I_{n+1}\cdots I_N} \) is the order of TR-cores in the subchain.
TR-ALS is a typical algorithm for updating TR-cores, which updates the nth TR-core by first computing the unfolding \(\textbf{G}_{n(2)}\) via Eq. (11), and then reshape \(\textbf{G}_{n(2)}\) into a third-order tensor  , for \(n = 1,2, \ldots ,N\), and repeated until the relative error \(\delta = \left\| \textbf{X}_{[n]}-\textbf{G}_{n(2)} (\textbf{G}^{\ne n}_{[2]})^{\top }\right\| _{F}/\left\| \textbf{X}_{[n]}\right\| _{F}\) reaches the set tolerance \(\delta _p\) or reaches the maximum number of iteration p [6].
, for \(n = 1,2, \ldots ,N\), and repeated until the relative error \(\delta = \left\| \textbf{X}_{[n]}-\textbf{G}_{n(2)} (\textbf{G}^{\ne n}_{[2]})^{\top }\right\| _{F}/\left\| \textbf{X}_{[n]}\right\| _{F}\) reaches the set tolerance \(\delta _p\) or reaches the maximum number of iteration p [6].
However, the direct application of TR decomposition to large-scale data processing often results in inefficiency. Therefore, hierarchical tensor decomposition methods with randomized algorithm were extensively studied for reducing the computation and storage cost [17, 19, 20, 29]. In this subsection, a hierarchical tensor decomposition based on rBKI method is developed to improve the scalability of the rBKI-TK method and the efficiency of TR method. In the rBKI-TK-TR model, the rBKI-TK can efficiently obtain factors and reduce noise interference, and the TR decomposition can further reduce the data storage cost when the TR-ranks are much smaller than the Tucker-rank.
Generally, such hierarchical framework can be extended to other tensor decomposition methods. The proposed rBKI-TK-TR method is detailed in Algorithm 2, and a tensor network diagram of TK, TD, hierarchical TK-TR decomposition and contraction operations among them are shown in Fig. 2.
4 Experiments
This section evaluates the efficiency and accuracy of the proposed method for large-scale processing and noise reduction. All evaluations were conducted on a computer with an Intel Core i5 3 GHz CPU and 8GB of RAM. The algorithms were coded in MATLAB 2020r.
4.1 Evaluation metric
The following metrics were employed for evaluations. Note that all results were the average of 10 runs.
-
Fitting rate, Fit
 , where
, where  and
and  is the original tensor and the sketched rank-k approximation, respectively. A larger value indicates higher recovery accuracy.
is the original tensor and the sketched rank-k approximation, respectively. A larger value indicates higher recovery accuracy. -
Frobenius norm error (Eq. 4), FErr
 , where
, where  is the deterministic rank-k approximation obtained by truncated SVD (T-SVD). When FErr = 1, the randomized rank-k approximation
is the deterministic rank-k approximation obtained by truncated SVD (T-SVD). When FErr = 1, the randomized rank-k approximation  captures the main information as well as the deterministic one
captures the main information as well as the deterministic one  . The larger the ratio, the worse the results [35].
. The larger the ratio, the worse the results [35]. -
Peak-Signal-Noise-Ratio, PSNR \(= 10 \log _{10} (255^2 / \text {MSE})\), where MSE is the Mean-Square-Error denoted by
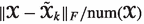 , and \(\text {num}(\cdot )\) denotes the number of components.
, and \(\text {num}(\cdot )\) denotes the number of components. -
Running time in seconds. For the TR-ALS, the iterations were repeated until the maximum number of iterations 50 is reached, or the relative error \(\delta < \delta _p = 10^{-3}\).
4.2 Datasets
4.2.1 Synthetic data
The generation of tensor data followed  , where the original data
, where the original data  was corrupted by a noise term
was corrupted by a noise term  , and \(\lambda \) was a parameter for tuning the noise level of
, and \(\lambda \) was a parameter for tuning the noise level of  via Signal-to-Noise-Ratio,
via Signal-to-Noise-Ratio,  A relatively comprehensive test was provided that considers higher and lower rank tensors with Gaussian random noise.
A relatively comprehensive test was provided that considers higher and lower rank tensors with Gaussian random noise.
Specifically, in the higher rank case, 3D tensors  with dimension of 200 and rank of 10 were given by Tucker model (1), where the entries of latent factor matrices \(\textbf{U}^{(n)}\in \mathbb {R}^{I_n \times R_n}, n=1,2,3\) and core tensor
with dimension of 200 and rank of 10 were given by Tucker model (1), where the entries of latent factor matrices \(\textbf{U}^{(n)}\in \mathbb {R}^{I_n \times R_n}, n=1,2,3\) and core tensor  were drawn from \(\mathcal {N}(0,1)\). In the lower rank case, the singular values of the data decay rapidly. The 3D tensors
were drawn from \(\mathcal {N}(0,1)\). In the lower rank case, the singular values of the data decay rapidly. The 3D tensors  were given by a power function \(x_{i,j,k} = 1/\root p \of {i^p + j^p +k^p}\), where p is a power parameter controlling the singular values of
were given by a power function \(x_{i,j,k} = 1/\root p \of {i^p + j^p +k^p}\), where p is a power parameter controlling the singular values of  (here, p \(=\) 10). It is noted that, for the additional noise, SNR \(=\) 0dB indicates that the power of signal is equal to the volume of noise, while SNR>0 and SNR<0 represents a less noisy and a much noisier case, respectively.
(here, p \(=\) 10). It is noted that, for the additional noise, SNR \(=\) 0dB indicates that the power of signal is equal to the volume of noise, while SNR>0 and SNR<0 represents a less noisy and a much noisier case, respectively.
4.2.2 Real-world datasets
Three YUV video sequences (“News”, “Hall”, “M &D”)Footnote 1 were utilized for denoising evaluations. The sequences were converted into fourth-order RGB tensors with a size of 288 pixels \(\times \) 352 pixels \(\times \) 3 RGB \(\times \) 300 frames. The 123th-frame of “News” video, the 15th-frame of “M &D” video, and the 120th-frame of “Hall” video were randomly selected for demonstration. Moreover, two large-scale image datasets were used for comparison of efficiency: COIL-100 dataset of size \(32 \times 32 \times 3 \times 7200 \), and a subset of CIFAR-10 dataset of size \(32 \times 32 \times 3 \times 10000 \). Both datasets contain a number of elements at the \(10^7\) level.
4.3 Evaluation of rBKI-TK
In this section, the proposed rBKI-TK is compared with the deterministic truncated higher-order SVD (T-SVD) [11] and existing randomized tensor decomposition methods based on different sketching techniques. The non-iterative series includes Gaussian random projection (GR-SVD) [19], CountSketch sampling (CS-SVD) [21], leverage score sampling [23], importance sampling (IS-SVD) [13] and subsampled randomized Hadamard transform [13]. The iterative series includes Gaussian random power iteration (GRpi-SVD) [27], Gaussian random iteration (GR3i-SVD, GR2i-SVD) [19, 25], and Gaussian random rank revealing (GRrr-SVD) [29]. Besides, the sketch size was set by \(S_n = R_n+1/\gamma \), where the overlapping parameter \(\gamma \) was set to 0.2, as suggested in [15].
The experimental results of synthetic data were detailed in Table 3, where the the best results were shown in bold. Specifically, iterative methods obtained higher accuracy than non-iterative methods, except GR3i-SVD [25] in the lower rank case (PF-data). With different noise setting, non-iterative methods and two Gaussian random iteration methods (GR3i-SVD, GR2i-SVD) were severely invalidated by noise interference, while our method remained valid as T-SVD in terms of FErr and Fit in most cases. These results show that the proposed method was superior in terms of accuracy and efficiency in both lower and higher rank data types, as well as in severe and slight noise interference.
Moreover, to evaluate the denoising performance of rBKI-TK in real-world case, Gaussian noise with an SNR of 5dB were added to video sequences. The approximate rank was set to \(85 \times 90 \times 3 \times 30\), which was selected by T-SVD and yielded satisfactory results in terms of both accuracy and efficiency. The T-SVD, two competitive iterative methods: GRpi-SVD, GRrr-SVD, and three non-iterative methods: GR-SVD, CS-SVD, IS-SVD were adopted in comparisons. The average results were given in Table 4, and a visual comparison of denoising performance was shown in Fig. 3.
As shown, iterative methods also outperform non-iterative methods in terms of approximation accuracy in real-world data, which produced a clear foreground (e.g., the letters “MPEG4 WORLD” in the “News” video). Besides, the proposed rBKI-TK and T-SVD both provided more details of contents (e.g., moving objects in the “Hall” video) that were not captured by the other methods, which are important information.
4.4 Evaluation of rBKI-TK-TR
In the subsection, the proposed rBKI-TK-TR model were compared with the deterministic TR-ALS [6] and two existing hierarchical TR models, i.e., Gaussian random TK-TR model (GR-TK-TR) [20] and rank revealing TK-TR model (RR-TK-TR) [29] on two large-scale image datasets. For large-scale data, higher rank leads to huge computational costs, we empirically chose several sets of TR-ranks for comparison and evaluation. The TR-ranks \(J_n\) was set ranged from [3,3,3,3], [6,6,3,6] to [9,9,3,9], while the Tucker-rank was set to \({R_n =} \min (5{J_n},I_n)\), and in order to minimize information loss without reducing efficiency, the Tucker-rank \(R_n\) and sketch-size \(S_n\) were set to the same value in the hierarchical TK-TR model.
The efficiency and recovery accuracy of comparison models were detailed in Table 5. Moreover, the visual comparison in terms of fitting rate and running time were provided in Figs. 4 and 5, respectively. Comparable to the deterministic TR-ALS, our method achieved the best recovery accuracy and time efficiency among randomized methods. In all cases, the Fit of non-iterative GR-TK-TR was lower than the other methods and slightly unstable, while iterative methods, i.e., RR-TK-TR and the proposed rBKI-TK-TR performed stably and better (see Fig. 4). Besides, the consumed time by the TR-ALS was extremely larger than the other randomized methods. Our method was the most time efficient, and as the rank increases the efficiency became more prominent, even 86 times faster than TR-ALS (see Fig. 5).
5 Conclusion
In this work, a randomized Tucker decomposition method is proposed by leveraging the strength of rBKI algorithm in reducing computational complexity and noise inferences, which achieves efficient and accurate low-rank approximation for large-scale and noisy tensors. Besides, a hierarchical rBKI-TK-TR method is developed for further reducing the storage cost. Experimental results promisingly validate the superior performance of the proposed methods in large-scale processing and noise reduction. Recently, adversarial attacks in visual data has attracted much attention. Therefore, randomized tensor decomposition and its application to machine learning for improving adversarial robustness will be explored in future work.
Data availability
Data is provided within the manuscript or supplementary information files.
References
Kolda, T.G., Bader, B.W.: Tensor decompositions and applications. SIAM Rev. 51, 455–500 (2009)
Cichocki, A., Mandic, D.P., Lathauwer, L.D., Zhou, G., Zhao, Q., Caiafa, C.F., Phan, A.: Tensor decompositions for signal processing applications: from two-way to multiway component analysis. IEEE Signal Process. Mag. 32, 145–163 (2015)
Tucker, L.R.: Some mathematical notes on three-mode factor analysis. Psychometrika 31, 279–311 (1966)
Harshman, R.A., et al.: Foundations of the parafac procedure: models and conditions for an “explanatory’’ multi-modal factor analysis. UCLA Working Papers Phonet. 16(1), 84 (1970)
Oseledets, I.: Tensor-train decomposition. SIAM J. Sci. Comput. 33, 2295–2317 (2011)
Zhao, Q., Zhou, G., Xie, S., Zhang, L., Cichocki, A.: Tensor ring decomposition. arXiv:1606.05535 (2016)
Zheng, Y., Huang, T., Zhao, X., Zhao, Q., Jiang, T.-X.: Fully-connected tensor network decomposition and its application to higher-order tensor completion. In: Proceedings of the AAAI conference on artificial intelligence, vol. 35, pp. 11071–11078 (2021)
Novikov, A., Podoprikhin, D., Osokin, A., Vetrov, D.P.: Tensorizing neural networks. In: Proceedings of the 28th international conference on neural information processing systems (2015)
Yu, J., Zhou, G., Li, C., Zhao, Q., Xie, S.: Low tensor-ring rank completion by parallel matrix factorization. IEEE Trans. Neural Netw. Learn. Syst. 32, 3020–3033 (2021)
Qiu, Y., Sun, W., Zhang, Y., Gu, X., Zhou, G.: Approximately orthogonal nonnegative tucker decomposition for flexible multiway clustering. Sci. China Technol. Sci. 64, 1872–1880 (2021)
Lathauwer, L.D., Moor, B.D., Vandewalle, J.: A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 21, 1253–1278 (2000)
Lathauwer, L.D., Moor, B.D., Vandewalle, J.: On the best rank-1 and rank-(r1 , r2, ... , rn) approximation of higher-order tensors. SIAM J. Matrix Anal. Appl. 21, 1324–1342 (2000)
Wang, S.: A practical guide to randomized matrix computations with matlab implementations. CoRR arXiv:1505.07570 (2015)
Tropp, J.A., Yurtsever, A., Udell, M., Cevher, V.: Practical sketching algorithms for low-rank matrix approximation. SIAM J. Matrix Anal. Appl. 38(4), 1454–1485 (2017)
Halko, N., Martinsson, P.G., Tropp, J.A.: Finding structure with randomness: probabilistic algorithms for constructing approximate matrix decompositions. SIAM Rev. 53(2), 217–288 (2011)
Szlam, A., Tulloch, A., Tygert, M.: Accurate low-rank approximations via a few iterations of alternating least squares. SIAM J. Matrix Anal. Appl. 38(2), 425–433 (2017)
Che, M., Wei, Y.-M.: Randomized algorithms for the approximations of tucker and the tensor train decompositions. Adv. Comput. Math. 45, 395–428 (2019)
Feng, Y., Zhou, G.: Orthogonal random projection for tensor completion. IET Comput. Vis. 14, 233–240 (2020)
Qiu, Y., Zhou, G., Zhang, Y., Cichocki, A.: Canonical polyadic decomposition (cpd) of big tensors with low multilinear rank. Multimed. Tools Appl. 80(15), 22987–23007 (2020)
Yuan, L., Li, C., Cao, J., Zhao, Q.: Randomized tensor ring decomposition and its application to large-scale data reconstruction. In: IEEE international conference on acoustics, speech and signal processing (ICASSP), pp. 2127–2131 (2019)
Malik, O.A., Becker, S.: Low-rank tucker decomposition of large tensors using tensorsketch. In: Proceedings of the 32nd international conference on neural information processing systems. NIPS’18, pp. 10117–10127. Curran Associates Inc., Red Hook, NY, USA (2018)
Wang, Y., Tung, H.-Y., Smola, A., Anandkumar, A.: Fast and guaranteed tensor decomposition via sketching. In: Proceedings of the 28th international conference on neural information processing systems - Volume 1. NIPS’15, pp. 991–999. MIT Press, Cambridge, MA, USA (2015)
Larsen, B.W., Kolda, T.G.: Practical leverage-based sampling for low-rank tensor decomposition. arXiv:2006.16438 (2022)
Malik, O.A.: More efficient sampling for tensor decomposition with worst-case guarantees. In: International conference on machine learning, pp. 14887–14917 (2022). PMLR
Ma, L., Solomonik, E.: Fast and accurate randomized algorithms for low-rank tensor decompositions. Adv. Neural. Inf. Process. Syst. 34, 24299–24312 (2021)
Erichson, N.B., Manohar, K., Brunton, S.L., Kutz, J.N.: Randomized cp tensor decomposition. Mach. Learn.: Sci. Technol. 1(2), 025012 (2020)
Ahmadi-Asl, S., Abukhovich, S., Asante-Mensah, M.G., Cichocki, A., Phan, A., Tanaka, T., Oseledets, I.: Randomized algorithms for computation of tucker decomposition and higher order svd (hosvd). IEEE Access 9, 28684–28706 (2021)
Minster, R., Saibaba, A.K., Kilmer, M.E.: Randomized algorithms for low-rank tensor decompositions in the tucker format. arXiv:1905.07311 (2020)
Ahmadi-Asl, S., Cichocki, A., Phan, A.H., Asante-Mensah, M.G., Ghazani, M.M., Tanaka, T., Oseledets, I.: Randomized algorithms for fast computation of low rank tensor ring model. Mach. Learn.: Sci. Technol. 2(1), 011001 (2020)
Lanczos, C.: An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. J. Res. Natl. Bur. Stand. 45, 255–282 (1950)
Golub, G., Kahan, W.: Calculating the singular values and pseudo-inverse of a matrix. J. Soc. Indus. Appl. Math. Series B Numer. Anal. 2(2), 205–224 (1965)
Cullum, J., Donath, W.E.: A block lanczos algorithm for computing the q algebraically largest eigenvalues and a corresponding eigenspace of large, sparse, real symmetric matrices. In: 1974 IEEE conference on decision and control including the 13th symposium on adaptive processes, pp. 505–509 (1974). IEEE
Savas, B., Eldén, L.: Krylov-type methods for tensor computations i. Linear Algebra Appl. 438(2), 891–918 (2013)
Eldén, L., Dehghan, M.: A krylov-schur-like method for computing the best rank-(r1, r2, r3) approximation of large and sparse tensors. Numer. Algorithms 91, 1315–1347 (2022)
Musco, C., Musco, C.: Randomized block krylov methods for stronger and faster approximate singular value decomposition. In: Proceedings of the 28th international conference on neural information processing systems. NIPS’15, pp. 1396–1404. MIT Press, Cambridge, MA, USA (2015)
Tropp, J.A.: Randomized block krylov methods for approximating extreme eigenvalues. Numer. Math. 150, 217–255 (2021)
Wang, C., Yi, Q., Liao, X., Wang, Y.: An improved frequent directions algorithm for low-rank approximation via block krylov iteration. IEEE Transactions on Neural Networks and Learning Systems (2023)
Yu, G., Feng, J., Chen, Z., Cai, X., Qi, L.: A randomized block krylov method for tensor train approximation. arXiv preprint arXiv:2308.01480 (2023)
Eckart, C., Young, G.M.: The approximation of one matrix by another of lower rank. Psychometrika 1, 211–218 (1936)
Woodruff, D.P.: Sketching as a tool for numerical linear algebra. Found. Trends Theor. Comput. Sci. 10(1–2), 1–157 (2014)
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under Grant 62073087 and Grant U1911401.
Author information
Authors and Affiliations
Contributions
1. Yichun Qiu (First author): Conceptualization, Investigation, Methodology, Software, Writing - Original Draft. 2. Weijun Sun (Corresponding author): Resources, Funding Acquisition, Writing - Review & Editing. 3. Guoxu Zhou: Supervision, Writing - Review & Editing. 4. Qibin Zhao: Supervision, Writing - Review & Editing.
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no Conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Qiu, Y., Sun, W., Zhou, G. et al. Towards efficient and accurate approximation: tensor decomposition based on randomized block Krylov iteration. SIViP 18, 6287–6297 (2024). https://doi.org/10.1007/s11760-024-03315-w
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11760-024-03315-w







 , and obtain the low multilinear-rank approximation by
, and obtain the low multilinear-rank approximation by  .
.


 , where
, where  and
and  is the original tensor and the sketched rank-k approximation, respectively. A larger value indicates higher recovery accuracy.
is the original tensor and the sketched rank-k approximation, respectively. A larger value indicates higher recovery accuracy. , where
, where  is the deterministic rank-k approximation obtained by truncated SVD (T-SVD). When FErr = 1, the randomized rank-k approximation
is the deterministic rank-k approximation obtained by truncated SVD (T-SVD). When FErr = 1, the randomized rank-k approximation  captures the main information as well as the deterministic one
captures the main information as well as the deterministic one  . The larger the ratio, the worse the results [
. The larger the ratio, the worse the results [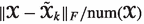 , and
, and 
