Multi-phase level set method for precise segmentation and correction of brain MRI

Abstract

Medical image segmentation as an earlier application field in image segmentation is the key technology of medical image analysis and is also a key point and difficulty in clinical application. This paper proposes an accurate and robust active contour model based on the four-phase level set for medical MR images. First we define a new energy functional by combining the data term and the length term, where the data term is defined by transforming the energy functional of the multiplicative intrinsic component optimization (MICO) model into the level set framework after adding an edge detector function. Then, when we minimize the energy functional, we use the split Bregman method to improve the convergence speed. To test the performance of our model, we do lots of experiments according to the different brain MR images, which show that even under the severe influence of bias field or shadows, our model can still segment these images well, and our model is robust to the initial contours and noise. Moreover, our model is compared with the MICO model by experimental results and the numerical values, concluding that our model is better than the MICO model no matter in segmentation accuracy or in correction effect.

1 Introduction

Magnetic resonance imaging (MRI) is based on the principle that atomic nuclei with magnetic field spacing can produce transitions between energy levels under the action of magnetic field. MRI is helpful to examine the brain energy state and cerebral blood flow of epilepsy patients and has great diagnostic value for degenerative diseases. Compared with other imaging methods, the anatomical structure revealed by MRI is very realistic, and the lesion image is shown on the basis of a good and clear anatomical background, which makes the relationship between the lesion and the anatomical structure more clear. There are many articles [1, 2, 9, 12, 16, 20, 24] to deal with magnetic resonance (MR) images, where the first five articles mainly talk about the image segmentation while others are mainly for the bias field correction.

With the development of computer technology, a large number of traditional image processing methods and models have been widely used in medical image automatic segmentation, such as threshold methods, region growing methods, statistical models, the active contour models, clustering methods, and so on. [13, 26]

Chan and Vese [3] proposed the classical active contour model based on region information in 2001, which is named the Chan–Vese (CV) model. The principle of the CV model depends on global energy minimization. When the intensity level of the target is different from the background, the CV model has a significant effect. But when the target intensity is similar to or overlapped with the background, the CV model often loses its effect and gets wrong segmentation results. In order to improve the effect of CV model to divide the different regions with similar gray values, a large number of scholars have transformed the CV model in the literature [7, 15, 17, 27]. However, in real life, the image usually has uneven intensity, especially for medical images which have more complex backgrounds and the effects of the image acquisition device. Li et al. used the Gaussian function as the kernel function to propose a local energy functional model named the region-scalable fitting energy (RSF) model [5, 11], thus effectively solving the intensity inhomogeneity problem. However, the downside of the RSF model is that it requires precise parameter setting, which is a complex process that wastes time.

To deal with the problem caused by the bias field and intensity inhomogeneity, Li et al. proposed the multiplicative intrinsic component optimization (MICO) model [10] by defining the bias field in the form of a vector product.

However, the MICO model uses the differentiation minimization method to obtain the optimal solutions, which makes the model unsmooth and cannot handle the situation of pseudo-boundary such as noise in the real life.

In order to improve the convergence rate, Goldstein and Osher [6] proposed the split Bregman algorithm which avoided the weakness that the calculation of iterative amount of the above gradient descent method is too large. The split Bregman method is a special method to rapidly solve the L1-regularization optimization problems, and now it is used in many articles [4, 6, 21,22,23, 25]. The basic idea of the split Bregman method is to transform the constrained optimization problem with regular terms of $L_1$ norm into an equivalent unconstrained optimization problem with auxiliary variables and quadratic penalty functionals according to the method of variable separation, and then decompose it into several sub-optimization problems by using Bregman iteration [14].

This paper presents a multi-phase level set method for precise segmentation and correction. The proposed model is based on the MICO model but improves it a lot. We first change the energy functional of the MICO model into a level set formulation, then a weighted length term is added into the energy. Then the split Bregman method is used to achieve faster minimization rather than the gradient descent method. The proposed model is tested with many brain MR images with promising segmentation and correction results, which demonstrates the usability of our model. Qualitative and quantitative comparisons with the MICO model also show the superior of our model in aspects of accuracy and robustness to initials and noises.

In this paper, we begin with a brief introduction of the MICO model in Sect. 2. In Sect. 3, we propose our model, respectively, in four-phase formulation, and we apply the split Bregman method to minimize energy functionals efficiently. In Sect. 4, our model is applied to a number of brain MR images and experimental results demonstrate the advantages of our model. We give a short conclusion in Sect. 5.

2 The MICO model

Li et al. [10] proposed the energy functional of the MICO model as:

$$\begin{aligned} E({\mathbf {u}},{\mathbf {c}},{\mathbf {w}})=\int _\Omega \sum \limits _{i=1}^N|I({\mathbf {x}})-{\mathbf {w}}^TG({\mathbf {x}})c_i|^2u_i({\mathbf {x}})d{\mathbf {x}}, \end{aligned}$$

(1)

where $I({\mathbf {x}})$ is the intensity of the observed image at voxel ${\mathbf {x}}$, ${\mathbf {w}}^T=(w_1,w_2,\ldots ,w_M)$ is the weight coefficient vector, the base function vector is $G^T({\mathbf {x}})=(g_1({\mathbf {x}}),g_2({\mathbf {x}}),\ldots$ $,g_M({\mathbf {x}}))$, $c_i$ is a constant and $u_i({\mathbf {x}})$ is the membership function.

The optimal solutions of the MICO model by energy minimization are as follows:

$$\begin{aligned}&{\left\{ \begin{array}{ll} \hat{c}_i&{}=\frac{\int _\Omega I({\mathbf {x}})b({\mathbf {x}})u_i({\mathbf {x}})d{\mathbf {x}}}{\int _\Omega b^2({\mathbf {x}})u_i({\mathbf {x}})\mathrm{d}{\mathbf {x}}},\quad i=1,\ldots ,N,\\ \hat{{\mathbf {w}}}&{}=\left[ \int _\Omega G({\mathbf {x}})G^T({\mathbf {x}})\left( \sum \limits _{i=1}^N c_i^2 u_i({\mathbf {x}})\right) \mathrm{d}{\mathbf {x}}\right] ^{-1}\\ &{}\quad \times \, \int _\Omega G({\mathbf {x}})I({\mathbf {x}})\left( \sum \limits _{i=1}^Nc_iu_i({\mathbf {x}})\right) \mathrm{d}{\mathbf {x}}, \end{array}\right. } \end{aligned}$$

(2)

$$\begin{aligned}&\hat{u}_i({\mathbf {x}})= {\left\{ \begin{array}{ll} 1,\quad \text {i}=\text {i}_{\text {min}}({\mathbf {x}}),\\ 0,\quad \text {i} \ne \text {i}_{\text {min}}({\mathbf {x}}), \end{array}\right. } \end{aligned}$$

(3)

where $i_{min}({\mathbf {x}})=\arg \min _{i} \{\tau _i(I({\mathbf {x}}))\}$ and $\tau _i({\mathbf {x}})=|I({\mathbf {x}})-{\mathbf {w}}^T G({\mathbf {x}})c_i|^2$.

3 The proposed model

In [10], the authors use the piecewise membership function and the derivative method directly to minimize the energy functional, and do not make any optimization on the results, making the model regard all areas different from the background as the target areas, so that it cannot solve the situation of pseudo-boundary such as noise. In this paper, we first present the four-phase level set formulations of the proposed model. Then we use the split Bregman method to minimize our new energy functionals more efficiently.

In order to build a four-phase model, let N be equal to 4. In other words, we divide the whole domain $\Omega$ into four parts $\Omega _i,i=1,2,3,4$. We rewrite the energy functional of the MICO model as:

$$\begin{aligned} E=\int _\Omega \sum \limits _{i=1}^4\lambda _i|I({\mathbf {x}})-{\mathbf {w}}^TG({\mathbf {x}})c_i|^2M_i \mathrm{d}{\mathbf {x}}, \end{aligned}$$

(4)

where we need to select two level set functions $\phi _1({\mathbf {x}})$ and $\phi _2({\mathbf {x}})$, and $M_i$ is the member function defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} M_1=H(\phi _1({\mathbf {x}}))H(\phi _2({\mathbf {x}})), \\ M_2=H(\phi _1({\mathbf {x}}))(1-H(\phi _2({\mathbf {x}}))), \\ M_3=(1-H(\phi _1({\mathbf {x}})))H(\phi _2({\mathbf {x}})), \\ M_4=(1-H(\phi _1({\mathbf {x}})))(1-H(\phi _2({\mathbf {x}}))). \\ \end{array}\right. } \end{aligned}$$

(5)

where H(z) is the Heaviside function defined as:

$$\begin{aligned} H(z)= {\left\{ \begin{array}{ll} 1&{}\quad z \ge 0,\\ 0&{}\quad z <0. \end{array}\right. } \end{aligned}$$

(6)

Taking E in (4) as a data term and combining a length term, we get a new energy functional:

$$\begin{aligned} \begin{aligned} F(\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})=E(\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})+\nu _1 L(\phi _1)+\nu _2 L(\phi _2), \end{aligned} \end{aligned}$$

(7)

where $L(\phi _i)=\int |\triangledown H(\phi _i(x))|dx,i=1,2$ represents the length of the zero level set of $\phi _i$, and $v_i$ is a positive parameter, which can be chosen as $\nu _1=\nu _2=1$ for simplicity.

In practice, a smooth function $H_\varepsilon$ is always used to approximate the Heaviside function, which is defined as:

$$\begin{aligned} H_\varepsilon (z)=\frac{1}{2}\left[ 1+\frac{1}{\pi }\arctan \left( \frac{z}{\varepsilon }\right) \right] . \end{aligned}$$

(8)

Then the energy functional becomes:

$$\begin{aligned} F_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})=E_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})+L_\varepsilon (\phi _1)+L_\varepsilon (\phi _2). \end{aligned}$$

(9)

Now we need to minimize the energy functional. Since there are four variables $\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}}$, we can fix the other three variables when solving the optimal value of one variable.

First of all, let us fix $\phi _1,\phi _2,{\mathbf {w}}$ to minimize $F_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})$ with respect to ${\mathbf {c}}$. Let $\frac{\partial F_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})}{\partial {\mathbf {c}}}={\mathbf {0}}$, we can get:

$$\begin{aligned} \hat{c}_i=\frac{\int _\Omega I({\mathbf {x}}){\mathbf {w}}^TG({\mathbf {x}})M_i^\varepsilon \mathrm{d}{\mathbf {x}}}{\int _\Omega {\mathbf {w}}^TG({\mathbf {x}}){\mathbf {w}}^TG({\mathbf {x}})M_i^\varepsilon \mathrm{d}{\mathbf {x}}},\ i=1, 2, 3, 4, \end{aligned}$$

(10)

where

$$\begin{aligned} {\left\{ \begin{array}{ll} M_1^\varepsilon =H^\varepsilon (\phi _1({\mathbf {x}}))H^\varepsilon (\phi _2({\mathbf {x}})), \\ M_2^\varepsilon =H^\varepsilon (\phi _1({\mathbf {x}}))(1-H^\varepsilon (\phi _2({\mathbf {x}}))), \\ M_3^\varepsilon =(1-H^\varepsilon (\phi _1({\mathbf {x}})))H^\varepsilon (\phi _2({\mathbf {x}})), \\ M_4^\varepsilon =(1-H^\varepsilon (\phi _1({\mathbf {x}})))(1-H^\varepsilon (\phi _2({\mathbf {x}}))). \\ \end{array}\right. } \end{aligned}$$

(11)

Then, let us fix $\phi _1,\phi _2,{\mathbf {c}}$ to minimize $F_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})$ with respect to ${\mathbf {w}}$. Let $\frac{\partial F_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})}{\partial {\mathbf {w}}}={\mathbf {0}}$, we can get:

$$\begin{aligned} {\mathbf {0}}=\frac{\partial F_\varepsilon }{\partial {\mathbf {w}}}=-2{\mathbf {l}}+2A\omega , \end{aligned}$$

(12)

where ${\mathbf {l}}$ is an M-dimensional column vector since $G({\mathbf {x}})$ is a vector defined as:

$$\begin{aligned} {\mathbf {l}}=\int _\Omega G({\mathbf {x}})I({\mathbf {x}})\left( \sum \limits _{i=1}^4c_iM_i^\varepsilon \right) \mathrm{d}{\mathbf {x}}, \end{aligned}$$

(13)

and A is an $M\times M$ matrix defined as:

$$\begin{aligned} A=\int _\Omega G({\mathbf {x}})G^T({\mathbf {x}})\left( \sum \limits _{i=1}^4c_i^2M_i^\varepsilon \right) \mathrm{d}{\mathbf {x}}. \end{aligned}$$

(14)

Thus, we have $\hat{{\mathbf {w}}}=A^{-1}{\mathbf {l}}$. Hence, the optimal solution of the bias field $\hat{b}$ is $\hat{b}=\hat{{\mathbf {w}}}^TG$.

At last, let us fix ${\mathbf {c}},{\mathbf {w}}$ and use the standard gradient descent method to minimize $F_\varepsilon (\phi _1,\phi _2,{\mathbf {c}},{\mathbf {w}})$ with respect to $\phi _i$. In other words, we should solve the following gradient flow equation:

$$\begin{aligned} \frac{\partial \phi _i}{\partial t}=-\frac{\partial F_\varepsilon }{\partial \phi _i}=-\delta _\varepsilon (\phi _i)R_i+\delta _\varepsilon (\phi _i)\text {div}\left( \frac{\bigtriangledown \phi _i}{|\bigtriangledown \phi _i|}\right) , \end{aligned}$$

(15)

where $\delta _\varepsilon (z)=H_\varepsilon '(z)=\frac{\varepsilon }{\pi (\varepsilon ^2+z^2)}$,   $i=1,2$ and

$$\begin{aligned} {\left\{ \begin{array}{ll} R_1=\lambda _1((e_3-e_1)H^\varepsilon (\phi _2({\mathbf {x}})))+\lambda _2((e_4-e_2)(1-H^\varepsilon (\phi _2({\mathbf {x}})))), \\ R_2=\lambda _3((e_2-e_1)H^\varepsilon (\phi _1({\mathbf {x}})))+\lambda _4((e_4-e_3)(1-H^\varepsilon (\phi _1({\mathbf {x}})))), \\ \end{array}\right. } \end{aligned}$$

and for $i=1,2,3,4$, $e_i({\mathbf {x}})=|I({\mathbf {x}})-{\mathbf {w}}^TG({\mathbf {x}})c_i|^2$.

By using the idea of the global convex segmentation method, we learn that the gradient flow Eq. (15) has the same stable solution with the following simplified equation:

$$\begin{aligned} \frac{\partial \phi _i}{\partial t}=-R_i+\text {div}\left( \frac{\bigtriangledown \phi _i}{|\bigtriangledown \phi _i|}\right) ,\quad i=1,2. \end{aligned}$$

(16)

For Eq. (16), we can get the energy functional as:

$$\begin{aligned} E(\phi _1,\phi _2)=\sum _{h=1}^2\left( \int _\Omega |\bigtriangledown \phi _i({\mathbf {x}})|\mathrm{d}{\mathbf {x}}+\int _\Omega \phi _i({\mathbf {x}})R_i({\mathbf {x}})\mathrm{d}{\mathbf {x}}\right) . \end{aligned}$$

(17)

In addition, in order to find the boundary more easily, we add a non-negative edge detector function $g(\sigma )=\frac{1}{1+\beta |\sigma |^2}$ into the energy functional (17), where $\beta$ is a non-negative parameter. Thus, the final energy functional is:

$$\begin{aligned} F(\phi _1,\phi _2)= & {} \int _\Omega g(|\bigtriangledown I({\mathbf {x}})|)|\bigtriangledown \phi _1({\mathbf {x}})|\mathrm{d}{\mathbf {\mathbf {x}}}\nonumber \\&\quad +\, \int _\Omega \phi _1({\mathbf {x}})R_1({\mathbf {x}})\mathrm{d}{\mathbf {x}}\nonumber \\&\quad +\, \int _\Omega g(|\bigtriangledown I({\mathbf {x}})|)|\bigtriangledown \phi _2({\mathbf {x}})|\mathrm{d}{\mathbf {x}}\nonumber \\&\quad +\, \int _\Omega \phi _2({\mathbf {x}})R_2({\mathbf {x}})\mathrm{d}{\mathbf {x}}. \end{aligned}$$

(18)

When we minimize $F(\phi _1,\phi _2)$ with respect to $\phi _1$ and $\phi _2$, limiting $\phi _i\in [q,q],q = 1\ or \ 2$, we can simply rewrite it as:

$$\begin{aligned} \min _{-q\le \phi _i\le q}F(\phi _1,\phi _2)=\min _{-q\le \phi _i\le q}\sum _{h=1}^2(|\bigtriangledown \phi _i|_g+\langle \phi _i,R_i\rangle ), \end{aligned}$$

(19)

where $|\cdot |_g$ and $\langle \cdot ,\cdot \rangle$ are the weight $L_1$ norm and the inner product, respectively, defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} |\bigtriangledown \phi _i|_g=\int _\Omega g(|\bigtriangledown I({\mathbf {x}})|)|\bigtriangledown \phi _i({\mathbf {x}})|\mathrm{d}{\mathbf {x}},\quad i=1, 2 \\ \langle \phi _i,R_i\rangle =\int _\Omega \phi _i({\mathbf {x}})R_i({\mathbf {x}})\mathrm{d}{\mathbf {x}},\quad i=1, 2. \\ \end{array}\right. } \end{aligned}$$

(20)

When solving the four-phase formulation by using the split Bregman method, two auxiliary variables ${\mathbf {d}}_1$ and ${\mathbf {d}}_2$ are needed because there are two level set functions at this moment, where ${\mathbf {d}}_1=\bigtriangledown \phi _1({\mathbf {x}})$ and ${\mathbf {d}}_2=\bigtriangledown \phi _2({\mathbf {x}})$. Adding two auxiliary variables ${\mathbf {m}}_1$ and ${\mathbf {m}}_2$, we have:

$$\begin{aligned}&(\phi _1^{k+1},\phi _2^{k+1},{\mathbf {d}}_1^{k+1},{\mathbf {d}}_2^{k+1})\nonumber \\&\quad =\arg \min \limits _{\begin{array}{c} {-q\le \phi \le q} {\mathbf {d}}_1,{\mathbf {d}}_2 \end{array}}\left[ \sum _{h=1}^2 |{\mathbf {d}}_h|_g+\langle \phi _h,R_h\rangle \right. \nonumber \\&\quad \left. +\, \frac{\mu _h}{2}\Vert {\mathbf {d}}_h-\bigtriangledown \phi _h-{\mathbf {m}}_h^k\Vert ^2\right] , \end{aligned}$$

(21)

where the iteration formula of ${\mathbf {m}}_h$ is:

$$\begin{aligned} {\mathbf {m}}_h^{k+1}={\mathbf {m}}_h^k+(\bigtriangledown \phi _h^{k+1}-{\mathbf {d}}_h^{k+1}),\ h=1,2. \end{aligned}$$

(22)

Keeping ${\mathbf {d}}_h$ $(h=1,2)$ fixed, we can get the following Eula-Lagrange equation with respect to $\phi _h$:

$$\begin{aligned} \triangle \phi _h^{k+1}=\frac{R_h^{k}}{\mu _h}+\bigtriangledown \cdot ({\mathbf {d}}_h^{k}-{\mathbf {m}}_h^{k}). \end{aligned}$$

(23)

Using the central difference and backward difference, respectively, to make $\triangle \phi _h$ and $\bigtriangledown \cdot ({\mathbf {d}}_h-{\mathbf {m}}_h)$ discretized, we can get the following iterative system:

$$\begin{aligned} {\left\{ \begin{array}{ll} \alpha _{h,i,j}^{k}&{}=d_{x,h,i-1,j}^k-d_{x,h,i,j}^k+d_{y,h,i,j-1}^k-d_{y,h,i,j}^k\\ &{}\quad -\, (m_{x,h,i-1,j}^k-m_{x,h,i,j}^k+m_{y,h,i,j-1}^k-m_{y,h,i,j}^k),\\ \beta _{h,i,j}^{k}&{}=\frac{1}{4}(\phi _{h,i-1,j}^k+\phi _{h,i+1,j}^k+\phi _{h,i,j-1}^k+\phi _{h,i,j+1}^k\\ &{}\quad -\, \frac{R_{h,i,j}^k}{\mu _h}+\alpha _{h,i,j}^k),\\ \phi _{h,i,j}^{k+1}&{}=\max \{\min \{\beta _{h,i,j}^k,q\},-q\}. \end{array}\right. } \end{aligned}$$

Keeping $\phi _1$ and $\phi _2$ fixed, we can obtain the iteration formula for updating ${\mathbf {d}}_i(i=1,2)$ with the shrinkage operator:

$$\begin{aligned} \begin{aligned} {\mathbf {d}}_i^{k+1}&=\text {shrink}_g\left( {\mathbf {m}}_i^k+\bigtriangledown \phi _i^{k+1},\frac{1}{\mu _i}\right) \\&=\text {shrink}\left( {\mathbf {m}}_i^k+\bigtriangledown \phi _i^{k+1},\frac{g}{\mu _i}\right) . \end{aligned} \end{aligned}$$

4 Numerical results and analysis

In this section, we first apply our model to brain MRI to demonstrate its performance, then we compare the experimental results between our model and the MICO model to show its superiority.

In all figures, the blue line and the red line are the active contours which are the zero level sets of the two level set functions. The blue line separates the cerebrospinal fluid and background from the gray matter and the white matter, while the red line separates the white matter and background from the gray matter and the cerebrospinal fluid, where we are interested in the white matter and the gray matter. All the experiment images can be downloaded from https://mrbrains18.isi.uu.nl/data/download/ and the data in [10]. In this paper, we use the competition data only to compare the results of our model and the MICO model numerically. We run the codes for all experiments with MATLAB 2010b on Windows 7 operating system on a Dell desktop with Intel(R) Core(TM) i5-7500 CPU, 3.40GHz 8GB RAM, and it requires 33s for our model to segment a $512\times 512$ MR image.

In order to enable readers to see the advantages and disadvantages of our model and the MICO model more clearly, we compare the image results and numerical results between the two models.

Why we only compare our model with the MICO model is because that our model is an improved model of the MICO model, where we enhance the ability of the MICO model for dealing with the images effected by noises. Meanwhile, the MICO model has already been compared with results from other software, such as SPM, FSL and FANTASM by Li et al. in [10]. Hence, we only compare our model with the MICO model. The main function of our model is to improve the noise sensitivity of the MICO model. Therefore, in this paper, we compared our model with the MICO model and obtained that the noise robustness was superior to the MICO model, rather than to compare the results with other methods in the challenge.

In the following experiments, we can divide 8 parameters including $\beta$, $\varepsilon$, $\mu _{1}$, $\mu _{2}$, $\lambda _{1}$, $\lambda _{2}$, $\lambda _{3}$, $\lambda _{4}$ into four groups according to their effects. The parameter $\beta$ in the edge detection function determines the detail level of the segmentation. When $\beta$ takes a large value, our model can get more contours to give more detailed segmentation results. So, if we only want to get a rough contour, we can choose a relatively small $\beta$. The parameter $\varepsilon$ is used in the smooth approximation function $H_{\varepsilon }$ of the Heaviside function H. The parameters $\lambda _{i},i=1,2,3,4$ are used to balance the energy inside and outside the contour, where the parameters $\lambda _{1}$, $\lambda _{2}$ are for the first level set function and the parameters $\lambda _{3}$, $\lambda _{4}$ are for the second level set function, respectively. The parameters $\mu _{i},i=1,2$ are the coefficients of the quadratic penalty functions in the minimization process of applying the split Bregman method, and its main effect is to strictly constrain the equations $d_{i}=\nabla \phi _{i},i=1,2$. In our experiment, we set $\beta =5$, $\varepsilon =0.0001$, $\lambda _{1}=\lambda _{2}=0.0025$, $\lambda _{3}=\lambda _{4}=0.0023$, $\mu _{1}=\mu _{2}=1$ for all clinical images.

4.1 Performance of our model

First, we apply our model to five brain MR images with different initial contours in Fig. 1. Original images with initial contours, bias fields, bias corrected images and segmentation results are shown from top to bottom. From these five groups of results, especially the segmentation results in the last row, the final brain image can be segmented into four regions by the active contours. Therefore, the proposed model is able to successfully deal with images affected by bias fields.

Fig. 1

Results of our model for five brain MR images. Row 1: Original images with initial contours. Row 2: Bias fields. Row 3: Bias corrected images. Row 4: Segmentation results. The blue line and the red line are the active contours which are the zero level sets of the two level set functions

In order to test our model’s ability to handle images with different inhomogeneity, we add different shadows to the same images and add different shadows to different images, respectively, in Fig. 2. Column 1 shows original images, Column 2 shows images after adding shadows with initial contours, Column 3 shows bias fields, Column 4 shows corrected results, and Column 5 shows segmentation results. In the first two rows, we add different shadows to the same image, where a serious over dark shadow is added to the top in Row 1, while a dark shadow of “snake” shape is added in Row 2. In the last two rows, we add different shadows to two different images, where the darkness is more serious in Row 3. We can see that all added shadows are with serious inhomogeneity, especially in the top part for all images and the left part in the second image in Row 3. It is really a big challenge to detect the boundaries from the background; however, our model can segment them very well, which can be observed from the last column. Besides, the added bias can be removed and we can obtain much more homogeneous corrected images shown in Column 4, which are very close to original images. In a word, our model has strong robustness to intensity inhomogeneity.

Fig. 2

Results of our model for four brain MR images with different intensity inhomogeneity and initials. Column 1: Original images. Column 2: Images with shadows and initial contours. Column 3: Bias fields. Column 4: Bias corrected images. Column 5: Segmentation results

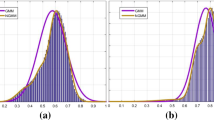
In order to explain more specifically that our model can deal with inhomogeneity, we, respectively, listed the histograms of the shadow images in Fig. 2 and the corrected result images, as shown in Fig. 3. The shadow images and their histograms are, respectively, shown in Column 1 and Column 2, while the bias field corrected results and their corresponding histograms are shown in Column 3 and Column 4. By comparing Column 2 and Column 4, we can clearly see that in Column 2 the histogram peaks are concentrated or multiple peaks occur, while in Column 4 there are only four histogram peaks which represent the background, the cerebrospinal fluid, the gray matter (GM) and the white matter (WM), respectively, from left to right. This suggests that our model can effectively reduce the influence of the inhomogeneity and give more homogeneous correction images.

Fig. 3

Histogram comparison of the shadow images and bias corrected images with our model. Column 1: Shadow images. Column 2: Histograms of shadow images. Column 3: Bias corrected images. Column 4: Histograms of bias corrected images

Fig. 4

Results of our model for a brain MR image with different initial contours. Column 1: Different initials. Column 2: Bias fields. Column 3: Bias corrected images. Column 4: Segmentation results

Although the initial contours we use in the above experiment are rectangular, our model is also applicable with other shapes of initial contours. In Fig. 4, we show that our model is insensitive to initial contours by using different initial contours for the same experimental MR image. Different shapes of initial contours are used in this experiment, including the square initials in (a), the triangle initials in (e), the circular initials in (i) and the random initials in (m). Through the consistency of segmentation results in the last column, we can see that our model is insensitive to initial contours.

4.2 Comparison with the MICO model

In Fig. 5, we compare our model with the MICO model. In Row 1, we present original images, while Row 2 and Row 3 show segmentation results of our model and the MICO model, respectively. For the segmentation results of these test images, our model and the MICO model are very similar. But careful observation in the green contour shows that our model can reduce the impact of background compared to the MICO model.

Fig. 5

Comparison of segmentation results between our model and the MICO model. Row 1: Original images. Row 2: Our model. Row 3: The MICO model. The green line contours the difference.

Therefore, in order to see the advantages of our model more clearly, we compared our model with the MICO model by adding different noises to the same images, as shown in Fig. 6. Column 1 shows original images, where the first two rows are different levels of Gaussian noise with mean 0, and variance 20 or 30, and the last two rows are different levels of Rician noise[8] with SNR (signal-to-noise ratio) 10 or 15. Column 3 and Column 4, respectively, show the segmentation results of our model and the MICO model. From the comparison of segmentation results in Fig. 6, we can distinct that compared with the MICO model, our model can segment noisy images more accurately, so our model can be used for false boundary images.

Fig. 6

Segmentation results of our model and the MICO model for four brain MR images with Gaussian noise. Column 1: Original images. Column 2: Images with different levels of Gaussian noise. Column 3: Segmentation results of our model. Column 4: Segmentation results of the MICO model. Row 1 to Row 2: Gaussian noise with mean 0, and variance 20 or 30. Row 3 to Row 4: Rician noise with SNR 10 or 15

Fig. 7

Comparison of bias corrected images among our model, the MICO model and the N4ITK algorithm. Column 1: Original images. Column 2: Our model. Column 3: The MICO model. Column 4: The N4ITK algorithm

In Fig. 7, we show the comparison of bias corrected images among our model, the MICO model and the N4ITK algorithm. The first column shows the original images, and the other three columns show the different bias corrected images with our model, the MICO model and the N4ITK algorithm. The corrected images from the N4ITK algorithm [18] in Column 4 can be downloaded directly from https://mrbrains18.isi.uu.nl/data/download/. This figure shows that our model can avoid the influence of bias field and get better correction results.

4.3 Numerical analysis

In this section, we do some numerical analysis to show the superiority of segmenting and correcting MRI with our model. To evaluate our model from two aspects of the correction effect and segmentation effect, respectively, four indexes are used in this paper, including the coefficient of joint variation (CJV) value, the coefficient of variations (CV) value, the Jaccard similarity (JS) index and the DICE similarity (DICE) value. The CV and CJV values are mostly used to evaluate the correction effect of the model. A good bias correction algorithm will make the CV and CJV values get small in each different region of the corrected image. In general, the smaller the CV and CJV values, the better bias field correction results.

For any target region C, the CV value and the CJV value are defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} CV(C)=\frac{\sigma (C)}{\mu (C)}, \\ CJV(C_1,C_2)=\frac{\sigma (C_1)+\sigma (C_2)}{|\mu (C_1)-\mu (C_2)|}, \end{array}\right. } \end{aligned}$$

(24)

where $\mu$ and $\sigma$ are the mean and variance of intensity values in the region, respectively, and $C_1$ and $C_2$ are two regions in the same image. According to the definition in (24), the CV value is defined by the ratio of the mean to the variance for one region. The smaller the value is, the smaller the difference of image intensity in a region is, namely the more uniform it is. The disadvantage of CV is that it does not provide any information about the overlap of the intensity distributions of different tissue categories. Therefore, we introduce the CJV value to estimate the overlap between the two organization categories. The CJV value is calculated from two regions which illustrates that the means of image intensity in the two regions are significantly different, if the CJV value is small, hence we can separate the different regions clearly. Hence the CV and the CJV values can be used to compare the correction results of different models even if there is no standard segmentations as ground truth [19].

The DICE value and the JS index are two indicators to measure the similarity of two regions A and B given by the algorithm and the ground truth, respectively, and they are often used to evaluate the quality of segmentation. They are defined as:

$$\begin{aligned} {\left\{ \begin{array}{ll} DICE(A,B)=\frac{2*|A\bigcap B|}{|A|+|B|},\\ JS(A,B)=\frac{|A\bigcap B|}{|A\bigcup B|}, \end{array}\right. } \end{aligned}$$

(25)

where $|\cdot |$ is the number of pixels in regions. The DICE value is satisfied $0\le DICE(A,B)\le 1$, and the higher the similarity of A and B is, the closer the DICE value is to 1, which means the better the segmentation result is. The JS value has the same properties.

Fig. 8

Numerical comparison of CV and CJV values for 50 images with our model and the MICO model

We compare the CV value and the CJV value of correction images with our model and the MICO model for almost 50 images, as shown in Fig. 8. From the box plots, we can see that our model is better than MICO model in terms of bias field correction, since the CV value and the CJV value for WM and GM with our model are smaller than those with the MICO model.

Fig. 9

Numerical comparison of DICE and JS values for 50 images with our model and the MICO model

We compare the DICE values and the JS index for WM and GM with our model and the MICO model for almost 50 MR images, and we show the box plots of DICE values in Fig. 9, where we can see that the DICE values and the JS index for both WM and GM are significantly higher than those of the MICO model. In the part of the statistical test, the null hypothesis is that there is no significant difference in DICE values between our model and the MICO model. And the alternative hypotheses is that the DICE values between our model and the MICO model have significant difference. Besides, we set the significance level equal to 5% here. According to the above definitions, we use the one-way ANOVA to obtain the P value by using the SPSS software. Due to the P values of white matter 0.038 and gray matter 0.032 are both less than 0.05, we can conclude that the null hypothesis is rejected, and the alternative hypothesis is established, that is, the DICE values of these two models are significantly different. Figure 9 demonstrates that our model can obtain more accurate segmentation results than the MICO model.

5 Conclusion

This paper presents a multi-phase level set method for precise segmentation and correction of brain MRI. The energy functional is given especially in the four-phase formulation and then minimized by the split Bregman method. In order to show the segmentation and correction ability of our model, lots of experimental results are presented. During the experiment, we firstly demonstrate the feasibility of our model based on the segmentation results of a large number of images. Different kinds of shadows are added to the brain images to verify our model’s ability to deal with different inhomogeneity. Furthermore, we also verify that our model is robust to initial contours. Compared with the MICO model, another advantage of our model is its insensitivity to noises. Meanwhile, we compare the bias-corrected results among our model, the MICO model and the N4ITK algorithm. Furthermore, we also verify that our model is robust to initial contours. Besides, we also calculate some numerical values, such as the CV, CJV and DICE, JS values, to demonstrate the superiority of our model. The segmentation results and the corrected results all declare that our model is an accurate and robust active contour model for brain MR image segmentation and correction. In conclusion, our model has superiority in segmentation and correction of inhomogeneous and noisy brain MRI in practical application.