A level set method for brain MR image segmentation under asymmetric distributions

Abstract

Magnetic resonance (MR) image segmentation plays an essential role for brain disease diagnosis; however, suffered from low contrast, intensity inhomogeneity, noise and asymmetry of the intensity distribution, segmentation methods are always difficult to achieve satisfactory results. In this paper, we propose a novel level set method for brain MR image segmentation with consideration of these problems. We firstly generate a new region descriptor based on asymmetric Gaussian distributions in order to fit different shapes of observed nonsymmetric data. Secondly, we utilize the spatial distance and intensity similarity information of neighborhood pixels to extract local anisotropic spatial information to balance the noise reduction and detail preservation. After that, the extracted information and bias field information are combined to improve the asymmetric region descriptor utilized in the level set framework. Finally, we define a maximum likelihood energy functional on the whole image, integrating the local anisotropic spatial information, the bias field information and the asymmetric distributions. The experimental results on synthetic and clinical images demonstrated that our method can achieve desirable performance in spite of the severe noise and intensity inhomogeneity.

1 Introduction

Segmenting brain MR images into non-overlapped regions (gray matter (GM), white matter (WM) and cerebrospinal fluid (CSF)) is an important first step in almost every task of brain clinical diagnosis and neuroscience research. Accurate segmentation can provide more and useful information [1]. However, suffered from low contrast, noise and intensity inhomogeneity [2], automated MR image segmentation is still a very challenging research topic.

Several classic models have been proposed for medical image segmentation [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17]. The active contour model [3], also named as Snake model, is a widely applied model with sub-pixel accuracy. However, the active contour model is sensitive to the choice of weighted parameters and thus is difficult to deal with adaptability topological changes. To solve these problems, Osher and Sethican presented a level set model [4], which performs curves/surfaces on a fixed Cartesian grid without any parameters so that it is easy to capture the changes that change topology. The level set-based approaches have been increasingly applied to image segmentation in the past decade [4,5,6,7,8,9,10,11,12,13,14,15,16,17] and can be categorized into two major classes: edge-based methods [4,5,6] and region-based methods [7,8,9,10,11,12,13,14,15].

The edge-based methods use edge information to guide the evolution of the curves/surfaces. These models are sensitive to the initial conditions and sensitive to noise and weak object boundaries. To tackle this problem, the region-based models aim to divide images into different regions by using a global or local certain region descriptor. The global region-based approaches [8] used global information to eliminate noise and weak edges. However, most of them depend on the assumption of non-intensity homogeneity. The local region-based methods [9,10,11,12,13] assume that the intensity of neighborhood is homogeneity and thus define the local descriptor of the level set model. Typical examples are local binary fitting (LBF) model [9, 10], local Gaussian distribution fitting (LGDF) model [11] and Zhang’s model [14]. The LBF only used local mean information to extract the local region descriptor, which makes it sensitive to variance changes. The LGDF model introduced the local Gaussian distribution to generate the descriptor to achieve performances that are more accurate; however, Brox [16] has proved that the spatially varying variance might be unstable because of its local property, which leads to inaccurate results when segmenting small objects. Based on this theoretical analysis, Zhang’s method [14] define a region descriptor by using the Gaussian distributions with local means and global variances. In order to improve the segmentation performance with severe intensity inhomogeneity, the Zhang’s method transformed pixel intensities into another domain, where the intensity distribution of each object is still Gaussian but better separated. The method can obtain the bias field and segment the images simultaneously, even when they have severe intensity inhomogeneity. But the constant convolutional kernel applied in the Zhang’s method leads the estimated bias field unsmoothness. Furthermore, in clinical brain MR image evaluation, the intensity distribution of each tissue is usually nonsymmetric. For this reason, the regions segmented by level set models based on the symmetric distribution, such as Gaussian distribution, cannot achieve satisfying results in a nonsymmetric situation [17]. Recently, machine learning methods have been successfully employed for image segmentation in the medical domain, such as brain segmentation based on 3D convolutional network and transfer learning [18], blood vessels detection via learning approaches [19, 20] and skin lesion segmentation using scale-oriented neural network [21].

In this paper, we present an improved level set method for brain MR image segmentation. By exploiting the local region statistics, we found that spatial information could improve the accuracy of level set methods. In order to balance the noise reduction and detail preservation, we utilize the local spatial Euclidean distance and intensity similarity to extract local anisotropic spatial information from the neighbor patch. To extract the asymmetric information, we defined an asymmetric region descriptor in each tissue region as a mixture descriptor to model the inhomogeneous tissue region. The bias field is then denoted as a linear combination of a set of orthogonal basis functions and coupled into the asymmetric region descriptor. Then, the final energy functional is presented combining local anisotropic spatial information, the bias field information and the asymmetric region descriptor. The proposed method can achieve satisfying results with a smooth bias field in spite of severe intensity inhomogeneity, low contrast and noise. We also demonstrate extensive simulations to prove that the proposed model is superior to other region-based level set methods.

2 Notations

2.1 Local binary fitting model (LBF)

Given an image $I$, the LBF model [9] assumed that the intensity values of each object in each local region are constant and defined the energy functional as:

$$ \begin{aligned} & E_{\text{LBF}} (\phi ,f_{1} ,f_{2} ) \\ & \quad = \mu \int_{\varOmega } {|\nabla H(\phi (x))|} {\text{d}}x + v\int_{\varOmega } {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} (|\nabla \phi (x)| - 1)^{2} {\text{d}}x \\ & \quad\quad + \lambda_{1} \int_{\varOmega } {\int_{\varOmega } {K_{\sigma } } } (x - y)|I(y) - f_{1} (x)|^{2} H(\phi (y)){\text{d}}y{\text{d}}x \\ & \quad \quad + \lambda_{2} \int_{\varOmega } {\int_{\varOmega } {K_{\sigma } } } (x - y)|I(y) - f_{2} (x)|^{2} (1 - H(\phi (y))){\text{d}}y{\text{d}}x \\ \end{aligned} $$

(1)

where $\lambda_{1} ,\lambda_{2} ,\mu$ and $\nu$ are fixed positive parameters. $K_{\sigma }$ is a Gaussian kernel function with fixed standard deviation $\sigma$. $f_{1}$ and $f_{2}$ are local fitting functions to approximate the local mean intensities inside and outside of the contour. $H(\phi )$ is the Heaviside function, which satisfies:$H(\phi ) = \left\{ {\begin{array}{*{20}c} 0 & {\phi < 0} \\ 1 & {\phi \ge 0} \\ \end{array} } \right.$. In practice, the Heaviside function is approximated by using a smooth function $H_{\varepsilon }$:$H_{\varepsilon } (x) = \frac{1}{2}[1 + \frac{2}{\pi }\arctan (\frac{x}{\varepsilon })]$. The first term of the energy function is a regular term of the curve length. The second term is a penalty term to preserve $|\nabla \phi (x)| = 1$.

The LBF model extracts the local region descriptor by local mean values to alleviate the effect of intensity inhomogeneity; however, the descriptor only utilizes the local mean values without any variance information, which may lead to inaccurate results when segmenting images with variance changes [11].

2.2 Local Gaussian distribution fitting model (LGDF)

In order to utilize more information into the model, Wang et al. [11] presented the region descriptor by using a Gaussian distribution. The energy functional is denoted as:

$$ \begin{aligned} & E_{\text{LGDF}} (\phi ,\mu_{1} ,\sigma_{1}^{2} ,\mu_{2} ,\sigma_{2}^{2} ) \\ & \quad = \mu \int_{\varOmega } {|\nabla H(\phi (x))|} {\text{d}}x + v\int_{\varOmega } {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} (|\nabla \phi (x)| - 1)^{2} {\text{d}}x \\ & \quad \quad + \lambda_{1} \int_{\varOmega } {\int_{\varOmega } { - K_{\sigma } } } (x - y)\log p_{i,x} (I(y))H(\phi (y)){\text{d}}y{\text{d}}x \\ & \quad \quad + \lambda_{2} \int_{\varOmega } {\int_{\varOmega } { - K_{\sigma } } } (x - y)\log p_{i,x} (I(y))(1 - H(\phi (y))){\text{d}}y{\text{d}}x \\ \end{aligned} $$

(2)

where $p_{i,x} (I(y))$ is estimated by using a Gaussian distribution with mean $\mu_{i}$ and variance $\sigma_{i}^{2}$:

$$ p_{i,x} (I(y)) = \frac{1}{{\sqrt {2\pi } \sigma_{i} }}\exp \left( { - \frac{{(I(y) - \mu_{i} (x))^{2} }}{{2\sigma_{i}^{2} (x)}}} \right) $$

(3)

By introducing more local information, the LGDF model improved the accuracy of segmentation performance; however, the Gaussian distribution only uses the intensity distribution information that makes the LGDF method still sensitive to severe noise without considering any spatial information. Furthermore, the Gaussian is symmetric and thus causes segmentation sensitive to the outlier.

2.3 Bayesian bounded asymmetric mixture model (BAMM)

In order to fit different data shapes, Nguyen et al. [22] proposed an asymmetric Gaussian distribution to model the component density in each class. The proposed probability density function is written as:

$$ p(I_{i} |\varOmega_{j} ) = \sum\limits_{k = 1}^{{K_{j} }} {u_{jk} N(I_{i} |\mu_{jk} ,\varSigma_{jk} )} $$

(4)

where $N(I_{i} |\mu_{jk} ,\varSigma_{jk} )$ is the Gaussian distribution with parameters: mean $\mu_{jk}$ and variance $\varSigma_{jk}$. $K_{j}$ is the number of the Gaussian distributions that is used to denote the region $\varOmega_{j}$. $u_{jk}$ is the weighting factor and satisfies: $u_{jk} \ge 0$ and $\sum\nolimits_{k = 1}^{{K_{j} }} {u_{jk} } = 1$.

Figure 1 shows the tissue distributions based on a manual partition of a real dataset generated from the Internet Brain Segmentation Repository (IBSR2_02). It can be observed that the histograms of the GM and WM are nonsymmetric. For this reason, the result of the symmetric distribution such as Gaussian distribution might be poor. By using the nonsymmetric Gaussian distribution, with $K_{j} = 4$, makes the more flexibility to fit the shape of nonsymmetric and non-Gaussian images than the Gaussian distribution.

Fig. 1

Comparison of the component. a The histogram of the GM in IBSR2_02 and the result of Gaussian distribution and nonsymmetric Gaussian distribution. b The corresponding results on WM in IBSR2_02

3 Proposed algorithm

Suppose there are $N$ regions in the observed image $I$. The segmentation model aims to divide the image into a set of disjoint regions $\{ \varOmega_{i} \}_{i = 1}^{N}$, which satisfies the following two conditions: $\varOmega = \cup_{i = 1}^{N} \varOmega_{i}$ and $\varOmega_{i} \cap \varOmega_{j} = \emptyset ,\forall i \ne j$. For brain MR image segmentation, the image region is divided into WM, GM, CSF and the background. The four regions can be represented by using two level sets $\phi_{1}$ and $\phi_{2}$. The objective function of the level set model can be written as:

$$ \begin{aligned} E(\phi_{1} ,\phi_{2} ) & = \int_{\varOmega } {\sum\limits_{i = 1}^{N} {M_{i} (\phi_{1} ,\phi_{2} )} } F_{i} (x){\text{d}}x \\ & \quad + \alpha \sum\limits_{j = 1}^{2} {\int_{\varOmega } {|\nabla H(\phi_{j} (x))|{\text{d}}x} } \\ & \quad + \nu \sum\limits_{j = 1}^{2} {\int_{\varOmega } {1/2(|\nabla (\phi_{j} (x)| - 1)^{2} {\text{d}}x} } \\ \end{aligned} $$

(5)

The region membership function $M_{i} (\phi_{1} ,\phi_{2} )$ is denoted as: $M_{1} (\phi_{1} ,\phi_{2} ) = H(\phi_{1} )H(\phi_{2} )$, $M_{ 2} (\phi_{1} ,\phi_{2} ) = H(\phi_{1} )( 1 { - }H(\phi_{2} ))$, $M_{ 3} (\phi_{1} ,\phi_{2} ) = ( 1 { - }H(\phi_{1} ))H(\phi_{2} )$, $M_{4} (\phi_{1} ,\phi_{2} ) = ( 1 { - }H(\phi_{1} ))( 1 { - }H(\phi_{2} ))$.

$F_{i} (x)$ is the region descriptor, motivated by the BAMM [17]. In this paper, we propose an asymmetric region descriptor by using the asymmetric Gaussian distribution to fit different shapes of observed data and incorporating the spatial information.

3.1 Asymmetric region descriptor

In order to fit nonsymmetric data of each region, the region descriptor is defined as:

$$ F_{i} (x) = \sum\limits_{j = 1}^{{K_{i} }} {u_{i,j}^{m} ( - \log p_{ij} (R_{x}^{'} ,P_{x}^{'} ,B_{x} |\mu_{ij} ,\varSigma_{ij} ))} $$

(6)

where $p_{ij} ( \cdot ) = (2\pi )^{ - D/2} |\varSigma_{ij} |^{ - 1/2} \exp ( - \frac{1}{2}(R_{x}^{'} \cdot (P_{x}^{'} - B_{x} \mu_{ij} ))^{\text{T}} \varSigma_{ij}^{ - 1} (R_{x}^{'} \cdot (P_{x}^{'} - B_{x} \mu_{ij} )))$.

$u_{ij}$ is within-region membership which represents the probability of current pixel in the label $\varOmega_{ij}$ and satisfies: $u_{ij} \ge 0$ and $\sum\nolimits_{j = 1}^{{K_{i} }} {u_{ij} } = 1$. The $\mu_{ij}$ and $\varSigma_{ij}$ are the mean and variance.$m \in (1,\infty )$ is the fuzzy coefficient. In this paper, we set $m = 2$. $P_{x}$ is the square neighbor patch centered at $x$ with size $r$.$R_{x}$ is the anisotropic inner relationship of $P_{x}$, which will be illustrated in Sect. 3.2. $P_{x}^{'} \in R^{M}$ and $R_{x}^{'} \in R^{M}$ are arranged from $P_{x}$ and $R_{x}$, respectively.$M = (2r + 1)^{2}$. $B_{x}$ is the bias field. The proposed region descriptor is then degraded into the descriptor of LBF when $K_{i} = 1$, $r = 1$ and $B_{x} = 1$.

3.2 Improved anisotropic spatial information

The traditional Gaussian distribution or asymmetric Gaussian distribution only applies intensity information without any spatial information, which makes it sensitive to noise. In this section, we utilize improved anisotropic spatial information, which can be combined with the Gaussian distribution or asymmetric Gaussian distribution easily.

The spatial information has been widely used in noise reduction. Caldairou et al. [23] introduced the nonlocal information that contained more detailed information. In the definition of the nonlocal information, the similarity value of two pixels is calculated by using the Euclidean distance of their neighbor patches:

$$ d(x,y) = \left\| {P_{x} - P_{y} } \right\|_{F}^{2} $$

(7)

Pixels with small distance will be regarded as similar points. All the pixels in the neighbor patch have the same inner weights to represent the isotropy. Figure 2 illustrates the defect of traditional neighbor patch representation within $3 \times 3$ square neighbor patches. The image has object points, including edge points ($A$), corner points ($C$), inner points ($F$) and end points ($E$).$B$ is a background point. $D$ is a noise point (single point). $d(C,B) = 3$ is more less than $d(C,A) = 6$ and $d(C,F) = 5$, which leads the point $C$ be regarded to be a background point. Similarly, the end point $E$ will be determined as a background point. The example demonstrates the segmentation without any inner relationship information.

Fig. 2

Analysis of the neighborhood similarities of edge point, corner point, noise point and end point. Points A, B, C, D, E and F are edge point(object point), background point, corner point(object point), background point, end point(object point) and inner point(object point), respectively

As analyzed above, the traditional nonlocal information is difficult to preserve the detail information for its isotropy. To overcome this shortcoming, we propose a local similarity function to balance between noise reduction and detail preservation:

$$ R_{x} = \left\{ {\begin{array}{*{20}l} {\frac{{d_{s} (x,y)}}{{\int_{{y \in \{ P_{x} \} }} {d_{s} (x,y)\,{\text{d}}y} }}} \hfill & {{\text{if}}\quad \, x \in \{ {\text{single point}}\} } \hfill \\ {\frac{d(x,y)}{{\int_{{y \in \{ P_{x} \} }} {d(x,y)\,{\text{d}}y} }}} \hfill & {\text{else}} \hfill \\ \end{array} } \right. $$

(8)

where $d_{s} (x,y) = \exp ( - \left\| {{\text{Mean}}(P_{x} ) - I(y)} \right\|^{2} /\zeta )/d_{l} (x,y)$ is distance between the single point $x$ and its neighbor pixel $y$, $d_{l} (x,y)$ is the spatial Euclidean distance, ${\text{Mean}}(P_{x} )$ is the mean value of $P_{x}$, $\zeta$ is a positive constant and depends on the standard deviation of the noise [24]. $d(x,y) = \frac{{\exp ( - \left\| {I(x) - I(y)} \right\|^{2} /\zeta )}}{{d_{l} (x,y)}}$ is the distance between the normal pixel and its neighbor pixel $y$. In each neighbor patch, the points with similar intensity values of the center point will have higher weights. We found that the single point had much larger or less intensity values than the neighbor points, and the end point had at least one or two neighbor pixels with similar intensity values. Based on this assumption, we regard $x$ as a single point when $1/(\int_{{y \in \{ P_{x} \} }} {\exp ( - \left\| {I(x) - I(y)} \right\|^{2} /\zeta ){\text{d}}y} ) > T$. $T$ is a nonnegative parameter and set as 3/4 in this paper. This similarity function (Eq. (8)) is different with our previous work [24], which has not considered the spatial Euclidean distance. Based on the Markov random field theory, the pixel with small Euclidean distance should have a higher similarity. Therefore, our improved similarity function can preserve more details.

The inner relationships in the neighbor patches of $C$(corner point), $D$(single point) and $E$(end point) are shown in the right side of Fig. 2. From these values, we can observe that the improved inner relationship is anisotropic. The traditional Euclidean distances between the neighbor patch of $E$ and the neighbor patch of $A$(edge point), $F$(inner point), $D$ (background point) are 6, 7 and 1, respectively. In this condition, point $E$ will be determined as a background point. To obtain a reasonable distance measurement, we modify the Euclidean distance as:$d(P_{x} ,P_{y} |R_{x} ) = \left\| {R_{x} \cdot (P_{x} - P_{y} )} \right\|_{F}^{2}$, where $R_{x}$ is defined in Eq. (8). The improved corresponding distances are $0.2499$, $2.56 \times 10^{ - 9}$ and 0.2499, respectively. Based on the new distance measurement, the point $E$ is regarded as an object point.

3.3 Bias field estimation

The bias field is generated during machine shooting and leads to inaccurate segmentation [11]. It is smooth across the image region and makes the intensity values of the same tissues vary with the location. Based on its property, the bias field can be modeled by using a linear combination of orthogonal polynomials [20, 21, 23,24,25]:

$$ B(x) = \sum\limits_{l = 1}^{L} {q_{l} s_{l} (x) = Q^{\text{T}} S(x)} $$

(9)

where $q_{l}$ is the combination coefficient, $P$ is the maximal degree of the polynomials $s(x)$. Then, for the 2D case, $L = (P + 1)(P + 2)/2$, and for 3D case, $L = (P + 1)(P + 2)(P + 3)/6$. $s(x)$ satisfies

$$ \int_{\varOmega } {s_{i} (x)s_{j} (x){\text{d}}x = \delta_{ij} } $$

(10)

When $i = j,\delta_{ij} = 1$, otherwise $\delta_{ij} = 0$.

Then, the functional of the proposed method can be written as:

$$ E(\phi_{1} ,\phi_{2} ) = E_{1} (\phi_{1} ,\phi_{2} ) + \alpha E_{2} (\phi_{1} ,\phi_{2} ) + \nu E_{3} (\phi_{1} ,\phi_{2} ) $$

(11)

where $E_{1} (\phi_{1} ,\phi_{2} ) = \int_{\varOmega } {\sum\nolimits_{i = 1}^{N} {M_{i} (\phi_{1} ,\phi_{2} )} } F_{i} (x){\text{d}}x$, $E_{2} (\phi_{1} ,\phi_{2} ) = \sum\nolimits_{j = 1}^{2} {\int_{\varOmega } {|\nabla H(\phi_{j} (x))|{\text{d}}x} }$, $E_{3} (\phi_{1} ,\phi_{2} ) = \sum\nolimits_{j = 1}^{2} {\int_{\varOmega } {1/2(|\nabla (\phi_{j} (x)| - 1)^{2} {\text{d}}x} }$.

Remark

Our method is superior to LGDF for several reasons: Firstly, the LGDF only uses a local Gaussian distribution to extract the local region descriptor, which is symmetric and only utilizes intensity information, so that the LGDF is hard to achieve satisfying results from segmenting images with severe noise. The local region descriptor can be regarded as a special case of our asymmetric region descriptor. Secondly, the LGDF used a local Gaussian kernel convolution to preserve the smoothness of the bias field. When an image has a different intensity inhomogeneity level, the parameter of the kernel needs to be changed. Furthermore, the LGDF cannot estimate the bias field. It can only define a local region descriptor to alleviate the effect of the bias field, which leads the method to have double integrations. In our method, we have considered the bias estimation and utilized the asymmetric region descriptor. Therefore, our method only needs one integration and is more efficient.

4 Parameter learning

Fixing $u,\mu ,\varSigma$ and $B$, minimizing $E$ with respect to each variable to $\phi_{1}$ and $\phi_{2}$, respectively, we have corresponding gradient-descent formulas:

$$\begin{aligned} & \frac{{\partial \phi_{1} }}{\partial t} = \alpha \delta (\phi_{1} ){\text{div}}\left( {\frac{{\nabla \phi_{1} }}{{\left| {\nabla \phi_{1} } \right|}}} \right) \\ & \quad + \nu \left( {\nabla^{2} \phi_{1} - {\text{div}}\left( {\frac{{\nabla \phi_{1} }}{{\left| {\nabla \phi_{1} } \right|}}} \right)} \right) - \delta (\phi_{1} )N_{1} \end{aligned} $$

(12)

$$\begin{aligned} & \frac{{\partial \phi_{2} }}{\partial t} = \alpha \delta (\phi_{2} ){\text{div}}\left( {\frac{{\nabla \phi_{2} }}{{\left| {\nabla \phi_{2} } \right|}}} \right) \\ & \quad + \nu \left( {\nabla^{2} \phi_{2} - {\text{div}}\left( {\frac{{\nabla \phi_{2} }}{{\left| {\nabla \phi_{2} } \right|}}} \right)} \right) - \delta (\phi_{2} )N_{2} \end{aligned} $$

(13)

where $N_{1} = H(\phi_{2} )(F_{1} - F_{3} ) + (1 - H(\phi_{2} ))(F_{2} - F_{4} )$, $N_{2} = H(\phi_{1} )(F_{1} - F_{2} ) + (1 - H(\phi_{1} ))(F_{3} - F_{4} )$.

For fixed $\phi$ and $B$, we can find the optimal $u$, $\mu$ and $\varSigma$ that minimize $E$:

$$ u_{ij} (x) = \frac{{(M_{i} (\phi )( - \log p_{ij} (R_{x}^{'} ,P_{x}^{'} ,B_{x} )))^{1/(1 - m)} }}{{\sum\nolimits_{k = 1}^{{K_{i} }} {(M_{i} (\phi )( - \log p_{ik} (R_{x}^{'} ,P_{x}^{'} ,B_{x} )))^{1/(1 - m)} } }} $$

(14)

$$\begin{aligned} & \mu_{ij} = \int_{\varOmega } {M_{i} (\phi )u_{ij}^{m} (x)B_{x} R_{x}^{'} \cdot R_{x}^{'} \cdot P_{x}^{'} {\text{d}}x} \\ & \quad \cdot /\int_{\varOmega } {M_{i} (\phi )u_{ij}^{m} (x)B_{x}^{2} R_{x}^{'} \cdot R_{x}^{'} {\text{d}}x}\end{aligned} $$

(15)

$$ \varSigma_{ij} = \frac{{\int_{\varOmega } {M_{i} (\phi )u_{ij}^{m} (x)(R_{x}^{'} \cdot (P_{x}^{'} - B_{x} \mu_{ij} ))(R_{x}^{'} \cdot (P_{x}^{'} - B_{x} \mu_{ij} ))^{\text{T}} {\text{d}}x} }}{{\int_{\varOmega } {M_{i} (\phi )u_{ij}^{m} (x){\text{d}}x} }} $$

(16)

In Eq. (9), the bias field $B_{x}$ can be defined as $B_{x} = Q^{T} S_{x}$, where $Q = [q_{1} , \ldots ,q_{L} ]^{\text{T}}$,$S = [s_{1} , \ldots ,s_{L} ]^{\text{T}}$. Fixing $\phi ,u,\mu ,\varSigma$, the optimal $Q$ that minimizes $E$:

$$ \left[ {\begin{array}{*{20}l} {\frac{\partial E}{\partial Q} = \frac{{\partial \int_{\varOmega } {\sum\nolimits_{i = 1}^{N} {M_{i} } (\phi )F_{i} {\text{d}}x} }}{\partial Q}} \hfill \\ { \propto \frac{{\partial \int_{\varOmega } {\sum\nolimits_{i = 1}^{N} {M_{i} } (\phi )\sum\nolimits_{j = 1}^{{K_{i} }} {u_{ij}^{m} (x)} (R_{x}^{'} \cdot (P_{x}^{'} - B_{x} \mu_{ij} ))^{T} \varSigma_{ij}^{ - 1} (R_{x}^{'} \cdot (P_{x}^{'} - B_{x} \mu_{ij} ))){\text{d}}x} }}{\partial Q}} \hfill \\ \end{array} } \right]_{{Q = Q^{\# } }} = 0 \\ $$

(17)

Then, we can obtain:

$$ Q^{\# } = A^{ - 1} W $$

(18)

Where $A = \int_{\varOmega } S_{x} S_{x}^{T} \sum\nolimits_{i = 1}^{N} \sum\nolimits_{j = 1}^{{K_{i} }} {M_{i} (\phi )u_{ij}^{m} (x)} (R_{x}^{'} \cdot \mu_{ij} )^{T} \varSigma_{ij}^{ - 1} (R_{x}^{'} \cdot \mu_{ij} )){\text{d}}x$ is a $L \times L$ inverse-able matrix [26] and.

$$ W = \int_{\varOmega } {S_{x} \sum\limits_{i = 1}^{N} {\sum\limits_{j = 1}^{{K_{i} }} {M_{i} (\phi )u_{ij}^{m} (x)(R_{x}^{'} \cdot P_{x}^{'} )^{T} \varSigma_{ij}^{ - 1} (R_{x}^{'} \cdot \mu_{ij} )){\text{d}}x} } } $$

The procedures of our method are summarized as:

• Step 1 Initialization: $\phi_{1} ,\phi_{2}$.

• Step 2 Update $u,\mu ,\varSigma$ by using Eqs. (14–16), respectively.

• Step 3 Update $Q$ by using Eq. (18).

• Step 4 Evolve the level set functions $\phi_{1}$ and $\phi_{2}$ according to Eqs. (12) and (13)

• Step 5 If $\phi_{1}$ and $\phi_{2}$ satisfy the stationary condition, stop; otherwise, return to Step 2.

5 Experimental results

To illustrate the advantage of the proposed method, we generated a simulated image containing three object regions (WM, GM and CSF) as shown in Fig. 3a. Figure 3b shows the histogram of the initial image and the fitting results of the Gaussian mixture model and the nonsymmetric Gaussian mixture model. It can be clearly observed from the histogram that the intensity distribution is not symmetric in each region and the tissue label (CSF) is a very small amount compared to other labels (WM and GM). We employ the misclassification ratio (MCR) to evaluate the segmentation performance quantitatively in this experiment. The MCR is defined as the number of misclassified pixels divided by the total number of pixels. The results demonstrate that the nonsymmetric Gaussian distribution-based method can obtain better results.

Fig. 3

Illustration on asymmetric distributions. a is the initial image. b denotes the histogram of the image and the mixture distributions of Gaussian mixture (MCR = 9.2%) and nonsymmetric Gaussian mixture (MCR = 6.4%)

Unless otherwise specified, the parameters of our method used in the next experiments are set as follows: the radius of the neighbor patch $r = 1$, the nonnegative constant $\varsigma = 400$, the degree of the basis functions of the bias field $P = 4(L = 15)$, the fuzzy coefficient $m = 2$, the level set parameter $\alpha = 0.00001 \times 255 \times 255$, $\nu = .1$.

All the synthetic images in the next experiments are downloaded from BrainWeb (http://www.bic.mni.mcgill.ca/brainweb/). BrainWeb provides full three-dimensional data volumes with a variety of slice thicknesses, noise levels and levels of intensity inhomogeneity. In this paper, we selected T1-weighted images with 1-mm slice thickness. The clinical data volumes are downloaded from the Internet Brain Segmentation Repository (IBSR, http://www.cma.mgh.harvard.edu/ibsr/). We use Jaccard similarity (JS) values [27] to quantitatively evaluate the performance of the competing methods.

5.1 Segmentation of 3T brain MR images

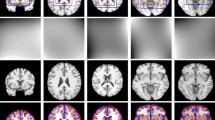
In this section, the first experiments are carried out on three 3T-weighted brain MR images. The initial images, segmentation results, the estimated bias fields and bias field-corrected images are shown in Fig. 4. The intensities within each tissue regions in the initial images are quite imhomogeneous. By comparison, it can be found that intensities in the bias field-corrected images are more homogeneous. The segmentation results demonstrate that our method can obtain expected tissue regions. In clinical applications, the brain MR images have non-brain tissues (also named as the skull), which have similar intensities and always affect the accuracy of the segmentation methods. In the second experiments, we perform our method on three 3T brain MR images with skulls. The initial images, segmentation results, the estimated bias fields and bias field-corrected images are shown in Fig. 5. It can be clearly found that our method can obtain satisfactory results without being affected by the skull. In the next experiments, all the brain MR images are skull stripped by using a learning-based method [28].

Fig. 4

Segmentation results on skulled brain MR images. From the left column to right column are three 3T-weighted brain MR images, segmentation results, estimated bias fields and bias-corrected images, respectively

Fig. 5

Segmentation results on un-skulled brain MR images. From the left column to right column are three 3T-weighted brain MR images, segmentation results, estimated bias fields and bias-corrected images, respectively

5.2 Quantitative comparison

In this section, we quantitatively compared our method with six existing methods including CV model [8], LBF [10], LGDF [11], Zhang’s [14], MICO [28] and RLSF [27]. All these methods are representative level set methods, and the parameters are set as default values in their manuscripts. More details can be found in the corresponding references. All the methods are initialized by using the K-means clustering method.

In this section, we compared our method to mentioned six segmentation methods on clinical T1-weighted brain MR images. Figure 6 shows the segmentation results on the dataset from IBSR (1-24#). The initial image appears intensity inhomogeneity and weak edges. From the results, we can observe that our method is more robust to weak edges. The partially enlarged details of the segmentation results are shown in Fig. 7. Figure 8 shows the segmentation results on another clinical image (2_4#) with severe intensity inhomogeneity and low contrast. Figure 9 shows the corresponding partial enlarged details. The segmentation accuracy of those methods is measured by JS and shown in Table 1.

Fig. 6

Segmentation results in a clinical brain MR image (11th of 1_24#). a Initial image (b–h) are the results of the CV model, LBF, LGDF, Zhang’s, MICO, RLSF and our method, respectively

Fig. 7

Details of the segmentation results shown in Fig. 9. From the left to right, the details of the initial images, the ground truth, CV model, LBF, LGDF, Zhang’s, MICO, RLSF and our method, respectively, are shown

Fig. 8

Segmentation results in a clinical brain MR image (40th of 2_4#). (a–h) are the initial image, the results of the CV model, LBF, LGDF, Zhang’s, MICO, RLSF and our method, respectively

Fig. 9

Details of the segmentation results shown in Fig. 11. The left to right column shows the details of the initial images, the ground truth, CV model, LBF, LGDF, Zhang’s, MICO, RLSF and our method, respectively

Table 1 Js values of the segmentation results. (%)

In order to show the robustness for bias field estimation, we compared our method with Wells method [22], Leemput method [29] and MICO [30] on a clinical brain MR image with severe intensity inhomogeneity. Figure 10 shows the segmentation results, estimated bias field and corrected images of the four mentioned methods. The Wells method used a low-pass filter to smooth the estimated bias field in each iteration, which caused the estimated bias field unsmooth. The Leemput method and the MICO method utilized the orthogonal basis function to fit the bias field. The estimated bias fields are smooth; however, the segmentation results are not accurate enough without using any spatial information. Our method can achieve the best performance.

Fig. 10

Segmentation results in a clinical brain MR image. The left column to the right column shows the initial image, the segmentation result, estimated bias field and corrected image of Wells method, Leemput method, MICO and our method, respectively

5.3 Evaluation with 3D image data

In this experiment, we compared our method with Wells method, Leemput method, LBF method, LGD method and MICO method on a 3D clinical brain MR image(ISBR 2.0(7#)), which has severe intensity inhomogeneity and low contrast. From the left column to right column, Fig. 11 shows the results of the ground truth, Wells method, Leemput method, LBF method, LGD method, MICO method and our method, respectively. Our method obviously obtains the best result.

Fig. 11

3D segmentation results of a T1-weighted clinical 3D brain MR image. (a–g) shows the ground truth, the segmentation results of Wells method, Leemput method, LBF method, LGD method, MICO method and our method, respectively. The first row shows the results of GM, and the second row shows the results of WM

6 Discussion

In our method, we utilized the proposed anisotropic information to noise reduction and detail preservation. The radius of the neighbor patch and the nonnegative constant $\zeta$ can affect the accuracy of our method. Based on exhausted experiments on brain MR images, we observed that a larger radius considers more pixels with similar intensities and makes the method sensitive to weak edges. The weight of each pixel in the neighbor patch is affected by the value of nonnegative constant $\zeta$. If $\zeta$ is small, the weight of each pixel is much smaller than that of the center pixel, so that our method is difficult to reduce the effect of noise. On the opposite, the weight of each pixel is similar to that of the center pixel, which leads the neighbor information to be isotropic and lose detail information. Figure 12 shows the effect of the radius of the neighbor patch and $\zeta$ on a simulated image with noise level 3% and intensity inhomogeneity level 80%. It is observed that the radius is set as 1 and $\zeta = 400$ to achieve the best performance. In further work, it is possible to learn the optimized value of $\zeta$ automatically. In our method, there are three parts in the objective function. We performed an experiment on a synthetic image (noise level 3% and intensity inhomogeneity level 40%) to evaluate the effect of each part. Figure 13b shows the segmentation result using the whole objective function, while Fig. 13c shows the segmentation result only with $E = E_{1} + E_{3}$. The second part ($E_{2}$) is the regular term of the curve length, which forces the curves/surfaces smoother and reduces the effect of noise. The third part ($E_{3}$) is a penalty term to preserve $|\nabla \phi (x)| = 1$. The method cannot achieve satisfying performance without the penalty term.

Fig. 12

Illustration of the effect of the radius of the neighbor patch and ς on a simulated brain MR image data with parameter: noise level 3% and intensity inhomogeneity level 80%

Fig. 13

Segmentation results on a synthetic image. a The initial image with noise level 3% and intensity inhomogeneity level 40%. b The segmentation results with $E = E_{1} + E_{2} + E_{3}$. c The segmentation results with $E = E_{1} + E_{3}$

7 Conclusion

In this paper, we present a new region descriptor based on asymmetric Gaussian distribution, to fit different shapes of the observed data. In order to alleviate the effect of noise, the anisotropic neighbor information is introduced to improve the ability of the asymmetric region descriptor, which is utilized by the level set model for brain MR image segmentation. Our method coupled the bias field information into the energy functional in order to segment the image and estimate the bias field simultaneously. Comparisons with several state-of-the-art methods on synthetic and real images datasets have demonstrated the robustness of the proposed method.