1 Introduction

As a typical digital modulation signal, the MPSK (multiple phase-shift keying) signal has the advantages of wide band of frequencies, low peak power, and good concealment and it has been used widely in radar and communication systems. For such systems, the extraction of characteristic parameters is a significant problem, and many solutions have been proposed.

At present, there are several methods used to estimate MPSK signal parameters, such as time-domain phase difference method [1, 2], wavelets [3, 4], short-time Fourier transform [5], and cyclic spectrum method [6,7,8]. When there is only one receiving channel in battlefield environments, it is easy to receive multiple signals at the same time; this makes it difficult to analyze multi-component mixed MPSK signals when using the above methods. Although the cyclic spectrum [9] solves the symbol rates estimation problem of two-component signals mixed in single channel, the method will be invalid when there are more than 2 components.

Single-channel source separation is a rather challenging endeavor; some researchers suggest using time–frequency distribution of sources to accomplish separation. For example, the fractional Fourier transform [10,11,12] is a very effective tool to process LFM signals. Li [13] used time–frequency filter and Viterbi algorithm to separate micro-Doppler signals. Liu [14] used an energy operator to estimate the modulation information of a multi-component radar signal. Adaptive decomposition [15,16,17,18,19] can be purposefully designed to separate multi-component frequency modulation signals. Although these methods can separate multi-component frequency modulation radar signals, they cannot be used to separate most multi-component communication signals (such as a BPSK/QPSK signal).

It is useful to accomplish separation by using the periodicity; Kanjilal [20] used singular value decomposition to successfully separate periodic source signals, Zou [21] and Cheng [22] separated periodic source signals with an algebraic approach, and Shen [23] successfully separated multi-component DSSS signal by using the periodicity of PN sequence with prior knowledge.

By analyzing the modulation period (symbol rate) of BPSK/QPSK signal, this paper is inspired to propose an effective method of source separation and parameter estimation for multi-component BPSK/QPSK signal.

2 Multi-component BPSK/QPSK signal in single channel

For a single-input communication system, the received multiple-component mixed rectangular pulse-shaped BPSK/QPSK signal with noise can be written as:

$$ \begin{aligned} x\left( t \right) & = s\left( t \right) + v\left( t \right) = \sum\limits_{i = 1}^{K} {s_{i} \left( t \right)} + v\left( t \right) \\ & = \sum\limits_{i = 1}^{K} {\left\{ {A_{i} \cdot U_{i} \left( t \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} t + \varphi_{i} } \right)} \right]} \right\} + v\left( t \right)} \\ \end{aligned} $$
(1)

where \( v\left( t \right) \) is the complex additive white Gaussian noise with zero mean and variance \( \sigma^{2} \) and \( s\left( t \right) \) is the received multi-component BPSK/QPSK signal. The number of components is \( K \). For the ith component \( s_{i} \left( t \right) \), \( A_{i} \) is the amplitude, where \( A_{i} > 0\left( {i = 1,2, \ldots ,K} \right) \) and \( A_{1} > A_{2} > \cdots > A_{K} \). \( f_{i} \) is the carrier frequency, and \( \varphi_{i} \in \left[ {0,\frac{\pi }{2}} \right) \) is the initial phase. The expression of the rectangular pulse sequence \( U_{i} \left( t \right) \) is:

$$ U_{i} \left( t \right) = \sum\limits_{p = 1}^{\infty } {b_{i,p}^{{m_{i} }} \cdot {\text{rect}}\left( {\frac{{t - \left( {p - 1} \right)T_{ci} - T_{ci} /2}}{{T_{ci} }}} \right)} $$
(2)

where \( {\text{rect}}\left( {\frac{t}{{T_{ci} }}} \right) = \left\{ {\begin{array}{*{20}c} {1,\left| t \right| \le T_{ci} /2} \\ {0,{\text{otherwise}}} \\ \end{array} } \right. \), \( T_{ci} \) is the symbol period. The ith component is a \( m_{i} {\text{PSK}} \) signal (\( m_{i} = 2,4 \)); \( b_{i,p}^{{m_{i} }} = e^{{j\left( {\frac{{q_{i,p} }}{{m_{i} }} \cdot 2\pi } \right)}} ,\left( {q_{i,p} = 0 \sim m_{i} - 1} \right) \) is the pth symbol.

Considering the time delay \( \Gamma _{i} \) of each component:

$$ x\left( t \right) = s\left( t \right) + v\left( t \right) = \sum\limits_{i = 1}^{K} {s_{i} \left( {t -\Gamma _{i} } \right)} + v\left( t \right) $$
(3)

With sampling period Ts, the discrete form is:

$$ x\left[ n \right] = x\left( {n \cdot T_{s} } \right) $$
(4)

3 Principle for the source separation and parameters estimation

3.1 Non-standard periodicity of BPSK/QPSK signal

A component can be represented as (when \( \tau_{i} = 0 \)):

$$ s_{i} \left[ n \right] = A_{i} \cdot U_{i} \left( {nT_{s} } \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} nT_{s} + \varphi_{i} } \right)} \right] $$
(5)

For positive integers \( c \) and \( d \), we have:

$$ \begin{aligned} & \left. {\frac{{s_{i} \left[ {n + cN} \right]}}{{s_{i} \left[ {n + dN} \right]}}} \right|_{{N = N_{ci} }} \\ & \quad = \frac{{A_{i} \cdot U_{i} \left( {nT_{s} + cT_{ci} } \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} \left( {nT_{s} + cT_{ci} } \right) + \varphi_{i} } \right)} \right]}}{{A_{i} \cdot U_{i} \left( {nT_{s} + dT_{ci} } \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} \left( {nT_{s} + dT_{ci} } \right) + \varphi_{i} } \right)} \right]}} \\ & \quad = \frac{{b_{{i,\left( {c + 1} \right)}}^{{m_{i} }} \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} cT_{ci} } \right)} \right]}}{{b_{{i,\left( {d + 1} \right)}}^{{m_{i} }} \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} dT_{ci} } \right)} \right]}} \\ &\quad = \exp \left\{ {j \cdot \left[ {2\pi \left( {\frac{{q_{i,c + 1} - q_{i,d + 1} }}{{m_{i} }} + f_{i} T_{ci} \left( {c - d} \right)} \right)} \right]} \right\}, \quad 1 \le n \le N_{ci} \\ \end{aligned} $$
(6)

where \( N_{ci} = {\raise0.7ex\hbox{${T_{ci} }$} \!\mathord{\left/ {\vphantom {{T_{ci} } {T_{s} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${T_{s} }$}} \), and as shown in Eq. (2), \( U_{i} \left( {nT_{s} + cT_{ci} } \right) = b_{{i,\left( {c + 1} \right)}}^{{m_{i} }} = e^{{j\left( {\frac{{q_{{i,\left( {c + 1} \right)}} }}{{m_{i} }} \cdot 2\pi } \right)}} \) when \( 1 \le n \le N_{ci} \). We found that the waveforms of two \( N_{ci} \) periods have repeating patterns that are scaled differently by a scale complex constant factor \( \exp \left\{ {j \cdot \left[ {2\pi \left( {\frac{{q_{i,c + 1} - q_{i,d + 1} }}{{m_{i} }} + f_{i} T_{ci} \left( {c - d} \right)} \right)} \right]} \right\} \) with unit amplitude, and it suggests that the BPSK/QPSK signal is a non-standard periodic signal [24, 25]. We can define the basic waveform \( h_{i} \left[ n \right] \) of each component that satisfied:

$$ s_{i} \left[ {n + \left( {d - 1} \right)N_{ci} } \right] = \lambda_{{dN_{ci} }} \cdot h_{i} \left[ n \right], \quad 1 \le n \le N_{ci} $$
(7)

where \( \lambda_{{dN_{ci} }} \) is the scale factor [24, 25].

3.2 Estimation of symbol period

At each separation, we remove the reconstructed component signal with maximum amplitude, so before the rth (r = 1,2,…,K) separation, the remaining signal is:

$$ x^{{\left( {r - 1} \right)}} \left[ n \right] = x\left[ n \right] - \sum\limits_{i = 1}^{r - 1} {\hat{s}_{i} \left[ {n - \hat{\tau }_{i} } \right]} \approx \sum\limits_{i = r}^{K} {s_{i} \left[ {n - \tau_{i} } \right]} + v\left[ n \right] $$
(8)

where \( \hat{s}_{i} \left[ n \right] \) is the reconstructed component, \( \tau_{i} =\Gamma _{i} /T_{s} \), \( \hat{\tau }_{i} \) is the estimated value of \( \tau_{i} \), and \( x\left[ n \right] = x^{\left( 0 \right)} \left[ n \right] \). There are \( K - r + 1 \) BPSK/QPSK components in the remaining signal, and their amplitudes satisfy \( A_{r} > A_{r + 1} > \cdots > A_{K} \); then, eigenvalue decomposition (EVD) [20,21,22] is applied to estimate the symbol period. Consider an \( R \) row \( M \) column matrix D with time delay \( \tau =\Gamma /T_{s} \) expressed as:

$$ D = \left[ {\begin{array}{*{20}c} {x^{{\left( {r - 1} \right)}} \left[ {\tau + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau + 2} \right]} &\quad \cdots &\quad {x^{{\left( {r - 1} \right)}} \left[ {\tau + M} \right]} \\ {x^{{\left( {r - 1} \right)}} \left[ {\tau + M + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau + M + 2} \right]} &\quad \cdots &\quad {x^{{\left( {r - 1} \right)}} \left[ {\tau + 2M} \right]} \\ \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left( {R - 1} \right)M + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left( {R - 1} \right)M + 2} \right]} &\quad \cdots &\quad {x^{{\left( {r - 1} \right)}} \left[ {\tau + RM} \right]} \\ \end{array} } \right] $$
(9)

For different values of variables \( \tau \) and \( M \), calculating the EVD of matrix \( D^{H} D \), and we can get R eigenvalues \( \sigma_{1}^{{\left( {\tau ,M} \right)}} > \sigma_{2}^{{\left( {\tau ,M} \right)}} > \cdots > \sigma_{R}^{{\left( {\tau ,M} \right)}} \) and define:

$$ {\text{EVR}}_{D} \left( {\tau ,M} \right) = \frac{{\left( {R - 1} \right)\sigma_{1}^{{\left( {\tau ,M} \right)}} }}{{\sum\nolimits_{i = 2}^{R} {\sigma_{i}^{{\left( {\tau ,M} \right)}} } }} $$
(10)

Then, we get a 3-D EVR (eigenvalue ratio) spectrum \( {\text{EVR}}\left( {\tau ,M} \right) \). For \( i = r, \ldots ,K \), if \( \tau - \tau_{i} = LN_{ci} ,\left( {L = 1,2, \ldots } \right) \) and \( M = N_{ci} \), there is a peak in the 3-D spectrum corresponding to the ith components, the peak value is proportional to the amplitude \( A_{i} \), and the position of the maximum peak value is \( \left( {\tau = LN_{ci} + \tau_{i} ,M = N_{cr} } \right) \), as shown in Fig. 1.

Fig. 1
figure 1

3-D EVR spectrum

Full size image

Finding out the location of peak value:

$$ \left( {\tau_{\rm max} ,M_{{\rm max} } } \right) = \mathop {\arg {\rm max} }\limits_{\tau ,M} \left[ {{\text{EVR}}_{D} \left( {\tau ,M} \right)} \right] $$
(11)

where the location \( \left( {\tau_{{\rm max} } = LN_{cr} + \tau_{r} ,M_{{\rm max} } = \frac{{N_{cr} }}{P}} \right) \) is corresponding to the rth component with maximum amplitude, (the value of P will be discussed in Sect. 3.2). Here, we assume that \( M_{{\rm max} } = N_{cr} \), then a new multi-dimensional matrix can be structured as:

$$ D_{{\rm max} } = \left[ {\begin{array}{*{20}c} {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + 2} \right]} &\quad \cdots &\quad {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + M_{{\rm max} } } \right]} \\ {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + M_{{\rm max} } + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + M_{{\rm max} } + 2} \right]} &\quad \cdots &\quad {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + 2M_{{\rm max} } } \right]} \\ \vdots &\quad \vdots &\quad \ddots &\quad \vdots \\ {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + \left( {R - 1} \right)M_{{\rm max} } + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + \left( {R - 1} \right)M_{{\rm max} } + 2} \right]} &\quad \cdots &\quad {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + RM_{{\rm max} } } \right]} \\ \end{array} } \right] $$
(12)

where \( \tau_{r,m} = \left( {\tau_{{\rm max} } \bmod M_{{\rm max} } } \right) \). Performing EVD of \( D_{{\rm max} }^{H} D_{{\rm max} } \) and the eigenvector corresponding to the maximum eigenvalue is the estimation \( \hat{h}_{r} \left[ n \right] \) of rth component \( s_{r} \left[ n \right] \); then, we get the carrier frequency with a rough value:

$$ \tilde{f}_{r} = \mathop {\arg {\rm max} }\limits_{f} \left\{ {\left| {\tilde{H}_{r} \left[ f \right]} \right|} \right\} = \mathop {\arg {\rm max} }\limits_{f} \left\{ {\left| {FFT\left( {\hat{h}_{r} \left[ n \right]} \right)} \right|} \right\} $$
(13)

For \( x^{{\left( {r - 1} \right)}} \left[ n \right] \), if we have estimated the time delay \( \tau_{r,m} = \left( {\tau_{{\rm max} } \bmod M_{{\rm max} } } \right) \), then we can get the following equation by removing the carrier frequency and initial phase (here we assumed that \( \tau_{r,m} = LN_{cr} + \tau_{i} ,\forall i = r, \ldots ,K \)):

$$ \begin{aligned} x_{\Delta }^{{\left( {r - 1} \right)}} \left[ n \right] & = x^{{\left( {r - 1} \right)}} \left[ {n + \tau_{r,m} } \right] \cdot {\text{conj}}\left\{ {\exp \left[ {j \cdot \left( {2\pi fnT_{s} + \varphi } \right)} \right]} \right\} \\ & = \sum\limits_{i = r}^{K} {A_{i} \cdot U_{i} \left( {nT_{s} } \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{\Delta i} nT_{s} + \varphi_{\Delta i} } \right)} \right]}\\ &\quad + v\left[ n \right] \cdot \exp \left[ { - j \cdot \left( {2\pi fnT_{s} + \varphi } \right)} \right] \\ & = \sum\limits_{i = r}^{K} {s_{\Delta i} \left[ n \right]} + v_{\Delta } \left[ n \right] \\ \end{aligned} $$
(14)

where \( f_{\Delta i} = f_{i} - \varphi \), \( \varphi_{\Delta i} = \varphi_{i} - \varphi \), and \( U_{i} \left( {nT_{s} } \right) = b_{{i,\left\lceil {n/N_{ci} } \right\rceil }}^{{m_{i} }} = e^{{j\left( {\frac{{q_{{i,\left\lceil {n/N_{ci} } \right\rceil }} }}{{m_{i} }} \cdot 2\pi } \right)}} ,\left( {q_{{i,\left\lceil {n/N_{ci} } \right\rceil }} = 0 \sim m_{i} - 1} \right) \).

Consider a cost function:

$$ \begin{aligned} {\text{CF}}\left( {f,\varphi } \right) & = \frac{1}{{N_{{s_{\Delta r} }} }}\sum\limits_{n} {\left| {\text{Re} \left\{ {x^{{\left( {r - 1} \right)}}_{\Delta } \left[ n \right]} \right\} \cdot \text{Im} \left\{ {x^{{\left( {r - 1} \right)}}_{\Delta } \left[ n \right]} \right\}} \right|^{2} } \\ & = \frac{1}{{N_{{s_{\Delta r} }} }}\sum\limits_{n} {\left| {CF^{\prime } \left( {f,\varphi } \right)} \right|^{2} } \\ \end{aligned} $$
(15)

and let \( x_{\Delta }^{{\left( {r - 1} \right)}} \left[ n \right] = s_{\Delta r} \left[ n \right] + w_{r} \left[ n \right] \), where \( w_{r} \left[ n \right] \) is:

$$ w_{r} \left[ n \right] = x^{{\left( {r - 1} \right)}}_{\Delta } \left[ n \right] - s_{\Delta r} \left[ n \right] = A_{{w_{r} }} \left[ n \right] \cdot \exp \left\{ {j \cdot \varphi_{{w_{r} }} \left[ n \right]} \right\} $$
(16)

then \( {\text{CF}}^{\prime } \left( {f,\varphi } \right) \) can be rewritten as:

$$ \begin{aligned} {\text{CF}}^{\prime } \left( {f,\varphi } \right) & = \text{Re} \left\{ {x^{{\left( {r - 1} \right)}}_{\Delta } \left[ n \right]} \right\}\text{Im} \left\{ {x^{{\left( {r - 1} \right)}}_{\Delta } \left[ n \right]} \right\} \\ & = \left\{ {A_{r} \cos \left[ {2\pi f_{\Delta r} nT_{s} + \varphi_{\Delta r} + \frac{{q_{{\left\lceil {n/N_{cr} } \right\rceil }} }}{{m_{i} }} \cdot 2\pi } \right] + A_{{w_{r} }} \left[ n \right] \cdot \cos \left[ {\varphi_{{w_{r} }} \left[ n \right]} \right]} \right\} \\ & \cdot \left\{ {A_{r} \sin \left[ {2\pi f_{\Delta r} nT_{s} + \varphi_{\Delta r} + \frac{{q_{{\left\lceil {n/N_{cr} } \right\rceil }} }}{{m_{i} }} \cdot 2\pi } \right] + A_{{w_{r} }} \left[ n \right] \cdot \sin \left[ {\varphi_{{w_{r} }} \left[ n \right]} \right]} \right\} \\ \end{aligned} $$
(17)

If \( w_{r} \left[ n \right] = 0 \), it could be found that \( {\text{CF}}\left( {f,\varphi } \right) \ge 0 \) and equality holds when:

$$ 2\pi f_{\Delta r} nT_{s} + \varphi_{\Delta r} + \frac{{q_{{\left\lceil {n/N_{cr} } \right\rceil }} }}{{m_{r} }} \cdot 2\pi = \frac{k\pi }{2},\quad \forall n \in N^{ + } ,\left( {k = 0,1,2,3, \ldots } \right) $$
(18)

where \( m_{r} = 2,4 \), \( \varphi_{\Delta r} \in \left( { - \frac{\pi }{2},\frac{\pi }{2}} \right) \) as \( \hat{\varphi }_{r} \in \left[ {0,\frac{\pi }{2}} \right) \). In such a situation, \( \varphi_{\Delta r} = 0 \) and \( f_{\Delta r} = kf_{s} /4 \) are the necessary and sufficient condition of Eq. (18), and normally \( f_{\Delta r} /f_{s} \ll 1 \), so \( {\text{CF}}\left( {f,\varphi } \right) \) would be the minimum value 0 as \( \left( {\varphi_{\Delta r} = 0,f_{\Delta r} = 0} \right) \).

In most cases, \( w_{r} \left[ n \right] \ne 0 \). Since \( s_{i} \left[ n \right] \) has the greatest amplitude among all the component signals in \( x^{{\left( {r - 1} \right)}} \left[ n \right] \), there would also be a local minimum value in \( {\text{CF}}\left( {f,\varphi } \right) \) when \( \left\| {f_{\Delta r} ,\varphi_{\Delta r} } \right\| = \left\| {f_{r} - f,\varphi_{r} - \varphi } \right\| \) is small enough. So we can estimate the carrier frequency and the initial phase of the rth component at the same time through a 2-D search:

$$\begin{aligned} &\left( {\hat{f}_{r} ,\hat{\varphi }_{r} } \right) = \mathop {\arg \hbox{min} }\limits_{f,\varphi } \left\{ {{\text{CF}}\left( {f,\varphi } \right)} \right\},\quad \\ &\quad\left( {f \in \left[ { - n_{f} \Delta f + \tilde{f}_{r} ,n_{f} \Delta f + \tilde{f}_{r} } \right],\varphi \in \left[ {0,n_{\varphi } \Delta \varphi } \right],n_{\varphi } \Delta \varphi < \frac{\pi }{2}} \right) \end{aligned} $$
(19)

where \( \Delta f \) and \( \Delta \varphi \) are the search intervals and \( 2n_{f} + 1 \) and \( n_{\varphi } + 1 \) are the numbers of search points.

3.3 Removal method of periodic ambiguity and optimization calculation

In Eq. (6), let \( N = \frac{{N_{ci} }}{P},\left( {P = 1,2,3, \ldots } \right) \), then

$$ \begin{aligned} & \left. {\frac{{s_{i} \left[ {n + cN} \right]}}{{s_{i} \left[ {n + dN} \right]}}} \right|_{{N = N_{ci} /P}} \\ & = \frac{{A_{i} \cdot U_{i} \left( {nT_{s} + cT_{ci} /P} \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} \left( {nT_{s} + cT_{ci} /P} \right) + \varphi_{i} } \right)} \right]}}{{A_{i} \cdot U_{i} \left( {nT_{s} + dT_{ci} /P} \right) \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} \left( {nT_{s} + dT_{ci} /P} \right) + \varphi_{i} } \right)} \right]}} \\ & = \frac{{b_{{i,\left( {\left\lfloor {c/P} \right\rfloor + 1} \right)}}^{{m_{i} }} \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} cT_{ci} /P} \right)} \right]}}{{b_{{i,\left( {\left\lfloor {d/P} \right\rfloor + 1} \right)}}^{{m_{i} }} \cdot \exp \left[ {j \cdot \left( {2\pi f_{i} dT_{ci} /P} \right)} \right]}} \\ & = \exp \left\{ {j \cdot \left[ {2\pi \left( {\frac{{q_{{\left\lfloor {c/P} \right\rfloor + 1}} - q_{{\left\lfloor {d/P} \right\rfloor + 1}} }}{{m_{i} }} + \frac{{f_{i} T_{ci} \left( {c - d} \right)}}{P}} \right)} \right]} \right\},\quad 1 \le n \le N_{ci} /P \\ \end{aligned} $$
(20)

which suggested that there are also several peaks in the spectrum of Eq. (10) when \( \tau + \tau_{i} = LN_{ci} ,\left( {L = 1,2, \ldots } \right) \) and \( M = N_{ci} /P \), as shown in Fig. 2, the value of \( P \) cannot be determined directly and it can be any integer value between \( \left[ {1,\infty } \right) \); we consider it be a periodic ambiguity problem and it is effective to solve the ambiguity through wavelet analysis.

Fig. 2
figure 2

Peaks with \( \tau + \tau_{i} = LN_{ci} \) and \( M = N_{ci} /P \)

Full size image

Construct a single frequency signal:

$$ s_{cr} \left[ n \right] = \exp \left[ {j\left( {2\pi \hat{f}_{r} nT + \hat{\varphi }_{r} } \right)} \right] $$
(21)

and it can be used to generate a reference signal \( s_{rr} \left[ n \right] \) which can approximately fit the symbol changes \( s_{r} \left[ n \right] \):

$$\begin{aligned} & s_{rr} \left[ {n + LM_{{\rm max} } } \right] \\&\quad= \exp \left\{ {j \cdot {\text{phase}}\left[ {\frac{1}{{M_{{\rm max} } }}\sum\limits_{m = 1}^{{M_{{\rm max} } }} {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} + m + LM_{{\rm max} } } \right]s_{cr} *\left[ m \right]} } \right]} \right\},\quad \\&\quad\quad \left( {n = 1,2, \ldots M_{{\rm max} } ;L = 0,1, \ldots } \right) \end{aligned}$$
(22)

where \( \tau_{r,m} = \left( {\tau_{{\rm max} } \bmod M_{{\rm max} } } \right) \).

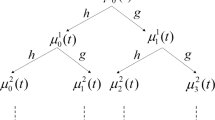
We can get the wavelet coefficient spectrums with different scales \( a \) by making continuous Haar wavelet transform to \( \text{Re} \left[ {s_{rr} \left[ n \right]} \right] \) or \( \text{Im} \left[ {s_{rr} \left[ n \right]} \right] \):

$$ {\text{RWC}}_{r} \left[ {a,n} \right] = {\text{CWT}}_{\text{Haar}} \left\{ {\text{Re} \left[ {s_{rr} \left[ n \right]} \right]} \right\} $$
(23a)
$$ {\text{IWC}}_{r} \left[ {a,n} \right] = {\text{CWT}}_{\text{Haar}} \left\{ {\text{Im} \left[ {s_{rr} \left[ n \right]} \right]} \right\} $$
(23b)

As shown in Fig. 3, the positions where symbol value changes are distinguishable in the spectrograms. We may get the average waveform to get more accurate information:

Fig. 3
figure 3

Wavelet coefficient a RWC[a,n],b symbol sequence, c IWC[a,n]

Full size image
$$ {\text{AWC}}_{r} \left[ n \right] = \sum\limits_{a} {\left| {{\text{RWC}}_{r} \left[ {a,n} \right]} \right|} + \sum\limits_{a} {\left| {{\text{IWC}}_{r} \left[ {a,n} \right]} \right|} $$
(24)

The symbol period of the component \( s_{r} \left[ n \right] \) could be estimated accurately by finding out the greatest common divisor of all the peak intervals in \( {\text{AWC}}_{r} \left[ n \right] \), as shown in Fig. 4. For \( {\text{AWC}}_{r} \left[ n \right] \), we only retain the values large enough:

Fig. 4
figure 4

The average waveform of \( {\text{AWC}}_{r} \left[ n \right] \)

Full size image
$$ {\text{AWC}}_{r} \left[ n \right] = \left\{ {\begin{array}{*{20}l} {{\text{AWC}}_{r} \left[ n \right],} \hfill & {{\text{AWC}}_{r} \left[ n \right] \ge 0.6{\rm max} \left\{ {{\text{AWC}}_{r} \left[ n \right]} \right\}} \hfill \\ {0,} \hfill & {{\text{otherwise}}\text{ }} \hfill \\ \end{array} } \right.. $$
(25)

Then, assuming that there are \( r_{p} \) peaks in \( {\text{AWC}}_{r} \left[ n \right] \), let \( P_{{{\text{AWC}}_{r} }} \left[ m \right] = {\text{Findpeaks}}\left\{ {{\text{AWC}}_{r} \left[ n \right]} \right\}{ = }\left[ {n_{1} ,n_{2} , \ldots ,n_{{r_{p} }} } \right] \) be the vector contains all the locations of peaks, and the accurate symbol period can be estimated:

$$ M_{pr} = \mathop {\hbox{min} }\limits_{{ \ge M_{{\rm max} } }} \left\{ {\left| {{\text{LOC}}\left[ m \right]} \right|} \right\} $$
(26)

where \( {\text{LOC}}\left[ m \right] = {\text{diff}}\left\{ {P_{{{\text{AWC}}_{r} }} \left[ m \right]} \right\} = [ n_{2} - n_{1} ,n_{3} - n_{2} , \ldots ,n_{{r_{p} }} - n_{{r_{p} - 1}} ] \) means the difference vector. With Eq. (26), we can get the minimum value among all the peak intervals which are not smaller than \( M_{{\rm max} } \) and therefore solved the problem of periodic ambiguity; if \( M_{{\rm max} } \) changed compared with the value gotten through Eq. (11), then let \( M_{{\rm max} } = M_{pr} \) be the accurate symbol period and re-estimate the time delay \( \tau_{{\rm max} } = \mathop {\arg {\rm max} }\limits_{\tau } {\text{SVR}}_{D} \left( {\tau ,M_{{\rm max} } } \right) \) and \( \tau_{r,m} = \left( {\tau_{{\rm max} } \bmod M_{{\rm max} } } \right) \).

In Eq. (19), we have got good estimation values of carrier frequency and initial phase; in order to improve estimation accuracy, we may apply gradient steepest descent method to do an optimization calculation to increase estimation precise. The derivative functions are given as:

$$ \frac{{{\text{dCF}}\left( {f,\varphi } \right)}}{{{\text{d}}f}} = \sum\limits_{n} {2\text{Re} \left\{ { - j2\pi n \cdot y\left[ n \right]\left[ {2\left( {x_{\Delta }^{{\left( {r - 1} \right)}} \left[ n \right]} \right)^{2} + 2\left( {x_{\Delta }^{{\left( {r - 1} \right)}} *\left[ n \right]} \right)^{2} } \right]} \right\}} $$
(27a)
$$ \frac{{{\text{dCF}}\left( {f,\varphi } \right)}}{{{\text{d}}\varphi }} = \sum\limits_{n} {2\text{Re} \left\{ { - j \cdot y\left[ n \right]\left[ {2\left( {x_{\Delta }^{{\left( {r - 1} \right)}} \left[ n \right]} \right)^{2} + 2\left( {x_{\Delta }^{{\left( {r - 1} \right)}} *\left[ n \right]} \right)^{2} } \right]} \right\}} $$
(27b)

where \( y\left[ n \right] = \text{Re} \left( {x_{\Delta }^{{\left( {r - 1} \right)}} \left[ n \right]} \right) \cdot \text{Im} \left( {x_{\Delta }^{{\left( {r - 1} \right)}} \left[ n \right]} \right) \).

3.4 Amplitude estimation

Get a new \( s_{cr} \left[ n \right] \) in Eq. (21) with updated carrier frequency and initial phase and then get a new reference signal \( s_{sr} \left[ n \right] \):

$$\begin{aligned} &s_{sr} \left[ {n + LM_{{\rm max} } } \right] = s_{cr} \left[ n \right] \\ &\quad\cdot \exp \left\{ {j \cdot {\text{phase}}\left[ {\frac{1}{{M_{{\rm max} } }}\sum\limits_{m = 1}^{{M_{{\rm max} } }} {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} { + }m + LM_{{\rm max} } } \right]s_{cr} *\left[ m \right]} } \right]} \right\},\quad\\ &\quad \left( {n = 1,2, \ldots M_{{\rm max} } ;L = 0,1, \ldots } \right) \end{aligned} $$
(28)

which can be used to obtain the amplitude:

$$ \hat{A}_{r} = \left| {\frac{{\sum\limits_{n = 1}^{{{\text{length}}\left[ {s_{sr} } \right]}} {x^{{\left( {r - 1} \right)}} \left[ {\tau_{r,m} { + }n} \right]s_{sr} *\left[ n \right]} }}{{{\text{length}}\left[ {s_{sr} } \right]}}} \right|. $$
(29)

Then, the component signal can be reconstructed as:

$$ \hat{s}_{r} \left[ n \right] = \left[ {\left[ {O_{{1 \times \tau_{r,m} }} } \right],\hat{A}_{r} \cdot s_{sr} \left[ n \right]} \right] $$
(30)

We may remove it to get \( x^{\left( r \right)} \left[ n \right] = x^{{\left( {r - 1} \right)}} \left[ n \right] - \hat{s}_{r} \left[ n \right] \), and the remaining components can also be reconstructed by repeating the steps in this section with the new mixture.

3.5 Stopping separation adaptively by estimating SNR

In this paper, we apply the subspace-based decomposition to estimate SNR [26,27,28] and assume that the energy of each component is not too small compared with noise; so for the remaining signal \( x^{\left( r \right)} \left[ n \right] \) after rth separation, if the estimated signal–noise ratio \( \widehat{\text{SNR}}_{r} < {\text{TH}} \) (\( {\text{TH}} \) is the threshold with small value), then, the separation should be stopped.

Here, we introduce the concept of waveform similarity as shown in Eq. (31) to measure the level of similarity of source and reconstructed signals, where \( \rho \left( {y,s} \right) \) is the similarity coefficient, \( y\left( t \right) \) and \( s\left( t \right) \) are the reconstructed and source signals, and \( E\left[ \cdot \right] \) means the value of expectation. For 300 different sets of parameters, we used the proposed method to complete estimation of mono-component BPSK/QPSK signal under different SNRs; we find that when \( {\text{SNR}} < - 8\;{\text{dB}} \), the mean waveform similarity value is lower than 0.8; in this case, we consider that the reconstruction performance is not good. For the multi-component signal, in order to get a better reconstruction effect, the threshold can be set \( {\text{TH}} = - 8\;{\text{dB}} \) as an empirical value. In Fig. 5, we give out the flowchart of the proposed method.

Fig. 5
figure 5

The flowchart of the method proposed in this paper

Full size image
$$ \rho \left( {y,s} \right) = \frac{{\left| {E\left[ {y\left( t \right)s\left( t \right)} \right]} \right|}}{{\sqrt {\left| {E\left[ {y^{2} \left( t \right)} \right]E\left[ {s^{2} \left( t \right)} \right]} \right|} }} $$
(31)

4 Simulation and analysis

In simulation, we use the method to analyze a three-component BPSK/QPSK signal in single channel, the signal is under Gaussian white noise, and the SNR is 10 dB. The parameters are shown in Table 1.

Table 1 All the parameters of the multi-component BPSK/QPSK signal
Full size table

The sampling frequency is 1 MHz, and we use 13,200 samples of the signal to complete the analysis.

In Fig. 6, we give the process of estimation of delay time and symbol period; here, we got that \( M_{{\rm max} } = \frac{132}{P = 3} = 44 \) and \( \tau_{r,m} = 10 \), and then by using EVD, we can get the basic waveform and estimate the carrier frequency with a rough value \( \tilde{f}_{r} = 227.7\;{\text{kHz}} \), which is shown in Fig. 7.

Fig. 6
figure 6

The search process of 3-D EVR spectrum

Full size image
Fig. 7
figure 7

The estimated basic waveform a time domain and b frequency domain

Full size image

The more accurately estimated value can be obtained through 2-D search with \( {\text{CF}}\left( {f,\varphi } \right) \), as shown in Fig. 8, \( \left( {\hat{f}_{1} ,\hat{\varphi }_{1} } \right) = \left( {230\;{\text{kHz}},1.382} \right) \); For the cost function \( {\text{CF}}\left( {f,\varphi } \right) \), to escape from local traps; it is necessary to improve accuracy of the 2-D search by reducing search intervals \( \Delta f \) and \( \Delta \varphi \) to make the initial value of optimization calculation better; in this simulation, we set that \( \left( {\Delta f{ = }50,\Delta \varphi { = }\pi /200} \right) \).

Fig. 8
figure 8

2-D search for carrier frequency and initial phase

Full size image

The waveform of \( {\text{AWC}}_{1} \left[ n \right] \) is given in Fig. 9, from which we can estimate the accurate symbol period \( N_{c1} = M_{p1} = 132 \) by finding out the greatest common divisor of all the peak intervals. Let \( M_{{\rm max} } = M_{p1} = 132 \), we can re-estimate the time delay \( \tau_{r,m} = 10 \) through EVR spectrum with \( M{ = }132 \), as shown in Fig. 10. After optimization calculation with gradient steepest descent method, we finally get \( \left( {\hat{f}_{1} ,\hat{\varphi }_{1} } \right) = \left( {230.0015\;{\text{kHz}},1.2501} \right) \), and then we can estimate the amplitude \( \hat{A}_{1} = 0.8122 \);

Fig. 9
figure 9

The waveform of \( {\text{AWC}}_{1} \left[ n \right] \)

Full size image
Fig. 10
figure 10

Re-estimation of delay time through EVR spectrum with \( M = 132 \)

Full size image

The estimated values of the parameters are shown in Table 2, the constellation diagrams of all the reconstructed signals are shown in Fig. 11, and the symbol information sequences after demodulation with estimated parameters are shown in Fig. 12 compared with sources. After the third separation, the estimated \( \widehat{\text{SNR}}_{3} = - 10.9165\;{\text{dB}} \) and it is smaller than the threshold TH = −8 dB, so the separation can stop.

Table 2 Comparison of the estimated and the true parameters
Full size table
Fig. 11
figure 11

The constellation diagrams of the reconstructed signals a component 1, b component 2, and c component 3

Full size image
Fig. 12
figure 12

The symbol sequences after demodulation for a component, 1 b component 2, and c component 3

Full size image

In Fig. 13, we give the estimation precision (NRMSE curves) of all the parameters under different sampling frequencies (Fs = 1–8 MHz) and SNRs, and we see that there are more accurate results with high sampling frequency.

Fig. 13
figure 13

The NRMSE curves of different sampling frequencies and SNRs a 5 dB, b 10 dB, c 15 dB, and d 20 dB

Full size image

Some times, the value \( T_{ci} /F_{s} \) may not be a integer when the sampling frequency is not appropriate, so by searching the peak of EVR spectrum when changing M by step value 1, the resulting value of \( M_{{\rm max} } \) is only the integer part of \( T_{ci} /F_{s} \). In order to avoid this situation, we may re-search the peak of the spectrum of the advanced matrix shown as Eq. (32) by changing the value M with step value 0.01 within a small range around \( M_{{\rm max} } \).

By using the advanced matrix of Eq. (32) and searching the location \( \hat{M}_{{\rm max} } \) of peak value, \( \hat{M}_{{\rm max} } \) may be not an integer, if \( \left| {\frac{{\hat{M}_{{\rm max} } - M_{{\rm max} } }}{{M_{{\rm max} } }}} \right| \le \delta_{c} \) (where \( \delta_{c} \) is a very small value), we can consider that the sampling frequency is appropriate; otherwise, let \( F_{s} = F_{s} \cdot \left( {{\raise0.7ex\hbox{${M_{{\rm max} } }$} \!\mathord{\left/ {\vphantom {{M_{{\rm max} } } {\hat{M}_{{\rm max} } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\hat{M}_{{\rm max} } }$}}} \right) \) be the appropriate one to complete separation.

In Fig. 14, we give the success rate that the delay times and symbol periods of all the components were estimated correctly.

Fig. 14
figure 14

The success rate of estimation of delay times and symbol periods

Full size image

The NRMSE curves of the three parameters under different input SNRs are drawn in Fig. 15 when there is only one-component signal and the CRLB curves are also shown in this figure. In addition, we compare the estimation performance with the spectral correlation method. It can be seen from Fig. 15 that the precision of the proposed method is higher than the spectral correlation method under high SNR, and its advantage lies in its ability to deal with single-channel multi-component problems.

Fig. 15
figure 15

The NRMSE and the CRLB curves of parameters a carrier frequency, b initial phase, and c amplitude

Full size image
$$ D = \left[ {\begin{array}{*{20}c} {x^{{\left( {r - 1} \right)}} \left[ {\tau + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau + 2} \right]} & \cdots & {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left\lceil M \right\rceil } \right]} \\ {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left\lceil M \right\rceil + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left\lceil M \right\rceil + 2} \right]} & \cdots & {x^{{\left( {r - 1} \right)}} \left[ {\tau + 2\left\lceil M \right\rceil } \right]} \\ \vdots & \vdots & \ddots & \vdots \\ {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left\lceil {\left( {R - 1} \right)M} \right\rceil + 1} \right]} & {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left\lceil {\left( {R - 1} \right)M} \right\rceil + 2} \right]} & \cdots & {x^{{\left( {r - 1} \right)}} \left[ {\tau + \left\lceil {\left( {R - 1} \right)M} \right\rceil + \left\lceil M \right\rceil } \right]} \\ \end{array} } \right] $$
(32)

5 Conclusion

This paper proposes a useful method of single-channel source separation and parameters estimation of multi-component BPSK/QPSK signal. Simulation results indicate that the method is effective with a high estimation precision. Future studies would be needed to construct an advanced cost function with limitations or improve resolution method to reduce computation of 2-D search and optimization calculation. Further, it is also necessary to consider the situation that the component signal is shaped by more complex pulse shaping filter and modulated with more complex digital phase modulation system.