1 Introduction

Adaptive filters have been used in many applications such as prediction, noise cancellation and system identification [1]. Recently, the LAF algorithms are the most widely used adaptive filter algorithms [2,3,4,5,6,7,8], because they are designed to construct an energy surface having a single global minimum point in contrast to the gradient descent-based algorithms [2]. Furthermore, they always guarantee asymptotic stability according to the Lyapunov stability theory (LST) due to the fact that their error signals can converge to zero asymptotically [2,3,4,5,6,7,8]. However, since these LAF algorithms are designed without considering measurement noise effects, they cannot estimate optimal weight vector coefficients of an unknown system. To overcome many of the limitations on existing LAF algorithms [2,3,4,5,6,7,8], we proposed an LAF algorithm with a fixed step size for the noisy desired signal in [9]. The proposed algorithm in [9] has provided the distinct advantages over the conventional LAF algorithm [2] by controlling the fixed step size parameter. However, there are conflicting requirements between the convergence rate and the steady-state MSD error for the proposed LAF algorithm in [9]. Also, the analysis of the proposed algorithm in terms of convergence in the mean has not been investigated in [9], and hence, the lower and upper bounds for the step size parameter have not been statistically determined yet.

In this paper, we propose a novel LAF algorithm and its some VSS versions. A novel Lyapunov function is first determined as \(V(k) = \left| {e(k)} \right| \), and then, the proposed filter design is expressed as a constrained optimization problem by considering LST. As a result of the solution of the optimization problem, we obtain the FSS-LAF algorithm. Thus, the proposed FSS-LAF algorithm, which ensures negative definiteness in the sense of Lyapunov, iteratively updates the weight vector coefficients of the adaptive filter. Use of the step size parameter in the proposed algorithm improves the convergence capability, provides the estimation of the optimal weight vector coefficients of the unknown system and controls both steady-state and transient MSD errors. Furthermore, we present the convergence analysis of the proposed FSS-LAF algorithm for the first time in this paper. However, the selection of the step size parameter plays a critical role in the convergence performance of the proposed algorithm. Hence, the step size parameter in the FSS-LAF needs to be optimized and adaptively controlled during the filtering process.

To deal with this problem, a number of widely used gradient VSS algorithms are also adapted to the proposed FSS-LAF algorithm to further improve the performance for the first time in this paper. These VSS algorithms adjusting the step size parameter are the BVSS [10], MVSS [11] and FVSS [12] algorithms. To iteratively update and optimize the step size in the FSS-LAF algorithm, similar to studies in [10,11,12,13], the BVSS-LAF algorithm is rigorously derived without considering the independence assumptions, whereas the MVSS-LAF algorithm uses instantaneous gradients. The FVSS-LAF algorithm is also proposed to reduce the computational complexity of the BVSS-LAF algorithm. Furthermore, computational complexities of the proposed VSS algorithms are analyzed in this study. Finally, the performances of the proposed algorithms are comparatively illustrated on benchmark system identification problems.

2 The proposed FSS-LAF algorithm formulation

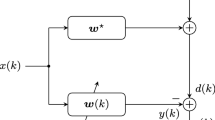
In the classical structure of a system identification problem, the desired signal consists of the following model:

$$\begin{aligned} d(k) = s(k) + n(k) = {{\mathbf{w }}_o}^\mathrm{T}\mathbf{x }(k) + n(k) \end{aligned}$$
(1)

where \(s(k) = {\mathbf{w }_o}^\mathrm{T}\mathbf{x }(k)\) represents the unknown system output, \(\mathbf{x }(k) = {[x(k),x(k - 1),\ldots ,x(k - M + 1)]^\mathrm{T}}\) is the input vector, \({\mathbf{w }_o} = {[{w_0},{w_1},\ldots ,{w_{M - 1}}]^\mathrm{T}}\) is the optimal weight vector of the unknown system to be estimated, n(k) is the measurement noise, and M is the filter order.

The filter output y(k) and the error signal e(k) are defined in (2) and (3), respectively.

$$\begin{aligned} y(k)&= \mathbf w ^{T}(k) \mathbf{x }(k) \end{aligned}$$
(2)
$$\begin{aligned} e(k)&= d(k) - y(k) \end{aligned}$$
(3)

For the design of the proposed adaptive filter, a candidate Lyapunov function should be determined after the error signal e(k) is defined in (3). According to LST, the Lyapunov function in our design is selected as \(V(k) = \left| {e(k)} \right| \) to construct a linear inequality constraint in our optimization problem. In order to ensure the asymptotic stability of the proposed algorithm in the sense of Lyapunov, the determined Lyapunov function V(k) should also provide the negative definiteness condition as \(\Delta V(k) = V(k) - V(k - 1) < 0\), \(\forall \,k\). Therefore, this condition is integrated into the constraint part of the proposed optimization problem as follows:

$$\begin{aligned} {\mathbf{w }_o} = \mathop {\text {min}}\limits _{\mathbf{w }(k)} \left( {\frac{1}{2}\delta {\mathbf{w }^\mathrm{T}}\delta \mathbf{w }} \right) \quad \text {subject to}\quad \Delta V(k)< 0 \end{aligned}$$
(4)

where \(\delta \mathbf{w } = \mathbf{w }(k) - \mathbf{w }(k - 1)\) and \(\Delta V(k) = \left| {e(k)} \right| -\left| {e(k-1)} \right| \).

In order to solve the optimization problem having the quadratic cost function and the linear inequality constraint, we use the method of Lagrange multipliers. We primarily define the Lagrangian function \(F(\mathbf{w }(k),\lambda )\) as follows:

$$\begin{aligned} F(\mathbf{w }(k),\lambda )&= {\frac{1}{2}(\mathbf{w }(k) - \mathbf{w }(k - 1))^\mathrm{T}}(\mathbf{w }(k) - \mathbf{w }(k - 1)) \nonumber \\&\quad + \lambda \left( {\left| {e(k)} \right| - \left| {e(k - 1)} \right| } \right) \end{aligned}$$
(5)

where \(\lambda \) is the Lagrange multiplier.

Then, the derivative of \(F(\mathbf{w }(k),\lambda )\) is taken with respect to \(\mathbf{w }\) and \(\lambda \) and these results are equal to zero. Thus, we obtain the two optimality conditions as follows.

$$\begin{aligned} \text {Condition 1:} \quad \frac{{\partial F(\mathbf{w }(k),\lambda )}}{{\partial \mathbf{w }(k)}}&= 0 \end{aligned}$$
(6)
$$\begin{aligned} \text {Condition 2:} \quad \frac{{\partial F(\mathbf{w }(k),\lambda )}}{{\partial \lambda }}&= 0 \end{aligned}$$
(7)

By implementing optimality Condition 1, (8) is obtained as follows:

$$\begin{aligned} \mathbf{w }(k) - \mathbf{w }(k - 1) = \lambda \left( {\text {sgn}(e(k))\mathbf{x }(k)} \right) . \end{aligned}$$
(8)

In order to obtain the Lagrange multiplier \(\lambda \) from (8), we can multiply both sides of (8) by \({\mathbf{x }^\mathrm{T}}(k)\). Thus, we can get the Lagrange multiplier \(\lambda \) in (9) after rearrangement of terms.

$$\begin{aligned} \lambda = \frac{{\alpha (k) - e(k)}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}\text {sgn}(e(k))}} \end{aligned}$$
(9)

where \(\alpha (k)\) represents the a priori estimation error given by:

$$\begin{aligned} \alpha (k) = d(k) - \mathbf w ^{T}(k-1) \mathbf{x }(k) \end{aligned}$$
(10)

Finally, Condition 2 in (7) is obtained as follows:

$$\begin{aligned} \frac{{\partial F(\mathbf{w }(k),\lambda )}}{{\partial \lambda }} = \left| {e(k)} \right| - \left| {e(k - 1)} \right| = 0. \end{aligned}$$
(11)

Here, Condition 2 is obtained as \(\left| {e(k)} \right| = \left| {e(k - 1)} \right| \) under the optimum conditions. However, this result does not ensure the negative definiteness of the Lyapunov function, \(\Delta V(k) < 0\). Therefore, in order to ensure \(\Delta V(k)\) \(= \left| {e(k)} \right| - \left| {e(k-1)} \right| < 0\) in all cases, we modify the error signal \(\left| {e(k)} \right| \) by using adaptation gain rate \(\kappa \in [0,1)\), as follows:

$$\begin{aligned} \left| {e(k)} \right| = \kappa \left| {e(k - 1)} \right| . \end{aligned}$$
(12)

Thus, the asymptotic stability of the proposed algorithm in the sense of Lyapunov, that is, \(\Delta V(k) = \kappa \left| {e(k - 1)} \right| - \left| {e(k - 1)} \right| < 0\) is ensured for \(\kappa \in [0,1)\). Therefore, the error function \(\left| {e(k)} \right| \) for \(\kappa \in [0,1)\) asymptotically converges to zero when the time index k approaches to infinity. This case can easily be verified by using (12) as follows:

$$\begin{aligned} \left| {e(k)} \right| = \mathop {\lim }\limits _{k \rightarrow \infty } {\kappa ^k}\left| {e(0)} \right| = 0. \end{aligned}$$
(13)

Remark

The use of the adaptation gain rate parameter \(\kappa \) in the proposed algorithm controls and improves the transient response of the adaptive filter. If \(\kappa \) is set to a small value, the proposed algorithm can achieve a faster convergence rate.

The Lagrange multiplier defined in (9) is rewritten in (14) by using (12).

$$\begin{aligned} \lambda \,\, = \frac{{\left( {\left| {\alpha (k)} \right| - \kappa \left| {e(k - 1)} \right| } \right) \text {sgn}(\alpha (k))}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}\text {sgn}(e(k))}} \end{aligned}$$
(14)

Finally, substituting (14) into (8), the proposed weight vector updates law is obtained as follows:

$$\begin{aligned} \mathbf{w }(k)&= \mathbf{w }(k - 1) \nonumber \\&\quad + \frac{{\mathbf{x }(k)}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}}}\left( {\alpha (k) - \kappa \left| {e(k - 1)} \right| \text {sgn}\left( {\alpha (k)} \right) } \right) . \end{aligned}$$
(15)

The weight vector update law of the proposed algorithm in (15) can be multiplied by a positive constant step size \(\mu \) in order to govern the steady-state and transient behaviors of the proposed algorithm. In addition, (15) can be modified in order to avoid singularity by adding a small positive constant \(\epsilon \). Consequently, the weight vector update law of the generalized FSS-LAF algorithm is given as in (16).

$$\begin{aligned} \mathbf{w }(k)&= \mathbf{w }(k - 1) \nonumber \\&\quad + \mu \frac{{\mathbf{x }(k)}}{\epsilon +{{{\left\| {\mathbf{x }(k)} \right\| }^2}}}\left( {\alpha (k) - \kappa \left| {e(k - 1)} \right| \text {sgn}\left( {\alpha (k)} \right) } \right) \end{aligned}$$
(16)

3 Stability of the FSS-LAF algorithm

In this section, we will represent the stability of the proposed FSS-LAF algorithm in terms of the convergence in the mean. The convergence analysis of the proposed algorithm can be done mathematically tractable if we use independence assumptions given in [1, 13, 14]. The desired signal first can be defined without loss of generality as follows:

$$\begin{aligned} d(k) = {\mathbf{w }_o}^\mathrm{T}\mathbf{x }(k) + n(k) \end{aligned}$$
(17)

where n(k) is zero-mean white Gaussian noise with variance \(\sigma _n^2\) which is uncorrelated with the input signal \(\mathbf{x }(k)\) [1, 13, 14].

Then, the a priori estimation error \(\alpha (k)\) is expressed by using (17) as follows:

$$\begin{aligned} \alpha (k)\, = {\mathbf{w }_o}^\mathrm{T}\mathbf{x }(k) + n(k) - {\mathbf{w }^\mathrm{T}}(k - 1)\mathbf{x }(k). \end{aligned}$$
(18)

Thus, using (18), (16) can be rewritten for \(\epsilon =0\) as:

$$\begin{aligned} \mathbf{w }(k)&= \mathbf{w }(k - 1) + \mu \frac{{\mathbf{x }(k)}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}}}\left( {{\mathbf{w }_o}^\mathrm{T}\mathbf{x }(k) + n(k)} \right. \nonumber \\&\quad \left. { - {\mathbf{w }^\mathrm{T}}(k - 1)\mathbf{x }(k) - \kappa \left| {e(k - 1)} \right| \text {sgn}\left( {\alpha (k)} \right) } \right) . \end{aligned}$$
(19)

After subtracting \({\mathbf{w }_o}\) from both sides of (19) [1, 13, 14], the weight error vector \(\mathbf{c }(k) = \mathbf{w }(k) - {\mathbf{w }_o}\) can be obtained by using (13), as follows:

$$\begin{aligned} \mathbf{c }(k)&= \mathbf{c }(k - 1) - \mu \frac{{\mathbf{x }(k) \mathbf x ^{T}(k)}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}}}\mathbf{c }(k - 1) + \mu \frac{{\mathbf{x }(k)n(k)}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}}}\nonumber \\&\quad - \mu \frac{{\mathbf{x }(k)}}{{{{\left\| {\mathbf{x }(k)} \right\| }^2}}}\left( {{\kappa ^k}\left| {e(0)} \right| \text {sgn}\left( {\alpha (k)} \right) } \right) . \end{aligned}$$
(20)

The statistical expectation operator is employed to both sides of (20), and then, the error signal vanishes in (20) (that is, \(\kappa \left| {e(k - 1)} \right| = {\kappa ^k}\left| {e(0)} \right| = 0\)) if the time index k approaches to infinity. Thus, (20) is easily obtained again under these assumptions as follows:

$$\begin{aligned} E\left\{ {{\mathbf{c }}(k)} \right\} = \left( {{\mathbf{I }} - \mu \frac{{\mathbf{R }}}{{\text {tr}[{\mathbf{R }}]}}} \right) E\left\{ {{\mathbf{c }}(k - 1)} \right\} . \end{aligned}$$
(21)

Using the unitary transformation similar to [1, 13, 14], we can define the correlation matrix \(\mathbf{R }\) as \(\mathbf{R }=\mathbf{Q }{\varvec{\varLambda }}\mathbf{Q }^\mathrm{T}\). Thus, we have:

$$\begin{aligned} E\left\{ {{\mathbf{v }}(k)} \right\} = \left( {{\mathbf{I }} - \mu \frac{{\varvec{\varLambda }}}{\lambda _{\max }}} \right) E\left\{ {{\mathbf{v }}(k - 1)} \right\} \end{aligned}$$
(22)

where \({\varvec{\varLambda }}\) is the diagonal matrix which has diagonal elements of \(\mathbf{R }\), \(\mathbf{Q }\) is the unitary matrix of transformation, \(\lambda _{\max }\) is the maximum eigenvalue of \(\mathbf{R }\), and \(\mathbf{v }(k)=\mathbf{Q }^\mathrm{T}\mathbf{c }(k)\).

If the nth natural mode of (22) is solved by considering the initial condition, we obtain the following solution:

$$\begin{aligned} E\left\{ {v_n}(k) \right\} = \left( {1 - \mu \frac{\lambda _n}{{\lambda _{\max }}}} \right) ^kE\left\{ {v_n(0)} \right\} \end{aligned}$$
(23)

where \(\lambda _n\) is the nth eigenvalue of \(\mathbf{R }\).

If the step size \(\mu \) in (23) is chosen as \( 0< \mu < 2\), \(\mathbf{w }(k)\) converges to \(\mathbf{w }_o\) when the time index k approaches infinity. In addition to this, assume that the error signal e(k) is equal to a priori estimation error \(\alpha (k)\) when the weight vector of the adaptive filter is close to the optimal weight vector.

4 Variable step size algorithms

In this section, we will design a number of widely used gradient VSS algorithms for the FSS-LAF algorithm. A gradient variable step size \(\mu (k)\) can be derived based on the following equation:

$$\begin{aligned} \mu (k) = \mu (k - 1) - {\left. {\rho {\nabla _\mu }J(k)} \right| _{\mu = \mu (k - 1)}} \end{aligned}$$
(24)

where the parameter \(\rho \) is the learning rate.

Using the cost function \(J(k) = \frac{1}{2}{\alpha ^2}(k)\), the gradient \(\nabla _\mu J(k)\) is calculated as [10]:

$$\begin{aligned} {\left. {{\nabla _\mu }J(k)} \right| _{\mu = \mu (k - 1)}} = - \alpha (k) \mathbf x ^{T}(k) \frac{{\partial \mathbf{w }(k - 1)}}{{\partial \mu (k - 1)}}. \end{aligned}$$
(25)

Assuming \(\mu (k - 1) \approx \mu (k)\) for a small step size value [10], we obtain the following equation:

$$\begin{aligned} \frac{{\partial \mathbf{w }(k - 1)}}{{\partial \mu (k - 1)}} \approx \frac{{\partial \mathbf{w }(k - 1)}}{{\partial \mu (k)}} = {\varvec{\psi }} (k) \end{aligned}$$
(26)

where \({\varvec{\psi }} (k)\) represents the sensitivity term [13].

Thus, a general update rule for the step size is obtained by using the sensitivity term \({\varvec{\psi }} (k)\), as follows:

$$\begin{aligned} \mu (k) = \mu (k - 1) + \rho \alpha (k) \mathbf x ^{T}(k) {\varvec{\psi }} (k). \end{aligned}$$
(27)

In the subsections, the design of VSS algorithms will be presented by evaluating the sensitivity term \({\varvec{\psi }} (k)\).

Table 1 Summary and complexity of the proposed algorithms
Full size table

4.1 BVSS-LAF algorithm

In this algorithm, the sensitivity term \({\varvec{\psi }} (k)\) is rigorously evaluated based on (16) as follows:

$$\begin{aligned}&\frac{{\partial \mathbf{w }(k - 1)}}{{\partial \mu (k - 1)}} = \frac{{\partial \mathbf{w }(k - 2)}}{{\partial \mu (k - 1)}}+ \frac{{\partial \mu (k - 1)}}{{\partial \mu (k - 1)}}\nonumber \\&\quad \left[ {\frac{{\mathbf{x }(k - 1)}}{{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}\left( {\left| {\alpha (k - 1)} \right| - \kappa \left| {e(k - 2)} \right| } \right) \text {sgn}\left( {\alpha (k - 1)} \right) } \right] \nonumber \\&\quad +\, \mu (k - 1)\left[ {\frac{{\mathbf{x }(k - 1)}}{{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}} \right. \left( {\frac{{\partial \left| {\alpha (k - 1)} \right| }}{{\partial \mu (k - 1)}}} \right. \nonumber \\&\quad \left. {\left. { -\, \kappa \frac{{\partial \left| {e(k - 2)} \right| }}{{\partial \mu (k - 1)}}} \right) \text {sgn}\left( {\alpha (k - 1)} \right) } \right] \nonumber \\&\quad +\, \mu (k - 1)\left[ {\frac{{\partial \left( {\mathbf{x }(k - 1)/{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}} \right) }}{{\partial \mu (k - 1)}}} \right. \nonumber \\&\quad \cdot \left. {\left( {\left| {\alpha (k - 1)} \right| - \kappa \left| {e(k - 2)} \right| } \right) \text {sgn}\left( {\alpha (k - 1)} \right) } \right] . \end{aligned}$$
(28)

The last term in (28) equals to zero because the input \(\mathbf{x }(k - 1)\) is independent of the step size \(\mu (k - 1)\). Therefore, only the terms \(\partial \left| {\alpha (k - 1)} \right| /\partial \mu (k - 1)\) and \(\partial \left| {e(k - 2)} \right| /\partial \mu (k - 1)\) are obtained as follows:

$$\begin{aligned} \frac{{\partial \left| {\alpha (k - 1)} \right| }}{{\partial \mu (k - 1)}}\,&= -\text {sgn}(\alpha (k - 1))\nonumber \\&\quad \cdot \left( \mathbf{x ^{T}(k-1) \frac{{\partial \mathbf{w }(k - 2)}}{{\partial \mu (k - 1)}}} \right) \end{aligned}$$
(29)
$$\begin{aligned} \frac{{\partial \left| {e(k - 2)} \right| }}{{\partial \mu (k - 1)}}&= - \text {sgn}(e(k - 2)) \nonumber \\&\quad \cdot \left( \mathbf{x ^{T}(k-2)\frac{{\partial \mathbf{w }(k - 2)}}{{\partial \mu (k - 1)}}} \right) . \end{aligned}$$
(30)

Using (29) and (30), (28) is rewritten as follows:

$$\begin{aligned} \frac{{\partial \mathbf{w }(k - 1)}}{{\partial \mu (k - 1)}}&= \left[ {\mathbf{I } - \mu (k - 1)\text {sgn}\left( {\alpha (k - 1)} \right) \frac{{\mathbf{x }(k - 1)}}{{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}} \right. \nonumber \\&\quad \cdot \left[ {\text {sgn}\left( {\alpha (k - 1)} \right) \mathbf x ^{T}(k-1)} \right. \nonumber \\&\quad \left. {\left. { -\, \kappa \text {sgn}\left( {e(k - 2)} \right) \mathbf{x ^{T}(k-2)}} \right] } \right] \nonumber \\&\quad \cdot \frac{{\partial \mathbf{w }(k - 2)}}{{\partial \mu (k - 1)}} + \frac{{\mathbf{x }(k - 1)}}{{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}\left( {\left| {\alpha (k - 1)} \right| } \right. \nonumber \\&\quad \left. { -\, \kappa \left| {e(k - 2)} \right| } \right) \text {sgn}\left( {\alpha (k - 1)} \right) . \end{aligned}$$
(31)

Thus, the sensitivity term \({\varvec{\psi }} (k)\) is expressed as follows:

$$\begin{aligned} {\varvec{\psi }}(k)&= {\varvec{\varLambda }} (k-1){\varvec{\psi }} (k-1) + \frac{{\mathbf{x }(k - 1)}}{\epsilon +{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}\nonumber \\&\quad \cdot \left( {\left| {\alpha (k - 1)} \right| - \kappa \left| {e(k - 2)} \right| } \right) \text {sgn}\left( {\alpha (k - 1)} \right) \end{aligned}$$
(32)

where \(\varvec{\varLambda }(k-1)\) is a time-varying adaptive filter that enables low-pass filtering of instantaneous gradients. Thus, the BVSS-LAF algorithm exhibits more accurate and robust behaviors against uncertainties resulted from the noisy instantaneous gradients [13].

Fig. 1
figure 1

Comparison of the proposed FSS-LAF algorithm in terms of MSD (dB) for correlated input at different fixed step sizes, a SNR \(=\) 0 dB, b SNR \(=\) 10 dB

Full size image

4.2 FVSS-LAF algorithm

In order to simplify the BVSS-LAF algorithm, the time-varying term \(\varvec{\varLambda }(k-1)\) is replaced by a constant \(0< a < 1\). Thus, \({\varvec{\psi }}(k)\) can be written as follows:

$$\begin{aligned} {\varvec{\psi }} (k)&= a{\varvec{\psi }} (k - 1)+ \frac{{\mathbf{x }(k - 1)}}{\epsilon +{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}\nonumber \\&\quad \cdot \left( {\left| {\alpha (k - 1)} \right| - \kappa \left| {e(k - 2)} \right| } \right) \text {sgn}\left( {\alpha (k - 1)} \right) . \end{aligned}$$
(33)

As seen from (33), the FVSS-LAF algorithm has a low-pass filter with a fixed coefficient a and thus provides the filtering of the noisy instantaneous gradients [13].

4.3 MVSS-LAF algorithm

By setting \(a=0\) in (33), the calculation of the sensitivity term can be further simplified as follows:

$$\begin{aligned} {\varvec{\psi }} (k)&= \frac{{\mathbf{x }(k - 1)}}{\epsilon +{{{\left\| {\mathbf{x }(k - 1)} \right\| }^2}}}\nonumber \\&\quad \cdot \left( {\left| {\alpha (k - 1)} \right| - \kappa \left| {e(k - 2)} \right| } \right) \text {sgn}\left( {\alpha (k - 1)} \right) . \end{aligned}$$
(34)

As seen from (34), the MVSS-LAF algorithm only uses the noisy instantaneous gradient estimates [13].

5 Computational complexities

As seen from Table 1, the BVSS-LAF algorithm has a higher computational complexity than the other VSS algorithms because of the detailed evaluation of \({\varvec{\psi }} (k)\). However, since the MVSS-LAF algorithm does not contain the information of the past values of \({\varvec{\psi }}(k)\), its computational complexity is less than those of the BVSS-LAF and FVSS-LAF algorithms.

6 Simulation results and discussion

In this section, the performance of the proposed algorithms is illustrated on identification scenarios. The unknown system H(z) including ten coefficients is randomly generated, and it has the same number of coefficients with the adaptive filter. The unknown system and the adaptive filter are fed by two Gaussian input signals [15] which are generated by filtering zero-mean white Gaussian random sequence through a first-order system (correlated input) \({G_1}(z) = {1}/({1 - 0.9{z^{ - 1}}})\) or a third-order system (nonwhite Gaussian input) \({G_2}(z) = {0.44}/({1 - 1.5{z^{ - 1}} + {z^{ - 2}}-0.25}{z^{ - 3}})\). The unknown system output s(k) is corrupted by the measurement noise n(k) with 0 and 10 dB signal-to-noise ratio (SNR) levels. To measure the performance of the proposed algorithms, the MSD is used as \(\text {MSD} = E{{{\left\| {{\mathbf{w }_o}-\mathbf{w }(k)} \right\| }^2}}\) [16]. All the following simulation results are obtained by ensemble averaging over 50 independent trials. The adaptation gain rate parameter of the proposed algorithms is chosen as \(\kappa =0.01\) in all the simulations to satisfy stability in the sense of Lyapunov. Also, \(\epsilon \) is chosen as 0.001.

Fig. 2
figure 2

Comparison of the proposed FSS-LAF algorithm in terms of MSD (dB) for nonwhite Gaussian input at different fixed step sizes, a SNR \(=\) 0 dB, b SNR \(=\) 10 dB

Full size image
Table 2 MSE performance of the proposed FSS-LAF algorithm at different step sizes and SNR levels
Full size table
Fig. 3
figure 3

a Comparison of the algorithms in terms of MSD (dB) for correlated input when SNR \(=\) 0 dB. b Variation of step sizes of the proposed VSS algorithms for correlated input when SNR \(=\) 0 dB

Full size image
Fig. 4
figure 4

a Comparison of the algorithms in terms of MSD (dB) for correlated input when SNR \(=\) 10 dB. b Variation of step sizes of the proposed VSS algorithms for correlated input when SNR \(=\) 10 dB

Full size image
Fig. 5
figure 5

a Comparison of the algorithms in terms of MSD (dB) for nonwhite Gaussian input when SNR \(=\) 0 dB. b Variation of step sizes of the proposed VSS algorithms for nonwhite Gaussian input when SNR \(=\) 0 dB

Full size image
Fig. 6
figure 6

a Comparison of the algorithms in terms of MSD (dB) for nonwhite Gaussian input when SNR \(=\) 10 dB. b Variation of step sizes of the proposed VSS algorithms for nonwhite Gaussian input when SNR \(=\) 10 dB

Full size image

Figures 1 and 2 show the effect of the step size on the MSD error of the proposed FSS-LAF algorithm at 0 and 10 dB SNRs for the correlated and nonwhite input signals. As seen from Figs. 1 and 2, a small step size slows down the convergence rate but provides a lower steady-state MSD error. On the other hand, a large step size accelerates the convergence but produces a higher steady-state MSD error. When \(\mu = 2\), the proposed algorithm demonstrates an unstable behavior because the step size \(\mu \) must be chosen less than 2 to ensure the stability of the proposed FSS-LAF algorithm. Note that the FSS-LAF algorithm for \(\mu = 1\) is equivalent to the classical LAF algorithm [2] which does not find the optimal weight vector coefficients as seen from Figs. 1 and 2. However, the proposed algorithm with a small step size value can estimate the optimal weight vector of the unknown system. Furthermore, Table 2 shows steady-state MSE performance of the proposed FSS-LAF algorithm for the correlated and nonwhite Gaussian inputs at different step sizes and SNR levels. As can be observed from both Figs. 1, 2 and Table 2, the proposed FSS-LAF algorithm provides a lower steady-state MSD and MSE errors for \(\mu = 0.05\). Therefore, its step size is chosen to be \(\mu = 0.05\) in the following simulations. For a fair comparison, while the initial values of the step sizes of the proposed VSS algorithms are initialized a small value such that as \(\mu (0) = 0.01\), other parameters of them for each simulation are chosen experimentally to achieve both the best convergence rate and the minimum level of the MSD (dB) error. In our simulations, we also compare the proposed algorithms with the recursive least square (RLS) algorithm, where the forgetting factor \(\lambda \) and the parameter \(\delta \) for initializing the inverse autocorrelation matrix \(\mathbf P (0)\) are chosen as 0.999 and 0.01, respectively.

Table 3 Coefficients of unknown system found by algorithms for correlated input signal
Full size table
Table 4 Coefficients of unknown system found by algorithms for nonwhite Gaussian input signal
Full size table

Figure 3a shows the convergence performances of the algorithms in terms of the MSD (dB) for the uncorrelated input signal when SNR \(=\) 0 dB. As seen from Fig. 3a, proposed BVSS-LAF and FVSS-LAF algorithms provide a good trade-off between the convergence rate and the steady-state MSD error due to the use of a low-pass filter for the noisy instantaneous gradients when compared to the other two proposed algorithms. As seen from Fig. 3a, the RLS algorithm exhibits a faster convergence rate than the proposed algorithms but achieves the same steady-state MSD error with the FVSS-LAF algorithm. Note that the faster convergence rate of the RLS algorithm comes at the cost of high computational complexity which is \(3(M+1)^2 + 2(M+1)\) [14]. The variations of step sizes of the corresponding VSS algorithms for the uncorrelated input signal and SNR \(=\) 0 dB are also shown in Fig. 3b. As seen from Fig. 3b, the step sizes \(\mu (k)\) of the BVSS-LAF and FVSS-LAF algorithms, unlike the MVSS-LAF algorithm, go up to higher values initially and then come down very fast to lower values. Thus, the BVSS-LAF and FVSS-LAF algorithms exhibit a faster initial convergence behavior and then improve the identification of the unknown system in order to obtain a lower MSD error in the steady state. For SNR \(=\) 10 dB, results similar to those in Fig. 3a, b are observed in Fig. 4a, b, respectively.

Figure 5a shows the convergence performances of the algorithms in terms of MSD (dB) for the nonwhite Gaussian input signal when SNR \(=\) 0 dB. As seen from Fig. 5a, the BVSS-LAF and FVSS-LAF algorithms outperform the FSS-LAF and MVSS-LAF algorithms in terms of the convergence rate and steady-state MSD error. Also, in Fig. 5a, although RLS algorithm for nonwhite Gaussian input shows a faster convergence rate, it produces a higher steady-state MSD error when compared to the proposed algorithms. In Fig. 5b, for the nonwhite Gaussian input signal at SNR \(=\) 0 dB, the step sizes \(\mu (k)\) of the BVSS-LAF and FVSS-LAF algorithms quickly converge to high values and then very fast descend to small values, unlike the MVSS-LAF algorithm. Also, in Fig. 6a, b, results similar to those in Fig. 5a, b are observed for 10 dB SNR. Moreover, Tables 3 and 4 summarize the coefficients of the unknown system obtained by the algorithms for the correlated and nonwhite Gaussian input signals at 0 and 10 dB SNR levels. Tables 3 and 4 show that, in the steady-state, all the algorithms approximately converge to the optimal weight vector coefficients.

7 Conclusion

In this paper, we have proposed a generalized FSS-LAF algorithm and its VSS versions. The proposed FSS-LAF algorithm ensuring asymptotic stability has improved the performance in the presence of the measurement noise. Furthermore, three VSS algorithms have been adapted to the FSS-LAF algorithm to further improve the performance. The performances of the proposed algorithms have been tested on system identification problems in terms of the MSD (dB) and the convergence rate. The simulation results have shown that the derived bounds of step size for the FSS-LAF algorithm are justified, and especially, the BVSS-LAF and FVSS-LAF algorithms provide a better trade-off between the steady-state MSD (dB) error and the convergence rate.