An ALNS to optimize makespan subject to total completion time for no-wait flow shops with sequence-dependent setup times

Abstract

In this article, we address the no-wait flow shop scheduling problem with sequence dependent setup times. The objective is to minimize makespan subject to an upper bound on total completion time. Although these performance measures and constraints have been extensively studied, they have never been considered together in this problem before. To solve the problem, we propose an adaptive large neighborhood search algorithm called $\textit{ALNS}_\textit{A}$. Essentially, $\textit{ALNS}_\textit{A}$ improves an initial solution by dynamically selecting and executing a pair of destroy and repair methods based on their performance history. In addition to classic greedy and random methods used, we present two new mechanisms in which the greediness-randomness behavior is balanced. To evaluate performance, the proposed approach is compared with three heuristic methods—GL, HH1 and TOB—developed for the most similar problems found in the literature. Computational experiments show that the proposed method outperforms state-of-the-art approaches in the literature for the no-wait flow shop scheduling problem with sequence dependent setup times and is therefore recommended to solve the problem.

1 Introduction

In this article, we address the flow shop scheduling problem (FSP) with two processing constraints: no-wait (NWT) and sequence dependent setup times (SDST). The FSP is a system where a set of jobs have to be processed through a series of machines in the same processing routing. In this system, often the same job sequence occurs on all machines, so that a schedule can be defined by a single permutation of jobs. When the NWT constraint is in place, there is no waiting time between successive operations. Therefore, no job is permitted to utilize a buffer or to wait in an upstream machine. NWT may occur due to process requirements or unavailability of waiting space. Having setup constraints means that a machine requires some preparation before processing a particular job. This preparation may include cleaning, retooling, adjustments, inspection and rearrangement of the work station. In SDST, the length of these times depends on the difficulty involved in switching from one processing configuration to another. SDST are common in multipurpose machines or when a single facility produces a variety of products. In those situations, instead of absorbing the setup times in the processing times, it is recommended to make explicit considerations (Emmons and Vairaktarakis 2013; Pinedo 2016).

The problem is considered with makespan and total completion time. Makespan and total completion time are among the most important performance measures in the field of scheduling. Makespan represents the maximal completion time among all jobs in the system. Minimizing makespan is appropriate when a complete batch of jobs needs to be dispatched as quickly as possible. A reduced makespan also allows an efficient use of resources, that is, it decreases equipment idle time. Total completion time is defined by the sum of all completion times. Schedulers try to minimize total completion time to increase processing rate, which decreases work-in-process inventory and increases the response to demands (Baker and Trietsch 2019). Optimization problems involving two (or more) conflicting objectives, such as these, need to be considered in the presence of trade-offs because no single solution optimizes each objective simultaneously. The approach adopted in this work is to optimize makespan subject to total completion time. This objective function is appropriate when makespan needs to be minimized, but there is no need to optimize total completion time as long as it does not exceed an upper bound. A practical example is when a scheduler sets an upper bound on total completion time to prevent inventory from growing beyond the facility’s capacity, but no benefit is gained by reducing it further after achieving this.

Many researchers have proposed algorithms to minimize makespan or total completion time in NWT–FSP–SDST. The most relevant studies include greedy algorithms (Bianco et al 1999; Xu et al 2012), simulated annealing (Lee and Jung 2005), hybrid genetic algorithm (Franca et al 2006), constructive heuristics (Araújo and Nagano 2011; Nagano et al 2015), differential evolution (Qian et al 2011, 2012), greedy randomized adaptive search and evolutionary local search based (Zhu et al 2013b), iterative algorithm (Zhu et al 2013a), hybrid evolutionary cluster search (Nagano and Araújo 2014), hybrid greedy algorithm (Zhuang et al 2014), particle swarm optimization (Samarghandi and ElMekkawy 2014), genetic algorithms (Samarghandi 2015a, b) and local search (Miyata et al 2019).

Despite the extensive research on multi-objective optimization of NWT–FSP, few studies have addressed objectives of type A subject to B. Moreover, none of them have considered the SDST feature, to the best of our knowledge. Allahverdi (2004) tried to minimize a linear combination of makespan and maximum tardiness under the condition of not allowing maximum tardiness to exceed a given value. Framinan and Leisten (2006) studied the FSP with the objective of minimizing makespan, such that maximum tardiness is not greater than an acceptable limit. Aydilek and Allahverdi (2012) and Nagano et al (2020) addressed the NWT–FSP with the objective of minimizing makespan under the constraint that mean completion time (or the equivalent total completion time) does not exceed a maximum value. Allahverdi and Aydilek (2013) addressed the NWT–FSP and tried to minimize total completion time while keeping makespan less than or equal to an upper bound, and Allahverdi and Aydilek (2014) considered the same problem with separate setup times. Recently, Allahverdi et al (2018) proposed an algorithm to solve the NWT–FSP with the objective of minimizing total tardiness, such that makespan does not exceed a given value, and Allahverdi et al (2020) studied the same problem with separate setup times.

The NWT–FSP–SDST belongs to the class of NP-hard problems (Bianco et al 1999). As exact methods are often impractical or ineffective for solving large or complex problems, heuristic methods are preferable. Heuristics use simple rules and shortcuts to find satisfactory solutions for various combinatorial optimization problems in a reasonable time. Unfortunately, this flexibility comes at a cost: there is no unique optimal parameter setting suitable for all problems and instances. This means that it will always take some effort to properly calibrate the algorithms in each new instance configuration if the scheduler really wants to extract maximum performance. The possibility of improvement can even be assumed to heuristics targeting the most convenient instance configuration, since heuristic solutions are not guaranteed to be optimal. Furthermore, the complexity of the algorithm and its computational time are always properties to be improved. In other words, there will always be possibilities for improvement, whether to get easier, better or faster solutions.

Focusing on these opportunities, we present the algorithm called $ALNS_{A}$ for the NWT–FSP–SDST to minimize makespan subject to total completion time. This method is based on the adaptive large neighborhood search (ALNS) algorithm originally presented by Ropke and Pisinger (2006), which extends the large neighborhood search (LNS) heuristic proposed by Shaw (1998). In LNS, a destroy and a repair method iteratively rebuild an initial solution in an attempt to improve it. In ALNS, multiple destroy and repair methods are used, and the performance of each destroy/repair method determines how often that particular method is executed during the search. This allows the algorithm to adapt to search conditions, reducing the need for calibration for different instance configurations. ALNS has been mainly applied in vehicle routing problems (VRP), e.g., Hemmelmayr et al (2012), Qu and Bard (2012), Demir et al (2012) and Azi et al (2014). However, the number of scheduling applications has also grown in recent years, e.g., Lin and Ying (2014), Rifai et al (2016) and Beezão et al (2017). In this work, our proposed $ALNS_{A}$ accesses a set of distinct mechanisms and dynamically selects a pair of destroy and repair methods based on their performance history. Among the mechanisms used, we present two new ones in which the greediness–randomness behavior is balanced to obtain better results. Extensive experiments are made to compare $ALNS_{A}$ with three heuristics for similar problems found in the literature. In addition, we present a mathematical model to be used as benchmark for small instances problems. All results are statistically verified.

The remainder of this article is organized as follows. The problem definition is described in Sect. 2. The mathematical model is presented in Sect. 3 and the algorithms are presented in Sect. 4. Section 5 is dedicated to the experimental design and analysis of results. Some concluding remarks are given in Sect. 6.

2 Problem definition

The FSP consists of a set $J = \left\{ i \mid i \in \mathbb {N}, 1 \le i \le n \right\}$ of n jobs which needs to be processed on a set $M = \left\{ k \mid k \in \mathbb {N}, 1 \le k \le m \right\}$ of m machines. Each machine can process only one job at a time. All jobs are processed once on each of the m machines, where the operation $O^k_i$ of job i on machine k is executed during the processing time $p^k_i$ without preemption. Moreover, all jobs follow the same processing order and the job sequence is kept fixed through all machines. It is assumed that all jobs are ready at time 0.

Fig. 1

Gantt chart of an example problem with three jobs and three machines

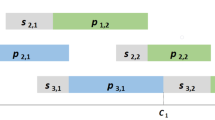
The NWT constraint imposes that operation $O^{k+1}_i$ must begin immediately after operation $O^k_i$ is completed. The SDST constraint implies that, after operation $O^k_i$ is processed, machine k requires a sequence dependent setup $s^k_{ij}$ before being able to start $O^k_j$. Therefore, setup times are not-attached; that is, a setup process must begin before the next job is ready for a given machine. It is assumed that there is no initial setup required by any machine before starting its first operation, and there is no final setup required to bring any machine back to its initial state after its last operation is executed. Figure 1 shows an example of the NWT–FSP–SDST. In particular, an instance with $n=3$ jobs and $m=3$ machines is represented.

Given the set $I = \{ q \mid q \in \mathbb {N}, 1 \le q \le n \}$ of n positions of a production sequence of J, let $t^k_q$ be the starting time of the qth job on machine k, and $c^k_q$ the completion time of the qth job on machine k. For simplicity, let $t_q$ = $t^1_q$ and $c_q$ = $c^m_q$. Based on the formulation of Bianco et al (1999), we have

$$\begin{aligned} t_{q+1} = t_q + \max \limits _{1 \le k \le m} \left[ s^k_{q,q+1} + \sum _{h=1}^{k} \left( p^h_q - p^h_{q+1} \right) + p^k_{q+1} \right] , \quad q \in I / \{n\} \end{aligned}$$

(1)

and

$$\begin{aligned} c_q = t_q + \sum _{k \in M} p^k_q, \quad q \in I. \end{aligned}$$

(2)

Equation (1) defines $t_{q+1}$ as $t_{q}$ plus its distance to $t_{q+1}$. And since the problem has the no-wait constraint, the completion time $c_q$ of a job is equal to its starting time $t_q$ plus the sum of its processing times, as defined in Eq. (2). Moreover, let $C_{max}$ and TCT represent the performance measures makespan and total completion time, respectively. Hence, we have $C_{max} = c_n$ and $TCT = \sum _{q \in I} c_q$.

The optimization problem modeling the NWT–FSP–SDST minimizing makespan subject to an upper bound on total completion time can be described as follows. The search space is defined by the set of feasible solutions $X = \{\pi \mid TCT(\pi ) \le K\}$, where $TCT(\pi )$ is the total completion time value of the solution $\pi$ and K is a constant used as upper bound. The objective is to find a solution with the lowest makespan value among all feasible solutions, that is, find a $\pi ^* \in X$, so that $C_{max}(\pi ^*) \le C_{max}(\pi ), \; \forall \pi \in X$. Each solution $\pi \in X$ defines a production sequence which we represent by a vector $\pi = (\pi _1,...,\pi _n)$, being $\pi _i \in J$ and $\pi _i \ne \pi _j$ if $i \ne j$. Clearly this is a permutation problem.

Using the notation proposed by Graham et al (1979) and T’kindt and Billaut (2006) the addressed problem can be written as

$$\begin{aligned} \textit{Fm} \; / \; \textit{nwt}, s^{k}_{i,j} \; / \; \epsilon (C_{max} / TCT). \end{aligned}$$

where $\epsilon (C_{max} / TCT)$ represents the objective function of minimizing $C_{max}$ subject to an upper bound on TCT, while Fm and nwt represent flow shop and no-wait, respectively.

3 Mixed-integer linear programming model

We formulate a mixed-integer linear programming model (MIP) for $\textit{Fm} \; / \; \textit{nwt}, s^{k}_{i,j} \; / \; \epsilon (C_{max} / TCT)$ as follows. Let $x^q_i$ be a binary decision variable, such that $x^q_i$ = 1 if job i is the qth job processed, otherwise $x^q_i$ = 0. Now, let $y^{q}_{ij}$ be a binary auxiliary variable, such that $y^{q}_{ij}$ = 1 if job i is the qth job processed immediately before job j, otherwise $y^{q}_{ij}$ = 0. Hence, MIP is defined as follows:

$$\begin{aligned} z = \text {min } c_n \end{aligned}$$

(3)

Subject to:

$$\begin{aligned}&\sum _{q \in I} c_q \le K \end{aligned}$$

(4)

$$\begin{aligned}&\quad \sum _{i \in J} x^q_i = 1, \quad q \in I \end{aligned}$$

(5)

$$\begin{aligned}&\quad \sum _{q \in I} x^q_i = 1, \quad i \in J \end{aligned}$$

(6)

$$\begin{aligned}&\quad \sum _{j \in J} y^{q}_{ij} = x^q_i, \quad q \in I / \{n\}, \quad i \in J, \quad i \ne j \end{aligned}$$

(7)

$$\begin{aligned}&\quad \sum _{i \in J} y^{q}_{ij} = x^{q+1}_i, \quad q \in I / \{n\}, \quad j \in J, \quad i \ne j \end{aligned}$$

(8)

$$\begin{aligned}&\quad c^k_q = t^k_q + \sum _{i \in J}(p^k_i \cdot x^q_i), \quad q \in I, \quad k \in M \end{aligned}$$

(9)

$$\begin{aligned}&\quad t^{k+1}_q = c^k_q, \quad q \in I, \quad k \in M / \{m\} \end{aligned}$$

(10)

$$\begin{aligned}&\quad t^k_{q+1} \ge c^k_q + \sum _{i \in J}\sum _{j \in J}(s^{k}_{ij} \cdot y^{q}_{ij}), \quad q \in I / \{n\}, \quad k \in M, \quad i \ne j \end{aligned}$$

(11)

$$\begin{aligned}&\quad t_1 = 0 \end{aligned}$$

(12)

$$\begin{aligned}&\quad x^q_i = \{0, 1\}, \quad i \in J, \quad q \in I \end{aligned}$$

(13)

$$\begin{aligned}&\quad y^{q}_{ij} = \{0, 1\}, \quad q \in I / \{n\}, \quad i, j \in J, \quad i \ne j \end{aligned}$$

(14)

$$\begin{aligned}&\quad t^k_q \ge 0, \quad q \in I, \quad k \in M \end{aligned}$$

(15)

$$\begin{aligned}&\quad c^k_q \ge 0, \quad q \in I, \quad k \in M \end{aligned}$$

(16)

The objective function (3) minimizes makespan. Constraint (4) imposes the upper bound K on TCT. Constraints (5) and (6) are the job assignment constraints, and constraints (7) and (8) are the precedence constraints. Constraints (9) state the right difference between the start time and the end time of a job on a machine according to the job assigned. Constraints (10) guarantee NWT more easily than Eq. (2), because they ensure no gap between successive processing of a job with a simple equality. Constraints (11) ensure the SDST constraints with a simple inequality. This avoids dealing with the “max” term from Eq. (1). Constraint (12) states that the first job on the first machine starts processing at time zero. Constraints (13)–(16) give the domains of the variables.

4 Heuristic algorithms

As mentioned earlier, the problem $\textit{Fm} / \textit{nwt} / \epsilon (C_{max} / TCT)$—without SDST constraints—has already been addressed by Aydilek and Allahverdi (2012) and Nagano et al (2020). Ye et al (2020) also proposed an algorithm for a similar environment. In this work, the best algorithm from each study is adapted to be used as a benchmark. The three methods are briefly explained in the next subsection, followed by a complete description of our proposed algorithm $\textit{ALNS}_\textit{A}$ to solve the problem (3)–(16).

4.1 Literature algorithms

Aydilek and Allahverdi (2012) proposed the algorithm HH1, composed by the algorithms called mSA and HA. The algorithm mSA is a modified simulated annealing, which tries to improve the incumbent solution by iteratively moving a random job to a random position. The algorithm HA iteratively applies an insertion local search. Then, it tries to improve the solution generated by using an interchange local search (local search that swaps random pairs of jobs). Only solutions with TCT less than or equal to a given upper bound can be candidates to update the incumbent solution. The final solution generated by mSA is used as initial solution of HA.

Nagano et al (2020) proposed the algorithm GL for the same problem. GL iterates through a reconstruction procedure followed by an insertion local search. The reconstruction step creates candidate solutions by removing random jobs from the incumbent solution and reinserting them back by using a constructive heuristic based on NEH (Nawaz et al 1983). This loop repeats until a defined number of iterations is achieved. Finally, a transposition local search (local search that swap pairs of adjacent jobs) tries to improve the incumbent solution. Throughout the execution, only sequences with TCT less than or equal to the upper bound are considered candidate solutions.

Ye et al (2020) proposed the algorithm called TOB. First, this method performs a reconstruction process that combines the NEH heuristic with an interchange local search. Then, a modified insertion local search is applied (local search that inserts jobs only ahead of its original position). The algorithm repeats these steps until a maximum number of iterations is achieved. The objective function was defined as a mathematical relationship between the two performance measures.

4.2 Algorithm $ALNS_{A}$

The adaptive large neighborhood search (ALNS), originally proposed by Ropke and Pisinger (2006), has access to a set of destructive and constructive heuristics. At each iteration, a given solution is destroyed by a destructive procedure and rebuilt by a constructive procedure. A weight is assigned to each heuristic according to its performance, giving to those that perform well a higher probability to be selected again. Usually, the weights are updated, so that all heuristics have at least some chance to be executed. This dynamic selection adapts the algorithm to the instance and the state of the search at hand (Pisinger and Ropke 2019).

The proposed ALNS ($ALNS_A$) starts with a permutation $\pi ^{0}$ as initial solution. Algorithm is the main structure that uses other heuristics to perform the search, and the performance of these methods determines how often each one is executed. Given the set $\Omega ^{-}$ of destroy heuristics and the set $\Omega ^{+}$ of repair heuristic, Algorithm iteratively tries to improve the incumbent solution $\pi ^*$ by using a destroy heuristic $d \in \Omega ^{-}$ and a repair mechanism $r \in \Omega ^{+}$ to create a new candidate solution $\pi '$, so that $\pi '$ = $r(d(\pi ^*))$.¹²

Algorithm 1

$ALNS_{A}$

Algorithm 2

Destroy d

Algorithm 3

Repair r

The set $\Omega ^{-}$ is composed by three destroy algorithms. Destroy algorithm $d = 1$ removes a predefined number of jobs from a sequence at random. Destroy algorithm $d = 2$ tries to remove from a sequence the best set of jobs that optimize the objective. Destroy algorithm $d = 3$ is similar to the previous one, but it differs by skipping some jobs at probability of 50%. These three heuristics are represented by the generic destroy Algorithm 2. The set $\Omega ^{+}$ is composed by three repair algorithms. Repair algorithm $r = 1$ reinserts the removed jobs back to the partial sequence at random positions. Repair algorithm $r = 2$ reinserts each removed job back to the partial sequence in the best possible position. Repair algorithm $r = 3$ is similar to the previous one, but it differs by skipping some insertion options at probability of 50%. These three heuristics are represented by the generic repair Algorithm 3.

Line 5 of Algorithm 2 works as follows.

• insert$_1$($\pi$, $\pi ^{e}$) inserts a random job from $\pi$ into the start of $\pi ^{e}$;

• insert$_2$($\pi$, $\pi ^{e}$) removes the job that minimizes $C_{max}$ of the remainder of $\pi$ and insert it at the start of $\pi ^{e}$;

• insert$_3$($\pi$, $\pi ^{e}$) removes the job that minimizes $C_{max}$ of the remainder of $\pi$ and insert it at the start of $\pi ^{e}$, but skipping some job options at probability of 50%;

Line 3 of Algorithm 3 works as follows.

• insert$_1$($\pi ^{e}$, $\pi$) inserts the first job of $\pi ^{e}$ into a random position of $\pi$;

• insert$_2$($\pi ^{e}$, $\pi$) inserts the first job of $\pi ^{e}$ into the best position of $\pi$ that minimizes its new $C_{max}$;

• insert$_3$($\pi ^{e}$, $\pi$) inserts the first job of $\pi ^{e}$ into the best position of $\pi$ that minimizes its new $C_{max}$, but skipping some position options at probability of 50%;

Pure random procedures as $d = 1$ and $r = 1$ have low performance but provide high diversification. On the other hand, pure greedy procedures as Algorithms $d = 2$ and $r = 2$ have high performance but provide low diversification and therefore tend to get stuck in a local optimum. Algorithms $d = 3$ and $r = 3$ have been developed to provide balanced options on these behaviors. The balance is achieved by adding to standard greedy mechanisms the simple but effective procedure of skipping some job manipulations at random, rather than testing every insertion or removal option. If the mechanisms selected are not able to produce a candidate solution $\pi '$, so that $TCT(\pi ') \le K$, the search proceeds to the next iteration without changes.

The parameters $\rho _{i}^{-} \in \mathbb {R}^{\Vert \Omega ^{-}\Vert }$ and $\rho _{i}^{+} \in \mathbb {R}^{\Vert \Omega ^{+}\Vert }$ store the weights of destroy and repair methods, respectively. Equation 17 describes how Algorithm calculates the probabilities $\phi _{i}^{-}$ and $\phi _{i}^{+}$ to select the ith destroy and repair heuristics, respectively.

$$\begin{aligned} \phi _{i}^{-}&= \frac{\rho _{i}^{-}}{\sum _{k=1}^{\Vert \Omega ^{-}\Vert }\rho _{k}^{-}}&\phi _{i}^{+}&= \frac{\rho _{i}^{+}}{\sum _{k=1}^{\Vert \Omega ^{+}\Vert }\rho _{k}^{+}} \end{aligned}$$

(17)

After each iteration of Algorithm , a score $\Psi$ is assigned to the methods used, so that

$$\begin{aligned} \Psi = {\left\{ \begin{array}{ll} \text {4,\quad if generated solution is a new global best;} \\ \text {3,\quad if generated solution is a new local best;} \\ \text {2,\quad if generated solution is accepted;} \\ \text {1,\quad if generated solution is rejected.} \end{array}\right. } \end{aligned}$$

(18)

Initially, we define $\rho ^{-} = (1, 1, 1)$ and $\rho ^{+} = (1, 1, 1)$. Then, the methods have their weights updated by computing

$$\begin{aligned} \rho _{i}^{-}&= \lambda \rho _{i}^{-} + (1-\lambda )\Psi \alpha _{i}^{-} \end{aligned}$$

(19)

and

$$\begin{aligned} \rho _{i}^{+}&= \lambda \rho _{i}^{+} + (1-\lambda )\Psi \alpha _{i}^{+}, \end{aligned}$$

(20)

with $\lambda \in [0,1]$. The parameters $\alpha _{i}^{-}$ and $\alpha _{i}^{+}$ represent the values used to normalize the score $\Psi \in \{1, 2, 3, 4\}$ with a measure of the CPU time of the corresponding heuristic. This is important, because some methods can be significantly slower than others, so the normalization ensures a proper trade-off between CPU time and solution quality. Note that the values of $\Psi$ {1, 2, 3, 4} are just a sequence of numbers in ascending order to establish a status ranking. The parameter that really controls the sensibility to change in performance is $\lambda$. Furthermore, only the weights $\rho _{i}^{-}$ and $\rho _{i}^{+}$ corresponding to the methods used in the current iteration are updated.

5 Computational experiments

We implemented all algorithms in C++ and ran them on a Windows 11 PC with a processor Intel$\circledR$ Core$^{\hbox {TM}}$ i5-11400 H and 16 GB of RAM. The literature methods HH1, GL and TOB were adapted and re-implemented. The source code and scripts can be downloaded from 10.5281/zenodo.10577724. To find optimal solutions for the proposed MIP, we employ the Gurobi Optimizer solver version 10.0.2. This solver is widely used in the field of operations research and has proven to be efficient and robust for solving large-scale linear and mixed-integer programming problems.

We defined the stopping criterion for the heuristic methods as $n \times (m/2) \times t$ milliseconds, with $t \in \{10, 20, 30, 40\}$ to analyze consistency across different computational times. In real life, the initial solution $\pi ^{0}$ and the upper bound K must be given by the scheduler. For our experimental purposes, each $\pi ^{0}$ is obtained by optimizing a random permutation through a simple local search that swaps pairs of adjacent jobs and has a neighborhood space of size $(n-1)$. The K value is defined as the total completion time of the initial solution, that is, $K = TCT(\pi ^{0})$. The same initial solutions and upper bounds were used for all methods for a fair comparison.

The solutions were evaluated by using the Average Relative Percentage Deviation (ARPD) defined as

$$\begin{aligned} ARPD_{h} = \frac{100}{N} \sum _{i=1}^{N} \frac{{C_{max}}_{i}^{h} - {C_{max}}_{i}^{best}}{{C_{max}}_{i}^{h}}, \end{aligned}$$

(21)

where h represents the evaluated solution, i is a problem instance, best is the best known solution for that instance and N is the number of instances. In summary, this measure represents the arithmetic mean of the deviations from the best solutions found. Therefore, the best method is the one with lowest ARPD value.

The experiments are divided in three phases. In the first phase, a parameter tuning for $ALNS_{A}$ is performed. In the second phase, the heuristics methods are compared with an exact method for small instances. And in the third phase, the heuristics are tested in large instance benchmarks from literature. These three phases are presented in the next subsections.

5.1 $ALNS_{A}$ parameters tuning

The parameter tuning had been performed for $ALNS_{A}$ as follows. Parameter $\lambda$ was calibrated in a set of 120 instances, with 5 different problems for each combination $n \in$ {5, 10, 20, 40, 80, 160} $\times$ $m \in$ {4, 8, 12, 16} by using the IRACE software package (Lopez-Ibanez et al 2016). We separate the tuning and validation instances to reduce the risk of over-fitting the parameters tuned to the validation instances. This tuning set has processing times with a uniform distribution in the range [1, 99]. The SDST have a uniform distribution in the range [1, 9]. The tuning was performed by using a computation time limit of $n \times (m/2) \times 25$ milliseconds as stopping criterion (Ruiz and Stützle 2008). We consider $\lambda \in \{0, 0.1, 0.2,..., 1\}$ for tuning in IRACE and the result obtained was $\lambda = 0.3$. We obtained the normalization values $\alpha ^{-} = (0.98, 0.3, 0.72)$ and $\alpha ^{+} = (0.99, 0.44, 0.57)$ by dividing the average time of each method by the maximum time of its set (destroy or repair) after running them 10 times on a random instance. The parameters $T_{0}$ (initial temperature), and $c_{f}$ (cooling factor) control the convergence of the algorithm. Based on the similar approach used in the simulated annealing heuristic presented by Aydilek and Allahverdi (2012), we take directly from these works the values $T_{0} = 0.1$ and $c_{f} = 0.98$.

5.2 Experiment with small instances

In this section, we create a set of instances with 5 different problems for each combination $n \in$ {6, 8, 10, 12} $\times$ $m \in$ {3, 4, 5, 6}. The processing times have a uniform distribution in the range [1, 99]. The set has setup times uniformly distributed in the ranges [1, 9], [1, 49], [1, 99] and [1, 124]. Therefore, 320 different problem instances were generated.

Table 1 ARPD of jobs (n) $\times$ machines (m)—[small instances]

The ARPD results with their standard deviations for jobs and machines are presented in Table 1. These values are averages of 80 measures (5 problems $\times$ 4 setups $\times$ 4 times). Obviously, MIP has all values equal to zero, as it always produces optimal solutions. Note that $ALNS_{A}$ performs consistently better when compared to the literature methods and very close to the MIP benchmark. Figure 2 illustrates the aggregated ARPD and CPU time values for each parameter. As can be seen, the heuristics are not very sensitive to parameter variation, except GL which performs better as the number of jobs increases, and worst as the number of machines increases. The methods HH1 and TOB have the worst performances which are very similar. In general, the exact method can be used until a number of 8 jobs. Above that, its CPU time starts to increase exponentially, so that a heuristic method is recommended. Because MIP failed to produce feasible solutions in many cases with stopping criterion, we run it without a time limit and presented its results over time in Figs. 2e and f instead of Fig. 2d. The overall ARPD values of $ALNS_{A}$, GL, HH1, TOB are 0.02%, 0.23%, 1.21% and 1.16%, respectively.

Fig. 2

Aggregated ARPD and CPU times

5.3 Experiment with large instances

This phase considers the problem instances of Ruiz and Stützle (2008), which are extensions of the Taillard’s benchmark (Taillard 1993). The extensions are divided in four sets, each consisting of 10 problems for each combination $n \times m$ for {20, 50, 100} $\times$ {5, 10, 20} and 200 $\times$ {10, 20}. The processing times have a uniform distribution in the range [1, 99]. Each set has setup times uniformly distributed in the ranges [1, 9], [1, 49], [1, 99] and [1, 124], respectively. This means that in total, there are 440 different problem instances.

Table 2 ARPD for jobs (n) $\times$ machines (m)—[large instances]

Table 3 ARPD for setup (s) $\times$ time (t)—[large instances]

The ARPD results for jobs and machines are presented in Table 2. These values are averages of 160 measures (10 problems $\times$ 4 setups $\times$ 4 times). Table 3 gives the results for setup and time, where the values are averages over 110 measures (the size of each instance set). Note that $ALNS_{A}$ performs consistently better when compared to the literature methods in each table. Figure 3 illustrates the ARPD values aggregated for each parameter. As can be seen, the heuristics are not very sensitive to variations on the parameters, except TOB which have values disproportionately high especially for 200 jobs (Fig. 3a) and $t = 10$ (Fig. 3c). These are extreme conditions because computational time is the main resource for the search and the amount spend by a heuristic increases exponentially with the number of jobs. It seems that the complex constructive mechanisms of TOB have not enough time to finish with these parameters. However, the other methods converge much faster and are therefore less influenced by the lack of time. The overall ARPD values of $ALNS_{A}$, GL, HH1, TOB are 0.03%, 1.32%, 2.85% and 4.02%, respectively.

Fig. 3

ARPD values aggregated for each parameter

Table 4 Multiple comparison of means—Tukey’ HSD test

Fig. 4

Boxplot of the ARPD results

The Tukey’ honestly significant difference (HSD) test was conducted to analyze the statistic difference between the methods. The null hypotheses that two algorithms have equal performances was tested at a significance level of 5%. The results in Table 4 show that all algorithms are statistically different from each other. Figure 4 shows the quartile distributions of the results. $ALNS_{A}$ has a less skewed distribution than the literature methods, indicating its consistent performance. It’s worth noting that TOB has many outliers with ARPD over 50 (omitted to prevent excessive image compression), which mainly reflect its poor performance for $n = 200$ and $t = 10$.

6 Conclusion

In this work, we propose the algorithm called $ALNS_{A}$ to solve the no-wait flow shop scheduling problem with sequence-dependent setup times to minimize makespan subject to an upper bound on total completion time. First, the proposed method was tested with small instance problems and compared with a mixed-integer linear programming model along with three existent algorithms—GL, HH1 and TOB—designed to solve the most similar problems found in the literature. This experiment shows that $ALNS_{A}$,GL, HH1 and TOB obtained overall ARPD values of 0.02%, 0.23%, 1.21% and 1.16%, respectively. Furthermore, the heuristic methods were tested by using a large instances problems $ALNS_{A}$,GL, HH1 and TOB obtained overall ARPD values of 0.03%, 1.32%, 2.85% and 4.02%, respectively. Therefore, $ALNS_{A}$ outperforms the literature methods.

Despite the superior performance of $ALNS_{A}$, there are still possibilities for improvement. For example, regarding the heuristic evaluation process, it can be appropriate to assign weights to pairs of methods instead of each method individually because their performances may not be the same across different combinations. Another option is to calibrate more parameters. Here, the randomness levels that determine the number of jobs removed and reinserted by the algorithm have been fixed at 50%. Therefore, it could be possible to increase performance with additional tuning. Algorithms for different applications can be adapted and included in future experiments to further test its efficiency.

The objective function makespan subject to total completion time is an example of how to provide more realistic solutions to scheduling problems that in practice often involve more than one objective. But this approach has a limitation: it does not provide recommendations for the upper bound on total completion time and therefore it must be given by the scheduler. And since the objectives involved are conflicting, this choice must be made carefully, as a tight upper bound makes the search for a feasible solution very difficult.