Reliability and optimal replacement policy for a generalized mixed shock model

Abstract

A generalized mixed shock model, which mixes two run shock models, is developed and analyzed. According to the model, the system subject to both internal degradation and external shocks fails upon the occurrence of $k_1$ consecutive shocks whose magnitude is between predefined critical values of $d_1$ and $d_2$ such that $d_1<d_2$, or $k_2$ consecutive shocks whose magnitude is above $d_2$. The system’s reliability, mean time to failure, and mean residual lifetime are all calculated under the assumption that the lifetime of the system due to internal wear and external shock arrival times follows a phase-type distribution. The best policy for replacement is also discussed. There are also graphical representations and numerical examples for the proposed model, in which both lifetime distribution of internal degradation and the interarrival periods between external shocks follow the Erlang distribution.

1 Introduction

In applied probability and reliability engineering, internal degradation mechanisms and external shocks models are crucial. A system (or component) is subjected to both internal wear degradation and external shocks of varying magnitudes and durations in a shock model, and the system fails if a predetermined pattern of shocks and/or times between shocks emerges. As a consequence, the system’s failure time can be represented as a compound random variable that evolves as a function of shock magnitudes and time intervals between subsequent shocks. The run shock model is one of the most extensively researched shock models in the literature on reliability. A system that is subjected to random magnitude shocks at random times fails after k consecutive critical shocks, according to run shock model ( Mallor and Omey (2001), Ozkut and Eryilmaz (2019)). When $k = 1$, the run shock model is equivalent to the extreme shock model. That is, a system’s breakdown occurs as a result of a single critical shock. A critical shock is one that surpasses a preset threshold. Shanthikumar and Sumita (1983), Gut and Hüsler (1999), Cha and Finkelstein (2011), Cirillo and Husler (2011) and Bozbulut and Eryilmaz Bozbulut and Eryilmaz (2020) have looked into the extreme shock model. Eryilmaz and Tekin (2019) recently introduced and investigated a new mixed shock model that incorporates extreme and run shock models. According to this model, if a series of k successive shocks with magnitudes are between $d_1$ and $d_2$ $(d_1<d_2)$ or a single shock with a magnitude greater than $d_2$, the system fails. On the whole, the focus of these studies is only due to external shocks without considering the internal wear. However, system failures can be induced by also internal degradation even if any external shocks do not occur (fatigue, erosion and wear). Therefore, taking into account internal degradation is more realistic in the real-life systems.

Shock model reliability and optimal replacement strategies have piqued attention in reliability engineering and operational research. To find the ideal replacement cycle, Tabriz et al. (2016) proposed age-based replacement models were exposed to shocks and failure rates. Eryilmaz (2017) calculated the mean residual lifetime and optimal replacement time of a system under a specific class of shock events using matrix-based techniques. When the system’s failure mechanism varies during operation, Zhao et al. (2018) studied the best replacement strategies using a mixed shock model. Li et al. (2018) presented a model of reliability for phased-mission systems that are subject to random shocks. Huang et al. (2019) performed research on coherent systems that were subject to both internal and external shocks. Zarezadeh and Asadi (2019) examined the reliability and preventive maintenance of coherent systems whose components are subject to breakdown due to a range of external shocks. The reliability and optimal replacement policy for a k-out-of-n system vulnerable to shocks were investigated by Eryilmaz and Devrim (2019).

For modelling times between shocks, phase-type distributions are acceptable and helpful. Because of their mathematical tractability, they can produce fascinating and useful results. Some processes, e.g., close phase-type distributions, are useful in reliability analysis Assaf and Levikson (1982). Montoro-Cazorla et al. (2009), Segovia and Labeau (2013) and Montoro-Cazorla et al. (2007) studied the reliability of shock models using the phase-type distributions. Neuts and Meier (1981) utilized phase-type distributions to model the reliability of systems with two components. When the time intervals between shocks follow a phase-type distribution, Eryilmaz (2017) determined the system’s optimal replacement time and mean residual life.

In this study, we define and investigate an extended version of the mixed shock model, which combines an extreme shock model with a run shock model previously investigated by Eryilmaz and Tekin (2019) without consideration of internal wear. According to this new model, the system has three failure conditions. The system fails if either $k_1$ consecutive shocks whose magnitude is between the predefined threshold values $d_1$ and $d_2$ $(d_1<d_2)$ or the occurrence of $k_2$ consecutive shocks whose magnitude is above the threshold value $d_2$ or the internal wear degradation occurs, whichever occurs first. Clearly, for $k_2 = 1$, we have a typical mixed shock model of extreme and run shock model studied by Eryilmaz and Tekin (2019). Similarly, when $d_2\rightarrow \infty$, the new model can be considered a usual run shock model. Therefore, this study is a more realistic and general form of the previous ones. In the suggested setting, the number of shocks that cause the system to fail, as well as the time between shocks, is assumed to have phase-type distributions with closure properties.

The following is a description of the current article’s structure. In Sect. 2, we establish the model and provide some properties of phase-type distributions that will be relevant in our process. The generalized mixed shock model is used to calculate the system’s dependability and mean time to failure in Sect. 3. The mean residual life (MRL) computations for the proposed model are shown in Sect. 4. In Sect. 5, we look at the challenge of determining the best replacement time. Finally, in Sect. 6, we offer numerical results that are intended to illuminate.

2 Model description

Consider a system subject to a sequence of shocks with a random magnitude $D_{1},D_{2},...$ over time. Let $T_{1}$ denote the waiting time for the first shock and $T_{i}$ denote the interarrival time between $(i-1)$th and ith shocks, $i\ge 2.$ Assume that the interarrival time $T_{i}$ between $(i-1)$th and ith shocks, the corresponding magnitude $D_{i}$ are independent for all i. Let us consider two fixed critical values $d_{1}$ and $d_{2}$ such that $d_{1}<d_{2}.$ The conventional run shock model suggests that the system will fail if k critical shocks occur in a row. However, in the present setup, the system fails upon $k_{1}$ consecutive shocks, having a magnitude between $d_{1}$ and $d_{2}$ or $k_{2}$ consecutive shocks of size at least $d_{2}$ or occurrence of the internal wear degradation. If we create a random variable N to represent the amount of shocks required to bring the system down, we may describe the system’s lifespan due to external shocks as

$$\begin{aligned} S=\sum _{i=1}^{N}T_{i} \end{aligned}$$

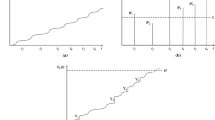
in the current model. Figure 1 shows a hypothetical implementation of the failure process to help to understand the suggested model.

Fig. 1

A possible realization of the model

According to Fig. 1, the system breaks after the fourth shock for $k_{1}=3$ or $k_{2}=2$, and the lifespan of the system is $S=T_{1}+T_{2}+T_{3}+T_{4}$. If $k_{1}=4$ and $k_{2}=2,$ the seventh shock causes the system to collapse, at which point the system’s lifespan due to external shocks is $S=T_{1}+\cdots +T_{7}$. Two run shock models are combined in this mixed shock model. The interval between consecutive shocks $T_1,T_2,...$ is considered to be a continuous phase-type with a common cumulative distribution function

$$\begin{aligned} F(t)=P(T_{i}\le t)=1-\varvec{\alpha }\exp \left( \textbf{A}t\right) \textbf{e}^{\prime }, \end{aligned}$$

(1)

for $i=1,2,...$ where $\textbf{e}=\left( 1,...,1\right) _{1\times m}.$ $\varvec{\alpha }$ is a substochastic vector of order m, all elements of the row vector $\varvec{\alpha }=\left( \alpha _{1},...,\alpha _{m}\right)$ are nonnegative, and $\varvec{\alpha e}^{\prime }\le 1$. $\textbf{A}$ is a subgenerator of order m, i.e., $\textbf{A}$ is an $m\times m$ nonsingular matrix such that all diagonal elements are negative, and all off-diagonal elements are nonnegative. All row sums are nonpositive. We will use the notation $T\sim PH_{c}(\varvec{\alpha },\textbf{A})$ to show that the random variable T has a continuous phase-type distribution of order m, with a PH-generator $\textbf{A}$ and a substochastic vector $\varvec{\alpha }$.

The expected value of T can be calculated from

$$\begin{aligned} E(T)=-\left( \varvec{\alpha A}^{-1}\textbf{e}^{\prime }\right) . \end{aligned}$$

(2)

To model the distribution of shock interarrival times, a lot of researchers use phase-type distributions. For more information and properties about the phase-type distribution, see Huang et al. (2019), Segovia and Labeau (2013), Neuts and Meier (1981), Cui and Wu (2019), He (2006) and Perez-Ocon and Segovia (2009). In an absorbing Markov chain, a discrete phase-type distribution is the distribution of the time to absorption. The probability mass function (PMF) of the discrete phase-type random variable N is represented by:

$$\begin{aligned} P\left\{ N=n\right\} =\textbf{aQ}^{n-1}\textbf{u}^{\prime }, \end{aligned}$$

for $n\in \mathbb {N},$ where $\mathbf {Q=}\left( \textbf{q}_{ij}\right) m\times m$ is a matrix that includes the transition probabilities among the m transient states, and $\textbf{u}^{\mathbf {\prime }}=\left( \textbf{I}-\textbf{Q}\right) \textbf{e}^{\prime }$ is a vector that includes the transition probabilities from transient states to the absorbing state, $\mathbf {a=}\left( \textbf{a}_{1},...,\textbf{a}_{m}\right)$ with ${\displaystyle \sum \nolimits _{i=1}^{m}} a_{i}=1,$ and $\textbf{I}$ is the identity matrix. In addition, the matrix $\textbf{Q}$ must satisfy the condition that $\textbf{I}-\textbf{Q}$ is nonsingular. To express that the random variable N has a discrete phase-type distribution, we will use $N\sim PH_{d}(\textbf{a},\textbf{Q})$. The expected value of N can be computed by

$$\begin{aligned} E(N)=\mathbf {a(I-Q)}^{-1}\textbf{e}^{\prime } \end{aligned}$$

(3)

Lemma 1

Let $p_{1}=P(d_{1}\le D_{i}<d_{2})$ and $p_{2}=P(D_{i}\ge d_{2})$ for $i=1,2,...$ then $N\sim PH_{d}(\textbf{a,Q})$ with $\textbf{a}=(1,0...,0),$

(4)

and $\mathbf {u=}\left( \mathbf {I-Q}\right) \textbf{e}^{\prime }$ where $\textbf{e}=(1,...,1)_{1\times \left( k_{1}+k_{2}-1\right) }$.

Proof

The random variable N can be described as the time to absorption of a Markov chain based on a sequence of trials $I_{1},I_{2},...$ such that

$$\begin{aligned} I_{i}=\left\{ \begin{array}{ll} 0, &{}\,\,\hbox { if} \,\,D_{i}<d_{1}\\ 1, &{} \,\,\hbox {if}\,\, d_{1}\le D_{i}<d_{2}\\ 2 &{} \,\,\hbox {if}\,\, D_{i}\ge d_{2} \end{array} \right. . \end{aligned}$$

The corresponding Markov chain has $\left( k_{1}+k_{2}-1\right)$ transient states and four absorbing states which are defined by $\left\{ 0,1,11,...,\underset{k_{1} -1}{\underbrace{11...1}},2,22,...,\underset{k_{2}-1}{\underbrace{22...2} }\right\}$ and $\left\{ \underset{k_{1} }{\underbrace{11...1}},\underset{k_{2}}{\underbrace{22...2}},\underset{k_{1}-1}{\underbrace{11...1}}\underset{k_{2}}{\underbrace{22...2}},\underset{k_{2}-1}{\underbrace{22...2}}\underset{k_{1}}{\underbrace{11...1} }\right\}$, respectively. More precisely,

transient states	0	$\Rightarrow$ a shock of magnitude less than or equal to $d_{1}$.
	1	$\Rightarrow$ a shock of magnitude between $d_{1}$ and $d_{2}$.
	$\vdots$	$\vdots$
	$\underset{k_{1}-1}{\underbrace{11\ldots 1}}$	$\Rightarrow k_{1}-1$ successive shocks with magnitudes between $d_{1}$ and $d_{2}$.
	2	$\Rightarrow$ a shock of magnitude greater than or equal to $d_{2}$.
	$\vdots$	$\vdots$
	$\underset{k_{2}-1}{\underbrace{22\ldots 2}}$	$\Rightarrow$ $k_{2}-1$ successive shocks with magnitudes greater than or equal to $d_{2.}$

absorbing states	$\underset{k_{1}}{\underbrace{11\ldots 1}}$	$\Rightarrow$ $k_{1}$ successive shocks with magnitudes between $d_{1}$ and $d_{2}$.
	$\underset{k_{2}}{\underbrace{22\ldots 2}}$	$\Rightarrow$ $k_{2}$ successive shocks with magnitudes greater than
		or equal to $d_{2.}$
	$\underset{k_{1}-1}{\underbrace{11\ldots 1}}\underset{k_{2}}{\underbrace{ 22\ldots 2}}$	$\Rightarrow$ $k_{1}-1$ successive shocks with magnitudes between $d_{1}$ and $d_{2}$,
		and $k_{2}$ successive shocks with magnitudes greater than or
		equal to $d_{2.}$
	$\underset{k_{2}-1}{\underbrace{22\ldots 2}}\underset{k_{1}}{\underbrace{ 11\ldots 1}}$	$\Rightarrow$ $k_{2}-1$ successive shocks with magnitudes greater than or
		equal to $d_{2},$
		and $k_{1}$ successive shocks with magnitudes between $d_{1}$ and $d_{2}.$

The proof is completed considering the probabilities between transient states and phase-type representation. $\square$

Corollary 2

Using Lemma 1 and (3)

$$\begin{aligned} E(N)=\frac{\left( {\displaystyle \sum \nolimits _{i=1}^{k_{1}}} p_{1}^{i-1}\right) \left( {\displaystyle \sum \nolimits _{j=1}^{k_{2}}} p_{2}^{j-1}\right) }{p_{1}^{k_{1}}\left( {\displaystyle \sum \nolimits _{j=1}^{k_{2}}} p_{2}^{j-1}\right) +p_{2}^{k_{2}}\left( {\displaystyle \sum \nolimits _{i=1}^{k_{1}}} p_{1}^{i-1}\right) }. \end{aligned}$$

(5)

The following proposition considers that the random variable N, which describes the waiting time, has a discrete phase-type distribution. For the proof, we refer to He (2006).

Proposition 3

Assume that $T_{1},$ $T_{2},\ldots$ are independent and $T_{i}\sim PH_{c} (\varvec{\alpha },\textbf{A}),$ $i=1,2,...$ and independently $N\sim PH_{d}(\textbf{a},\textbf{Q}).$ If $\varvec{\alpha }$ and $\textbf{a}$ are stochastic vectors, i.e. $\textbf{ae}^{\prime }=1$ and $\varvec{\alpha e}^{\prime }=1,$ then

$$\begin{aligned} S= {\displaystyle \sum \limits _{i=1}^{N}} T_{i}\sim PH_{c}(\varvec{\alpha \otimes a},\textbf{A}\otimes \mathbf {I+(-Ae} ^{\prime })\mathbf {\otimes Q}), \end{aligned}$$

(6)

where $\mathbf {\otimes }$ is the Kronecker product.

The next closure property will be used in the following section. For the proof, we refer to He (2006).

Proposition 4

Let $X\sim PH_c(\varvec{\alpha },\textbf{A})$ and $Y\sim PH_c(\varvec{\beta },\textbf{B})$ be two independent phase-type random variables. Then

$$\begin{aligned} \min (X,Y)\sim PH_c(\varvec{\alpha }\otimes \varvec{\beta },\textbf{A}\otimes \textbf{I}+\textbf{I}\otimes \textbf{B}). \end{aligned}$$

(7)

3 Reliability and mean time to failure of the system

According to the proposed model, the system will fail if either $k_1$ successive shocks with a strength between the predefined thresholds $d_1$ and $d_2$ $(d_1<d_2)$ or the occurrence of $k_2$ successive shocks with a strength above the threshold $d_2$ or internal wear degradation occurs, whichever comes first. Thus, the system lifetime can be represented as:

$$\begin{aligned} R=\min (S,W) \end{aligned}$$

(8)

where W is the lifetime of the system due to internal wear degradation.We assume that the interarrival time $T_{i}$ between $(i-1)$th and ith shocks, the corresponding magnitude $D_{i}$ are independent for all i. If $T_{i}\sim PH_{c}(\varvec{\alpha },\mathbf {A)}$, $N\sim PH_{d}(\textbf{a},\textbf{Q})$ and $W\sim PH_{c}(\varvec{\zeta },\textbf{Z})$, then from (1),(6),(7) and (8) we can compute the survival function of R from

$$\begin{aligned} P(R>t)=(\varvec{v\otimes \zeta })\exp \left( \left( \mathbf {Y\otimes I+I\otimes Z} \right) t\right) \textbf{e}^\prime , \end{aligned}$$

(9)

where $\textbf{Y}=\textbf{A}\otimes \mathbf {I+(-Ae}^{\prime })\mathbf {\otimes Q}$ and $\varvec{v=\alpha \otimes a}$

Using (2), one can easily calculate the mean time to the system failure under the proposed model from

$$\begin{aligned} E(R)=-\left( \left( \varvec{v\otimes \zeta }\right) \left( \mathbf {Y\otimes I+I\otimes Z}\right) ^{-1} \textbf{e}^{\prime }\right) . \end{aligned}$$

(10)

The following proposition will be helpful in the next section.

Proposition 5

If R $\sim PH_{c}(\varvec{\alpha },\textbf{A}),$ then

$$\begin{aligned} \left( R-t|R>t\right) \sim PH_{c}(\frac{\varvec{\alpha }\exp \left( \textbf{A}t\right) }{\varvec{\alpha }\exp \left( \textbf{A}t\right) \textbf{e}^{\prime }},\textbf{A}). \end{aligned}$$

4 Mean residual lifetime

The mean residual life (MRL) function is vital in reliability and system analysis. Assume that the system has a lifetime R, then the function $E(R-t|R>t)$ is called the system’s MRL function. In technical systems, the MRL function is an important feature that characterizes the system’s lifetime distribution function. We refer to Lai and Xie (2006) for more details and applications.

Since the system has a lifetime random variable R with a phase-type distribution, from Proposition 5 and (2), the mean residual lifetime at time t can be calculated from:

$$\begin{aligned}&E(R-t|R>t)= \nonumber \\&-\left( \frac{(\varvec{v\otimes \zeta })\exp \left( \left( \mathbf {Y\otimes I+I\otimes Z}\right) t\right) }{(\varvec{v\otimes \zeta })\exp \left( \left( \mathbf {Y\otimes I+I\otimes Z}\right) t\right) \textbf{e} ^{\prime }}\left( \mathbf {Y\otimes I+I\otimes Z}\right) ^{-1}\textbf{e}^{\prime }\right) . \end{aligned}$$

(11)

Phase-type distributions have been widely employed in numerous fields, including reliability theory in the literature, due to the fact that the phase-type distribution is closed under the influence of different operators and equations appear theoretically tractable when compared to other distributions.

5 Optimal replacement time

It is also crucial to choose the best replacement time that reduces the long-term average cost. The age replacement policy states that the system is replaced when it fails or reaches the age of t, whichever comes first. Let $c_{1}$ represent the cost of replacement before failure and $c_{2}$ represent the cost of replacement after failure. Since system failure causes an additional cost, we assume that $c_{1}<c_{2}$. Then, if a system has a lifetime T, the mean cost rate is given by

$$\begin{aligned} C(t)&=\frac{c_{1}P(R>t)+c_{2}P(R<t)}{E(\min (R,t))}\nonumber \\&=\frac{c_{2}+(c_{1}-c_{2})P(R>t)}{E(\min (R,t))}, \end{aligned}$$

(12)

where E(min(R, t)) denotes the mean time for replacement and is calculated as

$$\begin{aligned} E(min(R,t))=\int _{0}^{t}P(R>u)du. \end{aligned}$$

This section aims to find the $t^{*}$ that minimizes (12) when $c_{1}$ and $c_{2}$ are known. The following proposition is related to calculating the mean time for a replacement under the Phase-type distribution class.

Proposition 6

Let R denote the lifetime of the system having a continuous phase-type distribution with the representation $PH_{c}(\varvec{\alpha },\textbf{A})$; then, the mean time for replacement E(min(R, t)) can be calculated as:

$$\begin{aligned} E(min(R,t))=\varvec{\alpha A}^{-1}\exp (\mathbf {At)e}^{\prime }-\varvec{\alpha A}^{-1}\textbf{e}^{\prime }. \end{aligned}$$

(13)

See Appendix for the proof.

Using formula (12), the optimal value $t^{*}$, which minimizes the mean cost rate, can be found numerically.

6 Numerical illustrations

As seen in Fig. 2, a timing belt is a component, designed with a precise hard tooth that interlocks with the cogwheel of a crankshaft and the two camshafts, used in an internal combustion engine to synchronize the movement of the crankshaft and camshafts. A timing belt is often made of rubber with high tensile fibers in its structure and design. The entire belt is made of strong materials like molded polyurethane, neoprene, or welded urethane of varying levels. Rubber degrades at higher temperatures and when exposed to oil. Timing belt lifespan is compromised in hot, oil-leaking engines. Water and antifreeze can also shorten the life of reinforcing cables. Because of their trapezoid-shaped teeth, older timing belts typically have a high rate of wear. According to working principle of timing belt, exposing high degrees of temperatures or other materials such as oil, antifreeze or even just water can be considered external shocks. Occurrence of $k_1$ consecutive of these kind of external shocks whose magnitude is between $d_1$ and $d_2$ such that $d_1<d_2$, or $k_2$ consecutive shocks whose magnitude is above $d_2$ may cause the failure of the timing belt. On the other hand, the wear on the rubbing face of the timing belt because of trapezoid-shaped teeth of crankshaft and camshafts may also cause to break of the component without of occurrence. Therefore, the timing belt may fail because of wear degradation and external shocks.

Fig. 2

Timing belt Auto and Inc (2023)

Consider a system that is exposed to shocks on a regular basis in a job. As mentioned before, in the proposed model, for $d_{1}<d_{2},$ when there are $k_1$ successive shocks having magnitude between $d_{1}$ and $d_{2}$ or $k_{2}$ consecutive shocks of size at least $d_{2}$ or internal wear degradation occurs, the system fails. In this section, with the help of the methodology described in the previous sections, we will present the computation of reliability, MTTF, MRL, and optimal replacement time for the system under the proposed model. Assume that the system lifetime under internal wear degradation W and the intervals between shocks $T_{1},T_{2},...$ follow a continuous phase-type Erlang distribution with parameters m and $\lambda$. The Erlang distribution has cumulative distribution function (cdf)

$$\begin{aligned} F(t)=1-\varvec{\alpha }\exp (\textbf{A}t)\textbf{e}^{\prime }, \end{aligned}$$

$t\ge 0,$ where $\varvec{\alpha }=(0,...,1),$ and $\textbf{A}=\left[ \begin{array}{cccc} -\lambda &{} 0 &{} \cdots &{} 0\\ \lambda &{} -\lambda &{} &{} 0\\ \vdots &{} \ddots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} \lambda &{} -\lambda \end{array} \right] _{m\times m}.$

To illustrate, we first present a phase-type representation of the lifetime of the system under a generalized mixed shock model when $k_{1}=3$ and $k_{2}=2$ when the interarrival times and the lifetime of the system due to internal wear degradation follow the Erlang distribution with $m=2$ and $\lambda ^{IAT}=1$ and $m=2$ and $\lambda ^{IWD}=0.5$, respectively. From (4), the discrete phase-type random variable N,  which represents the total amount of shocks before the system fails, has phase-type representation $N\sim PH_{d}(\textbf{a,Q})$ where

$$\begin{aligned} \textbf{Q}=\left[ \begin{array}{llll} 1-p_{1}-p_{2} &{} p_{1} &{} 0 &{} p_{2} \\ 1-p_{1}-p_{2} &{} 0 &{} p_{1} &{} p_{2} \\ 1-p_{1}-p_{2} &{} 0 &{} 0 &{} p_{2} \\ 1-p_{1}-p_{2} &{} p_{1} &{} 0 &{} 0 \end{array} \right] , \end{aligned}$$

$\textbf{a}=(1,0,0,0)$ and $\mathbf {u=}\left( 0,0,p_{1},p_{2}\right)$. To present system’s survival function in (9), we need

$$\begin{aligned} \varvec{v\otimes \zeta } \end{aligned}$$

where $\varvec{v=\alpha \otimes a}$,

$$\begin{aligned} \varvec{v\otimes \zeta }&=(0,0,0,0,1,0,0,0)\mathbf {\otimes }(0,1)\\&=(0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0) \end{aligned}$$

and

$$\begin{aligned}{} & {} \mathbf {Y\otimes I+I\otimes Z} \nonumber \\{} & {} \quad =\left[ \begin{array}{llllllllllllllll} -1.5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} p_{1} &{} 0 &{} 0 &{} 0 &{} p_{2} &{} 0 \\ 0.5 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} p_{1} &{} 0 &{} 0 &{} 0 &{} p_{2} \\ 0 &{} 0 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} 0 &{} 0 &{} p_{1} &{} 0 &{} p_{2} &{} 0 \\ 0 &{} 0 &{} 0.5 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} 0 &{} 0 &{} p_{1} &{} 0 &{} p_{2} \\ 0 &{} 0 &{} 0 &{} 0 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} p_{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0.5 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} p_{2} \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1.5 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} p_{1} &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.5 &{} -1.5 &{} 0 &{} 1-p_{1}-p_{2} &{} 0 &{} p_{1} &{} 0 &{} 0 &{} 0 &{} 0 \\ 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} p_{1} &{} 0 &{} 0 &{} 0\\ 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.5 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} p_{1} &{} 0 &{} 0\\ 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.5 &{} -1.5 &{} 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1.5 &{} 0 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.5 &{} -1.5 &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} -1.5 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0.5 &{} -1.5 \end{array} \right] \nonumber \\ \end{aligned}$$

(14)

where $\textbf{Y}=\textbf{A}\otimes \mathbf {I+(-Ae}^{\prime })\mathbf {\otimes Q}$. Therefore, the system’s survival function in (9) under generalized mixed shock model with $k_{1}=3$ and $k_{2}=2$ is obtained as:

Fig. 3

Under the generalized mixed shock model, the survival function of the systems

Table 1 MTTF of the system

In Fig. 3, we plot the survival function of the system under a generalized mixed shock model for different values of $k_{1}$ and $k_{2}$ when $p_1=0.4, p_2=0.45$ and $\lambda ^{IAT}=1$ for interarrival times and $\lambda ^{IWD}=0.5$ for internal wear degradation.

As it is clear from the graphs, an increase in the values of $k_{1}$ or $k_{2}$ leads to an increase in system reliability, as expected. Similarly, since the MRL and the MTTF of the system formulae contain (14), one can easily obtain expressions for the MRL in (11) and the MTTF in (10). For a set of parameter values and for $\lambda ^{IAT}=1$ in Table 1, we calculate the system’s MTTF using a generalized mixed shock model.

From Table 1, we can see that the MTTF of the system increases as the value of $k_{1}$ or $k_{2}$ increases and decreases as the probability of a shock with a magnitude between the thresholds $d_{1}$ and $d_{2}$ or the probability of a shock greater than the threshold $d_{2}$ ($p_2$) or $\lambda ^{IWD}$ increases as expected. In Fig. 4, we plot the MRL function of the system under the proposed model for different values of $k_{1}$ and $k_{2}$ for $p_1 = 0.45$, $p_2 = 0.50$, and $\lambda ^{IAT}=1$ and $\lambda ^{IWD}=0.001$.

Fig. 4

Under the generalized mixed shock model, the MRL function of the systems

Table 2 Optimal replacement time and average cost rate

The MRL function increases in both $k_1$ and $k_2$, as shown in Fig. 4. In Table 2, for several values of the parameters under the generalized mixed shock model, we get the best replacement time $t^{*}$ for minimizing (12) and also its average cost rates $C(t^{*})$ using the equations (9) and (13) in (12).

From Table 2, it can be easily observed that an increase in the $k_2$ value causes a longer optimal replacement time and a lower mean cost rate. However, an increase in $p_{2}$ (probability that shock magnitude is above the threshold value $d_{2})$ or in $\lambda ^{IWD}$ leads to a decrease in optimal replacement time and an increase in mean cost rate. Lastly, to illustrate the shape of the cost function, in Figs. 5 and 6, we plot the mean cost rate function using (12) under the proposed model for different values of the parameters.

Fig. 5

The long-run average cost functions under generalized mixed shock model for $k_1=3$ and $k_2=1,2,3$

Fig. 6

The long-run average cost functions under generalized mixed shock model for $k_1=4,5,6$ and $k_2=3$

From Figs. 5 and 6, it is clear that the graph of the mean cost rate is always U-shaped for different values of $k_{1}$,$k_{2}$ and $p_{2}$. More precisely, a U-shape is a function with exactly one turning point. When the process begins to increase, it does not decrease.

7 Summary and conclusions

We define and investigate an extended version of the mixed shock model in this study, which combines the extreme and run shock models described by Eryilmaz and Tekin (2019) without considering the internal wear. However, we include the internal wear degradation in the proposed model. Therefore, without occurrence of external shocks, the system may also fail. The inclusion of internal wear makes the proposed model more realistic. The interarrival time of the shocks was supposed to follow phase-type distributions, which provided a number of benefits. In the proposed model, the system’s lifetime was computed using a compound random variable and the closure properties of phase-type distributions. We were also able to display mean time to failure and mean residual lifetimes without having to take integration into account. In addition, we examined the best replacement policy based on the mean cost rate function minimization. As future work, we aim to include repairability in the model and also derive other important reliability measures such as availability and rate of occurrence of failures (ROCOF).

Appendix

Proof of (13): Since continuous phase-type random variable R has representation $PH_c(\varvec{\alpha },\textbf{A})$ and from (1), we have

$$\begin{aligned} P(R>t)=\varvec{\alpha }\exp (\textbf{A}t)\textbf{e}'=\varvec{\alpha }\left( \sum _{n=0}^\infty \frac{t^n}{n!}\textbf{A}^n\right) \textbf{e}' \end{aligned}$$

and

$$\begin{aligned} E(min(R,t))&=\int _0^\infty P(min(R,t)>u)du \\&=\int _0^t P(R>u)du \\&=\int _0^t \varvec{\alpha }\left( \sum _{n=0}^\infty \frac{u^n}{n!}\textbf{A}^n\right) \textbf{e}' du \\&=\varvec{\alpha }\left( \textbf{A}^{-1}\sum _{n=0}^\infty \frac{t^{n+1}}{(n+1)!}\textbf{A}^{n+1}\right) \textbf{e}' \\&=\varvec{\alpha }\left( \textbf{A}^{-1}\sum _{n=-1}^\infty \frac{t^{n+1}}{(n+1)!}\textbf{A}^{n+1}-\textbf{I}\right) \textbf{e}' \\&=\varvec{\alpha }\left( \textbf{A}^{-1}(\exp (\textbf{A}t)-\textbf{I}) \right) \textbf{e}' \\&=\varvec{\alpha }\textbf{A}^{-1}\exp (\textbf{A}t)\textbf{e}' -\varvec{\alpha }\textbf{A}^{-1}\textbf{e}'. \end{aligned}$$