Abstract
We consider the change-point detection in a general class of time series models, including multivariate continuous and integer- valued time series. We propose a Wald-type statistic based on the estimator performed by a general contrast function, which can be constructed from the likelihood, a quasi-likelihood, a least squares method, etc. Sufficient conditions are provided to ensure that the test statistic convergences to a well-known distribution under the null hypothesis (of no change) and diverges to infinity under the alternative, which establishes the consistency of the procedure. Some examples of models are detailed to illustrate the scope of application of the proposed change-point detection tool. The procedure is applied to simulated and real data examples for numerical illustration.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Since Page (1955), the change-point problem has been widely studied. Several approaches and procedures have been developed for univariate and multivariate processes with continuous or integer- valued variables.
Consider observations \((Y_{1},\ldots ,Y_{n})\), generated from a multivariate continuous or integer-valued process \(Y=\{Y_{t},\,t\in \mathbb {Z}\}\). These observations depend on a parameter \(\theta ^* \in \Theta \subset \mathbb {R}^d \) (\(d \in \mathbb {N}\)) which may change over time. More precisely, consider the following test hypotheses:
- \(\hbox {H}_0\)::
-
\((Y_1,\ldots ,Y_n)\) is a trajectory of the process \(Y=\{Y_{t},\,t\in \mathbb {Z}\}\) which depends on \(\theta ^*\).
- \(\hbox {H}_1\)::
-
There exists \(((\theta ^{*}_1,\theta ^{*}_2),t^{*}) \in \Theta ^{2}\times \{2,3,\ldots , n-1 \}\) (with \(\theta ^{*}_1 \ne \theta ^{*}_2\)) such that \((Y_1,\ldots ,Y_{t^{*}})\) is a trajectory of a process \(Y^{(1)} = \{Y^{(1)}_{t},\, t \in \mathbb {Z}\}\) that depends on \(\theta ^*_1\) and \((Y_{t^{*}+1},\ldots ,Y_n)\) is a trajectory of a process \(Y^{(2)} = \{Y^{(2)}_{t}, \,t \in \mathbb {Z}\}\) that depends on \(\theta ^*_2\).
Note that under H\(_1\), \((Y_1,\ldots ,Y_n)\) is a trajectory of the process \(\{(Y^{(1)}_{t})_{t \le t^*}, (Y^{(2)}_{t})_{t > t^*} \}\) which depends on \(\theta ^*_1\) and \(\theta ^*_2\). In the whole paper, it is assumed that \(\Theta \) is a fixed compact subset of \(\mathbb {R}^d\) (\(d \in \mathbb {N}\)).
This test for change-point detection is often addressed with a Wald-type statistic based on the likelihood, quasi-likelihood, conditional least-squares or density power divergence estimator. Likelihood estimate-based procedure has been proposed for continuous and integer-valued time series; see, for instance, Lee and Lee (2004), Kang and Lee (2014), Doukhan and Kengne (2015), Diop and Kengne (2017), Lee et al. (2018). Several authors have pointed out some restrictions of these procedures and proposed a Wald-type statistic based on a quasi-likelihood estimators; see, among others papers, Lee and Song (2008), Kengne (2012), Diop and Kengne (2021). Other procedures have been developed with the (conditional) least-squares estimator (see, for instance, Lee and Na 2005a; Kang and Lee 2009) or the density power divergence estimator (see, among others, Lee and Na 2005b; Kang and Song 2015). Lee et al. (2003) proposed a procedure for change-point detection in a large class of time series models, but this procedure does not take into account the change-point alternative and does not ensure the consistency in power. We refer also to the works of Qu and Perron (2007) and Kim and Lee (2020) and the references therein, for some procedures for change-point detection in multivariate regressions and systems, and to Franke et al. (2012), Hudecová (2013), Fokianos et al. (2014), Hudecová et al. (2017), for other procedures for change-point detection in time series of counts.
In this new contribution, we consider a multivariate continuous or integer-valued process and deal with a general contrast, where the likelihood, quasi-likelihood, conditional least-squares or density power divergence can be seen as a specific case.
Let \({\widehat{C}} \big ((Y_t)_{t \in T},\theta \big )\) be a contrast function defined for any segment \(T \subset \{1,\ldots ,n\}\) and \(\theta \in \Theta \) by:
where \({\widehat{\varphi }}_t\) depends on \(Y_1,\ldots ,Y_t\), and is such that the minimum contrast estimator (MCE), computed on a segment \(T \subset \{1,\ldots ,n\}\) is given by
See also Killick et al. (2012) for the use of a general cost/contrast function in a context of the multiple change-points detection. In the sequel, we use the notation \({\widehat{C}} (T,\theta ) = {\widehat{C}} \big ((Y_t)_{t \in T},\theta \big )\) and address the following issues.
-
(i)
We propose a Wald-type statistic based on the MCE for testing H\(_0\) against H\(_1\). The asymptotic studies under the null and the alternative hypotheses show that the test has correct size asymptotically and is consistent in power. This test unifies the treatment of a large class of models, including multivariate continuous and count processes, and many existing results in the literature can be seen as specific cases of the results obtained below.
-
(ii)
Application to a large class of multivariate causal processes is carried out. We provide sufficient conditions under which the asymptotic results of the change-point detection hold.
-
(iii)
A general class of multivariate integer-valued models is considered. In the case where the conditional distribution belongs to the m-parameter exponential family, we provide sufficient conditions that ensure the existence of a stationary and ergodic \(\tau \)-weakly dependent solution. The inference is carried out, and the consistency and the asymptotic normality of the Poisson quasi maximum likelihood estimator (PQMLE) are established. This inference question has been addressed by Ahmad (2016) with the equation-by-equation PQMLE, Lee et al. (2018) for bivariate Poisson INGARCH model, Cui et al. (2020) for flexible bivariate Poisson integer-valued GARCH model, Fokianos et al. (2020) for linear and log-linear multivariate Poisson autoregressive models. The model considered in Sect. 4 appears to be more general, and the conditions imposed for asymptotic studies seem to be more straightforward. Also, we show that the asymptotic results of the change-point detection hold for this class of models.
The paper is structured as follows. Section 2 contains the general assumptions and the construction of the test statistic for change-point detection, as well as the main asymptotic results under H\(_0\) and H\(_1\). Section 3 is devoted to the application of the proposed change-point detection procedure to a general class of continuous-valued processes. Section 4 focuses on a general class of observation-driven integer-valued time series. In Sect. 5, we present some numerical results.
Section 6 contains the proofs of the main results.
2 General change-point detection procedure
2.1 Assumptions
Throughout the sequel, the following norms will be used:
-
\( \Vert x \Vert :=\sum _{i=1}^{p} |x_i| \)for any \(x \in \mathbb {R}^{p}\) (with \(p \in \mathbb {N}\));
-
\( \Vert x \Vert :=\underset{1\le j \le q}{\max } \sum _{i=1}^{p} |x_{i,j}| \)for any matrix \(x=(x_{i,j}) \in M_{p,q}(\mathbb {R})\);where \(M_{p,q}(\mathbb {R})\)denotes the set of matrices of dimension \(p\times q\)with coefficients in \(\mathbb {R}\);
-
\(\left\| g\right\| _{{\mathcal {K}}} :=\sup _{\theta \in {\mathcal {K}}}\left( \left\| g(\theta )\right\| \right) \)for any compact set \({\mathcal {K}} \subseteq \Theta \)and function \(g:{\mathcal {K}} \longrightarrow M_{p,q}(\mathbb {R})\);
-
\(\left\| Y\right\| _r :=\mathbb {E}\left( \left\| Y\right\| ^r\right) ^{1/r}\)for any random vector Ywith finite \(r-\)order moments.
Let \(Y=\{Y_{t},\,t\in \mathbb {Z}\}\) be a multivariate continuous or integer- valued process depending on a parameter \(\theta ^* \in \Theta \) and denote by \(\mathcal {F}_{t-1}=\sigma \left\{ Y_{t-1},\ldots \right\} \) the \(\sigma \)-field generated by the whole past at time \(t-1\). In the sequel, we assume that \((j_n)_{n\ge 1}\) and \((k_n)_{n\ge 1}\) are two integer-valued sequences such that \(j_n \le k_n\), \(k_n \rightarrow \infty \) and \(k_n - j_n \rightarrow \infty \) as \(n \rightarrow \infty \), and use the notation \(T_{\ell ,\ell '}=\{\ell ,\ell +1,\ldots ,\ell '\}\) for any \((\ell ,\ell ') \in \mathbb {N}^2\) such as \(\ell \le \ell '\). We consider a segment \(T_{j_n,k_n}\) and set the following assumptions for \((Y,\theta ^*)\) under H\(_0\).
- (A1)::
-
The process \(Y=\{Y_{t},\,t\in \mathbb {Z}\}\) is assumed to be stationary and ergodic.
- (A2)::
-
Assume that the MCE \({\widehat{\theta }}(T_{j_n,k_n})\) (defined in (2)) converges a.s. to \(\theta ^*\).
- (A3)::
-
For all \( t \in T_{j_n,k_n}\), the function \(\theta \mapsto {\widehat{\varphi }}_t(\theta )\) (see (1)) is assumed to be continuously differentiable on \(\Theta \), in addition, assume there exists a sequence of random function \((\varphi _t(\cdot ))_{t \in \mathbb {Z}}\) such that the mapping \(\theta \mapsto \varphi _t(\theta )\) is continuously differentiable on \(\Theta \) and for all \(\theta \in \Theta \), the sequence \((\partial \varphi _t(\theta )/ \partial \theta )_{t \in \mathbb {Z}}\) is stationary and ergodic, satisfying:
$$\begin{aligned}&\mathbb {E}\Big \Vert \dfrac{\partial }{\partial \theta } \varphi _t(\theta ) \Big \Vert ^2_\Theta < \infty ; ~ ~ \dfrac{1}{\sqrt{k_n - j_n}} \sum _{t \in T_{j_n,k_n}} \Big \Vert \dfrac{\partial }{\partial \theta } {\widehat{\varphi }}_t(\theta ) - \dfrac{\partial }{\partial \theta } \varphi _t(\theta ) \Big \Vert _\Theta = o_P(1) ~ \text { and } \nonumber \\&\quad \dfrac{1}{k_n - j_n} \sum _{t \in T_{j_n,k_n}} \Big \Vert \dfrac{\partial }{\partial \theta } {\widehat{\varphi }}_t(\theta ) \dfrac{\partial }{\partial \theta ^T} {\widehat{\varphi }}_t(\theta ) - \dfrac{\partial }{\partial \theta } \varphi _t(\theta ) \dfrac{\partial }{\partial \theta ^T} \varphi _t(\theta ) \Big \Vert _\Theta = o(1) ~ a.s. . \end{aligned}$$(3)Furthermore, assume that \(\left( \frac{\partial }{\partial \theta } \varphi _t(\theta ^*),\mathcal {F}_{t}\right) _{t \in \mathbb {Z}}\) is a stationary ergodic, square integrable martingale difference sequence with covariance \(G = \mathbb {E}\bigg [ \dfrac{\partial \varphi _0(\theta ^*)}{\partial \theta } \dfrac{\partial \varphi _0(\theta ^*)}{\partial \theta ^T}\bigg ] \) assumed to be positive definite.
- (A4)::
-
For all \( t \in T_{j_n,k_n}\), the function \(\theta \mapsto {\widehat{\varphi }}_t(\theta )\) is assumed to be 2 times continuously differentiable on \(\Theta \), moreover, under the assumption (A3), assume that the function \(\theta \mapsto \frac{\partial \varphi _t(\theta )}{\partial \theta }\) is continuously differentiable on \(\Theta \), such that the sequence \((\partial ^2 \varphi _t(\theta )/ \partial \theta \partial \theta ^T)_{t \in \mathbb {Z}}\) is stationary and ergodic, satisfying:
$$\begin{aligned} \mathbb {E}\Big \Vert \dfrac{\partial ^2 \varphi _t(\theta )}{\partial \theta \partial \theta ^T} \Big \Vert _\Theta < \infty , ~ ~ \dfrac{1}{ k_n - j_n} \sum _{t \in T_{j_n,k_n}} \Big \Vert \dfrac{\partial ^2 {\widehat{\varphi }}_t(\theta )}{\partial \theta \partial \theta ^T} - \dfrac{\partial ^2 \varphi _t(\theta )}{\partial \theta \partial \theta ^T} \Big \Vert _\Theta = o(1) ~ a.s., \nonumber \\ \end{aligned}$$(4)and the matrix \(F = \mathbb {E}\Big [ \dfrac{\partial ^2 \varphi _0(\theta ^*)}{\partial \theta \partial \theta ^T} \Big ]\) assumed to be invertible.
The conditions (A1) and (A2) assume the stationarity of the process under H\(_0\) and ensure that the MCE computed on each segment converges to the parameter of the stationary solution of the segment. Assumptions (A3) and (A4) allow to unify the theory for any model that satisfies such conditions and ensures the asymptotic normality of the MCE. More precisely, under (A1)–(A4), standard arguments can be used to get,
The examples detailed in Sects. 3 and 4 show that the assumptions (A1)–(A4) hold for many classical time series models.
Now, for any \(\ell , \ell ' \in \mathbb {N}\) with \(\ell \le \ell '\), define the matrices:
According to (A1)–(A4), \({{\widehat{F}}}(T_{j_n,k_n})\) and \({{\widehat{G}}}(T_{j_n,k_n})\) converges almost surely to F and G, respectively. Indeed, for example,
The first term of the right-hand side of the above inequality is a.s. o(1) from (4) and the second term is also a.s. o(1) since \( {\widehat{\theta }}(T_{j_n,k_n}) \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^*\) and by applying the uniform law of large numbers to the sequence \((\partial ^2 \varphi _t(\theta )/ \partial \theta \partial \theta ^T)_{t \in \mathbb {Z}}\). Under the assumption (A3), similar arguments yield \(\Vert {{\widehat{G}}}(T_{j_n,k_n}) - G \Vert = o(1) ~ a.s.\).
Therefore, \({{\widehat{F}}}(T_{j_n,k_n}) {{\widehat{G}}}(T_{j_n,k_n})^{-1} {{\widehat{F}}}(T_{j_n,k_n})\) is a consistent estimator of the covariance matrix \(\Omega \).
2.2 Change-point test and asymptotic results
We derive a retrospective test procedure based on the MCE of the parameter.
For all \(n \ge 1\), define the matrix \({\widehat{\Omega }}(u_n)\) and the subset \({\mathcal {T}}_n\) by
where \((u_n,v_n)_{n\ge 1}\) is a bivariate integer-valued sequence such that: \( (u_n,v_n) =o(n)\) and \( u_n,v_n \begin{array}{c} \overset{}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}+\infty \). Note that the asymptotic properties of \({\widehat{\Omega }}(u_n)\) are very important to prove consistency of the procedure. Indeed, under H\(_0\), \({\widehat{\Omega }}(u_n)\) is a consistent estimator of the matrix \(\Omega \). Under the alternative and the classical Assumption B (see below), one can show that the first component of \({\widehat{\Omega }}(u_n)\) converges to the inverse of the covariance matrix of the stationary model of the first regime and second component (even if its consistency is not ensured) is positive semi-definite. This will play a key role in proving the consistency under the alternative.
For any \(1< k < n\), let us introduce
Therefore, consider the following test statistic:
The construction of this statistic follows the approach of Doukhan and Kengne (2015); that is, \({\widehat{Q}}_{n,k}\) evaluates a distance between \({\widehat{\theta }}(T_{1,k})\) and \({\widehat{\theta }}(T_{k+1,n})\) for all \(k \in {\mathcal {T}}_n\). Let us stress that for n large enough, \({\widehat{\theta }}(T_{1,k})\) and \({\widehat{\theta }}(T_{k+1,n})\) are close to \({\widehat{\theta }}(T_{1,n})\) which converges to \(\theta ^*\) under H\(_0\) (from the consistency of the MCE in Assumption (A2)). The null hypothesis will thus be rejected if there exists a time \(k \in {\mathcal {T}}_n\) such that the distance between \({\widehat{\theta }}(T_{1,k})\) and \({\widehat{\theta }}(T_{k+1,n})\) is too large.
The following theorem gives the asymptotic behavior of the test statistic under H\(_0\).
Theorem 1
Under H\(_0\) with \(\theta ^* \in \overset{\circ }{\Theta }\), assume that (A1)–(A4) hold for \((Y,\theta ^*)\). Then,
where \(W_d\) is a d-dimensional Brownian bridge.
For a nominal level \(\alpha \in (0,1)\), the critical region of the test is then \(({\widehat{Q}}_{n}>c_{d,\alpha })\), where \(c_{d,\alpha }\) is the \((1-\alpha )\)-quantile of the distribution of \(\underset{0\le \tau \le 1}{\sup }\left\| W_d(\tau )\right\| ^{2}\). The critical values \(c_{d,\alpha }\) can be easily obtained through a Monte Carlo simulation; see, for instance, Lee et al. (2003).
Under the alternative hypothesis, we consider the following additional condition for the break instant.
Assumption B: There exists \(\tau ^* \in (0,1)\) such that \(t^*=[n\tau ^*]\),where [x]denotes the integer part of x.
We obtain the following main result under H\(_1\).
Theorem 2
Under H\(_1\) with \(\theta ^*_1\) and \(\theta ^*_2\) belonging to \(\overset{\circ }{\Theta }\), assume that (A1)–(A4) hold for \((Y^{(1)},\theta ^*_1)\) and \((Y^{(2)},\theta ^*_2)\). If Assumption B is satisfied, then
Note that under H\(_1\), Theorem 2 needs, in particular, the stationarity of the processes \(Y^{(1)}\) and \(Y^{(2)}\), but the independence between these two processes is not needed.
In the next two sections, we will detail some examples of classes of multivariate time series with a quasi-likelihood contrast function. We also show that under some regularity conditions, the general assumptions required for Theorems 1 and 2 are satisfied for these classes.
Let us stress that the scope of the proposed procedure is quite extensive and is not only restricted to the examples below. This procedure can be applied for instance, for change-point detection in models with exogenous covariates (see Diop and Kengne 2022a; Aknouche and Francq 2021), for integer-valued time series with negative binomial quasi-likelihood contrast (see Aknouche et al. 2018) or with density power divergence contrast (see Kim and Lee 2020), for general time series model with the conditional least-squares contrast (see Klimko and Nelson 1978). In fact, one can easily see in these papers that the assumptions (A1)–(A4) hold.
3 Application to a class of multidimensional causal processes
Let \(\{Y_{t},\,t\in \mathbb {Z}\}\) be a multivariate time series of dimension \(m \in \mathbb {N}\). For any \({\mathcal {T}} \subseteq \mathbb {Z}\) and \(\theta \in \Theta \), consider the general class of causal processes defined by
Class \(\mathcal{AC}\mathcal{}_{{\mathcal {T}}}(M_{\theta },f_{\theta })\): A process \(\{Y_{t},\,t\in {\mathcal {T}} \}\) belongs to \(\mathcal{AC}\mathcal{}_{{\mathcal {T}}}(M_\theta ,f_\theta )\) if it satisfies:
where \(M_{\theta }(Y_{t-1}, Y_{t-2}, \ldots )\) is a \(m \times p\) random matrix having almost everywhere (a.e) full rank m, \(f_{\theta }(Y_{t-1}, Y_{t-2}, \ldots )\) is a \(\mathbb {R}^m\)-random vector and \((\xi _t)_{t \in \mathbb {Z}}\) is a sequence of \(\mathbb {R}^p\)-random vector with zero-mean, independent, identically distributed (i.i.d) satisfying \(\xi _t=(\xi ^{(k)}_t)_{1\le k \le p}\) with \(\mathbb {E}\big [\xi ^{(k)}_0 \xi ^{(k')}_0\big ]=0\) for \(k \ne k'\) and \(\mathbb {E}\big [\xi ^{{(k)}^2}_0\big ]=\text {Var}(\xi ^{(k)}_0)=1\) for \(1\le k \le p\). \(M_\theta (\cdot )\) and \(f_\theta (\cdot )\) are assumed to be known up to the parameter \(\theta \). This class has been studied in Doukhan and Wintenberger (2008), Bardet and Wintenberger (2009).
We would like to carry out the change-point test presented in Sect. 1 for the class \(\mathcal{AC}\mathcal{}_{\mathcal T}(M_{\theta },f_{\theta })\). For this purpose, we assume that \((Y_1,\ldots ,Y_n)\) is a trajectory generated from one or two processes satisfying (9).
For all \(t \in \mathbb {Z}\), denote by \(\mathcal {F}_{t}=\sigma (Y_s,\, s \le t)\) the \(\sigma \)-field generated by the whole past at time t. For any segment \(T \subset \{1,\ldots ,n\}\) and \(\theta \in \Theta \), we define the contrast function based on the conditional Gaussian quasi-log-likelihood given by (up to an additional constant)
where \({{\widehat{f}}}^t_\theta := f_\theta (Y_{t-1},\ldots ,Y_{1},0,\ldots )\), \({{\widehat{M}}}^t_\theta := M_\theta (Y_{t-1},\ldots ,Y_{1},0,\ldots )\), \({{\widehat{H}}}^t_\theta := {{\widehat{M}}}^t_\theta ({\widehat{M}}^{t}_\theta )^T\).
Thus, the MCE computed on T is defined by
Let \(\Psi _\theta \) be a generic symbol for any of the functions \(f_\theta \), \(M_\theta \) or \(H_\theta =M_\theta M_\theta ^T\) and \({\mathcal {K}} \subseteq \Theta \) be a compact subset. To study the stability properties of the class (9), Bardet and Wintenberger (2009) imposed the following classical Lipschitz-type conditions on the function \(\Psi _\theta \).
Assumption A\(_i (\Psi _\theta ,\mathcal K)\) (\(i=0,1,2\)): For any \(y \in (\mathbb {R}^m)^{\infty }\), the function \(\theta \mapsto \Psi _\theta (y)\) is i times continuously differentiable on \({\mathcal {K}}\) with \( \big \Vert \frac{\partial ^i \Psi _\theta (0)}{\partial \theta ^i}\big \Vert _{{\mathcal {K}}}<\infty \), and there exists a sequence of nonnegative real numbers \((\alpha ^{(i)}_{k}(\Psi _\theta ,{\mathcal {K}}))_{k \in \mathbb {N}} \) satisfying: \( \sum \limits _{k=1}^{\infty } \alpha ^{(i)}_{k}(\Psi _\theta ,{\mathcal {K}}) <\infty \), for \(i=0, 1, 2\); such that for any \(x, y \in (\mathbb {R}^m)^{\infty }\),
where \(x,y,x_k,y_k\) are, respectively, replaced by \(xx^T\), \(yy^T\), \(x_kx^T_k\), \(y_ky^T_k\) if \(\Psi _\theta =H_\theta \).
For \(r\ge 1\), define the set
The following regularity conditions are also considered in Bardet and Wintenberger (2009) to assure the consistency and the asymptotic normality of \({\widehat{\theta }}(T_{1,n})\) under H\(_0\).
(\(\mathcal{AC}\mathcal{}.{\textbf {A0}}\)): For all \(\theta \in \Theta \) and some \(t \in \mathbb {Z}\), \( \big ( f^t_{\theta ^*}= f^t_{\theta } \ \text {and} \ H^t_{\theta ^*}= H^t_{\theta } \ \ a.s. \big ) \Rightarrow ~ \theta = \theta ^*\).
(\(\mathcal{AC}\mathcal{}.{\textbf {A1}}\)): \(\exists \underline{H}>0\) such that \(\displaystyle \inf _{ \theta \in \Theta } \det \left( H_\theta (y)\right) \ge \underline{H}\), for all \(y \in (\mathbb {R}^m)^{\infty }\).
(\(\mathcal{AC}\mathcal{}.{\textbf {A2}}\)): \( \alpha ^{(i)}_{k}(f_\theta ,\Theta )+\alpha ^{(i)}_{k}(M_\theta ,\Theta ) +\alpha ^{(i)}_{k}(H_\theta ,\Theta ) = O(k^{-\gamma }) \) for \(i=0,1,2\) and some \(\gamma >3/2\).
(\(\mathcal{AC}\mathcal{}.{\textbf {A3}}\)): One of the families \(\big (\frac{\partial f^0_{\theta ^*}}{\partial \theta _i}\big )_{1\le i \le d}\) or \(\big (\frac{\partial H^0_{\theta ^*}}{\partial \theta _i}\big )_{1\le i \le d}\) is a.e linearly independent.
Under A\(_0(\Psi _\theta ,\Theta )\) (for \(\Psi _\theta =f_\theta , M_\theta , H_\theta \)) with \(\theta ^* \in \Theta \cap \Theta (1)\), Bardet and Wintenberger (2009) established the existence of a strictly stationary and ergodic solution to the class \(\mathcal{AC}\mathcal{}_{\mathbb {Z}}(M_{\theta ^*},f_{\theta ^*})\), which shows that the assumption (A1) holds. Under H\(_0\), if A\(_0(f_\theta ,\Theta )\), A\(_0(M_\theta ,\Theta )\) (or A\(_0(H_\theta ,\Theta )\)) and (\(\mathcal{AC}\mathcal{}.{\textbf {A0}}\))–(\(\mathcal{AC}\mathcal{}.{\textbf {A2}}\)) hold with \(\theta ^* \in \Theta \cap \Theta (2)\), then \({\widehat{\theta }}(T_{j_n,k_n}) \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^*\) (from Theorem 1 of Bardet and Wintenberger 2009). Therefore, (A2) is satisfied.
Let us define
with \(f^t_\theta := f_\theta (Y_{t-1},\ldots )\), \(M^t_\theta := M_\theta (Y_{t-1},\ldots )\) and \(H^t_\theta := M^t_\theta ({M^t_\theta })^T\).
Now, consider the change-point test presented in Section, where the observations \((Y_1,\ldots ,Y_n)\) depend on \(\theta ^*\) under H\(_0\) and on (\(\theta ^*_1\),\(\theta ^*_2\)) under H\(_1\). Under H\(_0\), A\(_i(f_\theta ,\Theta )\), A\(_i(M_\theta ,\Theta )\) (or A\(_i(M_\theta ,\Theta )\)) for \(i=0,1,2\) and (\(\mathcal{AC}\mathcal{}.{\textbf {A0}}\))–(\(\mathcal{AC}\mathcal{}.{\textbf {A3}}\)) with \(\theta ^* \in \overset{\circ }{\Theta } \cap \Theta (4)\), Bardet and Wintenberger (2009) have proved that \({\widehat{\theta }}(T_{j_n,k_n})\) is asymptotically normal. Then, using the sequence of functions \(\left( \varphi _t(\cdot )\right) _{t \in \mathbb {Z}}\) defined in (12), one can see that the assumptions (A3) and (A4) also hold. For the condition (3) and those imposed on the sequence \((\frac{\partial }{\partial \theta } \varphi _t(\theta ^*),\mathcal {F}_{t})_{t \in \mathbb {Z}}\) in (A3), see the proof of their Theorem 2 and the arguments in the proof of Lemma 2 (ii). Thus, under the null hypothesis, all the required assumptions (A1)–(A4) are verified for \((Y,\theta ^*)\), which assures that Theorem 1 applies to this class of models. Note that, by the same arguments, one can also see that these assumptions hold for \((Y^{(1)},\theta ^*_1)\) and \((Y^{(2)},\theta ^*_2)\) under H\(_1\). Therefore, Theorem 2 also applies to this class.
The models VAR(1) considered in (20) and (22) are examples of processes belonging to the class \(\mathcal{AC}\mathcal{}_{{\mathcal {T}}}(M_{\theta },f_{\theta })\). Such examples have been studied; see, for instance, Dvořák and Prášková (2013) and Kirch et al. (2015). But, the models (20) and (22) below are quite general, since the matrix \(M_{\theta }\) is part of the parameters of the model and a change might occur in this matrix.
4 Inference and application in general multivariate count process
4.1 Model formulation and inference
Consider a multivariate count time series \(\{Y_{t}= (Y_{t,1},\ldots ,Y_{t,m})^T,\,t\in \mathbb {Z}\}\) with value in \(\mathbb {N}_0^{m}\) (with \(m \in \mathbb {N}\), \(\mathbb {N}_0 = \mathbb {N}\cup \{ 0 \}\)) and denote by \(\mathcal {F}_{t-1}=\sigma \left\{ Y_{t-1},\ldots \right\} \) the \(\sigma \)-field generated by the whole past at time \(t-1\). For any \({\mathcal {T}} \subseteq \mathbb {Z}\) and \(\theta \in \Theta \), define the class of multivariate observation-driven integer-valued time series given by
Class \(\mathcal {MOD}_{{\mathcal {T}} }(f_{\theta })\): The multivariate count process \(Y=\{Y_{t},\,t\in {\mathcal {T}} \}\) belongs to \(\mathcal {MOD}_{{\mathcal {T}} }(f_{\theta })\) if it satisfies:
where \(f_{\theta }(\cdot )\) is a measurable multivariate function with nonnegative components, assumed to be known up to the parameter \(\theta \).
In this section, it is assumed that any \(\{Y_{t} ,\,t\in \mathbb {Z}\}\) belonging to \(\mathcal {MOD}_{{\mathcal {T}} }(f_{\theta })\) is a stationary and ergodic process (i.e., the condition (A1) imposed for the change-point detection holds) satisfying:
Proposition 1 provides sufficient conditions for the existence of a stationary and ergodic solution of (13) when the conditional distribution belongs to a m-parameter exponential family. The condition (14) is a classical assumption which ensures that the process \(\{Y_{t},\,t\in \mathcal T \}\) has moments of order slightly greater than 1 (see, for instance, Ahmad and Francq 2016).
Let \((Y_{1},\ldots ,Y_{n})\) be observations generated from \(\mathcal {MOD}_{\mathbb {Z}}(f_{\theta ^{*}})\) with \(\theta ^* \in \Theta \). The conditional Poisson quasi-log-likelihood computed on \(\{1,\ldots ,n\}\) is given by (up to a constant)
where \( \lambda _t(\theta ) :=\big (\lambda _{t,1}(\theta ), \ldots , \lambda _{t,m}(\theta ) \big ) =f_\theta (Y_{t-1}, Y_{t-2}, \ldots )\). An approximated conditional quasi-log-likelihood is given by
where \( {\widehat{\lambda }}_t(\theta ) :=\big ({\widehat{\lambda }}_{t,1}(\theta ), \ldots , {\widehat{\lambda }}_{t,m}(\theta ) \big )^T = f_\theta (Y_{t-1}, \ldots , Y_{1},0,\ldots )\). Therefore, the Poisson quasi-maximum likelihood estimator (QMLE) of \( \theta ^*\) is defined by
Note that under the assumption of independence among components and conditionally Poisson distributed, this Poisson QMLE is equivalent to the maximum likelihood estimator. Let us highlight that we deal with an arbitrary dependence among components and arbitrary conditional distribution; that is, the distribution of the components could differ from each other.
For a process \(\{Y_t,\, t \in \mathbb {Z}\}\) belonging to \(\mathcal {MOD}_{\mathbb {Z}}(f_{\theta ^{*}})\), we set the following assumptions in order to establish the consistency and the asymptotic normality of the Poisson QMLE.
Assumption A\(_i (\Theta )\) (\(i=0,1,2\)): For any \(y \in \big (\mathbb {N}_0^{m} \big )^{\infty }\), the function \(\theta \mapsto f_\theta (y)\) is i times continuously differentiable on \(\Theta \) with \( \left\| \partial ^i f_\theta (0)/ \partial \theta ^i\right\| _\Theta <\infty \), and there exists a sequence of nonnegative real numbers \((\alpha ^{(i)}_k)_{k\ge 1} \) satisfying \( \sum \nolimits _{k=1}^{\infty } \alpha ^{(0)}_k <1 \) (or \( \sum \nolimits _{k=1}^{\infty } \alpha ^{(i)}_k <\infty \) for \(i=1, 2\)); such that for any \(y, y' \in \big (\mathbb {N}_0^{m} \big )^{\infty }\),
(\(\mathcal {MOD}.{\textbf {A0}}\)): For all \(\theta \in \Theta \), \( \big ( f_{\theta ^*}(Y_{t-1}, Y_{t-2}, \ldots ) \overset{a.s.}{=}f_{\theta }(Y_{t-1}, Y_{t-2}, \ldots ) ~ \text { for some } t \in \mathbb {Z}\big ) \Rightarrow ~ \theta ^* = \theta \); moreover, \(\exists \underline{c}>0\) such that \( f_\theta (y) \ge \underline{c} {\textbf {1}}_m\) componentwise, for all \(\theta \in \Theta \), \( y \in \big ( \mathbb {N}_0^{m} \big )^{\infty } \), where \({\textbf {1}}^T_m=(1,\ldots ,1)\) is a vector of dimension m.
(\(\mathcal {MOD}.{\textbf {A1}}\)): \(\theta ^* \) is an interior point of \(\Theta \subset \mathbb {R}^{d}\).
(\(\mathcal {MOD}.{\textbf {A2}}\)): The family \(\big (\frac{\partial \lambda _{t} (\theta ^* )}{\partial \theta _i} \big )_{1\le i \le d} \) is a.e. linearly independent.
Proposition 1 establishes the existence of a stationary and ergodic solution of the model (13) for the m-parameter exponential family conditional distribution. Consider a m-dimensional process \(\{Y_t, ~ t \in \mathbb {Z}\}\) satisfying
where \(p(\cdot | \cdot )\) is a multivariate discrete distribution belonging to the m-parameter exponential family; that is
where \(\eta \) is the natural parameter (i.e., \(\eta _t\) is the natural parameter of the distribution of \(Y_t|\mathcal {F}_{t-1}\)) and \(A(\eta )\), h(y) are known functions. It is assumed that the function \(\eta \mapsto A(\eta )\) is twice continuously differentiable on the natural parameter space; therefore, the mean and variance of this distribution are \(\partial A(\eta )/ \partial \eta \) and \(\partial ^2 A(\eta )/ \partial \eta ^2\), respectively. See Khatri (1983) for more details on such class of distribution. For the model (15), it holds that
Proposition 1
Assume that A\(_0(\Theta )\) holds. Then, there exists a \(\tau -weakly\) dependent, stationary and ergodic solution \(\{ Y_t, ~ t \in \mathbb {Z}\}\) to (15), satisfying \(\mathbb {E}\Vert Y_t \Vert < \infty \).
Let \((S,\mathcal {A}, \mathbb {P})\) be a probability space, \(\mathcal {M}\) a \(\sigma \)-subalgebra of \(\mathcal {A}\) and Z a random variable with values in a Banach space \((E, \Vert \cdot \Vert )\). Assume that \(\Vert Z \Vert _1 < \infty \) and define the coefficient \(\tau \) as
where \(\Lambda _1(E)\) is the set of functions \(h:E \rightarrow \mathbb {R}\) such that \(\text {Lip}(h) :={\sup }\, {x, y \in E, ~ x\ne y} |h(x) - h(y)|/ \Vert x- y \Vert \le 1\). Consider an E-valued strictly stationary process \((Z_t)_{t \in \mathbb {Z}}\) and set for all \(i \in \mathbb {Z}\), \(\mathcal {M}_i = \sigma (Z_t, ~ t\le i)\). The dependence between the past of the process \((Z_t)_{t\in \mathbb {Z}}\) and its future k-tuples may be assessed as follows. Consider the norm \(\Vert x-y\Vert = \Vert x_1-y_1\Vert + \cdots +\Vert x_{k}-y_{k}\Vert \) on \(E^k\) and define
If \(\tau (s)\) tends to 0 as \(s \rightarrow \infty \), then the process \((Z_t)_{t \in \mathbb {Z}}\) is said to be \(\tau \)-weakly dependent. The weak dependence concept has been introduced by Doukhan and Louhichi (1999) for the purpose of taking into account some situations where the mixing conditions are not satisfied. We refer to the lecture notes Dedecker et al. (2007) for an overview on this dependence concept.
In the sequel, we deal with the more general class of model (13), where the distribution of \(Y_t|\mathcal {F}_{t-1}\) may be outside the m-parameter exponential family. The following theorem shows that the Poisson QMLE for the class of models (13) is strongly consistent.
Theorem 3
Assume that A\(_0(\Theta )\), (\(\mathcal {MOD}.{\textbf {A0}}\)) and (14) (with \(\epsilon \ge 1\)) hold with
Then
For any \(t \in \mathbb {Z}\) and \(\theta \in \Theta \), denote \(\Gamma _t (\theta ):=(Y_t -\lambda _{t}(\theta ))(Y_t -\lambda _{t}(\theta ))^T\) and \(D_t(\theta )\) the \(m \times m\) diagonal matrix with the ith diagonal element is equal to \(\lambda _{t,i}(\theta )\) for any \(i=1,\ldots ,m\). From the assumption (\(\mathcal {MOD}.{\textbf {A0}}\)), the matrix \(D_t(\theta )\) is a.s. positive definite. Combining all the regularity assumptions and notations given above, we obtain the asymptotic normality of the Poisson QMLE, as shown in the following theorem.
Theorem 4
Assume that A\(_i(\Theta )\) (\(i=0,1,2\)), (\(\mathcal {MOD}.{\textbf {A0}}\))–(\(\mathcal {MOD}.{\textbf {A2}}\)) and (14) (with \(\epsilon \ge 3\)) hold with
then
where
In comparison with the results of Lee et al. (2018), Cui et al. (2020) and Fokianos et al. (2020), Theorems 3 and 4 are applied to the class \(\mathcal {MOD}_{\mathbb {Z}}(f_{\theta ^*})\) with a general structure of the conditional mean, whereas these authors deal with linear and log-linear models. Moreover, Lee et al. (2018) and Cui et al. (2020) consider a parametric framework, with the assumption that the conditional distribution given the whole past is known, which is quite restrictive in practice. Theorems 3 and 4 are established in a semi-parametric setting.
4.2 Change-point detection
Now, assume that the trajectory \((Y_1,\ldots ,Y_n)\) is generated from one or two processes satisfying the general model (13) and consider the change-point test of Sect. 1, where the observations depend on \(\theta ^*\) under H\(_0\) and on (\(\theta ^*_1\),\(\theta ^*_2\)) under H\(_1\). Let us define the contrast function based on the conditional Poisson quasi-log-likelihood for any segment \(T \subset \{1,\ldots ,n\}\) and \(\theta \in \Theta \):
Thus, the MCE computed on T is given by
Under the null hypothesis, the assumption (A2) holds from Theorem 3. Letting \(\varphi _t(\theta ):= -\ell _t(\theta )\) for all \( t \in \mathbb {Z}\) and \(\theta \in \Theta \), one can see that (A3) and (A4) are also satisfied from Theorem 4. The relation (3) in (A3) holds from Lemma 2 (i) (see below), the proof of Lemma 3 (a) and the arguments in the proof of Lemma 2 (ii), whereas the relation (4) in (A4) holds from Lemme 2 (ii), Lemma 3 (c). See also Lemma 3(b) for the required properties about the sequence \((\frac{\partial }{\partial \theta } \varphi _t(\theta ^*),\mathcal {F}_{t})_{t \in \mathbb {Z}}\). Hence, in absence of change, all the conditions of Theorem 1 are verified for \((Y,\theta ^*)\), which assures that the first result about the asymptotic behavior of the test statistic \({\widehat{Q}}_n\) applies to the class of models (13). Under the change point alternative H\(_1\), one can go along similar lines to verify that (A1)–(A4) are satisfied for \((Y_1,\theta ^*_1)\) and \((Y_2,\theta ^*_2)\). This shows that Theorem 1 can also be applied to this class.
5 Numerical results
In this section, the statistic \({\widehat{Q}}_{n}\) will be computed with \(u_n=[\left( \log (n)\right) ^{2}]\) and \(v_n=[\left( \log (n)\right) ^{5/2}]\) for a sample size n. The procedure is implemented in the R software (developed by the CRAN project).
5.1 Simulation study
We investigate the performance (level and power) of the test statistic through two examples of two-dimensional processes, with sample size \(n = 250, 500, 1000\) and the nominal level \(\alpha = 0.05\). Let us consider the following models.
-
A bivariate AR (1) model. Consider the two-dimensional AR(1) model (with zero-mean) expressed as
$$\begin{aligned} Y_t={A_0}Y_{t-1}+ \gamma _0 \xi _t \quad \text {for all}\quad t \in \mathbb {Z}, \end{aligned}$$(20)where \(Y_{t}= (Y_{t,1},Y_{t,2})^T\), \({A_0}=(a_{i,j})_{i,j=1,2}\) is a \(2 \times 2\) matrix with eigenvalues inside the complex unit circle, \(\gamma _0\) is a nonzero real number and \((\xi _t=(\xi _{t,1},\xi _{t,2})^T)_{t \in \mathbb {Z}}\) is a bivariate white noise satisfying the conditions of the class (9). This process belongs to the class \(\mathcal{AC}\mathcal{}_{\mathcal T}(M_{\theta },f_{\theta })\) with \(f_{\theta }(Y_{t-1}, \ldots ) ={A_0}Y_{t-1}\) and \(M_{\theta }(Y_{t-1}, \ldots ) = \begin{pmatrix} \gamma _0 &{}\!\! 0 \\ 0&{} \!\! \gamma _0 \end{pmatrix}\). The parameter of the model is denoted by \(\theta _0=(a_{1,1},a_{1,2},a_{2,1},a_{2,2},\gamma _0)\). At the nominal level \(\alpha = 0.05\), the critical value of the test is therefore \(c_{5,\alpha } \approx 3.899\) (see Lee et al. 2003). The performance will be evaluated in cases where the innovation \((\xi _{t})_{t \in \mathbb {Z}}\) is obtained from the standardized Student distributions with 5 and 8 degrees of freedom for the first and the second component, respectively. In the scenarios of change, we assume that the parameter \(\theta _0 \equiv (A_0,\gamma _0)\) changes to \(\theta _1 \equiv (A_1,\gamma _1)\).
-
A bivariate INARCH(1) model.
Assume that \(\{Y_{t}= (Y_{t,1},Y_{t,2})^T,\,t\in \mathbb {Z}\}\) is a count time series with value in \(\mathbb {N}_0^{2}\), where \(\{Y_{t,1},\,t\in \mathbb {Z}\}\) and \(\{Y_{t,2},\,t\in \mathbb {Z}\}\) are two processes with conditional distribution following a Poisson distribution and a negative binomial distribution, respectively. More precisely,
$$\begin{aligned} \left\{ \begin{array}{l} Y_{t,1} | \mathcal {F}_{t-1} \sim \text {Poisson}(\lambda _{t,1})\\ Y_{t,2} | \mathcal {F}_{t-1} \sim \text {NB}(r,r/(r+\lambda _{t,2})) \end{array} \right. \quad \text {with}\quad \lambda _{t}:= (\lambda _{t,1},\lambda _{t,2})^T = {d_0}+{B_0}Y_{t-1},\nonumber \\ \end{aligned}$$(21)where \({d_0}=(d^{(1)},d^{(2)})^T \in (0,\infty )^2\), \({B_0}=(b_{i,j})_{i,j=1,2}\) is a \(2 \times 2\) matrix with nonnegative coefficients, and NB(r, p) denotes the negative binomial distribution with parameter (r, p) and mean \(r(1-p)/p\). It is assumed that for all \(t \in \mathbb {Z}\), \(Y_{t,1}\), and \(Y_{t,2}\) are conditionally independent given \(\mathcal {F}_{t-1}\) and that the parameter r is known for each simulation; that is, the parameter of interest is \(\theta _0=(d^{(1)},d^{(2)}, b_{1,1},b_{1,2},b_{2,1},b_{2,2})\) and the critical value of the test is \(c_{6,\alpha } \approx 4.375\) (see also Lee et al. 2003).
In situations of break, we also assume that the parameter changes from \(\theta _0\) (which is characterized here by \(({d_0},{B_0})\)) to \(\theta _1\) that we will characterize by \(({d_1},{B_1})\) for this model.
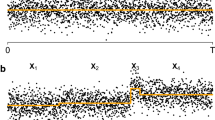
Figure 1 is an illustration of a typical realizations of the statistics \({\widehat{Q}}_{n,k}\) for two trajectories of length 1000 generated from bivariate AR(1) processes: a trajectory without change and a trajectory with a change at time \(t^*=500\). One can see that, for the trajectory without change, the statistics \({\widehat{Q}}_{n,k}\) are well below the critical value (see Fig. 1a). For the scenario with change, the maximum (which represents the value of \({\widehat{Q}}_{n}\)) of the statistics \({\widehat{Q}}_{n,k}\) is higher than the limit of the critical region and that it is obtained at a point very close to the instant of break (see Fig. 1b). This empirically comforts the common use of the classical estimator \({\widehat{t}}_n = {\text {argmax}}\, {k \in \mathcal T_n} \left( {{\widehat{Q}}}_{n,k}\right) \) to determine the break-point.
To evaluate the empirical level and power, we consider trajectories generated from the two models (20) and (21) in the following situations: (i) scenarios with a constant parameter \(\theta _0\) and (ii) scenarios with a parameter change (\(\theta _0 \rightarrow \theta _1\)) at time \(t^*=n/2\). The replication number in each simulation is 500. For different scenarios, Table 1 indicates the proportion of the number of rejections of the null hypothesis computed under H\(_0\) (for the levels) and H\(_1\) (for the powers). As can be seen from this table, the empirical levels are close to the nominal level for each of the two models. One can see that the statistic is quite sensitive for detecting the change for both the cases considered under the alternative: the scenario with dependent components and independent components (i.e., the scenario where the matrix \(A_1\) or \(B_1\) is diagonal) after the breakpoint. For both the classes of models, the results of the test are quite accurate; the empirical level approaching the nominal one when n increases and the empirical power increases with n and is close to 1 when \(n=1000\). This is consistent with the asymptotic results of Theorem 1 and 2.
Typical realizations of the statistics \({\widehat{Q}}_{n,k}\) for two trajectories generated from bivariate AR(1) processes defined in (20). a Is a realization for 1000 observations with a constant parameter \(\theta _0=(0.5,-0.2,0.35,0.1,1)\). b Is a realization for 1000 observations in a scenario where the parameter changes from \(\theta _0=(0.5,-0.2,0.35,0.1,1)\) to \(\theta _1=(0.5,-0.2,0.1,0.1,1)\) at \(t^*=500\). The horizontal line represents the limit of the critical region of the test
5.2 Real data example
We consider the bivariate time series whose variables represent the average daily concentrations of particulate matter with a diameter less than 10\(\mu m\) and carbon monoxide (PM\(_{10}\),CO), collected at some monitoring stations in the Vitória metropolitan area. We deal with the data from January 31, 2010 to December 30, 2010 (observations on 334 days); see Fig. 2a and b. This series is a part of a dataset obtained from the State Environment and Water Resources Institute (available at https://rss.onlinelibrary.wiley.com/pb-assets/hub-assets/rss/Datasets/RSSC%2067.2/C1239deSouza-1531120585220.zip ), which were analyzed by de Souza et al. (2018).
To apply the proposed test procedure, we consider a two-dimensional AR(1) model (with nonzero mean) given for \(t \in \mathbb {Z}\), by
where \(Y_{t}= (PM_{10,t},CO_{t})^T\) (the value of the corresponding vector at day t), \(\omega _0\) is a 2-dimensional vector, \(A_0\), M are \(2 \times 2\) matrices and \((\xi _t)\) a bivariate white noise satisfying the conditions of the class (9). The parameter of the model is \(\theta = (\omega _0, A_0, M) \in \mathbb {R}^{10}\).
The realizations of \({\widehat{Q}}_{n,k}\) (for all \(k \in \mathcal T_n\)) displayed in Fig. 2c show that the resulting test statistic \({\widehat{Q}}_{n}\) is higher than the critical value of the test, which indicates that a change-point is detected in this series. The breakpoint is estimated as \({\widehat{t}}_n=184\) (see Fig. 2), which corresponds to the date August 02, 2010. The estimated model with two regimes is given by:
where in brackets are the standard errors of the estimators obtained from the sandwich matrix \({{\widehat{\Omega }}}_T^{-1}\), a consistent estimator of the covariance matrix \(\Omega ^{-1}\) defined in (5), computed on the segment \(T \subset \{ 1,\ldots ,n\}\). Simulations carried out with the parameters in (23) show that the procedure works well (in term of empirical level and power) in that case. Also, this result is in accordance with those obtained by Diop and Kengne (2022b) who have found a break on August 06, 2010 with an epidemic procedure in the carbon monoxide series. The first regime (from January 31, 2010 to August 08, 2010) includes the austral winter and a period where the winds are weaker. These meteorological factors are known to increase the concentration of some pollutants (such as the carbon monoxide), which are important determinants associated to the \(PM_{10}\) concentration (see, for instance, Ng and Awang 2018 and the references therein).
Plot of the time series and the statistic \({\widehat{Q}}_{n,k}\) for the change-point detection applied to the bivariate real data (PM\(_{10}\),CO) with the VAR(1) process defined in (22). The horizontal line represents the limit of the critical region of the test. The vertical line represents the estimated breakpoint
6 Proofs of the main results
Let \( (\psi _n)_{n \in \mathbb {N}} \) and \( (r_n)_{n \in \mathbb {N}} \) be sequences of random variables or vectors. Throughout this section, we use the notation \( \psi _n = o_P(r_n) \) to mean: for all \( \varepsilon > 0, ~ \mathbb {P}( \Vert \psi _n \Vert \ge \varepsilon \Vert r_n \Vert ) \begin{array}{c} \overset{}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}0\). Write \( \psi _n = O_P(r_n)\) to mean: for all \( \varepsilon > 0 \), there exists \(C>0\) such that \(\mathbb {P}( \Vert \psi _n \Vert \ge C \Vert r_n \Vert )\le \varepsilon \) for n large enough. In the sequel, C denotes a positive constant whose the value may differ from one inequality to another.
6.1 Proof of the results of Section 2
6.1.1 Proof of Theorem 1
Define the statistic
where \(\Omega \) is the covariance matrix defined in the assumption (A4). For any segment \(T \subset \{1,\ldots ,n\}\) and \(\theta \in \Theta \), we also define the function
Let \(1\le k \le k^{\prime } \le n\), \({\bar{\theta }} \in \Theta \) and \(i \in \{1,2,\ldots ,d\}\). By the mean value theorem applied to the function \(\theta \mapsto \frac{\partial }{\partial \theta _i}C({T_{k,k^{\prime }}},\theta )\), there exists \(\theta _{n,i}\) between \({\bar{\theta }}\) and \(\theta ^*\) such that
which implies
with
The following lemma will be useful in the sequel.
Lemma 1
Assume that the conditions of Theorem 1 hold.
-
(i)
\(\underset{k \in {\mathcal {T}}_n}{\max }\big |{{\widehat{Q}}}_{n,k}-Q_{n,k}\big |=o_P(1)\).
-
(ii)
If \((j_n)_{n\ge 1}\) and \((k_n)_{n\ge 1}\) are two integer-valued sequences such that \(j_n \le k_n\), \(k_n \begin{array}{c} \overset{}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}\infty \) and \(k_n - j_n \begin{array}{c} \overset{}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}\infty \), then \( F_n(T_{j_n,k_n},{\widehat{\theta }}(T_{j_n,k_n})) \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }F, \) where F is the matrix defined in (A4).
Proof
-
(i)
Let \(k \in {\mathcal {T}}_n\). As \(n \rightarrow \infty \), from the asymptotic normality of the MCE and the consistency of \({\widehat{\Omega }}(u_n)\), we obtain:
$$\begin{aligned} \big \Vert {\sqrt{k}} \big ({\widehat{\theta }}(T_{1,k}) -\theta ^*\big )\big \Vert= & {} O_P(1), \big \Vert {\sqrt{n-k}} \big ({\widehat{\theta }}(T_{k+1,n}) -\theta ^*\big )\big \Vert \nonumber \\= & {} O_P(1) \quad \text {and} \quad \big \Vert {\widehat{\Omega }}(u_n)-\Omega \big \Vert =o(1). \end{aligned}$$(26)Then, it holds that
$$\begin{aligned}&\big |{{\widehat{Q}}}_{n,k}-Q_{n,k}\big |\\&\quad = \frac{\left( k(n-k)\right) ^{2}}{n^{3}} \Big | \big ({\widehat{\theta }}(T_{1,k})-{\widehat{\theta }}(T_{k+1,n})\big )^T \big ( {\widehat{\Omega }}(u_n)-\Omega \big ) \big ({\widehat{\theta }}(T_{1,k})-{\widehat{\theta }}(T_{k+1,n})\big ) \Big |\\&\quad \le C\frac{\left( k(n-k)\right) ^2}{n^{3}} \big \Vert {\widehat{\Omega }}(u_n)-\Omega \big \Vert \big \Vert {\widehat{\theta }}(T_{1,k})-{\widehat{\theta }}(T_{k+1,n}) \big \Vert ^2\\&\quad \le C\big \Vert {\widehat{\Omega }}(u_n)-\Omega \big \Vert \bigg [ \frac{k(n-k)^2}{n^{3}} \big \Vert \sqrt{k} \big ({\widehat{\theta }}(T_{1,k}) -\theta ^*\big )\big \Vert ^2 \\&\qquad + \frac{k^2(n-k)}{n^{3}} \big \Vert \sqrt{n-k} \big ({\widehat{\theta }}(T_{k+1,n}) -\theta ^*\big )\big \Vert ^2 \bigg ]\\&\quad \le o(1)O_P(1); \end{aligned}$$which allows to conclude.
-
(ii)
Applying (25) with \({\bar{\theta }} = {\widehat{\theta }}(T_{j_n,k_n})\), we obtain
$$\begin{aligned} F_n(T_{j_n,k_n},{\widehat{\theta }}(T_{j_n,k_n}))&= \left( \frac{1}{k_n-j_n+1}\frac{\partial ^{2}}{\partial \theta \partial \theta _i} C(T_{j_n,k_n},\theta _{n,i})\right) _{1\le i \le d}\\&=\frac{1}{k_n-j_n+1}\left( \sum _{t \in T_{j_n,k_n}}\frac{\partial ^{2} \varphi _t(\theta _{n,i})}{\partial \theta \partial \theta _i} \right) _{1\le i \le d}, \end{aligned}$$where \(\theta _{n,i}\) belongs between \({\widehat{\theta }}(T_{j_n,k_n})\) and \(\theta ^*\). Since \({\widehat{\theta }}(T_{j_n,k_n}) \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^*\), \(~ \theta _{n,i} ~ \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^*\) (for any \(i=1,\ldots ,d\)) and that \(F=\mathbb {E}\big [\frac{\partial ^{2} \varphi _0(\theta ^*)}{\partial \theta \partial \theta ^T} \big ]\) exists (see the assumption (A4)), by the uniform strong law of large numbers, for any \(i =1,\ldots ,d\), we get
$$\begin{aligned}&\left\| \frac{1}{k_n-j_n+1}\sum _{t \in T_{j_n,k_n}}\frac{\partial ^{2} \varphi _t(\theta _{n,i})}{\partial \theta \partial \theta _i} - \mathbb {E}\left[ \frac{\partial ^{2} \varphi _0(\theta ^*)}{\partial \theta \partial \theta _i}\right] \right\| \\&\quad \le \left\| \frac{1}{k_n-j_n+1}\sum _{t \in T_{j_n,k_n}}\frac{\partial ^{2} \varphi _t(\theta _{n,i})}{\partial \theta \partial \theta _i} - \mathbb {E}\Big [\frac{\partial ^{2} \varphi _0(\theta _{n,i})}{\partial \theta \partial \theta _i}\Big ] \right\| \\&\qquad + \left\| \mathbb {E}\left[ \frac{\partial ^{2} \varphi _0(\theta _{n,i})}{\partial \theta \partial \theta _i}\right] - \mathbb {E}\left[ \frac{\partial ^{2} \varphi _0(\theta ^*)}{\partial \theta \partial \theta _i}\right] \right\| \\&\quad \le \left\| \frac{1}{k_n-j_n+1}\sum _{t \in T_{j_n,k_n}}\frac{\partial ^{2} \varphi _t(\theta )}{\partial \theta \partial \theta _i} - \mathbb {E}\left[ \frac{\partial ^{2} \varphi _0(\theta )}{\partial \theta \partial \theta _i}\right] \right\| _\Theta \\&\quad + o(1) = o(1) + o(1)= o(1). \end{aligned}$$This completes the proof of the lemma.
\(\square \)
Now, we use (26) and the part (ii) of Lemma 1 to show that
Let \(k \in {\mathcal {T}}_n\). Applying (24) with \({\bar{\theta }}={\widehat{\theta }}(T_{1,k})\) and \(T_{k,k^\prime }=T_{1,k}\), we get
With \({\bar{\theta }}={\widehat{\theta }}(T_{k+1,n})\) and \(T_{k,k^\prime }=T_{k+1,n}\), (24) becomes
Moreover, as \(n\rightarrow +\infty \), Lemma 1(ii) implies
Then, according to (26), for n large enough, (28) gives
This is equivalent to
For n large enough, \({\widehat{\theta }}(T_{1,k})\) is an interior point of \(\Theta \) and we have \( \frac{\partial }{\partial \theta } {{\widehat{C}}}(T_{1,k},{\widehat{\theta }}(T_{1,k}))=0\).
Hence, for n large enough, we get from (30)
Similarly, we can use (29) to obtain
The subtraction of (31) and (32) gives
Since the matrix G is positive definite (see (A3)), the above equality is equivalent to
and that \(Q_{n,k}\) can be rewritten as
Moreover, applying the central limit theorem for the martingale difference sequence \(\left( \frac{\partial }{\partial \theta } \varphi _t(\theta ^*),\mathcal {F}_{t}\right) _{t \in \mathbb {Z}}\) (see Billingsley 1968), we have
where [x] denotes the integer part of x and \(B_{G}\) is a Gaussian process with covariance matrix \(\min (s,t)G\).
Then,
where \(B_d\) is a d-dimensional standard motion and \(W_d\) is a d-dimensional Brownian bridge.
Therefore, using (33) and (34), we obtain
For n large enough, we deduce
which shows that (27) holds. Hence, we can conclude the proof of the theorem from Lemma 1(i). \(\square \)
6.1.2 Proof of Theorem 2
Under the alternative, we can write
where \(t^*=[\tau ^* n]\) (with \(0<\tau ^*<1\)) and \(\{Y^{(j)}_{t}, t \in \mathbb {Z}\}\) (\(j=1,2\)) is a stationary and ergodic process depending on the parameter \(\theta ^{*}_j\) (with \(\theta ^{*}_1 \ne \theta ^{*}_2\)) satisfying the assumptions (A1)–(A4).
Remark that \( {\widehat{Q}}_n = \underset{k \in {\mathcal {T}}_n}{\max }\big ({\widehat{Q}}_{n,k}\big ) \ge {\widehat{Q}}_{n,t^*} \). Then, to prove the theorem, we will show that \({\widehat{Q}}_{n,t^*} \begin{array}{c} \overset{\mathcal {P}}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}+\infty \).
For any \(n\in \mathbb {N}\), we have
with
Moreover, the two matrices in the formula of \({\widehat{\Omega }}(u_n)\) are positive semi-definite. Then, we obtain
By the consistency and asymptotic normality of the MCE, we have: (i) \( {\widehat{\theta }}(T_{1,t^{*}})-{\widehat{\theta }}(T_{t^*+1,n}) \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^{*}_1-\theta ^{*}_{2}\ne 0 \) and (ii) \(\widehat{F}(T_{1,u_n}) {{\widehat{G}}}(T_{1,u_n})^{-1} {{\widehat{F}}}(T_{1,u_n}) \) converges to the covariance matrix of the stationary model of the first regime which is positive definite. Therefore, (35) implies \({\widehat{Q}}_{n,t^*} \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }+\infty \). This establishes the theorem. \(\square \)
6.2 Proof of the results of Section 4
6.3 Proof of Proposition 1
Let \(F_\lambda (y)\) be the cumulative distribution function of \(p(y|\eta )\) with marginals \(F_{\lambda _{1},1}, \ldots , F_{\lambda _{m},m}\), where \(\lambda = (\lambda _{1},\ldots ,\lambda _{m})^T = \partial A (\eta )/\partial \eta \). From the Sklar’s theorem (see Sklar 1959), one can find a copula \(\mathcal {C}\) such that, for all \(y=(y_1,\ldots , y_m) \in \mathbb {R}^m\)
For \(i=1,\ldots ,m\), denote by \(F_{\lambda ,i}^{-1}(u) := \inf \{ y_i \ge 0, ~ F_{\lambda ,i}(y_i) \ge u \} \) for all \(u \in [0,1]\). Let \(\{ U_t = (U_{t,1},\ldots ,U_{t,m})^T, ~ t \in \mathbb {Z}\}\) be a sequence of independent random vectors with distribution \(\mathcal {C}\). We will prove that there exists a \(\tau \)-weakly dependent, stationary and ergodic solution \((Y_t, \lambda _t)\) of (15) satisfying:
with \(\lambda _t = \left( \lambda _{t,1},\ldots ,\lambda _{t,m} \right) ^T= f_\theta (Y_{t-1},\ldots )\). For a process \((Y_t)_{t \in \mathbb {Z}}\) that fulfills (15) and (36), we get,
where \(\Psi \) is a function defined in \((\mathbb {N}_0^m)^\infty \times [0,1]^m\). According to Doukhan and Wintenberger (2008), it suffices to show that: (i) \(\mathbb {E}\Vert \Psi (\pmb {y};U_t) \Vert < \infty \) for some \(\pmb {y} \in (\mathbb {N}_0^m)^\infty \) and (ii) there exists a sequence of nonnegative real numbers \((\alpha _k(\Psi ))_{k \ge 1}\) satisfying \(\sum _{k \ge 1} \alpha _k(\Psi ) < 1\) such that, for all \(\pmb {y}, \pmb {y}' \in (\mathbb {N}_0^m)^\infty \), \(\mathbb {E}\Vert \Psi (\pmb {y};U_t) - \Psi (\pmb {y}';U_t) \Vert \le \sum _{k \ge 1} \alpha _k(\Psi ) \Vert y_k - y'_k \Vert \).
Proof of (i)
Set \(f_\theta (0,\ldots ) = \lambda = (\lambda _{1},\ldots ,\lambda _{m})^T\). The random vector \(\big (F_{\lambda _{1},1}^{-1}(U_{t,1},\ldots , F_{\lambda _{m},m}^{-1}(U_{t,m}) \big )^T\) is \(F_\lambda \) distributed. Thus,
where this inequality holds from the assumption A\(_0(\Theta )\). \(\square \)
Proof of (ii)
For all \(\pmb {y}, \pmb {y}' \in (\mathbb {N}_0^m)^\infty \), set \(\lambda = f_\theta (\pmb {y},\ldots ) = (\lambda _{1},\ldots ,\lambda _{m})^T\) and \(\lambda ' = f_\theta (\pmb {y}',\ldots ) = (\lambda _{1}',\ldots ,\lambda _{m}')^T\). We have,
where the equality in (38) holds from the Proposition A.2 of Davis and Liu (2016) and the inequality in (39) holds from the assumption A\(_0(\Theta )\). Thus, take \(\alpha _k(\Psi )=\alpha ^{(0)}_k\), which completes the proof of the proposition. \(\square \)
6.3.1 Proof of Theorem 3
To simplify, we will use the following notations in the sequel:
where \( f_\theta ^{t,i}\) and \({{\widehat{f}}}_\theta ^{t,i}\) (for \(i=1,\ldots ,m\)) represent the ith component of \(f^t_\theta \equiv f_\theta (Y_{t-1}, Y_{t-2}, \ldots )\) and \({\widehat{f}}^t_\theta \equiv f_\theta (Y_{t-1}, Y_{t-2}, \ldots ,Y_1 )\), respectively.
-
(i)
Firstly, we will show that
$$\begin{aligned} \frac{1}{n}\big \Vert {{\widehat{L}}}_{n}(\theta ) - L_{n}(\theta ) \big \Vert _\Theta \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }0 . \end{aligned}$$(40)Remark that
$$\begin{aligned} \frac{1}{n}\big \Vert {{\widehat{L}}}_{n}(\theta ) - L_{n}(\theta ) \big \Vert _\Theta&\le \frac{1}{n}\sum _{t=1}^{n}\Vert {\widehat{\ell }}_{t}(\theta )-\ell _{t}(\theta ) \Vert _\Theta \nonumber \\&\le \frac{1}{n}\sum _{i=1}^{m}\sum _{t=1}^{n}\Vert {\widehat{\ell }}_{t,i}(\theta )-\ell _{t,i}(\theta ) \Vert _\Theta . \end{aligned}$$(41)Using \({\textbf {A}}_0(\Theta )\) with the condition (16) and the existence of the moment of order 2 (i.e., (14) with \(\epsilon \ge 1\)), one can proceed as in the proof of Theorem 3.1 in Doukhan and Kengne (2015) to prove that
$$\begin{aligned} \frac{1}{n}\sum _{t=1}^{n}\Vert {\widehat{\ell }}_{t,i}(\theta )-\ell _{t,i}(\theta ) \Vert _\Theta \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }0\quad \text {for all}\quad i=1,\ldots ,m. \end{aligned}$$ -
(ii)
Let us establish that: for all \(t \in \mathbb {Z}\),
$$\begin{aligned} \mathbb {E}\big [ \Vert \ell _t(\theta ) \Vert _{\Theta } \big ] < \infty . \end{aligned}$$(42)We have
$$\begin{aligned} \mathbb {E}\big [ \Vert \ell _t(\theta ) \Vert _{\Theta } \big ] \le \sum _{i=1}^m \mathbb {E}\big [ \sup _{\theta \in \Theta } |\ell _{t,i}(\theta ) | \big ], \end{aligned}$$From \({\textbf {A}}_0(\Theta )\), (\(\mathcal {MOD}.{\textbf {A0}}\)), (14) (with \(\epsilon \le 1\)) and by going along similar lines as in the proof of Theorem 3.1 in Doukhan and Kengne (2015), we get: \(\mathbb {E}\big [ \sup _{\theta \in \Theta } |\ell _{t,i}(\theta ) | \big ] < \infty \) for all \(i=1,\ldots ,m\). Thus, (42) holds.
Since \(\{Y_{t},~t\in \mathbb {Z}\}\) is stationary and ergodic, the process \(\{\ell _{t}(\theta ),~t\in \mathbb {Z}\}\) is also a stationary and ergodic sequence. Then, by the uniform strong law of large numbers applied to \(\{\ell _{t}(\theta ),~t\in \mathbb {Z}\}\), it holds that
$$\begin{aligned} \Big \Vert \frac{1}{n}L_{n}(\theta )-\mathbb {E}[\ell _{0}(\theta )]\Big \Vert _{\Theta }= \left\| \frac{1}{n} \sum _{t=1}^{n} \ell _{t}(\theta )-\mathbb {E}[\ell _{0}(\theta )]\right\| _{\Theta } \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }0. \end{aligned}$$Thus, from (40), we obtain
$$\begin{aligned} \Big \Vert \frac{1}{n}{\widehat{L}}_{n}(\theta )-\mathbb {E}[\ell _{0}(\theta )]\Big \Vert _{\Theta }\le & {} \frac{1}{n}\big \Vert {\widehat{L}}_{n}( \theta )-L_{n}(\theta )\big \Vert _{\Theta }\\&+\left\| \frac{1}{n}L_{n}(\theta )-\mathbb {E}[\ell _{0}(\theta )]\right\| _{\Theta } \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }0. \end{aligned}$$ -
(iii)
To complete the proof of the theorem, it suffices to show that the function \(\theta \mapsto L(\theta ) = \mathbb {E}[\ell _0 (\theta )]\) has a unique maximum at \(\theta ^*\). Let \(\theta \in \Theta \), such that \(\theta \ne \theta ^*\). We have
$$\begin{aligned} L(\theta ^*) - L(\theta )&= \sum _{i=1}^m \big ( \mathbb {E}\ell _{0,i}(\theta ^*) - \mathbb {E}\ell _{0,i}(\theta ) \big ) \\&= \sum _{i=1}^m \left( \mathbb {E}\left[ Y_{0,i}\log f_{\theta ^*}^{0,i} - f_{\theta ^*}^{0,i}\right] - \mathbb {E}\left[ Y_{0,i}\log f_{\theta }^{0,i} - f_{\theta }^{0,i}\right] \right) \\&= \sum _{i=1}^m \left( \mathbb {E}\left[ f_{\theta ^*}^{0,i} \log f_{\theta ^*}^{0,i} - f_{\theta ^*}^{0,i}\right] - \mathbb {E}\left[ f_{\theta ^*}^{0,i} \log f_{\theta }^{0,i} - f_{\theta }^{0,i}\right] \right) \\&= \sum _{i=1}^m \left( \mathbb {E}\left[ f_{\theta ^*}^{0,i} \left( \log f_{\theta ^*}^{0,i} - \log f_{\theta }^{0,i} \right) \right] - \mathbb {E}\left( f_{\theta ^*}^{0,i} - f_{\theta }^{0,i}\right) \right) . \end{aligned}$$According to the identifiability assumption \({\textbf {A}}_0(\Theta )\) and since \(\theta \ne \theta ^*\), there exists \(i_0\) such that \(f_{\theta }^{0,i_0} \ne f_{\theta ^*}^{0,i_0}\). By going as in the proof of Theorem 3.1 in Doukhan and Kengne (2015), we get \(\mathbb {E}\big [ f_{\theta ^*}^{0,i_0} \big (\log f_{\theta ^*}^{0,i_0} - \log f_{\theta }^{0,i_0} \big ) \big ] - \mathbb {E}[f_{\theta ^*}^{0,i_0} - f_{\theta }^{0,i_0}] > 0\) and \(\mathbb {E}\big [ f_{\theta ^*}^{0,i} \big (\log f_{\theta ^*}^{0,i} - \log f_{\theta }^{0,i} \big ) \big ] - \mathbb {E}[f_{\theta ^*}^{0,i} - f_{\theta }^{0,i}] \ge 0\) for \(i=1,\ldots ,m, ~ i \ne i_0\). This establishes (iii), which consequently yields the theorem. \(\square \)
6.3.2 Proof of Theorem 4
Applying the mean value theorem to the function \(\theta \mapsto \frac{\partial }{\partial \theta _i} L_n (\theta )\) for all \(i \in \{1,\ldots ,d\}\), there exists \({{\bar{\theta }}}_{n,i}\) between \({\widehat{\theta }}_n\) and \(\theta ^*\) such that
which is equivalent to
with
The following lemma is needed.
Lemma 2
Assume that the conditions of Theorem 4 hold. Then,
-
(i)
\( \mathbb {E}\Big [ \frac{1}{\sqrt{n}} \Big \Vert \frac{\partial }{\partial \theta }{{\widehat{L}}}_n (\theta )- \frac{\partial }{\partial \theta } L_n (\theta )\Big \Vert _\Theta \Big ] \begin{array}{c} \overset{}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}0. \)
-
(ii)
\( \frac{1}{n} \Big \Vert \frac{\partial ^2}{\partial \theta \partial \theta ^T}{{\widehat{L}}}_n (\theta )- \frac{\partial ^2}{\partial \theta \partial \theta ^T} L_n (\theta )\Big \Vert _\Theta = o(1) ~ a.s.\).
Proof
-
(i)
We have
$$\begin{aligned}&\frac{1}{\sqrt{n}} \Big \Vert \frac{\partial }{\partial \theta }\widehat{L}_{n}(\theta ) - \frac{\partial }{\partial \theta } L_{n}(\theta ) \Big \Vert _\Theta \nonumber \\&\quad \le \frac{1}{\sqrt{n}} \sum _{t=1}^{n} \Big \Vert \frac{\partial }{\partial \theta }{\widehat{\ell }}_{t}(\theta )-\frac{\partial }{\partial \theta }\ell _{t}(\theta ) \Big \Vert _\Theta \nonumber \\&\quad \le \frac{1}{\sqrt{n}}\sum _{i=1}^{m}\sum _{t=1}^{n}\Big \Vert \frac{\partial }{\partial \theta }{\widehat{\ell }}_{t,i}(\theta )-\frac{\partial }{\partial \theta }\ell _{t,i}(\theta ) \Big \Vert _\Theta . \end{aligned}$$(45)Moreover, by proceeding as in Lemma 7.1 of Doukhan and Kengne (2015), we can use A\(_i(\Theta )\) (\(i=0,1\)), (14) and the condition (17) to establish that
$$\begin{aligned} \mathbb {E}\Big [\frac{1}{\sqrt{n}} \sum _{t=1}^{n}\Big \Vert \frac{\partial }{\partial \theta }{\widehat{\ell }}_{t,i}(\theta )-\frac{\partial }{\partial \theta }\ell _{t,i}(\theta ) \Big \Vert _\Theta \Big ] \begin{array}{c} \overset{}{\longrightarrow } \\ {n\rightarrow \infty } \end{array}0\quad \text {for all}\quad i=1,\ldots ,m. \end{aligned}$$Thus, we can conclude the proof of (i) from (45).
-
(ii)
It holds that
$$\begin{aligned}&\frac{1}{n} \Big \Vert \frac{\partial ^2}{\partial \theta \partial \theta ^T}{{\widehat{L}}}_n (\theta )- \frac{\partial ^2}{\partial \theta \partial \theta ^T} L_n (\theta )\Big \Vert _\Theta \\&\quad \le \frac{1}{n} \sum _{t=1}^{n} \Big \Vert \frac{\partial ^2}{\partial \theta \partial \theta ^T}{\widehat{\ell }}_{t}(\theta )-\frac{\partial ^2}{\partial \theta \partial \theta ^T}\ell _{t}(\theta ) \Big \Vert _\Theta \\&\quad \le \frac{1}{n}\sum _{i=1}^{m}\sum _{t=1}^{n}\Big \Vert \frac{\partial ^2}{\partial \theta \partial \theta ^T}{\widehat{\ell }}_{t,i}(\theta )-\frac{\partial ^2}{\partial \theta \partial \theta ^T}\ell _{t,i}(\theta ) \Big \Vert _\Theta . \end{aligned}$$By going as in the proof of Lemma 7.1 of Doukhan and Kengne (2015), one easily get for \(i=1,\ldots ,m\), \( \frac{1}{n} \sum _{t=1}^{n}\Big \Vert \frac{\partial ^2}{\partial \theta \partial \theta ^T}{\widehat{\ell }}_{t,i}(\theta )-\frac{\partial ^2}{\partial \theta \partial \theta ^T}\ell _{t,i}(\theta ) \Big \Vert _\Theta = o(1)\), which shows that (ii) holds.
\(\square \)
The following lemma will also be needed.
Lemma 3
If the assumptions of Theorem 4 hold, then
-
(a)
the matrices \( J_{\theta ^*} = \mathbb {E}\big [\frac{\partial \lambda ^T_{0}(\theta ^* )}{ \partial \theta } {D}^{-1}_0(\theta ^*) \frac{\partial \lambda _{0}(\theta ^* )}{ \partial \theta ^T} \big ]\) and \(I_{\theta ^*}= \mathbb {E}\big [ \frac{\partial \lambda ^T_{0}(\theta ^* )}{ \partial \theta } {D}^{-1}_0(\theta ^*) \Gamma _0 (\theta ^*) {D}^{-1}_0(\theta ^*) \frac{\partial \lambda _{0}(\theta ^* )}{ \partial \theta ^T} \big ]\) exist and are positive definite;
-
(b)
\(\left( \frac{\partial \ell _t(\theta ^*)}{\partial \theta },\mathcal {F}_{t}\right) _{t \in \mathbb {Z}}\) is a stationary ergodic, square integrable martingale difference sequence with covariance matrix \(I_{\theta ^*}\);
-
(c)
\(\mathbb {E}\big [ \Vert \frac{\partial ^{2} \ell _0 (\theta )}{\partial \theta \partial \theta ^T} \Vert _\Theta \big ] < \infty \) and \(\mathbb {E}\big [\frac{\partial ^{2} \ell _0 (\theta ^*)}{\partial \theta \partial \theta ^T}\big ]=-J_{\theta ^*}\);
-
(d)
\(J({{\widehat{\theta }}}_{n}) \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }J_{\theta ^*}\) and that the matrix \(J_{\theta ^*}\) is invertible.
Proof
- (a):
-
From the assumption (\(\mathcal {MOD}.{\textbf {A0}}\)), we can find a constant \(C>0\) such that it holds a.s.
$$\begin{aligned}&\mathbb {E}\Big \Vert \frac{\partial \lambda ^T_{0}(\theta )}{ \partial \theta } {D}^{-1}_0(\theta ) \frac{\partial \lambda _{0}(\theta )}{ \partial \theta ^T} \Big \Vert _\Theta \\&\quad \le C \mathbb {E}\Big \Vert \frac{\partial \lambda _{0}(\theta )}{ \partial \theta } \Big \Vert ^2_\Theta \\&\quad \le C \sum _{i=1}^m \mathbb {E}\Big \Vert \frac{\partial \lambda _{0,i}(\theta )}{ \partial \theta } \Big \Vert ^2_\Theta . \end{aligned}$$
One can show as in the proof of Lemma 7.1 of Doukhan and Kengne (2015) that for any \(i=1,\ldots ,m\), \(\mathbb {E}\big \Vert \frac{\partial \lambda _{0,i}(\theta )}{ \partial \theta } \big \Vert ^2_\Theta < \infty \). Hence,
which establishes the existence of \(J_{\theta ^*}\).
Using (\(\mathcal {MOD}.{\textbf {A0}}\)) and Hölder’s inequality, we have
According to the existence of the moment of order 4 (from (14) with \(\epsilon \ge 3\)), \(\mathbb {E}\Vert Y_0\Vert ^4<\infty \). Furthermore, proceeding as in the proof of Theorem 3.1 and Lemma 7.1 in Doukhan and Kengne (2015), one can also get \(\mathbb {E}\Vert \lambda _{0,i}(\theta ) \Vert ^4_\Theta < \infty \) and \(\mathbb {E}\big \Vert \frac{\partial \lambda _{0,i}(\theta )}{ \partial \theta } \big \Vert ^4_\Theta <\infty \) for any \(i=1,\ldots ,m\). Therefore,
which establishes that \(I_{\theta ^*}\) exists.
Now, let \(U \in \mathbb {R}^d\) be a nonzero vector. We have \( \frac{\partial \lambda _{0}(\theta ^* )}{ \partial \theta ^T} \cdot U \ne 0\) a.s. from the assumption (\(\mathcal {MOD}.{\textbf {A2}}\)), which implies
and
Hence, \(J_{\theta ^*}\) and \(I_{\theta ^*}\) are positive definite.
- (b):
-
For any \(\theta \in \Theta \), we have
$$\begin{aligned} \frac{\partial \ell _t(\theta )}{\partial \theta } = \sum _{i=1}^{m} \left( \frac{Y_{t,i}}{\lambda _{t,i}(\theta )}-1\right) \frac{\partial }{\partial \theta }\lambda _{t,i}(\theta ) = \frac{\partial \lambda ^{T}_{t}(\theta )}{ \partial \theta } { D}^{-1}_t(\theta ) (Y_t- \lambda _{t}(\theta )). \nonumber \\ \end{aligned}$$(47)Then, according to the stability properties of \(\{Y_{t},~t\in \mathbb {Z}\}\), the process \(\big \{\frac{\partial \ell _t(\theta )}{\partial \theta },~t\in \mathbb {Z}\big \}\) is also stationary and ergodic. Moreover, since \(\lambda _t(\theta ^*)\) and \(\frac{\partial \lambda _t(\theta ^*)}{\partial \theta } \) are \(\mathcal {F}_{t-1}\)-measurable, we have
$$\begin{aligned} \mathbb {E}\left[ \frac{\partial \ell _t(\theta ^*)}{\partial \theta }\right]&= \sum _{i=1}^{m} \mathbb {E}\left[ \mathbb {E}\left[ \frac{\partial \lambda ^{T}_{t}(\theta ^*)}{ \partial \theta } { D}^{-1}_t(\theta ^*) (Y_t- \lambda _{t}(\theta ^*)) | \mathcal {F}_{t-1}\right] \right] \\&= \sum _{i=1}^{m} \mathbb {E}\left[ \frac{\partial \lambda ^{T}_{t}(\theta ^*)}{ \partial \theta } { D}^{-1}_t(\theta ^*) \cdot \mathbb {E}\left[ \left( Y_t- \lambda _{t}(\theta ^*)\right) | \mathcal {F}_{t-1}\right] \right] =0 \end{aligned}$$In addition, \(\mathbb {E}\big [ \frac{\partial \ell _0(\theta ^*)}{\partial \theta } \frac{\partial \ell _0(\theta ^*)}{\partial \theta ^{T}}\big ] =I_{\theta ^*}\). Hence, the part second part of the lemma holds.
- (c):
-
We have,
$$\begin{aligned} \mathbb {E}\Big \Vert \frac{\partial ^2 \ell _0(\theta )}{\partial \theta \partial \theta ^{T}} \Big \Vert _\Theta = \sum _{i=1}^m \mathbb {E}\Big \Vert \frac{\partial ^2 \ell _{0,i}(\theta )}{\partial \theta \partial \theta ^{T}} \Big \Vert _\Theta < \infty , \end{aligned}$$where the above inequality holds since \(\mathbb {E}\Big \Vert \frac{\partial ^2 \ell _{0,i}(\theta )}{\partial \theta \partial \theta ^{T}} \Big \Vert _\Theta < \infty \) for \(i=1,\ldots ,m\) by going as in the proof of Lemma 7.2 in Doukhan and Kengne (2015). Moreover, according to (47), for any \(\theta \in \Theta \), we have
$$\begin{aligned} \frac{\partial ^2 \ell _t(\theta )}{\partial \theta \partial \theta ^{T}} = \sum _{i=1}^{m} \left( \frac{Y_{t,i}}{\lambda _{t,i}(\theta )}-1\right) \frac{\partial ^2 \lambda _{t,i}(\theta )}{\partial \theta \partial \theta ^{T}} - \sum _{i=1}^{m} \frac{Y_{t,i}}{\lambda ^2_{t,i}(\theta )} \frac{\partial \lambda _{t,i}(\theta )}{\partial \theta } \frac{\partial \lambda _{t,i}(\theta )}{\partial \theta ^{T}} . \end{aligned}$$Then, using conditional expectations, we obtain
$$\begin{aligned} \mathbb {E}\left[ \frac{\partial ^2 \ell _0(\theta ^*)}{\partial \theta \partial \theta ^{T}} \right]= & {} - \mathbb {E}\left[ \sum _{i=1}^{m} \frac{1}{\lambda _{0,i}(\theta ^*)} \frac{\partial \lambda _{0,i}(\theta ^*)}{\partial \theta } \frac{\partial \lambda _{0,i}(\theta ^*)}{\partial \theta ^{T}} \right] \\= & {} - \left[ \frac{\partial \lambda ^{T}_{0}(\theta ^* )}{ \partial \theta } {D}^{-1}_0(\theta ^*) \frac{\partial \lambda _{0}(\theta ^* )}{ \partial \theta ^{T}} \right] =- J_{\theta ^*} . \end{aligned}$$ - (d):
-
We have
$$\begin{aligned} J({\widehat{\theta }}_n) = \left( -\frac{1}{n}\frac{\partial ^2}{\partial \theta \partial \theta _i} L_n ({{\bar{\theta }}}_{n,i})\right) _{1 \le i \le d} = \left( -\frac{1}{n}\sum _{t=1}^{n}\frac{\partial ^{2} \ell _t({{\bar{\theta }}}_{n,i})}{\partial \theta \partial \theta _i}\right) _{1 \le i \le d}. \end{aligned}$$Since \({\widehat{\theta }}_n \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^*\), \(~ \bar{\theta }_{n,i} ~ \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }\theta ^*\) (for any \(i=1,\ldots ,d\)) and that \(\mathbb {E}\big [\frac{\partial ^{2} \ell _0 (\theta ^*)}{\partial \theta \partial \theta ^{T}}\big ]=-J_{\theta ^*}\) exists, by the uniform strong law of large numbers, for any \(i =1,\ldots ,d\), we get
$$\begin{aligned} \frac{1}{n}\sum _{t=1}^{n}\frac{\partial ^{2} \ell _t({{\bar{\theta }}}_{n,i})}{\partial \theta \partial \theta _i} \overset{a.s.}{=}\frac{1}{n}\sum _{t=1}^{n}\frac{\partial ^{2} \ell _t(\theta ^*)}{\partial \theta \partial \theta _i} \overset{a.s.}{\longrightarrow } \mathbb {E}\left[ \frac{\partial ^{2} \ell _0(\theta ^*)}{\partial \theta \partial \theta _i}\right] \quad \text {as}\quad n \rightarrow \infty . \end{aligned}$$Therefore,
$$\begin{aligned} J({\widehat{\theta }}_n)= & {} \left( -\frac{1}{n}\sum _{t=1}^{n}\frac{\partial ^{2} \ell _t(\bar{\theta }_{n,i})}{\partial \theta \partial \theta _i}\right) _{1 \le i \le d} \overset{a.s.}{\longrightarrow } { n \rightarrow \infty }-\left( \mathbb {E}\left[ \frac{\partial ^{2} \ell _0(\theta ^*)}{\partial \theta \partial \theta _i}\right] \right) _{1\le i \le d}\\= & {} J_{\theta ^*}. \end{aligned}$$This completes the proof of the lemma. \(\square \)
Now, let us use the results of Lemmas 2 and 3 to complete the proof of Theorem 4.
Since \({\widehat{\theta }}_n\) is a local maximum of the function \(\theta \mapsto {{\widehat{L}}}_n (\theta )\) for n large enough (from the assumption (\(\mathcal {MOD}.{\textbf {A1}}\)) and the consistency of \({\widehat{\theta }}_n\)), \(\frac{\partial }{\partial \theta } \widehat{L}_n ( {\widehat{\theta }}_n)=0\).
Thus, according to Lemma 2, the relation (43) becomes
Moreover, applying the central limit theorem to the sequence \(\left( \frac{\partial \ell _t(\theta ^*)}{\partial \theta } ,\mathcal {F}_{t}\right) _{t \in \mathbb {Z}}\), it holds that
Therefore, for n large enough, using Lemma 3(d) and the relation (48), we obtain
This establishes the theorem. \(\square \)
References
Ahmad A (2016) Contribution à l’économétrie des séries temporelles à valeurs entières. Ph.D. Thesis, Université de Lille
Ahmad A, Francq C (2016) Poisson QMLE of count time series models. J Time Ser Anal 37(3):291–314
Aknouche A, Francq C (2021) Count and duration time series with equal conditional stochastic and mean orders. Economet Theor 37(2):248–280
Aknouche A, Bendjeddou S, Touche N (2018) Negative binomial quasi-likelihood inference for general integer-valued time series models. J Time Ser Anal 39(2):192–211
Bardet JM, Wintenberger O (2009) Asymptotic normality of the quasi-maximum likelihood estimator for multidimensional causal processes. Ann Stat 37(5B):2730–2759
Billingsley P (1968) Convergence of probability measures. Wiley, New York
Cui Y, Li Q, Zhu F (2020) Flexible bivariate Poisson integer-valued Garch model. Ann Inst Stat Math 72(6):1449–1477
Davis RA, Liu H (2016) Theory and inference for a class of nonlinear models with application to time series of counts. Stat. Sinica 1673–1707
de Souza JB, Reisen VA, Franco GC, Ispány M, Bondon P, Santos JM (2018) Generalized additive models with principal component analysis: an application to time series of respiratory disease and air pollution data. J Roy Stat Soc: Ser C (Appl Stat) 67(2):453–480
Dedecker J, Doukhan P, Lang G, José Rafael LR, Louhichi S, Prieur C (2007) Weak dependence. In: Weak dependence: with examples and applications. Springer, pp 9–20
Diop ML, Kengne W (2021) Poisson QMLE for change-point detection in general integer-valued time series models. Metrika 1–31
Diop ML, Kengne W (2017) Testing parameter change in general integer-valued time series. J Time Ser Anal 38(6):880–894
Diop ML, Kengne W (2022) Inference and model selection in general causal time series with exogenous covariates. Electron J Stat 16(1):116–157
Diop ML, Kengne W (2022) Epidemic change-point detection in general causal time series. Stat Probab Lett 184:109416
Doukhan P, Kengne W (2015) Inference and testing for structural change in general Poisson autoregressive models. Electron J Stat 9:1267–1314
Doukhan P, Louhichi S (1999) A new weak dependence condition and applications to moment inequalities. Stoch Process Their Appl 84(2):313–342
Doukhan P, Wintenberger O (2008) Weakly dependent chains with infinite memory. Stoch Process Their Appl 118(11):1997–2013
Dvořák M, Prášková Z (2013) On testing changes in autoregressive parameters of a VAR model. Commun Stat Theory Methods 42(7):1208–1226
Fokianos K, Gombay E, Hussein A (2014) Retrospective change detection for binary time series models. J Stat Plan Inference 145:102–112
Fokianos K, Støve B, Tjøstheim D, Doukhan P (2020) Multivariate count autoregression. Bernoulli 26(1):471–499
Franke J, Kirch C, Kamgaing JT (2012) Changepoints in times series of counts. J Time Ser Anal 33(5):757–770
Hudecová Š (2013) Structural changes in autoregressive models for binary time series. J Stat Plan Inference 143(10):1744–1752
Hudecová Š, Hušková M, Meintanis SG (2017) Tests for structural changes in time series of counts. Scand J Stat 44(4):843–865
Kang J, Lee S (2009) Parameter change test for random coefficient integer-valued autoregressive processes with application to polio data analysis. J Time Ser Anal 30(2):239–258
Kang J, Lee S (2014) Parameter change test for Poisson autoregressive models. Scand J Stat 41(4):1136–1152
Kang J, Song J (2015) Robust parameter change test for Poisson autoregressive models. Stat Probab Lett 104:14–21
Kengne WC (2012) Testing for parameter constancy in general causal time-series models. J Time Ser Anal 33(3):503–518
Khatri CG (1983) Multivariate discrete exponential family of distributions and their properties. Commun Stat Theory Methods 12(8):877–893
Killick R, Fearnhead P, Eckley IA (2012) Optimal detection of changepoints with a linear computational cost. J Am Stat Assoc 107(500):1590–1598
Kim B, Lee S (2020) Robust estimation for general integer-valued time series models. Ann Inst Stat Math 72(6):1371–1396
Kirch C, Muhsal B, Ombao H (2015) Detection of changes in multivariate time series with application to EEG data. J Am Stat Assoc 110(511):1197–1216
Klimko LA, Nelson PI (1978) On conditional least squares estimation for stochastic processes. Ann Stat 629–642
Lee S, Lee T (2004) Cusum test for parameter change based on the maximum likelihood estimator. Seq Anal 23(2):239–256
Lee S, Na O (2005) Test for parameter change in stochastic processes based on conditional least-squares estimator. J Multivar Anal 93(2):375–393
Lee S, Na O (2005) Test for parameter change based on the estimator minimizing density-based divergence measures. Ann Inst Stat Math 57(3):553–573
Lee S, Song J (2008) Test for parameter change in ARMA models with GARCH innovations. Stat Probab Lett 78(13):1990–1998
Lee S, Ha J, Na O, Na S (2003) The cusum test for parameter change in time series models. Scand J Stat 30(4):781–796
Lee Y, Lee S, Tjøstheim D (2018) Asymptotic normality and parameter change test for bivariate Poisson INGARCH models. Test 27(1):52–69
Ng KY, Awang N (2018) Multiple linear regression and regression with time series error models in forecasting pm10 concentrations in peninsular Malaysia. Environ Monit Assess 190(2):1–11
Page E (1955) A test for a change in a parameter occurring at an unknown point. Biometrika 42(3/4):523–527
Qu Z, Perron P (2007) Estimating and testing structural changes in multivariate regressions. Econometrica 75(2):459–502
Sklar M (1959) Fonctions de repartition an dimensions et leurs marges. Publ Inst Statist Univ Paris 8:229–231
Acknowledgements
The authors are grateful to the two anonymous referees for many relevant suggestions and comments which helped to improve the contents of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
M. L. DIOP: Supported by the MME-DII center of excellence (ANR-11-LABEX-0023-01) and the ANR BREAKRISK: ANR-17-CE26-0001-01.
M. L. DIOP and W. KENGNE: Developed within the CY Initiative of Excellence (grant “Investissements d’Avenir” ANR-16-IDEX-0008), Project “EcoDep” PSI-AAP2020-0000000013.
Rights and permissions
About this article
Cite this article
Diop, M.L., Kengne, W. A general procedure for change-point detection in multivariate time series. TEST 32, 1–33 (2023). https://doi.org/10.1007/s11749-022-00824-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11749-022-00824-z
Keywords
- Change-point
- Multivariate time series
- Minimum contrast estimation
- Consistency
- Causal processes
- Integer-valued time series