The multiple filter test for change point detection in time series

Abstract

A framework for the detection of change points in the expectation in sequences of random variables is presented. Specifically, we investigate time series with general distributional assumptions that may show an unknown number of change points in the expectation occurring on multiple time scales and that may also contain change points in other parameters. To that end we propose a multiple filter test (MFT) that tests the null hypothesis of constant expectation and, in case of rejection of the null hypothesis, an algorithm that estimates the change points.

The MFT has three important benefits. First, it allows for general distributional assumptions in the underlying model, assuming piecewise sequences of i.i.d. random variables, where also relaxations with regard to identical distribution or independence are possible. Second, it uses a MOSUM type statistic and an asymptotic setting in which the MOSUM process converges weakly to a functional of a Brownian motion which is then used to simulate the rejection threshold of the statistical test. This approach enables a simultaneous application of multiple MOSUM processes which improves the detection of change points that occur on different time scales. Third, we also show that the method is practically robust against changes in other distributional parameters such as the variance or higher order moments which might occur with or even without a change in expectation. A function implementing the described test and change point estimation is available in the R package MFT.

1 Introduction

The statistical testing and estimation of structural breaks in time series is of high importance in various applications, such as econometrics (Fryzlewicz 2014), mobile communication (Zhang et al. 2009), machine learning (Harchaoui and Lévy-Leduc 2008), ocean engineering (Killick et al. 2010) or also neurophysiological data analysis (Staude et al. 2010). Accordingly, there is a vast literature on change point analysis (for an overview and review see Basseville and Nikiforov 1993; Brodsky and Darkhovsky 1993; Aue and Horváth 2013; Jandhyala et al. 2013; Brodsky 2017).

In this paper we investigate an unknown number of change points in the expectation occurring on multiple time scales in time series with general distributional assumptions in which also other parameters are allowed to change. Also other methods address these aspects. Nonparametric methods have been proposed by Horváth et al. (2008); Eichinger and Kirch (2018). The detection of change points on multiple time scales is investigated by, e.g., Frick et al. (2014), Fryzlewicz (2014) and Matteson and James (2014), some of these methods also requiring only relatively weak distributional assumptions. Other approaches provide robustness against changes in other parameters when aiming at detecting changes in the expectation. Recently, Pein et al. (2017) developed a method on multiscale change point inference for Gaussian sequences using likelihood ratio statistics, which detects change points in the expectation where the variance is allowed to change simultaneously. In general, few results can be found concerning change point detection in the expectation that is robust against changes in the variance. Applied approaches using leave-one-out cross validation and segmentation are proposed in Arlot and Celisse (2011) and Muggeo and Adelfio (2011). Among the existing literature, however, we are not aware of a method that combines all three properties, i.e., (1) that makes weak distributional assumptions on the data, (2) that captures the aspect of change points occurring on multiple time scales and (3) that also turns out to be robust against changes in other parameters than the expectation.

Here we consider a method, abbreviated MFT, that tests the null hypothesis of constant expectation and that, after rejection of the null hypothesis, aims at estimating the change points in the expectation. We translate a framework for change point detection that was designed for point processes (Messer et al. 2014) to a model that is based on piecewise sequences of i.i.d. random variables. This transition requires the formulation of a multiple change point model as well as underlying moving sum (MOSUM) type processes (compare, e.g., Eichinger and Kirch 2018), which also contain parameter estimating processes. It is also necessary to derive the processes’ limit behavior under the null hypothesis of no change in the expectation. The results of the transition show that the translated MFT exhibits two important properties that proved to be beneficial in the point process scenario. First, the MFT works under relatively general distributional assumptions on sequences of random variables, i.e., also on non-Gaussian sequences. We also discuss extensions to sequences of independent random variables showing a certain variability in their variances (heteroscedasticity) or a certain degree of dependence. Second, by simultaneous application of multiple MOSUM processes, change points occurring on different time scales can be investigated.

Additionally, we derive results under alternative scenarios of change points that support the methods’ robustness against changes in other parameters than the expectation. The results of the paper show that the MFT is sensitive to changes in the expectation while it proves robust against changes in other parameters such as the variance or higher order moments. Also, a routine is provided in the R-package MFT (Messer et al. 2017a) that complements the theoretical results of the MFT by enabling its straightforward practical applicability.

The paper is organized as follows. The set of model assumptions is presented in Sect. 2. Then the MFT is derived in Sect. 3. There we formulate the MOSUM process which includes a parameter estimating auxiliary process. Then we investigate an asymptotic setting in which the MOSUM process converges weakly to a functional L of a standard Brownian motion, which depends only on the window size—i.e., the MOSUM bandwidth—and is independent of the distribution of the data. This limit process L can therefore be used to derive the rejection threshold of the statistical test via simulations. This approach is suitable for relatively general distributional assumptions, since it is based on Donsker type limit theorems. Further, the MFT allows the combination of multiple window sizes, i.e., simultaneous application of multiple MOSUM processes, in order to detect change points at multiple time scales. In case of rejection of the null hypothesis, we combine the MOSUM processes of different window sizes and provide an algorithm that estimates the change points in multiple time scales (Sect. 4). This combines the advantages of small windows, which can be more precise for changes occurring in fast time scales, with the advantages of larger windows, which can be more sensitive to smaller changes. Finally, we show robustness of the procedure against changes in other distributional parameters if there is no change in expectation. The properties of the test are entirely unchanged as long as the expectation and variance remain unchanged. In case of changes in the variance, we show that for constant expectation, there is only a negligible change in the limit behavior of the MOSUM process, which affects only the covariance structure in the neighborhood of the variance change point (Sect. 5). In Sect. 6, we complement our theoretical findings in exemplary simulations, where we show the procedures’ sensitivity to changes in the expectation (occurring on multiple time scales) and its robustness against changes in other parameters.

2 The model

Let $\mathbf {X} = (X_i)_{i=1,2\ldots }$ be a sequence of i.i.d. real-valued, square-integrable random variables with positive variances. These constitute the null hypothesis of constant expectation $\mu :=\mathbb {E}[X_1]$.

The full model $\mathcal M$ with changes in the expectation is given by piecewise combination of null elements. We assume the observation regime to be $1,\ldots ,T$, for a total time $T\in \mathbb {N}\backslash \{0,1\}$. We consider a set of change points $C \subset \{2,\ldots ,T\}$ with elements $c_1< c_2 \ldots < c_k$ fixed, but unknown. Given C, consider $k+1$ independent null processes $\mathbf X^{[1]},\ldots ,\mathbf X^{[k+1]}$, with $\mathbf X^{[j]}=(X_{i,[j]})_{i=1,2,\ldots }$ having expectations $\mu _{[j]}:=\mathbb {E}[X_{1,[j]}]$ for $j=1,\ldots ,k$. Unless otherwise stated we assume $\mu _{[j]} \not =\mu _{[j+1]}$ for all j which means that the expectation changes at every $c_j$, while also other parameters are allowed to change. Then the compound process is given by

$$\begin{aligned} X_{1,[1]},\ldots ,X_{c_1-1,[1]}, X_{c_1,[2]},\ldots ,X_{c_2-1,[2]},\ldots , X_{c_k,[k+1]},\ldots ,X_{T,[k+1]}, \end{aligned}$$

i.e., at each change point $c_j$, we enter a process $\mathbf X^{[j+1]}$ with new expectation $\mu _{[j+1]}$.

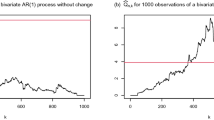
Here we aim at testing the null hypothesis of no change points, i.e., $C=\emptyset$, when the observed process is a null element with constant expectation (for an example of a null element see Fig. 1a). In case of rejection of the null hypothesis, we aim at estimating the set of change points C. An example with three change points is shown in Fig. 1b.

Fig. 1

Examples of time series. a A null element without change point. b A process $\mathbf X \in \mathcal M$ with three change points, where the first change point $c_1=500$ shows a small change in expectation while the change points $c_2=1200$ and $c_3=1290$ occur rapidly with large changes in expectation. a $X_i \sim \mathcal N(0,1)$, $T=2000$. b All random variables independent and normally distributed with variance 1 and means $\mu _{[1]}=0, \mu _{[2]}=0.3,\mu _{[3]}=2.2,\mu _{[4]}=1.4$, $T=2000$

Note that the assumption of i.i.d. random variables is used here for simplicity, while the methods and proofs require only relaxations of this assumption (see Sect. 3).

3 The multiple filter test (MFT)

In the following we construct the MFT for the null hypothesis $C=\emptyset$. This is an asymptotic method and in the formulation of the model $\mathcal M$ therefore we let time and the change points grow linearly in a parameter n. That is, for the asymptotics below, we switch from the parameters $T, c_1, \ldots , c_k$ and the window size h introduced in the following to parameters $nT, nc_1,\ldots ,nc_k$ and nh, $n \in \mathbb {N}$.

Let $\mathbf X\in \mathcal M$. The MFT is based on multiple MOSUM statistics which compare the empirical means of the observations in adjacent windows. At first consider a single window $h\in \{1,2,\ldots ,\lfloor T/2\rfloor \}$ for which we consider the time horizon $[h,T-h]$. It denotes $\lfloor \cdot \rfloor$ the floor function. For all $t\in [h,T-h]$ we set

$$\begin{aligned} D_{h,t}^{(n)} := \frac{\bar{X}_r - \bar{X}_\ell }{\hat{s}_{h,t}^{(n)}}, \end{aligned}$$

(1)

with $\bar{X}_\ell := (1/nh)\sum _{i=\lfloor nt\rfloor -nh +1}^{\lfloor nt \rfloor } X_i$ and $\bar{X}_r := (1/nh)\sum _{i=\lfloor nt\rfloor +1}^{\lfloor nt\rfloor +nh} X_i$ and further

$$\begin{aligned} (\hat{s}_{h,t}^{(n)})^2 := \frac{\hat{\sigma }_r^2 + \hat{\sigma }_\ell ^2}{nh}, \end{aligned}$$

(2)

with empirical variances being evaluated locally from the observations within the windows, i.e., $\hat{\sigma }_\ell ^2 := (1/nh)\sum _{i=\lfloor nt\rfloor -nh +1}^{\lfloor nt\rfloor } (X_i-\bar{X}_\ell )^2$ and $\hat{\sigma }_r^2 := (1/nh)\sum _{i=\lfloor nt\rfloor +1}^{\lfloor nt\rfloor +nh} (X_i -\bar{X}_r)^2$.

Simply put, $D^{(n)}_{h,t}$ is the common (unpooled) two-sample t-statistic, which at every time point compares two adjacent subsamples of sample size nh. We are interested in large deviations of $D^{(n)}_{h,t}$ from zero as these indicate a change in expectation. Shifting the window continuously in time results in càdlàg-valued step-processes $D^{(n)}:=(D^{(n)}_{h,t})_{t\in [h,T-h]}$ that take values in $(\mathcal D[h,T-h],d_{SK})$ which denotes the space of all càdlàg-functions on $[h,T-h]$ endowed with the Skorokhod topology.

The MFT is based on an approximation of the MOSUM process $D^{(n)}$ by a Gaussian process L. By letting $n\rightarrow \infty$ we show weak convergence to the limit process $L:=(L_{h,t})_{t\in [h,T-h]}$, which is a functional of a standard Brownian motion W given by

$$\begin{aligned} L_{h,t} =\frac{(W_{t+h} - W_t) - (W_t - W_{t-h})}{\sqrt{2h}}, \end{aligned}$$

(3)

see Proposition 3.1. Note that L is a Gaussian process with zero mean and unit variance. Accordingly, $D^{(n)}$ typically fluctuates around zero under the null. The process convergence enables us to pursue two ideas. First, due to continuity of the maximum operator, the convergence of the temporal maximum is preserved, i.e.

$$\begin{aligned} \max _{t\in [h,T-h]} |D_{h,t}^{(n)}| {\mathop {\longrightarrow }\limits ^{d}} \max _{t\in [h,T-h]} |L_{h,t}|, \end{aligned}$$

while ${\mathop {\longrightarrow }\limits ^{d}}$ denotes convergence in distribution. As a consequence, we can simulate a quantile of the distribution of the right hand side which is used as a rejection threshold for the statistical test. And second, again due to continuity, we can also maximize over different windows

$$\begin{aligned} M^{(n)}:=\max _{h\in H}\max _{t\in [h,T-h]} |D_{h,t}^{(n)}| {\mathop {\longrightarrow }\limits ^{d}} \max _{h\in H}\max _{t\in [h,T-h]} |L_{h,t}|, \end{aligned}$$

(4)

for any finite window set $H\subset \{1,2,\ldots ,\lfloor T/2\rfloor \}$. This allows the simultaneous application of multiple windows, which is particularly advantageous for the estimation of change points that occur on different time scales. Smaller windows are more sensitive to change points occurring in fast succession, while larger windows provide higher power when changes are small. The global maximum $M:=M^{(1)}$, with T being large, serves as the test statistic of the MFT. Again, a quantile Q of the limit distribution can be derived via simulations as, to the best of our knowledge, there is no closed formula available.

Proposition 3.1

For $\mathbf X\in \mathcal M$ with $C=\emptyset$ and $h\in \{1,2,\ldots ,\lfloor T/2\rfloor \}$ it holds in $(\mathcal D[h,T-h],d_{SK})$ as $n\rightarrow \infty$

$$\begin{aligned} D^{(n)} {\mathop {\longrightarrow }\limits ^{d}} L. \end{aligned}$$

Proof

Let W denote a standard Brownian motion. Let $\mathbf X=X_1,X_2\ldots$ with $\mu =\mathbb {E}[X_1]$ and $\sigma ^2=\mathbb {V}\!ar(X_1)$ and for $n=1,2,\ldots$ define the rescaled random walk $S^{(n)}:=(S_{t}^{(n)})_{t\in [0,T]}$ by

$$\begin{aligned} S_{t}^{(n)} := \frac{1}{\sigma \sqrt{n}} \sum _{i=1}^{\lfloor nt \rfloor } (X_i - \mu ). \end{aligned}$$

(5)

Then, by Donsker’s theorem, in $(\mathcal D[0,T], d_{SK})$ the process $S^{(n)}$ converges weakly to W as $n\rightarrow \infty$. Now we map the process $S^{(n)}$ based on the life times up to time t to a process based on the life times in the adjacent windows in $[t-h,t+h]$. For that we define the continuous map $\varphi : (\mathcal D[0,T], d_{SK})\rightarrow (\mathcal D[h,T-h],d_{SK})$ via

$$\begin{aligned} (f(t))_{t\in [0,T]} {\mathop {\longmapsto }\limits ^{\varphi }} \left( \frac{(f(t+h)-f(t)) - (f(t)-f(t-h))}{\sqrt{2h}} \right) _{t\in [h,T-h]}. \end{aligned}$$

Mapping $S^{(n)}$ via $\varphi$, continuity yields in $(\mathcal D[h,T-h],d_{SK})$ as $n\rightarrow \infty$

$$\begin{aligned} \left( \frac{\bar{X}_r - \bar{X}_\ell }{(2\sigma ^2 / nh)^{1/2}}\right) _{t} {\mathop {\longrightarrow }\limits ^{d}} (L_{h,t})_t. \end{aligned}$$

(6)

In Lemma 3.2, the consistency of the estimator $\hat{s}_{h,t}^{(n)}$ is shown i.e., in $(\mathcal D[h,T-h],d_{SK})$ we have $(\hat{s}_{h,t}^{(n)} / (2\sigma ^2 / nh)^{1/2})_t\rightarrow (1)_t$ almost surely as $n\rightarrow \infty$. This allows us to exchange the denominator in (6) with $\hat{s}_{h,t}^{(n)}$ by Slutsky’s Lemma, which finishes the proof. $\square$

Let $(\mathcal D[h,T-h],d_{\Vert \cdot \Vert })$ denote the space of all càdlàg-functions on $[h,T-h]$ endowed with the supremum norm. Analogously define $(\mathcal D[0,T],d_{\Vert \cdot \Vert })$. Note that convergence w.r.t. $d_{\Vert \cdot \Vert }$ implies convergence w.r.t. $d_{SK}$.

Lemma 3.2

For $\mathbf X\in \mathcal M$ with $C=\emptyset$, $h\in \{1,2,\ldots ,\lfloor T/2\rfloor \}$ and $\hat{s}_{h,t}^{(n)}$ given in (2) it holds in $(\mathcal D[h,T-h],d_{\Vert \cdot \Vert })$ as $n\rightarrow \infty$ almost surely

$$\begin{aligned} \left( \frac{\hat{s}_{h,t}^{(n)}}{(2\sigma ^2/nh)^{1/2}}\right) _{t} {\mathop {\longrightarrow }\limits ^{}} (1)_t. \end{aligned}$$

Proof

By construction of $\hat{s}_{h,t}^{(n)}$ it is sufficient to show that in $(\mathcal D[h,T-h],d_{\Vert \cdot \Vert })$ it holds $(\hat{\sigma }_\ell ^2)_t\rightarrow (\sigma ^2)_t$ a.s. and $(\hat{\sigma }_r^2)_t\rightarrow (\sigma ^2)_t$ a.s. as $n\rightarrow \infty$. We show the first convergence. The second follows analogously. Indeed, it is sufficient to show a.s. process convergence of the first two empirical moments $(\overline{X_\ell ^m})_t \rightarrow (\mu ^m)_t$, with $\overline{X_\ell ^m} :=(1/nh)\sum _{i=\lfloor nt\rfloor -nh +1}^{\lfloor nt \rfloor } X_i^m$ for $m=1,2$, since we can decompose $\hat{\sigma }_\ell ^2 = \overline{X_\ell ^2} - \overline{X_\ell }^2$. We show that in $(\mathcal D[0,T],d_{\Vert \cdot \Vert })$ as $n\rightarrow \infty$ a.s.

$$\begin{aligned} \left( \frac{1}{n} \sum \nolimits _{i=1}^{\lfloor nt \rfloor } X_i^m\right) _t \rightarrow \left( t \nu ^{\langle m\rangle }\right) _t, \end{aligned}$$

(7)

with $\nu ^{\langle 1\rangle }:=\mu$ and $\nu ^{\langle 2\rangle }:=\sigma ^2+\mu ^2$ denoting the first two moments of the observations such that we obtain in $(\mathcal D[h,T-h],d_{\Vert \cdot \Vert })$ as $n\rightarrow \infty$ almost surely

$$\begin{aligned} (\overline{X_\ell ^m})_t&= \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor nt\rfloor } X_i^m\right) _t - \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor n(t-h)\rfloor } X_i^m\right) _t \longrightarrow \left( \frac{t }{h}\nu ^{\langle m\rangle }\right) _t - \left( \frac{t - h }{h}\nu ^{\langle m\rangle } \right) _t \\&= (\nu ^{\langle m\rangle })_t. \end{aligned}$$

We deduce (7) from the strong law of large numbers (SLLN) using a discretization argument. For uniform convergence we first bound the suprema

$$\begin{aligned} \sup _{0\le t\le T}\left| \frac{1}{n}\sum _{i=1}^{\lfloor nt \rfloor } X_i^m - t\nu ^{\langle m\rangle }\right|&\le \sup _{0\le t\le T}\left| \frac{1}{n}\sum _{i=1}^{\lfloor nt \rfloor } X_i^m - \frac{\lfloor nt\rfloor }{n}\nu ^{\langle m\rangle }\right| + r_n\\&= \max _{j \in \{1, 2,\ldots ,nT\}}\left| \frac{1}{n}\sum _{i=1}^{j} X_i^m - \frac{j}{n}\nu ^{\langle m\rangle } \right| \! + r_n, \end{aligned}$$

with remainder $r_n := \sup _{t\in [0,T]}|t - \lfloor nt \rfloor /n| \; \nu ^{\langle m\rangle }\le (1/n) \;\nu ^{\langle m\rangle }\rightarrow 0$ as $n\rightarrow \infty$ and we need to show that also the maximum vanishes almost surely. Let $\varepsilon >0$, then by the SLLN for almost every realization we find $j_0\in \mathbb {N}$ such that $|(1/j)\sum _{i=1}^j X_i^k - \nu ^{\langle m\rangle }|<\varepsilon /2$ for all $j> j_0$ and thus

$$\begin{aligned} \max _{j \in \{1, 2,\ldots ,nT\}}\left| \frac{1}{n}\sum _{i=1}^{j} X_i^m - \frac{j}{n}\nu ^{\langle m\rangle } \right|&\le \frac{1}{n} \max _{j\le j_0}\left| \sum _{i=1}^j X_i^m -j\nu ^{\langle m\rangle }\right| \\&\quad + \frac{j}{n}\max _{j_0<j\le nT} \left| \frac{1}{j}\sum _{i=1}^j X_i^m -\nu ^{\langle m\rangle }\right| \le \varepsilon \end{aligned}$$

for n large enough, because the maximum in the first summand does not depend on n and the maximum of the second summand becomes small according to the SLLN. Since $\varepsilon$ can be chosen arbitrarily small the left hand side vanishes with probability one and (7) holds. $\square$

Relaxations of model assumptions As noted above, the assumption of i.i.d. random variables is used here for simplicity, rather than being necessary for the convergence of the maximum in Eq. (4). Technically, to establish the procedure, we made use of first, Donsker’s theorem for the proof of Proposition 3.1 and second, the SLLN to ensure consistent parameter estimation in Lemma 3.2. Both results may also hold true when the i.i.d. assumption is relaxed. For example, the identical distribution of the random variables can be relaxed by allowing a certain variability in the variances of the random variables (heteroscedasticity), as proposed in Messer et al. (2014, Lemma A.9.): letting the random variables to have constant expectation ($\mathbb {E}(X_i)=\mu$ for all $i\in \mathbb {N}$), but allowing the variances to vary slightly by assuming them to be uniformly bounded and their mean to converge $(1/n)\sum _{i=1}^n \mathbb {V}\!ar(X_i)\rightarrow \sigma ^2$ as $n\rightarrow \infty$ for some constant $\sigma ^2>0$, a functional central limit theorem was proven assuming also the Lindeberg condition for the random variables to hold true. This formulation of null elements of constant expectation is particularly useful to describe data in which certain variability in variances is observed on small time scales.

Further, also the independence assumption can be weakened assuming the random variables to form a stationary and ergodic sequence. In these models the ergodic theorem substitutes the SLLN, and versions of Donsker’s theorem are well known, see e.g., Billingsley (1999, Theorem 19.1.). In these cases, the variance $\sigma ^2$ has to be exchanged by $\rho ^2=\sigma ^2+2\sum _{i=2}^\infty \mathbb {C}ov(X_1,X_i)$ in order to account for the dependencies of the data. (Further, the assumption $\sum _{i=2}^{\infty }\Vert \mathbb {E}[X_1-\mathbb {E}[X_1] | \{X_k|k\ge i\}]\Vert <\infty$, while $\Vert \cdot \Vert$ denotes the $L^2$ norm, ensures the absolute converge of the series of covariances.) Given a consistent estimator for the true order of scaling $\sqrt{2\rho /nh}$ in the MOSUM statistic, the procedure can be adapted (see Messer et al. 2017b, Proposition 2.2., for a detailed discussion in the scenario of point processes).

Illustration of the MFT The construction of the MFT is depicted again in Eqs. (8)–(11). First, under the null hypothesis the rescaled random walk $S^{(n)}$ based on the observations $\mathbf X$ converges weakly to a standard Brownian motion W. Given h, the process $D^{(n)}$ converges to L. This convergence holds for all $h\in H$. The crucial point is that on the empirical (left) side all functionals are based on the single process $\mathbf X$, while on the limit (right) side all functionals are evaluated from a single Brownian motion W, while all mappings in (9)–(11) are continuous, such that convergence is preserved. For the simulation of the rejection threshold Q, we can therefore simulate realizations of Brownian motions, and for each realization evaluate the maximum of all functionals $\{(|L_{h,t}|)_{t\in [h,T-h]}| h\in H\}$. Taking the maximum of $D^{(n)}$ across all window sizes as a test statistic thus avoids multiple testing in the test of the null hypothesis.

$$\begin{aligned} S^{(n)}(\mathbf X)&{\mathop {\longrightarrow }\limits ^{d}} W \end{aligned}$$

(8)

$$\begin{aligned} D^{(n)}(\mathbf X)&{\mathop {\longrightarrow }\limits ^{d}} L(W) \end{aligned}$$

(9)

$$\begin{aligned} \max _t |D^{(n)}_{h,t}(\mathbf X)|&{\mathop {\longrightarrow }\limits ^{d}} \max _t |L_{h,t}(W)| \end{aligned}$$

(10)

$$\begin{aligned} \max _h \max _t |D^{(n)}_{h,t}(\mathbf X)|&{\mathop { \longrightarrow }\limits ^{d}} \max _h \max _t |L_{h,t}(W)| \end{aligned}$$

(11)

In the example in Fig. 2, the distributions of $\max _t |D_{h,t}(\mathbf X)|$ and $\max _h \max _t |D_{h,t}(\mathbf X)|$ (red) correspond closely to the distributions of their asymptotic analogues $\max _t |L_{h,t}(W)|$ and $\max _h \max _t |L_{h,t}(W)|$ (blue). Given $\alpha \in (0,1)$, we derive Q as the $(1-\alpha )$-quantile of the simulated distribution of the asymptotic quantity $\max _h \max _t L_{h,t}(W)$.

Fig. 2

Distribution of $\max _t |D_{h,t}(\mathbf X)|$ (a) and $\max _h \max _t |D_{h,t}(\mathbf X)|$ (b), red, and their asymptotic analogues $\max _t |L_{h,t}(W)|$ and $\max _h \max _t |L_{h,t}(W)|$, blue. Red distributions are derived from time series of length $T=1000$ with $\mathcal N(0,1)$-distributed random variables and a window choice of $h=80$ (a) and $H=\{80, 180, 280\}$ (b). Q denotes the $95\%$ quantile of the simulated (red) distribution of the global maximum and corresponds closely to the true $95\%$ quantile (dashed blue line) (color figure online)

In practice, this method can be well applicable, i.e., when $n=1$, but T is large, in spite of being based on asymptotic results. One only needs to choose the smallest window sufficiently large. For example, for normally distributed random variables, the pointwise distribution can be considered sufficiently close to the normal distribution for values of h of about 30 in analogy to the t-distribution (simulation results not shown). For corresponding simulation studies with gamma distributed random variables in the case of point processes, see, e.g., Messer et al. (2014).

4 The multiple filter algorithm

In Fig. 3a, the MFT is illustrated for the data taken from Fig. 1a where no change in the mean occurs. Accordingly, the global maximum M lies below Q, and the null hypothesis is not rejected. If, however, the null hypothesis is rejected, we aim at estimating the set of change points C. To that end, we adopt a heuristic algorithm, called the multiple filter algorithm (MFA) originally proposed for point processes in Messer et al. (2014) to the analysis of time series. Figure 3c, d illustrate the analysis of the data from Fig. 1b with three change points.

First, we see that M lies above Q, and the null hypothesis is rejected (panel c). The MFA then detects change point candidates separately with every individual window $h\in H$ as follows. For every $h\in H$ the MOSUM process $D^{(1)}$ is successively searched for maximizers. Start with the entire (discrete) observation region $t\in \{h,h+1,\ldots ,T-h\}$ and if the maximum lies above Q, its argument $\hat{c}_{h,1}$ is accepted as a first change point candidate. Then restrict the previous observation region by deleting the h-neighborhood $\{\hat{c}_{h,1}-h,\ldots ,\hat{c}_{h,1}+h-1\}$ of $\hat{c}_{h,1}$ and search for the next maximizer. This procedure is repeated until the remaining process lies below Q, yielding a set of change point candidates for every $h\in H$ (Fig. 3d, diamonds, two candidates for the smallest window (blue), one for the second smallest window (gray) and two for the largest window (red)). Note that it is sufficient to restrict to the discrete observation region (instead of $[h,T-h]$) since $D^{(1)}$ has step-function paths.

Fig. 3

Application of the MFA to the data in Fig. 1. a, c Processes $D^{(1)}$ for three different window sizes. d Change point candidates of the second process and their h-neighborhoods of all windows (two candidates with $h_1$ (blue), one with $h_2$ (gray) and two with $h_3$ (red)). b, e Final set of change point estimates and estimates of means (gray) compared to the true means (orange) (color figure online)

In the second step the MFA integrates the change point candidates across all windows resulting in a final set of estimates $\hat{C}$. Here we argue that large windows may be affected by subsequent change points and may therefore yield less precise estimates. Therefore, let $h_1<h_2<\cdots h_{|H|}$ be the ordered elements of H. We start with including all change point candidates referring to the smallest window $h_1$ (in Fig. 3d two blue candidates). Then, by moving to successively larger windows, we add change point estimates $\hat{c}_{h_j,i}$ of larger windows $h_j$ only if their $h_j$-neighborhood $(\hat{c}_{h_j,i}-h_j,\hat{c}_{h_j,i}+h_j)$ does not contain an already accepted change point. In Fig. 3d we update $\hat{C}$ by a third estimate resulting from the largest window $h_3$ (red). Finally, we estimate the expectation in the segments given by the estimated set of change points $\hat{C}$ (Fig. 3e).

Figure 3 illustrates the advantage of the simultaneous use of multiple windows: Smaller windows are more sensitive to fast changes (blue), while larger windows have more power when the change in expectation is small (red). The function MFT.mean() in the R package MFT (Messer et al. 2017a) performs the MFT and the corresponding MFA for a given time series.

Note that the MFA does not represent a statistical test but an algorithm that can be used after rejection of the null hypothesis in order to estimate the change points. It makes use of the fact that change point effects are only local, i.e., a given change point affects the process $D^{(n)}$ only in its h-neighborhood. This is because the process $D^{(n)}$ is 2h-dependent by construction, resulting also from local parameter estimation. As the h-neighborhood is cut out after estimation of the change point, multiple distinct crossings of the rejection threshold are a good indication of multiple change points. Accordingly, true change points did not increase the frequency of falsely detected change points in simulations (cmp. Messer et al. 2014 Section 5.1.3 and Table 2). Similar procedures were shown to yield consistent change point estimates under mild conditions in Gaussian sequence change point models (Hušková and Slabý 2001; Eichinger and Kirch 2018).

5 Robustness against changes in other parameters

In the previous sections we assumed that a change point describes a change in the expectation, implying that under the null hypothesis of no change in the expectation, no change point occurred and thus, no parameter change is observed, yielding a sequence of i.i.d. random variables under the null hypothesis.

Here we consider a situation in which a change point does not change the expectation but potentially the variance or higher order moments, while we still test the null hypothesis of no change in expectation. Interestingly, the MFT is robust against such violations of the model assumptions. More precisely we show that, given no change in expectation, the MOSUM process $D^{(n)}$ can still be approximated by a 2h-dependent Gaussian process $\widetilde{L}:=(\widetilde{L}_{h,t})_t$ with mean zero and unit variance. The only difference to the limit process L (Eq. (3)) is a small deviation in the covariance structure in the h-neighborhood of a change point. As we show in a one change point model, this is practically negligible with respect to the maximum of the MOSUM process and thus to the derivation of the rejection threshold Q.

In the following assume a one change point model $C=\{nc\}$ associated with two independent processes $\mathbf X^{[1]}$ and $\mathbf X^{[2]}$ such that the asymptotic setting is given by

$$\begin{aligned} X_{1,[1]},\ldots ,X_{nc-1,[1]}, X_{nc,[2]},\ldots ,X_{nT,[2]}. \end{aligned}$$

We explicitly assume $\mu :=\mu _{[1]}=\mu _{[2]}$ (no change in expectation), while other parameters are allowed to change. Let $\sigma _{[1]}^2:=\mathbb {V}\!ar(X_{1,[1]})$ and $\sigma _{[2]}^2:=\mathbb {V}\!ar(X_{1,[2]})$. The following Proposition 5.1 states that in $(\mathcal D[h,T-h],d_{SK})$ the MOSUM process $D^{(n)}$ converges weakly to $\widetilde{L}$ given by

$$\begin{aligned} \widetilde{L}_{h,t}&:= {\left\{ \begin{array}{ll} \frac{(W_{t+h}-W_t)-(W_t-W_{t-h})}{\sqrt{2h}}, &{} \text {if }\; |t-c|>h,\\ \frac{\sigma _{[2]}(W_{t+h}-W_c) + \sigma _{[1]}[(W_c-W_t)-(W_t-W_{t-h})]}{h\cdot s_{h,t}^{(1)}}, &{} \text {if }\; c-h\le t\le c,\\ \frac{\sigma _{[2]}[(W_{t+h}-W_t)-(W_t-W_{c})] - \sigma _{[1]}(W_{c}-W_{t-h})}{h\cdot s_{h,t}^{(1)}}, &{} \text {if }\; c<t\le c+h, \end{array}\right. } \end{aligned}$$

(12)

for a standard Brownian motion W. There $(s_{h,t}^{(n)})^2$ is given by $2\sigma _{[1]}^2/(nh)$ for $t<c-h$ and $2\sigma _{[2]}^2/(nh)$ for $t>c-h$ and for a linear interpolation within the h-neighborhood of the change point, i.e., in $t\in [c-h,c+h]$ it is

$$\begin{aligned} (s_{h,t}^{(n)})^2 = \frac{(t+h-c)\sigma _{[2]}^2 + (c-(t-h))\sigma _{[1]}^2}{n h^2}. \end{aligned}$$

(13)

The idea is that $(s_{h,t}^{(n)})^2$ approximates the asymptotic variance of the numerator $\bar{X}_r - \bar{X}_{\ell }$. We find $\widetilde{L}$ to be a Gaussian process with $\mathbb {E}[\widetilde{L}_{h,t}]=0$ and $\mathbb {V}\!ar(\widetilde{L}_{h,t})=1$ that equals L for $|t-c|>h$, i.e., outside the h-neighborhood of c. The only difference between L and $\widetilde{L}$ is a slight deviation in the covariance structure around the change point (Fig. 4b), resulting in minor differences between the individual processes L and $\widetilde{L}$ in this neighborhood that hardly affect their maximum (Fig. 4a). Further note that, if also the variance remains unchanged $\sigma _{[1]}^2 = \sigma _{[2]}^2$ (but potentially other parameters do change) then the two limit processes coincide for all $t\in [h,T-h]$.

Fig. 4

The two limit processes L (blue) and $\widetilde{L}$ (red) in and around the neighborhood of a change point in the variance at time c (a). The two processes coincide for $|t-c|>h$ and show a slight difference in the autocovariance around the change point. b compares the autocovariance of L (blue) as a function of the lag v with the simulated covariance of $\widetilde{L}$ (red) at the change point c (color figure online)

Proposition 5.1

Let $\mathbf X\in \mathcal M$ with $C=\{nc\}$ such that $c\in [h,T-h]$ and $\mu _{[1]}=\mu _{[2]}$. Then it holds in $(\mathcal D[h,T-h],d_{SK})$ as $n\rightarrow \infty$

$$\begin{aligned} D^{(n)} {\mathop {\longrightarrow }\limits ^{d}} \widetilde{L}. \end{aligned}$$

Proof

We proceed similarly to the proof of Proposition 3.1, applying Donsker’s theorem and continuous mapping to obtain the MOSUM statistic. The difference is that joint convergences w.r.t. the two underlying processes $\mathbf X^{[1]}$ and $\mathbf X^{[2]}$ are used to obtain the result concerning the compound process $\mathbf X$.

First observe that $(\sigma _{[k]} / (nh \cdot s_{h,t}^{(n)}))_{t\in [0,T]} = (\sigma _{[k]} / (h\cdot s_{h,t}^{(1)})_{t\in [0,T]}$ is continuous and does not depend on n. For $k=1,2$ denote the rescaled random walk w.r.t. $\mathbf X^{[k]}$ by $S_{[k]}^{(n)}$ (see (5)). Further define $(\widetilde{S}_{t,[k]}^{(n)})_{t\in [0,T]}$ via $\widetilde{S}_{t,[k]}^{(n)} := (\sigma _{[k]}/(nh\cdot s_{h,t}^{(n)})) S_{t,[k]}^{(n)}$. For two independent standard Brownian motions $W^{[1]}$ and $W^{[2]}$ we then obtain in $(\mathcal D[0,T]\times \mathcal D[0,T], d_{SK}\otimes d_{SK})$ as $n\rightarrow \infty$ joint convergence

$$\begin{aligned} \left( (\widetilde{S}_{t,[1]}^{(n)})_t, (\widetilde{S}_{t,[2]}^{(n)})_t\right) {\mathop {\longrightarrow }\limits ^{d}} \left( \left( \frac{\sigma _1}{h\cdot s_{h,t}^{(1)}} W_t^{[1]} \right) _{t}, \left( \frac{\sigma _2}{h\cdot s_{h,t}^{(1)}} W_t^{[2]}\right) _{t}\right) \end{aligned}$$

(14)

according to Donsker’s theorem and due to the independence of $\mathbf X^{(1)}$ and $\mathbf X^{(2)}$. We now map these pairs to the scenario of the MOSUM statistic merging the information of both processes in the neighborhood of the change point. For that we define the continuous map $\varphi : (\mathcal D[0,T]\times \mathcal D[0,T], d_{SK} \otimes d_{SK}) \rightarrow (\mathcal D[h,T-h],d_{SK})$ given by

$$\begin{aligned}&((f(t))_{t\in [0,T]},(g(t))_{t\in [0,T]})\\&\quad {\mathop {\longmapsto }\limits ^{\varphi }} \left( \begin{array}[c]{l} (f(t+h)-f(t)) - (f(t)-f(t-h))\mathbb {1}_{[h,c-h)}(t) \\ +(g(t+h)-g(c))+(f(c)-f(t)) - (f(t)-f(t-h))\mathbb {1}_{[c-h,c)}(t) \\ +(g(t+h)-g(t))-(g(t)-g(c)) - (f(c)-f(t-h))\mathbb {1}_{[c,c+h)}(t)\\ +(g(t+h)-g(t)) - (g(t)-g(t-h))\mathbb {1}_{[c+h,T-h]}(t)\\ \end{array}\right) _{t\in [h,T-h]}. \end{aligned}$$

Applying $\varphi$ to (14) yields in $(\mathcal D[h,T-h], d_{SK})$ as $n\rightarrow \infty$

$$\begin{aligned} \left( \frac{\bar{X}_r -\bar{X}_\ell }{s_{h,t}^{(n)}} \right) _t{\mathop {\longrightarrow }\limits ^{d}} (\widetilde{L}_{h,t})_t. \end{aligned}$$

(15)

To see this we exemplarily calculate the left hand side of the convergence of $\varphi (\cdot )$ for $t\in [c-h,c)$

$$\begin{aligned} \left. \varphi \left( (\tilde{S}_{t,[1]}^{(n)})_{t \in [0,T]},(\tilde{S}_{t,[2]}^{(n)})_{t \in [0,T]}\right) \right| _{t}= & {} (\widetilde{S}_{t+h,[2]}^{(n)} - \widetilde{S}_{c,[2]}^{(n)})+(\widetilde{S}_{c,[1]}^{(n)}- \widetilde{S}_{t,[1]}^{(n)})\\&- (\widetilde{S}_{t,[1]}^{(n)} - \widetilde{S}_{t-h,[1]}^{(n)}) \\= & {} \frac{\bar{X}_r - \bar{X}_\ell }{s_{h,t}^{(n)}}. \end{aligned}$$

Here we used that all $\mu$ are equal and thus, cancel out. Then $\sigma _k$ cancels out by construction of $\widetilde{S}_{t,[k]}^{(n)}$, and finally it is $s_{h,t}^{(1)}/\sqrt{n} = s_{h,t}^{(n)}$ by definition of $s^{(n)}$. For the right hand side we see by definition of $\widetilde{L}_{h,t}$ in (12) that it holds e.g., for $t\in [c-h,c)$

$$\begin{aligned}&\left. \varphi \left( \left( \frac{\sigma _1}{h\cdot s_{h,t}^{(1)}} W_t^{[1]} \right) _{t}, \left( \frac{\sigma _2}{h\cdot s_{h,t}^{(1)}} W_t^{[2]}\right) _{t} \right) \right| _t \\&\quad = \frac{\sigma _{[2]}(W_{t+h}^{[2]}-W_c^{[2]}) + \sigma _{[1]}[(W_c^{[1]}-W_t^{[1]})-(W_t^{[1]}-W_{t-h}^{[1]})]}{h\cdot s_{h,t}^{(1)}}. \end{aligned}$$

Let now $(W_t)_t$ denote a standard Brownian motion. Then we can omit the superscripts on the r.h.s. of the latter display without changing the distribution while continuity of the sample paths is preserved, which results in the maintained limit $\widetilde{L}_{h,t}$. Finally we can exchange the true order of scaling in (15) with $\hat{s}_{h,t}^{(n)}$ by Slutsky’s Lemma using Lemma 5.2. $\square$

Lemma 5.2

Let $\mathbf X\in \mathcal M$ with $C=\{nc\}$ such that $c\in [h,T-h]$ and $\mu _{[1]}=\mu _{[2]}$. Further let $\hat{s}_{h,t}^{(n)}$ be given in (2) and $s_{h,t}^{(n)}$ as in (13). Then it holds in $(\mathcal D[h,T-h],d_{\Vert \cdot \Vert })$ as $n\rightarrow \infty$ almost surely

$$\begin{aligned} \left( \frac{\hat{s}_{h,t}^{(n)}}{s_{h,t}^{(n)}}\right) _{t} {\mathop {\longrightarrow }\limits ^{}} (1)_t. \end{aligned}$$

This Lemma basically states that the local parameter estimation is consistent as long as there is no change in expectation, even if other parameters potentially change. Note that this result is an extension of Lemma 3.2; it reduces to Lemma 3.2 in the case of $\sigma ^2:=\sigma _{[1]}^2 = \sigma _{[2]}^2$.

Proof

First we decompose the true order of variance $(s_{h,t}^{(n)})^2=:s_r^2 +s_\ell ^2$ w.r.t. both window halves, i.e., for the left window we find $nh\cdot s_\ell ^2 = \sigma _1^2$ for $t<c$, $nh\cdot s_\ell ^2=\sigma _2^2$ for $t>c+h$ and it describes a linear interpolation when the window overlaps the change point, for $t\in [c,c+h]$

$$\begin{aligned} nh\cdot s_\ell ^{2}= \frac{t-c}{h}\sigma _2^2 + \frac{c-(t-h)}{h}\sigma _1^2. \end{aligned}$$

A similar decomposition for the right window yields $nh\cdot s_r^2 = \sigma _1^2$ for $t<c-h$, $nh\cdot s_r^2=\sigma _2^2$ for $t>c$ and $nh\cdot s_r^{2}= ((t+h)-c)\sigma _2^2/h + (c-t)\sigma _1^2/h$ for $t\in [c-h,c]$. By definition of the estimator $(\hat{s}_{h,t}^{(n)})^2 = (\hat{\sigma }_r^2+ \hat{\sigma }_\ell ^2)/nh$ it suffices to show that in $(\mathcal D[h,T-h],d_{\Vert \cdot \Vert })$ it holds almost surely as $n\rightarrow \infty$

$$\begin{aligned} \left( \frac{\hat{\sigma }_{\ell }^2}{nh\cdot s_\ell ^2}\right) _t \longrightarrow (1)_t \end{aligned}$$

(16)

while an analogous statement for the right window half follows in the same manner. Because $\mu :=\mu _{[1]}=\mu _{[2]}$ we find the second moment of the observations in $\mathbf X^{[k]}$ as $\nu _{[k]}^{\langle 2\rangle } :=\sigma _{[k]}^2+ \mu ^2$ for $k=1,2$. For $t\in [h,T-h]$ we define $(\nu _\ell ^{\langle 2 \rangle })_t$ via

$$\begin{aligned} \nu _\ell ^{\langle 2\rangle }&:= nh\cdot s_{\ell }^2 - \mu ^2 = {\left\{ \begin{array}{ll} \nu _{[1]}^{\langle 2\rangle } &{} \text {if }\; t< c,\\ \frac{t-c}{h} \nu _{[2]}^{\langle 2\rangle } + \frac{c-(t-h)}{h} \nu _{[1]}^{\langle 2\rangle } &{} \text {if }\; c\le t\le c+h,\\ \nu _{[2]}^{\langle 2\rangle } &{} \text {if }\; t> c+h, \end{array}\right. } \end{aligned}$$

(17)

which we understand as the true order of the second moment $\overline{X_{\ell }^2}$. We decompose $\hat{\sigma }_{\ell }^2=\overline{X_{\ell }^2} - \overline{X_{\ell }}^2$ and note that in $(\mathcal D_{[h,T-h]},d_{\Vert \cdot \Vert })$ a.s. process convergence $(\overline{X}_\ell )_t \rightarrow (\mu )_t$ follows with analogous arguments as in the proof of Lemma 3.2 (since $\mu _{[1]}=\mu _{[2]}$). Thus it remains to show process convergence of the second empirical moment $(\overline{X_{\ell }^2})_{t}\rightarrow (\nu _{\ell }^{\langle 2 \rangle })_t$ uniformly almost surely as $n\rightarrow \infty$. From (7) we know that it holds for $k=1,2$ in $(\mathcal D[0,T],d_{\Vert \cdot \Vert })$ almost surely as $n\rightarrow \infty$

$$\begin{aligned} \left( \frac{1}{n} \sum \nolimits _{i=1}^{\lfloor nt \rfloor } X_{i,[k]}^2\right) _t \rightarrow \left( t \nu _{[k]}^{\langle 2 \rangle }\right) _t. \end{aligned}$$

Representing $(\overline{X_{\ell }^2})_{t}$ accordingly as

$$\begin{aligned} (\overline{X_{\ell }^2})_{t}= & {} {\left\{ \begin{array}{ll} \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor nt\rfloor } X_{i,[1]}^2\right) _t - \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor n(t-h)\rfloor } X_{i,[1]}^2\right) _t \qquad \text {with }\; t\in (h,c),\\ \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor nt\rfloor } X_{i,[2]}^2\right) _t - \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor nc\rfloor } X_{i,[2]}^2\right) _t\\ \qquad + \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor nc\rfloor } X_{i,[1]}^2\right) _t - \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor n(t-h)\rfloor } X_{i,[1]}^2\right) _t\\ \qquad \text {with }\; t\in [c,c+h],\\ \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor nt\rfloor } X_{i,[2]}^2\right) _t - \left( \frac{1}{nh} \sum \nolimits _{i=1}^{\lfloor n(t-h)\rfloor } X_{i,[2]}^2\right) _t \qquad \text {with }\; t\in (c+h,T-h),\\ \end{array}\right. } \end{aligned}$$

gives uniform a.s. convergence to $(\nu _{\ell }^{\langle 2\rangle } )_t$ in all three subdivisions and thus also regarding the entire time horizon $[h,T-h]$ proves (16) and thus the statement of the Lemma. $\square$

Thus, in case of constant expectation, a change in the variance leads to only minor deviations of the limit process. Therefore we argue that L can be used in practice to derive the rejection threshold Q also in cases with variance changes, while the significance level is practically unchanged.

The practical negligibility of changes in the variance is also supported by the marginal behavior of the MOSUM process at the change point c when any parameters are allowed to change. It follows as $n\rightarrow \infty$

$$\begin{aligned} D^{(n)}_{h,c} - \frac{\mu _{[2]}-\mu _{[1]}}{(\sigma _{[2]}^2 + \sigma _{[1]}^2)^{1/2}}\sqrt{nh} {\mathop {\longrightarrow }\limits ^{d}} N(0,1) \end{aligned}$$

(18)

which basically states the test power of a t-test as a simple application of the Delta method. Thus, it is the (scaled) difference of the expectations that results in large values of the MOSUM process. Conversely, as long as the mean does not change, i.e., $\mu _{[2]}=\mu _{[1]}$, the MOSUM process will converge to a zero mean, unit variance Gaussian process, as stated in Proposition 5.1. Also note that in the extended case of simultaneous changes in the expectation and variance, Proposition 5.1 and Lemma 5.2 can be extended analogously (see Messer and Schneider (2017) for corresponding results in the framework of point processes). In that case, the expectation of $D^{(n)}$ locally shows a systematic deviation from zero: in the h-neighborhood of a change point, it takes the form of a hat if the variance stays constant and the form of a shark if both parameters change (compare also Bertrand 2000; Bertrand et al. 2011). In any case, the maximal expected deviation lies at the change point itself. As a consequence, the procedure is sensitive to changes in the expectation while it does not tend to falsely detect changes in other parameters.

6 Simulation example

In this section we support our theoretical findings, illustrating the performance of the MFT with respect to the sensitivity to change points in the expectation as well as its robustness to other parameter changes. Sequences of independent random variables with three change points in the expectation ($c_1,c_3,c_4$) on different time scales and one change point in the variance ($c_2$) are simulated (Fig. 5a). While the magnitude of the first change in expectation at $c_1$ is small, the other two change points in the expectation ($c_3,c_4$) occur close to each other. To stress the applicability under general distributional assumptions we use samples of normally distributed random variables (panel b) as well as gamma distributed (panel c) random variables. We apply the MFA using a 5% significance level for the statistical test. Panels b and c show temporal histograms of the number of detected change points in 1000 simulations.

Fig. 5

Number of detected change points in 1000 simulations under the alternative with expectations and variances given in a. The mean changes at $c_1=400, c_3=1200,c_4=1305$ and the variance changes at $c_2=800$. Parameters: $\mu _{[1]}=0.5, \mu _{[2]}=0.85, \mu _{[3]}=0.85, \mu _{[4]}=1.9, \mu _{[5]}=1, \sigma ^2_{[1]}=\sigma ^2_{[2]}=0.25, \sigma ^2_{[3]}=\sigma ^2_{[4]}=\sigma ^2_{[5]}=1$, $T=2000$, $H=\{100,150,200,250,300\}$. All random variables are independent and normal (b) or gamma-distributed (c)

The results support again the three properties of the MFT. First, the histograms for the numbers of detected change points are highly similar for both simulated distributions, illustrating the applicability of the MFT under general distributional assumptions. Second, all three change points in the expectation are correctly detected in 98.3% (96.9%) in the normal (gamma) case, where we call a change point correctly detected if it is located in the $h_1/2=50$-neighborhood of an estimated change point. The change at $c_1$ was correctly detected in 98.6% (97.8%) of the cases, the change at $c_3$ in 99.9% (99.8%) and the change at $c_4$ in 99.8% (99.3%) of the simulations, supporting sensitivity to changes in the expectation on multiple time scales. Third, the percentage of simulations with falsely detected change points is 4.6% (5.0%) for the normal (gamma) distributed random variables, which does not exceed the $5\%$ significance level. The variance change point was falsely detected in only five (six) out of the 1000 simulations.

Interestingly, the robustness of the MFT to changes in variance and other parameters also allows extensions of the MFT to the detection of other change points than the expectation, for example in the variance. To that end the MFT could be extended in a straightforward manner by suitable modification of the MOSUM statistic, which would then compare estimates of the empirical variances within the two windows by including the information of the estimated changes in expectation (compare Albert et al. 2017, for the respective method in point processes).

In summary, these simulations support the theoretical results and suggest good performance and practical applicability of the multiple filter test.

7 Discussion

We proposed a method that extends the MFT for change point detection in point processes (Messer et al. 2014, 2017b) to sequences of events. The MFT contains a test for the null hypothesis of constant expectation and, in case of rejection of the null, an algorithm for the detection of change points in the expectation. It is based on multiple MOSUM processes depending on different window sizes. Both, the test as well as the algorithm depend on a rejection threshold which is derived in a two-step procedure of first, showing weak process convergence of all involved MOSUM processes (see Proposition 3.1) and second a Monte Carlo simulation of the distribution of the global maximum over all corresponding limit processes.

Technically, the translation from point processes to sequences of random variables involved introducing the procedure to the inverted point process. For a given window size h we evaluate a fixed number of 2h observations at each time point, rather than a random number of observations. We are now able to evaluate real-valued sequences of events, in contrast to the point process framework, where positivity of the data was assumed. We proposed a local, i.e., time dependent, estimator for the process parameters in order to account for alternatives that contain changes in the expectation: local estimation results in consistent parameter estimation at those points in time where the corresponding window of the MOSUM process does not overlap a change point in the expectation. Particularly, on a functional level consistency of the estimator was shown for sequences of events where no changes in the expectation occur, while change points in other parameters may exist, see Lemma 5.2.

The present MFT has three important benefits. First, it does not require specific parametric assumptions but works for sequences of independent and identically distributed random variables. For the theoretical results of Sect. 3, sufficient conditions were given that also allow for relaxations of these assumptions. This is because the MFT is based on a functional central limit theorem, which is known to hold true for i.i.d. random variables and also for relaxations of the assumption of independence or identical distribution. Second, change points occurring on different time scales can be detected. This is achieved by simultaneous evaluation of all MOSUM processes. The adequate derivation of the rejection threshold is a consequence of the fact that all processes are continuous functionals of the same underlying rescaled random walk. Third, our theoretical findings support the robustness of the MFT against changes in parameters other than the expectation. This is stated in Proposition 5.1 where we showed that the limit of the MOSUM process is a Gaussian process with zero mean and unit variance as long as the expectation remains unchanged while other parameters are allowed to change. We also discussed the sensitivity of the procedure to change points in the expectation (see Eq. (18)): the asymptotic marginal of the MOSUM statistic at a change point is normal and its mean is given as a scaled difference of the expectations of the populations. The three benefits of the MFT were also supported in simulations. For practical applicability, the procedure is made accessible in the R-package MFT (Messer et al. 2017a).