1 Introduction

Varying coefficient models proposed by Hastie and Tibshirani (1993) are fashionable nonparametric fitting techniques. A salient feature of varying coefficient models is that the response is linear in the covariates, but the regression coefficients are smooth nonparametric functions which depend on certain covariates such as the measurement time. Thus, varying coefficient models can be regarded as a natural extension of multiple linear regression models. Due to its flexibility to explore the dynamic features, many procedures had been proposed to estimate the varying coefficient functions. Wu et al. (1998) obtained kernel estimators of the coefficient functions by minimizing local least-squares criterion and established its asymptotic normality. Combined with a polynomial spline, Huang et al. (2002, 2004) considered the estimation of the coefficient functions by employing the least-squares method. Noh and Park (2010) developed a regularized estimation procedure for variable selection by linearizing the group smoothly clipped absolute deviation penalty. Other related literature includes Wang et al. (2008), Wang and Xia (2009) and Wang and Lin (2015).

An important feature of longitudinal data is that subjects are often measured repeatedly over a given period, which results in possible correlations between repeated measures. Thus, it is important to account for the correlation to improve the efficiency of statistical inference. However, the mentioned references above did not consider the correlations, which will result in a great loss of efficiency. Although it is an interesting topic to estimate the covariance functions in the analysis of longitudinal data, we will meet some challenges. The reasons are as follows. (i) Longitudinal data are frequently collected at irregular and possibly subject-specific time points, which leads to different dimensions of the covariance matrix for each subject. (ii) It involves more parameters to be estimated in the covariance matrix, and the positive definiteness of the covariance matrix also needs to be assured. To overcome these difficulties, the modified Cholesky decomposition approach (Pourahmadi 1999) is developed to decompose the covariance matrix, which has been demonstrated to be effective and attractive. Recently, Ye and Pan (2006) constructed several sets of parametric generalized estimating equations by utilizing the modified Cholesky decomposition. In order to relax the parametric assumption in Ye and Pan (2006), Leng et al. (2010) constructed the joint partially linear mean–covariance model based on the B-spline basis approximation. Liu and Li (2015) studied a class of marginal models with time-varying coefficients for longitudinal data by using the modified Cholesky decomposition.

However, these mentioned articles are focused on longitudinal mean regression. Quantile regression has become a powerful complement to the mean regression. Its main merits include the following two aspects. On the one hand, it can offer a more complete description of the entire distribution of the response variable. On the other hand, it does not require specification of the error distribution, and thus it is a robust regression approach. So far, quantile regression has become a widely used technique for analyzing longitudinal data. Tang and Leng (2011) applied the empirical likelihood (Owen 2001) to account for the within-subject correlations, which yields more efficient estimators than the conventional quantile regression. Leng and Zhang (2014) proposed a new quantile regression approach to account for correlations through combining multiple sets of unbiased estimating equations. Tang et al. (2015) extended this method to composite quantile regression. Yuan et al. (2017) used a similar strategy to construct a new weighted quantile regression model with longitudinal data. However, the above literature only considered some commonly used working correlation structures (e.g., compound symmetry (CS) and first-order autoregressive [AR(1)]). When the specified working correlation structure is far from the true one, it seriously affects the estimation efficiency. However, it is difficult to justify a correct working correlation matrix in quantile regression with longitudinal data (Leng and Zhang 2014; Fu and Wang 2016). This paper focuses on longitudinal varying coefficient models and proposes a data-driven approach to estimate the covariance matrix through the modified Cholesky decomposition. The proposed method does not need to specify a working correlation structure to improve the efficiency of statistical inference, which is more flexible than the existing methods.

The confidence interval construction for varying coefficient functions is also an interesting issue. Empirical likelihood (Owen 2001) is a popular nonparametric inference method for the interval estimation. The confidence region based on empirical likelihood has many advantages. On the one hand, it does not require estimating either the unknown error density function or any covariance matrix. On the other hand, it does not impose prior constraints on the region shape, and the shape and orientation of confidence regions are determined entirely by the data. Xue and Zhu (2007) applied the local empirical likelihood technique to construct confidence intervals for varying coefficient functions, which is more accurate than the normal approximation and bootstrap methods. However, they did not consider the possible correlation between repeated measures, which will result in rough confidence intervals. Meanwhile, they only consider mean regression rather than quantile regression. Under the framework of longitudinal quantile regression, we propose an efficient smoothed empirical likelihood procedure to construct more accurate confidence intervals for varying coefficient functions.

The rest of this paper is organized as follows. In Sect. 2, we propose the smoothed estimating equations for varying coefficient functions and establish its asymptotic theories. Furthermore, we define a empirical log-likelihood ratio function and prove that its asymptotic distribution is a standard Chi-squared under mild conditions. Section 3 discusses the bandwidth choice and reports the simulation results. In Sect. 4, the proposed approach is illustrated by a longitudinal progesterone data. Section 5 ends the article with a discussion. Finally, the proofs of the main results are provided in “Appendix.”

2 Methodology

We consider the varying coefficient model with longitudinal data

$$\begin{aligned} {Y_{ij}} = \varvec{X}_i^\mathrm{T}\left( {{t_{ij}}} \right) \varvec{\beta } \left( {{t_{ij}}} \right) + {\varepsilon _i}\left( {{t_{ij}}} \right) ,\quad i = 1,\ldots ,n,\quad j = 1,\ldots ,{m_i}, \end{aligned}$$
(1)

where \(Y_{ij}=Y_i\left( {{t_{ij}}} \right) \), \({\varvec{X}_i}\left( {{t_{ij}}} \right) = {\left( {{X_{i1}}\left( {{t_{ij}}} \right) ,\ldots , {X_{ip}}\left( {{t_{ij}}} \right) } \right) ^\mathrm{T}}\), \({t_{ij}} \in {\mathscr {R}}\), \(\varvec{\beta } \left( t \right) = {\left( {{\beta _1} \left( t \right) ,\ldots ,{\beta _p}\left( t \right) } \right) ^\mathrm{T}}\), \(\beta _r \left( t \right) \) are smooth functions of t and \(\beta _r \left( t \right) \in {\mathscr {R}} \) for all \(r=1,\ldots ,p\), \({\varepsilon _i}\left( {{t}} \right) \) are stochastic processes and independent of \({\varvec{X}_i}\left( t \right) \). In this paper, we assume that the design points \(\left\{ {{t_{ij}},i = 1,\ldots ,n,j = 1,\ldots ,{m_i}} \right\} \) are random and iid according to an underlying density function \(f_T\left( \cdot \right) \) with respect to the Lebesgue measure, and \(S(f_T)\) is the support of \(f_T\). We assume that the random error \(\varepsilon _{ij}={\varepsilon _i}\left( {{t_{ij}}} \right) \) satisfies \(P\left( {{\varepsilon _i}\left( {{t_{ij}}} \right) < 0\mid t_{ij}} \right) = \tau \) and with an unspecified density function \(f_{ij} \left( \cdot \right) \). Then it is easy to show that

$$\begin{aligned} E\left\{ {\tau - I\left( {{Y_{ij}} - \varvec{X}_i^\mathrm{T}\left( {{t_{ij}}} \right) \varvec{\beta } \left( {{t_{ij}}} \right) } < 0\right) \mid t_{ij}} \right\} = 0, \end{aligned}$$
(2)

where \(I\left( \cdot \right) \) is a indicator function. Note that the random errors are correlated within the same subject but independent across the subjects.

2.1 Efficient estimating equations for regression coefficients \({\varvec{\beta }}\left( t \right) \)

Based on the local constant approximation, the standard quantile regression estimator \( \varvec{\hat{\beta }}\left( {t;h_1} \right) \) of \(\varvec{\beta } \left( t \right) \) can be obtained by minimizing

$$\begin{aligned} \sum \limits _{i = 1}^n {\sum \limits _{j = 1}^{{m_i}} {{\rho _\tau }\left( {{Y_{ij}} - \varvec{X}_i^\mathrm{T} \left( {{t_{ij}}} \right) \varvec{\beta } \left( t \right) } \right) {K_{h_1}}\left( {t - {t_{ij}}} \right) } } \end{aligned}$$

with respect to \(\varvec{\beta } \left( t \right) \), where \({K_{h_1}}\left( \cdot \right) = K\left( {{ \cdot \big / {h_1}}} \right) \), \(K( \cdot )\) is a kernel function and \({h_1}\) is a bandwidth, \({\rho _\tau }\left( u \right) = u\left\{ {\tau - I\left( {u < 0} \right) } \right\} \) is the quantile loss function. And equivalently, the resulting estimator \(\varvec{{\hat{\beta }}} \left( {t;{h_1}} \right) \) is the solution of the following estimating equations

$$\begin{aligned} \sum \limits _{i = 1}^n {\varvec{X}_i^\mathrm{T} {\varvec{\mathrm{K}}_i}\left( t;h_1 \right) {\psi _\tau }\left( {{\varvec{Y}_i} - {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) } = \varvec{0}, \end{aligned}$$
(3)

where \({\varvec{\mathrm{K}}_i}\left( t;h_1 \right) = \hbox {diag}\left( {{K_{h_1}}\left( {t - {t_{i1}}} \right) ,\ldots ,{K_{h_1}}\left( {t - {t_{i{m_i}}}} \right) } \right) \), \({\varvec{X}_i} = \left( {\varvec{X}_i}\left( {{t_{i1}}} \right) ,\ldots ,\right. \left. {\varvec{X}_i}\left( {{t_{i{m_i}}}} \right) \right) ^\mathrm{T}\), \({\varvec{Y}_i} = {\left( {{Y_{i1}},\ldots ,{Y_{i{m_i}}}} \right) ^\mathrm{T}}\), \({\psi _\tau }\left( u \right) = \tau - I\left( {u < 0} \right) \) is the quantile score function and

$$\begin{aligned} {\psi _\tau }\left( {{\varvec{Y}_i} \!-\! {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) = {\left\{ {{\psi _\tau }\left( {{Y_{i1}} \!-\! \varvec{X}_i^\mathrm{T}\left( {{t_{i1}}} \right) \varvec{\beta } \left( t \right) } \right) ,\ldots ,{\psi _\tau }\left( {{Y_{i{m_i}}}\! -\!\varvec{X}_i^\mathrm{T}\left( {{t_{i{m_i}}}} \right) \varvec{\beta } \left( t \right) } \right) } \right\} ^\mathrm{T}}. \end{aligned}$$

Estimating equations (3) are obtained under the independent working model; hence, the efficiency of the estimators \(\varvec{{\hat{\beta }}} \left( {t;{h_1}} \right) \) can be improved if the within correlations are incorporated. To incorporate the correlation within subjects, we can use the estimating equations that take the form

$$\begin{aligned} \sum \limits _{i = 1}^n {\varvec{X}_i^\mathrm{T}{\varvec{\mathrm{K}}_i}\left( t;h_1 \right) \varvec{\varSigma } _i^{ - 1}{\psi _\tau }\left( {{\varvec{Y}_i} - {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) } = \varvec{0}, \end{aligned}$$
(4)

where \({\varvec{\varSigma } _i} = \hbox {Cov}\left( {{\psi _\tau }\left( {{\varvec{\varepsilon } _i}} \right) } \right) \) and \({\varvec{\varepsilon } _i} = {\left( {{\varepsilon _{i1}},\ldots ,{\varepsilon _{i{m_i}}}} \right) ^\mathrm{T}}\). But we cannot directly obtain the estimator of \(\varvec{\beta } \left( t \right) \) by solving (4) because the estimating equations include the unknown covariance matrix \(\varvec{\varSigma _i}\).

In this paper, we estimate \({\varvec{\varSigma } _{i}}\) via the modified Cholesky decomposition. That is, \({\varvec{\varSigma } _{i}} = {\varvec{L}_{i}}{\varvec{D}_{i}}\varvec{L}_{i}^\mathrm{T},\) where \(\varvec{L}_{i}\) is a lower triangular matrix with 1’s on its diagonal and \({\varvec{D}_{i}}= \hbox {diag}\left( {d _{i1}^2,\ldots ,d _{i{m_i}}^2} \right) \). Let \(\varvec{e}_i=\varvec{L}_i^{-1}{{\psi _\tau }\left( {{\varvec{\varepsilon } _{i}}} \right) }= {\left( {{e_{i1}},\ldots ,{e_{i{m_i}}}} \right) ^\mathrm{T}}\) with \(e_{ij}={e_{i}\left( t_{ij }\right) }\), we have

$$\begin{aligned} {{\psi _\tau }\left( {{\varepsilon _{ij}}} \right) }= \sum \limits _{k = 1}^{j - 1} {{l_{ijk }}} {e_{ik}} + {e_{ij}}, \end{aligned}$$
(5)

where \(l_{ijk}\) are the below diagonal entries of \(\varvec{L}_{i}\). The sum \(\sum \nolimits _{k = 1}^{j - 1} \) is interpreted as zero when \(j=1\) throughout this paper. Note that \(E\left( {{\varvec{e}_{i}}} \right) = \varvec{0}\) and \(\hbox {Cov}\left( {{\varvec{e}_{i}}} \right) = {\varvec{D}_{i}}= \hbox {diag}\left( {d _{i1}^2,\ldots ,d _{i{m_i}}^2} \right) \) for \(i=1,\ldots ,n\). Thus we know that \(e_{ij}, j=1,\ldots ,m_i\) are uncorrelated and \(d _{ij}^2=d ^2\left( t_{ij }\right) \) is called as innovation variance for \(j=1,\ldots ,m_i\). The merit of this decomposition is that the parameters \(l_{ijk }\) and \( {d _{ij}^2} \) are unconstrained. In the spirit of Pourahmadi (1999), we construct the following regression models to estimate \(l_{ijk }\) and \( {d _{ij}^2} \)

$$\begin{aligned} {l_{ijk}} =\varvec{w}_{ijk }^\mathrm{T}{\varvec{\gamma } }, {d _{ij}^2} =g\left( t_{ij }\right) , \end{aligned}$$
(6)

where \({\varvec{\gamma } } = {\left( {{\gamma _{1}},\ldots ,{\gamma _{q}}} \right) ^\mathrm{T}}\), \(g\left( t\right) \) is an unknown smooth function of t, and \(\varvec{w}_{ijk }\) is usually taken as a polynomial of time difference \(t_{ij}-t_{ik}\). Some authors applied similar parametric models to parsimoniously parameterize the covariance matrix \(\varvec{\varSigma }_i\) when considering the modified Cholesky decomposition (Ye and Pan 2006; Zhang and Leng 2012). Compared with parametric models, we relax the parametric assumption and propose a nonparametric model to estimate innovation variance \( {d _{ij}^2} \), which reduce the risk of model misspecification. Eyeballing (6), we can use regression models to describe the within-subject correlation among repeated measures. Furthermore, model-based analysis of \(l_{ijk }\) and \( {d _{ij}^2} \) permits more accessible statistical inference.

Now we give specific details to estimate \(l_{ijk }\) and \( {d _{ij}^2} \). Based on \(\varvec{{\hat{\beta }}} \left( {t;{h_1}} \right) \), we can obtain the estimated residuals

$$\begin{aligned} {{{\hat{\varepsilon }} }_{ij}} = {Y_{ij}} - \varvec{X}_i^\mathrm{T}\left( {{t_{ij}}} \right) \varvec{{\hat{\beta }}} \left( {{t_{ij}};{h_1}} \right) ,\quad i = 1,\ldots ,n,\quad j = 1,\ldots ,{m_i}. \end{aligned}$$
(7)

From (5)–(7), we can obtain the estimator \(\varvec{{\hat{\gamma }}}\) of \(\varvec{\gamma }\) by using the GEE method

$$\begin{aligned} \sum \limits _{i = 1}^n \varvec{V}_i^\mathrm{T}{\varvec{{\tilde{e}}}_{i}} =\varvec{0}, \end{aligned}$$

where \({\varvec{ \tilde{e}}_{i}} = \varvec{L}_{i}^{ - 1}{{\psi _\tau }\left( {{{\hat{\varepsilon }} _i}} \right) }=({{\tilde{e}}_{i1}},\ldots ,{{\tilde{e}}_{im_i}})^\mathrm{T}\) with \({{\tilde{e}}_{ij}} = {\psi _\tau }\left( {{{\hat{\varepsilon }} _{ij}}} \right) - \sum \nolimits _{k = 1}^{j - 1} {{l_{ijk}}{{\tilde{e}}_{ik}}} \) and \(\varvec{V}_i^\mathrm{T}={{\partial \varvec{{\tilde{e}}}_i^\mathrm{T}} \big / {\partial \varvec{\gamma } }}\) is a \(q \times m_i\) matrix with the first column zero and the jth \(j\ge 2\) column \({{\partial {{\tilde{e}}_{ij}}} \big / {\partial {\varvec{\gamma }}}} = - \sum \nolimits _{k = 1}^{j - 1} {\left[ {{\varvec{w}_{ijk }}{{\tilde{e}}_{ik }} + {l_{ijk }}{{\partial {{\tilde{e}}_{ik }}} \big / {\partial {\varvec{\gamma }}}}} \right] } \). Then, we have \({{\hat{l}}_{ijk}} =\varvec{w}_{ijk }^\mathrm{T}{\varvec{{\hat{\gamma }} }}\). Please note that \(E\left( {e_{ ij }^2} \right) = \hbox {Var}\left( {{e_{ ij }}} \right) + {\left[ {E\left( {{e_{ ij }}} \right) } \right] ^2}=\hbox {Var}\left( {{e_{ ij }}} \right) = d_{ ij }^2\) due to \(E\left( {{\varvec{e}_{i}}} \right) = \varvec{0}\) and \(\hbox {Cov}\left( {{\varvec{e}_i}} \right) = {\varvec{D}_i}\). Thus, a local polynomial regression technique can be used to estimate the nonparametric function \(g(\cdot )\) (Fan and Yao 1998). Specifically, we can obtain the estimator \({\hat{d}}^2\left( t \right) ={\hat{a}}\) by minimizing the following weighted least-squares problem

$$\begin{aligned} \left( {{\hat{a}},{\hat{b}}} \right) =\mathop {\arg \min }\limits _{a,b} \sum \limits _{i = 1}^n {\sum \limits _{j = 1}^{{m_i}} {{{\left\{ {{\hat{e}}_{ij}^2 - a - b\left( {{t_{ij}} - t} \right) } \right\} }^2}} } {K_{{h_2}}}\left( {t - {t_{ij}}} \right) , \end{aligned}$$

where \({{\hat{e}}_{ij}} = {\psi _\tau }\left( {{{\hat{\varepsilon }} _{ij}}} \right) - \sum \nolimits _{k = 1}^{j - 1} {{{\hat{l}}_{ijk}}{{\hat{e}}_{ik}}} \). Therefore, we can obtain \(\hat{\varvec{\varSigma } _{i}} = \hat{\varvec{ L}_{i}}\hat{\varvec{ D}_{i}}\hat{\varvec{ L}}_{i}^\mathrm{T},\) where \(\varvec{{\hat{L}}}_{i}\) is an \(m_i \times m_i\) lower triangular matrix with 1’s on its diagonal and the below diagonal entries of \(\hat{\varvec{ L}}_{i}\) are \({\hat{l}}_{ijk}= \varvec{w}_{ijk }^\mathrm{T}\hat{\varvec{\gamma } }\) and \(\hat{\varvec{ D}}_{i}= \hbox {diag}\left( {{\hat{d}} _{i1}^2,\ldots ,{\hat{d}} _{i{m_i}}^2} \right) \) with \({\hat{d}} _{ij}^2= {\hat{d}}^2 \left( {{t_{ij}}} \right) \).

Replacing \({\varvec{\varSigma } _{i}} \) by \({\hat{\varvec{\varSigma }} _{i}} \), estimating equations (4) can be rewritten as

$$\begin{aligned} \sum \limits _{i = 1}^n {\varvec{X}_i^\mathrm{T} {\varvec{\mathrm{K}}_i}\left( t;h_1 \right) \varvec{{\hat{\varSigma }}} _i^{ - 1}{\psi _\tau }\left( {{\varvec{Y}_i} - {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) } =\varvec{0}. \end{aligned}$$
(8)

However, proposed estimating equations (8) are neither smooth nor monotone. In order to overcome the calculation difficulty, we approximate \({\psi _\tau }\left( \cdot \right) \) by a smooth function \({\psi _{\tau {h}} }\left( \cdot \right) \) based on the idea of Wang and Zhu (2011). Define \(G\left( x \right) = \int _{u < x} {K_1\left( u \right) } \hbox {d}u\) and \({G_h}\left( x \right) = G\left( {{x \big / h}} \right) \), where \(K_1\left( \cdot \right) \) is a kernel function and h is a positive bandwidth parameter. Then, we approximate \({\psi _\tau }\left( \cdot \right) \) by \({\psi _{\tau {h} }}\left( \cdot \right) =\tau -1+{G_{h}}\left( \cdot \right) \). Therefore, based on the approximation, estimating equations (8) can be replaced by the following smoothed estimating equations

$$\begin{aligned} \sum \limits _{i = 1}^n {\varvec{X}_i^\mathrm{T}{\varvec{\mathrm{K}}_i}\left( t;h_1 \right) \varvec{{\hat{\varSigma }}} _i^{ - 1}{\psi _{\tau {h}}}\left( {{Y_i} - {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) } =\varvec{0}, \end{aligned}$$
(9)

where \({\psi _{\tau {h}}}\left( {{Y_i} - {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) =\left( {\psi _{\tau {h} }}\left\{ {{Y_{i1}} -\varvec{X}_i^\mathrm{T}\left( {{t_{i1}}} \right) \varvec{\beta } \left( t \right) } \right\} ,\ldots ,{\psi _{\tau {h} }}\left\{ {Y_{im_i}} -\varvec{X}_i^\mathrm{T}\left( {{t_{im_i}}} \right) \right. \right. \left. \left. \varvec{\beta } \left( t \right) \right\} \right) ^\mathrm{T}\). We assume that \( \varvec{\bar{\beta }} \left( t;h_1 \right) \) is the solution of estimating equations (9).

We assume that \(t_0\) is an interior point of \(S(f_T)\). Next, we derive the asymptotic distribution of \(\varvec{{\hat{\gamma }}}\) and establish the large sample properties of \({{\hat{d}}}^2\left( t_0 \right) \) and \(\varvec{{\bar{\beta }}} \left( {t_0;h_1} \right) \) at a fixed point \(t_0\). Let \({\rho _\varepsilon }\left( {{t_0}} \right) = \mathop {\lim }\nolimits _{\delta \rightarrow 0} E\left\{ {\left[ {{\psi _\tau }\left( {{\varepsilon _1}\left( {{t_0} + \delta } \right) } \right) } \right] \left[ {{\psi _\tau }\left( {{\varepsilon _1}\left( {{t_0}} \right) } \right) } \right] } \right\} \), \({\eta _{lr}}\left( {{t_0}} \right) = E\left[ {{X_{il}}\left( {{t_{ij}}} \right) {X_{ir}}\left( {{t_{ij}}} \right) \left| {{t_{ij}} = {t_0}} \right. } \right] \), \({\mu _j} = \int {{u^j}} K\left( u \right) \hbox {d}u\) and \({\nu _j} = \int {{u^j}} {K^2}\left( u \right) \hbox {d}u\). In this paper, \(\dot{d} (t)\) and \(\ddot{d} (t)\) stand for the first and second derivative of d(t) respectively.

Theorem 1

Let \(\varvec{\gamma }_{0}\) be the true value of \(\varvec{\gamma }\). Under conditions (C1)–(C8) stated in “Appendix,” the proposed estimator \(\varvec{{\hat{\gamma }}}\) is \(\sqrt{n} \)-consistent and asymptotically normal, that is,

$$\begin{aligned} \sqrt{n} \left( {\varvec{{\hat{\gamma }}} - {\varvec{\gamma } _0}} \right) \mathop \rightarrow \limits ^d N\left( {\varvec{0},{\varvec{\varXi }^{ - 1}}\varvec{\varGamma } {\varvec{\varXi }^{ - 1}}} \right) , \end{aligned}$$

where \(\mathop \rightarrow \limits ^d\) means the convergence in distribution, \(\varvec{\varXi }= \mathop {\lim }\nolimits _{n \rightarrow \infty } \frac{1}{n}\sum \nolimits _{i = 1}^n {\varvec{V}_i^\mathrm{T}} {\varvec{V}_i}\) and \(\varvec{\varGamma } = \mathop {\lim }\limits _{n \rightarrow \infty } \frac{1}{n}\sum \nolimits _{i = 1}^n {\varvec{V}_i^\mathrm{T}{\varvec{D}_i}} {\varvec{V}_i}\).

In order to obtain the asymptotic result of \({{{\hat{d}}}^2}\left( t \right) \), we rewrite (5) as follows:

$$\begin{aligned} {\psi _\tau }\left( {{\varepsilon _{ij}}} \right) = \sum \limits _{k = 1}^{j - 1} {{l_{ijk}}{d_{ik}}{\varsigma _{ik}}} + {d_{ij}}{\varsigma _{ij}}, \end{aligned}$$
(10)

where \({e_{ij}} = {d_{ij}}{\varsigma _{ij}}\), \(E\left( {{\varsigma _{ij}}|{t_{ij}}} \right) = 0\) and \({{\hbox {Var}}}\left( {{\varsigma _{ij}}|{t_{ij}}} \right) = 1\).

Theorem 2

Under the same set of conditions as in Theorem 1, together with \(Nh_2 \rightarrow \infty \) as \(n\rightarrow \infty \) and \(\lim {\sup _{n \rightarrow \infty }}N{h_2^5} < \infty \), we have

$$\begin{aligned}&\sqrt{Nh_2} \left\{ {{{{\hat{d}}}^2}\left( t_0 \right) - {d^2}\left( t_0 \right) - \frac{1}{2}{\mu _2}{h_2^2}{{\ddot{d}}^2}\left( t_0 \right) } \right\} \\&\quad \mathop \rightarrow \limits ^d N\left( {0,\frac{{{\nu _0}}}{{f_T\left( t_0 \right) }}\mathop {\lim }\limits _{n \rightarrow \infty }\frac{1}{N}\sum \limits _{i = 1}^n {\sum \limits _{j = 1}^{{m_i}} {E\left[ {{{\left( {\varsigma _{ij}^2 - 1} \right) }^2}\left| {{t_{ij}} = t_0} \right. } \right] {d^4}\left( t_0 \right) } } } \right) . \\ \end{aligned}$$

Let \({b_l}\left( {{t_0}} \right) = {\mu _2}h_1^2\sum \nolimits _{r = 1}^p \left[ {{\dot{\beta }} _r}\left( {{t_0}} \right) {{\dot{\eta }} _{lr}}\left( {{t_0}} \right) {f_T}\left( {{t_0}} \right) + \frac{1}{2}{\ddot{\beta }_r}\left( {{t_0}} \right) {\eta _{lr}}\left( {{t_0}} \right) {f_T}\left( {{t_0}} \right) + {{\dot{\beta }} _r}\left( {{t_0}} \right) \right. \left. {\eta _{lr}}\left( {{t_0}} \right) {\dot{f}_T}\left( {{t_0}} \right) \right] \) and \(\varvec{b}\left( {{t_0}} \right) = {\left( {{b_1}\left( {{t_0}} \right) ,\ldots ,{b_p}\left( {{t_0}} \right) } \right) ^\mathrm{T}}\). Let \({\hat{\sigma }} ^{jj'}\) be the \((j,j')\)th element of \(\varvec{{\hat{\varSigma }}}_i^{-1}\) and \(\varvec{\varPhi }\left( {{t_0}} \right) \) be given in condition (C7).

Theorem 3

Suppose that conditions (C1)–(C10) hold, we have

$$\begin{aligned} \sqrt{N{h_1}} \left( {\varvec{{\bar{\beta }}} \left( {{t_0};{h_1}} \right) - \varvec{\beta } \left( {{t_0}} \right) } -\varvec{B}\left( {{t_0}} \right) \right) \mathop \rightarrow \limits ^d N\left( {\varvec{0},\varvec{\varOmega }_1^{ - 1}\left( {{\varvec{\varOmega }_2} + {\varvec{\varOmega }_3}} \right) \varvec{\varOmega }_1^{ - 1}} \right) , \end{aligned}$$

where \(\varvec{B}\left( {{t_0}} \right) = { {{f_T^{ - 1}}\left( {{t_0}} \right) } }{\varvec{\varPhi }^{ - 1}}\left( {{t_0}} \right) \varvec{b}\left( {{t_0}} \right) \), \({\varvec{\varOmega }_1} = {\lim _{n \rightarrow \infty }}\frac{1}{N}\sum \nolimits _{i = 1}^n \sum \nolimits _{j = 1}^{{m_{i}}} \sum \nolimits _{j' = 1}^{{m_i}} {f_T}\left( t_0 \right) {{{\hat{\sigma }}}^{jj'}}{f_{ij'}} \left( 0 \right) \varvec{\varPhi }\left( {{t_0}} \right) \),

$$\begin{aligned} \begin{array}{ll} {\varvec{\varOmega }_2} =&{} {\lim _{n \rightarrow \infty }}\frac{1}{N}\sum \limits _{i = 1}^n \sum \limits _{j = 1}^{{m_{i}}} {\nu _0}{f_T}\left( {{t_0}} \right) \\ &{}\times \left[ \sum \limits _{j' = 1}^{{m_i}}{ {{{\left( {{{{\hat{\sigma }} }^{jj'}}} \right) }^2}\tau \left( {1 - \tau } \right) + \sum \limits _{{j_1} \ne {j_2}} {{{{\hat{\sigma }} }^{j{j_1}}}{{{\hat{\sigma }} }^{j{j_2}}}{\rho _\varepsilon }\left( {{t_0}} \right) } } } \right] \varvec{\varPhi }\left( {{t_0}} \right) , \\ {\varvec{\varOmega }_3} =&{} {\lim _{n \rightarrow \infty }}\frac{1}{N}\sum \limits _{i = 1}^n \sum \limits _{{j_1} \ne {j_2}} {h_1}f_T^2\left( {{t_0}} \right) \\ &{}\times \left[ {\sum \limits _{j' = 1}^{{m_i}} {{{{\hat{\sigma }} }^{{j_1}j'}}{{{\hat{\sigma }} }^{{j_2}j'}}\tau \left( {1 - \tau } \right) + \sum \limits _{j'' \ne j'''} {{{{\hat{\sigma }} }^{{j_1}j''}}{{{\hat{\sigma }} }^{{j_2}j'''}}{\rho _\varepsilon }\left( {{t_0}} \right) } } } \right] \varvec{\varPhi }\left( {{t_0}} \right) . \\ \end{array} \end{aligned}$$

2.2 Empirical likelihood method

To construct the empirical likelihood ratio function for \(\varvec{\beta } \left( t \right) \), based on Owen (2001) and Qin and Lawless (1994), we introduce an auxiliary random vector as follows \({\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) = {\varvec{X}_i^\mathrm{T}{\varvec{\mathrm{K}}_i}\left( t;h_1 \right) \varvec{{\hat{\varSigma }}} _i^{ - 1}{\psi _{\tau {h}}}\left( {{Y_i} - {\varvec{X}_i}\varvec{\beta } \left( t \right) } \right) }.\) Note that \(\left\{ {{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) :1 \le i \le n} \right\} \) are independent. Invoking (2), it can be shown that \(E\left\{ {\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) \right\} =o(1)\) when \({\varvec{\beta } \left( t \right) }\) is the true value.

Let \(p_1,\ldots ,p_n\) be nonnegative numbers satisfying \(\sum \nolimits _{i = 1}^n {{p_i}} = 1\), where \({p_i} = {p_i}\left( t \right) , i=1,\ldots ,n\). Using such information, a natural block empirical log-likelihood ratio for \( {\varvec{\beta } \left( t \right) }\) is defined as

$$\begin{aligned} l\left( \varvec{\beta }\left( t \right) \right) = - 2\max \left\{ {\sum \limits _{i = 1}^n {\log \left( {n{p_i}} \right) \left| {{p_i} \ge 0, \sum \limits _{i = 1}^n {{p_i}} = 1,\sum \limits _{i = 1}^n {{p_i}{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) } = 0} \right. } } \right\} .\nonumber \\ \end{aligned}$$
(11)

Tang and Leng (2011) pointed out that for finite sample, existence of a solution to empirical likelihood for a given \(\varvec{\beta }\left( t \right) \) requires that 0 is inside the convex hull of the points \(\left\{ {{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) ,i = 1,\ldots ,n} \right\} \). By the Lagrange multiplier method, the optimal value for \(p_i\) is given by

$$\begin{aligned} {p_i} = {n^{ - 1}}{\left\{ {1 + \varvec{\lambda }^\mathrm{T}{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) } \right\} ^{ - 1}}, \end{aligned}$$
(12)

where \(\lambda \) is a p-dimensional Lagrange multiplier satisfying

$$\begin{aligned} \sum \limits _{i = 1}^n {\frac{{{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) }}{{1 + \varvec{\lambda }^\mathrm{T}{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) }}} = 0. \end{aligned}$$
(13)

By (11) and (12), \(l\left( \varvec{\beta }\left( t \right) \right) \) can be represented as

$$\begin{aligned} l\left( \varvec{\beta }\left( t \right) \right) =2\sum \limits _{i = 1}^n {\log \left\{ {1 + \varvec{\lambda }^\mathrm{T}{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) } \right\} } \end{aligned}$$
(14)

with \(\varvec{\lambda }\) satisfying (13). In our numerical studies, we can employ the modified Newton–Raphson algorithm of Chen et al. (2002) to obtain the estimator of \(\varvec{\lambda }\). We further define the maximum empirical likelihood (EL) estimator of \(\varvec{\beta }\left( t \right) \) as

$$\begin{aligned} \varvec{{\hat{\beta }}}\left( t \right) _\mathrm{EL}=\mathop {\arg \min }\limits _{\varvec{\beta }\left( t \right) \in \mathscr {R}^p}l\left( \varvec{\beta }\left( t \right) \right) . \end{aligned}$$

Remark 1

From (14) and (A.20), we can prove that the maximum empirical likelihood estimator \(\varvec{{\hat{\beta }}}\left( t \right) _\mathrm{EL}\) is asymptotically the solution of \(\sum \nolimits _{i = 1}^n {{\varvec{Z}_{ih}}\left( {\varvec{\beta } \left( t \right) } \right) } = \varvec{0}\). Let

$$\begin{aligned} \varvec{{\hat{V}}}\left( {{t}} \right) = \frac{1}{{N{h_1}}}\sum \limits _{i = 1}^n {\varvec{X}_i^\mathrm{T}{\varvec{\mathrm{{K}}}_i}\left( {{t};{h_1}} \right) \varvec{{\hat{\varSigma }}} _i^{ - 1}{\varvec{\tilde{\varLambda }} _i}{\varvec{X}_i}} , \end{aligned}$$

and

$$\begin{aligned} {\varvec{{\tilde{\varLambda }} }_i}= & {} \hbox {diag}\left\{ h^{ - 1}{K_1}\left[ {{{\left( {{Y_{i1}} - {\varvec{X}_i}{{\left( {{t_{i1}}} \right) }^\mathrm{T}}\varvec{\beta } \left( t \right) } \right) } \Big / {{h}}}} \right] ,\right. \\&\dots , \left. h^{ - 1}{K_1}\left[ {{{\left( {{Y_{i{m_i}}} - {\varvec{X}_i}{{\left( {{t_{i{m_i}}}} \right) }^\mathrm{T}}\varvec{\beta } \left( t \right) } \right) } \Big / {{h}}}} \right] \right\} . \end{aligned}$$

If we assume that the matrix \(\varvec{{\hat{V}}}\left( {{t}} \right) \) is invertible together with (14), then we can obtain

$$\begin{aligned} \begin{array}{l} \varvec{{\hat{\beta }}}\left( t \right) _\mathrm{EL} - \varvec{\beta } \left( {{t}} \right) = \varvec{{\hat{V}}}\left( {{t}} \right) ^{-1}\left\{ {\frac{1}{{N{h_1}}}\sum \limits _{i = 1}^n {\varvec{X}_i^\mathrm{T}{\varvec{\mathrm{{K}}}_i}\left( {{t};{h_1}} \right) \varvec{{\hat{\varSigma }}} _i^{ - 1}{\psi _{\tau h} }\left( {{\varvec{Y} _i-\varvec{X}_i \varvec{\beta }(t)}} \right) } } \right\} \\ ~~~~~~~~~~~~~~~~~~~~~~~~~~~~+ {o_p}\left( {{{\left( {N{h_1}} \right) }^{{{ - 1}/ 2}}}} \right) . \end{array} \end{aligned}$$

Then we can see that the leading term is that of \( \varvec{\bar{\beta }} \left( t;h_1 \right) \), seeing the proof of Theorem 3 in “Appendix.” In other words, the \(\varvec{{\hat{\beta }}}\left( t \right) _\mathrm{EL}\) is asymptotically equivalent to the \( \varvec{\bar{\beta }} \left( t;h_1 \right) \).

Theorem 4

Suppose that conditions (C1)–(C10) hold. If \(\varvec{\beta }\left( t_0 \right) \) is the true parameter, then \(l\left( {\varvec{\beta } \left( {{t_0}} \right) } \right) \mathop \rightarrow \limits ^d \chi _p^2\), where \(\chi _p^2\) is the standard Chi-squared distribution with p degrees of freedom.

Remark 2

By Theorem 4, we can use the test statistic \(l\left( {\varvec{\beta } \left( {{t_0}} \right) } \right) \) to obtain confidence regions for \({\varvec{\beta } \left( {{t_0}} \right) }\). Specifically, we define \(\left\{ {\varvec{\beta } \left( t \right) :l\left( {\varvec{\beta } \left( t \right) } \right) \le \chi _{1 - \alpha }^2\left( p \right) } \right\} \) as the EL confidence regions for \({\varvec{\beta } \left( {{t_0}} \right) }\), where \({\chi _{1 - \alpha }^2\left( p \right) }\) is the \((1 - \alpha )\)th quantile of \(\chi _p^2\).

In addition, we can apply the profile empirical log likelihood ratio test statistic to obtain the confidence region of the subset of \({\varvec{\beta } \left( {{t_0}} \right) }\). Let \(\varvec{\beta } \left( {{t_0}} \right) \! \!=\! {\left( {{\varvec{\beta } ^{(1)}}\left( {{t_0}} \right) ^\mathrm{T}\!,{\varvec{\beta } ^{(2)}}\left( {{t_0}} \right) ^\mathrm{T}} \right) ^\mathrm{T}}\), where \(\varvec{\beta } ^{(1)}\left( {{t_0}} \right) \) and \(\varvec{\beta } ^{(2)}\left( {{t_0}} \right) \) are \(p_1 \times 1\) and \((p-p_1) \times 1\) vectors, respectively. If we are interested in testing \({H_0}:{\varvec{\beta } ^{(1)}}\left( {{t_0}} \right) = \varvec{b}\left( {{t_0}} \right) \), where \( \varvec{b}\left( {{t_0}} \right) \) is some known \(p_1 \times 1\) vector. The profile log likelihood ratio test statistic is defined as

$$\begin{aligned} {\bar{l}}\left( {\varvec{b}\left( {{t_0}} \right) } \right) = l\left( {\varvec{b}\left( {{t_0}} \right) ,{\varvec{{\tilde{\beta }} }^{(2)}}\left( t \right) } \right) - l\left( {{\varvec{{\hat{\beta }} }^{(1)}}\left( t \right) ,{\varvec{{\hat{\beta }} }^{(2)}}\left( t \right) } \right) , \end{aligned}$$

where \({{\varvec{{\tilde{\beta }} }^{(2)}}\left( t \right) }\) minimizes \(l\left( {\varvec{b}\left( {{t_0}} \right) ,{\varvec{\beta } ^{(2)}}\left( t \right) } \right) \) with respect to \({{\varvec{\beta } ^{(2)}}\left( t \right) }\), and \({\left( {{\varvec{{\hat{\beta }} }^{(1)T}}\left( t \right) ,{\varvec{{\hat{\beta }} }^{(2)T}}\left( t \right) } \right) ^\mathrm{T}}\) are the EL estimators.

Corollary 1

Under the conditions of Theorem 4 and \({H_0}:{\varvec{\beta } ^{(1)}}\left( {{t_0}} \right) =\varvec{b}\left( {{t_0}} \right) \), we have \({\bar{l}}\left( {\varvec{b}\left( {{t_0}} \right) } \right) \mathop \rightarrow \limits ^d \chi _{p_1}^2\) as \(n\rightarrow \infty \).

Remark 3

According to Corollary 1, we can construct the confidence region for \({{\varvec{\beta } ^{(1)}}\left( {{t_0}} \right) }\), namely \(\left\{ {\varvec{b}\left( t \right) :l\left( {\varvec{b}\left( t \right) } \right) \le \chi _{1 - \alpha }^2\left( p_1 \right) } \right\} \).

3 Simulation studies

In this section, we conduct simulation studies to investigate the finite sample performance of the proposed method. In the following examples, we fix the kernel function to be the Epanechnikov kernel, that is, \(K(u) = 0.75{(1 - {u^2})_ + }\). We apply the fivefold cross-validation to choose the optimal bandwidths \(h_1\) and \(h_2\). Taking an example of the \(h_1\), let \(T - {T^v}\) and \({T^v}\) be the cross-validation training and test set respectively for \(v=1,\ldots ,5\), where T is the full dataset. Note that in model (1), the observations are dependent within each subject. To retain this dependence structure, we treat the observations in each subject as a block. For each \(h_1\) and v, we find the estimator \(\varvec{{\hat{\beta }}}(t;h_1,v)\) of \(\varvec{\beta }(t)\) using the training set \(T - {T^v}\); then, we can form the fivefold cross-validation criterion as

$$\begin{aligned} \hbox {CV}\left( {{h_1}} \right) = \sum \limits _{v = 1}^5 {\sum \limits _{\left( {{Y_{ij}},{\varvec{X}_{ij}}} \right) \in {T^v}} {{\rho _\tau }\left( {{Y_{ij}} - \varvec{X}_i^\mathrm{T}\left( {{t_{ij}}} \right) \varvec{{\hat{\beta }}} \left( {t_{ij};h_1,v} \right) } \right) } }. \end{aligned}$$

By using the grid search method, we find \({h_{1\mathrm{opt}}} = {\min _{h_1}}\hbox {CV}\left( h_1 \right) \). Based on the idea of Wang and Zhu (2011), we smooth the quantile score function by the following second-order (\(\nu =2\)) Bartlett kernel

$$\begin{aligned} K_1\left( u \right) = \frac{3}{{4\sqrt{5} }}\left( {1 - {{{u^2}} \big / 5}} \right) I\left( {\left| u \right| \le \sqrt{5} } \right) . \end{aligned}$$

Wang and Zhu (2011) had proved that the smoothed approach is robust to the bandwidth h. Thus, we fix \(h=n^{-0.4}\) which satisfies the theoretical requirement \( n{h^{2\nu }} \rightarrow 0\) with \(\nu =2\).

In addition, we compare the following estimation approaches. (i) The conventional quantile regression estimator \(\varvec{{\hat{\beta }}}\left( t;h_1 \right) \) without considering possible correlations denoted as \(\varvec{{\hat{\beta }}}_\mathrm{qr}\). (ii) The estimator proposed by Xue and Zhu (2007) denoted as \(\varvec{{\hat{\beta }}}_\mathrm{ls}\). (iii) The proposed estimator \(\varvec{{\bar{\beta }}}\left( t;h_1 \right) \) denoted as \(\varvec{{\hat{\beta }}}_\mathrm{pr}\). (iv) The proposed empirical likelihood (EL) estimator \(\varvec{{\hat{\beta }}}\left( t \right) _\mathrm{EL}\) denoted as \(\varvec{{\hat{\beta }}}_\mathrm{el}\). For \(\varvec{{\hat{\beta }}}_\mathrm{ls}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\), we construct confidence regions/intervals based on the estimated empirical likelihood (EL) as suggested in Sect. 2.2; for \(\varvec{{\hat{\beta }}}_\mathrm{qr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{pr}\), we construct confidence regions/intervals based on the normal approximation (NA). To assess the performance of the empirical likelihood, we make a comparison between the EL and NA in terms of coverage accuracies and average widths of the confidence intervals. In the following simulation studies, we focus on \(\tau =0.5\) and 0.75, and choose \(n=50\) and 200 representing moderate and large sample sizes. The number of simulation replications is set to 500.

Example 1

For simplicity, we consider model (1) with a time-independent covariate \( \varvec{X}_{i}={\left( {{X_{i1}},{X_{i2}}} \right) ^\mathrm{T}}\), where \(\varvec{X}_{i}\) follows a multivariate normal distribution \(N(\varvec{0},\varvec{\varSigma }_{\varvec{x} })\) with \((\varvec{\varSigma }_{\varvec{x} })_{k,l}=0.5^{|k-l|}\) for \(1\le k,l\le 2\). The coefficient functions are given by \({\beta _1}\left( t \right) = 6-0.2t\), \({\beta _2}\left( t \right) = - 4 + {{{{\left( {20 - t} \right) }^3}} \big / {2000}}\). Each subject is measured \(m_i\) times with \(m_i-1 \sim \hbox {Binomial}(9,0.8)\), which results in different numbers of repeated measurements for each subject. Here, we define \({\varepsilon _{ij }} ={\xi _{ij}}- {c_\tau } \), and \(c_\tau \) is the \(\tau \)th quantile of the random error \(\xi _{ij}\), which implies the corresponding \(\tau \)th quantile of \(\varepsilon _{ij}\) is zero. Meanwhile, we consider two error distributions of \(\varvec{\xi }_{i}=\left( \xi _{i1},\ldots ,\xi _{im_i} \right) ^\mathrm{T}\) for assessing the robustness and effectiveness of the proposed method.

Case 1: correlated normal error, \({\varvec{\xi }}_i\), is generated from a multivariate normal distribution \(N(\varvec{0},\varvec{\varXi }_i)\), where \(\varvec{\varXi }_i\) will be listed later.

Case 2: \({\varvec{\xi }}_i\) is generated from a multivariate t-distribution with degree 3 and covariance matrix \(\varvec{\varXi }_i\).

We construct the covariance matrix \(\varvec{\varXi }_i\) of \({\varvec{\varepsilon } _i} \) as \({\varvec{\varXi }_i} = \varvec{\varDelta }_i^{ - 1}{\varvec{B}_i}{\left( {\varvec{\varDelta }_i^\mathrm{T}} \right) ^{ - 1}}\), where \(\varvec{B}_i\) is an \(m_i \times m_i\) diagonal matrix with the jth element \({{\sin \left( {\pi {t_{ij}}} \right) } \big / 3} + 1.5\) and \(\varvec{\varDelta }_i \) is a unit lower triangular matrix with (j, k) element \(-\delta _{j,k}^{(i)}\)\((k<j)\), \(\delta _{j,k}^{(i)} = 0.3 + 0.6\left( {{t_{ij}} - {t_{ik}}} \right) \) and \(t_{ij} \sim U(0,1)\). Similar to Zhang and Leng (2012), we take the covariate in model (6) as \({\varvec{w}_{ijk }} = {\left\{ {1,{t_{ij}} - {t_{ik}},{{\left( {{t_{ij}} - {t_{ik }}} \right) }^2},{{\left( {{t_{ij}} - {t_{ik }}} \right) }^3}} \right\} ^\mathrm{T}}\).

Example 2

The coefficient functions are given by \({\beta _1}\left( t \right) = \cos \left( {2\pi t} \right) \), \({\beta _2}\left( t \right) = 4t\left( {1 - t} \right) \). We set the covariance matrix as \( {\varvec{\varXi }_i} = \varvec{D}_i^{{1 \big / 2}}\varvec{R}\left( \rho \right) \varvec{D}_i^{{1 \big / 2}}\), \({\varvec{D}_i} = \hbox {diag}\left( {\sigma _{i1}^2,\ldots ,\sigma _{i{m_i}}^2} \right) \), with \(\sigma _{ij}^2 = \sigma \left( t_{ij}\right) \), where

$$\begin{aligned} \sigma \left( t \right) = \left\{ \begin{array}{ll} \left| {50{t^2} - 2} \right| ,&{}~~~0 \le t \le 0.3 \\ \left| {2t} \right| ,&{}~~~0.3< t \le 0.6 \\ \left| {4t} \right| ,&{}~~~0.6 < t \le 1 \\ \end{array} \right. \end{aligned}$$

In addition, \(\varvec{R}\left( \rho \right) \) is AR(1) or compound symmetry structure with correlation coefficient \(\rho =0.9\). Other settings are the same as that in Example 1.

Table 1 Simulation results of the bias, SD, estimated coverage probabilities (CP) and average lengths (AL) for different methods with \(n=50, \tau =0.5\) at \(t_0=0.2,0.7\) in Example 1
Full size table
Table 2 Simulation results of the bias, SD, estimated coverage probabilities (CP) and average lengths (AL) for different methods with \(n=50,\tau =0.75\) at \(t_0=0.2,0.7\) in Example 1
Full size table
Table 3 Simulation results of the bias, SD, estimated coverage probabilities (CP) and average lengths (AL) for different methods with \(\tau =0.5\) at \(t_0=0.7\) in Example 2
Full size table
Table 4 Simulation results of the bias, SD, estimated coverage probabilities (CP) and average lengths (AL) for different methods with \(\tau =0.75\) at \(t_0=0.7\) in Example 2
Full size table
Fig. 1
figure 1

The sample standard deviations of different methods at \(\tau =0.5\) and \(\tau =0.75\) with \(n=50\) in Example 1. Here “ls” is the estimator proposed by Xue and Zhu (2007); “qr” is the conventional quantile regression estimator \(\varvec{\hat{\beta }}\left( t;h_1 \right) \) without considering possible correlations; “pr” stands for the proposed estimator \(\varvec{\bar{\beta }}\left( t;h_1 \right) \)

Full size image

Tables 1, 2, 3 and 4 give the biases, the standard deviations (SD), estimated coverage probabilities (CP) and average lengths (AL) of 95% confidence intervals for different methods at \(\tau =0.5\) and 0.75. Tables 2 and 4 only list the results of \(\varvec{{\hat{\beta }}}_\mathrm{qr}\), \(\varvec{{\hat{\beta }}}_\mathrm{pr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\) at \(\tau =0.75\). The reason is that there is no comparison between the least-squares estimator and the quantile estimation at \(\tau =0.75\). From the four tables, we can obtain the following findings. (1) All methods yield asymptotic unbiased estimators, since the corresponding biases are small for the large sample size \(n=200\). (2) For the point estimation, \(\varvec{\hat{\beta }}_\mathrm{pr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\) have similar performances for all settings due to similar biases and standard deviations. In other words, the \(\varvec{{\hat{\beta }}}_\mathrm{pr}\) is asymptotically equivalent to the \(\varvec{{\hat{\beta }}}_\mathrm{el}\), which is consistent with our theory. (3) For the interval estimation, it is easy to find that \(\varvec{{\hat{\beta }}}_\mathrm{el}\) has the shortest confidence intervals and achieves the highest empirical coverage probabilities among all methods. Thus, the proposed empirical likelihood method \(\varvec{{\hat{\beta }}}_\mathrm{el}\) significantly improves the accuracy of the confidence intervals. Finally, Fig. 1 depicts the sample standard deviations of different methods at \(\tau =0.5\) and 0.75 in Example 1, and we can see that \(\varvec{\hat{\beta }}_\mathrm{pr}\) has the smallest sample standard deviations.

Overall, the simulation results show that the proposed estimators \(\varvec{{\hat{\beta }}}_\mathrm{pr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\) generally work well and outperform other existing methods.

4 Real data analysis

In this section, we illustrate the proposed method by analyzing a longitudinal progesterone data (Zhang et al. 1998). The dataset used here consists of 492 observations of progesterone level within a menstrual cycle from 34 women clinical participants. Zheng et al. (2013) constructed robust parametric mean-covariance regression model to analyze this dataset. Here we consider the following quantile varying coefficient model

$$\begin{aligned} Q\left( { {{Y_{ij}}} |{\varvec{X}_i}\left( {{t_{ij}}} \right) } \right)= & {} {\beta _0}\left( {{t_{ij}}} \right) + {X_{i1}}\left( {{t_{ij}}} \right) {\beta _1}\left( {{t_{ij}}} \right) + {X_{i2}}\left( {{t_{ij}}} \right) {\beta _2}\left( {{t_{ij}}} \right) ,\quad i=1,\ldots ,34;\\&\quad j=1,\ldots ,m_i, \end{aligned}$$

where \(Q\left( Y_{ij}|{\varvec{X}_i}\left( t_{ij} \right) \right) \) is the \(\tau \)th conditional quantile of \(Y_{ij}\) given \({\varvec{X}_i}\left( t_{ij} \right) \). Here \(X_{i1}\) and \(X_{i2}\) represent patient’s age and body mass index, \(t_{ij} \) is taken as the repeated measurement time, and the log-transformed progesterone level is defined as the response \(Y_{ij}\). Then \({\beta _0}\left( t \right) \) stands for the intercept, and \({\beta _1}\left( t \right) \) and \({\beta _2}\left( t \right) \) describe the effects of woman’s age and body mass index on the progesterone level at time t. Before implementing estimation procedures, we normalize all predictor variables and rescale the repeated measurement time \(t_{ij}\) into interval [0,1]. In this real data analysis, we consider conventional quantile regression estimator \(\varvec{{\hat{\beta }}}_\mathrm{qr}\) and the proposed estimation approaches \(\varvec{{\hat{\beta }}}_\mathrm{pr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\) at quantile levels \(\tau = 0.25\) and \(\tau =0.5\). For \(\varvec{{\hat{\beta }}}_\mathrm{qr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{pr}\), we use normal approximation to construct the confidence intervals, and the corresponding standard error is calculated by the bootstrap resampling method. The confidence intervals of \(\varvec{{\hat{\beta }}}_\mathrm{el}\) are constructed by the empirical likelihood method. For covariance model (6), we take the covariate \({\varvec{w}_{ijk }}\) as \({\varvec{w}_{ijk }} = {\left\{ {1,{t_{ij}} - {t_{ik}},{{\left( {{t_{ij}} - {t_{ik }}} \right) }^2},{{\left( {{t_{ij}} - {t_{ik }}} \right) }^3}} \right\} ^\mathrm{T}}\).

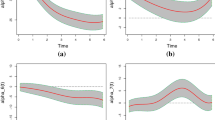
Figure 2 displays the estimated varying coefficient functions and their \(95\%\) confidence intervals for \(\tau =0.25\) and \(\tau =0.5\). For the estimated values, there is little difference for \(\varvec{{\hat{\beta }}}_\mathrm{pr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\), which has been confirmed by simulations given in Sect. 3. So we do not display the estimated curves of \(\varvec{{\hat{\beta }}}_\mathrm{el}\) in Fig. 2. Obviously, the effects of AGE and BMI are insignificant for all methods due to the large standard errors. These results are consistent with that of Zheng et al. (2013). Eyeballing Fig. 3, it is clear that \(\varvec{{\hat{\beta }}}_\mathrm{el}\) performs best among all methods because it has the shortest widths of confidence intervals. This indicates that the proposed estimation procedure is more efficient.

5 Conclusion and discussion

This paper considers robust GEE analysis for varying coefficient quantile regression models with longitudinal data based on the modified Cholesky decomposition. Asymptotic normalities for the estimators of the coefficient functions and the parameters in the decomposition of covariance matrix are established. Smoothed quantile score estimating equations are proposed to facilitate computation. We also developed block empirical likelihood-based inference procedures for varying coefficient functions to improve the accuracy of interval estimation. Simulations and an real data analysis have showed that the proposed methods are clear superior to other existing methods.

Fig. 2
figure 2

Estimated nonparametric curves and their \(95\%\) confidence intervals of different methods at \(\tau = 0.25\) and \(\tau = 0.5\). The red and black solid lines stand for the estimated values of \(\varvec{\hat{\beta }}_\mathrm{qr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{pr}\). The red and black dotted lines represent \(95\%\) confidence intervals of \(\varvec{\hat{\beta }}_\mathrm{qr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{pr}\). The black dashed lines represent \(95\%\) confidence intervals of \(\varvec{\hat{\beta }}_\mathrm{el}\)

Full size image
Fig. 3
figure 3

Average lengths of \(95\%\) confidence intervals for different methods at \(\tau = 0.25\) and \(\tau = 0.5\). The red solid lines, black dotted lines and black dashed lines represent average interval lengths of \(\varvec{\hat{\beta }}_\mathrm{qr}\), \(\varvec{{\hat{\beta }}}_\mathrm{pr}\) and \(\varvec{{\hat{\beta }}}_\mathrm{el}\) respectively

Full size image

This paper does not prove that the proposed method is more efficient than the conventional quantile approach which does not deal with the within-subject correlation among repeated measures over time. The main reason is that we cannot guarantee covariance model (6) is always correct. In practice, all models are wrong since no one knows which model is optimal for estimating \(l_{ijk}\) and \(d^2_{ij}\). Although theoretical results about estimation efficiency cannot be established in this article, the efficiency of our method is investigated by simulations and real data analysis, which indicates that our method is more useful in practice. Recently, Li (2011) utilized the nonparametric kernel technique to estimate the within-subject covariance matrix. There is no model assumption to estimate the covariance matrix, and thus his method is robust against misspecification of covariance models. Furthermore, he proved that the proposed nonparametric covariance estimation is uniformly consistent. The semiparametrical efficiency of mean regression coefficients is also established. However, he only focused on mean regression. Therefore, nonparametric covariance estimation procedures for quantile regression should be developed to estimate the covariance matrix \(\varvec{\varSigma }_i\) involved in formula (6), but this is beyond the scope of this paper. We will focus on the study of these aspects in the future.