1 Introduction

When comparing the survival times from two independent groups (\(j=1,2\)), the Mann–Whitney effect is an intuitive measure; see e.g. Koziol and Jia (2009). In a classical survival setting with continuous life-time distributions and random censoring, it is given by the probability \(P(T_{1} > T_{2})\) that a random subject from group \(j=1\) (with survival time \(T_1\)) survives longer than a randomly chosen person from group \(j=2\) (with survival time \(T_2\)). In case of uncensored data, this effect reduces to the well-known Wilcoxon functional underlying the nonparametric Wilcoxon–Mann–Whitney test. Depending on the field of application, it is also known as nonparametric treatment effect (e.g. Brunner and Munzel 2000), stress–strength characteristic (e.g. Kotz et al. 2003) or probabilistic index (e.g. Thas et al. 2012). Moreover, in case of diagnostic tests it has a direct interpretation as the area under the corresponding ROC curve, see e.g. Lange and Brunner (2012), Pauly et al. (2016) and Zapf et al. (2015) as well as Zhou et al. (2002) for more details on diagnostic accuracy measures. The Mann–Whitney effect is often estimated by the c-index for concordance (e.g. Koziol and Jia 2009). As pointed out by Acion et al. (2006), the Mann–Whitney effect is “a simple, clinically relevant, and robust index” and thus “an ideal effect measure”, see also Kieser et al. (2013). The same still holds true in case of survival outcomes that may be subject to independent random censoring, see e.g. the glorification of the c-index in Hess (2010) or Dunkler et al. (2010). An R-package for a general Wilcoxon–Mann–Whitney test was propagated in De Neve et al. (2014).

In the present paper, we face the practically relevant situation where tied data are often inevitable. Thus, to take ties appropriately into account, we use a generalized definition of the Mann–Whitney effect: \(p=P(T_{1} > T_{2}) + \frac{1}{2} P(T_{1} = T_{2})\), also known as ordinal effect size measure in case of complete data (Ryu and Agresti 2008; Konietschke et al. 2012). As an alternative to the log-rank test in group-sequential designs, Brückner and Brannath (2016) analysed the average hazard ratio which is related to p. They describe it as an “alternative effect parameter in situations with non-proportional hazards, where the hazard ratio is not properly defined”.

Recently, a related effect measure, the so-called win ratio (for prioritized outcomes), has been investigated considerably by several authors (Pocock et al. 2012; Rauch et al. 2014; Luo et al. 2015; Abdalla et al. 2016; Bebu and Lachin 2016 as well as Wang and Pocock 2016). It is given by the odds of the Mann–Whitney effect p, i.e. \(w = {p}/{(1-p)}\), also referred to as the odds of concordance; see Martinussen and Pipper (2013) for a treatment in the context of a semiparametric regression model. In our situation, p and w describe the probability that a patient of group 1 survives longer than a patient of group 2. That is, \(p > 1/2\), or equivalently \(w > 1\), implies a protective survival effect for group 1. Note that until now, ties have been excluded for estimating these quantities which particularly led to the recent assessment of Wang and Pocock (2016) that “we caution that the win ratio method should be used only when the amount of tied data is negligible”.

In this paper, we propose and rigorously study different statistical inference procedures for both parameters p and w in a classical survival model with independent random censoring, even allowing for ties in the data. While several authors (e.g. Nandi and Aich 1994; Cramer and Kamps 1997; Kotz et al. 2003, and references therein) have considered inference for p under specific distributional assumptions, we here focus on a completely nonparametric approach, not even assuming continuity of the data. Apart from confidence intervals for p and w, this also includes one- and two-sided test procedures for the null hypothesis of no group effect (tendency) \(H_0^p\,{:}\,\{p = 0.5 \} = \{w = 1 \}\). In the uncensored case, this is also called the nonparametric Behrens–Fisher problem, see e.g. Brunner and Munzel (2000) and Neubert and Brunner (2007). To this end, the unknown parameters p and w are estimated by means of normalized versions of Kaplan–Meier estimates. These are indeed their corresponding nonparametric maximum likelihood estimates, see Efron (1967) as well as Koziol and Jia (2009) for the case of continuous observations. Based on their asymptotic properties, we derive asymptotically valid tests and confidence intervals. These may be regarded as extensions of the Brunner–Munzel test Brunner and Munzel (2000) to the censored data case. Since, for small sample sizes, the corresponding tests may lead to an invalid \(\alpha \)-level control (e.g. Medina et al. 2010 or Pauly et al. 2016 without censoring), we especially discuss and analyse two different resampling approaches (bootstrapping and permuting) to obtain better small sample performances.

The resulting tests are innovative in several directions compared to other existing procedures for the two-sample survival set-up:

  1. 1.

    We focus on the null hypothesis \(H_0^p\) of actual interest. Before, only the more special null hypothesis \(H_0^S\,{:}\,\{S_1 = S_2 \}\) of equal survival distributions between the two groups has been investigated, see e.g. Efron (1967), Akritas and Brunner (1997) and Akritas (2011). Corresponding one-sided testing problems (for null hypotheses involving distribution functions) based on the related stochastic precedence were treated in Arcones et al. (2002) and Davidov and Herman (2012). Instead, our procedures will not only assess the similarity of two survival distributions but also quantify the degree of deviation by confidence intervals for meaningful parameters.

  2. 2.

    The more complex null \(H_0^p\) has so far only been studied in the uncensored case; see e.g. Janssen (1999), Brunner and Munzel (2000), De Neve et al. (2013), Chung and Romano (2016a), Pauly et al. (2016) and the references cited therein. The present focus on the effect size p while allowing for survival analytic complications is achieved by utilizing empirical process theory applied to appropriate functionals.

  3. 3.

    We do not rely on the (elsewhere omnipresent) assumption of existing hazard rates. Instead, we adjust for ties by using normalized versions of the survival function and the Kaplan–Meier estimator (leading to mid-ranks in the uncensored case). This more realistic assumption of ties in the observations accounts for a phenomenon which is oftentimes an intrinsic problem by study design. Therefore, a methodology for continuous data (even for only testing \(H_0^S\)) should not be applied. Notable exceptions for the combination of survival methods and discontinuous data are provided in Akritas and Brunner (1997) and Brendel et al. (2014) where the hypothesis \(H_0^S\) is tested.

  4. 4.

    Finally, small sample properties of inference procedures relying on the asymptotic theory are greatly improved by applications of resampling techniques. These utilized resampling techniques are shown to yield consistent results even in the case of ties. Thereof, the permutation procedure succeeds in being even finitely exact in the case of exchangeable survival data in both sample groups; see e.g. Lehmann and Romano (2010), Good (2010), Pesarin and Salmaso (2010), Pesarin and Salmaso (2012), and Bonnini et al. (2014) for the classical theory of permutation tests. In this perspective, the present paper not only states the first natural extension of point estimates for p to tied survival data but especially introduces the first inference procedures for \(H_0^p\) (tests and confidence intervals) with rigorous consistency proofs. The latter have formerly not even been known in the continuous survival case. An early reference for applications of permutation techniques in survival analysis is Neuhaus (1993) who considered extensions of the log-rank test; see Neuhaus (1994) for a treatment of tied data and Brendel et al. (2014) for further generalizations. As an alternative method, we will also examine a pooled bootstrap approach. A textbook overview of permutation techniques applied in the survival context is given in Chapter 9 of Pesarin and Salmaso (2010). See also Basso et al. (2009) who treated permutation tests for stochastic ordering. In a comparative simulation study, Arboretti et al. (2009) compared various permutation and asymptotic tests for two-sample equality of survival functions under right-censoring. Furthermore, Arboretti et al. (2010) combined multiple permutation tests in a survival analytic framework. In the recent article Arboretti et al. (2017), permutation combination tests are proposed to test differences in two samples of survival data under both treatment-dependent and -independent censoring while allowing for various weight functions.

With our assessment of the bootstrap and the permutation approach, we also contribute to recent analyses in the statistical literature in which both methods, the bootstrap and random permutation, have been compared in various contexts; see e.g. Pauly (2011), Gel and Chen (2012), Santos and Ferreira (2012), Bonnini (2014), Yan et al. (2015), Albert et al. (2015), and Friedrich et al. (2017). Usually, the permutation technique is found to be preferable to the bootstrap.

The article is organized as follows. Section 2 introduces all required notation and estimators, whose combination with the variance estimator in Sect. 3 yields (non-resampling) inference procedures. Theoretical results concerning the resampling techniques are presented in Sect. 4. A simulation study in Sect. 5.1 reports the improvement of the level \(\alpha \) control by the proposed permutation and bootstrap techniques and in Sect. 5.2 all developed test procedures are evaluated in terms of power via an additional simulation study in which we also included the log-rank test. A final application of the developed methodology to a tongue cancer data set Klein and Moeschberger (2003) is presented in Sect. 6. This article’s results are discussed in Sect. 7 and theoretically proven in Online Resource which also contains additional simulations results.

2 Notation, model, and estimators

Throughout the article, let \((\varOmega ,\mathcal {A},P)\) be a probability space. For a more formal introduction of the concordance index p and the win ratio w, we employ some standard notation from survival analysis. Thus, we consider two independent groups \((j=1,2)\) of independent random variables \( \tilde{T}_{j1}, \ldots , \tilde{T}_{jn_j}\,{:}\,(\varOmega ,\mathcal {A},P) \rightarrow (0,\infty ),\) with distribution function \(\tilde{F}_j, j=1,2,\) and total sample size \(n = n_1 + n_2, n_1, n_2 \in \mathbb {N}\). We will refer to these random variables as survival times and assume that they are identically distributed within each group. Their distributions may have discrete components, which reflects the situation in most clinical studies (i.e. survival times rounded to days or weeks). Since most studies pre-specify a point of time \(K > 0\) after which no further observation is intended, we also truncate the above survival times to \( T_{ji} = \tilde{T}_{ji} \wedge K, i=1,\ldots , n_j, j=1,2,\) where \(\wedge \) denotes the minimum operator. Denote their survival functions as \(S_j(t) = 1 - F_j(t) \equiv P(T_{j1} > t), j=1,2\). Thus, both sample groups may have different, even heteroscedastic distributions. Their cumulative hazard functions are given by \(\varLambda _j(t) = - \int _0^t \frac{\mathrm dS_j}{S_{j-}}\) where the index minus (here in \(S_{j-}\)) always indicates the left-continuous version of a right-continuous function. Note that this definition of \(\varLambda _j\) implies that the survival functions have the representations , where denotes the product integral, i.e. the limit of products over fine partitions of the interval (0, t]; see Gill and Johansen (1990) for details. The survival times are randomly right-censored by independent, positive variables \( C_{j1}, \ldots , C_{jn_j} \) with possibly discontinuous, group-specific censoring survival functions \(G_j, j=1,2\). Observation is thus restricted to \( \mathbf X _j = \{(X_{ji}, \delta _{ji}): i = 1, \ldots , n_j \}, j=1,2,\) where \(X_{ji} = {T_{ji} \wedge C_{ji}}, \delta _{ji} = \mathbf 1 \{X_{ji} = T_{ji} \}, 1 \le i \le n_j\). Note that the choice of K shall imply a positive probability of each event \(\{\tilde{T}_{ji} > K\}\). This constant K could, for example if all individuals enter into the study at time 0, be the end-of-study time, i.e. the largest censoring time. For later use, we introduce the counting process notation

$$\begin{aligned} N_{j;i}(u)&= \mathbf 1 \{\text {``observed event for ind}.\,i\,\mathrm{of group}\,j\,\mathrm{until}\,u\text {''} \} = \mathbf 1 \{X_{ji} \le u, \delta _{ij} = 1 \},\\ Y_{j;i}(u)&= \mathbf 1 \{\text {``ind.}\,i\,\mathrm{of}~\mathrm{group}~j~\mathrm{is}~\mathrm{under}~\mathrm{observation}~\mathrm{at}~\mathrm{time}~u\text {''} \} = \mathbf 1 \{X_{ji} \ge u \}. \end{aligned}$$

Summing up these quantities within each group results in \(Y_j(u) = \sum _{i = 1}^{n_j} Y_{j;i}(u)\), the number of group-j subjects under study shortly before u, and \(N_{j}(u) = \sum _{i=1}^{n_j} N_{j;i}(u)\), the number of observed events in group j until time u. Denote by \(f^\pm = \frac{1}{2} (f + f_-) \) the so-called normalized version of a right-continuous function f. With this notation, the Mann–Whitney effect and the win ratio are given as

$$\begin{aligned} p = P(T_{11} > T_{21}) + \frac{1}{2} P(T_{11} = T_{21}) = - \int S_1^\pm \mathrm dS_2 = 1 - \int F_1^\pm \mathrm dF_2 \end{aligned}$$
(1)

and \(w= {p}/{(1-p)}\), respectively. If not specified, integration is over [0, K]. In this set-up, we test the null hypothesis \(H_0^p: \{p = 1/2 \} = \{w = 1 \}\) that the survival times from both groups are tendentiously equal against one- or two-sided alternatives. We note that the usually considered null hypothesis \(H_0^S\,{:}\,\{S_1 = S_2\}\) of equal survival distributions is more restrictive and implies \(H_0^p\). Similarly, a stochastic order or precedence (Davidov and Herman 2012) such as \(F_1 \lneq F_2\) implies \(p\ge 1/2\).

To test \(H_0^S\) for continuous survival times, Efron (1967) has introduced a natural estimator for p, see also Koziol and Jia (2009), replacing the unknown survival functions \(S_j{(t)}\) in (1) with the Kaplan–Meier estimators . Since their normalized versions \(\widehat{S}_j^\pm \) are nonparametric maximum likelihood estimators for the normalized survival functions \(S_j^\pm \), we obtain

$$\begin{aligned} \widehat{p} = \widehat{P}(T_{11} > T_{21}) + \frac{1}{2} \widehat{P}(T_{11} = T_{21}) = - \int \widehat{S}_1^\pm \mathrm d\widehat{S}_2 \end{aligned}$$
(2)

and \(\widehat{w}= \widehat{p}/(1-\widehat{p})\) as nonparametric maximum likelihood plug-in estimators of p and w, respectively. Similar estimators for p have been proposed by Akritas and Brunner (1997) and Brunner and Munzel (2000). The latter quantity \(\widehat{w}\) has been introduced by Pocock et al. (2012) for uncensored observations (without ties) with the nice interpretation as total number of winners divided by the total number of losers in group 1 (where \(T_{1i}\) wins against \(T_{2\ell }\) if \(T_{1i} > T_{2\ell }\)).

Thus, the statistics \(V_n(\frac{1}{2}) = \sqrt{\frac{n_1 n_2}{n}} (\widehat{p} - \frac{1}{2})\) or \(U_n(1) = \sqrt{\frac{n_1 n_2}{n}} (\widehat{w} - 1)\) may measure deviations from \(H_0^p\). In order to obtain adequate critical values for testing \(H_0^p\) or constructing one- or two-sided confidence intervals for the Mann–Whitney effect p and the win ratio w, we study their limit behaviour under the asymptotic frameworks

$$\begin{aligned} 0< \liminf {({n_1}/{n})}&\le \limsup {({n_1}/{n})} < 1 \end{aligned}$$
(3)
$$\begin{aligned} {\text {or} \qquad {n_1}/n}&\rightarrow \kappa \in (0,1) \end{aligned}$$
(4)

as \({\min (n_1, n_2)} \rightarrow \infty \). Here, (4) is used in intermediate results, whereas our main theorems will only rely on the weaker assumption (3).

We denote by “\({\mathop {\longrightarrow }\limits ^{d}}\)” and “\({\mathop {\longrightarrow }\limits ^{p}}\)” convergence in distribution and in outer probability as \(n \rightarrow \infty \), respectively, both in the sense of van der Vaart and Wellner (1996). The following central limit theorem for \(\widehat{p} \) is the normalized counterpart of the asymptotics due to Efron (1967) and is proven by means of the functional \(\delta \)-method in combination with the weak convergence theorem for the Kaplan–Meier estimator as stated in van der Vaart and Wellner (1996, Section 3.9). Throughout, let \(a_n = \sqrt{n_1 n_2/n}\).

Theorem 1

(i) Suppose (4) holds, then the Mann–Whitney statistic \(V_n=V_n(p) = {a_n} (\widehat{p} - p)\) is asymptotically normal distributed, i.e. \(V_n{\mathop {\longrightarrow }\limits ^{d}}Z \sim N(0, \sigma ^2)\) as \(n \rightarrow \infty \). The limit variance is \(\sigma ^2 = (1-\kappa ) \sigma ^2_{12} + \kappa \sigma ^2_{21}\), where for \(1 \le j \ne k \le 2\),

$$\begin{aligned} \sigma ^2_{jk} = \int \int \varGamma _j^{\pm \pm }(u,v) \mathrm dS_k(u) \mathrm dS_k(v) \quad \text {and}\quad \varGamma _j(u,v) = \int _0^{u \wedge v} \frac{{S_j(u) S_j(v)} \mathrm d\varLambda _j}{S_{j-} G_{j-}}. \end{aligned}$$
(5)

Moreover, \(\varGamma _j^{\pm \pm }\) denotes the covariance function normalized in both arguments given by \( \varGamma _j^{\pm \pm }(u,v) = [\varGamma _j(u,v) + \varGamma _j(u-,v) + \varGamma _j(u,v-) + \varGamma _j(u-,v-)]/4. \)

(ii) Under the conditions of (i), the win ratio statistic \( U_n(w) = {a_n} (\widehat{w} - w)\) asymptotically follows a normal-\(N(0, \sigma ^2/(1-p)^4)\)-distribution.

Remark

(a) Efron (1967) used a version of the Kaplan–Meier estimator that always considered the last observation as uncensored. Moreover, the restrictive null hypothesis \(H_0^S\,{:}\,\{S_1 = S_2 \}\) was used to simplify the variance representation under the null.

(b) Without a restriction at some point of time K, a consistent estimator for the Mann–Whitney effect requires consistent estimators for the survival functions on their whole support. This involves the condition \(-\int (\mathrm dS_j)/G_{j-} < \infty , j=1,2,\) which is obviously only possible if the support of \(S_j\) is contained in the support of \(G_j\); see e.g. Gill (1983), Ying (1989) and Akritas and Brunner (1997). However, this assumption is often not met in practice, e.g. if \(G_j(u) = 0 < S_j(u)\) for some point of time \(u > 0\).

Since the variances \(\sigma ^2_{jk}\) are unknown under the null \(H_0^p\), the test statistics \(V_n(\frac{1}{2})\) and \(U_n(1)\) are asymptotically non-pivotal. Thus, their estimation from the data is mandatory in order to obtain consistent tests and confidence intervals for p and w.

3 Variance estimation and studentized test statistics

Asymptotically pivotal test statistics result from studentized versions of \(\widehat{p}\) and \(\widehat{w}\). Replacing all unknown quantities in (5) with consistent estimators, a plug-in estimator for the limit variance \(\sigma ^2\) of \(V_n= {a_n} (\widehat{p} - p)\) is \(\widehat{\sigma }^2 = {a_n^2} (\widehat{\sigma }^2_{12} + \widehat{\sigma }^2_{21})\), where

$$\begin{aligned} \widehat{\sigma }^2_{jk} = \int \int \widehat{\varGamma }_j^{\pm \pm }(u,v) \mathrm d\widehat{S}_k(u) \mathrm d\widehat{S}_k(v) \quad \text {and} \quad \widehat{\varGamma }_j(u,v) = \int _0^{u \wedge v} \frac{\widehat{S}_j(u) \widehat{S}_j(v) \mathrm dN_j}{(Y_j - \Delta N_j)Y_j} \end{aligned}$$
(6)

for \(1 \le j \ne k \le 2\). Here, the function \(\Delta f(u) = f(u) - f(u-)\) contains all jump heights of a right-continuous function f.

Lemma

Under (4), \(\widehat{\sigma }^2\) is consistent for \(\sigma ^2\) defined in Theorem 1, i.e. \(\widehat{\sigma }^2 {\mathop {\longrightarrow }\limits ^{p}}\sigma ^2\).

This result directly leads to the studentized statistics \(T_n(p) = {a_n} {(\widehat{p} - p)}/{\widehat{\sigma }}\) and \(W_n(w) = {a_n} (\widehat{w} - w) {(1-\widehat{p})^2}/{\widehat{\sigma }} = {{a_n(\widehat{w} - w)}}/[{\widehat{\sigma }(1+\widehat{w})^2}] \) which are both asymptotically standard normal as \({\min (n_1,n_2)} \rightarrow \infty \) by Slutzky’s theorem and the \(\delta \)-method only assuming (3). Indeed, under (3), Theorem 1 and Lemma 3 might be applied along each convergent subsequence of \(n_1/n\). Since all resulting limit distributions of \(T_n(p)\) and \(W_n(p)\) are pivotal, i.e. independent of \(\kappa \), this weak convergence must hold for the original sequence as well. Thus, two-sided confidence intervals for p and w of asymptotic level \((1-\alpha ) \in (0,1)\) are given by

$$\begin{aligned} {I}_n = \left[ \widehat{p} \mp {z_{1-\alpha /2}\widehat{\sigma }/a_n} \right] (\text {for}\,p)\quad \text {and}\quad \left[ \widehat{w} \mp {z_{1-\alpha /2}\widehat{\sigma }(1 + \widehat{w})^2/a_n} \right] (\text {for}\,w), \end{aligned}$$
(7)

respectively, where \(z_{1-\alpha }\) denotes the \((1-\alpha )\)-quantile of N(0, 1). Moreover,

$$\begin{aligned} \varphi _n = \mathbf {1}\{T_n({1}/{2})> {z_{1-\alpha }}\} \quad \text {and} \quad \psi _n = \mathbf {1}\{W_n(1) > {z_{1-\alpha }}\} \end{aligned}$$
(8)

are consistent asymptotic level \(\alpha \) tests for \(H_0^p\,{:}\,\{p=\frac{1}{2}\} = \{w = 1 \}\) against the one-sided alternative hypothesis \(H_1^p\,{:}\,\{p>\frac{1}{2}\} = \{w > 1 \}\), i.e. as \(n \rightarrow \infty \), \(E(\varphi _n) \rightarrow \alpha \mathbf {1}\{p=1/2\} + \mathbf {1}\{p>1/2\}\) and \(E(\psi _n) \rightarrow \alpha \mathbf {1}\{w=1\} + \mathbf {1}\{w>1\}\). One-sided confidence intervals and two-sided tests can be obtained by inverting the above procedures. For larger sample sizes (\(n_j > 30\) depending on the magnitude of censoring), the above inference methods (7) and (8) are fairly accurate; see the simulation results in Sect. 5. For smaller sample sizes, however, these procedures tend to have inflated type-I error probabilities. Therefore, we propose different resampling approaches and discuss their properties in the following section. For ease of presentation, we only consider resampling tests for \(H_0^p\,{:}\,\{p=\frac{1}{2}\}\) in order to concentrate on one parameter of interest (i.e. on p) only. Nevertheless, the results directly carry over to construct resampling-based confidence intervals for p and w, respectively.

4 Resampling the Mann–Whitney statistic

Even in the continuous case, Koziol and Jia (2009) pointed out that “with small samples sizes a bootstrap approach might be preferable” for approximating the unknown distribution of \(V_n=V_n(p) = {a_n} (\widehat{p} - p)\). To this end, we consider different resampling methods, starting with Efron’s classical bootstrap. Here the bootstrap sample is generated by drawing with replacement from the original data pairs; see Efron (1981). Large sample properties of the bootstrapped Kaplan–Meier process and extensions thereof have been analysed e.g. in Akritas (1986), Lo and Singh (1986), Horvath and Yandell (1987), and Dobler (2016). Calculating the bootstrap version of \(\widehat{p}\) via bootstrapping for each sample group and using their quantiles leads to a slightly improved control of the type-I error probability in comparison with the asymptotic test (8). However, this way of bootstrapping results in a still too inaccurate behaviour in terms of too large deviations from the \(\alpha =5\%\) level (results not shown). This technique is typically improved by resampling procedures based on the pooled data \(\mathbf Z = \{(Z_i, \eta _i): i=1,\ldots ,n\}\) given by

$$\begin{aligned} (Z_i, {\eta _i}) = (X_{1i}, \delta _{1i}) \mathbf {1}\{i \le n_1 \} + (X_{2 (i-n_1)}, \delta _{2 (i-n_1)}) \mathbf {1}\{i > n_1 \}, \quad i=1,\ldots , n {,} \end{aligned}$$

i.e. the pairs \((Z_i, {\eta _i})\) successively take all the values of the first (\(i \le n_1\)) and of the second sample group (\(i > n_1\)). See e.g. Boos et al. (1989), Janssen and Pauls (2005) and Neubert and Brunner (2007) for empirical verifications for other functionals in this matter. Boos et al. (1989) and Konietschke and Pauly (2014) also demonstrate that random permuting of and bootstrapping from pooled samples may yield superior results, where the first has the additional advantage of leading to finitely exact testing procedures in case of \(S_1=S_2\) and \(G_1=G_2\). We investigate both techniques in more detail below. The dependence of the underlying probability space of \(p \in (0,1)\) is subsequently denoted by \(P_p\) and the corresponding expectation by \(E_p\). Online Resource contains asymptotic results on the pooled (bootstrap) and permutation Kaplan–Meier estimator. Therefore, only the description of both resampling methods and the resulting final theorems are given here.

The pooled bootstrap We independently draw n times with replacement from the pooled data \(\mathbf Z \) to obtain the pooled bootstrap samples \(\mathbf Z _1^* = (Z_{1i}^*, \eta _{1i}^*)_{i=1}^{n_1}\) and \(\mathbf Z _2^* = (Z_{2i}^*, \eta _{2i}^*)_{i=1}^{n_2}\). Denote the corresponding Kaplan–Meier estimators based on these bootstrap samples as \(S_{1}^*\) and \(S_{2}^*\). These may also be regarded as the \(n_j\) out of n bootstrap versions of the Kaplan–Meier estimator \(\widehat{S}\) based on the pooled sample \(\mathbf Z \). All in all, this results in the pooled bootstrap version \(p^* = - \int S_1^{*\pm } \mathrm dS_2^*\) of \(\widehat{p}\). A suitable centring term for \(p^*\) is based on the pooled Kaplan–Meier estimator and is given by \( - \int \widehat{S}^\pm \mathrm d\widehat{S} = \frac{1}{2}\). Thus, we study the distribution of \(V_n^* = {a_n} (p^* - \frac{1}{2})\) for approximating the null distribution of \(V_n(\frac{1}{2}) = {a_n} (\widehat{p} - \frac{1}{2})\).

The large sample properties of \(V_n^*\) are studied with the help of empirical process theory. In the convergence results stated below the càdlàg space D[0, K] is always equipped with the \(\sup \)-norm; cf. van der Vaart and Wellner (1996). The technical Lemma 2 and Theorem 4 in Online Resource show the large sample behaviour of \(\widehat{S}\) and the bootstrapped counterpart \(S^*\), respectively.

Since pooled sampling affects the covariance structure of the Kaplan–Meier estimator, a studentization for \(V_n^*\) becomes mandatory. Following the general recommendation to bootstrap studentized statistics (see e.g. Hall and Wilson 1991; Janssen and Pauls 2005, or Delaigle et al. 2011), we introduce the bootstrap variance estimator

$$\begin{aligned} \sigma ^{* 2} = \frac{n_2}{n} \int \int {n_1 \varGamma _1^{*\pm \pm }(u,v)} \mathrm dS_{2}^*(u) S_{2}^*(v) + \frac{n_1}{n} \int \int {n_2 \varGamma _2^{*\pm \pm }(u,v)} \mathrm dS_{1}^*(u) S_{1}^*(v), \end{aligned}$$

with bootstrapped Greenwood-type covariance \(\varGamma _j^{*}(u,v) = \int _0^{u \wedge v} \frac{{S_{j}^*(u) S_{j}^*(v)} \mathrm dN_j^*}{(Y_j^* - \Delta N_j^*)Y_j^{*}}\) in which \(N_j^*\) and \(Y_j^*\) are the pooled bootstrapped counting processes based on the jth bootstrap sample \(\mathbf Z _j^*\), \(j=1,2\). We state our main result on the pooled bootstrap.

Theorem 2

Assume (3). Then the studentized bootstrap statistic \(T_{n}^*=V_{n}^*/ \sigma ^{*}\) always approximates the null distribution of \(T_n(1/2)\) in outer probability, i.e. we have for any choice of p and as \({\min (n_1,n_2)} \rightarrow \infty \):

$$\begin{aligned} \sup _x \left| P_p(T_{n}^*\le x|\mathbf Z ) - P_{1/2}\left( T_n(1/2)\le x\right) \right| {\mathop {\longrightarrow }\limits ^{p}}0. \end{aligned}$$
(9)

Moreover, denoting by \(c_{n}^*({1-}\alpha )\) the conditional \((1-\alpha )\)-quantile of \(T_{n}^*\) given \(\mathbf Z \), it follows that \(\varphi _{n}^* = \mathbf {1}\{T_n(1/2) > c_{n}^*({1-}\alpha )\}\) is a consistent asymptotic level \(\alpha \) test for \(H_0^p\,{:}\,\{p=\frac{1}{2}\}\) against \(H_1^p\,{:}\,\{p>\frac{1}{2}\}\) that is asymptotically equivalent to \(\varphi _n\), i.e. we have \(E_p(|\varphi _n^* - \varphi _n|)\rightarrow 0\).

Random permutation

An alternative resampling technique to Efron’s bootstrap is the permutation principle. The idea is to randomly interchange the group association of all individuals while maintaining the original sample sizes. The test statistic is then calculated anew based on the permuted samples. A big advantage of permutation resampling over the pooled bootstrap is the finite exactness of inference procedures on the smaller null hypothesis \(H_0^{S,G}: \{S_1 = S_2\,\text {and}\,G_1 = G_2 \} \subset H_0^p\); see e.g. Neuhaus (1993) and Brendel et al. (2014) in case of testing \(H_0^S\) and Janssen (1997), Janssen (1999), Neubert and Brunner (2007), Chung and Romano (2013, 2016b), Pauly et al. (2015) as well as Pauly et al. (2016) for uncensored situations.

Therefore, let \(\pi \,{:}\,\varOmega \rightarrow \mathcal {S}_n\) be independent of \(\mathbf Z \) and uniformly distributed on the symmetric group \(\mathcal {S}_n\), the set of all permutations of \((1,\ldots ,n)\). The permuted samples are obtained as \(\mathbf Z _1^\pi = (Z_{\pi (i)}, \eta _{\pi (i)})_{i=1}^{n_1}\) and \(\mathbf Z _2^\pi = (Z_{\pi (i)}, \eta _{\pi (i)})_{i=n_1+1}^{n}\). Plugging the Kaplan–Meier estimators \(S_1^{\pi }\) and \(S_2^\pi \) based on these permuted samples into the Wilcoxon functional (1) leads to the permutation version \( {p}^\pi = - \int S_1^{\pi \pm } \mathrm dS_2^\pi \) of \(\widehat{p}\). The permutation sampling is equivalent to drawing without replacement from the pooled sample \(\mathbf Z \). Again, the limit variance of \(V_n^\pi = {a_n} ( p^\pi - \frac{1}{2})\) is in general different from \(\sigma ^2\) and again studentizing \(V_n^\pi \) is necessary. This is achieved by utilizing the permutation version \(\sigma ^{\pi 2}\) of \(\widehat{\sigma }^2\) which is the same as \(\sigma ^{*2}\) while replacing all \({}^*\) with \({}^\pi \). Thereby, the permutation counting processes \(N_j^\pi \) and \(Y_j^\pi \) based on the jth permuted sample \(\mathbf Z _j^\pi , j=1,2\), are used. This yields the studentized permutation statistic \(T_n^\pi =V_n^\pi /\sigma ^{\pi }\). Note that it is indeed the permutation version of \(T_n(1/2)\) which is necessary for maintaining the exactness property under \(H_0^{S,G}\). Below, we prove that \(T_n^\pi \) also approximates the asymptotic null distribution of \(T_n(\frac{1}{2})\) in general.

Theorem 3

Assume (3). Then the studentized permutation statistic \(T_n^\pi =V_n^\pi /\sigma ^{\pi }\) always approximates the null distribution of \(T_n(1/2)\) in outer probability, i.e. we have for any choice of p and as \({\min (n_1,n_2)} \rightarrow \infty \):

$$\begin{aligned} \sup _x \left| P_p\left( T_n^\pi \le x|\mathbf Z \right) - P_{1/2}\left( T_n(1/2)\le x\right) \right| {\mathop {\longrightarrow }\limits ^{p}}0. \end{aligned}$$
(10)

Moreover, denoting by \(c_{n}^\pi ({1-}\alpha )\) the conditional \((1-\alpha )\)-quantile of \(T_n^\pi \) given \(\mathbf Z \), it follows that \(\varphi _{n}^\pi = \mathbf {1}\{T_n(1/2) > c_{n}^\pi ({1-}\alpha )\}\) possesses the same asymptotic properties as \(\varphi _n^*\) in Theorem 2. Furthermore, \(\varphi _n^\pi \) is even a finitely exact level \(\alpha \) test under \(H_0^{S,G}\).

5 Finite sample properties

5.1 Coverage probabilities of confidence intervals

In this section, we study the finite sample properties of the proposed approximations. In particular, we compare the actual coverage probability of the asymptotic two-sided confidence interval \(I_n\) given in (7) with that of the corresponding bootstrap and permutation confidence intervals

$$\begin{aligned} I_n^* = \left[ \widehat{p} \mp {c_n^*(1-\alpha /2)\widehat{\sigma }/a_n} \right] \quad \text {and} \quad I_n^\pi = \left[ \widehat{p} \mp {c_n^\pi (1-\alpha /2)\widehat{\sigma }/a_n} \right] , \end{aligned}$$

respectively. To this end, the following distribution functions \(\tilde{F}_1\) and \(\tilde{F}_2\), frequently occurring in the survival context, have been chosen in our simulation study:

  1. (1)

    Group 1: Exponential distribution with mean 1 / 2, i.e. \({\tilde{F}_1}=Exp(1/2)\). Group 2: Exponential mixture distribution: \({\tilde{F}_2}= \frac{1}{3}Exp(1/1.27) + \frac{2}{3}Exp(1/2.5)\).

  2. (2)

    Group 1: Weibull distribution with scale parameter 1.65 and shape parameter 0.9. Group 2: Standard lognormal distribution.

  3. (3)

    Both groups: Weibull distribution with unit scale and shape parameter 1.5.

  4. (4)

    Group 1: Weibull distribution with scale parameter 2 and shape parameter 1.5. Group 2: Gamma distribution with scale 0.5 and shape parameter 3.4088.

For achieving \(p \approx 1/2\) in each set-up, the terminal times were chosen as \(K \approx 1.6024, 1.7646, 2\), and 3, respectively. Censoring is realized using i.i.d. exponentially distributed censoring variables \(C_{ji}\) with different means such that the (simulated) censoring probability (after truncation at K) for each of both sample groups is between 41.0 and 43.6% (strong), between 21.2 and 26.4% (moderate), and exactly \(0\%\) (no censoring). See e.g. Chapter 1 in Bagdonavičius and Nikulin (2002), Chapter 2 in Klein and Moeschberger (2003) or Sections 2.4 and 10.4 in Moore (2016) as well as Model 3 in Bajorunaite and Klein (2008) for similar survival and censoring distributions.

The sample sizes range over \(n_1 = n_2 \in \{10,15,20,25,30{,50,100}\}\) as well as \(n_2 = 2 n_1 \in \{20,30, 40,50, 60{, 100,200}\}\) and finally \(n_1 = 2 n_2\) running through the same set. Simulating 10,000 individuals each, the approximate percentages of observations greater than K for strong, moderate, and no censoring are, respectively:

\(\bullet \) Set-up (1):

0.36/0.32

1.19/1.35

4.12/4.26

\(\bullet \) Set-up (2):

12.16/10.44

22.3/17.43

34.26/28.37

\(\bullet \) Set-up (3):

1.54

3.28

6.02

\(\bullet \) Set-up (4):

5.58/3.6

10.16/6.59

15.94/10.35

where the values for both sample groups are separated by “/” in case of set-ups (1), (2), or (4). The pre-specified confidence level is \(1-\alpha = 95\%\). Each simulation was carried out using \(N= 10{,}000\) independent tests, each with \(B= 1999\) resampling steps in R version 3.2.3 (R Development Core Team 2016). All Kaplan–Meier estimators were calculated using the R package etm by Allignol et al. (2011). In comparison with the pooled bootstrap confidence interval \(I_n^*\), the permutation-based confidence interval \(I_n^\pi \) provides even finitely exact inference if the restricted null hypothesis \(H_0^{S,G} {: \{S_1 = S_2 \,\text {and}\, G_1 = G_2 \}}\) is true (as in the third set-up).

The simulation results for all scenarios are summarized in Tables 1, 2, and 3; the latter is given in Online Resource. Considering first the asymptotic confidence interval \(I_n\), we see quite satisfactory coverage probabilities in the uncensored case in any of the set-ups (1)–(4) for \(n_1, n_2 \ge 20\) even though they are still slightly too low (93.1–94.9%). This is in line with previous findings of \(\alpha \)-level control of rank-based tests for \(H_0^p\) (e.g. Neubert and Brunner 2007 or Pauly et al. 2016). The undercoverage, however, gets much worse if the sample sizes are smaller (90.9–93.2%) or if the censoring rates are increased (coverage partially below 89%). The bootstrap-based confidence intervals \(I_n^*\) and the permutation-based confidence intervals \(I_n^\pi \) appear to be much more reliable, even under censoring and for small sample sizes. While the bootstrap-based intervals \(I_n^*\) tend to be slightly conservative (i.e. have too large coverage probabilities) in case of strong censoring and very small samples sizes \(n_1, n_2 \in \{10,15,20\}\), the permutation-based intervals \(I_n^\pi \) show excellent coverage probabilities even in these extreme scenarios. Furthermore, we see empirical evidence for the finite exactness of \(I_n^\pi \) in set-up (3) in which \(I_n\) and \(I_n^*\) are generally outperformed, especially under strong censoring. Apart from that, the empirical coverage probabilities of \(I_n^\pi \) and \(I_n^*\) are generally comparable and clearly support our conjecture of a greater reliability in comparison with \(I_n\).

Table 1 Simulated coverage probabilities (in %) of two-sided asymptotic 95% confidence intervals for \(p = 0.5\) and equal sample sizes \(n_1=n_2\)
Full size table
Table 2 Simulated coverage probabilities (in %) of two-sided asymptotic 95% confidence intervals for \(p = 0.5\) and unequal sample sizes \(2n_1=n_2\)
Full size table

All in all, the permutation procedure can be generally recommended, even for very small sample sizes such as \(n_1 = n_2 = 10\) and even in case of censoring rates of about 40%. In the censored case, the bootstrap procedure shows a similar coverage (with a minor conservativeness for strong censoring) but does not possess the nice exactness property under \(H_0^{S,G}\). The asymptotic procedure \(I_n\) can only be recommended for larger sample sizes, especially in the presence of strong censoring. For the latter, sample sizes of at least \(n_1, n_2 \ge 100\) are required to obtain coverage probabilities close to the nominal confidence level of 95%.

5.2 Power comparisons

In a second set of simulations, we assessed the power of all two-sided counterparts of \(\varphi _n, \varphi _n^*\), and \(\varphi _n^\pi \) to detect one-sided shift alternatives. For notational convenience, we will use the same names for the present tests. The shift alternatives are obtained by subtracting a shift parameter \(\mu \in \{0, 0.1, \ldots , 1\}\) from the survival times of the second group, i.e. \(\tilde{F}_{2, \mu }(x) = \tilde{F}_2(x + \mu )\). To have another competitor to the present tests, we also simulated the power of the log-rank test which is actually a test for the null hypothesis \(H_0^S\) instead of \(H_0^p\). However, in the present shift model, the distribution functions only imply \(H_0^p\) in case of \(\mu = 0\) for the subsequent choices of \(\tilde{F}_1\) and \(\tilde{F}_2\). We utilized the function survdiff of the R package survival (Therneau and Lumley 2017) for calculating the log-rank test outcomes. We focused on the above set-ups (2) and (3) and coupled those, respectively, with those choices of the above censoring distributions leading to the moderate and strong censoring regimes under \(H_0^p\).

Fig. 1
figure 1

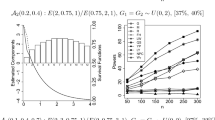
Power comparisons between \(\varphi _n\) (solid line), \(\varphi _n^*\) (dashed line), \(\varphi _n^\pi \) (dotted line), and the log-rank test (dot-dashed line) for small sample sizes \({n_1 = 10,} \ n_2 \in \{10,20\}\) and set-ups (2) and (3). The narrow, horizontal line represents the nominal level \(\alpha =5\%\)

Full size image

The results are presented in Fig. 1 for the sample sizes \(n_1 = 10, n_2 \in \{10,20\}\) (and Figure 3 in Online Resource for \(n_1 = 20, n_2 = 10\)). As expected, the powers of all test procedures generally increase if the sample size is increased. Among the Mann–Whitney statistic-based tests \(\varphi _n, \varphi _n^*\), and \(\varphi _n^\pi \), we see that the asymptotic test \(\varphi _n\) has the highest power. This is no surprise, though, as it comes at the cost of an inflated type-I error rate under \(H_0^p\,{:}\,\mu =0\); see the simulation results of Sect. 5.1 above. Therefore, we exclude \(\varphi _n\) from further discussion. The remaining two tests, \(\varphi _n^*\), and \(\varphi _n^\pi \), keep the nominal level approximately equally well. The power of both is comparable under set-up (2), but it is greater for \(\varphi _n^\pi \) in the third set-up.

In contrast, the log-rank test is slightly liberal under \(H_0^p\) (type-I error rates of 5.3–6.6%). However, this does not even result uniformly in the greatest power: While it is clearly greater than the power of \(\varphi _n^*\) and \(\varphi _n^\pi \) under set-up (3) and \(n_1=20, n_2=10\), the power is only slightly elevated in the cases \(n_1=20, n_2=10\) (second set-up) and \(n_1 = n_2=10\) (third set-up). In the remaining three combinations, the power of the log-rank test is apparently inferior to the power of \(\varphi _n^*\), and \(\varphi _n^\pi \).

Again, it needs to be emphasized that the log-rank test is originally constructed for a different testing problem under proportional hazards. If \(H_0^p\) is true while \(H_0^S\) is not, this necessarily implies that the involved cumulative hazard functions cross. Therefore, slight departures from such null hypotheses still result in crossing hazards which usually imply a sub-optimal power of the log-rank test. Of course, its power would be greater in case of proportional hazards alternatives; see e.g. Tables 1 and 2 in Brückner and Brannath (2016) or Figures 5 to 7 in Brendel et al. (2014) for the loss of power of the log-rank test when a proportional hazards alternative is replaced by a non-proportional hazards alternative.

As a final conclusion, we summarize that \(\varphi _n^*\) and \(\varphi _n^\pi \) appear to be the most reliable procedures (with a view towards control of the nominal level and power) whereof the permutation test is slightly preferable. In terms of power, \(\varphi _n^*\) and \(\varphi _n^\pi \) seem to be at least competitive to the log-rank test, while their test statistic is based on a meaningful, real-valued quantity, whereas the interpretation of the log-rank test statistic is cumbersome in the absence of proportional hazards.

6 Application to a data example

To illustrate the practical applicability of our novel approaches, we reconsider a data set containing survival times of tongue cancer patients, cf. Klein and Moeschberger (2003). The data set is freely available in the R package KMsurv via the command data(tongue). It contains 80 patients of which \(n_1=52\) are suffering from an aneuploid tongue cancer tumour (group 1) and \(n_2=28\) are suffering from a diploid tumour (group 2). Observation of 21 patients in group 1 and of six patients in group 2 have been right-censored; for all others, the time of death has been recorded. Thus, the corresponding censoring proportions are intermediate between the “strong” and “moderate” scenarios of Sect. 5. Note that the data set actually contains ties: among the uncensored survival times, there are 27 different times of death in the first group, 20 different in the second group, and 39 different in the pooled sample. Moreover, there are three individuals in group 1 with censoring time exceeding the greatest recorded time of death in this group; for group 2 there is one such individual. As a reasonable value for restricting the time interval, we may thus choose \(K=200\) weeks which still precedes all just mentioned censoring times.

The Kaplan–Meier estimators of both recorded groups are plotted in Fig. 2. It shows that the aneuploid Kaplan–Meier curve is always above the Kaplan–Meier curve of the diploid group. We would, therefore, like to examine whether this gap already yields significant results concerning the probability of concordance.

Fig. 2
figure 2

Kaplan–Meier estimators for diploid (dashed line) and aneuploid tumour (solid line) patients

Full size image

The data evaluation resulted in a point estimate \(\widehat{p} \approx 0.6148\) indicating a larger survival probability of the aneuploid group in comparison with the diploid. To infer this, we obtained these one- and two-sided 95% confidence intervals (based on normal, bootstrap, and permutation quantiles) for the probability p, that a randomly chosen individual with an aneuploid tumour survives longer than a patient with diploid tumour:

\(\bullet \) Asymptotic intervals:

Two-sided: [0.490, 0.740],

One-sided: [0.510, 1.000],

\(\bullet \) Bootstrap intervals:

Two-sided: [0.457, 0.772],

One-sided: [0.505, 1.000],

\(\bullet \) Permutation intervals:

Two-sided: [0.467, 0.763],

One-sided: [0.506, 1.000].

The intervals were calculated using the asymptotic normal quantile as well as \(B=9999\) resampling iterations for each of the bootstrap and the permutation technique.

By inverting these confidence intervals, it can be readily seen that the two-sided null hypothesis \(H_0^p\,{:}\,\{p=1/2\}\) cannot be rejected by any of the two-sided procedures since \(p=1/2\) is contained in all two-sided intervals. Here, slightly larger sample sizes might have caused significant results as the lower bounds of all three intervals are not far from 1 / 2. We like to note that the asymptotic two-sided interval is the shortest one which is in line with our simulation results from Sect. 5: the corresponding empirical coverage probabilities for \(I_n\) in Table 3 for \(n_1 = 50\) and \(n_2 = 25\) suggest that the actual coverage probability (for \(p=1/2\)) is somewhere between 93 and 94.5%, that is, \(I_n\) is slightly liberal. On the other hand, \(I_n^*\) and \(I_n^\pi \) turned out to be much more reliable under these scenarios such that their widths seem to be much more realistic. That the permutation-based interval is slightly smaller than the bootstrap-based interval is in line with the power simulations as presented in Fig. 1: the permutation method always seemed to yield a slightly more powerful inference method than the pooled bootstrap.

However, if we were only interested in detecting an effect in favour of the aneuploid group, we have to consider the corresponding one-sided tests to avoid possible directional errors. In particular, the results for testing the one-sided hypothesis \(H_{0,\le }^p\,{:}\,\{p\le 1/2\}\) are borderline significant: it can be rejected by all three approaches at level 5%, but the lower bounds of the intervals are just above 1/2. We note that multiplicity issues have not been taken into account.

7 Summary and discussion

In this article, novel inference procedures for the Mann–Whitney effect p and the win ratio w are introduced both of which are meaningful and well-established effect measures (especially in biometry and survival analysis). In comparison with the usual survival hypothesis \(H_0^S\,{:}\,\{S_1=S_2\}\), we were the first who particularly developed asymptotic confidence intervals for p and w as well as tests for the more interesting composite null hypothesis \(H_0^p\,{:}\,\{p= 1/2\}\) in the two-sample survival model with right-censored data. By utilizing normalized Kaplan–Meier estimates, these can even be constructed for discontinuously distributed survival times that may be subject to independent right-censoring. Applying empirical process theory, we showed that point estimates of p and w are asymptotically normal. By introducing novel variance estimates, this leads to asymptotic inference procedures based on normal quantiles. To improve their finite sample performance, bootstrap and permutation approaches have been considered and shown to maintain the same asymptotic properties. In our simulation study, it could be seen that the proposed permutation procedure considerably improves the finite sample performance of our procedure. Moreover, it is even finitely exact if data is exchangeable (i.e. whenever both survival and censoring distributions are equal) and can thus be recommended as the method of choice. In the special continuous situation with complete observations, a similar result has recently been proven in Chung and Romano (2016a).

Note that the proposed method can also be applied in the ‘winner-loser’ set-ups considered in Pocock et al. (2012) or Wang and Pocock (2016), where now even the neglected ties can be taken into account. We plan to do this in the near future. Moreover, extensions of the proposed techniques to other models such as multiple samples and multivariate or specific paired designs (e.g. measurements before and after treatment) will also be considered in a forthcoming paper.