Bootstrap and permutation rank tests for proportional hazards under right censoring

Abstract

We address the testing problem of proportional hazards in the two-sample survival setting allowing right censoring, i.e., we check whether the famous Cox model is underlying. Although there are many test proposals for this problem, only a few papers suggest how to improve the performance for small sample sizes. In this paper, we do exactly this by carrying out our test as a permutation as well as a wild bootstrap test. The asymptotic properties of our test, namely asymptotic exactness under the null and consistency, can be transferred to both resampling versions. Various simulations for small sample sizes reveal an actual improvement of the empirical size and a reasonable power performance when using the resampling versions. Moreover, the resampling tests perform better than the existing tests of Gill and Schumacher and Grambsch and Therneau . The tests’ practical applicability is illustrated by discussing real data examples.

1 Introduction

The famous model of Cox (1972) for proportional hazards is very popular in practice. That is why we need tests to check its model assumptions, i.e., $\alpha _2(t)=\vartheta \alpha _1(t)$ for all $t \in [0,\infty )$ in the two-sample case, where $\alpha _j$ denotes the group-specific hazard rate. Since the Cox model is more than 40 years old it is not surprising that several statisticians already suggested how to check the proportional hazard assumption. It is not possible to comment the whole recent literature but we want to give at least a (not complete) list of contributions to this topic: Cox (1972), Schoenfeld (1982), Lin (1991), Lin et al. (1993), Grambsch and Therneau (1994), Hess (1995), Sengupta et al. (1998), Scheike and Martinussen (2004), Kraus (2009) and Chen et al. (2015). Under the assumption of proportional hazards in the two-sample case weighted rank estimators of Andersen (1983) can be used to estimate the unknown proportionality factor $\vartheta$. The idea of Gill and Schumacher (1987) was to compare two different of these estimators. A similar approach is coming from Bluhmki et al. (2019). They measured the discrepancy of the ratio process of the group-specific Nelson–Aalen estimators from being constant. In contrast to the main contributions basing on Gaussian approximations the method of Bluhmki et al. (2019) based on a resampling technique, namely the wild bootstrap of Wu (1986). Resampling techniques are well known to improve the tests’ finite sample performance. In this paper, we suggest a (further) new test for checking the Cox model in the two-sample case. The novelty is not the test statistic itself, which is similar to the one of Wei (1984), but that the test can be conducted as a permutation as well as a wild bootstrap test. For small sample sizes resampling tests are known to perform (often) better than their asymptotic version. That is why they should be preferred. Moreover, the favorable benefit of the permutation test is its finite exactness under exchangeability. At the first sight it is, maybe, surprising that the permutation works for the whole null of proportional hazards since the data is not exchangeable in general because of two reasons: (1) we allow different censoring distribution for the two groups (2) the proportionality factor $\vartheta$ may differ from 1. Neuhaus (1993) already showed that his permutation approach works despite the first point for testing of distributional equality in the two-sample setting, confer Janssen and Pauls (2003) and Pauly (2011) for a general setting, and in this paper we prove the extension of this idea to the null of proportional hazards.

The paper is organized as follows. In Sect. 2, we introduce the survival set-up, the counting process notation, the logrank process and Andersen’s estimator for the proportionality factor $\vartheta$. The asymptotic exactness of the test under the null and the test’s consistency are derived in Sect. 3. The resampling techniques, permutation and wild bootstrapping, are introduced in Sect. 4. Moreover, we transfer the theoretical asymptotic properties of the test to both resampling versions. Simulations for various scenarios comparing our method with the ones of Gill and Schumacher (1987) and of Grambsch and Therneau (1994), respectively, are presented in Sect. 5. In Sect. 6, we apply our tests to two real data sets to demonstrate the practical applicability. All proofs are deferred to the “Appendix”.

2 Two-sample survival set-up

Let the usual two-sample survival set-up be given by survival times $T_{j,i}\sim F_j$ and censoring times $C_{j,i}\sim G_j$ for all individuals $i=1,\ldots ,n_j$ within the two groups $j\in \{1,2\}$, where $F_j$ and $G_j$ are continuous distribution functions on the positive line. All random variables $T_{1,1},C_{1,1},\ldots ,T_{2,n_2}, C_{2,n_2}$ are assumed to be independent. We denote by $n=n_1+n_2$ the pooled sample size which is supposed to tend to infinity in our asymptotic considerations below. To shorten the notation, all subsequent limits are meant as $n\rightarrow \infty$ if not explicitly stated otherwise. The functions of interests are the (group specific) cumulative hazard functions $A_1,A_2$ of the survival times defined by $A_j(t)=-\log (1-F_j(t))=\int _0^t(1-F_j{(s)})^{-1}\,\mathrm { d }F_j{(s)}$$(t>0)$. To be more specific, we want to test the proportional hazard assumption, i.e.,

$$\begin{aligned} { H_0} : A_2 = \vartheta A_1,\;\vartheta >0, \end{aligned}$$

while only the possibly censored times $X_{j,i}=\min (T_{j,i},C_{j,i})$ and their censoring status $\delta _{j,i}={\mathbf {1}}\{X_{j,i}=T_{j,i}\}$$(j=1,2;\,i=1,\ldots ,n_j)$ can be observed.

In the following, we introduce important statistics and estimators by adopting the counting process notation of Andersen et al. (1993). Define $N_{j,i}(t)={\mathbf {1}}\{X_{j,i}\le t,\,\delta _{j,i}=1\}$ and $Y_{j,i}(t)={\mathbf {1}}\{X_{j,i}\ge t\}$$(t\ge 0)$. Then $N_j(t)=\sum _{i=1}^{n_j}N_{j,i}(t)$ equals the amount of uncensored survival times, so-called events, in group j up to the time point t and $Y_j(t)=\sum _{i=1}^{n_j}Y_{j,i}(t)$ counts the individuals belonging to group j under risk at the time point t. In a similar way, we can interpret the pooled versions $N=N_1+N_2$ and $Y=Y_1+Y_2$. The Nelson–Aalen estimator ${{\widehat{A}}}_j$ for $A_j$ is given by

$$\begin{aligned} {{\widehat{A}}}_j(t)=\int _0^t \frac{{\mathbf {1}}\{Y_j{(s)}>0\}}{Y_j{(s)}}\,\mathrm { d }N_j{(s)}\quad (t\ge 0;\ j=1,2). \end{aligned}$$

It is well known that this nonparametric estimator obeys a central limit theorem, see Andersen et al. (1993). Heuristically, we have ${\widehat{A}}_2 \approx \vartheta {{\widehat{A}}}_1$ under ${ H_0}$. Based on this idea Andersen (1983) as well as Begun and Reid (1983) suggested to estimate the underlying $\vartheta$ by weighted rank estimators given by

$$\begin{aligned} {{\widehat{\vartheta }}}_{K} = \frac{ \int K{(s)} \,\mathrm { d }{{\widehat{A}}}_2{(s)}}{\int K{(s)} \,\mathrm { d }{{\widehat{A}}}_1{(s)} } \end{aligned}$$

(1)

for an appropriate (predictable) weight function K. Famous weight functions K corresponding to weighted logrank tests have the shape $K=(w\circ {{\widehat{F}}}) n^{-1}Y_1Y_2/(Y_1+Y_2)$ for $w\in \mathscr {W}=\{w:[0,1]\rightarrow (0,\infty )$ continuous and of bounded quadratic variation$\}$, where ${{\widehat{F}}}$ denotes the Kaplan–Meier estimator of the pooled sample, i.e.,

$$\begin{aligned} 1-{{\widehat{F}}}(t) = \prod _{(j,i):X_{j,i}\le t} \Bigl ( 1- \frac{\delta _{j,i} }{Y(X_{j,i})} \Bigr )\quad (t\ge 0). \end{aligned}$$

This class includes, among others, the classical logrank weight $K_L=n^{-1}Y_1Y_2/(Y_1+Y_2)$ and the weight $K_{\text {HF}}=K_{\text {L}} {{\widehat{F}}}^\rho$ suggested by Harrington and Fleming (1982). By Gill (1980) the estimator ${{\widehat{\vartheta }}}_K$ obeys a central limit theorem. The test for ${ H_0}$ of Gill and Schumacher (1987) is based on the observation that the quotient of two different rank estimators ${\widehat{\vartheta }}_1$ and ${{\widehat{\vartheta }}}_2$ is approximately equal to 1, independently of the true proportionality factor $\vartheta$. Closely related to these rank estimators are (extended) rank tests for the null of equal distributions $H^=_0: F_1=F_2$, or equivalently $H^=_0: A_1=A_2$. Probably, the most famous member is the classical logrank test corresponding to the weight $K_L$. This specific test, which was first proposed by Mantel (1966) and Peto and Peto (1972), is asymptotically efficient for proportional hazard alternatives. Enlarging the restricted null $H^=_0$ to our null $H_0$ of proportional hazards we need to correct, among others, $K_L$. The corrections lead to the following rescaled logrank statistic:

$$\begin{aligned} S_n(t,\vartheta )= \Bigl ( \frac{n}{n_1n_2} \Bigr )^{1/2}\int _{[0,X_{([nt])}]} \frac{Y_1Y_2}{Y_1+\vartheta Y_2} ( \,\mathrm { d }{{\widehat{A}}}_2-\vartheta \,\mathrm { d }{{\widehat{A}}}_1), \end{aligned}$$

(2)

where [x] denotes the integer part of x, we set $X_{(0)}=0$ and $X_{(1)}\le \cdots \le X_{(n)}$ are the order statistic of the pooled sample. $S_n(1,1)$ is the classical logrank statistic. The additional argument $\vartheta$ is a correction for the case $A_2=\vartheta A_1$, details are carried out in the subsequent section. By Gill (1980) $S_n(1,1)$ is asymptotically normal. An extension of his estimator for the limiting variance to our situation is

$$\begin{aligned} {{\widehat{\sigma }}}^2(t,\vartheta ) = \frac{n}{n_1n_2} \int {\mathbf {1}}_{[0,X_{([nt])}]} \frac{\vartheta Y_1Y_2}{(Y_1+\vartheta Y_2)^2 }\,\mathrm { d }(N_1+N_2). \end{aligned}$$

(3)

Both, $S_n(t,\vartheta )$ and ${{\widehat{\sigma }}}^2(t,\vartheta )$, can be rewritten as linear rank statistics noting that all involved processes only jump at the order statistics $X_{(i)}$. Let $\delta _{(i)}$ be the censoring status corresponding to $X_{(i)}$. Moreover, we introduce the group status $c_{(i)}$ of the individual corresponding to $X_{(i)}$. To be more specific, let $c_{(i)}=1$ if $X_{(i)}$ belongs to the second group and $c_{(i)}=0$ if it is a member of the first group. Then

$$\begin{aligned}&S_n(t,\vartheta )=\Bigl ( \frac{n}{n_1n_2} \Bigr )^{1/2}\sum _{i=1}^{[nt]} \delta _{(i)} \Bigl ( c_{(i)} - \frac{\vartheta \sum _{m=i}^nc_{(m)}}{\sum _{m=i}^n(1-c_{(m)}) + \vartheta \sum _{m=i}^nc_{(m)}} \Bigr ), \end{aligned}$$

(4)

$$\begin{aligned}&{{\widehat{\sigma }}}^2(t,\vartheta ) = \frac{n}{n_1n_2} \sum _{i=1}^{[nt]} \delta _{(i)} \frac{\vartheta \sum _{m=i}^nc_{(m)}\sum _{m=i}^n(1-c_{(m)})}{(\sum _{m=i}^n(1-c_{(m)}) + \vartheta \sum _{m=i}^nc_{(m)})^2}. \end{aligned}$$

(5)

3 Our test statistic and its asymptotic properties

For our asymptotic consideration we need two (common) assumptions. Let $\tau _j=\sup \{x>0: (1-F_j(x))(1-G_j(x))>0\}$$(j=1,2)$ be the upper limit of the observation times $X_{j,i}$ of group j, where $\tau _j =\sup [0,\infty )=\infty$ is allowed. Due to the weighting integrands in (2) and (3) only observations $X_{j,i}\le \tau =\min (\tau _1,\tau _2)$ have an impact in our statistic analysis. To observe not pure censored times we suppose that $F_1(\tau )>0$ or $F_2(\tau )>0$ holds. Moreover, we suppose that no group vanishes, i.e.,

$$\begin{aligned} 0< \liminf _{n\rightarrow \infty } \frac{n_1}{n} \le \limsup _{n\rightarrow \infty }\frac{n_1}{n}<1. \end{aligned}$$

The continuous martingale techniques are a favorable tool to obtain distributional convergence of the weighted rank estimators as well as the weighted rank statistics, or, more generally, the weighted rank processes. Since the most of these statistic can easily be written as linear rank statistics, compare to (4), discrete martingale techniques seems to be more natural. In our situation, it can be shown that $i\mapsto S_n(i/n,\vartheta )$ is a discrete martingale with respect to the filtration

$$\begin{aligned} \mathscr {F}_{n,i} = \sigma ( d_{(1)},\ldots ,d_{(i)}, \delta _{(1)},\ldots ,\delta _{(i+1)}), \end{aligned}$$

(6)

where $d_{(1)},\ldots ,d_{(n)}\in \{(j,i):\,1\le i \le n_j;\,j=1,2\}$ are the so-called anti ranks, i.e., if $d_{(k)}=(j,i)$ then $X_{(k)}$ is the value of individual i in group j. Compared to the usual filtration for the continuous approach we know a little bit about the future under $\mathscr {F}_{n,i}$, namely the next censoring status $\delta _{(i+1)}$. By using this discrete filtration Janssen and Neuhaus (1997) pointed out that the summands of $S_n(1,1)$ in (4) can be interpreted as “observed minus expected” under the restricted null $H_0^=:A_1=A_2$, see also Lemma 5.3 of Janssen and Werft (2004). We show that this can be extended to general $\vartheta$ and our general null $H_0$. Consequently, we can apply an appropriate discrete martingale central limit theorem, see Hall and Heyde (1980) and Jacod and Shiryaev (2003) as well as the references therein. We obtain under $A_2=\vartheta A_1$ that $t\mapsto S_n(t,\vartheta )$ converges in distribution to a rescaled Brownian motion $B\circ \sigma ^2$ on the Skorohod space D[0, 1] containing all right-continuous functions $x:[0,1]\rightarrow { {\mathbb {R}} }$ with existing left-hand limits. The rescaling function $t\mapsto \sigma ^2(t)$ can be estimated by ${{\widehat{\sigma }}}^2(t,\vartheta )$. Since the proportionality factor $\vartheta$ is unknown the canonical solution is to plug-in an appropriate estimator for it. For the readers’ convenience we restrict here to the (logrank) estimator ${\widehat{\vartheta }}={{\widehat{\vartheta }}}_{K}$ from (1) with $K= K_{\text {L}}$. In the “Appendix” the regularity conditions for more general estimators can be found, for instance, for weight functions of the shape $K=(w\circ {{\widehat{F}}})K_L$ with $w\in \mathscr {W}$. The plug-in-estimator leads to a non-vanishing rest term $R_n(t)=S_n( t,\vartheta )-S_n( t,{{\widehat{\vartheta }}})$ converging in distribution to $Z_K\sigma ^2(t)$ for all $t>0$, where $Z_K$ is a normal distributed random variable. To eliminate this rest term and the dependence on the unknown $\sigma ^2$ we suggest the following transformation of the statistic

$$\begin{aligned} T_n = {\widehat{\sigma }}^2(1,{\widehat{\vartheta }})^{-1/2}\sup _{t\in [0,1]}\Bigl \{ \Bigl | S_{n}(t,{{\widehat{\vartheta }}}) - \frac{{\widehat{\sigma }}^2(t,{\widehat{\vartheta }})}{{\widehat{\sigma }}^2(1,{\widehat{\vartheta }})}S_n(1,{{\widehat{\vartheta }}}) {\Bigr |} \Bigr \}. \end{aligned}$$

Theorem 1

Under ${ H_0}$ our $T_n$ converges in distribution to $T=\sup \{|B_0(t)|:t\in [0,1]\}$, where $B_0$ is a Brownian bridge.

Note that the classical Kolmogorov–Smirnov test converges in distribution to the same T. Hence, the distribution of T is well-known. Tables consisting its quantiles can be found in Hall and Wellner (1980) and Schumacher (1984). Let $\alpha \in (0,1)$ be a fixed level and $q_\alpha$ be the $\alpha$-quantile of T. Then we obtain by $\varphi _{n,\alpha }={\mathbf {1}}\{T_n>q_{1-\alpha }\}$ an asymptotically exact test of size $\alpha$, i.e., ${ E }(\varphi _{n,\alpha })\rightarrow \alpha$ under $H_0$. In contrast to the test of Gill and Schumacher (1987), which was designed for monotonic hazard ratio alternatives, our test is an omnibus test, as the one of Wei (1984), i.e., the test is consistent for any relevant alternative.

Theorem 2

Consider a general alternative $H_1$:$\{$ for every $\vartheta >0$ there is some $x\in (0,\tau )$ such that $A_2(x)\ne \vartheta A_1(x)\}$. Then our test $\varphi _{n,\alpha }$ is consistent for $H_1$, i.e., ${ E }(\varphi _{n,\alpha })\rightarrow 1$ under $H_1$ for all $\alpha \in (0,1)$.

4 Resampling tests

4.1 Permutation test

Let $c^{(n)}=(c_{(1)},\ldots ,c_{(n)})$ and $\delta ^{(n)}=(\delta _{(1)},\ldots ,\delta _{(n)})$. It is easy to check that our test statistic $T_n$ only depends on $(c^{(n)}, \delta ^{(n)})$ and, thus, we write $T_n(c^{(n)}, \delta ^{(n)})$ instead of just $T_n$ throughout this section. Instead of permuting the pairs $(c_{(i)},\delta _{(i)})$ we follow the approach of Neuhaus (1993) and Janssen and Mayer (2001), both studied weighted logrank test for testing $H_0^=: F_1=F_2$. Simulations of Neuhaus (1993) and Heller and Venkatraman (1996) promise a good finite sample performance of these weighted logrank tests. Their approach is to keep $\delta ^{(n)}$ fixed and only permute randomly the group membership $c_{(i)}$. In this spirit let $c^\pi _n=(c_{n,1}^\pi ,\ldots ,c_{n,n}^\pi )$ be a uniformly distributed permutation of $c^{(n)}$ independent of the data $\{(X_{j,i}, \delta _{j,i}): 1\le i \le n_j;\,j=1,2\}$.

Theorem 3

Let T be defined as in Theorem 1. Then we have under $H_0$ as well as under any fixed alternative $H_1$ from Theorem 2 that in probability

$$\begin{aligned} \sup _{t\ge 0}\Bigl | P (T_n(c_n^\pi , \delta ^{(n)})\le t \vert \delta ^{(n)} ) - P (T\le t) \Bigr | \rightarrow 0. \end{aligned}$$

Let $q_{n,\alpha }^\pi ({{\widetilde{\delta }}}_n)$$(\alpha \in (0,1);\,{{\widetilde{\delta }}}_n\in \{0,1\}^n)$ be the (left continuous) $\alpha$-quantile of the distribution of $T_n(c_n^\pi ,{\widetilde{\delta }}_n)$. Then $\varphi _{n,\alpha }^\pi = {\mathbf {1}}\{T_n(c^{(n)},\delta ^{(n)})>q_{n,1-\alpha }^\pi (\delta ^{(n)})\}$$(\alpha \in (0,1))$ is an asymptotically exact test for $H_0$, i.e., ${ E }(\varphi _{n,\alpha }^\pi )\rightarrow \alpha$ under $H_0$. Since the statement of Theorem 3 is also valid under fixed alternatives $H_1$ we can deduce from Lemma 1 of Janssen and Pauls (2003) that $\varphi _{n,\alpha }^\pi$ is consistent for general alternatives $H_1$ introduced in Theorem 2. To sum up, the permutation test and the asymptotic test have the same asymptotic behavior under the null as well as under fixed alternatives. However, our simulations show that for finite sample size the permutation test outperformed the asymptotic test. Partially, this can be explained by the following observation:

Since the distribution of $T_n(c_n^\pi ,{\widetilde{\delta }}_n)$ is discrete for all ${{\widetilde{\delta }}}_n\in \{0,1\}^n$ we may consider a randomized version

$$\begin{aligned} {{\widetilde{\varphi }}}_{n,\alpha }^\pi =\varphi _{n,\alpha }^\pi + \gamma ^\pi _{n,\alpha }(\delta ^{(n)}) {\mathbf {1}}\{T_n(c^{(n)},\delta ^{(n)})=q^\pi _{n,1-\alpha }(\delta ^{(n)})\} \end{aligned}$$

with $\gamma ^\pi _{n,\alpha }({{\widetilde{\delta }}}_n)\in [0,1]$$(\alpha \in (0,1),{{\widetilde{\delta }}}_n\in \{0,1\}^n)$. The advantage of the permutation approach compared, for instance, to the bootstrap approach and, of course, to the asymptotic test is that the (randomized) permutation test is usually finitely exact for at least a restricted null. In our situation, $c^{(n)}$ and $\delta ^{(n)}$ are independent under the restricted null $H^=_0: \{F_1=F_2,G_1=G_2\}$, see Neuhaus (1993). Hence, the randomized permutation test is even finitely exact, i.e., ${ E }({{\widetilde{\varphi }}}_{n,\alpha }^\pi )=\alpha$ under $H_0^=$.

4.2 Wild bootstrap

In this section, we apply the wild bootstrap technique of Wu (1986). Introduce n independent and identical distributed real-valued $G_{1,1},\ldots ,G_{1,n_1},G_{2,1},\ldots ,G_{2,n_2}$ with ${ E }(G_{j,i})=0$ and $\text {Var} (G_{j,i})=1$. Then the wild bootstrap version ${{\widehat{A}}}_j^G$$(j=1,2)$ of the Nelson–Aalen estimator ${{\widehat{A}}}_j$ is given by

$$\begin{aligned} {{\widehat{A}}}_j^G(t)&= \int _0^t \frac{{\mathbf {1}}\{Y_j{(s)}>0\}}{Y_j{(s)}}\,\mathrm { d }\Bigl ( \sum _{i=1}^{n_j}G_{j,i}N_{j,i}{(s)} \Bigr )=\sum _{i=1}^{n_j}G_{j,i}\int _0^t \frac{{\mathbf {1}}\{Y_j{(s)}>0\}}{Y_j{(s)}}\,\mathrm { d }N_{j,i}{(s)}. \end{aligned}$$

Now, we replace in the definition of $S_n$ the usual Nelson–Aalen estimators ${{\widehat{A}}}_1$ and ${{\widehat{A}}}_2$ by their wild bootstrap versions ${{\widehat{A}}}_1^G$ and ${{\widehat{A}}}_2^G$, respectively, and we denote the resulting statistic by $S_n^G$. Since the limit of $S_n^G$ is Gaussian a choice of normal distributed multipliers $G_{j,i}$ seems to be plausible, as used, for example, in a competing risk setting by Lin (1997). But taking the (discrete) structure of counting processes into account we should also consider discrete distributions for the multipliers $G_{j,i}$. For example, the Rademacher distribution, i.e., the uniform distribution on $\{-1,1\}$, see Liu (1988), or a centred Poisson distribution, see Beyersmann et al. (2013) and Mammen (1992). The latter is highly connected to the classical bootstrap, drawing with replacement, see the previously mentioned references. Janssen and Pauls (2003) offered a unified general approach for bootstrap and permutation statistics. Now, replacing $S_n$ by $S_n^G$ in our test statistic $T_n$ we get our wild bootstrap test statistic denoted by $T_n^G$. All other statistics, for instance ${{\widehat{\sigma }}}^2$ and ${{\widehat{\vartheta }}}$, remain unchanged. In contrast to the permutation approach, where we kept only the censoring status fixed, we keep here the whole data fixed.

Theorem 4

Let T be defined as in Theorem 1. Then under $H_0$ we have in probability

$$\begin{aligned} \sup _{x\ge 0}\Bigl | P (T_n^G\le x \vert (X_{j,i},\delta _{j,i}):1\le i \le n_j;\;j=1,2 ) - P (T\le x) \Bigr | \rightarrow 0. \end{aligned}$$

(7)

Let $q_{n,\alpha }^G=q_{n,\alpha }^G((X_{j,i},\delta _{j,i})_{1\le i \le n_j,j=1,2})$$(\alpha \in (0,1))$ be an $\alpha$-quantile of $T_n^G$ given the data $(X_{j,i},\delta _{j,i})_{1\le i \le n_j,j=1,2}$. Then $\varphi _{n,\alpha }^G= {\mathbf {1}}\{T_n^G>q_{n,\alpha }^G\}$$(\alpha \in (0,1))$ is an asymptotically exact test for $H_0$, i.e., ${ E }(\varphi _{n,\alpha }^\pi )\rightarrow \alpha$ under $H_0$. In contrast to the permutation statistic, see Theorem 3, the convergence in (7) is only valid under the null. But we can show that the conditional distribution of $T_n^G$ is tight under alternatives $H_1$ introduced in Theorem 2. As a result we get the bootstrap test’s consistency.

Theorem 5

For all alternatives $H_1$ discussed in Theorem 2 we have ${ E }(\varphi _{n,\alpha }^G)\rightarrow 1$ under $H_1$ for all $\alpha \in (0,1)$.

5 Simulations

5.1 Type I error

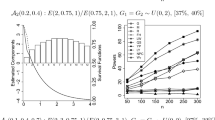
To compare the behavior of our asymptotic and resampling tests with the test of Gill and Schumacher (1987) and the one of Grambsch and Therneau (1994), we performed a simulation study for small sample sizes under different scenarios. The simulations were conducted with R (version 3.5.0), see R Core Team (2019). In this section, we consider the behavior of the tests mentioned before under the null $H_0:A_2=\vartheta A_1, \,\vartheta >0$. Since we are dealing with rank tests, monotone transformations of the data do not affect the outcome of the test statistic. That is why we can assume without loss of generality that $F_1$ belongs to a standard exponential distribution $\text {Exp}(1)$ and, thus, under the null $H_0$ the second group follows also a exponential distribution $\text {Exp}(\vartheta )$ with general parameter $\vartheta >0$. We considered 9 different proportionality factors $\vartheta \in \{0.2,0.4,0.6,0.8,1,2,3,4,5\}$ and two different sample sizes $n\in \{56,224\}$. To discuss balanced and unbalanced sample size cases as well as different censoring settings, we took 3 different Scenarios into account, which are summarized in Table 1. The group sizes are $n_1=\kappa _1n$ and $n_2=n-n_1$. For the censoring distribution, we used exponential distributions $C_{j,i}\sim \text {Exp}(\mu _{j,\vartheta })$ and uniform distributions $C_{j,i}\sim \textit{Unif}(0,\mu _{j,\vartheta })$ on the interval $(0,\mu _{j,\vartheta })$. The parameters $\mu _{j,\vartheta }$ are chosen such that they lead to an average censoring rate of $r_j$ specified in Table 1. In the supplement, we explain how these parameters can be determined. The empirical sizes were estimated based on 5000 iterations and the resampling tests’ quantiles were estimated by 1000 iterations.

Table 1 Simulation scenarios

For our tests we used the estimator ${{\widehat{\vartheta }}}={{\widehat{\vartheta }}}_K$ with the logrank weight $K=K_{\text {L}}$ as recommended before. For the test of Gill and Schumacher (1987) we followed their suggestion and used the two weights corresponding to the logrank test and the Peto–Prentice version, see Peto and Peto (1972) and Prentice (1978), of the generalized Wilcoxon test, respectively. The test of Grambsch and Therneau (1994) is already implemented in R, see the function cox.zph in the package survival.

For the wild bootstrap we considered three different distributions for the multipliers, namely the Rademacher, the standard normal distribution and the centred Poisson distribution, see Sect. 4.2 for details to these distributions. To not overload the plots we compare in Fig. 1 only the three bootstrap tests. The curves of the empirical sizes are very close to each other and nearly indistinguishable in most of the cases. In the comparison with the other tests, see Fig. 2, we just include the Rademacher multipliers. In the small sample size setting $n=56$, it is apparent that the test of Gill and Schumacher (1987) leads to quite liberal decisions with empirical sizes between 5.5 and 8.4% and in average around $7\%$. For the larger sample size case ($n=224$), the empirical sizes are closer to the $5\%$ benchmark with an overall average of $5.5\%$. The test of Grambsch and Therneau (1994) is quite conservative, in particular, for $\vartheta$ far away from 1. Our asymptotic test is also very conservative with empirical sizes around 2–3% for $n=56$ and around 3–5% for $n=224$. The permutation and Rademacher bootstrap tests’ empirical sizes are always close to the nominal level $5\%$ even in the small sample size setting $n=56$. But the Rademacher wild bootstrap and so the other two wild bootstrap multipliers are slightly liberal in some settings, see in particular the close-up in Fig. 1, whereas the permutation test’s empirical sizes are mainly below the $5\%$ level.

Fig. 1

Empirical sizes of the three bootstrap tests based on the Rademacher (Rade), the normal (Norm) and the centred Poisson (Pois) distribution

Fig. 2

Empirical sizes of our permutation (Per), bootstrap (Bo) and asymptotic (Asy) test as well as the tests’ empirical sizes of Gill and Schumacher (1987) (GS) and Grambsch and Therneau (1994) (GT)

5.2 Power simulations

In this section, we present simulations about the tests’ power behavior under different alternatives. Since the test of Gill and Schumacher (1987) was quite liberal in our simulations for small sample sizes we exclude it here. Again, we restricted to the case that the survival times of the first group are $\text {Exp}(1)$-distributed. For the second group, we disturbed the null assumption $A_2={0.6}A_1$ in different hazard directions:

$$\begin{aligned} A_2(t)=\int _0^t 0.6 + w(F_1(s)) \,\mathrm { d }A_1{(s)} \quad (t\ge 0), \end{aligned}$$

(8)

where the hazard direction $w:[0,1]\rightarrow { {\mathbb {R}} }$ is continuous and of bounded variation. To be more specific, we considered two different hazard directions:

• 1. (central hazards) $w(x)={50}x(1-x)$.

• 2. (late hazards) $w(x)={70}x^3(1-x)$.

Moreover, we included an alternative, which was already discussed by Kraus (2009):

$$\begin{aligned} A_2(t)=\int _0^t \alpha _2(t)\,\mathrm { d }t\quad \text {with }\alpha _2(t)= \frac{3}{2}(t-1)^2. \end{aligned}$$

(9)

For the group sizes as well as the censoring, we considered again Scenarios 1–3 introduced in the previous section. Of course, the censoring parameters $\mu _{j,\vartheta }$ needed to be updated for the second group. Due to the complex nature of the alternatives, it is not as easy as before to determine $\mu _{j,\vartheta }$ and, thus, we decided to find appropriate parameters by trial and error. The concrete values, which we used, can be found in the supplement. The tests’ empirical power values were estimated based on 5000 iterations and the resampling tests’ quantiles were estimated by 1000 iterations. In Tables 2, 3 and 4 we summarized the results for various sample sizes, where the highest values are marked in boldface.

To summarize the results, we can observe that the GT test leads to the highest empirical power values in scenario 2 for the late and central hazard alternative as well as in scenario 3 for the late hazard alternative when $n=112$. Nevertheless, our permutation and our Rademacher wild bootstrap test can compete with it in these settings. For all the other situations, our resampling tests lead to higher power values than the GT test. In particular, our tests outperform the GT test for the alternative given by (9). It can be seen that among the wild bootstrap approaches the Rademacher multipliers are favorable. Moreover, we can observe that either all resampling test lead to quite similar sizes or the permutation test’s size is the highest.

Table 2 Empirical power values (highest ones boldfaced) of the test of Grambsch and Therneau (1994) (GT), our permutation (Per), our asymptotic (Asy) as well as our three different bootstrap test based on Rademacher (Rade), normal (Norm) and centered Poisson (Pois) multipliers, respectively, for the central hazard alternative

Table 3 Empirical power values (highest ones boldfaced) of the test of Grambsch and Therneau (1994) (GT), our permutation (Per), our asymptotic (Asy) as well as our three different bootstrap test based on Rademacher (Rade), normal (Norm) and centered Poisson (Pois) multipliers, respectively, for the late hazard alternative

Table 4 Empirical power values (highest ones boldfaced) of the test of Grambsch and Therneau (1994) (GT), our permutation (Per), our asymptotic (Asy) as well as our three different bootstrap test based on Rademacher (Rade), normal (Norm) and centered Poisson (Pois) multipliers, respectively, for alternative given by (9)

6 Real data examples

In this section, we illustrate the applicability of our tests by discussing two examples. The first data set is taken from Fleming et al. (1980) and consists of times from treatment to disease progression for 35 patients suffering on ovarian cancer, where 15 patients (9 censored) are categorized to stage II ovarian cancer and the remaining 20 individuals (4 censored) are stage IIa patients. The group balancing parameter $\kappa _1$ and the censoring rates of Scenario 2 from the previous section correspond exactly to the situation here. The data set is available in the R package coin, see Hothorn et al. (2006), and is denoted by ocarcinoma there. Gill and Schumacher (1987) already used this data set. In Fig. 3 the group-specific Nelson–Aalen estimators are plotted. In Table 5 we present the p values of the tests already used in the previous section. Hereby, we restrict ourselves to the wild bootstrap test with Rademacher multipliers, due to our findings in Sect. 5.1. It can be seen that all tests reject the null of proportional hazards for the nominal level of $5\%$, which is in line with the impression of non-proportionality getting by the plot in Fig. 3.

The second data set is taken from Collett (2015), the data set can be found in Appendix B.1 therein. The data set consists of the survival times of 44 patients suffering from chronic active hepatitis. 22 of these patients were selected by random and got the drug Prednisolone. The other 22 patients served as a control group and did not get any treatment. The censoring rates are $50\%$ in the treatment group and $27\%$ in the control group. Observe that Scenario 1 from the previous section reflects exactly the group balancing and the censoring rates of this data set. The details of this clinical trial were described by Kirk et al. (1980). In Fig. 3 the group-specific Nealson–Aalen estimators are plotted and in Table 5 the tests’ p values can be found. Again, the plot suggests non-proportionality of the hazards. However, in contrast to the previous example only one test, namely the Rademacher wild bootstrap test, can reject the null hypothesis of proportionality for the nominal level of $5\%$. It was already recognized by Kraus (2009) that the test of Gill and Schumacher (1987) cannot detect the presence of non-proportional hazards for this data set. The reason is that the test was designed for alternatives with a monotone ratio of the hazard rates, which is not the case in this example. But also our asymptotic and our permutation test are not able to reject the null, where the permutation test’s p value is quite close to the $5\%$ benchmark compared to the other tests.

Fig. 3

Group-specific Nelson–Aalen estimators for the ovarian data set (left) and the hepatitis data set (right). The solid line corresponds to the patients with stage II (in the left plot) and to the control group (in the right plot), respectively

7 Summary and discussion

Our simulations reveal that for small sample sizes both resampling techniques are a real improvement of our asymptotic test and they lead to better results than the existing (asymptotic) methods of Gill and Schumacher (1987) and Grambsch and Therneau (1994). Regarding this observation, one may try to improve the finite sample performance of other (existing) tests by using wild bootstrapping or permutation techniques as a future project. The simulation results show that the (slightly conservative) permutation test leads to higher power values than the (slightly liberal) wild bootstrap approach in most of the cases. Moreover, we favor, in general, the permutation test due to its finite exactness under the restricted null $H_0^{=}:F_1=F_2,\,G_1=G_2$. Altogether, we recommend using the permutation approach. But, as explained in the following two paragraphs, the wild bootstrap approach is more flexible regarding extensions.

As pointed out be one of the referees, other types of our statistic may be interesting as well, e.g., an integral-type statistic in the spirit of Cramér and von Mises. Since the wild bootstrap version directly recovers the covariance structure of the process $S_n$, we can transfer our results concerning wild bootstrapping to other statistic types by a simple modification of the proofs. However, the situation for the permutation approach is more delicate because the asymptotic covariance structure differs from the one of $S_n$. The solution for this problem is to use a studentized test statistic, as already done several times in the literature (Neuhaus 1993; Janssen 1997, 2005; Janssen and Pauls 2003; Pauly 2011; Konietschke and Pauly 2012; Omelka and Pauly 2012; Chung and Romano 2013; Pauly et al. 2015). A studentized version of, e.g., the integral-type statistic is rather complicated in comparison to our sup-statistic. One reason for this is the time invariance of the latter. That is why we prefer the sup-statistic in this paper.

Table 5 p values for the ovarian data set and the hepatitis data set of our asymptotic (Asy), permutation (Per) and Rademacher wild bootstrap (Bo) tests as well as the test of Gill and Schumacher (GS) and Grambsch and Therneau

We want to suggest two different ways to extend our approach to the k-sample case. On the one hand, pairwise testing $H_0^{ij}:A_i=\vartheta _{ij}A_j$ for all $1\le i < j \le k$ can be done in a first step followed by the classical Bonferroni adjustment of the resulting $m=k(k-1)/2$ tests. If m is large, this leads to very conservative decisions and we suggest to apply the FDR-controlling procedure of Benjamini and Yekutieli (2001) instead. On the other hand, by more technical effort the process convergence of $S_n$ proven in the “Appendix” can be extended to the multivariate case. Then we may use ${{\widetilde{T}}}_n=\max _{i,j} T_n^{ij}$ as our test statistic, where $T^{ij}_n$ denotes the sup-statistic for the pairwise comparison of groups i and j. But the limiting distribution of ${{\widetilde{T}}}_n$ is not distribution-free in the case $k>2$ and depends on the unknown distribution functions $F_1,G_1,\ldots$ This problem may be solved by wild bootstrapping again or, alternatively, by group-wise bootstrapping, where the bootstrap sample for group j is drawn from the observations of group j only and not from the pooled observations, as in the classical bootstrap of Efron (1979). In contrast to these bootstrap methods, we do not expect the permutation approach to work because the statistic ${{\widetilde{T}}}_n$ cannot be studentized appropriately as in the two-sample case.

Appendix: Proofs

In the following we give all the proofs. Considering appropriate subsequences we can assume without loss of generality that $n_1/n\rightarrow \kappa _1\in (0,1)$ and $n_2/n\rightarrow \kappa _2=1-\kappa _1$. Note that the final statements of all our theorems do not depend on $\kappa _1$ and $\kappa _2$ as well as the considered subsequence. For the readers’ convenience we present some technical, known results before giving the actual proofs.

1.1 Preliminaries

One basic tool for our proofs are discrete martingale theorems, see Hall and Heyde (1980) and references therein. For our purposes, a simplified version of Theorem 8.3.33 from Jacod and Shiryaev (2003) is sufficient, see also their Theorem 2.4.36.

Proposition 1

[c.f. Jacod and Shiryaev (2003)] For each $n\in { {\mathbb {N}} }$ let $(\xi _{n,i})_{1\le i \le n}$ be a martingale difference scheme with respect to some filtration $({\mathscr {F}}_{n,i})_{0\le i \le n}$, i.e., ${ E }(\xi _{n,i}\vert {\mathscr {F}}_{n,i-1})=0$ for every $1\le i \le n$. Assume that the conditional Lindeberg condition, $\sum _{i=1}^{n} { E }(\xi _{n,i}^2{\mathbf {1}}\{|\xi _{n,i}|\ge \varepsilon \}\vert \mathscr {F}_{n,i-1})\rightarrow 0$ in probability for all $\varepsilon >0$, is fulfilled. Define $M_n$ by $M_n(t)=\sum _{i=1}^{[nt]}\xi _{n,i}$$(t\in [0,1])$. Suppose that the predictable quadratic variation process $\langle M_n\rangle$ given by $\langle M_n\rangle (t)=\sum _{i=1}^{[nt]} { E }(\xi _{n,i}^2\vert \mathscr {F}_{n,i-1})$$(t\in [0,1])$ converges in probability pointwisely to a continuous function $\sigma ^2:[0,1]\rightarrow [0,\infty )$. Then $M_n$ converges in distribution on the Skorohod space D[0, 1] to the rescaled Brownian motion $B\circ \sigma ^2$, where B denotes a classical Brownian motion.

Proposition 2

[c.f. Janssen and Mayer (2001)] Assume that all assumptions of our paper are underlying. Let ${{\widetilde{\delta }}}_n=({\widetilde{\delta }}_{n,1},\ldots ,{{\widetilde{\delta }}}_{n,n})\in \{0,1\}^n$ and $w_n=(w_{n,1},\ldots ,w_{n,n})\in { {\mathbb {R}} }^n$ such that $\lim _{n\rightarrow \infty }n^{-1}\sum _{i=1}^n{{\widetilde{\delta }}}_{n,i}w_{n,i}^2\in (0,\infty )$ and $\max \{|w_{n,i}|:i=1,\ldots ,n\}\le M\in (0,\infty )$ for all $n\in { {\mathbb {N}} }$. Define for all $t\in [0,1]$

$$\begin{aligned}&W_n(t){=}\Bigl ( \frac{n}{n_1n_2} \Bigr )^{1/2} \sum _{i=1}^{[nt]}w_{n,i}{{\widetilde{\delta }}}_{n,i} \Bigl ( c^\pi _{n,i} - \frac{\sum _{j=i}^nc_{n,j}^\pi }{n-i+1} \Bigr ),\\&V_n(t)=\Bigl ( \frac{n}{n_1n_2} \Bigr )^{1/2} \sum _{i=1}^{[nt]}w_{n,i}^2{{\widetilde{\delta }}}_{n,i} \Biggl [ \frac{\sum _{j=i}^n(c_{n,j}^\pi )^2}{n-i+1}- \left( \frac{\sum _{j=i}^nc_{n,j}^\pi }{n-i+1} \right) ^2 \Biggr ],\\&\beta ^2_n(t)=\frac{1}{n-1}\sum _{i=1}^{[nt]}w_{n,i}^2{{\widetilde{\delta }}}_{n,i} \frac{n-i}{n-i+1},\\&\alpha _n(t)=\inf \{s\in [0,1]: \beta _n^2(s)>t \beta _n^2(1)\}, \end{aligned}$$

where for the latter we set $\inf \emptyset = 1$. Then $V_n(\alpha _n(t))/V_n(1)$ converges in probability to t for all $t\in [0,1]$ and $V_n(1)^{-1/2}W_n\circ \alpha _n$ tends in distribution to a Brownian motion B on the Skorohod space D[0, 1]. Moreover, the sequences $(V_n(1))_{n\in { {\mathbb {N}} }}$ and $(W_n(1))_{n\in { {\mathbb {N}} }}$ are tight, i.e., we have $\lim _{t\rightarrow \infty }\limsup _{n\rightarrow \infty } P ( |W_n(1)| \ge t)+ P ( |V_n(1)| \ge t)=0$.

Proof

It is easy to check that due to the assumptions on $w_n$ and ${{\widetilde{\delta }}}_n$ we have $0<\liminf _{n\rightarrow \infty }\beta _n^2(1)\le \limsup _{n\rightarrow \infty }\beta _n^2(1)<\infty$ and, thus, condition (15) of Janssen and Mayer (2001) is fulfilled. Moreover, the conditions for the regression coefficients in the paper of Janssen and Mayer (2001) hold for our (rescaled) coefficients ${{\widetilde{c}}}_{(i)}= (n_1n_2/n)^{-1/2} c_{(i)}$. Consequently, we can apply their Theorem 1 and Lemma 3. Note that $\beta _n^2(1)=1$ is assumed in their Lemma 3 as well as in the proof of their Theorem 1, but this can always be ensured by rescaling the weight coefficients ${{\widetilde{w}}}_{n,i}= w_{n,i}/\beta _n(1)$. Now, the desired distributional convergence of $V_n(1)^{-1/2}W_n\circ \alpha _n$ follows from their Theorem 1. In the proof of Lemma 3 Janssen and Mayer (2001) showed $\beta _n^2(\alpha _n(t))/\beta _n^2(1)\rightarrow t$ for all $t\in [0,1]$ and by their (33) we have $[1/\beta _n^{2}(1)]\sup _{t\in [0,1]}|\beta _n^2(t)-V_n(t)|\rightarrow 0$ in probability. Combining both we obtain the convergence in probability of $V_n(\alpha _n(t))/V_n(1)$. Moreover, their Theorem 1 implies that $W_n(1)V_n(1)^{-1/2}$ converges in distribution to a standard normal distributed random variable. Finally, the tightness of $(V_n(1))_{n\in { {\mathbb {N}} }}$ and $(W_n(1))_{n\in { {\mathbb {N}} }}$, respectively, follows from $\limsup _{n\rightarrow \infty }\beta _n^2(1)<\infty$. $\square$

The subsequent result concerning linear rank tests is well-known and can be found, for example, in the book of Hájek et al. (1999). Combining their Theorem 3 in Section 3.3.1 and Chebyshev’s inequality we obtain:

Proposition 3

[c.f. Hájek et al. (1999)] Let $w_{n,1},\ldots ,w_{n,n}$ be real-valued constants. Introduce the linear rank statistic $\xi _n^\pi =\sum _{i=1}^{n}w_{n,i}(c_{n,i}^\pi -{{\bar{c}}})$, where $\bar{c}=n^{-1}\sum _{i=1}^nc_{n,i}^\pi =n_2/n$. Then ${ E }(\xi _n^\pi )=0$ and

$$\begin{aligned} \text {Var} (\xi _n^\pi ) = \frac{n_1n_2}{n(n-1)}\sum _{i=1}^{n} (w_{n,i}-{\bar{w}})^2,\quad {{\bar{w}}} = n^{-1}\sum _{i=1}^nw_{n,i}. \end{aligned}$$

In particular, if $\max _{1\le i \le n}|w_{n,i}|\le M/n$ for all $n\in { {\mathbb {N}} }$ and some fixed $M>0$ then $\text {Var} (\xi _n^\pi )\rightarrow 0$ and $\xi _n^\pi$ converges in probability to 0.

1.2 Proof of Theorem 1

The following lemma and the corresponding proof are extensions of Lemma 5.3 and its proof of Janssen and Werft (2004).

Lemma 1

Suppose that $A_2=\vartheta A_1$ for some $\vartheta >0$. Then $(\xi _{n,i})_{1\le i \le n}$ given by

$$\begin{aligned} \xi _{n,i}= \Bigl ( \frac{n}{n_1n_2} \Bigr )^{1/2} \delta _{(i)} \Bigl ( c_{(i)} - \frac{\vartheta \sum _{m=i}^nc_{(m)}}{\sum _{m=i}^n(1-c_{(m)}) + \vartheta \sum _{m=i}^nc_{(m)}}\Bigr ) \end{aligned}$$

is a martingale difference scheme with respect to the filtration $({\mathscr {F}}_{n,i})_{0\le i \le n}$ defined in (6). Moreover, the predictable quadratic variation process $\langle M_n\rangle$ of the martingale $M_n$ given by $M_n(t)=S_n(t)=\sum _{i=1}^{[nt]}\xi _{n,i}$$(t\in [0,1])$ equals ${{\widehat{\sigma }}}^2$ from (5).

Proof

Fix $1\le i\le n$. First, observe that $\sum _{m=i}^nc_{(m)}$ and $\delta _{(i)}$ are predictable, i.e., $\mathscr {F}_{n,i-1}$-measurable. Since $c_{(i)}$ equals either 0 or 1 it is easy to see that all postulated statements follow from

$$\begin{aligned} { E }( \delta _{(i)} c_{(i)} \vert {\mathscr {F}}_{n,i-1}) = \delta _{(i)}\frac{ \vartheta \sum _{m=i}^nc_{(m)}}{\sum _{m=i}^n(1-c_{(m)}) + \vartheta \sum _{m=i}^nc_{(m)}}. \end{aligned}$$

(10)

Clearly, (10) is true in the case $\delta _{(i)}=0$. Hence, it is sufficient for the proof of (10) to consider events $A\in {\mathscr {F}}_{n,i-1}$ of the form $A= \{ \delta _{(i)}=1,\,\delta _{(m)}= \delta _m, \,d_{(m)}= d_m;\;m\le i-1\}$ with constants $\delta _1, \ldots ,\delta _{i-1}\in \{0,1\}$ and pairwise different $d_1,\ldots ,d_{i-1}\in \{(j,k): 1\le k \le n_j;\,j=1,2\}$. Introduce $Z_{j,k}={\mathbf {1}}\{d_{(i)}=(j,k)\}$$(1\le k \le n_j;\, j=1,2)$. Clearly, $1-c_{(i)}= \sum _{k=1}^{n_1} Z_{1,k}$ and $c_{(i)}= \sum _{k=1}^{n_2} Z_{2,k}$. That is why we analyse $Z_{j,k}$ in the next step. For this purpose we define the set $B_x=\bigl \{ X_{ d_{1}}<\cdots<X_{d_{i-1}}< x\,\, ,\,\, \delta _{d_{(m)}} = \delta _{m}\,\,\text {for}\,\,m\le i-1\,\bigr \}\quad (x>0)$. From Fubini’s theorem and $\mathrm dF_j / \mathrm dA_j = 1- F_j$ we obtain for all $(j,k)\in J=\{(j,k): 1\le k \le n_j;\,j=1,2\}{\setminus } \{ d_1,\ldots , d_{i-1}\}$ that

$$\begin{aligned} P \left( \left\{ Z_{j,k} = 1 \right\} \cap A \right)&= \int _0^\infty P ( B_x) [1-G_j(x)] \prod _{(r,s)\in J{\setminus } \{(j,k)\} } [1-F_r(x)] [1-G_r(x)]\,\mathrm dF_j\nonumber \\&= \int _0^\infty P ( B_x)\;\prod _{(r,s)\in J } [1-F_r(x)] [1-G_r(x)] \;\mathrm dA_j(x) \nonumber \\&= C^* \left( \, \vartheta + \left( 1 - \vartheta \right) {\mathbf {1}}\{ j = 1 \} \,\right) \end{aligned}$$

(11)

for some $C^*\ge 0$. Obviously, $P ( \{ Z_{j,k} = 1 \} \cap A )=0$ for $(j,k)\notin J$. Remind in the following that $n_1-\sum _{m=1}^{i-1}(1-c_{d_m})$ and $n_2-\sum _{m=1}^{i-1}c_{d_m}$ elements of J belong to the first and second group, respectively. Thus, we can deduce from summing up all probabilities $P ( \{ Z_{j,k} = 1 \} \cap A )$ that

$$\begin{aligned} C^*= P (A) / \Bigl [\vartheta \Bigl (n_2-\sum _{m=1}^{i-1}c_{d_m}\Bigr )+ n_1-\sum _{m=1}^{i-1}(1-c_{d_m})\Bigl ]. \end{aligned}$$

Finally, inserting $C^*$ into (11) and recalling $c_{(i)}= \sum _{k=1}^{n_2} Z_{2,k}$ proves (10) since $n_2-\sum _{m=1}^{i-1}c_{d_m}$ equals $\sum _{m=i}^nc_{(m)}$ under A. $\square$

It is easy to see that there is a sequence $(b_n)_{n\in { {\mathbb {N}} }}$ converging to 0 such that $\max _{1\le i \le n}|\xi _{n,i}|\le b_n$. This implies immediately the conditional Lindeberg condition. Thus, to apply Proposition 1 it remains to show convergence of the corresponding predictable quadratic variation ${{\widehat{\sigma }}}^2$. For this purpose we prefer the following slight modification of its representation in (3)

$$\begin{aligned} {{\widehat{\sigma }}}^2(t,\vartheta ) = \int {\mathbf {1}}\Bigl \{\frac{Y}{n}\ge \frac{n-[nt]+1}{n}\Bigr \} w_{n} \,\mathrm { d }\frac{N}{n},\quad w_{n}=\frac{n^2}{n_1n_2}\frac{\vartheta Y_1Y_2}{(Y_1+\vartheta Y_2)^2}. \end{aligned}$$

(12)

Clearly, the integrand is bounded. As well known, we can deduce from the extended Glivenko–Cantelli theorem that $\sup \{|Y_{j}(t)/n-y_j(t)|:t\in [0,\infty )\}\rightarrow 0$ as well as $\sup \{|w_{n}(t)-w(t)|:t\in [0,s]\}\rightarrow 0$ for every $s<\tau$, both in probability, where $y_j=\kappa _j(1-F_j)(1-G_j)$ and $w=(\kappa _1\kappa _2)^{-1}y_1y_2/( y_1 + \vartheta y_2)^2$. Set $y=y_1+y_2$. Moreover, by the law of large numbers $N_j(t)/n$ converges in probability to $L_j(t)=\kappa _j P (X_{j,1}\le t, \Delta _{j,1}=1)=\kappa _j\int _{[0,t]}(1-G_j)\,\mathrm { d }F_j$$(t\ge 0; \,j=1,2)$ and, thus, $N(t)/n\rightarrow L(t)=L_1(t)+L_2(t)$. Since $|w_{n}|$ is uniformly bounded and $\mathrm dF_j / \mathrm dA_j = 1- F_j$ we obtain that $\sigma _n^2(t,\vartheta )$ converges in probability to

$$\begin{aligned} \sigma ^2(t,\vartheta )= \frac{\vartheta }{\kappa _1\kappa _2}\int {\mathbf {1}}\{y\ge 1-t\} \frac{y_1y_2}{(y_1+\vartheta y_2)^2}\,\mathrm { d }L. \end{aligned}$$

Applying Proposition 1 yields that $S_n(\cdot ,\vartheta )$ converges in distribution to $B\circ \sigma ^2(\cdot , \vartheta )$ on the Skorohod space D[0, 1], where B is a Brownian motion.

In the next step, we plug-in the estimator ${{\widehat{\vartheta }}}$ of the proportionality factor $\vartheta$. The statement of Theorem 1 holds for general estimators ${{\widehat{\vartheta }}}$ of the proportionality factor $\vartheta$ fulfilling the subsequent Assumption I. As already mentioned in Sect. 2, by Gill (1980) ${{\widehat{\vartheta }}}_K$ with $K=(w\circ {{\widehat{F}}})K_L$ obeys a central limit theorem and, in particular, fulfills the subsequent Assumption I.

Assumption I Let ${{\widehat{\vartheta }}}$ be a positive random variable which is bounded with probability one, i.e., $P ({{\widehat{\vartheta }}} \le \eta _\vartheta )\rightarrow 1$ for some $\eta _\vartheta$. Suppose that $n^{1/2}({{\widehat{\vartheta }}} - \vartheta )$ converges in distribution to a real-valued random variable $Z_\vartheta$.

Obviously, ${{\widehat{\vartheta }}}$ is a consistent estimator for $\vartheta$ under Assumption I, i.e., ${{\widehat{\vartheta }}}$ tends in probability to $\vartheta$. Analogously to the convergence of ${{\widehat{\sigma }}}^2(t,\vartheta )$, we can deduce from the consistency that ${{\widehat{\sigma }}}^2(t,{{\widehat{\vartheta }}})$ converges in probability to $\sigma ^2(t,\vartheta )$ for every $t\in [0,1]$. It is easy to check that $S_n(t,\vartheta ) - S_n(t,{{\widehat{\vartheta }}})$ equals $Z_{n,\vartheta }{{\widetilde{\sigma }}}_n^2(t,\vartheta )$, where

$$\begin{aligned} Z_{n,\vartheta }&= \Bigl (\frac{n_1n_2}{n}\Bigr )^{1/2} \vartheta ^{-1}({{\widehat{\vartheta }}}-\vartheta ),\\ {{\widetilde{\sigma }}}^2(t,\vartheta )&=\frac{n^2}{n_1n_2}\int {\mathbf {1}}\Bigl \{\frac{Y}{n}\ge \frac{n-[nt]+1}{n}\Bigr \} \frac{\vartheta Y_1Y_2}{(Y_1+\vartheta Y_2)(Y_1+{{\widehat{\vartheta }}} Y_2)} \,\mathrm { d }\frac{N}{n}. \end{aligned}$$

Clearly, $Z_{n,\vartheta }$ converges in distribution to ${{\widetilde{Z}}}_\vartheta = (\kappa _1\kappa _2)^{1/2} Z_\vartheta /\vartheta$. Analogously to the argumentation above, ${{\widetilde{\sigma }}}^2(t,\vartheta )$ converges in probability to $\sigma _n^2(t,\vartheta )$ for all $t\in [0,1]$. Hence, for every $t\in [0,1]$

$$\begin{aligned} R_n(t,\vartheta )= S_n(t,\vartheta )-S_n(t,{{\widehat{\vartheta }}}) - \frac{{\widehat{\sigma }}^2_n(t,{{\widehat{\vartheta }}})}{{{\widehat{\sigma }}}^2(1,{{\widehat{\vartheta }}})}[S_n(1,\vartheta )-S_n(1,{{\widehat{\vartheta }}})] \rightarrow 0 \end{aligned}$$

in probability. Consequently, $(S_n(\cdot ,\vartheta ), {{\widehat{\sigma }}}^2(\cdot ,{{\widehat{\vartheta }}}), R_n(\cdot ,\vartheta ))$ converges in distribution to $(B\circ \sigma ^2(\cdot ,\vartheta ),\sigma ^2 (\cdot ,\vartheta ), 0)$ on $D[0,1]\times D[0,1]\times D[0,1]$. By the continuous mapping theorem, respecting that $t\mapsto \sigma ^2(t,\vartheta )$ is continuous and nondecreasing,

$$\begin{aligned} T_n&= {\widehat{\sigma }}^2_n(1,{\widehat{\vartheta }})^{-1/2}\sup _{t\in [0,1]}\Bigl \{ \Bigl | S_{n}(t,\vartheta ) - \frac{ {\widehat{\sigma }}^2_n(t,{\widehat{\vartheta }})}{{\widehat{\sigma }}^2_n(1,{\widehat{\vartheta }})}S_n(1,\vartheta ) + R_n(t,\vartheta )\Bigr | \Bigr \}\\&\rightarrow \sigma ^2(1,\vartheta )^{-1/2}\sup _{t\in [0,1]}\Bigl \{ \Bigl | B\Bigl (\sigma ^2(1,\vartheta ) t \Bigr ) - t B\Bigl ( \sigma ^2(1,\vartheta ) \Bigr ) {\Bigr |} \Bigr \}={{\widetilde{T}}}. \end{aligned}$$

Note that the assumptions ensure $\sigma ^2(1,\vartheta )>0$. Let $B_0$ be a Brownian bridge on [0, 1]. Since $B(c^2\cdot )$ and cB for every $c>0$ as well as $t\mapsto B(t)-tB(1)$$(t\in [0,1])$ and $B_0$ have the same distribution, respectively, we obtain that the distribution of ${{\widetilde{T}}}$ equals the one of T.

1.3 Proof of Theorem 2

Let ${{\widehat{\vartheta }}}={{\widehat{\vartheta }}}_K$ with $K=(w\circ {{\widehat{F}}})K_L$ for some $w\in {\mathscr {W}}$. Following the argumentation of the convergence of ${\widehat{\sigma }}^2(t,{{\widehat{\vartheta }}})$ in the proof of Theorem 1 we obtain under $H_1$ that in probability

$$\begin{aligned} -\log (1-{{\widehat{F}}}(x))&= \int _0^x \log (1-Y^{-1})^n \,\mathrm { d }\frac{N}{n} \nonumber \\&\rightarrow \int _0^x (1-y^{-1})\,\mathrm { d }L\equiv -\log [1-F(x)]\quad (x<\tau ), \end{aligned}$$

(13)

$$\begin{aligned} {{\widehat{\vartheta }}}_K&\rightarrow \frac{ \int {{\widetilde{K}}} \,\mathrm { d } A_2}{\int {{\widetilde{K}}} \,\mathrm { d } A_1 } \equiv \vartheta _0>0, \quad {{\widetilde{K}}} = (w\circ S) \frac{y_1y_2}{y}, \end{aligned}$$

(14)

where $y_1,y_2,y,L$ are defined as in the proof of Theorem 1. Similarly, we can deduce that $n^{-1/2}T_n$ converges in probability under $H_1$ to

$$\begin{aligned} {\sigma }^2(t,{\vartheta _0})^{-1/2}\sup _{t\in [0,1]}\Bigl \{ \Bigl | S(t,\vartheta _0) - [{\sigma }^2(t,{\vartheta _0})/{\sigma }^2(1,{\vartheta _0})]S(1,\vartheta _0) {\Bigr |}\Bigr \} \equiv {{\widetilde{T}}}, \end{aligned}$$

where

$$\begin{aligned}&S(t,\vartheta _0) = ( \kappa _1\kappa _2)^{-1/2}\int {\mathbf {1}}\{y\ge 1-t\} \frac{y_1y_2}{y_1+\vartheta _0 y_2} ( \,\mathrm { d } A_2-\vartheta _0\,\mathrm { d } A_1),\\&\sigma ^2(t,\vartheta _0)= \vartheta _0( \kappa _1\kappa _2)^{-1}\int {\mathbf {1}}\{y\ge 1-t\} \frac{y_1y_2}{(y_1+\vartheta _0 y_2)^2}(y_2\,\mathrm { d }A_2+y_1\,\mathrm { d }A_1). \end{aligned}$$

Clearly, the consistency of our test follows if ${{\widetilde{T}}}>0$. Contrary to this, suppose that ${{\widetilde{T}}} =0$. Then there is some $\eta _0\ne 0$ such that $S(t,\vartheta _0)=\eta _0 \sigma ^2(t,\vartheta _0)$ for all $t\in [0,1]$. It can easily be seen that

$$\begin{aligned}&\int {\mathbf {1}}\{y\in [s,t)\} \frac{y_1y_2}{y_1+\vartheta _0 y_2} ( \,\mathrm { d } A_2-\vartheta _0\,\mathrm { d } A_1) \nonumber \\&\quad = \eta _1 \int {\mathbf {1}}\{y\in [s,t)\} \frac{y_1y_2}{(y_1+\vartheta _0 y_2)^2}(y_2\,\mathrm { d }A_2+y_1\,\mathrm { d }A_1) \end{aligned}$$

(15)

follows for every $0\le s<t\le 1$ and some $\eta _1\ne 0$. Assume that $\eta _1>0$. The case $\eta _1<0$ can be treated analogously and, thus, we omit it to the reader. Since the right hand side of Eq. (15) is nonnegative and $(y_1+\vartheta _0 y_2){{\widetilde{K}}}/(y_1y_2)\ge 0$ we can deduce

$$\begin{aligned} \int {\mathbf {1}}\{y\in [s,t)\} {{\widetilde{K}}} ( \,\mathrm { d } A_2-\vartheta _0\,\mathrm { d } A_1)\ge 0 \end{aligned}$$

(16)

for all $0\le s<t\le 1$. Note that due to the definition of $\vartheta _0$, see (14), we have equality in (16) for $s=0$ and $t=1$. Hence, we get equality in (16) for all $0\le s<t\le 1$. But this implies $A_2(x)=\vartheta _0 A_1(x)$ for all $x {>} 0$ with ${{\widetilde{K}}}(x)>0$ or, equivalently, for all $x\in (0,\tau )$.

1.4 Proof of Theorem 3

To distinguish between the processes depending on the original data and the permuted data, respectively, we add a superscript $\pi$ to these processes if the permutation versions are meant, namely ${{\widehat{A}}}_j^\pi$, $Y_j^\pi$, $N_j^\pi$, $K_L^\pi$, $K^\pi$, $S_n^\pi$, ${\widehat{\sigma }}^{2,\pi }$$(1\le j\le 2)$. Note that the processes N and Y as well as the pooled Kaplan–Meier estimator ${{\widehat{F}}}$ do not depend on the group membership vector.

Assumption II Let ${{\widehat{\vartheta }}}={{\widehat{\vartheta }}}(c^{(n)},\delta ^{(n)})$ be an estimator fulfilling Assumption I, which depends only on the group memberships $c^{(n)}$ and the censoring status $\delta ^{(n)}$ of the ordered values. Let ${{\widehat{\vartheta }}}^\pi ={{\widehat{\vartheta }}}(c_n^\pi ,\delta ^{(n)})$ be the corresponding permutation version of the estimator. Moreover, suppose that a certain conditioned tightness assumption is fulfilled for $(n^{1/2}({{\widehat{\vartheta }}}^\pi -1))_{n\in { {\mathbb {N}} }}$, namely that for every subsequence there is a further sub-subsequence such that along this sub-subsequence we have with probability one

$$\begin{aligned} \lim _{t\rightarrow \infty }\limsup _{n\rightarrow \infty }\, P \Bigl (n^{1/2}\bigl |{{\widehat{\vartheta }}}^\pi -1\bigr |\ge t \bigr \vert \delta ^{(n)} \Bigr )=0. \end{aligned}$$

At the proof’s end, we verify that Assumption II holds for the estimators considered in the paper.

Lemma 2

Let $w\in {\mathscr {W}}$. Then the estimator ${{\widehat{\vartheta }}}={{\widehat{\vartheta }}}_K$ with $K=(w\circ {{\widehat{F}}})K_L$ fulfills Assumption II.

As in the proof of Theorem 1, we obtain that $n^{-1}\sum _{i=1}^{n}\delta _{(i)}\rightarrow \int \mathrm { d }L\ge L(\tau )>0$ in probability, where L and y were defined there. Now, we start with an arbitrary subsequence of ${ {\mathbb {N}} }$. Since we are interested in the conditional distributional convergence we treat the censoring status $\delta _{(1)},\ldots ,\delta _{(n)}$ as constants. Considering an appropriate sub-subsequence of the pre-chosen subsequence we can assume that $\lim _{n\rightarrow \infty }n^{-1}\sum _{i=1}^{n}\delta _{(i)}>0$ and that by Assumption II the sequence $(\sqrt{n}({{\widehat{\vartheta }}}^\pi -1))_{n\in { {\mathbb {N}} }}$ is tight. The latter implies, in particular, ${\widehat{\vartheta }}^\pi \rightarrow 1$ in probability. The proof’s rest goes along the argumentation of the proof of Theorem 1. Nevertheless, we carry out the important steps.

Observe that $S_n^\pi (t,1)=W_n(t,\delta ^{(n)},w_n)$ and ${\widehat{\sigma }}^{2,\pi }(t,1)=V_n(t,\delta ^{(n)},w_n)$ for $w_n=(1,\ldots ,1)$. By Proposition 2${\widehat{\sigma }}^{2,\pi }(1,1)^{-1/2}S_n^\pi \circ \alpha _n$ converge in distribution to a Brownian motion B and ${\widehat{\sigma }}^{2,\pi }(\alpha _n(t),1)/{\widehat{\sigma }}^{2,\pi }(1,1)$ tends in probability to t for all $t\in [0,1]$, where $\alpha _n$ is defined as in Proposition 2. Moreover, $({{\widehat{\sigma }}}^{2,\pi }(1,1))_{n\in { {\mathbb {N}} }}$ is tight. Let us now discuss what happens when we plug-in the estimator ${\widehat{\vartheta }}^\pi$. First, for all $t\in [0,1]$

$$\begin{aligned}&\Bigl | {\widehat{\sigma }}^{2,\pi }(t,1)- {\widehat{\sigma }}^{2,\pi }(t,{{\widehat{\vartheta }}}^\pi ) \Bigr |\nonumber \\&\quad =\frac{n^2}{n_1n_2} \Bigl | \int _0^{X_{([nt])}}\, \frac{Y_1^\pi Y_2^\pi }{Y^2} ({\widehat{\vartheta }}^\pi -1)\, \frac{(Y_1^\pi )^2-{{\widehat{\vartheta }}}^\pi (Y_2^\pi )^2 }{(Y_1^\pi +{{\widehat{\vartheta }}}^\pi Y_2^\pi )^2}\,\mathrm { d }\frac{N}{n} \Bigr |\nonumber \\&\quad \le |1-{{\widehat{\vartheta }}}^\pi | \frac{n^2}{n_1n_2}\int \frac{Y_1^\pi Y_2^\pi }{Y^2} \Bigl ( 1 + \frac{1}{{{\widehat{\vartheta }}}^\pi } \Bigr )\,\mathrm { d }\frac{N}{n} = \frac{|1-{{\widehat{\vartheta }}}^\pi |(1+{{\widehat{\vartheta }}}^\pi )}{{{\widehat{\vartheta }}}^\pi } {\widehat{\sigma }}^{2,\pi }(1,1). \end{aligned}$$

(17)

Thus, ${\widehat{\sigma }}^{2,\pi }(\alpha _n(t),{\widehat{\vartheta }}^\pi )/{\widehat{\sigma }}^{2,\pi }(1,1)$ as well as ${\widehat{\sigma }}^{2,\pi }(\alpha _n(t),{\widehat{\vartheta }}^\pi )/{\widehat{\sigma }}^{2,\pi }(1,{\widehat{\vartheta }}^\pi )$ tend to t for all $t\in [0,1]$. It remains to study $S_n^\pi (t,1)-S_n^\pi (t,{\widehat{\vartheta }}^\pi )$. This difference equals, compare to the proof of Theorem 1, $Z_{n}^\pi {\widehat{\sigma }}^{2,\pi }(t)$$(t\in [0,1])$, where

$$\begin{aligned} Z_{n}^\pi&= \Bigl (\frac{n_1n_2}{n}\Bigr )^{1/2} ({{\widehat{\vartheta }}}^\pi -1),\quad {{\widetilde{\sigma }}}^{2,\pi }(t)\\&=\frac{n}{n_1n_2}\int {\mathbf {1}}\Bigl \{\frac{Y}{n}\ge \frac{n-[nt]+1}{n}\Bigr \} \frac{Y_1^\pi Y_2^\pi }{Y(Y_1^\pi +{{\widehat{\vartheta }}}^\pi Y_2^\pi )} \,\mathrm { d }N. \end{aligned}$$

Analogously to (17), we get ${\widetilde{\sigma }}^{2,\pi }(\alpha _n(t))/{\widehat{\sigma }}^{2,\pi }(1,1)\rightarrow t$ for all $t\in [0,1]$. Since $(Z_n^\pi )_{n\in { {\mathbb {N}} }}$ and $({\widehat{\sigma }}^{2,\pi }(1,1))_{n\in { {\mathbb {N}} }}$ are tight we obtain

$$\begin{aligned} R_n^\pi (t)&=S_n^\pi (\alpha _n(t),1)-S_n^\pi (\alpha _n(t),{{\widehat{\vartheta }}}^\pi ) - \frac{{\widehat{\sigma }}^{2,\pi }(\alpha _n(t),{{\widehat{\vartheta }}}^\pi )}{{{\widehat{\sigma }}}^{2,\pi }(1,{{\widehat{\vartheta }}}^\pi )}[S_n^\pi (1,1)-S_n^\pi (1,{{\widehat{\vartheta }}}^\pi )] \\&= Z_n^\pi {\widehat{\sigma }}^{2,\pi }(1,1) \Bigl ( \frac{ {{\widetilde{\sigma }}}^{2,\pi }(\alpha _n(t))}{{\widehat{\sigma }}^{2,\pi }(1,1)}-\frac{{{\widetilde{\sigma }}}^{2,\pi }(1)}{{\widehat{\sigma }}^{2,\pi }(1,1)} \frac{{{\widehat{\sigma }}}^{2,\pi }(\alpha _n(t),{{\widehat{\vartheta }}}^\pi )}{{\widehat{\sigma }}^{2,\pi }(1,{{\widehat{\vartheta }}}^\pi )} \Bigr ) \rightarrow 0 \end{aligned}$$

in probability. Finally, the statement follows from the continuous mapping theorem, compare to the proof of Theorem 1.

Proof (Lemma 2)

As already mentioned in the proof of Theorem 1, ${{\widehat{\vartheta }}}$ fulfills Assumption I. Now, define $w_{n,i}=w( {{\widehat{F}}}(X_{(i)}))$ and set $w_n=(w_{n,1},\ldots ,w_{n,n})$. Analogously to the proof of Theorem 1, we obtain that in probability

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^n w_{n,i} \delta _{(i)} = \int w({\widehat{F}}(t))^2 \,\mathrm { d }\frac{N}{n}(t) \rightarrow \int w(F(t))^2\,\mathrm { d }L(t)>0, \end{aligned}$$

(18)

$$\begin{aligned}&\frac{1}{n}\sum _{i=1}^{[n_2/2]} w_{n,i} \delta _{(i)} \rightarrow \int {\mathbf {1}}\{y\ge 1- \kappa _2/2\} w(F(t))^2\,\mathrm { d }L>0, \end{aligned}$$

(19)

where y and L are defined in the proof of Theorem 1 as well as F is given by (13). It is well known that for every subsequence of ${ {\mathbb {N}} }$ there exists a further sub-subsequence such that the convergences in (18) and (19) hold with probability one along this sub-subsequence. Since we are interested in the probability conditioned under $\delta ^{(n)}$ we can treat the censoring status $\delta _{(1)},\ldots ,\delta _{(n)}$ as constants and, hence, $w_{n,1},\ldots ,w_{n,n}$ as constants with $\lim _{n\rightarrow \infty }\sum _{i=1}^nw_{n,i}\delta _{(i)}\in (0,\infty )$ as well as $\lim _{n\rightarrow \infty }n^{-1}\sum _{i=1}^{[n_2/2]} w_{n,i} \delta _{(i)}\in (0,\infty )$ along an appropriate subsequence. Thus, we can apply Proposition 2 to the numerator of

$$\begin{aligned} n^{1/2}({{\widehat{\vartheta }}}^\pi -1)&= \frac{ n^{-1/2}\int (w\circ {{\widehat{F}}}) (Y_1^\pi Y_2^\pi /Y^\pi ) \,(\mathrm { d }{{\widehat{A}}}_2^\pi -\mathrm { d }{{\widehat{A}}}_1^\pi )}{\int K^\pi \,\mathrm { d }{{\widehat{A}}}_1^\pi }\\&=\Bigl ( \frac{n_1n_2}{n^2} \Bigr )^{1/2}\frac{ W_n(1, \delta ^{(n)},w_n)}{\int K^\pi \,\mathrm { d }{{\widehat{A}}}_1^\pi }. \end{aligned}$$

Note that we always have $Y^\pi _2(X_{(i)})/Y(X_{(i)})\ge (n_2-1)/(2n)$ for $i=1,\ldots ,[n_2/2]$. Hence, we can bound the denominator $D_n$ from below as follows:

$$\begin{aligned} \int K^\pi \,\mathrm { d }{{\widehat{A}}}_1^\pi&\ge \frac{n_2-1}{2n} \frac{1}{n} \sum _{i=1}^{[n_2/2]} w_{n,i}\delta _{(i)} (1-c_{n,i}^\pi )\\&=\frac{n_2-1}{2n}\frac{n_1}{n}\frac{1}{n} \sum _{i=1}^{[n_2/2]} ( w_{n,i}\delta _{(i)} ) - \frac{n_2-1}{2n}\sum _{i=1}^{[n_2/2]} \frac{w_{n,i}\delta _{(i)}}{n} (c_{n,i}^\pi - {{\bar{c}}} ), \end{aligned}$$

where ${{\bar{c}}} = n^{-1}\sum _{i=1}^n c_{(i)}=n_2/n$. Applying Proposition 3 for ${{\widetilde{w}}}_{n,i}= (w_{n,i}\delta _{n,i}/n) {\mathbf {1}}\{ i \le [n_2/2]\}$ yields that the second summand converges in probability to 0. The first summand converges to $M>0$, say. To sum up, $P (D_n\ge M/2)\rightarrow 1$. Combining this and the tightness result for the numerator according to Proposition 2 gives us the desired tightness of $(n^{1/2}({{\widehat{\vartheta }}}^\pi -1))_{n\in { {\mathbb {N}} }}$. $\square$

1.5 Proof of Theorems 4 and 5

For simplicity we restrict here to estimators ${{\widehat{\vartheta }}}={{\widehat{\vartheta }}}$ of the form ${{\widehat{\vartheta }}}_K$ with $K=(w\circ {{\widehat{F}}})K_L$ for $w\in {\mathscr {W}}$. We give the proof of Theorems 4 and 5 simultaneously. First, we verify that (7) holds for some real-valued random variable $T_0$, say, under $H_0$ as well as under $H_1$, respectively, where the distribution of $T_0$ depends on the underlying distributions $F_1,F_2,G_1,G_2$. From this convergence we can immediately deduce the bootstrap test’s consistency (i.e., Theorem 5) since we already know that $T_n$ converges in probability to $\infty$ under $H_1$, compare to Theorem 7 of Janssen and Pauls (2003). In the second step, we show that $T_0$ has the same distribution as T under $H_0$ and, thus, Theorem 4 follows.

Recall from the proof of Theorem 1 that ${{\widehat{\sigma }}}^2(t,{{\widehat{\vartheta }}})\rightarrow \sigma ^2(t,\vartheta )$ ($t\in [0,1]$), $\sup \{|Y_{j}(x)/n-y_j(x)|: x\in [0,\infty )\}\rightarrow 0$$(j=1,2)$ and $N_j(s)/n\rightarrow L_j(s)$ ($s\ge 0;\,j=1,2$), all in probability under $H_0$. It is easy to check that the same is valid under $H_1$. Restricting to t and s coming from dense subsets of [0, 1] and $[0,\infty )$, respectively, for every subsequence we can construct a further sub-subsequence such that all the convergences mentioned above hold simultaneously with probability one under $H_0$ as well as under $H_1$, respectively. Due to the monotonicity and the continuity of the limits the convergences carry over to the whole intervals [0, 1] and $[0,\infty )$, respectively. Regarding (14) ${\widehat{\vartheta }}$ converges in probability to some $\vartheta >0$ under $H_0$ as well as under $H_1$, where $\vartheta$ equals the proportionality factor under $H_0$. Since we are interested in the conditional distribution of $T_n^G$ given the whole data we can treat ${{\widehat{\sigma }}}^2(\cdot ,{{\widehat{\vartheta }}})$, $Y_j$, $N_j$ as nonrandom functions and ${{\widehat{\vartheta }}}$ as a constant. Starting with an arbitrary subsequence we can always construct a further sub-subsequence, compare to the explanation above, that along this sub-subsequence ${{\widehat{\sigma }}}^2(t,{{\widehat{\vartheta }}})\rightarrow \sigma ^2(t,\vartheta )$ ($t\in [0,1]$), $\sup \{|Y_{j}(x)/n-y_j(x)|:x \in [0,\infty )\}\rightarrow 0$$(r=1,2)$ and $N_j(s)/n\rightarrow L_j(s)$ ($s\ge 0$) as well as ${{\widehat{\vartheta }}}\rightarrow \vartheta$. All following considerations are along this sub-subsequence.

Let $G_{(i)}$ be the multiplier corresponding to $X_{(i)}$. Clearly, $G_{(1)},\ldots ,G_{(n)}$ are (given the data) still independent and identical distributed with the same distribution as $G_{1,1}$. We can now rewrite the statistic $S_n^G$ as a linear rank statistic:

$$\begin{aligned} S_n^G(t,{{\widehat{\vartheta }}})= \sum _{i=1}^{[nt]} \Bigl ( \frac{n}{n_1n_2} \Bigr )^{1/2}G_{(i)}\delta _{(i)} \Bigl ( c_{(i)} - \frac{{{\widehat{\vartheta }}} \sum _{m=i}^nc_{(m)}}{\sum _{m=i}^n(1-c_{(m)}) + {{\widehat{\vartheta }}} \sum _{m=i}^nc_{(m)}} \Bigr ). \end{aligned}$$

(20)

To obtain the asymptotic behavior of the process $t\mapsto S_n^G(t,{{\widehat{\vartheta }}})$ ($t\in [0,1]$) we apply Proposition 1. In contrast to the two previous proofs, we have already replaced $\vartheta$ by ${{\widehat{\vartheta }}}$ here. That is why we do not need to discuss the difference $S_n^G(t,\vartheta )-S_n^G(t,{{\widehat{\vartheta }}})$ at the proof’s end. Let us now introduce the natural filtration $\mathscr {G}_{n,i}=\sigma (G_{(1)},\ldots ,G_{(i)})$ ($0\le i \le n$). Denoting the summands in (20) by $\xi _{n,i}$$(1\le i \le n)$ we, clearly, have ${ E }(\xi _{n,i}\vert \mathscr {G}_{n,i-1})={ E }(\xi _{n,i})=0$. To verify the conditional Lindeberg condition, first note that there is a constant $\eta >0$ independent of i and n such that $|\xi _{n,i}|\le \eta n^{-1/2}|G_i|$. Hence, it is sufficient to show for all $\varepsilon >0$ that

$$\begin{aligned} \sum _{i=1}^n { E }( n^{-1}G_{(i)}^2 {\mathbf {1}}\{|G_{(i)}|\ge n^{1/2} \varepsilon \eta ^{-1}\}) = { E }( G_{(1)}^2 {\mathbf {1}}\{|G_{(1)}|\ge n^{1/2} \varepsilon \eta ^{-1}\}) \end{aligned}$$

tends to 0. This follows immediately from Lebesgue’s dominated limit theorem and ${ E }(G_{(1)}^2)=1$. In the final step we discuss the asymptotic behavior of the predictable quadratic variation process $t\mapsto \sigma _n^{2,G}(t,{{\widehat{\vartheta }}})$ ($t\in [0,1]$) given by

$$\begin{aligned} \sigma _n^{2,G}(t,{{\widehat{\vartheta }}})&=\sum _{i=1}^{[nt]}{ E }(\xi _{n,i}^2\vert {\mathscr {G}}_{n,i-1}) \\&= \frac{n}{n_1n_2} \sum _{i=1}^{[nt]} \delta _{(i)}\Bigl ( c_{(i)} - \frac{{{\widehat{\vartheta }}} \sum _{m=i}^nc_{(m)}}{\sum _{m=i}^n(1-c_{(m)}) + {{\widehat{\vartheta }}} \sum _{m=i}^nc_{(m)}} \Bigr )^2. \end{aligned}$$

Rewriting $\sigma _n^{2,G}(t,{{\widehat{\vartheta }}})$ in terms of the (nonrandom) functions $Y_j$, $N_j$ we obtain for $t\in [0,1]$

$$\begin{aligned}&\sigma _n^{2,G}(t,{{\widehat{\vartheta }}})\\&\quad = \frac{n}{n_1n_2} \Bigl ( \int _0^{X_{([nt])}}1 - 2 {{\widehat{\vartheta }}}\frac{Y_2}{Y_1+{{\widehat{\vartheta }}} Y_2}\,\mathrm { d }N_2 + \int _0^{X_{([nt])}} \frac{ {{\widehat{\vartheta }}}^2 Y_2^2}{(Y_1+{{\widehat{\vartheta }}} Y_2)^2} \,\mathrm { d }N \Bigr )\\&\quad =\frac{n^2}{n_1n_2} \Bigl ( \int _{\{ \frac{Y}{n}\ge \frac{n-[nt]+1}{n} \}} \frac{Y_1^2}{(Y_1+{{\widehat{\vartheta }}} Y_2)^2} \,\mathrm { d }\frac{N_2}{n} + \int _{\{ \frac{Y}{n}\ge \frac{n-[nt]+1}{n} \}} \frac{{{\widehat{\vartheta }}}^2 Y_2^2}{(Y_1+{{\widehat{\vartheta }}} Y_2)^2} \,\mathrm { d }\frac{N_1}{n}\Bigr )\\&\qquad \rightarrow \frac{1}{\kappa _1\kappa _2}\Bigl ( \int _{\{y\ge 1-t\}} \frac{y_1^2}{(y_1+\vartheta y_2)^2} \,\mathrm { d }L_1 + \int _{\{y\ge 1-t\}} \frac{\vartheta ^2 y_2^2}{(y_1+\vartheta y_2)^2} \,\mathrm { d }L_1 \Bigr ) \equiv \sigma ^{2,G}(t,\vartheta ). \end{aligned}$$

Applying Proposition 1 yields distributional convergence of $S_n^G(\cdot ,{{\widehat{\vartheta }}})$ to the rescaled Brownian motion $B(\sigma ^{2,G}(\cdot ,\vartheta ))$ on the Skorohod space D[0, 1]. Similarly to the proofs of Theorems 1 and 3, we can conclude from the continuous mapping theorem that

$$\begin{aligned} T_n^G \rightarrow \sigma ^2(t,\vartheta )^{-1/2}\sup _{t\in [0,1]}\{ |B(\sigma ^{2,G}(t,\vartheta )) - \frac{\sigma ^{2}(t,\vartheta )}{\sigma ^{2}(1,\vartheta )}B(\sigma ^{2,G}(t,\vartheta )){|} \} \equiv T_0. \end{aligned}$$

Finally, it remains to show $\sigma ^{2,G}(t,{{\widehat{\vartheta }}})= \sigma ^{2}(t,\vartheta )$ under $H_0$. By inserting $L_j(t)=\int y_j(1+(\vartheta -1){\mathbf {1}}\{j=2\})\,\mathrm { d }A_1$ in the formulas of $\sigma ^{2,G}(t,{{\widehat{\vartheta }}})$ and $\sigma ^{2}(t,\vartheta )$ the equality follows immediately.