Flexible cutoff values for fit indices in the evaluation of structural equation models

Abstract

Researchers often struggle when applying ‘golden rules of thumb’ to evaluate structural equation models. This paper questions the notion of universal thresholds and calls for adjusted orientation points that account for sample size, factor loadings, the number of latent variables and indicators, as well as data (non-)normality. This research explores the need for flexible cutoffs and their accuracy in single- and two-index strategies. Study 1 reveals that many indices are biased; thus, rigid cutoffs can become imprecise. Flexible cutoff values are shown to compensate for the unique distorting patterns and prove to be particularly beneficial for moderate misspecification. Study 2 sheds further light on this ‘gray’ area of misspecification and disentangles the different sources of misspecification. Study 3 finally investigates the performance of flexible cutoffs for non-normal data. Having substantiated higher performance for flexible reference values, this paper provides to managers an easy-to-use tool that facilitates the determination of adequate cutoffs.

Introduction

Structural equation modeling (SEM) is widely applied as a theory-testing tool and the technique is extensively used in many domains of the marketing discipline, especially in marketing strategy and consumer behavior research. In their analysis of the major marketing journals, Kumar et al. (2017) recently observed that SEM ranked second in currently used analytical techniques. Reliance on SEM, which has been found to boost strategic insights, is a “pioneer[s] in contributing to the citations” (Kumar et al. 2017, p. 180). SEM is also often the method of choice for validating multi-item scales (Hulland et al. 2017) and for assessing common method variance (Podsakoff et al. 2003). However, researchers sometimes struggle when testing theoretical models with the help of SEM. The once-promising concept of indicators of global model fit (referred to as fit indices) has received relatively little attention lately. This development (or lack thereof) is worrisome because a substantial body of research indicates that fit indices vary with model size (e.g., the number of latent and manifest variables) and data characteristics (e.g., sample size). When fit indices respond to factors other than model misspecification, this introduces nuisance variance in fit scores and, in turn, provokes misleading conclusions. To resolve this issue, the seminal work by Hu and Bentler (1999), which has been cited over 53,000 times to date (Google Scholar citations, as of June 2018), proposes relying on pairs of indicators instead of just one indicator. Still, the decision about the model is based on fixed reference values (cutoffs) that indicate ‘good fit’ (e.g., close to .95), regardless of the model or data characteristics, which are known to contaminate the fit indices’ ability to identify ‘correct’ models and reject ‘false’ ones.

The paper aims to tackle this weakness, using a contingency approach. The ‘sui generis’ principle (Cheung and Rensvold 2001) implies that each fit index has a unique distribution that is limited by the parameters of the model and the sample. In contrast to fixed cutoffs, flexible cutoff values are specific to these parameters. The present research proposes that this can be achieved by simulations that estimate correctly specified models under the specific model and data conditions. As we will show, flexible cutoffs improve precision when testing models for a vast range of configurations, from small to large models and samples. Unlike fixed cutoffs, this contingent approach allows to specify the assumed uncertainty about the cutoff values (α of .001 to .1). The flexible cutoffs are thus not only flexible in terms of model parameters but also flexible in the conclusions about a model. Depending on the certainty researchers have about the model or the data, this allows to adjust for more or less conservative evaluations and even makes sensitivity analyses of the decision about the model possible.

This paper first identifies the factors that distort fit indices, irrespective of the actual extent of misspecification. Flexible cutoffs, which serve as orientation points for decisions about a model, are then determined in a comprehensive simulation. As researchers place perhaps too much faith in gold standards (e.g., fixed thresholds for statistical significance or model fit), our flexible paradigm aims at balancing Type I errors (‘erroneously rejecting a correct model’) and Type II errors (‘erroneously accepting a misspecified model’), and thereof power.¹ Three studies set out to provide evidence that compared to fixed cutoffs, flexible cutoffs have preferable accuracy in detecting correct and misspecified models, especially in the ‘gray area’ of minor misspecifications and less ideal conditions (e.g., few degrees of freedom or small samples, (Kenny et al. 2015). Study 1 furnishes initial evidence that flexible cutoffs are capable of dampening the distorting impact of the factors that are unrelated to model misspecification. Study 2 then investigates a finer and continuous form of misspecification and disentangles the different sources of model misspecification. As non-normal data is not uncommon in practice, Study 3 finally examines the performance of fixed and flexible cutoffs under this data condition. We contribute to the literature in several ways. This research—to the best of our knowledge for the first time—in a ‘sui generis’ approach, develops cutoff values that (i) flexibly cater to data and model characteristics, (ii) are particularly effective in the critical gray area of misspecification, (iii) improve the detection of error in both the structural model and the measurement model, (iv) allow for the balancing of Type I and Type II errors, and (v) account for the non-normality of the data.

Note that the focus of this research is on the reference values with respect to making more accurate decisions about a model; however, the development or optimization of the fit indices themselves is not within the scope of this paper. Neither can a flexible approach remedy poorly performing fit indicators, nor should this be the sole basis for accepting or rejecting models. Flexible cutoffs should only serve as orientation points (i.e., what fit value of an index is to be expected for correctly specified models under these specific models and data conditions). To guide marketing managers, we illustrate the benefits of the flexible cutoff paradigm with examples from marketing research. We provide an easy-to-use tool at www.flexiblecutoffs.org that helps to derive adjusted cutoffs across a wide range of model configurations and sample sizes.

Literature review and conceptual background

Sources of variation in model fit indices

Covariance-based structural equation modeling (CBSEM) tests whether a theoretically modeled covariance matrix (as implied by the theoretical model) resembles the empirical (observed) covariance matrix of the data (e.g., Jöreskog and Sörbom 1982). This fit is indicated by low values of χ². As the χ² statistic increases with sample size, the probability of rejecting the model also increases, which leads to unreliable behaviors in the assessment of the theoretical model fit (e.g., Curran et al. 2002). To overcome this limitation, scholars have advocated the use of fit indices. Over the past decades, a multiplicity of fit measures has been suggested that can be roughly grouped into ‘goodness-of-fit indices’ (a value of 1 indicates good fit) and ‘badness-of-fit indices’ (a value of 0 indicates good fit). Goodness-of-fit indices can further be split into absolute indices (e.g., GFI) and incremental fit indices (e.g., IFI) for which the model under investigation is compared to a baseline model without any correlations or loadings (Bentler and Bonett 1980).

Scholars have developed various ‘golden rules’ (Marsh et al. 2004, p. 321) to draw a dividing line between models with ‘acceptable’ fit and models that are incorrectly specified. However, these cutoff values cannot be treated in the same way as test statistics, such as the χ² test. Theory testing by comparing an empirical value to a theoretical value with a given confidence level (e.g., α = 5%) is thus not possible for fit indices (Hayduk et al. 2007). Model misspecification, at least in theory, should be the sole source of variation in the indicators of model fit (Hu and Bentler 1998). However, a large body of research has identified various factors that are unrelated to misspecification but which also cause notable variation in model fit statistics. Five key factors appear to have the greatest potential in distorting fit values: the sample size, model size, measurement model, model type, and the normality of the data distribution (Table 1).

Table 1 Previous empirical studies on the variation in fit indices

Sensitivity to sample size and model size effects

Sample size is expected to induce variation in fit indices due to the aforementioned bias of the underlying χ² statistic. As fit indices often rely on χ² values, they inherit their sample size biases (e.g., Fan and Sivo 2007). Additionally, the size of the model is deemed to harm the precision of generic cutoffs. This model size effect stems from two sources that determine the amount of model variables: (a) the number of latent variables (Breivik and Olsson 2001) and (b) the indicators per latent variable (Kenny and McCoach 2003; Marsh et al. 1998). More variables in a model imply a larger covariance matrix that, all other parameters being equal, increases the degrees of freedom. Larger models therefore tend to increase the χ² statistic (Kenny and McCoach 2003) and make one’s standards for ‘fit’ more lenient. Fit indices that for reasons of parsimony penalize models with relatively few degrees of freedom, such as RMSEA (Steiger and Lind 1980), are sensitive to this effect (Sharma et al. 2005).

Sensitivity to the measurement model

The evidence is mixed as to whether fit indices are affected by factor loadings, the dependencies between latent and manifest variables (Gagne and Hancock 2006; Moshagen 2012; Savalei 2012) or the correlations (or covariances) among latent variables (Nasser and Wisenbaker 2003). As shown in Table 1, only a few studies have investigated both questions simultaneously. Sharma et al. (2005, p. 941) emphasized that dependency effects are only critical if factor loadings fall below a threshold of .5. Yet, such very low loadings (< .5) fail to meet the minimum requirements for reliability (Bagozzi and Yi 1988) and raise questions about the measurement. Nonetheless, the impact of factor loadings on cutoff accuracy is included in this research.

Sensitivity to the model type

CBSEM is used for different purposes, such as confirmatory factor analysis (CFA) or SEM. While both CFAs and SEMs are theory-driven, CFAs consider all relationships among latent variables and are therefore often more complex than SEMs. There are competing predictions as to whether fit indices differ between both types of models. On one hand, CFAs typically estimate more parameters than do SEMs (non-recursive SEMs contain even fewer degrees of freedom), which results in fewer degrees of freedom and a smaller χ² value. Fit indices might bear an imprint of this difference. On the other hand, the difference is only marginal considering the total degrees of freedom available, particularly for large models with many indicators. It is further plausible that SEMs already contain the theoretically relevant paths. CFAs and SEMs therefore primarily differ in dispensable and irrelevant relationships. Hence, the incremental bias should be rather low. Given these considerations, the results obtained for CFAs are traditionally extended to SEMs (Fan and Sivo 2007).

To determine the relevance of the model type, we reviewed articles that were recently published in this journal over a period of 5 years (2014 to 03/2018) and coded their application (Web Appendix 1). Of the 68 articles that made use of CBSEM, a vast majority (65 articles) used it for CFA to check for convergent and discriminant validity or common method bias. Twenty-nine articles used SEM to test a theoretical model, and a few papers (11) compared groups using multi-group SEM. It is therefore reasonable to assume that CFA is the most prominent and practically relevant application of SEM.

Sensitivity to data non-normality

Deviations from the multivariate normality of data (required for ML and GLS estimators) is known to bias the χ² statistic and therewith fit indices (Fouladi 2000). The relevant research (Table 1) addresses two parameters, specifically, the kurtosis (tailedness) and skewness (asymmetry) of a multivariate distribution. The more tailed or skewed a distribution is, the higher the degree of non-normality will be, although there is no general agreement on what non-normality constitutes. Some studies have solely varied kurtosis (e.g., Hu and Bentler 1998), examining peaked or flat symmetric distributions, while others jointly varied kurtosis and skewness (e.g., Muthén and Kaplan 1985). There is neither agreement on what degree of kurtosis or skewness constitutes a slight, moderate, or severe extent of non-normality nor what values constitute ‘acceptable’ non-normality (Curran et al. 1996; Marsh et al. 2004; Nye and Drasgow 2011). A general finding seems to be that fit indices that rely on the χ² statistic (e.g., RMSEA) are more sensitive to non-normal data than are indices that do not, such as SRMR (Bentler 1995). The accuracy of the decisions about a model should thus respond to deviations from the normality assumption of the data. Our review of recent CBSEM-papers in this journal indicates that eight papers mention non-normality regarding their data (e.g., Miao and Wang 2017; Sleep et al. 2015).

Sensitivity to the type of misspecification: Structural model vs. measurement model

Each fit index is not only subject to the aforementioned sources of variation but is also known to respond differently to the specific reasons of specification errors (Table 1). While certain fit indices are particularly sensitive to misspecified paths in the structural model (e.g., SRMR), others are more sensitive to a misspecification of the measurement model, such as CFI (Bentler 1990) or TLI (Tucker and Lewis 1973). In consideration of this sensitivity to one type of misspecification but insensitivity to the other, reliance on individual indices (single-index strategies) is deemed insufficient for the evaluation of model fit. Since no ‘one-fits-all’ indicator is yet available that is equally sensitive to both types of misspecification, Hu and Bentler (1999) argue that relying on a thoughtful combination of two indices and balancing their respective strengths and weaknesses is superior to relying on single indices. A two-index strategy combines the index that responds most sensitively to the misspecification of the structural model (SRMR) with another index that is equally sensitive to the misspecification of the measurement model (e.g., CFI).

To justify their decision about a model, researchers often report larger sets of indicators, and sometimes it appears that fit indices supporting the desired decision are ‘cherry-picked’. Such a ‘more is better’ approach is problematic for two reasons. First, reporting fit indices from the same group (e.g., CFI, TLI) leaves the problem that these indicators are only efficient in detecting one source of misspecification. Arbitrary combinations of similar indices are therefore prone to ignore cases of misspecification to which these indices are relatively insensitive. Second, untested combinations may introduce nuisance variance in the evaluation of model fit. Each fit index has a unique distribution and responds to the misspecification-unrelated factors in a different fashion. By cherry-picking untested combinations, researchers lose the key benefit of balancing the respective strengths and weaknesses of the selected index pairs.

Balancing different indices still overlooks one key problem. Despite being carefully selected, the cutoff values for the pairs of indices are fixed.² Apart from some limiting notes (e.g., TLI < .96 instead of .95 for N > 1000), the cutoffs for a given combinational rule are uniformly applied to small samples of 150 cases and larger samples of, say, 950 cases. Similarly, the very same cutoffs are used for simple models (e.g., four indicators of two latent variables) and complex models (e.g., 100 indicators for 20 latent variables). The distorting factors discussed above still contaminate the fit values of the indices being paired. It is therefore reasonable to assume that this also harms the precision of the two-index strategy, although to a lesser extent than for a single-index strategy. Because each fit index supposedly has its own ‘sui generis’ distribution (Cheung and Rensvold 2001), the cutoffs for different fit indices should inherently account for their unique distribution with regard to the relevant characteristics of the model and the data.

Flexible cutoff values

Principle

In consideration of the multiplicity of distortions outlined above, popular fixed cutoff points, such as .90 (Bentler and Bonett 1980), .95 (Hu and Bentler 1998) or .05 (Browne and Cudeck 1989) can be misleading (Chen et al. 2008; Sivo et al. 2006). To overcome this weakness of fixed cutoffs, this research proposes the idea of flexible reference values that follow a contingency approach in line with the ‘sui generis’ claim (Cheung and Rensvold 2001). As each index has its own unique distribution, flexible cutoffs must account for the imprint of the relevant distorting factors. Rather than applying a universal threshold (e.g., a value close to .95 for CFI), cutoff points for complex models with small samples should be more ‘forgiving’ (CFI below .95), while they should be stricter for simple models with large samples (CFI above .97). To enhance objectivity, cutoff points for model evaluation are not solely based on a predefined level of misspecification (Marsh et al. 2004). In a flexible cutoff paradigm, a case-specific lower confidence interval of correctly specified models (or an upper confidence interval for badness-of-fit indices) is derived depending on the model size, reliability of the measurement model, sample size, and normality of the distribution. The index’s lower margin for a correctly specified model defines the cutoff value, which serves as an orientation point for the decision about the model at hand. A fit value for a given model at or above this point suggests correct specification, as under the specific model and data conditions, a very large number of correctly specified models achieve at least this value. A fit value below this point can be regarded as the value of a distribution that differs from that of a correctly specified model and thus points to misspecification.

Unlike fixed cutoffs, a flexible paradigm allows accounting for uncertainty in the evaluation of the model’s fit. As for other means of theory testing, the acceptable error (Type I) is set to a certain value (e.g., .05). For more or less conservative evaluations, the width of the confidence intervals can be varied across different levels of acceptable error. This error is one-sided because cutoffs above (below) the median are irrelevant for goodness-of-fit indices (badness-of-fit indices). As illustrated in Fig. 1, an error (α) of .1 is rather conservative compared to an error of .01. Consider the example of a model that contains four latent variables with three items each, an average factor loading of .8, and 250 respondents. The flexible approach with an acceptable error α of .1 yields a cutoff point of .97 for CFI and a value of .05 for SRMR. Changing the accepted α to .01 results in less conservative cutoffs of .95 and .05, respectively. As this research will show, only levels of α = .05 and the wider confidence interval of α = .01 (if the researcher is certain about the model) should be applied in practice. More extreme conservative (α = .1) or lenient uncertainty levels (α = .001) will be included in the analyses to conduct sensitivity analyses.

Fig. 1

Flexible cutoff values for CFI and SRMR depending on the width of error interval. Notes. Empirical example (1000 replications), left: CFI, right: SRMR, normal distributed flexible cutoffs, gray bars: frequency, orange area: density, solid lines: ⍺ = .1, long dashed lines: ⍺ = .05, dashed lines: ⍺ = .01, dotted lines: ⍺ = .001

To summarize, flexible cutoffs allow for the contingent adjustment of threshold values to those factors that are known to harm a fit index’s ability to detect model misspecification. Integrating the level of assumed uncertainty (α) further allows for the adjustment of these cutoffs depending on prior theoretical considerations, ranging from more lenient to more conservative.

Method

To obtain flexible cutoffs for a large number of generalizable models, a comprehensive Monte Carlo simulation was run, estimating correctly specified CFAs (with all loadings equal, all correlations are .3 between latent variables) that vary systematically for a wide range of levels across the distorting factors. Sample size range between 100 and 1000 subjects in steps of 50. Model size is varied by the number of latent variables, and the indicators per latent variable range from two to ten indicators per latent variable. Factor loadings are varied in steps of .7, .8, and .9, assuming that only reliable latent variables are applied and that reliability is smaller than one (Bagozzi and Yi 1988, p. 82). In addition, normal (kurtosis = 0, skewness = 0) and non-normal data conditions (kurtosis = 3.5 or 7, skewness = 1 or 2) are available. We configure 13,851 CFA models with normally or non-normally distributed data. Empirical confidence intervals (α levels of .001, .01, .05, and .1) are determined based on at least 500 replications per model. Our dataset thus ranges from very small CFAs (two latent variables with two indicators and 100 cases) up to extensive models (ten latent variables with ten indicators each and 1000 cases).

All data is generated using R. For the estimation of the flexible cutoff values, multivariate normal or non-normal distributed datasets of the corresponding size and number of variables are generated by applying the simulateData function in the R package lavaan. Models are estimated with the help of the R package lavaan applying its standard settings for CFA models (free intercepts of manifest variables, free intercepts of latent variables, first indicator for each latent variable is fixed to 1, free residual variances and variances of latent variables, free covariances of latent variables, settings for limited variables do not apply). Median-unbiased and distribution-irrelevant empirical quantiles (Hyndman and Fan 1996) are then used to derive the cutoffs with a given width of error (α = .001, .01, .05, .1). We finally consolidate a dataset of all calculated model configurations. The 55,404 determined cutoff values are also implemented in a tool that can be accessed at www.flexiblecutoffs.org .

A first inspection of the data shows that the lower bound of fit scores for these correctly specified models varies considerably depending on the size of the model and the sample. This provides initial support for this paper’s premise. Figure 2 illustrates this susceptibility to misspecification-unrelated factors for a goodness-of-fit indicator (CFI) and a badness-of-fit indicator (SRMR). For CFI, the average fit score is below the widely noted threshold of close to .95 if the sample size is relatively small (≤ 300). Bear in mind that flexible cutoffs build on correctly specified models. Figure 2 also shows a drop in fit scores for very large models. Thus, if fixed golden rules were used under such conditions, even correctly specified models are likely to be rejected. This highlights the need to account for the distorting factors when evaluating model fit.

Fig. 2

Flexible cutoffs for selected fit indices depending on misspecification-unrelated factors. Notes. Fixed cutoffs: CFI = .95, SRMR = .08; correct models (flex) for α = .05; The shaded area indicates the sensitivity of the flexible cutoffs (α_.001 to α_.1)

Cutoffs in light of hypothesis testing and power

Type I vs. Type II errors

Following established theory-testing principles, cutoff values must balance Type I and Type II errors (Cohen 1988; Sedlmeier and Gigerenzer 1989). Similar to the case for the indices themselves, the trade-off between Type I and Type II errors will bear an imprint of the above discussed factors that are unrelated to model misspecification. Cutoffs that neglect to account for these sources of variation in fit scores will hence suffer in their attempt to minimize both errors. Accordingly, power has been found to suffer due to fixed cutoffs, especially for small samples for which the distributions of true and false models tend to overlap (Marsh et al. 2004, p. 328). Pairs of indicators also seem to have difficulties balancing Type I and Type II errors under non-normal data conditions. The appendix of Hu and Bentler (1999) indicates that for complex models, the pairing of CFI and SRMR results in large sums of errors of 45.6% (for N = 150) and 24.6% (for N = 250), respectively, which is predominantly due to failures in detecting correctly specified models (Type I error). Flexible cutoffs, by contrast, are specific to the situation with regard to the key model and data characteristics. Accounting for their distorting impact with a flexible approach is therefore expected to facilitate the balancing of Type I and Type II errors.

Acceptable error α

Prior approaches have been criticized for making recommendations about appropriate cutoffs based on arbitrary definitions of model misspecification (Marsh et al. 2004). As the acceptable Type I error is not set, generic approaches may boost the danger of Type II errors. Herein lie the major opportunities for flexible cutoffs. Given that flexible cutoffs are based on the distribution of fit values from a true model, misspecification is not subject to a potentially erroneous assumption about the ‘severity’ of misspecification. As for theory testing, a flexible approach allows specifying assumed uncertainty—the acceptable error α of the confidence interval—and thereby controls for Type I errors. This additionally allows the determination of the stability of the cutoff values. With sensitivity analyses (varying the confidence interval between the most conservative and optimistic α), researchers can draw conclusions about the robustness of the cutoff, and in turn, the decision about the model. Still, flexible cutoff points are only as precise as the respective fit index. As Fig. 2 shows, the stability of flexible values (indicated by the shaded area) is contingent on the model and data conditions. For example, the cutoffs for CFI are more robust for larger samples, while those for SRMR are slightly less robust when few model parameters are available. This stability of the flexibly derived cutoffs has to be considered when selecting the acceptable error α and when drawing conclusions about the estimated model.

Taking all of this together, with a ‘sui generis’ approach and by controlling the acceptable error α, flexible cutoffs are expected to be better at safeguarding against Type I and Type II errors and therefore loss in power than fixed cutoffs are. It is imperative to note that the flexible paradigm aims to ensure more accurate decisions about whether the data fits a theoretical model (i.e., by providing more precise cutoffs). Flexible cutoffs should not be mistaken for a remedy to correct the fit values of suboptimal indices that are per se less sensitive to model misspecification or a specific type of misspecification, such as GFI (Jöreskog and Sörbom 1981).

Overview of the series of simulation studies

Three simulation studies contrast the performance of fixed and flexible cutoffs. Study 1 examines the cutoffs’ performance for three discrete degrees of misspecification (no, moderate, and severe misspecification). Study 2 then introduces a finer, continuous form of model misspecification to spotlight the ‘gray’ area between correct and misspecified models. Study 2 further disentangles the misspecification of the structural model and the measurement model. Finally, Study 3 investigates the flexible cutoffs under non-normal data conditions. Although flexible cutoffs have been determined for a large set of fit indices, the following analyses focus on a subset of four indicators to allow greater detail. With CFI and the structurally close index TLI as well as RMSEA and SRMR, we examine the most frequently used fit indices in CFA (Jackson et al. 2009) that are recommended for a two-index strategy by Hu and Bentler (1999). This paper’s Web Appendix provides a detailed description of the selected indices and their specifics as well as additional analyses of the Studies 1 to 3.

Study 1: Accuracy of fixed and flexible cutoff values

Objectives

Study 1 examines the performance of fixed and flexible cutoff values. A Monte Carlo simulation first extracts the incremental impact of the major distorting factors. The analysis then assesses the extent of their imprint on the accuracy in identifying misspecification for both single-index and two-index strategies.

Data generation

In Study 1, we generated models that varied systematically across five factors pertaining to the characteristics of the model and the data used for estimation. The factors and their levels were selected on the basis of the literature review (Table 1). More detailed descriptions of the factors and variables applied in the literature are provided in the Web Appendix. To enhance generalizability, we focus on factor levels that are frequently used in the previous research:

• Factor 1: the degree of model misspecification, three levels (no, moderate, and severe misspecification of the conceptual model)

• Factor 2: sample size, three levels (N = 250, 500, and 1000 cases)

• Factor 3: the number of indicators, four levels (2, 3, 4, and 5 indicators per latent variable)

• Factor 4: the number of latent variables, five levels (4, 5, 6, 7, and 8 latent variables)

• Factor 5: factor loadings (.7, .8, and .9)

Model misspecification

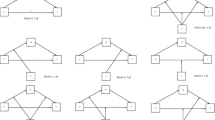
We adapted the approach by Hu and Bentler (1999) to manipulate the extent of model misspecification. Since this approach employed only two levels (a simple and a complex model), we followed Marsh et al. (2004) and Fan and Sivo (2007) and manipulated three levels of misspecification to enhance generalizability. In the ‘no misspecification’ condition, no adjustments were made. In the ‘moderate misspecification’ condition, sampling data were generated with an indicator of latent variable 3 loading on latent variable 2 and a correlation of r = .5 between latent variable 1 and 4. For the ‘severe misspecification’ condition, an indicator of latent variable 2 additionally loads on latent variable 1, and a second correlation with r = .5 between latent variables 2 and 4 was introduced. All factor loadings were simulated with a constant value of .7, .8 or .9 depending on the loading condition and all structural parameters were simulated with .3, except for the two correlations (r = .5) that are used to manipulate the different conditions. The ‘no misspecification’ models had no restrictions. In the ‘moderate’ condition models, one correlation among the latent variables (among variables 1 and 4) was constrained to zero, whereas in the ‘severe’ condition, this was the case for two correlations (1 and 4, 2 and 4). Thus, an equal number of ‘failures’ was simultaneously introduced into the structural models (0, 1, and 2) and the measurement models (0, 1, and 2), as proposed by Fan and Sivo (2007). The upper part of Fig. 3 illustrates the manipulation of misspecification in greater detail.

Fig. 3

Manipulation of model misspecification in Studies 1, 2 and 3. Notes. Examples for four latent variables with three indicators (loadings: .7) each. Ovals represent latent variables, rectangles indicators. Solid lines are constant in all models (loadings: .7; correlations: .3). Dashed lines in Study 1 are misspecifications for the moderate and severe conditions. Dotted lines in Study 1 are misspecifications for the severe condition (population values outside, manipulation values inside parentheses). Dashed lines in Studies 2 and 3 are pairwise switches of step 1 (e.g., a1 to B, b1 to A ➔ MM = 1). Dotted lines in Study 2 and 3 are pairwise switches of step 2 (e.g., a2 to B, b2 to A ➔ MM = 1). Dashed and dotted lines in Studies 2 and 3 are pairwise switches of step 3 (e.g., a3 to B, b3 to A ➔ MM = 0). In step 0 (MM = 0), all indicators belong to the correct latent variable (e.g., a1-a3 to A). Maximum MM is reached if the truncated half of the overall indicators is reached (here: 3/2 ➔ 1). Roman numerals indicate the order of restricting a correlation (true value: .3) to zero. In step 0 (SM = 0), all correlations are estimated. For example, in step 3 (SM = 3), correlations I, II and III are set to zero

Sample and model size

We varied the sample size in three levels (250, 500, and 1000) because these levels are expected to evoke an important (and unique) effect on the model interpretation. According to Hu and Bentler (1999), larger samples (e.g., N = 2500 or 5000) produce only marginal differences. Model complexity was varied in the steps that are commonly found in published models. We used 2, 3, 4, and 5 indicators per latent variable and configured models with 4, 5, 6, 7, or 8 latent variables. The factor loadings were varied in the levels of .7, .8, and .9.

We applied the simulation packages and data structure that were used to calculate the flexible cutoffs. For data generation, we specified a 3 (misspecification) × 3 (sample size) × 3 (factor loadings) × 4 (indicators) × 5 (latent variables) full factorial design with 200 replications, resulting in a total of 108,000 models.

Results

Distortion of the fit scores

First, we quantify the extent to which the fit indices are distorted. ANOVAs are run including the manipulated misspecification-factor, the four factors that are unrelated to model misspecification (number of latent variables, number of indicators, sample size, factor loading), and the fit indices as the dependent variables. Given the large number of replications, virtually all F-statistics (ANOVA) indicate significant results (Table 2). As we consider relevance to be more important than statistical significance, the analysis focuses on each factor’s incremental effect size (η²).

Table 2 ANOVA results for the simulation studies

The results imply that misspecification explains a large part of variance in most of the fit indices with effect sizes that are larger than the sum of all other factors. All indices are additionally driven by factors other than misspecification. Smaller samples consistently lead to smaller goodness-of-fit values (vice versa for badness-of-fit values), irrespective of model misspecification. In addition, the characteristics of the model affect the indices. For example, CFI and TLI decrease for larger models in terms of correct models, while both indices increase with model size for misspecified models. CFI and TLI thus discriminate better between correct and misspecified models for smaller rather than larger models. Also, RMSEA decreases with lower factor loadings (Savalei 2012), or SRMR is sensitive to the number of latent variables because the higher number of correlations that are present in the model expands the factor correlation matrix (Fan and Sivo 2005). Even more importantly, the interplay between the distorting factors explains a considerable share of variance. This implies that the distortions are not only of an additive nature. We observe several substantial two-way interactions (e.g., SRMR: η² = .08). Due to these intricate and complex influences, the reliance on fixed cutoffs that fail to account for the distorting factors and their interplay will be misleading, even for informed SEM users. The next steps examine whether flexible cutoffs are able to compensate for the implications of these distortions.

Accuracy of the cutoff values

To assess precision, we calculated the hit rates of fixed and flexible cutoff as follows. The cases in the no misspecification condition were coded 1 if the estimated fit score was at or above the fixed cutoff or the flexible value as derived with our tool (and 0 if the fit index was below the cutoff). The inverse coding was employed for the cases in the moderate and severe misspecification conditions. The hit rates for the badness-of-fit indices were generated in the opposite manner. Using the thresholds suggested by Hu and Bentler (1999), we derived single-index hit rates for CFI and TLI (.95), SRMR (.08) and RMSEA (.06). We also estimated the hit rates for the two-index strategy (pairs of CFI and SRMR, TLI and SRMR, RMSEA and SRMR), using the cutoffs of the single-index strategies and .09 for SRMR.

Table 3 (upper part) presents the (absolute) hit rates of fixed cutoffs for the three types of misspecification (no, moderate, and severe) and the average hit rates. For example, in the ‘no misspecification’ section, the ‘97’ in the TLI row and ‘Fix absolute’ column indicates that 97% of the samples with correctly specified models had a TLI that was greater or equal to the generic cutoff value of .95. Table 3 also presents the (relative) difference between the hit rates of the fixed and flexible cutoffs. The ‘+2’ in the same row under the ‘Δflex .01’ column indicates that the flexible cutoff outperforms the fixed value by 2%, meaning that 99% of the samples with correctly specified models had a TLI of greater than the flexible cutoff value for a .01 range of error. The hit rates that were below 100 in the ‘no misspecification’ column are indicative of Type I errors (correct models are erroneously rejected), whereas the entries below 100 in the ‘moderate misspecification’ and ‘severe misspecification’ columns are indicative of Type II errors (misspecified models are erroneously accepted). Ideally, effective cutoff values minimize both types of errors while reaching the maximum (e.g., 100 minus the accepted error).

Table 3 Accuracy of fixed and flexible cutoffs under different degrees of model misspecification (Studies 1, 2 and 3)

Table 3 indicates that established fixed cutoffs are sufficiently effective in identifying correct models. However, they had marked difficulties in detecting a moderate extent of misspecification. RMSEA (47%) and SRMR (75%) have even relatively low hit rates for a severe degree of misspecification. Table 3 further highlights that the hit rates improve when applying flexible cutoff values (except for TLI, which already shows good accuracy). For RMSEA, the increase in overall hit rate ranges between 38 and 42%, and it ranges between 33 and 36% for SRMR. Although the overall increase in accuracy is less prominent for CFI and TLI, the analysis still indicates improvement, particularly in terms of moderate misspecification in which the hit rates rise above 90% when applying flexible thresholds (α = .05). The analysis shows very similar patterns with regard to the two-index strategy. The best performing two-index strategy with fixed cutoffs (TLI and SRMR) identifies moderate misspecifications relatively reliably (89%). Flexible cutoffs improve these hit rates by 9 to 11%. The gain in precision in this condition is even stronger for CFI and SRMR (23 to 24%) or RMSEA and SRMR (82 to 83%).

The analysis also addressed the question of whether flexible cutoffs are able to dampen the impact of the distorting factors. As shown in Fig. 4, there is a distinct drop in the hit rates of fixed cutoffs, which is due to the size of the sample or the model (e.g., more latent variables or indicators in terms of RMSEA). By contrast, the relatively constant graphs (= similar hit rates) imply that flexible cutoffs compensate for the imprint of each distorting factor on the fit indices. Still, a sensitivity analysis (shaded area representing α = .001 to α = .1) clearly shows that for CFI, smaller samples result in less robust decisions about the model, while the decisions based on SRMR are relatively robust in this regard.

Fig. 4

Hit rates (in %) of fixed and flexible cutoff values across different distorting factors (Study 1). Notes. The shaded area indicates the sensitivity of the flexible cutoffs (α_.001 to α_.1)

Balancing type I and type II error rates

Table 3 also showcases how the precision of flexible indices depends on the applied error interval (α). While narrow intervals (e.g., α = .001) raise the likelihood of identifying correctly specified models, wider intervals (e.g., .1) better identify moderate and severe cases of misspecification. However, this also increases the danger of accepting a misspecified model (Type II error) and erroneously rejecting a correct model (Type I error), respectively. Figure 5 depicts this trade-off between Type I and Type II error rates for flexible cutoffs. Very low α of .001 are at times too lenient to detect moderate misspecification, whereas wider error intervals of .1 tend to reject even correct models. The results in Fig. 5 clearly indicate that an α of .05 and .01 appear to balance Type I and Type II errors best.

Fig. 5

Trade-off between Type I and Type II error rates depending on the width of the error interval

Discussion

Flexible cutoffs aim to adjust for the key characteristics of a model and sample that are known to substantially bias fit indices. Unlike ‘golden rules’ that endorse one fixed (and somewhat arbitrary) threshold, these cutoffs are contingent as they are based on the distribution of correctly specified models that are estimated under such conditions. Study 1 confirmed the potential of flexible cutoffs as reference points for model evaluation and showed when they outperform fixed cutoffs. A substantial gain was observed in identifying moderately misspecified models for both single indices and the two-index strategy.

Beyond higher hit rates, we consider cutoff points that balance Type I and Type II errors as critically important for model testing (Hu and Bentler 1999; Marsh et al. 2004). A trade-off between the acceptance of correct models and the rejection of misspecified models is commensurable. Our results revealed that an error level α of .05 provides a conservative test of the model. Correctly specified models are detected in no less than 94% of the cases for the single indices and 92% for two-index strategies, while the likelihood of detecting moderate misspecification increases substantially compared to fixed cutoffs. To avoid a cherry-picking of α (similar to p-hacking), our results prohibit against moving towards the more extreme α unless it is used for sensitivity analysis to determine the robustness of the decision about the model.

Study 1 has one major shortcoming. Adopting the approach by Hu and Bentler (1999), the models were manipulated to cause a ‘no’, ‘moderate’, or ‘severe’ level of misspecification. Although these discrete levels have proven to be effective, the manipulation may be somewhat arbitrary, as the question of what can be qualified as either a ‘moderate’ or ‘severe’ misspecification is subjective (Marsh et al. 2004) and has drawbacks. To manipulate the respective condition, one or two parameters are misspecified in the measurement model and the structural model. However, one or two missed loadings in the measurement (maximum five indicators) might be more ‘obvious’ than the relatively small variation of one or two missing correlations would be (eight latent variables have 28 correlations). The design of Study 1 might have thus favored indices that are sensitive to misspecifications of the measurement model, such as CFI or TLI. Hence, a more objective procedure is required that captures all possible combinations of loadings and correlations. Study 2 therefore applies a systematic variation of the extent of misspecification to better spotlight the ‘gray’ area between correct and moderately misspecified models. Since certain groups of fit indices are known to be sensitive to just one specific source of misspecification but less sensitive to another, Study 2 independently varies these major sources of misspecification: the misspecification of the structural model and the measurement model.

Study 2: Continuous manipulation of the degree of misspecification

Objective

Study 2 avoids the arbitrary specification of the extent of model misspecification by employing an objective, continuous manipulation in a Monte Carlo simulation. This is achieved by sequentially introducing errors into a CFA model. The investigation further sheds light on the basic principles. Beyond model and data characteristics, fit indices could be differentially sensitive to specific sources of model misspecification (i.e., the misspecifications that are related to the structural parameters or the measurement model). Further, the debate on the two-index strategy could suggest that simply relying on larger sets of fit indices is sufficient to resolve the issue of fixed cutoffs. Study 2 therefore tests whether this ‘more-is-better’ strategy helps or harms.

Manipulated factors

Model misspecification

The literature (Table 1) offers two approaches when manipulating model misspecification. First, the measurement model falsely assumes that a manifest variable loads on a latent variable to which it does not belong (measurement model misspecification, hereafter, MM). Second, the structural model restricts a correlation (or a directed structural parameter in SEM) to zero that is not zero in the data (structural model misspecification, SM). Either way, the correlations in the data are not captured by the model, increasing χ² and thereby altering fit indices. SM and MM are commonly pooled to manipulate model misconfiguration. Study 2, by contrast, independently manipulates both misspecification types in a full factorial design.

In terms of MM, each degree of misspecification is manipulated pairwise.³ The starting point is the ‘no misspecification’ condition (MM = 0) in which all indicators load on the latent variables to which they belong (e.g., the two indicators a1 and a2 load on latent variable A, while the indicators b1 and b2 load on variable B). Each new MM condition iteratively reverses the loading of one pair of indicators (e.g., a1 loading on B, b1 loading on A). When half of the indicators load on the incorrect latent variable, the maximum degree of MM is reached, which is 1 for two−/three-indicator constructs or 2 for four−/five-indicator constructs. When switching further pairs of indicators, the majority of incorrectly loading indicators simply reverses the meanings of those latent variables.⁴ This symmetric approach is applied to ensure MM objectivity. Any asymmetric loading pattern would either endanger model identification (e.g., if no items are left to measure B) or require subjective modifications (to achieve comparability by equal degrees of freedom).

Manipulating SM starts with unrestricted correlations, and every iteration restricts one additional correlation to zero until all correlations are restricted. SM is manipulated independently of MM. The number of SM-levels depends on the number of latent variables but not on the number of indicators. Two latent variables yield a maximum of two levels of SM (0 or 1). Four variables have a maximum of seven levels (0 to 6), six variables have a maximum of 16 levels, and eight variables have a maximum of 29 levels. Figure 3 (lower part) illustrates the manipulation. All possible combinations of MM and SM are calculated with a nearly exponentially increasing number of combinations of MM and SM (e.g., two latent variables and two indicators result in six combinations; eight latent variables and five indicators yield 609 combinations).

Model size, factor loadings, and sample size

The manipulation of the misspecification-unrelated factors builds on Study 1. As the fit indices are expected to respond differently to errors in the measurement model and the structural model, we again distinguish between the number of latent variables and the number of indicators. We used two, four, six, and eight latent variables to avoid the asymmetric patterns that evoke dependencies between MM and SM. Including more latent variables would have little incremental contribution because CFAs are usually limited by the available degrees of freedom (Kenny and McCoach 2003). We used the same levels regarding the indicators (two to five items) and factor loadings (.7 to .9) as in Study 1. The sample size had relatively little impact in Study 1 (except for SRMR). As Fig. 2 and the prior research (Marsh et al. 2004) suggest, ‘sui generis’ distributions of fit indices are particularly vulnerable to very small samples. To scrutinize these challenging conditions, we split the sample sizes by the factor 2, resulting in levels of 125, 250, and 500. We apply the procedure of Study 1 to generate the data and to estimate the models with 500 replications (standard CFAs using lavaan). The overall simulation sample sums to 2.43 million unique data points.

Manipulation check

Although the conditions of misspecification were varied systematically, we ensured that the manipulation was successful. To this end, the mean χ² values were regressed by all factors (SM, MM, sample size, factor loadings, and the number of latent variables and indicators). Strong positive coefficients for SM (beta = .225, SE = .353, p = .000) and MM (beta = .326, SE = 3.263, p = .000) substantiate the SM−/MM-induced increase in the empirical lack of model fit (inflated χ²-metric). To ensure that statistical stability is not impaired by very extreme conditions to estimate CFA (i.e., complex SEMs with very small samples), the following analyses exclude models with 13 parameters or more for the sample size of N = 125.

Results

Accuracy of cutoffs

In a first step, the analysis determines the hit rates as described in Study 1. We observe for the single indices and the two-index strategy that flexible cutoffs uplift the hit rates across the large number of different conditions being evaluated. The shaded area in Fig. 6 illustrates this gain in precision. The figure shows the cumulated hit rates for all models estimated in Study 2. As can be seen for SRMR, for example, flexible cutoffs produce a much larger share of models with high hit rates (shaded area) than fixed cutoffs do. This analysis further reveals that conditions exist under which fixed cutoffs completely fail to correctly evaluate the model (hit rate of 0%), even when applying a two-index strategy. By contrast, flexible cutoffs for index pairs achieved hit rates of at least 41% (RMSEA and SRMR) and 42% (CFI/TLI and SRMR), even under the most suboptimal conditions.

Fig. 6

Comparison of the hit rates for fixed and flexible (α = .05) cutoffs (Study 2)

Extent of misspecification

To examine the impact of elevating degrees of misspecification, we formed an index combining SM and MM (0 = no misspecified parameters to 30 parameters misspecified). The lower part of Table 3 shows the hit rates of the single fit indices and the two-index strategies for four prototypical cases of (mis)specification. Mirroring the findings for the discrete levels of misspecification in Study 1, flexible cutoffs outperform fixed cutoffs, especially for weak to moderate misspecification, when only few errors are present in the model.

Disentangling different types of misspecification

We now disentangle the sources of misspecification. ANOVA is conducted including SM and MM and the misspecification-unrelated factors (the number of latent variables and indicators, sample size, and factor loadings). The results in Table 2 show that SRMR is mostly driven by misspecified structural parameters (η²_SM = .35, all ps < .001); however, the index responds much less to the measurement model misspecification (η²_MM = .14). By contrast, the goodness-of-fit indices better detect misspecification in the measurement model (CFI: η²_MM = .42; η²_SM = .11; TLI: η²_MM = .26; η²_SM = .04). RMSEA is likewise less sensitive to misspecification of the structural model (η²_MM = .25; η²_SM = .04).

Manipulating SM and MM separately enabled us to disentangle their impact on hit rates. For reasons of simplicity, the analysis focuses on the two-index strategy and the pairs: CFI and SRMR, and RMSEA and SRMR. The results are similar for TLI and SRMR. As outlined in Fig. 7, hit rates appear to suffer, especially when few SM (or MM) occur in combination with correctly specified MM (or SM). The results further highlight that under such challenging conditions, flexible cutoffs have higher hit rates than flexible thresholds do. Pairing SRMR with the moderately performing RMSEA yields below-average hit rates for fixed cutoffs, which can be improved by flexible cutoffs. Also, these patterns are very similar for a single-index strategy.

Fig. 7

Interplay between the misspecification of the structural model and the misspecification of the measurement model (Study 2)

Dependency on model and sample size

Next, we focus on the factors that are unrelated to the misspecification of SM and MM, such as the size of the model or sample. Their impact on the fit indices is presented in Table 2. The pattern closely resembles that of Study 1. The study design also helps us to separate SM and MM from model size effects (number of latent variables, indicators) that lead to pronounced effects (e.g., RMSEA favors larger models). Furthermore, identical patterns with regard to the balancing of Type I and Type II errors are found (Fig. 5).

For a more detailed analysis of model complexity, we derived three groups of models: simple models consisting of four constructs and three indicators or less (5 to 18 parameters to be estimated); moderately complex models with a maximum of six constructs and three indicators (22 to 33 parameters), which seem quite elementary for marketing practice; and complex models with a maximum of eight constructs and five indicators (39 to 68 parameters). To contrast the performance of fixed and flexible cutoffs, we estimated a score capturing the difference between their hit rates. Positive values indicate the extent to which the hit rates for flexible cutoffs surpass those of fixed cutoffs. As Fig. 8 shows for two pairs (CFI and SRMR, RMSEA and SRMR), this difference is particularly prominent for one or few misspecified model parameters (structural paths or indicator loadings), and the gain increases even further with model size. In line with the prior research (Kenny et al. 2015), pairing RMSEA and SRMR leads to substantial differences, which is due to the poor performance of RMSEA. As this index strongly responds to model size (more degrees of freedom), RMSEA tends to accept misspecified models. It should be noted that the relative advantages of flexible cutoffs come at the cost of slightly lower hit rates for correct models (e.g., CFI and SRMR_α = .05: 92.5% instead of 97.5% for N = 250 and moderately complex models).

Fig. 8

Difference between the flexible and the fixed cutoffs depending on the interplay between model and sample size (Study 2)

Balancing quality and quantity—Is more better?

To safeguard against drawing false conclusions, conventional wisdom may suggest that fit index sets bigger than pairs are beneficial when evaluating model fit. As this ‘more-is-better’ principle is often asserted (e.g., Fan and Sivo 2005), we test whether larger sets improve the accuracy in evaluating a model. For this purpose, we estimated mean hit rates for the four fit indices (CFI, TLI, RMSEA, and SRMR), the three pairs suggested by Hu and Bentler (1999), as well as for combinations of three fit indices and all four indices. For fixed cutoffs, the hit rates averaged across all possible combinations show an incremental gain in accuracy when moving from single indices to pairs; however, the gain flattens for larger sets (average hit rates for single indices = 74.6%, two = 84.5%, three = 91.3%, four = 91.9%). By contrast, flexible cutoffs (α = .05) are less strongly affected in their performance by the size of the set (single indices = 94.5%, two = 99.1%, three = 99.1%, four = 99.1%).

Despite the incremental gain in accuracy, one aspect warrants attention with regard to Type I errors. The inclusion of further indices raises the danger of correct models being falsely rejected because each additional index introduces unique variance from sources other than misspecification (Table 2). For example, adding RMSEA to the pair CFI and SRMR introduces more error, as RMSEA is vulnerable to variations due to the factor loading or complex models. Consequently, this reduces the hit rates of fixed cutoffs for correctly specified models and even more so when adding TLI as a fourth index (CFI and SRMR = 96.9%, +RMSEA = 95.6%, + TLI = 92.5%). As flexible cutoffs cater to the misspecification-unrelated factors, the increase in Type I error is less pronounced (CFI and SRMR_.05 = 92.3%, + RMSEA = 91.9%, + TLI = 91.8%). Hence, carefully selected pairs of indicators seem optimal to balance Type I and Type II errors.

Discussion

Study 2 confirms our suspicion that often-advocated ‘golden rules’ have difficulties shedding light on the ‘gray’ area of misspecification. Flexible cutoffs are better for detecting few misspecified parameters, especially in the problematic conditions of complex models and/or small samples. It cannot be stressed enough that the width of error (α) affects the conclusions for model evaluation. The results for the continuous variation of misspecification corroborate that the error levels of .05 and .01 allow a decent trade-off between Type I and Type II errors. That being said, the accuracy of flexible cutoffs is still dependent on the fit index’s general ability to detect the different reasons for misspecification. Here, we observed notable differences among the fit indices. Our results strongly support the notion that combinations of indices are beneficial for compensating their respective disadvantages (Hu and Bentler 1999). However, simply considering larger sets of indices does not resolve the problem associated with fixed cutoffs. Including more indices raises the likelihood that weak misspecification is detected. Nevertheless, this carries the danger that one of the indices will erroneously flag misspecification for a correct model. Although flexible cutoffs appear to perform consistently with elevating numbers of fit indices, researchers are well advised to focus on the quality rather than quantity of their set of fit indices.

Thus far, this research has considered cutoffs for normally distributed data. It is yet not uncommon for the data obtained in marketing to violate the normality assumption. Study 3 tackles this issue and explores if the benefits of flexible cutoffs can be generalized to non-normal data.

Simulation study 3: Violation of the normality assumption

Objective

When the assumption of multivariate normality is violated, fixed cutoffs can be based on a non-normality scaled χ² statistic (Satorra and Bentler 2001). Also, a flexible paradigm allows for this issue to be addressed because flexible cutoffs can be calculated ‘sui generis’ for non-normal data (using the scaled χ² statistic). Study 3 investigates how the performance of fixed cutoffs is affected and whether flexible cutoff points are beneficial or detrimental under such conditions.

Manipulated factors

We employed the design of Study 2 and added an additional factor with two non-normality levels that may plausibly occur in practice. First, the literature review (Table 1) reveals that ‘severe’ levels of kurtosis = 7 (rather flat) and skewness = 2 (skewed right) are most frequently applied, for example, by Curran et al. (1996). Second, a ‘moderate’ non-normality level is manipulated by setting kurtosis to 3.5 and skewness to 1 (half the severe level). The flexible cutoffs and the test models are simulated by using the simulateData function of lavaan (with non-normality robust MLM estimator). We set the arguments kurtosis and skewness to our parameters. As non-normality can lead to the non-convergence of SEM, the number of replications for each model was raised to 1000.

Manipulation check

We used the scaling factors proposed by Satorra and Bentler (2001) to check for the manipulation of non-normality. The scaling factor describes the required correction of a normal χ² statistic for non-normal distributions. Values unequal to 1 indicate that the χ² statistic must be corrected for non-normality. We checked the scaling factors for each condition (non-normality: normal, moderate, severe) based on the data derived in Studies 2 and 3. As expected, the data in Study 2 has a mean scaling factor of 1.00, whereas the data in Study 3 averages 1.05 (moderate) and 1.19 (severe) for all simulated data points. We hence assume that our manipulation was successful.

Results

Split for the two conditions of non-normal data, Table 3 presents the hit rates of the fixed and flexible cutoffs regarding the four cases of misspecification. The results largely confirm the patterns observed in the previous two studies and support a higher accuracy of flexible cutoffs, especially when few misspecified parameters are present in a model. ANOVAs also confirm the principal sensitivity of the selected fit indices to SM and MM (Table 2). The analysis shows several notable differences between normal and non-normal data. Integrating non-normality variation introduces multiple interactions, so that the sources of variations other than misspecification become even more complex in their behavior, substantiating the need to account for them.

An inspection of the absolute fit scores confirms our assumption that non-normal data reduced the goodness-of-fit scores, regardless of the actual misspecification (CFI_normal = .823, CFI_non-moderate = .810, CFI_non-severe = .801). We also observe slightly higher badness-of-fit scores (SRMR_normal = .095, SRMR_non-moderate = .099, SRMR_non-severe = .096). This shift in the fit scores has implications for the accuracy of fixed cutoffs, which do not account for this condition. For CFI, non-normal data limit the chances of detecting a correct model (M_normal = 96.9%, M_non-moderate = 94.6%, M_non-severe = 92.2%) and thus boost Type I errors by 4.7%. Conversely, the general drop in the fit values makes it more likely that models with few misspecified parameters are rejected (e.g., one misspecified parameter, M_normal = 56.3%, M_non-moderate = 59.9%, M_non-severe = 62.0%). For the badness-of-fit indices, non-normal data hamper the chances of detecting weak misspecification (e.g., one misspecified parameter for SRMR: M_normal = 27.5%, M_non-moderate = 21.9%, M_non-severe = 23.1%). The consequences of non-normal data also affect the accuracy of index pairs. As outlined in Table 3, lower hit rates occur for CFI (or TLI) and SRMR with regard to correct models, while fewer misspecified models are detected by RMSEA and SRMR.

Flexible cutoffs tailored to non-normal data appear to dampen the impact of non-normality on the decision about the model. With regard to CFI, the hit rates for fixed cutoffs (M_normal = 88.7%, M_non-moderate = 90.3%, M_non-severe = 91.1%) are consistently lower than those for the flexible cutoffs (M_normal = 93.3%, M_non-moderate = 93.0%, M_non-severe = 92.1%). The relatively constant (= similar) hit rates for flexible cutoffs across the normal and non-normal data conditions imply that the flexible paradigm helps to compensate for the distorting imprint of this factor on the fit index. Additionally, flexible cutoffs dampen the non-normality-induced increase in Type I errors that is observed for fixed cutoffs. In terms of flexible cutoffs (M_normal = 94.9%, M_non-moderate = 94.8%, M_non-severe = 94.5%), the hit rates for normal versus severe non-normality drop by .4% (Δ_fix = −4.7%). Still, the likelihood that few misspecified parameters are rejected is somewhat reduced under such suboptimal data conditions (e.g., one misspecified parameter: M_normal = 65.7%, M_non-moderate = 64.9%, M_non-severe = 63.0%). Compared to the performance of single indices, a two-index strategy produces generally higher hit rates, and again, marked differences are apparent between fixed cutoffs (e.g., CFI and SRMR: M_normal = 90.2%, M_non-moderate = 91.0%, M_non-severe = 91.7%) and flexible cutoffs (M_normal = 99.1%, M_non-moderate = 99.1%, M_non-severe = 98.9%).

Discussion

Study 3 also substantiates the feasibility of the flexible paradigm for non-normal data. Such data conditions were found to increase Type I errors, particularly for fixed cutoffs: the number of correctly specified models detected is less than when the data does not meet the normality assumption. This can be traced back to scaling factors >1. Non-normality decreases the (now corrected) χ² statistic and, in turn, the values of CFI, TLI, and RMSEA. As a result, fewer correct but more misspecified models are appropriately flagged, which is in line with Hu and Bentler (1999). Very similar to the case for the normal data conditions (Studies 1 and 2), flexible cutoffs were shown to produce higher hit rates, especially in the problematic cases (Table 3). Because flexible cutoffs are determined under the respective data conditions (normal or non-normal data), the hit rates of flexible cutoffs remain relatively stable for correct models as well as for misspecified models.

General discussion

Conclusions

This research has explored the major sources of variation in fit indices and their consequences for model evaluation. Three simulation studies provide triangulating evidence with important implications for marketing and management research. Study 1 confirms that fit indices are affected by aspects that are unrelated to model misspecification. This unwanted nuisance variance harms the accuracy of fixed cutoffs in identifying slightly or moderately misspecified models because generic cutoff points do not account for distortions that are induced by characteristics of the data or the model. The issue is more acute for complex models that entail many latent and manifest variables. For such models, more degrees of freedom are available. It is hence more likely to go unnoticed that one or few structural paths or measurement indicators are falsely specified. Since standards, such as values close to .95, have been hand-selected for simpler models, fixed cutoffs are not well suited for the degrees of freedom present in more complex models (Chen et al. 2008; Marsh et al. 1988). Under certain conditions (small samples), the fit scores for correctly specified models do not tend to reach the popular .95-threshold, so that such models may remain in the file drawer.

As these observations run counter to the notion of universal ‘golden rules’, we proposed a contingent approach and posit that cutoff values should cater to the sample and the relevant characteristics of the core model. In line with the ‘sui generis’ claim (Cheung and Rensvold 2001), fit indices follow a distribution that can alter as a function of the underlying model and sample. By accounting for these misspecification-unrelated factors, flexible cutoffs reduce their distorting impact and—as orientation points for model evaluation—facilitate the detection of few misspecified parameters. Unlike existing cutoffs, flexible cutoff points can be adjusted with regard to the width of the error range to balance Type I and Type II errors. This, for example, allows sensitivity analysis to assess the stability of the decision to accept (or reject) a given model.

Study 2 then used a more objective, continuous approach for model misspecification that separated the effects of misspecification in the structural model and the measurement model. Some fit indices are more precise in detecting misspecified structural paths (SRMR), while others are more accurate in identifying errors in the measurement model (CFI, TLI). It was again observed that fixed cutoffs have difficulties in the important ‘gray’ area of slightly misspecified models that contain few problematic parameters. Flexible cutoffs perform better under these conditions. Finally, Study 3 has shown that these conclusions also apply to non-normal data because flexible cutoffs can be specifically determined under such data conditions.

In sum, our findings cast doubt on universal thresholds. Other than recommendations to completely omit specific fit indices (Kenny et al. 2015) or to use bootstrapping fits (Bone et al. 1989), a ‘sui generis’ approach provides case-specific cutoffs, which address the criticism that there is not one universal value or ‘golden rule’ (e.g., Marsh et al. 2004). Consistent with Hu and Bentler’s (1999) recommendation, certain pairs of indices (e.g., TLI and SRMR) might appear to be sufficient when using fixed cutoffs in absolute terms and relative to flexible cutoffs. Nonetheless, fixed cutoffs are here equally effective only for the more extreme cases of misspecification that are easier to identify. Flexible cutoffs display their usefulness, especially for the problematic cases of moderate misspecification. Fostered by conventional wisdom, researchers might also be tempted to base their decision about a model on a large set of (affirmative) indices. Yet, such ‘more-is-better’ strategies are shown to yield little incremental precision. The strategy can even backfire, as it provokes the rejection of correct models and thus boosts Type I errors.

Guidelines for using flexible cutoffs

SEM is an important technique and, as shown in the field of marketing strategy, the effort invested to employ the method should be rewarded with more citations (Kumar et al. 2017). As calls are getting louder for a paradigm shift towards methodological simplicity (Gupta et al. 2014; Lehmann 2014; Lehmann et al. 2013), we provide an easy-to-use tool that determines flexibly adjusted cutoff values for all major fit indices ( www.flexiblecutoffs.org ). The tool allows the determination of cutoffs by answering a few essential questions (e.g., How many latent and measured variables does my model have? How many cases do I have? What is the amount of accepted uncertainty?). Flexible cutoffs can be derived by indicating the number of indicators and latent variables, sample size, average factor loadings, additionally fixed parameters, non-normality⁵ and assumed uncertainty (α). A large set of fit indices is available, extending beyond those discussed in this research.

Figure 9 depicts in four steps the decisions researchers should make when applying a flexible approach. We strongly discourage researchers from selectively reporting only the fit indices that support their model. Sets of fit indices can be sensitive to certain sources of misspecification, while being insensitive to others. For example, SRMR has superior capacities to detect structural misspecification but is not as effective in identifying misspecification of the measurement model. Researchers should therefore refer to combinations of fit indices, balancing their strength and weaknesses (Hu and Bentler 1999). Our results suggest referring to CFI (or TLI) and SRMR rather than RMSEA and SRMR. As no ‘one-fits-all’ indicator emerged in this research, we do not recommend a single-index strategy or untested combinations (e.g., TLI and RMSEA), even with flexible cutoffs, because they have not been validated to compensate for their respective weaknesses. We also warn against using cutoffs as the sole decision criterion. Flexible cutoff points indicate whether a given empirical model is ‘close to’ (Hu and Bentler 1999, p. 27) the ideal model. Rejecting a theoretically sound model only because CFI is .94, while fixed rules demand .95, seems arbitrary. It should thereby be noted that our criticism on ‘golden rules’ is criticism solely based on their fixed nature (being constant for all types of model and data) and not criticism of the use of fit indices per se.

Fig. 9

Decisions to derive, interpret and report flexible cutoffs

SEM, and CFAs in particular, are complex techniques that require sufficiently large samples. As long as commonalities are reasonable, SEM will produce stable results for small samples (e.g., Bentler 2007; MacCallum et al. 2001). We still call for caution when applying flexible cutoffs here. In addition, the width of the confidence interval is crucial when adopting flexible cutoffs. Error intervals of α = .1 and .001 inherently assume very high and very low uncertainty, respectively, about the evaluated model. We advise against applying such extreme intervals. They should only be used for specific purposes, such as for sensitivity analyses when testing if a model is identified correctly even under extreme (un)certainty. Although an α of .01 (rather optimistic) worked reasonably well, we recommend using an α of .05 (rather conservative), as this seems to provide the best trade-off between Type I and Type II errors (Fig. 5). Still, researchers should check the sensitivity of their decision about the model because the flexible cutoff values are more or less sensitive depending on model size and sample size (see shaded area in Fig. 2). The level of assumed uncertainty should be based on prior theoretical considerations. In general, researchers may use a more conservative α (.05) if (i) the sample is relatively small (because of imprecise estimators), (ii) the model is simple with few latent variables and indicators (because even small deviations change fit values substantially), and (iii) the research is exploratory or the model not grounded in existing theory. If (i) the data offers greater certainty (e.g., larger sample), (ii) the model yields more degrees freedom, and (iii) the constructs, their dimensionality, and the model structure are well established, then researchers can assume less uncertainty when using a less conservative α (.01). Particularly interesting for some fields, SEM is a still neglected method for estimating effects in experimental design (Bagozzi and Yi 1989), thereby explaining measurement error. These models typically consist of few factors and levels.

Illustrative examples based on marketing data

To illustrate the usefulness of flexible cutoffs in a marketing context, we apply the approach to three widely noted papers on different phenomena in marketing.

Case I—Post-hoc examination of model fit

Flexible cutoffs can be used to evaluate model fit post-hoc. For example, Zboja et al. (2016) developed a scale of consumer perception of sales pressure. The authors report that their final CFA has appropriate fit (CFI = .99, TLI = .99, RMSEA = .05, SRMR missing). Applying our flexible cutoffs for this model with a relatively small sample (N = 275) confirms model fit (CFI_.05 ≥ .947, TLI_.05 ≥ .940) but not for RMSEA (RMSEA_.05 ≤ .029). Consulting SRMR (SRMR_.05 ≤ .054) could have provided clarification.

Case II—Gray area of misspecification

Mishra et al. (1993) explored the antecedents of the attraction effect (correlation matrices and standard deviations allow replication). For this illustration, we focus on the beer dataset (N = 359) and estimate the original CFA model, which includes six latent variables. The model (χ² = 344.184, df = 194, CFI = .972, TLI = .967, SRMR = .037) is accepted when applying both the fixed cutoffs (CFI and TLI ≥ .95, SRMR ≤ .09) and the flexible cutoffs (CFI_.05 ≥ .965, TLI_.05 ≥ .959, SRMR_.05 ≤ .045). The same is true for the two-index combinations. The flexible approach even allows for sensitivity analyses of the decision to accept the model. The model is confirmed when using the less conservative margin of error of α = .01 (CFI_.01 ≥ .951, TLI_.01 ≥ .943, SRMR_.01 ≤ .046). This decision would hold even when employing the very conservative cutoffs with α = .1 (CFI_.1 ≥ .970, TLI_.1 ≥ .966, SRMR_.1 ≤ .044).

To illustrate the performance of fixed and flexible cutoffs for the problematic ‘gray’ area of weak misspecification, we test whether missing out on a correlation is detected (between familiarity and task involvement, value = .231). This slightly misspecified model (χ² = 360.060, CFI = .970, TLI = .960, and SRMR = .059) would still be accepted by fixed cutoffs as well as when applying the two-index strategy. However, the flexible cutoff for SRMR (most sensitive to structural misspecification) rejects such a model (SRMR_.05 ≤ .045), as the two-index strategy would also do. Sensitivity analyses again demonstrate that this remains the case, even when applying less conservative margins of errors (SRMR_.01 ≤ .046; SRMR_.001 ≤ .047).

Case III— Exploratory use

Our review of 68 JAMS articles shows that 28 papers used fit indices (or χ²) for model comparison. However, comparing models with different parameters based on fit indices can be misleading because the indices respond to model and sample size. Given this sensitivity to the model parameters, authors may be prompted to selectively remove items or add constructs to inflate fit scores. We illustrate this by using the SERVQUAL scale (Parasuraman et al. 1988) and data from Babakus and Boller (1992), who compare the dimensionality of this established scale. The SERVQUAL configuration did not show an acceptable fit of data and model (CFI = .900, SRMR = .065), even for fixed cutoff standards. To mimic an exploratory approach, we modeled a five-factor CFA, using a a-priori principal axis factor analyis to calibrate (items are allocated to the factor they load highest and loadings < .3 are removed). Fixed cutoffs would suggest an appropriate fit (CFI = .960, SRMR = .038). However, and in line with issues raised by Babakus and Boller (1992), this empirical solution is questionable, as items load differently than originally proposed by SERVQUAL (e.g., nine items loaded on the responsiveness dimension). Consequentially, greater uncertainty has to be assumed due to the exploratory nature of the analysis. Since flexible cutoffs are also flexible with regard to the conclusions, α can be adjusted to the large uncertainty involved in the model assessment (α = .1). Flexible cutoffs clearly spark doubts about the fit (CFI_.10 ≥ .982, SRMR_.10 ≤ .036); the same holds true for an α of .05. By contrast, if this study served a confirmative purpose with very limited uncertainty (α = .001), flexible cutoffs would indicate that the empirical factor selection is close to an appropriate fit (CFI_.001 ≥ .955, SRMR_.001 ≤ .041).

Further research and limitations

As with all studies, there are limitations to our findings. The sample size and the parameters of the core model were carefully selected. Although we tried to capture the most common design levels, some scholars may have more complex CFA models in mind, or they might want to examine uneven combinations of indicators and latent variables (e.g., a latent variable with five indicators and another one with twelve). The simulations also assumed constant factor loadings across all indicators of a construct and structural relationships. Future research should extend our approach to asymmetric or unequal relationships among loadings (e.g., loadings of .5 to .9 for one latent variable) and correlations (e.g., .2 for one structural path, .4 for another). The studies in this research employed only a limited number of errors in the measurement model to retain symmetric patterns and maintain objectivity. More complex, asymmetric designs as well as other sources of misspecification, such as outliers, correlated errors, or omitted variables, and other levels of non-normal data, should be considered (e.g., positive or negative kurtosis, no skewness).

Our results clearly favor two-index strategies in model evaluation because each index has unique strengths and weaknesses. It is still worthwhile to continue the search for an index that is equally effective in detecting misspecified parameters in the structural model as well as in the measurement model. Such a ‘one-fits-all’ index should also be immune to aspects that are unrelated to model misspecification. If this proves impossible, a flexible approach as suggested in this paper may help to reduce the distortions by misspecification-unrelated factors.

The flexible cutoff paradigm allows researchers to set an acceptable Type I error that captures the amount of uncertainty they are willing to accept a-priori for the given theoretical model. When safeguarding against falsely accepted models (lower Type II errors), this comes at the expense of sometimes lowering chances to accept the model under consideration (possibly slightly increased Type I errors). Considering the balancing of Type I and Type II errors, we believe that this price is worth the overall higher chance to reliably detect a misspecified model.

In this research, fit indices have been investigated in absolute terms, particularly in light of theory testing (Jöreskog and Sörbom 1982). Flexible cutoffs may also be relevant for comparing alternative models (West et al. 2012). Applying the flexible cutoff approach for these relative purposes might be a venture for future research. The flexible cutoffs in this research were derived and validated for CFAs. Similar to previously used fixed cutoffs that were derived from CFAs, flexible cutoffs can be applied to other applications of SEMs. When doing this, one should be aware of the consequences arising from more parsimonious models. Unlike CFAs that capture all possible relationships, SEMs consider only the paths that are theoretically relevant. Future research should thus attempt to fine-tune flexible cutoff values with regard to SEM models that are often used in marketing research or specific issues in SEM, such as multi-group analysis or latent growth. Since flexible cutoffs are only investigated in a FIML (full information maximum likelihood) context, investigations for other estimators with and without missing data are welcome. Recent developments in SEM have also spawned a Bayesian approach (Muthén and Asparouhov 2012). We second this approach for cases in which informative priors rather than exact zeros for cross-loadings and residual correlations are used. Relative performance compared to the traditional ‘ML-SEM’ approach applied here has not been investigated systematically. We therefore advocate simulations that address the Bayesian ‘PP’ alternative to χ² and suggest comparing its performance to ML-based fit indices. Overall, this research provides a starting point for subsequent works on flexible interpretations of fit indices. Our basic premise coupled with the empirical findings hopefully encourages scholars to strengthen their efforts in the search for more accurate cutoffs to evaluate a model.