Goodness-of-fit assessment refers to how well our model reproduces the data-generating process. When fitting a regression model, researchers assess the goodness-of-fit of their model by inspecting a plot of the standardized residuals versus standardized fitted values in order to check the linearity and homoscedasticity assumption of the model. Failure to meet the model assumptions will likely result in incorrect parameter estimates. Simply put, when the fitted model is incorrectly specified, all inferences based on it are suspect.

In structural equation modeling (SEM), we fit a system of regression-like equations to our data (possibly involving latent variables), and procedures similar to those used in regression can be used to assess each of the equations in the model (Bollen & Arminger, 1991; Coffman & Millsap, 2006; Hildreth, 2013; Yuan & Hayashi, 2010). However, they hardly seem to be used in applications. Rather, for historical reasons, the assessment of model fit in structural equation models has relied on the use of grouped data (residual means, covariances, and correlations) as opposed to individual residual observations. There is evidence that residual covariances (i.e., the differences between observed and fitted covariances) are sensitive to linear mis-specifications (Raykov, 2000) but I am not aware of any research that has examined whether they are sensitive to the presence of heteroscedasticity. Residual summary statistics such as residual covariances can be summarized into a single test statistic to assess the overall goodness-of-fit of a structural equations model. Although overall test statistics are invariably reported in applications, they are most often ignored as they usually suggest that the model is incorrectly specified. Rather, current practice in SEM relies on the use of goodness-of-fit indices, summary statistics that are provided in a descriptive fashion, along with some cutoff values that suggest a “good” fit. In so doing, I feel that these current practices in SEM contradict the most basic statistical principles, as taught in introductory statistics courses. In fact, I believe that assessing the fit of a structural equation model is not fundamentally different from assessing a mean difference using a z test.

The aim of this presentation is to provide specific links between our practices in introductory statistics and in SEM in the hope that it helps to standardize current practices. To simplify the presentation, I discuss solely the frequentist approach. Also, I focus on “classical” structural equation models, in other words, on covariance structure models.

1 Why Should We Assess the Goodness-of-Fit of a SEM Model?

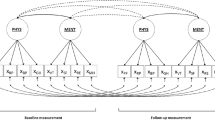
What do we gain by properly examining the fit of a SEM model? And what do we lose by not doing so? To answer these questions, it is best to use a simple model. Consider the mediation model involving variables Y, X and M sketched in Fig. 1 as Model 0. Edwards and Lambert (2007) discussed how to use regression analysis to estimate the moderating effects of a fourth variable (variable z in Fig. 1). Consider Model 0, in Fig. 1. Moderation may be present only in path a, leading to Model a, or only in path b, leading to Model b, etc. Assuming that Model 0 holds, there are seven possible moderated mediation models with these four variables (in addition to Model 0, no moderation). These models can be estimated by including the interactions ZX and ZM in the model leading to the eight models and their degrees of freedom sketched in Fig. 1.

Fig. 1
figure 1

Sketch of moderated mediation models.

Full size image

The purpose of the analysis is to estimate the mediation parameter (indirect effect) \(a \times b\). Because of the nature of the models involved, both regression and SEM provide the same parameter estimates for any of the models depicted. However, SEM methods provide an overall goodness of fit of the model being fitted, something not available using the equation by equation regression methods. What is the use of these goodness-of-fit tests? One could argue that they are not needed and that all that a researcher needs to do when confronted with this problem is to fit the saturated model, Model abc. This argument is incorrect. If any of the other models (Models a to bc) is the data-generating process and Model abc is fitted, one loses power for detecting the parameter of interest, \(a \times b\), because one uses up degrees of freedom in estimating unneeded parameters. More generally, if the data-generating process is nested within (but not equal to) the fitted model, the power to detect the mediational effect is reduced. For instance, if Model a is the data-generating model and Models ab, ac, or abc are fitted, the mediational effect will be consistently estimated, but power will be less (confidence intervals for the parameter \(a \times b\) will be wider) than the power resulting from using Model a. This is clearly undesirable if the population effect size is small, and/or if sample size is small. In contrast, if the data-generating model is not nested within the fitted model, the mediational effect will not be consistently estimated. For instance, if Model a is the data-generating model, and Models b, c, or bc are fitted, the estimate of the parameter of interest \(a\times b\) will be biased, regardless of sample size. Fitting an overparameterized SEM model will lead to a loss of power for detecting effects of interest, whereas fitting an underparameterized SEM model (or more generally, a mis-specified model) will lead to inconsistent estimates in one or more model parameters.

Correct model specification is critical for sound substantive inferences—not just in a SEM but for any model, even the simplest possible one. For instance, consider investigating the extent to which individuals in a high-stakes job assessment situation distort their responses to a personality questionnaire. Suppose we have baseline (B) measures of their personality as well as their scores obtained when they apply (A) for a job. To what extent did individuals distort their responses? Provided the sample size is large enough, this question can be answered using a paired samples z test.

What assumptions are needed to make an inference in this case given a large enough sample? Apparently, none. Although the data (difference scores) may appear remarkably non-normal, unless the sample size is small, the central limit theorem ensures the validity of the statistical inference. However, there are “hidden” model assumptions (Cohen, Cohen, West, & Aiken, 2003). The easiest way to see this is by rephrasing the problem as a regression model, \(y_A -y_B ={\beta }_0 +{\varepsilon } \). This regression model can be rewritten as \(y_A ={\beta }_0 +y_B +{\varepsilon } \), and we now realize a model assumption made when using a paired samples z test, namely, that the slope between the two assessments is 1. The slope between two psychological measurements taken a couple of weeks apart is never 1. Therefore, the model assumption made when performing our paired sample z test is likely to be incorrect, thus biasing the results. To investigate whether the assumption used in our paired sample z test is tenable, we could fit \(y_A ={\beta }_0 +{\beta }_1 y_B +{\varepsilon } \). However, this model in turn implies the standard assumption that the predictor (baseline score) is uncorrelated with the error (which contains unmodeled predictors of the assessment score). This assumption is likely to be incorrect as well, as we should expect individuals with a high level on a desirable trait to be less likely to distort their responses than those with a low level on the trait, leading to a heteroscedastic relationship between baseline and assessment scores. Thus, fitting a regression model to this problem is also likely to result in incorrect substantive conclusions. A model that accounts for the heteroscedasticity is likely to be needed. The morale of this digression is clear: even in extremely simple models such as a paired sample z test there are model assumptions that, when not met, lead to incorrect substantive conclusions.

2 Current Practices in Elementary Statistics

2.1 Classical Approach

Consider the paired sample z test for the score distortion example introduced above. A null hypothesis of no effect can be stated as \(H_0 :{\mu } ={\mu }_A -{\mu }_B =0\), where \({\mu }\) denotes the population mean of the difference scores. More generally, the null hypothesis can specify a non-null value, \(H_0 :{\mu } ={\mu }_0 \) versus say \(H_1 :{\mu } \ne {\mu }_0 \) and \(H_{0}\) can be tested in large samples using a z statistic. Should a statistically significant difference be found, we examine the magnitude of the difference using an effect size and judge it qualitatively.

To me, an effect size is a population parameter that conveys the magnitude of the effect. We can convey this information for a paired sample z test in different ways. One way is by providing an estimate of the mean difference. This is reasonable if the units are meaningful. For the score distortion example, such an effect size (e.g., 10 points) is not useful to convey the magnitude of the effect. In this case, we could provide an estimate of the percentage increase (e.g., assessment scores are on average 20% higher than baseline scores). Often, these relative effect sizes are more informative than raw (or unstandardized) effect sizes. However, relative effect sizes are most useful when (a) they are coupled with information on the baseline, and (b) baseline units can be substantively interpreted. When the baseline units cannot be substantively interpreted, preference has evolved for unitless (standardized) effect sizes. Regardless of whether unstandardized, relative, or standardized effect sizes are used, it is necessary to provide a confidence interval for them instead of simply a point estimate to convey the precision with which we estimate the effect size, a population parameter.

2.2 Interval Estimation Approach

Some authors (Schmidt & Hunter, 1997; Steiger & Fouladi, 1997; and references therein) have strongly argued for bypassing the significance test altogether and focusing the analysis on the estimation of a confidence interval for an effect size of interest. One basic argument put forth by these authors is that, from a substantive point of view, it is far more interesting (and fruitful) to ask the question of how large an effect is (in a probabilistic sense, i.e., with a confidence interval) than asking whether an effect is exactly zero (which is very unlikely). For a paired sample z test, the unstandardized effect size is simply \({{\varepsilon }}_\mathrm{u} ={\mu } -{\mu }_0 \) and the standardized effect size is \({{\varepsilon }}_\mathrm{s} =\frac{{\mu } -{\mu }_0 }{{\sigma } }\), where \({\sigma }\) denotes the population standard deviation of the difference scores and note that \({\varepsilon }_{s}\) is Cohen’s delta (e.g., Cohen, 1988). In large samples, a \((100 -\alpha )\)% confidence interval for \({\varepsilon }\) (that is, \({\varepsilon }_{s}\) or \({\varepsilon }_{u}\)), can be obtained using

$$\begin{aligned} \Pr \left( {{\hat{{\varepsilon } }}-z_{\alpha /2} \hbox {ASE}({\hat{{\varepsilon } }})\le {\varepsilon } \le {\hat{{\varepsilon } }}+z_{\alpha /2} \hbox {ASE}({\hat{{\varepsilon } }})} \right) =1-\alpha , \end{aligned}$$
(1)

where \({\hat{{\varepsilon }}}\) denotes the estimate of the effect size and ASE denotes its asymptotic standard error.

3 Current Practices in SEM

Before describing current practices in SEM, I shall provide some background. Covariance structure modeling most often begins by specifying a set of equations for mean-centered data, possibly involving latent variables. The model implies a covariance structure \({\varvec{{\upsigma }}}_{0}={\varvec{{\upsigma }}}({\varvec{\uptheta }}_{0})\). Let p denote the number of observed variables being modeled; then \({\varvec{{\upsigma }}}\) is a \(t=p(p+1)/2\) vector of population covariances, and \({\varvec{\uptheta }}_{0}\) is a \(q \le t\) vector of parameters to be estimated from the data. The two best known procedures for estimating the model parameters involve minimizing the discrepancy functions

$$\begin{aligned} F=\left( {\mathbf{s}-\varvec{{\upsigma }}_0 } \right) ^{\prime }{{\hat{\mathbf{W}}}}\left( {\mathbf{s}-\varvec{{\upsigma }}_0 } \right) , \end{aligned}$$
(2)

and

$$\begin{aligned} F_\mathrm{ML} =\ln \left| {\varvec{\Sigma }_0 } \right| -\ln \left| \mathbf{S} \right| +\hbox {tr}\left( {\mathbf{S}\varvec{\Sigma }_0^{-1} } \right) -p, \end{aligned}$$
(3)

with respect to \({\varvec{\uptheta }}\). In (3), S and \({\varvec{\Sigma }}_{0}\) denote the sample and population covariance matrices, respectively, whereas in (2), s is a t-vector of sample covariances and \({{\hat{\mathbf{W}}}}\mathop \rightarrow \limits ^{p} \mathbf{W}\), a fixed matrix. In covariance structure analysis, maximum likelihood (ML) parameter estimates under normality assumptions are frequently obtained by minimizing (3)—see Browne and Arminger (1995) for details. In contrast, (2) defines a class of functions. Different choices of the weight matrix \({{\hat{\mathbf{W}}}}\) lead to different estimators such as unweighted least squares, diagonally weighted least squares, or the asymptotically distribution free (ADF) weighted least squares proposed by Browne (1982, 1984).

One choice of weight matrix in (2) is

$$\begin{aligned} {{\hat{\mathbf{W}}}}=2^{-1}{} \mathbf{{D}'}\left( {\hat{\varvec{\Sigma }}_0^{-1} \otimes \hat{\varvec{\Sigma }}_0^{-1} } \right) \mathbf{D}, \end{aligned}$$
(4)

updated at each iteration, where D is a duplication matrix (see Browne & Arminger, 1995). I shall denote (2) with (4) as \(F_{\mathrm{IRLS}}\) (for Iteratively Reweighted Least Squares). Minimizing \(F_{\mathrm{IRLS}}\) has the same solution as (3) but a different minimum (for details see Lee & Jennrich, 1979). Thus, \(F_{\mathrm{IRLS}}\) can also be used to obtain normal theory (NT) ML estimates. NT ML is by far the most widely used estimator in covariance structure modeling both when normality assumptions are invoked but also under the ADF assumptions set forth by Browne (1982). In the latter case, asymptotic standard errors that are robust to non-normality are used (Satorra & Bentler, 1994).

3.1 Goodness-of-Fit Assessment: Classical Approach

Within a classical approach, the null hypothesis to be tested is \(H_0 :\varvec{{\upsigma }} =\varvec{{\upsigma }}_0 \) versus \(H_1 :\varvec{{\upsigma }} \ne \varvec{{\upsigma }}_0 \). There exist a number of test statistics with known asymptotic distribution under the null that can be used to test this hypothesis (Browne, 1984; Satorra & Bentler, 1994; Yuan & Bentler, 1997, 1998, 1999), some of which rely on normality assumptions, and others on ADF assumptions. These test statistics are simply a summary (often a weighted average) of the residual covariances, \(\mathbf{s}-\hat{\varvec{{\upsigma }}}\), where \(\hat{\varvec{{\upsigma }}}=\varvec{{\upsigma }} (\hat{\varvec{\uptheta }})\). For instance, for ML estimates obtained under normality assumptions, \({\hat{T}}_{\mathrm{IRLS}} =n{\hat{F}}_{\mathrm{IRLS}}\) is one suitable test statistic, where \(n=N-1\) and N denotes sample size. Under the null hypothesis, this statistic follows an asymptotic Chi-square distribution with \({ df}=t-q\) degrees of freedom. However, in applications involving ML estimation under normality assumptions, the most widely used test statistic is the likelihood ratio test of the model against a saturated model, \(LR=n{\hat{F}}_\mathrm{ML}\mathop \rightarrow \limits ^{d} {\chi }_{{ df}}^2\).

Yet, when (as is most often the case) the null hypothesis is rejected, the result of the goodness-of-fit test is usually disregarded on a number of grounds, such as (a) the model will be rejected for substantively trivial misfits when the sample size is very large, (b) the null hypothesis is a substantively uninteresting hypothesis, since by definition all models (that is, approximations) are wrong, or (c) we should focus on comparative model fit (i.e., model selection) rather than on model fit.

As a result, within a classical approach SEM practice usually relies on the use of goodness-of-fit indices. These are summary sample statistics used in a descriptive fashion such as

(a) the Comparative Fit Index (Bentler, 1990)

$$\begin{aligned} \widehat{\hbox {CFI}}=1-\frac{\max \left( {{\hat{T}}_0 -df_0 ,0} \right) }{\max \left( {{\hat{T}}_\mathrm{baseline} -df_\mathrm{baseline},0} \right) }, \end{aligned}$$
(5)

where \({\hat{T}}_0\) denotes the estimated value of the statistic used to test the fitted model (with \({ df}_{0}\)), and \({\hat{T}}_\mathrm{baseline}\) denotes the value of the statistic when testing a baseline model (with \({ df}_\mathrm{baseline}\)), usually the independence model,

(b) the Goodness-of-Fit Index (GFI: Jöreskog & Sörbom, 1981) which as presented in Tanaka and Huba (1989) is

$$\begin{aligned} \widehat{\hbox {GFI}}=1-\frac{\left( {\mathbf{s}-\hat{\varvec{{\upsigma } }}} \right) ^{\prime }{{\hat{\mathbf{W}}}}\left( {\mathbf{s}-\hat{\varvec{{\upsigma } }}} \right) }{\mathbf{s}^{\prime }{{\hat{\mathbf{W}}}{} \mathbf s }}, \end{aligned}$$
(6)

(c) the Standardized Root Mean Squared Residual (SRMR: Bentler, 1995; Jöreskog & Sörbom, 1988)

$$\begin{aligned} \widehat{\hbox {SRMR}}=\sqrt{\frac{(\mathbf{s}-\hat{\varvec{{\upsigma } }})'{{\hat{\mathbf{G}}}}^{-1}(\mathbf{s}-\hat{\varvec{{\upsigma }}})}{t}}=\sqrt{\frac{1}{t}\sum _{i\le j} {\frac{\left( {s_{ij} -\hat{\varvec{{\upsigma }}}_{ij} } \right) ^{2}}{\sqrt{s_{ii} s_{jj} }}} }, \end{aligned}$$
(7)

where \({{\hat{\mathbf{G}}}}\) is a \(t\times t\) diagonal matrix with elements \(s_{ii} s_{jj} \), that is, letting \(\mathbf{s}_{ii}\) be a p vector of sample variances, \({{\hat{\mathbf{G}}}}=\hbox {diag}\left( {\hbox {vecs}(\mathbf{s}_{ii} \mathbf{s}_{ii} ^{\prime })} \right) \), and vecs() denotes an operator that stacks onto a column vector the elements at or below the diagonal of a symmetric matrix,

(d) the Correlation Root Mean Squared Residual (CRMR: Bollen, 1989; Ogasawara, 2001)

$$\begin{aligned} \widehat{\hbox {CRMR}}=\sqrt{\frac{\left( {{{\hat{\mathbf{G}}}}^{-1/2}\mathbf{s}-{{\hat{\mathbf{G}}}}_0^{-1/2} \hat{\varvec{{\upsigma } }}} \right) ^{\prime }\left( {{{\hat{\mathbf{G}}}}^{-1/2}{} \mathbf{s}-{{\hat{\mathbf{G}}}}_0^{-1/2} \hat{\varvec{{\upsigma } }}} \right) }{t-p}}=\sqrt{\frac{1}{t-p}\sum _{i<j} {\left( {r_{ij} -{\hat{\rho }}_{ij} } \right) ^{2}} }, \end{aligned}$$
(8)

where \({{\hat{\mathbf{G}}}}_0 =\hbox {diag}( {\hbox {vecs}(\hat{\varvec{{\upsigma } }}_{ii} \hat{\varvec{{\upsigma }}}_{ii} ^{\prime })} )\).

Many more goodness-of-fit indices have been proposed in the literature. For an overview, see Marsh, Hau, and Grayson (2005) and Bollen and Long (1993). In practice, goodness-of-fit indices such as the GFI, CFI or SRMR are used as if they were test statistics in a classical null hypothesis testing framework using cutoff values that have been proposed in the literature (e.g., Hu & Bentler, 1999). Thus, if a goodness-of-fit index meets the recommended cutoff values, the model is retained and used as if it were correctly specified. In other words, fit indices coupled with fixed cutoff values are used as if they were test statistics of a vaguely specified hypothesis of “close” fit: the model fit is close if it meets the fixed cutoff criterion for that index, and not close if it exceeds the cutoff (Barrett, 2007; Marsh, Hau, & Wen, 2004; Saris, Satorra, & van der Veld, 2009). The problem is compounded by the existence of different fit indices, each one with one or more proposed cutoff values. As a result, unscrupulous researchers may choose the most favorable index and the most favorable cutoff value (McDonald & Ho, 2002).

There are several problems with current practices. I will just highlight three. First, they are pre-statistical. The parameter being estimated by each index is often not described, nor is care taken to ensure that the index is an asymptotically unbiased (or at least consistent) estimate of the parameter of interest. Furthermore, the sampling variability of the statistic is blatantly ignored. In many ways, retaining a model if, say, the sample CFI is larger than some cutoff value (say .99) is analogous to concluding in a z test that there is a mean difference worth speaking of if the observed mean percentage increase is larger than some fixed cutoff value (say 10%). Second, partly as a result of the approach being pre-statistical, no agreement is possible regarding which index to use, or what cutoff value. Third, and most importantly, inferences on the model parameters are made as if the model were correct, when in fact, it is mis-specified.

3.2 Goodness-of-Fit Assessment: Interval Estimation Approach

Within this approach, a confidence interval for an effect size of model misfit is estimated. The effect size of model misfit reported almost invariably in current SEM practice is the Root Mean Squared Error of Approximation (RMSEA). The RMSEA is often referred to as a goodness-of-fit index. I prefer to reserve the term “goodness-of-fit index” for sample statistics whose distribution is unknown, or if known, is not used in practice. The asymptotic distribution of the sample RMSEA is known under general conditions (Browne & Cudeck, 1993, Steiger, 1989), and is widely used in practice for statistical inference.

The RMSEA was introduced by Steiger (Steiger, 1989, 1990; Steiger & Lind, 1980) with contributions by Browne and Cudeck (1993). Consider a discrepancy function of the sample and model-implied population covariances such as (2) and (3). As described by Steiger (1989) and Browne and Cudeck (1993), the population RMSEA is defined as

$$\begin{aligned} \hbox {RMSEA}=\sqrt{\frac{F(\varvec{\Sigma } ,\varvec{\Sigma }_0 )}{df}} \end{aligned}$$
(9)

where \(F(\varvec{\Sigma }, \varvec{\Sigma }_0 )\) denotes the discrepancy between the true and unknown population covariance matrix, \(\varvec{\Sigma }\), and the covariance matrix specified under the null hypothesis, \(\varvec{\Sigma }_0 \).

The sample RMSEA is defined as (Browne & Cudeck, 1993; Steiger, 1989)

$$\begin{aligned} \widehat{\hbox {RMSEA}}=\sqrt{\max \left( {\frac{n{\hat{F}}-df}{n\times df},0} \right) }\quad . \end{aligned}$$
(10)

Provided \(n{\hat{F}}\) follows, asymptotically, a non-central Chi-square distribution under a sequence of local alternatives, confidence intervals for the population RMSEA can be obtained. Alternatively, the RMSEA may be used to test an hypothesis of approximate (or “close”) fit of the model, \(H_{0}^{*} :\hbox {RMSEA}\le c\hbox { versus }H_{1}^{*} :\hbox {RMSEA}>c\), where \(c > 0\) is some arbitrary cutoff value. When \(c = 0, H_{0}^{*}\) is equivalent to the null hypothesis of exact fit \(H_0 :\varvec{{\upsigma }} =\varvec{{\upsigma }} (\varvec{\uptheta })\). Browne and Cudeck (1993, p. 144) famously stated that, based on their practical experience, they felt that models with RMSEA \(\le 0.05\) provided a close fit to the unknown population covariance matrix (in relation to the degrees of freedom), that models with an RMSEA around 0.08 provided a reasonable approximation, and that models with an RMSEA greater than 0.1 provided a poor fit. As a result, the hypothesis of close fit being tested in applications is \(H_{0}^{*}:\hbox {RMSEA}\le 0.05\), which corresponds to Steiger’s (1989) cutoff for a very good fit.

4 Reconciling Current Practices in Introductory Statistics and in SEM

The use of the RMSEA effect size of the misfit (9) and accompanying statistical theory to obtain a confidence interval for it (within an interval estimation approach) or a p value for a test of close fit \(H_0^*:\hbox {RMSEA}\le 0.05\) (within a classical approach) provides a marked improvement over practices involving the comparison of sample goodness-of-fit indices to fixed cutoff values. However, upon realizing that the population RMSEA is an effect size of the misfit of a SEM model, I saw that we need to examine more closely than we have done so far how to assess the size of the misfit of a SEM model. For it is the notion of effect size of the misfit that will enable us to reconcile current practices in introductory statistics (e.g., when reporting z tests results) and in SEM.

Indeed, I believe that current practices in SEM will substantially improve by mimicking current practices elsewhere in statistics. Thus, within a classical approach, if the null hypothesis is tested and rejected, one should report the effect size of the misfit (with a confidence interval), and judge it qualitatively, just as in a z test. On the other hand, within an interval estimation approach, one should first judiciously choose the effect size of the misfit and report a confidence interval for it.

However, there are three key differences between the null hypothesis considered in covariance structure modeling [\(H_{0} :{\varvec{{\upsigma }}}={\varvec{{\upsigma }}}_{0}, \varvec{{\upsigma }}_{0}=\varvec{{\upsigma }}(\varvec{\uptheta }_{0} )\)] and a paired sample z test \((H_{0} :{\mu } ={\mu }_{0})\). The first is that in the z test, the parameter involved in the null hypothesis is the parameter of interest, whereas in SEM, the parameters involved in the null hypothesis of model fit, \({\varvec{{\upsigma }}}\), are most often simply a means to an end: the interest lies in the fundamental parameters \({\varvec{\uptheta }}\). A second difference is that \(H_{0}\) in a z test is univariate and only one parameter is involved, while in SEM we deal with a multivariate null hypothesis. A third difference is that in a z test \(H_{0}\) is a simple null hypothesis (\({\mu }_0 \) is fixed), whereas in SEM we deal with a composite null hypothesis \(({\varvec{\uptheta }}_{0}\) is to be estimated from the data).

The first difference implies that one needs to relate the model misfit results to the consistency with which parameters of interest are estimated. There is not much research on this topic, though see for instance Yuan, Marshall, and Bentler (2003) and Reise, Scheines, Widaman, and Haviland (2012). The second difference implies that in a z test there is only one effect size to consider, although we are free to choose the most suitable one for the analysis (e.g., unstandardized, standardized, or relative), whereas in SEM one may consider t effect sizes in which the overall effect size of the misfit will simply be a summary measure, however imperfect, of these t effect sizes. Also, because only one parameter is considered in a z test, assessing power involves a single dimension; in contrast, in SEM there are multiple possible directions of misfit to consider when assessing power. The third difference simply implies that the statistical theory for obtaining confidence intervals will necessarily be more involved in SEM than in a z test.

5 Effect Sizes of SEM Misfit

5.1 A Multivariate Problem

The size of the misfit in a covariance structure model cannot be captured by a single effect size parameter because of the multivariate nature of the data. Rather, for each variance and covariance we can define an unstandardized effect size \({{\varepsilon }}_{ij}^{(u)} \) as well as a standardized effect size parameter \({{\varepsilon }}_{ij}^{(s)} \) analogous to the ones used in a paired sample z test where \({{\varepsilon }}_{ij}^{(u)} ={\sigma }_{ij} -{\sigma }_{ij}^0 \) and

$$\begin{aligned} {{\varepsilon }}_{ij}^{(s)} =\frac{{\sigma }_{ij} -{\sigma }_{ij}^0 }{\sqrt{{\sigma }_{ii} {\sigma }_{jj} }}. \end{aligned}$$
(11)

Here, \({\sigma }_{ij}\) denotes the true and unknown population covariance between variables i and j (or variance if \(i=j\)) and \({\sigma }_{ij}^0 \) denotes the population covariance (or variance) under the fitted model obtained as the solution to (13)—see below. Almost invariably, we will not be able to interpret the magnitude of the unstandardized effect size \({{\varepsilon }}_{ij}^{(u)}\). Therefore, as an effect size it is most often useless. To obtain an effect size whose magnitude can be interpreted, in (11) the unstandardized effect size is standardized by dividing it by the product of the population standard deviations.

Another possible effect size is

$$\begin{aligned} {{\varepsilon }}_{ij}^{(r)} =\frac{{\sigma }_{ij} }{\sqrt{{\sigma }_{ii} {\sigma }_{jj} }}-\frac{{\sigma }_{ij}^0}{\sqrt{{\sigma }_{ii}^{0} {\sigma }_{jj}^{0}}}={\rho }_{ij} -{\rho }_{ij}^{0}. \end{aligned}$$
(12)

Here, the population covariance is standardized by dividing by the population standard deviations, and the covariance under the null hypothesis is standardized by dividing by the null standard deviations. \({{\varepsilon }}_{ij}^{(r)}\) is simply the population residual correlation between the population and the fitted model.

Letting \({\hat{{\sigma }}}_{ij} \equiv {\sigma }_{ij} (\hat{\varvec{{\uptheta }}})\), \({{\varepsilon }}_{ij}^{(u)} \) and \({{\varepsilon }}_{ij}^{(s)}\) can be consistently estimated using the sample residual covariance and standardized residual covariance respectively, \(e_{ij}^{(u)}=s_{ij} -{\hat{{\sigma } }}_{{{{\varvec{ij}}}}}\), \(e_{ij}^{(s)} =\frac{s_{ij}-{\hat{{\sigma }}}_{ij}}{\sqrt{s_{ii} s_{jj}}}\) and note that the standardized residual covariance need not be in the interval (\(-1\), 1), but one expects it to be within this metric in most cases. In contrast, the sample residual correlation, \(e_{ij}^{(r)} =\frac{s_{ij} }{\sqrt{s_{ii} s_{jj} }}-\frac{{\hat{{\sigma } }}_{ij} }{\sqrt{{\hat{{\sigma } }}_{ii} {\hat{{\sigma } }}_{jj} }}=r_{ij} -{\hat{\rho }}_{ij} \), is most often within the interval (\(-1\), 1).

Now, to obtain confidence intervals for these population effect sizes, I assume that the population covariances \({\varvec{{\upsigma }}}\) are related to the fitted model, \(\varvec{{\upsigma }}_0\), by the standard assumption of a sequence of local alternatives (aka parameter drift assumption), \(\varvec{{\upsigma }} = \varvec{{\upsigma }}_0 + \varvec{\updelta } /\sqrt{N}\), where \(\varvec{{\upsigma }}_0 =\varvec{{\upsigma }} (\varvec{\uptheta }_0 )\). I also assume that \(\varvec{{\upsigma }}_0 \) corresponds to the value of \({\varvec{\uptheta }}_{0}\) that minimizes \(\left( {\varvec{{\upsigma }} -\varvec{{\upsigma }}_0 } \right) ^{\prime }{} \mathbf{W}\left( {\varvec{{\upsigma }} -\varvec{{\upsigma }}_{0}} \right) \) so that \(\varvec{\uptheta }_0\) satisfies

$$\begin{aligned} \varvec{{\Delta }}'_0 \mathbf{W}\left( {\varvec{{\upsigma }} -\varvec{{\upsigma }}_0 } \right) =\mathbf{0}, \end{aligned}$$
(13)

where \(\varvec{\Delta }_0 =\left. {\frac{\partial \varvec{{\upsigma }} (\varvec{\uptheta })}{\partial {\varvec{\uptheta }}'}} \right| _{\varvec{\uptheta } =\varvec{\uptheta }_0 } \). Finally, with \(\varvec{\updelta } =\sqrt{N}(\varvec{{\upsigma }} -\varvec{{\upsigma }} _0 )\) I assume that

$$\begin{aligned} \sqrt{N}\left( {\mathbf{s}-\varvec{{\upsigma }} _0 } \right) \mathop \rightarrow \limits ^d N\left( {{\varvec{\updelta }}, \varvec{\Gamma }}\right) . \end{aligned}$$
(14)

Consider now the asymptotic distribution of the unstandardized, \(\mathbf{e}_\mathrm{u} =\mathbf{s}-{\hat{\varvec{{\upsigma }}}}\), standardized, \(\mathbf{e}_\mathrm{s} ={{\hat{\mathbf{G}}}}^{-1/2}(\mathbf{s}-{\hat{\varvec{{\upsigma }} }})\), and correlation residuals, \(\mathbf{e}_\mathrm{r} ={{\hat{\mathbf{G}}}}^{-1/2}{} \mathbf{s}-{{\hat{\mathbf{G}}}}_0^{-1/2} {\hat{\varvec{{\upsigma }} }}=\mathbf{r}-{\hat{{\varvec{\uprho }}}}\) respectively, with population parameters

$$\begin{aligned} \varvec{{\upvarepsilon }}_\mathrm{u} =\varvec{{\upsigma }} -\varvec{{\upsigma }}_0 ={\varvec{\updelta }} /{\sqrt{N}}, \quad \varvec{{\upvarepsilon }}_\mathrm{s} =\mathbf{G}^{-1/2}(\varvec{{\upsigma }} -\varvec{{\upsigma }}_0 ),\quad \hbox {and}\quad \varvec{{\upvarepsilon }}_\mathrm{r} =\mathbf{G}^{-1/2}\varvec{{\upsigma }} -\mathbf{G}_0^{-1/2} \varvec{{\upsigma }} _0, \end{aligned}$$
(15)

where \(\mathbf{G}=\hbox {diag}\left( {\hbox {vecs}(\varvec{{\upsigma }}_{ii} \varvec{{\upsigma }} _{ii} ^{\prime })} \right) \). With \(\mathbf{H}=\varvec{\Delta } ({\varvec{\Delta } }'{} \mathbf{W}\varvec{\Delta } )^{-1}{\varvec{\Delta }}'{} \mathbf{W}\), and \(\mathbf{F}=\left. {\frac{\partial (\mathbf{r}-{\hat{{\varvec{\uprho }} }})}{\partial {\hat{\varvec{{\upsigma }} }}^{\prime }}} \right| _{{\hat{\varvec{{\upsigma }}}}=\varvec{{\upsigma }}} \), we obtain \(\mathbf{e}_\mathrm{u} \mathop \rightarrow \limits ^{d} N\left( {{\varvec{{\upvarepsilon }}}_\mathrm{u} ,{\varvec{\Xi }}_\mathrm{u} } \right) \), \({\varvec{\Xi }}_\mathrm{u} =N^{-1}(\mathbf{I}-\mathbf{H}){\varvec{\Gamma }} (\mathbf{I}-\mathbf{H})'\),

$$\begin{aligned}&\mathbf{e}_\mathrm{s} \mathop \rightarrow \limits ^d N\left( {{\varvec{{\upvarepsilon }}}_\mathrm{s} ,{\varvec{\Xi }}_\mathrm{s} } \right) , \quad {\varvec{\Xi }}_\mathrm{s} =\mathbf{G}^{{^{-1}}/{_{2}}}{\varvec{\Xi }}_\mathrm{u} \mathbf{G}^{{^{-1}}/{_{2}}}, \end{aligned}$$
(16)
$$\begin{aligned}&\mathbf{e}_\mathrm{r} \mathop \rightarrow \limits ^d N\left( {{\varvec{{\upvarepsilon }}}_\mathrm{r} ,{\varvec{\Xi }}_\mathrm{r} } \right) ,\quad {\varvec{\Xi }}_\mathrm{r} =\mathbf{F}{\varvec{\Xi }}_\mathrm{u} \mathbf{{F}'}, \end{aligned}$$
(17)

where \({\varvec{\Gamma }}\) denotes the asymptotic covariance matrix of \(\sqrt{N}{} \mathbf{s}\), which can be computed under normality assumptions, \({\varvec{\Gamma }}_\mathrm{NT}\), or under ADF assumptions, \({\varvec{\Gamma }}_{{ ADF}}\) (see for instance Satorra & Bentler, 1994).

Therefore, the sample effect sizes are asymptotically unbiased estimators of their respective population effect sizes. Furthermore, using (1), for any estimator within the family of estimators (2)—which includes the MLE—one can obtain confidence intervals (under normality, or “robust” to non-normality) for these effect sizes of the misfit. Thus, for instance, the asymptotic standard error of a standardized residual covariance is \(\hbox {ASE}(e_{ij}^{(s)} )=\sqrt{{\varvec{\Xi }}_\mathrm{s}^{(ij)} }={\sqrt{{\varvec{\Xi }}_\mathrm{u}^{(ij)} }}\big /{\sqrt{\varvec{{\upsigma }}_{ii} \varvec{{\upsigma }}_{jj} }}\) (Ogasawara, 2001), where \({\varvec{\Xi }}_\mathrm{s}^{(ij)}\) is the corresponding diagonal element of \({\varvec{\Xi }}_{s}\).

5.2 Overall Effect Size of the Misfit

In practice, applied researchers will be interested in a single parameter that summarizes the effect of the misfit. A “natural” overall unstandardized effect size is the population Root Mean Squared Residual (RMSR), \({{\iota }}_\mathrm{u} :=\hbox {RMR}=\sqrt{\frac{{\varvec{{\upvarepsilon }}}_\mathrm{u}^{\prime }{\varvec{{\upvarepsilon }}}_\mathrm{u} }{t}}=\sqrt{\frac{(\varvec{{\upsigma }} -{\varvec{{\upsigma }}}_0)'(\varvec{{\upsigma }} -{\varvec{{\upsigma }}}_0 )}{t}}\). It is clear that this overall effect size cannot be substantively interpreted. In contrast, the population Standardized Root Mean Residual

$$\begin{aligned} {{\iota }}_\mathrm{s} :=\mathrm{SRMR}=\sqrt{\frac{{\varvec{{\upvarepsilon }}}_\mathrm{s} ^{\prime }{\varvec{{\upvarepsilon }}}_\mathrm{s} }{t}}=\sqrt{\frac{(\varvec{{\upsigma }} -{\varvec{{\upsigma }}}_0 )'{} \mathbf{G}^{-1}(\varvec{{\upsigma }} -{\varvec{{\upsigma }}}_0 )}{t}}, \end{aligned}$$
(18)

can be approximately interpreted as an average of the standardized effect sizes. Finally, we can define a population Correlation Root Mean Squared Residual

$$\begin{aligned} {{\iota }}_{r}:={\hbox {CRMR}}=\sqrt{\frac{{\varvec{{\upvarepsilon }}}_\mathrm{r} ^{\prime }{\varvec{{\upvarepsilon }}}_\mathrm{r}}{t-p}}=\sqrt{\frac{(\mathbf{G}^{{^{-1}}/{_{2}}}\varvec{{\upsigma }} -\mathbf{G}_0^{-1/2} \varvec{{\upsigma }}_0)'(\mathbf{G}^{{^{-1}}/{_{2}}}\varvec{{\upsigma }} -\mathbf{G}_0^{-1/2} \varvec{{\upsigma }}_0)}{t-p}}, \end{aligned}$$
(19)

which can be approximately interpreted as the average of the population residual correlations.

To obtain suitable estimators for these population parameters, consider the sum of squared residuals, \(T=T_{s}\) or \(T_{r}\), where \(T_\mathrm{s} =\mathbf{e}_\mathrm{s} ^{\prime }{} \mathbf{e}_\mathrm{s} \) and \(T_\mathrm{r} =\mathbf{e}_\mathrm{r} ^{\prime }{} \mathbf{e}_\mathrm{r} \) denote the sum of squared standardized and correlation residuals, respectively. The asymptotic mean and variance of T under parameter drift assumptions are (see the “Appendix”)

$$\begin{aligned} \hbox {E}(T)= & {} {\mu }_T =\hbox {tr}({\varvec{\Xi }} )+{{\varvec{{\upvarepsilon }}} }'{\varvec{{\upvarepsilon }}} , \end{aligned}$$
(20)
$$\begin{aligned} \hbox {var}(T)= & {} {\sigma }_T^2 =2\hbox {tr}({\varvec{\Xi }}^{2})+4{{\varvec{{\upvarepsilon }}} }'{\varvec{\Xi }} {\varvec{{\upvarepsilon }}} , \end{aligned}$$
(21)

where \({\varvec{\Xi }} = {\varvec{\Xi }}_{s}\) or \({\varvec{\Xi }}_{r}\). Therefore, using the method of moments, an asymptotically unbiased estimate of the population sum of squared residuals \({{\varvec{{\upvarepsilon }}} }'{\varvec{{\upvarepsilon }}} \) is \({\hat{{{\varvec{{\upvarepsilon }}} }'}}{\hat{{\varvec{{\upvarepsilon }}} }}=T-\hbox {tr}({\varvec{\Xi }})\) leading to the estimator for the overall effect sizes \({{\iota }}={{\iota }}_{s}\) or \({{\iota }}_{r}\, \tilde{{{\iota }}}=\sqrt{\frac{T-\hbox {tr}({\varvec{\Xi }})}{t}}\), where for \({{\iota }}_{r}\), we use \(t-p\) instead of t. In turn, the asymptotic mean and variance of this estimator are

$$\begin{aligned} \hbox {E}(\tilde{{\iota }})= & {} \left( {\frac{{\mu }_T -\hbox {tr}({\varvec{\Xi }} )}{t}} \right) ^{-\frac{3}{2}}\frac{8\left( {{\mu }_T -\hbox {tr}({\varvec{\Xi }})} \right) ^{2}-{\sigma } _T^2 }{8t^{2}}={{\iota }} \left( {1-\frac{{\sigma } _T^2 }{8({{\varvec{{\upvarepsilon }}} }'{\varvec{{\upvarepsilon }}} )^{2}}} \right) , \end{aligned}$$
(22)
$$\begin{aligned} \hbox {var}(\tilde{{\iota }})= & {} \frac{{\sigma } _T^2 }{4t\;\left( {{\mu }_T -\hbox {tr}({\varvec{\Xi }} )} \right) }. \end{aligned}$$
(23)

Equation (22) reveals that \(\tilde{{{\iota }}}\) is an asymptotically biased estimator of the overall population effect sizes and that an asymptotically unbiased estimator is \({\hat{{{\iota }}}}=k^{-1}\tilde{{{\iota }}}\), where \(k=1-\frac{{\sigma }_T^2}{8({{\varvec{{\upvarepsilon }}} }'{\varvec{{\upvarepsilon }}} )^{2}}\). As a result, asymptotically unbiased estimates of the population SRMR and CRMR can be obtained using

$$\begin{aligned} {\hat{{{\iota }}}}_\mathrm{s}= & {} {\hat{k}}_\mathrm{s}^{-1} \sqrt{\frac{\max \left( {T_\mathrm{s} -\hbox {tr}(\hat{\varvec{\Xi }}_\mathrm{s} ),0} \right) }{t}}, \quad {\hat{{{\iota }} }}_\mathrm{r} ={\hat{k}}_\mathrm{r}^{-1} \sqrt{\frac{\max \left( {T_\mathrm{r} -\hbox {tr}(\hat{\varvec{\Xi }}_\mathrm{r} ),0} \right) }{t-p}}, \end{aligned}$$
(24)
$$\begin{aligned} {\hat{k}}_\mathrm{s}= & {} 1-\frac{\hbox {tr}(\hat{\varvec{\Xi }}_\mathrm{s}^2 )+2\mathbf{{e}'}_\mathrm{s} \hat{\varvec{\Xi }}_\mathrm{s} \mathbf{e}_\mathrm{s} }{4T_\mathrm{s}^2 }, \quad {\hat{k}}_\mathrm{r} =1-\frac{\hbox {tr}\left( \hat{\varvec{\Xi }}_\mathrm{r}^2\right) +2\mathbf{{e}'}_\mathrm{r} \hat{\varvec{\Xi }}_\mathrm{r} \mathbf{e}_\mathrm{r} }{4T_\mathrm{r}^2 }. \end{aligned}$$
(25)

Equation (22) also reveals that the sample RMR (Jöreskog & Sörbom, 1988), \(\widehat{RMSR}=\sqrt{(\mathbf{s}-\hat{\varvec{{\upsigma }}}{)}'(\mathbf{s}-\hat{\varvec{{\upsigma }}})/t}\), and the samples SRMR and CRMR given in Eqs. (7) and (8) overestimate their population parameters.

6 Confidence Intervals for the SRMR and CRMR and Associated Tests of Close Fit

If the sampling distribution of \({\hat{{{\iota }} }}={\hat{{{\iota }}}}_\mathrm{s} ,{\hat{{{\iota }} }}_\mathrm{r} \) is well approximated in large samples by a normal distribution, then a \((100-{\alpha })\)% confidence interval for \({{\iota }} ={{\iota }} _\mathrm{s} ,{{\iota }} _\mathrm{r} \) can be obtained using an expression analogous to (1) where the asymptotic standard errors are (see “Appendix”)

$$\begin{aligned} \hbox {ASE}({\hat{{{\iota }}}}_\mathrm{s})=\sqrt{k_\mathrm{s}^{-2} \frac{\hbox {tr}({\varvec{\Xi }}_\mathrm{s}^2 )+2\mathbf{{e}'}_\mathrm{s} {\varvec{\Xi }}_\mathrm{s} \mathbf{e}_\mathrm{s} }{2t\times T_\mathrm{s} }},\quad +\,\, \hbox {ASE}({\hat{{{\iota }} }}_\mathrm{r} )=\sqrt{k_\mathrm{r}^{-2} \frac{\hbox {tr}({\varvec{\Xi }}_\mathrm{r}^2 )+2\mathbf{{e}'}_\mathrm{r} {\varvec{\Xi }}_\mathrm{r} \mathbf{e}_\mathrm{r}}{2(t-p)T_\mathrm{r} }}. \end{aligned}$$
(26)

If a test of close fit based on the SRMR or CRMR is desired, of the type

$$\begin{aligned} H_0^*:{{\iota }} \le {{\iota }}_0 \hbox { versus }H_{1}^{*} :{{\iota }} >{{\iota }}_0, \end{aligned}$$
(27)

where \({{\iota }} _0 >0\) is an arbitrary value of the SRMR or CRMR, p values are obtained using \(p=1-\Phi (z)\), where \(\Phi ()\) denotes a standard normal distribution function and \(z=\frac{{\hat{{{\iota }} }}-{{\iota }} _0 }{\hbox {ASE}({\hat{{{\iota }} }})}\).

7 Tests of Exact Fit Based on the SRMR and CRMR

For tests of exact fit of the type \(H_0 :{{\iota }} =0\hbox { versus }H_1 :{{\iota }} >0\), where \({{\iota }}\) denotes either the population SRMR or CRMR, I consider the statistics \(T^{*}=\widehat{SRMSR}\) or \(\widehat{CRMSR}\) given in Eqs. (7) and (8). Under this null hypothesis, the asymptotic mean and variance of the sample SRMR and CRMR are (see “Appendix”)

$$\begin{aligned} \hbox {E}(T^{*})= & {} {\mu }_{T^{*}} =\sqrt{\frac{\hbox {tr}({\varvec{\Xi }} )}{t}}\frac{4\hbox {tr}({\varvec{\Xi }} )^{2}-\hbox {tr}({\varvec{\Xi }} ^{2})}{4\hbox {tr}({\varvec{\Xi }})^{2}}, \end{aligned}$$
(28)
$$\begin{aligned} \hbox {var}(T^{*})= & {} {\sigma }_{T^{*}}^2 =\frac{\hbox {tr}({\varvec{\Xi }}^{2})}{2t\,\hbox {tr}({\varvec{\Xi }} )}, \end{aligned}$$
(29)

where for the CRMR \(t-p\) is used instead of t (see also Ogasawara, 2001). Again, assuming that the sampling distribution of \(T^{*}=\widehat{\hbox {SRMR}}\) or \(\widehat{\hbox {CRMR}}\) is well approximated in large samples by a normal distribution, p values for the null hypothesis of exact fit are obtained using

$$\begin{aligned} p=1-\Phi (z), \quad z=\frac{T^{*}-{\mu }_{T^{*}} }{\sqrt{{\sigma }_{T^{*}}^2 }}. \end{aligned}$$
(30)

8 Small Sample Behavior of SRMR and CRMR Confidence Intervals and Goodness-of-Fit Tests

To investigate the performance of the methods described above, I performed a small simulation study involving a two-factor model. More specifically, multivariate normal data for p = 8 variables were generated with mean zero and a covariance structure \({\varvec{\Sigma }} ={\varvec{\Lambda \Psi }} {{\varvec{\Lambda }} }'+{\varvec{\Theta }} \) with \({{\varvec{\Lambda }} }'=\left( {{\begin{array}{cccccccc} {0.8}&{}\quad {0.7}&{}\quad {0.7}&{}\quad {0.8}&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad 0 \\ 0&{}\quad 0&{}\quad 0&{}\quad 0&{}\quad {0.8}&{}\quad {0.7}&{}\quad {0.7}&{}\quad {0.8} \\ \end{array} }} \right) \), \({\varvec{\Psi }} =\left( {{\begin{array}{cc} 1&{}\quad \\ \rho &{}\quad 1 \\ \end{array} }} \right) \), and \({\varvec{\Theta }} =\mathbf{I}-\hbox {diag}({\varvec{\Lambda \Psi }} {{\varvec{\Lambda }} }')\). Sample sizes were 100, 200, 500, 1000, and 3000; interfactor correlations were \({\rho } = 0.7, 0.8\) and 0.9. A one-factor model was estimated in all cases by maximum likelihood under normality assumptions. 1000 replications per condition were used. In Table 1 I provide the population values corresponding to each condition, the average sample SRMR (7) and CRMR (8) and the unbiased estimates of the population parameters (24). We see in this table that the simulation setup yields an array of population values: the SRMR values investigated are 0.074, 0.049, and 0.025, and the CRMR values investigated are 0.084, 0.056 and 0.028.

Table 1 Standardized Root Mean Squared Residual (SRMR) and Correlation Root Mean Squared Residual (CRMR): population values, average and standard deviation of sample estimates, average and standard error of unbiased estimates, average standard errors for unbiased estimates, and coverage rates for 90% confidence intervals.
Full size table

We also see in Table 1 that the samples SRMR and CRMR overestimate their population parameters substantially as sample size and degree of misfit decreases. For instance, when the correlation between the two factors is 0.9 and sample size is 100, the population CRMR is 0.028, but the average sample CRMR is a whopping 0.048. In contrast, the unbiased estimates are right on target: for the above example, the average of the unbiased estimates is 0.027. I also provide in Table 1 the standard deviation of the unbiased estimates, the average of the standard errors (SEs) of the unbiased estimates, and coverage rates for 90% confidence intervals computed using a reference normal distribution. We see that the SEs slightly overestimate the true variability of the estimates when the sample size is 200 or less, particularly as the degree of misfit decreases. This is because of the use of a truncated estimate. As a result, coverage rates are unacceptably small when the sample size is 200 or less and the fitted model is rather close to the true model (population parameters of SRMR = 0.025 and CRMR = 0.028). In all other conditions, coverage is at or below nominal rates, but it is at least 0.86 even at the smallest sample size considered (\(N= 100\)). I also examined coverage rates for individual standardized residuals (11) and individual residual correlations (12). For the worst case (\(\rho = 0.9\), or SRMR = 0.025 and CRMR = 0.028) and smallest sample size considered (\(N = 100\)), coverage rates for 90% confidence intervals are at worst 0.86.

Table 2 shows the empirical rejection rates (Type I errors) for selected values of nominal rejection rates of the test of close fit (27) using a reference normal distribution. In all cases, the value being tested is whether the SRMR or CRMR parameter equals its true value. We see in this table that the proposed test provides accurate Type I errors for all levels of SRMR (0. 025–0. 074) and CRMR (0.028 to 0.084) even at the smallest sample size considered \((N = 100)\) and for all significance levels except when \({\alpha }>0.60, N < 500\) and at the smallest model discrepancy considered (\({\rho } = 0.9\), or SRMR = 0.025 and CRMR = 0.028).

Table 2 Test of close model fit based on the Standardized Root Mean Squared Residual (SRMR) and Correlation Root Mean Squared Residual (CRMR): empirical rejection rates for selected levels of significance level.
Full size table

To investigate the performance of the methods described above when the model holds, I used the same setup as before, except that now data were generated under a one-factor model. Table 3 shows the empirical rejection rates (Type I errors) for selected values of nominal rejection rates of the test of exact fit \(H_0 :{{\iota }} =0\hbox { versus }H_1 :{{\iota }} >0\) using a reference normal distribution. In this table, we see that the proposed test provides accurate Type I errors even at the smallest sample size considered (N = 100) and for all significance levels.

Additional Monte Carlo results on the accuracy of confidence intervals and tests for single standardized residuals and residual correlations are given in Maydeu-Olivares and Shi (2017)—see also Ogasawara (2001).

Table 3 Test of exact model fit based on the Standardized Root Mean Squared Residual (SRMR) and Correlation Root Mean Squared Residual (CRMR): empirical rejection rates for selected levels of significance level.
Full size table

8.1 The RMSEA as an Overall Effect Size

The population RMSEA (9) as defined by Steiger (1989) and Browne and Cudeck (1993) is not unique; rather, it changes depending on the method used to estimate the model parameters. For instance, when ML estimates under normality are obtained by minimizing \(F_\mathrm{IRLS}\)—i.e., (2) using the weight matrix (4)—the population RMSEA being estimated is

$$\begin{aligned} \hbox {RMSEA}_\mathrm{NT,1} =\sqrt{\frac{({\varvec{{\upsigma }}} -{\varvec{{\upsigma }}}_0 )'{\varvec{\Gamma }}_\mathrm{NT}^{-1} ({\varvec{{\upsigma }}} -{\varvec{{\upsigma }}}_0 )}{df}}, \end{aligned}$$
(31)

where \({\varvec{\Gamma }}_\mathrm{NT} \) denotes the asymptotic covariance matrix of \(\sqrt{N}\left( {\mathbf{s}-{\varvec{{\upsigma }}}} \right) \) under normality assumptions.

In contrast, when these ML estimates are obtained by minimizing the \(F_\mathrm{ML}\) function (3), the population RMSEA being estimated is

$$\begin{aligned} \hbox {RMSEA}_\mathrm{NT,2} =\sqrt{\frac{\ln \left| {{\varvec{\Sigma }}_0 } \right| -\ln \left| {\varvec{\Sigma }} \right| +\hbox {tr}\left( {{\varvec{\Sigma }} {\varvec{\Sigma }}_0^{-1} } \right) -p}{df}}\quad . \end{aligned}$$
(32)

Furthermore, if the model parameters are estimated by minimizing (2) using the weight matrix \({{\hat{\mathbf{W}}}}={\hat{{\varvec{\Gamma }} }}_\mathrm{ADF}^{-1} \), where \({\hat{{\varvec{\Gamma }} }}_\mathrm{ADF} \) denotes the consistent estimator of the asymptotic covariance matrix of \(\sqrt{N}\left( {\mathbf{s}-{\varvec{{\upsigma }}} } \right) \) under ADF assumptions, the RMSEA being estimated is

$$\begin{aligned} \hbox {RMSEA}_\mathrm{ADF} =\sqrt{\frac{({\varvec{{\upsigma }}} -{\varvec{{\upsigma }}}_0 {)}'{\varvec{\Gamma }}_\mathrm{ADF}^{-1} ({\varvec{{\upsigma }}} -{\varvec{{\upsigma }}}_0 )}{df}}\quad . \end{aligned}$$
(33)

I find it undesirable that the population parameter being estimated to communicate the size of the model misfit changes depending on the estimator used; I think that the same parameter should be estimated regardless of the estimator and distributional assumptions. I will return to this point later.

For now, let us assume for ease of exposition that the RMSEA parameter being estimated is (31). The \(\hbox {RMSEA}_\mathrm{NT,1}\) differs from the RMR in that (a) a weighted sum of the unstandardized effect sizes is used instead of an unweighted sum, and (b) the sum is divided by degrees of freedom instead of by the number of effect sizes. I will examine each of these features of \(\hbox {RMSEA}_\mathrm{NT,1}\) in turn.

In my opinion, the only weighting of population parameters that can be justified is one that facilitates the substantive interpretation of the parameter being estimated. The weight matrix used in the population SRMR (18) is one such choice. The weight matrix (4) does not facilitate the substantive interpretation of the parameter: quite the contrary. So why was such a weight matrix used? Because of computational convenience: under normality assumptions, an assumption of parameter drift, and if an asymptotically optimal estimator such as the MLE is used, the statistic \({\hat{T}}_\mathrm{IRLS} =n{\hat{F}}_\mathrm{IRLS}\) leads to a non-central Chi-square distribution which allows a straightforward computation of confidence intervals for the RMSEA (31)—see Steiger (1989) and Browne and Cudeck (1993) for details. The use of \({\hat{{\varvec{\Gamma }}}}_\mathrm{NT}^{-1}\) in \({\hat{T}}_\mathrm{IRLS}\) is fully justified: it takes into account the sampling variability of the statistics used in the quadratic form. But the use of \({\varvec{\Gamma }}_\mathrm{NT}^{-1} \) in (31) is not. The unstandardized population effect sizes \({\varvec{{\upsigma }}} -{\varvec{{\upsigma }}}_0 \) are parameters and therefore have no sampling variability. Recently, however, Wu and Browne (2015, see also Satorra, 2015) have provided one such justification. They show that if one is willing to assume that the data arise from a two-level setup in which the sampled population is an instance of a superpopulation, the RMSEA can be interpreted as a “distance” between the sampled population and the superpopulation. In many instances, I feel uncomfortable with this two-level setup because its main result is to widen the confidence intervals, whereas parameter estimates are unaffected. I prefer to rely on the usual setup in which inferences are made solely on the population from which the sample is drawn and, if indeed a superpopulation is of interest, samples from multiple populations from the superpopulation are drawn (as in any two-level model), thereby resulting in different parameter estimates than if only a single sample is used, as in Wu and Browne’s (2015) setup.

Leaving the superpopulation issue aside, the RMSEA parameter cannot be interpreted substantively. What does a population RMSEA of 0.07 mean? We believe it is a value that is not too large, but not small either. But we believe this because of the cutoff values given by Browne and Cudeck, or by Steiger (1989), which are slightly different; if they had not given their famous cutoff values, we would be left stranded with an RMSEA value we would be unable to interpret.

It is the uninterpretable nature of the RMSEA that makes cutoff values necessary. A close reading of Browne and Cudeck (1993) reveals that their cutoff values were largely based on their experience fitting exploratory factor models. However, any given population value of the RMSEA (say 0.05) has a different meaning depending on the structure and size of the model (Chen, Curran, Bollen, Kirby, & Paxton, 2008; Savalei, 2012). In contrast, a standardized effect size such as the CRMR always has the same interpretation: it can be interpreted as approximately the average of the residual correlations, which are in a (\(-1\), 1) interval. As a result, cutoff values for the CRMR can be avoided altogether, as we are able to interpret what a CRMR = 0.05 versus CRMR = 0.10 means.

Steiger (2000) anticipated many of the points made in the present article regarding inconveniences with the population non-centrality parameter and related measures such as the RMSEA. In particular, he pointed out how the fact that the weighting of the residuals is stochastically motivated makes precise population cutoff points problematic.

9 Adjusting for Model Parsimony: Model Selection Versus Goodness-of-Fit

The population RMSEA divides the (weighted) sum of unstandardized effect sizes by degrees of freedom to correct for model complexity. Indeed, models with more parameters will generally lead to smaller overall effect sizes. By doing so, the RMSEA attempts to “reduce the conflict between the desire for parsimony and the desire for close fit” (Browne & Cudeck, 1993: p. 136). Indeed, the sample RMSEA can be used as an index for model selection and also as a test statistic to assess the (approximate) goodness-of-fit of the model.

Model selection involves selecting the best model for the data at hand using a particular criterion. Goodness-of-fit proper addresses the question of how close our model is to the data-generating mechanism. I prefer to separate model selection from goodness-of-fit assessment proper. In applications, often both need to be performed. An investigator who performs model selection first, after selecting the best model for the data at hand, needs to examine the extent to which the selected model mirrors the unknown data-generating mechanism. This involves substantive considerations, but also a goodness-of-fit assessment, as the data at hand is what provides us the actual information on the data-generating mechanism.

On the other hand, an investigator who first assesses the goodness-of-fit of several substantively different models, after determining that more than one model provides a close fit to the data at hand, must select a model. This can involve a model selection statistic, but in my opinion, it will involve mostly substantive considerations. The extreme case, of course, involves choosing among equivalent models (MacCallum, Wegener, Uchino, & Fabrigar, 1993).

Fig. 2
figure 2

Overall effect size of the misfit when a one-factor model is fitted to an independent clusters two-factor model as the number of variables and the correlation between the factors increase.

Full size image

To help understand the effect that adjusting for model parsimony has on the overall effect sizes of the misfit, I computed the population \({\hbox {RMSEA}}_\mathrm{NT,2}\) (32), \({\hbox {RMSEA}}_\mathrm{NT,2 }\) (31), the SRMR (18), and the CRMR (19) when the discrepancy between the true data-generating mechanism and the fitted model substantively “stays the same” while model size (the number of variables being modeled) increases. The true data-generating mechanism is again a two-independent cluster factor model with equal number of indicators per factor where population factor loading values were in all cases 0.8 and error variances \(1-0.8^{2}=0.36\), the number of variables ranged from \(p=8\) to \(p= 48\), and \(\rho \) ranged from 0.8 to 0.9. The null model corresponds to the value of the parameter vector that minimizes the Kullback–Leibler discrepancy (i.e., the ML fitting function under normality) between the data-generating model and a one-factor model. Results are presented graphically in Fig. 2. We see in Fig. 2 that when a one-factor model is fitted to an independent cluster factor model and the correlation between the factors is held constant (say \(\rho =0.85\)), as the number of indicators per factor increases the population \({\hbox {RMSEA}}_\mathrm{NT,2}\) decreases. This implies that if a criterion such as a RMSEA = 0.05 is used to retain a model, and if the RMSEA is estimated using the likelihood ratio test statistic, it is easier to retain a model because the corresponding population parameter decreases as model size increases even when the discrepancy between the data-generating mechanism and the fitted model “stays the same.” In contrast, in this setup the value of the \(\hbox {RMSEA}_\mathrm{NT,1}\) parameter also decreases from \(p= 8\) to 16 and then flattens. Thus, the \(\hbox {RMSEA}_\mathrm{NT,1}\) is preferable in this setup. The SRMR shows the opposite pattern to the \(\hbox {RMSEA}_\mathrm{NT,1}\): it increases from p = 8 to 16 and then flattens. Finally, the CRMR shows the pattern that I would like to see in this setup: it reflects the fact that the overall effect of the misfit does not depend on model size, it only depends on \({\rho }\), the correlation between the factors.

This example serves to illustrate the following point: Almost invariably, a fixed cutoff for the RMSEA, such as RMSEA = 0.05, is used. Also, almost invariably the RMSEA is estimated using the likelihood ratio test (possibly after a mean and variance correction to account for non-normality). In my experience (see also Kenny & Mccoach, 2003), in these situations it is easier to retain the model when a large number of variables is used (say, p = 50, rather than, say, p = 10). This runs counter to the obvious fact that finding a well-fitting model is increasingly difficult as the number of variables to be modeled increases. In contrast, an average of standardized effect sizes, such as the CRMR, is invariant to increasing model size as the discrepancy between the data-generating mechanism and the fitted model “stays the same.” As a result, one should expect larger values of the SRMR or CRMR as the number of variables being modeled increases.

10 Assessing the Goodness-of-Fit of a SEM Model in Practice

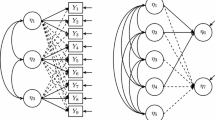
Figure 3 displays graphically a “typical” SEM model, taken from Alden, Steenkamp, and Batra (2006).Footnote 1 In this model, a number of indicators are used to measure the variables “media,” “migration,” “SNI,” “materia,” “ethno,” and “GBA” without error. In addition, the variables “GCO attitude” and “GCO intens” are measured with error, and a number of variables (e.g., age) are used as covariates. The hypotheses of interest are displayed graphically in Fig. 4.

The results obtained using robust methods are very similar to those obtained under normality assumptions, and here I just report the results obtained under normality. The R package lavaan (Rosseel, 2012) was used to obtain all the results presented here. The likelihood ratio statistic yields 1,090.99 on 267 df, \(p= 0\). We conclude that the proposed model is not the data-generating mechanism. This is not a surprising outcome, given the streamlined nature of the model and the number of variables being modeled.

Fig. 3
figure 3

“Typical” SEM model, taken from Alden et al. (2006).

Full size image
Fig. 4
figure 4

Alden et al.’s (2006) substantive hypotheses.

Full size image

How far away are we from the data-generating mechanism? In other words, what is the size of the misfit? If the size of the misfit is trivial, we may decide to ignore it. The current standard for judging the size of model misfit (adjusted for model parsimony) is to use the RMSEA. A 90% confidence interval (CI) for the RMSEA based on the likelihood ratio test yields (0.061, 0.069), the point estimate is 0.065, and notice that another CI could have been constructed using \(T_\mathrm{IRLS}\), yielding a slightly different result. Does this estimate of the RMSEA reveal a large or a small degree of misfit? We do not know. All we have are Browne and Cudeck’s famous cutoffs, based on their experience. But their experience is limited to just a handful of models and mis-specifications. As Savalei (2012) has shown, a RMSEA value (say 0.065) may indicate a large or small misfit depending on a number of factors such as the type of model, the number of variables being modeled, and so on. The magnitude of the RMSEA is uninterpretable because it is based on a weighted combination of unstandardized residuals. But the RMSEA also aims for model parsimony. Aiming for model parsimony makes sense in exploratory factor analysis, where we do not want to add another factor to the model to increase fit when the number of general factors may be correctly specified, but the model misfits for other reasons, such as the need of correlated residuals. But in a general model such as the one displayed in Fig. 3, do we want our model to be parsimonious? I think the answer is no. The aim of the study is to obtain accurate parameter estimates and standard errors to make inferences about the hypotheses outlined in Fig. 4.

Alternatively, the overall magnitude of the model misfit can be gauged using the CRMR (or the SRMR) without the need for any cutoff and without adjusting for model parsimony. The unbiased estimate of the CRMR, given by (24), equals 0.065, and a 90% CI for the population parameter is (0.059, 0.072). Notice that in this example the point estimates of the RMSEA and CRMR are equal (to three digits), whereas the CI for the CRMR is wider. Using the CRMR, is the magnitude of this model misfit large? In applications, I disregard statistically significant correlations smaller than \({\vert }0.1{\vert }\) as being of no substantive interest. I use the same criterion to judge the magnitude of residual correlations: I cannot disregard a statistically significant residual correlation larger than \({\vert }0.1{\vert }\). Of course, the smaller the residual correlations the better, and I consider that the degree of misfit of a model is negligible when all residual correlations are smaller than 0.05. Therefore, I consider that a model fits closely when CRMR \(\le \) 0.05, provided no statistically significant residual correlation is larger \({\vert }0.1{\vert }\). Do I consider a CRMR value of 0.065 to be acceptable? I cannot tell without examining the largest residual correlations (in absolute values), as the CRMR is only (roughly) the average of the residual correlations. This model yields many large residual correlations: nine of them are larger than \({\vert }0.20{\vert }\), and they cannot be attributed to chance. I conclude that the model fits poorly.

It has repeatedly been advised (Jöreskog & Sörbom, 1988; McDonald & Ho, 2002; Raykov, 2000) that all standardized residual covariances (or residual correlations) be examined carefully. To do so, the variables need to be ordered in consonance with the fitted model. No pattern between these residuals should be apparent: rather, they should be well scattered. The matrix of residuals will often reveal structural zeroes, residual correlations that must be zero under the fitted model and for the choice of estimator used. When there is a large number of structural zeroes in the model, the SRMR and CRMR do not provide an accurate representation of the overall fit of the model.

Researchers should examine the extent to which standardized residual covariances (or residual correlations) can be attributed to chance using confidence intervals, or z statistics based on their standard errors. In so doing, it is necessary to account for multiple testing, for instance using a Bonferroni correction.

To understand how the model misfits, I often find it helpful to compute the average of the absolute value of the residual correlations for each variable (Maydeu-Olivares, 2015). In this case, the average corresponding to i54 (one of the indicators of “migra”—mass mediation exposure), 0.138, is much larger than the averages for the other variables (which range from 0.013 to 0.087). The model needs to be modified to reduce the size of the residual correlations involving this variable. An alternative is to remove the variable from the model as it is not a key variable.

How to modify the model to obtain a better fit? I would begin by inspecting graphs of individuals’ residuals versus expected values for each equation in the model, just as in regression. These may be used to assess the linearity and homoscedasticity assumptions in each equation. In particular, the presence of heteroscedasticity may be an indication of a moderating relationship, possibly involving another variable in the dataset. Only after I am satisfied that these critical assumptions are met would I explore the modification indices (score tests) for the model in combination with their power and the expected parameter change, as described in Saris et al. (2009). Their procedure requires a fair amount of work, particularly with a model of this size, but this is as it should be: fitting a set of equations (possibly involving latent variables) involves considerably more work than fitting a single regression equation.

Hopefully, the application of Saris et al.’s (2009) method will shed some light into the validity of our inferences on the substantive hypotheses of interest outlined in Fig. 4. What do the residual correlations (or standardized residuals)—the size of the model misfit—tell us about the validity of our inferences? This matter requires further research.

11 Remarks on Some Recurring Themes in SEM Goodness-of-Fit Assessment

11.1 The Role of Sample Size

The role of sample size in assessing the goodness-of-fit of a SEM model is as it should be, and it is no different from a regression model or a simple z-test: increasing sample size leads to increasing power to detect discrepancies between the model and the data-generating mechanism. This is a good thing. Sample size should be as large as possible. I have yet to encounter a z-test application involving a mean difference in which researchers complained that their power was too high. And yes, the value of all test statistics (including the z test) depends on sample size, not just the value of the Chi-square statistic in SEM. Nonetheless, one encounters numerous applications in which the dependency of the SEM’s Chi-square test statistic on sample size is used to disregard its result, based on grounds of excessive power, without actually checking the power of the test against any meaningful alternative. In any case, the “antidote” against excessive power is to examine the effect size (in our case, the effect size of the misfit).

11.2 Relative Effect Sizes of the Overall Misfit

There exist population counterparts of the CFI (Bentler, 1990), and of the GFI (Steiger, 1990), as well of other popular relative goodness-of-fit indices. Therefore, we could use a parameter to convey the magnitude of the misfit of a model relative to that of another model. Should we do so? We could, but by construction, they are relative effect sizes of the misfit. Relative overall misfit effect sizes can be used to compare two substantively motivated models, or a substantively motivated model against a standard baseline model. The standard baseline model used in the CFI is the independence model, and the one used in the GFI is the saturated model. I believe that the independence model should never be used as a baseline model, because if, as our theory suggests, we believe that our variables are correlated and we model their dependencies, why do we use an independence model as a baseline to communicate how well we are modeling these dependencies? Put differently, if we believe that our variables are uncorrelated (our baseline model), why are we modeling their dependencies? The use of a saturated model as a standard baseline has some justification. For if the core features of our model are correctly specified (and this is a strong assumption) then hopefully our parameter estimates will be unbiased when a restricted model is fitted, and therefore it is of some interest to gauge our fitted model against a saturated model. In any case, if the relative effect sizes of the overall misfit are of interest, confidence intervals for the population parameters of interest should be used, not (possibly biased) point estimates.

12 Conclusions

As in any modeling enterprise, such as fitting a regression model, goodness-of-fit assessment in SEM should be performed judiciously. We wish to reproduce the features of the data-generating process, but not the idiosyncratic characteristics of the sample. The best way to distinguish them is by replication. Regrettably, in SEM not much value is assigned to replication studies, with the possible exception of factor analysis studies. In addition, it is often difficult to replicate the conditions of previous studies due to the non-experimental nature of most studies. By construction, a perfect replication study is a cross-validation. Since SEM estimation methods are asymptotic in nature, researchers use a sample as large as possible, with no data to spare in a cross-validation. However, with the increasing sample sizes available in some planned large scale studies, I expect that cross-validation methods in SEM will be more frequently used. This is good, because SEM is often used to generate new theoretical models (Jöreskog, 1993). The researcher begins with a tentative initial model. When the initial model does not fit well, the researcher repeatedly modifies the model using her substantive theory and the model-fit results, until a better fitting model is found that is a reasonable compromise between theory and data. There is nothing wrong with using SEM in this fashion. However, we need cross-validation (or replication) to ensure that we have not captured idiosyncrasies in the data. Browne (2000) and Browne and Cudeck (1989) are excellent sources on cross-validation methods.

Goodness-of-fit assessment is not an end in itself; it is simply a means to draw inferences about the world (Saris et al., 2009). The substantive inferences we make are the final objective of our analysis. There has been so much abuse of SEM fit indices as test statistics that one may be tempted to avoid examining the goodness-of-fit of the model altogether and simply perform model selection. However, I believe that model selection proper does not tell us anything about the validity of the inferences we make.

Assessing the goodness-of-fit of a SEM model is a time-consuming process. The time required is a function of a number of determinants, such as the complexity of the model, and the presence of latent variables. But to a large extent, it is a function of the number of equations in the model. A researcher modeling ten equations simultaneously in a SEM should expect to devote at least a tenfold increase of the time devoted to check the model assumptions of a single regression equation.

When only a few equations are being estimated, researchers should be able to find a well-fitting model. However, when fifty equations are being modeled, as is often the case in the social sciences, it is not realistic to expect to find a well-fitting model in the amount of time a researcher can devote to the enterprise and as a result, she is obliged to settle for a model that fits closely. Thus, it is time constraints and the number of equations being modeled that justify the use of approximate fit assessment, not sample size considerations. There is nothing wrong with the notion of testing for approximate fit in large models, as opposed to testing for exact fit, but one has to realize that an approximate model is, by definition, incorrect and that all inferences based on an approximate model are suspect (Yuan et al., 2003).

Here, I have introduced statistical theory for assessing the magnitude of the misfit in SEM models using standardized residual covariances and residual correlations. For if a model is rejected and due to time constraints we cannot find a well-fitting model, we may be able to gauge how far we are from the data-generating process and decide whether to retain it as a “close fitting model” based on a confidence interval for the SRMR or the CRMR. Alternatively, in a classical fashion one can use a test of close fit for these parameters. Because the interpretation of these parameters is straightforward, any arbitrary value, such as 0.05, can be used in such a test. However, as SEM is a multivariate technique, it is only meaningful to report the overall degree of misfit of the model if none of the standardized residual covariances (or residual correlations) is too large (\(< {\vert }0.1{\vert }\) is my personal criterion). Standardized residual covariances (or residual correlations) are seldom reported in applications. I would urge researchers to report the six largest standardized residual covariances (or residual correlations)—in absolute values—in applications, along with their statistical significance or CIs, for the SRMR and CRMR are simply summary measures of the model misfit.

The use of the sample SRMR and CRMR should be avoided, as they are biased upwards estimates of their corresponding parameters. For instance, the sample CRMR estimate in the application described previously is 0.072, \(N = 725\), but this equals the upper bound of the 90% CI for the population parameter; the asymptotically unbiased estimate of the population parameter is 0.065.

Hopefully, this presentation will spur further research on this topic. An immediate topic that requires attention is whether we should use standardized residual covariances or residual correlations. Personally, I have a mild preference for residual correlations, as their interpretation is more straightforward than for standardized residual covariances. However, their use in models that are not scale invariant needs to be investigated. Another topic that requires research is how to assess the degree of misfit in models with a mean structure. It seems to me that it is perhaps best to separate the model misfit in the mean structure from the model misfit in the covariance structure, rather than combining them. For the mean structure, a suitable standardized parameter is \({{\iota }} _{\mu } =\sqrt{\frac{1}{p}\sum \nolimits _{i=i}^{p} {\frac{\left( {{\mu }_i -{\mu }_i^0 } \right) ^{2}}{{\sigma }_i}}}\) where \({\mu }_i \) and \({\sigma }_{i}\) denote the unknown population mean and standard deviation and \({\mu }_i^0 \) denote the population mean under the fitted model. In models for ordinal data (Maydeu-Olivares, 2006; Muthén, 1984) and more generally in item response theory (IRT) models for ordinal data, the CRMR can certainly be used to gauge the size of model misfit at the bivariate level (Maydeu-Olivares, 2015) .

But, above all, when due to time constraints we are obliged to settle for a model that fits closely, what do the effect sizes of the misfit tell us about the validity of the inferences we make? This is the area where I would like to see much more research.