Measurement of Interdiffusion and Tracer Diffusion Coefficients in FCC Co-Cr-Fe-Ni Multi-Principal Element Alloy

Abstract

Average effective interdiffusion coefficients of individual components and tracer diffusion coefficient of Ni were experimentally determined in FCC CoCrFeNi high entropy alloys. Average effective interdiffusion coefficients of individual elements in CoCrFeNi alloys were determined using the Dayananda-Sohn approach. Cr had the highest while Ni had the lowest magnitude of the average effective interdiffusion coefficient in the CoCrFeNi alloy. The tracer diffusion coefficient of Ni was determined without the application of radiotracers using the novel analytical method proposed by Belova et al. based on linear response theory coupled with the Boltzmann-Matano approach and Gaussian distribution function. Both average effective interdiffusion coefficients and tracer diffusion coefficients in CoCrFeNi were compared with the relevant high entropy alloys with varying entropy of mixing. The diffusion of individual elements in Al-containing high entropy alloys (e.g., Al-Co-Cr-Fe-Ni and Al-Co-Cr-Fe-Ni-Mn), with higher entropy of mixing, was higher than that in CoCrFeNi alloy, with relatively lower entropy of mixing. Therefore, diffusion cannot a priori consider to be sluggish in alloys with higher configurational entropy. Moreover, potential energy fluctuations determined in quinary and senary Al-containing high entropy alloys were higher than that in quaternary CoCrFeNi alloy. This also suggests that the diffusivity of a component may not be always lower in the alloys which possess higher fluctuations in potential energy or configurational entropy of mixing.

1 Introduction

Metallic alloys for most engineering application are designed near one of the terminal ends of the multicomponent phase diagram with a primary solvent (concentration > 50 at.%), e.g. Co-based superalloys, Ni-based superalloys (IN718, IN625, etc.), steels (SS304, SS316, etc.), and various commercial Al-based alloys (e.g. AA5083, AA6061, AA7075, etc.). However, a new class of multicomponent alloys, i.e., high entropy alloys (HEAs), are designed in the middle of the multicomponent phase diagram, with a near equiatomic proportion of the constituent elements. Thermodynamically, HEAs would have a high configurational entropy of mixing, and therefore form in a simple solid solution instead of complex low entropy, enthalpy-driven intermetallic phases.[1] However, various researchers[2,3,4] had previously cast doubt on this theory of entropic stabilizations and suggested that the role of enthalpy of mixing cannot be neglected in the stability of a single phase. It has also been observed that prolonged annealing of HEAs (e.g., CoCrFeNiMn) can result in decomposition at intermediate temperatures (~ 500-900 °C).[5] Others[6,7] had also cast doubt on the solid-solution phase stability in HEAs (e.g., Al_0.5CrFeCoNiCu) as precipitation of the second phase was observed irrespective of different cooling rates (e.g., furnace cooling, quenching, etc.), further suggesting that the rate of elemental redistribution kinetics can be high in these alloys.

Initially, HEAs were postulated to exhibit sluggish diffusion kinetics as the formation of a new phase will require the co-operative movement of many atoms, which may be difficult to accomplish. This hypothesis was mainly motivated by indirect observations such as the absence of low-temperature phases in Al_0.5CoCrFeNiCu upon slow cooling from high temperature,[8] restricted growth of nanocrystals in as-cast Al_xCoCrFeNiCu alloy[9] and AlCrMoSiTi film.[10] This suggests that the stability of HEAs is directly related to the diffusion kinetics, as faster kinetics may result in the formation of low entropy phases. Therefore, knowledge of diffusion kinetics becomes imperative to understand HEAs, which may impart unique properties such as excellent creep resistance and high thermal stability, among many others.

Many studies in the literature explored the diffusion in CoCrFeNi based HEAs. Initial work by Tsai et al.[11] supported the sluggish diffusion in CoCrFeNiMn_0.5 alloy by experimental determination of interdiffusion coefficients using a pseudo-binary approach and extrapolating the tracer diffusion coefficients based on negligible marker movement and near-ideal solution behavior of CoCrFeNiMn_0.5 alloy.[2] The validity of this work was later challenged by Paul et al.[12] based on incorrect estimation of diffusion data using a pseudo-binary approach, which was subsequently rebutted by Tsai et al.[13] The following re-analysis by Beke and Erdelyi[14] based on the diffusion data reported by Tsai et al.[11] had also advocated that the diffusion is sluggish in CoCrFeNiMn_0.5 alloy. Dabrowa et al.[15] also supported the sluggish diffusion kinetics in Co-Cr-Fe-Ni-Mn and Al-Co-Cr-Fe-Ni alloys. However, more recent work by Vaidya et al.[16,17,18] measured the tracer diffusivity of each constituent element via radiotracer experiments and reported that diffusion may not be sluggish in CoCrFeNi and CoCrFeNiMn alloys when examined with absolute temperature, however, may be sluggish at temperature normalized with respect to the melting point. In addition, several other investigations on experimental determination of tracer diffusion coefficients[19,20,21,22,23,24] suggested that diffusion is not sluggish at absolute temperature but may be at inverse homologous temperature. Limited studies had measured interdiffusion coefficients in HEAs. Kulkarni and Chauhan[25] suggested that multicomponent diffusional interactions are more relevant and play an important role in HEAs. Verma et al.[26] also suggested that the interdiffusion flux of a diffusing component in HEAs can be increased (enhanced) or decreased (reduced) based on the direction of flux for a particular element with respect to other constituent elements. In follow-up work by Verma et al.,[27] the full matrix of the interdiffusion coefficients was experimentally determined using Body-diagonal diffusion couple[28] approach in quaternary Co-Cr-Fe-Ni and quinary Co-Cr-Fe-Ni-Mn alloys. Within the experimental uncertainty, this approach[27] allowed the intersection of multiple diffusion paths at near-equiatomic composition in multi-dimensional compositional space. However, the uncertainty in cross-over composition of diffusion path can increase with an increase in number of components in the alloy or the composition range of an element in the terminal alloys of diffusion couple.[27] Significant magnitude of off-diagonal interdiffusion coefficients suggested that there is a strong diffusional interaction among constituent elements, which was neglected by Tsai et al.[11] Recently, Mehta and Sohn,[3,4,19] suggested that the sluggish diffusion effect may not be generalized for all HEAs based on average effective interdiffusion coefficients measurement in Al-Co-Cr-Fe-Ni and Al-Co-Cr-Fe-Ni-Mn alloys. Other investigations[29,30,31] also suggested that the sluggish diffusion effect cannot be generalized for all HEAs. Recent review articles[32,33,34,35] comprehensively summarize the overall viewpoint on recent development on sluggish diffusion effect in HEAs.

Previously, the tracer diffusion coefficient in CoCrFeNi-based HEAs was experimentally determined by the radio-tracer technique.[16,17,18,20,21]. Few investigations had utilized the numerical approach method to estimate the tracer diffusion coefficients using interdiffusion data (e.g., Al-Co-Cr-Fe-Ni HEAs)[15,31] or suggested that intrinsic diffusivity is equal to tracer diffusivity based on ideal solution behavior of a HEA (e.g., CoCrFeNiMn_0.5 alloy).[11] In this work, tracer diffusion coefficient of Ni in equiatomic CoCrFeNi alloy was experimentally determined using sandwich diffusion couple experiment, wherein concentration profiles were analyzed by a novel mathematical formalism, established by Belova et al.[36] based on linear response theory coupled with Boltzmann-Matano approach and Gaussian distribution function.[36,37]. Average effective interdiffusion coefficients of individual elements were determined by analyzing the concentration profiles, from solid-to-solid diffusion couple experiments, using Dayananda and Sohn[38] method. Results were analyzed by comparing diffusion coefficients in different HEAs with varying entropy. The concept of the potential energy landscape was utilized to understand the diffusion process in HEAs, by analytically estimating the fluctuations in lattice potential energy using the potential energy fluctuation (PEF) model.[39].

2 Experimental Method

The single-phase solid solution alloys of quaternary Co₂₀Cr₂₈Fe₃₂Ni₂₀, Co₂₀Cr₃₀Fe₃₀Ni₂₀, and Co₃₀Cr₂₀Fe₂₀Ni₃₀ alloys were prepared using elemental Co, Cr, Fe, and Ni, with minimum 99.9% purity. Arc melting was performed in an Ar environment using Centorr^TM Arc furnace with water-cooled Cu drop-cast crucible. Before melting, the chamber was flushed with Ar, evacuated to a pressure of 5.0 × 10⁻⁵ torr or better, and backfilled with Ar. To promote the compositional homogeneity, alloy ingots were flipped and re-melted at least five times, and then homogenized at 1100 °C for 48 h in an Ar-filled quartz tube capsule. After the homogenization, alloys were water quenched to retain the high-temperature single phase microstructure at room temperature. Phase constituents, e.g., formation of single-phase and microstructural homogeneity were confirmed using Malvern Panalytical Empyrean™ x-ray diffraction system and Zeiss™ Ultra-55 field emission scanning electron microscope (FE-SEM) equipped with Thermo-Scientific™ x-ray energy dispersive spectroscopy (XEDS).

Homogenized alloys were sectioned into discs, approximately 3 mm in thickness and 9 mm in diameter using a low-speed diamond saw and metallographically polished down to 1 μm surface finish. For interdiffusion measurements, polished surfaces of two alloys were placed in intimate contact and held tightly by two stainless steel jigs. For tracer diffusion measurements, an alloy disc polished on both sides was sandwiched between two alloys of the same constituents. More details on the stacking of sandwich diffusion couples to measure the tracer diffusivity can be found elsewhere[37] and is also described in Sect. 3.2.1. One of the interfaces between two alloys contained a thin film of pure Ni. Electron-beam physical vapor deposition (EB-PVD), with a built-in plasma cleaning capability, was used to deposit Ni thin film on selected HEAs. EB-PVD chamber was evacuated to a pressure of approximately 1.2 $\times$ 10⁻⁷ torr, and sample surfaces were cleaned using Ar plasma. The electron beam was generated by passing a current (~80 mA) through the tungsten filament (electron source). Then, the electron beam was accelerated by applying an acceleration voltage (− 10 kV). During the deposition process, the substrate holder was allowed to rotate to achieve a uniform thin-film thickness. The deposition rate was maintained at approximately 0.7 Å/s, which was monitored using the resonant frequency of the oscillating quartz crystal. The thickness of the film deposited on alloys is proportional to the change in the resonant frequency of the quartz crystal (i.e., shift in frequency). The time of deposition was adjusted to achieve a film thickness of approximately 900 nm. To verify the film thickness, the focused ion beam (FEI™ TEM 200-FIB) was used to prepare a thin slice of the cross-section, which allowed the direct measurement of film thickness.

Thin alumina spacers were placed between the alloy and stainless-steel jig to avoid any interdiffusion between the HEAs and jigs. The assembled diffusion couple was placed in a quartz tube along with a tantalum foil (i.e., oxygen getter), evacuated to a pressure of 8.0 $\times$ 10⁻⁶ torr or better, and flushed alternately with high purity Ar and H₂ gas multiple times. Finally, quartz tube was sealed in a high purity Ar atmosphere using an oxy-acetylene torch. More details of diffusion couple fabrication can be found elsewhere.[37,40,41,42,43,44,45] Diffusion couples examined in this study for the measurement of interdiffusion and tracer diffusion coefficients are listed in Tables 1 and 2, respectively. After annealing, all diffusion couples were water quenched to preserve the high-temperature microstructure. Then, all diffusion couples were mounted in cold resin epoxy and cross-sectioned normal to the diffusion couple interface. All cross-sections were metallographically polished down to 1 μm surface finish. The microstructure of each diffusion couple was examined by SEM equipped with XEDS. A minimum of three concentration profiles, across the interdiffusion zone for each diffusion couple, were obtained by point-to-point acquisition to estimate the uncertainties in diffusion coefficients. XEDS data were converted to the concentration of various constituent elements in atom percent via standardless analysis.

Table 1 Diffusion couples investigated to determine interdiffusion coefficient

Table 2 “Sandwich” thin-film diffusion couples employed for the determination of tracer diffusion coefficient

3 Analytical Framework

3.1 Interdiffusion Coefficients

Interdiffusion flux of a component in an n-component system can be written as[46]:

$$\tilde{J}_{i} = ~ - \sum\limits_{{j = 1}}^{{n - 1}} {\tilde{D}_{{ij}}^{n} } \frac{{\partial C_{j} }}{{\partial x}}~\quad \left( {i = 1,~2, \ldots ,n - 1} \right)$$

(1)

where $\tilde{D}_{{ij}}^{n}$ are the (n − 1)² interdiffusion coefficients, and $\partial C_{j} /\partial x$ is the concentration gradient. When the composition-dependent variation of the molar volume is negligible, interdiffusion flux at any plane ‘x’ can be determined from the concentration profiles without the knowledge of interdiffusion coefficients using the following relationship[47]:

$$\tilde{J}_{i} = ~\frac{1}{{2t}}\mathop \smallint \limits_{{C_{i} ( \pm \infty )}}^{{C_{i} (x)}} (x{-}x_{{\text{o}}} ){\text{d}}C_{i} ~~~\left( {i = 1,~2 \ldots ,n - 1} \right)$$

(2)

An extension of the Boltzmann–Matano method can be implemented to the n-component system to measure the interdiffusion coefficients,[48] as expressed by:

$$\mathop \smallint \limits_{{C_{i} ( \pm \infty )}}^{{C_{i} (x)}} (x{-}x_{{\text{o}}} ){\text{d}}C_{i} = ~{-}2t\mathop \sum \limits_{{j = 1}}^{{n - 1}} \tilde{D}_{{ij}}^{n} \frac{{\partial C_{j} }}{{\partial x}}~~~\left( {i = 1,~2, \ldots ,n - 1} \right)$$

(3)

However, it is extremely challenging to measure the interdiffusion coefficients via the above method for n ≥ 4, because to determine (n − 1)² interdiffusion coefficients at a fixed composition, (n − 1) independent compositional gradients need to be correlated to (n − 1) independent interdiffusion fluxes. Therefore, (n − 1) diffusion couple experiments must be conducted in such a way that the diffusion paths of these diffusion couples intersect at a fixed composition in the n-dimensional compositional space of Gibbs polyhedron. In order to circumvent this problem, the average effective interdiffusion coefficient of component i, $~\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$, in an n-component system can be defined for a given element over the desired composition range, C_i(x₁) to C_i(x₂), using the relation[38]:

$$\mathop \smallint \limits_{{x_{1} }}^{{x_{2} }} \tilde{J}_{i} {\text{d}}x~ = ~{-}~\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}} ~(C_{i} (x_{1} ){-}C_{i} (x_{2} ))~ = ~{-}\frac{1}{{2t}}\mathop \smallint \limits_{{C_{i} (x_{1} )}}^{{C_{i} (x_{2} )}} \left( {x{-}x_{o} } \right)^{2} {\text{d}}C_{i} \quad ~~\left( {i = 1,2 \ldots ,n} \right)$$

(4)

The average effective interdiffusion coefficient can be determined from a single diffusion couple experiment and represents one magnitude for a single component, but it does not provide any information about multicomponent diffusional interactions. Experimental concentration profiles measured from XEDS in this study were smoothened using Origin^TM Pro 8.5 software, with non-linear curve fitting function given by[37,49,50]:

$$c\left( x \right) = ~\frac{{p_{1} + p_{3} x + p_{5} x^{2} + p_{7} x^{3} }}{{1 + p_{2} x + p_{4} x^{2} + p_{6} x^{3} }}~$$

(5)

3.2 Tracer Diffusion Coefficients

3.2.1 Tracer Diffusion Coefficient via Belova’s Formalism

Based on linear response theory coupled with Boltzmann–Matano method, Belova et al.[36] developed a mathematical formalism, to measure the tracer diffusion coefficient in multicomponent alloys using traditional diffusion couple experiments. Instead of the application of radiotracers, this formalism utilizes the same type of atoms (e.g., Ni) sandwiched as a thin film between two alloys with varying compositions on either side. Sandwich type diffusion couple arrangement, therefore, yields concentration profiles from both the interdiffusion and thin-film diffusion in the same experiment. Experimentally, three alloy discs are stacked in a sequence such that the first alloy (e.g., Co₃₀Cr₂₀Fe₂₀Ni₃₀) is sandwiched between two same alloys (e.g., Co₂₀Cr₃₀Fe₃₀Ni₂₀), and one of the interfaces between Co₃₀Cr₂₀Fe₂₀Ni₃₀ and Co₂₀Cr₃₀Fe₃₀Ni₂₀ has a thin film of metal (e.g., Ni), for which tracer diffusion coefficient can be determined, and the other interface can be used as the interdiffusion reference. Isothermal annealing of the sandwich diffusion couple will create a spike in the concentration profile of the thin film metal (Ni), as schematically shown in Figure 1. Spike profile (Ni = Ni₁ + Ni₂) at the spike interface includes the concentration profile due to both the interdiffusion (Ni₁) and thin-film diffusion (Ni₂). The concentration profile due to tracer movement (Ni₂) can be extracted by simple mathematical subtraction of interdiffusion profile (Ni₁), measured at the other interdiffusion interface, from the spike profile (Ni₁+ Ni₂), measured at the spiked interface. In comparison to the traditional radiotracer experiment, Ni₂ acts as a tracer in sandwich diffusion couple experiments to yield tracer diffusion. Tracer diffusion coefficient can be determined using the Belova et al.[36] mathematical formalism, given by:

$$D_{A}^{*} = - {{\left( {\frac{{x + a}}{{2t}} - \frac{{G_{2} }}{{c_{{{\text{Ni}}_{2} }} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{x + a}}{{2t}} - \frac{{G_{2} }}{{c_{{{\text{Ni}}_{2} }} }}} \right)} {\left( {\frac{{{\text{d}}\ln \left( {c_{{{\text{Ni}}_{1} }} /c_{{{\text{Ni}}i_{2} }} } \right)}}{{{\text{d}}x}}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\frac{{{\text{d}}\ln \left( {c_{{{\text{Ni}}_{1} }} /c_{{{\text{Ni}}i_{2} }} } \right)}}{{{\text{d}}x}}} \right)}}$$

(6)

Fig. 1

A schematic of sandwich diffusion couple utilized to determine tracer diffusion coefficient of Ni in CoCrFeNi, depicting the evolution of Ni concentration profile after isothermal annealing

where a is a constant and the value of G₂ can be determined using:

$$G_{2} = \frac{{c_{{{\text{Ni}}_{2} }}^{ + } - c_{{{\text{Ni}}_{2} }}^{ - } }}{{2t}}~ \times \left[ {\left( {1 - y_{{{\text{Ni}}_{2} }}^{*} } \right)\mathop \smallint \limits_{{ - \infty }}^{{x^{*} }} y_{{{\text{Ni}}_{2} }} {\text{d}}x + ~y_{{Ni_{2} }}^{*} \mathop \smallint \limits_{{x^{*} }}^{\infty } \left( {1 - y_{{{\text{Ni}}i_{2} }} } \right){\text{d}}x} \right]$$

(7)

Details of determining G₂ and a are described by Belova et al.[36] Recently, Schulz et al.[37] had implemented this formalism[36] to document tracer diffusion coefficients of Cu in an isomorphous Cu-Ni system. Their validation work suggested that the formalism was successful in determining the tracer diffusion coefficient of Cu, however, did not give a reliable compositional dependence due to uncertainty in concentration profiles. Alternatively, Schulz et al.[37] demonstrated that a Gaussian distribution function can be used for fitting the subtracted concentration profile with the determination of tracer diffusion coefficient at a fixed composition using full width at half maxima (FWHM) analysis. Therefore, Belova et al.[36] approach along with the Gaussian distribution function was used to determine the tracer diffusion coefficients for the composition of interest. It is also worth mentioning that the thickness of the thin-film at the spike interface should be below $\sqrt {D_{{{\text{Ni}}}}^{*} t}$. If the sandwich film thickness is greater than $\sqrt {D_{{{\text{Ni}}}}^{*} t}$, the film then will be considered as a thick-film[51,52] which would result in significant interdiffusion contribution from the thick-film, in addition to tracer diffusion contribution. This additional contribution of interdiffusion towards the width of the FWHM would yield an overestimation of tracer diffusion coefficient.

3.2.2 Tracer Diffusion Coefficient via Gaussian Distribution Function

Thin film solution for the diffusion of thin film metal in two semi-infinite medium on either side in the sandwich type diffusion couple configuration is given by[53]:

$$C\left( {x,t} \right) = \frac{{C_{{\text{o}}} \Delta x}}{{\sqrt {4\pi D^{*} t} }}~\exp \left( {~{-}\frac{{x^{2} }}{{4D^{*} t}}} \right)$$

(8)

where C_o is the thin film composition, Δx is the thickness of thin film, D* represents tracer diffusion coefficient, and t is the time of annealing. Gaussian/normal distribution function is a symmetric bell-shaped curve which can be expressed by[54]:

$$f\left( {x,\mu ,\sigma } \right) = \frac{1}{{\sigma ~\sqrt {2\pi } }}~\exp \left[ {{-}\frac{1}{2}~\left( {\frac{{x~{-}~\mu }}{\sigma }} \right)^{2} } \right]$$

(9)

where the pre-exponential term (i.e., $\frac{1}{{\sigma ~\sqrt {2\pi } }}$) represents the height of the bell curve’s peak, σ is the standard deviation (i.e., Gaussian RMS width) which controls the width of the bell curve, and µ is the mean value of x around which the bell curve is symmetric (i.e., position of the center of the peak).

Therefore, the exponential part of thin film solution for sandwich geometry in Eq 8 and Gaussian distribution function symmetric along the y-axis in Eq 9 can be expressed as:

$$\exp \left( {~{-}\frac{{x^{2} }}{{4D^{*} t}}} \right) = \exp ~\left[ {{-}\frac{1}{2}~\left( {\frac{{x~{-}~0}}{\sigma }} \right)^{2} } \right]$$

(10)

On further simplification, tracer diffusion coefficient can be expressed by:

$$D^{*} = ~\frac{{\sigma ^{2} }}{{2t}}$$

(11)

The standard deviation of the bell curve can be expressed in terms of other measurable quantity such as full-width half maxima (FWHM). Figure 2 represents the Gaussian distribution profile, where, α₁ and α₂ are the abscissas corresponding to half maxima position of the Gaussian distribution function. Therefore, half maxima position of the Gaussian distribution function via Eq (9) can be expressed by:

$$\frac{1}{2}f_{{\max }} ~ = ~\frac{1}{{\sigma ~\sqrt {2\pi } }}~\exp \left[ {{-}\frac{1}{2}~\left( {\frac{{\alpha ~{-}~\mu }}{\sigma }} \right)^{2} } \right]$$

(12)

Fig. 2

A schematic representation of Gaussian profile to measure the standard deviation as a function of full width half maxima (FWHM)

Maxima of Gaussian distribution function occurs at the center of peak (i.e., x = µ), which can be expressed by:

$$f_{{\max }} ~ = ~\frac{1}{{\sigma ~\sqrt {2\pi } }}~\exp \left[ {{-}\frac{1}{2}~\left( {\frac{{\mu ~{-}~\mu }}{\sigma }} \right)^{2} } \right] = ~\frac{1}{{\sigma ~\sqrt {2\pi } }}$$

(13)

On dividing Eq (13) by Eq (12), and solving for roots of α, i.e., α₁ and α₂, one gets:

$$\begin{aligned} \alpha _{1} & = ~{-}~\sigma \sqrt {2\ln 2} ~ + ~\mu \\ \alpha _{2} & ~ = ~~\sigma \sqrt {2\ln 2} ~ + ~\mu \\ \end{aligned}$$

(14)

Therefore, FWHM can be expressed as:

$${\text{FWHM}} = ~\alpha _{2} ~{-}~\alpha _{1} = ~\sigma ~2\sqrt {2\ln 2} ~$$

(15)

On substituting the value of σ in Eq (11), tracer diffusion coefficient can be expressed as:

$$D^{*} = ~\frac{{{\text{FWHM}}^{2} }}{{16~\ln 2~t}}$$

(16)

Schulz et al.[37] adopted an alternative approach wherein the Gaussian distribution function was used for fitting the subtracted composition profile, and full width at half maxima (FWHM) was used to determine the tracer diffusion coefficient. Therefore, Belova et al. approach along with the Gaussian distribution function was used to determine the tracer diffusion coefficients in this study.

4 Results

4.1 Average Effective Interdiffusion Coefficients

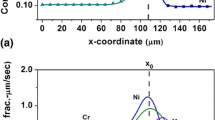
Figure 3 shows the concentration profiles superimposed on the secondary electron micrograph of Co₂₀Cr₂₈Fe₃₂Ni₂₀ versus Co₃₀Cr₂₀Fe₂₀Ni₃₀ diffusion couples, isothermally annealed at 900, 1000, 1100, and 1200 °C for 240, 240, 240, and 48 hours, respectively. Interdiffusion zone in all the diffusion couples exhibited the single-phase microstructure without any intermediate layers, precipitates, or interphase boundary. Diffusion couples annealed at 1000, 1100, and 1200 °C showed the formation of Kirkendall voids in the interdiffusion zone.

Fig. 3

Concentration profiles superimposed on secondary electron micrographs of Co₂₀Cr₂₈Fe₃₂Ni₂₀ vs Co₃₀Cr₂₀Fe₂₀Ni₃₀ diffusion couples, isothermally annealed at (a) 900 °C for 240 hours, (b) 1000 °C for 240 h, (c) 1100 °C for 240 hours, and (d) 1200 °C for 48 h

Table 3 reports the average effective interdiffusion coefficients, activation energies, and pre-exponential factor for Co, Cr, Fe, and Ni determined from the diffusion couple annealed at 900, 1000, 1100, and 1200 °C for the composition ranging from Co₂₀Cr₂₈Fe₃₂Ni₂₀ to Co₃₀Cr₂₀Fe₂₀Ni₃₀. Figure 4 shows the corresponding Arrhenius plot for the temperature dependence of these average effective interdiffusion coefficients. In general, Cr had the highest interdiffusion coefficient while Ni had the lowest in the CoCrFeNi alloy.

Fig. 4

Temperature dependence of average effective interdiffusion coefficients for Co, Cr, Fe and Ni determined from Co₂₀Cr₂₈Fe₃₂Ni₂₀ vs Co₃₀Cr₂₀Fe₂₀Ni₃₀ diffusion couples in temperature range from 900 to 1200 °C

Table 3 Average effective interdiffusion coefficients and the corresponding activation energy and pre-exponential factor for Co, Cr, Fe, and Ni determined from Co₂₀Cr₂₈Fe₃₂Ni₂₀ vs Co₃₀Cr₂₀Fe₂₀Ni₃₀ diffusion couples

4.2 Tracer Diffusion Coefficients of Ni in Equiatomic CoCrFeNi

As described in section 3.2, tracer diffusion coefficients of Ni$,~D_{{Ni}}^{*}$ in near equiatomic composition for quaternary CoCrFeNi alloys were determined using “sandwich” thin-film diffusion couple, for the temperature range from 900 to 1000 °C using Belova et al.[36] approach and Gaussian distribution function. Figure 5 shows the concentration profiles of Ni at the interdiffusion interface and thin-film interface (i.e., spike profile) overlaid, and the corresponding Gaussian fitted profile obtained after subtracting the interdiffusion profile at 900, 950, and 1000 °C. Table 4 reports the $D_{{{\text{Ni}}}}^{*}$ in equiatomic CoCrFeNi alloys. The $D_{{{\text{Ni}}}}^{*}$ in CoCrFeNi measured in present work is slightly higher than the $D_{{Ni}}^{*}$ determined using radiotracer techique by Vaidya et al.[18], possibly due to minor effect of compositional variation for Ni diffusion in the bulk alloy on either side of the diffusion couple.

Fig. 5

Concentration profile of Ni from the “spike” interface superimposed on the concentration profile of Ni from the “interdiffusion” interface, and the corresponding Gaussian fitted concentration profile obtained after subtraction of interdiffusion profile from the spike profile after isothermal annealing of the sandwich diffusion couple at (a, b) 900 °C for 24 hours, (c, d) 950 °C for 12 hours, and (e, f) 1000 °C for 8 h

Table 4 Tracer diffusion coefficient of Ni in CoCrFeNi alloy

5 Discussion

Based on the sluggish diffusion postulate, diffusion should be slow in alloys with higher configurational entropy of mixing. If so, average effective interdiffusion coefficients ($\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$) of various elements should vary as the reverse order of the configurational entropy of mixing, i.e., $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$(Al_pCo_qCr_rFe_sNi_tMn_u) < $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$(Al_pCo_qCr_rFe_sNi_t) ≈ $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$(Al_0.25CoCrFeNi) < $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$(CoCrFeNi). Figure 6 compares the temperature-dependence of $\overline{{\tilde{D}}} _{{{\text{Co}}}}^{{{\text{eff}}}}$,$~\overline{{\tilde{D}}} _{{{\text{Cr}}}}^{{{\text{eff}}}}$,$~\overline{{\tilde{D}}} _{{{\text{Fe}}}}^{{{\text{eff}}}}$, and $~\overline{{\tilde{D}}} _{{{\text{Ni}}}}^{{{\text{eff}}}}$ in Co-Cr-Fe-Ni, Al-Co-Cr-Fe-Ni[3, 19], and Al-Co-Cr-Fe-Ni-Mn[4] alloys. The $\overline{{\tilde{D}}} _{{{\text{Co}}}}^{{{\text{eff}}}}$,${\text{~}}\overline{{\tilde{D}}} _{{{\text{Cr}}}}^{{{\text{eff}}}}$, and $\overline{{\tilde{D}}} _{{{\text{Ni}}}}^{{{\text{eff}}}}$ is the lowest in quaternary Co-Cr-Fe-Ni alloy. Interestingly, the $\overline{{\tilde{D}}} _{{{\text{Cr}}}}^{{{\text{eff}}}}$ is the highest in the senary Al-Co-Cr-Fe-Ni-Mn alloy, while the $\overline{{\tilde{D}}} _{{{\text{Co}}}}^{{{\text{eff}}}}$ and $~\overline{{\tilde{D}}} _{{{\text{Fe}}}}^{{{\text{eff}}}} ~$ is the highest in quinary Al-Co-Cr-Fe-Ni alloy and contradicts the sluggish diffusion hypothesis based on $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$ determination.

Fig. 6

Comparison of $\overline{{\tilde{D}}} _{{{\text{Co}}}}^{{{\text{eff}}}}$,$~\overline{{\tilde{D}}} _{{{\text{Cr}}}}^{{{\text{eff}}}}$,$~\overline{{\tilde{D}}} _{{{\text{Fe}}}}^{{{\text{eff}}}}$, and $~\overline{{\tilde{D}}} _{{{\text{Ni}}}}^{{{\text{eff}}}}$ in near-equiatomic CoCrFeNi, Al_0.25CoCrFeNi[19], off-equiatomic Al_pCo_qCr_rFe_sNi_t[3], and Al_pCo_qCr_rFe_sNi_tMn_u[4] high entropy alloys

Figure 7 compares the temperature-dependent tracer diffusion coefficient of Ni, $D_{{{\text{Ni}}}}^{*}$ in various quaternary and quinary FCC HEAs, i.e., CoCrFeNi[18], CoCrFeNiMn_0.5[11], CoCrFeNiMn[18], and Al_0.25CoCrFeNi[19]. The $D_{{{\text{Ni}}}}^{*} ~$ is the lowest in quaternary CoCrFeNi alloy and the highest in quinary Al_0.25CoCrFeNi alloy. This result also contradicts the sluggish diffusion hypothesis in HEAs, which suggest that the $D_{{{\text{Ni}}}}^{*}$ should ideally vary as: $D_{{{\text{Ni}}}}^{*}$(CoCrFeNiMn) < $D_{{{\text{Ni}}}}^{*} ~$ (CoCrFeNiMn_0.5) < $D_{{{\text{Ni}}}}^{*} ~$ (Al_0.25CoCrFeNi) < $D_{{{\text{Ni}}}}^{*} ~$ (CoCrFeNi).

Fig. 7

Comparison of tracer diffusion coefficient of Ni in FCC Co-Cr-Fe-Ni, Co-Cr-Fe-Ni-Mn, and Al-Co-Cr-Fe-Ni alloys

Sluggish diffusion in high entropy alloys is typically correlated with potential energy fluctuation in lattice sites of diffusing elements. Tsai et al.[11] suggested that the alloys with higher configurational entropy of mixing would exhibit larger fluctuations in potential energy of lattice sites in comparison to alloys with lower configurational entropy of mixing, which would result in anomalously slower diffusion in alloys with higher configurational entropy. This is because, when an alloy exhibits a substantial variation in the potential energy of the lattice sites, diffusing elements would experience fluctuations in lattice potential energy (i.e. larger diffusion barrier), which may yield trapping of atoms in highly stable lower potential energy sites (i.e., deep traps in potential energy landscapes)[55]. Potential energy fluctuations (PEF) may arise from various interatomic interactions from electronic, magnetic, mechanical, or chemical origins. Pertaining to HEAs, two main sources of PEF were identified as a mismatch in atomic size and chemical bond misfit[39,56].

PEF normalized with respect to thermal energy (k_BT), due to intrinsic residual strain arising from the mismatch in atomic size can be expressed as[39]:

$$p_{{\text{e}}} ~ = ~4.12~ \times ~\sqrt {~\mathop \sum \limits_{{i = 1}}^{n} X_{i} \left( {1{-}\frac{{r_{i} }}{{\sum X_{i} r_{i} }}} \right)^{2} } ~ \times ~\sqrt {\frac{{\bar{K}\bar{V}}}{{k_{{\text{B}}} T}}}$$

(17)

where $X_{i}$ is the composition of constituent elements, $r_{i}$ is the atomic radius, $\bar{K}$ is the composition-weighted average bulk modulus and $\bar{V}$ is the composition-weighted average atomic volume. Normalized potential energy fluctuation arising due to the difference in chemical bond energy of various atomic pairs is given by[39]:

$$p_{{\text{c}}} ~ = ~2~\sqrt {\frac{{\sqrt {\mathop \sum \nolimits_{i} \mathop \sum \nolimits_{{j,i \ne j}} X_{i} X_{j} (\Delta H_{{ij}}^{{{\text{mix}}}} {-}\bar{H})^{2} } }}{{k_{{\text{B}}} T}}}$$

(18)

where $\Delta H_{{ij}}^{{{\text{mix}}}}$ represents the binary enthalpy of mixing of element i and j, determined using Miedema’s macroscopic model[57] and $\bar{H}$ is the average enthalpy of $\Delta H_{{ij}}^{{{\text{mix}}}}$. Therefore, the total potential energy fluctuation (p) is given by the sum of potential energy fluctuation due to atomic size and chemical bond misfit, i.e., $~p~ = ~p_{{\text{e}}} + ~p_{{\text{c}}}$.

Figure 8 compares the normalized PEF in various quaternary (CoCrFeNi), quinary (Al_0.25CoCrFeNi, Al_0.45CoCrFeNi, CoCrFeNiMn_0.5, CoCrFeNiMn) and senary (Al_0.435CoCrFeNiMn) HEAs. The magnitude of PEF follows the following order: p(CoCrFeNi) < p(CoCrFeNiMn_0.5) < p(CoCrFeNiMn) < p(Al_0.25CoCrFeNi) < p(Al_0.45CoCrFeNi) < p(Al_0.435CoCrFeNiMn). Nevertheless, configurational entropy of mixing (ΔS) varies as: ΔS(CoCrFeNi) < ΔS(Al_0.25CoCrFeNi) < ΔS(Al_0.45CoCrFeNi) < ΔS(CoCrFeNiMn_0.5) < ΔS(CoCrFeNiMn) < ΔS(Al_0.435CoCrFeNiMn). Therefore, a larger configurational entropy does not always result in larger fluctuations in the potential energy of the lattice sites, as suggested by the sluggish diffusion postulation[11].

Fig. 8

Temperature dependence of potential energy fluctuations in various FCC alloys

The potential energy fluctuations depends on the constituent element in an alloy system. Al in Al-Co-Cr-Fe-Ni and Al-Co-Cr-Fe-Ni-Mn alloys exhibits strong thermodynamic interaction with other constituent elements, which is evident from the larger magnitude of the binary pair enthalpy of mixing ($\Delta H_{{ij}}^{{{\text{mix}}}}$) for Al, as reported in Table 5. This larger magnitude of $\Delta H_{{{\text{Al}} - X}}^{{{\text{mix}}}}$ (X = Co, Cr, Fe, Ni, Mn) in Al-containing HEAs would result in a larger PEF in comparison to other HEAs with moderate $\Delta H_{{ij}}^{{{\text{mix}}}}$ (i,j = Co, Cr, Fe, Ni, Mn). Furthermore, comparison of diffusivities in Figs. 6 and 7 suggest that diffusivities were also composition-dependent, rather than PEF or ΔS dependent. In general, diffusivities of various elements in Al-containing HEAs were observed to be higher than that in other HEAs, despite larger PEF. This suggests that number of low energy sites in Al-containing HEAs were insufficient to significantly slow down the diffusion.

Table 5 Binary enthalpy of mixing (kJ/mol) calculated by Miedema’s model[57] for atomic pair between elements i and j (i, j = Al, Co, Cr, Fe, Ni, and Mn)

6 Summary

Average effective interdiffusion coefficients of individual elements and tracer diffusion coefficient of Ni were determined for CoCrFeNi alloy. Comparison of $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$, ${\text{~}}\overline{{\tilde{D}}} _{{{\text{Cr}}}}^{{{\text{eff}}}}$, $~\overline{{\tilde{D}}} _{{Fe}}^{{{\text{eff}}}}$, $~\overline{{\tilde{D}}} _{{{\text{Ni}}}}^{{{\text{eff}}}}$ in equiatomic CoCrFeNi, Al_0.25CoCrFeNi and off-equiatomic Al_pCo_qCr_rFe_sNi_t and Al_pCo_qCr_rFe_sNi_tMn_u alloys, demonstrated that the $\overline{{\tilde{D}}} _{i}^{{{\text{eff}}}}$ are generally lower in quaternary CoCrFeNi alloy. Similarly, comparison of Ni tracer diffusion coefficient in CoCrFeNi, CoCrFeNiMn_0.5, CoCrFeNiMn, and Al_0.25CoCrFeNi alloys demonstrated that Ni diffusion is slower in CoCrFeNi alloy. Estimated potential energy fluctuation for these alloy systems revealed that Al-containing HEAs exhibited larger fluctuations in lattice potential energy, however with faster diffusion kinetics. Therefore, alloys with higher configurational entropy of mixing may not always exhibit slow diffusion kinetics, and the overall diffusion phenomena cannot be always correlated with the lattice potential energy fluctuations in HEAs.