First-Principles Study of Structural, Electronic, Magnetic and Elastic Properties of the Mn₂XSb (X = Co, Fe) Inverse Heusler Alloys

Abstract

We predicted the electronic structure and half-metallic properties of the Mn₂XSb (X = Co, Fe) inverse Heusler alloys using the full-potential linearized augmented plane wave (FPLAPW) method. We used generalized gradient approximation (GGA) and GGA + U schemes to compute the electronic structure for both alloys. We employed the Tran and Blaha modified Becke–Johnson (TB-mBJ) potential to accurately estimate the band gap. The stability has been determined by calculating their formation energy and elastic constants under ambient conditions. Both alloys show a half-metallic ferromagnetic nature with a 100% spin polarization at the Fermi level. The calculated total spin magnetic moments of Mn₂XSb (X = Co, Fe) alloys are $4\upmu_{B}$ and $3\upmu_{B}$, respectively, which is a good agreement with the well-known Slater–Pauling rule of 24. The predicted Curie temperature for both alloys is greater than room temperature. The half-metallic and high spin polarization properties make them one of the promising candidates for spintronic device applications.

Introduction

Heusler alloys have a great importance in the field of spintronics due to their tunable band gap, half-metallic ferromagnetism, high spin polarization (P%) and high Curie temperature (T_C).1 The electronic structure of half-metallic materials has a finite band gap in one spin channel at the Fermi level E_F and metallic overlap in another spin channel. They can be used as electrodes for magnetic tunnel junctions (MTJs), giant magnetic resistive (GMR) devices and spin injectors for magnetic random-access memories (MRAMs). Inverse Heusler alloys have a stoichiometric ratio of Y₂XZ, where the X and Y are transition metal atoms, and Z is the main group element. The number of valence electrons of the Y element is larger than that for the X element. Inverse Heusler alloys are emerging as a promising subfamily of Heusler alloys in the search for low-magnetic-moment systems for spintronic applications. Various theoretical approaches for investigating the structural, thermal, mechanical and magnetic properties of the inverse Heusler alloys have appeared in the literature, but Heusler alloys containing Co and Mn have attracted particular attention because of their high Curie temperature and peculiar behavior of the magnetic moment of manganese atoms. The neighboring atoms order the magnetic moment alignment of manganese atoms, and the exchange interactions between Mn and Co atoms are found in short-range order.2,3,4 Several recent first-principles calculations confirm the presence of half-metallicity in Mn-based inverse Heusler alloys such as Mn₂VAl, Mn₂CrZ (Z = Al, Sb), Mn₂YGa (Y = V, Nb, Ta), Mn₂FeZ (Z = Al, Ga, Si, Ge, Sb) and Mn₃Ga.5,6,7,8 We mainly focused on structural stability, ground-state properties, electronic structure, total spin magnetic moment, Curie temperature and elastic constants of Mn₂XSb (X = Co, Fe) inverse Heusler alloys.

Method of Calculations

We calculated the structural stability, electronic, magnetic and elastic properties of Mn₂XSb (X = Co, Fe) using the full-potential linearized augmented plane wave (FPLAPW) method as implemented in WIEN2k code based on density functional theory (DFT).9 We employed a spin-polarized Perdew–Burke–Ernzerhof (PBE) scheme of generalized gradient approximation (GGA) for the exchange–correlation functional by treating onsite strong correlation of the 3d electrons by the Hubbard correction term of Coulomb repulsion U (GGA + U).10,11 The muffin-tin radii (RMT) were set to 2.24 a.u. for Mn, Co, Fe and Sb. The cut-off parameter RMT × Kmax = 9 and Gmax = 12 (a.u.⁻¹) was set for all calculations. The Monkhorst–Pack mesh of 700 k-points has been chosen in the irreducible Brillouin zone for both alloys to compute self-consistent field (SCF) calculations. The calculated values of U in the present systems were found to be U_Mn = 1.69 eV, U_Co = 1.92 eV and U_Fe = 1.80 eV.12 The iteration halted when the energy difference was set to 10⁻⁴ Ry/cell and the charge to 10⁻³ e. The Mn:[Ar] 3d⁵4s², Fe:[Ar] 3d⁶4s², Co:[Ar] 3d⁷4s² and Sb:[Kr] 5p³5s² electrons are treated as valence electrons. Also, the Tran and Blaha modified Becke–Johnson (TB-mBJ) potential was used to predict the band gap results in more accuracy.13

Result and Discussion

Structural Properties

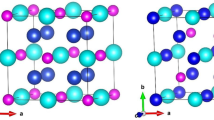
The inverse Heusler alloys consist of four interpenetrating face-centered cubic (FCC) sublattices. The three possible crystal structures of Mn₂XSb (X = Co, Fe) of XA type in cubic symmetry under a space group of $F\bar{4}3{\text{m}}$ (no. 216) are shown in Fig. 1, and the Wyckoff positions of three possible configurations are illustrated in Table I. Based on the data obtained from the total energy vs. volume optimization curve as shown in Table II, it is clear that for both alloys, the XA-I structure has the lowest energy than the other two types of structures, and all calculations have been carried out for the XA-I stable crystal structure.

Fig. 1

Schematic representation of thee possible crystal configurations of Mn₂XSb (X = Co, Fe): (a) XA-I, (b) XA-II and (c) XA-III.

Table I Three possible crystal configurations of Mn₂XSb (X = Co, Fe) inverse Heusler alloys

Table II The possible crystal structure, lattice parameters and obtained total energy of Mn₂XSb (X = Co, Fe)

The formation energy can be calculated by the following equation.

$$ E_{F} = E_{{{\text{Mn}}_{2} {\text{XSb}}}} - \left( {E_{\text{Mn1}} + E_{\text{Mn2}} + E_{X} + E_{\text{Sb}} } \right);X = {\text{Co}},{\text{Fe}} $$

(1)

where $E_{{{\text{Mn}}_{ 2} {\text{XSb}}}}$ is the ground-state energy of Mn₂XSb alloys per formula unit, and $E_{\text{Mn1}}$, $E_{\text{Mn2}}$, $E_{X}$ and $E_{\text{Sb}}$ are the total ground-state energies of the bulk Mn, Sb, and X (X = Co, Fe), respectively. The calculated formation energies of two alloys are listed in Table III. The negative enthalpy of formation energy implies that the material is thermally stable, and it can be possible to prepare experimentally.

Table III Calculated formation energy (E_F) of Mn₂XSb (X = Co, Fe)

We have shown the volume optimization curve for paramagnetic (PM) and ferromagnetic (FM) states to find out the most stable ground state that is represented in Fig. 2. Accordingly, in both alloys, the FM state is a most stable state. The ground-state properties, such as the equilibrium lattice parameter a, the bulk modulus and its pressure derivative, have been derived from a volume optimization fitted curve using Birch–Murnaghan's equation of states (EOS) and are listed in Table IV. The calculated lattice parameter was found to be 5.9998 Ǻ for Mn₂CoSb and 6.0035 Ǻ for Mn₂FeSb, and these calculated results are quite similar with the other experimental data and previous theoretical calculations.14,7

Fig. 2

Calculated variation of energy with the volume of (a) Mn₂CoSb and (b) Mn₂FeSb alloys for both the PM and FM states.

Table IV The calculated ground-state properties of M₂XSb (X = Co, Fe) alloys for both the PM and FM states

Electronic Properties

The calculated total density of states (TDOS), partial density of states (PDOS) and band structure of M₂XSb (X = Co, Fe) using the GGA + U scheme have been shown in Figs. 3 and 4. For both alloys, the spin-down DOS at E_F reveals the semiconducting nature with a finite band gap, and the spin-up DOS at E_F possesses a strong metallic nature. The values of band gap and Fermi energy for different approximations are reported in Table V. Due to the existence of a semiconductor band gap in one spin channel and metallic overlap in another spin channel, both alloys are considered as half-metallic ferromagnetic materials. The band structure contains an indirect minority band gap along the Γ-X direction. The TDOS of these alloys is mainly governed by all 3d transition metal atoms. The formation of a band gap in the spin-down channel can be understood by d–d hybridization represented in Fig. 5. In the spin-down channel, the d orbitals of Mn(1) and X atoms hybridize with each other and create five bonding d orbitals (2e_g and 3t_2g) and five non-bonding d orbitals (2e_u and 3t_u). Then, the five Mn(1)-X bonding d orbitals hybridize with the d orbitals of Mn(2) atoms and create bonding orbitals (2e_g and 3t_2g) and antibonding orbitals ($2e^{*}_{g}$ and $3{\text{t}}^{*}_{{ 2 {\text{g}}}}$). This hybridization makes the d orbitals split to three states i.e., (a) bonding orbitals below the E_F, (b) non-bonding orbitals around the E_F and c) an anti-bonding orbital above the E_F. The valence band of alloys is originated from hybridization of bonding orbitals (e_g and t_2g), and the conduction band is originated by hybridization of anti-bonding orbitals ($e^{*}_{g}$ and $t^{*}_{2g}$). The minority band gap has been created due to the splitting between the bonding 3t_2g and non-bonding 3t_1u orbitals. In the spin-up channel, the metallic overlap due to the exchange splitting effect between orbitals makes the energy bands shift towards lower energies, and the non-bonding 3t_u orbital crosses the Fermi level E_F.

Fig. 3

Calculated total and projected density of states of (a) Mn₂CoSb and (b) Mn₂FeSb for both majority and minority carriers using the GGA + U method.

Fig. 4

The calculated spin-dependent band structure of (a) Mn₂CoSb and (b) Mn₂FeSb for spin-up (pink color) and spin-down (blue color) channels using the GGA + U method (Color figure online).

Table V Calculated electronic parameters of Mn₂XSb (X = Co, Fe) inverse Heusler alloys using GGA, GGA + U and GGA + mBJ schemes

Fig. 5

Schematic representation of the origin of the half-metallic band gap in Mn₂XSb (X = Co, Fe) inverse Heusler alloys.

Magnetic Properties

The total and partial magnetic moments of Mn₂XSb (X = Co, Fe) in the FM phase using GGA are listed in Table VI. We obtained a total magnetic moment of 4 μ_B/f.u. for Mn₂CoSb and 2.99 μ_B/f.u. for Mn₂FeSb alloys using GGA and it obeys the Slater–Pauling rule, M_t = Z_t− 24. Table VI shows that a strong contribution to M_tot comes from the Mn(2) and X atoms. The Mn(1) atom has a negative magnetization due to a negative exchange splitting between spin-up and spin-down electrons in the d shell. The spin polarization (P%) of the Mn₂XSb (X = Co, Fe) alloys at the Fermi level has been calculated using the following equation, and results are shown in Table VI.

$$ P\left( {\text{\% }} \right) = \frac{n\left( \uparrow \right) - n\left( \downarrow \right)}{n\left( \uparrow \right) + n\left( \downarrow \right)} \times 100 $$

(2)

where n(↑) and n(↓) represent the number of spin-up and spin-down energy states at the Fermi level E_F in spin ↑ and spin ↓ configurations, respectively. By measuring n(↑) and n(↓) from the spin-polarized density of states in Fig. 3, both alloys exhibit 100% spin polarization which could be useful for spin injection. The Curie temperature of these alloys has been calculated using Eq. (3) within mapping the Heisenberg model in the mean field approximation as discussed in Refs. 15,16,17, where $\Delta E = E_{\text{PM}} - E_{\text{FM}}$ is the difference of the total energies of the Mn₂XSb (X = Co, Fe) alloys in their PM and FM states, and $K_{B}$ is the Boltzmann constant. The T_Cvalues for bulk Mn₂XSb (X = Co, Fe) were estimated for 427 K for Co and 415 K for Fe, and it has high T_C greater than room temperature, which indicated that both alloys are ideal candidates for spintronic device applications.

Table VI Calculated total and partial magnetic moments, spin polarization and Curie temperature of Mn₂XSb (X = Co,Fe) using GGA

$$ T_{C} = \frac{\Delta E}{{3K_{B} }} $$

(3)

Elastic Properties

The mechanical stability of the alloys was estimated by deriving the elastic constants C_ij, and it is important for various practical applications. The necessary and sufficient stability conditions of the elastic constants for cubic crystals are

$$ C_{11} > 0,C_{44} > 0,\left( {C_{11} - C_{12} } \right) > 0,\left( {C_{11} + 2C_{12} } \right) > 0 $$

(4)

Our calculated elastic constants as listed in Table VII satisfy the above conditions; therefore, all of our theoretically predicted alloys are mechanically stable. The elastic parameters such as bulk modulus (B), shear modulus (G), Young’s modulus (E), Poisson’s ratio ($v$) and anisotropic factor (A) of Mn₂XSb (X = Co, Fe) have been calculated using the Voigt–Reuss and Hill approximations as discussed in Refs. 18 and 19

Table VII Calculated elastic constants C_ij (GPa) and various elastic parameters of Mn₂XSb (X = Co, Fe) using GGA

$$ B = \frac{1}{6}\left( {C_{11} + 2C_{12} } \right) $$

(5)

$$ G = \frac{1}{2}\left( {G_{v} + G_{R} } \right) $$

(6)

where

$$ G_{V} = \frac{1}{5}\left( {C_{11} - C_{12} + 3C_{44} } \right) $$

(7)

$$ G_{R} = 5\frac{{\left( {C_{11} - C_{12} } \right)C_{44} }}{{3\left( {C_{11} - C_{12} } \right) + 4C_{44} }} $$

(8)

Here, $G_{V}$ is Voigt’s shear modulus, and $G_{R}$ is Reuss’s shear modulus.

$$ E = \frac{9GB}{3B + G} $$

(9)

$$ v = \frac{1}{2}\left( {\frac{3B - 2G}{3B + G}} \right) $$

(10)

$$ A = \frac{{2C_{44} }}{{C_{11} - C_{12} }} $$

(11)

B denotes the hardness and fracture resistance of the alloy, whereas G refers to resistance to plastic deformations. E quantifies the stiffness of the alloy, and here Mn₂FeSb is stiffer than Mn₂CoSb. Pugh’s ratio (B/G) of both alloys is lower than the critical value of 1.75, indicating that they are brittle in nature. The anisotropic factor (A) has been calculated to identify the anisotropic or isotropic nature of the alloy. Both alloys are elastically anisotropic in nature, and the value of anisotropic factor (A) for both alloys has a deviation from unity, which indicates occurrence of cracks during the process of crystal growth.

Conclusion

The structural stability, ground-state, electronic, magnetic and elastic properties of Mn₂XSb (X = Co, Fe) inverse Heusler alloys have been investigated using full-potential linearized augmented plane wave (FPLAPW) method with various schemes such as GGA, GGA + U and GGA + TB-mBJ. The calculated minimum lattice parameter is 5.9998 Ǻ for Mn₂CoSb and 6.0035 Ǻ for Mn₂FeSb which is in good agreement with the available theoretical and experimental data. Both alloys are found to be structurally stable at a XA-I crystal configuration. From calculating the formation energy Mn₂XSb (X = Co, Fe), the alloys are found to be thermally stable and may be synthesized experimentally. The electronic structure of Mn₂XSb (X = Co, Fe) shows half-metallic behavior, and the origin of the band gap at the Fermi level in the spin-down channel has been explained in terms of orbital hybridizations. The total magnetic moment is 4.00 μ_B/f.u. for Mn₂CoSb and 2.99 μ_B/f.u. for Mn₂FeSb, and both alloys obey the Slater–Pauling rule of M_t= Z_t− 24. The Mn₂XSb (X = Co, Fe) alloys are highly spin-polarized (100%), and the estimated Curie temperature is greater than room temperature. The two alloys are predicted as elastically stable, hard materials and brittle in nature. On the basis of the combination of structural, electronic, magnetic and elastic properties from the above predicted results, the Mn₂XSb (X = Co, Fe) inverse Heusler alloys represent a potential candidate for spintronics applications.