Introduction

Liquid silicon oxidation is a driving phenomenon in purification processes used in the “metallurgical route” to produce silicon for solar cells, at a lower energy cost than the classical chemical route used for electronic grade silicon.[1] A plasma process has been proposed to remove boron from liquid silicon, first investigated on silicon drops,[2] then at large scale in Japan with arc torches[3] and in France with inductive plasmas.[4,5] Other boron extraction processes were tested using gas mixtures in place of plasma torches.[6,7] All those processes use a common reaction mechanism at the interface between molten silicon and gas, involving silicon and boron in the liquid phase and hydrogen and oxygen in the gas phase (generally mixed with argon). Despite its industrial application, this mechanism is not completely understood, especially the rate limiting step that could be the surface reaction itself or the diffusion of oxidizing species toward the surface.[7,8]

One key point of such a process is that silicon is oxidized (to form SiO or SiO2) in parallel with boron that mainly produces HBO in the gas phase.[4,7] The concept of thermodynamic equilibrium at the surface[8] enables to deduce the boron extraction rate from the silicon oxidation rate.

The core of this paper is to study the mechanism of silicon oxidation for typical conditions used in the purification processes mentioned previously: atmospheric pressure, silicon temperature between 1683 K and 2073 K (1410 °C and 1800 °C), and a gas mixture blown on the surface, containing argon with some percents of oxygen (or water vapor) and a variable proportion of hydrogen. The oxidation of liquid silicon by dioxygen in a neutral gas was described in the literature,[10,11] but those models did not include hydrogen. A 1D model has been developed using the work of Ratto et al.[11] as a basis and adding new species due to the presence of hydrogen. This model is described in part 2. The main results are described in part 3, for conditions that could be encountered in purification processes.

In part 4, the flow of silicon oxidized from the melt is predicted using a combination of our numerical model with the theoretical predictions of the mass transfer boundary layer thickness for an impinging jet. These predictions are applied for a set of experiments of silicon purification with steam for which the mass loss was measured.[12] In part 5, we applied the same model to a plasma purification experiment to predict silicon oxidation rate, and from this value, a speed of removal of boron which was compared to the experimental value.[8] The discussion shows perspectives on the prediction of purification kinetics.

Oxidation Model in the Presence of Hydrogen

Following Reference 11, we use the concept of a stagnant film to study the transport of species across the gaseous boundary layer just above the liquid silicon. The flow of each gaseous species is then only diffusive, whereas chemical reactions in the gas produce some source terms in each transport equation for individual species.

Diffusive Transport and Effective Pressures

Molar balance equations for each species i (i = Ar, O2, Si, SiO, SiO2, H2, H2O) in an elementary layer dz of the 1D domain (from z min = 0 at the silicon surface to z max = δ, a prescribed boundary layer thickness) can be written using the diffusivities D i and partial pressures p i :

$$ - \frac{{D_{i} }}{RT}\frac{{\partial^{2} p_{i} }}{{{\text{d}}z^{2} }} = R_{i}, \;{\text{where}}\;R = 8. 3 1 4\;{\text{J}}/\left( {{\text{mol}}\;{\text{K}}} \right),R_{i} :\;{\text{source due to chemical reactions}}\left( {{\text{mol}}/\left( {{\text{m}}^{ 3} \;{\text{s}}} \right)} \right). $$
(1)

The production rate of atomic species (Si, O, or H) is the combination of reactive sources R i for all gaseous reactions involving that atomic species (with stoichiometric coefficients). Introducing the molar rate R sol of production of solid SiO2 (R sol =0 in purely gaseous zones), three combined equations (for Si, O, and H) can be written using the effective pressures introduced in Reference 11:

$$ \begin{array}{*{20}c} {\frac{{\partial^{2} p_{\text{Si}}^{\text{eff}} }}{{{\text{d}}z^{2} }} = \frac{RT}{{D_{{{\text{O}}_{2} }} }}R_{\text{sol}} } & {} & {p_{{{\text{O}}_{2} }}^{\text{eff}} = p_{{{\text{O}}_{2} }} + \psi_{{{\text{SiO}}_{2} }} p_{{{\text{SiO}}_{2} }} + \frac{{\psi_{\text{SiO}} }}{2}p_{\text{SiO}} + \frac{{\psi_{{{\text{H}}_{2} {\text{O}}}} }}{2}p_{{{\text{H}}_{2} {\text{O}}}} } \\ {\frac{{\partial^{2} p_{{{\text{O}}_{2} }}^{\text{eff}} }}{{{\text{d}}z^{2} }} = \frac{RT}{{D_{{{\text{O}}_{2} }} }}R_{\text{sol}} } & {\text{with}} & {p_{\text{Si}}^{\text{eff}} = \psi_{\text{Si}} p_{\text{Si}} + \psi_{{{\text{SiO}}_{2} }} p_{{{\text{SiO}}_{2} }} + \psi_{\text{SiO}} p_{\text{SiO}} } \\ {\frac{{\partial^{2} p_{{{\text{H}}_{2} }}^{\text{eff}} }}{{{\text{d}}z^{2} }} = 0} & {} & {p_{{{\text{H}}_{2} }}^{\text{eff}} = \psi_{{{\text{H}}_{2} }} p_{{{\text{H}}_{2} }} + \psi_{{{\text{H}}_{2} {\text{O}}}} p_{{{\text{H}}_{2} {\text{O}}}} } \\ \end{array}, $$
$$ {\begin{array}{*{20}l} {\psi_{\text{Si}} = D_{\text{Si}} /D_{{{\text{O}}_{2} }} = 0.914} \hfill \\ {\psi_{\text{SiO}} = D_{\text{SiO}} /D_{{{\text{O}}_{2} }} = 0.739} \hfill \\ {\psi_{{{\text{SiO}}_{2} }} = D_{{{\text{SiO}}_{2} }} /D_{{{\text{O}}_{2} }} = 0.58} \hfill \\ {\psi_{{{\text{H}}_{2} }} = D_{{{\text{H}}_{2} }} /D_{{{\text{O}}_{2} }} = 3.46} \hfill \\ {\psi_{{{\text{H}}_{2} {\text{O}}}} = D_{{{\text{H}}_{2} {\text{O}}}} /D_{{{\text{O}}_{2} }} = 1.20.} \hfill \\ \end{array} }. $$
(2)

We use numerical values of D i , valid at 1750 K (1477 °C), given in Reference 11 for oxygen and silicon-containing species, and from the commercial CFD code Fluent for H2 and H2O. Whatever the homogeneous reactions in the gas, the gradients of those effective pressures give atomic flows due to diffusion.

The combined balance Eq. [2] shows that the distribution of each effective pressure is linear across the boundary layer, when the whole layer is homogeneous (gaseous species only). The situation becomes more complicated when SiO2 condenses to form solid particles in a part of the boundary layer (heterogeneous sublayer). In such a mixed configuration (superposition of homogeneous and heterogeneous sublayers), the distributions of \( {p_{\text{Si}}^{\text{eff}} } \) and \( {p_{{{\text{O}}_{2} }}^{\text{eff}} } \) are not linear. However, eliminating the rate of formation of solid silica shows that \( {p_{\text{Si}}^{\text{eff}} - p_{{{\text{O}}_{2} }}^{\text{eff}} } \) varies linearly with the distance z to the interface in the whole layer.

Equilibrium in the Gas Phase

Ratto et al.[11] introduced a hypothesis of local chemical equilibrium in the gas phase at each point of the layer. Introducing the equilibrium constants, it means that

$$ \begin{array}{*{20}l} {p_{{{\text{SiO}}_{2} }} = K_{{{\text{P,SiO}}_{2} }} p_{\text{Si}} p_{{{\text{O}}_{2} }} \left( {p^{\varTheta } } \right)^{ - 1} } & {} & {K_{{{\text{P,SiO}}_{2} }} = 1.41 \times 10^{15} } & {} \\ {p_{\text{SiO}} = K_{\text{P,SiO}} p_{\text{Si}} p_{{{\text{O}}_{2} }}^{0.5} \left( {p^{\varTheta } } \right)^{ - 1/2} } & {\text{with}} & {K_{\text{P,SiO}} = 1.76 \times 10^{13} } & {{\text{at}}\;1750\;{\text{K}}\left( {1477\;^\circ {\text{C}}} \right)} \\ {p_{{{\text{H}}_{2} {\text{O}}}} = K_{{{\text{P,H}}_{2} {\text{O}}}} p_{{{\text{H}}_{2} }} p_{{{\text{O}}_{2} }}^{0.5} \left( {p^{\varTheta } } \right)^{ - 1/2} } & {} & {K_{{{\text{P,H}}_{2} {\text{O}}}} = 3.00 \times 10^{4} } & {} \\ \end{array}, $$
(3)

with \( p^{\theta } = 1 \;{\text{bar}}. \)

The values of the equilibrium constants were obtained from Reference 11 for silicon oxides and using the commercial code FactSage® for water vapor. Substituting Eq. [3] in Eq. [2] gives a system of three nonlinear equations with three unknowns (\( P_{\text{Si}} , P_{{{\text{O}}_{2} }} , P_{{{\text{H}}_{2} }} \)). By substitution, a polynomial equation for \( X = P_{{{\text{O}}_{2} }}^{ 1/ 2} \) is obtained and can be solved (we found only one real positive root) to give all the partial pressures as a function of \( {p_{\text{Si}}^{\text{eff}} ,p_{{{\text{O}}_{ 2} }}^{\text{eff}} ,{\text{ and }}p_{{{\text{H}}_{ 2} }}^{\text{eff}} } \) in homogeneous zones.

For heterogeneous zones, the pressure of SiO2 is known (\( {p_{{{\text{SiO}}_{2} }} = p_{{{\text{SiO}}_{2} }}^{\text{sat}} = 1.67 \times 10^{ - 4} \;{\text{Pa}}} \) at 1750 K (1477 °C)[11]), which gives a relation between \( {p_{\text{Si}} \;{\text{and}}\;p_{{{\text{O}}_{2} }} } \). Only two unknowns remain among the partial pressures, but \( {p_{\text{Si}}^{\text{eff}} {\text{ and }}p_{{{\text{O}}_{ 2} }}^{\text{eff}} } \) are not known individually. Subtracting the last two nonlinear equations gives a system of two equations with two unknowns (\( {p_{{{\text{O}}_{2} }} \;{\text{and}}\;p_{{{\text{H}}_{2} }} } \)), the solution of which gives all the partial pressures as a function of \( {p_{\text{Si}}^{\text{eff}} - p_{{{\text{O}}_{2} }}^{\text{eff}} ,\;{\text{and}}\;p_{{{\text{H}}_{2} }}^{\text{eff}} } \) in heterogeneous zones. After substitution, a polynomial equation is obtained for \( X = P_{{{\text{O}}_{2} }}^{ 1/ 2} \), and its only real positive root is used to calculate all the partial pressures from the effective pressures. The detailed equations are presented in annex.

Boundary Conditions and Sublayers

Following Reference 11, two types of configuration are considered, a homogeneous configuration (no solid silica) and a mixed configuration, which contains a heterogeneous sublayer (producing particles of SiO2) between two homogeneous sublayers. Boundary conditions at z = δ are based on the composition of the gas blown on the surface:

$$ \begin{aligned} p_{\text{Si}}^{\text{eff,ext}} = 0 \hfill \\ p_{{{\text{H}}_{2} }}^{\text{eff,ext}} = \psi_{{{\text{H}}_{2} }} p_{{{\text{H}}_{2} }}^{\text{ext}} + \psi_{{{\text{H}}_{2} {\text{O}}}} p_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}} \hfill \\ p_{{{\text{O}}_{2} }}^{\text{eff,ext}} = p_{{{\text{O}}_{2} }}^{\text{ext}} + 0.5\psi_{{{\text{H}}_{2} {\text{O}}}} p_{{{\text{H}}_{2} {\text{O}}}}^{\text{ext}} \hfill \\ \end{aligned}. $$
(4)

Let us note that \( {p_{{{\text{O}}_{ 2} }}^{\text{eff,ext}} } \) and \( {p_{{{\text{H}}_{ 2} }}^{\text{eff,ext}} } \) are here exclusively for the purpose of introducing atomic concentrations as an external condition and can apply for H2/H2O mixtures as well as O2/H2O mixtures since we have thermodynamical equilibrium in isothermal hypotheses. The effective external pressures should be calculated at thermodynamical equilibrium.

At z = 0, the silicon pressure is known (\( {p_{\text{Si}} = p_{\text{Si}}^{\text{sat}} = 0.104\;{\text{Pa}}} \) at 1750 K (1477 °C)[11]), and we consider that the dissolved oxygen and hydrogen concentrations in the liquid silicon are in equilibrium with the gas phase. Therefore, there is no net flux of oxygen or hydrogen atoms across the interface: \( {\frac{\partial }{\partial z}p_{{{\text{O}}_{ 2} }}^{\text{eff}} = \, \frac{\partial }{\partial z}p_{{{\text{H}}_{2} }}^{\text{eff}} = 0}. \) This flux condition shows that the effective pressure of oxygen is constant across the homogeneous zone touching the silicon, and the hydrogen effective pressure is constant across the whole layer, because the hydrogen atoms are not part of the silica particles formation.

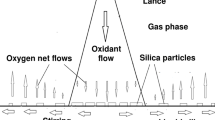
Whereas the value of \( {p_{{{\text{H}}_{ 2} }}^{\text{eff}} } \) is known in the whole layer from external conditions, for oxygen, this is only true if the whole layer is homogeneous. If a heterogeneous sublayer is present, its lower limit should obey \( {\partial p_{{{\text{O}}_{ 2} }}^{\text{eff}} /\partial z = 0} \), from the continuity of the flux of oxygen atoms with the lower homogeneous layer (where this flux is zero because of interface conditions). This additional equation makes this point monovariant, so that it is possible to calculate all the partial pressures at that point from the known value of \( {p_{{{\text{H}}_{ 2} }}^{\text{eff}} } \), and then we have \( {p_{\text{Si}}^{\text{eff}} {\text{ and }}p_{{{\text{O}}_{ 2} }}^{\text{eff}} } \) at that point (Figure 1).

Fig. 1
figure 1

Distribution of effective pressures across a layer of thickness 2 mm. \( p_{{{\text{O}}2}}^{\text{eff,ext}} = 0.05\;{\text{bar}}\;p_{{{\text{H}}_{2} }}^{\text{eff,ext}} = 0.20\;{\text{bar}}, \) HT: heterogeneous sublayer, HM: homogenous sublayer, Overall (left), Near from surface (right)

Full size image

It is possible to show that the heterogeneous layer appears when the oxygen contents out of the boundary layer (\( {p_{{{\text{O}}_{2} }}^{\text{ext}} } \)) is greater than the value of \( {p_{{{\text{O}}_{ 2} }}^{\text{eff}} } \) calculated at the monovariant point (plotted in Figure 3 as a function of \( {p_{{{\text{H}}_{ 2} }}^{\text{eff}} } \)). Because \( {p_{{{\text{H}}_{2} }}^{\text{eff}} } = \psi_{{{\text{H}}_{2} }} p_{{{\text{H}}_{2} }}^{\text{ext}} \) in the whole layer, we point out that there is a threshold in the oxygen contents of the blown gas, above which silica aerosols will appear in the boundary layer, and this threshold depends on the hydrogen contents of the blown gas.

Resolution and Exploitation

As shown above, the effective pressure of oxygen at the interface is known (from external conditions in a homogeneous situation or from the monovariant point in a mixed situation). The condition of saturation of silicon at the surface can be used to calculate \( {p_{\text{Si}}^{\text{eff}} } \) at the surface. The linear law for \( {p_{\text{Si}}^{\text{eff}} - p_{{{\text{O}}_{ 2} }}^{\text{eff}} } \) can then be drawn across the whole layer, and its intersection with the value representing the monovariant point gives the position of (the lower edge of the heterogeneous layer (if it exists). Knowing the \( {p_{{{\text{O}}_{ 2} }}^{\text{eff}} } \) is constant across the first homogeneous layer (or the whole layer if there is no aerosol), the solution can be completely calculated using the methods described in Section II–B. The corresponding equations are presented in details in annex.

The whole process was programmed using the Matlab® software and gives the distribution of reactive species in the boundary layer for given values of the oxygen and hydrogen partial pressures in the external gas. The program was validated by verifying that it gives the same results as[11] in H2-free situations. For a given thickness of the boundary layer, the results (part 3) make it possible to calculate the molar flux of silicon atoms extracted from the surface, and the molar flux of oxygen atoms drawn from the external gas to produce SiO or SiO2.

The first limitation of this model is due to the stagnant film technique: the thickness of the boundary layer has to be given, and the flux of oxygen to the surface is proportional to the inverse of this thickness. In part 4, the boundary layer thickness has been chosen according to theoretical correlations, and the oxidation flux was validated experimentally.

The second limitation of the model is its uniform temperature across the whole layer: this is not realistic at all for plasma processes, where the blown gas can be 6000 K (5727 °C) hotter than the silicon surface. Nevertheless, the model gives interesting qualitative information, and its results can be extrapolated qualitatively to hotter gases as shown in part 5.

Results of the 1D Model

Typical distributions of gaseous species calculated across the boundary layer are presented in Figure 2 for two different fractions of H2 in the outer flow, while the fraction of O2 is 5 pct for both cases [the total pressure has been set to 1 bar everywhere and the temperature to 1750 K(1477 °C)]. The thickness of the layer has been fixed to δ = 2 mm for illustration, but the species distribution (vs z/δ) would be the same for other values of δ. With 0 pct H2, case a) gives a much thinner heterogeneous sublayer, while with 20 pct H2, case b) gives a thicker heterogeneous sublayer. In both cases, there is a second homogeneous sublayer near the surface too small to be drawn. SiO2 is withdrawn as solid silica (not plotted) in the heterogeneous sublayer.

Fig. 2
figure 2

Distribution of gaseous species across a layer of thickness 2 mm. HT: heterogeneous sublayer HM: homogenous sublayer. (a) \( p_{{{\text{O}}_{2} }}^{\text{eff,ext}} = 0.05\;{\text{bar}}\;p_{{{\text{H}}_{2} }}^{\text{eff,ext}} = 0 \), (b) \( p_{{{\text{O}}_{2} }}^{\text{eff,ext}} = 0.05\;{\text{bar}}\;p_{{{\text{H}}_{2} }}^{\text{eff,ext}} = 0.20\;{\text{bar}} \)

Full size image

Figure 3 shows that the appearance of a heterogeneous zone is favored by an increase in the outer gas fraction of oxygen atoms (described here with the bulk effective pressure for O2) and a decrease of the outer gas fraction of hydrogen. We found the following empirical relationship using the data from Ratto for T = 1750 K for the critical oxygen pressure for \( P_{{{\text{H}}_{2} }}^{\text{EFF}} > 1\;{\text{Pa}}. \):

$$ p_{{{\text{O}}_{2} }}^{\text{eff,transition}} /p_{\text{ref}} \approx 0.235\left( {p_{{{\text{H}}_{2} }}^{\text{eff,ext}} /p_{\text{ref}} } \right)^{1/2}, $$
(5)

where pref = 1 Pa

Fig. 3
figure 3

Domain of existence of the heterogeneous sublayer depending on the outer partial pressure of H2

Full size image

.

Even at high fractions of H2 (~100 pct in 1 atm), the aerosols appear at very low fractions of O2, (0.7 pct, i.e., \( {p_{{{\text{O}}_{ 2} }}^{\text{ext}} } \) ~70 Pa, for \( {p_{{{\text{H}}_{ 2} }}^{\text{ext}} } \) ~1 bar). This means that under flows of H2 and O2 applied at industrial conditions, for the isothermal model at 1750 K (1477 °C), the aerosols are certain to appear. However, temperatures for plasma processes are usually much higher inside the gas phase.

The 1D model can also be used to study the oxidation rate of silicon for different compositions of the gas blown on the surface. Figure 4 presents the flux density for several compositions of the outer gas and for a boundary layer thickness δ = 2 mm. The flux density is inversely proportional to the thickness δ, so that Figure 4 makes it possible to calculate the oxidation rate at T = 1750 K (1477 °C) for any outer conditions (the thickness of the boundary layer depends on the outer flow). The external effective pressures in the blown gas describe the external atomic concentrations, whatever their form (H2O-O2 or H2O-H2), at thermodynamic equilibrium.

Fig. 4
figure 4

Flux density for silicon oxidized for different outer gas compositions

Full size image

An increase in oxygen concentration in the lines of Figure 4 at some point induces a transition from a homogeneous regime to a heterogeneous regime which divides the slope of the Si flow by 2. In the homogeneous regime, we have a ratio of oxidated silicon atoms over reduced oxygen atoms of 1, and 2 in the heterogeneous regime. We find, using the thermodynamical data from Ratto, for the temperature of 1750 K (1477 °C), the equation:

$$ \begin{aligned} J_{\text{Si}} \approx 2\frac{{{{D_{{{\text{O}}_{2} }} p_{{{\text{O}}_{2} }}^{\text{eff,ext}} } \mathord{\left/ {\vphantom {{D_{{{\text{O}}_{2} }} p_{{{\text{O}}_{2} }}^{\text{eff,ext}} } {RT}}} \right. \kern-0pt} {RT}}}}{\delta }\,{\text{if}} \,p_{{{\text{O}}_{2} }}^{\text{eff,ext}} < p_{{{\text{O}}_{2} }}^{\text{eff,transition}} \hfill \\ J_{\text{Si}} \approx 2\frac{{{{D_{{{\text{O}}_{2} }} p_{{{\text{O}}_{2} }}^{\text{eff,transition}} } \mathord{\left/ {\vphantom {{D_{{{\text{O}}_{2} }} p_{{{\text{O}}_{2} }}^{\text{eff,transition}} } {RT}}} \right. \kern-0pt} {RT}}}}{\delta } + \frac{{D_{{{\text{O}}_{2} }} {{\left( {p_{{{\text{O}}_{2} }}^{\text{eff,ext}} - p_{{{\text{O}}_{2} }}^{\text{eff,transition}} } \right)} \mathord{\left/ {\vphantom {{\left( {p_{{{\text{O}}_{2} }}^{\text{eff,ext}} - p_{{{\text{O}}_{2} }}^{\text{eff,transition}} } \right)} {RT}}} \right. \kern-0pt} {RT}}}}{\delta }\,{\text{if}} \,p_{{{\text{O}}_{2} }}^{\text{eff,ext}} > p_{{{\text{O}}_{2} }}^{\text{eff,transition}} , \hfill \\ \end{aligned}, $$
(6)

where JSi is the flow of silicon atoms expressed in mol/m2 s.

Application of the Model to a Set of Experiments: Impinging Jet on Liquid Silicon

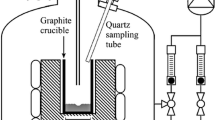
The oxidation rate of silicon is calculated in this part for a series of experiments from Sortland et al.,[12] where a steam-argon mixture has been injected onto a liquid silicon melt inductively stirred and heated to a homogeneous temperature of 1773 K (1500 °C) (Figure 5). The composition of the injected mixture was kept constant at 0.21 pct mass fraction of steam at constant pressure of 1.112 bar. Weighing the crucible before and after the experiment gave the experimental oxidation rate (data in Reference 12, p. 162). In order to calculate the mass flow boundary layer thickness, we are using formula for mass transfer coefficients for laminar impinging jet from Scholtz et al.[13,14] (those correlations were also used by Sortland,[12] p. 48):

Fig. 5
figure 5

Experimental Setup from Sortland (reprinted in Ref. [7])

Full size image

If r/d < 0.6 (stagnation zone):

$$ \begin{aligned} k = D_{{{\text{H}}_{2} {\text{O}}}} \text{Re}^{1/2} d^{ - 1} \left( {0.8242 Sc^{0.361} - 0.1351 Sc^{0.368} *\left( {\frac{2r}{d}} \right)^{2} } \right) \hfill \\ {\text{else}}\left( {{\text{wall}}\;{\text{jet}}\;{\text{zone}}} \right):k = 0.1590 D_{{{\text{H}}_{2} {\text{O}}}} Sc^{1/3} \text{Re}^{3/4} \frac{{d^{1/4} }}{{r^{5/4} }} \left( {1 + \left( {\frac{l}{r}} \right)^{3} } \right)^{ - 3/4} \hfill \\ \end{aligned} $$
(7)

where \( l = 0.1327 d \text{Re}^{1/3} , \)where Re is the Reynolds number at the lance outlet. The characteristic distance is the lance diameter of 2 mm at all experiments. The radiation on the lance by the melt and the crucible make the choice of a mixing temperature of 1773 K (1500 °C) at the outlet of the lance a reasonable choice. This temperature is determining the mixture viscosity, species diffusivities, as well as the outlet speed.

We use \( \upsilon_{{{\text{H}}_{2} }} \) = 1.86E−3 Pa s (with data from Svehla et al.[18] and formula from Byrd et al.[17]).The boundary layer thickness is then deduced from the transfer coefficient:

$$ \delta (r) = D_{{{\text{H}}_{2} {\text{O}}}} /k. $$
(8)

We use the diffusivity \( D_{{{\text{H}}_{2} {\text{O}}}} \) of H2O in H2 in Eq. [4] and to calculate the Schmidt number, but the thickness would not be very different using the diffusivity of SiO. We have integrated the oxidation flowrate using 100 discretization points along the radius r and checked that the relative sensitivity was less than 10−2 when more points are used. Similarly, the sensitivity to the discretization height from the surface melt was less than 10−2 when 100 points or more are used across the boundary layer. In this part, we used the thermodynamical data from the JANAF database[15] to calculate the equilibrium constants. For SiO2 particles, we used the data on SiO2-Quartz(h) at 1773 K (1500 °C) but we obtain identical results with data for SiO2(l).[16] Using Byrd et al.,[17] we deduced the diffusivities from Lennard–Jones parameters given by Svehla et al.,[18] so that \( D_{{{\text{H}}_{2} {\text{O}}}} \) = 1.62E−3 at 1773 K (1500 °C).

We found a systematic overestimate of the silicon flows going by a factor between 1.2 and 2.7 (Figure 6), with the worst results for lower speeds. It may be due to the fact that in the reactor outside of the boundary layer, the concentration of SiO is important while the model assumes it to be zero. The walls of the crucible can cause recirculations that reinject reaction products such a SiO in the direction of the boundary layer. Thus, the gradient of concentration of SiO is less than predicted by this model, which diminishes the diffusion of SiO. This is compatible with the fact that at higher jet speeds, the discrepancies between the model and the experimental results decrease (see Figure 6 and Table I). The higher the injection speed, the higher the wall jet speed, relatively the less diffusive interactions between the wall jet boundary layer and the reactor atmosphere. One may also consider the fact that the surface of the melt is not perfectly flat nor solid as assumed by the correlations. The temperature gradient at surface may also induce variations from the isothermal model by modification of the equilibrium constants.

Fig. 6
figure 6

Comparison between experimental results and simulations for silicon flows

Full size image
Table I Reynolds and Speed for the Experiments Using Information from Sortland et al.[7]
Full size table

Application to a Purification Experiment

The oxidation rate of silicon is reconstructed in this part from the purification rate of a plasma process, measured in experiments run in our laboratory pilot (sketched in Table II), in conditions summarized in Table II. An illustration of this experiment can be seen at Figures 7 and 8. The ratio of silicon atoms to boron atoms inside the gas phase at the facility outlet was recorded by ICP-MS analysis in real time during the experiment (Figure 9).

Table II Main Parameters of the Plasma Experiment Fig. 8: Parameters of the (Using Information From Ref. [8]) Plasma Torch
Full size table
Fig. 7
figure 7

Schema of the purification process Exhaust gas analysis by ICP and liquid sampling for concentration measurements of the silicon

Full size image
Fig. 8
figure 8

Parameters of the plasma torch

Full size image
Fig. 9
figure 9

Monitoring of the ratio B/Si atoms by ICP-MS during the purification experiment (reprinted in Ref. [8])

Full size image

Under those conditions, the boron fraction in the liquid silicon (initially 25 ppmw) decreases exponentially with time and is divided by two after a characteristic time τ0.5 related to the mass of silicon by the relation τ0.5/m Si= 31 min/kg.[8] We conclude to a first-order law relating the molar flux of boron \( \dot{N}_{\text{B}} \)(mol/s) extracted from the liquid phase, to the boron concentration in the liquid C LIQB (mol/m3), with a known rate constant \( \overline{k} S \):

$$ \dot{N}_{\text{B}} = \overline{k} S \cdot c_{\text{B}}^{\text{liq}} ,{\text{ where}}\;\overline{k} S = 6. 3 2 10^{ - 8} {\text{m}}^{ 3} /{\text{s}}, $$
(9)

k is the local value of the mass transfer coefficient of boron from the liquid to the boron free outer gas, and \( \overline{k} \) its mean value on the silicon-free surface of area S.

A hypothesis of chemical equilibrium at the surface is used to relate the experimental flux of boron to the associated oxidation rate of silicon: thermodynamic equilibrium laws give the ratio of boron to silicon in the gas phase, divided by the ratio of boron to silicon in the liquid phase, which was called “enrichment factor” in Reference 8. This equilibrium was calculated by the Factsage code with data from the database FactPS, taking data from JANAF,[15] then corrected to account for new values of the formation enthalpy,[9] that are not included in the FactPS database.

We chose the most realistic value for the enthalpy of formation of HBO according to Reference 12. The resulting enrichment factor, a function of the hydrogen molar fraction and temperature, is found to be R = 60 at [H2] = 4 pct mol, T = 1690 K (1417 °C) (the estimated silicon temperature for that experiment).

To calculate the boundary layer thickness, the properties of the diluted mixture (Table III) were approximated by those of Argon, calculated using the Lennard–Jones model with data from Svehla[18] and formula from Bird & Al.[17] DH2O is now the diffusivity of H2O in Ar.

Table III Transport Coefficients at Different Temperatures and Results Obtained by Choosing the Lennard–Jones Parameters from Svehla[16]
Full size table

The products of oxidation of silicon and boron are both evacuated by diffusion in the gas boundary layer. Assuming that HBO and SiO have comparable diffusivity, the rate of oxidation ratio verifies: \( \dot{N}_{\text{B}} /\dot{N}_{\text{Si}} = c_{\text{B}}^{\text{gas}} /c_{\text{Si}}^{\text{gas}} \), which is related to the boron concentration in the liquid by the enrichment factor:

$$ \dot{N}_{\text{B}} /\dot{N}_{\text{Si}} = R \cdot c_{\text{B}}^{\text{liq}} /c_{\text{Si}}^{\text{liq}}. $$
(10)

The results are given at Table III for the film temperature [3350 K (3077 °C)] and the mixing temperature at torch outlet [5000 K (4727 °C)]. Best results are obtained in the case of mixing temperature at outlet.

The predictions are quite good compared to experimental values (Eq. [9]) with both film temperature and outlet temperature. However, we should keep in mind other uncertainties, in addition to those exposed at the previous part, regarding the enthalpy of formation of HBO and the influence of radicals O and H as well as the higher temperature gradient between outlet and surface. The injection nozzle being larger in this case we have a lower speed of 27 m/s and a larger Reynolds of 732 compared to the cases from Sortland et al.

Discussion and Perspectives

The extension of the Ratto model to the case of liquid silicon oxidation in the presence of hydrogen enabled us to estimate mass transfer and concentration patterns in the boundary layer in the context of processes related to silicon purification. We combined the 1D isothermal diffusive model presented in parts 2 and 3 with theoretical calculations of boundary layer thickness for mass transfer with impinging jets in Part 4. We applied this combination to a case of liquid silicon oxidation and found some discrepancies, however, in a realistic range of order. We explain these discrepancies with the influence of the reactor atmosphere enriched in reaction products due to some recirculations and irregularities in the melt surface. This 1D model with theoretical calculations of boundary thickness for mass transfer has also been applied to a plasma process for deboration of silicon, which is currently employed for photovoltaic cells and in this case gave realistic results. In order to have a better insight into the mass transfer in the context of liquid silicon oxidation, a CFD model will be made to calculate the silicon oxidation rate in the correct experimental conditions (with hydrogen and SiO).