Passivation Threshold for the Oxidation of Liquid Silicon and Thermodynamic Non-equilibrium in the Gas Phase

Abstract

The present study focuses on a specific step of the metallurgical path of purification to provide solar-grade silicon: the removal of boron through the injection of H₂O(g)-H₂(g)-Ar(g) (cold gas process). A progressive increase of the oxidant H₂O(g) concentration at injection increases the speed of the process until a silica layer appears at the surface of the liquid silicon to be purified. It then stops the purification. During the process, silica aerosols may form in the gas boundary layer. This modifies the flows of oxidants and the gas concentrations at the liquid silicon surface. Using a monodimensional model, this article shows that a hypothesis of thermodynamic equilibrium of silica aerosols with the gas phase in the boundary layer has to be dropped in order to explain the appearance of a silica passivating layer. The passivation threshold is defined as the limit concentration of the oxidant at the injection below which there is no silica on the liquid silicon surface and beyond which silica particles appear on the liquid silicon surface. Three experiments of estimation of the passivation threshold with the injection of water vapor are used to confirm an empirical criterion for the prediction of the appearance of the silica layer. Two other sets of experiments with the injection of Ar-O₂ are also being studied where the kinetics of the formation of silica aerosols seems to be slower than when water vapor is used. An optimization of the speed of boron removal under the assumption of a maximal concentration of water vapor before the appearance of a passivating silica layer would require an increase of the liquid silicon surface temperature from the fusion temperature of silicon.

Introduction

Solar-grade silicon for photovoltaic cells has less purity requirements than electronic-grade silicon.[1] This creates a need for the exploration of new processes that consume less energy than processes from the chemical route for electronic-grade silicon such as the common Siemens process. Whereas the chemical route transforms the metallurgical-grade silicon (MG-Si) to be refined into gaseous species, the metallurgical route is made from a set of steps that extract the impurities from the MG-Si in its solid and liquid states.

Within the metallurgical route, solidification processes cannot remove boron efficiently because of its segregation coefficient near one. This is why other processes are needed to remove boron. One category of the processes involves an impurity-absorbing slag. Another category[2] involves the injection of cold gases or plasma with hydrogen and oxygen atoms onto electromagnetically stirred and heated liquid silicon. Regarding the cold gas and plasma processes, the goal is to optimize the efficiency in the choice of the geometry, flow rate of injection, composition of the injected mixture and silicon temperature. More specifically, an increase in the concentration of H₂O(g) at injection accelerates the process. However, if the concentration of H₂O(g) at injection is too high, a silica passivating layer appears at the surface of the liquid silicon and stops the process. Hence, it is necessary to be able to predict the passivation threshold. The passivation threshold is the highest concentration of H₂O(g) at injection at which there is no silica at the surface of the liquid silicon and beyond which silica particles appear on the liquid silicon surface.

CFD simulations have been realized with ©Ansys Fluent and used to model experiments from Sortland[3] to evaluate the mass transfer of H₂O(g) towards the liquid silicon surface.

Thermodynamic Non-equilibrium Regarding Silica Aerosols

Homogeneization of $P_\mathrm{{SiO}}^\mathrm{{surf}}$ at Passivation Threshold

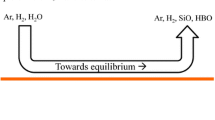
We suppose we are at the passivation threshold in stationary conditions. The first silica particles appear under the jet where the oxidant concentration is highest. Then, the stirring moves the particles from the center of the melt surface towards the crucible wall. The spreading of the particles maintains the partial pressure of SiO(g) at the surface at $P_\mathrm{{SiO}}^\mathrm{{lim}}$, which is the partial pressure of SiO(g) at equilibrium with Si(l) and SiO₂(s/l) according to the reaction $\mathrm{{Si(l)\,+\,SiO_2(s/l) \leftrightarrows 2 SiO(g)}}$. As illustrated in Figure 1, there is adsorption of oxygen under the jet and desorption nearer to the crucible wall. Thus, the hypothesis of a global net flow of oxygen equal to zero at the surface, necessary to the hypothesis of stationary conditions, can be maintained.

Fig. 1

Representation of adsorption and desorption flows of oxygen

Conditions of Existence of Silica Aerosols at the Passivation Threshold in Stationary Conditions

In this part, we use a monodimensional model for the gas boundary layer with silica aerosols at thermodynamic equilibrium, adapting the reasoning of Vadon et al.[4] to the specific case of the passivation threshold. The main purpose of the use of a monodimensional model for a boundary layer is to prove the impossibility of a thermodynamic equilibrium over the whole boundary layer between silica aerosols and the gas at the passivation threshold. Therefore, we first make a reasoning with a zero net flow of oxygen at the liquid surface ( Appendices B and C). Then, we make a similar reasoning with a positive net flow of oxygen towards the liquid (Appendix D). Showing that both situations are not compatible with the experimental observations, we deduce that the hypothesis of thermodynamic equilibrium between silica aerosols and the gas has to be dropped.

The structure of the boundary layer in the active case (i.e., without silica particles on the surface) is represented in Figure 2. The structure of the boundary layer in the case at the passivation threshold is represented in Figure 3. The corresponding model is described more in detail in the Appendix. In the active case, there is a homogeneous sublayer (i.e., without silica aerosols) near the liquid silicon at the surface due to the reduction by the liquid silicon. However, in the passivation threshold case, if we suppose the thermodynamic equilibrium, the presence of silica particles at the surface of the liquid silicon eliminates this homogeneous sublayer.

Fig. 2

Boundary layer representation in active conditions [Si(g) and SiO₂(g) are also included in the model just to show that they play no significant role]

Fig. 3

Boundary layer representation at the passivation threshold [Si(g) and SiO₂(g) are also included in the model just to show that they play no significant role]

Boundary layer with zero net flow of oxygen at the surface

The heterogeneous sublayer (Figure 3) is characterized by the presence of two phases (silica + gas) and thus has one degree of freedom less than the lower homogeneous sublayer in the case of active conditions (Figure 2). Let’s consider a simplified monodimensional model in the purification conditions with only the dominant species SiO(g), H₂O(g), Si(l), H₂(g) and SiO₂(s/l). Fixing a uniform temperature in the gas phase as well as a net flow of zero oxygen atoms from the surface becomes equivalent to having a flow of oxidant equal to zero at the surface because there is one less degree of freedom due to the thermodynamic equilibrium that links the concentration of H₂O(g) with those of SiO(g) in the presence of silica aerosols (see details in Appendix B). This leads to a uniform boundary layer with all concentrations equal to the concentrations at the surface, which is unrealistic if we consider a boundary layer under a jet with H₂O(g) and without SiO(g). Similarly, a more complex model including the minority species Si(g), O₂(g) and SiO₂(g) as described in Vadon et al.[4] leads to unrealistically high concentrations of H₂O(g) at injection to be at the passivation threshold.

If we suppose a negative temperature gradient in the non-isothermal case, this changes very little because a certain amount of SiO(g) at injection is still necessary to get into the passivation threshold, which is unrealistic (see Appendix C).

Boundary layer with non-zero net flow of oxygen at the surface

In case there is a positive net flow of oxygen atoms from the gas to the liquid, the thermodynamics says this will essentially be a flow of SiO(g). The reason is that SiO(g) is a dominant species in the presence of Si(l) over H₂O(g) and SiO₂(g), and the concentrations of SiO(g) and H₂O(g) are bound all over the layer by the presence of silica at thermodynamic equilibrium (see Appendix D). If there is no oxygen supplied in the form of SiO(g), there will be an excess of oxygen atoms over silicon atoms that leads to the complete passivation, since silica particles on the surface are already providing oxygen atoms. We thus come to a contradiction: a gas boundary layer at the thermodynamic equilibrium and passivation threshold becomes possible only in the desorption zones.

This means that to explain the appearance of a passivating layer in stationary conditions, we need to drop the hypothesis of thermodynamic equilibrium of silica aerosols with the gas phase.

Gap to Thermodynamic Equilibrium

In Appendix A, we have given an expression of the partial pressure of SiO (for active or passivation threshold conditions) at the surface using a simplified model at thermodynamic equilibrium under the isothermal hypothesis (see section Notation for the notations).

$$\begin{aligned} p_\mathrm{{SiO}}^\mathrm{{surf, eq}}= 2 \left( \frac{p_\mathrm{{SiO_2}}^\mathrm{{s}} \Psi _\mathrm{{H_2O}}p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{K_1 \Psi _\mathrm{{SiO}} \Psi _\mathrm{{H_2}}}\right) ^{1/2} \end{aligned}$$

(1)

Let’s assume that the pressure of gaseous silica $P_\mathrm{{SiO_2}}^*$ is higher than its equilibrium value by a factor $\alpha$ in the heterogeneous layer:

$$\begin{aligned} P_\mathrm{{SiO_2}}^*= \alpha P_\mathrm{{SiO_2}}^\mathrm{{s}} \end{aligned}$$

(2)

where $\alpha$ is assumed constant for this very first description of a non-equilibrium layer, then:

$$\begin{aligned} p_\mathrm{{SiO}}^\mathrm{{surf, neq}}= 2 \left( \frac{p_\mathrm{{SiO_2}}^* \Psi _\mathrm{{H_2O}}p_\mathrm{{H2}}^\mathrm{{eff,0}}}{K_1 \Psi _\mathrm{{SiO}} \Psi _\mathrm{{H_2}}}\right) ^{1/2}=\alpha ^{1/2}p_\mathrm{{SiO}}^\mathrm{{surf, eq}} \propto \alpha ^{1/2} \end{aligned}$$

(3)

In case of a negative temperature gradient from the surface (cold gas process), under an hypothesis of thermodynamic equilibrium, $p_\mathrm{{SiO}}^\mathrm{{surf, eq}}$ would be inferior to the value given in Eq. [1] because the evolution of the equilibrium constant of the reaction of nucleation $K_\mathrm{{nucl}}=K_1/p_\mathrm{{SiO_2}}^*$ would lead to more incoming oxygen atoms precipitating into silica. However, for simplicity, we are going to calculate $\alpha$ using a value of $p_\mathrm{{SiO}}^\mathrm{{surf, eq}}$ calculated with an isothermal hypothesis with surface temperature. This leads to an underevaluation of $\alpha$ in the case of a negative temperature gradient.

At the passivation threshold, the parameter $\alpha$ can be adjusted from $p_\mathrm{{SiO}}^\mathrm{{lim}}$ [the partial pressure of SiO at equilibrium with Si(l) and SiO₂(s/l)]:

$$\begin{aligned} p_\mathrm{{SiO}}^\mathrm{{surf, neq}}= p_\mathrm{{SiO}}^\mathrm{{lim}}=\alpha ^{1/2}p_\mathrm{{SiO}}^\mathrm{{surf, eq}} \end{aligned}$$

(4)

The parameter α > 1 describes the non-equilibrium of silica particles with the gas phase and non-isothermality. $p_\mathrm{{SiO}}^\mathrm{{surf, neq}}$ is the experimental value of the partial pressure of SiO at the surface, and $p_\mathrm{{SiO}}^\mathrm{{surf, eq}}$ is the value that the partial pressure of SiO at the surface would have had if there had been a thermodynamic equilibrium between the silica aerosols and the gas. It is related to the speed of nucleation and growth of the particles. It depends on the speed of injection, the concentration of oxidant at injection and the temperatures in the gas phase. The gap to thermodynamic equilibrium leads to increased SiO(g) concentrations at the surface. Since the densities are higher in the condensed phase, the collisions between molecules in the condensed phase could occur at a higher rate, and the hypothesis that at the passivation threshold there is a thermodynamic equilibrium at the surface among Si(l), SiO₂(s/l) and SiO(g) can still be reasonably maintained. Thus, the prediction of the passivation threshold depends on the accurate modeling of the nucleation and growth of silica aerosols and of the diffusion from the gas phase to the growing silica aerosols.¹

To achieve such an accurate modeling, a sufficient number of experiments to determine the passivation threshold are necessary, in particular experiments that test the influence of the speed of injection. In the next part, we present a few experiments to determine the passivation threshold to start the building of such a set of experiments.

Description of Experiments to Measure the Passivation Threshold

Experiments with the Injection of Water Vapor on Liquid Silicon in a Graphite Crucible

In this article, we analyze two sets of experiments to determine the passivation threshold.

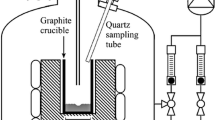
The first set is taken from Sortland.[3] This is a series of injections of Ar-H₂O or H₂-H₂O gaseous mixtures on liquid silicon through a lance. The concentration of H₂O(g) at injection is at different levels. The highest concentration at which there is no silica observed at the surface of liquid silicon and the lowest concentration at which there is silica at the surface of the liquid silicon are noted. The passivation threshold is in between. The diagram of the experiments is shown in Figure 4 and its representation in our CFD code in Figure 5. The liquid silicon is electromagnetically stirred.

Fig. 4

Configuration of the modeled cold gas experiments. Source Sortland.[3]

Fig. 5

Crucible representation in the CFD model

In the series of experiments Pass_Ar and H₂O_X (Table I), the injected mixture is Ar-H₂O. For experimental series Pass_H₂, it is H₂-H₂O.

Table I Parameters for the Passivation Experiments

Table II Results of the Passivation Experiments with the Highest Partial Pressure of H₂O(g) at Which There Is No Silica at the Surface of the Passivating Layer (a) and the Lowest Partial Pressure at Which There Is Silica at the Surface of the Passivating Layer (p)

The results for the experiments are shown in the Table II. They clearly show that an increase of surface temperature increases the passivation threshold and that the replacement of Ar by H₂ makes no significant difference.

Experiments with the Injection of O₂ on a Levitating Ball

The second set of experiments is made with the injection of an Ar-O₂ mixture on a levitating liquid silicon ball at an initial mass of 3.19 g (Figure 6 and Table III). The concentration of O₂(g) is increased progressively until the appearance of silica particles at the surface. A video of the ball is being filmed, and the temperature and injection flows are recorded simultaneously. Due to the small mass of the ball, the surface over mass ratio is high. Thus, the exothermic reaction of liquid silicon oxidation increases the temperature of the ball, and the increase in the concentration of O₂(g) at injection leads to an increase in the temperature of the ball. Thanks to the video, we write down the temperature and O₂(g) concentration at injection at the time of appearance of the first silica particles at the surface of the ball.

Fig. 6

Description of the device for electromagnetic levitation

Table III Material Used for the Levitation Experiments

Between 0.026 and 0.028 Nm³/h of injection flow of O₂ (for 0.4 Nm³/h of Ar), silica appears at 1928 K of liquid silicon temperature. A Brooks SLA 5850S flowmeter is used with a maximal precision of 1 pct for flows in the domain 0.1 to 1 Nm³/h. In our case, below 0.1 Nm³/h the precision is 0.0018 Nm³/h, which represents 6.4 pct of the measured value. Given that the pressure is maintained at about 1.1 bar, there is a partial pressure of O₂ at injection of about 0.070 bar. Thus, for a flow of 0.028 Nm³/h, the relative error is 0.0018/0.028 = 6.4 pct of the given value (Figure 7).

Fig. 7

Formation of silica particles at the surface of an electromagnetically levitating liquid silicon ball

Experiments on the Influence of the Temperature of the Liquid Silicon on the Passivation Threshold

A set of experiments from a technical report (Saadi et al.[6]) was carried out according to the geometry represented in Figure 8. A mixture of Ar and O₂ was injected on liquid silicon in a graphite crucible. The concentration of O₂ was increased progressively to determine the passivation threshold and its dependence on the liquid silicon temperature. The results are represented in Table IV.

Fig. 8

Geometry of the SNC experiments

Analysis of Experiments

Influence of the Temperature of the Liquid Silicon

Information on the influence of the temperature of the liquid silicon can be deduced from the results of experiments from Sortland[3] and the SNC report[6] shown in Tables I, II and IV. It shows a dependence on the passivation threshold that could be represented by an increasing exponential function of the temperature. This is compatible with the hypothesis of a passivation threshold characterized as an equilibrium between liquid silicon and surface silica particles (see Figure 9). This hypothesis already mentioned in Sortland[3] for experiments with the injection of Ar-H₂O is confirmed by new experiments with the injection of Ar-O₂ from the SNC report.[6]

Fig. 9

SiO partial pressure at equilibrium between Si(l) and SiO₂(s/l) (JANAF data[7])

Passivation Threshold with the Injection of H₂O(g)

In this part, we are going to check the validity of an empirical criterion from Sortland[3] for the prediction of the passivation threshold with the injection of H₂O(g)-Ar(g) or H₂O(g)-H₂(g) on liquid silicon. This empirical criterion is the following. Let’s define the efficiency efc as the fraction of oxidant injected that reacts with Si(l) to form SiO(g). According to the empirical formula from Sortland,[3] the partial pressure of H₂O at the passivation threshold $P^\mathrm{{0,max}}_\mathrm{{H_2O}}$ is given by the equation:

$$\begin{aligned} P^\mathrm{{0,max}}_\mathrm{{H_2O}}=efc^{-1}P_\mathrm{{SiO}}^\mathrm{{lim}} \end{aligned}$$

(5)

The efficiency can be measured experimentally by measuring the silicon mass loss. These measurements of silicon mass loss are taken from Sortland[3] for the experiments Pass_Ar and Pass_H₂. In addition, we have made CFD simulations with ©Ansys Fluent that predict the efficiency for the H₂O experiments and for Pass_Ar and Pass_H₂ as well as a verification. The ability of these simulations to predict the silicon flows has been validated in Vadon et al.[8]

We use an axisymmetric stationary laminar model taking into account mass (convection, diffusion) and heat transfer phenomena (convection, diffusion and radiation). The temperature at the exit boundary is supposed to be 1273 K but has no influence on the transport because the convection is dominant for heat and mass transport at the exit (see Figure 5). Similarly, the external gas at the exit is supposed to be made of pure argon but it has no impact because the convection outwards is dominant. The temperature of water vapor at injection is supposed to be 373 K, but the model also has little sensitivity to this parameter (Vadon[5]). The induction equations are not included in the model. Instead, the zone around the melt is set as a homogeneous zone at melt temperature. It is shown in Vadon[5] that due to the high speed of stirring, the mass transfer inside the melt is not limiting and the temperature of the melt can be considered as homogeneous. The crucible then conducts the heat with the conductivity of graphite.

We chose to model only the gas phase, while supposing the liquid silicon phase uniform in temperature and concentration. Regarding the cold gas experiments, Sortland[3] has made experiments with the same settings except for the furnace where the frequency of electromagnetic stirring of the silicon went from 11 to 4 kHz. He found identical transfer coefficients at least up to an inflow of Q = 2 nl/mn. Regarding the experiments with the highest inflow (Q16 with an inflow of Q = 16 nl/mn), simulations in Sortland[3] has also shown that the transport of boron in the liquid phase was probably non-limiting (with a ratio of 1 to 4 between the experimental transfer coefficient and the transfer coefficient calculated by the simulation for the liquid phase). Such results can be extrapolated regarding the concentrations of oxygen atoms inside the melt.

The equations were solved by the model under ©Ansys Fluent, in stationary conditions for a single phase, for 2D axisymmetric geometries with isotropic diffusivities.

Mass conservation equation:

$$\begin{aligned} \nabla . \left( \rho {\vec{v}} \right) = 0 \end{aligned}$$

(6)

Momentum conservation (F is the external forces, in our case the gravity, and I is the unity matrix):

$$\begin{aligned} \nabla . \left( \rho {\vec{v}} \vec{v}^T \right) = - \nabla p + \nabla . \left[ \mu \left( \nabla \vec{v} + \nabla \vec{v}^T \right) -\frac{2}{3} \nabla . \vec{v}I \right] +\vec{F} \end{aligned}$$

(7)

Species transport:

$$\begin{aligned} \nabla . \left( \rho \vec{v} Y_i \right) =-\nabla .\vec{J_i}+R_i \end{aligned}$$

(8)

where R_i is the net rate of production of species i by chemical reaction, and Y_i the mass fraction of species i. R_J is the diffusive flow (in kg m^–2 s^–1), and its expression is given in laminar conditions and for an ideal gas at constant pressure by a component taking into account the mass fraction gradients and thermodiffusion component. The choice for the laminar model was made after the comparison for the experiment with the highest speed (Q16a) had shown that the introduction of the $k-\omega$ SST model made no significant difference in the results.

$J_i$ is the solution of the equation of Maxwell Stefan (whose complex analytical solution is described in the explanatory notice) with a term that includes the thermodiffusion component:

$$\sum _{j=1,j \ne i}^N \frac{X_i X_j}{D_{ij}}\left( \frac{\vec{J_j}}{\rho _j} - \frac{\vec{J_i}}{\rho _i} \right) =\nabla X_i -\frac{\nabla T}{T} \sum _{j=1,j \ne i}^N \frac{X_i X_j}{D_{ij}}\left( \frac{D_{T,j}}{\rho _j}-\frac{D_{T,i}}{\rho _i} \right)$$

(9)

where Xⁱ is the mole fraction, T the temperature in K, D_ij the binary mass diffusivity of i in j in m² s^–1 and D_T,j the thermal diffusion coefficient of j. The binary mass diffusivities are calculated from the Lennard-Jones parameters and the temperature and the thermal diffusion coefficient from the molecular masses and the temperature. The energy equation is given by (viscous heating is neglected in the gases):

$$\nabla .\left( \vec{v}\left( \rho E + p \right) \right) = \nabla .\left( k_{eff} \nabla T - \sum _j h_j \vec{J}_j \right) +S_{\text{h}}$$

(10)

where k_eff is the effective thermal model equal to the thermal diffusivity due to the laminar model. The two terms on the right are the diffusion due to conduction and species diffusion. S_h includes the volumetric heat of reaction. In the absence of a volumetric reaction in the model, this term is equal to zero.

The radiation model is a surface-to-surface model (that is, the gases are transparent to radiations), where the surfaces are represented as black bodies.

The integration method was using the ISAT tables, a method that stores calculated parameters on different points and that calculates parameters by using previously stored parameters in points with input parameters that approximate those of the point for which the calculation is being performed (Ansys Manual[9] and Pope[10]).

We used method B validated in Vadon et al.[8] to calculate the silicon flows. In this method, only the species H₂O(g), H₂(g) and Ar(g) are included in the model, as well as a fictive species X(g), which has the thermodynamic properties of H₂O(g) and the diffusivity properties of H₂(g). The silicon flow is calculated by estimating the flow of H₂O(g) towards the surface. This flow of H₂O(g) towards the surface is given by the outflow of the fictive species X(g). This fictive species X(g) results from the conversion of the H₂O(g) molecules reaching the melt surface into X(g). This flow of X(g) represents the flow of SiO(g) from the surface. This flow is divided by two to take into account the nucleation and growth of silica aerosols. SiO(g) reacts entirely with H₂O(g) to form silica aerosols under similar conditions. Since SiO(g) comes exclusively from the oxidation of Si(l) by H₂O(g), it means that for one molecule of H₂O(g) that reaches the liquid silicon surface, one other molecule will react with SiO(g) to form silica aerosols. Apart from this, the transport towards the surface of H₂O(g) molecules that don’t react with SiO(g) seems not to be significantly modified by the reactions of the formation by SiO(g) and SiO₂(s/l). The diffusivity of H₂(g) for X(g) was chosen for reasons external to the present subject² and still gives an accurate description of the SiO(g) flows because the evacuation of SiO(g) is non-limiting for the silicon flows. As shown in Vadon et al.,[4,8] the reason for this non-limiting evacuation of SiO(g) is a steep decreasing gradient of SiO(g) at the surface due to the formation of silica aerosols at the surface with SiO(g) as a reactant. The high diffusivity of H₂(g) used for the species X(g) that represents SiO(g) also helps to represent such a non-limiting evacuation of SiO(g). This model supposes that the dilution from the surface reaction ${\text{Si(l)}} + {\text{H}}_{{\text{2}}} {\text{O(g)}} \leftrightarrows {\text{SiO(g)}} + {\text{H}}_{{\text{2}}}{\text{(g)}}$ and the concentration in equal proportions from reaction ${\text{SiO(g)}} + {\text{H}}_{{\text{2}}} {\text{O(g)}} \leftrightarrows {\text{SiO}}_{2}{\text{(s/l)}} + {\text{H}}_{2}{\text{(g)}}$ happen very close to the surface. Since H₂(g), a product of both reactions, has high diffusivity, the concentration and dilution compensate each other and thus have no significant influence on the transport of oxidant towards the surface. We still have to divide the calculated flow because the H₂O molecules (which experimentally react with SiO(g) to form silica) in the model react with Si(l). This model is well adapted for high oxidant concentrations because it takes the self-compensating phenomena of both dilution and concentration into account.

Figure 10 shows that the empirical formula from Sortland associated with our CFD prediction of the efficiency efc (Eq. [5]) is able to predict the passivation threshold quite accurately for experiments at very different temperatures. The curve of $P_{\rm{SiO}}^{\rm{lim}}$ is in between the curves for active and passive conditions.

Fig. 10

For each series, Pass_Ar, Pass_H₂ and H₂O_X, act designates the experiment in active conditions with the highest concentration of H₂O at injection and pass the experiment in passive conditions with the lowest concentration of H₂O at injection

We made a numerical application for the calculation of the α factor for the case Pass_H₂, which is easy to calculate because of the excess of H₂. At 1773 K, the equilibrium pressure of SiO₂(g) with silica is $P_{{{\text{SiO}}_{2} }}^{{\text{s}}} \, = \,2.85\, \times \,10^{{ - 9}} \,{\text{bar}}$ and $P_{{{\text{SiO}}}}^{{\text{s}}} /K_{1} \, = \,1.09\, \times \,10^{{ - 6}} \;{\text{bar}}$ ($p_{{{\text{SiO}}_{{\text{2}}} }}^{{\text{S}}} /K_{1}$ being the equilibrium constant of the reaction ${\text{SiO}}_{2}{\text{(s/l)}} + {\text{H}}_{2}{\text{(g)}} \leftrightarrows {\text{SiO(g)}} + {\text{H}}_{{\text{2}}} {\text{O(g)}}$) (source JANAF[7]). For $P_{{{\text{H}}_{{\text{2}}} }} = 1\;{\text{bar}}$, at thermodynamic equilibrium of silica aerosols with the gas phase, we have: $P_{{{\text{SiO}}}}^{{{\text{surf}},{\text{eq}}}} = 0.00236\;{\text{bar}}$. Thus, using the parameters in Table V, this leads to $\alpha = \left( {P_{{{\text{SiO}}}}^{{{\text{lim}}}} /P_{{{\text{SiO}}}}^{{{\text{surf}},{\text{eq}}}} } \right)^{2} = 130$. However, since we have a negative gradient from the surface, the value of α is undervalued since a lower temperature thermodynamically favors the precipitation of silica.

Optimization of the Temperature of the Liquid Silicon

The purification process is at its highest speed when the concentration of H₂O(g) is right at the maximum below the passivation threshold. An increase in the concentration of H₂O(g) causes an increase in purification speed. This was proved experimentally (Sortland[3]) and can also be shown by reasoning on a monodimensional diffusive reactive boundary layer (Eqs. [A8] and [A9] in Appendix A), which shows an increase of the silicon outflow with the increase of $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ at injection. Altenberend et al.[11] showed that, regarding the purification, there is a thermodynamic equilibrium at the surface between HBO(g), SiO(g), H2(g), Si(l) and B (in Si). Altenberend[11] also defined an enrichment factor as:

$$ R = \frac{{P_{{{\text{HBO}}}}^{{{\text{surf}}}} }}{{x_{B} P_{{{\text{SiO}}}}^{{{\text{surf}}}} }} \approx \gamma _{{\text{B}}} \left( {p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{surf}}}} } \right)^{{1/2}} K $$

(11)

where K is the equilibrium constant of the reaction $B({\text{in Si}}) + \frac{1}{2}{\text{H}}_{2}{\text{(g)}} + {\text{SiO(g)}} \leftrightarrows {\text{Si(l)}} + {\text{HBO(g)}}$ and γ_B the activity coefficient of boron in liquid silicon. Then, we use the approximation, verified in Vadon et al.,[8] that HBO(g) and SiO(g) diffuse similarly to link the flow of boron with the flow of silicon.

$$J_{\text{B}} =\eta R \times x_{\text{B}} \times J_{\text{Si}}$$

(12)

where J_B is the surface molar boron flow, J_Si the surface molar silicon flow and x_B the molar fraction of boron in silicon.

Given the decreasing evolution of the R factor with temperature, the purification speed decreases with the temperature for a fixed concentration of H₂O(g) at injection. However, it has been experimentally shown that the maximal oxidation speed before passivation increases with the temperature (Table I combined with Tables II and IV). This poses the question of the optimal temperature.

Table IV Dependence of the Passivation Threshold on the Liquid Silicon Temperature (SNC Report[6])

Table V Parameters of the Numerical Application for Case Pass_H₂ for the Calculation of the α Factor

Using the monodimensional model (see Appendix A for explanations) helps us to express the silicon flow as a function of $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{0}},{\text{max}}}}$ and $P_{{{\text{SiO}}}}^{{{\text{lim}}}}$ as in Eq. [13]³:

$$ \begin{array}{ll} {J_{{{\text{Si}}}} \approx \frac{{\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\,\Psi \,_{{{\text{SiO}}}} \,p_{{{\text{SiO}}}}^{{{\text{surf}}}} }}{{R\int_{0}^{\delta } {\frac{{T(z^{\prime})}}{{D_{{O_{2}}} (z^{\prime})}}} {\text{d}}z^{\prime}}}} \hfill \\ \end{array} $$

(13)

If we suppose $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{0,max}}}}$ proportional to $P_{{{\text{SiO}}}}^{{{\text{lim}}}}$ as in the empirical formula [5] from Sortland, then $J_{{{\text{Si}},{\text{max}}}}$ is proportional to $P_{{{\text{SiO}}}}^{{{\text{lim}}}} = P_{{{\text{SiO}}}}^{{{\text{surf}}}}$. Thus, under this assumption, $J_{{\text{B}}}^{{{\text{max}}}}$ depends on temperature as does $\left( {R/p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{1/2}},{\text{surf}}}} } \right)P_{{{\text{SiO}}}}^{{{\text{lim}}}}$, represented in Figure 11 (with the removal of the dependency on $p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{surf}}}}$).

We represented the function $\left( {R/p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{1/2,surf}}}} } \right)P_{{{\text{SiO}}}}^{{{\text{lim}}}}$ (Figure 11) because the maximal rate of deboration $J_{{\text{B}}}^{{{\text{max}}}}$ has the same evolution with the temperature as this function. For this function, we used the value recommended of Vadon et al.[8] for the standard enthalpy of the formation of HBO(g) ($\Delta _{f} ({\text{HBO(g)}}\, = \, - \,250.8\,{\text{kJ/mol}}$) and for the activity coefficient of boron from Freis et al.[12] (Eq. [14]). Regarding its standard molar entropy, we take the value from Gurvich[13] of 202.691 kJ/mol. Other values are taken from JANAF.[7]

$$\begin{array}{l} \log_{10}(\gamma _{\text{B}}^{\infty })=1105/T -0.1105 \end{array}$$

(14)

We deduce from Figure 11 that an increase of temperature from the fusion temperature of silicon may be advised for a maximization of the purification speed. The limit to this temperature increase should then be set by the maximal acceptation of silicon mass losses during the purification process.

Fig. 11

Maximum speed factor $Rp_{{{\text{SiO}}}}^{{{\text{lim}}}}$ where $p_{{{\text{H}}_{{\text{2}}} }} = 1\;{\text{bar}}$

Passivation Threshold with the Injection of O₂(g) on Levitating Liquid Silicon

At 1928 K, the partial pressure of SiO(g) at equilibrium with SiO₂(s/l) and Si(l) is 0.147 bar. Let’s suppose that there is no influence from silica aerosols on the transport, which is compatible with the experimental observations without any aerosols big enough to be observable, between the jet and the levitating silicon ball.

Let’s consider the equation for the mass transport of a uniform jet on a sphere from Whitaker[14] in Eq. [15].

$$ \begin{array}{ll} {{{Sh}}\, = \,2\, + \,\left( {0.4{{Re}}^{{1/2}} \, + \,0.06{{Re}}^{{2/3}} } \right){{Sc}}^{{0.4}} \left( {\frac{{\mu _{\infty } }}{{\mu _{s} }}} \right)^{{1/4}} } \hfill \\ {3.5\, < \,{{Re}}\, < \,76,000} \hfill \\ {0.71\, < \,{{Sc}}\, < \,380} \hfill \\ {{{Sh}}_{{\text{X}}} \, = \,\frac{{k_{{\text{X}}} }}{{D_{{\text{X}}} - {\text{Ar}}/L}}} \hfill \\ {{{Sc}}_{{\text{X}}} \, = \,\frac{\mu }{{\rho D_{X} - {\text{Ar}}}}} \hfill \\ \end{array} $$

(15)

where k_X is the transfer coefficient and L the diameter of the sphere.

The concentration of oxygen atoms due to the supposed absence of silica aerosols leads to the equation of conservation of oxygen atoms [16]:

$$ \begin{aligned} P_{{{\text{O}}_{{\text{2}}} }}^{0} & = \frac{1}{2}\frac{{D_{{{\text{SiO}}}} }}{{D_{{{\text{O}}_{{\text{2}}} }} }}\frac{{{{Sh}}_{{{\text{SiO}}}} }}{{{{Sh}}_{{{\text{O}}_{{\text{2}}} }} }}\, \times \,P_{{{\text{SiO}}}}^{{{\text{lim}}}} \, \approx \,\frac{1}{2}\frac{{D_{{{\text{SiO}}}} }}{{D_{{{\text{O}}_{{\text{2}}} }} }}\left( {\frac{{Sc_{{{\text{SiO}}}} }}{{Sc_{{{\text{O}}_{{\text{2}}} }} }}} \right)^{{0.4}} \\ {{Sc}}_{{\text{X}}} & \, = \,\frac{\mu }{{\rho D_{{{\text{X}} - {\text{Ar}}}} }} \\ P_{{{\text{O}}_{{\text{2}}} }}^{0} & \, = \,\frac{1}{2}\left( {\frac{{D_{{{\text{SiO}}}} }}{{D_{{{\text{O}}_{{\text{2}}} }} }}} \right)^{{0.6}} \, \times \,P_{{{\text{SiO}}}}^{{{\text{lim}}}} \\ \end{aligned} $$

(16)

Using the mixing temperature $(298\, + \,1923)\, \times \,0.5\, = \,1110\,{\text{K}}$, $\left( {\frac{{D_{{{\text{SiO}}}} }}{{D_{{{\text{O}}_{{\text{2}}} }} }}} \right)^{{0.6}} \, \approx \,0.88$⁴, the model for a flux of O₂ between 0.025 and 0.028 Nm³/h leads to a partial pressure of SiO(g) at the surface between 0.138 and 0.153 bar in homogeneous conditions, which includes the 0.142 bar of equilibrium pressure of SiO(g) between SiO2(s) and Si(l) at the measured temperature.

On the contrary, in this case, the empirical formula of Sortland does not give the right range for the prediction of the passivation threshold in these conditions. Remember there is indeed a partial pressure of about 0.070 bar of O₂ at injection, which means that there should be an unrealistic efficiency of about one to reach the value $\frac{1}{2}P_{{{\text{SiO}}}}^{{{\text{lim}}}} = 0.142\;{\text{bar}}$. It is then likely that in this case the kinetics of nucleation and growth of silica particles was too slow to influence the transport of oxidant towards the surface of the liquid silicon. A nucleation and growth of silica that is slower under an O₂(g) atmosphere than with an H₂O(g) atmosphere may be an explanation for this result. However, the absence of impurities such as carbon (no crucible) and boron (non-doped electronic-grade silicon) in the gas phase may also help to explain this result.

Conclusion and Perspectives

In the present article, we have shown that the appearance of a passivating silica layer on a liquid silicon layer under a jet of O₂(g) or H₂O(g) with excessive oxidant concentrations can be explained only through a thermodynamic non-equilibrium of silica particles with the gas. We have verified an empirical criterion related to the prediction of the appearance of silica particles on liquid silicon with a CFD model for three experiments. However, more experiments are needed as well as proper data and models for the kinetics of nucleation and growth of silica particles. An optimization of the speed of boron removal under the assumption of a maximal concentration of H₂O(g) before the appearance of a passivating silica layer would require an increase of the liquid silicon surface temperature. Such an increase would only be limited by the accepted losses of silicon.

Appendices

Appendix A: Simplified 1D isothermal model

We consider a boundary layer of thickness δ, where the only reactive species out of the boundary layer are H₂O(g) ($P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ at injection) and H₂(g) ($P_{{{\text{H}}_{{\text{2}}} }}^{0}$ at injection). Remember that the convection is not considered, and the model included only reactive and diffusive phenomena. At the reactive surface z = 0, there is liquid silicon. The structure of this layer is given in Figure 2, which means there is liquid silicon at the surface.

Hypotheses:

• Thermodynamic equilibrium everywhere

• Net flow of oxygen and hydrogen atoms at the surface equal to zero

• Sufficient dilution for the use of the Fick’s law

For this part, let’s define the effective pressures that will be used to express the flow of oxygen and silicon atoms in a more simple way.

$$ \begin{aligned} P_{{{\text{Si}}}}^{{{\text{eff}}}} \, = \, & \Psi _{{{\text{Si}}}} P_{{{\text{Si}}}} \, + \,\Psi _{{{\text{SiO}}}} P_{{{\text{SiO}}({\text{g}})}} \\ & + \,\Psi _{{{\text{SiO}}_{{\text{2}}} }} P_{{{\text{SiO}}_{{\text{2}}} ({\text{g}})}} \\ P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} \, = & \,\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} P_{{{\text{H}}_{{\text{2}}} {\text{O}}}} + \frac{1}{2}\Psi _{{{\text{SiO}}}} P_{{{\text{SiO}}({\text{g}})}} \\ & + \,\Psi _{{{\text{SiO}}_{{\text{2}}} }} P_{{{\text{SiO}}_{{\text{2}}} ({\text{g}})}} \\ P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}} & \, = \,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, + \,\Psi _{{{\text{H}}_{{\text{2}}} }} P_{{{\text{H}}_{{\text{2}}} }} \\ \end{aligned} $$

(A1)

These effective pressures are defined by rearranging the partial pressures and adimensionalized diffusivities $\Psi$ in such a way that the flow of atoms of Si, H and O can be found straightfowardly. The flows of atoms of Si, H and O can later be found by deriving these effective pressures via Fickian-type diffusive fluxes.

First, let’s write Fick’s law for a diluted gas at uniform pressure to express the diffusive fluxes at the surface of arbitrary gas species X:

$$ \begin{aligned} J_{{\text{X}}}^{{{\text{mol}}}} = & - D_{\text{X}} c\frac{{\partial x_{\text{X}} }}{{\partial z}} \\ = & - \frac{{D_{\text{X}} }}{{RT}}\frac{{\partial P_{\text{X}} }}{{\partial z}} \\ \end{aligned} $$

(A2)

Remember that the adimensionalized diffusivity for gas species X is written $\Psi _{{\text{X}}} = \frac{{D_{{\text{X}}} }}{{D_{{{\text{O}}_{{\text{2}}} }} }}$. Thus, using Eq. [A1] and Fick’s law for a diluted gas: $- \frac{{2D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}}$ gives the flow of oxygen atoms:

$$ - \,\frac{{2D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}}\, = \, - \,D_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \frac{{\partial P_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\, - \,D_{{{\text{SiO}}}} \frac{{\partial P_{{{\text{SiO}}}} }}{{\partial z}}\, - \,2D_{{{\text{SiO}}_{{\text{2}}} }} \frac{{\partial P_{{{\text{SiO}}_{{\text{2}}} }} }}{{\partial z}}\, = \,J_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, + \,J_{{{\text{SiO}}}} \, + \,2J_{{{\text{SiO}}_{{\text{2}}} }} \, = \,J_{{\text{O}}} {\text{ }} $$

(A3)

Similarly, $- \frac{{2D_{{{\text{H}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}}$ gives the flow of hydrogen atoms and $- \frac{{D_{{{\text{Si}}}} }}{{RT}}\frac{{\partial P_{{{\text{Si}}}}^{{{\text{eff}}}} }}{{\partial z}}$ the flow of silicon atoms. We used expressions similar to Ratto et al.[15] and Vadon et al.[4] Hence, $P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}}$ and $P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}}$ are used to follow flows of atoms (with a multiplicator of two) to simplify expressions further in the model.

A reasoning on an elementary layer of thickness dz shows that $\frac{{\partial ^{2} \left( {P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} - P_{{{\text{Si}}}}^{{{\text{eff}}}} } \right)}}{{\partial z^{2} }} = 0$ because one atom of silicon for every two atoms of oxygen goes from the gas phase to the silica phase, using Fick’s law:

$$ \begin{aligned} P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} - P_{{Si}}^{{eff}} = \, & Az + B \\ P_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}}}} = \, & {\text{constant}} \\ \end{aligned} $$

(A4)

The net flow of oxygen atoms at the surface is equal to zero by the hypothesis, and hence by Fick’s law, at the surface:

$$ {\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}} = 0} $$

(A5)

The flow of silicon atoms at the surface is given by Fick’s law for diluted gases; then, using Eqs. [A5] and [A4]:

$$ {J_{{{\text{Si}}}} \, = \, - \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial P_{{{\text{Si}}}}^{{{\text{eff}}}} }}{{\partial z}}\, = \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}A} $$

(A6)

Thus, by looking at the conditions at the surface (z = 0) and at the top of the boundary layer ($z =\delta$), the molar flow of silicon per m² J_Si can be written using Eq. [A4]:

$$ \begin{array}{ll} {J_{{{\text{Si}}}} \, = \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\,\frac{{\Psi _{{{\text{Si}}}} \,P_{{{\text{Si}}}}^{{{\text{sat}}}} \, + \,\frac{1}{2}\,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\,\Psi _{{{\text{SiO}}}} \,P_{{{\text{SiO}}}}^{{{\text{surf}}}} \, - \,\frac{1}{2}\,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{surf}}}} }}{\delta }} \hfill \\ \end{array} $$

(A7)

Then, using thermodynamic data from JANAF,[7] we can neglect $\Psi _{{{\text{Si}}}} \,P_{{{\text{Si}}}}^{{{\text{sat}}}}$ and $\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{surf}}}}$ compared with $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ for $P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0}$ more than a 100 Pa like in the studied cases.

$$ {J_{{{\text{Si}}}} \, \approx \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\Psi _{{{\text{SiO}}}} \,P_{{{\text{SiO}}}}^{{{\text{surf}}}} }}{\delta }} $$

(A8)

Let’s remark that from Vadon et al.,[8] there is a similar equation for non-isothermal cases, which neglects the effect of Soret thermodiffusion:

$$ {J_{{{\text{Si}}}} \, \approx \,\frac{{\frac{1}{2}\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} \, + \,\frac{1}{2}\Psi _{{{\text{SiO}}}} \,p_{{{\text{SiO}}}}^{{{\text{surf}}}} }}{{R\int_{0}^{\delta } {\frac{{T(z^{\prime})}}{{D_{{{\text{O}}_{{\text{2}}} }} (z^{\prime})}}} dz^{\prime}}}} $$

(A9)

SiO₂(g) is a minority species (${P_{{{\text{SiO}}_{{\text{2}}} }} \, \ll \,P_{{{\text{SiO}}}} }$) at thermodynamic equilibrium. The gradient of ${P_{{{\text{SiO}}_{{\text{2}}} }} }$ does not play any role in the heterogeneous sublayer at thermodynamic equilibrium because its concentration is fixed by the reaction ${{\text{SiO}}_{2}{\text{(g)}} \leftrightarrows {\text{SiO}}_{2}{\text{(s/l)}}}$.

$$ {\frac{{\partial P_{{{\text{SiO}}_{{\text{2}}} }} }}{{\partial z}} = 0} $$

(A10)

By using the conditions at the intersection of the lower homogeneous sublayer (zero flow of oxygen atoms) and the heterogeneous sublayer like in Figure 2, we can thus find an analytical expression of the partial pressure of SiO(g) at the surface in Eq. [1]. In the lower homogeneous sublayer, the zero net flow of oxygen atoms at the surface and the absence of silica particles give the conservation of oxygen atoms:

$$ {\frac{{\partial P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} }}{{\partial z}} = 0} $$

(A11)

In the heterogeneous sublayer we have (using ${K_{{{\text{nucl}}}} }$ the equilibrium constant of the reaction ${{\text{SiO(g)}} + {\text{H}}_{{\text{2}}} {\text{O(g)}} \leftrightarrows {\text{SiO}}_{2}{\text{(s/l)}} + {\text{H}}_{{\text{2}}}{\text{(g)}}}$):

$$ p_\mathrm{{SiO}}=K_\mathrm{{nucl}}^{-1}p_\mathrm{{H_2}}/p_\mathrm{{H_2O}}$$

(A12)

Therefore, at at the limit between the homogeneous sublayer and the heterogeneous sublayer (the superscript “inf” is used for a variable located at this limit):

$$ {p_{{{\text{SiO}}}}^{{{\text{inf}}}} \, = \,K_{{{\text{nucl}}}}^{{ - 1}} \,p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{inf}}}} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} } $$

(A13)

With a derivation of the expression of ${\begin{array}{ll} {P_{{{\text{O}}_{{\text{2}}} }}^{{{\text{eff}}}} } \hfill \\ \end{array} }$ in $z=z_{inf}$ at the intersection between the homogeneous sublayer and the heterogeneous sublayer, using Eqs. [A1], [A12], [A10] and [A11]:

$$ {0\, = \,\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, - \,\Psi _{{{\text{SiO}}}} \,K_{{{\text{nucl}}}}^{{ - 1}} \,p_{{{\text{H}}_{{\text{2}}} }} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} } \right)\, + \,\frac{{\partial p_{{{\text{H}}_{{\text{2}}} }} }}{{\partial z}}\,\Psi _{{{\text{SiO}}}} \,K_{{{\text{nucl}}}}^{{ - 1}} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} } $$

(A14)

Then, with a simplification using the conservation of hydrogen atoms (Eqs. [A1] and [A4]):

$$ \begin{aligned} 0 & = \;\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \;p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} \; - \;\frac{{\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \Psi _{{{\text{SiO}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} }}K_{{{\text{nucl}}}}^{{ - 1}} \;p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \; - \;\Psi _{{{\text{SiO}}}} \;K_{{{\text{nucl}}}}^{{ - 1}} \;(p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \; - \;\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} )/\Psi _{{{\text{H}}_{{\text{2}}} }} } \right) \\ 0 & = \;\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} }} \;\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \;p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} \; - \;\Psi _{{{\text{SiO}}}} \;K_{{{\text{nucl}}}}^{{ - 1}} \;p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} } \right) \\ \end{aligned} $$

(A15)

which, given the fact that the gradient of H₂O is non-zero everywhere, using Eq. [A13] for ${p_{{{\text{SiO}}}}^{{{\text{inf}}}} }$, gives the expression:

$$ \begin{aligned} p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} & = \left( {\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \Psi _{{{\text{SiO}}}} }}{{K_{{{\text{nucl}}}} \Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \Psi _{{{\text{H}}_{{\text{2}}} }} }}} \right)^{{1/2}} \\ p_{{{\text{SiO}}}}^{{{\text{inf}}}} & = \left( {\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{K_{{{\text{nucl}}}} \Psi _{{{\text{SiO}}}} \Psi _{{{\text{H}}_{{\text{2}}} }} }}} \right)^{{1/2}} \\ & = \frac{{\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\Psi _{{{\text{SiO}}}} }}p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} \\ \end{aligned} $$

(A16)

Then, using the conservation of oxygen atoms in the lower homogeneous sublayer (Eq. [A1] combined with the integration of [A11] between $z=0$ and $z=z_{inf}$) and with the thermodynamic equilibrium, since in the presence of Si(l), $p_\mathrm{{H_2O}}^\mathrm{{surf}} \ll p_\mathrm{{SiO}}^\mathrm{{surf}}$ and everywhere $p_\mathrm{{SiO_2}} \ll p_\mathrm{{SiO}}$:

$$ {\Psi _{{{\text{SiO}}}} p_{{{\text{SiO}}}}^{{{\text{surf}}}} \, = \,\Psi _{{SiO}} \,p_{{{\text{SiO}}}}^{{{\text{inf}}}} \, + \,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{{{\text{inf}}}} } $$

(A17)

hence:

$$ {p_{{{\text{SiO}}}}^{{{\text{surf}}}} \, = \,2\left( {\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} \,\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{K_{{{\text{nucl}}}} \,\Psi _{{{\text{SiO}}}} \,\Psi _{{{\text{H}}_{{\text{2}}} }} }}} \right)^{{1/2}} } $$

(A18)

All other data can be reconstructed from known conditions at the surface and above the layer, including the thickness of the lower homogeneous sublayer, which is always non-zero.

Appendix B: Configuration of the boundary layer at the passivation threshold, isothermal case with zero oxygen atoms net flow

First, let’s remark that:

$$ {p_{{{\text{SiO}}}} \, = \,K_{{{\text{nucl}}}}^{{ - 1}} \frac{{p_{{{\text{H}}_{{\text{2}}} }} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\, < \,K_{{{\text{nucl}}}}^{{ - 1}} \frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} \,p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}} $$

(B1)

Now, let’s consider the equation of net zero oxygen atom flux at the surface, deriving Eq. [A1], the difference from the previous case of non-passivation being that this time Eq. [A12] of the thermodynamic equilibrium of the silica aerosols is also valid all the way down to z = 0:

$$ {\begin{aligned} {0 = - \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} - \Psi _{{{\text{SiO}}}} K_{{{\text{nucl}}}}^{{ - 1}} \frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{2} }}} \right)} \hfill \\ {= - \,\frac{{D_{{{\text{O}}_{{\text{2}}} }} }}{{RT}}\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} - \Psi _{{{\text{SiO}}}} \frac{{p_{{{\text{SiO}}}} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H}}_{{\text{2}}} }} }}} \right)} \hfill \\ \end{aligned} } $$

(B2)

Since in the presence of Si(l) ${p_{{{\text{SiO}}}} /p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} \gg 1}$ and ${\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} }$,${\Psi _{{{\text{SiO}}}} }$ and ${\Psi _{{{\text{H}}_{{\text{2}}} }} }$ are of the same order, from Eq. [B1], we deduce ($P_\mathrm{{H_2}}^\mathrm{{eff}}$ non-infinitesimal because ${P_{{{\text{H}}_{{\text{2}}} {\text{O}}}}^{0} }$ non-infinitesimal):

$$ {\left( {\Psi _{{{\text{H}}_{{\text{2}}} {\text{O}}}} \, - \,\Psi _{{{\text{SiO}}}} \frac{{p_{{{\text{SiO}}}} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H2}}}} }}} \right)\, \simeq \, - \,\Psi _{{SiO}} \frac{{p_{{{\text{SiO}}}} }}{{p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}\frac{{p_{{{\text{H}}_{{\text{2}}} }}^{{{\text{eff}},{\text{0}}}} }}{{\Psi _{{{\text{H}}_{{\text{2}}} }} p_{{{\text{H}}_{{\text{2}}} }} }}\, \ne \,0} $$

(B3)

Hence, ${\frac{{\partial p_{{{\text{H}}_{{\text{2}}} {\text{O}}}} }}{{\partial z}}\,(z = 0) = 0}$ and the flow is zero for all species at the surface. Using the relationship, [A4] we deduce that the concentrations are all uniform, equal to the concentrations at the surface. This is an absurdity because experimentally we have a passivation while ${p_{{{\text{SiO}}}}^{0} = 0}$ at injection. Therefore, we need to drop the hypothesis of the thermodynamic equilibrium of the silica aerosols with the gas phase at the passivation threshold in the isothermal case with zero oxygen atom net flow.

Appendix C: Configuration of the boundary layer at the passivation threshold, non-isothermal case with zero oxygen atom net flow

We suppose we have a case of injection of cold gases ($\frac{\partial T}{\partial z}<0$ ). We suppose that the ratio of diffusivities does not vary with temperature, which is realistic at these high temperatures (Vadon et al.[8]). This time, we rewrite Eqs. [A14] and [A15] at the surface:

$$\begin{aligned} \begin{array}{ll} 0&=\frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{H_2O}}- \frac{\Psi _\mathrm{{SiO}}K_\mathrm{{nucl}}^{-1}p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H_2}}p_\mathrm{{H_2O}}^2} \right) +\Psi _\mathrm{{SiO}} \frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T} \frac{\partial T}{\partial z} \frac{p_\mathrm{{H_2}}}{p_\mathrm{{H_2O}}} \end{array} \end{aligned}$$

(C1)

Using Eq. [B1] and remarking again that in the presence of Si(l) $p_\mathrm{{SiO}}/p_\mathrm{{H_2O}} \gg 1$ and $\Psi _\mathrm{{H_2O}}$,$\Psi _\mathrm{{SiO}}$ and $\Psi _\mathrm{{H_2}}$ are of the same order:

$$\begin{aligned} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \approx \frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T} \frac{\partial T}{\partial z} \frac{p_\mathrm{{H_2O}}}{p_\mathrm{{SiO}}} \frac{p_\mathrm{{H2}}\Psi _\mathrm{{H_2}}}{p_\mathrm{{H_2}}^\mathrm{{eff,0}}} \end{aligned}$$

(C2)

Let’s now express the gradient of SiO at the surface, starting from the zero flux of oxygen at the surface.

$$\begin{aligned} 0=\Psi _\mathrm{{SiO}}\frac{\partial p_\mathrm{{SiO}}}{\partial z} + \Psi _\mathrm{{H_2O}}\frac{\partial p_\mathrm{{H_2O}}}{\partial z} \end{aligned}$$

(C3)

and then using Eq. [C2]:

$$\begin{aligned} \frac{\partial p_\mathrm{{SiO}}}{\partial z} = -\frac{\Psi _\mathrm{{H_2O}}}{\Psi _\mathrm{{SiO}}} \frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T} \frac{\partial T}{\partial z} \frac{p_\mathrm{{H_2O}}}{p_\mathrm{{SiO}}} \frac{p_\mathrm{{H_2}}\Psi _\mathrm{{H_2}}}{p_\mathrm{{H_2}}^\mathrm{{eff,0}}} \end{aligned}$$

(C4)

Since $\frac{\partial K_\mathrm{{nucl}}^{-1}}{\partial T}>0$ and $\frac{\partial T}{\partial z}<0$, this means there must be $\frac{\partial p_\mathrm{{SiO}}}{\partial z}>0$ to be at the passivation threshold and thus an influx of silicon atoms in the form of SiO(g), which is absurd. Therefore, we need to drop the hypothesis of the thermodynamic equilibrium of the silica aerosols with the gas phase at the passivation threshold in the non-isothermal case with zero oxygen atom net flow.

We neglect the thermodiffusion effect in this demonstration, which is all the more understandable since the molecular mass of Ar (0.040 kg/mol) is near the molecular mass of SiO(g).

Appendix D: Configuration of the boundary layer at the passivation threshold, isothermal case with non-zero oxygen atom net flow

If we have a net density of flow of oxygen atoms J from the surface, we rewrite Eq. [A15] for the flow of oxygen atoms at the surface:

$$\begin{aligned} \begin{array}{ll} J_O &{}= -\frac{D_\mathrm{{O_2}}}{RT} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{H_2O}}-\Psi _\mathrm{{SiO}}K_\mathrm{{nucl}}^{-1} \frac{p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H_2}}p_\mathrm{{H_2O}}^2} \right) \\ &{}=-\frac{D_\mathrm{{O_2}}}{RT} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{H_2O}}-\Psi _\mathrm{{SiO}} \frac{p_\mathrm{{SiO}}}{p_\mathrm{{H_2O}}} \frac{p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H2}}p_\mathrm{{H_2}}} \right) \end{array} \end{aligned}$$

(D1)

Reasoning similarly as previously, neglecting the concentration of H₂O(g) at the surface to take into account the presence of Si(l):

$$\begin{aligned} \begin{array}{ll} J_O&\approx \frac{D_\mathrm{{O_2}}}{RT} \frac{\partial p_\mathrm{{H_2O}}}{\partial z} \left( \Psi _\mathrm{{SiO}} \frac{p_\mathrm{{SiO}}}{p_\mathrm{{H_2O}}} \frac{p_\mathrm{{H_2}}^\mathrm{{eff,0}}}{\Psi _\mathrm{{H_2}}p_\mathrm{{H_2}}} \right) =-\frac{D_\mathrm{{O_2}}}{RT}\Psi _\mathrm{{SiO}} \frac{\partial p_\mathrm{{SiO}}}{\partial z} =J_\mathrm{{Si}} \end{array} \end{aligned}$$

(D2)

Thus, at the passivation threshold, the oxygen must be supplied in the form of SiO(g) at the surface in the absorption/adsorption zones. This is absurd. Therefore, we need to drop the hypothesis of the thermodynamic equilibrium of the silica aerosols with the gas phase at the passivation threshold in the non-isothermal case with a positive oxygen atoms net flow towards the liquid.