Robust mixture regression modeling based on two-piece scale mixtures of normal distributions

Abstract

The inference of mixture regression models (MRM) is traditionally based on the normal (symmetry) assumption of component errors and thus is sensitive to outliers or symmetric/asymmetric lightly/heavy-tailed errors. To deal with these problems, some new mixture regression models have been proposed recently. In this paper, a general class of robust mixture regression models is presented based on the two-piece scale mixtures of normal (TP-SMN) distributions. The proposed model is so flexible that can simultaneously accommodate asymmetry and heavy tails. The stochastic representation of the proposed model enables us to easily implement an EM-type algorithm to estimate the unknown parameters of the model based on a penalized likelihood. In addition, the performance of the considered estimators is illustrated using a simulation study and a real data example.

1 Introduction

Mixture regression models (MRM) have broad applications in many fields including Engineering, Biology, Biometrics, Genetics, Medicine, Econometrics, Psychology and Marketing. These models are used to investigate the relationship between variables which come from several unknown latent homogeneous groups. The MRM was first introduced by Quandt (1972) and Quandt and Ramsey (1978) as switching regression models and Späth (1979) as cluster wise linear regression models. For a comprehensive survey see McLachlan and Peel (2000).

The maximum likelihood (ML) estimation of the parameter of the MRM is usually based on the normality assumption. In this regard, many extensive literatures are available. Applications include marketing (DeSarbo and Cron 1988; DeSarbo et al. 1992; Naik et al. 2007), finance (Engel and Hamilton 1990), economics (Cosslett and Lee 1985; Hamilton 1989), agriculture (Turner 2000), nutrition (Arellano-Valle et al. 2008), psychometrics (Liu et al. 2011), health (Maleki et al. 2019a), sports (Maleki et al. 2019b; Maleki and Wraith 2019), telecommunication (Hajrajabi and Maleki 2019; Maleki et al. 2020a; Mahmoudi et al. 2020). The estimators of the parameters of the normal MRM work well when the error distribution is indeed normal, but these estimators are very sensitive to the departures from normality. These departures often appear when the datasets contain outliers, or the error distribution displays an asymmetric shape or heavy tail. To deal with the departures from normality, many extensions of this classic model have been proposed. For example, Markatou (2000) proposed a weight function to robustly estimate the mixture regression parameters. Bai et al. (2012) used a robust estimation procedure based on M-regression estimation to robustly estimate the mixture regression parameters. Yao et al. (2014) studied the MRM assuming that the error terms follow a t distribution which is a generalization of the mixture of t distribution proposed by Peel and McLachlan (2000). Also, Song et al. (2014) introduced a robust model and method to estimate the parameters of MRM when the error distribution is a mixture of Laplace distribution. Another robust MRM based on the skew normal distribution has been studied by Liu and Lin (2014). Recently, Zeller et al. (2016) proposed a unified robust MRM when the error term follows scale mixtures of skew-normal distributions and examined the performance of the estimation procedure. In this regard, Doğru and Arslan (2017) investigated a MRM based on the skew-t distribution as a special case of the model proposed by Zeller et al. (2016).

In this paper, a general class of robust mixture regression models based on two-piece scale mixtures of normal (TP-SMN) distributions proposed by Maleki and Mahmoudi (2017) is presented. The class of TP-SMN distributions is a rich class of distributions that includes the well-known family of scale mixtures of normal (SMN; Andrews and Mallows 1974) distributions which covers symmetrical/asymmetrical and lightly/heavy-tailed distributions (see also e.g., Arellano-Valle et al. (2005), Maleki and Mahmoudi (2017), Moravveji et al. (2019), Bazrafkan et al. (2021), Hoseinzadeh et al. (2021), Maleki et al. (2021, 2022) and Maleki (2022)). Here, the family of two-piece scale mixtures of normal distributions is considered and this class of distribution is extended to the mixture regression setting.

In addition, the class of TP-SMN distributions is an attractive family for modeling the skewed and heavy-tailed data sets in a much wider range (see e.g., Maleki et al. (2019c, 2020b), Ghasami et al. (2020) and Maleki (2022)). So, our mixture regression model based on the two-piece scale mixtures of normal (TP-SMN-MRM) is very flexible and robust, and can efficiently deal with skewness and heavy-tailed-ness in the MRM setting. In this work, a penalized likelihood function is also considered to set the best number of component and after using the stochastic representation of the suggested model, two extensions of the EM-algorithm (Dempster et al. 1977) are developed, including the ECM algorithm (Meng and Rubin 1993) and the ECME algorithm (Liu and Rubin 1994).

The rest of this paper is organized as follows. In Sect. 2, the researchers review some properties of the TP-SMN distributions. In Sect. 3, the TP-SMN-MRM is introduced and maximum penalized estimates (MPL) of the proposed model based on an EM-type algorithm are obtained. In Sect. 4, numerical studies involving simulations with some applications of the proposed models and estimates on real datasets are presented. In addition, comparison is made with well-known normal competitor and then symmetrical/asymmetrical and lightly/heavy-tailed scale mixtures of skew-normal (SMSN; Branco and Dey, 2001) family in Zeller et al. (2016) which had been studied previously. Some conclusive remarks are presented in Sect. 4.

2 TP-SMN distributions

2.1 Preliminaries

The two-piece scale mixtures of normal (TP-SMN) family of distributions were constructed by the celebrated well-known scale mixtures of normal (SMN; Andrews and Mallows 1974) family, based on the methodology of constructing the general two-piece distributions. The SMN random variable $X$ has the following probability density function (pdf) and denoted by $X \sim SMN \left(\mu ,\sigma ,{\varvec{\nu}}\right)$:

$${f}_{SMN}\left(x; \mu ,\sigma ,{\varvec{\nu}}\right)={\int }_{0}^{\infty }\phi \left(x; \mu ,k\left(u\right){\sigma }^{2}\right)dH\left(u;{\varvec{\nu}}\right), x\in R,$$

(1)

where $\phi \left(\cdot ; \mu ,{\sigma }^{2}\right)$ represents the pdf of $N\left(\mu ,{\sigma }^{2}\right)$ distribution, $H\left(\cdot ;{\varvec{\nu}}\right)$ is the cumulative distribution function (cdf) of the scale mixing random variable $U$ which was indexed by parameter ${\varvec{\nu}}$. By letting $k(u)=1/u$, some suitable mathematical properties (such as appropriate hierarchical forms in the classical inferences and closed form posteriors in the Bayesian inferences, (see e.g., Zeller et al. (2016) and Barkhordar et al. (2020)) are obtained. Also $X \sim SMN \left(\mu ,\sigma ,{\varvec{\nu}}\right)$ has the stochastic representation given by

$$X=\mu +\sigma {k}^{1/2}\left(U\right)W,$$

(2)

where $W$ is a standard normal random variable that is assumed independent of $U$.

The TP-SMN is a rich family of distributions that covers the symmetric/asymmetric lightly/heavy-tailed distributions and its main members are two-piece normal (TP-N or Epsilon-Skew-Normal: Mudholkar and Hutson 2000; Maleki and Nematollahi 2017), two-piece t (TP-T), and two-piece slash (TP-SL) distributions.

Definition 2.1

Following general two-piece distributions from Arellano-Valle et al. (2005), the pdf of random variable $Y \sim TP-SMN\left(\mu ,\sigma ,\gamma ,{\varvec{\nu}}\right)$, for $y\in R$ is represented as.

$$ f\left( {y;\mu ,\sigma ,\gamma ,\varvec{\nu} } \right) = \left\{ {\begin{array}{ll} {2\left( {1 - \gamma } \right)f_{{SMN}} \left( {y;\mu ,\sigma \left( {1 - \gamma } \right),\varvec{\nu} } \right),y \le \mu ,} & {y \le \mu ,} \\ {2\gamma f_{{SMN}} \left( {y;\mu ,\sigma \gamma ,\varvec{\nu} } \right),} & {y > \mu ,} \\ \end{array} } \right. $$

(3)

where $\gamma \in \left(\mathrm{0,1}\right)$ is the slant parameter, ${f}_{SMN}\left(\cdot ; \mu ,\sigma ,{\varvec{\nu}}\right)$ is given by (1).

Proposition 2.1

Let $Y \sim TP-SMN\left(\mu ,\sigma ,\gamma ,{\varvec{\nu}}\right)$, then $Y$ has a stochastic representation given by.

$$Y=\mu -\sigma \left(1-\gamma \right){S}_{1}{k}^{1/2}\left(U\right)\left|W\right|+\sigma \gamma {S}_{2}{k}^{1/2}\left(U\right)\left|W\right|,$$

(4)

where $W$ is a standard normal random variable that is assumed independent of scale mixing random variable $U \sim H\left(u;{\varvec{\nu}}\right)$, and under reparameterization ${\sigma }_{1}=\sigma \left(1-\gamma \right)$ and ${\sigma }_{2}=\sigma \gamma$, ${\varvec{S}}={\left({S}_{1},{S}_{2}\right)}^{\top } \sim \mathrm{Multinomial}(1,\frac{{\sigma }_{1}}{{\sigma }_{1}+{\sigma }_{2}},\frac{{\sigma }_{2}}{{\sigma }_{1}+{\sigma }_{2}})$, with the following probability mass function (pmf):

$$P\left({\varvec{S}}={\varvec{s}}\right)=\frac{{\sigma }_{1}^{s}{\sigma }_{2}^{1-s}}{{\sigma }_{1}+{\sigma }_{2}}; {s}_{1}=1-{s}_{2}=s=\mathrm{0,1}.$$

Proof

The pdf of the $Y \sim TP-SMN\left(\mu ,\sigma ,\gamma ,{\varvec{\nu}}\right)$ in (3) is a piecewise function, which according to the Eq. (2), on its top piece, the $2{f}_{SMN}\left(y; \mu ,\sigma {\left(1-\gamma \right)},{\varvec{\nu}}\right) \mathrm{for} y\le \mu ,$ pdf, has the following stochastic representation.

$$\left[\mu -\sigma \left(1-\gamma \right){k}^{1/2}\left(U\right)\left|W\right|\right] \sim SMN\left(\mu ,\sigma \left(1-\gamma \right),{\varvec{\nu}}\right)I\left(-\infty ,\mu \right],$$

and also on its bottom piece, $2{f}_{SMN}\left(y; \mu ,\sigma {\gamma },{\varvec{\nu}}\right)\mathrm{ for} y>\mu ,$ has the following stochastic representation

$$\left[\mu +\sigma \gamma {k}^{1/2}\left(U\right)\left|W\right|\right] \sim SMN\left(\mu ,\sigma \gamma ,{\varvec{\nu}}\right)I\left(\mu ,+\infty \right).$$

So the random variable $Y$ can obey from the top piece with probability $\left(1-\gamma \right)\left(=\frac{{\sigma }_{1}}{{\sigma }_{1}+{\sigma }_{2}}\right)$ when ${S}_{1}=1$, and can obey from the bottom piece with probability $\left(\gamma \right)\left(=\frac{{\sigma }_{2}}{{\sigma }_{1}+{\sigma }_{2}}\right)$ when ${S}_{2}=1$. So combining these stochastic representations and latent variable ${\varvec{S}}={\left({S}_{1},{S}_{2}\right)}^{\top }$ conclude the (4) ${\ominus }$

Proposition 2.2

Let $Y \sim TP-SMN(\mu ,\sigma ,\gamma ,{\varvec{\nu}})$,

• $E\left(Y\right)=\mu -b\Delta ;$

• $\mathrm{Var}\left(Y\right)={\sigma }^{2}\left[{c}_{2}{k}_{2}\left({\varvec{\nu}}\right)-{b}^{2}{c}_{1}^{2}\right]$,

where $\Delta =\sigma \left(1-2\gamma \right)$, $b=\sqrt{2/\pi }{k}_{1}\left({\varvec{\nu}}\right)$, ${c}_{r}={\gamma }^{r+1}+{\left(-1\right)}^{r}{\left(1-\gamma \right)}^{r+1}$ and ${k}_{r}\left({\varvec{\nu}}\right)=E\left({U}^{-r/2}\right)$, for which $U$ is the scale mixing variable in (2).

Proof

Considering the Proposition 2.4. from Maleki and Mahmoudi (2017), these results have been obtained ${\ominus }$

More statistical properties along with the details of the TP-SMN family were introduced by Arellano-Valle et al. (2005) and Maleki and Mahmoudi (2017).

Proposition 2.3

The TP-SMN distributions with the pdf given in (3) can be represented as the two-component mixture of left and right half SMN distributions with special component probabilities as follows:

$$f\left(y; \mu ,{\sigma }_{1},{\sigma }_{2},{\varvec{\nu}}\right)=2\frac{{\sigma }_{1}}{{\sigma }_{1}+{\sigma }_{2}}{f}_{SMN}\left(y; \mu ,{\sigma }_{1},{\varvec{\nu}}\right){I}_{(-\infty ,\mu ]}\left(y\right)+2\frac{{\sigma }_{2}}{{\sigma }_{1}+{\sigma }_{2}}{f}_{SMN}\left(y; \mu ,{\sigma }_{2},{\varvec{\nu}}\right){I}_{(\mu ,+\infty )}\left(y\right),$$

where as in (4), ${\sigma }_{1}=\sigma \left(1-\gamma \right)$, ${\sigma }_{2}=\sigma \gamma$, and the scale parameter $\sigma$ and skewness parameter $\gamma$ in (3) are recovered in the form of $\sigma ={\sigma }_{1}+{\sigma }_{2}$ and $\gamma ={\sigma }_{2}/\left({\sigma }_{1}+{\sigma }_{2}\right)$.

Proof

Considering the pdf (3) and reparameterization ${\sigma }_{1}=\sigma \left(1-\gamma \right)$ and ${\sigma }_{2}=\sigma \gamma$, the results have been obtained.

Note that in the symmetric positions ($\gamma =0.5$), the TP-SMN distributions are the well-known SMN distributions attributed to Andrews and Mallows (1971).

2.2 Examples of the TP-SMN distributions

In this section, some particular cases of TP-SMN distributions are considered. Let $Y \sim TP-SMN(\mu ,\sigma ,\gamma ,{\varvec{\nu}})$, different members of the TP-SMN family accordance of different distributions for the scale mixing variable $U$ in (4) are as follows:

• Two-piece normal (TP-N):

In this case U=1, with the following pdf,

$$f\left(y; \mu ,\sigma ,\gamma \right)=\left\{\begin{array}{ll}2\left(1-\gamma \right)\phi \left(y;\mu ,{\sigma }^{2}{\left(1-\gamma \right)}^{2}\right) , y\le \mu ;\\ \\ 2\gamma \phi \left(y;\mu ,{\sigma }^{2}{\gamma }^{2}\right) , y>\mu .\end{array}\right.$$

• Two-piece t (TP-T) with $\nu$ degrees of freedom:

In this case $U\sim \mathrm{ Gamma}\left(\frac{\nu }{2},\frac{\nu }{2}\right)$, for which ${k}_{r}\left({\varvec{\nu}}\right)={\left(\frac{\nu }{2}\right)}^{r/2}\frac{\Gamma \left(\frac{\nu -r}{2}\right)}{\Gamma \left(\frac{\nu }{2}\right)}, \nu >r$, with the following pdf,

$$f\left(y; \mu ,\sigma ,\gamma ,{\varvec{\nu}}\right)=\left\{\begin{array}{c}2\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\Gamma \left(\frac{\nu }{2}\right)\sqrt{\pi \nu }\sigma }{\left(1+\frac{1}{\nu }{\left(\frac{y-\mu }{\sigma \left(1-\gamma \right)}\right)}^{2}\right)}^{- \frac{\nu +1}{2}} , y\le \mu ;\\ \\ 2\frac{\Gamma \left(\frac{\nu +1}{2}\right)}{\Gamma \left(\frac{\nu }{2}\right)\sqrt{\pi \nu }\sigma }{\left(1+\frac{1}{\nu }{\left(\frac{y-\mu }{\sigma \gamma }\right)}^{2}\right)}^{- \frac{\nu +1}{2}} , y>\mu .\end{array}\right.$$

• Two-piece slash (TP-SL):

In this case $U\sim \mathrm{Beta}\left(\nu ,1\right)$, for which ${k}_{r}\left({\varvec{\nu}}\right)=\frac{2\nu }{2\nu -r}, \nu >\frac{r}{2}$, with the following pdf,

$$ f\left( {y;\mu ,\sigma ,\gamma ,\varvec{\nu} } \right) = \left\{ {\begin{array}{ll} {2\nu \left( {1 - \gamma } \right)\smallint _{0}^{1} u^{{\nu - 1}} \phi \left( {y;\mu ,u^{{ - 1}} \sigma ^{2} \left( {1 - \gamma } \right)^{2} } \right)du,} & {y \le \mu ;} \\ {2\nu \gamma \smallint _{0}^{1} u^{{\nu - 1}} \phi \left( {y;\mu ,u^{{ - 1}} \sigma ^{2} \gamma ^{2} } \right)du,} & { y> \mu .} \\ \end{array}} \right. $$

Note that the TP-N is a light-tailed density while the TP-T and TP-SL are heavy-tailed densities. Some asymmetry (with various values of shape parameter $\gamma =0.3 \mathrm{and} 0.9$,) and symmetry ($\gamma =0$) graphs of the light-tailed TP-N and heavy-tailed TP-T densities with various scale ($\sigma =\mathrm{1,2},3$) and degrees of freedom ($\nu =\mathrm{2,4},40$) parameters are provided in Fig. 1.

Fig. 1

Some typical graphs of the light-tailed TP-N densities (left) and heavy-tailed TP-T densities (right) with various shape, scale and degrees of freedom parameters

Proposition 2.4

Let $Y \sim TP-SMN(\mu ,\sigma ,\gamma ,{\varvec{\nu}})$. Considering the stochastic representation (4) and $k(U)=1/U$, conditional expectation $\tau =E\left[S\left.U\right|y\right]$ for the TP-SMN distribution members are given by:

• TP-N: $\tau ={I}_{\left.\left(-\infty ,\mu \right.\right]}\left(y\right),$

• TP-T: $\tau =\frac{\nu +1}{\nu +d} ,$

• TP-SL: $\tau =\frac{2\nu +1}{d}\frac{{P}_{1}\left(\nu +3/2,d/2\right)}{{P}_{1}\left(\nu +1/2,{d}_{j}/2\right)} ,$

where $d={\left(\frac{y-\mu }{{{m}_{1}\sigma }_{1}+{{m}_{2}\sigma }_{2}}\right)}^{2}$, for which ${m}_{1}={I}_{\left.\left(-\infty ,\mu \right.\right]}\left(y\right)$ and ${m}_{2}=1-{m}_{1}$, and ${P}_{x}\left(a,b\right)$ denote the distribution function of the Gamma $\left(a,b\right)$ distribution evaluated at $x$. Note the conditional expectations in Proposition 2.4 are used in the E-step of the EM-algorithm to obtain the MPL estimates.

3 Mixture Regression model using the TP-SMN distributions

3.1 The TP-SMN-MRM

In this section, the mixture regression model where the random errors follow the two-piece scale mixtures of normal distributions (TP-SMN-MRM) is examined. It is defined as

$$\left.Y\right|\left({Z}_{\mathrm{g}}=1\right)={{\varvec{x}}}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}+{\varepsilon }_{\mathrm{g}},\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\mathrm{g}=1,\dots ,G,$$

(5)

where $G$ is the number of components (groups) in mixture regression model, ${Z}_{\mathrm{g}}=1, \mathrm{g}=1,\dots ,G$, set for the gth component, such that $P\left({Z}_{\mathrm{g}}=1\right)={\pi }_{\mathrm{g}}, \mathrm{g}=1,\dots ,G$, ${{\varvec{\beta}}}_{\mathrm{g}}={({\beta }_{1\mathrm{g}},\dots , {\beta }_{p\mathrm{g}})}^{\top }$ is a vector of regression coefficient (fixed explanatory variables) parameters, $Y$ is a response variable, and ${\varvec{x}}={({x}_{1},\dots , {x}_{p})}^{\top }$ is a vector of fixed explanatory variables which is independent of the random errors ${\varepsilon }_{\mathrm{g}}$. In the presented methodology ${\varepsilon }_{\mathrm{g}} \sim TP-SMN\left({\mu }_{\mathrm{g}},{\sigma }_{\mathrm{g}},{\gamma }_{\mathrm{g}},{{\varvec{\nu}}}_{\mathrm{g}}\right), \mathrm{g}=1,\dots ,G,$ where ${\mu }_{\mathrm{g}}={b}_{\mathrm{g}}\left(1-2{\gamma }_{\mathrm{g}}\right){\sigma }_{\mathrm{g}} (\mathrm{or} {\mu }_{\mathrm{g}}={b}_{\mathrm{g}}{\Delta }_{\mathrm{g}}, {\Delta }_{\mathrm{g}}=\left(1-2{\gamma }_{\mathrm{g}}\right){\sigma }_{\mathrm{g}})$ for which ${b}_{\mathrm{g}}=\sqrt{2/\pi }{k}_{1}\left({{\varvec{\nu}}}_{\mathrm{g}}\right)$, and ${k}_{1}\left(\cdot \right)$ was defined in proposition 2.2. Also, note that due to the Proposition 2.2., the errors have zero mean $\left(E\left({\varepsilon }_{\mathrm{g}}\right)=0\right)$. For computational convenience, the parameter of mixing distribution $H\left(\cdot ;{{\varvec{\nu}}}_{\mathrm{g}}\right), \mathrm{g}=1,\dots ,G$ are assumed equal as ${{\varvec{\nu}}}_{1}=\dots ={{\varvec{\nu}}}_{\mathrm{G}}={\varvec{\nu}}$. The identifiability of finite mixtures has been studied by Teicher (1963) to ensure that our MRM is identifiable. In addition, in this study, the maximum likelihood inferential paradigm is used and so label switching has no practical implications and arises only as a theoretical identifiability issue that can usually be resolved by specifying some ordering on the mixing proportions in the form of ${\pi }_{1}>\dots >{\pi }_{G}.$ Note that in cases where mixing proportions are equal, a total ordering on other model parameters can be considered.

Using an auxiliary random variable ${\varvec{Z}}={\left({Z}_{1},\dots ,{Z}_{G}\right)}^{\top }$ (independent of ${\varvec{x}}$), for which ${Z}_{\mathrm{g}}=1, \mathrm{g}=1,\dots ,G$, set the regression model in (5) for the gth component, such that $P\left({Z}_{\mathrm{g}}=1\right)={\pi }_{\mathrm{g}}, \mathrm{g}=1,\dots ,G$, then the density of response variable $Y$ is given by

$${f}_{MR}\left(y; {\varvec{x}},{\varvec{\Theta}}\right)=\sum_{\mathrm{g}=1}^{G}{\pi }_{\mathrm{g}}f\left(y; {\varvec{x}},{{\varvec{\theta}}}_{\mathrm{g}}\right),$$

(6)

where $f\left(\cdot ; {\varvec{x}},{{\varvec{\theta}}}_{\mathrm{g}}\right)$ is the pdf of $TP-SMN\left({{\varvec{x}}}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}+{\mu }_{\mathrm{g}},{\sigma }_{\mathrm{g}},{\gamma }_{\mathrm{g}},{\varvec{\nu}}\right)$ and ${{\varvec{\theta}}}_{\mathrm{g}}=\left({{\varvec{\beta}}}_{\mathrm{g}}^{\top },{\sigma }_{\mathrm{g}},{\gamma }_{\mathrm{g}},{{\varvec{\nu}}}^{\top }\right),$ $\mathrm{g}=1,\dots ,G$ or according to the representation of Proposition 2.3, ${{\varvec{\theta}}}_{\mathrm{g}}=\left({{\varvec{\beta}}}_{\mathrm{g}}^{\top },{\sigma }_{1\mathrm{g}},{\sigma }_{2\mathrm{g}},{{\varvec{\nu}}}^{\top }\right), \mathrm{g}=1,\dots ,G$ and ${\varvec{\Theta}}={\left({\pi }_{1},\dots ,{\pi }_{G},{{\varvec{\theta}}}_{1}^{\top },\dots ,{{\varvec{\theta}}}_{G}^{\top }\right)}^{\top }$. In the viewpoint of classical inferences, using the observations $\left({Y}_{i},{{\varvec{x}}}_{i}\right), i=1,\dots ,n$, the parameter ${\varvec{\Theta}}$ is traditionally estimated by maximization of the log-likelihood of an IID sample ${\left({\varvec{Y}},{\varvec{x}}\right)}^{\top }$, where ${\varvec{Y}}={\left({Y}_{1},\dots ,{Y}_{n}\right)}^{\top }$ and ${\varvec{x}}={\left({{\varvec{x}}}_{1}^{\top },\dots ,{{\varvec{x}}}_{n}^{\top }\right)}^{\top }$ as

$$\mathbf{\ell}\left({\varvec{\Theta}}\right)=\sum_{i=1}^{n}\mathrm{log}{f}_{MR}\left({y}_{i}; {{\varvec{x}}}_{i},{\varvec{\Theta}}\right).$$

In applications, existence of too many components imply that the mixture models may overfit the data and yield poor interpretations, while existence of too few components, imply that the mixture models may not be flexible enough to approximate the true underlying data structure. So, estimating the true number of components in the mixture models is very important. In order to solve this issue, we have used a penalized log-likelihood function to avoid overestimating or underestimating them, given by

$${\mathbf{\ell}}_{P}\left({\varvec{\Theta}}\right)=\mathbf{\ell}\left({\varvec{\Theta}}\right)-n\lambda {D}_{f.MR}\sum_{\mathrm{g}=1}^{G}\left[\mathrm{log}\left(\epsilon +{\pi }_{\mathrm{g}}\right)-\mathrm{log}\left(\epsilon \right)\right],$$

(7)

where $\mathbf{\ell}\left({\varvec{\Theta}}\right)$ is the log-likelihood function, $\lambda$ is a tuning parameter, $\epsilon$ is a very small positive number, say ${10}^{-6}$, and ${D}_{f.\mathrm{MR}}$ is the number of free parameters for each component. For the TP-N-MRM, TP-T-MRM and TP-SL-MRM, each component has ${D}_{f.MR}= p+ 4$, and for TP-CN-MRM each component has ${D}_{f.MR}= p+ 5$ number of free parameters. Huang et al. (2017) had used this penalty term in the structure of likelihood function of the mixture of Gaussian model.

To obtain the proposed maximizer given by penalized log-likelihood (7), there is not an explicit solution, so an EM-type algorithm (Dempster et al. 1977; McLachlan and Peel, 2000) is considered.

3.2 The observed information matrix

In this section, the observed information matrix of the TP-SMN-MRM, defined as $\mathbf{J}\left(\left.{\varvec{\Theta}}\right|{\varvec{y}}\right)=-\frac{{\partial }^{2}{\mathbf{\ell}}_{P}\left({\varvec{\Theta}}\right)}{\partial{\varvec{\Theta}}\partial {{\varvec{\Theta}}}^{\top }}$, where ${\mathbf{\ell}}_{P}\left({\varvec{\Theta}}\right)=\sum_{i=1}^{n}{\mathbf{\ell}}_{Pi}\left({\varvec{\Theta}}\right)$, for which

$${\mathbf{\ell}}_{Pi}\left({\varvec{\Theta}}\right)=\mathrm{log}\sum_{\mathrm{g}=1}^{G}{\pi }_{\mathrm{g}}f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)-\lambda {D}_{f.MR}\sum_{\mathrm{g}=1}^{G}\left[\mathrm{log}\left(\epsilon +{\pi }_{\mathrm{g}}\right)-\mathrm{log}\left(\epsilon \right)\right].$$

It is well known that, under some regularity conditions, the covariance matrix of the MPL estimates $\widehat{{\varvec{\Theta}}}$ can be approximated by the inverse of $\mathbf{J}\left(\left.{\varvec{\Theta}}\right|{\varvec{y}}\right)$. So, the square roots of its diagonal elements have been considered as the standard deviations of the MPL estimates in the real applications. Thus, following Basford et al. (1997) and Lin et al. (2007),

$$\mathbf{J}\left(\left.{\varvec{\Theta}}\right|{\varvec{y}}\right)=\sum_{i=1}^{n}{\widehat{{\varvec{j}}}}_{i}^{\top }{\widehat{{\varvec{j}}}}_{i},$$

where ${\widehat{{\varvec{j}}}}_{i}={\left.\frac{\partial {\mathbf{\ell}}_{Pi}\left({\varvec{\Theta}}\right)}{\partial{\varvec{\Theta}}}\right|}_{{\varvec{\Theta}}=\widehat{{\varvec{\Theta}}}}$, and now consider the vector ${\widehat{{\varvec{j}}}}_{i}$ which is partitioned into components corresponding to all the parameters in ${\varvec{\Theta}}$ as

$${\widehat{{\varvec{j}}}}_{i}={\left({\widehat{j}}_{i,{\pi }_{1}},\dots ,{\widehat{j}}_{i,{\pi }_{G-1}},{\widehat{{\varvec{j}}}}_{i,{{\varvec{\beta}}}_{1}}^{\top },\dots ,{\widehat{{\varvec{j}}}}_{i,{{\varvec{\beta}}}_{G}}^{\top },{\widehat{j}}_{i,{\sigma }_{1}},\dots ,{\widehat{j}}_{i,{\sigma }_{G}},{\widehat{j}}_{i,{\gamma }_{1}},\dots ,{\widehat{j}}_{i,{\gamma }_{G}},{\widehat{{\varvec{j}}}}_{i,{\varvec{\nu}}}^{\top }\right)}^{\top },$$

where its coordinate elements for $\mathrm{g}=1,\dots ,G$ are given by

$${\widehat{j}}_{i,{\pi }_{\mathrm{g}}}=\frac{f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)-f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{G},{\varvec{\nu}}\right)}{{f}_{MR}\left({y}_{i}|{{\varvec{x}}}_{i},{\varvec{\Theta}}\right)}-\lambda {D}_{f.MR}\left[\frac{1}{\epsilon +{\pi }_{\mathrm{g}}}-\frac{1}{\epsilon +{\pi }_{\mathrm{G}}}\right],$$

$${\widehat{{\varvec{j}}}}_{i,{{\varvec{\beta}}}_{\mathrm{g}}}=\frac{{\pi }_{\mathrm{g}}{D}_{{{\varvec{\beta}}}_{\mathrm{g}}}\left(f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right)}{{f}_{MR}\left({y}_{i}; {{\varvec{x}}}_{i},{\varvec{\Theta}}\right)}, {\widehat{j}}_{i,{\sigma }_{\mathrm{g}}}=\frac{{\pi }_{\mathrm{g}}{D}_{{\sigma }_{\mathrm{g}}}\left(f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right)}{{f}_{MR}\left({y}_{i}; {{\varvec{x}}}_{i},{\varvec{\Theta}}\right)}, {\widehat{j}}_{i,{\gamma }_{\mathrm{g}}}=\frac{{\pi }_{\mathrm{g}}{D}_{{\gamma }_{\mathrm{g}}}\left(f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right)}{{f}_{MR}\left({y}_{i}; {{\varvec{x}}}_{i},{\varvec{\Theta}}\right)},$$

and

$${\widehat{{\varvec{j}}}}_{i,{\varvec{\nu}}}=\frac{\sum_{\mathrm{g}=1}^{G}{\pi }_{\mathrm{g}}{D}_{{\varvec{\nu}}}\left(f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right)}{{f}_{MR}\left({y}_{i}; {{\varvec{x}}}_{i},{\varvec{\Theta}}\right)},$$

for which ${D}_{\boldsymbol{\alpha }}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]=\partial f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)/\partial \boldsymbol{\alpha }$, for $\boldsymbol{\alpha }={{\varvec{\beta}}}_{\mathrm{g}},{\sigma }_{\mathrm{g}},{\gamma }_{\mathrm{g}},{\varvec{\nu}}$. To determine the coordinate elements of the ${\widehat{{\varvec{j}}}}_{i}$, let us define ${\zeta }_{i\mathrm{g}}\left(\omega \right)={E}_{H}\left[{u}^{\omega }\mathrm{exp}\left(-\frac{1}{2}u{m}_{i\mathrm{g}}\right)\right]$, where ${m}_{i\mathrm{g}}=\frac{{d}_{i\mathrm{g}}^{2}}{{\sigma }_{\mathrm{g}}^{2}{\rho }_{\mathrm{g}}^{2}}$ is the Mahalanobis distances for which ${d}_{i\mathrm{g}}={y}_{i}-{{\varvec{x}}}_{i}^{\mathrm{\top }}{{\varvec{\beta}}}_{\mathrm{g}}-{\mu }_{\mathrm{g}}$, and hereafter ${\rho }_{\mathrm{g}}=1-{\gamma }_{\mathrm{g}}$ if ${d}_{i\mathrm{g}}\le 0$ and ${\rho }_{\mathrm{g}}={\gamma }_{\mathrm{g}}$ if ${d}_{i\mathrm{g}}>0$. So, we have

$${D}_{{{\varvec{\beta}}}_{\mathrm{g}}}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]=\frac{2}{\sqrt{2\pi }}\left[\frac{1}{{\sigma }_{\mathrm{g}}^{3}}{\zeta }_{i\mathrm{g}}\left(\frac{3}{2}\right){d}_{i\mathrm{g}}{{\varvec{x}}}_{i}\right]$$

$${D}_{{\sigma }_{\mathrm{g}}}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]=\frac{2}{\sqrt{2\pi }}\left[\frac{1}{{\sigma }_{\mathrm{g}}^{4}{\rho }_{\mathrm{g}}^{2}}\left({d}_{i\mathrm{g}}+{\mu }_{\mathrm{g}}/2\right){\zeta }_{i\mathrm{g}}\left(\frac{3}{2}\right)-\frac{1}{{\sigma }_{\mathrm{g}}^{2}}{\zeta }_{i\mathrm{g}}\left(\frac{1}{2}\right)\right],$$

$${D}_{{\gamma }_{\mathrm{g}}}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]=\frac{2}{\sqrt{2\pi }}\left(\mathrm{sign}\left({d}_{i\mathrm{g}}\right)\frac{{d}_{i\mathrm{g}}}{{\sigma }_{\mathrm{g}}^{3}{\rho }_{\mathrm{g}}^{3}}-\frac{b}{{\sigma }_{\mathrm{g}}^{2}{\rho }_{\mathrm{g}}^{2}}\right){\zeta }_{i\mathrm{g}}\left(\frac{3}{2}\right),$$

where ${\zeta }_{i\mathrm{g}}\left(\cdot \right)$ in the above relations, and also ${D}_{{\varvec{\nu}}}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]$ for the TP-SMN-MRM members, are given by:

• (i) TP-N-MRM:

  $${\zeta }_{i\mathrm{g}}\left(\omega \right)=\mathrm{exp}\left(-\frac{1}{2}{m}_{i\mathrm{g}}\right),$$
  $${D}_{{\varvec{\nu}}}\left[f\left({y}_{i}|{{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]=0;$$

• (ii) TP-T-MRM:

  $${\zeta }_{i\mathrm{g}}\left(\omega \right)=\frac{{2}^{\omega }{\nu }^{\nu /2}\Gamma \left(\nu /2+\omega \right)}{\Gamma \left(\nu /2\right){\left(\nu +{m}_{i\mathrm{g}}\right)}^{\nu /2+\omega }} ,$$
  $${D}_{{\varvec{\nu}}}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]=\frac{1}{2}f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\left[\psi \left(\frac{\nu +1}{2}\right)-\psi \left(\frac{\nu }{2}\right)-\frac{1}{\nu }-\mathrm{log}\left(1+\frac{{m}_{i\mathrm{g}}}{\nu }\right)+\left(\nu +1\right)\frac{{m}_{i\mathrm{g}}+{\mu }_{\mathrm{g}}\left[1+\nu \psi \left(\frac{\nu -1}{2}\right)-\nu \psi \left(\frac{\nu }{2}\right)\right]\sqrt{{m}_{i\mathrm{g}}}}{{\nu }^{2}+\nu {m}_{i\mathrm{g}}}\right];$$

• (iii) TP-SL-MRM:

  $${\zeta }_{li\mathrm{g}}\left(\omega \right)=\frac{\nu\Gamma \left(\nu +\omega \right)}{{\left({m}_{i\mathrm{g}}/2\right)}^{\nu +\omega }}{P}_{1}\left(\nu +\omega ,{m}_{i\mathrm{g}}/2\right),$$
  $${D}_{{\varvec{\nu}}}\left[f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},{\varvec{\nu}}\right)\right]={\nu }^{-1}f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},\nu \right)+\nu f\left({y}_{i}; {{\varvec{x}}}_{i},{{\varvec{\theta}}}_{\mathrm{g}},\nu -1\right);$$

where ${P}_{x}\left(a,b\right)$ denotes the distribution function of the Gamma $\left(a,b\right)$ distribution evaluated at $x$.

3.3 Maximum penalized estimation of the model parameters

In this section, an efficient EM-type algorithm for MPL estimation of the parameters of TP-SMN-MRM is developed using an incomplete-data framework. To do this procedure, beside all the observations $\left({Y}_{i},{{\varvec{x}}}_{i}\right), i=1,\dots ,n$ defines the latent random vector as ${{\varvec{Z}}}_{i}={\left({Z}_{i1},\dots ,{Z}_{iG}\right)}^{\top }, i=1,\dots ,n$, where

$$ Z_{{ig}} = \left\{ {\begin{array}{ll} {1,\quad {\text{if}}\;{\text{the}}\;i{\text{th}}\;{\text{observation}}\;{\text{belongs}}\;{\text{the}}\;g{\text{th}}\;{\text{component}};} \hfill \\ {0,\quad {\text{otherwise}}.} \hfill \\ \end{array} } \right. $$

Therefore, under the above approach the latent random vector ${{\varvec{Z}}}_{i}, i=1,\dots ,n$ has the following multinomial pmf:

$$P\left({{\varvec{Z}}}_{i}={{\varvec{z}}}_{i}\right)=\prod_{\mathrm{g}=1}^{G}{\pi }_{\mathrm{g}}^{{z}_{i\mathrm{g}}}; i=1,\dots ,n,$$

such that $\sum_{\mathrm{g}=1}^{G}{\pi }_{\mathrm{g}}=1$, ${\pi }_{\mathrm{g}}>0,\mathrm{ g}=1,\dots ,G$ and

$${Y}_{i}\left|{z}_{i\mathrm{g}}=1\right. \sim TP-SMN\left({{\varvec{x}}}_{i}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}+{\mu }_{\mathrm{g}},{\sigma }_{\mathrm{g}},{\gamma }_{\mathrm{g}},{\varvec{\nu}}\right), \mathrm{g}=1,\dots ,G.$$

So, using the stochastic representation of the TP-SMN family given by (4), the following hierarchical representation is considered

$${Y}_{i}\left|{U}_{i}\right.,{S}_{ij}=1, {Z}_{i\mathrm{g}}=1 \begin{array}{c}\begin{array}{c} \\ {\underset{\sim}{ind.}}\end{array}\\ \\ \end{array} N\left({{\varvec{x}}}_{i}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}+{\mu }_{\mathrm{g}},{u}_{i}^{-1}{\sigma }_{\mathrm{g}j}^{2} \right){I}_{{A}_{i}}{\left({y}_{i}\right)}^{2-j}{I}_{{A}_{i}^{c}}{\left({y}_{i}\right)}^{j-1},$$

$${U}_{i}\left|{Z}_{i\mathrm{g}}=1\right. \begin{array}{c}\begin{array}{c} \\{\underset{\sim}{ind.}}\end{array}\\ \\ \end{array} H\left({u}_{i};\boldsymbol{ }{\varvec{\nu}}\right), $$

$$\left.{{\varvec{S}}}_{i}\right|{Z}_{i\mathrm{g}}=1 \begin{array}{c}\begin{array}{c} \\ {\underset{\sim}{ind.}}\end{array}\\\\ \end{array}\mathrm{ Multinomial}\left(1,\frac{{\sigma }_{\mathrm{g}1}}{{\sigma }_{\mathrm{g}1}+{\sigma }_{\mathrm{g}2}},\frac{{\sigma }_{\mathrm{g}2}}{{\sigma }_{\mathrm{g}1}+{\sigma }_{\mathrm{g}2}}\right),$$

$${{\varvec{Z}}}_{i}\begin{array}{c}\begin{array}{c} \\ {\underset{\sim}{i{.}i{.}d.}} \end{array}\\\\ \end{array} \mathrm{Multinomial}\left(1,{\pi }_{1},\dots ,{\pi }_{G}\right),$$

(8)

for $i=1,\dots ,n$, $\mathrm{g}=1,\dots ,G$ and $j=\mathrm{1,2}$, where ${A}_{i}=\left.\left(-\infty ,{{\varvec{x}}}_{i}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}+{\mu }_{\mathrm{g}}\right.\right]$ and $N\left(\cdot \right){I}_{A}\left(\cdot \right)$ denotes the univariate normal distribution truncated on the interval $A$.

The hierarchical representation (8) of the TP-SMN-MRM is used to obtain the MPL estimates via an EM-algorithm called ECME algorithm. It is a generalization of the ECM algorithm introduced by Meng and Rubin (1993). It can be obtained by replacing some CM-steps which maximize the constrained expected complete-data penalized log-likelihood function with steps that maximize the correspondingly constrained actual likelihood function.

Let ${\varvec{y}}={({y}_{1},\dots , {y}_{n})}^{\top }$, ${\varvec{u}}={({u}_{1},\dots , {u}_{n})}^{\top }$,${\varvec{s}}={({{\varvec{s}}}_{1}^{\top },\dots , {{\varvec{s}}}_{n}^{\top })}^{\top }$ and ${\varvec{z}}={({{\varvec{z}}}_{1}^{\top },\dots , {{\varvec{z}}}_{n}^{\top })}^{\top }$ for which ${{\varvec{s}}}_{i}={({s}_{i1}, {s}_{i2})}^{\top }$, and ${{\varvec{z}}}_{i}={({z}_{i1},\dots , {z}_{iG})}^{\top }$ for $i=1,\dots ,n$, so considering the complete data ${{\varvec{y}}}_{c}={({{\varvec{y}}}^{\top },{{\varvec{u}}}^{\top },{{\varvec{s}}}^{\top }, {{\varvec{z}}}^{\top })}^{\top }$ and using the hierarchical representation in (8) of the TP-SMN-MRM, the complete log-likelihood function is given by

$${\mathbf{\ell}}_{cp}\left({\varvec{\Theta}}|{{\varvec{y}}}_{c}\right)=c+\sum_{i=1}^{n}\sum_{\mathrm{g}=1}^{G}{z}_{i\mathrm{g}}\mathrm{log}{\pi }_{\mathrm{g}}-\sum_{i=1}^{n}\sum_{\mathrm{g}=1}^{G}{z}_{i\mathrm{g}}\mathrm{log}\left({\sigma }_{\mathrm{g}1}+{\sigma }_{\mathrm{g}2}\right)-\frac{1}{2}\sum_{i=1}^{n}\sum_{\mathrm{g}=1}^{G}\sum_{j=1}^{2}\frac{{z}_{i\mathrm{g}}{s}_{ij}{u}_{i}}{{\sigma }_{\mathrm{g}j}^{2}}{\left({Y}_{i}-{{\varvec{x}}}_{i}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}-{\mu }_{\mathrm{g}}\right)}^{2}-n\lambda {D}_{f.MR}\sum_{\mathrm{g}=1}^{G}\left[\mathrm{log}\left(\epsilon +{\pi }_{\mathrm{g}}\right)-\mathrm{log}\left(\epsilon \right)\right],$$

where $c$ is a constant and independent of ${\varvec{\Theta}}$.

Letting ${\widehat{{\varvec{\Theta}}}}^{\left(k\right)}$ the estimates of ${\varvec{\Theta}}$ at the kth iteration, the conditional expectation of complete log-likelihood function ignoring constant is given by

$$ \begin{aligned} Q\left( {\varvec{\Theta} |\widehat{\varvec{\Theta }}^{{\left( k \right)}} } \right) & = \sum\limits_{{i = 1}}^{n} {\sum\limits_{{{\text{g}} = 1}}^{G} {\hat{z}_{{i{\text{g}}}}^{{\left( k \right)}} } } {\text{log}}\pi _{{\text{g}}} - \sum\limits_{{i = 1}}^{n} {\sum\limits_{{{\text{g}} = 1}}^{G} {\hat{z}_{{i{\text{g}}}}^{{\left( k \right)}} } } {\text{log}}\left( {\sigma _{{{\text{g}}1}} + \sigma _{{{\text{g}}2}} } \right) \\ & \quad - \frac{1}{2}\sum\limits_{{i = 1}}^{n} {\sum\limits_{{{\text{g}} = 1}}^{G} {\sum\limits_{{j = 1}}^{2} {\frac{{\widehat{{zsu}}_{{i{\text{g}}j}}^{{\left( k \right)}} }}{{\sigma _{{{\text{g}}j}}^{2} }}} } } \left( {Y_{i} - {\varvec{x}}_{i}^{{ \top }} {\varvec{\beta}}_{{\text{g}}} - \mu _{{\text{g}}} } \right)^{2}\\ & - n\lambda D_{{f.MR}} \sum\limits_{{{\text{g}} = 1}}^{G} {\left[ {{\text{log}}\left( {\epsilon + \pi _{{\text{g}}} } \right) - {\text{log}}\left( \epsilon \right)} \right]} , \\ \end{aligned} $$

where ${\widehat{z}}_{i\mathrm{g}}^{\left(k\right)}=E\left[\left.{Z}_{i\mathrm{g}}\right|{y}_{i}, {\widehat{{\varvec{\Theta}}}}^{\left(k\right)}\right]$ is determined by using known properties of conditional expectation, as

$${\widehat{z}}_{i\mathrm{g}}^{\left(k\right)}=\frac{{\widehat{\pi }}_{\mathrm{g}}^{\left(k\right)}f\left({y}_{i}; {{\varvec{x}}}_{i},{\widehat{{\varvec{\theta}}}}_{\mathrm{g}}^{\left(k\right)}\right)}{\sum_{\mathrm{g}=1}^{G}{\widehat{\pi }}_{\mathrm{g}}^{\left(k\right)}f\left({y}_{i}; {{\varvec{x}}}_{i},{\widehat{{\varvec{\theta}}}}_{\mathrm{g}}^{\left(k\right)}\right)}; i=1,\dots ,n, \mathrm{g}=1,\dots G,$$

for which $f\left(\cdot ; {\varvec{x}},{{\varvec{\theta}}}_{\mathrm{g}}\right)$ was defined in the (6), and ${\widehat{zsu}}_{i\mathrm{g}j}^{\left(k\right)}=E\left[{Z}_{i\mathrm{g}}\left.{S}_{ij}{U}_{i}\right|{y}_{i}, {\widehat{{\varvec{\Theta}}}}^{\left(k\right)}\right]={\widehat{z}}_{i\mathrm{g}}^{\left(k\right)}{\widehat{\tau }}_{i\mathrm{g}j}^{\left(k\right)}$, for which ${\widehat{\tau }}_{i\mathrm{g}j}^{\left(k\right)}$ values can be easily derived from the Proposition 2.4.

Now, this EM-type algorithm (ECME) is described to obtain the MPL estimates of the parameters of TP-SMN-MRM.

E-step Given ${\varvec{\Theta}}={\widehat{{\varvec{\Theta}}}}^{\left(k\right)}$ and using the above calculations, we compute ${\widehat{z}}_{i\mathrm{g}}^{\left(k\right)}$ and ${\widehat{zsu}}_{i\mathrm{g}j}^{\left(k\right)}$ for$j = 1, 2$, $\mathrm{g}=1,\dots ,G$ and$i = 1, . . . , n$.

CM-step Update ${\widehat{{\varvec{\Theta}}}}^{\left(k+1\right)}$ by maximizing $Q\left(\left.{\varvec{\Theta}}\right|{\widehat{{\varvec{\Theta}}}}^{\left(k\right)}\right)$ over ${\varvec{\Theta}}$ with the following updates:

Update ${\widehat{\pi }}_{\mathrm{g}}; \mathrm{g}=1,\dots ,G$, with given $\epsilon$ is very close to zero, by using straightforward calculations, we obtain

$${\widehat{\pi }}_{\mathrm{g}}^{\left(k+1\right)}=Max\left\{0,\frac{1}{1-\lambda {GD}_{f.MR}}\left[\frac{\sum_{i=1}^{n}{\widehat{z}}_{i\mathrm{g}}^{\left(k\right)}}{n}-\lambda {D}_{f.MR}\right]\right\}.$$

The penalized log-likelihood and the number of effective clusters (with non-zero proportions) evolved during the iterations of the ECME algorithm works as follows: it starts with a pre-specified large number of components (for example G = 10 in the last section), and whenever a mixing probability is shrunk to zero by CM-step (for example ${\widehat{\pi }}_{\mathrm{g}}^{\left(k\right)}<0.01 \mathrm{for g}=\mathrm{1,2},\dots G\mathrm{ in the last section}$), the corresponding component is deleted, thus fewer components are retained for the remaining ECME iterations. Here we abuse the notation $G$ for the number of components at beginning of each ECME iteration, and through the updating process, $G$ becomes smaller and smaller. For a given ECME iteration step, it is possible that none, one, or more than one components are deleted (see e.g., Huang et al. (2017)). Note that our proposed penalized likelihood method is significantly different from various Bayesian methods in the objective function and theoretical properties. When a component is eliminated, i.e., the mixing weight of that component is shrunk to zero, the objective function of our proposed method changes continuously. So above estimation of ${\pi }_{\mathrm{g}}$ is different of any maximum a posteriori (MAP) estimation of them.

Update ${\widehat{{\varvec{\beta}}}}_{\mathrm{g}}; \mathrm{g}=1,\dots ,G$, by

$${\widehat{{\varvec{\beta}}}}_{\mathrm{g}}^{\left(k+1\right)}={\left(\sum_{i=1}^{n}{\widehat{\varrho }}_{i\mathrm{g}}^{\left(k\right)}{{\varvec{x}}}_{i}{{\varvec{x}}}_{i}^{\top }\right)}^{-1}\sum_{i=1}^{n}{\widehat{\varrho }}_{i\mathrm{g}}^{\left(k\right)}\left({Y}_{i}-{\widehat{\mu }}_{\mathrm{g}}^{\left(k\right)}\right){{\varvec{x}}}_{i},$$

where ${\widehat{\varrho }}_{i\mathrm{g}}^{\left(k\right)}={\widehat{zsu}}_{i\mathrm{g}1}^{\left(k\right)}/{\sigma }_{\mathrm{g}1}^{2}+{\widehat{zsu}}_{i\mathrm{g}2}^{\left(k\right)}/{\sigma }_{\mathrm{g}2}^{2}$.

Update ${\widehat{\sigma }}_{\mathrm{g}j}; \mathrm{g}=1,\dots ,G, j=\mathrm{1,2}$, by solving the following equations

$$\sum_{i=1}^{n}{\widehat{z}}_{i\mathrm{g}}^{\left(k\right)}{\left({\sigma }_{\mathrm{g}1}+{\sigma }_{\mathrm{g}2}\right)}^{-1}=\sum_{i=1}^{n}\left[{\sigma }_{\mathrm{g}j}^{-3}{\widehat{zsu}}_{i\mathrm{g}j}^{\left(k\right)}{\widehat{e}}_{i\mathrm{g}}^{2\left(k+1\right)}+{\left(-1\right)}^{j+1}b{\widehat{\varrho }}_{i\mathrm{g}}^{\left(k\right)}{\widehat{e}}_{i\mathrm{g}}^{\left(k+1\right)}\right],$$

where ${e}_{i\mathrm{g}}={Y}_{i}-{{\varvec{x}}}_{i}^{\top }{{\varvec{\beta}}}_{\mathrm{g}}-b\left({\sigma }_{\mathrm{g}1}-{\sigma }_{\mathrm{g}2}\right)$. Note that the above equation is a cubic equation for each ${\sigma }_{\mathrm{g}j}$ in the form of ${\sigma }_{\mathrm{g}j}^{3}+{c}_{1}{\sigma }_{\mathrm{g}j}+{c}_{2}=0$ such that ${c}_{1},{c}_{2}<0$, so this cubic equation has unique root in the $\left(0,+\infty \right)$ interval.

CML-step In the last step, update $\widehat{{\varvec{\nu}}}$ by maximizing the actual marginal log-likelihood function, as

$${{\varvec{\nu}}}^{\left(k+1\right)}={\mathrm{argmax}}_{{\varvec{\nu}}}\sum_{i=1}^{n}\mathrm{log}\sum_{\mathrm{g}=1}^{G}{\widehat{\pi }}_{\mathrm{g}}^{\left(k\right)}f\left({y}_{i}; {{\varvec{x}}}_{i},{\widehat{{\varvec{\beta}}}}_{\mathrm{g}}^{\left(k+1\right)},{\widehat{\sigma }}_{\mathrm{g}1}^{\left(k+1\right)},{\widehat{\sigma }}_{\mathrm{g}2}^{\left(k+1\right)},{\varvec{\nu}}\right),$$

where $f\left(\cdot ; {\varvec{x}},{{\varvec{\theta}}}_{\mathrm{g}}\right)$ is defined in (6).

The proposed ECME algorithm works as follows: it starts with a pre-specified large number of components, and due to updating ${\widehat{\pi }}_{\mathrm{g}}^{\left(k+1\right)}, \mathrm{g}=1,\dots ,G$, whenever a mixing probability is shrunk to zero, the corresponding component is deleted, and as result fewer components are retained for the remaining EM iterations. The iterations are repeated until a suitable convergence rule is satisfied, e.g., $\left|\mathbf{\ell}\left({\widehat{{\varvec{\Theta}}}}^{\left(k+1\right)}\right)/{\mathbf{\ell}}\left({\widehat{{\varvec{\Theta}}}}^{\left(k\right)}\right)-1\right|\le {10}^{-4}$ where ${\mathbf{\ell}}\left(\cdot \right)$ is the actual log-likelihood, was defined in the Sect. 3.1.

3.4 Selection of tuning parameter and model selection

To obtain the final estimate of the mixture model by maximizing (7), one needs to select the tuning parameter $\lambda$. For standard LASSO (Tibshirani 1996) and SCAD (Fan and Li 2001) penalized regressions, there are many methods to select $\lambda$, and in this work we have used BIC function in Wang et al. (2007). Here we define a $BIC\left(\lambda \right)$ value as

$$BIC\left(\lambda \right)=\sum_{i=1}^{n}\mathrm{log}\sum_{\mathrm{g}=1}^{\widehat{G}}{\widehat{\pi }}_{\mathrm{g}}f\left({y}_{i}; {{\varvec{x}}}_{i},{\widehat{{\varvec{\beta}}}}_{\mathrm{g}},{\widehat{\sigma }}_{\mathrm{g}1},{\widehat{\sigma }}_{\mathrm{g}2},\widehat{{\varvec{\nu}}}\right)-\frac{1}{2}\widehat{G}{D}_{f.MR}\mathrm{log}n,$$

and estimate $\lambda$ by

$$\widehat{\lambda }={\mathrm{argmax}}_{\lambda }BIC\left(\lambda \right),$$

where $\widehat{G}$ is the estimate of the number of TP-SMN-MRM components.

The $BIC\left(\lambda \right)$ value is useful for selecting an appropriate model with the best number of components, for the given data with adequate sample size, but in this study, four criteria are also considered in simulations in order to select the best fitted MRM. They are maximized log-likelihood values, the Akaike information criterion (AIC; Akaike 1974), the Bayesian information criterion (BIC; Schwarz 1978) and the efficient determination criterion (EDC; Resende and Dorea 2016). The above criteria have the general following form

$$k{r}_{n}-2\mathbf{\ell}\left(\left.\widehat{{\varvec{\Theta}}}\right|{\varvec{y}}\right),$$

where $\mathbf{\ell}\left(\left.\widehat{{\varvec{\Theta}}}\right|{\varvec{y}}\right)$ is the actual log-likelihood, $k$ is the number of free parameters that has to be estimated in the model and the penalty term ${r}_{n}$ is a convenient sequence of positive numbers. Additionally, the values ${r}_{n}=2$, ${r}_{n}=\mathrm{log}n$ and ${r}_{n}=0.2\sqrt{n}$, for the AIC, BIC and EDC are used respectively. Fewer values of the AIC, BIC and EDC criteria indicate choosing the best model.

4 Numerical study

In this section, some simulations and a real dataset to show the satisfactory performances of the proposed model are considered.

4.1 Simulations

In this section, three parts of simulations are presented. In the first part, we have some simulations for TP-SMN-MRM parameters recovery by simulating from them and estimating the proposed MPL estimates to show the satisfaction of the proposed estimations. In the second part, by choosing some various sample sizes, the consistency properties of the proposed model and estimation methods are shown. Finally, in the third part of simulations, using an asymmetry and heavy-tailed distribution that belong to the class of scale mixtures of skew-normal (SMSN) distributions, a similar MRM to ours is generated to show the performances (robustness, misspecification and right classification) of our models to model the data with unknown structure. Note that in the all parts of numerical studies, the search range of tuning parameter is interval of $(\mathrm{0,10})$, and the maximum initial (pre-specified) number of components is set to be 10.

4.1.1 Part1: recovery of parameters

The following TP-SMN-MRM with two components was considered in three scenarios. In the first one, both components had skewed behavior between week up to moderate, in the second one, both components had skewed behavior between moderate up to strong, and in the third one, a component had skewed behavior between week up to moderate and another component had skewed behavior between moderate up to strong. The simulated model is given by

$$ \left\{ {\begin{array}{ll} {Y_{i} = {\varvec{x}}_{i}^{ \top } {\varvec{\beta}} _{1} + \varepsilon _{1} ,{\text{with}}\;{\text{Probability}}\;\pi } \hfill \\ {Y_{i} = {\varvec{x}}_{i}^{\top } {\varvec{\beta}} _{2} + \varepsilon _{2} ,{\text{with}}\;{\text{Probability}}\;1 - \pi ,} \hfill \\ \end{array} } \right. $$

where ${{\varvec{x}}}_{i}^{\top }=\left(1,{x}_{i1},{x}_{i2}\right)$ for $i=1,\dots ,n$, such that ${x}_{i1}\sim U(\mathrm{0,1})$ and independent of ${x}_{i2}\sim N(\mathrm{0,1})$, and, ${\varepsilon }_{1}$ and ${\varepsilon }_{2}$ follow the TP-SMN distributions, as the assumption given in (5).

700 samples were generated from the above model with $n=400$ from the TP-N, TP-T and TP-SL models the following parameter values:

$${{\varvec{\beta}}}_{1}={\left({\beta }_{01},{\beta }_{11},{\beta }_{21}\right)}^{\top }={\left(1,\mathrm{3,5}\right)}^{\top },\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }{{\varvec{\beta}}}_{2}={\left({\beta }_{02},{\beta }_{12},{\beta }_{22}\right)}^{\top }={\left(5,-2,-6\right)}^{\top },\boldsymbol{ }\boldsymbol{ }\boldsymbol{ }\pi =0.4, {\sigma }_{1}={\sigma }_{2}=2,$$

and, ${\gamma }_{1}=0.45, {\gamma }_{2}=0.55$ (for the first scenario), ${\gamma }_{1}=0.05, {\gamma }_{2}=0.95$ (for the second scenario) and ${\gamma }_{1}=0.1, {\gamma }_{2}=0.6$ (for the third scenario), for which $\nu =4$ has used in the TP-T-MRM and TP-SL-MRM.

The maximum likelihood estimation via the proposed ECME algorithm for each sample was calculated, and the average values of MPL estimates and the corresponding standard deviations (SD) of the MPL estimates across all samples were computed and recorded in Tables 1, 2 and 3. The results indicated us that all the point estimates are quite accurate in all the three considered scenarios. Thus, the results suggest that the proposed EM-type algorithm produced satisfactory estimates of the proposed models on the all proposed scenarios.

Table 1 Mean and standard deviations (SD) of MPL estimates based on 700 samples from the TP-SMN-MRM with true values of parameters in the parentheses (Scenario 1)

Table 2 Mean and standard deviations (SD) of MPL estimates based on 700 samples from the TP-SMN-MRM with true values of parameters in the parentheses (Scenario 2)

Table 3 Mean and standard deviations (SD) of ML estimates based on 700 samples from the TP-SMN-MRM with true values of parameters in the parentheses (Scenario 3)

4.1.2 Part2: consistency of estimations and convergence of BIC

In the further simulation study with various sample sizes, generating the following model given by

$$\left\{\begin{array}{ll}{Y}_{i}=1-2{x}_{i1}+{\varepsilon }_{1}, with Probability \pi =1/2 \\ {Y}_{i}=2+3{x}_{i1}+{\varepsilon }_{2}, with Probability 1-\pi =1/2,\end{array}\right.$$

for $i=1,\dots ,n$, such that ${x}_{i1}\sim U(\mathrm{0,1})$, and, ${\varepsilon }_{1}$ and ${\varepsilon }_{2}$ follow the TP-SMN distributions with the following parameters and as the assumption given in (5),

$${\sigma }_{1}=1, {\sigma }_{2}=2, {\gamma }_{1}=0.25, {\gamma }_{2}=0.75, \nu =3.$$

1000 samples from the above model for sample sizes $n=50, 100, 250$ and $n=450$ were generated respectively. Table 4 reports the mean squared errors (MSE) and the absolute bias (Bias) of the MPL estimates in each sample $j\left(=1,\dots ,1000\right)$ in a way that for each parameter $\theta \in{\varvec{\Theta}}$, is defined respectively by.

Table 4 Absolute bias and MSE (in parentheses) of point estimates

$$Bias\left(\theta \right)=\frac{1}{1000}\sum_{j=1}^{1000}\left|{\widehat{\theta }}_{j}-{\theta }_{j}\right|\mathrm{ and }MSE \left(\theta \right)=\frac{1}{1000}\sum_{j=1}^{1000}{\left({\theta }_{j}-{\widehat{\theta }}_{j}\right)}^{2}.$$

As it can be noticed from the Table 4, by increasing the sample size, the absolute biases and MSE of the MPL estimates tend to approach zero. These results indicate that the proposed MPL estimates of the TP-SMN-MRM based on the ECME algorithm do possess good consistency properties.

We consider further simulations with 100 samples with lengths of $n=300$ from the above TP-SMN-MRM, where ${\varepsilon }_{1}$ and ${\varepsilon }_{2}$ follow the proposed TP-T distribution. We plotted the $BIC(\lambda )$ for each sample during the ECME algorithm in Fig. 2 (left) and also Barplot of mean of estimated numbers of components from 100 samples in Fig. 2 (right). Diagrams of $BIC(\lambda )$ show their monotonic behavior and converging during the ECME algorithm. Also Barplot of mean of estimated numbers of components show the true number of components (which is two-components) has the most frequency, which are convergence of the number of components during the ECME algorithm. These results together show the performances of the proposed estimates of the work with reasonability of choosing the best number of components.

Fig. 2

$\mathrm{BIC}(\uplambda )$ of 100 samples during the ECME algorithm (left) and Barplot of mean of estimated numbers of components from 100 samples (right)

4.1.3 Part3: robustness, misspecification and classification

In this part, the performance of the TP-SMN-MRM to cluster observations with unknown structure in the weakly and strongly separated datasets (homogeneous and heterogeneous, respectively) was investigated. In addition, a comparison was made to find the applicability of some classic procedures to choose between the underlying TP-SMN-MRM for simulated data from another similar model which is an MRM based on the skew-t distributions (Branco and Day, 2001). To do the proposed simulations, the number of components $(G=2)$, sample size ($n=700$) and the following parameter values were fixed in the two schemes strongly and weakly separated models. Then, without loss of generality, 700 samples from the proposed skew-t-MRM were artificially generated and, for each sample, the Normal-MRM, TP-N-MRM, TP-T-MRM and the TP-SL-MRM were fitted. The proposed skew-t-MRM had the asymmetric and heavy tails behavior and it was expected that the TP-T-MRM and (possibly the TP-SL-MRM) has the best fitting on them to have a robust inference.

Also, the quality of the classification of each mixture model is important. In this study, the methodology proposed by Liu and Lin (2014) is followed. The correct classification rate ($CCR$) index is based on the estimate of the posterior probability (${\widehat{z}}_{i\mathrm{g}}$) assigned to each subject, i.e., the maximum value of the ${\widehat{z}}_{i\mathrm{g}}, \mathrm{g}=1,\dots ,G$ determines that an observation ${y}_{i}$ belongs to its corresponding component of the mixture. So for tth ($t=1,\dots ,700$) sample of the 700 samples, the number of correct allocations (which are known in simulations) divided by the sample size $n=700$, has been embedded as ${CCR}_{t}$ and mean of correct classification rate ($MCCR$) was computed using the mathematical average of correct classification rate in the form of $MCCR=\frac{1}{700}\sum_{t=1}^{700}{CCR}_{t}$. Also mean of the number of the correct allocation ($MCA$) which is the average number of correct allocations on 700 samples has been considered.

Two schemes of the strongly and weakly separated models are given by:

• Strongly separated model:

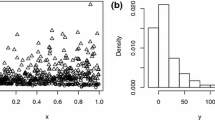
  $$\left\{\begin{array}{l}{Y}_{i}=3+2{x}_{i1}+{\varepsilon }_{1}, with \;Probability\; \pi =0.3 \\ {Y}_{i}=-1-2{x}_{i1}+{\varepsilon }_{2}, with \;Probability \;1-\pi =0.7 ,\end{array}\right.$$

  for $i=1,\dots ,700$, such that ${x}_{i1}\sim U(\mathrm{0,1})$, and, ${\varepsilon }_{1}$ and ${\varepsilon }_{2}$ follow the skew-t distributions with zero mean, scale parameters ${\sigma }_{1}=1, {\sigma }_{2}=1$, shape parameters ${\lambda }_{1}=-3, {\lambda }_{2}=+3$, and degrees of freedom $\nu =4$. Figure 3 shows a scatter plot and a histogram for one of these simulated samples.

• Weakly separated model:

  $$\left\{\begin{array}{l}{Y}_{i}=3+2{x}_{i1}+{\varepsilon }_{1}, with Probability \; \pi =0.3 \\ {Y}_{i}=1-1{x}_{i1}+{\varepsilon }_{2}, with Probability \; 1-\pi =0.7 ,\end{array}\right.$$

for $i=1,\dots ,700$, such that ${x}_{i1}\sim U(\mathrm{0,1})$, and, ${\varepsilon }_{1}$ and ${\varepsilon }_{2}$ follow the skew-t distributions with zero mean, scale parameters ${\sigma }_{1}=2, {\sigma }_{2}=1$, shape parameters ${\lambda }_{1}=-5, {\lambda }_{2}=+5$, and degrees of freedom $\nu =2$. Figure 3 shows scatter plots and histograms for one of these simulated samples on each scheme.

Fig. 3

a Histogram and b scatterplot of the strongly separated simulated skew-t MRM. c Histogram and d scatterplot of the weakly separated simulated skew-t MRM

Fitting the several models that belong to the TP-SMN-MRM on the generated datasets from the skew-t-MRM in the both strongly and weakly separated schemes, the MCA and standard deviation (SD) of correct allocations on 700 samples, as well as the MCCR are presented in Table 5. Note larger values indicate better classification results.

Table 5 Correctness of classification analysis of the TP-SMN-MRM for 700 samples artificially generated from the skew-t-MRM

For each fitted model, the AIC, EDC and the log-likelihood criterion were computed. The percentage rates at which the best model was chosen for each criterion are recorded in Table 6. Note that as it was expected, all the criteria have satisfactory behavior, in that, they favor the best model, that is, the TP-T-MRM. Figure 4 shows the AIC values for each sample and the best (expected and robust) TP-T-MRM and TP-N-MRM.

Table 6 Percentages that the best fitted TP-SMN-MRM are chosen using some model selection criteria

Fig. 4

AIC values of 700 samples with blue line for TP-T-MRM and black dashed line for TP-N-MRM

4.2 Application

In this section, the proposed models and methods on datasets which the first represent the perception of musical tones by musicians are illustrated as they are described in Cohen (1984), and the second represent the US census population and poverty percentage estimates by county.

4.2.1 Tone perception data

In the well-known data, a pure fundamental tone with electronically generated overtones added was played to a trained musician. In this experiment, the subjects were asked to tune an adjustable tone to one octave above the fundamental tone and their perceived tone was recorded versus the actual tone. A number of 150 trials from the same musician were recorded in this experiment. The overtones were determined by a stretching ratio which is the ratio between the adjusted and the fundamental tone. The experiment was designed to find out how the tuning ratio affects the perception of the tone and decide which of the two musical perception theories was reasonable. So we consider the actual tune ratio as the explanatory variable $x$ and perceived tone ratio as the response variable $Y$.

The scatter plot and the histogram of the perceived tone ratio are plotted in Fig. 5. These plots demonstrate that there are two groups with separate trends in the dataset and they have a non-normal distribution. Based on the realizations of the data, Cohen (1984) discussed two hypotheses which were called the interval memory hypothesis and the partial matching hypothesis. Many have considered and modeled this data using a mixture of linear regressions framework, see DeVeaux (1989), Viele and Tong (2002), Hunter and Young (2012), Yao et al. (2014), Zeller et al. (2016) and Doğru and Arslan (2017). Zeller et al. (2016) and Doğru and Arslan (2017) propose the robust mixture regression using the SMSN distributions which are similar counterparts of the TP-SMN distributions.

Fig. 5

a Scatterplot and b histogram of the tone perception data

The proposed TP-SMN-MRM was expanded to model the data. Using the ECME algorithm, the MPL estimates together with their corresponding standard errors (based on the square root of invers of the observed information matrix form Sect. 3.2) of the parameters from the Normal-MRM, TP-N-MRM, TP-T-MRM, TP-SL-MRM and the skew-t-MRM (as asymmetry heavy-tailed competitor) are presented in Table 7. According to the recorded model selection criteria, numbers and elapsed time (s) of algorithm iterations (N.I. and E.T., respectively) in Table 8, the best fitted TP-SMN-MRM of the tone perception data is the TP-T-MRM. Observing the estimated parameters of the best fitted model, it is concluded that the model which is based on the asymmetric distribution with heavier tails provides a better fit compared to the ordinary, normal and the TP-N distribution.

Table 7 MPL estimation results with their standard errors for fitting several TP-SMN-MRM and skew-t-MRM on the tone perception data

Table 8 Some model selection criteria, numbers and elapsed time of algorithm iterations (N.I. and E.T., respectively) for the fitted TP-SMN-MRM and skew-t-MRM of the tone perception data

Figure 6 shows the scatter plot of the data set with the lightly and heavy tailed fitted TP-N-MRM and TP-T-MRM, respectively, and clustering of the dataset. Clustering of the data based on the fitted skew-t-MRM is also in the Fig. 7. In Fig. 8, we plot the profile log-likelihood of the parameter $\nu$ for the TP-T-MRM and skew-t-MRM in all of ECME algorithm iterations.

Fig. 6

The scatterplots and clustering of the tone perception data based on the lightly and heavily tailed fitted TP-N-MRM and TP-T-MRM

Fig. 7

The scatter plot and clustering of the tone perception data based on the skew-t-MRM

Fig. 8

Plots of the profile log-likelihood on the EM-algorithm iterations of the parameter $\nu$ for fitting the perception data with a two component TP-T-MRM (left) and skew-t-MRM (right)

4.2.2 US population and poverty percentage counties data

In this subsection we consider a dataset which is provided in “usmap” package from R software called “countypop” and “countypov” which are the 2015 population estimate (in number of people) for the corresponding county (see also, https://www.census.gov/programs-surveys/popest.html), and the 2014 poverty percentage estimate (in percent of county population) for the corresponding county (see also, https://www.census.gov/topics/income-poverty/poverty.html), respectively. We consider the logarithm of population estimate as the explanatory variable and poverty estimate as the response variable. MPL estimates and their corresponding standard errors of the parameters from the TP-T-MRM (the best fitted TP-SMN-MRM) and the skew-t-MRM on the dataset are presented in Table 9. The estimations of the shape parameters (${\gamma }_{\mathrm{g}},\mathrm{ g}=\mathrm{1,2}$) and degrees of freedom ($\nu$) of the fitted TP-T-MRM, show that both of the fitted components have skew behavior and are heavy-tailed. Also, the estimation of regression coefficients of components and Fig. 9, which are the clustering the US counties dataset based on the fitted TP-T-MRM the skew-t-MRM, demonstrates us that, in the first component the levels of poverty percentage are more than the second. Also in the first component by increasing the population estimates, poverty percentage estimates are decreasing, while in the second component it seems the population estimates are not effective on the poverty percentage estimates. Clustering the US counties based on the proposed fitted TP-T-MRM is provided in the US map in Fig. 10.

Table 9 MPL estimation results with their standard errors for fitting TP-T-MRM on the US population and poverty percentage counties data

Fig. 9

Clustering of the US counties based on the estimated TP-T-MRM to population and poverty percentage estimate data (light color is due to the first cluster and dark color is due to the second cluster

Fig. 10

The scatterplot and clustering of the US population and poverty percentage estimate data based on the TP-T-MRM (left) and skew-t-MRM. Top members (red color) are due to the first cluster and bottom members (blue color) are due to the second cluster

5 Conclusion

Finite mixture of regression models is a research area with several applications. In the current study, a model called the TP-SMN distributions was proposed based on a flexible class of symmetric/asymmetric and lightly/heavy tailed distribution. In fact, the proposed model is a generalization of the work carried out by Yao et al. (2014) and Liu and Lin (2014) that can efficiently and simultaneously deal with skewness and heavy-tailed-ness in the mixture regression model setting. Also we have used the penalized likelihood to have the best number of components, and the robust proposed model allows the researchers on different areas to analyze data in an extremely flexible methodology. An EM-type algorithm was employed and some simulation studies were presented to show that this algorithm gives reasonable estimates. After obtaining the MPL estimates via the ECME algorithm, they were easily implemented and coded with existing statistical software such as the R package, and the R code is available from us upon request. Results of the work indicated that using the TP-SMN-MRM leads to a better fit, solves the outliers’ issues and gives a more precise picture of robust inferences. It is intended to pursue a fully Bayesian inference via the Markov chain Monte Carlo method on the proposed model in future research.