Robust Mixture Regression Using Mixture of Different Distributions

Abstract

In this paper, we examine the mixture regression model based on mixture of different type of distributions. In particular, we consider two-component mixture of normal-t distributions, and skew t-skew normal distributions. We obtain the maximum likelihood (ML) estimators for the parameters of interest using the expectation maximization (EM) algorithm. We give a simulation study and real data examples to illustrate the performance of the proposed estimators.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

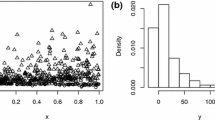
Mixture regression models were first introduced by Quandt (1972), Quandt and Ramsey (1978) as switching regression models, which are used to explore the relationship between variables that come from some unknown latent groups. These models are widely applied in areas such as engineering, genetics, biology, econometrics and marketing. These mixture regression models are used to model data sets which contain heterogeneous groups. Figure 1 shows the scatter plots of this type of real data sets used in literature. A pure fundamental tone electronically obtained overtones added was played to a trained musician in the tone perception data which given by Cohen (1984) in Fig. 1a. The overtones were determined by a stretching ratio which is between the adjusted tone and the fundamental tone. 150 trials were performed by the same musicians in this experiment. This experiment was to reveal how the tuning ratio affects the perception of the tone and to choose if either of two musical perception theories was reasonable (see Cohen 1984 for more detail). The other data contains a number of green peach aphids which were released at various times over 51 small tobacco plants (used as surrogates for potato plants) and the number of infected plants was recorded after each release given in Fig. 1b (see Turner 2000 for more detailed explanations). From these figures, we can observe that there are two groups in both examples. Therefore, these data sets should be modeled by using the mixture regression models.

Fig. 1

a The scatter plot of the tone perception data. b The scatter plot of the aphids data

In general, the parameters of a mixture regression model are estimated under normality assumption. Since the estimators based on normal distribution are sensitive to the outliers, robust mixture regression models have been proposed by Bai (2010) and Bai et al. (2012) to estimate the parameters of mixture regression using the M-estimation method. Wei (2012), Yao et al. (2014) proposed the mixture regression model based on the mixture of t distribution. Liu and Lin (2014) studied the mixture regression model based on the skew normal (Azzalini 1985, 1986) distribution. Doğru (2015), Doğru and Arslan (2016) propose a robust mixture regression procedure using the mixture of skew t distribution (Azzalini and Capitaino 2003) to model skewness and heavy-tailedness in the data with the groups.

Up to now mixture regression models are considered using the finite mixture of the same type of distributions such as mixture of normal or mixture of t distributions. The purpose of this work is to deal with the mixture regression model using the mixture of different type of distributions. This is due to the fact that the subclasses of data may not have same type of behavior. For example some of them may be heavy-tailed, skew or heavy-tailed skew. Using the same type of distributions to model such heterogeneous data may not produce efficient estimators. To accurately model this type of data we may need a mixture of distributions with different type of components. For example, it is clear that in the tone perception data (Fig. 1) two groups should have different type of error distributions. This is due to the fact that the observations around each line has differently scattered.

The rest of the paper is organized as follows. In Sect. 2, we give the mixture regression estimation based on mixture of different distributions. We consider two different mixtures. First, we consider the mixture of symmetric distributions. In particular, we take the mixture of normal and t distribution to estimate the regression parameters in a mixture regression model. Second model will be the mixture of skew distributions. In this context, we study the mixture of skew t and skew normal distribution to estimate the parameters of the mixture regression model. In both cases we give the EM algorithms in details. In Sect. 3, we provide a simulation study to demonstrate the performances of the proposed mixture regression estimators over the counterparts. In Sect. 4, we explore two real data examples to see the capability of the proposed estimators for real data sets. The paper is finalized with a conclusion section.

2 Mixture Regression Model Using the Mixture of Different Type of Distributions

In this section, we will carry out the mixture regression procedure based on the mixture of different distributions. We will only consider the mixture of two distributions, but mixture of more than two different types of distributions can be easily done using the methodology given in this paper.

2.1 Mixture Regression Estimation Based on the Mixture of Normal and t Distributions

A two-component mixture regression model can be defined as follows. Let Z be a latent class variable which is independent of explanatory variable $\mathbf {x}$. Then given $Z = i$, the response variable y and the p-dimensional explanatory variable $\mathbf {x}$ have the following linear model

$$\begin{aligned} y_j=\mathbf {x}_j^{{\prime }} {\varvec{\beta }}_i + \epsilon _i, i=1,2, \end{aligned}$$

(1)

where $\mathbf {x}_j$ contains both the predictors and constant 1. Let $w_i=P(Z=i|\mathbf {x}),i=1,2,$ be the mixing probability with ${\sum _{i=1}^2}w_i=1$. The conditional density of y given $\mathbf {x}$ has the following form

$$\begin{aligned} f(y_{j};\mathbf {x}_{j},\varvec{\varTheta })=w{\phi }\left( y_{j};\mathbf {x} _{j}^{^{\prime }}{{\varvec{\beta }}_{1}},{\sigma _{1}^{2}}\right) +(1-w)f_{t}\left( y_{j};\mathbf {x}_{j}^{^{\prime }}{{\varvec{\beta }} _{2}},{\sigma _{2}^{2}},{\nu }\right) , \end{aligned}$$

(2)

where Z is not observed. This implies that the distribution of the first error term is a normal distribution with 0 mean and the variance ${\sigma _1^{2}}$ and the distribution of the second error term is a t distribution with 0 mean, the scale parameter ${\sigma _2^{2}}$ and the degrees of freedom ${\nu }$. Let $\varvec{\varTheta }=(w,{{\varvec{\beta }}_1},{\sigma _1^{2}},{\varvec{\ \beta }}_2,{\sigma _2^{2}},{\nu })^{\prime }$ be the vector of all the unknown parameters in the model (2).

The ML estimator of the unknown parameter $\varvec{\varTheta }$ is obtained by maximizing the following log-likelihood function

$$\begin{aligned} \ell (\varvec{\varTheta })=\sum _{j=1}^{n}log(w{\phi }(y_{j};\mathbf {x} _{j}^{{\prime }}{{\varvec{\beta }}_{1}},{\sigma _{1}^{2}} )+(1-w)f_{t}(y_{j};\mathbf {x}_{j}^{{\prime }}{{\varvec{\beta }}_{2}},{ \sigma _{2}^{2}},{\nu })). \end{aligned}$$

(3)

However, the maximizer of the log-likelihood function does not have an explicit solution. Therefore, the numerical methods should be used to obtain the estimators for the parameters of interest. Because of the mixture structure of the model the EM algorithm (Dempster et al. 1977) will be the convenient numerical method to obtain the estimators for the parameters.

Let $z_{j}$ be the latent variable with

$$\begin{aligned} z_{j}=\left\{ \begin{array}{l} 1,\ if\ j^{th}\ observation\ is\ from\ 1^{th}\ component \\ 0,\ otherwise, \end{array} \right. \end{aligned}$$

(4)

for $j=1,\ldots ,n$. The joint density function of two-component mixture regression model is

$$\begin{aligned} f(y_j,z_j) = \left( w {\phi } (y_j;\mathbf {x} _j^{{\prime }} {{\varvec{\beta }}_1}, {\sigma _1^{2}})\right) ^{z_j} \left( (1-w) f_t (y_j ; \mathbf {x}_j^{{\prime }} {{\varvec{\beta }}_2}, {\sigma _2^{2}}, { \nu })\right) ^{(1-z_j)}. \end{aligned}$$

(5)

To further simplify the steps of the EM algorithm, we will use the scale mixture representation of the t distribution. Let the random variable u has a gamma distribution with the parameters $(\nu /2,\nu /2)$. Then, the conditional distribution of $\epsilon _2$ given u will be $N(0,\sigma ^2/u)$. With the scale mixture representation of the t distribution this joint density can be further simplified as

$$\begin{aligned} f\left( y_{j},u_{j},z_{j}\right) =\left( w\frac{1}{\sqrt{2\pi \sigma _{1}^{2} }}e^{-\frac{\left( y_{j}-\mathbf {x}_{j}^{{\prime }}{\varvec{\beta }} _{1}\right) ^{2}}{2\sigma _{1}^{2}}}\right) ^{z_{j}}\left( \left( 1-w\right) \frac{\left( \nu /2\right) ^{\nu /2}u_{j}^{\frac{\nu }{2}-1}e^{-\frac{\nu }{2 }u_{j}}}{\varGamma \left( \frac{\nu }{2}\right) \sqrt{2\pi \sigma _{2}^{2}/u_{j}}}e^{-\frac{\left( y_{j}-\mathbf {x}_{j}^{{\prime }}{ \varvec{\beta }}_{2}\right) ^{2}}{2\sigma _{2}^{2}/u_{j}}}\right) ^{1-z_{j}}. \end{aligned}$$

(6)

In this model, $(\mathbf {z},\mathbf {u})$ are regarded as missing data and y is taken as observed data, where $\mathbf {y}=(y_1,\ldots ,y_n),\mathbf {u}=(u_1,\ldots ,u_n)$ and $\mathbf {z}=(z_1,\ldots ,z_n)$. Equation (6) is the joint density function of the complete data $(\mathbf {y},\mathbf {u},\mathbf {z})$. Using this joint density function the complete data log-likelihood function for $\varvec{\varTheta }$ can be written as follows

$$\begin{aligned} \ell (\varvec{\varTheta };\mathbf {y},\mathbf {u},\mathbf {z})= & {} \sum \limits _{j=1}^{n}z_{j}\left( \log w- \frac{\log 2\pi }{2} -\frac{\log \sigma _{1}^{2}}{2}-\frac{\left( y_{j}- \mathbf {x}_{j}^{{\prime }}{\varvec{\beta }}_{1}\right) ^{2}}{2\sigma _{1}^{2}}\right) \nonumber \\+ & {} \left( 1-z_{j}\right) \bigg ( \log \left( 1-w\right) -\frac{\log 2\pi }{2} -\frac{\log \sigma _{2}^{2}}{2}+\frac{\log u_{j}}{2}-\frac{\nu }{2} u_{j} \nonumber \\- & {} \frac{\left( y_{j}-\mathbf {x}_{j}^{{\prime }}{\varvec{\beta }} _{2}\right) ^{2}}{2\sigma _{2}^{2}/u_{j}}-\log \varGamma \left( \frac{\nu }{2}\right) +\frac{\nu }{2}\log \left( \frac{\nu }{2}\right) +\left( \frac{\nu }{2}-1\right) \log u_{j} \bigg ). \end{aligned}$$

(7)

Since $u_j$ and $z_j$ for $j=1,\ldots ,n,$ are taken as missing observations this log-likelihood function cannot be directly used to obtain the estimator for $\varvec{\varTheta }$. To overcome this latency problem we have to take the conditional expectation of the complete data log-likelihood function given $y_j$. This will be the E-step of the EM algorithm:

E-step:

$$\begin{aligned} E\left( \ell (\varvec{\varTheta } ;\mathbf {y},\mathbf {u},\mathbf {z})|y_{j}\right)= & {} \sum \limits _{j=1}^{n}E\left( z_{j}|y_{j}\right) \left( \log w-\frac{\log 2\pi }{2} -\frac{\log \sigma _{1}^{2}}{2}-\frac{\left( y_{j}-\mathbf {x} _{j}^{{\prime }}{\varvec{\beta }}_{1}\right) ^{2}}{2\sigma _{1}^{2}} \right) \nonumber \\+ & {} \left( 1-E\left( z_{j}|y_{j}\right) \right) \left( \log \left( 1-w\right) -\frac{\log 2\pi }{2} -\frac{\log \sigma _{2}^{2}}{2}\right. \nonumber \\+ & {} \frac{1}{2}E\left( \log u_{j}|y_{j}\right) -\frac{\left( y_{j}-\mathbf {x} _{j}^{{\prime }}{\varvec{\beta }}_{2}\right) ^{2}E\left( u_{j}|y_{j}\right) }{2\sigma _{2}^{2}}-\frac{\nu }{2}E\left( u_{j}|y_{j}\right) \nonumber \\- & {} \left. \log \varGamma \left( \frac{\nu }{2}\right) +\frac{\nu }{2} \log \left( \frac{\nu }{2}\right) +\left( \frac{\nu }{2}-1\right) E\left( \log u_{j}|y_{j}\right) \right) . \end{aligned}$$

(8)

To obtain this conditional expectation of the complete data log-likelihood function we have to find $\hat{z}_{j} =E(z_{j}|y_{j},\varvec{\hat{\varTheta }})$, $\hat{u}_{1j} =E( u_{j}|y_{j},\varvec{\hat{\varTheta }})$ and $\hat{u}_{2j} =E(\log u_{j}|y_{j},\varvec{\hat{\varTheta }})$ given in (36), (37) and (38), where $\varvec{\hat{\varTheta }}$ is the current estimate for $\varvec{\varTheta }$.

The M-step of the EM algorithm will be as follows.

M-step: Maximize the following function with respect to $\varvec{\varTheta }$

$$\begin{aligned} Q\left( \varvec{\varTheta };\varvec{\hat{\varTheta }}\right)= & {} \sum \limits _{j=1}^{n}\hat{z} _{j}\left( \log w-\frac{\log 2\pi }{2} -\frac{\log \sigma _{1}^{2}}{2}- \frac{\left( y_{j}-\mathbf {x}_{j}^{{\prime }}{\varvec{\beta }} _{1}\right) ^{2}}{2\sigma _{1}^{2}}\right) \nonumber \\+ & {} \left( 1-\hat{z}_{j}\right) \left( \log \left( 1-w\right) -\frac{\log 2\pi }{2} -\frac{\log \sigma _{2}^{2}}{2}+\frac{\hat{u}_{2j}}{2}-\frac{\nu }{2}\hat{u}_{1j}\right. \nonumber \\- & {} \left. \frac{\left( y_{j}-\mathbf {x}_{j}^{{\prime }}{\varvec{\beta }}_{2}\right) ^{2}\hat{u}_{1j}}{2\sigma _{2}^{2}}-\log \varGamma \left( \frac{ \nu }{2}\right) +\frac{\nu }{2}\log \left( \frac{\nu }{2} \right) +\left( \frac{\nu }{2}-1\right) \hat{u}_{2j}\right) . \end{aligned}$$

(9)

Then, E- and M-steps of the EM algorithm will form the following iteratively reweighting algorithm.

Iteratively reweighting algorithm (EM algorithm)

• 1. Set initial parameter estimate $\varvec{\varTheta }^{(0)}$ and a stopping rule $\varDelta$.

• 2. Calculate the conditional expectations $\hat{z}_{j}^{(k)},\hat{u}_{1j}^{(k)}$ and $\hat{u}_{2j}^{(k)}$ for the $(k+1)th$ for $k=0,1,2,\ldots$ iteration using the Eqs. (36), (37) and (38) given in appendix.

• 3. Insert the current values $\hat{z}_{j}^{(k)},\hat{u}_{1j}^{(k)},\hat{u}_{2j}^{(k)}$ and $\varvec{\hat{\varTheta }}^{(k)}$ in $Q(\varvec{\varTheta } ;\varvec{\hat{\varTheta }})$ to form $Q(\varvec{\varTheta };\varvec{\hat{\varTheta }}^{(k)})$ and maximize $Q(\varvec{\varTheta };\varvec{\hat{\varTheta }}^{(k)})$ with respect to the parameters $(w,{{\varvec{\beta }}_1},{\sigma _1^{2}},{\varvec{\beta }}_2,{\sigma _2^{2}},{\nu })$ to get new estimates for the parameters. This maximization will give the following updating equations:

  $$\begin{aligned} \hat{w}^{(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\hat{z}_{j}^{(k)}}{n}, \end{aligned}$$

  (10)
  $$\begin{aligned} \hat{{\varvec{\beta }}}_{1}^{(k+1)}= & {} \left( \sum \limits _{j=1}^{n} \hat{z}_{j}^{(k)}\mathbf {x}_{j}\mathbf {x}_{j}^{{\prime }}\right) ^{-1}\left( \sum \limits _{j=1}^{n}\hat{z}_{j}^{(k)}\mathbf {x} _{j}y_{j}\right) , \end{aligned}$$

  (11)
  $$\begin{aligned} \hat{\sigma }_{1}^{2(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\hat{z} _{j}^{(k)}\left( y_{j}-\mathbf {x}_{j}^{{\prime }}\hat{{ \varvec{\beta }}}_{1}^{(k)}\right) ^{2}}{\sum \limits _{j=1}^{n}\hat{z} _{j}^{(k)}}, \end{aligned}$$

  (12)
  $$\begin{aligned} \hat{{\varvec{\beta }}}_{2}^{(k+1)}= & {} \left( \sum \limits _{j=1}^{n}\left( 1-\hat{z}_{j}^{(k)}\right) \hat{u} _{1j}^{(k)}\mathbf {x}_{j}\mathbf {x}_{j}^{{\prime }}\right) ^{-1}\left( \sum \limits _{j=1}^{n}\left( 1-\hat{z}_{j}^{(k)}\right) \hat{u} _{1j}^{(k)}\mathbf {x}_{j}y_{j}\right) , \end{aligned}$$

  (13)
  $$\begin{aligned} \hat{\sigma }_{2}^{2(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\left( 1- \hat{z}_{j}^{(k)}\right) \hat{u}_{1j}^{(k)}\left( y_{j}-\mathbf {x} _{j}^{{\prime }}\hat{{\varvec{\beta }}} _{2}^{(k)}\right) ^{2}}{\sum \limits _{j=1}^{n}\left( 1-\hat{z} _{j}^{(k)}\right) }. \end{aligned}$$

  (14)

• 4. To obtain the $\hat{\nu }^{(k+1)}$ solve the following equation

  $$\begin{aligned} \sum \limits _{j=1}^{n}\left( 1-\hat{z}_{j}^{(k)}\right) \left( DG\left( \frac{\nu }{2}\right) -\log \left( \frac{\nu }{2}\right) -1-\hat{u} _{2j}^{(k)}+\hat{u}_{1j}^{(k)}\right) =0, \end{aligned}$$

  (15)

  where $DG(\frac{\nu }{2})=\frac{\varGamma ^\prime (\frac{\nu }{2})}{\varGamma (\frac{\nu }{2})}$ is the digamma function.

• 5. Repeat E and M steps until the convergence rule $\Vert \varvec{\hat{\varTheta }}^{(k+1)}-\varvec{\hat{\varTheta }}^{(k)}\Vert <\varDelta$ is satisfied.

  Note that the Eq. (15) can be solved by using some numerical methods.

2.2 Mixture Regression Estimation Based on the Mixture of Skew t (ST) and Skew Normal (SN) Distributions

Next we will consider the parameter estimation for the mixture regression model assuming that the error terms have mixture of skew t and skew normal distributions. By taking this mixture of two different skew distributions we attempt to model skewness, as well as, the heavy-tailedness in the sub groups of the data.

For two-component mixture regression model given in (1), the conditional density of y given $\mathbf {x}$ is

$$\begin{aligned} f(y_{j};\mathbf {x}_{j},\varvec{\varTheta })=w{f}_{ST}\left( y_{j};\mathbf {x} _{j}^{{\prime }}{{\varvec{\beta }}_{1}},{\sigma _{1}^{2},\lambda }_{1},\nu \right) +(1-w)f_{SN}\left( y_{j};\mathbf {x}_{j}^{{\prime }}{{ \varvec{\beta }}_{2}},{\sigma _{2}^{2}},{\lambda }_{2}\right) , \end{aligned}$$

(16)

where $f_{ST}(\cdot )$ is the density function of the skew t distribution proposed by Azzalini and Capitaino (2003) with the parameters $(\sigma _{1}^{2},\lambda _1,\nu )$ and $f_{SN}(\cdot )$ is the density function of the skew normal distribution proposed by Azzalini (1985, 1986) with the parameters $(\sigma _{2}^{2},\lambda _2)$. Note that the skew t is the distribution of $\epsilon _1$ and the skew normal is the distribution of $\epsilon _2$. Let $\varvec{\varTheta }=(w,{{\varvec{\beta }}_1},{\sigma _1^{2}},{\lambda _1},{\nu },{\varvec{\beta }}_2,{\sigma _2^{2}},{\lambda _2})^{^{\prime }}$ be the unknown parameter vector for this model. Notice that we have extra two skewness parameters to be estimated compare to the model given in Sect. 2.1. In this mixture regression model we note that different from the symmetric case $E(\epsilon )\ne 0$. Therefore, when we estimate the intercept we take into consideration $\widehat{E(\epsilon )}$.

To find the ML estimator of the unknown parameter $\varvec{\varTheta }$ we should maximize the following log-likelihood function

$$\begin{aligned} \ell (\varvec{\varTheta })=\sum _{j=1}^{n}\log \left( w{f}_{ST}(y_{j}; \mathbf {x}_{j}^{{\prime }}{{\varvec{\beta }}_{1}},{\sigma _{1}^{2},\lambda }_{1},\nu )+(1-w)f_{SN}(y_{j};\mathbf {x}_{j}^{{\prime }}{{ \varvec{\beta }}_{2}},{\sigma _{2}^{2}},{\lambda }_{2})\right) . \end{aligned}$$

(17)

Since the log-likelihood function does not have an explicit maximizer, the estimates for the unknown parameter vector $\varvec{\varTheta }$ can be again obtained by using the EM algorithm.

Let $z_j$ define as in Eq. (4), for $j=1,\ldots ,n$. The joint density function of two-component mixture regression model is

$$\begin{aligned} f( y_{j},z_{j}) =\left( w{f}_{ST}(y_{j};\mathbf {x} _{j}^{{\prime }}{{\varvec{\beta }}_{1}},{\sigma _{1}^{2},\lambda }_{1},\nu )\right) ^{z_{j}}\left( (1-w) f_{SN}(y_{j};\mathbf {x} _{j}^{{\prime }}{{\varvec{\beta }}_{2}},{\sigma _{2}^{2}},{\lambda } _{2})\right) ^{1-z_{j}}. \end{aligned}$$

(18)

To represent this joint density function in terms of the normal distribution, we will use the stochastic representation of the skew t and the skew normal distributions. By doing this we will simplify the steps of the EM algorithm. One can see the papers proposed by Azzalini and Capitaino (2003), Azzalini (1986, p. 201), Henze (1986, Theorem 1) to get more details for the stochastic representation of the skew t and the skew normal distributions. Using the scale mixture representation of the skew t distribution and the stochastic representation of the skew t and the skew normal distribution following conditional distributions can be given (Lin et al. 2007; Liu and Lin 2014). Let $\gamma$ and $\tau$ be the latent variables. Then, we have

$$\begin{aligned}&\left. y_{j}\right| \gamma _{j},\tau _{j}\sim N\left( \mathbf {x} _{j}^{{\prime }}{{\varvec{\beta }}_{1}}+\alpha _{1}\gamma _{j},\frac{\kappa _{1}^{2}}{\tau _{j}}\right) , \\&\left. y_{j}\right| \tau _{j}\sim TN\left( 0,\frac{1}{\tau _{j}};(0,\infty )\right) ,\tau _{j}\sim Gamma \left( \frac{\nu }{2},\frac{\nu }{2}\right) , \\&\left. y_{j}\right| \gamma _{j}\sim N\left( \mathbf {x} _{j}^{{\prime }}{{\varvec{\beta }}_{2}+\alpha _{2}}\gamma _{j},\kappa _{2} ^{2}\right) , \gamma _{j}\sim TN\left( 0,1;(0,\infty )\right) , \end{aligned}$$

where $\delta _{\lambda _1}=\lambda _{1}/\sqrt{1+\lambda _{1}^{2}},\delta _{\lambda _2}=\lambda _{2}/\sqrt{1+\lambda _{2}^{2}},\alpha _{1}=\sigma _{1}\delta _{\lambda _1},\alpha _{2}=\sigma _{2}\delta _{\lambda _2},\kappa _{1}^2=\sigma _{1}^{2}(1-\delta _{\lambda _1}^{2})$, $\kappa _{2}^2=\sigma _{2}^{2}(1-\delta _{\lambda _2}^{2})$ and $TN(\cdot )$ shows the truncated normal distribution.

Using the conditional distributions given above the joint density function given in (18) can be rewritten as

$$\begin{aligned} f(y_{j},\gamma _{j},\tau _{j},z_{j})= & {} \left( w\frac{(\nu /2)^{\nu /2}\tau _{j}^{\nu /2}}{\pi \varGamma \left( \frac{\nu }{2}\right) \sqrt{\kappa _{1}^{2}}}e^{-\frac{\nu \tau _{j}}{2}-\frac{\tau _{j}(y_{j}- \mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{1}-\alpha _{1}\gamma _{j})^{2}}{2\kappa _{1}^{2}}-\frac{\tau _{j}\gamma _{j}^{2}}{2}}\right) ^{z_{j}} \nonumber \\&\left( \frac{(1-w)}{\pi \sqrt{\kappa _{2}^{2}}}e^{-\frac{\left( y_{j}- \mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{2}-\alpha \gamma _{j}\right) ^{2}}{2\kappa _{2}^{2}}-\frac{\gamma _{j}^{2}}{2}}\right) ^{1-z_{j}}. \end{aligned}$$

(19)

Note that in this model $(\varvec{\gamma },\varvec{\tau },\mathbf {z})$ will be regarded as the missing and $\mathbf {y}$ will be the observed data, where $\mathbf {y}=(y_1,\ldots ,y_n ),\varvec{\gamma }=(\gamma _1,\ldots ,\gamma _n),\varvec{\tau }=(\tau _1,\ldots ,\tau _n )$ and $\mathbf {z}=(z_1,\ldots ,z_n )$. Let $(\mathbf {y},\varvec{\gamma },\varvec{\tau },\mathbf {z})$ be the complete data. Then, using the complete data joint density function given in (19), the complete data log-likelihood function can be obtained as follows

$$\begin{aligned} \ell _{c}(\varvec{\varTheta } ; \mathbf {y},\varvec{\gamma },\varvec{\tau },\mathbf {z})&=\sum \limits _{j=1}^{n}z_{j}\bigg ( \log w-\log \pi -\frac{\log \kappa _{1}^{2}}{2}+\frac{\nu }{2}\log \left( \frac{\nu }{2}\right) -\log \left( \varGamma \left( \frac{\nu }{2}\right) \right) \nonumber \\&+\frac{\nu }{2}\log \tau _{j}-\frac{\nu \tau _{j}}{2}-\frac{(y_{j}-\mathbf { x}_{j}^{^{\prime }}{\varvec{\beta }}_{1}-\alpha _{1}\gamma _{j})^{2}}{ 2\kappa _{1}^{2}/\tau _{j}}-\frac{\tau _{j}\gamma _{j}^{2}}{2}\bigg )+(1-z_{j}) \nonumber \\&\bigg (\log {(1-w)}-\log \pi -\frac{\log \kappa _{2}^{2}}{2}-\frac{( y_{j}- \mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{2}-\alpha _{2}\gamma _{j})^{2}}{2\kappa _{2}^{2}}-\frac{\gamma _{j}^{2}}{2}\bigg ). \end{aligned}$$

(20)

Since we cannot be able to observe the missing data $(\varvec{\gamma },\varvec{\tau },\mathbf {z})$ this complete data log-likelihood function cannot be used to obtain the estimator for $\varvec{\varTheta }$. To overcome this problem we have to take the conditional expectation of the complete data log-likelihood function given the observed data $\mathbf {y}$. This will be the E-step of the EM algorithm

E-step

$$\begin{aligned} E\left( \ell _{c}(\varvec{\varTheta } ;\mathbf {y},\varvec{\gamma } ,\varvec{\tau },\mathbf {z})|y_{j}\right)= & {} \sum \limits _{j=1}^{n}E( z_{j}|y_{j}) \bigg ( \log w-\frac{\log \kappa _{1}^{2}}{2}+\frac{\nu }{2}\log \left( \frac{\nu }{2}\right) -\log \varGamma \left( \frac{\nu }{2}\right) \bigg ) \nonumber \\+ & {} \frac{\nu E( z_{j}\log \tau _{j}|y_{j}) }{2}-\frac{\nu E( Z_{j}\tau _{j}|y_{j}) }{2}-\frac{E( Z_{j}\tau _{j}|y_{j}) \left( y_{j}-\mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{1}\right) ^{2} }{2\kappa _{1}^{2}} \nonumber \\- & {} \frac{\alpha _{1}^{2}E( z_{j}\tau _{j}\gamma _{j}^{2}|y_{j}) }{ 2\kappa _{1}^{2}}+\frac{\alpha _{1}E( Z_{j}\tau _{j}\gamma _{j}|y_{j}) ( y_{j}-\mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{1}) }{\kappa _{1}^{2}} \nonumber \\+ & {} ( 1-E( z_{j}|y_{j}) ) \bigg ( \log (1-w)-\frac{\log \kappa _{2}^{2}}{2}-\frac{\left( y_{j}-\mathbf {x}_{j}^{^{\prime }}{ \varvec{\beta }}_{2}\right) ^{2}}{2\kappa _{2}^{2}} \nonumber \\+ & {} \frac{\alpha _{2}E( \gamma _{j}|y_{j}) ( y_{j}- \mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{2}) }{\kappa _{2}^{2} }-\frac{\alpha _{2}^{2}E( \gamma _{j}^{2}|y_{j}) }{2\kappa _{2}^{2}}\bigg ) . \end{aligned}$$

(21)

To obtain the conditional expectation of the complete data log-likelihood function we have to find $\hat{z} _{j}=E(z_{j}|y_{j},\varvec{\hat{\varTheta }})$, $\hat{s} _{1j}=E(z_{j}\tau _{j}|y_{j},\varvec{\hat{\varTheta }})$, $\hat{s} _{2j}=E(z_{j}\gamma _{j}\tau _{j}|y_{j},\varvec{\hat{\varTheta }})$, $\hat{s} _{3j}=E(z_{j}\gamma _{j}^{2}\tau _{j}|y_{j},\varvec{\hat{\varTheta }})$, $\hat{s} _{4j}=E(z_{j}\log (\tau _{j})|y_{j},\varvec{\hat{\varTheta }})$, $\hat{t} _{1j}=E(\gamma _{j}|y_{j},\varvec{\hat{\varTheta }})$ and $\hat{t} _{2j}=E(\gamma _{j}^{2}|y_{j},\varvec{\hat{\varTheta }})$ given in (39)–(45).

M-step: For the M step of the EM algorithm, the expected complete data log-likelihood function will be maximized with respect to the parameter $\varvec{\varTheta }$

$$\begin{aligned} Q\left( \varvec{\varTheta };\varvec{\hat{\varTheta } }\right)&=\sum \limits _{j=1}^{n}\hat{z} _{j}\left( \log w-\frac{1}{2}\log (\kappa _{1}^{2})+\frac{\nu }{2}\log \left( \frac{\nu }{2}\right) -\log \left( \varGamma \left( \frac{\nu }{2} \right) \right) \right) -\frac{\nu \hat{s}_{1j}}{2} \nonumber \\&+\frac{\nu \hat{s}_{4j}}{2}-\frac{\hat{s} _{1j}(y_{j}-\mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{1})^{2}}{ 2\kappa _{1}^{2}}+\frac{\alpha _{1}\hat{s}_{2j}(y_{j}-\mathbf {x} _{j}^{^{\prime }}{\varvec{\beta }}_{1})}{\kappa _{1}^{2}}-\frac{\alpha _{1}^{2}\hat{s}_{3j}}{2\kappa _{1}^{2}}+(1-\hat{z}_{j}) \nonumber \\&{}\bigg (\log (1-w)-\frac{\log \kappa _{2}^{2}}{2}-\frac{(y_{j}- \mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }}_{2})^{2}-2\alpha _{2} \hat{t}_{1j}(y_{j}-\mathbf {x}_{j}^{^{\prime }}{\varvec{\beta }} _{2})+\alpha _{2}^{2}\hat{t}_{2j}}{2\kappa _{2}^{2}}\bigg ). \end{aligned}$$

(22)

Similar to the iteratively reweighting algorithm given in Sect. 2.1, we can give the following algorithm based on the steps of the EM algorithm for the two-component mixture regression model obtained from the skew t and skew normal distributions.

Iteratively reweighting algorithm (EM algorithm)

• 1. Set an initial parameter estimates $\varvec{\varTheta }^{(0)}$ and stopping rule $\varDelta$.

• 2. Use $\varvec{\hat{\varTheta }}^{(k)}$ to compute the conditional expectations $\hat{z}_{j}^{(k)},\hat{s}_{1j}^{(k)},\hat{s}_{2j}^{(k)},\hat{s}_{3j}^{(k)},\hat{s}_{4j}^{(k)},\hat{t}_{1j}^{(k)},\hat{t}_{2j}^{(k)}$ for $k=0,1,2,\ldots$ from the Eqs. (39)–(45) given in appendix.

• 3. Insert $\hat{z}_{j}^{(k)},\hat{s}_{1j}^{(k)},\hat{s}_{2j}^{(k)},\hat{s}_{3j}^{(k)},\hat{s}_{4j}^{(k)},\hat{t}_{1j}^{(k)},\hat{t}_{2j}^{(k)}$ and $\varvec{\hat{\varTheta }}^{(k)}$ in $Q(\varvec{\varTheta };\varvec{\hat{\varTheta }})$ to form $Q(\varvec{\varTheta };\varvec{\hat{\varTheta }}^{(k)})$. Maximize the function $Q(\varvec{\varTheta };\varvec{\hat{\varTheta }}^{(k)})$ given in (22) with respect to the parameters $(w,{{\varvec{\beta }}_1},{\sigma _1^{2}},{\lambda _1},{\varvec{\beta }}_2,{\sigma _2^{2}},{\lambda _2})$ to get $(k+1)$ iterated values

  $$\begin{aligned} \hat{w}^{(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\hat{z}_{j}^{(k)}}{n}, \end{aligned}$$

  (23)
  $$\begin{aligned} \hat{{\varvec{\beta }}}_{1}^{(k+1)}= & {} \left( \sum \limits _{j=1}^{n} \hat{s}_{1j}^{(k)}\mathbf {x}_{j}\mathbf {x}_{j}^{^{\prime }}\right) ^{-1}\left( \sum \limits _{j=1}^{n}\left( y_{j}\hat{s}_{1j}^{(k)}-\hat{ \delta }_{\lambda _{1}}^{(k)}\hat{s}_{2j}^{(k)}\right) \mathbf {x} _{j}\right) , \end{aligned}$$

  (24)
  $$\begin{aligned} \hat{\alpha }_{1}^{(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\hat{s} _{2j}^{(k)}(y_{j}-\mathbf {x}_{j}^{^{\prime }}\hat{{\varvec{\beta }}} _{1}^{(k)})}{\sum \limits _{j=1}^{n}\hat{s}_{3j}^{(k)}}, \end{aligned}$$

  (25)
  $$\begin{aligned} \hat{\kappa }_{1}^{2(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\hat{s} _{1j}^{(k)}(y_{j}-\mathbf {x}_{j}^{^{\prime }}\hat{{\varvec{\beta }}} _{1}^{(k)})^{2}-2\hat{\alpha }_{1}^{(k)}\hat{s}_{2j}^{(k)}(y_{j}- \mathbf {x}_{j}^{^{\prime }}\hat{{\varvec{\beta }}}_{1}^{(k)})+ \hat{\alpha }_{1}^{2(k)}\hat{s}_{2j}^{(k)}}{\sum \limits _{j=1}^{n} \hat{z}_{j}^{(k)}}, \end{aligned}$$

  (26)
  $$\begin{aligned} \hat{{\varvec{\beta }}}_{2}^{(k+1)}= & {} \left( \sum \limits _{j=1}^{n}\left( 1-\hat{z}_{j}^{(k)}\right) \mathbf {x}_{j} \mathbf {x}_{j}^{^{\prime }}\right) ^{-1}\left( \sum \limits _{j=1}^{n}\left( 1- \hat{z}_{j}^{(k)}\right) \left( y_{j}-\hat{\alpha }_{2}^{(k)} \hat{t}_{1j}^{(k)}\right) \mathbf {x}_{j}\right) , \end{aligned}$$

  (27)
  $$\begin{aligned} \hat{\alpha }_{2}^{(k+1)}= & {} \frac{\sum \limits _{j=1}^{n}\left( 1- \hat{z}_{j}^{(k)}\right) \hat{t}_{1j}^{(k)}(y_{j}-\mathbf {x} _{j}^{^{\prime }}\hat{{\varvec{\beta }}}_{2}^{(k)})}{ \sum \limits _{j=1}^{n}\left( 1-\hat{z}_{j}^{(k)}\right) \hat{t} _{2j}^{(k)}}, \end{aligned}$$

  (28)
  $$\begin{aligned} \hat{\kappa }_{2}^{2(k+1)}= & {} \frac{1}{\sum \limits _{j=1}^{n}\left( 1- \hat{z}_{j}^{(k)}\right) }\sum _{j=1}^{n}\left( 1-\hat{z} _{j}^{(k)}\right) \left( (y_{j}-\mathbf {x}_{j}^{^{\prime }}\hat{{ \varvec{\beta }}}_{2}^{(k)})^{2}\right. \nonumber \\- & {} \left. 2\hat{\alpha }_{2}^{(k)}\hat{t}_{1j}^{(k)}(y_{j}-\mathbf {x} _{j}^{^{\prime }}\hat{{\varvec{\beta }}}_{2}^{(k)})+\hat{\alpha } _{2}^{2(k)}\hat{t}_{2j}^{(k)}\right) . \end{aligned}$$

  (29)

  Then, we obtain the $\hat{\sigma }_1^{2(k+1)}, \hat{\lambda }_1^{(k+1)}, \hat{\sigma }_2^{2(k+1)}$ and $\hat{\lambda }_2^{(k+1)}$ parameter estimates

  $$\begin{aligned} \hat{\sigma }_{1}^{2(k+1)}= & {} \hat{\kappa }_{1}^{2(k+1)}+\hat{ \alpha }_{1}^{2(k+1)}, \end{aligned}$$

  (30)
  $$\begin{aligned} \hat{\lambda }_{1}^{(k+1)}= & {} \hat{\delta }_{\lambda _{1}}^{(k+1)}\left( 1-\hat{\delta }_{\lambda _{1}}^{2(k+1)}\right) ^{-1/2}, \end{aligned}$$

  (31)
  $$\begin{aligned} \hat{\sigma }_{2}^{2(k+1)}= & {} \hat{\kappa _{2} }^{2(k+1)}+\hat{\alpha _{2} }^{2(k+1)}, \end{aligned}$$

  (32)
  $$\begin{aligned} \hat{\lambda }_{2}^{(k+1)}= & {} \hat{\delta }_{\lambda _{2}}^{(k+1)}\left( 1-\hat{\delta }_{\lambda _{2}}^{2(k+1)}\right) ^{-1/2}, \end{aligned}$$

  (33)

  where $\hat{\delta }_{\lambda _1}^{(k+1)}=\hat{\alpha _{1}}^{(k+1)}/\hat{\sigma }_1^{(k+1)}$ and $\hat{\delta }_{\lambda _2}^{(k+1)}=\hat{\alpha _{2}}^{(k+1)}/\hat{\sigma }_2^{(k+1)}$.

• 4. Also $(k+1)$th value of $\lambda _1$ can be found by solving following equation

  $$\begin{aligned} \delta _{\lambda _{1}}(1-\delta _{\lambda _{1}}^{2})\sum _{j=1}^{n}\hat{ z}_{j}^{(k)}-\delta _{\lambda _{1}}\left( \sum _{j=1}^{n}\hat{s} _{1j}^{(k)}\frac{(y_{j}-\mathbf {x}_{j}^{{\prime }}{\hat{\varvec{\beta }}} _{1}^{(k)})^{2}}{\hat{\sigma } _{1}^{2(k)}}+\sum _{j=1}^{n}\hat{s}_{3j}^{(k)}\right) \nonumber \\ +(1+\delta _{\lambda _{1}}^{2})\sum _{j=1}^{n}\hat{s}_{2j}^{(k)}\frac{ (y_{j}-\mathbf {x}_{j}^{{\prime }}{\hat{\varvec{\beta }}}_{1}^{(k)})}{\hat{\sigma } _{1}^{(k)}}=0. \end{aligned}$$

  (34)

  The $(k+1)$th values of $\nu$ can be calculated solving the following equation

  $$\begin{aligned} \log \left( \frac{\nu }{2}\right) +1-DG\left( \frac{\nu }{2} \right) +\frac{\sum _{j=1}^{n}\left( \hat{s}_{4j}^{(k)}- \hat{s}_{1j}^{(k)}\right) }{\sum _{j=1}^{n}\hat{z}_{j}^{(k)}}=0. \end{aligned}$$

  (35)

• 5. Repeat E and M steps until the convergence rule $\Vert \varvec{\hat{\varTheta }}^{(k+1)}-\varvec{\hat{\varTheta }}^{(k)}\Vert <\varDelta$ is satisfied.

Note that we can solve the Eqs. (34) and (35) using some numerical algorithms.

3 Simulation Study

In this section we will give a simulation study to assess and compare the performances of the mixture regression estimators proposed in this paper with the existing mixture regression estimators in the literature. We specifically compare the mixture regression estimators obtained from normal and t (MixregNt) distributions with the estimators obtained from normal (MixregN) and t (Mixregt) distributions for the two-component mixture regression models for the symmetric case. For the skew case, we compare the mixture regression estimators obtained from the skew t and the skew normal (MixregSTSN) distributions with the estimators obtained from skew normal (MixregSN) and skew t (MixregST) distributions for the two-component mixture regression models. The compression will be done in terms of bias and mean square error (MSE) which are given the following formulas

$$\begin{aligned} \widehat{bias}(\hat{\theta })=\bar{\theta }-\theta ,\> \widehat{MSE}(\hat{\theta })=\frac{1}{N}\sum _{i=1}^{N}{(\hat{\theta _i}-\theta )^2}, \end{aligned}$$

where $\theta$ is the true parameter value, $\hat{\theta _i}$ is the ith simulated parameter estimate, $\bar{\theta }=\frac{1}{N}\sum _{i=1}^{N}{\hat{\theta _i}}$ and $N=500$ is the replication number. For the sample sizes, we take $n=200$ and $n=400$. The simulation is conducted using MATLAB R2013a. The MATLAB codes can be obtained upon request.

Alternatively, the MSE for the $\varvec{\hat{\varTheta }}$ which can be defined as $\Vert \varvec{\hat{\varTheta }}-\varvec{\varTheta }_0\Vert ^2$, where $\varvec{\varTheta }_0$ is the true parameter, can be also used to illustrate the performance of the parameter vector as is suggested by one of the referee. However, to see the performance of each parameter we prefer computing the MSE for each parameter separately. We compare the both the MSE values and observe the similar behavior.

The data $\{(x_{1j},x_{2j},y_{j}),j=1,\ldots ,n\}$ are generated from the following two-component mixture regression model (Bai et al. 2012)

$$ Y=\left\{ \begin{array}{c} 0+X_{1}+X_{2}+\epsilon _{1},Z=1, \\ 0-X_{1}-X_{2}+\epsilon _{2},Z=2, \end{array} \right. $$

where $P(Z=1)=0.25=w_1,X_1\sim N(0,1)$ and $X_2\sim N(0,1)$. The values of the regression coefficients are $\varvec{\beta }_1{=}\,(\beta _{10},\beta _{11},\beta _{12} )^{'}{=}\,{(0,1,1)}^{'}$ and $\varvec{\beta }_2{=}(\beta _{20},\beta _{21},\beta _{22} )^{'}=(0,-1,-1)^{'}$, respectively.

We consider the following error distributions for the symmetric (i) and skew (ii) cases.

(i) Case I: $\epsilon _1,\epsilon _2\sim N(0,1)$, the standard normal distribution.

Case II: $\epsilon _1,\epsilon _2\sim t_3 (0,1)$, the t distribution with 3 degrees of freedom.

Case III: $\epsilon _1\sim N(0,1)$ and $\epsilon _2\sim t_3 (0,1)$.

Case IV: $\epsilon _1,\epsilon _2\sim N(0,1)$ and we also added $\% 5$ outliers at $X_1=20,X_2=20$ and $Y=100$.

(ii) Case I: $\epsilon _1,\epsilon _2\sim SN(0,1,0.5)$, the skew normal distribution.

Case II: $\epsilon _1,\epsilon _2\sim ST(0,1,0.5,3)$, the skew t distribution with 3 degrees of freedom.

Case III: $\epsilon _1\sim ST(0,1,0.5,3)$ and $\epsilon _2\sim SN(0,1,0.5)$.

Case IV: $\epsilon _1,\epsilon _2\sim N(0,1)$ and we also added $\% 5$ outliers at $X_1=20,X_2=20$ and $Y=100$.

Table 1 MSE (bias) values of estimates for $n=200$

Table 2 MSE (bias) values of estimates for $n=400$

Table 3 MSE (bias) values of estimates for $n=200$

Table 4 MSE (bias) values of estimates for $n=400$

The simulation results are summarized in Tables 1, 2, 3 and 4. Tables 1 and 2 show the simulation results for the estimators based on MixregNt with the error distributions given in case (i). For the Case I the best result is obtained from the estimators based on MixregN. For this case, the estimators based on Mixregt and the estimators based on MixregNt have similar behavior. For the error distribution given in Case II the best behavior is obtained, as expected, from Mixregt. In this case, the estimators based on MixregN are drastically affected. The proposed estimators (MixregNt) again have similar behavior with the estimators obtained from Mixregt which shows that it tolerates the heavy-tailedness. The estimators obtained from MixregNt perform the best for the error distribution given in Case III. In this case the estimator obtained from MixregN again has the worst performance. On the other hand, the performance of the estimators based on Mixregt is comparable with the estimators based on MixregNt. Finally, for the outlier case (Case IV) the behavior of the estimators based on MixregN and Mixregt is very similar. In both cases the worst performance is obtained for small groups. That is, they fail to find the regression line for the smaller group. In contrast, the estimators based on MixregNt can be able to accommodate the regression lines for both groups. This can be seen from the smaller bias and the MSE values. In summary, for all the cases considered in this part of the simulation the behavior of the proposed estimators is comparable with the counterparts.

In Tables 3 and 4 we summarize the simulation results obtained from the skew distributions with the error distributions given in case (ii). From this table we can observe that when the error distribution is the mixture of skew normal distribution, the estimators obtained from MixregSN behave better than the other cases. The same behavior can be noticed for the skew t distribution as well. When the error distribution is the mixture of the skew t and the skew normal the estimators obtained from MixregSTSN outperform the counterparts in terms of the MSE values. In this case, the estimators based on MixregSN have the worst performance. When we add the leverage point (the error distribution given in Case IV) the behavior of all the estimators are similarly worse. However, the estimators obtained from MixregST and MixregSTSN give comparable results which have smaller bias and MSE than MixregSN.

Note that from the computational point of view, computing the estimators based on MixregSTSN is less intensive than the estimators obtained from MixregST. Therefore, even they show similar behavior MixregSTSN should be preferred.

4 Real Data Examples

In this section, we will analyze two real data examples to show the performances of the proposed estimators over the estimators given in literature for the cases with and without outliers.

Example 1 In this example, we use the aphids data introduced in Sect. 1 which can be accessed by using mixreg package (Turner 2000) in R. We first fit the lines using the estimates based on MixregN, Mixregt and MixregNt. These fitted lines along with the scatter plot of the data are shown in Fig. 2a. We can see that all methods successfully find the groups and give the correct fitted lines. Also, we summarize the ML estimates and the values of some information criteria in Table 5. Note that for the t distribution we assume that $\nu =2$. We observe that MixregN has the best fit than the other mixture regression models in terms of the Akaike information criterion (AIC) (Akaike 1973), consistent AIC (CAIC) (Bozdogan 1993) and the Bayesian information criterion (BIC) (Schwarz 1978) values.

Fig. 2

a Fitted mixture regression lines without outlier. b Fitted mixture regression lines with outliers at (50, 50)

Table 5 ML estimates and some information criteria for fitting mixture regression models to the aphids data

Table 6 ML estimates and some information criteria for fitting mixture regression models to the aphids data with five outliers at (50, 50)

Fig. 3

a Fitted mixture regression lines without outlier. b Fitted mixture regression lines with outliers at (0, 5)

Table 7 ML estimates and some information criteria for fitting mixture regression models to the tone perception data

Table 8 ML estimates and some information criteria for fitting mixture regression models to the tone perception data with ten outliers at (0, 5)

To see the performances of our estimators when there are outliers in the data, we add five pairs of high leverage outliers at point (50, 50). These points are shown in Fig. 2b by asterisk. Also, the fitted lines and the scatter plot of the data are displayed in Fig. 2b. We give the ML estimates in Table 6. We can see that the fitted lines obtained from MixregN are drastically affected by the outliers. On the other hand, the estimators obtained from Mixregt and MixregNt correctly identifies the groups and fit the regression lines. However, when we compare all methods MixregNt provides the best model in terms of the values of the information criteria.

Example 2. In this example, we use the tone perception data described in Sect. 1 which is given in fpc package (Hennig 2013) in R. This data analyzed by Bai et al. (2012) to model robust mixture regression model. Also, Yao et al. (2014) and Song et al. (2014) used the same data to test performances of the mixture regression estimators based on t and Laplace distributions. The results of these papers show that there should be two groups in the data. We fit mixture of skew normal, mixture of skew t and mixture of skew t and skew normal to check the performances of estimators based on these finite mixture models. We first consider this data without outlier and obtain the fitted lines from the mixture models mentioned above. The fitted lines along with the scatter plot are displayed in Fig. 3a. This figure shows that all the models give similar fits. Also, we give the ML estimates and some values of the information criteria in Table 7. The value of the degrees of freedom of the skew t distribution is taken as 2. We see that MixregSTSN gives the best fit than the other mixture regression models in terms of the AIC, CAIC and the BIC values.

To see the performances of the estimators when there are outliers in the data we added ten identical outliers at point (0, 5). The results for the data with outliers are shown in Fig. 3b. Note that the asterisk in this figure shows the location of outliers. It is clear from this figure that the outliers badly affect the estimators obtained from MixregSN. On the other hand, the estimators based on MixregST and MixregSTSN are not affected from the outliers. From the results of information criteria given in Table 8, MixregSTSN has the best fit to model to the tone perception data.

5 Conclusions

In this paper, we have proposed an alternative robust mixture regression model based on the mixture of different type of distributions. We have specifically considered two-component mixture regression based on mixture of t and normal distributions for the symmetric case, and the mixture of skew t and skew normal distributions for the skew case. We have given the EM algorithms for the mixture of different distributions. We have provided a simulation study and two real data examples. The simulation results and the real data examples have shown that the proposed method based on the mixture of different distributions is superior to or comparable with the method based on mixture of the same type of distributions such as mixture of (skew) normal and mixture of (skew) t distribution. If the groups in the data set have different tail behavior using the mixture of different type of distributions should be preferred. For example, in two group case if one of the groups has heavier tails but the other one is not then instead of using mixture of (skew) t distribution one can use mixture of (skew) t and (skew) normal and get the similar result. Using the mixture of t and normal will be computationally less intensive.

Appendix

To get the conditional expectation of the complete data log-likelihood function given in (8), the following conditional expectations should be calculated given $y_j$ and the current parameter estimate $\varvec{\hat{\varTheta }}=({\varvec{\hat{\beta }}}_{1},\hat{\sigma }_{1}^{2},{\varvec{\hat{\beta }}}_{2},\hat{\sigma }_{2}^{2},\hat{\nu })$

$$\begin{aligned} \hat{z}_{j}= & {} E(z_{j}|y_{j},\varvec{\hat{\varTheta }}) =\frac{ \hat{w}\phi ( y_{j};\mathbf {x}_{j}^{{\prime }} \hat{{\varvec{\beta }}}_{1},\hat{\sigma }_{1}^{2}) }{ \hat{w}\phi ( y_{j};\mathbf {x}_{j}^{{\prime }} \hat{{\varvec{\beta }}}_{1},\hat{\sigma }_{1}^{2}) +( 1-\hat{w}) f_{t}( y_{j};\mathbf {x}_{j}^{{\prime }}\hat{{\varvec{\beta }}}_{2},\hat{\sigma }_{2}, \hat{\nu }) } , \end{aligned}$$

(36)

$$\begin{aligned} \hat{u}_{1j}= & {} E( u_{j}|y_{j},\varvec{\hat{\varTheta }}) =\frac{ \hat{\nu }+1}{\hat{\nu }+\left( \left( y_{j}-\mathbf {x} _{j}^{^{\prime }}{\varvec{\hat{\beta }}}_{2}\right) /\hat{\sigma } _{2}\right) ^{2}} , \end{aligned}$$

(37)

$$\begin{aligned} \hat{u}_{2j}= & {} E(\log u_{j}|y_{j},\varvec{\hat{\varTheta }}) =DG\left( \frac{\hat{\nu }+1}{2}\right) -\log \left( \frac{\hat{\nu }}{2} +\frac{\left( y_{j}-\mathbf {x}_{j}^{{\prime }}{\varvec{\hat{\beta }}}_{2}\right) ^{2}}{2\hat{\sigma }_{2}^{2}}\right) . \end{aligned}$$

(38)

These conditional expectations will be used in EM algorithm given in Sect. 2.1.

Similarly, to obtain the conditional expectation of the complete data log-likelihood function given in (21) the following expectations should be computed given $y_j$ and the current parameter estimate $\varvec{\hat{\varTheta }}=({\varvec{\hat{\beta }}}_{1},\hat{\sigma }_{1}^{2},\hat{\lambda }_{1},\hat{\nu },{\varvec{\hat{\beta }}}_{2},\hat{\sigma }_{2}^{2},\hat{\lambda }_{2})$

$$\begin{aligned} \hat{z}_{j}= & {} E(z_{j}|y_{j},\varvec{\hat{\varTheta }}) =\frac{ \hat{w}f_{ST}(y_{j};\mathbf {x}_{j}^{^{\prime }}\hat{{ \varvec{\beta }}}_{1},\hat{\sigma }_{1}^{2},\hat{ \lambda }_{1},\hat{\nu }) }{\hat{w}f_{ST}( y_{j};\mathbf {x} _{j}^{^{\prime }}\hat{{\varvec{\beta }}}_{1},\hat{\sigma } _{1}^{2},\hat{\lambda }_{1},\hat{\nu }) +( 1-\hat{w} )f_{SN}(y_{j};\mathbf {x}_{j}^{^{\prime }}\hat{{\varvec{ \beta }}}_{1},\hat{\sigma }_{2}^{2},\hat{\lambda }_{2}) } , \end{aligned}$$

(39)

$$\begin{aligned} \hat{s}_{1j}= & {} E(z_{j}\tau _{j}|y_{j},\varvec{\hat{\varTheta }}) = \hat{z}_{j}\bigg ( \frac{\hat{\nu }+1}{\hat{\eta }_{1j}^{2}+ \hat{\nu }}\bigg ) \frac{T_{\hat{\nu }+3}\bigg ( \hat{M}_{j}\sqrt{ \frac{\hat{\nu }+3}{\hat{\nu }+1}}\bigg ) }{T_{\hat{\nu } +1}(\hat{M}_{j}) } , \end{aligned}$$

(40)

$$\begin{aligned} \hat{s}_{2j}= & {} E(z_{j}\gamma _{j}\tau _{j}|y_{j},\varvec{\hat{\varTheta }} ) =\frac{\hat{\delta }_{\lambda _{1}}( y_{j}-\mathbf {x}_{j}^{^{\prime }}\hat{{\varvec{\beta }}} _{1}) \hat{s}_{1j}}{\hat{\sigma }_{1}} +\frac{\hat{z}_{j}\sqrt{1-\hat{\delta } _{\lambda _{1}}^{2}}}{\pi \hat{\sigma }_{1}\hat{f}(y_{j})}\bigg ( \frac{\hat{\eta }_{1j}^{2}}{\hat{\nu }(1-\hat{\delta }_{\lambda _{1}}^{2})}+1\bigg ) ^{-(\frac{\hat{\nu }}{2}+1) }, \end{aligned}$$

(41)

$$\begin{aligned} \hat{s}_{3j}= & {} E(z_{j}\gamma _{j}^{2}\tau _{j}|y_{j},\varvec{\hat{\varTheta }}) =\hat{\delta }_{\lambda _{1}}^{2}\bigg ( \frac{y_{j}- \mathbf {x}_{j}^{^{\prime }}\hat{{\varvec{\beta }}}_{1}}{\hat{ \sigma }_{1}}\bigg ) ^{2}\hat{s}_{1j}+\hat{z}_{j}\bigg \{ (1-\hat{ \delta }_{\lambda _{1}}^{2}) \nonumber \\+ & {} \frac{\hat{\delta }_{\lambda _{1}}( y_{j}-\mathbf {x} _{j}^{^{\prime }}\hat{{\varvec{\beta }}}_{1}) \sqrt{1-\hat{ \delta }_{\lambda _{1}}^{2}}}{\pi \hat{\sigma }_{1}^{2}\hat{f}(y_{j}) }\bigg ( \frac{\hat{\eta }_{1j}^{2}}{\hat{\nu }(1-\hat{\delta } _{\lambda _{1}}^{2})}+1\bigg ) ^{-(\frac{\hat{\nu }}{2}+1)}\bigg \} , \end{aligned}$$

(42)

$$\begin{aligned} \hat{s}_{4j}= & {} E( z_{j}\log (\tau _{j})|y_{j},\varvec{\hat{\varTheta }} ) =\hat{z}_{j}\bigg \{ DG\bigg ( \frac{\hat{\nu }+1}{2}\bigg ) -\log \bigg ( \frac{\hat{\eta }_{1j}^{2}+\hat{\nu }}{2}\bigg ) \nonumber \\+ & {} \bigg ( \frac{\hat{\nu }+1}{\hat{\eta }_{1j}^{2}+\hat{\nu }} \bigg ) \left( \frac{T_{\hat{\nu }+3}\bigg ( \hat{\lambda }_{1} \hat{\eta }_{1j}\sqrt{\frac{\hat{\nu }+3}{\hat{\nu }+\hat{ \eta }_{1j}^{2}}}\bigg ) }{T_{\hat{\nu }+1}\bigg ( \hat{\lambda }_{1} \hat{\eta }_{1j}\sqrt{\frac{\hat{\nu }+1}{\hat{\nu }+\hat{ \eta }_{1j}^{2}}}\bigg ) }-1\right) \nonumber \\+ & {} \frac{\hat{\lambda }_{1}\hat{\eta }_{1j}(\hat{\eta } _{1j}^{2}-1)}{\sqrt{(\hat{\nu }+1)(\hat{\nu }+\hat{\eta } _{1j}^{2})^{3}}}\frac{t_{\hat{\nu }+1}\bigg ( \hat{\lambda }_{1} \hat{\eta }_{1j}\sqrt{\frac{\hat{\nu }+1}{\hat{\nu }+\hat{ \eta }_{1j}^{2}}}\bigg ) }{T_{\hat{\nu }+1}\bigg ( \hat{\lambda }_{1} \hat{\eta }_{1j}\sqrt{\frac{\hat{\nu }+1}{\hat{\nu }+\hat{ \eta }_{1j}^{2}}}\bigg ) } \nonumber \\+ & {} \frac{1}{T_{\hat{\nu }+1}\bigg ( \hat{\lambda }_{1}\hat{ \eta }_{1j}\sqrt{\frac{\hat{\nu }+1}{\hat{\nu }+\hat{\eta } _{1j}^{2}}}\bigg ) }\int \limits _{-\infty }^{\hat{M}_{j}}g_{\hat{\nu } }(x)t_{\hat{\nu }+1}(x)dx\bigg \} , \end{aligned}$$

(43)

$$\begin{aligned} \hat{t}_{1j}= & {} E( \gamma _{j}|y_{j},\varvec{\hat{\varTheta }}) = \hat{\delta }_{\lambda _{2}}\hat{\eta }_{2j}+\sqrt{1-\hat{\delta }_{\lambda _{2}}^{2}}\frac{\phi \left( \hat{\lambda }_{2}\hat{\eta } _{2j}\right) }{\Phi \left( \hat{\lambda }_{2}\hat{\eta }_{2j}\right) } , \end{aligned}$$

(44)

$$\begin{aligned} \hat{t}_{2j}= & {} E(\gamma _{j}^{2}|y_{j},\varvec{\hat{\varTheta }}) =1-\hat{\delta }_{\lambda _{2}}^{2}+\hat{\delta }_{\lambda _{2}} \hat{\eta }_{2j}\hat{t}_{1j} , \end{aligned}$$

(45)

where

$$\begin{aligned} \hat{\eta }_{1j}= & {} \frac{(y_{j}-\mathbf {x}_{j}^{{\prime }}\hat{{\varvec{\beta }}}_{1})}{\hat{\sigma }_{1}},\hat{ \delta }_{\lambda _{1}}=\frac{\hat{\lambda }_{1}}{\sqrt{1+\hat{ \lambda }_{1}^{2}}}, \\ \hat{\eta }_{2j}= & {} \frac{(y_{j}-\mathbf {x}_{j}^{{\prime }}\hat{{\varvec{\beta }}}_{2})}{\hat{\sigma }_{2}},\hat{ \delta }_{\lambda _{2}}=\frac{\hat{\lambda }_{2}}{\sqrt{1+\hat{\lambda }_{2}^{2}}},\hat{M}_{j} =\hat{\lambda }_{1}\hat{\eta }_{1j}\sqrt{\frac{\hat{\nu }}{\hat{\nu }+\hat{\eta }_{1j}^{2}}},\\ g_{\hat{\nu }} (x)= & {} DG\bigg (\frac{\hat{\nu }+2}{2}\bigg )-DG\bigg (\frac{\hat{\nu }+1}{2}\bigg )-\log \bigg (1+\frac{x^2}{\hat{\nu }+1}\bigg )+\frac{x^2(\hat{\nu }+1)-\hat{\nu }-1}{(\hat{\nu }+1)(\hat{\nu }+1+x^2)},\\ \hat{f} (y_{j})= & {} \hat{w_{1}}\frac{2}{\hat{\sigma }_{1}}t_{\hat{\nu }}(\hat{ \eta }_{1j})T_{\hat{\nu }+1}(\hat{M}_{j})+(1-\hat{w_{1}})\frac{2}{\hat{\sigma }_{2}}\phi (\hat{\eta }_{2j})\Phi (\hat{\lambda _{2}}\hat{\eta }_{2j}). \end{aligned}$$

These conditional expectations will be used in EM algorithm given in Sect. 2.2.