1 Introduction

Consider a set of nodes that are deployed to estimate an unknown parameter using the data collected at nodes. Such an estimation problem (known as distributed estimation problem) arises in several applications, e.g., environment monitoring, target localization and sensor network application[1–4]. Different distributed estimation algorithms have been proposed in [5–10]. In general, the available algorithms can be categorized based on the presence or absence of a fusion center (FC) for data processing (see for example [5] and references therein). In many applications, we need to perform estimation when the statistical information of the underlying processes of interest is not available or it varies over time. This issue motivated the development of novel distributed estimation algorithms that are known as adaptive networks.

We adopt the term adaptive networks from [6, 7] to refer to a collection of nodes that interact with each other and function as a single adaptive entity that is able to track statistical variations of data in real-time. In fact, in an adaptive network, each node collects local observations and at the same time, interacts with its immediate neighbors. At every instant, the local observation is combined with information from the neighboring nodes in order to improve the estimate at the local node. By repeating this process of simultaneous observation and consultation, the nodes are constantly exhibiting updated estimates that respond to observations in real time[7].

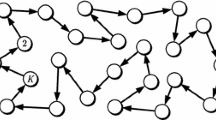
Based on the mode of cooperation between nodes, distributed adaptive estimation algorithms may be referred to as incremental algorithms or diffusion algorithms (see Fig. 1). The distributed incremental least-mean square (DILMS)[8], distributed recursive least square (DRLS) algorithm[9], affine projection algorithm[10] and parallel projections[11] are examples of distributed adaptive estimation algorithms that use incremental cooperation. In these algorithms, there is a Hamiltonian cycle through which the estimates are sequentially circulated from node to node.

Fig. 1
figure 1

Different types of cooperation mode in adaptive networks: incremental (left), diffusion (right)

Full size image

On the other hand, in the diffusion cooperative mode each node updates its estimate using all available estimates from its neighbors as well as data and its own past estimate. Both least-mean square (LMS)-based and recursive least square (RLS)-based diffusion algorithms have been considered in [12, 13]. In [13], a multi-level diffusion algorithm was proposed, where a network running a diffusion algorithm is enhanced by adding special nodes that can perform different processing. In [14], an efficient adaptive combination strategy for diffusion algorithms over adaptive networks was proposed in order to improve the robustness against the spatial variation of signal-to-noise ratio (SNR) over the network.

In the previous incremental adaptive estimation algorithms[7–11], the node profile has not been considered in the algorithm structure. Therefore, the performance of such algorithms will deteriorate if the SNR at some nodes is lower than others, because the noisy estimates of such nodes pervade the entire network by incremental cooperation among the nodes. To address this issue, Panigrahi and Panda have proposed an efficient step size assignment for every node in the incremental least mean squares (ILMS) adaptive learning algorithm[14]. The aim in [14] is to improve the robustness of the ILMS algorithm against the spatial variation of observation noise statistics over the network. The algorithm provides improved steady-state performance in comparison with ILMS algorithm with static step-sizes. However, it needs the noise variance information of all the nodes. In [15], the authors have proposed an efficient step size assignment for every node in the ILMS algorithm so that the convergence of the proposed algorithm is the same as the ILMS algorithm with static step-sizes.

In this paper, we propose a new incremental LMS algorithm with an adaptive combination strategy, which assigns each node a suitable weight according to its reliability of measurement. We formulate the weight assignment as a constrained optimization problem and then recast it into a distributed form and give finally an adaptive solution to the problem. Simulation results are also provided to show the performance of the proposed algorithm.

Notations. We adopt boldface letters for random quantities and normal font for nonrandom (deterministic) quantities. The symbol * denotes conjugation for scalars and Hermitian transpose for matrices. The notation \(||x||_\Sigma ^2 = {x^*}\Sigma x\) stands for the weighted square norm of x. The exact meaning of this notation will be clear from the context.

2 Estimation problem and the adaptive distributed solution

2.1 Incremental LMS solution

Consider a network composed of N distributed nodes as shown in Fig. 2. The purpose is to estimate an unknown parameter M × 1 vector w o from multiple spatially independent but possibly time-correlated measurements collected at N nodes in a network. Each node k has access to time-realizations {d k (i), U k,i } of zero-mean spatial data {d k , u k } where each d k is a scalar measurement and each u k is a 1 × M row regression vector that are related via

$${d_k}(i) = {u_{k,i}}{w^o} + {v_k}(i)$$
(1)

where w o is the M × 1 unknown vector parameter and v k (i) is the observation noise term with zero-mean and variance of \(\sigma _{v,k}^2\). In practice, w o may represent different physical quantities, e.g., location of a target, parameter of an autoregressive (AR) model taps of a communication channel, or the location of food sources[16]. Collecting regression and measurement data into global matrices results in

$$U \buildrel \Delta \over = {\left[ {\matrix{{{u_1}} \cr {{u_2}} \cr \vdots \cr {{u_N}} \cr } } \right]_{N \times M}},\;\;d \buildrel \Delta \over = {\left[ {\matrix{{{d_1}} \cr {{d_2}} \cr \vdots \cr {{d_N}} \cr } } \right]_{N \times 1}}.$$
(2)
Fig. 2
figure 2

A distributed network with N nodes. Note to our definition for the neighborhood of a node N k in the incremental cooperation

Full size image

The objective is to estimate the M × 1 vector w that solves

$${\min\limits_w}J(w)\;\quad {\rm{where}}\;J(w) = {\rm{E}}\{ ||d - Uw|{|^2}\}.$$
(3)

The optimal solution w o satisfies the normal equations[6]

$${R_{du}} = {R_u}{w^o}$$
(4)

where

$${R_{du}} = {\rm{E}}\{ {U^*}d\} = \sum\limits_{k = 1}^N {{R_{du,k}}} $$
(5)
$${R_u} = {\rm{E}}\{ {U^*}U\} = \sum\limits_{k = 1}^N {{R_{u,k}}}.$$
(6)

Note that in order to use (4) to compute w o, each node must have access to the global statistical information {R u , R du } which, in turn, needs a lot of communication and computational resources. Moreover, such an approach, does not enable the network to response to the changes in statistical properties of data.

2.2 Incremental LMS solution

In [6, 8], a fully distributed adaptive estimation algorithm, known as DILMS algorithm has been proposed. To develop our proposed algorithm, we introduce the DILMS algorithm first. To this end, we first consider the gradientdescent method. The standard gradient-descent implementation to solve the normal equation (4) is

$${w_i} = {w_{i - 1}} + {\mu _k}{\left[ {\nabla J\left({{w_{i - 1}}} \right)} \right]^*}$$
(7)

where is a suitably chosen step-size parameter, w i is an estimate of w o at iteration i and ΔJ (·) denotes the gradient vector of J(w) evaluated at w i −1. In order to obtain a distributed solution, first the cost function J(w)is decomposed as follows:

$$J(w) = \sum\limits_{k = 1}^N {{J_k}(w)} $$
(8)

where

$${J_k} \buildrel \Delta \over = {\rm{E}}\{ {\left| {{d_k} - {u_k}w} \right|^2}\}.$$
(9)

Using (8) and (9) the standard gradient-descent implementation of (7) can be rewritten as (8)

$${w_i} = {w_{i - 1}} - {\mu _k}{\left[ {\sum\limits_{k = 1}^N {\nabla {J_k}\left({{w_{i - 1}}} \right)} } \right]^*}.$$
(10)

By defining \(\psi _k^{(i)}\) as the local estimate of w o at node k and time i, w i can be evaluated as[6, 8]

$$\psi _k^{(i)} = \psi _{k - 1}^{(i)} - {\mu _k}{\left[ {\nabla {J_k}\left({{w_{i - 1}}} \right)} \right]^*},\>k = 1,2, \cdots, N.$$
(11)

This scheme still requires all nodes to share the global information w i −1. The fully distributed solution can be achieved by using the local estimate \(\psi _{k - 1}^{(i)}\) at each node k instead of w i −1[6]:

$$\psi _k^{(i)} = \psi _{k - 1}^{(i)} - {\mu _k}{\left[ {\nabla {J_k}\left({\psi _{k - 1}^{(i)}} \right)} \right]^*},\>k = 1,2, \cdots, N.$$
(12)

Now, we need to determine the gradient of J and replace it in (10). To do this, the following approximations are used

$$\matrix{{{R_{du,k}} \approx {d_k}(i)\,u_{k,i}^*} \hfill \cr {{R_{u,k}} \approx u_{k,i}^*{u_{k,i}}.} \hfill \cr }$$
(13)

The resulting DILMS algorithm is as[6, 8]

$$\left\{ {\matrix{{\psi _0^{(i)} \leftarrow {w_{i - 1}}} \hfill \cr {\psi _k^{(i)} = \mathop {\psi _{k - 1}^{(i)} + {\mu _k}}\limits_{k = 1,2, \cdots, N} u_{k,i}^*\left[ {{d_k}(i) - {u_{k,i}}\psi _{k - 1}^{(i)}} \right]} \hfill \cr {{w_i} \leftarrow \psi _N^{(i)}.} \hfill \cr } } \right.$$
(14)

The block diagram of the distributed incremental least-mean square (DILMS) algorithm is shown in Fig. 3.

Fig. 3
figure 3

The block diagram of the DILMS algorithm

Full size image

3 Effect of noisy nodes

Suppose that we have a network so that the SNR at some nodes is lower than others (noisy nodes). The performance of DILMS algorithm in such a network deteriorates because the noisy estimate of such a node pervades the entire network by incremental cooperation among the nodes. To see this, let us consider a network with N = 20 nodes and assume M = 5, µ = 0.01, and \({w^o} = {1_M}/\sqrt M \). The regression vectors u k,i are considered to be independent Gaussian where their eigenvalue spread is ρ = 3Footnote 1. We assume that there are 5 noisy nodes with \(\sigma _{v,k}^2 \in (0,2)\) in the network while for other nodes we consider \(\sigma _{v,k}^2 \in (0,0.1)\). Fig. 4 shows the node profile for our set up. Fig. 5 shows the global average excess mean-square error (ESME) in different conditions when noisy nodes are included and excluded from the network. The global average EMSE is defined as

$${\zeta _g}(i) = {1 \over N}\sum\limits_{k = 1}^N {{\rm{E}}\left\{ {{{\left| {{u_{k,i}}({w^o} - {\psi _{k - 1,i}})} \right|}^2}} \right\}}$$
Fig. 4
figure 4

The node profile, \(\sigma _{v,k}^2\) and tr{R u,k }

Full size image
Fig. 5
figure 5

The global average EMSE for DILMS algorithm in different conditions

Full size image

We can see from Fig. 5 that the noisy nodes strongly affect the performance of DILMS algorithm. More precisely, the performance of DILMS algorithm (in terms of steady-state EMSE) is reduced by about 9 dB because of noisy nodes.

4 Proposed algorithm

The block diagram of the proposed algorithm is shown in Fig. 6. As we can see, at the first step, we need to modify the DILMS algorithm (14) as

$$\left\{ {\matrix{{{\phi _{k,i}} = {c_{k,k - 1}}{\psi _{k - 1,i}} + {c_{k,k}}{\psi _{k,i - 1}}} \hfill \cr {{\psi _{k,i}} = {\phi _{k,i}} + {\mu _k}u_{k,i}^*({d_k}(i) - {u_{k,i}}{\phi _{k,i}})} \hfill \cr } } \right.$$
(15)

where {c k,k−1, c k,k } ∈ R are combination coefficients used at node k. Thus, in the modified DILMS, each node updates its local estimate by combing the local estimate of previous node (i.e., ψ k −1,i ) and its previous time local estimate (i.e., ψ k,i −1,). It must be noted that at node k = 1, due to incremental cooperation in the DILMS algorithm, we have c 1,0 = c 1,N .

Fig. 6
figure 6

The block diagram of the proposed algorithm

Full size image

To formulate the problem of finding combination coefficients, we define the N × 1 vector c k = [c k,1,c k,2 , ⋯,c k , N ]T ∈ R N for every node k, where we have c k,ℓ = 0, ℓ ≠{k − 1, k}. Now, suppose that for each node k, the local estimates {ψ k,i , i = 0, 1, ⋯} are realizations of some random vector ψ k . Then, we would like to find a vector of coefficients c k ∈ R N that solves the following problem

$$\left\{ {\matrix{{\mathop {\min }\limits_{\{ {c_1}, \cdots, {c_N}\} \in {{\bf{R}}^N}} \quad \sum\limits_{k = 1}^N {{\rm{E}}\{ \left| {|\Psi {c_k} - {w^o}} \right|{|^2}\} } } \hfill \cr {{\rm{subject}}\>{\rm{to}}\>\>{c_{k,\ell }} = 0\quad {\rm{for}}\>\ell \notin {{\cal N}_k},\>\>{{\cal N}_k} = \{ k - 1,k\} } \hfill \cr } } \right.$$
(16)

where Ψ = [ψ 1, ψ 2, ⋯, ψ N ]is an M × N random matrix. To have a distributed solution we use the fact that the optimization problem (16) can be decomposed into N subproblems for each k = {1, ⋯, N} as

$$\left\{ {\matrix{{\mathop {\min }\limits_{{c_k} \in {{\bf{R}}^N}} \quad J({c_k}) = {\rm{E}}\{ {{\left\Vert {\Psi {c_k} - {w^o}} \right\Vert}^2}\} } \hfill \cr {{\rm{subject}}\>{\rm{to}}\>\>{c_{k,\ell }} = 0\quad {\rm{for}}\>\ell \notin {{\cal N}_k},\>\>{{\cal N}_k} = \{ k - 1,k\}.} \hfill \cr } } \right.$$
(17)

There is a difficulty to use the optimization problem (17): due to the presence of the unknown quantity w o the optimization problem (17) cannot be solved directly. To address this issue, we can assume that every local estimate ψ k is unbiased, i.e., E{ψ k } = w o for all k = 1, ⋯, N. Now we can use this assumption to say \({\rm{E}}\{ \Psi \} = {w^o}1_N^{\rm{T}}\). Then, we apply the bias-variance decomposition[18, 19]

$$J({c_k}) = c_k^{\rm{T}}{Q_\Psi }{c_k} + {\left\Vert {({\bf{1}}_N^{\rm{T}}{c_k} - 1){w^o}} \right\Vert^2}$$
(18)

where Q Ψ is an N × N matrix defined as

$${Q_\Psi } \buildrel \Delta \over = {\rm{E}}\{ {(\Psi - {\rm{E}}\{ \Psi \})^*}(\Psi - {\rm{E}}\{ \Psi \})\}.$$
(19)

Therefore, by imposing \(1_N^{\rm{T}}{c_k} = 1\), the second term involving the unknown quantity w o is eliminated and we arrive at the following problem

$$\left\{ {\matrix{{\mathop {\min }\limits_{{c_k} \in {{\bf{R}}^N}} \quad c_k^{\rm{T}}{Q_\Psi }{c_k}} \hfill \cr {{\rm{subject}}\>{\rm{to}}\>\>\>{\bf{1}}_N^{\rm{T}}{c_k} = 1\>\>\,\>{\rm{and}}\>\,{c_{k\ell }} = 0\>{\rm{for}}\>\ell \notin {{\cal N}_k}.} \hfill \cr } } \right.$$
(20)

As it is shown in [18], the dimension of the problem like (20) can be reduced from N unknowns to the cardinality of N k , say 2, by introducing the following N × 2 auxiliary variable

$${P_k} = {[{\tau _{k - 1}},{\tau _k}]_{N \times 2}}$$
(21)

where τ k is the N × 1 vector whose components are all zeros except k, for example τ 2 = [010 ⋯ 0]T. Note that due to incremental cooperation we define P 1 as P 1 = [τ 1 τ N ].

Then, any vector c k that satisfies c kℓ = 0 for ℓ ∈ N k can be represented as[18, 19]

$${c_k} = {P_k}{a_k}\>{\rm{with}}\,\;{\rm{some}}\>{a_k}\; \in {{\bf{R}}^2}.$$
(22)

Therefore, substituting (22) into (20) we get

$$\left\{ {\matrix{{\mathop {\min }\limits_{{c_k} \in {{\bf{R}}^N}} \quad {f_k}({a_k}) \buildrel \Delta \over = a_k^{\rm{T}}{Q_{\Psi, k}}{a_k}} \hfill \cr {{\rm{subject}}\>{\rm{to}}\>\>\,{a_k} \in {V_N} \buildrel \Delta \over = \{ a \in {{\bf{R}}^2}|{\bf{1}}_2^{\rm{T}}a = 1\} } \hfill \cr } } \right.$$
(23)

where Q Ψk is the 2 × 2 matrix which is defined as

$${Q_{\Psi, k}} \buildrel \Delta \over = P_k^{\rm{T}}{Q_\Psi }{P_k}$$
(24)

and \({1_2} \triangleq P_k^{\rm{T}}{1_N}\) is the vector whose components are all unity. The solution to (23) is well-known to be[18, 19]

$$a_k^o \buildrel \Delta \over = {{Q_{\Psi, k}^{ - 1}{{\bf{1}}_2}} \over {{\bf{1}}_2^{\rm{T}}Q_{\Psi, k}^{ - 1}{{\bf{1}}_2}}}.$$
(25)

To have an adaptive distributed solution, we need to eliminate the constraint V k from the constrained optimization problem in (23). By applying a similar technique introduced in [18, 19], we finally arrive at the following iterative solution

$$\left\{ {\matrix{{{b_{k,i}} = {b_{k,i - 1}} - {\lambda _k}(i)\Lambda {Q_{\Psi, k}}{b_{k,i - 1}}} \hfill \cr {{c_k} = {P_k}{b_{k,i}}} \hfill \cr } } \right.$$
(26)

where λ k (i) is the step-size and Λ is the following matrix

$$\Lambda = \left[ {\matrix{{0.5} & { - 0.5} \cr { - 0.5} & {0.5} \cr } } \right].$$
(27)

To derive an adaptive solution, we replace Q Ψ,k by its instantaneous approximation as

$${Q_{\Psi, k}} \approx {(\Delta \phi)^*}(\Delta \phi)$$
(28)

where Δϕ is an M × 2 matrix as

$$\Delta \phi = [{\psi _{k - 1,i}} - {\psi _{k - 1,i - 1}}\quad {\psi _{k,i - 1}} - {\psi _{k,i - 2}}].$$
(29)

Now by substituting (28) into (26) and using the modified DILMS algorithm (10), our proposed algorithm with adaptive combination algorithm yields

$$\left\{ {\matrix{{{g_{k,i}} = \Lambda {{(\Delta \phi)}^*}(\Delta \phi){b_{k,i - 1}}} \hfill \cr {{b_{k,i}} = {b_{k,i - 1}} - {\lambda _k}(i){g_{k,i}}} \hfill \cr {{c_k} = {P_k}{b_{k,i}}} \hfill \cr {{\phi _{k,i}} = {c_{k,k - 1}}{\psi _{k - 1,i}} + {c_{k,k}}(i){\psi _{k,i - 1}}} \hfill \cr {{\psi _{k,i}} = {\phi _{k,i}} + {\mu _k}\,u_{k,i}^*({d_k}(i) - {u_{k,i}}{\phi _{k,i}}).} \hfill \cr } } \right.$$
(30)

A possible choice for λ k (i) is the normalized step-size[18, 19]

$${\lambda _k}(i) = \gamma {{\min \{ {b_{k,i - 1}}(1),{b_{k,i - 1}}(2)\} } \over {\parallel {g_{k,i}}{\parallel _\infty } + \varepsilon }}$$
(31)

where γ ∈ (0, 1) and ε are constants, ∥ · ∥∞ denotes the maximum norm, and b k , i −1(m) is the m-th component of b k , i −1. The pseudo code of the proposed algorithm is shown in sequel.

Algorithm 1. The pseudo code of the proposed algorithm

figure Graphic1

5 Simulation results

In this section, we present the simulation results to evaluate the performance of our proposed algorithm. To this aim, we consider again the set up in Section 3. We further choose γ = 0.01 and ε = 10−5. We examine the network performance by the global average mean-square deviation (MSD) and global average EMSE. Note that global average MSD is defined as

$${\eta _g}(i) = {1 \over N}\sum\limits_{k = 1}^N {{\rm{E}}\left\{ {{{\left\Vert {{w^o} - {\psi _{k - 1,i}}} \right\Vert }^2}} \right\}}.$$
(32)

The curves are generated by averaging over 100 independent experiments. In Fig. 7, we have shown the global average MSD and global average EMSE for the DILMS with noisy nodes, the proposed algorithm, and DILMS without noisy nodes. As it is clear from Fig. 7, the proposed algorithm outperforms the DILMS algorithm in a sense of steady-state performance. In fact, in this special set up, the performance of the proposed algorithm is increased by about 7 dB in comparison with the DILMS algorithm. The main disadvantage of the proposed algorithm is its convergence rate, as it is obvious from Fig. 8. In Fig. 8, we have plotted the EMSE learning curves for the DILMS with noisy nodes and the proposed algorithm by manipulating the step size so that both the algorithms have the same convergence speed. The approximation of Q Ψ,k in (28) is the main reason for low convergence speed of the proposed algorithm, which needs time to know the exact variance of a node. The smaller convergence rate in adaptive networks means that the algorithm needs more iterations to converge, which in turn increases the required power, and reduces the network life. The convergence rate of the proposed algorithm can be improved by using a variable step-size LMS algorithm. It is possible to use the block adaptive algorithm concept to minimize the communication overhead involved in the algorithm[20, 21].

Fig. 7
figure 7

The global average MSD and ESME for DILMS and our proposed algorithm

Full size image
Fig. 8
figure 8

The EMSE learning curves for the DILMS with noisy nodes and the proposed algorithm. Note that we have manipulated the step size so that both the algorithm have same convergence speed

Full size image

6 Conclusions and future work

In this paper, we proposed a new incremental LMS algorithm with adaptive combination strategy. The adaptive combination strategy improves the robustness of the proposed algorithm to the spatial variation of SNR. We formulated the weight assignment as a constrained optimization problem and then changed it into a distributed form and finally derived an adaptive solution to the problem. The simulation results showed the effectiveness of our proposed algorithm. In this paper, we assumed ideal links between nodes in the networks. As we have shown in [22, 23], the performance of incremental adaptive networks deteriorates in the presence of noisy links. Moreover, the performance of adaptive networks can vary significantly when they are implemented in finite-precision arithmetic, which makes it vital to analyze their performance in a quantized environment. In the future work, we will consider these issues to modify the structure of our proposed algorithm.