Optimal online algorithms for MapReduce scheduling on two uniform machines

Abstract

We study online scheduling on two uniform machines in the MapReduce system. Each job consists of two sets of tasks, namely the map tasks and reduce tasks. A job’s reduce tasks can only be processed after all its map tasks are finished. The map tasks are fractional, i.e., they can be arbitrarily split and processed on different machines in parallel. Our goal is to find a schedule that minimizes the makespan. We consider two variants of the problem, namely the cases involving preemptive reduce tasks and non-preemptive reduce tasks. We provide lower bounds for both variants. For preemptive reduce tasks, we present an optimal online algorithm with a competitive ratio of $\frac{\sqrt{s^{2}+2s+5}+1-s}{2}$, where $s\ge 1$ is the ratio between the speeds of the two machines. For non-preemptive reduce tasks, we show that the ${ LS}$-like algorithm is optimal and its competitive ratio is $\frac{2s+1}{s+1}$ if $s<\frac{1+\sqrt{5}}{2}$ and $\frac{s+1}{s}$ if $s\ge \frac{1+\sqrt{5}}{2}$.

1 Introduction

In this paper we consider the problem of online scheduling on two uniform machines in the MapReduce system [3], which is a programming model and the associated implementation for processing large-scale data. It is a two-phase paradigm consisting of the map phase and the reduce phase. Specifically, when a job is submitted for processing by the system, the system partitions it into two types of tasks, namely the map tasks and reduce tasks. The map tasks take the raw data as input and output the key-value pairs, while the reduce tasks take the pairs output by the map tasks and compute the final results. All the map tasks and reduce tasks are processed on a number of parallel processors.

Formally, we introduce the problem under study as follows. A sequence ${\mathcal {J}}$ of independent jobs $J_{1},J_{2},\ldots ,J_{n}$ arrive one by one that are to be scheduled irrevocably onto two uniform machines $\sigma _1$ and $\sigma _2$. Machine $\sigma _i$ has speed $s_i\ge 1$. Without loss of generality, we assume $s=s_1\ge s_2=1$. Each job $J_j$ has a set of map tasks $M_j=\{m_j^1, m_j ^2, \ldots , m_j^{u_j}\}$ and a set of reduce tasks $R_j=\{r_j^1, r_j ^2, \ldots , r_j^{v_j}\}$, i.e., the job has $u_j$ map tasks and $v_j$ reduce tasks. The reduce tasks of $J_j$ can only be processed after all the map tasks of $J_j$ are finished. We assume that the map tasks are fractional, i.e., each map task can be arbitrarily split and parts of the same task can be processed on different machines in parallel. Our goal is to minimize the makespan, i.e., the maximum completion time of all the jobs. We consider two variants of the problem, namely the cases involving preemptive reduce tasks and non-preemptive reduce tasks. In the former case, each reduce task may be cut into a few pieces, which are assigned to possibly different machines for processing in non-overlapping time slots, while in the latter case, each reduce task must be processed on one machine in a continuous time interval. Using the three-field notation for scheduling problems, we denote our problem as $Q2|M({ frac})R({ pmtn})|C_{\mathrm{max}}$ for the case involving preemptive reduce tasks and $Q2|M({ frac})R|C_{\mathrm{max}}$ for the case involving non-preemptive reduce tasks.

The performance of an online algorithm A is measured by its competitive ratio, which is defined as $\rho _{A}=\inf \{\rho \ge 1|C^A({\mathcal {J}})\le \rho \cdot C^*({\mathcal {J}}),\forall {\mathcal {J}}\}$, where $C^A({\mathcal {J}})$ (or in short $C^A$) denotes the objective value produced by A and $C^*({\mathcal {J}})$ (or in short $C^*$) denotes the optimal value in the offline version. An online problem has a lower bound if no online algorithm has a competitive ratio smaller than the lower bound. An online algorithm is called optimal if its competitive ratio matches its largest lower bound.

For MapReduce scheduling on parallel machines to minimize the makespan, Zhu et al. [13] considered offline scheduling on m identical machines where the map tasks are fractional, i.e., $Pm|M({ frac}), { offline}|C_{\mathrm{max}}$. They presented an algorithm that produces an optimal solution for preemptive reduce tasks and an algorithm with a worst-case ratio of $\frac{3}{2}-\frac{1}{2m}$ for non-preemptive tasks. They also considered the problem to minimize the total completion time, and gave an approximation algorithm and a heuristic for the non-preemptive and preemptive cases, respectively. For the offline version of the problem on m uniform machines, i.e., $Qm|M({ frac}), { offline}|C_{\mathrm{max}}$, Jiang et al. [6] provided an approximation algorithm with a worst-case ratio of 2 for the preemptive case and an approximation algorithm with a worst-case ratio of $\max \{1+\frac{\Delta }{2}-\frac{1}{m}, \Delta \}$, where $\Delta$ is the speed ratio between the fastest and slowest machines, for the non-preemptive case.

For the online version of the problem in [13], Jiang et al. [7] considered preemptive scheduling on two machines, i.e., $P2|M({ frac})R({ pmtn}), { online}|C_{\mathrm{max}}$. They presented an optimal online algorithm with a competitive ratio of $\sqrt{2}$. Luo et al. [8] considered the online version under the assumption that a job’s reduce tasks are unknown until its map tasks are finished. They provided online optimal algorithms with the same competitive ratio of $2-\frac{1}{m}$ for both the preemptive and non-preemptive cases. Huang et al. [5] studied a special case of online over-list MapReduce model on two identical machines where each job consists of only one map task and one reduce task. When jobs are released over time, Chen et al. [2] presented an algorithm with a competitive ratio $2-\frac{1}{m}$ for the non-preemptive case and an optimal algorithm for the preemptive case involving two machines. Besides, some researchers studied different online MapReduce scheduling models with different objectives. Le et al. [9] considered online MapReduce load balancing with skewed data input. They presented a 2-competitive ratio algorithm and a sample-based enhancement that probabilistically achieves a 3 / 2-competitive ratio with a bounded error. Zheng et al. [12] introduced the criterion of efficiency ratio to measure the performance of online algorithms for the problem to minimize the total completion time. Under the assumption that the length of each map task is one unit, they provided an algorithm based on the shortest remaining processing time (SRPT) and showed that it has a small efficiency ratio for the preemptive case. Chang et al. [1] considered the MapReduce scheduling to minimize the weighted total completion time and presented an online algorithm that achieves a $30\%$ improvement over FIFO via simulation. Moseley et al. [10] considered the problem to minimize the total flowtime in the two-stage hybrid flow shop where the speed of each machine is $1+\epsilon$, $0<\epsilon \le 1$. They presented an online $1+\epsilon$-speed $O(\frac{1}{\epsilon ^{2}})$-competitive algorithm.

In this paper we consider online MapReduce scheduling on two uniform machines in which the map tasks are fractional. Though Jiang et al. [6] presented online heuristics for the problem and confirmed the advantage of the algorithms through simulation, they did not provide the competitive ratios of the online algorithms. Our contribution is to provide two optimal online algorithms for the cases involving preemptive and non-preemptive reduce tasks. For the variant $Q2|M({ frac})R({ pmtn}), { online}|C_{\mathrm{max}}$, we propose an optimal online algorithm with a competitive ratio of $\frac{\sqrt{s^{2}+2s+5}+1-s}{2}$, which is strictly greater than the competitive ratio $\frac{(s+1)^2}{s^2+s+1}$ for the classical preemptive uniform-machine scheduling problem $Q2|{ pmtn}, { online}|C_{\mathrm{max}}$ [11], as shown in Fig. 1. Note that $\frac{\sqrt{s^{2}+2s+5}+1-s}{2}=\sqrt{2}$ when $s=1$, so it is a general result for the problem in [7]. For the variant $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$, we propose an optimal online algorithm with a competitive ratio of $\frac{2s+1}{s+1}$ if $s<\frac{1+\sqrt{5}}{2}$ and $\frac{s+1}{s}$ if $s\ge \frac{1+\sqrt{5}}{2}$, which is the same as that of the classical non-preemptive uniform-machine scheduling problem $Q2|{ online}|C_{\mathrm{max}}$ [4].

Fig. 1

Comparison between two competitive ratios

We organize the rest of the paper as follows: in Sect. 2 we derive lower bounds for the problem. In Sects. 3 and 4 we present optimal online algorithms for the preemptive and non-preemptive variants, respectively. Finally, we conclude the paper in Sect. 5.

2 Lower bounds

For the sake of simplicity in the remainder of this paper, we use $r_j^i$ to denote the length of a task, and $M_j$ ($R_j$) to denote the total length of the tasks in $M_j$ ($R_j$). We assume that $r_j^1\ge r_j^2\ge \cdots \ge r_j^{v_j}$ for every $1\le j\le n$. Let $P_j=\sum \nolimits _{i=1}^j(M_i+R_i)$ be the total length of the first j jobs. Let $C_{j}^{A}$ and $C_j^*$ denote the makespan produced by algorithm A and the optimal makespan after scheduling the first j jobs.

Lemma 2.1

For both variants $Q2|M({ frac})R({ pmtn}), { online}|C_{\mathrm{max}}$ and $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$, we have

$$\begin{aligned} C_j^*\ge \max \left\{ \frac{P_j}{1+s}, \max _{1\le i\le j}\left\{ \frac{r_i^1}{s}+\frac{M_i}{1+s}\right\} \right\} . \end{aligned}$$

(1)

We first derive a lower bound for the preemptive variant $Q2|M({ frac})R({ pmtn}), { online}|C_{\mathrm{max}}$.

Theorem 2.2

For the variant $Q2|M({ frac})R({ pmtn}), { online}|C_{\mathrm{max}}$, the competitive ratio of any online algorithm is at least $\frac{\sqrt{s^{2}+2s+5}+1-s}{2}$.

Proof

Assume that there exists an algorithm A with a competitive ratio $\rho$. The first job $J_1=\{M_{1},\emptyset \}$ arrives. Let $l_i$ be the completion time of machine $\sigma _i$ after job $J_1$ has been scheduled by algorithm A, $i=1, 2$. It is clear that the current optimal makespan is $\frac{M_1}{s+1}=\frac{sl_1+l_2}{s+1}$. We consider two cases with respect to the values of $l_1$ and $l_2$.

Case 1$l_1\ge l_2$. The makespan produced by A is $l_1$, so

$$\begin{aligned} \rho \ge \frac{l_1}{\frac{sl_1+l_2}{s+1}}\doteq \rho _1. \end{aligned}$$

(2)

Then the second and last job $J_2=\{M_2, R_2\}$ arrives, where $M_{2}=l_1-l_2$ and $R_{2}$ has only one task $r_2^1=(sl_1+l_2)s$. It is easy to see that the makespan produced by algorithm A is at least $l_1+sl_1+l_2=(s+1)l_1+l_2$. On the other hand, we find that the optimal makespan is $\frac{l_1-l_2}{s+1}+sl_1+l_2$ by scheduling all the map tasks in $M_2$ on the two machines evenly, $r_2^1$ on $\sigma _1$, and all the map tasks in $M_1$ on $\sigma _2$. Thus, we have

$$\begin{aligned} \rho \ge \frac{(s+1)l_1+l_2}{\frac{l_1-l_2}{s+1}+sl_1+l_2}\doteq \rho _2. \end{aligned}$$

(3)

If $l_2=0$, we have $\rho \ge \frac{s+1}{s}>\frac{\sqrt{s^{2}+2s+5}+1-s}{2}$ by (2). So we assume $l_2>0$ and let $q=\frac{l_1}{l_2}$. From (2) and (3), we have

$$\begin{aligned} \rho _1=\frac{q}{\frac{1+sq}{s+1}}=\frac{(s+1)q}{sq+1} \end{aligned}$$

and

$$\begin{aligned} \rho _2=\frac{1+(s+1)q}{\frac{q-1}{s+1}+1+sq}=\frac{(s+1)q+1}{(s^2+s+1)q+s}. \end{aligned}$$

It is easy to see that for $q \ge 1$, $\rho _1$ is increasing and $\rho _2$ is decreasing. Since $\rho \ge \max \{\rho _1,\rho _2\}$, we establish the equation $\rho _1=\rho _2$. Solving the equation, we obtain $q=\frac{s+1+\sqrt{s^{2}+2s+5}}{2}$, so $\rho \ge \frac{\sqrt{s^{2}+2s+5}+1-s}{2}$.

Case 2$l_1\le l_2$. The makespan produced by A is $l_2$, so

$$\begin{aligned} \rho \ge \frac{l_2}{\frac{sl_1+l_2}{s+1}}. \end{aligned}$$

(4)

Then the second and last job $J_2=\{M_2, R_2\}$ arrives, where $M_{2}=(l_2-l_1)s$ and $R_{2}$ has only one task $r_2^1=(sl_1+l_2)s$. It is easy to see that the makespan produced by algorithm A is at least $l_2+sl_1+l_2=sl_1+2l_2$. On the other hand, we find that the optimal makespan is $\frac{(l_2-l_1)s}{s+1}+sl_1+l_2$. Thus,

$$\begin{aligned} \rho \ge \frac{sl_1+2l_2}{\frac{(l_2-l_1)s}{s+1}+sl_1+l_2}. \end{aligned}$$

(5)

Using similar arguments in Case 1, we obtain the desired result from (4) and (5). $\square$

For the non-preemptive variant, note that $Q2|{ online}|C_{\mathrm{max}}$ is a special case of our problem $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$, so a lower bound for $Q2|{ online}|C_{\mathrm{max}}$ [4] is also a lower bound for of $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$.

Theorem 2.3

For the variant $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$, the competitive ratio of any on-line algorithm is at least

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{2s+1}{s+1}, &{}\quad \text{ if } \ s<\frac{1+\sqrt{5}}{2};\\ \frac{s+1}{s}, &{}\quad \text{ if } \ s\ge \frac{1+\sqrt{5}}{2}. \end{array} \right. \end{aligned}$$

3 An optimal on-line algorithm for the preemptive variant

In this section we provide an online algorithm $A_1$ with a competitive ratio $\alpha =\frac{\sqrt{s^{2}+2s+5}+1-s}{2}>1$ for the preemptive variant $Q2|M({ frac})R({ pmtn}), { online}|C_{\mathrm{max}}$. Let $l_j^{i}$ denote the completion time of machine $\sigma _{i}$ at the moment right after the jth job $J_j$ has been scheduled, $i=1, 2$.

Before presenting our algorithm $A_1$, we introduce a useful lemma as follows:

Lemma 3.1

If $l_j^1=\frac{\alpha }{1+s-\alpha s}l_j^2$ for some $1\le j \le n$, we have $\frac{C_{j}^{A_{1}}}{C_j^*}\le \alpha$.

Proof

Noting that $\frac{\alpha }{1+s-\alpha s}>1$, we have $C_{j}^{A_{1}}=l_j^1=\frac{\alpha }{1+s-\alpha s}l_j^2$. By (1), we have $C_j^*\ge \frac{P_j}{1+s}= \frac{sl_j^1+l_j^2}{1+s}=\frac{1}{1+s-\alpha s}l_j^2$, so $\frac{C_{j}^{A_{1}}}{C_j^*}\le \alpha$. $\square$

The main idea of our algorithm $A_{1}$ is inspired by Lemma 3.1. To achieve the desired competitive ratio, algorithm $A_1$ always tries to schedule the jobs so that the completion times of the two machines keep the ratio $\alpha {:}\,1+s-\alpha s$. In other words, it only needs to schedule the current job $J_j$ so that $l_j^1=\frac{\alpha }{1+s}P_j$ and $l_j^2=\frac{1+s-\alpha s}{1+s}P_j$. If the ratio cannot be maintained, we conclude that the current job $J_j$ has a very large reduce task $r_j^1$ (the details are provided in the algorithm). In that case, the optimal makespan is also determined by this job, i.e., $C_j^*\ge \frac{p(M_j)}{1+s}+\frac{r_j^1}{s}$, and we show that $\frac{C_j^{A_1}}{C_j^*}\le \alpha$ still holds.

In our algorithm, we introduce the procedure $P(M_j, R_j)$ to schedule job $J_j$ when the current completion times of the two machines are the same, i.e., $l_{j-1}^1=l_{j-1}^2$.

Procedure $P(M_j,R_j)$

• 0. Denote $\Delta _{1}=\frac{\alpha }{1+s}P_j-l_{j-1}^1-\frac{M_j}{1+s}$ and $\Delta _{2}=\frac{1+s-\alpha s}{1+s}P_j-l_{j-1}^1-\frac{M_j}{1+s}$.

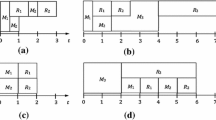
• 1. If $s\Delta _{1}>R_j$, schedule the portion $(1+s-\alpha s)(M_j+R_j-\frac{s(s+1)(\alpha -1)}{1+s-\alpha s}l_{j-1}^1)$ (denoted by $M_j^1$) of the map tasks in $M_j$ on the two machines evenly, and the leftover of the map tasks (denoted by $M_j^2$) and all the reduce tasks on $\sigma _1$ (see Fig. 2a).

• 2. If $r_j^1<s\Delta _{1}\le R_j$, schedule all the map tasks on the two machines evenly. For the reduce tasks:

  • 2.1 If $r_j^1\le \Delta _{2}$, find $k=\min \{q|\sum \nolimits _{i=1}^qr_j^i\ge \Delta _{2}, 1\le q \le v_j\}$ and partition $r_j^k$ into two parts $r_j^{k_1}$ and $r_j^{k_2}$ such that $\sum \nolimits _{i=1}^{k-1}r_j^i+r_j^{k_1}=\Delta _{2}$. Then schedule $r_j^1, \ldots , r_j^{k-1}, r_j^{k_1}$ on $\sigma _2$ and $r_j^{k_2},r_j^{k+1}, \ldots , r_j^{v_j}$ on $\sigma _1$. (see Fig. 2b, where $R_j^1=\{r_j^2, \ldots , r_j^{k-1}\}$ and $R_j^1=\{r_j^{k+1}, \ldots , r_j^{v_j}\}$.)

  • 2.2 If $r_j^1>\Delta _{2}$, partition $r_j^1$ into two parts $r_j^{1_1}$ and $r_j^{1_2}$ such that $r_j^{1_1}=\Delta _{2}$. Then schedule $r_j^{1_1}$ on $\sigma _2$ in the time interval $[l_{j-1}^1+\frac{M_j}{1+s}, \frac{1+s-\alpha s}{1+s}P_j]$ and $r_j^{1_2}$ on $\sigma _1$ in the time interval $[\frac{1+s-\alpha s}{1+s}P_j, \frac{1+s-\alpha s}{1+s}P_j+\frac{r_j^{1_2}}{s}]$, and the leftover on $\sigma _1$ as early as possible (see Fig. 2c, Where $R_j^1\bigcup R_j^2=R_j{\setminus }\{r_j^1\}$ and $R_j^1=r_j^{1_1}$).

• 3. If $s\Delta _{1}\le r_j^1$, schedule all the map tasks on the two machines evenly, the largest reduce task $r_j^1$ on $\sigma _1$, and the leftover of the reduce tasks on $\sigma _2$ (see Fig. 2d).

Fig. 2

Assignment of job $J_j$ by procedure P

Algorithm $A_{1}$

• 1. Let $l_0^1=l_0^2=0$ and invoke procedure $P(M_1, R_1)$ for the first job $J_1$.

• 2. For every job $J_j$, $2\le j\le n$, denote $\Gamma _1=\frac{1+s-\alpha s}{1+s}P_j-l_{j-1}^2$, $\Gamma _2=\frac{\alpha }{1+s}P_j-l_{j-1}^2$, $\Gamma _3=\frac{1+s-\alpha s}{1+s}P_j-l_{j-1}^1$, and $\Gamma _4=\frac{\alpha }{1+s}P_j-l_{j-1}^1$. Clearly, $\Gamma _1<\Gamma _2$ and $\Gamma _3<\Gamma _4$. If $M_j\le l_{j-1}^1-l_{j-1}^2$, go to Step 3; otherwise, go to Step 4.

• 3. For $M_j\le l_{j-1}^1-l_{j-1}^2$.

  • 3.1 If $M_j+R_j\le \Gamma _1$, schedule all the map tasks and reduce tasks on $\sigma _2$.

  • 3.2 If $M_j+r_j^1\le \Gamma _1<M_j+R_j$, schedule all the map tasks on $\sigma _2$. For the reduce tasks:

    • (a) If $r_j^1\le \Gamma _3$, schedule $r_j^1$ on $\sigma _2$ in the time interval $[l_{j-1}^1, l_{j-1}^1+r_j^1]$, and the leftover on $\sigma _2$ in the time intervals $[l_{j-1}^2+M_j, l_{j-1}^1]$ and $[l_{j-1}^1+r_j^1, \frac{1+s-\alpha s}{1+s}P_j]$, and on $\sigma _1$ in the time interval $[l_{j-1}^1, \frac{\alpha }{1+s}P_j]$ (see Fig. 3).

    • (b) If $r_j^1> \Gamma _3$, schedule $r_j^1$ on $\sigma _2$ in the time interval $[\frac{1+s-\alpha s}{1+s}P_j-r_j^1, \frac{1+s-\alpha s}{1+s}P_j]$, and the leftover on $\sigma _2$ in the time intervals $[l_{j-1}^2+M_j, \frac{1+s-\alpha s}{1+s}P_j-r_j^1]$ and on $\sigma _1$ in the time interval $[l_{j-1}^1, \frac{\alpha }{1+s}P_j]$ (see Fig. 4).

  • 3.3 If $M_j+r_j^1> \Gamma _1$, schedule all the map tasks on $\sigma _2$. For the reduce tasks:

    • (a) If $\frac{r_j^1}{s}\le \Gamma _3$, partition $r_j^1$ into two parts $r_j^{1_1}$ and $r_j^{1_2}$ such that $r_j^{1_1}+\frac{r_j^{1_2}}{s}=\Gamma _3$. Then schedule $r_j^{1_1}$ on $\sigma _2$ in the time interval $[l_{j-1}^1,l_{j-1}^1+r_j^{1_1}]$ and $r_j^{1_2}$ on $\sigma _1$ in the time interval$[l_{j-1}^1+r_j^{1_1}, \frac{1+s-\alpha s}{1+s}P_j]$, and the leftover on $\sigma _2$ in the time intervals $[l_{j-1}^2+M_j, l_{j-1}^1]$ and $[l_{j-1}^1+r_j^{1_1}, \frac{1+s-\alpha s}{1+s}P_j]$, and on $\sigma _1$ in the time intervals $[l_{j-1}^1, l_{j-1}^1+r_j^{1_1}]$ and $[\frac{1+s-\alpha s}{1+s}P_j, \frac{\alpha }{1+s}P_j]$ (see Fig. 6a).

    • (b) If $\Gamma _3<\frac{r_j^1}{s}\le \Gamma _4$, schedule $r_j^1$ on $\sigma _1$ in the time interval $[l_{j-1}^1, l_{j-1}^1+\frac{r_j^1}{s}]$, and the leftover on $\sigma _2$ in the time interval $[l_{j-1}^2+M_j, \frac{1+s-\alpha s}{1+s}P_j]$ and on $\sigma _1$ in the time interval $[l_{j-1}^1+\frac{r_j^1}{s}, \frac{\alpha }{1+s}P_j]$ (see Fig. 6b).

    • (c) If $\frac{r_j^1}{s}>\Gamma _4$, partition $r_j^1$ into two parts $r_j^{1_1}$ and $r_j^{1_2}$ such that $l_{j-1}^1+\frac{r_j^{1_2}}{s}=\frac{\alpha }{1+s}P_j$.

      • (1) If $l_{j-1}^2+M_j+r_j^{1_1}\le l_{j-1}^1$, schedule $r_j^{1_1}$ on $\sigma _2$ in the time interval $[l_{j-1}^1-r_j^{1_1}, l_{j-1}^1]$ and $r_j^{1_2}$ on $\sigma _1$ in the time interval $[l_{j-1}^1, \frac{\alpha }{1+s}P_j]$, and the leftover on $\sigma _2$ in the time interval $[l_{j-1}^2+M_j, l_{j-1}^1-r_j^{1_1}]$ and $[l_{j-1}^1, \frac{1+s-\alpha s}{1+s}P_j]$ [see Fig. 6(c1)].

      • (2) If $l_{j-1}^2+M_j+r_j^{1_1}> l_{j-1}^1$, partition $r_j^1$ into two parts $r_j^{1'_1}$ and $r_j^{1'_2}$ such that $l_{j-1}^2+M_j+r_j^{1'_1}=l_{j-1}^1$. Then schedule $r_j^{1'_1}$ on $\sigma _2$ in the time interval $[l_{j-1}^1-r_j^{1_1}, l_{j-1}^1]$, $r_j^{1'_2}$ on $\sigma _1$ in the time interval $[l_{j-1}^1, l_{j-1}^1+\frac{r_j^{1'_2}}{s}]$, and the leftover on $\sigma _2$ at time $l_{j-1}^1$ [see Fig. 6(c2)].

    Fig. 3

    

    Step 3.2(a)

    Fig. 4

    

    Step 3.2(b)

• 4. For $M_j>l_{j-1}^1-l_{j-1}^2$

  • 4.1 If $M_j+R_j\le \Gamma _2$, schedule the portion $M_j^1=\Gamma _1$ of $M_j$ on $\sigma _2$, and the leftover of the map tasks $M_j^2$ and all the reduce tasks on $\sigma _1$ (see Fig. 5).

  • 4.2 If $M_j+R_j>\Gamma _2$, schedule the portion $M_j^1=l_{j-1}^1-l_{j-1}^2$ of the map tasks such that $l_{j-2}^2+M_j^1=l_{j-1}^1$ and denote the remainder of the map tasks as $M_j'=M_j{\setminus } M_j^1$. Invoke procedure $P(M_j', R_j)$ for the job $J_j'=\{M_j', R_j\}$.

Fig. 5

Step 4.1

Remark By the rules of procedure P and algorithm $A_{1}$, we always have $l_j^1\ge \frac{\alpha }{1+s-\alpha s} l_j^2$ after scheduling any job $J_j$. Specifically,

• (i) $l_j^1=\frac{\alpha }{1+s-\alpha s} l_j^2$ after Steps 1 and 2 in procedure P, and Steps 3.2, 3.3(a), 3.3(b), 3.3(c1), and 4.1 in algorithm $A_{1}$.

• (ii) $l_j^1>\frac{\alpha }{1+s-\alpha s} l_j^2$ after Step 3 in procedure P, and Steps 3.1 and 3.3(c2) in algorithm $A_{1}$.

In addition to obtaining the desired competitive ratio, we have to consider the feasibility of the resulting schedule. The assignment of the map tasks is obviously feasible because it is fractional and can be scheduled arbitrarily. To ensure the feasibility of the reduce tasks, the algorithm must follow two rules. One is that the reduce tasks must be processed after the map tasks and the other is that the time slots assigned to the different parts of any preempted reduce task do not overlap.

Theorem 3.2

For any $1\le j\le n$, we have $l_j^1\ge \frac{\alpha }{1+s-\alpha s}l_j^2$ and $\frac{C_{j}^{A_{1}}}{C_j^*}\le \alpha$.

Proof

We use mathematical induction to prove the result.

First, we consider the case where $j=1$, i.e., the assignment of the first job $J_1$. Note that $l_{j-1}^1=l_{j-1}^2=0$, so the algorithm schedules job $J_1$ by procedure P.

• (i) If $J_j$ is scheduled by Step 1, the assignment of the job is obviously feasible as shown in Fig. 2a. Noting that $l_{j-1}^1=l_{j-1}^2=\frac{P_{j-1}}{1+s}$ and $P_j=M_j+R_j+P_{j-1}$, we have

  $$\begin{aligned} l_j^2= & {} l_{j-1}^{2}+ \frac{M_j^1}{1+s}=l_{j-1}^{2}+ \frac{1+s-\alpha s}{1+s}\left( \phantom {\left. -\,\frac{s(s+1)(\alpha -1)}{1+s-\alpha s}l_{j-1}^2\right) =\frac{1+s-\alpha s}{1+s}P_j} M_j+R_j \right. \\&\left. -\,\frac{s(s+1)(\alpha -1)}{1+s-\alpha s}l_{j-1}^2\right) =\frac{1+s-\alpha s}{1+s}P_j \end{aligned}$$

and $l_j^1=P_j-\frac{1+s-\alpha s}{1+s}P_j=\frac{\alpha }{1+s}P_j$. Thus, we have $\frac{C_{j}^{A_1}}{C_j^*}\le \alpha$ by Lemma 3.1.

• (ii) If $J_j$ is scheduled by Step 2. It is easy to verify that $l_j^1=\frac{\alpha }{1+s}P_j$ and $l_j^2=\frac{1+s-\alpha s}{1+s}P_j$ by the rule of the algorithm. If the reduce tasks are scheduled by Step 2.1, we only need to consider the assignment of the preempted task $r_j^k$. Since $r_j^{k_2}\le r_j^k\le r_j^1$ by the assumption that $r_j^1\ge \cdots \ge r_j^{v_j}$, we have $\frac{r_j^{k_2}}{s}\le r_j^1$. This means that the start time of $r_j^{k_1}$ is not earlier than the finish time of $r_j^{k_2}$ as shown in Fig. 2b. Thus the time slots assigned to $r_j^{k_1}$ and $r_j^{k_2}$ do not overlap. On the other hand, if the reduce tasks are scheduled by Step 2.2, the assignment of the reduce tasks is obviously feasible as shown in Fig. 2c. Thus, the desired result holds.

• (iii) If $J_j$ is scheduled by Step 3, feasibility is trivial. From the rule of the algorithm as shown in Fig. 2d and $l_{j-1}^1=0$, we have $C_{j}^{A_1}=l_j^1=l_{j-1}^1+\frac{M_j}{1+s}+\frac{r_j^1}{s}=\frac{M_j}{1+s}+\frac{r_j^1}{s}=C_j^*$. By the assumption that $r_j^1\ge s\Delta _1$, we obtain $r_j^1\ge \frac{\alpha s}{1+s}P_j-\frac{s}{1+s}M_j$. It follows that $l_j^1=\frac{M_j}{1+s}+\frac{r_j^1}{s}\ge \frac{\alpha }{1+s}P_j$ and $l_j^2\le \frac{1+s-\alpha s}{1+s}P_j$, i.e., $l_j^1\ge \frac{\alpha }{1+s-\alpha s}l_j^2$.

Hence, the result holds when $j=1$.

Suppose that the result is true for $j-1$ ($j\ge 2$), i.e., $l_{j-1}^1\ge \frac{\alpha }{1+s-\alpha s}l_{j-1}^2$ and $\frac{C_{j-1}^{A_1}}{C_{j-1}^*}\le \alpha$. We consider the assignment of $J_j$ below.

• (I) $J_j$ is scheduled by Step 3.1. Note that all the tasks are scheduled on $\sigma _1$, so the schedule is obviously feasible and we have $l_j^2=l_{j-1}^2+M_j+R_j\le l_{j-1}^2+\Gamma _{1}-l_{j-1}^2\le \frac{1+s-\alpha s}{1+s}P_j$ by the assumption that $M_j+R_j\le \Gamma _1=\frac{1+s-\alpha s}{1+s}P_j-l_{j-1}^2$. So we have $l_j^1=l_{j-1}^1\ge \frac{\alpha }{1+s}P_j$, i.e., $l_{j}^1\ge \frac{\alpha }{1+s-\alpha s}l_{j}^2$. It is clear that $C_{j}^{A_{1}}=C_{j-1}^{A_{1}}$ and $C_j^*\ge C_{j-1}^*$. Hence,

  $$\begin{aligned} \frac{C_{j}^{A_{1}}}{C_j^*}\le \frac{C_{j-1}^{A_{1}}}{C_{j-1}^*}\le \alpha . \end{aligned}$$

• (II) $J_j$ is scheduled by Step 3.2. We have $l_{j}^2=l_{j-1}^2+\Gamma _{1}=\frac{1+s-\alpha s}{1+s}P_j$ and $l_{j}^1=\frac{\alpha }{1+s}P_j$ as shown in Figs. 2 and 3. If the job is scheduled by Step 3.2(a), we only need to consider the assignment of the preempted task $r_j^k$. Since $r_j^{k_2}\le r_j^k\le r_j^1$, we have $\frac{r_j^{k_2}}{s}\le r_j^1$, which implies that the start time of $r_j^{k_1}$ is not earlier than the finish time of $r_j^{k_2}$, as shown in Fig. 3. If the job is scheduled by Step 3.2(b), the assignment of the job is obviously feasible as shown in Fig. 4.

• (III) $J_j$ is scheduled by Steps 3.3(a), 3.3(b), or 3.3(c1). It is not hard to verify that $l_j^1=\frac{\alpha }{1+s}P_j$ and $l_{j}^2=\frac{1+s-\alpha s}{1+s}P_j$ by the rule of the algorithm as shown in Fig. 6. If the job is scheduled by Step 3.3(a), as shown in Fig. 6a, the time slots assigned to $R_j^1$, $R_j^2$, $R_j^3$, and $R_j^4$ do not overlap. If the job is scheduled by Step 3.3(b), we see that the time slots assigned to $R_j^1$ and $R_j^2$ do not overlap because the completion time of $r_j^1$ is greater than $\frac{1+s-\alpha s}{1+s}P_j$. If the job is scheduled by Step 3.3(c1), the assignment of the job is obviously feasible as shown in Fig. 6(c1).

• (IV) $J_j$ is scheduled by Step 3.3(c2). We have $C_{j}^{A_{1}}=l_{j-1}^1+\frac{r_j^{1'_2}}{s}>\frac{\alpha }{1+s}P_j$ as can been seen in Fig. 6(c2) and $C_j^*\ge \frac{M_j}{1+s}+\frac{r_j^1}{s}$ by Lemma 2.1. Since $l_{j-1}^1=l_{j-1}^2+M_j+r_j^{1'_1}$,

  $$\begin{aligned} P_j= & {} M_j+R_j+sl_{j-1}^1+l_{j-1}^2\ge M_j+r_j^{1'_1}+r_j^{1'_2}+sl_{j-1}^1+l_{j-1}^2 \\ {}= & {} (s+1)l_{j-1}^1+r_j^{1'_2}. \end{aligned}$$

Thus,

$$\begin{aligned} \frac{r_j^{1'_2}}{s}>\frac{(\alpha -1)s(s+1)}{1+s-\alpha s}l_{j-1}^1. \end{aligned}$$

Fig. 6

Step 3.3

With the induction assumption that $l_{j-1}^2\le \frac{1+s-\alpha s}{\alpha }l_{j-1}^1$, we have

$$\begin{aligned} \frac{C_{j}^{A_{1}}}{C_j^*}&\le \frac{l_{j-1}^1+\frac{r_j^{1'_2}}{s}}{\frac{M_j}{1+s}+\frac{r_j^1}{s}} \le \frac{l_{j-1}^1+\frac{r_j^{1'_2}}{s}}{\frac{l_{j-1}^1-l_{j-1}^2}{1+s}+\frac{r_j^{1'_2}}{s} +\frac{r_j^{1'_1}}{s}-\frac{r_j^{1'_1}}{1+s}} \\&<\frac{l_{j-1}^1+\frac{r_j^{1'_2}}{s}}{\frac{l_{j-1}^1-l_{j-1}^2}{1+s}+\frac{r_j^{1'_2}}{s}} \le \frac{l_{j-1}^1 +\frac{(\alpha -1)(s+1)}{1+s-\alpha s}l_{j-1}^1}{\frac{(1-\frac{1+s-\alpha s}{\alpha })l_{j-1}^1}{1+s}+\frac{(\alpha -1)(s+1)}{1+s-\alpha s}l_{j-1}^1}=\alpha . \end{aligned}$$

Finally, we have $l_{j}^1\ge \frac{\alpha }{1+s-\alpha s}l_{j}^2$ from the fact that $l_{j}^1>\frac{\alpha }{1+s}P_j$ and $l_{j}^2<\frac{1+s-\alpha s}{1+s}P_j$.

• (V) $J_j$ is scheduled by Step 4.1, feasibility is trivial. We have $l_{j}^2=l_{j-1}^2+\Gamma _{1}=\frac{1+s-\alpha s}{1+s}P_j$ and $l_{j}^1=\frac{\alpha }{1+s}P_j$ as shown in Fig. 6. Thus, the result is true.

• (VI) $J_j$ is scheduled by Step 4.2. From the algorithm, we see that the loads of the two machines are the same after scheduling the portion $M_j^1=l_{j-1}^1-l_{j-1}^2$. Then the leftover $J_j'=\{M_j',R_j\}$ is scheduled by procedure P. If $J_j'$ is scheduled by Step 1 (or Step 2) in procedure P, then we obtain the desired result by the same discussion in (i) [or (ii)]. So we only need to consider the case where $J_j'$ is scheduled by Step 3.

It is easy to obtain that $C_{j}^{A_{1}}=l_{j-1}^1+\frac{M_j'}{1+s}+\frac{r_j^1}{s}>\frac{\alpha }{1+s}P_j$ by the assumption that $r_j^1\ge s\Delta _1$ and $C_j^*\ge \frac{M_j}{1+s}+\frac{r_j^1}{s}$ by Lemma 2.1. Since $M_j^1=l_{j-1}^1-l_{j-1}^2$, we have

$$\begin{aligned} P_j=M_j^1+M_j'+R_j+sl_{j-1}^1+l_{j-1}^2\ge r_j^1+(s+1)l_{j-1}^1. \end{aligned}$$

So we obtain

$$\begin{aligned} r_j^1\ge \frac{(\alpha -1)s(s+1)}{1+s-\alpha s}l_{j-1}^1>\frac{(\alpha -1)s(s+1)}{1+s-\alpha s}l_{j-1}^1. \end{aligned}$$

By the induction assumption that $l_{j-1}^2\le \frac{1+s-\alpha s}{\alpha }l_{j-1}^1$, we have

$$\begin{aligned} \frac{C_{j}^{A_{1}}}{C_j^*}\le \frac{l_{j-1}^1+\frac{M_j'}{1+s}+\frac{r_j^1}{s}}{\frac{M_j^1}{1+s}+\frac{M_j'}{1+s}+\frac{r_j^1}{s}} \le \frac{l_{j-1}^1+\frac{r_j^1}{s}}{\frac{l_{j-1}^1-l_{j-1}^2}{1+s}+\frac{r_j^1}{s}}\le \frac{l_{j-1}^1 +\frac{(\alpha -1)(s+1)}{1+s-\alpha s}l_{j-1}^1}{\frac{(1-\frac{1+s-\alpha s}{\alpha })l_{j-1}^1}{1+s}+\frac{(\alpha -1)(s+1)}{1+s-\alpha s}l_{j-1}^1}=\alpha . \end{aligned}$$

Clearly, we have $l_{j}^1\ge \frac{\alpha }{1+s-\alpha s}l_{j}^2$ in this case.

In sum, we conclude that the result holds for any $j\ge 2$ and the proof is complete.    $\square$

4 An optimal online algorithm for the non-preemptive variant

In this section we provide an optimal online algorithm $A_2$ for the variant $Q2|M({ frac})R, { onine}|C_{\mathrm{max}}$. The main idea of the algorithm is to schedule the map tasks as early as possible and then schedule all the reduce tasks by the List Scheduling (LS) rule.

Algorithm $A_{2}$

• 1. For every job $J_j$, $1\le j\le n$, schedule the map tasks as early as possible.

• 2. Schedule the reduce tasks by the LS rule.

• 3. Output the schedule.

Theorem 4.1

For the variant $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$, the competitive ratio of algorithm $A_2$ is

$$\begin{aligned} \gamma =\left\{ \begin{array}{ll} \frac{2s+1}{s+1}, &{}\quad \text{ if } \ s<\frac{1+\sqrt{5}}{2};\\ \frac{s+1}{s}, &{}\quad \text{ if } \ s\ge \frac{1+\sqrt{5}}{2} \end{array} \right. . \end{aligned}$$

Proof

The proof is similar to that for the problem $Q2|{ online}|C_{\mathrm{max}}$. Let r be the last finished reduce task and $L_{j}$ be the completion time of the machine $\sigma _i$ before scheduling the reduce task r, $i=1, 2$. By the rule of Algorithm $A_2$, we have

$$\begin{aligned} C^{A_2}=\min \left\{ L_{1}+\frac{r}{s}, L_{2}+r\right\} . \end{aligned}$$

(6)

It is clear that

$$\begin{aligned} P_n=sL_{1}+L_{2}+r\le (1+s)C^{*} \end{aligned}$$

(7)

and

$$\begin{aligned} \frac{r}{s}\le C^{*}. \end{aligned}$$

(8)

From (6), we have $C^{A_2}\le L_{1}+\frac{r}{s}$ and $C^{A_2}\le L_{2}+r$. Combining with (7) and (8), we get

$$\begin{aligned} (s+1) C^{A_2}-r\le (s+1)C^{*}. \end{aligned}$$

Thus, we have $\frac{ C^{A_2}}{C^{*}}\le \frac{2s+1}{s+1}$.

By $C^{A_2}\le L_{1}+\frac{r}{s}$ and (7), we have

$$\begin{aligned} C^{A_2}\le \frac{sL_{1}+r}{s}\le \frac{sL_{1}+L_{2}+r}{s}\le \frac{(1+s)C^{*}}{s} \end{aligned}$$

so $\frac{ C^{A_2}}{C^{*}}\le \frac{s+1}{s}$.

Hence,

$$\begin{aligned} \frac{ C^{A_2}}{C^{*}}\le \min \left\{ \frac{2s+1}{s+1},\frac{s+1}{s}\right\} = \left\{ \begin{array}{ll} \frac{2s+1}{s+1}, &{}\quad \text{ if } \ s<\frac{1+\sqrt{5}}{2};\\ \frac{s+1}{s}, &{}\quad \text{ if } \ s\ge \frac{1+\sqrt{5}}{2}. \end{array} \right. \end{aligned}$$

$\square$

From the proof and the result, we conclude that the problem $Q2|M({ frac})R, { online}|C_{\mathrm{max}}$ is not harder than the classical problem $Q2|{ online}|C_{\mathrm{max}}$.

5 Conclusion

In this paper we study online MapReduce scheduling on two uniform machines to minimize the makespan. Under the assumption that the map tasks are fractional, we consider the cases involving preemptive and non-preemptive reduce tasks. For both variants, we derive lower bounds and optimal online algorithms. We find that the preemptive variant is more complicated than the classical preemptive problem $Q2|{ pmtn}, { online}|C_{\mathrm{max}}$, while the non-preemptive variant is the same as complicated as the classical problem $Q2|{ online}|C_{\mathrm{max}}$. Possible future research directions include studying the general case with $m\ge 3$ machines and online algorithms with partial information.