Online MapReduce scheduling problem of minimizing the makespan

Abstract

MapReduce system is a popular big data processing framework, and the performance of it is closely related to the efficiency of the centralized scheduler. In practice, the centralized scheduler often has little information in advance, which means each job may be known only after being released. In this paper, hence, we consider the online MapReduce scheduling problem of minimizing the makespan, where jobs are released over time. Both preemptive and non-preemptive version of the problem are considered. In addition, we assume that reduce tasks cannot be parallelized because they are often complex and hard to be decomposed. For the non-preemptive version, we prove the lower bound is $\frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))}$, higher than the basic online machine scheduling problem, where k is the root of the equation $k=\big \lfloor {\frac{m-k}{1+\Psi (m)-\Psi (k)}+1 }\big \rfloor$ and m is the quantity of machines. Then we devise an $(2-\frac{1}{m})$-competitive online algorithm called MF-LPT (Map First-Longest Processing Time) based on the LPT. For the preemptive version, we present a 1-competitive algorithm for two machines.

1 Introduction

MapReduce (Dean and Ghemawat 2008) has been an important model in many big data processing applications such as search indexing, distribution sorts, log analysis, machine learning, etc. While popularized by Google, MapReduce is used by several companies including Microsoft, Yahoo, Facebook in their clusters for many of their applications today (Chang et al. 2011).

Fig. 1

MapReduce execution sequence

At a high-level, MapReduce processing essentially consists of two phases: the map phase and the reduce phase (Fig. 1). When a job is submitted to the MapReduce systems, it has to be processed sequentially in these two phases. During the map phase the entire data is divided into several smaller splits and assigned to different machines (workers) for parallel computation of results by centralized scheduler called master node. The map phase will output key-value pairs which are used as inputs of the reduce phase. During the reduce phase the machines process the pairs and output the final results. In short, a single job can be taken as a combination of map task and reduce task: map task executed in the map phase and reduce task in reduce phase, and the reduce phase cannot begin until the map phase ends.

Although MapReduce is a framework for distributed computation, it is integrated in decision making by the centralized scheduler. The scheduler makes the overall scheduling decisions, such as which machine to assign a particular task to and when to execute it. Hence, the effectiveness of MapReduce system is closely related to the efficiency of the centralized scheduler. In recent years, the scheduling problem has been one of the active research topics in MapReduce because of the need to guarantee the performance of system like response times, system utilization, etc. Besides several papers based on practical insights like Zaharia et al. (2008, 2010), Isard et al. (2009), Sandholm and Lai (2009), a great deal of theoretical works have also emerged (Chang et al. 2011; Moseley et al. 2011; Chen et al. 2012; Tan et al. 2012; Wang et al. 2013; Zheng et al. 2013; Yuan et al. 2014; Zhu et al. 2014; Luo et al. 2015). Most of these works concentrate on the offline scheduling problem, where job arrivals are known beforehand. In practice, however, the scheduler can hardly know all the information in advance. As a result, the theoretical research of the online scheduling is in need of urgent attention. To the best of our knowledge, there are little work with respect to it (Moseley et al. 2011; Zheng et al. 2013; Chang et al. 2011; Luo et al. 2015).

For the online MapReduce scheduling problem, Moseley et al. (2011) model the MapReduce scheduling problem as a generalization of the two-stage flexible flow-shop problem (FFS) for minimize the total flow-time. However, the competitive ratio of their online algorithm will be unbounded without resource augmentation. To solve this problem, Zheng et al. (2013) construct a slightly weaker metric of the online algorithm performance called the efficiency ratio. Then they design an online algorithm and claim that it guarantees a small efficiency ratio. Furthermore, Chang et al. (2011) focus on minimizing the total completion time, and devise an online algorithm that achieved 30% improvements compared to FIFO in the view of simulations. However, there is no constant bound to guarantee the online algorithm. For minimizing the makespan, Luo et al. (2015) consider the problem with complex reduce tasks, which means the reduce tasks are non-parallelizable. When the jobs are released over list (i.e. list model), they give two optimal algorithms for both preemptive and non-preemptive versions.

In this paper, we focus on the theoretical study of online MapReduce scheduling problem where jobs are released over time, which is more close to the reality compared to the list model. Moreover, most of the existing studies assume that reduce tasks can be arbitrarily split between multiple servers. However, this may not be true in reality. In practice, the number of reduce processors is much less than that of map processors, and in some cases there is only one reduce processor (like the grep program and so on) (Dean and Ghemawat 2008). These are mainly because reduce tasks are much more complex compared to map tasks, and there are many operations that must be processed in sequence. So far, only Zhu et al. (2014) and Luo et al. (2015) have considered this issue, which is important and needs more attention. Thus, in this paper we assume the reduce task is the minimum level of parallel processing, which means each reduce task cannot be handled by more than one machine at the same time. Detailed problem formulation will be presented in Sect. 2.

The mainly contributions of this paper are as follows:

• 1) When preemption is not allowed, we prove that the lower bound of this problem is $\frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))}$, where k is the root of the equation $k=\big \lfloor {\frac{m-k}{1+\Psi (m)-\Psi (k)}+1 }\big \rfloor$. For the basic online machine scheduling problem (only contains the reduce tasks compared to our problem), Chen and Vestjens (1997) give a lower bound 1.3473 for $m\ge 3$ and 1.3820 for $m=2$ where m represents the quantity of machines. Our new lower bound is proved to be higher than the lower bound of them for $m\ge 3$, which means adding map tasks leads to increasing the basic lower bound. (Sect. 3)

• 2) We present an $(2-\frac{1}{m})$-competitive algorithm called MF-LPT for our problem based on the online LPT algorithm, where m represents the quantity of machines. (Sect. 4)

• 3) For the preemptive version, we devises a 1-competitive algorithm for two machines, which is optimal. (Sect. 5)

2 System model and problem statement

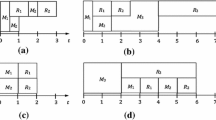
As mentioned above, MapReduce system essentially consists of the map phase and the reduce phase. Each job submitted to the MapReduce system will first go into the map phase and then the reduce phase. Denote a set of jobs by $\mathcal {J}=\{J_1,J_2,\ldots ,J_n\}$, which can be processed on m identical machines $\{\sigma _1,\sigma _2,\ldots ,\sigma _m\}$. Let $M_i$ and $R_i$ denote the total processing time during the map phase and the reduce phase of job $J_i$, respectively. So we can denote each job by $J_i(M_i,R_i,r_i)$ where $r_i$ represents the release time of $J_i$. We also use $M_i$ and $R_i$ to represent the map task and reduce task itself for simplicity if there is no confusion.

Fig. 2

Schematic of MapReduce scheduling

For each job in MapReduce system: (1) The reduce task cannot be processed unless the map task has been finished ($R_1$ follows $M_1$ in Fig. 2), due to the input data of the reduce task relies on the output of the map task. (2) Map task can be arbitrarily split between different machines for distributed computing, however the reduce task is often complex, which means a single reduce task can not be executed on multiple machines at the same time (see $M_1$ and $R_1$ in Fig. 2). (3) When preemption is not allowed, the assignment and scheduling of either map task or reduce task being executed cannot change then, i.e. once $M_2$ is being processed by machine $\sigma _2$ at the time $r_2$, the assignment and scheduling of $M_2$ won’t change even though part of $M_2$ has not yet begun in machine $\sigma _1$ in Fig. 2. On the contrary, when preemption is allowed, any task may be interrupted and resumed at a later time during processing.

From the above formulation, we can notice that if all map tasks equal to zero ($M_i=0 \mathrm {~for~}i=1,2,\ldots ,n)$, this problem becomes the same as the basic online machine scheduling problem (Chen and Vestjens 1997).

The objective of our online algorithm is to minimize the makespan, i.e. the completion time of the last job that finishes. The metric of an online algorithm is usually competitive ratio, which is also known as the worst-case performance. An algorithm A is called $\rho$-competitive if, for any instance, the objective function value of the schedule generated from this algorithm A is no worse than $\rho$ times the objective value of the optimal offline schedule (Fiat and Woeginger 1998), i.e. $C_A(\mathcal {J}) \le \rho \cdot C_{opt}(\mathcal {J})$ for any $\mathcal {J}$, where $C_A(\mathcal {J})$ denotes the objective function value produced by A and $C_{opt}(\mathcal {J})$ denotes the optimal objective value.

3 Lower bound for the non-preemptive version

In this section, we consider the non-preemptive version of the Online MapReduce Scheduling problem of minimizing the Makespan (OMRSM). We first give the lower bound of the problem, i.e. no online algorithm can perform better than it from a worst-case point of view.

Theorem 1

When preemption is not allowed, any $\rho$-competitive online algorithm has

$$\begin{aligned} \rho \ge \frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))} \end{aligned}$$

where Digamma function $\Psi (n+1)=\sum _{i=1}^n \frac{1}{i}-\gamma$, and k is the root of the equation

$$\begin{aligned} k=\bigg \lfloor {\frac{m-k}{1+\Psi (m)-\Psi (k)}+1 }\bigg \rfloor \end{aligned}$$

Proof

First of all, suppose A is a $\rho$-competitive online algorithm for the problem. Then the offline adversary will present several kinds of sets of jobs to set constraints on $\rho$.

Fig. 3

The schedule of $J_1$ obtained by online algorithm A

At time 0, the first job $J_1(M_1,R_1,r_1)=J_1(1,0,0)$ is released. The algorithm A can arbitrarily split the $M_1$ into several pieces and assign them to m machines in parallel. We use $x_i$ to denote the completion time of $M_1$ on each machine $\sigma _i$ $(i=1,2,\ldots ,m)$. Without loss of generality, we assume that the completion times of different machines are arranged in descending order, i.e. $x_1\ge x_2\ge \cdots \ge x_m$ (shown in Fig. 3). Then denote by $s_j$ the starting time of the j-th started piece of $M_1$ on a particular machine, i.e. $s_1\le s_2\le \cdots \le s_m$. It’s obvious that $s_1\le x_m$ and

$$\begin{aligned} \sum _{i=1}^m x_i=\sum _{i=1}^m s_i+1 \end{aligned}$$

(3.1)

For $J_1$, the online cost of the algorithm A will be $C_A(J_1)=x_1$. The optimal offline server (offline scheduler), however, will be able to finish the job by time $C_{opt}(J_1)=\frac{1}{m}$. The online server (online scheduler) is not sure about whether there will be the second job in the future. Thus, to guarantee A is $\rho$-competitive, the online cost must satisfy

$$\begin{aligned} \frac{C_A(J_1)}{C_{opt}(J_1)}=m\cdot x_1\le \rho \end{aligned}$$

(3.2)

Note that, after time $s_1$ when the process of $J_1$ has started, the online server can not change the schedule of $J_1$ according to the assumption before.

At time $s_1$, the offline adversary will present different kinds of sets of jobs for $m-1$ cases. For any case, the online cost $C_A(\mathcal {J})$ must be no worse than $\rho$ times the optimal offline cost $C_{opt}(\mathcal {J})$.

Case $i~(i=1,2,\ldots ,m-1)$: At time $s_1$, a set of jobs $\mathcal {J}^2=\{J_2,J_3,\ldots ,J_{i+1}\}$ are released where $J_2=J_3=\cdots =J_{i+1}(0,\frac{1-m\cdot s_1}{m-i},s_1)$, and no more jobs will be released after then.

According to the differences of the jobs assignment, we consider two subcases of the online server:

(i-a): If the online server assigns different jobs of $\mathcal {J}^2$ to different machines, we have that:

For the online server, $\sigma _{m-i+1}$ is the i-th machine which has finished the $J_1$. Noticing that the $\mathcal {J}^2$ contains i jobs which are assigned to different machines, the online cost is at least $x_{m-i+1}+\frac{1-m\cdot s_1}{m-i}$. However, the offline server can make all machines finish at the same time with a optimal cost $C_{opt}=(1+i\cdot \frac{1-m\cdot s_1}{m-i})/m=\frac{1-i\cdot s_1}{m-i}$. Thus, to guarantee A is $\rho$-competitive, the online cost must satisfy

$$\begin{aligned} \rho \ge \frac{C_A(\mathcal {J})}{C_{opt}(\mathcal {J})} \ge \frac{x_{m-i+1}+\frac{1-m\cdot s_1}{m-i}}{\frac{1-i\cdot s_1}{m-i}} =\frac{(m-i)(x_{m-i+1}-s_1)}{1-i\cdot s_1}+1 \end{aligned}$$

(3.3)

(i-b): If the online server assigns no less than two jobs of $\mathcal {J}^2$ to a single machine, we have that:

For the online server, when two jobs of $\mathcal {J}^2$ are assigned to a single machine, the online cost is at least $x_m+2(\frac{1-m\cdot s_1}{m-i})$. For the offline server, the optimal cost is the same as before $C_{opt}=\frac{1-i\cdot s_1}{m-i}$. Thus, to guarantee A is $\rho$-competitive, the online cost must satisfy

$$\begin{aligned} \rho \ge \frac{C_A(\mathcal {J})}{C_{opt}(\mathcal {J})} \ge \frac{x_m+2\left( \frac{1-m\cdot s_1}{m-i}\right) }{\frac{1-i\cdot s_1}{m-i}} =2-\frac{(m-i)(2s_1-x_m)}{1-i\cdot s_1} \end{aligned}$$

(3.4)

Up to now, we have listed all the constraints of $\rho$. Then, we will analyze how good $\rho$ can be with these constraints.

• 1. When the online server assigns different jobs of $\mathcal {J}^2$ to different machines in all cases:

  Due to the offline adversary can arbitrarily decide the $\mathcal {J}^2$, to guarantee A is $\rho$-competitive, the online cost must satisfy (3.1), (3.2), (3.3). So the problem can be taken as the minimization of $\rho$ with these constraints:

  $$\begin{aligned} \min&\quad \rho =b \nonumber \\ \text{ s.t. }&~ {\left\{ \begin{array}{ll} \sum \limits _{i=1}^m x_i=\sum \limits _{i=1}^m s_i+1\\ m\cdot x_1\le b\\ \frac{(m-i)(x_{m-i+1}-s_1)}{1-i\cdot s_1}+1 \le b,\quad i=1,2,\ldots ,m-1\\ 0\le s_1\le s_2\le \cdots \le s_m\\ x_1\ge x_2\ge \cdots \ge x_m\ge s_1 \end{array}\right. } \end{aligned}$$

  (3.5)

  By solving (3.5), we find the minimum value of $\rho$ (for details see Appendix A):

  $$\begin{aligned} \rho ^* = \frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))} \end{aligned}$$

  where Digamma function $\Psi (n+1)=\sum _{i=1}^n \frac{1}{i}-\gamma$, and k is the root of the equation

  $$\begin{aligned} k=\bigg \lfloor {\frac{m-k}{1+\Psi (m)-\Psi (k)}+1 }\bigg \rfloor \end{aligned}$$

• 2. On the contrary, when the online server assigns no less than two jobs of $\mathcal {J}^2$ to a single machine in certain case:

The online cost must satisfy (3.1),(3.2),(3.4). Considering (3.1) and (3.2), we have $\rho \ge m\cdot x_1 \ge \sum _{i=1}^m x_i = \sum _{i=1}^m s_i+1 \ge m\cdot s_1+1$, i.e. $m\cdot s_1 \le \rho -1$. Thus, we can get the bound of $\rho$ from (3.4):

$$\begin{aligned} \begin{aligned} \rho&\ge 2-\frac{(m-i)(2s_1-x_m)}{1-i\cdot s_1} \ge 2-\frac{(m-i)s_1}{1-i\cdot s_1} \ge 2-\frac{\rho -1-i\cdot s_1}{1-i\cdot s_1} \\&=1+\frac{2-\rho }{1-i \cdot s_1} \ge 3-\rho \end{aligned} \end{aligned}$$

Therefore, $\rho \ge \frac{3}{2}$.

Above all, we conclude that the lower bound of this problem is $\min \{\rho ^*,\frac{3}{2}\}$. After further analysis in Appendix B, we have $\rho ^*<\frac{3}{2}$ and the theorem is proved. $\square$

Because we can hardly know the analytical solution of k, we list several numerical results (Table 1) of the lower bound for comparison.

Table 1 Numerical results

Letting $M_i=0$ (for any i), the problem becomes the same as the basic online machine scheduling problem. Chen and Vestjens (1997) gives a lower bound 1.3473 for $m\ge 3$ and 1.3820 for $m=2$ where m represents the quantity of machines. Compared with the basic lower bound, the Table 1 shows that we get a higher lower bound for $m\ge 3$ by adding map tasks.

4 The online MF-LPT algorithm

In this section, for the non-preemptive version of the problem, we present a new algorithm called MF-LPT (Map First-Longest Processing Time) based on the online LPT algorithm (Chen and Vestjens 1997). It guarantees a competitive ratio of $(2-\frac{1}{m})$ for the OMRSM where jobs are released over time. The MF-LPT is described completely by its behavior at the moment when any machine becomes available. Letting $\mathcal {M}$ denote all the unscheduled map tasks and $\mathcal {R}$ denote all the unscheduled reduce tasks, the MF-LPT can be formally described as follows.

Let $\mathcal {J}_s$ be any set of jobs with no common idle throughout the online schedule, i.e. at any time before $C_{\texttt {MF-LPT}}(\mathcal {J}_s)$ in the online schedule, at least one machine is busy.

Lemma 1

If $C_{{{\texttt {MF-LPT}}}}(\mathcal {J}_s) \le \rho \cdot C_{opt}(\mathcal {J}_s)$ for any $\mathcal {J}_s$, the MF-LPT algorithm is $\rho$-competitive.

The proof of Lemma 1 can be easily obtained from the proof of Observation 1 in Chen and Vestjens (1997).

Theorem 2

When preemption is not allowed, the online MF-LPT algorithm is $(2-\frac{1}{m})$-competitive, and the ratio is tight.

Fig. 4

Online schedule for $\mathcal {J}_s$

Proof

According to Lemma 1, we just need to prove the MF-LPT is $(2 - \frac{1}{m})$-competitive for any $\mathcal {J}_s$. Let $J_l(M_l,R_l,r_l)$ be the last finished job in online schedule of $\mathcal {J}_s$, and $S_l$ be the starting time of $R_l$. As we know, during the period $[0,r_l]$, there may be sometime when some machine is idle. Let I denote the summation of the time during which at least one machine is idle (we put the idle time together for convenience in Fig. 4). Note that: (1) There is at least one machine is busy during the interval I, because there is no common idle in online schedule we has assumed in previous. (2) Besides the idle time I, there will be a $(r_l-I)$ long period of time with no idle machine before $r_l$. (3) No machine can be idle during the interval $[r_l,S_l]$, otherwise the $R_l$ will start before $S_l$ according to the LPT-rule.

Thus, we can obtain a lower bound of the offline cost:

$$\begin{aligned} \begin{aligned} C_{opt}(\mathcal {J}_s)&\ge (r_l-I)+(S_l-r_l)+\frac{I+R_l}{m}\\&= S_l-\frac{m-1}{m}I+\frac{1}{m}R_l \end{aligned} \end{aligned}$$

(4.1)

Moreover, noting that the $J_l$ is released at $r_l$, and I is at most $r_l$, we can obtain another lower bound of the offline cost:

$$\begin{aligned} C_{opt}(\mathcal {J}_s) \ge r_l+R_l \ge I+R_l \end{aligned}$$

(4.2)

To sum up, from the two lower bounds (4.1) and (4.2) displayed above, we can have

$$\begin{aligned} C_{opt}(\mathcal {J}_s) \ge \max \{S_l-\frac{m-1}{m}I+\frac{1}{m}R_l,I+R_l\} \end{aligned}$$

(4.3)

For the online cost, obviously

$$\begin{aligned} C_{{{\texttt {MF-LPT}}}}(\mathcal {J}_s) = S_l+R_l \end{aligned}$$

(4.4)

• 1. When $S_l-\frac{m-1}{m}I+\frac{1}{m}R_l \ge I+R_l$, according to (4.3) and (4.4) we have:

  $$\begin{aligned} \begin{aligned} \frac{C_{{{\texttt {MF-LPT}}}}(\mathcal {J}_s)}{C_{opt}(\mathcal {J}_s)}&\le \frac{S_l+R_l}{S_l-\frac{m-1}{m}I+\frac{1}{m}R_l}\\&= 1+\frac{m-1}{m}\cdot \frac{I+R_l}{S_l-\frac{m-1}{m}I+\frac{1}{m}R_l}\\&\le 2-\frac{1}{m} \end{aligned} \end{aligned}$$

  (4.5)

• 2. When $S_l-\frac{m-1}{m}I+\frac{1}{m}R_l < I+R_l$, according to (4.3) and (4.4) we have:

  $$\begin{aligned} \begin{aligned} \frac{C_{{{\texttt {MF-LPT}}}}(\mathcal {J}_s)}{C_{opt}(\mathcal {J}_s)}&\le \frac{S_l+R_l}{I+R_l}\\&= \frac{S_l-\frac{m-1}{m}I+\frac{1}{m}R_l}{I+R_l}+\frac{m-1}{m}\\&< 2-\frac{1}{m} \end{aligned} \end{aligned}$$

  (4.6)

Therefore, (4.5) and (4.6) proves that the algorithm is $(2-\frac{1}{m})$-competitive.

The following example shows that the ratio of $2-\frac{1}{m}$ is asymptotically tight. At time 0, $J_1(M_1,0,0)$ is released, and at time $\epsilon$, $J_2(0,\frac{{{M_1}}}{{m - 1}} - (\frac{m}{m-1})\epsilon ,\epsilon )$ is released, where $\epsilon$ is some small positive number. Due to the online server will schedule the $M_1$ parallelly between machines and assign $J_2$ after that, the online cost is $C_{\texttt {MF-LPT}}(\mathcal {J}) = \frac{M_1}{m} + \frac{M_1}{m - 1} - (\frac{m}{m-1})\epsilon$. However, the optimal cost is $C_{opt}(\mathcal {J})=\frac{M_1-\epsilon }{m-1}$. The ratio tends to $2-\frac{1}{m}$ as $\epsilon$ tends to 0. $\square$

5 A 1-competitive preemptive algorithm for two machines

In this section, we consider the preemptive version, where the processing of any operation may be interrupted and resumed at a later time. For the preemptive scheduling problem, Algorithm 5.2.3 in Pinedo (2012) shows a common way to deal with the preemptive jobs. Guo and Kang (2013) devised an algorithm which well solved the online parallel jobs scheduling problem with preemption, but the parallel jobs are different from the map tasks in our paper. The parallel job must be processed on multiple machines simultaneously, while the map task can be processed on either multiple machines or an arbitrary single machine. Based on these two algorithms, we present a 1-competitive algorithm called Algorithm M for two machines in the following.

Recall that each job $J_i$ in the job set $\mathcal {J}=\{J_1,J_2,\ldots ,J_n\}$ has a release time $r_i$. We separate the job set $\mathcal {J}$ into different groups by release time, putting the jobs with same release time into a same group, and denote the release time of jobs in the ith group by $t_i$ ($t_1 <t_2 <\dots < t_p$). The Algorithm M makes decisions at every $t_i$. If a job is processing at time $t_i$, we stop it and take the remaining part of it as a new job with release time $t_i$, since the preemption is allowed. We denote by $\mathcal {J}^i$ the set of all jobs available at time $t_i$. $\mathcal {J}^i$ may contain “new” jobs that arrive at time $t_i$, remaining parts of jobs that are being processed at time $t_i$ and “old” jobs that have not been processed in $\mathcal {J}^{i-1}$. We denote by $J^i_j$ the job $J_j$ or the remaining part of job $J_j$ appearing in set $\mathcal {J}^i$, $M^i_j$ and $R^i_j$ the length of map task and reduce task of job $J^i_j$ respectively. Let $\overline{M^i}$ be the total length of all map tasks in $\mathcal {J}^i$, and $\overline{R^i}$ be the total length of all reduce tasks in $\mathcal {J}^i$. Denote by $J^i_l(M^i_l,R^i_l)$ the job who has the longest reduce task than other reduce tasks of any job in $\mathcal {J}^i$, i.e. $l=\hbox {arg max}_{j}R^i_j$. The algorithm will produce three different types of schedule for different $R^i_j$. The Algorithm M can be formally described as follows.

Lemma 2

The schedule produced by Algorithm M is feasible, i.e. (1) for any job $J^i_j(M^i_j,R^i_j)$, $R^i_j$ is processed after $M^i_j$ has been finished, and (2) there is no reduce task that is processed on two machines simultaneously.

Proof

When $R^i_l \le \frac{1}{2}\overline{R^i}$, the Algorithm M schedules all map tasks first, thus it’s obvious that $R^i_j$ is processed after $M^i_j$ has been finished for any i. Note that there is at most one reduce task $R^i_d$ that will be divided into two parts in the reduce tasks list formed by the Algorithm M, and one part at the end of the first half list, while the other part at the beginning of the second half list (as $R^i_3$ exhibited in Fig. 5). Hence, if the two parts of the reduce task $R^i_d$ are processed on two machines simultaneously, $R^i_d$ must be larger than $\frac{1}{2}\overline{R^i}$, which is contradictory to $R^i_d \le R^i_l \le \frac{1}{2}\overline{R^i}$.

When $\frac{1}{2}\overline{R^i} < R^i_l \le \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$, according to Algorithm M, there is no reduce task that will be split, which means no reduce task will be processed on two machines simultaneously. Moreover, $R^i_j$ is processed after $M^i_j$ has been finished for any i, because $R^i_l$ is processed after $M^i_l$, and all other reduce tasks are processed after all map tasks (see Fig. 6).

Fig. 5

A possible temporary 1-type schedule (i.e. $R^i_l \le \frac{1}{2}\overline{R^i}$)

Fig. 6

A possible temporary 2-type schedule (i.e. $\frac{1}{2}\overline{R^i} < R^i_l \le \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$)

Fig. 7

A possible temporary 3-type schedule (i.e. $R^i_l > \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$)

The case when $R^i_l > \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$ is similar to the previous case (see Fig. 7). Therefore, the lemma is proved. $\square$

Without loss of generality, we assume that there is no common idle throughout the online schedule, i.e. at least one machine is busy during the schedule. From the assumption, we have that the first group of jobs is released at time 0, i.e. $t_1=0$.

Lemma 3

Algorithm M is 1-competitive when all jobs are released at time 0.

Proof

If all jobs are released at time 0, there is only one job set $\mathcal {J}^1$ and one schedule produced by the Algorithm M. We will consider three different types of schedule produced by Algorithm M in the following.

• 1. If the schedule is 1-type schedule, i.e. $R^i_l \le \frac{1}{2}\overline{R^i}$:

  According to Algorithm M, the 1-type schedule guarantees that the two machines have the same completion time $C_\texttt {M}(\mathcal {J}^1)$, and there is no idle time during the period $[0,~C_\texttt {M}(\mathcal {J}^1)]$. Hence, $C_{opt}(\mathcal {J}^1)=C_\texttt {M}(\mathcal {J}^1)$ (as shown in Fig. 5).

• 2. If the schedule is 2-type schedule, i.e. $\frac{1}{2}\overline{R^i} < R^i_l \le \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$:

  According to Algorithm M, $M^i_l$ and part of other map tasks will be scheduled in parallel. So the total length of the rest map tasks is $\overline{M^i}-(M^i_l+(\overline{R^i}+\overline{M^i}-M^i_l-2R^i_l))=2R^i_l-\overline{R^i}$. Then the $R^i_l$ is scheduled on machine $\sigma _1$. Finally, the rest of the map tasks with length $2R^i_l-\overline{R^i}$ along with the rest of the reduce tasks with length $\overline{R^i}-R^i_l$ are scheduled on machine $\sigma _2$. Therefore, the completion time of $\sigma _1$ is $\frac{M^i_l}{2}+\frac{\overline{R^i}+\overline{M^i}-M^i_l-2R^i_l}{2}+R^i_l=\frac{\overline{R^i}+\overline{M^i}}{2}$, and the completion time of $\sigma _2$ is $\frac{M^i_l}{2}+\frac{\overline{R^i}+\overline{M^i}-M^i_l-2R^i_l}{2}+(2R^i_l-\overline{R^i})+(\overline{R^i}-R^i_l)=\frac{\overline{R^i}+\overline{M^i}}{2}$, i.e. $C_\texttt {M}(\mathcal {J}^1)=\frac{\overline{R^i}+\overline{M^i}}{2}$. Due to $C_{opt}(\mathcal {J}^1)\ge \frac{\overline{R^i}+\overline{M^i}}{2}$, the Algorithm M is optimal (as shown in Fig. 6).

• 3. If the schedule is 3-type schedule, i.e. $R^i_l > \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$:

  After $M^i_l$ is scheduled in parallel, the $R^i_l$ is scheduled on $\sigma _1$ and the rest of the map tasks with length $\overline{M^i}-M^i_l$ along with the rest of the reduce tasks with length $\overline{R^i}-R^i_l$ are scheduled on $\sigma _2$. Therefore, the completion time of $\sigma _1$ is $\frac{M^i_l}{2}+R^i_l$, and the completion time of $\sigma _2$ is $\frac{M^i_l}{2}+\overline{M^i}-M^i_l+\overline{R^i}-R^i_l$. Due to $R^i_l > \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$, $C_\texttt {M}(\mathcal {J}^1)=\max \{\frac{M^i_l}{2}+R^i_l,\frac{M^i_l}{2}+\overline{M^i}-M^i_l+\overline{R^i}-R^i_l\}=\frac{M^i_l}{2}+R^i_l$. Because $C_{opt}\ge \frac{M^i_l}{2}+R^i_l$, the Algorithm M is optimal (as shown in Fig. 7).

Therefore, the Algorithm M is optimal when all jobs are released at 0. $\square$

Lemma 4

If $J_j$ is released at time $t_{i_0}$ and its reduce task in job set $\mathcal {J}^k$ satisfies $R^k_j > \frac{1}{2}(\overline{R^k}+\overline{M^k}-M^k_j)$, then for any $i \in [i_0,k]$ it satisfies $R^i_j > \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_j)$.

Proof

Suppose to the contrary that $\exists ~i \in [i_0,k]$, $R^i_j \le \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_j)$ and $R^k_j > \frac{1}{2}(\overline{R^k}+\overline{M^k}-M^k_j)$. At time $t_i$, the Algorithm M produces a schedule and then keeps processing tasks according to the schedule until the next group of new jobs are released at time $t_{i+1}$. Denote by $R^{i^+}_j$ the remaining length of $R^i_j$ at time $t_{i+1}$, and $M^{i^+}_j,~\overline{R^{i^+}},~\overline{M^{i^+}}$ in a similar fashion.

• 1. If Algorithm M produces a 1-type schedule at time $t_i$, we have $R^i_j \le R^i_l\le \frac{1}{2}\overline{R^i}$. According to the Algorithm M, at time $t_{i+1}$, the remaining length of $R^i_j$, i.e. $R^{i^+}_j$, is no more than $\frac{1}{2}\overline{R^{i^+}}$. Note that $R^{i^+}_j$ and $R^{i+1}_j$ are equal in value and $\overline{R^{i^+}} \le \overline{R^{i+1}}$. Therefore, $R^{i+1}_j =R^{i^+}_j \le \frac{1}{2}\overline{R^{i^+}} \le \frac{1}{2}\overline{R^{i+1}} \le \frac{1}{2}(\overline{R^{i+1}}+\overline{M^{i+1}}-M^{i+1}_j)$.

• 2. If Algorithm M produces a 2-type schedule at time $t_i$, we have $\frac{1}{2}\overline{R^i} < R^i_l \le \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$. According to Algorithm M, $M^i_l$ and part of the rest map tasks will be processed first (see Fig. 6).

  • (1) If at time $t_{i+1}$ the $R^i_l$ has not been started, then besides $M^i_l$ there is at most $\overline{R^i}+\overline{M^i}-M^i_l-2R^i_l$ map tasks have been processed during the period $[t_i,~t_{i+1}]$. So, $R^{i^+}_l=R^{i}_l$, $\overline{R^{i^+}}=\overline{R^i}$ and $\overline{M^{i^+}} -M^{i^+}_l \ge \overline{M^i}-(\overline{R^i}+\overline{M^i}-M^i_l-2R^i_l)-M^i_l=2R^i_l-\overline{R^i}$. Therefore, $\frac{1}{2}(\overline{R^{i^+}}+\overline{M^{i^+}}-M^{i^+}_l) \ge \frac{1}{2}(\overline{R^i}+2R^i_l-\overline{R^i})=R^i_l=R^{i^+}_l$. Due to $\overline{R^{i^+}} \le \overline{R^{i+1}}$ and $\overline{M^{i^+}} \le \overline{M^{i+1}}$, we can finally get that $R^{i+1}_j\le R^{i^+}_l \le \frac{1}{2}(\overline{R^{i^+}}+\overline{M^{i^+}}-M^{i^+}_l) \le \frac{1}{2}(\overline{R^{i+1}}+\overline{M^{i+1}}-M^{i+1}_l)$.

  • (2) If at time $t_{i+1}$ the $R^i_l$ has been started, obviously $R^{i^+}_l = \frac{1}{2}(\overline{R^{i^+}}+\overline{M^{i^+}}-M^{i^+}_l)$. Due to $\overline{R^{i^+}} \le \overline{R^{i+1}}$ and $\overline{M^{i^+}} \le \overline{M^{i+1}}$, we can get that $R^{i+1}_j\le R^{i^+}_l = \frac{1}{2}(\overline{R^{i^+}}+\overline{M^{i^+}}-M^{i^+}_l) \le \frac{1}{2}(\overline{R^{i+1}}+\overline{M^{i+1}}-M^{i+1}_l)$.

    To sum up, we have $R^{i+1}_j \le \frac{1}{2}(\overline{R^{i+1}}+\overline{M^{i+1}}-M^{i+1}_l)$.

• 3. If Algorithm M produces a 3-type schedule at time $t_i$, we have $R^i_l > \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$. As $R^i_j < \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_l)$, so $j\ne l$. According to Algorithm M, the inequation $R^{i^+}_j<\frac{1}{2}\overline{R^{i^+}}$ will always be true. Therefore, $R^{i+1}_j=R^{i^+}_j<\frac{1}{2}\overline{R^{i^+}}\le \frac{1}{2}\overline{R^{i+1}} \le \frac{1}{2}(\overline{R^{i+1}}+\overline{M^{i+1}}-M^{i+1}_l)$.

To conclude, if $R^i_j \le \frac{1}{2}(\overline{R^i}+\overline{M^i}-M^i_j)$, then $R^{i+1}_j \le \frac{1}{2}(\overline{R^{i+1}}+\overline{M^{i+1}}-M^{i+1}_j)$ for any i. By this analogy, we have $R^k_j \le \frac{1}{2}(\overline{R^k}+\overline{M^k}-M^k_j)$, a contradiction. $\square$

Lemma 4 implies that if $J^k_j$ in job set $\mathcal {J}^k$ leads to 3-type schedule at time $t_k$, $J_j$ always leads to 3-type schedule from its release time.

Theorem 3

When preemption is allowed, Algorithm M is 1-competitive.

Proof

According to Lemma 3, we have $C_{opt}(\mathcal {J}^1)=C_\texttt {M}(\mathcal {J}^1)$. Thus, we suppose $C_{opt}(\mathcal {J}^i)=C_\texttt {M}(\mathcal {J}^i)$ for any $i \le k$ where $k\ge 1$. Then we will show that the equation $C_{opt}(\mathcal {J}^{k+1})=C_\texttt {M}(\mathcal {J}^{k+1})$ still holds in any cases.

Case 1: $R^{k+1}_l \le \frac{1}{2}(\overline{R^{k+1}}+\overline{M^{k+1}}-M^{k+1}_l)$, i.e. the Algorithm M produces a 1-type or 2-type schedule for job set $\mathcal {J}^{k+1}$.

In this case, the two machines have the same completion time $C_\texttt {M}(\mathcal {J}^{k+1})$. If there is no idle time in the online schedule during the period $[0,~C_\texttt {M}(\mathcal {J}^{k+1})]$, we can easily get that $C_{opt}(\mathcal {J}^{k+1})=C_\texttt {M}(\mathcal {J}^{k+1})$. So we consider the case there are some idle time in the online schedule. Suppose the last idle time ends at time $t_{i_0}$, when the job set $\mathcal {J}^{i_0}$ arrived. From the Algorithm M, we know that the schedule of $\mathcal {J}^{i_0-1}$ is a 3-type schedule, and the remaining task of $\mathcal {J}^{i_0-1}$ at time $t_{i_0}$ is only a reduce task with length $C_\texttt {M}(\mathcal {J}^{i_0-1})-t_{i_0}$. Due to the fact that all machines are busy during $[t_{i_0},~C_\texttt {M}(\mathcal {J}^{k+1})]$, the total workload of jobs released after $t_{i_0}$ is $2(C_\texttt {M}(\mathcal {J}^{k+1})-t_{i_0})-(C_\texttt {M}(\mathcal {J}^{i_0-1})-t_{i_0})$.

For the offline schedule, due to $C_{opt}(\mathcal {J}^{i_0-1})=C_\texttt {M}(\mathcal {J}^{i_0-1})$, there is at least $C_{opt}(\mathcal {J}^{i_0-1})-t_{i_0}$ length of tasks that have not been processed at time $t_{i_0}$. Considering the jobs released after time $t_{i_0}$, we have

$$\begin{aligned}&C_{opt}(\mathcal {J}^{k+1}) \\&\quad \ge t_{i_0}+\frac{1}{2}\Big (C_{opt}(\mathcal {J}^{i_0-1})-t_{i_0}+2\big (C_\texttt {M}(\mathcal {J}^{k+1})-t_{i_0}\big )-\big (C_\texttt {M}(\mathcal {J}^{i_0-1})-t_{i_0}\big )\Big ) \\&\quad =C_\texttt {M}(\mathcal {J}^{k+1})+\frac{1}{2}\big (C_{opt}(\mathcal {J}^{i_0-1})-C_\texttt {M}(\mathcal {J}^{i_0-1})\big ) \\&\quad =C_\texttt {M}(\mathcal {J}^{k+1}) \end{aligned}$$

Case 2: $R^{k+1}_l > \frac{1}{2}(\overline{R^{k+1}}+\overline{M^{k+1}}-M^{k+1}_l)$, i.e. the Algorithm M produces a 3-type schedule for job set $\mathcal {J}^{k+1}$.

In this case, according to Lemma 4, the job $J^{k+1}_l$ always causes 3-type schedule from its release time. Suppose $l=i_1$, so the $J^{k+1}_l$ is released at time $r_{i_1}$. According to the Algorithm M, the process of $J_{i_1}$ never be interrupted. Hence, $C_\texttt {M}(\mathcal {J}^{k+1})=r_{i_1}+\frac{1}{2}M_{i_1}+R_{i_1}$. Due to $C_{opt}(\mathcal {J}^{k+1})\ge r_{i_1}+\frac{1}{2}M_{i_1}+R_{i_1}$, we have $C_{opt}(\mathcal {J}^{k+1})\ge C_\texttt {M}(\mathcal {J}^{k+1})$.

Above all, we can conclude that the equation $C_{opt}(\mathcal {J}^{k+1})= C_\texttt {M}(\mathcal {J}^{k+1})$ is also true. So $C_{opt}(\mathcal {J}^i)= C_\texttt {M}(\mathcal {J}^i)$ is true for all i, i.e. the Algorithm M is optimal. $\square$

6 Conclusion

In this paper, we mainly focus on the theoretical study of the online MapReduce scheduling problem of minimizing the makespan, where jobs are released over time. Both preemptive and non-preemptive version of the problem are considered. Besides the precedence between the map and reduce tasks, we also consider the complexity difference between them (Zhu et al. 2014; Luo et al. 2015). With the assumption that the reduce tasks are non-parallelizable due to the complexity, this problem can be viewed as an extended online machine scheduling problem (only contains the reduce tasks compared to us). We proved that, when preemption is not allowed, no online algorithm can achieve a better competitive ratio than $\frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))}$, where k is the root of the equation $k=\big \lfloor {\frac{m-k}{1+\Psi (m)-\Psi (k)}+1 }\big \rfloor$. The numerical results in Table 1 show that we get an increased lower bound compared with the basic online machine scheduling problem (Chen and Vestjens 1997). Then we present an online MF-LPT algorithm with a competitive ratio of $(2-\frac{1}{m})$. In addition, when preemption is allowed, we give an 1-competitive algorithm for two machines, which is optimal obviously. However, future work is needed to consider the m machines case of the preemptive version problem.

Appendices

Appendix 1: The solution of $\rho ^*$

To make (3.5) easier to solve, we transform it into:

$$\begin{aligned} \min \quad \rho =\max \{b_1,b_2,\ldots ,b_m\} \end{aligned}$$

Substituting (7.1b) and (7.1c) into (7.1a), we have

$$\begin{aligned} \sum _{i=1}^m x_i = \frac{b_1}{m}+\sum _{i=1}^{m-1}\frac{(b_{m-i+1}-1)(1-i\cdot s_1)}{m-i} +(m-1)s_1 = \sum _{i=1}^m s_i+1 \end{aligned}$$

(7.2)

Noticing that, in (7.2), $\frac{\partial b_1}{\partial s_i}=m>0 ~ (\forall i\in \{2,3,\ldots ,m\})$ and $\frac{\partial b_j}{\partial s_i}=\frac{j-1}{1-(m-j+1)s_1}>0 ~ (\forall i,j\in \{2,3,\ldots ,m\})$, we have that $\forall j\in \{1,2,\ldots ,m\}$, $b_j$ is monotonically increasing in $s_i$ for any $i\in \{2,3,\ldots ,m\}$. Thus, to minimize the objective function $\rho =\max \{b_1,b_2,\ldots ,b_m\}$, the $s_i$ must be as small as possible. As well as (7.1d), we conclude that $s_1=s_2=\cdots =s_m$. So we can simplify (7.2) into the following equation

$$\begin{aligned} \frac{b_1}{m}+\sum _{i=1}^{m-1}\frac{(b_{m-i+1}-1)(1-i\cdot s_1)}{m-i}-s_1 = 1 \end{aligned}$$

(7.3)

For (7.3), we have that

$$\begin{aligned} \left\{ \! \begin{aligned} \frac{{\partial {b_1}}}{{\partial {s_1}}}&= m\left( {1 + \sum \limits _{i = 1}^{m - 1} {\frac{{\left( {{b_{m + 1 - i}} - 1} \right) \cdot i}}{{\left( {m - i} \right) }}} } \right) > 0\\ \frac{{\partial {b_j}}}{{\partial {s_1}}}&= \frac{{\left( {j - 1} \right) \left( {1 + \sum \nolimits _{i = 1}^{m - 1} {\frac{{\left( {{b_{m + 1 - i}} - 1} \right) \cdot i}}{{\left( {m - i} \right) }}} } \right) }}{{1 - \left( {m - j + 1} \right) {s_1}}} > 0,\quad j = 2,3,\ldots ,m \end{aligned} \right. \end{aligned}$$

Since $\forall j\in \{1,2,\ldots ,m\}$, $b_j$ is monotonically increasing in $s_1$, to minimize the objective function $\rho =\max \{b_1,b_2,\ldots ,b_m\}$, the $s_1$ must be as small as possible, i.e. $s_1=0$. As well as (7.1e), we can simplify (7.3) into the following

$$\begin{aligned}&\frac{{{b_1}}}{m} + \frac{{{b_2} - 1}}{1} + \frac{{{b_3} - 1}}{2} + \dots + \frac{{{b_m} - 1}}{{m - 1}} = 1 \end{aligned}$$

(7.4)

$$\begin{aligned}&\frac{{{b_1}}}{m} \ge \frac{{{b_2} - 1}}{1} \ge \frac{{{b_3} - 1}}{2} \ge \dots \ge \frac{{{b_m} - 1}}{{m - 1}} \end{aligned}$$

(7.5)

Suppose the number $p\in \{1,2,\ldots ,m\}$ such that $b_p=\max \{b_1,b_2,\ldots ,b_m\}$. For (7.4), $\forall j \in \{1,2,\ldots ,p-1,p+1,\ldots ,m\}$, $\frac{{\partial {b_p}}}{{\partial {b_j}}} < 0$ obviously. Hence, $\forall j\in \{1,2,\ldots ,m\}$, $b_p$ is monotonically increasing in $b_j$. To minimizie $b_p$, $b_j$ must be as large as possible with the constraints $b_j\le b_p$ and (7.5).

Firstly, For $b_1$, it should be equal to $b_p$. Then, if we temporarily ignore the first inequation in (7.5), $\forall j\in \{2,3,\ldots ,m\}$, $b_j$ can freely increase to $b_p$. But taking the first inequation into account may lead to some $b_j$ can not reach $b_p$. We denote the last $b_j$ who can not reach $b_p$ by $b_k$, i.e. $\{b_2,b_3,\ldots ,b_k\}$ cannot increase to $b_p$. To minimizie $b_p$, $\forall i\in \{2,3,\ldots ,k\}$, $b_i$ can increase to $\frac{i-1}{m}b_p+1$ so that $\frac{b_p}{m}=\frac{b_i-1}{i-1}$. Lastly, $\{b_{k+1},b_{k+2},\ldots ,b_m\}$ can increase to $b_p$. Eventually, after each $b_j$ become as large as possible, (7.4) turn into

$$\begin{aligned} \begin{array}{l} \underbrace{\frac{{{b_p}}}{m} + \frac{{{b_p}}}{m} + \cdots +\frac{{{b_p}}}{m}}_k + \underbrace{\frac{{{b_p} - 1}}{{{k}}} + \frac{{{b_p} - 1}}{{{k} + 1}} + \cdots + \frac{{{b_p} - 1}}{{m - 1}}}_{m - k} \\ = \displaystyle {k} \cdot \frac{{{b_p}}}{m} + \left( {{b_p} - 1} \right) {\sum _{{k}}^{m - 1} {\frac{1}{i}} } = 1 \end{array} \end{aligned}$$

(7.6)

where k satisfy

$$\begin{aligned} \left\{ \! \begin{aligned} \frac{{{b_p} - 1}}{{k - 1}}&\ge \textstyle \frac{{{b_p}}}{m}\\ \frac{{{b_p} - 1}}{k}&< \textstyle \frac{{{b_p}}}{m}\\ \end{aligned} \right. \end{aligned}$$

(7.7)

From (7.6) and (7.7), we have:

$$\begin{aligned} \rho ^* =b_p = \frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))} \end{aligned}$$

where $\Psi (n+1)=\sum _{i=1}^n \frac{1}{i}-\gamma$, and k is the root of $k =\Big \lfloor {\frac{m-k}{1+\Psi (m)-\Psi (k)}+1 }\Big \rfloor$.

Appendix 2: The proof of $\rho ^*<\frac{3}{2}$

To prove $\rho ^*=\frac{m+m(\Psi (m)-\Psi (k))}{k+m(\Psi (m)-\Psi (k))}<\frac{3}{2}$, we just need to prove

$$\begin{aligned} \frac{{3k}}{m} + \Psi (m)-\Psi (k) > 2 \end{aligned}$$

(8.1)

Since we can hardly know the exact value of $\frac{{3k}}{m} + \Psi (m)-\Psi (k)$ in (8.1), we have to use inequation to bound it. DeTemple (1993) propose that

$$\begin{aligned} \frac{1}{24n^2} < \Psi (n)-\ln \left( n-\frac{1}{2}\right) < \frac{1}{24(n-1)^2} \end{aligned}$$

(8.2)

Substituting (8.2) into (8.1), we have

$$\begin{aligned} \frac{3k}{m} + \Psi (m)-\Psi (k) > \frac{{3k}}{m} + \frac{1}{{24{m^2}}} - \frac{1}{{24{{\left( {k - 1} \right) }^2}}} + \ln \left( \frac{m - \frac{1}{2}}{k - \frac{1}{2}} \right) \end{aligned}$$

After calculation, for $k \ge 2$, we have

$$\begin{aligned} \frac{{3k}}{m} + \frac{1}{{24{m^2}}} - \frac{1}{{24{{\left( {k - 1} \right) }^2}}} + \ln \left( \frac{m - \frac{1}{2}}{k - \frac{1}{2}} \right) > 2 \end{aligned}$$

For $k=1$, $\frac{{3k}}{m} + \Psi (m)-\Psi (k)=\frac{{3}}{m} + \Psi (m) + \gamma$, which is increasing in m when $m\ge 2$. Hence, $\frac{{3}}{m} + \Psi (m) + \gamma \ge \frac{3}{2}+\Psi (2)+ \gamma =\frac{5}{2}>2$. From the above we can draw a conclusion that $\rho ^*<\frac{3}{2}$.