Modeling of the solid oxide fuel cell anode based on a new analytical model using nonlinear Butler-Volmer expression

Abstract

In this study, a new analytical model of solid oxide fuel cell (SOFC) anode is derived base on nonlinear BV equation. The error of the analytical solution is analyzed in detail. The effect of microstructure parameters and operation conditions on electrochemical performance is investigated. Results show that the analytical solution can obtain relatively good agreement with the numerical solution. As the overpotential increases, relative error quickly decreases. Using the nonlinear BV equation is important for obtaining more accurate prediction results. Due to the existence of an impossible zone in the composition of Ni-YSZ anode, TPB density cannot reach to peak value when the porosity is 0.15 or 0.20. Temperature and H₂ molar fraction have a more remarkable effect on active thickness than total overpotential. When concentration overpotential cannot be neglected, our analytical solution may cause big error and cannot be used to quantitative prediction.

Introduction

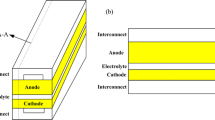
Solid oxide fuel cells (SOFCs) can efficiently convert chemical energy into electrical energy directly. They consist of anode, electrolyte, and cathode layers, forming a sandwich structure. The anode of an SOFC consists of three phases: Ni, YSZ, and pore phases. H₂ diffuses within the pores, and electrons and oxygen ions transfer within the Ni and YSZ phases, respectively. At the three-phase boundary (TPB), an electrochemical reaction occurs, generating reaction current and mass sources. The performance of SOFC is directly decided by the mass transfer, charge transfer, and electrochemical reaction in porous electrodes. Therefore, many models, including numerical [1, 2] and analytical models [3, 4], have been built to disclose the inner coupling mechanism of SOFC.

Numerical models can provide detailed distributions of physical fields, while analytical models can help to understand the native of physicochemical phenomena and reveal the mechanism of complex physical phenomena by direct analytical expressions. However, the nonlinear exponential terms in the BV equation make it difficult to obtain an analytical expression of overpotential. In the case of small overpotential, the BV equation can be simplified by linearizing the exponent items, leading to an analytical solution of overpotential [3]. Kenjo et al. [4] obtained the analytical solution of the Pt/ZrO2 cathode of high-temperature SOFCs, while the BV equation is approximated by a linear function. Then, Costamagna et al. [3] derived an analytical model using linearly approximated BV equation and analyzed the effect of microstructure parameters based on random particle packing model. However, linearizing BV equation under small current density or overpotential does not give a picture of electrode function at median and large overpotentials. Kulikovsky [5] derived analytical solutions for the cases of low and high current density regimes of SOFC anode operation without considering the concentration loss of electrodes. In the intermediate region, analytical solution had not been obtained, and a “patching” function is used to connect two analytical solutions. Thus, the functional relationship between current density and overpotential is expressed as different functions, which is inconvenient to use. Bao et al. [6] solved overpotential equations using perturbation method. They obtained approximate (asymptotic) solutions under the assumption that the perturbation parameter is sufficiently large or small. The solution is rather complex, and its applicability is limited by the magnitude of the perturbation parameter closely related to the square of the electrode thickness. Recently, they have obtained an approximately analytical solution of a wide range of SOFC operations, including high current density and thin electrode by using linear translation and power law approaches [7]. However, using the power function to approximate the exponent function changes the physical meaning of original equations. Recently, Miyawaki et al. [8] derived a piecewise semianalytical expression of overpotential and active thickness for high and low overpotential cases, while the gap between numerical and analytical solutions is relatively large.

Microstructure of the electrode closely related with electrode performance [9, 10], analytical model can be used to quickly obtain the performance of reconstructed microstructures [11] or synthetic microstructures [12]. One way to investigate the relation between the microstructure and the performance is the random particle packing model together with percolation theory. Costamagna et al. [3] firstly investigated the composition and ratio of particle size on electrode performance. Farhad et al. [13, 14] used the random particle packing model to study the effect of the microstructure parameters, including the porosity, thickness, particle-size ratio, and particle size, on the electrochemical performance. However, these studies used a single particle size and did not consider the distribution of different particle sizes. Zhang et al. [12] further developed the particle packing model by introducing particle size distribution. Chen et al. [15] also derived a multi-phase mixed model which regards particles with different size as multiple phases. All these studies are beneficial for the optimizing electrode performance. Particle packing model only considers the binary solid particles, and then, pore phase has been considered separately. Particle packing model can be safely applied to SOFC cathode, like LSM-YSZ cathode. However, when the model is applied to Ni-YSZ anode, the coupling of the three-phase volume fractions of the anode should be considered, because experimental study [16] showed that volume fractions of three phases are dependent because most pores of anode are formed by the conversion of NiO to Ni at a reduction process. So predicted microstructure parameters should be different when the coupling of three phase volume fractions is considered.

On the basis of the author’s knowledge, the analytical solutions in the references are usually based on linearly approximating BV equation. Some analytical solutions are complex piecewise functions for different cases, which are inconvenient to use. In this work, we report a new analytical model based on the nonlinear BV equation. The derivation process is simple, and the solution is accurate enough. The model is validated by comparing with experimental data. The error source of the analytical model is analyzed in detail. The particle packing model is used to analyze the effect of microstructure parameters on anode performance, such as specific area resistance and active thickness. The effects of initial porosity and porosity of anode are investigated based on the experimental result. Then, the effect of operation conditions is analyzed through the analytical expressions of area resistance and active thickness. This study is helpful for the simulation and design of SOFCs.

Mathematical model of a SOFC anode

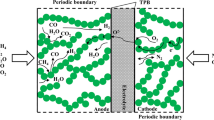
Figure 1 shows the working principle diagram of a SOFC anode. Charges (electron and ion) and mass transfers occur mainly along the anode thickness direction. Anode contains three phases: Ni, YSZ, and pore. Solid phase can be regarded as a composite material stacked by Ni and YSZ particles randomly. The gaps between the particles form the pore phase. Fuel transfers in the pore phase, oxygen ion transfers in the YSZ phase, and electron transfers in the Ni phase. Substances (H₂ and H₂O) in channel diffuse into the anode via the anode–channel interface, providing reactant for electrochemistry reaction. O²⁻ of the electrolyte diffuses into the anode via the anode–electrolyte interface under the driving force of the ion potential difference. The intersection of the three phases is TPB line (black line in the enlarged view) where electrochemical reaction occurs under the driving force of activation overpotential, generating electrons and consuming O²⁻. Generated electrons diffuse to anode–channel interface under the driving force of the electron potential difference, forming current. The electron potential at channel–anode interface is equal to total overpotential η_tot. The ion potential at channel–electrolyte interface is equal to zero.

Fig. 1

The working principle diagram of a SOFC anode

Activation overpotential

The analytical solution can be obtained under some assumptions. The diffusivity of H₂ is large, so the concentration loss is very low and commonly negligible. We assume that the concentration overpotential is zero; this assumption has been used by many studies [4,5,6,7, 17] to decouple mass transfer and electrochemical reaction. The electronic conductivity in the Ni phase is extremely high; hence, we assume that electron potential is constant.

Along the positive direction from the anode–channel interface to the anode–electrolyte interface (x coordinate), the charge transfer in two phases is described using ohm’s law, Eq. (1), in which σ_io^eff and σ_el^eff are effective electrical ion and electron conductivities, respectively. Equation (2) describes the relationship among electron conductor potential φ_el, ion conductor potential φ_io, and activation overpotential η_act. Substituting Eq. (2) into Eq. (1), we can obtain Eq. (3).

$$ -{\sigma}_{\mathrm{io}}^{\mathrm{eff}}\frac{d^2{\varphi}_{\mathrm{io}}}{d{x}^2}={\sigma}_{\mathrm{el}}^{\mathrm{eff}}\frac{d^2{\varphi}_{\mathrm{el}}}{d{x}^2}=i $$

(1)

$$ {\eta}_{\mathrm{act}}={\varphi}_{\mathrm{el}}-{\varphi}_{\mathrm{io}} $$

(2)

$$ -{\sigma}_{\mathrm{io}}^{\mathrm{eff}}\frac{d^2{\varphi}_{\mathrm{io}}}{d{x}^2}=-{\sigma}_{\mathrm{io}}^{\mathrm{eff}}\frac{d^2\left({\varphi}_{\mathrm{el}}-{\eta}_{\mathrm{act}}\right)}{d{x}^2}={\sigma}_{\mathrm{io}}^{\mathrm{eff}}\frac{d^2{\eta}_{\mathrm{act}}}{d{x}^2}=i $$

(3)

The BV equation can be expressed as Eq. (4), where i₀ is exchange current density per unit TPB length and l_tpb is TPB density [8]. Equation (5) is modified exchange current density model, where ${p}_{{\mathrm{H}}_2}$ is the partial pressure of H₂. Equation (6) is the original exchange current density model. The original exchange current density model come from the study of Kanno et al. [18] who fitted the Bieberle et al.’s [19] and Boer’s [20] experimental data and then obtained the two models. Both the models caused relative big errors in predicting electrode performance. Boer’s model shows weaker dependence on steam partial pressure than the experimental data, and the dependence on steam partial pressure is somewhat improved by the Bieberle et al.’s model. The exponent of p_H2O in Bieberle et al.’s exchange current density i₀ is preferred than the Boer’s model. [18], but a relative big discrepancy between simulation and experiment results still exists. In this study, we use Bieberle et al.’s model. In order to make the prediction results consistent with the experimental data in Model validation, we only adjusted one parameter to reduce the changes to the original model. We select to tune the exponent of ${p}_{{\mathrm{H}}_2}$ because the exponent of ${p}_{{\mathrm{H}}_2\mathrm{O}}$, 0.67, in the Eq. (6) is preferred [18]. The exponent of ${p}_{{\mathrm{H}}_2}$ has been tune to 0.04 from original 0.11 to enhance the dependence of the original model on fuel composition. The comparison between the modified and original i₀ models is shown in Model validation.

A correction coefficient χ is introduced to correct the asymmetrical charge transfer coefficients in the nonlinear terms, that is, α and β. If α is equal to β, then χ is one. If α is not equal to β, then χ is less than one and can be evaluated using the integral approach method, Eq. (6). Let η_act be between 0 and 0.3 V because η_act of the anode is usually lower than 0.3 V (an overestimated value). For α = 2 and β = 1 in this study, χ = 0.998 is obtained. The corrected Eq. (4) is still nonlinear.

$$ {\displaystyle \begin{array}{c}i={i}_0{l}_{\mathrm{tpb}}\left[\exp \left(\frac{\alpha F{\eta}_{\mathrm{act}}}{RT}\right)-\exp \left(\frac{-\beta F{\eta}_{\mathrm{act}}}{RT}\right)\right]\\ {}={i}_0{l}_{\mathrm{tpb}}\left[\exp \left(a{\eta}_{\mathrm{act}}\right)-\exp \left(-b{\eta}_{\mathrm{act}}\right)\right]\approx 2{i}_0{l}_{\mathrm{tpb}}\chi \sinh \left(a{\eta}_{\mathrm{act}}\right)\end{array}} $$

(4)

$$ {i}_0=0.0013{p}_{{\mathrm{H}}_2}^{0.04}{p}_{{\mathrm{H}}_2\mathrm{O}}^{0.67}\exp \left(\frac{-84900}{RT}\right) $$

(5)

$$ {i}_0=0.0013{p}_{{\mathrm{H}}_2}^{0.11}{p}_{{\mathrm{H}}_2\mathrm{O}}^{0.67}\exp \left(\frac{-84900}{RT}\right) $$

(6)

$$ \chi =\frac{\underset{0}{\overset{0.3}{\int }}\exp \left(a{\eta}_{\mathrm{act}}\right)-\exp \left(-b{\eta}_{\mathrm{act}}\right)}{2\underset{0}{\overset{0.3}{\int }}\sinh \left(a{\eta}_{\mathrm{act}}\right)}=\frac{\frac{e^{0.3a}-1}{a}+\frac{e^{-0.3b}-1}{b}}{\frac{2}{a}\left(\cosh (0.3a)-1\right)} $$

(7)

For an anode-supported SOFC, the anode thickness is much thicker than active thickness. Thus, boundary can be easily defined. At the anode–channel interface, x = 0, the gradient of η_act is zero because the gradient of the ionic potential is zero, and η_act is zero because no reaction current occurs. At the anode–electrolyte interface, x = l, the ionic potential is zero. These boundary conditions can be expressed as Eqs. (8) and (9).

$$ \frac{d{\eta}_{act}}{dx}{\left|{}_{x=0}=0,\kern0.5em {\eta}_{\mathrm{act}}\right|}_{x=0}=0 $$

(8)

$$ {\left.{\eta}_{\mathrm{act}}\right|}_{x=l}=\left({\varphi}_{\mathrm{el}}-{\varphi}_{\mathrm{io}}\right){\left|{}_{x=l}=\left({\varphi}_{\mathrm{el},\mathrm{bulk}}-0\right)\right|}_{x=l}={\eta}_{\mathrm{tot}} $$

(9)

Dimensionless equation is helpful for understanding the essence of physical phenomena. Using Eq. (10) to nondimensionalize Eq. (3) and boundary conditions (8) and (9), we have control equation (11) and boundary conditions (12) and (13).

$$ {\eta}_{\mathrm{act}}^{\ast }=a{\eta}_{\mathrm{act}},\kern0.5em X=x/l $$

(10)

$$ \frac{d^2{\eta}_{act}^{\ast }}{d{X}^2}=\xi sinh\left({\eta}_{act}^{\ast}\right),\kern0.75em \xi =2a\frac{i_0{l}_{\mathrm{tpb}}\chi }{\sigma_{\mathrm{io}}^{\mathrm{eff}}}{l}^2 $$

(11)

$$ \frac{\mathrm{d}{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}X}{\left|{}_{X=0}=0,{\eta}_{\mathrm{act}}^{\ast}\right|}_{X=0}=0 $$

(12)

$$ {\left.{\eta}_{\mathrm{act}}^{\ast}\right|}_{X=1}=a{\eta}_{\mathrm{tot}}=m $$

(13)

In accordance with Eq. (11), we can obtain:

$$ 2\frac{\mathrm{d}{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}X}\frac{{\mathrm{d}}^2{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}{X}^2}=2\xi \sinh \left({\eta}_{\mathrm{act}}^{\ast}\right)\frac{d{\eta}_{\mathrm{act}}^{\ast }}{dX} $$

(14)

When the boundary condition is applied to X = 0, Eq. (15) can be obtained. Given the gradient of ${\eta}_{\mathrm{act}}^{\ast }$ is positive in the anode, Eq. (16) can be obtained.

$$ {\left(\frac{\mathrm{d}{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}X}\right)}^2=2\xi \cosh \left({\eta}_{\mathrm{act}}^{\ast}\right)\kern0.5em {C}_1,{C}_1=-2\xi $$

(15)

$$ \frac{\mathrm{d}{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}X}=\sqrt{2\xi \left(\cosh \left({\eta}_{\mathrm{act}}^{\ast}\right)-1\right)} $$

(16)

Equation (16) can be rewritten as:

$$ \frac{dX}{d{\eta}_{act}^{\ast }}=\frac{1}{2\sqrt{\xi}\mathit{\sinh}\left(\frac{\eta_{act}^{\ast }}{2}\right)}\kern0.5em \left({\eta}_{\mathrm{act}}^{\ast}\ne 0,0<X\le 1\right) $$

(17)

Equation (17) is integrated, and we have Eq. (18):

$$ X-1=\underset{m}{\overset{\eta_{\mathrm{act}}^{\ast }}{\int }}\frac{1}{2\sqrt{\xi}\sinh \left(\frac{\eta_{\mathrm{act}}^{\ast }}{2}\right)}\mathrm{d}{\eta}_{\mathrm{act}}^{\ast }=\frac{1}{\sqrt{\xi }}\left(\ln \frac{e^{\eta_{\mathrm{act}}^{\ast }/2}-1}{e^{\eta_{\mathrm{act}}^{\ast }/2}+1}-\ln \frac{e^{m/2}-1}{e^{m/2}+1}\right) $$

(18)

A constant f is defined in Eq. (19), and Eq. (18) can be written as Eq. (20) or (21), which are the functions of dimensionless activation overpotential and coordinate.

$$ f=\frac{e^{m/2}-1}{e^{m/2}+1} $$

(19)

$$ X=\frac{1}{\sqrt{\xi }}\left(\ln \frac{e^{\eta_{\mathrm{act}}^{\ast }/2}-1}{e^{\eta_{\mathrm{act}}^{\ast }/2}+1}-\ln f\right)+1\kern0.75em \left({\eta}_{\mathrm{act}}^{\ast}\ne 0\right) $$

(20)

$$ {\eta}_{\mathrm{act}}^{\ast }(X)=2\ln \left(\frac{2}{1-f{e}^{\sqrt{\xi}\left(X-1\right)}}-1\right)\kern0.5em \left(0<X\le 1\right) $$

(21)

Output current density

Using I to denote the output current density of the anode, then, we have Eq. (22), where ${I}^{\ast }$ is the dimensionless output current density.

$$ I=\underset{0}{\overset{l}{\int }} idx=\underset{0}{\overset{l}{\int }}2{i}_0{l}_{\mathrm{tpb}}\chi \sinh \left(a{\eta}_{\mathrm{act}}\right) dx=2{i}_0{l}_{\mathrm{tpb}}\chi l\underset{0}{\overset{1}{\int }}\sinh \left({\eta}_{\mathrm{act}}^{\ast}\right)\mathrm{d}X=2{i}_0{l}_{\mathrm{tpb}}\chi l{I}^{\ast } $$

(22)

The dimensionless output current density can be obtained as:

$$ {\displaystyle \begin{array}{c}{I}^{\ast }=\underset{0}{\overset{1}{\int }}\sinh \left({\eta}_{\mathrm{act}}^{\ast}\right)\mathrm{d}X=\frac{1}{\xi}\underset{0}{\overset{1}{\int }}\frac{{\mathrm{d}}^2{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}{X}^2}\mathrm{d}X=\frac{1}{\xi}\frac{\mathrm{d}{\eta}_{\mathrm{act}}^{\ast }}{\mathrm{d}X}{\left|{}_{X=0}^{X=1}=\frac{1}{\xi}\sqrt{2\xi \left(\cosh \left({\eta}_{\mathrm{act}}^{\ast}\right)-1\right)}\right|}_{X=0}^{X=1}\\ {}=\frac{1}{\xi}\left(\sqrt{2\xi \left(\cosh (0)-1\right)}-\sqrt{2\xi \left(\cosh (m)-1\right)}\right)=\frac{-1}{\sqrt{\xi }}\sqrt{2\left(\cosh (m)-1\right)}\end{array}} $$

(23)

Then, the area specific resistance of anode can be defined as:

$$ AR=\frac{\eta_{\mathrm{tot}}}{I}=\frac{\sqrt{\xi }{\eta}_{\mathrm{tot}}}{2{i}_0{l}_{\mathrm{tpb}}\chi l\sqrt{2\left(\cosh (m)-1\right)}}=\sqrt{\frac{a}{2{i}_0{l}_{\mathrm{tpb}}{\sigma}_{\mathrm{io}}^{\mathrm{eff}}\chi }}\frac{\eta_{\mathrm{tot}}}{\sqrt{2\left(\cosh (m)-1\right)}} $$

(24)

Active thickness

In the anode, electrochemical reaction occurs at a thin zone in the vicinity of the anode–electrolyte interface. Evaluating the active thickness of electrochemical reaction is helpful for the anode design, especially the anode function layer. Equation (25) is used to define the active thickness, where the dimensionless overpotential becomes 10% of its value at the anode–electrolyte interface. Using δ^∗ to denote the dimensionless active thickness that can be evaluated by Eq. (26), real active thickness is denoted as δ, δ = δ^∗l and can be evaluated by Eq. (27). It can be found that δ is the function of total overpotential, temperature, exchange current density, TPB density, and effective ionic conductivity.

$$ {\eta}_{\mathrm{act}}^{\ast}\left(1-{\delta}^{\ast}\right)=0.1{\eta}_{\mathrm{act}}^{\ast }(1) $$

(25)

$$ {\delta}^{\ast }=\sqrt{\frac{RT{\sigma}_{\mathrm{io}}^{\mathrm{eff}}}{2\alpha F{i}_0{l}_{\mathrm{tpb}}\chi {l}^2}}\left(\ln \frac{\exp \left(m/2\right)-1}{\exp \left(m/2\right)+1}-\ln \frac{\exp \left(0.1m/2\right)-1}{\exp \left(0.1m/2\right)+1}\right) $$

(26)

$$ \delta =\sqrt{\frac{RT{\sigma}_{\mathrm{io}}^{\mathrm{eff}}}{2\alpha F{i}_0{l}_{\mathrm{tpb}}\chi }}\left(\ln \frac{\exp \left(m/2\right)-1}{\exp \left(m/2\right)+1}-\ln \frac{\exp \left(0.1m/2\right)-1}{\exp \left(0.1m/2\right)+1}\right) $$

(27)

Anode effective properties

Microstructure parameters in the above equations are evaluated by random particles packing model, together with percolation theory. The equations of random packing model are listed in Appendix 1. In the random packing systems, active TPBs are formed by the contacts of percolating Ni particles and YSZ particles. The active TPB density l_tpb (m·m^–3) is determined as Eq. (28), where n_t is the number density of all particles (total number of particles per unit volume) and θ_c (30^o) is the contact angle between the Ni and YSZ particle. d_i is the diameter of particle i. P_i is the percolation probability of i phase. γ is the size ratio of YSZ particle to Ni particle (γ = d_io/d_el), and Z is the average coordination number for random packing systems, which is 6. n_el is the number fraction of Ni. ε denotes the anode porosity.

$$ {l}_{\mathrm{t}\mathrm{pb}}=\pi \sin \left(\frac{\theta_c}{2}\right)\min \left({d}_{\mathrm{io}},{d}_{\mathrm{el}}\right){n}_{\mathrm{t}}{n}_{\mathrm{el}}{n}_{\mathrm{io}}\frac{Z_{\mathrm{el}}{Z}_{\mathrm{io}}}{Z}{P}_{\mathrm{el}}{P}_{\mathrm{io}} $$

(28)

$$ {n}_{\mathrm{t}}=\frac{1-\varepsilon }{\pi /6{d}_{\mathrm{el}}^3\left({n}_{\mathrm{el}}+\left(1-{n}_{\mathrm{el}}\right){\gamma}^3\right)} $$

(29)

The effective conductivity of YSZ phase can be evaluated by Eq. (30) that considers the effects of the volume fraction, percolation probability P_io, and tortuosity factor τ of the YSZ phase, where σ_io is the intrinsic ion conductivity [21]. Tortuosity factor τ is equal to 8.85 in this study as shown in Table 1.

$$ {\sigma}_{\mathrm{io}}^{\mathrm{eff}}=\frac{\left(1-\varepsilon \right){V}_{\mathrm{io}}}{\tau }{P}_{\mathrm{io}}{\sigma}_{\mathrm{io}} $$

(30)

$$ {\sigma}_{\mathrm{io}}=3.4\times {10}^4\exp \left(\frac{-10350}{T}\right) $$

(31)

Table 1 The experimental parameters used in the study

Model validation

The analytical model is validated by comparing with the experimental data of Kishimoto et al. [22] and Kanno et al. [18]. Kishimoto et al. tested the polarization curve of a SOFC anode with a thickness of 50 μm and reconstruction the microstructure using FIB-SEM. Kanno et al. tested the polarization curve of a SOFC anode with a thickness of 22.3 μm. The microstructure parameters of two anodes are shown in Table 1. Figure 2 shows the comparison between the experiment results and the predicted results using two different exchange current density model. It can be found that total overpotential–current density curves predicted by our model using the modified exchange density model agree well with the experimental data at median and high current density, expecially for the data of Kanno et al. The original exchange current density model causes big errors at all conditions. Nagasawa and Hanamura [23] used their analytical model to fit the experimental data of six different patterns of anodes. In order to determine certain model parameters, they used the experimental data of Kanno et al. as benchmark data. If we use Kanno et al.’s experimental data as benchmark data, it can be found that the main source of the discrepancy in Fig. 2a is the experimental error. At a current of 500 A m⁻², the relative error is about 30%. After calculation, we found that that the analytical solution itself causes a relative error of 14% at 500 A m⁻². This is because our analytical model has a relatively big error at small current density, which is analyzed in Error of the analytical solution.

Fig. 2

Comparison of experimental data and the analytical solution: (a) comparing with the experimental data of Kishimoto et al. [22]; (b) comparing with the experimental data of Kanno et al. [18]

Results and discussion

Error of the analytical solution

In the derivation process of the analytical solution, concentration loss is neglected, and a correction coefficient χ is introduced to approximately treat the asymmetrical charge transfer coefficients α and β. So the analytical may cause error under extreme conditions. Evaluating the accuracy and error source of analytical solution is important for engineering application. A coupling 1D numerical model is built and solved in COMSOL 5.4, and its results can be regard as right solution for comparison. Appendix 2 shows the equations of 1D numerical model. The model considers the mass and electron transfer resistances. Substance concentration is coupled with electrochemical reaction rate.

Firstly, two kinds of BV equation (Eq. (4)) are used to compare one with same values of charge transfer coefficient α and β and another with different values. For the SOFC anode in this study, α = 2 and β = 1 are used, while it is more common that α = β = 1 in other studies [13, 24, 25]. Figure 3a shows the current density–overpotential curves of α = 2 and β = 1 predicted by analytical and numerical solutions under the same conditions. It can be find that current density monotonely increases with overpotential. From low overpotential to high overpotential (0–0.3 V), the analytical solution obtains good agreement with the numerical solution. The relative error of two models, defined aserror = (I_analitical − I_numerical)/I_analitical × 100%, exponentially decreases with the increasing of the overpotential. Under a small overpotential, such as 0.01 V, the relative error is big, about 16%. But the relative error is quickly reduced to less than 10% at 0.05 V.

Fig. 3

(a) Current density–overpotential curves when α = 2 and β = 1; (b) current density–overpotential curves when α = β = 1; (c) activation overpotentials predicted by two models

Figure 3b shows the current density–overpotential curves of α = 1 and β = 1 predicted by two models under same conditions. The results of the two models are in good agreement. The relative error varies from positive to negative when overpotential increases. At high current density, the current densities predicted by 1D numerical solution is slightly higher than those predicted by the analytical solution. For analytical model, a constant exchange current density and zero concentration loss are used, so the consumption of H₂ cannot affect the current density. While for 1D numerical model, the consumption of H₂ will  increase the concentration loss on the one hand, leading to a decrease in current density. But on the other hand, it will increase the exchange current density, leading to an increase in current density. This is the opposite effect. Because the H₂ consuming has a more significant effect on the exchange current density than concentration loss, relative error is negative at a high current density. The maximun relative errors in Fig. 3b are lower than 2% and are much less than 17% in Fig. 3a, which implies that the main error source of the analytical solution is the approximate treatment of the asymmetrical charge transfer coefficient in Eq. (4).

Another problem is the difference between the analytical solutions based on nonlinear and linear BV equations, respectively. Paola Costamagna et al. [3] obtained an analytical solution after linearly approximating the exponent terms of the BV equation. They use current density I as boundary condition, but our analytical solution uses overpotential as boundary condition, so I and η_tot are firstly obtained using the 1D numerical model and then were applied on two analytical solutions, respectively. Appendix 3 shows the analytical solution of Paola Costamagna et al. expressed as the symbols of this study. Same exchange current density i₀ and TPB density l_tpb are used for comparison in this study as shown in Appendix 3. Figure 3c shows the comparison of predicted activation overpotentials. Paola Costamagna et al. used symmetrical charge transfer coefficients, so we set α = β = 1 to compare. It can be found that the solution of Paola Costamagna et al. predicts too high activation overpotential and causes big error under a high current density of I = 3125 A m⁻², while our analytical solution only causes small error. Therefore, using the nonlinear BV equation is significantly important, and our analytical model is more accurate and is suitable for wider working conditions.

Overpotential of different thicknesses of anodes

Above analysis shows that the main error source of the analytical solution is the approximate treatment of the asymmetrical charge transfer coefficients. In the following, α = 2 and β = 1 are still used because the BV equation has been validated by experiment. The analytical solution is derived under the assumptions that the anode is thick enough and the concentration overpotential can be neglected at the same time. For some conditions, such as extremely high current density or too thick anode, concentration overpotential cannot be neglected, and therefore, our analytical solution will cause big error and cannot be used to quantitative forecast.

Figure 4 shows the overpotentials and activation overpotentials of 400 and 30-μm-thick anodes predicted by analytical solution and 1D numerical solution. The parameters of two models are same. In Fig. 4a and c, it can be found that the analytical solution presents a good agreement with the numerical solution. At 0.05 V, relative errors are about 15% and 7% for 400 and 30-μm-thick anodes, respectively, indicating that analytical solution causes smaller error for thin electrode. But as the overpotential increases, relative errors quickly decrease.

Fig. 4

(a) Overpotentials of a 400-μm-thick anode; (b) activation overpotentials of a 400-μm-thick anode; (c) overpotentials of a 30-μm-thick anode; (d) activation overpotentials of a 30-μm-thick anode

As the Fig. 4b shows, the activation overpotentials predicted by two models agree well although at high overpotential of 0.21 V. The active zone predicted by the analytical solution almost completely overlap with that of numerical solution, implying that our analytical expression of active thickness is credible. The main difference is that at X = 1, analytical solution predicts higher overpotential because it has not considered concentration loss. For 30-μm thick anode in Fig. 4d, concentration loss is very small, but there is also a small gap at 0.6 < X < 0.8, which is caused by the approximate treatment of asymmetrical charge transfer coefficients. When the total overpotential varies from 0.09 to 0.21 V, the gap decreases in accordance with the decrease of relative error in Fig. 4c.

Effect of microstructure parameters on anode

Above analysis shows that analytical solution can predict the overpotential and activation overpotential of anode well. Therefore, the analytical expressions of AR and activation thickness can be used to predict the electrochemical performance of anode. AR and activation thickness are two important indexes in electrode design and optimization. Initial porosity ε₀ and porosity ε significantly affect both indexes. In this section, the effects of ε₀ and ε are investigated by particle packing model combined with experimental observation. In the particle packing model, ε is an independent parameter that has no effect on volume fraction of electron or ion conducting phase in solid, which is reasonable for cathode like LSM-YSZ cathode. However, for a Ni-YSZ anode, ε is dependent with the volume fractions of Ni and YSZ. When NiO converts to Ni at reduction process, new pores can be formed. These pores with the addition of initial pores of NiO-YSZ anode form the final pore phase. Mori et al. [16] measured the porosity of anodes of different Ni contents after reduction. All oxide anode samples (NiO-YSZ) have a very low initial porosity, 0.01 to 0.04. When these samples are reduced, new pores are generated in the samples. We fitted the experimental data with an initial porosity of 0.031. Then, the volume fractions of three phases under different porosities can be obtained by the fitting equation as Fig. 5a shows. When porosity increases, Ni content in solid also increases, and YSZ content decreases. It can be found that most pores are formed by the reduction of NiO. ε₀ must be bigger than 0, and thus, the gray zone in Fig. 5a is impossible. When ε is small, the variation range of V_el is narrow. Figure 5b shows the effect of the volume fraction of the Ni on anode TPB density under different porosities. When ε = 0.15 and 0.20, TPB densities cannot reach to peak value because of the impossible zone. As the increase of ε, the variation range of V_el also increases. When ε = 0.25, TPB density reaches to maximum at V_el = 0.5, but when V_el = 0.15, TPB density reaches to maximum at V_el≈0.2.

Fig. 5

(a) Porosity as a function of Ni content; (b) effect of Ni content on TPB density of anode; (c) effect of initial porosity on TPB density of anode; (d) effect of initial porosity on area specific resistance of anode

Figure 5c and d show the TPB density and area specific resistance AR of different initial porosities. It can be found that percolation range is affected by the initial porosity ε₀. As the ε₀ increases, the maximum TPB density decreases. When porosity is between 0.2 and 0.25, the anode with initial porosity of 0.100 has a high AR, and the anode with initial porosity of 0.150 is not percolating, so an initial porosity of 0.031 is more advantaging. When porosity ε is between 0.25 and 0.30, AR is very low for the anode with initial porosity of 0.100. When porosity ε is 0.30 to 0.35, an initial porosity of 0.150 is more advantaging. Minimum AR increases with the increase of ε₀ due to the decrease of TPB density. However, minimum AR of different ε₀ are closing. Therefore, in the following analysis, ε₀ = 0.031 is used.

Figure 6a shows the effect of porosity on the TPB density. It can be found that TPB density firstly increases and then decreases with the increase of porosity. When porosity is 0.24 (V_el = 0.5), TPB density reaches the maximum. When particles (with γ = 1) become smaller from 1.6 to 0.4 μm, TPB density increases largely because total number density n_t increases with reducing particle size. Additionally, due to the coupling of volume fractions of three phases, the curves in Fig. 6a are asymmetric, which is more outstanding when γ is 0.5 and 2. When γ is 0.5, smaller particles (0.4 μm and 0.8 μm) are mixed, which make total number density and TPB density higher. When γ is 2, big particles (1.6 μm and 0.8 μm) are mixed, so total number density and TPB density are low. For a common porosity (0.2 to 0.4), TPB density changes largely with porosity and particle size. When TPB density is larger than 1 μm⁻², particle size must be smaller than 1.6 μm. Figure 6b shows the effects of porosity on effective ion conductivity. The change of effective ion conductivity is monotonous and almost linear. As the porosity increases, the content and percolation possibility of YSZ phase monotonously reduce. When YSZ and Ni particles size are the same (γ = 1), effective ion conductivity is independent with the particle size because percolation possibility is unchanged, which shows that YSZ content dominates the ion conductivity.

Fig. 6

(a) Effect of porosity on the TPB density; (b) effect of porosity on effective ion conductivity; (c) the effect of porosity on area specific resistance; (d) effect of porosity on active thickness

Figure 6c shows the effects of porosity on area specific resistance AR. It can be found that the curves are also asymmetric because contents of Ni and YSZ are not equal at different porosities. At the vicinity of percolation threshold, AR increases quickly, which should be avoided. For γ = 2, AR is very high due to low TPB density and low effective ion conductivity, and the range with low AR is narrow. For different particle size, reasonable porosity zone is different. For γ = 1, reasonable porosity zone is 0.2 to 0.25, and the zone will become narrow when particle size increases. For γ = 0.5, the reasonable porosity zone is 0.25 to 0.3.

Figure 6d shows the effect of porosity on active thickness. According to Eq. (26),$\delta \propto \sqrt{\sigma_{\mathrm{io}}^{\mathrm{eff}}/{l}_{\mathrm{tpb}}}$, active thickness is independent of anode thickness l based on the assumption that the anode is sufficiently thick. As the figure shows, at the vicinity of the left percolation porosity, active thickness rises rapidly due to the quick reduce of TPB density. As the porosity increases, active thickness decreases monotonously, although TPB density increases firstly and then decreases, implying that active thickness is dominated by effective ion conductivity. At the vicinity of right percolation porosity, both ${\sigma}_{\mathrm{io}}^{\mathrm{eff}}$ and l_tpb decrease at same rate with porosity increasing, which makes active thickness almost unchanging.

Effect of operation condition

Operation condition also affects the area specific resistance and active thickness. Figure 7a shows the effect of temperature on AR. Increasing temperature not only increases effective ion conductivity but also increases exchange current density. According to Eq. (24), we have $AR\propto {\left({\sigma}_{\mathrm{io}}^{\mathrm{eff}}{i}_0\right)}^{-1/2}$. Temperature largely affects ${i}_0{\sigma}_{\mathrm{io}}^{\mathrm{eff}}$ because T appears at the exponent term. So increasing temperature extremely reduces the polarization resistance of the electrode. When temperature is higher than 800 °C, the change of AR with temperature is slight. When temperature is lower than 800 °C, AR quickly increases with reducing temperature, and thus, optimizing microstructure is extremely important for low-temperature SOFC.

Fig. 7

(a)Area specific resistance at different temperatures; (b) active thicknesses at different temperatures; (c) area specific resistance at different H₂ molar fractions; (d) active thicknesses at different H₂ molar fractions; (e) area specific resistance at different overpotentials; (f) active thicknesses at different overpotentials

Figure 7b shows the effect of temperature on active thicknesses. For comparison, we add the solution of Miyawaki et al. [8]. Miyawaki et al. gave a piecewise function of active thickness in accordance with the magnitude of the total overpotential. As figure shows, our solutions fall in between the solutions of Miyawaki et al., which implies that our analytical expression of active thickness is accurate, but with a simpler function. It can be found that the active thickness increases with temperature, which is consistent with results of studies [26, 27] and contrary with the result of Zheng et al. [25]. In Eq. (27), $\delta \propto \sqrt{T{\sigma}_{\mathrm{io}}^{\mathrm{eff}}/{i}_0}$, and thus, $\sqrt{T{\sigma}_{\mathrm{io}}^{\mathrm{eff}}/{i}_0}$ is the independent variable of active thickness, and other parameters can be regarded as constants. Then, active thickness is mainly affected by temperature, ion diffusion, and electrochemical reaction rate. When the temperature increases, the ionic conductivity ${\sigma}_{\mathrm{io}}^{\mathrm{eff}}$ increases and enables ions to transfer further from the anode–electrolyte interface, increasing the active thickness. High temperature enhances the exchange current density i₀, and high i₀ causes high electrochemical reaction rate. Consequently, substantial ions are consumed in the active zone, which reduces the active thickness. T appears at the exponent terms of the expressions of ${\sigma}_{\mathrm{io}}^{\mathrm{eff}}$ and i₀ (Eqs. (29) and (5)), and the effect of T on $\sqrt{\sigma_{\mathrm{io}}^{\mathrm{eff}}/{i}_0}$ is weak in accordance with our evaluation. Thus, the effect of temperature on active thickness is dominated by T^0.5, which agrees with the profile of curves in Fig. 7b. Due to there are different equations in literatures to describe the effect of T on i₀ and ${\sigma}_{\mathrm{io}}^{\mathrm{eff}}$, $\sqrt{\sigma_{\mathrm{io}}^{\mathrm{eff}}/{i}_0}$ sometimes decreases as T increases, resulting in a decrease in active thickness as T increases.

Figure 7c shows the effect of H₂ molar fraction on AR. It can be found that increasing H₂ molar fraction increases AR. H₂ molar fraction affects the exchange current density and then affects AR. AR ∝ i₀^−1/2. At low temperature, such as 700 °C, the change of AR with H₂ molar fraction is more outstanding. At 900 °C, increasing H₂ molar fraction slightly increases AR. Figure 7d shows the effect of H₂ molar fraction on active thickness. Active thickness is thicker at a higher H₂ molar fraction, which is consistent with the results of studies [25,26,27]. From Eq. (27), H₂ molar fraction is related only to the exchange current density i₀. An increase in H₂ molar fraction decreases the reaction rate, resulting in reducing ion consumption rate. Then, the ions can diffuse further, resulting in an increase in active thickness.

Figure 7e shows the effect of total overpotential on AR. It shows that AR slightly decreases with the increase of total overpotential, which indicates that main polarization loss is ohmic loss. At low temperature, the effect of overpotential on AR is more outstanding. In Fig. 7f, high overpotential can reduce active thickness, but this effect is negligible. Although the ions can diffuse further under high overpotential, high reaction rate also increases the consumption rate of ions, which counteracts the increase in active thickness.

Conclusions

In this study, a new analytical model of SOFC anode is derived base on nonlinear BV equation. Simple analytical solutions of activation overpotential, current density, area specific resistance, and active thickness are obtained. The analytical solution is validated by comparing with the experimental data. The results of analytical solution are compared with the 1D numerical solution and other researchers’ solutions. The error of analytical solution is analyzed in detail. The effect of microstructure parameters and operation conditions on electrochemical performance is investigated. Following conclusions can be obtained:

The analytical solution can obtain relatively good agreement with the numerical solution. The main error source of the analytical solution is the approximate treatment of the asymmetrical charge transfer coefficient. As the overpotential increases, relative error quickly decreases. Using nonlinear BV equation is significantly important, and our analytical model is more accurate when compared with the analytical model using a linear BV equation. The analytical solution causes smaller error for a thinner electrode. When concentration overpotential cannot be neglected, our analytical solution may cause big error and cannot be used to quantitative forecast.

Due to the coupling of volume fractions of three phases, when the porosity is 0.15 or 0.20, TPB densities cannot reach to peak value. The minimum area specific resistance slightly increases with the increase of initial porosity. Because area specific resistance is proportional to ${\left({\sigma}_{\mathrm{io}}^{\mathrm{eff}}{i}_0\right)}^{-1/2}$, increasing temperature extremely reduces the polarization resistance of the electrode. Active thickness is proportional to $\sqrt{T{\sigma}_{\mathrm{io}}^{\mathrm{eff}}/{i}_0}$. Temperature and H₂ molar fraction have a more remarkable effect on active thickness than the overpotential.

Appendices

Appendix 1: Random packing model

Random packing of binary spherical particles, together with percolation theory, has been applied to calculate microstructure parameters of electrodes by several researchers [14, 28,29,30,31]. The coordination numbers (number of contacts with other particles) for electron conductor (Ni) and ion conductor (YSZ) particles are denoted by Z_el and Z_io, respectively, and can be evaluated using Eqs. (32) and (33).

$$ {Z}_{\mathrm{el}}=3+\frac{Z-3}{n_{\mathrm{el}}+\left(1-{n}_{\mathrm{el}}\right){\gamma}^2} $$

(32)

$$ {Z}_{\mathrm{io}}=3+\frac{\left(Z-3\right){\gamma}^2}{n_{\mathrm{el}}+\left(1-{n}_{\mathrm{el}}\right){\gamma}^2} $$

(33)

The number fraction n_el can be obtained with volume fraction of Ni phase in solid, V_el, as:

$$ {n}_{\mathrm{el}}=\frac{\gamma^3{V}_{\mathrm{el}}}{1-{V}_{\mathrm{el}}+{\gamma}^3{V}_{\mathrm{el}}} $$

(34)

The coordination number between i-phase particle and j-phase particle is Z_i–j, given as Eqs. (35)–(37).

$$ {Z}_{\mathrm{el}\hbox{-} \mathrm{io}}={n}_{\mathrm{io}}\frac{Z_{\mathrm{el}}{Z}_{\mathrm{io}}}{Z} $$

(35)

$$ {Z}_{\mathrm{el}\hbox{-} \mathrm{el}}=\frac{Zn_{\mathrm{el}}}{n_{\mathrm{el}}+\left(1-{n}_{\mathrm{el}}\right){\gamma}^2} $$

(36)

$$ {Z}_{\mathrm{io}\hbox{-} \mathrm{io}}=\frac{Zn_{\mathrm{io}}}{n_{\mathrm{io}}+\left(1-{n}_{\mathrm{io}}\right){\gamma}^{-2}} $$

(37)

For Ni-YSZ anode, only percolated Ni and YSZ phases are useful. The percolation probability of i-phase is given by P_i [29]:

$$ {P}_{\mathrm{el}}={\left[1-{\left(\frac{4.236-{Z}_{\mathrm{el}-\mathrm{el}}}{2.472}\right)}^{2.5}\right]}^{0.4}, $$

(38)

$$ {P}_{\mathrm{io}}={\left[1-{\left(\frac{4.236-{Z}_{\mathrm{io}-\mathrm{io}}}{2.472}\right)}^{2.5}\right]}^{0.4.} $$

(39)

Appendix 2: Control equations of 1D numerical model

1D numerical model has no approximation and considers the coupling of mass and charge transfers and electrochemical reaction. Charge transfer is defined as Eq. (40), where i is the reaction current per unit volume.

$$ -{\sigma}_{\mathrm{io}}^{\mathrm{eff}}\frac{d^2{\varphi}_{\mathrm{io}}}{dx^2}={\sigma}_{\mathrm{el}}^{\mathrm{eff}}\frac{d^2{\varphi}_{\mathrm{el}}}{dx^2}=i $$

(40)

The electrical chemistry reaction rate is defined as Eq. (41), where l_tpb is the TPB density.

$$ i={i}_0{l}_{\mathrm{tpb}}\left[\exp \left(\frac{\alpha F{\eta}_{\mathrm{act}}}{RT}\right)-\exp \left(\frac{-\beta F{\eta}_{\mathrm{act}}}{RT}\right)\right] $$

(41)

Considering the concentration loss η_conc, we have:

$$ {\eta}_{\mathrm{act}}={\varphi}_{\mathrm{el}}-{\varphi}_{\mathrm{ion}}-{\eta}_{\mathrm{conc}}, $$

(42)

$$ {\eta}_{\mathrm{conc}}=\frac{RT}{2F}\ln \left(\frac{p_{{\mathrm{H}}_2}^{\mathrm{bulk}}}{p_{{\mathrm{H}}_2}}\frac{p_{{\mathrm{H}}_20}}{p_{{\mathrm{H}}_20}^{\mathrm{bulk}}}\right) $$

(43)

Mass source term s_i is proportional to the reaction current density. Effective diffusivity Deff i is corrected using Eq. (46). D_ij is the binary diffusivity, and D_Kn,i is the Knudsen diffusivity [32].

$$ \nabla \cdotp \left({D}_i\frac{1}{RT}\nabla {p}_i\right)={s}_i $$

(44)

$$ {s}_{{\mathrm{H}}_2}=-\frac{i}{2F},{s}_{{\mathrm{H}}_2\mathrm{O}}=\frac{i}{2F}\kern0.5em $$

(45)

$$ {D}_i^{\mathrm{eff}}=\frac{V_{\mathrm{pore}}}{\tau_{\mathrm{pore}}}{D}_i $$

(46)

$$ {D}_i={\left(\frac{1}{D_{ij}}+\frac{1}{D_{\mathrm{Kn},i}}\right)}^{-1} $$

(47)

$$ {D}_{\mathrm{Kn},i}=\frac{d_{\mathrm{p}}}{3}\sqrt{\frac{8 RT}{\pi {M}_i}} $$

(48)

$$ {D}_{ij}=\frac{3.198\times {10}^{-4}{T}^{1.75}\sqrt{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${M}_i$}\right.+\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${M}_j$}\right.}}{p_{\mathrm{t},\mathrm{bulk}}{\left[{\left({v}_i\right)}^{1/3}+{\left({v}_j\right)}^{1/3}\right]}^2} $$

(49)

Appendix 3: Analytical solution using linear BV equation

Paola Costamagna et al. [3] obtained an analytical solution after linearly approximating exponent terms of the BV equation. Neglecting the resistance of electron transfer, we have:

$$ {\sigma}_{\mathrm{io}}^{\mathrm{eff}}\frac{d^2{\eta}_{\mathrm{act}}}{d{x}^2}=2\frac{i_0{l}_{\mathrm{tpb}}\alpha F}{RT}{\eta}_{\mathrm{act}}. $$

(50)

Introducing the dimensionless parameter Γ, the activation overpotential can be expressed as Eq. (52). Note that we have neglected the resistance of electron transfer of origin analytical solution of Paola Costamagna et al.

$$ {\Gamma}^2=\frac{2{i}_0{l}_{\mathrm{tpb}}\alpha F}{\sigma_{\mathrm{io}}^{\mathrm{eff}} RT}{l}^2 $$

(51)

$$ {\eta}_{\mathrm{act}}=\frac{Il}{\Gamma \sinh \left(\Gamma \right){\sigma}_{\mathrm{io}}^{\mathrm{eff}}}\cosh \left(\Gamma \frac{x}{l}\right) $$

(52)