Probabilistically segregated neural circuits and subcritical linguistics

Abstract

Early studies of cortical information codes and memory capacity have assumed large neural networks, which, subject to evenly probable binary (on/off) activity, were found to be endowed with large storage and retrieval capacities under the Hebbian paradigm. Here, we show that such networks are plagued with exceedingly high cross-network connectivity, yielding long code words, which are linguistically non-realistic and difficult to memorize and comprehend. Noting that the neural circuit activity code is jointly governed by somatic and synaptic activity states, termed neural circuit polarities, we show that, subject to subcritical polarity probability, random-graph-theoretic considerations imply small neural circuit segregation. Such circuits are shown to represent linguistically plausible cortical code words which, in turn, facilitate storage and retrieval of both circuit connectivity and firing-rate dynamics.

Introduction

Any representation of information involves a language. Natural languages, such as English, consist of elementary alphabets, comprising letters, which connect into words. Words, being the smallest embodiment of meaning, are normally short, consisting of two to about ten letters. Numbering in the millions and normally grouped into sentences, paragraphs, sections, chapters, articles and whole books, words carry the entire burden of linguistic information. Without such structures, information would be difficult to comprehend or memorize. Computer languages have conceptually similar structures. Their lowest-level alphabet consists of (0, 1) bits. Computer words normally consist of 2–32 bits. Yet, computer programs, consisting of “commands” can be arbitrarily long. Both natural and artificial manifestations of information extend beyond the formal linguistic domain, employing vision, hearing, smell, touch and motion in the generation and memorization of information. Highly inspiring progress has been made in the formal conceptualization of cognitive functions, including behavioral decision making (Wei et al. 2017), communicational behaviour linkage to neural dynamics (Bonzon 2017), feeling of understanding (Mizraji and Lin 2017), multisensory learning (Rao 2018) and bilingual language control (Tong et al. 2019).

Early studies of cortical information codes and memory capacity (McEliece et al. 1987; Amit et al. 1987; Baram and Sal’ee 1992) have pertained to a particular, largely simplified and unified binary (on/off) neural network model (McCulloch and Pitts 1943; Amari 1972; Hopfield 1982), employing the Hebbian learning paradigm (Hebb 1949). Such connected neural network, representing a single cortical word, would imply, however, a long code word, which not only consumes many neurons, but also seems linguistically difficult to comprehend. Neural circuit segregation into smaller circuits seems necessary, then, for the generation and memorization of reasonably short code words in cortical language. It is widely accepted that the neural consistency of the brain is highly heterogeneous (e.g, Stefanescu and Jirsa 2008; Hu et al. 2013; Han et al. 2018), representing a large variety of specifically defined neuronal types and neural circuit structures. As our main purpose in this work is to present a new, linguistically plausible approach to memory by small neural circuits, contrasting those earlier information-theoretic results, it seems appropriate, for comparison purposes, to limit the discussion, in essence, to the same model.

As we show in this paper, the segregation of large neural assemblies into small circuits is implied by graph theoretic considerations. We show that linguistic characteristics, such as the lengths of cortical code words, are strongly dependent on the probability of inter-neuron connectivity. On a conceptual level, the binary nature of neural networks in those early information-theoretic studies is replaced in the present study by the more recently discovered molecularly and physiologically based notions of electrical somatic (Melnick 1994) and synaptic (Atwood and Wojtowicz 1999) potentials being above or below a certain value (about − 60 mV). As this binary distinction, which may take different mathematical representations, defines the excitability, or silence, of the corresponding neuronal components and, consequently, inter-neural connectivity, they have been called cortical circuit polarities (Baram 2018). The diversion from the original information-theoretic models is represented by a graph-theoretic notion of criticality pertaining to node connection probability. The resulting segregated neural circuits constitute a form of cortical linguistics. While the dynamics of membrane and synapse polarities have been mathematically analyzed (Baram 2018), here we argue that the convergent nature of synaptic plasticity implies another form of cortical linguistics, namely, the dynamic modes of neural firing-rate, associated with cortical functionality.

Neuronal polarity codes

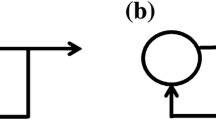
Neuronal membrane (Melnick 1994) and synapse (Atwood and Wojtowicz 1999) polarities can be described as on/off gates which, in the “off” (“disconnect”) position, represent negative polarity, and, in the “on” (“connect”) position, represent positive polarity. The binary polarity states of a neural circuit will represent a code word. The polarity gates of a single neuron are described graphically in Fig. 1a by angular discontinuities in line segments representing membranes and synapses as specified. Neuronal self-feedback, employing an intermediate synapse between axonal output and neuronal input, has been suggested (Groves et al. 1975), although this is not a generic concept, and there are other self-feedback models (such as the axonal discharge model, Carlsson and Lindquist 1963; Smith and Jahr 2002). As in the rest of this paper, our intent here is to address certain concepts, rather than attempt to provide a complete account of the highly heterogeneous neural consistency of brain. Since the neuron-external inputs directly affect the membrane polarity, they are accounted for in the 3-word polarity code depicted in Fig. 1b and c as: (b) positive membrane and self-synapse polarities, (c) positive membrane polarity and negative self-synapse polarity and (d) neuronal silence, implied by negative membrane and self-synapse polarities. Figure 2 shows a 2-neuron circuit, revealing all somatic and synaptic polarities in the negative (“off”) state for illustration.

Fig. 1

Neuronal polarity gates (a) and their code (b–d). As the neuron-external inputs directly affect the membrane polarity, they are accounted for in the neuronal 3-words polarity code, which, for graphical clarity, specifies the connected elements only, without the “off” gates

Fig. 2

Two-neuron polarity-gated circuit. All polarity gates are open for graphical clarity

In order to derive the $n$-neuron circuit polarity code, it is first noted that there can be up to $n$ active neurons (neurons with positive membrane polarities) and $n^{2}$ synapses (including self-synapses). A synapse can be either active or silent. It follows that there can be up to

$$ R^{(1)} (n) = 2^{{n^{2} }} $$

(1)

different circuits involving only active membranes and active or silent synapses. In addition, there can be circuits with $i = 1, \ldots ,n$ silent membranes, yielding

$$ R^{(2)} (n) = \sum\limits_{i = 1}^{n} {\left( \begin{aligned} n \hfill \\ i \hfill \\ \end{aligned} \right)2^{{(n - i)^{2} }} } $$

(2)

different polarity patterns. It follows that there is a maximum total of

$$ R(n) = R^{(1)} (n) + R^{(2)} (n) = 2^{{n^{2} }} + \sum\limits_{i = 1}^{n} {\left( \begin{aligned} n \hfill \\ i \hfill \\ \end{aligned} \right)2^{{(n - i)^{2} }} = } \,\sum\limits_{i = 0}^{n} {\left( \begin{aligned} n \hfill \\ i \hfill \\ \end{aligned} \right)2^{{(n - i)^{2} }} } $$

(3)

different circuits, constituting the size of the circuit polarity code of $n$ polarity-gated neurons (Eq. 3 corrects an error in Baram 2018, Eq. 3.3).

Equation 3 yields $R(1) = 3$, $R(2) = 21$, $R(3) = 567$, $R(4) = 67,689$, $R\left( 5 \right) = 33,887,403$, $R\left( 6 \right) = O(10^{10} )$, $R\left( 7 \right) = O(10^{14} )$, $R(8) = O(10^{19} )$, $R(9) = O(10^{24} )$, $R(10) = O(10^{30} )$. The polarity code for a circuit of 2 neurons is illustrated in Fig. 3, where “off” (negative) polarity gates are omitted for graphical clarity.

Fig. 3

Polarity code of 2-neuron circuits. Each row represents one inter-neuron connectivity pattern with the four different possible states of self-feedback. a bidirectional interneuron connectivity, b both neurons active with directional connectivity from right to left neuron, c both neurons active with directional connectivity from left to right neuron, d two segregated active neurons, e one active neuron and one silent neuron and f two silent neurons

Subcritical neural circuit segregation

Cortical activity segregation and integration have been argued on grounds of thalamocortical simulations (Stratton and Wiles 2015). A mathematical foundation for the relationship between polarity, segregation and firing dynamics has been established (Baram 2018). Synaptic polarization may clearly result in circuit segregation.

Graph-theoretic considerations (Erdos and Rény 1959, 1960) imply that, if the connectivity probability $p(n)$ between pairs of neurons in an assembly of $n$ neurons with $n \to \infty$ satisfies the subcriticality condition $p(n) = c/n$ for fixed $c < 1$, then, with high probability, the largest connected circuit will be of maximal size $\log (n)$. On the other hand, if $p(n)$ satisfies the supercriticality condition $p(n) = c/n$ for fixed c > 1, then, with high probability, the largest connected circuit will be of maximal size linear in $n$. Finally, if $p(n)$ satisfies the criticality condition $p(n) = 1/n$, then, with high probability, the largest connected circuit will be of maximal size $n^{2/3}$ (Bollobás 1984).

For reasons that will become apparent in the subsequent sections, we relax the above formal definitions somewhat by leaving the criticality condition $p(n) = 1/n$ as is, changing its notation to $p(n) \equiv q(n) = 1/n$ and defining subcriticality as the condition $p(n) < q(n)$ and supercriticality as the condition $p(n) > q(n)$.

Figure 4a displays a 2-neuron circuit with a certain polarity pattern. As shown in Fig. 4b, the mixed polarities of Fig. 4a yield two mutually segregated 1-neuron circuits, with the polarity gates in the “off” states concealed for graphical simplicity.

Fig. 4

Given a a 2-neuron circuit with all polarity gates in the “off” states revealed. The mixed polarity pattern yields b two segregated 1-neuron circuits in different polarity states, with the “off” states expressed by disconnect

An average of $7 \times 10^{3}$ synapses per neuron (Drachman 2005) in the average human brain of $n = 10^{11}$ neurons (von Bartheld et al. 2016) would yield an average connectivity probability of

$$ p(n) = 7000/10^{22} < 10^{ - 18} = 10^{ - 7} \times 10^{ - 11} = 10^{ - 7} /n $$

(4)

which, satisfying the sub-criticality condition $p(n) = c/n,\,\,0 < c < 1$, implies an upper bound of $\log (n)$ on the neural circuit size, which, in turn, implies a lower bound

$$ C(n) = \frac{n}{\log (n)} $$

(5)

on the number of externally disconnected, internally connected neural circuits.

Equation 5 constitutes, then, a lower bound on the average information capacity (in number of code words) of $n$ subcritically connected neurons. The number $n$ may take different values corresponding to the sizes of different cortical structures, hence, different maximal segregated circuit sizes $\log (n)$. For instance, for $n = 1000$ we have $\log (n) = O(7)$ (more precisely 6.91), for $n = 25 \times 10^{9}$ (which is about the size of the human cerebral cortex) we have $\log (n) = O(24)$ and for $n = 10^{11}$ (which is about the size of the human brain) we have $\log (n) = O(25)$. As we have noted, the manipulation and memory of such long words (e.g., 24, 25 letters) is not normally attempted in natural languages, and seems linguistically unrealistic in cortical terms as well.

The linguistic impasse of probabilistically supercritical neural polarity

The linguistic difficulties associated with the memorization and manipulation of brain-size code words in cortical language does not appear to have been explicitly noted in early studies of cortical information coding. In fact, experimental observations of simultaneous activity in large cortical areas have seemed to justify a large network approach to cortical information processing. Seminal studies on networks of binary neurons (McCulloch and Pitts 1943; Amari 1972; Hopfield 1982) were followed by studies of their memory capacity. Mathematical manifestations of the Hebbian learning paradigm have produced a variety of bounds on the memory capacity of such networks (e.g., McEliece et al. 1987; Amit et al. 1987; Baram and Sal’ee 1992). As these bounds increase with the number of neurons in the network, so do the lengths of the code words. While the first (McEliece et al. 1987) and the third (Baram and Sal’ee 1992) studies assumed that the network size $n$ satisfies $n \to \infty$, the second study (Amit et al. 1987) assumed a finite network size $n$, which was, however, allowed to grow indefinitely. Below, we consider all three models, so as to show that the linguistic impasse is inherent under probabilistically supercritical polarity. In order to put these earlier binary models in the same context as the polarity models considered in the present work, let us assume that all synapses are in positive polarity (1-valued) state, while the membrane polarities of the neurons are in positive (1-valued) polarity state with probability $p$ and in negative (0-valued) polarity state otherwise. It might also be noted that, beyond this section, which is tailored to correspond with the noted earlier models employing membrane polarity alone (with post-axonal synaptic polarity adhering accordingly), only changes in synaptic polarity will be considered, with the somatic polarity kept positive for simplicity.

In the first model (McEliece et al. 1987), Hebbian storage is represented by the sum of outer products

$$ W = \sum\limits_{i}^{M} {\omega^{(i)} \omega^{(i)T} } $$

(6)

where $\omega^{(i)} ,\,\;i = 1, \ldots ,M$ are $n$-dimensional vectors of equiprobable $\pm \;1$ (hence, supercritical) network polarities. Retrieval is performed according to

$$ \begin{aligned} x_{k} = \left\{ \begin{aligned} 0,\,\,\,\,\,\,\,{\text{if }}\,\,\,{\text{u}}_{k} \le 0 \hfill \\ 1,\,\,\,\,\,\,\,\,{\text{if }}\,\,\,{\text{u}}_{k} > 0 \hfill \\ \end{aligned} \right. \hfill \\ \hfill \\ \end{aligned} $$

(7)

where

$$ u_{k} = \sum\limits_{j = 1}^{n} {\omega_{k,j} x_{j} } $$

(8)

with $\omega_{k,j}$ the corresponding element of the matrix $W$ in Eq. 6. An upper bound on the number of stored patterns

$$ M < \frac{n}{2\log (n)} $$

(9)

yields equilibrium

$$ W\omega^{(i)} = \omega^{(i)} $$

(10)

at each of the stored vectors $\omega^{(i)} ,\,\;i = 1, \ldots ,M$ (McEliece et al. 1987).

Storage to full capacity would yield the inter-neuron connectivity probability

$$ P(n) = 1 - (1 - p(n))^{M} $$

(11)

which, under the capacity bound implied by Eq. 9. Yields

$$ P(n) = 1 - (1 - p(n))^{n/2\log (n)\,} $$

(12)

$P(n)$ now takes the place of $p(n)$ as the neural network’s probabilistic criticality measure, following the storage of $M$ polarity patterns. Specifically,$P(n)$ is critical if $P(n) = q(n) = 1/n$, subcritical if $P(n) < q(n)$ and supercritical if $P(n) > q(n)$. The value of $P(n)$ as specified by Eq. 12 is plotted, along with the critical value $q(n) = 1/n$, against $n$ in Fig. 5. The intersection point $P(n) = q(n)$ is at $n = 2$. It can be seen that as $n$ approaches the value 100, $P(n)$ approaches the value 1, and becomes closer to 1 as $n$ grows larger. This means that the circuit becomes, with high probability, connected, with maximal size linear in $n$ (in fact, specifically $n$), which is consistent with the graph-theoretic property of supercriticality, and which, as we have noted, may be of little linguistic use, if any.

Fig. 5

For supercritical polarity probability $p(n) = 0.5$ and the storage capacity bound specified by Eq. 9, the inter-neuron connectivity probability $P(n)$, specified by Eq. 12, is plotted along with the critical connectivity probability $q(n) = 1/n$. Beyond the critical (intersection) point at $n = 2$, $P(n)$ quickly converges to 1, which, implying large circuit connectivity, is increasingly unacceptable for linguistic purposes. (Color figure online)

In the second model (Amit et al. 1987), Hebbian storage is represented by the attenuated sum of outer products

$$ W = \frac{1}{n}\sum\limits_{i}^{M} {\omega^{(i)} \omega^{(i)T} } $$

(13)

where $\omega^{(i)} ,\,\;i = 1, \ldots ,M$ are $n$-dimensional vectors of equiprobable $\pm \;1$ network polarities. Employing the physical spin-glass model (Hopfield 1982), equilibrium stability was found to be destroyed beyond the following upper bound on the number of stored patterns

$$ M < 0.14n $$

(14)

(Amit et al. 1987). While, in contrast to the other models noted (McEliece et al. 1987; Baram and Sal’ee 1992), the number of neurons, $n$, assumed in the present model (Amit et al. 1987) is finite, the supercriticality effect is similar, as we show next. The inter-neuron connectivity probability, Eq. 11, takes, in the present case, the form

$$ P(n) = 1 - (1 - p(n))^{0.14n} $$

(15)

The value of $P(n)$ according to Eq. 15 is plotted in Fig. 6, along with the critical value $q(n) = 1/n$. The critical (intersection) point $P(n) = q(n)$ is at $n = 3$. It can be seen that as $n$ approaches the value 100, $P(n)$ quickly approaches the value 1, which, implying large circuit connectivity, is increasingly unacceptable for linguistic purposes.

Fig. 6

For supercritical polarity probability $p(n) = 0.5$ and the storage capacity bound specified by Eq. 14, the inter-neuron connectivity probability $P(n)$, specified by Eq. 15, is plotted along with the critical connectivity probability $q(n) = 1/n$. Beyond the critical (intersection) point at $n = 3$, $P(n)$ quickly converges to 1, which, implying large circuit connectivity, is increasingly unacceptable for linguistic purposes. (Color figure online)

In the third model (Baram and Sal’ee 1992), $p(n)$ can, with appropriate modification, approach the subcritical domain, which will become useful in the following section. Given an $n$-neuron assembly, the synaptic weight connecting the $k$’th and the $j$’ th neurons is obtained from a set of vectors over $\omega^{(i)} \in \left\{ {0,1} \right\}^{n}$, $i = 1, \ldots ,M$. In the present context, these will be called the stored polarity patterns. Storage is performed by the modified Hebbian rule (Tsodyks and Feigel’man 1988; Vincente and Amit 1989)

$$ \omega_{k,j} = \sum\limits_{i}^{M} {(\omega_{k}^{(i)} - p)(\omega_{j}^{(i)} - p)} $$

(16)

where $p$ is the probability of a stored polarity having the value 1.

The recalled polarity states $x_{k} ,\;k = 1, \ldots ,n$ are obtained by the McCulloch–Pitts rule

$$ x_{k} = \left\{ \begin{aligned} 0,\,\,\,\,\,\,\,{\text{if }}\,\,\,{\text{u}}_{k} \le t \hfill \\ 1,\,\,\,\,\,\,\,\,{\text{if }}\,\,\,{\text{u}}_{k} > t \hfill \\ \end{aligned} \right. $$

(17)

where

$$ u_{k} = \sum\limits_{j = 1}^{n} {\omega_{k,j} x_{j} } $$

(18)

and $t = \alpha np$, with $\alpha = \,(4 - \tau )/4(2 - \tau )$, is a threshold.

Let us denote the probability that any of the stored polarity vectors is not an equilibrium point $P_{e}$, and, further, let $p = p(n) = cn^{ - \tau }$, with $0 {\text{ < c}} \le 0. 5$ and $0 { < }\tau < 1$. Then $P_{e} \to 0\,\,{\text{as}}\,\,n \to \infty$ if (Baram and Sal’ee 1992, Theorem 1)

$$ M \le \gamma \frac{n}{p(n)\log \,n} $$

(19)

for any $\gamma < 1/4(2 - \tau )$. Equation 19 represents, then, an upper bound on the equilibrium polarity capacity of a neural circuit. While the latter study has also addressed the error correction capacity of the network, here we restrict the analysis to equilibrium capacity for simplicity.

Clearly, for any $0 {\text{ < c}} \le 0. 5$ and $0 < \tau < 1$, $p(n) = cn^{ - \tau } \,$ is supercritical. The smaller the value of $c$ (say, $c = 0.01$) and the larger the value of $\tau$ (say, $\tau = 0.99$), the smaller (yet, supercritical) the value of $p(n)$, and the larger the bound in Eq. 19. Storage to full capacity would yield inter-neuron connectivity probability which, under Eqs. 11 and 19, yields

$$ P(n) = 1 - (1 - p(n))^{\gamma n/p(n)\log (n)} $$

(20)

The value of $P(n)$ as specified by Eq. 20, where $p(n) = cn^{ - \tau }$ with $c = 0.01$ and $\tau = 0.99$, is plotted, along with the critical value $q(n) = 1/n$, against the value of $n$ in Fig. 7. The intersection point $P(n) = q(n)$ is at $n = 1$. It can be seen that, as $n$ approaches the value 100, $P(n)$ approaches the value 1. This means that the circuit becomes connected with increasingly high probability, which, as we have noted, may be of little linguistic use, if any. It might be noted that, since the shapes of the curves depicted in Figs. 5, 6 and 7 are similar, the language of their corresponding descriptions is also similar. The distinction between these figures is specifically expressed by the corresponding equations, 12, 15 and 20, which, while yielding similar results, are clearly different.

Fig. 7

For supercritical polarity probability $p(n) = 0.01n^{ - 0.99}$ and the storage capacity bound specifies by Eq. 19, the inter-neuron connectivity probability is $P(n)$ and the critical connectivity probability is $q(n)$. Beyond the critical (intersection) point at $n = 1$, $P(n)$ quickly converges to 1, which, implying large circuit connectivity, is increasingly unacceptable for linguistic purposes. (Color figrue online)

The subcritical Hebbian linguistic limit of neural polarity

Of the three models considered above, only the third (Baram and Sal’ee 1992) allows for a variable polarity probability. Let us assume a subcritical membrane polarity probability, $p(n) = c/n$ with $0 < c \le 0.5$. The linguistic capacity will be controlled by the parameter $c$, which is characteristically dependent on the size and the functionality of the corresponding cortical domain. Subcritical polarity implies that the largest connected circuit (having a sequence of connections between any two neurons) is of size $\log (n)$ (Erdos and Rény 1959, 1960).

As, for large $n$, a subcritical value of $p(n)$ implies a highly sparse connectivity, the storage of

$$ M = \log (n) $$

(21)

circuit polarity vectors according to Eq. 6 implies that these vectors are, with high probability, mutually orthogonal, and are, therefore, equilibrium points of the circuit satisfying

$$ W\omega^{(i)} = \omega^{(i)} $$

(22)

where $W$ is the matrix whose elements, $\omega_{k,j}$, are defined by Eq. 6, $\omega^{(i)} ,\,\,i = 1, \ldots ,M$ are the $n$-dimensional polarity vectors stored, and $M = O(\log (n))$.

The equilibrium storage capacity of the segregated circuit is, then $O(\log (n))$, and, employing Eq. 21, the storage and retrieval capacity for the entire assembly of $n$ neurons is

$$ B(n) = O(C(n)\log (n)) = O(n) $$

(23)

where $C(n)$ is defined by Eq. 5. From a linguistic viewpoint, the significance of circuit segregation is that each of the words is, with high probability, of maximal length $\log (n)$, which is, for large $n$, considerably smaller than $n$.

The inter-neuron connectivity probability is, by Eqs. 11 and 21

$$ P(n) = 1 - (1 - p(n))^{\log (n)} $$

(24)

For $c = 0.5$, the polarity probability $p(n) = c/n$ is subcritical. The critical point, defined by $P(n) = q(n) = 1/n$ is found to be $n = 7$, as depicted in Fig. 8. The corresponding maximal connected circuit size is $s = [\log (7)] = 2$ (with $[x]$ representing the integer closest to $x$), which is the critical linguistic limit of the neural polarity code word size. For $n > 7$, $P(n)$ becomes supercritical, and the maximal connected circuit size becomes linear in $n$ (Bollobás 1984), which makes it linguistically implausible for large $n$.

Fig. 8

For subcritical $p = c/n$ with c = 0.5, the inter-neuron connectivity probability is $P(n)$ and the critical connectivity probability is $q(n)$. The critical point satisfying $P(n) = q(n) = 1/n$ is at $n = 7$. (Color figrue online)

For c = 0.1, the polarity probability $p(n) = c/n$ is subcritical. The inter-neuron connectivity probability is $P(n)$, as specified by Eq. 24. The critical point satisfying $P(n) = q(n) = 1/n$ is found to be $n = 22,030$, as depicted in Fig. 9. The corresponding maximal connected circuit size is $s = [\log (22,030)] = 10$, which is the critical linguistic limit of the neural polarity code word size. For $n > 22,030$,$P(n)$ becomes supercritical, and the maximal connected circuit size becomes linear in $n$ (Bollobás 1984), which makes it linguistically implausible.

Fig. 9

For subcritical $p = c/n$ with c = 0.1, the critical point satisfying $P(n) = q(n) = 1/n$ is at $n = 22,030$

It follows that while, for large neural assemblies under supercritical polarity probability, the connected neural circuits are, rather uniformly, large, producing linguistically implausible long codewords, the range of subcritical polarity probabilities produces a variety of linguistically plausible, relatively short (2–10 letters/neurons) code words/circuits. The smaller the value of $p(n)$, the greater the linguistic range.

Hebbian random graphs and neural circuit connectivity linguistics

We next demonstrate that, under capacity constraint, neural circuit segregation is a natural outcome of the Hebbian storage of subcritical randomly generated polarity patterns. Let $n = 10,\,p = 0.5/n$ and ${\text{M = 10}}$. It can be seen that, in terms of random graph theory (Erdos and Rény 1959, 1960), $p$ is subcritical. The storage of $M\,n$-dimensional randomly generated polarity vectors according to Eq. 6 has produced the synaptic weights matrix W depicted in Fig. 10a. The connectivity represented by this matrix can be seen to translate into the 5 segregated (externally disconnected) circuits depicted in Fig. 10b, whose neurons are numbered according to the rows (or columns) of the matrix W. Four segregated circuits consist of one neuron each (neurons 1, 4, 5 and 7), while one segregated circuit consists of two neurons (neurons 2 and 9). As implied by both Fig. 10a and b, all synaptic weights are valued at 1.

Fig. 10

Subcritical Hebbian segregation corresponding to $n = 10,\,$$p = 0.5/n\,$ and $\,{\text{M = 10}}$: a synaptic weights matrix, b segregated neural circuits. The neuronal numbering corresponds to the rows (or columns) of the matrix W, while the synaptic weights are all 1, as implied by the matrix

Now let $n = 10,\,p = 1.5/n\,\,{\text{and}}\,\,{\text{M = 10}}$, making $p$ supercritical by graph theoretic terminology. The storage of $M\, n$-dimensional randomly generated polarity vectors according to Eq. 6 has produced the synaptic weights matrix W depicted in Fig. 11a. With some of the weights exceeding the value 1, the connectivity represented by this matrix can be seen to translate into the 3 segregated (externally disconnected) circuits depicted in Fig. 11b, whose neurons are numbered according to the rows (or columns) of the matrix W. One of these circuits consists of a single neuron (neuron 4), one consists of three neurons (neurons 2, 9 and 10) and one consists of four neurons (neurons 3, 5, 7 and 8).

Fig. 11

Supercritical Hebbian segregation corresponding to $n = 10,\,$ $p = 1.5/n\,$ and $\,{\text{M = 10}}$: a synaptic weights matrix, b segregated neural circuits

The transition from subcritical ($p(n) = 0.5/n$) to supercritical ($p(n) = 1.5/n$) has resulted, then, in a dramatic linguistic change. In the subcritical case (Fig. 10), the maximal segregated circuit size of 2 satisfies the Erdos–Renyi condition on maximal connected circuit size (as $2 < log\left( {10} \right) = 2.3$), while in the supercritical case (Fig. 11) the maximal segregated circuit size of 4 does not satisfy the condition (as $4 > log\left( {10} \right)$).

Next, let $n = 10\,\,{\text{and}}\,p = 0.5/n\,$, as in the case depicted in Fig. 10, but let ${\text{M}}$ increase to 20. The storage of 20 $n$-dimensional randomly generated polarity vectors according to Eq. 6 has produce the synaptic weights matrix W depicted in Fig. 12a, which can be seen to have elements greater than 1, as in the case depicted in Fig. 11. The connectivity represented by this matrix translates into the four segregated circuits depicted in Fig. 12b, whose neurons are numbered according to the rows (or columns) of the matrix W depicted in Fig. 12a. It can be seen that three of the circuits consist of a single neuron each (neurons 1, 6 and 8), and one circuit consists of three neurons (neurons 2, 4 and 9). While, from a graph theoretic viewpoint, $p$ is subcritical, as in the case depicted by Fig. 10 ($p = 0.5/n$), the maximal segregated circuit size of 3 violates the Erdos–Renyi size condition (as $3 > \log (10) = 2.3$). The reason is that, in contrast to the case $M = n\,( = 10)$ corresponding to Fig. 10, the present case of $M = 20 > n = 10$ does not yield full mutual orthogonality of the $M$ stored polarity patterns, resulting in excessively larger connectivity and capacity smaller than $M$, in spite of the subcritical value of $p$.

Fig. 12

Hebbian segregation under increased Hebbian storage, corresponding to $n = 10,\,$ $p = 0.5/n\,$ and $\,{\text{M = 20}}$ a synaptic weights matrix, b segregated neural circuits. While $p$ is subcritical, the maximal connected circuit size exceed the Erdos–Renyi limit of $\log (n)$ due to excessive Hebbian storage

Firing-rate mode reproduction by polarity recall

Neuronal firing rate models (Lapicque 1907; Hodgkin and Huxley 1952; Gerstner 1995) have been put in discrete-time forms for computational purposes (Baram 2017a, b, 2018). The nature of neural circuit firing-rate dynamics, having direct impact on cortical function, is closely associated with synaptic plasticity (Bienenstock et al. 1982). The latter, in contrast to circuit polarity, is not binary. The convergence of time-varying synaptic plasticity weights to limit modes (Cooper et al. 2004) results in a high variety of dynamic firing-rate modes, characterized, in maturity, by a code of global attractors (Baram 2013, 2017a). However, as we argue and demonstrate next, given neuronal internal properties, a neural circuit’s firing-rate dynamics are completely determined by a vector-valued probe, retrieving a memorized polarity pattern by the mechanism represented by Eqs. 6–8. This implies that, once a neural circuit is probed, revealing a stored polarity vector, it can only evolve into one final mode of synaptic plasticity weights. Consequently the circuit’s firing rate dynamics can only evolve into one final set of dynamic firing-rate modes, which may be synchronous and identical for all the circuit’s neurons, or unequally and asynchronously produced by different neurons.

The discrete-time firing rate model for the $i$th neuron in a circuit is given by (Baram 2017a, b, 2018)

$$ \upsilon_{i} (k) = \alpha_{i} \,\upsilon_{i} (k - 1) + \beta_{i} f_{i} \left( {{\varvec{\upomega}}_{i}^{T} (k){\varvec{\upupsilon}}_{i} (k - 1) + u_{i} } \right) $$

(25)

where $\upsilon_{i} (k)$, is the neuron’s firing rate, ${\varvec{\upupsilon}}_{i} (k)$ is the vector of firing rates of the neuron’s pre-neurons,$\alpha_{i} = \exp ( - 1/\tau_{{m_{i} }} )\,$ and $\beta_{i} = 1 - \alpha_{i}$, with $\tau_{{m_{i} }}$ the membrane time constant of the neuron, ${\varvec{\upomega}}_{i} (k)$ is the vector of synaptic weights corresponding to the neuron’s pre-neurons (including self-feedback), $u_{i} = I_{i} - r_{i}$, with $I_{i}$ the neuron’s circuit-external activation input and $r_{i}$ the neuron’s membrane resting potential, and $f_{i}$ the conductance-based rectification kernel defined as (Carandini and Ferster 2000)

$$ f_{i} (x) = \left\{ \begin{aligned} x\,\,\,{\text{if}}\,\,x \ge 0 \hfill \\ 0\,\,\,\,{\text{if}}\,\,\,x < 0 \hfill \\ \end{aligned} \right. $$

(26)

The BCM plasticity rule (Bienenstock et al. 1982) of the pre-neuron’s synaptic weights takes the discrete-time form (Baram 2017a, b, 2018)

$$ {\varvec{\upomega}}_{i} (k) = \varepsilon_{i} {\varvec{\upomega}}_{i} (k - 1) + \gamma_{i} \left[ {\upsilon_{i} (k - 1) - \theta_{i} (k - 1)} \right]\,{\varvec{\upupsilon}}_{i}^{2} (k - 1) $$

(27)

where ${\varvec{\upupsilon}}_{i}^{2} (k - 1)$ is the vector whose components are the squares of the components of ${\varvec{\upupsilon}}_{i} (k - 1)$ and

$$ \theta_{i} (k) = \delta_{i} \sum\limits_{\ell = 0}^{N} {\exp ( - \ell /\tau_{{\theta_{i} }} )\upsilon_{i}^{2} (k - \ell )} $$

(28)

with $\varepsilon_{i} = \exp ( - 1/\tau_{{\omega_{i} }} ),\,\,\gamma_{i} = 1 - \,\varepsilon_{i} ,\,\,\delta_{i} = 1/\tau_{{\theta_{i} }} \,$, where $\tau_{{\omega_{i} }}$ and $\tau_{{\theta_{i} }}$ are time constants, and $N$ is sufficiently large to guarantee convergence of the sum.

Next, we examine and demonstrate the effects of synapse polarization on circuit structure and firing dynamics. The essence of these findings will be demonstrated for small circuits of 2 neurons, as the simulation of large circuit firing is highly elaborate, tedious, and space consuming. Consider a 2-neuron circuit having the following identical parameters

$$ u_{1} = u_{2} = 1,\,\tau_{m,1} = \tau_{m,2} = 1,\,\,\tau_{w,1} = \tau_{w,2} = 5,\,\tau_{\theta ,1} = \tau_{\theta ,2} = 1. $$

Starting with full connectivity, changes in circuit connectivity due to synapse silencing are illustrated in Fig. 13. Different initial values of the firing rates, $\upsilon_{1} (0)$ and $\upsilon_{2} (0)$, were applied, so as to check robustness of the results and the claims made. We establish the Hebbian memory of the polarity patterns in the three cases depicted in Fig. 13 by employing the mechanism represented by Eqs. 6–8. We assume for illustrative purposes that in each of the cases we have a synaptic weights matrix which, calculated by Eq. 6 in two time steps, corresponds to the circuit polarity states displayed in Fig. 13.

Fig. 13

Two-neuron circuit modification and segregation by synapse silencing. a Fully connected circuit. b Asymmetric circuit connectivity and c circuit segregation into 2 single isolated neurons by inter-neuron synapse silencing

In case (a) we have

$$ {\mathbf{w}} = 2\left( \begin{aligned} 1\,\,\,\,\,1 \hfill \\ 1\,\,\,\,\,1 \hfill \\ \end{aligned} \right)\, = \left( \begin{aligned} 2\,\,\,\,2 \hfill \\ 2\,\,\,\,2 \hfill \\ \end{aligned} \right) $$

(29)

This is the initial condition in the calculation of the time-varying plasticity weights according to Eq. 27, and reaching the limit

$$ \omega_{1,1} = \,\omega_{1,2} = \omega_{2,1} = \omega_{2,2} = \, - 0. 1 2 9 1. $$

In case (b) we have

$$ {\mathbf{w}} = 2\left( \begin{aligned} 1\,\,\,\,\,0 \hfill \\ 1\,\,\,\,\,1 \hfill \\ \end{aligned} \right)\, = \left( \begin{aligned} 2\,\,\,\,\,0 \hfill \\ 2\,\,\,\,\,2 \hfill \\ \end{aligned} \right) $$

(30)

which, in the appropriate positions, represents the initial condition for the continuous-time plasticity weights. The limit values of the plasticity weights calculated according to Eq. 27 were found to be

$$ \omega_{1,1} = \, - 0.1216,\,\omega_{1,2} = - 0.1375,\,\omega_{2,1} = 0,\,\omega_{2,2} = - 0.1925. $$

In case (c) we have

$$ {\mathbf{w}} = 2\left( \begin{aligned} 1\,\,\,\,\,0 \hfill \\ 0\,\,\,\,\,1 \hfill \\ \end{aligned} \right)\, = \left( \begin{aligned} 2\,\,\,\,\,0 \hfill \\ 0\,\,\,\,\,2 \hfill \\ \end{aligned} \right) $$

(31)

which constitutes the initial condition for the continuous plasticity weights calculated according to Eq. 27. The final values of the plasticity weights were found to be

$$ \omega_{1,1} = \, - 0. 1 9 2 5,\,\omega_{1,2} = 0,\,\omega_{2,1} = 0,\,\omega_{2,2} = - 0. 1 9 2 5. $$

The values of the synaptic weights $\omega_{2,1} ,\,\omega_{1,2}$ and the firing rates $\upsilon_{1} ,\,\upsilon_{2}$ sequences in the three cases, simulated by running Eqs. 25–28, are displayed in Fig. 14. It can be seen that, subject to different initial transients due to different initial conditions, the two neurons in circuits that have symmetric connectivity [cases (a) and (c)] converge to the same firing-rate dynamics, while the two neurons in a circuit which has a non-symmetric connectivity [case (b)] converge to different firing-rate dynamics. Indeed, the final values of $\upsilon_{1}$ and $\upsilon_{2}$ in the three cases are:

Fig. 14

Temporal plasticity evolution $\omega_{2,1}$ and $\omega_{1,2}$ and firing rate sequences, $\upsilon_{1}$ and $\upsilon_{2}$, corresponding to the three circuits depicted in Fig. 13. The plasticity synaptic weights were initialized at the convergence values of the polarity synaptic weights

• (a) $\upsilon_{1} (k = 100) = \upsilon_{2} (k = 100) = 0. 7 9 4 7$ (symmetric, as original polarity)

• (b) $\upsilon_{1} (k = 100) = 0. 7 8 8 8,\,\,\upsilon_{2} (k = 100) = 0. 8 3 8 5$ (asymmetric, as original polarity)

• (c) $\upsilon_{1} (k = 100) = \upsilon_{2} (k = 100) = 0. 8 3 8 5$ (symmetric, as original polarity).

Subject to internal neural parameters, the cortical languages of polarity, on the one hand, and firing-rate dynamics, on the other, are, then, interchangeable in representing such neural circuit properties as symmetry, synchrony and asynchrony. The expression of such properties in a variety of firing rate modes has been noted (Baram 2018).

Discussion

Linguistic considerations, such as the number and the sizes of code words, appear to be as significant for the language of cortical information representation as they are for natural and artificial languages. Extending fundamental results from the theory of random graphs, we have shown that subcritical probability of positive polarity holds the key to small circuit segregation, which, in turn, holds the key to linguistically plausible short code words. It might be noted that, as a consequence of small circuit segregation, the notion of information storage capacity is transformed from the storage of few long code words to the storage of many short code words, which is more plausible from a linguistic viewpoint. In contrast, we have shown that supercritical probability of positive polarity, yielding inherently long code words, misrepresents efficient cortical linguistics. The subcritical linguistic range of cortical codewords, resembling the one found in natural languages, is between 2 and 10 “letters”, represented by neuronal membrane polarity states. We have argued and demonstrated the effects of subcritical polarity probability on segregated neural circuit sizes employing theoretical as well as computational reasoning. We have further shown that cortical linguistics, represented by membrane and synapse polarities, and defining neural circuit connectivity, pave the way for another expression of cortical information, namely, neural circuit firing-rates. The transition from polarity linguistics to firing-rate linguistics constitutes a mechanism for transforming memory, stored in the form of circuit polarities, to memory retrieval by firing-rate manifestation. The correspondence between firing-rate modes and cortical functions has been noted before (e.g., Baram 2013, 2017a, b, 2018), but their storage and retrieval by transforming circuit polarity codes into convergent plasticity modes appears to be suggested here for the first time. The interaction and collaboration of the seemingly different mechanisms of neuronal polarization and synaptic plasticity in the definition of firing-rate modes also appears to be suggested here for the first time, and is suggested for further investigation in future studies.