Introduction

Understanding neural coding is an important part of understanding informational neurodynamics in our brains. For example, the rate codes play an important role in identifying the regulation of the neuronal firing trains (Guo et al. 2016a, b). For temporal codes, two different types of encoding, namely, the frequency of firing and the exact temporal occurrence of spikes, are reported in experimental recordings (Rabinovich et al. 2006). Spike trains’ similarity and dissimilarity can thus have two kinds of metrics, the inter spike interval (ISI) distance (Kreuz et al. 2007) and the spike distance (Kreuz et al. 2011, 2013). A measure by introducing a kernel function was proposed by van Rossum (2001), whereby the distance could interpolate between coincidence detection and spike count difference via changing the time constant, which gave rise to a continuous prototype of spike train topology. A similar approach is proposed recently by Rusu and Florian (2014), where they show their max-metric and modulus-metric are particularly suitable for measuring distances in spike trains where information is encoded in the identity of bursts as unitary events. For classifications of spike train distance, one can also refer to Victor (2015) and references therein, where he classified spike train metrics into embedding-based (Houghton and Sen 2008; van Rossum 2001) and cost-based (Victor and Purpura 1998) distances.

Synchronization (Pikovsky et al. 2003) as a collective behavior has attracted much attention in neuroscience partly due to its relation with many brain disorders, e.g. schizophrenia, epilepsy, autism, Alzheimer’s disease, and Parkinson’s disease, all of which are considered associated with abnormal neural synchronizations (Uhlhaas and Singer 2006). In neuronal ensembles, synchronizations may be impacted by connection topologies (Bera et al. 2017; Majhi et al. 2016) and other systematic parameters, e.g. time delay (Dhamala et al. 2004b; Sun et al. 2017; Zhu et al. 2016), coupling strength (Dhamala et al. 2004a; Ivanchenko et al. 2004), network size (Zhu et al. 2016), etc. For coupled spiking neurons, the lag synchronization (LG) can be measured by using the similarity function (Rosenblum et al. 1997), e.g. in the Rulkov map neurons (Zhu et al. 2016) and in the Morris–Lecar neurons (Wang et al. 2013). However, it has been shown that LG does not occur in coupled Hindmarsh–Rose (HR) neurons (Hindmarsh and Rose 1984) which is related to the burst process (Shuai and Durand 1999). Moreover, for information encoded only in the precise spike timing, synchronization should not be related with the spike amplitude where the latter will certainly affect the value of the similarity function. Generally, for two coupled HR neurons, absolute phase difference or frequency difference can serve as a simple criterion for phase synchronization (Shuai and Durand 1999), but the value may be influenced by the missing recorded data or noise, while the latter is ubiquitous in neurons (Lindner et al. 2004) and the phase definition can be quite puzzling in bursting neurons. Other measures, e.g. transverse Lyapunov exponent is frequently used in coupled bursting neurons (Dhamala et al. 2004a, b; Ivanchenko et al. 2004), which is significant in determining the stability of synchronization. Yet, it shares the same feature as the similarity function that the amplitude of the action potential is considered in the synchronization manifold. Noise may play a constructive role on the amplification of information transfer (Perc and Marhl 2005) and on the activation process (Franović et al. 2015a, b), which will also influence the synchronization between neuronal ensembles (Lindner et al. 2004). In this paper, a new spike timing distance which is simple but efficient is introduced to quantify the spike train distance between the HR neurons with information only encoded in the precise timing of the spikes. It can be used to measure the degree of synchronization and desynchronization in coupled or noise-stimulated HR neurons.

This paper is organized as follows. In “Model and bifurcation analysis” section, dynamical behaviors of a single HR neuron model are briefly discussed including the bifurcation analysis. In “Spike timing distance” section, the definition of the new spike timing distance is introduced. Comparisons with previous measures are given in “Comparison with previous measures” section. Next, in “Synchronization with electrical coupling” section, the degree of synchronization of two electrically coupled HR neurons is investigated in both bursting and spiking states by using the distance measure. Furthermore, because of the inevitable noise in neuronal population, especially of recent increasing interest in the influence of common noise (Sunada et al. 2014; Vidne et al. 2012; Zambrano et al. 2010), the roles of common noise acting on uncoupled and coupled HR neurons are studied in “The influences of common noise” section. In “Possible extensions and applications” section, possible extensions and applications are given. Finally, conclusions and discussions are presented in “Conclusions and discussions” section.

Model and bifurcation analysis

We consider the Hindmarsh–Rose neuron model. It is an extension of the Fitzhugh–Nagumo neuron model which demonstrates the bursting behavior of neurons by adding a slow adaptation current. The governing equations are as follows:

$$\begin{aligned} \frac{dx}{dt} & = y - ax^{3} + bx - z + I_{\text{ext}} \\ \frac{dy}{dt} & = c - dx^{2} - y \\ \frac{dz}{dt} & = r\left( {s\left( {x - x_{0} } \right) - z} \right) \\ \end{aligned}$$
(1)

where x and y represent the membrane potential and the recovery variable respectively. The parameter I ext is the external current. The variable z is the aforementioned adaptation current. In the following, we shall choose parameters traditionally as: a = 1, b = 3, c = 1, d = 5, r = 0.001, s = 4, x 0 = − 1.6. As r « 1, the variable z changes slowly, so z − I ext can be viewed as the bifurcation parameter for the first two equations in Eq. (1). The corresponding bifurcation diagram is plotted in Fig. 1a [see e.g. (Innocenti et al. 2007; Wang 1993) for similar bifurcation analyses]. For the original model, the interspike interval (ISI) bifurcation versus the external current is illustrated in Fig. 1b. It is shown in Fig. 1 that for I ext = 4 and 1.5, the HR neuron will be in the tonic spiking and bursting states, respectively.

Fig. 1
figure 1

a Bifurcation diagram by setting z-I ext as the bifurcation parameter. The black solid (green dotted) lines represent the stable (unstable) equilibrium points. The red dotted line represents the saddles and the blue cycles represent the extrema of the limit cycles. b Bifurcation diagram for the interspike interval versus the external current I ext. Typical time series for I ext = 1.5 and 4 are plotted in purple and green, which have also been plotted in a of the same colors

Full size image

In the following sections, the spike train distance of uncoupled and coupled neurons in both states will be investigated. Before doing so, an appropriate distance measure should be defined. It should be noted that the synchronization in this paper is similar to the phase synchronization as we consider that the information is encoded in the precise timing of the spikes not the amplitude of them, although the difference of complete synchronization (considering the amplitude of the spikes) and phase synchronization (considering only the phase of the spikes) may be important in oscillators.

Spike timing distance

For information encoded only in the precise timing of the spikes, the needed data for calculating the distances between different neurons are merely the simultaneously measured spike trains for the same length of the time window. Suppose \(S = \left\{ {s_{1} ,\;s_{2} , \ldots ,\;s_{m} } \right\}\) and \(P = \left\{ {p_{1} ,\;p_{2} , \ldots ,\;p_{n} } \right\}\) are the corresponding series for neuron S and P, where s i and p i are the ith precise timing of the spikes in each neuron. Our measure for the spike train distance of the neurons is defined as follows:

$$S_{td} \left( {S,P} \right) = {\text{mean}}\left\{ {S_{1} ,S_{2} } \right\}$$
(2)
$$\begin{aligned} S_{1} = \sqrt {\frac{1}{m}\sum\limits_{i = 1}^{m} {\left( {s_{i} - p_{i*} } \right)^{2} } } \hfill \\ S_{2} = \sqrt {\frac{1}{n}\sum\limits_{i = 1}^{n} {\left( {p_{i} - s_{i*} } \right)^{2} } } \hfill \\ \end{aligned}$$
(3)

where p i* is the nearest spike to s i in neuron P, and similarly for s i* . \({\text{mean}}\left\{ {S_{1} ,S_{2} } \right\} = \frac{{S_{1} + S_{2} }}{2}\).

A distance metric should satisfy nonnegativity, symmetry and triangle inequality (Victor 2015). However, one can verify that the measure defined as in Eq. (2)–(3) is not a metric. The nonnegativity and symmetry of the metric are obvious because of the variance-like type in Eq. (3) and \({\text{mean}}\left\{ {S_{1} ,S_{2} } \right\} = {\text{mean}}\left\{ {S_{2} ,S_{1} } \right\}\). But an example is as follows: let S = {0}, P = {a} and T = {0, a} be three spike trains (a > 0). It is easy to calculate that \(S_{td} \left( {S,T} \right) + S_{td} \left( {T,P} \right) = {a \mathord{\left/ {\vphantom {a {\sqrt 2 }}} \right. \kern-0pt} {\sqrt 2 }} < a = S_{td} \left( {S,P} \right)\), which certainly violates the triangle inequality. Despite that our measure is not a metric (It could be controversial that the concept of metrics is not important in neuroscience), the measure defined as above could be useful in measuring synchrony for bursting and spiking neurons.

It is possible to use a simpler measure as \(S_{1} = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left| {s_{i} - p_{i*} } \right|}\) (This definition is similar to the averaged phase difference of coupled neurons). However, this kind of measure cannot distinguish between the two cases in Fig. 2a (since for case 1, the two spike trains have different interspike intervals while for case 2, the interspike intervals are the same). In contrast, the spike timing distance S td defined in Eq. (2)–(3) can solve the problem that S td in case 1 is larger than in case 2. This can be explained by Cauchy inequality that \(\sqrt {\frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left( {s_{i} - p_{i*} } \right)^{2} } } \ge \frac{1}{n}\sum\nolimits_{i = 1}^{n} {\left| {s_{i} - p_{i*} } \right|}\), where they are equal if and only if all \(\left| {s_{i} - p_{i*} } \right|\) are the same. This feature is important in distinguishing between entrainment and phase locking (Izhikevich 2007).

Fig. 2
figure 2

a Two cases of spike timing distance. The black horizontal lines are the timelines. The red and green small rectangles represent spikes for each neuron on the timeline. b Spike timing distance between two uncoupled HR neurons versus different initial conditions for two kinds of firing states (spiking for I ext = 4 and bursting for I ext = 1.5; the time window is [10,000, 19,000] for calculating S td ). c Phase portraits and time series for I ext = 1.5 with different initial differences, where x 1 and x 2 represent the membrane potentials of the two uncoupled HR neurons

Full size image

As a start, we calculate the spike timing distance S td in uncoupled identical HR neurons but with different initial conditions and compare it with other measures to validate its effectiveness later in “Comparison with previous measures” section. Let two uncoupled neurons have initial conditions as: {x 1, y 1, z 1} = {0.1, 0, 0} and {x 2, y 2, z 2} = {0.1 + dx, 0, 0}, where dx is the initial difference between the membrane potential of the neurons. The results are in Fig. 2b. It can be seen that for the spiking state (I ext = 4), the spike timing distance increases monotonically as the initial difference increases while for the bursting state (I ext = 1.5), it shows a counterintuitive peak which means two uncoupled HR neurons with a larger initial difference in the membrane potential (x variable) don’t guarantee a larger final spike timing distance. The results of the bursting state can be further demonstrated by the phase portraits and time series of the corresponding initial differences [see Fig. 2c], which clearly shows the maximal difference for dx = 0.44 as compared with the peak in Fig. 2b.

Comparison with previous measures

There are lots of spike train distance measures (Victor 2015) that could be used to characterize the similarity and dissimilarity between spike trains. Some of them are concerned with the spike series’ waveforms, i.e., both the phase and amplitude of them (e.g. the similarity function (Rosenblum et al. 1997)) while the others are interested in the spike timing which consider the neuron activity as a point process (Victor 2015), e.g. van Rossum spike train metric (van Rossum 2001) and Kreuz et al. ISI-distance measure(Kreuz et al. 2007). Since the measure defined in this paper considers the spike timing as the essential information, we compared the performance of our measure with the latter.

van Rossum spike train metric

Consider two spike trains as \(S = \left\{ {s_{1} ,\;s_{2} , \ldots ,\;s_{m} } \right\}\) and \(P = \left\{ {p_{1} ,\;p_{2} , \ldots ,\;p_{n} } \right\}\), so the spike train could be given in the continuous time form as

$$\begin{aligned} f_{s}^{\text{orig}} \left( t \right) & = \sum\limits_{i}^{m} {\delta \left( {t - s_{i} } \right)} , \\ g_{p}^{\text{orig}} \left( t \right) & = \sum\limits_{i}^{n} {\delta \left( {t - p_{i} } \right)} . \\ \end{aligned}$$
(4)

According to van Rossum, each spike will be associated with an exponential function as

$$\begin{aligned} f_{s} \left( t \right) & = \sum\limits_{i}^{m} {H\left( {t - s_{i} } \right)e^{{ - \left( {t - s_{i} } \right)/t_{c} }} } \\ g_{p} \left( t \right) & = \sum\limits_{i}^{n} {H\left( {t - p_{i} } \right)e^{{ - \left( {t - p_{i} } \right)/t_{c} }} } \\ \end{aligned}$$
(5)

where H is the Heaviside step function (H(x) = 0 for x < 0 and H(x) = 1 for \(x \ge 0\)). The variable t c is a free parameter. Finally, the van Rossum spike train metric (van Rossum 2001) can be calculated as

$$D_{vr} = \frac{1}{{t_{c} }}\int_{0}^{\infty } {\left[ {f_{s} \left( t \right) - g_{p} \left( t \right)} \right]^{2} dt}$$
(6)

This measure can be used as a coincidence detection for small enough t c and a spike count difference measure for large t c .

Kreuz et al. ISI-distance measure

Different from the previous van Rossum metric which can be interpreted as a time coding measure, Kreuz et al. (2007) defined a rate coding measure. For the same spike trains considered above, the Kreuz et al. ISI-distance measure is introduced as follows:

$$I\left( t \right) = \frac{{x_{isi} \left( t \right) - y_{isi} \left( t \right)}}{{\hbox{max} \left( {x_{isi} \left( t \right),y_{isi} \left( t \right)} \right)}}$$
(7)

where \(x_{isi} \left( t \right) = \hbox{min} \left( {s_{i} |s_{i} > t} \right) - \hbox{max} \left( {s_{i} |s_{i} < t} \right)\) and similarly for \(y_{isi} \left( t \right)\). To be a measure of spike train distance, we adopt the following definition (Eq. (4) in Ref. (Kreuz et al. 2007)):

$$D_{tk} = \int_{0}^{T} {\left| {I\left( t \right)} \right|dt}$$
(8)

Comparison between spike train distance measures for Std, Dvr and Dtk

In order to compare these three measures, we normalize the values to the interval [0, 1]. The results are in Fig. 3. It is shown in Fig. 3a that all of these measures exhibit a maximum at dx = 0.44. The general tendency is similar. However, for Kreuz et al. ISI-distance measure, there is only one extremum, but for the other two, there are more than one. The difference is more remarkable in Fig. 3b that S td and D vr show a similar trend while D tk exhibit large fluctuations. It can be explained that our measure is by definition a time coding measure which is, not surprising, closer to the van Rossum spike train measure, thus could be totally different from the Kreuz et al. ISI-distance measure when measuring various spike trains (although for complete synchronization, they all equal to zero). The brief summary of their comparison between these three measures is given Table 1.

Fig. 3
figure 3

Comparison between different spike train distance measures (normalized). a I ext = 1.5. b I ext = 4. For van Rossum spike train distance, the time constant t c  = 5. The time window is [10,000, 19,000] for calculating the distances

Full size image

It should be noted that the spike timing distance defined in this paper is parameter-free compared with van Rossum spike train metric (van Rossum 2001) and Victor–Purpura spike train metric (Victor and Purpura 1998). However, one should keep in mind that parameter-free implies less controllability of the measure. If one wants to consider the sensitivity of the measure to the temporal pattern, a controllable parameter should be considered like van Rossum metric or Victor–Purpura metric. Note that our measure is applicable to neurons in the steady state. To measure the transient process for neurons from desynchronization to synchronization, one can refer to (Kreuz et al. 2007, 2013).

Synchronization with electrical coupling

In this section, the electrically coupled HR neurons will be investigated. The equations are as follows:

$$\begin{aligned} \frac{{dx_{i} }}{dt} & = y_{i} - ax_{i}^{3} + bx_{i} - z_{i} + I_{ext} + D\left( {x_{j} - x_{i} } \right) \\ \frac{{dy_{i} }}{dt} & = c - dx_{i}^{2} - y_{i} \\ \frac{{dz_{i} }}{dt} & = r\left( {s\left( {x_{i} - x_{0} } \right) - z_{i} } \right) \\ \end{aligned}$$
(9)

where i = 1, 2 and j = 2, 1, represent the labels of the neurons. The variable D is the coupling strength. By increasing the coupling strength, it is expected that the degree of synchronization will be enhanced. However, as is shown in Fig. 4a and b, the spike timing distance does not decrease monotonically. In fact, it is larger than that without coupling for a wide range of coupling strengths, which means the degree of synchronization is weakened by the addition of the coupling between the two identical neurons (for both bursting and spiking states). For neurons at the bursting state, i.e. I ext = 1.5, at most coupling strengths, the spike timing distance remains a small value, which can be seen in the insets of Fig. 4a for D = 0.128 and D = 0.132. While there are values e.g. D = 0.13, the spike timing distance of the two coupled neurons becomes considerably large. Another feature which should be noted is that for the former (D = 0.128 and D = 0.132), the spike counts in each burst are not fixed but for the latter (D = 0.13), the spike counts are fixed (note the waveforms of the two identical neurons are different which is a phenomenon of symmetry breaking since the coupling is symmetric). For neurons at the spiking state, i.e. I ext = 4, the electrical coupling transforms the spiking states into the bursting states (see the inset of Fig. 4b for D = 0.163). It shows for HR neurons, the route to synchronization of spiking neurons should undergo bursting processes with the increase of the coupling strength.

Fig. 4
figure 4

Spike timing distance versus coupling strength. a For I ext = 1.5. The insets are time series of x 1 (dotted green) and x 2 (solid red) for different coupling strengths. The time series are shifted for a better illustration. b For I ext = 4. The time window for calculating S td is [100,000, 180,000], and the initial conditions are {0.1, 0, 0} for one neuron and {0.2, 0, 0} for the other

Full size image

The results are compared with van Rossum spike train metric and Kreuz et al. ISI-distance measure in Fig. 5 (To reveal the details, the resolution of the D-axis is reduced). The results show that the desynchronization induced by moderate coupling strength is observed by all these three measures. However, details can be quite different among them. The shapes of the curves for our measure and the van Rossum spike train metric are more similar although their maxima exhibit at different values for I ext = 4 [see Fig. 5b]. This is consistent with the statement in “Comparison with previous measures” section that they are both time coding measures. The critical values for complete synchronization in these measures are also divided into two groups. The first one is our measure and the van Rossum metric and the other is the Kreuz et al. ISI-distance measure. So one should keep in mind that different coding measures may come into different critical values as they focus on different properties of the series.

Fig. 5
figure 5

Comparison between different spike train distance measures (normalized). a I ext = 1.5. b I ext = 4. For van Rossum spike train distance, the time constant t c  = 5. The time window for calculating these distances is [100,000, 180,000], and the initial conditions are {0.1, 0, 0} for one neuron and {0.2, 0, 0} for the other

Full size image

The influences of common noise

There is evidence for synchronization via common stimulation between uncoupled neurons (Kruscha and Lindner 2015, 2016). In this section, the influences of common noise on the synchronization between coupled and uncoupled HR neurons will be investigated. The equations go as:

$$\begin{aligned} \frac{{dx_{i} }}{dt} & = y_{i} - ax_{i}^{3} + bx_{i} - z_{i} + I_{ext} + D\left( {x_{j} - x_{i} } \right) + \sqrt w \xi \left( t \right) \\ \frac{{dy_{i} }}{dt} & = c - dx_{i}^{2} - y_{i} \\ \frac{{dz_{i} }}{dt} & = r\left( {s\left( {x_{i} - x_{0} } \right) - z_{i} } \right) \\ \end{aligned}$$
(10)

where w is the strength of the Gaussian white noise with \(\left\langle {\xi \left( t \right)} \right\rangle = 0,\;\left\langle {\xi \left( t \right)\xi \left( {t - \tau } \right)} \right\rangle = \delta \left( \tau \right)\).

In the first situation, the two HR neurons are uncoupled, i.e. D = 0. It is shown in Fig. 6 that initially, the increase of the noise strength will not contribute to the enhancement of synchronization. Until a critical value is exceeded (around 1e-6 for I ext = 1.5 and 1e-5 for I ext = 4), the degree of synchronization decreases which is demonstrated by the increase of S td . There is a peak for both bursting and spiking states that the spike timing distance between two uncoupled neurons reaches the maximum value, after which the input of common noise begins to enhance the synchronization of the neurons. Two different initial condition mismatches are tested, which shows no qualitative distinction. The critical value of the noise strength for complete synchronization is observed about w = 5 for I ext = 1.5 and w = 6 for I ext = 4, which is consistent with previous studies (He et al. 2003). It should be noted that the critical values in both cases are too large for neurons that the dynamics of the neurons are dominated by noise. It remains to be validated whether such strong noises can be used in real neurons under the promise of not destroying the functioning of them.

Fig. 6
figure 6

Spike timing distance versus noise strength in uncoupled HR neurons. a I ext = 1.5. b I ext = 4. Initial conditions: {x 1, y 1, z 1} = {0.1, 0, 0} and {x 2, y 2, z 2} = {0.1 + dx, 0, 0}. Euler method is used and S td is obtained by averaging over 20 samples. The considered noise strength is [1e-8, 1e1]

Full size image

The results are again compared with van Rossum spike train metric and Kreuz et al. ISI-distance measure. As is shown in Fig. 7, all these measures show the process from desynchronization to synchronization by increasing the noise strength. And the critical values for complete synchronization match well for them. But the shape of them differ significantly. The reason for the narrow width of the D vr curve may be explained by the small value of the time constant t c that for small noise strengths the spike counts for two HR neurons differ negligibly while for large noise strengths they may differ considerably.

Fig. 7
figure 7

Comparison between different spike train distance measures (normalized). a I ext = 1.5. b I ext = 4. For van Rossum spike train distance, the time constant t c  = 5. Initial conditions: {x 1, y 1, z 1} = {0.1, 0, 0} and {x 2, y 2, z 2} = {0.11, 0, 0}. Euler method is used and the result is obtained by averaging over 20 samples. The considered noise strength is [1e-8, 1e1]

Full size image

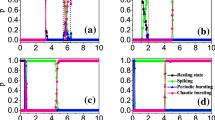
In the second situation, the influences of common noise in coupled HR neurons are researched. For I ext = 1.5, as in Fig. 8a, we can see that with the increase of the noise strength, the abnormal peak around D = 0.13 disappeared which shows the symmetry breaking behavior discussed previously in Fig. 4a cannot be preserved at the presence of noise. Moreover, the peak moves toward larger coupling strengths for larger noise strengths (although the peak height decreases). For I ext = 4, as in Fig. 8b, the multiple peaks in Fig. 4b are merged into one peak as the noise strength increases. Detailed analysis shows the common noise plays different roles for weak and strong coupling strengths. For D = 0, as is illustrated in Fig. 8c, the degree of synchronization decreases with the increase of the noise strength. While for large enough D, the results are reversed, whereby larger strength of noise enhances the synchronization [see Fig. 8d]. This shows the evidence for the cooperation between noise and coupling in the induction of synchronization which is opposite to the observation in two coupled oscillators (Garcia-Alvarez et al. 2009) (Table 1).

Fig. 8
figure 8

Spike timing distance versus noise strength for weak and strong coupling strengths. Parameters: a I ext = 1.5; b I ext = 4; c D = 0; d D = 0.46. Initial conditions: {x 1, y 1, z 1} = {0.1, 0, 0} and {x 2, y 2, z 2} = {0.2, 0, 0}

Full size image
Table 1 The comparison between three measures
Full size table

Possible extensions and applications

Although the distance measure is in a symmetric form (by the “mean” sign) in this paper which is consistent with the symmetry of system itself and electrical coupling, it could be transformed into other asymmetric or more generalized forms in different cases. For example, in the driver/response system as is illustrated in Fig. 9a, instead of applying the mean value of the spike timing distance as in Eq. (2), one of Eq. (3) is selected. For the sake of certainty, we assume S and P being the spike trains of the driver and response respectively. Then S 1 in Eq. (3) can be a quantitative measure of the interdependences between the driver and response system. Similarly, it can be applied to systems with hubs to measure the degree of correlation between the neurons which connected with the same hub as in Fig. 9b. Table 2 summarizes all the applications in this paper and in possible future extensions.

Fig. 9
figure 9

a Typical driver/response system. b Neuronal system with a hub

Full size image
Table 2 The applications of S td and in future extensions
Full size table

Conclusions and discussions

In summary, a simple spike timing distance is defined in this paper which is suitable for determining synchronization between neurons with information only encoded in the precise timing of spikes. By using this measure, we investigate the spike train distance for uncoupled HR neurons with different initial conditions. It is shown that with the increase of the deviation between the initial conditions, the spiking timing distance for spiking neurons increases as is expected, but exhibits a peak for bursting neurons which means that a larger initial difference doesn’t make a larger final spike timing distance. To evaluate our measure, we compare it with the van Rossum spike train metric and Kreuz et al. ISI-distance measure. Since the spike timing distance defined in this paper is a time coding measure, the result reveals the similarity of it to the van Rossum spike train metric while the dissimilarity of it to the Kreuz et al. ISI-distance measure as the latter is a rate coding measure. Next, we use our measure to study the synchronization in coupled or noise-stimulated HR neurons. When the electrical coupling is added, it is quite counterintuitive that as the coupling strength enhances, the spike timing distance doesn’t decrease monotonically, instead there is a wide range of strength that the addition of coupling destroyed the synchronization between both bursting and spiking HR neurons. It is interesting that the spiking neurons undergo the bursting process before the final synchronization (the spikes in each burst is much more than that in the bursting state). Further, the common noise induced synchronization (CNIS) in uncoupled HR neurons is investigated. It is found that a small common noise doesn’t enhance or weaken the synchronization. After a critical value is exceeded, the degree of synchronization decreases as the increase of the noise strength. For strong enough noise, synchronization is achieved. However, it remains to be verified if the too strong noise will influence the functioning of real neurons. Finally, for coupled HR neurons, the common noise plays opposite roles in neurons with weak and strong coupling strengths which shows the cooperation between coupling and noise in the induction of synchronization.

The spike timing distance defined in this paper has been shown to be useful in both spiking and bursting neurons. It has an advantage of not dealing with the definition of instantaneous phases, which is hard to define for a busting neuron. The only information needed to calculate the degree of synchronization is the simultaneously measured spike trains, which is beneficial to theoretical and experimental studies. It can be easily extended to multiple spike timing distances for large neuronal ensembles. Moreover, higher order moments, e.g. \(\sqrt {\text{var} \left( {s_{i} - p_{i*} } \right)^{2} }\) can be used in measuring the regularity and other details between spike trains. It should be noted that the lag synchronization (Rosenblum et al. 1997) is not considered in this paper but it is easy to translate the spike trains via plus or minus a time lag to investigate the lag synchronization in our future works.